Motion guidance lines for robust data -consistency based retrospective motion correction in 2D and 3D MRI

Abstract

Purpose:

To develop a robust retrospective motion correction technique based on repeating k-space guidance lines for improving motion correction in cartesian 2D and 3D brain MRI.

Methods:

The motion guidance lines are inserted into the standard sequence orderings for 2D TSE and 3D MPRAGE to inform a data-consistency based motion estimation and reconstruction, which can be guided by a low-resolution scout prior. The extremely limited number of required guidance lines are repeated during each echo train and discarded in the final image reconstruction. Thus, integration within a standard k-space acquisition ordering ensures the expected image quality/contrast and motion sensitivity of that sequence.

Results:

Through simulation and in vivo 2D multi-slice and 3D motion experiments, we demonstrate that respectively 2 or 4 optimized motion guidance lines per shot enables accurate motion estimation and correction. Clinically acceptable reconstruction times are achieved through fully separable on-the-fly motion optimizations (~1 sec/shot) using standard scanner GPU hardware.

Conclusion:

The addition of guidance lines to scout accelerated motion estimation facilitates robust retrospective motion correction that can be effectively introduced without perturbing standard clinical protocols and workflows.

Introduction

Patient motion during MRI examinations causes disruptive motion artifacts, such as image ghosting, blurring, ringing and signal dropouts which can degrade diagnostic utility to the point where scans must be repeated, or patients called back [1]. According to a recent study at a US hospital, about 20% of brain scans were repeated due to excessive patient motion [2]. Many methods to address this issue have been explored, including faster scanning which implicitly reduces the chance of unintended patient motion [3], tracking devices [4]–[10] or motion navigator acquisitions [1], [11]–[16] which can either retrospectively or prospectively reduce motion artifacts. Unfortunately, motion mitigation techniques have not found widespread clinical adoption apart from prescribing anesthesia which increases risk, examination duration, and cost [17].

The adoption of new motion correction techniques into routine clinical service is challenging due to high demands on reliability, robustness, and intolerance to any disruptions in the examination workflow, e.g., difficult tracker alignment/calibration or changes in sequence timings to accommodate the acquisition of full navigator images. Successful adoption of a motion mitigation method requires that (i) image quality is significantly improved for severe motion cases to prevent repeats or call-backs, (ii) the expected high level of image quality must be maintained when there is limited or no patient motion and (iii) the clinical workflow cannot be impeded to accommodate the technique. Because severe motion is only present in a fraction of examinations, it is crucial to avoid image quality compromises in studies without significant motion artifacts. Moreover, motion correction is expected to generalize across a broad range of imaging sequences, and an easy to integrate one-size-fits-all solution would be highly desirable.

Several approaches that directly measure and correct for motion have been developed. Optical [4]–[7] and RF [8]–[10] tracking devices provide position information in real time allowing the mitigation of motion artifacts through updates of the imaging FOV. In theory, this prospective correction approach is desirable as patient motion is compensated in real-time, however, widespread clinical adoption is challenging due to the high demands on reliability and robustness. MR-based motion navigators are advantageous as they provide tracking information without additional hardware requirements. Self-navigated techniques [18] typically use non-cartesian k-space trajectories that are inherently more motion robust and allow for extraction of motion information from the over-sampled central region of k-space. Alternatively, additional navigators ([1], [11]–[16]) can be inserted into cartesian imaging sequences, and then patient motion can be estimated by applying image registration techniques to the supplemental navigator data. However, acquiring sufficient data to produce complete navigator images can cause disruptions to the sequence timing and the “shadows” left by slice-select spin-history have limited their use mainly to 3D sequences with significant time gaps such as MPRAGE.

These issues led to the development of navigator/tracking-free retrospective approaches that estimate patient motion in a purely data-driven manner using only the raw k-space data from the standard data acquisition. This is possible as the complex coil sensitivities of multi-channel receiver arrays encode the motion information into the raw k-space data [19]. Through non-linear inversion of a physics model that describes the effect of patient motion on the acquired k-space data, these methods extract the motion information along with the motion-corrected image. This is achieved by either minimizing an image quality metric associated with motion [20]–[23] or by jointly optimizing over the data consistency error of a SENSE+motion model [24]–[28]. Unfortunately, these methods entail large-scale non-linear inverse problems which are most often solved using alternating/joint optimization. In this approach, the optimization alternates between updating the motion parameters and the image estimate while keeping the other variable type fixed. Iterating in this manner is computationally costly due to the large number of optimization variables and slow convergence, and often requires clinically disruptive reconstruction times. To maintain the efficiency of existing clinical workflows it is critical that the technologist has information on the suitability of the acquired data before the next scan has been completed.

SAMER [29] augments the joint or alternating optimization by exploiting a single 3–5 sec scout scan to significantly reduce the computational burden of motion estimation. The highly accelerated scout provides sufficient motion free k-space data to guide the non-convex motion trajectory search without requiring repeated full [27], [28] or partial [26] image updates. Moreover, SAMER permits the motion state to be separately determined (“on-the-fly”) using only the acquired k-space data from one shot. This allows for the 2–5 minutes of image acquisition time to be used for computing motion information, rather than having to wait until the scan finishes to initiate the joint optimization.

Although SAMER in its original form provides computationally efficient and accurate motion estimation, it relied on a non-standard distributed sequence acquisition ordering that ensures overlap with the central region of k-space in every shot [29]. While this sequence ordering facilitates the estimation of the motion parameters, it can also amplify the sequence’s sensitivity to patient motion. This can lead to a more severe appearance of motion artifacts in the standard SENSE reconstruction, i.e., without motion correction than that obtained from the clinically accepted sequence ordering. In practice, retrospective correction will not always produce the true image, e.g., due to non-idealities in the motion estimation, and hence it is important that radiologists can always review the original non-corrected image series with image quality/contrast and motion robustness that matches the standard acquisition.

In this work, we utilize conventional k-space acquisition orderings for MPRAGE and TSE acquisitions and introduce the concept of “motion guidance lines” into the SAMER framework. This facilitates robust retrospective motion correction while being minimally intrusive to standard acquisition timing and ordering. A limited number of motion guidance lines (2–4 per echo train) are required to accurately guide data-consistency based SAMER motion estimation which allows for them to be excluded during reconstruction. This ensures that the imaging data is minimally different from the clinical baseline and that even without motion correction, the quality of reconstructed images will be similar to conventional scans. We demonstrate the accuracy of the motion estimation and motion mitigation performance using simulation and in vivo experiments for standard cartesian 2D TSE and 3D MPRAGE.

Methods

Algorithm overview

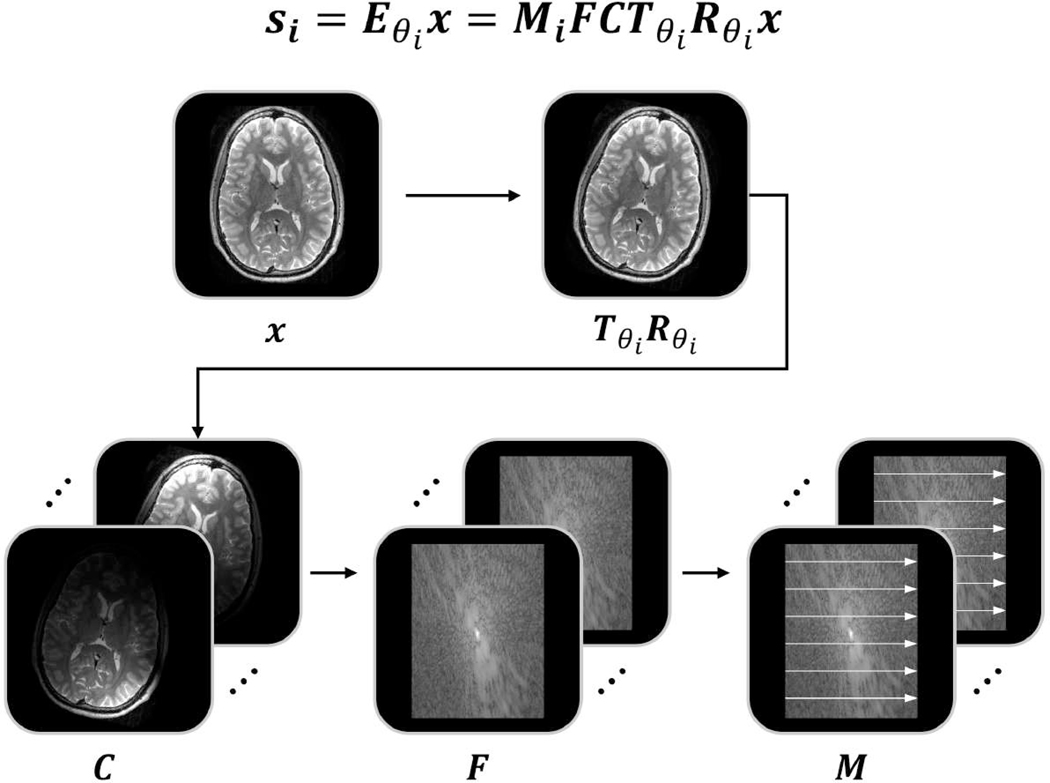
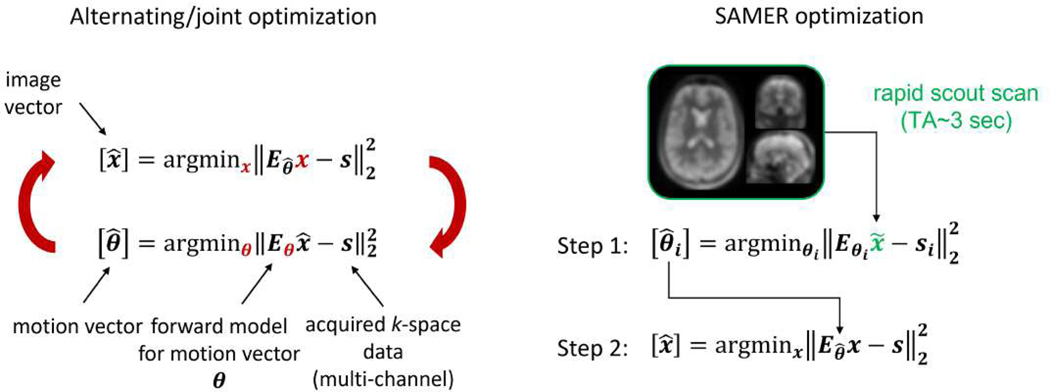
SAMER exploits an ultra-fast (~3–5 sec) scout and optimized k-space acquisition ordering to help separate the motion trajectory and motion-free image estimation, which would otherwise be a more difficult joint-optimization problem [26], [27]. In its simplest form, SAMER is an extension of the SENSE [30], [31] parallel imaging reconstruction with the addition of rigid-body motion parameters $\mathit{\theta }$ added into the forward model ${\mathit{E}}_{\mathit{\theta }}$ and the use of the scout prior:

$${\mathit{s}}_{\mathit{i}}={\mathit{E}}_{{\mathit{\theta }}_i}\mathit{x}={\mathit{M}}_i\mathit{F}\mathit{C}{\mathit{T}}_{{\mathit{\theta }}_i}{\mathit{R}}_{{\mathit{\theta }}_i}\mathit{x}$$

The k-space data ${\mathit{s}}_{\mathit{i}}$ for a given shot $i$ is related to the image volume $\mathit{x}$ through image translations $\mathit{T}$, image rotations $\mathit{R}$, coil sensitivity matrix $\mathit{C}$, Fourier operator $\mathit{F}$ and undersampling operator for each shot $\mathit{M}$ (Fig. 1). The goal of SAMER is to create an efficient method for directly (non-jointly) optimizing (estimating) the motion trajectory $\mathit{\theta }$ using an ultra-fast low-resolution scout $\tilde{\mathit{x}}$. This strategy avoids the difficult non-linear and non-convex joint optimization that contains millions of unknowns (SAMER only considers 6 degrees of rigid body motion at any time during the motion trajectory estimation) and it does not require computationally costly full or partial updates to the image estimate. The computational advantages of SAMER in comparison to alternating or joint optimization methods are summarized in Fig. 2. A key computational benefit of the SAMER approach is the ability to independently determine the motion state for each shot of the sequence:

$$\left[{\widehat{\mathit{\theta }}}_i\right]={\mathrm{a}\mathrm{r}\mathrm{g}\mathrm{m}\mathrm{i}{\mathrm{n}}_{{\mathit{\theta }}_{\mathit{i}}}‖{\mathit{s}}_i-{\mathit{E}}_{{\mathit{\theta }}_{\mathit{i}}}\tilde{\mathit{x}}‖}_2$$

Figure 1: Illustration of the SAMER forward model.

The k-space data for a given shot $i$ is related to the 3D image volume, $\mathit{x}$, through: (1) image motion: rotations $\mathit{R}$ and translations $\mathit{T}$, (2) coil sensitivity matrix $\mathit{C}$, (3) Fourier operator $\mathit{F}$, (4) undersampling operator for each shot $\mathit{M}$.

Figure 2: Comparison between alternating/joint optimization and SAMER.

The rapid SAMER scout facilitates fully separable motion estimation across the shots. This removes the need for computationally costly iterative updates to the image volume.

Note, that the scout prior $\tilde{\mathit{x}}$ must be available prior motion estimation and can be obtained from a rapid pre-scan (c.f. Tab. 1). Although each shot’s optimization problem can be solved concurrently, the non-linear and non-convex nature of each smaller optimization still presents a challenge; however, the stability can be improved by considering k-space sampling strategies that broaden the distribution across k-space for each shot while maintaining significant overlap with the low-resolution scout region. For the conventional linear ordering of an 3D MPRAGE scan, each shot is restricted to a single phase-encoding position and adjacent partition encoding lines are acquired in one shot. In this case, not all of the shots will overlap sufficiently with the scout’s central k-space region (Fig. 3A) which is needed to provide robust motion parameter estimation. Distributed orderings (Fig. 3A) were shown to have computational advantages by uniformly distributing a shot’s samples across k-space. This provides overlap with the scout’s data, facilitating robust fully separable per shot motion estimation [29], [32].

Table 1:

Imaging and scout acquisition parameters for 3D MPRAGE and 2D TSE (T2w).

		3D MPRAGE	2D TSE (T2w)
Scout scan	Resolution [mm]	1×4×4	0.4×5.8
	Acceleration	2×2	2
	Turbo factor	192	19
	TE/TI/TR [ms]	3.5/1100/2500	200/-/6000
	Scan time [min]	0:03	0:06
Imaging scan	Resolution [mm]	1×1×1	0.4×0.6
	Acceleration	2×2	1
	Turbo factor	188 (+ 4 guidance lines)	17 (+2 guidance lines)
	TE/TI/TR [ms]	3.5/1100/2500	100/-/6000
	Scan time [min]	2:42	2:21
Scout & imaging scan	FOV [mm]	256×256×192	220×220
	Bandwidth [Hz/px]	200	222
	Slices	-	27
	Slice thickness [mm]	-	4
	Slice gap [mm]	-	1.2

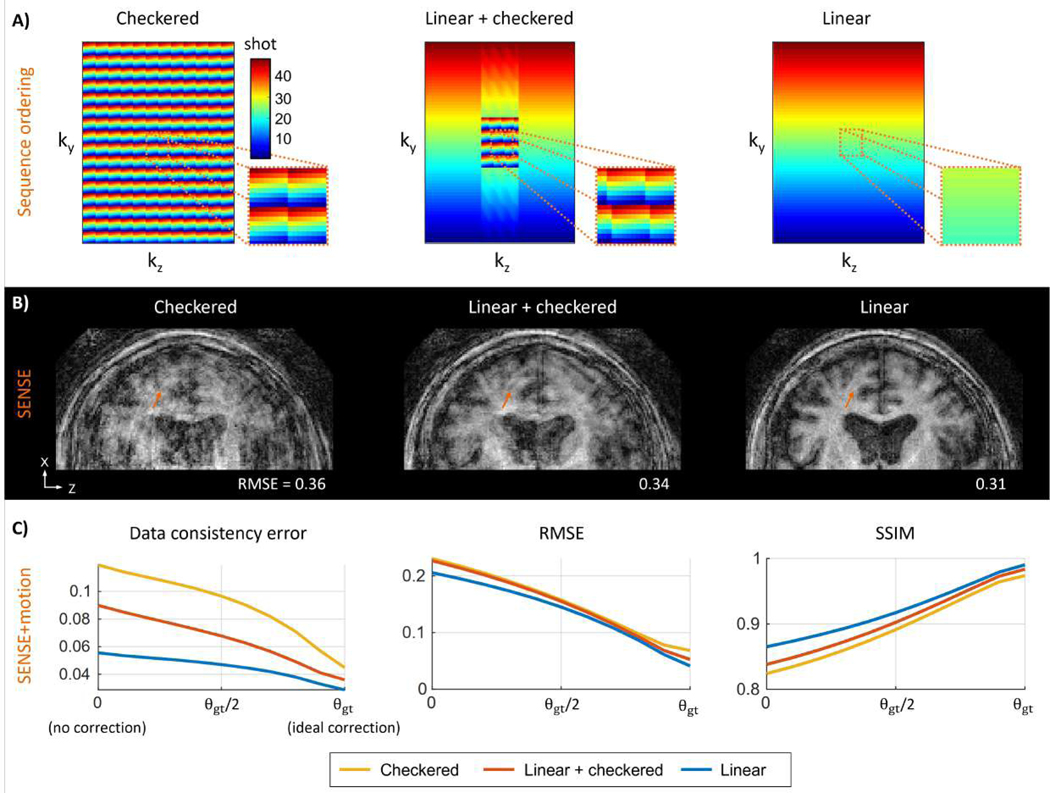
Figure 3: Analysis of motion sensitivity for different sequence orderings:

(A) Distributed sequence orderings (checkered and linear+checkered) broaden the k-space distribution and ensure overlap with the central region of k-space in every shot. (B) Example SENSE reconstruction (no motion correction) for simulated motion data. Linear sampling is inherently less sensitive to motion than distributed orderings (orange arrows). (C) Motion mitigated image quality metrics as a function of motion estimation accuracy computed across 41 clinical motion trajectories. SENSE+motion reconstructions were performed using motion values linearly scaled from 0 to θ_gt. The image quality metrics improved for all ordering schemes as the motion parameters approach the ground truth values, where linear sampling provided the best result for all cases.

Sequence ordering and motion sensitivity

While the choice of acquisition ordering can improve the ability to perform per-shot motion estimations, it can also fundamentally change how sensitive the sequence is to motion, i.e., there is often a direct relationship between motion observability and estimation robustness. To produce the desired image contrast, clinical imaging sequences utilize different cartesian sampling schemes. For example, T2w TSE is typically acquired with a distributed sampling (broad distribution of k-space per shot), while T1w MPRAGE often uses a linear ordering (narrow per shot k-space distribution). Interleaving the k-space sampling across shots is known to increase the sensitivity to motion, i.e., for the same motion trajectory TSE typically shows more severe motion artifacts than MPRAGE. At the same time, distributed sampling was shown to improve the ability to estimate motion [29], [32] further highlighting the relationship between motion sensitivity and estimation stability.

In motion simulations, we analyzed the motion sensitivity of linear and two recently proposed distributed sequence orderings (checkered [32] and linear+checkered [29] sampling, c.f. Fig. 3A). Here, we compared the quantitative image quality metrics: data consistency (DC), root-mean-squared error (RMSE) and structural-similarity (SSIM) of the non-corrected SENSE reconstructions to the ground truth. Motion sensitivity was first assessed qualitatively using a single clinical motion trajectory (maximum translation: 5 mm and maximum rotation: 2°) and then quantitatively across 41 clinical motion patterns [33]. In addition, motion sensitivity was investigated as a function of deviation from the ground truth motion (representing estimation error). For this analysis, the motion parameters used during the motion correction reconstructions were linearly scaled, and the artifact severity was examined as the assumed motion parameters approached the ground truth values (θ=αθ_gt; αϵ[0,1]).

Optimization of guidance lines

Previous implementations of SAMER [29] relied on a distributed sequence acquisition ordering for MPRAGE that ensures overlap with the central region of k-space in every shot. However, this sequence ordering was found to lead to more severe motion artifacts in the standard SENSE reconstruction than the conventional ordering where neighboring lines are acquired in each shot. Thus, the sequence ordering change had the unfortunate effect of improving the correction but exacerbating the motion sensitivity problem as demonstrated in Fig. 3. In this work, we introduce a very limited number of additional k-space lines (motion guidance lines) that when acquired along with the standard sequence sampling can accurately guide the data-consistency driven SAMER motion estimation. These small number of guidance lines can be readily excluded from the image reconstruction thereby ensuring that the image quality/contrast and motion robustness of the standard acquisition ordering is maintained.

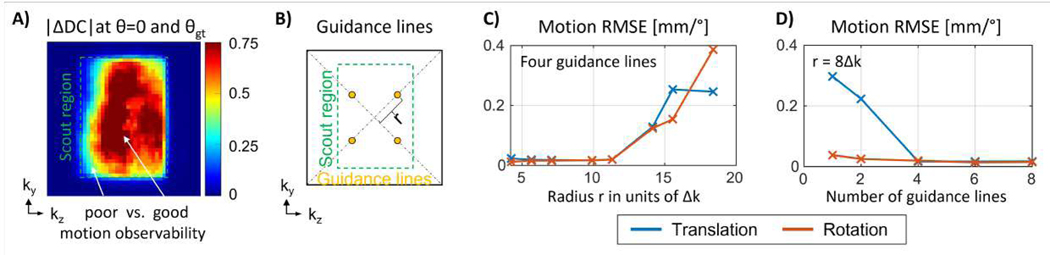
We first determined the minimal number and optimal k-space location of the motion guidance lines. Specifically, we examined k-space areas that are most suitable to observe motion when utilizing the rapid scout scan $\tilde{\mathit{x}}$ within the SENSE+motion model. Through simulation, the data consistency (DC) metric can be used for this purpose. We compute the DC distance between the case where no motion is assumed θ=0 (initial state of motion optimization) and the DC achieved when the ground truth parameters, θ_gt, are used. We define this DC distance metric as:

$$\mathrm{\Delta }DC={‖\mathit{s}-{\mathit{E}}_{\mathit{\theta }=0}\tilde{\mathit{x}}‖}_2-{‖\mathit{s}-{\mathit{E}}_{{\mathit{\theta }}_{\mathit{g}\mathit{t}}}\tilde{\mathit{x}}‖}_2$$

A large |ΔDC| indicates good observability of motion through the rapid scout, i.e., effective contribution to the data consistency driven motion optimization. In simulation using MPRAGE data and a low-resolution scout prior, absolute |ΔDC| was evaluated per k-space voxel across 41 clinical motion trajectories in MPRAGE data reconstructed with a low-resolution scout prior, $\tilde{\mathit{x}}$. This reveals the guidance line k-space locations that enable the highest level of motion accuracy. The motion error was first computed for a fixed number of guidance lines (4) while the distance r from the center of k-space was varied. Next, the k-space distance (r=8Δk) was held fixed, and |ΔDC| was studied as the number of lines was changed.

Implementation of guidance lines

Given that as little as 4 guidance lines per shot are needed to provide an accurate motion estimation (Fig. 4), our objective is to include these lines into 2D and 3D imaging sequences, with as little alteration of the standard sequence timing and contrast as possible. We consider two strategies for the implementation of guidance lines into multi-shot sequences:

Figure 4: Optimization of location for motion guidance lines:

(A) Mean absolute difference in data consistency (DC) error at θ=0 and θ_gt as measured across 41 clinical motion trajectories. The observability of motion (ΔDC) is high as long as there is sufficient distance from the scout boundary. (B) Illustration of four guidance lines located at radius r from the k-space center. (C) Motion estimation error (RMSE) as a function of radius r for four guidance lines. Statistics generated for simulated motion across 41 trajectories. The motion accuracy improves as the radius r increases, given sufficient overlap with the scout region in k-space. (D) Motion estimation error as a function of number of guidance lines (fixed radius) as observed across 41 motion patterns. Additional guidance lines (>4) do not provide significant improvement in motion accuracy.

• Small reductions of the nominal spatial resolution (≤2%) for minimal impact on clinical readings as it is not typically visible by the human eye and several established methods can effectively compensate for it, e.g., POCS or deep learning super resolution.

• Small increases of the echo train length. Standard TSE sequences have been optimized to retain image quality/contrast under varying echo distribution conditions. They are generally robust to small echo train length changes which can better exploit sequence dead-times.

Using these strategies, motion guidance lines were implemented into 2D TSE and 3D MPRAGE. The acquisition of the scout scan was optimized to ensure that motion guidance lines and scout data share similar image contrast, since large deviations can lead to unstable motion estimation [29]. In addition, the acquisition time of the scout was minimized to reduce the chance of their motion corruption (the scout is typically assumed to be motion-free [29]).

In vivo motion experiments

The stability of the guidance line approach was assessed in vivo using instructed motion experiments. Scans were performed on two healthy volunteers with written consent using a 3T MR scanner (MAGNETOM Vida, Siemens Healthcare, Erlangen, Germany) and a 20-channel head coil. Our proposed technique was first evaluated in 3D MPRAGE using conventional linear ordering and four motion guidance lines, c.f. Tab. 1, and was compared against the previously proposed linear+checkered ordering without guidance lines [29]. For this experiment, a healthy volunteer was trained to perform a consistent supervised step motion during two consecutive MPRAGE scans that employed the different sequence orderings. In addition, motion experiments with instructed nodding (breathing) and unsupervised (free) motion were conducted to validate our approach across a broader range of motion trajectories that closely match clinical scenarios. Each motion experiment was followed by a matched protocol where the subject was instructed to remain still. This served as a motion-free ground truth for qualitative and quantitative analyzes. Our approach was also validated in TSE (c.f. Tab. 1 for acquisition details) to assess the performance of the motion guidance lines with the most commonly used form of 2D imaging. To evaluate the motion estimation accuracy as well as potential computational advantages, SAMER was compared against an alternating/joint motion optimization (our implementation follows ref. [28]). In this case, the same TSE datasets were used to directly compare the retrospective techniques.

All motion correction reconstructions were performed offline using MATLAB and a Linux workstation with a NVIDIA GPU (Quadro RTX 6000, 24 GB). In 3D MPRAGE, motion parameters were estimated once per TR with a temporal resolution of 2.5 sec. In multi-slice 2D TSE, updates of the 3D motion trajectory were calculated twice per TR. For the interleaved 2D acquisitions this separated each shot across odd and even slices into different motion states with a temporal motion resolution of 3 sec. We utilized shears for all 3D image warps, since image interpolation errors in SENSE+motion reconstructions can lead to noise amplification [29]. The shear operations were implemented efficiently using position dependent phase ramps in k-space [27]. To reduce the computational cost of the SAMER algorithm, the raw k-space data of all acquisitions was compressed (6 SVD channels for motion estimation, 12 SVD channels for image reconstruction). Coil sensitivity maps were calculated using ESPIRiT [34] and the standard vendor 2-sec external reference scan. Note that 3D ESPIRiT was used in all experiments since 2D ESPIRiT can lead to varying image phase offsets across the slice/partition dimension. A standard quasi-newton non-linear solver (MATLAB’s fminunc) was used for the SAMER separable motion estimation and the alternating/joint technique. For all image reconstructions an iterative linear solver (MATAB’s lsqr) was employed.

Results

Figure 3 demonstrates the variation in motion sensitivity when considering different 3D sequence orderings in simulated motion data. Checkered and linear+checkered orderings have been proposed to improve motion estimation accuracy and convergence speed. They each provide distributed overlap with the center of k-space in every shot, unlike the standard linear ordering where k-space is traversed sequentially (c.f. Fig 3A). In a qualitative comparison using a single motion trajectory (derived from a clinical patient exam), the SENSE reconstructions using checkered and linear+checkered sampling show more severe streaking artifacts and higher loss of spatial resolution than linear ordering. This reduction in image quality corresponds to a 10–20% increase in RMSE when compared to a no motion ground truth scan (Fig. 3B). The same trend is also observed across the 41 clinical motion trajectories (Fig. 3C). For all acquisition orderings, the mean data consistency error of SENSE+motion improved as the motion parameters were varied from θ=0 (no motion assumed) toward the ground truth values θ_gt. Across this representative set of clinical patient motion, linear sampling consistently produced the lowest error, i.e., the best agreement with the SENSE+motion model. This trend was also observed for other quantitative image quality metrics such as RMSE and SSIM.

The optimization of the location and number of motion guidance lines is illustrated in Fig. 4. The change in data consistency error |ΔDC| between the nominal motion state θ=0 and the ground truth θ_gt used to simulate the data is shown in Fig. 4A as a function of k-space location. The observability of motion is high as long as there is sufficient distance from the scout boundary. As expected, the k-space area outside of the scout region is not well suited for motion estimation as evidenced by a small change in |ΔDC|. Fig. 4C shows the motion estimation accuracy using four guidance lines located at distance r from the k-space center (c.f. Fig. 4B). The motion accuracy is high for a large range of radii r, however, insufficient k-space overlap between the low-resolution scout and the guidance samples eventually degrades the estimation accuracy. Fig. 4D illustrates the motion error for varying number of guidance lines at a fixed radius r. High levels of motion accuracy are observed using at least four guidance lines.

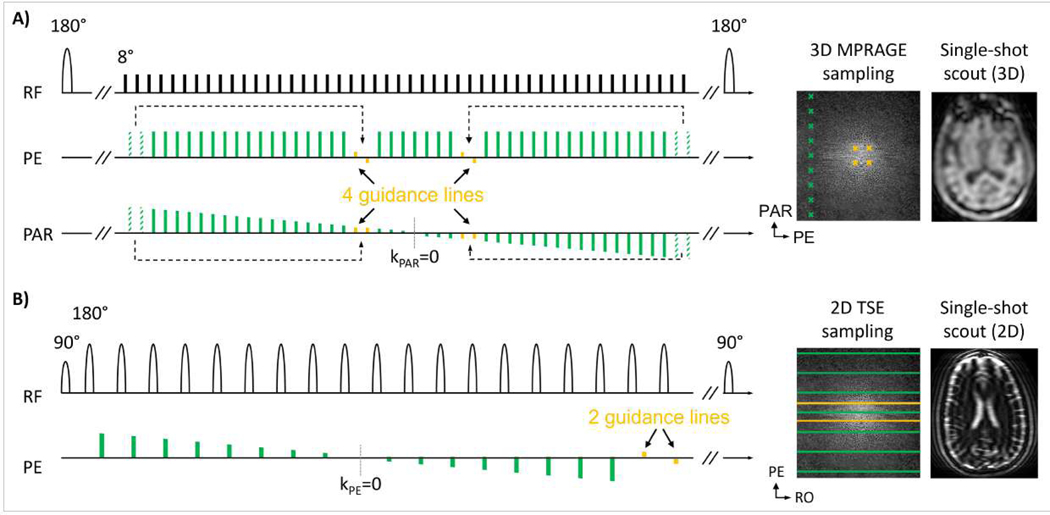
Figure 5 illustrates the implementation of motion guidance lines into 3D MPRAGE and 2D TSE. As shown in the sequence diagram of MPRAGE (Fig. 5A), four guidance lines (yellow) were inserted into an echo train. Moreover, the same number of imaging samples (dashed green) were removed from the periphery of k-space. This trade-off avoids changes to the sequence timing (fixed total echo train duration) while incurring only ~2% loss of spatial resolution for standard protocols. All motion guidance lines are located near the center of k-space and the acquisition order across both imaging and guidance lines provides the desired linear k-space partition (PAR) direction traversal in every echo train. The single-shot low-resolution MPRAGE scout scan (TA=3sec, c.f. Tab. 1) was acquired with linear acquisition ordering resulting in similar image contrast to that of the guidance lines.

Figure 5: Implementation of motion guidance lines into 3D MPRAGE and 2D TSE:

(A) In MPRAGE with linear ordering, four imaging scan echoes (dashed green) were removed from the echo train to accommodate for four guidance lines (yellow) located near the center of k-space. The single-shot, low-resolution MPRAGE scout (TA=3 sec) is acquired with linear sampling and matches the contrast of the guidance samples. (B) In 2D TSE (T2w), standard distributed ordering is used, and two guidance lines are appended at the end of each echo train. The single-shot scout scan matches the contrast of the guidance lines, here heavily T2w due to long TE~200 ms.

The echo train length of 2D TSE (c.f. Tab. 1) is much shorter than that of MPRAGE and insertion of guidance lines near the center of k-space can be disruptive to the sequence ordering which can lead to noticeable image contrast changes. Therefore, the turbo factor was increased to accommodate the acquisition of motion guidance lines. The 2D multi-slice acquisition inherently provides encoding along the third spatial direction and only two guidance lines were required at the end of the echo train (Fig. 5B). This strategy avoids any signal modulation of the TSE imaging data since motion guidance lines are acquired after the standard TSE echo train. For widely adopted clinical protocols the sequence dead-times in T2w TSE (TR=6 sec) proved sufficient for this very small number of additional readouts. The low-resolution, single-shot scout matches the contrast of the guidance lines, now heavily T2w due to long TE~200 ms (c.f. Tab. 1).

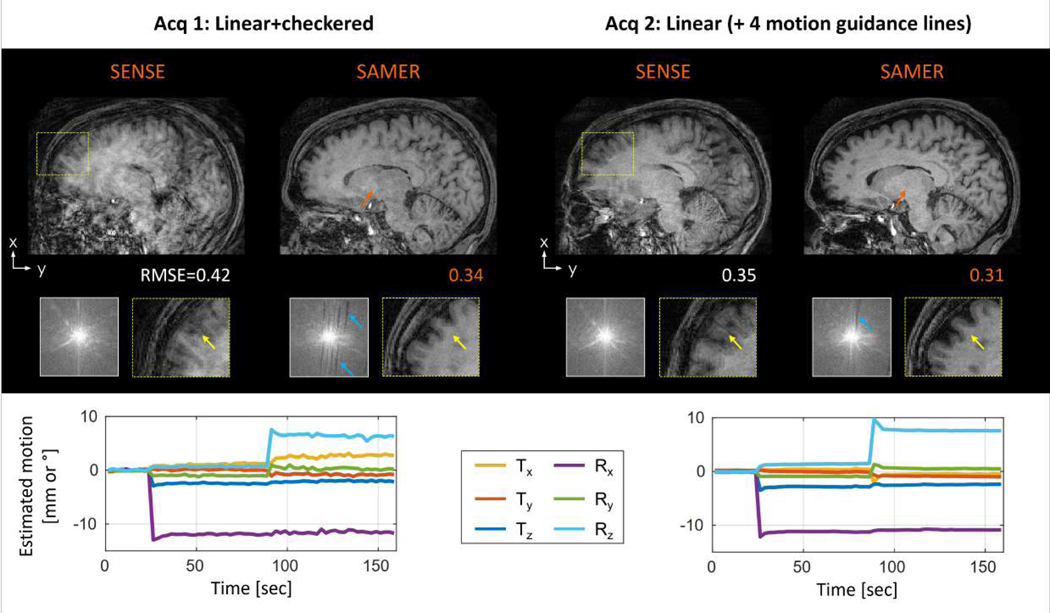
Figure 6 compares the motion correction performance of our approach in 3D MPRAGE to linear+checkered sampling. The proposed linear sampling with guidance lines was less motion sensitive as indicated by fewer motion artifacts in the initial SENSE reconstruction. The motion trajectory was estimated well in both methods, but the guidance lines provided more stable motion estimation with fewer fluctuations. This is due to the consistency of the spectral content for the guidance lines that are used in the data-consistency driven optimization. In comparison, the distributed sampling patterns of linear+checkered will have fluctuating biases as the sampling pattern shifts across the shots. After applying the motion correction, motion artifacts are significantly reduced in both cases. The linear ordering produced more homogenous contrast and had better preservation of the spatial resolution, as supported by the lower RMSE and fewer gaps in k-space.

Figure 6: Comparison of linear+checkered and standard linear sampling with motion guidance lines, in vivo 3D MPRAGE:

The SENSE reconstruction with linear sampling shows fewer motion artifacts which also led to a lower RMSE (computed w.r.t to motion-free reference). The instructed step motion trajectory was estimated reliably by both approaches, but fewer fluctuations were observed using motion guidance lines. After correction, substantial image quality improvement is demonstrated for both strategies, but linear sampling resulted in more homogenous contrast (orange arrows) and better preservation of the spatial resolution (yellow arrows) due to fewer gaps in k-space (blue arrows).

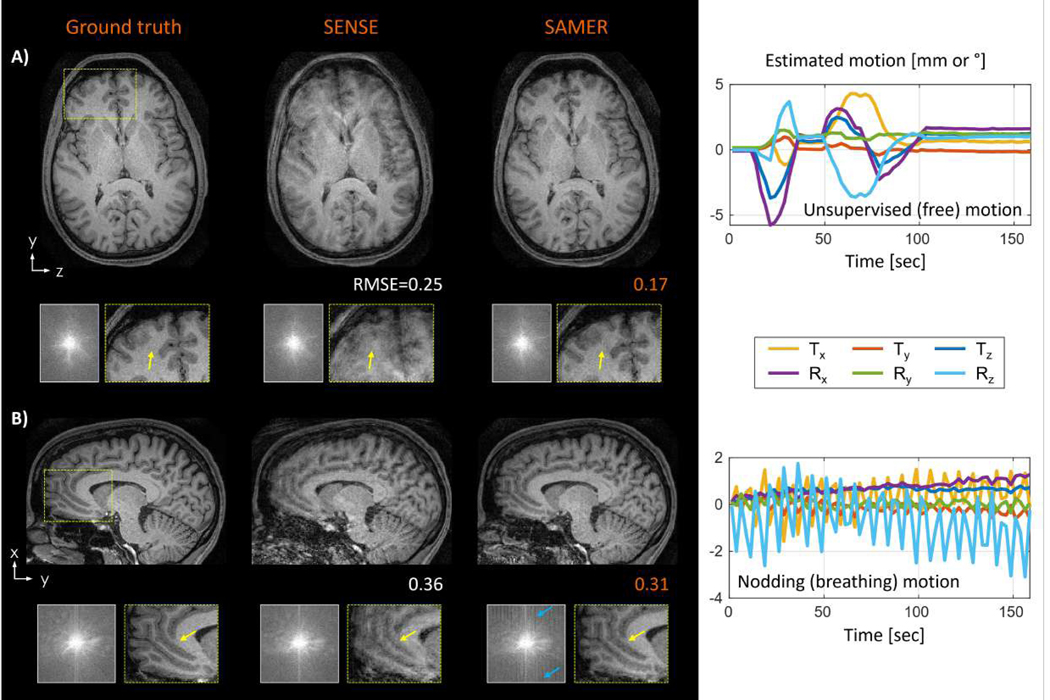
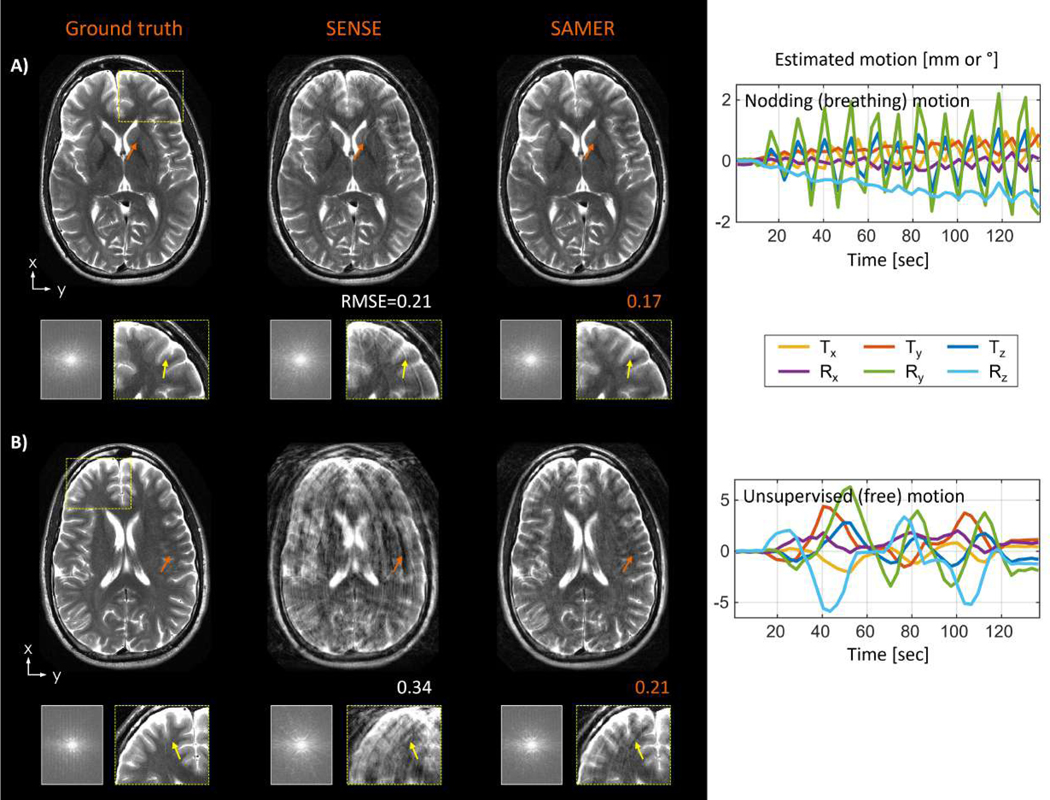
Additional in vivo motion experiments were conducted to probe the robustness of SAMER MPRAGE with linear ordering and guidance lines. In a scan with unsupervised (free) motion (Fig. 7A), SAMER removed most blurring artifacts and enabled better differentiation of gray- and white matter in the frontal cortex. The image quality improvement was also reflected by a 32% improvement in RMSE. The mean per shot motion estimation time in MATLAB was T_MotEst=0.8 sec/shot, facilitating fully separable on-the-fly motion optimizations; the image reconstruction time was T_Recon=32 sec. In Fig. 7B, SAMER was applied to a scan with instructed head nodding to mimic breathing motion. The sinusoidal motion trajectory was estimated robustly (T_MotEst=0.8 sec/shot) leading to reduced blurring and streaking artifacts after the motion correction (T_Recon=35 sec). Note that while motion correction led to a reduction of motion artifacts and an overall improvement in image quality, there were still residual artifacts in the corrected image associated with gaps in k-space that the algorithm was unable to fill-in given the strong nodding motion.

Figure 7: In vivo motion correction of representative motion patterns for 3D MPRAGE with linear ordering and guidance lines:

(A) SAMER improved the image quality in a scan with unsupervised (free) motion enabling better differentiation of gray- and white matter in the frontal cortex (yellow arrows). (B) For a scan with instructed nodding motion (breathing), SAMER also reduced streaking artifacts and loss of spatial resolution (yellow arrows), however, repetitive gaps in k-space (blue arrows) are still visible due to the large sinusoidal motion.

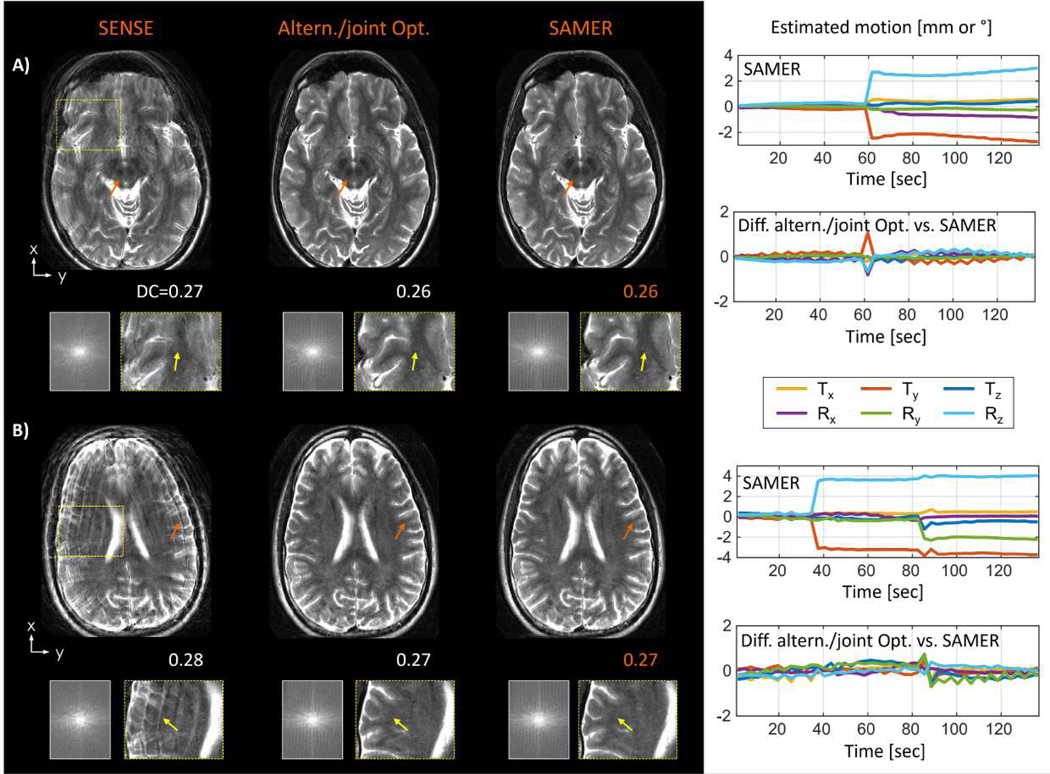
SAMER was also evaluated in 2D TSE (T2w) and compared against an alternating/joint optimization (Fig. 8) to assess the motion estimation accuracy and potential computational advantages of motion guidance lines. The instructed step motion pattern was estimated reliably using both methods and the small differences in the motion trajectories (standard deviation of motion difference < 0.31 mm/°) suggest good accuracy when using the guidance lines. It is important to note that the computation time of SAMER was roughly 300-times faster as each shot can be treated as a separable motion optimization problem (SAMER: T_MotEst=1.6 sec/shot, alternating/joint optimization: T_MostEst=508 sec/shot for the step motion trajectory shown in Fig. 8A). The very small differences in estimated motion trajectories result in comparable image quality improvement and similar final data-consistency error. As expected, the scan with only in-plane motion showed superior final image quality (Fig. 8A) compared to the scan with through-plane motion (Fig. 8B).

Figure 8: Estimation accuracy and computational scalability comparison of joint/alternating optimization and SAMER in 2D TSE (T2w) scans with instructed step motion.

Mostly in-plane motion under (A), combined in-plane and through-plane motion under (B). Comparable motion trajectories (standard deviation of motion difference < 0.31 mm/°) were estimated by both methods yielding similar reconstructed image quality improvement (c.f. orange and yellow arrows) and final data consistency error (DC). Fully separable motion optimization in SAMER resulted in ~300x smaller computation time.

Additional in vivo motion experiments were performed for 2D TSE to demonstrate the performance of guidance lines under realistic motion conditions. SAMER estimated the instructed nodding motion robustly (Fig. 9A) and removed most streaking artifacts and loss of spatial resolution which is also reflected by a reduction in RMSE. In a more difficult unsupervised (free) motion example (Fig. 9B), SAMER also achieved substantial image quality improvement, but some residual streaking artifacts and localized signal dropouts are still visible.

Figure 9: In vivo motion correction for 2D TSE (T2w):

(A) SAMER improved the image quality in a scan with supervised nodding (breathing) motion which reduced streaking artifacts and loss of spatial resolution (yellow arrows). (B) Substantial image quality improvement (orange arrows) was also observed in a case with unsupervised (free) motion. However, SAMER was unable to remove all streaking artifacts (yellow arrows) due to large through-plane motion (>8°).

Discussion

In this work, we introduced motion guidance lines within the SAMER framework to facilitate robust retrospective motion correction with minimal disruption to standard clinical sequences and protocols. Our approach relies on the high motion observability of 2 or 4 additional k-space lines which are acquired in each shot and are used to guide the data-consistency based motion optimization in SAMER. The extremely limited number of motion guidance lines allows them to be excluded for the final image reconstruction. This enables the method to produce a true “original image series” with image quality/contrast and motion robustness that matches the standard acquisition. We validated our approach both in simulation and in vivo through supervised motion experiments. The method produced highly accurate and robust artifact correction in standard 2D and 3D sequences with clinically acceptable reconstruction times.

Our proposed method offers a “do-no-harm” strategy to ensure that the baseline image quality/contrast and clinical workflow are maintained, and that the motion mitigated reconstruction will only add value to the exam (i.e., the motion-corrected images can be ignored if correction does not improve the image quality). Compared to image navigator-based methods the changes to sequence timings and k-space ordering required by the inclusion of the few guidance lines are minimal and lead to a negligible effect on image resolution, image contrast and motion sensitivity. This distinguishes our method from previous retrospective data-driven methods where distributed encoding orderings [29], [32] often led to more severe appearance of motion artifacts. In contrast, the proposed technique retains the image quality and motion robustness from the original sequence ordering which allows radiologists to always compare the motion mitigated SAMER images against the non-corrected original image series. Moreover, separable motion optimization using the SAMER scout prior facilitates on-the-fly motion estimation. Thus, the computational cost of the method is only the final very rapid image reconstruction time (~ 1 min for online implementation with standard scanner GPU hardware). This post-scan reconstruction time is less than a typical MRI scan duration and should not interfere with the clinical workflow.

Motion guidance lines were placed at fixed k-space locations to reduce fluctuations in the estimated motion trajectory. Distributed sampling, such as linear+checkered, was originally designed to provide center of k-space information in every shot. Fully separable motion estimation can be achieved when the sampling pattern is combined with a low-resolution scout prior. However, as shown, changing the sampling pattern in this interleaving manner can lead to small fluctuations in the estimated motion trajectory as different shifted k-space patterns are used in every per shot motion optimization. These instabilities are caused by small biases in the k-space data, e.g., different level of contrast mismatch between the scout and imaging data that varies with k-space location. Therefore, the proposed method utilizes a small number of motion guidance lines acquired at fixed k-space locations, making any potential k-space biases consistent across all shots which led to smoother trajectories. This increased stability should benefit scans that contain little or no motion, as inaccurate motion trajectory estimation may introduce small artifacts in the motion corrected reconstruction.

The acquisition of the scout scan was optimized to minimize scan time while maintaining accurate and robust motion estimation driven by a fixed set of motion guidance lines. In the original SAMER framework [29], the scout was acquired at 4 mm spatial resolution to ensure 100% k-space overlap with the low-resolution checkered k-space region of the imaging scan. Alternatively, when considering the optimized placement of the motion guidance lines, a much smaller k-space window is required. We demonstrated a total 4-fold reduction in the scout scan’s spatial resolution without compromising on motion accuracy. This enabled the scout to be acquired very rapidly using just a single shot and R=4 acceleration for 3D MPRAGE. We anticipate improved robustness in clinical settings as previous implementations either required longer scan time (e.g., 5–7 sec) which increases the chance of motion during the scout, or utilized higher acceleration (e.g., R=6–12) which could lead to instabilities due to parallel imaging artifacts.

In this work, the k-space locations of motion guidance lines were optimized for a fixed acquisition scenario. However, the concept should generalize across a large range of clinical sequences and protocols. The accuracy of SAMER will be independent of the spatial resolution, but it will depend on the size of the FOV. Larger FOVs require denser sampling in k-space (i.e., smaller Δk) and hence the absolute k-space distance from the center will be reduced. As was demonstrated in Fig. 4C, there is a wide range of radius values ($4\Delta k$ to $16\Delta k$) for the guidance lines that provided accurate motion estimation. The flexibility afforded by the model should accommodate the modest FOV changes seen in clinical practice.

Motion guidance lines were inserted into standard 2D and 3D cartesian sequences to obtain accurate motion information at the temporal resolution of the underlying sequence, e.g., TR=2.5 sec in MPRAGE. However, this temporal resolution may be insufficient for very rapid and extreme head motion. This issue can be addressed by placing multiple sets of guidance lines across the echo train (e.g., at the beginning, middle and end) and estimating the patient’s position for each set of guidance lines independently. Note, the large signal intensity/contrast variation across the echo train may require the acquisition of separate (contrast-matched) scout scans for each set of guidance lines. We envision that this intra-shot motion correction approach will increase the temporal resolution of the motion estimates and thus improve the image quality in cases with very rapid and extreme subject motion.

Given the successful utilization of deep learning (DL) for stabilizing difficult image reconstructions, it is reasonable to expect DL techniques to further improve the image quality of retrospective motion correction. In standard parallel imaging, priors/constraints were shown to help stabilize ill-conditioned image reconstruction at high acceleration. In addition to explicit regularizers (compressed sensing [35], LORAKS [36]), there has also been increasing interest in learned image priors [37]. DL has been applied to a variety of reconstruction tasks, where predominantly image-to-image networks have been proposed for motion correction [38]–[40]. We anticipate that DL can also be synergistically combined with the SENSE+motion model. This will be helpful in acquisitions with distributed sequence ordering, such as TSE, where retrospective motion correction is likely to cause large repetitive gaps in k-space. These gaps cannot always be filled using standard coil spatial encoding and this may result in image ghosting and loss of spatial resolution. Note, that high parallel imaging acceleration and sub-optimal receiver coil geometries can further increase the severity of these artifacts. SENSE+motion reconstructions with learned image priors are expected to better fill these gaps which should improve the image quality under poor parallel imaging stability conditions. Moreover, motion correction in 2D imaging sequences is often limited by the inability to accurately interpolate through thick slices and missing information due to slice gaps. Recent successes in deep learning super-resolution [41], [42] may help to overcome these limitations by generating data at higher through-plane resolution and reduce the image interpolation errors.

In conclusion, motion guidance lines enabled robust retrospective motion correction with minimal potential disruption to the standard sequences and clinical workflows. Our approach generalizes across 2D and 3D sequences and was demonstrated to achieve robust artifact mitigation with clinically feasible reconstruction times.

Data Availability Statement

The data that support the findings of this study are openly available in GitHub at https://github.com/reconmri/samer.