Abstract
Population-scale single-cell RNA-seq (scRNA-seq) data sets create unique opportunities for quantifying expression variation across individuals at the gene coexpression network level. Estimation of coexpression networks is well established for bulk RNA-seq; however, single-cell measurements pose novel challenges owing to technical limitations and noise levels of this technology. Gene–gene correlation estimates from scRNA-seq tend to be severely biased toward zero for genes with low and sparse expression. Here, we present Dozer to debias gene–gene correlation estimates from scRNA-seq data sets and accurately quantify network-level variation across individuals. Dozer corrects correlation estimates in the general Poisson measurement model and provides a metric to quantify genes measured with high noise. Computational experiments establish that Dozer estimates are robust to mean expression levels of the genes and the sequencing depths of the data sets. Compared with alternatives, Dozer results in fewer false-positive edges in the coexpression networks, yields more accurate estimates of network centrality measures and modules, and improves the faithfulness of networks estimated from separate batches of the data sets. We showcase unique analyses enabled by Dozer in two population-scale scRNA-seq applications. Coexpression network–based centrality analysis of multiple differentiating human induced pluripotent stem cell (iPSC) lines yields biologically coherent gene groups that are associated with iPSC differentiation efficiency. Application with population-scale scRNA-seq of oligodendrocytes from postmortem human tissues of Alzheimer's disease and controls uniquely reveals coexpression modules of innate immune response with distinct coexpression levels between the diagnoses. Dozer represents an important advance in estimating personalized coexpression networks from scRNA-seq data.
The advent of single-cell RNA sequencing (scRNA-seq) has provided unparalleled insights into the transcriptional programs of cell types and cellular stages (Zeisel et al. 2015; Chen et al. 2017; Travaglini et al. 2020). Emerging population-scale scRNA-seq data sets are enabling investigations of population-level phenotypic variability as a function of transcriptomic variability at the single-cell level (Bernardes et al. 2020; Cuomo et al. 2020; van der Wijst et al. 2020; Jerber et al. 2021; Soskic et al. 2022). When combined with individual-level genetic information, population-scale scRNA-seq data sets enable mapping expression quantitative trait loci (eQTL) across different cell types and in dynamic processes (van der Wijst et al. 2018; Soskic et al. 2022).
A key opportunity unveiled by emerging scRNA-seq data sets is the construction of personalized gene coexpression networks that can be leveraged to link network-level properties to phenotypic variation, for example, discovering therapeutic targets in cancer (Forbes et al. 2022) and identifying genetic variants (e.g., network QTLs) that associate with network properties such as modules (Langfelder and Horvath 2008) and network centrality (Savino et al. 2020) measures. Gene coexpression network analysis (Zhang and Horvath 2005), which estimates gene–gene correlations, is a key inference tool for detecting latent relationships that might be obscured in standard analysis of clustering and differential expression. Studies examining protein–protein interactions on a genome-wide scale have shown that proteins with a high number of connections in protein–protein interaction networks are more vital for survival than proteins with fewer connections (Jeong et al. 2001; He and Zhang 2006). In a similar vein, research on coexpression networks has pinpointed genes with high centrality that participate in processes specific to the studied phenotypes. One such study conducted on zebrafish heart regeneration found that genes associated with tissue regeneration occupied central positions within the coexpression network (Azuaje 2014). These results underscore the importance of gene centrality when identifying genes that influence the phenotypes of interest (Lareau et al. 2015). Instead of focusing on high centrality genes within a single coexpression network, detecting genes with differential centrality between phenotypic groups can elucidate regulatory alterations. Savino et al. (2020) offer insights into the potential regulatory relationships that a gene with differential centrality, but no differential expression, might signify. Modifications in post-translational processes, the involvement of a cofactor, or epigenetic mechanisms like DNA methylation can modify the regulatory function of a transcription factor (TF) without impacting its expression.
Workflows, including data preprocessing, normalization, and network transformation, for estimation of gene–gene correlations in coexpression networks are well established for bulk RNA-seq (Johnson and Krishnan 2022); however, single-cell measurements of expression pose unique challenges owing to technical limitations and noise levels inherent to the technology. Past research innovated numerous approaches to mitigate the noise and sparsity issues related to scRNA-seq technology when estimating gene–gene correlations. MetaCell (Baran et al. 2019) aggregated profiles of disjoint and homogeneous groups of cells to reduce sparsity in expression counts. BigSCale2 (Iacono et al. 2019) leveraged patterns of differential expression between clusters of cells to calculate correlations from transformed scRNA-seq data. State-of-the-art scRNA-seq data normalization and imputation methods, such as SCTransform (Hafemeister and Satija 2019), MAGIC (Van Dijk et al. 2018), SAVER (Huang et al. 2018), and DCA (Eraslan et al. 2019), perform well in estimating expression, removing technical variability, and improving downstream dimension reduction and clustering tasks. However, these widely used methods, notably except for SAVER, rarely account for the estimation uncertainty in their expression estimates and were observed to introduce correlation artifacts for gene pairs that are not expected to coexpress (Zhang et al. 2021). A noise regularization approach was introduced by Zhang et al. (2021) to eliminate such correlation artifacts. However, none of the existing methods have been evaluated within the scope of population-scale scRNA-seq data sets with varying levels of technical artifacts across individual data sets for their reproducibility and stability. Furthermore, their performances in terms of estimating network centrality measures have not been assessed.
Here, we aim to fill this gap by developing Dozer to estimate gene–gene correlations from scRNA-seq data. Unlike existing approaches, Dozer accounts for the noise in the normalized expression and automatically generates a “noise-to-signal” metric as an index to select genes for reliable coexpression analysis. Through large-scale simulations and data-driven computational experiments, we show that Dozer yields robust estimates of gene–gene correlations that are less sensitive to the overall expression levels of the genes and the sequencing depths of the data sets compared with alternatives. Furthermore, Dozer outperforms other methods in estimating network centrality measures such as degree, pagerank, betweenness, eigenvector centrality, and modules. We show the utility of Dozer in two population-scale scRNA-seq data sets in which Dozer-constructed coexpression networks have a higher proportion of edges validated by external data sets compared with others. These applications further showcase how network centrality measures from personalized coexpression networks can be leveraged to exploit phenotypic variation.
Results
Correction factors for correlations estimated from normalized expression data
We consider a biologically motivated hierarchical model to disentangle the biological signal and the measurement error resulting from the sequencing procedure. Let gj represent the expression level of gene j, ℓ represent cell sequencing depth, and X represent cell-level covariates, for example, batch labels; mitochondrial percentage denoting the mitochondrial transcript counts as a percentage of the total transcript counts. The observed UMI count of gene j, Yj, is modeled as
| (1) |
This Poisson measurement model succeeds in capturing variation driven by sampling noise and stochastic technical noise (Sarkar and Stephens 2021; Choudhary and Satija 2022) and is particularly well suited for data sets with shallow depths common to population-scale scRNA-seq studies. Although an explicit expression model for gj is not required for correlation estimation, in our simulation studies, we consider a Gamma prior , where vj and uj are shape and scale parameters. With this expression model, UMI counts follow the widely used negative binomial distribution (Huang et al. 2018; Hafemeister and Satija 2019). Let denote the normalizing size factor and denote the normalized counts. Elementary calculations result in
| (2) |
| (3) |
Hence, the magnitude of the correlation of the normalized counts and is an underestimate of the true correlation, cor(gj, gk), of genes j and k. We use the ratio to define a “noise ratio” indicating the quality of normalized expression of gene j. Quantification of this ratio across a wide range of genes in both simulated and actual data sets indicates that the high noise ratio corresponds to low expression and high sparsity (Supplemental Fig. S1; Supplemental Sec. S2.1). This aligns well with the intuition that the sparser the gene expression, the harder to recover the underlying signal. The corrected correlation between the expression values of gene j and k is then given by
| (4) |
For a given data set, Yj, are the observed UMI counts of the genes. The cell sequencing depth ℓ is typically approximated with the total number of UMI counts per cell (e.g., work by Hafemeister and Satija 2019), which is further justified with an approximation error under the Poisson measurement model and probability simplex constraint (Zhang et al. 2020a). We used trimmed total UMI counts (Methods), a modification of total UMI counts, to reduce the influence of high expression genes on the estimation, as a default estimator for the sequencing depth. Parameters for the covariates {βj}j are estimated through a Poisson regression. The numerator and denominator of the noise ratio , , and the gene pair correlation are estimated through the sample mean, variance, and correlation. We denote Sj = 1/(1 − Rj) as the correlation correction factor for gene j and represent cor(gj, gk) in Equation 4 as . Because the variance of a plug-in estimator is inflated for genes with a high noise ratio (Rj close to one), we adopt two strategies to stabilize the estimation of the corrected gene–gene correlations: a weighting scheme that allocates higher weights to cells with higher depths in the estimation of gene noise ratio, and a variance reduction transformation to stabilize the gene correction factor estimates (Methods; Supplemental Fig. S2). Direct evaluation of biases and variances in the gene–gene correlations estimated by Dozer validates the effectiveness of our strategies in achieving a well-balanced trade-off between estimation bias and variance (Supplemental Sec. S2.2; Supplemental Figs. S3–S5).
Dozer reduces false positives in coexpression network edge estimation
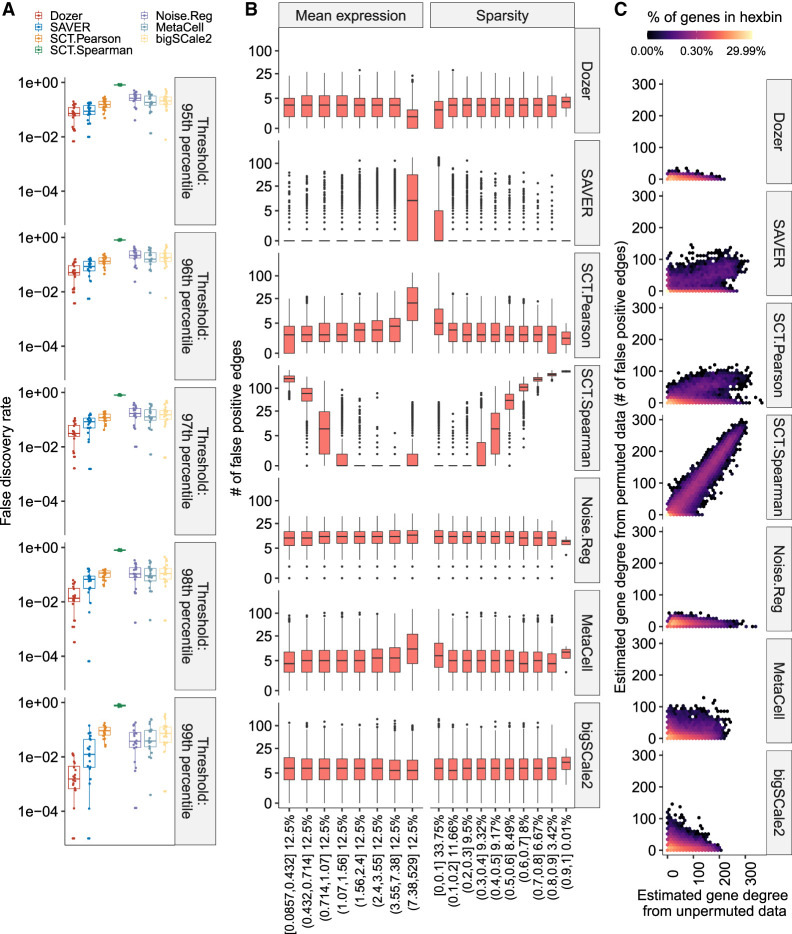
We first designed a data-driven permutation experiment with the Jerber_2021 data (Jerber et al. 2021), leveraging proliferating floor plate progenitor (P_FPP) cells from 20 donors, each with at least 500 cells, to study the overall false-discovery rates of coexpression network construction methods in terms of edge estimation (Supplemental Secs. S1.1, S1.2). We also leveraged these computational experiments to investigate the factors that affected the number of false-positive edges associated with each gene within each method. Given an expression matrix, we randomly split genes into two disjoint sets and permuted the cell ordering in one set so that gene pairs with one gene in each set have zero correlation by construction. We then constructed a coexpression network for gene pairs with one gene from each set using the permuted data set by each method. Because the networks with permuted data are null networks, all the discovered edges are deemed as false positives.
Quantification of the empirical false-discovery rates of each method across the data splitting experiments revealed that Dozer has a smaller false-discovery rate than the other methods irrespective of the correlation threshold (one-sided Wilcoxon rank-sum test P-values comparing Dozer vs. the next best method are ≤0.077 across all percentile thresholds) (Fig. 1A). We next asked how the numbers of false-positive edges of genes varied as a function of the overall expression of the genes and their sparsity, that is, proportion of cells with zero expression for a given gene (high proportion indicating high sparsity) (Fig. 1B). Networks constructed by SAVER and SCT.Pearson have more false positives among genes with high expression or low sparsity. SCT.Spearman tends to overestimate the number of edges for genes with high sparsity. This appears to be an artifact owing to oversmoothing of the normalization procedure and has been observed by others as well (Supplemental Fig. S6; Zhang et al. 2021). In contrast, Dozer, MetaCell, Noise.Reg, and bigSCale2 do not show any discernible association between the numbers of false-positive edges and the overall sparsity levels of the genes or the overall expression levels of the genes. Next, to elucidate the aggregated effect of the overall mean expression and sparsity levels of the genes, we compared the estimated degrees of the genes, that is, the total number of edges of a gene, obtained from the networks with the permuted and the unpermuted data. The gene degrees estimated from the networks with unpermuted and permuted data are correlated for methods SAVER, SCT.Pearson, and SCT.Spearman (Fig. 1C). This indicates that some of the high centrality genes in these networks are driven by the edge identification bias toward genes of certain expression patterns, for example, high expression genes for SAVER and SCT.Pearson and sparse genes for SCT.Spearman. Dozer, MetaCell, Noise.Reg, and bigSCale2, to a large extent, show a uniform behavior across the genes, with Dozer having a lower number of false-positive edges compared with MetaCell, Noise.Reg, and bigSCale2, respectively (an average of 3.4 vs. 9.2, 11.3, and 9.8 in Fig. 1C).
Figure 1.
Impact of the overall expression and sparsity levels of genes on false-discovery rates of coexpression network edge detection. (A) Empirical false-discovery rates of the methods across multiple permutation experiments with the Jerber_2021 samples at multiple distinct thresholds set by the percentiles of the absolute values of the estimated correlations. The P-values from a one-sided Wilcoxon rank-sum test between Dozer and the second-best method, SAVER, for the five quantile thresholds are 0.077, 0.0014, 4.1 × 10−5, 9.5 × 10−6, and 0.00016, respectively. (B) Numbers of false-positive edges of genes stratified by mean expression levels and the proportion of zeros in gene counts (sparsity). Percentages on the x-axis denote the percentage of genes in the expression and sparsity intervals. (C) Estimated gene degrees (i.e., numbers of edges connected to a gene) from the coexpression network with the permuted (y-axis) versus unpermuted (x-axis) data. Coexpression networks are constructed between the two groups of genes that result from splitting of the genes. Gene degrees are estimated from coexpression networks with the original data (unpermuted; x-axis) and data in which cells are permuted for one set of the genes (permuted; y-axis). Because the correlation of genes in the permuted data is zero, the corresponding gene degrees are contributed by falsely detected edges, highlighting the aggregated impact of mean expression levels and proportion of zeros in deriving the genes’ overall associations. Results are pooled from multiple permutation replicates across the genes.
Dozer yields more accurate estimates of gene centrality scores and modules in coexpression networks
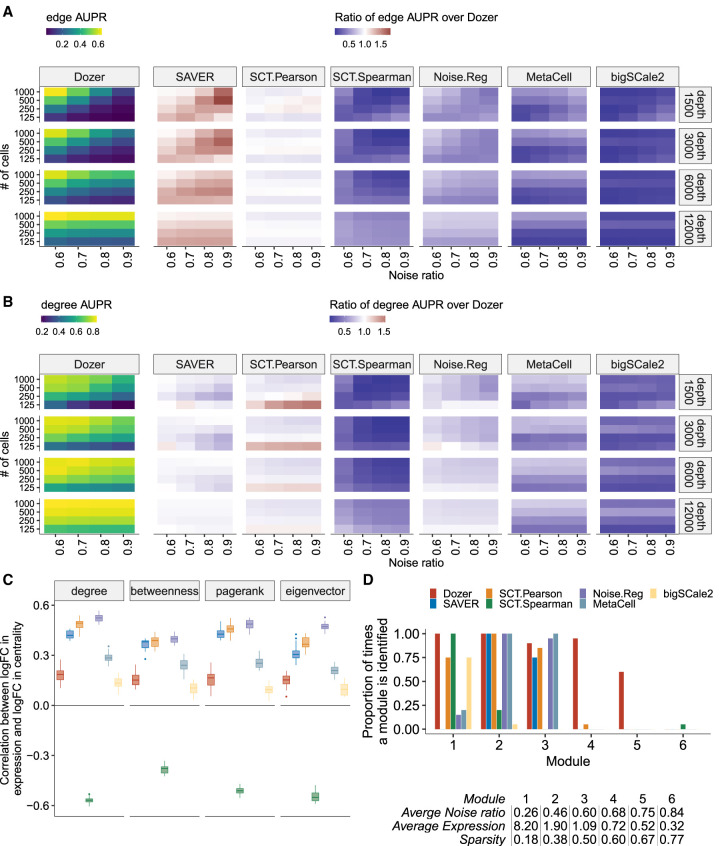
Coexpression network construction methods are traditionally benchmarked for their accuracy in detecting individual edges using the area under precision recall curve (AUPR) and F1 score metrics (Pratapa et al. 2020; Johnson and Krishnan 2022; McCalla et al. 2023). Although inferential analysis of coexpression networks commonly use gene centrality measures and modules to prioritize genes and elucidate biological processes (Iacono et al. 2019; Wang et al. 2021), existing methods for estimating coexpression networks from scRNA-seq data are not benchmarked for their performance in estimating these inferential parameters.
To create simulation scenarios that accurately reflect real-world conditions, we relied on Cuomo_2020 (Cuomo et al. 2020), which provides a high sequencing depth per cell (averaging about 530,000 total counts per cell), to simulate from realistic gene–gene correlation structures. We combined these correlations with marginal gene distributions and sequencing depth estimates obtained from Jerber_2021 (Jerber et al. 2021) to simulate population-scale scRNA-seq data (Methods). In addition to the standard evaluation of network edge recovery, we evaluated each method's performance in identifying top centrality genes, as defined by a variety of network centrality measures (setting A). We also assessed their abilities to avoid confounding between differential gene expression and differential gene centrality (setting B) and the performance in gene module identification in terms of identifying gene modules in the ground truth network (setting C). The former is important for coexpression analysis of population-scale scRNA-seq data because genes that are differentially expressed between populations might also spuriously show differential network centralities owing to the computational biases as observed in the false-discovery analysis (Fig. 1).
Performances of the methods in terms of edge and high centrality gene identification as a function of noise ratios of the genes (i.e., with four different noise ratio thresholds as {0.6, 0.7, 0.8, 0.9}), the numbers of cells (four different cell sample sizes as {125, 250, 500, 1000}), and average sequencing depths (four different sequencing depths as {1500, 3000, 6000, 12000}) in the first simulation setting (setting A) are summarized in Figure 2, A and B, and Supplemental Figures S7 and S8. Specifically, SAVER tends to outperform the rest in terms of edge identification, whereas Dozer shows superior performance in terms of identifying high centrality genes. The discrepancy in edge and high centrality gene identification performances of SAVER can be attributed to its upward bias toward high expression genes, which was also prevalent in the FDR analysis (Fig. 1B). Correlation estimation from SAVER tends to be larger in magnitude for high expression genes. This upward bias favors higher rankings for correlations between high expression genes, resulting in a greater number of selected edges among these genes (Supplemental Fig. S9). Exploring the impact of the noise ratio and the numbers of cells for coexpression analysis yielded that, for all methods, noise ratio and sample size have a large impact on edge identification but a much smaller impact on the centrality measures of the genes (Fig. 2A,B; Supplemental Figs. S7, S8). For the three top-performing methods, Dozer, SAVER, and SCT.Pearson, the AUPR of edges reduces by 47% (F1 score reduces by 38%) when we relax the noise ratio threshold from 0.6 to 0.9 or decrease the numbers of cells from 1000 to 250, whereas the AUPR of gene centrality is attenuated by only 18% (F1 score reduces by 15%). Visualizing the general trends in the leftmost panels of Figure 2, A and B (also Supplemental Figs. S7, S8), we observe a clear drop in performance when going from 250 to 125 cells (AUPRs of edge and degree centrality identification are (0.22, 0.58) with 250 cells and (0.12, 0.42) with 125 cells), especially for data sets with low sequencing depths. This indicates the importance of extra caution and additional robustness checks when constructing networks with fewer than 100 cells. Further extension of these simulations by varying the sequencing depths of the cells reveals that the sequencing depth is not a key factor for network construction performance as long as genes with high noise ratio are filtered. However, sequencing depth plays a key role on the numbers of genes retained, hence the size of the network that can be accurately recovered (Supplemental Fig. S10).
Figure 2.
Evaluation for gene centrality and module estimation. (A,B) Summary of simulation results in terms of AUPR scores for edge and high degree centrality gene identification. The leftmost panel depicts the average AUPR scores of Dozer for edge (A) and degree (B) centrality identification as a function of gene noise ratios (x-axis), number of cells (y-axis), and average sequencing depths (rows). The remaining panels highlight the performances of other methods as quantified by the ratio of their AUPR scores over the AUPR score of Dozer. Results for the identification of high centrality genes with respect to pagerank, betweenness, and eigenvector centrality are in Supplemental Figure S7. (C) Robustness of estimated gene centrality measures against differential expression. Box plots of Spearman's correlations between log2 fold changes (logFCs) of expression and centrality across genes are displayed for individual methods. Although the two batches of simulated data sets have induced differential expression, they share the same coexpression network structure, leading to differential expression but similar centrality measures of the genes across the two batches. (D) Proportion of times each module is identified by each method. A gene module was deemed as identified by a method if it has a Jaccard index overlap of at least 0.5 with WGCNA estimated modules of the method. The table below the bar plot provides the average sparsity, expression, and noise ratio of genes in each module.
Although Dozer does not assume a Gamma expression model, we further evaluated its robustness under additional data-generative settings. Specifically, we compared Dozer with the other state-of-the-art methods using scDesign2 (Supplemental Sec. S2.3; Sun et al. 2021). scDesign2 chooses the marginal distributions of the genes adaptively among a larger set of count distributions (Poisson, negative binomial, zero-inflated Poisson, and zero-inflated negative binomial) and uses a Copula model to generate gene–gene correlations. In experiments with scDesign2, Dozer showed robustness to the violation of the Poisson-Gamma assumption and outperformed other methods (Supplemental Figs. S11, S12).
Next, we designed a second batch of simulations (simulation setting B) to evaluate potential confounding between changes in expression and changes in network centrality of the genes. This type of confounding can lead to inaccurate inference. For example, an increase in expression of a group of genes owing to perturbation might be inferred as having interactions with larger groups of genes owing to biased correlation estimation. Each simulation instance contains two data sets generated from the same underlying network (i.e., same gene–gene correlation matrix) but with different gene expression levels controlled by the shape and scale parameters of the Gamma-Poisson distribution. After constructing coexpression networks with each method, we quantified, for each gene, the log2 fold change (logFC) of centrality between the two data sets in the same simulation instance. We also quantified the logFC of gene expression across the same twodata sets for each gene. Figure 2C displays the associations of these twofold changes as quantified by the Spearman's correlation across the genes. Because the centralities are estimated from data originating from the same underlying network, methods robust to differences in expression levels are expected not to yield significant associations between logFC of gene centrality measures and expression. We observe that bigSCale2 and Dozer shows relatively small correlations between differential expression and centrality measures. In contrast, the logFCs of gene expression and centrality have strong positive associations for SAVER, SCT.Pearson, and Noise.Reg and strong negative association for SCT.Spearman. This result aligns with the upward bias of edges toward high expression genes for methods SAVER and SCT.Pearson and the oversmoothing issue with SCT.Spearman observed in the FDR analysis.
Finally, we evaluated the methods in terms of their coexpression module identification performances (simulation setting C). The ground-truth modules, which were balanced with 80 to 100 genes per module, were set as WGCNA (Langfelder and Horvath 2008) computational modules with the true network as input to the WGCNA. The table in Figure 2D summarizes the general characteristics of the modules in terms of the sparsity, expression, and noise ratio, calculated by averaging over genes in each module. Each method's coexpression modules were derived by WGCNA. In a simulation instance, a true module was considered as identified by a given method if one of its coexpression modules overlapped with the true model with a Jaccard index of at least 0.5 (overall results appeared robust to this choice of cutoff). Figure 2D displays the proportion of times the modules are identified by each method and indicates that modules with high noise ratios (modules 4, 5, and 6 with noise ratios greater than 0.65) are harder to identify for all the methods. Dozer shows a robust performance for all the modules with an average noise ratio less than 0.75. None of the methods were able to consistently identify module 6 because the correlation among genes with such high noise ratios shrank toward zero, leaving these genes as singletons in the network. SAVER, Noise.Reg, and MetaCell are also challenged in identifying module 1 despite the lowest noise ratio of this module. A closer investigation revealed that, without correction, these genes tend to have high spurious correlations with the other genes. As a result, genes in module 1 were merged with genes in other modules, which hindered the identification of module 1. Overall, Dozer is more robust in identifying modules with an average accuracy of 0.74 across the modules, 68% higher than the second-best method SCT.Pearson.
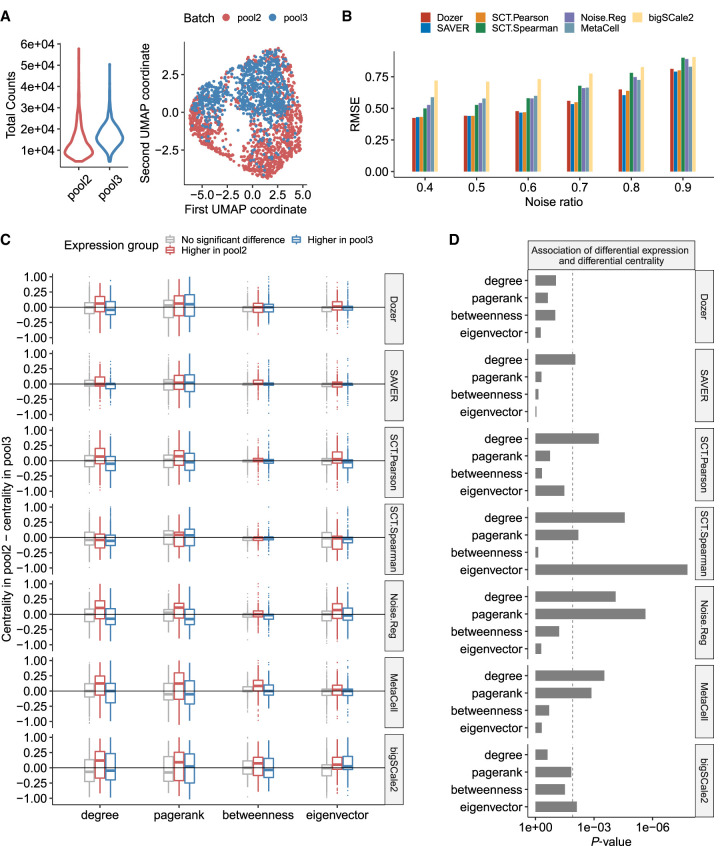
Dozer is robust against sequencing depth differences of the scRNA-seq data sets
In large-scale scRNA-seq studies, data are typically generated in separate batches owing to logistical constraints, for example, at different times, laboratories, with different library preparation technologies, and so on. Although this can cause systematic differences in expression between batches and requires correction (Tran et al. 2020) before the data can be analyzed jointly, it further provides an opportunity to evaluate the impact of sequencing depth on estimated network features as the underlying coexpression networks of these batches are realizations from the true coexpression network. Although we evaluated the robustness of estimated network features against differential expression with simulation setting B in the previous section, we reasoned that the multiple batches setting can further corroborate our findings with actual data. Figure 3A displays sequencing depths of two biological replicate data sets sequenced in different batches (labeled as pool2 and pool3) from the Jerber_2021 (Jerber et al. 2021) study. Median total read counts in pool2 is 70% of the median total counts in pool3. There is also a clear separation of cells in the two batches in the UMAP (Becht et al. 2019) visualization (Fig. 3A). We used gene–gene correlations estimated from pool3 (with the higher depth) as the reference to quantify the effect of lower sequencing depth on correlation estimation. Specifically, we evaluated the root mean square error of the absolute correlations (Fig. 3B) to quantify the similarity of the correlations from the two batches. Dozer, SAVER, and SCT.Pearson yielded lower root mean squares than other methods regardless of the noise ratios of the genes, indicating robustness of estimated correlations against sequencing depth differences of the scRNA-seq data sets.
Figure 3.
Robustness in coexpression networks against sequencing depth differences of the scRNA-seq data sets. (A) Distribution of sequencing depths across cells and UMAP visualization of the cells in biological replicates pool2 and pool3. (B) The root mean square error (RMSE) of absolute correlation estimates in pool2 using the higher depth pool3 as the gold standard. Before computing the RMSE, the absolute correlations in pool2 and pool3 were scaled by the standard error of all absolute correlations. (C) Genes are separated into three groups as “higher expression in pool2,” “higher expression in pool3,” and “no significant differential expression” using an adjusted P-value threshold of 0.05. For each gene group, the boxplot displays the differences in gene centrality scores between the pool2 and pool3 data sets. Methods robust to sequencing depth differences have centrality differences centered at zero regardless of the gene group. (D) P-values from testing the association of differential expression and differential centrality. Dashed line is the Bonferroni-corrected P-value threshold of 0.05/4.
Next, we considered the impact of expression differences owing to batch effects on gene centrality estimates from the coexpression networks. With population-scale data, a key downstream analysis is to detect network-level differences associated with phenotypic or genotypic variation (van der Wijst et al. 2018). If a network construction method is biased by the actual expression levels of the genes, differential expression will impact the detection of network-level changes. We reasoned that although the differences in sequencing depths or other experimental artifacts would lead to differentially expressed genes between the two batches, robust estimation of gene correlations should not result in genes with differential network centrality measures. A differential expression analysis with DESeq2 (Love et al. 2014) identified 231 (270) genes with significantly higher expression in pool2 (pool3) compared with pool3 (pool2). The choice of DESeq2 ensured that all the methods had access to the same set of differentially expressed genes. We then assessed if a spurious change in expression is performed to a change in gene centrality measures. This revealed significant associations between differential expression and centrality, including degree, pagerank, and eigenvector centralities, for all methods except Dozer (Fig. 3C,D). Overall, Dozer provides the most protection against the carry-over effects from changes in expression to centrality.
Personalized coexpression network analysis of donor iPSC lines under neuronal differentiation identifies genes central to differentiation efficiency
The Jerber_2021 (Jerber et al. 2021) study, with multiple human induced pluripotent stem cell (iPSC) lines differentiating toward a midbrain neural fate, is one of the pioneering population-scale genetic studies with scRNA-seq profiling. The neuronal differentiation efficiency score is quantified for each donor iPSC line in the original study as a phenotypic trait. We specifically focused on the P_FPP cells to discover genes related to neuronal differentiation efficiency and evaluate the resulting coexpression networks from different methods with external data sources.
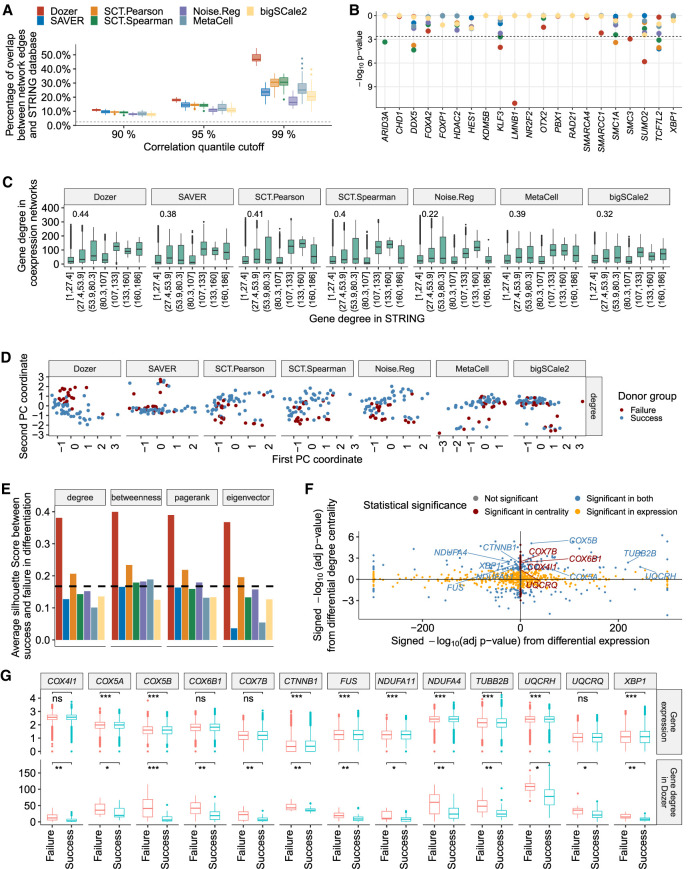
For each donor, we constructed a gene coexpression network, by keeping edges with absolute estimated correlations greater than the xth percentile, x ∈ {90, 95, 99}, of all of the absolute estimated correlations. We first evaluated the edges identified in the coexpression networks with the STRING protein–protein interaction database (Supplemental Sec. S1.3; Szklarczyk et al. 2021). Across all the methods, a larger fraction of network edges overlapped with the interactions in the STRING database with a higher threshold (Fig. 4A), suggesting that the gene pairs with large absolute correlations are better supported by the corresponding protein–protein interactions. Overall, edges from Dozer network had the highest validation rate with the STRING database for all thresholds, with an average increase of 13%, 25%, and 56% in the percent validations, for the percentile thresholds of 90%, 95%, and 99%, compared with the next best method (one-sided Wilcoxon rank-sum test P-values for Dozer vs. the next best method in Fig. 4A are 1.1 × 10−11, 3.9 × 10−12, and 4.1 × 10−12 under the three thresholds, respectively).
Figure 4.
Coexpression network analysis of the Jerber_2021 multiple donor scRNA-seq data. (A) The percentage of coexpression network edges validated by the STRING protein interaction database across donors. The x-axis denotes the percentile cutoff for thresholding the estimated correlations. The dashed line is the percentage of randomly selected gene pairs validated in the STRING database. The P-values from one-sided Wilcoxon rank-sum test between Dozer and the second-best method for the three percentile thresholds are 1.1 × 10−11, 3.9 × 10−12, and 4.1 × 10−12, respectively. (B) Transcription factors (TFs) enriched in gene coexpression networks of the donors, evaluated using TF–target pairs documented in the hTFtarget database. (C) Comparison of estimated gene degrees from coexpression networks with gene degrees in the STRING database. (D) Visualization of donor-specific networks using the first two principal components of the network degree centralities. (E) Average silhouette scores from the first two principal components of the two groups of donors based on their gene centralities in neuronal differentiation. The dashed line represents the average silhouette score based on principal components of donors’ bulkified expression. (F) Comparison of differential degree centralities of the genes from the Dozer coexpression networks with their differential expression. The x-axis displays the signed –log10 (adjusted P-value) from differential expression with positive (negative) values denoting higher (lower) expression in the failure group. The y-axis denotes the signed –log10 (adjusted P-value) from differential degree centrality with positive (negative) values showing higher (lower) centrality in the failure group. (G) Comparison of the degree centralities from the Dozer coexpression networks and expressions of select genes associated with “neurodegeneration” across the donors in the two neuronal differentiation efficiency groups. Significance levels are coded as follows: (*) adjusted P-value < 0.05, (**) adjusted P-value < 0.01, (***) adjusted P-value < 0.001.
Next, we used hTFtarget (Zhang et al. 2020b), a database of human TF targets, for further validation of the edges connected to TFs. Specifically, we tested whether the targets of TFs were enriched among the edge genes of TFs in the coexpression networks (Supplemental Sec. S1.4). Four TFs showed significant enrichment in the Dozer networks (Fig. 4B), whereas most networks did not yield any enrichment (MetaCell, Noise.Reg, bigSCale2), and SAVER, SCT.Spearman, and SCT.Pearson resulted in one, four, and three TFs enriched for edges by their hTFtarget targets, respectively. Of these, lamin B1 (LMNB1), which is identified only by Dozer, modulates differentiation into neurons (Mahajani et al. 2017). SMC3 is a member of the cohesion complex, which plays a critical role in regulating changes in chromatin structure and gene expression (Ball et al. 2014). In a study with Smc3-knockout mice, reduced cohesion expression in the developing brain resulted in alterations in gene expression, which subsequently caused distinct and abnormal neuronal characteristics (Fujita et al. 2017).
We next turned our attention to gene centrality measures estimated from these coexpression networks. First, to validate gene degrees, we compared the network gene degrees in the coexpression networks and in the networks formed by gene pairs with interactions in the STRING database (Fig. 4C). The Spearman's correlation between the degrees of the genes in coexpression network and the STRING network is the highest for Dozer, at a level of 0.44. This reinstates that Dozer does not sacrifice accuracy of gene degrees for edge accuracy.
In the Jerber_2021 (Jerber et al. 2021) study, the donors are divided into two groups in terms of their neuronal differentiation efficiency, namely, neuron differentiation failure (neuronal differentiation efficiency <0.2) and neuron differentiation success (neuronal differentiation efficiency ≥ 0.2). We asked whether network gene centrality measures can highlight differences between the two phenotype groups. After estimating a variety of gene centrality measures from each donor's coexpression network, we visualized the separation of the two donor groups with principal components (PCs) and assessed the level of separation with the silhouette score (Rousseeuw 1987), higher positive values of which indicate good separation between the two groups (Methods). Centrality measures estimated from the Dozer coexpression networks show a clear separation between the two neuronal differentiation efficiency groups in the PC plots for all the four centrality measures (Fig. 4D; Supplemental Fig. S13). The silhouette score associated with Dozer is also the largest, with an average of 0.38 among the four centrality types (Fig. 4E).
Centrality measures from coexpression networks can lead to identification of biologically relevant genes that might be missed by standard analysis of differential expression and clustering. To this end, we tested for differences in gene centrality measures of the two phenotype groups and compared the differential centrality and differential expression quantification of the genes (Supplemental Sec. S1.5). This analysis identified 51 genes that showed differential degree but equal expression between the success and failure groups at an FDR of 0.05 (Fig. 4F; for the other centrality measures, see Supplemental Fig. S14). We performed gene set enrichment analysis (Supplemental Sec. S1.6) separately on KEGG pathways and GO biological processes for genes that showed significantly higher centralities in the failure group (adjusted P-value < 0.05 and logFC(failure/success) > 0) and the success group (adjusted P-value < 0.05 and logFC(failure/success) < 0). We identified a set of 13 genes (COX5A, COX5B, COX4I1, COX6B1, COX7B, CTNNB1, FUS, NDUFA11, NDUFA4, TUBB2B, UQCRH, UQCRQ, XBP1) that showed significantly higher centrality in the failure group and were associated with “Pathways of neurodegeneration.” This set of genes does not appear to be identifiable through differential expression analysis, with four genes showing higher expression in the failure group, five genes with higher expression in the success group, and four genes yielding equal expression in both groups (Fig. 4F,G). Furthermore, this set of genes overlapped with gene sets enriched in neurodegenerative diseases, such as Parkinson's disease, amyotrophic lateral sclerosis, and Alzheimer's disease (AD), as well as GO terms related to mitochondrial electron transport (Supplemental Figs. S15–S17). The biological relevance of the latter is supported by the growing body of literature that suggests that mitochondria are central regulators in neurogenesis (Arrázola et al. 2019; Brunetti et al. 2021). Mitochondrial dysfunction, especially in the electron transport chain, is responsible for neurodegenerative diseases (Guo et al. 2013; Hroudová et al. 2014; Kausar et al. 2018). We next asked whether bigSCale2, which had been used for identifying genes with coexpression network centrality differences (Iacono et al. 2019), could similarly reveal biologically relevant gene groups with differential centrality between the two phenotype groups. Although bigSCale2 identified a total of 11 genes with differential centrality across the four centrality measures (with only two genes in the gene set not showing differential expression), this set of genes lacked enrichment for neuronal differentiation GO and KEGG terms.
Differential analysis of personalized coexpression networks uniquely identifies a dense innate immune response module in the AD diagnosis donors
The Morabito_2021 data set (Morabito et al. 2021) profiled transcriptome of nuclei isolated from the prefrontal cortex (PFC) of postmortem human tissues from 11 late-stage AD subjects and seven age-matched cognitively healthy controls. A coexpression analysis is performed in the original paper with single-nucleus consensus WGCNA (scWGCNA) using both single-cell and bulk RNA-seq data. To directly compare donor-specific coexpression networks with the scWGCNA results, we started with the same set of 1252 genes that scWGCNA used leveraging both the snRNA-seq and bulk RNA-seq data. When using only the snRNA-seq data, 682 of these were filtered either because of their zero expression in one or more donor data sets or because of high gene noise ratios (Supplemental Fig. S18). We primarily focused on oligodendrocytes because this cell type constituted, on average, 60% of donor cells, hence providing a sizable sample per donor.
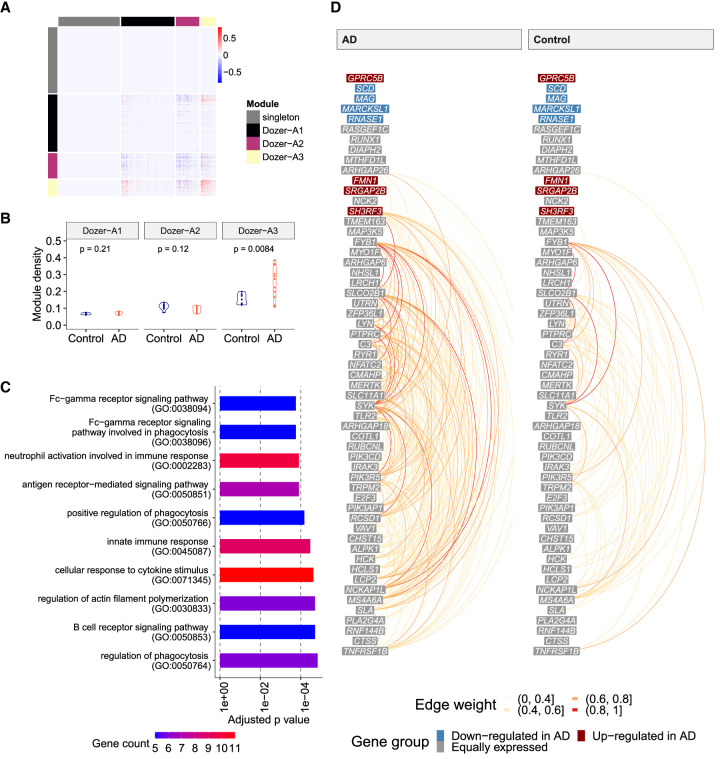
We first established that donor-specific coexpression networks are biologically sound by a largest-clique, that is, a largest fully connected subnetwork, analysis that was validated in the independent snRNA-seq data set from Nagy et al. (2020) (Supplemental Sec. S4.1; Supplemental Fig. S19). Next, to identify subnetworks, that is, modules, driving the variation of coexpression networks between the AD and control diagnoses, we constructed a “difference network” by first averaging the donor-specific unsigned Dozer networks within the AD and the control diagnoses separately and then taking the differences of these two averaged networks. Hierarchical clustering of the difference network yielded three gene modules: Dozer-A1, Dozer-A2, and Dozer-A3 (Fig. 5A). Taking advantage of the coexpression networks at the donor level, we asked whether densities (i.e., connectedness) of these modules varied between the two diagnoses and observed that module Dozer-A3, with 57 genes, has significantly higher module density in AD compared with the control diagnosis (t-test P-value of 0.0084) (Fig. 5B). We found that the majority of the GO terms enriched in this module are related to innate immune response (Fig. 5C). We next explored the expression patterns of the genes in Dozer-A3 (Fig. 5D; Supplemental Figs. S20–S22). It is evident, especially in the hive plots of Dozer-A3 (Fig. 5D; Supplemental Fig. S22), that the genes with high degrees are not expressed at high levels. More critically, genes driving the differences in the connectivities of the AD and control groups are also not differentially expressed. Further investigation into these genes revealed that they tend to coexpress in a small group of immune oligodendrocyte cells (immune ODCs) (cluster ODC13 in Morabito et al. 2021) and suggested immune ODCs as the primary source driving the module density differences between the AD and control groups. This is corroborated by the significant coexpression levels of Dozer-A3 module genes in cells of immune ODCs (Supplemental Fig. S23). Furthermore, the association between the coexpression of Dozer-A3 genes and whether a cell is an immune ODC cell is stronger among the AD diagnosis compared with the control (Supplemental Sec. S1.7; Supplemental Fig. S24). To further validate that immune ODCs are driving the discovery of Dozer-A3, we repeated the difference network analysis with Dozer with a restricted ODC cell population excluding the immune ODCs and observed that the immune-related gene module Dozer-A3 was no longer discoverable (Supplemental Fig. S25). This corroborated the driver role of immune ODCs in the original Dozer-A3 module.
Figure 5.
Coexpression network analysis of the Morabito_2021 multiple donor scRNA-seq data. (A) Heatmap of the “difference network” (average of AD networks − average of control networks). Genes are ordered by gene modules (singleton, Dozer-A1, Dozer-A2, Dozer-A3), which are obtained by hierarchical clustering on the “difference network” (Methods). (B) Violin plots of module densities for AD and control donor networks. Module density is a function of the average absolute correlation of gene pairs in the given module (Methods). (C) Bar plot of GO enrichment terms for module Dozer-A3. (D) Hive plot visualization of module Dozer-A3 in AD and control groups. Genes are ordered from high (top) to low (bottom) by their average expression across all donors. Genes are further divided into three groups as “down-regulated in AD,” “up-regulated in AD,” and “equally expressed” according to their differential expression status between the control and AD diagnoses. The arcs between the genes in this linear layout depict the edges in the average networks of AD (left) and control (right) donors, with colors representing edge weights.
We next performed differential centrality analysis for degree, pagerank, betweenness, and eigenvector centralities to infer the key genes in the Dozer-A3 module. This revealed that TLR2, which encodes a primary receptor for Alzheimer's amyloid beta-peptide to trigger neuroinflammatory activation (Liu et al. 2012), has significantly higher degree centrality in AD than in the control (Supplemental Fig. S26). In the broader context, innate and adaptive immune responses play a key role in the pathological processes of AD as well as other neurodegenerative diseases (Shi and Holtzman 2018). Recent studies have shown that oligodendroglia becomes immune-reactive in a mouse model of multiple sclerosis (Kirby et al. 2019) and in human iPSC-derived oligodendrocytes from Parkinson's disease and multiple system atrophy patients (Azevedo et al. 2022), providing further support for the discovery of this module by Dozer.
Repeating the same type of difference network analysis with the other methods revealed that Dozer, SAVER, and SCT.Pearson are the only three network construction methods that unearthed coexpression modules with densities significantly correlated with diagnoses and significantly enriched GO terms (Supplemental Figs. S27–S32). The three modules that show changes in densities between diagnoses are Dozer-A3, SAVER-A3, and SCT.Pearson-A3. These three modules from independent methods are supportive of each other, as they share 23 genes (Supplemental Fig. S33) and as the common set of genes are significantly enriched for the GO term “innate immune response” (Supplemental Fig. S34).
Finally, we asked whether the association of the diagnosis with the coexpression networks of innate immune response genes is also revealed with the scWGCNA analysis (Morabito et al. 2021) that combines data from all donors to construct a single coexpression network. Although Morabito et al. (2021) observed that the cell-type composition of late-stage AD shifted toward more immune ODCs, the eigengene expression of their immune response–related gene module (OM3) within oligodendrocytes is not correlated with the AD diagnosis in the scWGCNA analysis (Fig. 8 of Morabito et al. 2021). As a consensus clustering approach, scWGCNA used external bulk RNA-seq data from the UCI (Morabito et al. 2021) and ROSMAP (Mostafavi et al. 2018) cohorts to mitigate the issue of sparsity in expression data. Nevertheless, the inclusion of these external data may have obscured signals that are unique to single-cell RNA-seq. To elucidate the factors that contribute to the differences in findings between scWGCNA and personalized gene coexpression networks, we reimplemented scWGCNA on data set Morabito_2021, following the gene filtering procedure used in Dozer to exclude genes with high sparsity and noise ratios. Our implementation considered two comparable variants of scWGCNA as follows: (1) scWGCNA-I, data were combined from donors within a diagnosis group to construct diagnosis-specific coexpression networks, and then the consensus modules were computed; and (2) scWGCNA-II, a difference network between the diagnoses from diagnosis-specific coexpression networks was constructed, and modules on the difference network were inferred. scWGCNA-I follows the prescribed scWGCNA pipeline of Morabito et al. (2021) with a small modification by using diagnosis-specific networks, whereas scWGCNA-II is more similar to our difference network analysis for personalized networks, and it aims to detect modules showing differences in connectivity between diagnoses. A key difference of both of these implementations from our approach is that they pool the donor data before constructing networks; hence, the resulting networks are not at the individual donor level. In these analysis, scWGCNA-I detected three coexpression modules (scWGCNA-brown, scWGCNA-blue, and scWGCNA-turquoise) and left a large group of genes as singletons, that is, deemed as not forming a coexpression module (scWGCNA-gray) (Supplemental Fig. S35). Eigengene analysis of these modules revealed only the scWGCNA-brown module as weakly associated with the AD diagnosis (Supplemental Sec. S1.8; Supplemental Fig. S35). Furthermore, innate immune response genes, discovered in our personalized networks analysis, appeared as singletons, prohibiting them to be identified as enriched within a module. This can be explained by scWGCNA-I's intrinsic focus on modules common to both diagnoses, as a result of which it loses power to detect module-level differences between the diagnoses. scWGCNA-II builds modules on the difference network between the AD and control diagnoses. One of its eight coexpression modules (scWGCNA-A4) harbors the innate immune response genes. However, expression of none of the module eigengenes of scWGCNA-II has a significant association with the AD diagnoses (Supplemental Fig. S36). In fact, visualization of the Dozer-A3 genes within the scWGCNA networks of the AD and control groups does not show any discernible differences between the two (Supplemental Fig. S37). scWGCNA-II pools cells from all donors and loses the ability to directly test differences in module connectivity between diagnoses through module density. This further reinstates that although module eigengene expression is representative of module gene expression level, when the differences in the expression levels between the diagnoses are small, it might hinder the association of the module with the diagnosis. Constructing personalized coexpression networks, as we do with Dozer, enables a formal testing framework for downstream association analysis with the modules.
Discussion
Excess sparsity and measurement error in scRNA-seq data sets distort gene–gene correlation estimation, introducing downward bias for genes with low expression and in low-depth data sets. The distortion of estimated correlations has a major influence on the construction of coexpression networks, by uplifting high expression genes to be network hub genes and confounding differential expression with changes in coexpression networks. Dozer, built on a Poisson measurement model, provides correction for gene–gene correlation estimates and offers a gene-specific noise ratio score to reliably filter genes for coexpression network analysis. In our analysis, no restrictions were put on the expression model, that is, distributional assumption on gi in Equation 1, except for simulation purposes. A large variety of observation models, including negative binomial (Love et al. 2014; Huang et al. 2018), zero-inflated negative binomial (Risso et al. 2018), and other flexible models used by Wang et al. (2018), can be accounted for by combining Poisson measurement error model with Gamma, point Gamma, or point exponential family expression models (Sarkar and Stephens 2021). Although the Poisson measurement model usually suffices in practice, in the cases in which a more complex measurement model is more adequate, a gene correction factor should be derived accordingly to adjust for the underestimation of absolute corrections owing to measurement error.
For network validation, instead of solely focusing on network edges, that is, highly correlated gene pairs, we also validated a broader set of network features used in downstream inference, including gene modules and gene centrality measures. We observed a significant discrepancy between edge accuracy and centrality/module accuracy. Most notably, our computational experiments revealed that an upward bias toward high expression genes could lead to an increase in edge accuracy; however, this comes at the cost of decreased accuracy for identifying high centrality genes among low expression genes. This broadly suggests that benchmarking studies of coexpression networks focusing solely on network edges may be inadequate. Both data-driven simulation and computational experiments showed Dozer's superior performance in mitigating the sequencing depth differences between donor-specific data sets and faithfully preserving the coexpression network structures both at edge, centrality, and module levels, in the presence of expression differences owing to technical reasons.
Construction of donor-specific networks enables exploring association of multiple classes of network features with phenotype or genotype information. In contrast, with the existing scWGCNA analysis that pools individual level data before network construction, only the expression of eigengenes of modules can be associated with subject-level information. The Morabito_2021 reanalysis showcased how constructing donor-level coexpression networks can discover a module of genes with significantly different module density between the diagnosis groups even when these genes are coexpressed only in a small subpopulation of the cells and are not differentially expressed between the diagnosis groups. Similarly, in the analysis of Jerber_2021, we identified a group of neurodegeneration-associated genes with differences in network centrality between the donors that succeeded or failed in neuronal differentiation. However, a considerable proportion of these genes were not differential expressed between the two phenotype groups. This further highlights that donor-specific coexpression networks offer an opportunity to quantify a broader set of network traits. In our implementation, we integrated four commonly used centrality measures in Dozer, namely, degree, pagerank, betweenness, and eigenvector centrality. Degree centrality detects hub genes with extensive connections (Prifti et al. 2010; Serin et al. 2016), whereas pagerank and eigenvector centrality pinpoint influential genes (Mistry et al. 2017; Iacono et al. 2019). In contrast, elevated betweenness values signify genes functioning as bottlenecks for information transfer (Prifti et al. 2010; Serin et al. 2016). The framework for calculating these centrality measures is general and can be extended to include other customized centrality measures. We recommend exploring multiple centrality measures because their significance depends on the topology of the coexpression network in specific biological contexts.
In conclusion, Dozer is tailored for coexpression analysis with population-scale scRNA-seq data sets and enables further downstream analysis such as network differences between different phenotypic groups with the constructed individual coexpression networks. We envision that similar differential analysis might be of interest between coexpression networks of different cell types. Alternatively, one can formally test whether coexpression networks of different cell types are the same by using recent theoretical developments on testing of large dimensional correlation matrices (Zheng et al. 2019). Additionally, we expect that Dozer-derived coexpression networks, when combined with genetic information, can facilitate network QTL analysis.
Methods
Gene–gene correlations in the Poisson measurement model
Let random variable gj represent the expression level of gene j, ℓ represent cell sequencing depth, and X represent cell-level covariates. The UMI count of gene j, Yj, follows a Poisson measurement model (Sarkar and Stephens 2021),
| (5) |
The correlation between the expression levels of gene j and k, cor(gj, gk), is the signal we aim to recover for quantifying coexpression between genes j and k.
Let denote the size factor per cell and represent the normalized counts. Under the conditional independence of the observed UMI counts given the true expression levels and cell sequencing depths
| (6) |
we have
| (7) |
| (8) |
Because of the inflation in the compared with the true variance var(gj), the proxy is an underestimate of cor(gj, gk) in terms of its magnitude. The deviation between the true expression variance of gene j and the variance of normalized expression depends on the ratio , which we denote as gene j’s “noise ratio,” indicating the quality of gene j’s normalized expression. Let , and then the expression correlation of genes j and k can be represented through the following equation with the correction factors:
| (9) |
Estimation of the gene correction factors in the Poisson measurement model
Given the UMI counts Yj and sequencing depths of the cells ℓ, we fit the Poisson measurement model in Equation 5 and estimate {βj}j via a Poisson generalized linear model,
| (10) |
The cell size factor is estimated by plugging in as . The numerator and denominator of the noise ratio are estimated through sample mean and variance with weights w as
| (11) |
Similarly, the correlation of normalized counts is estimated through sample correlation:
| (12) |
where μw( · ), , and ρw( · , · ) denote weighted sample mean, variance, and correlation with weights w = ℓ, to account for the heteroscedasticity of Yj/ℓ conditional on ℓ. Without loss of generality, the setting with βj = 0 provides further insights into this apparent heteroscedasticity. We express the var(Yj/ℓ|ℓ) by using the law of total variance,
| (13) |
and observe that the conditional variance of Yj/ℓ given ℓ decreases with depth ℓ. The weight, inspired by the weighted least-square approach, is proportional to . The second term in the denominator of the weight is the overdispersion parameter of gene j. To avoid the extra variability introduced by estimation of overdispersion, we use ℓ as weights for cells.
The correction factors Sj, cannot be reliably estimated directly by plugging in corresponding because the resulting plug-in estimator can be arbitrarily large for sparse genes with noise ratios close to one. To robustly estimate the gene correction factor Sj, we opted to balance the bias and variance by shrinking the estimator of Sj toward one when its variance is large. Given a plug-in estimator of correction factor Sj with the estimated noise ratio as
| (14) |
we obtain an initial plug-in estimator of the variance of as
| (15) |
Because the variance of increases with its mean, we consider a penalized correction factor and obtain a shrinkage estimator as
| (16) |
Finally, to borrow information across genes, we fit a local polynomial regression of with the R (R Core Team 2021) function loess. The fitted function is naturally unimodal, because for genes with a noise ratio close to one, is close to one. However, the true value of Sj increases with Rj. To turn it into a monotone function, we set the turning point , where is the estimated local polynomial regression function, and set the final estimate that we refer to as truncated shrinkage estimator as
| (17) |
Sequencing depth estimation
Sequencing depth in cells is typically estimated by the total UMI counts per cell (Vallejos et al. 2017). Normalizing gene counts by the total UMI counts imposes a “sum to one” constraint on the normalized expression. This constraint can result in negative correlations between highly expressed genes. For instance, in a simulation setting without any correlation between gene pairs, this simple normalization process induced a negative correlation of −0.07 between pairs of genes, which accounted for 10% of the total UMI counts (Supplemental Fig. S38). Prior research has suggested approaches for clipping influential genes, such as the “median of ratios” estimator proposed by Love et al. (2014) and “trimmed mean of M values” of Robinson and Oshlack (2010). Following these ideas, we consider “trimmed total UMI count” as an estimator designed to mitigate the influence of highly expressed genes. First, we compute the expression proportion of each gene across all cells. These proportions serve as gene weights. Subsequently, we normalize the UMI counts for each gene, ensuring an average value of one. We then set a threshold for gene weights to prevent any single gene from dominating the sequencing depth estimation (e.g., empirically set as 0.02 as this reduced the apparent negative correlation to −0.01 in the simulation setting of Supplemental Fig. S38). By limiting the weights of highly expressed genes to the threshold value, we effectively trim their contributions. Finally, we compute the trimmed total UMI count for each cell by summing the weighted UMI counts across all genes as its estimated sequencing depth.
Next, to determine whether a global normalization factor (i.e., same for all the genes) is sufficient for normalization, we perform a diagnostic analysis. Global normalization factors are used to account for a presumed count-sequencing depth relationship that is consistent across all genes. However, when genes of different expression levels grow disproportionately with sequencing depth, normalization through global scale factors can result in overcorrection for weakly and moderately expressed genes (Bacher et al. 2017). As part of the diagnostic process, raw gene counts and trimmed total UMI counts are divided by their mean to achieve an average value of one. Then, for each gene j, scaled gene counts are regressed on scaled trimmed total UMI counts as
| (18) |
and the slope is estimated from this regression using cell-level data. The diagnostic plots visualize (1) the distribution of these estimated slopes of genes across multiple expression groups and (2) distribution of the correlations between the expression of genes normalized with the trimmed total UMI counts. Proportionate growth yields regression slopes around one and correlations near zero, whereas disproportionate growth causes regression slopes and correlations to diverge from these values. When disproportionate growth is detected for a given data set, Dozer adopts a regression-based gene-specific cell size factor approach for sequencing depth adjustment. This involves first grouping genes into K bins based on their raw mean expression quantiles. Next, the trimmed total UMI counts of each gene group, denoted as , are used as regressors in a Poisson regression to facilitate gene-specific adjustment for sequencing depth. More specifically, for gene j with UMI counts Yj, we conduct a Poisson regression analogous to Equation 5 while replacing the global cell size factor ℓ with a set of covariates L,
| (19) |
where X represents cell-level covariates as before (e.g., batch labels, percentage of mitochondrial genes), and L = [logl1, …, loglK] denotes the design matrix that harbors the trimmed total UMI counts of each gene group for each cell. K is chosen incrementally by starting from one and gradually increasing it up to 10 until the mode of the correlation between normalized expression and trimmed UMI drops below 0.1 for all gene groups. The estimated cell size factor for gene j is then given by
| (20) |
An illustration of how these diagnostics plots and the resulting gene-specific size factors work are provided in Supplemental Figure S39 for two donors from the Jerber_2021 data set. The right panels of the Supplemental Figure S39, A and B, display the density of correlations between expression normalized with the gene specific cell size factors and trimmed total UMI counts across all the genes. These plots highlight how the apparent correlations between the global size factor and expression normalized with the global size factor are reduced when gene-specific size factors are adopted.
Simulations
Three simulation settings were considered to evaluate the performances of the coexpression network construction methods in recovering network edges and gene centrality measures (setting A), reducing false discoveries in differential network centrality measures in the presence of differential expression (setting B), and detecting modules (setting C). The following base procedure was used in settings (A–C) to generate the gene expression Yij for gene j, , in cell i, . First, a G-dimensional relative gene abundance vector g was generated through a multivariate Gamma distribution, with shape parameters v, scale parameters u, and correlation matrix Σ. The sequencing depth ℓi of cell i was simulated from a log normal distribution Lognormal(lℓ, sℓ). The UMI count for each gene j was sampled independently from Poisson distribution for cell i as . Under this simulation framework, Σ specifies the coexpression structure of the genes.
To ensure that these simulations yield data with high fidelity to actual population-scale scRNA-seq data, the Cuomo_2020 scRNA-seq data (Cuomo et al. 2020), which offer high sequencing depth per cell (averaging ∼530,000 total counts per cell) was used to generate realistic gene–gene correlations. These correlations were then combined with marginal expression count distributions from Jerber_2021 (Jerber et al. 2021). Realistic data sets similar to those of Jerber_2021 and Morabito_2021 were simulated by modulating the library sizes. The shape and the scale parameters vj, uj for gene j were estimated by
| (21) |
The scaling in Equation 21 for the scale parameter ensures that the total counts in cell i are approximately equal to its sequencing depth ℓi. The parameters (lℓ, sℓ) of the sequencing depth distribution were estimated by fitting a log normal distribution to the total read counts. The correlation matrix Σ was estimated through a SCTransform normalized expression matrix of the data set Cuomo_2020.
Further details on the parameters of the simulation settings A, B, and C are as follows.
Setting A
This setting considered four average sequencing depth levels (1500, 3000, 6000, 12,000) and four sample sizes (125, 250, 500, 1000 cells). For each depth and sample size combination, 10 simulation replications were generated from the base model described above. When generating coexpression networks, four noise ratio thresholds, namely, 0.6, 0.7, 0.8, and 0.9, were used for gene filtering. Gene pairs with the top 1% of absolute correlations and genes with the top 10% gene centrality measures were set as true edges and true high centrality genes. The same quantiles were applied to estimated networks for AUPR and F1 score calculations.
Setting B
For each simulation instance out of 20 replications, two data sets with the same gene–gene correlation structure but different gene expression levels were generated by reshuffling the Gamma shape and scale vectors. Gene pairs with the top 1% of absolute correlations were used to set the network edges. Both the logFC of gene expression and the logFC of centrality were computed across the two data sets of the simulation instance. To avoid taking log of zeros, the first percentile of positive centrality values across all genes was added to centrality values before taking the log. The Spearman's correlation between logFC in expression and logFC in centrality was computed to assess the impact of differential expression on detecting spurious differential centrality.
Setting C
Across 20 simulation replications, six gene modules, with balanced module sizes of 80 to 100 genes and large differences in average gene noise ratios, were simulated with a block diagonal correlation matrix, with six gene modules and 2434 singletons. Module detection was performed with WGCNA (with default parameter settings) that took as input the estimated correlation matrices to generate modules. Module detection performances were quantified with the Jaccard index between the inferred and the true gene modules after excluding singletons. If a true gene module had a Jaccard index of 0.5 or larger with an inferred gene module, it was deemed as detected for the purposes of quantifying the empirical probability of detecting gene modules.
Computation of network metrics and gene centrality measures
Thresholding correlations for edges and network centrality measures of genes
Unless otherwise specified, hard-thresholding was adapted for keeping edges between the genes in the coexpression networks and labeling genes based on their network centrality measures. Genes i and j were set to be connected with an edge in the coexpression network if the absolute value of their estimated expression correlation was larger than threshold τ. τ was set using the percentiles of the absolute values of the correlations as specified in the analyses throughput the paper.
Centrality measures in coexpression networks
Four centrality measures, namely, degree, pagerank, betweenness, and eigenvector centrality, were considered to quantify the “importance” of a gene in the coexpression networks. These were computed using the following functions from the R package igraph (https://cran.r-project.org/web/packages/igraph): degree, page_rank, betweenness, and evcent.
Module
Module identification from coexpression networks was performed through the R package WGCNA (Langfelder and Horvath 2008) with the default parameter settings with an exception for the difference networks. The canonical WGCNA module identification pipeline starts out with unsigned coexpression similarity measures between nodes/genes as weights. However, the edge weight between two genes in the “difference network,” with positive and negative values, represents whether the association of the genes is higher in AD or in the control rather than a similarity between the two. To accommodate this, we considered a network transformation while still keeping the hierarchical clustering and dynamic tree cut components of the WGCNA pipeline. Specifically, we let [djk]j,k∈{1,…,G} denote the edge weight between genes j and k in the “difference network.” Then, defines a connectivity similarity for genes j and k. A distance between nodes j and k can be obtained as . Finally, the gene modules of the “difference networks” are inferred by hierarchical clustering and dynamic tree cut algorithm (R function hclust and cutreeDynamic) using the distance matrix with entries Djk and the default parameter settings.
Module density
Module density, D(M), measuring the average connectivity of genes within a module, was calculated as follows for module M with n genes: , where sij ∈ [0, 1] is the absolute correlation between gene i and j.
Largest clique
The largest clique was computed using function largest_ cliques from the R package igraph.
Silhouette score
Silhouette score (Rousseeuw 1987) is used to measure the consistency of gene centrality profile of donors under the same phenotypic group. Silhouette score is computed using function silhouette in R package cluster (https://cran.r-project.org/web/packages/cluster) with Euclidean distance as the distance metric.
Data sets
The single-cell RNA-seq data set Jerber_2021 (Jerber et al. 2021) is available from Zenodo (https://doi.org/10.5281/zenodo.4333872); the data set Cuomo_2020 is available from Zenodo (https://zenodo.org/record/3625024); and the data set Morabito_2021 is available from Synapse (https://www.synapse.org/#!Synapse:syn22079621/). Comprehensive details regarding the description and specific utilization of the three data sets can be found in Supplemental Section S6.
Software availability
The R (R Core Team 2021) package Dozer, along with its vignette, can be accessed at GitHub (https://github.com/keleslab/Dozer), and the Supplemental Code files also provide additional resources for reference.
Supplementary Material
Acknowledgments
This work was supported by National Institutes of Health (NIH) grant HG003747 and a Chan Zuckerberg Initiative (CZI) single-cell data insights grant.
Author contributions: S.K. conceived the project. S.L. and S.K. designed the research and developed the methods. Both authors contributed to the preparation of the manuscript and approved the final manuscript.
Footnotes
[Supplemental material is available for this article.]
Article published online before print. Article, supplemental material, and publication date are at https://www.genome.org/cgi/doi/10.1101/gr.277363.122.
Competing interest statement
The authors declare no competing interests.
References
- Arrázola MS, Andraini T, Szelechowski M, Mouledous L, Arnauné-Pelloquin L, Davezac N, Belenguer P, Rampon C, Miquel MC. 2019. Mitochondria in developmental and adult neurogenesis. Neurotox Res 36: 257–267. 10.1007/s12640-018-9942-y [DOI] [PubMed] [Google Scholar]
- Azevedo C, Teku G, Pomeshchik Y, Reyes JF, Chumarina M, Russ K, Savchenko E, Hammarberg A, Lamas NJ, Collin A, et al. 2022. Parkinson's disease and multiple system atrophy patient iPSC-derived oligodendrocytes exhibit α-synuclein–induced changes in maturation and immune reactive properties. Proce Natl Acad Sci 119: e2111405119. 10.1073/pnas.2111405119 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Azuaje FJ. 2014. Selecting biologically informative genes in co-expression networks with a centrality score. Biol Direct 9: 12. 10.1186/1745-6150-9-12 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bacher R, Chu LF, Leng N, Gasch AP, Thomson JA, Stewart RM, Newton M, Kendziorski C. 2017. SCnorm: robust normalization of single-cell RNA-seq data. Nat Methods 14: 584–586. 10.1038/nmeth.4263 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ball AR Jr, Chen YY, Yokomori K. 2014. Mechanisms of cohesin-mediated gene regulation and lessons learned from cohesinopathies. Biochim Biophys Acta 1839: 191–202. 10.1016/j.bbagrm.2013.11.002 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Baran Y, Bercovich A, Sebe-Pedros A, Lubling Y, Giladi A, Chomsky E, Meir Z, Hoichman M, Lifshitz A, Tanay A. 2019. MetaCell: analysis of single-cell RNA-seq data using K-nn graph partitions. Genome Biol 20: 206. 10.1186/s13059-019-1812-2 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Becht E, McInnes L, Healy J, Dutertre CA, Kwok IW, Ng LG, Ginhoux F, Newell EW. 2019. Dimensionality reduction for visualizing single-cell data using UMAP. Nat Biotechnol 37: 38–44. 10.1038/nbt.4314 [DOI] [PubMed] [Google Scholar]
- Bernardes JP, Mishra N, Tran F, Bahmer T, Best L, Blase JI, Bordoni D, Franzenburg J, Geisen U, Josephs-Spaulding J, et al. 2020. Longitudinal multi-omics analyses identify responses of megakaryocytes, erythroid cells, and plasmablasts as hallmarks of severe COVID-19. Immunity 53: 1296–1314.e9. 10.1016/j.immuni.2020.11.017 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brunetti D, Dykstra W, Le S, Zink A, Prigione A. 2021. Mitochondria in neurogenesis: implications for mitochondrial diseases. Stem Cells 39: 1289–1297. 10.1002/stem.3425 [DOI] [PubMed] [Google Scholar]
- Chen YJJ, Friedman BA, Ha C, Durinck S, Liu J, Rubenstein JL, Seshagiri S, Modrusan Z. 2017. Single-cell RNA sequencing identifies distinct mouse medial ganglionic eminence cell types. Sci Rep 7: 45656. 10.1038/srep45656 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Choudhary S, Satija R. 2022. Comparison and evaluation of statistical error models for scRNA-seq. Genome Biol 23: 27. 10.1186/s13059-021-02584-9 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cuomo AS, Seaton DD, McCarthy DJ, Martinez I, Bonder MJ, Garcia-Bernardo J, Amatya S, Madrigal P, Isaacson A, Buettner F, et al. 2020. Single-cell RNA-sequencing of differentiating iPS cells reveals dynamic genetic effects on gene expression. Nat Commun 11: 810. 10.1038/s41467-020-14457-z [DOI] [PMC free article] [PubMed] [Google Scholar]
- Eraslan G, Simon LM, Mircea M, Mueller NS, Theis FJ. 2019. Single-cell RNA-seq denoising using a deep count autoencoder. Nat Commun 10: 390. 10.1038/s41467-018-07931-2 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Forbes AN, Xu D, Cohen S, Pancholi P, Khurana E. 2022. Discovery of novel therapeutic targets in cancer using patient-specific gene regulatory networks. bioRxiv 10.1101/2022.01.31.478503 [DOI] [Google Scholar]
- Fujita Y, Masuda K, Bando M, Nakato R, Katou Y, Tanaka T, Nakayama M, Takao K, Miyakawa T, Tanaka T, et al. 2017. Decreased cohesin in the brain leads to defective synapse development and anxiety-related behavior. J Exp Med 214: 1431–1452. 10.1084/jem.20161517 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Guo C, Sun L, Chen X, Zhang D. 2013. Oxidative stress, mitochondrial damage and neurodegenerative diseases. Neural Regen Res 8: 2003–2014. 10.3969/j.issn.1673-5374.2013.21.009 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hafemeister C, Satija R. 2019. Normalization and variance stabilization of single-cell RNA-seq data using regularized negative binomial regression. Genome Biol 20: 296. 10.1186/s13059-019-1874-1 [DOI] [PMC free article] [PubMed] [Google Scholar]
- He X, Zhang J. 2006. Why do hubs tend to be essential in protein networks? PLoS Genet 2: e88. 10.1371/journal.pgen.0020088 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hroudová J, Singh N, Fišar Z. 2014. Mitochondrial dysfunctions in neurodegenerative diseases: relevance to Alzheimer's disease. Biomed Res Int 2014: 175062. 10.1155/2014/175062 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Huang M, Wang J, Torre E, Dueck H, Shaffer S, Bonasio R, Murray JI, Raj A, Li M, Zhang NR. 2018. SAVER: gene expression recovery for single-cell RNA sequencing. Nat Methods 15: 539–542. 10.1038/s41592-018-0033-z [DOI] [PMC free article] [PubMed] [Google Scholar]
- Iacono G, Massoni-Badosa R, Heyn H. 2019. Single-cell transcriptomics unveils gene regulatory network plasticity. Genome Biol 20: 110. 10.1186/s13059-019-1713-4 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jeong H, Mason SP, Barabási AL, Oltvai ZN. 2001. Lethality and centrality in protein networks. Nature 411: 41–42. 10.1038/35075138 [DOI] [PubMed] [Google Scholar]
- Jerber J, Seaton DD, Cuomo AS, Kumasaka N, Haldane J, Steer J, Patel M, Pearce D, Andersson M, Bonder MJ, et al. 2021. Population-scale single-cell RNA-seq profiling across dopaminergic neuron differentiation. Nat Genet 53: 304–312. 10.1038/s41588-021-00801-6 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Johnson KA, Krishnan A. 2022. Robust normalization and transformation techniques for constructing gene coexpression networks from RNA-seq data. Genome Biol 23: 1. 10.1186/s13059-021-02568-9 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kausar S, Wang F, Cui H. 2018. The role of mitochondria in reactive oxygen species generation and its implications for neurodegenerative diseases. Cells 7: 274. 10.3390/cells7120274 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kirby L, Jin J, Cardona JG, Smith MD, Martin KA, Wang J, Strasburger H, Herbst L, Alexis M, Karnell J, et al. 2019. Oligodendrocyte precursor cells present antigen and are cytotoxic targets in inflammatory demyelination. Nat Commun 10: 3887. 10.1038/s41467-019-11638-3 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Langfelder P, Horvath S. 2008. WGCNA: an R package for weighted correlation network analysis. BMC Bioinformatics 9: 559. 10.1186/1471-2105-9-559 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lareau CA, White BC, Oberg AL, McKinney BA. 2015. Differential co-expression network centrality and machine learning feature selection for identifying susceptibility hubs in networks with scale-free structure. BioData Min 8: 5. 10.1186/s13040-015-0040-x [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu S, Liu Y, Hao W, Wolf L, Kiliaan AJ, Penke B, Rübe CE, Walter J, Heneka MT, Hartmann T, et al. 2012. TLR2 is a primary receptor for Alzheimer's amyloid β peptide to trigger neuroinflammatory activation. J Immunol 188: 1098–1107. 10.4049/jimmunol.1101121 [DOI] [PubMed] [Google Scholar]
- Love MI, Huber W, Anders S. 2014. Moderated estimation of fold change and dispersion for RNA-seq data with DESeq2. Genome Biol 15: 550. 10.1186/s13059-014-0550-8 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mahajani S, Giacomini C, Marinaro F, De Pietri Tonelli D, Contestabile A, Gasparini L. 2017. Lamin B1 levels modulate differentiation into neurons during embryonic corticogenesis. Sci Rep 7: 4897. 10.1038/s41598-017-05078-6 [DOI] [PMC free article] [PubMed] [Google Scholar]
- McCalla SG, Fotuhi Siahpirani A, Li J, Pyne S, Stone M, Periyasamy V, Shin J, Roy S. 2023. Identifying strengths and weaknesses of methods for computational network inference from single-cell RNA-seq data. G3 (Bethesda) 13: jkad004. 10.1093/g3journal/jkad004 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mistry D, Wise RP, Dickerson JA. 2017. DiffSLC: a graph centrality method to detect essential proteins of a protein-protein interaction network. PLoS One 12: e0187091. 10.1371/journal.pone.0187091 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Morabito S, Miyoshi E, Michael N, Shahin S, Martini AC, Head E, Silva J, Leavy K, Perez-Rosendahl M, Swarup V. 2021. Single-nucleus chromatin accessibility and transcriptomic characterization of Alzheimer's disease. Nat Genet 53: 1143–1155. 10.1038/s41588-021-00894-z [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mostafavi S, Gaiteri C, Sullivan SE, White CC, Tasaki S, Xu J, Taga M, Klein HU, Patrick E, Komashko V, et al. 2018. A molecular network of the aging human brain provides insights into the pathology and cognitive decline of Alzheimer's disease. Nat Neurosci 21: 811–819. 10.1038/s41593-018-0154-9 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nagy C, Maitra M, Tanti A, Suderman M, Théroux JF, Davoli MA, Perlman K, Yerko V, Wang YC, Tripathy SJ, et al. 2020. Single-nucleus transcriptomics of the prefrontal cortex in major depressive disorder implicates oligodendrocyte precursor cells and excitatory neurons. Nat Neurosci 23: 771–781. 10.1038/s41593-020-0621-y [DOI] [PubMed] [Google Scholar]
- Pratapa A, Jalihal AP, Law JN, Bharadwaj A, Murali T. 2020. Benchmarking algorithms for gene regulatory network inference from single-cell transcriptomic data. Nat Methods 17: 147–154. 10.1038/s41592-019-0690-6 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Prifti E, Zucker JD, Clément K, Henegar C. 2010. Interactional and functional centrality in transcriptional co-expression networks. Bioinformatics 26: 3083–3089. 10.1093/bioinformatics/btq591 [DOI] [PubMed] [Google Scholar]
- R Core Team. 2021. R: a language and environment for statistical computing. R Foundation for Statistical Computing, Vienna. https://www.R-project.org/. [Google Scholar]
- Risso D, Perraudeau F, Gribkova S, Dudoit S, Vert JP. 2018. A general and flexible method for signal extraction from single-cell RNA-seq data. Nat Commun 9: 284. 10.1038/s41467-017-02554-5 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Robinson MD, Oshlack A. 2010. A scaling normalization method for differential expression analysis of RNA-seq data. Genome Biol 11: R25. 10.1186/gb-2010-11-3-r25 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rousseeuw PJ. 1987. Silhouettes: a graphical aid to the interpretation and validation of cluster analysis. J Comput Appl Math 20: 53–65. 10.1016/0377-0427(87)90125-7 [DOI] [Google Scholar]
- Sarkar A, Stephens M. 2021. Separating measurement and expression models clarifies confusion in single-cell RNA sequencing analysis. Nat Genet 53: 770–777. 10.1038/s41588-021-00873-4 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Savino A, Provero P, Poli V. 2020. Differential co-expression analyses allow the identification of critical signalling pathways altered during tumour transformation and progression. Int J Mol Sci 21: 9461. 10.3390/ijms21249461 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Serin EA, Nijveen H, Hilhorst HW, Ligterink W. 2016. Learning from co-expression networks: possibilities and challenges. Front Plant Sci 7: 444. 10.3389/fpls.2016.00444 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shi Y, Holtzman DM. 2018. Interplay between innate immunity and Alzheimer disease: APOE and TREM2 in the spotlight. Nat Rev Immunol 18: 759–772. 10.1038/s41577-018-0051-1 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Soskic B, Cano-Gamez E, Smyth DJ, Ambridge K, Ke Z, Matte JC, Bossini-Castillo L, Kaplanis J, Ramirez-Navarro L, Lorenc A, et al. 2022. Immune disease risk variants regulate gene expression dynamics during CD4+ T cell activation. Nat Genet 54: 817–826. 10.1038/s41588-022-01066-3 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sun T, Song D, Li WV, Li JJ. 2021. scDesign2: a transparent simulator that generates high-fidelity single-cell gene expression count data with gene correlations captured. Genome Biol 22: 163. 10.1186/s13059-021-02367-2 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Szklarczyk D, Gable AL, Nastou KC, Lyon D, Kirsch R, Pyysalo S, Doncheva NT, Legeay M, Fang T, Bork P, et al. 2021. The STRING database in 2021: customizable protein–protein networks, and functional characterization of user-uploaded gene/measurement sets. Nucleic Acids Res 49: D605–D612. 10.1093/nar/gkaa1074 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tran HTN, Ang KS, Chevrier M, Zhang X, Lee NYS, Goh M, Chen J. 2020. A benchmark of batch-effect correction methods for single-cell RNA sequencing data. Genome Biol 21: 12. 10.1186/s13059-019-1850-9 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Travaglini KJ, Nabhan AN, Penland L, Sinha R, Gillich A, Sit RV, Chang S, Conley SD, Mori Y, Seita J, et al. 2020. A molecular cell atlas of the human lung from single-cell RNA sequencing. Nature 587: 619–625. 10.1038/s41586-020-2922-4 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vallejos CA, Risso D, Scialdone A, Dudoit S, Marioni JC. 2017. Normalizing single-cell RNA sequencing data: challenges and opportunities. Nat Methods 14: 565–571. 10.1038/nmeth.4292 [DOI] [PMC free article] [PubMed] [Google Scholar]
- van der Wijst MG, Brugge H, De Vries DH, Deelen P, Swertz MA, Franke L. 2018. Single-cell RNA sequencing identifies celltype-specific cis-eQTLs and co-expression QTLs. Nat Genet 50: 493–497. 10.1038/s41588-018-0089-9 [DOI] [PMC free article] [PubMed] [Google Scholar]
- van der Wijst MG, de Vries DH, Groot HE, Trynka G, Hon CC, Bonder MJ, Stegle O, Nawijn M, Idaghdour Y, van der Harst P, et al. 2020. Science forum: the single-cell eQTLGen consortium. eLife 9: e52155. 10.7554/eLife.52155 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Van Dijk D, Sharma R, Nainys J, Yim K, Kathail P, Carr AJ, Burdziak C, Moon KR, Chaffer CL, Pattabiraman D, et al. 2018. Recovering gene interactions from single-cell data using data diffusion. Cell 174: 716–729.e27. 10.1016/j.cell.2018.05.061 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang J, Huang M, Torre E, Dueck H, Shaffer S, Murray J, Raj A, Li M, Zhang NR. 2018. Gene expression distribution deconvolution in single-cell RNA sequencing. Pro Natl Acad Sci 115: E6437–E6446. 10.1073/pnas.1721085115 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang X, Choi D, Roeder K. 2021. Constructing local cell-specific networks from single-cell data. Pro Natl Acad Sci 118: e2113178118. 10.1073/pnas.2113178118 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zeisel A, Muñoz-Manchado AB, Codeluppi S, Lönnerberg P, La Manno G, Juréus A, Marques S, Munguba H, He L, Betsholtz C, et al. 2015. Cell types in the mouse cortex and hippocampus revealed by single-cell RNA-seq. Science 347: 1138–1142. 10.1126/science.aaa1934 [DOI] [PubMed] [Google Scholar]
- Zhang B, Horvath S. 2005. A general framework for weighted gene co-expression network analysis. Stat Appl Genet Mol Biol 4: Article17. 10.2202/1544-6115.1128 [DOI] [PubMed] [Google Scholar]
- Zhang MJ, Ntranos V, Tse D. 2020a. Determining sequencing depth in a single-cell RNA-seq experiment. Nat Commun 11: 774. 10.1038/s41467-020-14482-y [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang Q, Liu W, Zhang HM, Xie GY, Miao YR, Xia M, Guo AY. 2020b. hTFtarget: a comprehensive database for regulations of human transcription factors and their targets. Genomics Proteomics Bioinformatics 18: 120–128. 10.1016/j.gpb.2019.09.006 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang R, Atwal GS, Lim WK. 2021. Noise regularization removes correlation artifacts in single-cell RNA-seq data preprocessing. Patterns 2: 100211. 10.1016/j.patter.2021.100211 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zheng S, Cheng G, Guo J, Zhu H. 2019. Test for high dimensional correlation matrices. Ann Stat 47: 2887–2921. 10.1214/18-AOS1768 [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.