Machine learning based brain signal decoding for intelligent adaptive deep brain stimulation

Abstract

Sensing enabled implantable devices and next-generation neurotechnology allow real-time adjustments of invasive neuromodulation. The identification of symptom and disease-specific biomarkers in invasive brain signal recordings has inspired the idea of demand dependent adaptive deep brain stimulation (aDBS). Expanding the clinical utility of aDBS with machine learning may hold the potential for the next breakthrough in the therapeutic success of clinical brain computer interfaces. To this end, sophisticated machine learning algorithms optimized for decoding of brain states from neural time-series must be developed. To support this venture, this review summarizes the current state of machine learning studies for invasive neurophysiology. After a brief introduction to the machine learning terminology, the transformation of brain recordings into meaningful features for decoding of symptoms and behavior is described. Commonly used machine learning models are explained and analyzed from the perspective of utility for aDBS. This is followed by a critical review on good practices for training and testing to ensure conceptual and practical generalizability for real-time adaptation in clinical settings. Finally, first studies combining machine learning with aDBS are highlighted. This review takes a glimpse into the promising future of intelligent adaptive DBS (iDBS) and concludes by identifying four key ingredients on the road for successful clinical adoption: i) multidisciplinary research teams, ii) publicly available datasets, iii) open-source algorithmic solutions and iv) strong world-wide research collaborations.

1. Introduction

The opportunity to modulate neural circuits with deep brain stimulation (DBS) has changed the way brain disorders are treated and understood. By means of an implantable DBS pulse generator (IPG), neurostimulation combined with invasive neural sensing has created novel possibilities for demand dependent neuromodulation (Krauss et al., 2021; Neumann et al., 2019). DBS can improve the quality of lives of patients suffering from a variety of neural disorders, such as essential tremor (ET), Parkinson’s disease (PD), dystonia, Tourette syndrome and obsessive-compulsive disorder (Starr, 2018), where the target structure for stimulation depends on the condition and symptoms to be treated.

In open-loop conventional DBS (cDBS), therapeutic stimulation parameters are programmed in the outpatient environment, in which symptoms may not manifest. Suboptimal or static stimulation parameters may not evoke the desired treatment effect and/or come at the cost of producing adverse effects (Steigerwald et al., 2018; van Westen et al., 2020). cDBS does not take into account short-term changes in patient behavior, medication efficacy and fluctuation, or/and external environmental factors, that reflect the clinical state and hour-to-hour quality of life in DBS patients. Stimulation setting adjustments required returning to a specialized clinic, which is not practical for daily or even weekly adjustments of DBS settings due to symptom fluctuations or changes in the patients’ lifestyles. Adaptive closed-loop DBS (aDBS) aims to overcome such limitations by automatically adjusting the stimulation parameters to the fluctuating clinical state of the patient. Ideally, stimulation would be applied only when necessary. In the design, implementation, and application of aDBS, several challenges need to be addressed. These include the optimal choice of the control algorithm and control variables, such as stimulation frequency, stimulation amplitude and pulse width, as well as the identification of robust neural biomarkers.

Oscillatory activity has proven to carry relevant clinical information that can trigger the adaptive control algorithms. In Parkinson’s disease, first successful aDBS studies have used local field potentials (LFP) directly from the DBS target area (Arlotti et al., 2018; Golshan et al., 2018a, 2018b; Golshan et al., 2020; Little et al., 2013, 2016). Recently electrocorticography (ECoG) recordings have been explored as an additional source of input to inform DBS (Swann et al., 2018). Indeed, ECoG is being used more frequently within the brain computer interface (BCI) community, including with ML methods in various fields, such as speech and movement decoding (Goli and Rad, 2019; Merk et al., 2021; Ramsey et al., 2018; Schalk et al., 2008; Xie et al., 2018).

These pioneering efforts thus far have relied on single oscillatory biomarkers (e.g. pathologically enhanced beta activity in PD) that capture important but not extensive information about the patients’ clinical states. Here, multivariate brain signal decoding with machine learning (ML) may further augment the capabilities of clinical BCI for invasive neuromodulation. For future aDBS applications, machine learning-based algorithms may be able to detect the presence of disease-specific symptoms, side effects and normal human behavior (Neumann et al., 2019), allowing the construction of intelligent aDBS (iDBS) devices. To this end, the multiple neural activity patterns underlying specific signs and symptoms of brain disorders may inform sophisticated machine learning-based iDBS algorithms. These brain signals can represent the inputs for models which are built to decode the physiological and/or pathological states of DBS patients. Fig. 1 compares a schematic representation of a conventional aDBS approach compared to a machine learning-based intelligent aDBS approach, based upon multimodal (cortical and subcortical) invasive brain recordings. While first breakthrough studies have demonstrated convincing proof of concept for the utility of machine learning for aDBS (He et al., 2021; Opri et al., 2020; Wan et al., 2019; Watts et al., 2020), there is still a wide gap between experimental ML solutions, device capabilities and clinical reality. This review aims to provide guidance to DBS researchers by synthesizing initial studies that apply ML algorithms toward, or otherwise set the stage for the development of intelligent adaptive DBS.

Fig. 1.

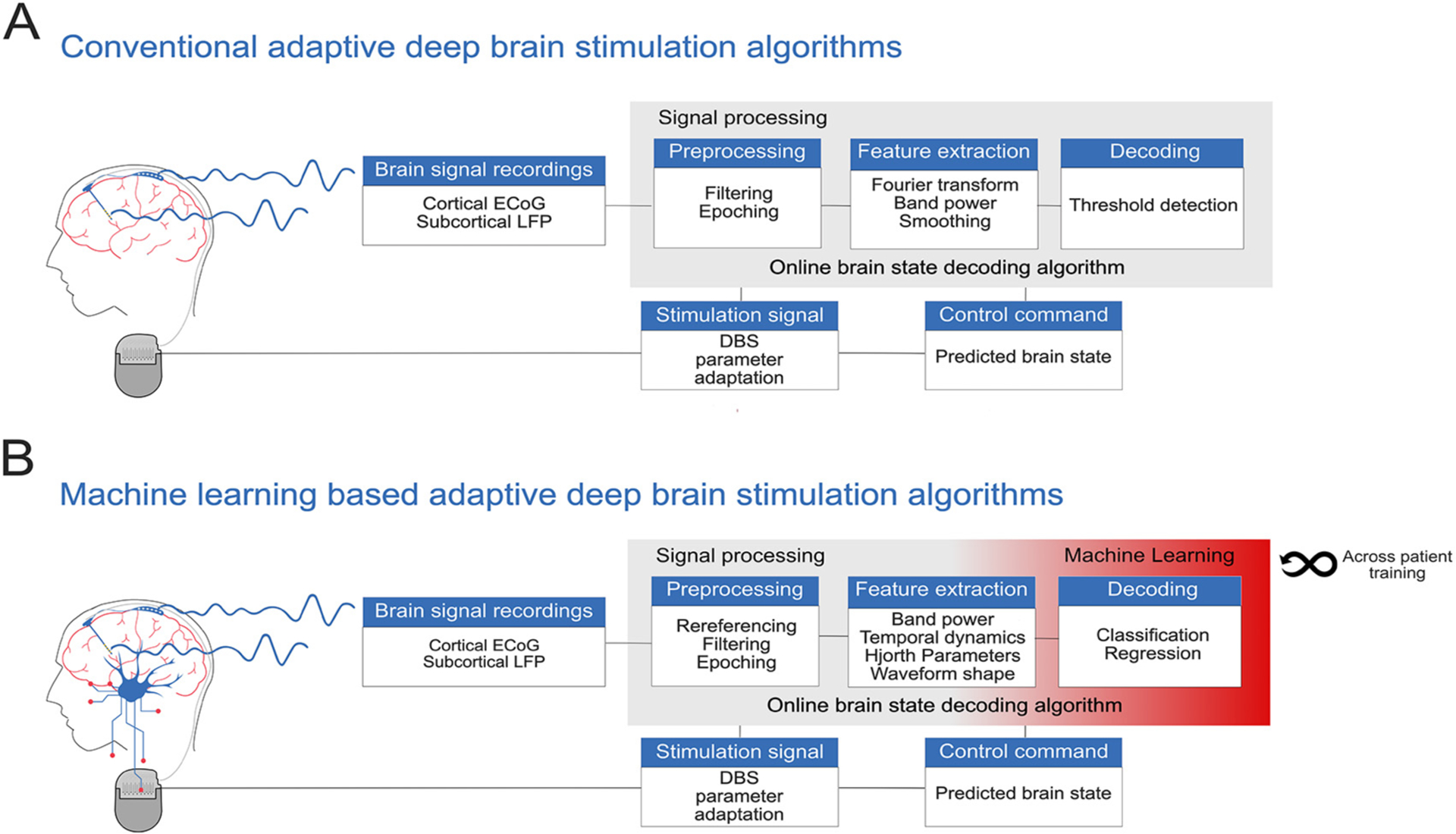
Schematic representation of a conventional adaptive deep brain stimulation algorithm compared to a machine learning-based adaptive deep brain stimulation system. (A) Input signals are cortical ECoG and subcortical LFP brain signal recordings. New incoming data packets are preprocessed (e.g. normalization, rereferencing, artifact detection and subsequent rejection applied) and features are extracted (e.g. Fourier transformation, band power averaging and smoothing). The control algorithm is a simple threshold detection of a predefined feature: the brain state (e.g. pathological or non-pathological state) is predicted, and translated into a control command, such that the DBS stimulation parameters are adapted. (B) Machine learning-based adaptive deep brain stimulation can use multimodal features to decode a variety of brain states (e.g. classification for decoding of tremor or regression for indication of severity of bradykinesia in PD). In addition to brain signals, the decoding model can also be re-adjusted based on the information delivered by the stimulation signal. Moreover, information from previous patients could be used to feed the decoding algorithms and potentially avoid time-consuming individual training sessions.

2. A brief introduction to general machine learning methodology

Machine learning algorithms can “learn” the relationship between data and the target outcome, without having to rely on direct human instructions (Bishop, 2006). For doing so, a model is constructed based upon input data. In the case of what is called supervised learning, the algorithm’s goal is to learn a mapping between the input data and the target variables. To accomplish this task, representative data of the problem at hand is provided to the algorithm. Such data, which is called training data, comprises input–output pairs. The inputs are generally multi-dimensional vectors that represent features of the data, i.e., relevant information characterizing and describing certain brain states or behaviors that are to be decoded. Most commonly, features are first constructed from raw data and sometimes manually optimized through feature engineering, before the features deemed most promising or appropriate are selected. The mapping that links features to desired outputs is learned during training. The response variable, also known as the dependent variable, is the output of interest that is associated with these features, i.e. the brain state or behavior itself. The response variable can either be discrete (e.g. absence or presence of symptoms or movement) or continuous (e.g. severity of a symptom or degree of grip force), representing either a classification or a regression problem, respectively (Mitchell et al., 2013). As a first step, an ML model needs to be trained. This is typically done by providing the model a training set of input features and corresponding known target variables. In the training process the model learns to map input features to target variables by optimizing model parameters, typically by minimizing a cost function. The cost function estimates the loss or error as an indicator of model performance, e.g. the difference between model output and target variable. Various optimization algorithms can minimize the cost function, but the most prominent is gradient descent, which enables a model to learn the gradient or direction model parameters should take to improve model performance. Depending on the model complexity, it is susceptible to overfitting, which describes the attribution of target irrelevant noise in the training data to model parameters, leading to high performance in the training dataset but low generalization for new or left out data. The risk for overfitting increases with higher model complexity, i.e. the bigger the number of model parameters, the higher the risk for the model to assign unrelated or noisy input to these parameters. Therefore, the model performances must be objectively validated on a set of unseen data, called a test set. Such data should never be examined by the algorithm during training and should be as representative of the real setting as possible.

An objectively good ML model generalizes well to unseen data (not part of the training set), when its performance for left out or new test sets is as good as for the training set. A model is described as overfitted when it performs well on the training set but poorly on new, unseen test sets. To avoid overfitting, several strategies can be adopted, such as feature selection, data augmentation and regularization techniques. To avoid an overestimation of the performance metrics, cautious (cross-) validation routines must be cleared of any circularity, which can arise when the same model learns from shuffled consecutive samples that are correlated, e.g., by autocorrelation of the signals, see for example (Lemm et al., 2011). In the following sections, detailed insight into these topics within the framework of invasive brain signal decoding will be provided. Representative test sets are required to estimate and quantify the generalization capability, which is evaluated by performance metrics for both classification and regression problems.

Finally, many models require tweaking the hyperparameters, which are defined as parameters that are not optimized through model training, but can either be set manually, or can be subjected to a so-called hyperparameter grid search (a systematic run through a set of predefined grid of values) or random search (run through a set of randomly defined values). Optimal hyperparameters are often unknown, which makes manual optimization inefficient. Grid and random hyperparameter searches, however, are uninformed by past evaluations, meaning that the entire training process is repeated for the entire predefined grid, regardless of the performance metrics. More recently, Bayesian hyperparameter optimization routines have evolved, which form a probabilistic model for identifying optimal hyperparameters by learning from previous performance metrics.

In summary, a training set comprising input features (e.g. oscillatory gamma band activity) and corresponding target variables (e.g. hand grip-force) is used to train a machine learning model, by optimizing model parameters (e.g. linear model coefficients) to minimize the loss or difference of model output (predicted grip-force) and target variable (observed true grip-force). Once the decoding model is built, yielding a pre-defined “satisfactory” prediction performance metric, the learned parameters and model functions can be directly applied to unseen testing data. This training-testing procedure is represented in Fig. 2, where raw data is transformed into features, features are selected, and the prediction model is adjusted. The model then is applied to testing data, to make novel predictions or to evaluate performance metrics. In the particular case of deep learning, features will be constructed during model training. In this review, we explore how these specific ML definitions become relevant in the case of real-time decoding for intelligent adaptive DBS based on invasive electrophysiological neural population activity.

Fig. 2.

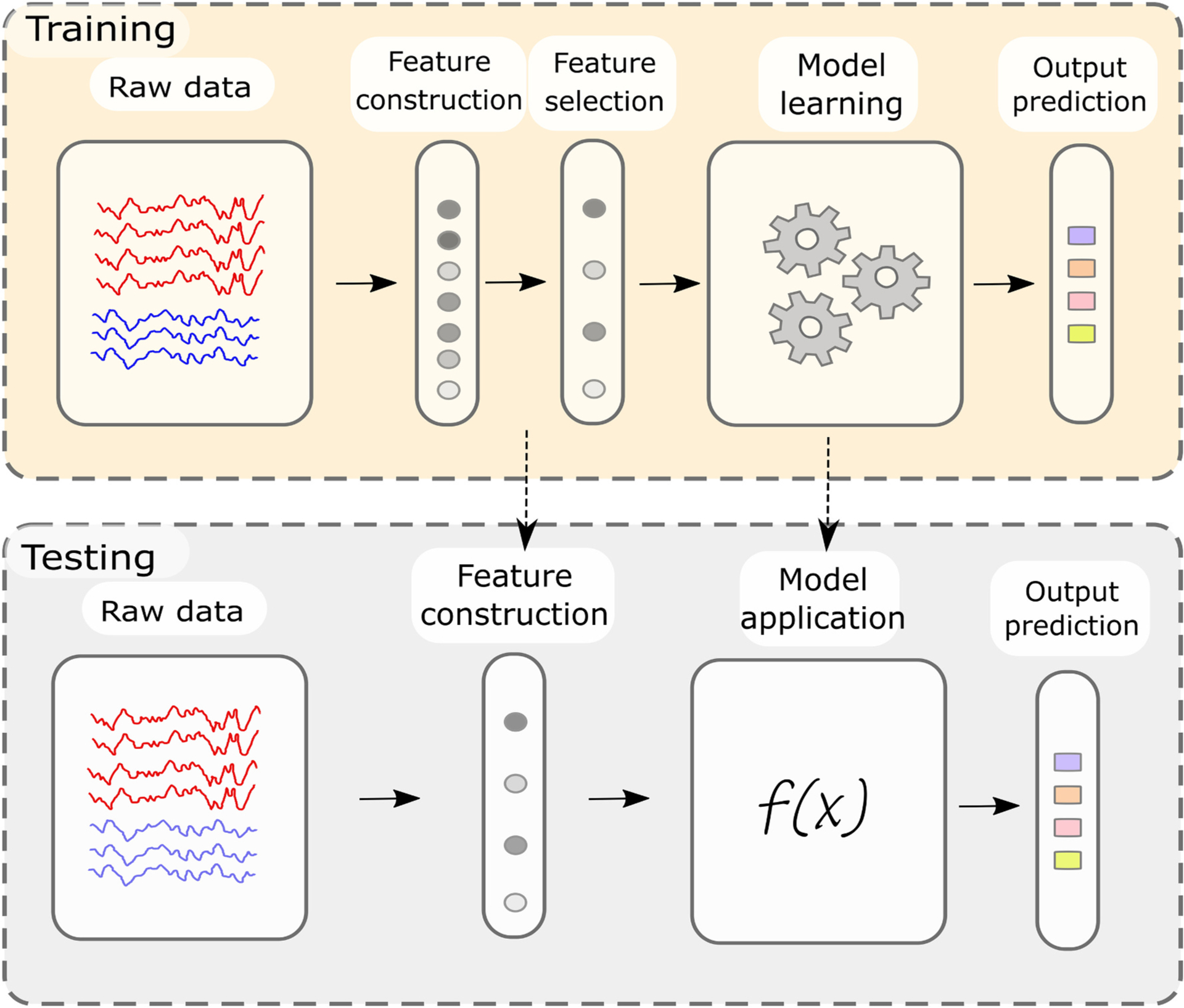
Architecture of a representative machine-learning pipeline. During model training, features are extracted from training data. The most relevant features can then be selected. The prediction model, either for classification or regression, is based on optimized parameters that transform input features into predicted model output. During training, parameters are optimized, until the performance saturates, and no further improvement is gained. Once the model yields satisfactory performance metrics on training data, the learned parameters can be directly applied to new input features for test set model predictions. A good decoding model is a model in which training and testing performance remain similar. Deep learning architectures enable feature construction and selection within the model training step.

3. Features

In general, the performance of machine learning models depends highly on the choice of input features. Identification of stable and representative features greatly facilitates the work of the subsequent decoding algorithm. Consequently, less time needs to be spent in finding the right model that can predict meaningful output from those features. Especially in the context of invasive neuromodulation, it is crucial to identify the most reliable and mechanistically relevant correlates of target output in order to optimize the therapy in a robust and stable manner. E.g. subthalamic beta activity in PD has been shown robustly to be associated with akinesia/rigidity symptoms (Neumann et al., 2016), which will likely yield good performance for the purpose of symptom decoding (Gilron et al., 2021). False prediction on the other hand, may lead to suboptimal treatment of a patient’s symptoms or even produce adverse effects. It is therefore an important task to identify relevant physiological and pathological biomarkers, to combine them as features in a model, and then to establish which features have the highest importance. This process, known as feature engineering, can be conducted with prior knowledge of known well-performing features. High-quality feature engineering ensures that the underlying problem is understood and is often a key to success in machine learning competitions. Both, model choice and feature engineering can be critical to successful learning. On the other hand, automatic feature construction, commonly also referred to as feature learning, constitutes the identification of features from raw data via a pre-defined algorithm. A problem that can emerge with automatic feature learning is that the resulting conceptual insight is not accessible to the researcher and the domain knowledge is “trapped” with limited potential for further improvement and translation (Brownlee, 2014).

Electrophysiological data comprises at least five dimensions: time, space, frequency, amplitude and phase. This multidimensionality allows exploration of different feature categories, namely from the frequency, time and spatial domains. The most common features from these domains used in machine learning are reviewed in the following subsections. How these features relate to certain physiological or pathological states is described in Section 6.

3.1. Frequency-domain features

The electrical activity of the brain can be separated into canonical frequency bands (delta: 0–4 Hz, theta: 4–7.5 Hz, alpha: 8–13 Hz, beta: 13–30 Hz, gamma: 30–100 Hz, high frequency activity: 100–600 Hz) to aid analyses. Changes at the level of the relative power of specific frequency bands are associated with different human behavioral states, like movement planning (Little et al., 2019; Szurhaj et al., 2003), imagination (Kühn et al., 2006; McFarland et al., 2000) and performance (Branco et al., 2017; Brücke et al., 2012; Fischer et al., 2020; Lofredi et al., 2018; Wang et al., 2012). In addition, the low-frequency component (< 3 Hz), has been useful for movement decoding with ECoG recordings (Hammer et al., 2013; Volkova et al., 2019). Such band-power changes can also reveal pathological states. It was shown that oscillatory beta activity is elevated in the STN as well as Globus Pallidus internus (GPi) in PD patients and is reduced by medication (Kühn et al., 2006; Neumann et al., 2017; Silberstein, 2003) as well as DBS (Eusebio et al., 2011; Kühn et al., 2008; Merkl et al., 2016; Neumann et al., 2016; Quinn et al., 2015). This has led to the inspiration of aDBS strategies based on beta activity as a neural marker (Arlotti et al., 2018; Little et al., 2013).

A plethora of different approaches exist for the extraction of features from the frequency domain. The simplest and most computationally efficient method is to perform a temporal band-pass filtering of the signal in a particular frequency band of interest (Widmann et al., 2015). To this end, digital filters can be used, which are routinely classified as finite impulse response (FIR) or infinite impulse response (IIR), depending on whether the output relies only on previous input values or on both previous input and output values, respectively. In electrophysiological data analysis, mainly due to its stability and well-defined passband, FIR filters are recommended (Widmann et al., 2015). Since the variance of a band-pass filtered signal is proportional to its band-power, frequency-band features can be easily extracted by calculating the variance of a bandpass filtered signal. Frequency band information can also be extracted by the instantaneous amplitude, for example after applying a Hilbert transform (Cagnan et al., 2019).

Spectral decomposition analysis can also be used for extracting frequency-based features. In this context, the power spectral density (PSD) is estimated after applying a transformation of the temporal signal to the frequency domain. In particular, the fast Fourier transform (FFT) provides a way of decomposing the signal at different frequency bins. After applying FFT the power spectrum of the signal at a particular frequency band can be easily computed by calculating the square of the amplitude spectrum at the frequency band of interest. Absolute or relative band features can be extracted, with the latter being most informative when a particular brain pattern is aimed to be detected from baseline (Zhang and Parhi, 2016). Popular alternatives to Fourier- or Hilbert-based methods are multitaper and wavelet-based time-frequency decomposition. Each of these methods offers individual advantages in time and frequency resolution - and potentially computational speed - that should be considered in every specific use-case (Bruns, 2004).

These frequency domain analyses can also be used to extract the phase of the signal, which together with amplitude values can be used to calculate measures of phase amplitude coupling (PAC) (Tort et al., 2010). Here, the phase of a lower carrier frequency is correlated with the amplitude of a higher frequency band. In Parkinson’s disease, an increased level of beta – gamma PAC has been described (De Hemptinne et al., 2015). A difficulty for using PAC as a brain signal decoding input feature, is the fact that relatively long segment periods are required for robust estimates. Nevertheless, PAC has been reported as one of multiple features, for detecting mental fatigue from ECoG recordings in non-human primates (Yao et al., 2020a). A novel method for estimating PAC based on mutual information has recently been proposed (Martínez-Cancino et al., 2019), suggesting that this measure could be used for constructing viable machine learning models for brain state decoding.

3.2. Time-domain features

Frequency domain features are obtained by fitting certain band-power estimates to raw data. This process can be error-prone if the underlying time-domain signal is not well characterized by the spectral analysis. Therefore, current research investigates the importance of specific waveform shape characteristics (Cole et al., 2017). This process can be driven by specific knowledge of certain temporal events like asymmetric sharp waves or bursts (Anderson et al., 2020; Jackson et al., 2019; Lofredi et al., 2019b; Tinkhauser et al., 2018). In Parkinson’s Disease for instance a positive correlation of longer beta bursts and clinical impairment has been found, where Levodopa treatment leads to a relative increase of shorter bursts (Tinkhauser et al., 2017b). Characterization between Parkinson’s Disease and Dystonia showed that prolonged burst duration is indeed a disease specific biomarker for Parkinson’s Disease, where Parkinson’s Disease Medication ON and Dystonia showed similar burst characteristics (Lofredi et al., 2019a). Since bursting is a transient non-stationary event, this time domain feature holds strong promise for adaptive DBS use cases (Tinkhauser et al., 2017a). Additionally, entropy or sample entropy can be estimated. During Freezing of Gait in Parkinson’s Disease, freezers showed during locomotion without Freezing of Gait higher beta sample entropy than non-freezers. Greater alpha sample entropy on the other hand was observed during walking without Freezing of Gait (Syrkin-Nikolau et al., 2017). With regard to temporal waveform shape, waveform sharpness asymmetry has been suggested to reflect cortical pathophysiology in Parkinson’s disease (Cole et al., 2016; Cole and Voytek, 2017; Jackson et al., 2019). Therefore, sharp wave characteristics like sharp ratio, rise and decay time, peak and trough amplitudes may be used as machine learning feature for neural decoding.

Another commonly used time-domain feature are Hjorth parameters. Hjorth activity measures the broadband variance or power of a time signal, Hjorth mobility measures the mean frequency or proportion of standard deviation of the power spectrum and Hjorth complexity quantifies the frequency change, or pure sine wave similarity (Hjorth, 1970). Hjorth parameters were successfully used in EEG analysis (Oh et al., 2014; Vidaurre et al., 2009) and showed high feature importance for ECoG analysis (Shah et al., 2018; Yao et al., 2020c, 2020a).

3.3. Spatial features

Beyond signal features in the time and frequency domain, the brain activity measured by sensors can be viewed as a spatial superposition of different sources of cerebral activity. Statistical spatial filtering approaches offer the possibility to demix the sensor measurements into statistical sources. These methods are commonly known in the literature as blind-source separation methods, in which a forward linear mixing model is hypothesized, with the goal of learning a demixing matrix to make the decomposition. The properties of the estimated sources are depending on the final objective for which spatial filtering is being implemented. For example, principal component analysis (PCA) or independent component analysis (ICA) can be used as dimensionality reduction steps for a) isolating important sources with larger variability (Naeem et al., 2009), b) data cleaning (Zhou and Gotman, 2009) or c) multi-channel data correlation finding (Rogers et al., 2019). Principal component analysis has also been evaluated as a tool for feature selection in discriminative pattern recognition problems (Liao et al., 2014; Yu et al., 2014). Along these lines, the common spatial patterns (CSP) method is a well-known and widely used method in the field of brain-computer interfaces (Blankertz et al., 2008; Hämäläinen and Hari, 2002). It allows identification of discriminative sources and extraction of spectral-power related features for a subsequent classification problem. In the context of invasive brain recordings, it has been used for band-power feature extraction in hand movement decoding (Jiang et al., 2017). While CSP was designed for discrete targets (classification), the source power comodulation (SPoC) method can be thought as an extension of CSP for continuous output signals. By means of SPoC, highly correlated sources to the continuous target can be estimated (Dähne et al., 2014). Here again, spatio-spectral features can then be learned to feed a model (Castaño-Candamil et al., 2020b). Recently, a spatial filtering approach combining frequency, phase, and spatial distribution of invasive neural signals from epilepsy patients was proposed to reconstruct stimulus features in the motor and speech domain (Delgado Saa et al., 2020).

3.4. Connectivity

Intra- or inter-regional connectivity can be used to estimate information transfer within a specific functional area or between two different areas (Cohen, 2014). In one example, connectivity features extracted by the time-varying dynamic Bayesian networks (TV-DBN) have been used to decode a motor task in humans using ECoG signals (Benz et al., 2012). More recently, a decoding model to predict movement intention was constructed based upon estimating intra- and inter-regional connectivity in dorsolateral prefrontal cortex and primary motor cortex using mutual information (Kang et al., 2018).

Interactions between oscillations in different frequency bands can also be used as informative features. Coherence has been proposed to be a relevant mechanism of neuronal communication (Fries, 2015). For Parkinson’s disease and dystonia patients, motor cortex and basal ganglia coherence was reported to be coupled to its power in the beta and gamma bands during voluntary movement (Talakoub et al., 2016). Recently, STN - motor cortex coherence was also shown to differentiate motor states in Parkinson’s disease patients (Gilron et al., 2020).

Phase amplitude coupling (PAC), as described in the frequency domain section, can also be considered as a connectivity metric as it constitutes the interaction of two different signals, a lower frequency carrier phase signal and a higher frequency amplitude signal. These signals may be recorded from a single local or from distant electrodes. In the latter case, significant PAC may result from interregional connectivity as described for thalamocortical PAC in essential tremor patients undergoing DBS, that is modulated with movement (Opri et al., 2019). However, the utility of interregional PAC as a brain signal decoding feature remains unexplored, potentially because the signal to noise ratio can be relatively low and correlated with other coupling and activity features that are less computationally expensive.

3.5. Kalman filtering

Kalman filters model system dynamics to estimate a system state based on input and control data. The robustness to noise and random/unexpected signal changes with uncertain impact for output predictions makes this approach particularly useful for neural decoding. While similar to a supervised machine learning algorithm, one method of implementing Kalman filtering, is that it can be used for feature engineering to create more robust inputs to subsequent machine learning models. It is thus a step in between signal preprocessing and model-based output prediction. Therefore, it is not considered in the following section on machine learning architectures. More specifically, A Kalman Filter is a recursive optimal estimator that infers parameters of interest from uncertain, inaccurate and indirect observations (Kleeman, 1996). A time-domain linear dynamical system, defined by a state transition model, observation model, process and observation covariance noise and a state vector, need to be described under the assumption of additive white noise. Kalman filtering can be used to reduce undesired noisy signal fluctuations and thus false positive detections. It has been applied to band power features (Yao et al., 2020c) and has been shown to significantly improve the false positive rate and thus, specificity. Similar results have been obtained for different analysis of Epilepsy seizure prediction (Chisci et al., 2010; Zhang and Parhi, 2016). A white noise acceleration model is commonly employed, which uses the sensor signal and its derivative in the state space. The linear dynamic system is chosen such that the signal representation has a nearly constant rate of change (Chisci et al., 2010). The smoother, filtered first component of the state space then is used instead of the observation. In the white noise acceleration system, the Kalman gain defining the state and sensor noise covariance is the only design parameter for filter performance tuning. In addition to improving stability of input features, this method can also be applied for smoothing and improved robustness of model prediction output (Yao et al., 2020c). For certain machine learning methods outliers can cause a severe performance loss. Next to clipping or rank transformation, Kalman filtering of features before model training is a promising preprocessing method to reduce signal fluctuations. Using more in-depth knowledge of the underlying data generation, a source estimate can also be constructed by specifying a more sophisticated observation model and linear dynamic system.

4. Machine learning methodology

4.1. Hyperparameters

Many methods have hyperparameters associated with model learning. The model performance also depends on finding the optimal values for model specific hyperparameters. If the number of hyperparameters is low, they can be explored through grid or random search (Zeiler and Fergus, 2014). But, when the number of hyperparameters of the model is high, adaptive methods such as Bayesian optimization are recommended (Frazier, 2018) in order to minimize computational cost and maximize hyperparameter search ranges, which can identify optimal model hyperparameters.

While higher complexity of a model can boost the predictive capacity, it is important to understand advantages and disadvantages of specific model architectures. On the other hand, high decoding performance is often driven by investigative feature engineering. Through optimized feature extraction the model choice becomes less critical. If the main underlying hidden predictive structure is understood, simple models will yield high performances. An important aspect is therefore to understand task relevant features and circumvent “black box” implementations. In addition to the explained model designs, stacking predictions of different architectures has shown significant advantages in machine learning competitions (Michailidis, 2017). Stacked predictions of different model types are fed as features to following models using multiple hidden layers, each with an own model architecture (Pavlyshenko, 2018). This approach thus combines different underlying function approximators in a potentially multi-model-based learning approach (Michailidis, 2017).

4.2. Architectures

Each model family has its own fundamental data representation and transformation mechanisms, model assumptions, and consequently varying advantages and disadvantages. Fig. 3 illustrates the different ML models considered in this review, from simpler models, like linear regression to more complex architectures, such as deep neural networks, while Table 1 expands the information summarized in Fig. 3 and may serve as a more detailed reference for interested readers.

Fig. 3.

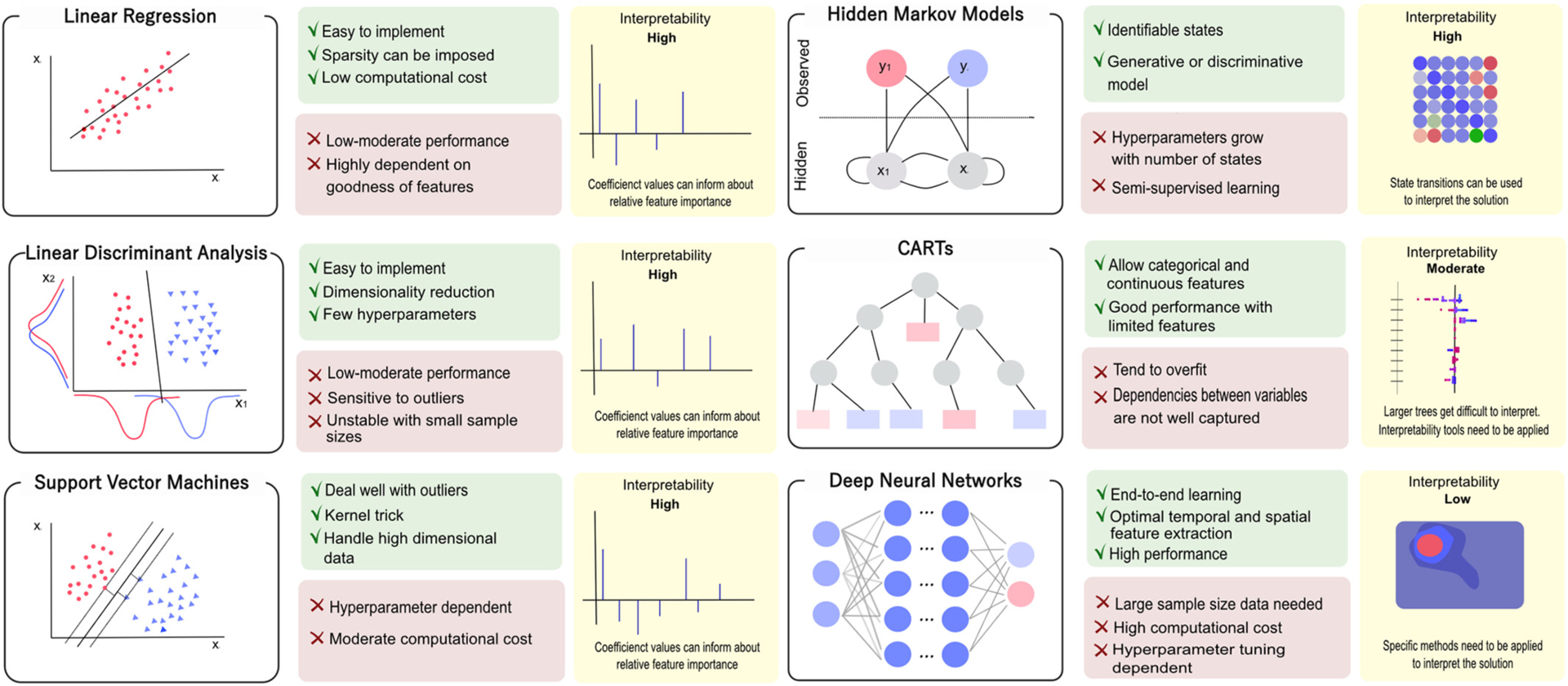
Overview of common Machine learning model architectures. The most commonly used machine learning models for invasive neural decoding are shown, ranging from simple linear methods to more complex models. Each method is built under different model assumptions and comes with specific advantages and disadvantages. Interpretability of the solution plays a key role in invasive neuromodulation.

Table 1.

Comparison of different machine learning models.

Method	Advantages	Disadvantages	Interpretability	Paper
Linear models: Linear and logistic regression	Fast, tractable (solution can be calculated non-iteratively) Simple implementation Simplest model architecture Regularization terms add desired properties to the solution vector, i.e. the l2-norm (RIDGE and ENET) adds more stability to small sample sizes and outliers, while the l1-norm (LASSO and ENET) allows feature selection	Performance (low model complexity) Becomes unstable with few samples The goodness of the solution highly depends on the choice of regularization parameters When the l1-norm is being used, the solution is found via optimization Performance is highly dependent of the input features	High: Coefficient values can be regarded as a measure of feature importance	Tan et al. (2019), Flamary and Rakotomamonjy (2012), Herff et al. (2016), Castaño-Candamil et al. (2020a), Houston et al. (2019)
Statistical Machine Learning: Linear discriminant analysis	Fast, tractable (solution is calculated non-iteratively) Can be used as dimensionality reduction method Little hyperparameter tuning needed Was already shown to work in essential tremor closed-loop DBS (Opri et al., 2020)	Homogeneity and gaussian assumption of equal covariance matrix (workaround can be quadratic discriminant analysis) Independence assumptions	High: Coefficient values can be regarded as a measure of feature importance	Opri et al. (2020), Ferleger et al. (2020), Gruenwald et al. (2019)
Statistical Machine Learning: Support Vector Machines	Diminished outlier influence because of soft margin SVM, thus performs usually better than linear discriminant analysis Can be extended to nonlinear classification through the kernel trick Was already shown to work in Essential Tremor Closed Loop DBS (He et al., 2021)	Hyperparameter tuning, if nonlinear structure is known, the ideal kernel needs to be specified	High: Coefficient values can be regarded as a measure of feature importance Non-zero entries identify decision boundaries and represent samples that are hard to classify	Golshan et al. (2018a, 2018b), Zhang and Parhi, 2016, Horn et al. (2019), He et al. (2021)
Hidden Markov models	Identifiable states Generation of data Less prone to overfitting	Hyperparameter is the number of states that may be unknown in advance	High: State transitions give intuition how states change data generation can be compared to real acquired data	Zaker et al. (2015), Zaker et al. (2016), Jiang et al. (2013), Hirschmann et al. (2017), Sun et al. (2020)
CART	Performs well with limited number of features Continuous and categorical features can be used Limited preprocessing necessary: data does not need to be scaled Certain architectures e.g. XGBOOST can make use of a validation set during training therefore early stopping is supported Typically very limited hyperparameter tuning is necessary Some architectures allow NaN values being fed to the model	Model complexity can easily lead to overfitting by simply “storing” training samples Sometimes linear dependencies cannot be captured	Moderate: Feature importance can be computed based on different criteria	Yao et al. (2020a), Yao and Shoaran (2019), Yao et al. (2020b), Yao et al. (2020c)
Deep Learning	End-to-end learning capability Optimal time domain feature extraction (RNN, LSTM, GRU, Transformer) Optimal spatial domain feature extraction (CNNs) It is thought to take optimal advantage of bigger dataset Early Stopping and implementation of callbacks	Hyperparameter tuning, deep learning models hardly perform out of the box Additional hardware requirements (GPU) More advanced techniques need to be utilized to combine features of different modality (categorical and non categorical) Preprocessing need to be directly addressed by the model architecture (Batch Normalization)	Moderate: Methods exist though for feature importance (Shrikumar et al., 2017) Permutation and ablation of input features can be informative	Haddock et al. (2019), Xie et al. (2018), Hashimoto et al. (2020), Petrosyan et al. (2021)

Each machine learning model is presented in one row, in which advantages and disadvantages are listed. The interpretability of the learned model is also described. Selected studies in which such a model was used in the context of invasive neuromodulation are cited in the last column.

Less complex models, like linear models, assume well defined preprocessed features. The function approximation is limited through architectural constraints. Linear discriminant analysis (LDA) finds a linear projection that maximizes inter-class separability and minimizes intra-class distance. Through this dimensionality reduction step, data can be classified under the Gaussian distribution and equal covariance matrix assumption. The latter one can be circumvented by quadratic discriminant analysis. Unlike LDA, Support Vector Machines (SVM) are motivated by statistical learning theory and do not provide probability estimates. Individual training points resemble the decision functions, which are called support vectors. Through optional non-linear data transformation and regularization, support vector machines represent a high dimensional effective, memory efficient and well performing classification and regression method. Different non-linear models, such as Classification and Regression Tree (CART) based methods, like random forests, provide nontrivial splitting strategies that implicitly generate novel features. Such non-linear models could be used for multimodal embedding (Gray et al., 2013), for example by adding boosted decision tree outputs as inputs to linear classifiers (He et al., 2014). In addition to feature generation, CART methods can successfully incorporate categorical and continuous features without additional architecture adaptation (Dorogush et al., 2018). Data samples are segmented into leaf nodes, combining features in a non-linear and hierarchical manner. This constitutes a different approach to neural networks, where features are linearly weighted and non-linearly scaled by an activation function before being combined.

Furthermore, compared to other ML methods, CART methods can handle feature combinations without the need of feature scaling (e.g. min-max scaling or rank transformation). Deep learning methods, on the other hand, allow for automated spatio-temporal feature extraction and are designed to beneficially incorporate known preprocessing steps (Chung et al., 2014; Miotto et al., 2018; Vaswani et al., 2017), leading to what are known as end-to-end architectures (Arik and Pfister, 2019). Interestingly, hybrid combinations of deep learning and CART methods were shown to outperform deep learning and CART methods individually on a wide range of non-neurophysiological tabular datasets, e.g. for predicting cartographic variables (Arik and Pfister, 2019). Such combinations may be valuable for invasive neurophysiology research but have not been reported in this setting to date.

For most model architectures feature importance measures are defined. For linear regression and statistical models such as LDA or SVM, the associated coefficient values or solution vectors can be evaluated with respect to feature – target relationships. On the other hand, CART methods can define feature importance through mean performance change of the splitting criterion. Here, in specific use-cases feature importance can be estimated after the definitive performance evaluation on the test set to prevent influence from model overfitting. In particular, test set estimated permutation scores of non-correlated features, “column drop” methods in addition to other approaches have been proposed (Lundberg et al., 2020). Interpretability for deep learning methods can be achieved through perturbation methods, which have been successfully applied to convolutional neural networks (CNN) (Zeiler and Fergus, 2014). Backward pass activation contributions can be calculated by the commonly applied DeepLIFT method (Shrikumar et al., 2017), and Shapley additive explanation approaches have been described for deep learning methods (Lundberg and Lee, 2017). For the specific domain of interpretable invasive decoding, Petrosyan et al. proposed an interpretable CNN architecture (Petrosyan et al., 2021). It should be noted that ‘important’ features identified by these approaches may not be guaranteed to bear any direct statistical dependency to the predicted target variable themselves – their predictive value may derive from a conditional dependency through other features. Different architectures such as hidden Markov models were shown to learn behavioral states and can also be used to generate data in order to validate identified states (Sun et al., 2020). This semi-supervised generative approach thus yields high model interpretability.

To conclude, a great variety of machine learning models can be used for invasive neurophysiology decoding. A list of the most relevant studies that have used ML models in this context are summarized in Table 1. The advantages and disadvantages of each method are described as well as the interpretability of the learned model.

5. Validation strategies

5.1. Data splitting strategies

In order to obtain a meaningful estimation of performance, this performance must be estimated on data that was not seen before, in particular not for feature selection/engineering and not for hyperparameter selection. Machine learning models are only able to generalize well in real-time applications if the feature engineering and hyperparameter optimization have been validated and tested on data (generally with label information) that are not part of the training and optimization procedure. That is, data should be split in at least two parts: the training set for learning the model, and the testing set to evaluate the model. When hyperparameters are being learned, it is also recommended to split training data into a training and validation set. In the case where just one dataset is available and validation is not possible on additional data, cross-validation must be used. The simplest cross-validation strategy is to randomly split or hold out 30% of the dataset for testing, while using 70% for training. Importantly, in comparison to other machine learning problems, neural time-series are temporally dependent. For example, in image classification, one image (i.e. of a cat) is independent of the next image (i.e. of a dog). For such problems, the data can simply be randomly held out. When working with time-series data, each sample can be partly predicted by the previous and next one. That is particularly true if the features are already in the frequency domain, where amplitude of oscillations can by definition only be estimated as part of an oscillation that consists of multiple samples. Therefore, training and testing folds should consist of consecutive data chunks, e.g. for a target variable with meaningful changes at a pace of 5 s, one should take out ~5 s of consecutive data instead of multiple single samples or 100 ms snippets. Not adhering to this will lead to two problems, first random shuffling of single samples will not enable the model to learn time dependencies and second the model will overfit, because neighboring samples can populate both training and test sets, while being highly correlated and violating the training test set label independence assumption. This could lead to artificially inflated test set performances, which would not survive further validation e.g. in a novel real-time prediction or across patient scenario.

The split into training and test sets can be repeated multiple times. In particular, in the k-fold cross-validation strategy, data is partitioned into k subparts or folds, where each fold is the test hold-fold once, while the model is trained on the remaining k-1 folds. The resulting performance is then the average performance across all testing folds. Given that the entire dataset is utilized for both training and testing, the model evaluation has lower bias than when random split is being used. When working with datasets of segmented blocks or groups, a group shuffle split k-fold cross validation is advised (Fig. 4). In the context of movement decoding, individual resting or movement blocks can be specified for training or testing respectively. To counteract imbalances, data can either be up- or downsampled, or class weights can be attributed within the training cost function.

Fig. 4.

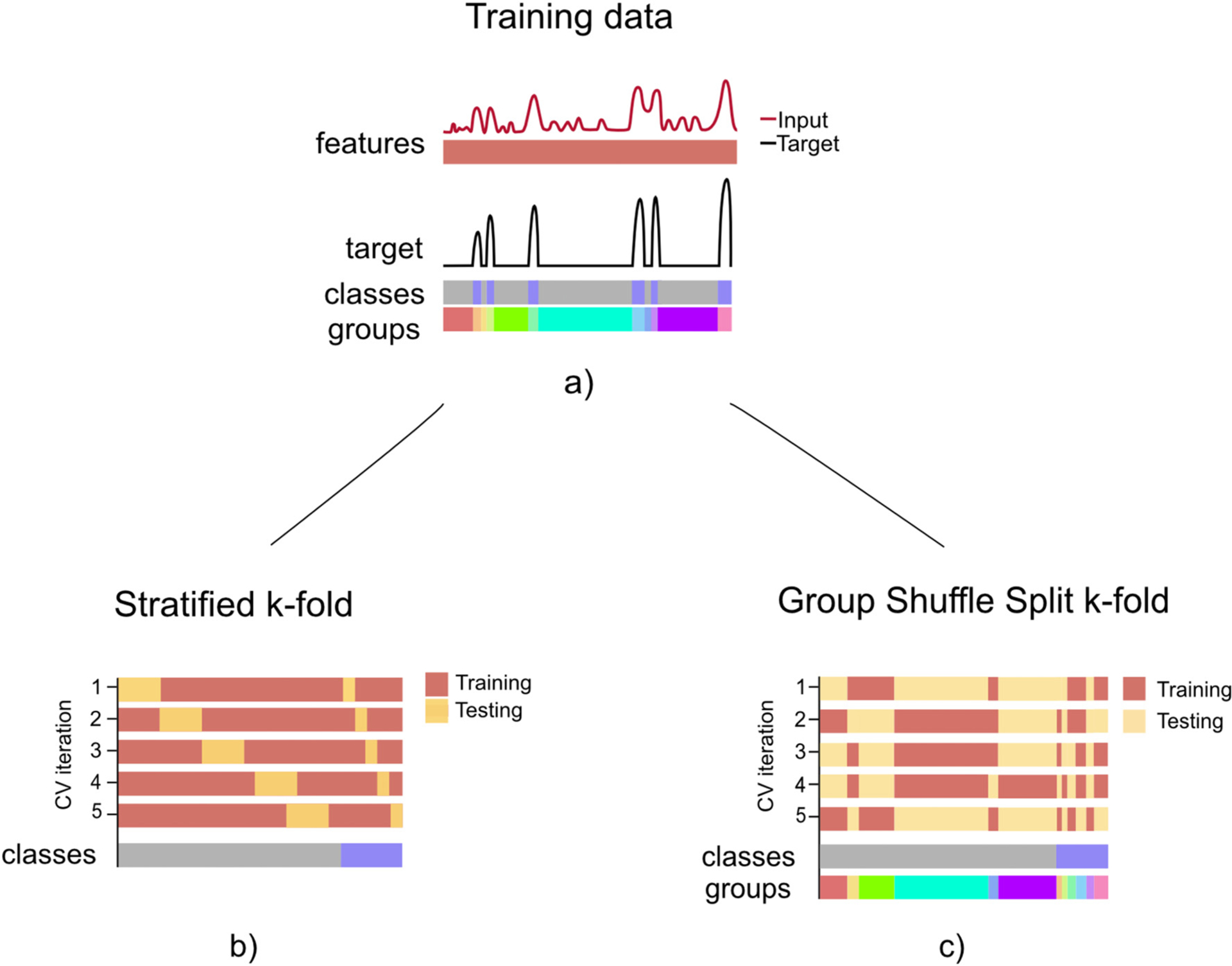
Schematic representation of different k-fold cross-validation (CV) strategies. a) Training data, corresponding to an input vector of features (red) and an output target vector (black), e.g. movement trace, where two classes are involved and same sized groups are defined according to movement/no movement consecutive data chunks. b) In the standard stratified k-fold CV data is split into train and test sets, preserving class ratios in both sets. c) For invasive neurophysiological decoding we propose a group shuffled split k-fold CV strategy. While in the stratified k-fold CV class distributions are preserved along the CV iterations, features coming from the same group can be used for training and testing. The group k-fold CV ensures that group structure is preserved during training and testing set construction, but information about individual group blocks may not be preserved. For imbalanced class distributions data can either be rebalanced or cost function weights can be attributed class specific.

Different strategies for splitting neural time-series data in a cross-validation (CV) scheme are highlighted in Fig. 4. For this exemplary scenario, training data (Fig. 4a) comprises an input array of features and an output array of classes (i.e. movement, no-movement). When the stratified k-fold strategy is being used, the class proportion is aimed to be preserved along the CV splits. When working with time-series data, the CV iterations should be constructed without shuffling single samples (Fig. 4b stratified k-fold). Although, this strategy can be used for working with time-series data, the temporal relationship between two consecutive segments of different classes is disregarded. This could influence test performance, when not considered in the training and testset design, for example through introducing incremental group affiliations for multiple occurrences of the different classes. The k-fold CV cannot guarantee that features coming from a given group will appear in only either of the sets. Grouping data can be an important step for time-series training/test splitting strategies, since consecutive feature or raw data samples can show high temporal correlations. Additionally, when working with imbalanced datasets, there might be a need to balance the class distributions when training. This can be conducted by means of adding associated weights of class proportions to groups and constructing the training set with resampling strategies over the morerepresented class (here, non-movement). This proposed strategy is shown in Fig. 4c, in which some groups of the higher represented class are randomly discarded when constructing the training set. In addition, training and testing sets are constructed considering group definitions, and thus it guarantees that a group will be used entirely in one of the datasets. During training, the information regarding class-ratio is added as weights.

When learning multi-subject models, the leave-one-patient-out strategy is the most commonly utilized approach. It has the advantage of learning from other subjects the problem at hand, but subject-specific features that could improve performance for that individual, can be missed during the training. For such scenarios, transfer learning strategies should be applied to transfer domain specific features to a different data aspect, such as the recording hardware used, the surgical implantation technique, medications, disease progression and other potential sources of bias.

Regardless of the model training strategy, it is of utmost importance that ML-based studies report in detail how data was partitioned, to verify that there is always a testing set that has never been used during the model learning process.

5.2. Performance indices

Machine learning applications are usually optimized with respect to a certain performance measure. The general separation lies here between regression, where continuous values can be learned (e.g. grip force) and classification, where categorical or discrete values should be assigned to data to predict the class membership (e.g. tremor vs. no tremor present). Defining the evaluation metric is an important domain-knowledge driven process. Optimally, for application of machine learning in the medical field this is conducted in interdisciplinary discussions with clinical experts and practicing medical advisors. The model evaluation metric should be representative of the medical treatment and desired outcome. With respect to movement actuated deep brain stimulation, false positive and false negative predictions should not be treated in an equal fashion. The therapeutic risk of not applying stimulation in a critical setting (false negative) may be higher than applying stimulation when not needed (false positive), since the current standard is the uninterrupted delivery of electrical stimulation. In concordance with the medical evaluation requirement, the machine learning model can also be trained and optimized according to certain metric definitions (Nedel’ko, 2018). Therefore, the model choice is highly affected by the chosen performance measure. Additionally, distribution imbalances of the state that is to be predicted should be investigated to mitigate potential danger from biased results in both regression and classification problems.

5.2.1. Regression

The most common regression metrics are mean absolute error (MAE), mean squared error (MSE), correlation coefficient R, coefficient of determination R² and Spearman’s correlation ρ. With respect to distribution balance, it is important to assess if regression events occur with a certain ratio which are also expected in test data and the real time application. For example, decoding of gripping force can be affected by the number and duration of gripping events with respect to a resting condition. Therefore, data subsampling of regression groups can be a performance beneficial method. Defining the model optimization metric according to the model evaluation metric would also be an optimal training approach. For example, the mean squared error could be used as a deep neural network loss function as well as performance metric report. In summary, for regression problems, the aim is to predict a continuous variable. The variance of that variable in the training data should reflect that entire spectrum of expected occurrence in a balanced way. Finally, performance for regression is often the Mean Squared Error, i.e. the difference between predicted and ground truth target, which can be used to assess model performance and can be plugged in to the model optimization process, i.e. as the loss function.

5.2.2. Classification

Common classification metrics are accuracy, area under the curve (AUC), F1 score, sensitivity, precision and quadratic weighted kappa. In a review of 154 papers on Deep Learning methods for EEG published from 2010 till 2018, by far the most common performance metric was accuracy, defined as the percentage of correct classifications of the test set. Accuracy is being used in more than 70% of all classification problems (Roy et al., 2019). Unfortunately, accuracies can be highly biased if class label distributions are not balanced. If data is unbalanced (see section above), it is important to report the class label ratios. Cross validation methods can then weight the class frequencies for training sets, but the reported metric on the test however should be without any resampling adjustment, to approximate real time applications as close possible. Special attention needs to be taken, when reporting performance indices for baseline or above chance classifications, that can yield significant results if the model predicts only the more prevalent class. For example in a setting where most samples are considered to be a “resting class” and fewer samples belong to a “movement class”, a model that always predicts presence of the resting class will give seemingly above-chance results, but would be useless in a real-world scenario. Therefore, the precision-recall area under the curve (AUC-PR) performance metric is in some cases advised to be chosen over the commonly used receiver operating characteristic area under the curve (ROC-AUC). The researchers should make an informed decision about the correct metrics to be used. In general, confusion matrices can help the interpretation of classification performance. As an example, for seizure predictions it is common to report not only the sensitivity, but also the false positive rate per hour (Zhang and Parhi, 2016), which will help to determine the relationship of true and false alarms in a clinical application.

6. Decoding human behavioral states for adaptive DBS

For conventional deep brain stimulation, a chronic DBS parameter setting including active stimulation contact, stimulation frequency, pulse width and amplitude is programmed by an experienced clinician and iteratively optimized according to the patient’s reports. Consequently, DBS parameter adjustments are inherent compromises to accommodate “one setting fits all situations” solutions, without the ability to accommodate dynamic fluctuations of therapeutic demand. Strategies to understand potential input signals have been initiated, using electrophysiological biomarkers of certain symptom states. In the case of movement disorders, a direct measurement of the motor or symptom state may be achieved directly via accelerometry or electro-myography (EMG) (Cagnan et al., 2017; Malekmohammadi et al., 2016). One of the very first case reports on the use of adaptive DBS for essential tremor used EMG of the deltoid muscle for triggering stimulation (Brice and Mclellan, 1980). As an alternative to recording the motor activity itself, the patient’s behavioral state can be indirectly assessed through intracranial electrophysiology recordings. This approach provides the substantial advantage that no additional external sensing device is needed. In addition, by using neurological sensors it is possible to anticipate the need for changes in stimulation settings by predicting symptoms or actions before their onset (Khawaldeh et al., 2020; Meisel and Bailey, 2019; Ryun et al., 2014; Zhang and Parhi, 2016). Such intracranial measurements may be obtained from ECoG electrodes, microelectrode arrays, or even from DBS electrodes themselves. The use of DBS lead electrodes as the sole sensing device could potentially eliminate the need for additional intracranial implants. While the first successful studies on aDBS relied on single biomarkers (e.g. beta activity) with predefined thresholds, intracranial recordings can also be used to train ML algorithms that learn to infer the patient’s needs and that can determine the optimal stimulation parameters.

To date, only a few investigations implementing ML methods to directly adapt DBS parameters in humans have been published. Table 2 summarizes these works. All studies were performed with patients undergoing DBS implantation for ET. Most notably, the feasibility of a fully embedded long-term, ML-based stimulation protocol in an out-of-clinic setting was recently demonstrated in three ET patients (Opri et al., 2020). Stimulation was delivered whenever the pre-trained, individual patient-tailored algorithm detected movement or tremor-provoking postures from ECoG signals using LDA classifiers (see section above). Follow-up performance, training and clinical results were reported to be stable with dramatically reduced stimulation times at comparable clinical outcome that was stable over the reported time-period. Among the implemented ML algorithms were LDA classifiers (Ferleger et al., 2020; Opri et al., 2020) and a logistic regression classifier (Houston et al., 2019), all relying on additional ECoG electrodes. Two published investigations estimated pathological tremor intensity (as a regression problem) from intracranial signals (Castaño-Candamil et al., 2020a; He et al., 2021) of which one study implemented a non-binary stimulation paradigm which adjusted stimulation intensity according to tremor severity (Castaño-Candamil et al., 2020a).

Table 2.

Studies demonstrating intelligent adaptive DBS with machine learning approaches.

Investigated states	Recording location	Recording modality	Features	Models	Performancea
Essential Tremor
Houston et al. (2019) Tremor-provoking postures Upper limb movements	Primary motor cortex Primary somatosensory cortex	ECoG	BP in patient-specific bins from the theta-beta range (4–28 Hz)	Logistic regression	Accuracy: 0.75–0.84 Sensitivity: 0.77–0.81
Opri et al. (2020) Tremor-provoking postures Upper limb movements	Primary motor cortex	ECoG	BP in 1 or 2 “low-frequency“bands	LDA	Accuracy: 0.86–0.96
Ferleger et al. (2020) Upper limb movements	Thalamus, VIM Primary motor cortex	LFP ECoG	VIM: beta-BP Cortex: gamma-BP	LDA	Error Rate (1-Accuracy): 0.12–0.57
Castaño-Candamil et al. (2020a) Postural tremor intensity	Primary motor cortex	ECoG	BP in 8 frequency bins (3–25 Hz)	Linear classifier	Pearson correlation coefficient: −0.15–0.39
He et al. (2021) Tremor-provoking postures Upper limb movements	Thalamus, VIM Zona incerta	LFP	BP in 8 frequency bands (1–195 Hz) Hjorth parameters Mean signal	Logistic regression LDA SVM Naïve Bayes Decision tree k-NN	Accuracy: Movement: 0.84/0.83 Tremor: 0.82/0.79 (SVM)

BP – band power; ECoG – Electrocorticography; k-NN – k-nearest neighbors; LDA – Linear discriminant analysis; LFP – Local field potential; STN – subthalamic nucleus; SVM – Support vector machine; VIM – ventral intermediate nucleus.

^aClassification performance is not strictly comparable between studies, as design of the performance metrics was highly variable. If more than one algorithm was compared, only the score of best-performing algorithm is reported in this table.

While almost all investigations relied on signals obtained from either ECoG or a combination of ECoG and subcortical LFP, a single study reported the successful implementation of a ML-based stimulation paradigm based solely on LFP recordings (He et al., 2021). The authors implemented an algorithm detecting voluntary movement and tremor-provoking postures which then triggered electrical stimulation in a cohort of 8 ET patients. A number of different ML-architectures were compared offline (see first row in Table 2). Based on the best offline decoding performance, an SVM-based classifier was chosen for online aDBS testing. This report was the only study to use features from the time and statistical domain and additional features derived from a wide spectrum in the frequency range (1–195 Hz).

When moving toward more refined stimulation paradigms, a broad spectrum of conditions should be detected from intracranial recordings. Tables 3 and 4 provide examples of studies exploring ML methods for the detection of pathological and physiological human states. Potential target states for aDBS comprise disease-specific symptoms or medication-induced side effects, as well as physiological activities such as sleep, speech or eating. In Parkinson’s disease (PD) patients, prediction of resting tremor (Bakstein et al., 2012; Camara et al., 2015; Hirschmann et al., 2017; Pan et al., 2012; Wu et al., 2010; Yao et al., 2020c), dyskinesia (Swann et al., 2016), and states of hypo- and hypermobility representing ON/OFF dopaminergic medication fluctuations (Gilron et al., 2021) have been demonstrated. In Tourette syndrome detection of tics (Shute et al., 2016) and in epilepsy patients’ prediction of seizures (Chisci et al., 2010; Meisel and Bailey, 2019; Zhang and Parhi, 2016) have been reported. As a consequence of their importance in day-to-day life, the dynamics of upper limb movements have been addressed by a number of studies. Apart from the separation of a general state of upper limb activity during sitting and walking (Haddock et al., 2019) promising results have been reported for the more specific decoding of finger movement (Liang and Bougrain, 2012; Quandt et al., 2012; Xie et al., 2018; Yao and Shoaran, 2019), reaching gestures (Bansal et al., 2012; Bundy et al., 2016; Nakanishi et al., 2013) and gripping force (Jiang et al., 2020; Merk, 2020; Merk et al., 2021; Shah et al., 2018; Tan et al., 2016). Moreover, neural signals during the pre-movement period contain a significant amount of information about the task to be performed. It has been demonstrated that this information can be leveraged to make predictions about the nature of a movement even before its onset (Khawaldeh et al., 2020; Loukas and Brown, 2004; Ryun et al., 2014). Other investigations have studied the decoding of swallowing (Hashimoto et al., 2020), sleep (Sun et al., 2020), mental fatigue (Yao et al., 2020a) and mood (Kirkby et al., 2018; Sani et al., 2018).

Table 3.

Machine learning studies for decoding of pathological states from intracranial recordings.

Investigated states	Recording location	Recording modality	Features	Models	Performancea
Epilepsy
Zhang and Parhi (2016) Preictal/interictal state	Three focal, three extrafocal electrodes	ECoG	3 features each in 8 frequency bins (4–128 Hz): Absolute BP Relative BP BP ratio	Cost-sensitive linear SVM	Sensitivity: 1.0 FPR: 0.0324 per hour
Meisel and Bailey (2019) Preictal/interictal state	Three focal, three extrafocal electrodes	ECoG EEG EKG	Average PSD across all channels PSD of single channels EKG PSD	Deep learning k-NN SGD AdaBoost	IoC-F1 score: ≈ 0.7
Essential Tremor
Tan et al. (2019) Postural tremor Upper limb movements	Thalamus, VIM	LFP	BP in 8 frequency bands (1–195 Hz)	Logistic regression	AUC: Movement: 0.74–0.99 Tremor: 0.79–0.88
Parkinson’s Disease
Gilron et al. (2021) Dyskinesia Mobile and immobile states labelled by Parkinson’s KinetiGraph watch	STN Primary motor cortex	LFP ECoG	STN: BP of peak frequency in beta band Cortex: BP of peak frequency in gamma band LFP-ECoG coherence	LDA Supervised clustering Unsupervised (density-based) clustering	ROC-AUC: 0.81–1.0 Clustering concordance: 74%
Swann et al. (2016) Dyskinesia	STN Primary motor cortex	LFP ECoG	BP in 2 Hz-bins (2–50 Hz) (Phase-) coherence	Logistic regression	ROC-AUC: 0.8–0.94
Hirschmann et al. (2017) Resting tremor	STN	LFP	BP at tremor frequency Beta-BP Low gamma-BP HFO BP ratio	Hidden Markov models	Accuracy: 0.84 ROC-AUC: 0.82
Yao et al. (2020c) Resting tremor	STN	LFP	BP Hjorth parameters Entropy PAC Tremor power Peak tremor power	XGBoost LDA Logistic Regression SVM (RBF and linear) MLP-NN Random forest	F1 score: 0.88 (XGBoost)
Camara et al. (2015) Resting tremor Tremor subtypes Across-patient classification	STN	LFP	5 features each in 6 frequency bins (3–30 Hz): energy, average, variance, first derivative, entropy	K-means clustering MLP-NN	Accuracy: 0.64–1.00 (0.90 mean)
Tourette Syndrome
Shute et al. (2016) Tics Upper limb movements	Primary motor cortex Thalamus, CM-PF	ECoG LFP	BP of three 10 Hz-bins (1–100 Hz)	SVM	Recall: 0.39–0.89 Precision: 0.37–0.96

AUC – Area under the curve; CM-PF - centromedian-parafascicular complex; ECoG – Electrocorticography; HFO – High-frequency oscillation; IoC – Improvement over chance; k-NN - k-nearest neighbors; LDA – Linear discriminant analysis; LFP – Local field potential; MLP-NN – Multi-layer perceptron neural network; PAC – Phase-amplitude coupling; PSD – Power spectral density; RBF – radial basis function; ROC – Receiver operating characteristic; SGD – Stochastic gradient descent; STN – subthalamic nucleus; SVM – Support vector machine; XGBoost – Extreme gradient boosted decision tree.

^aClassification performance is not strictly comparable between studies, as design of the performance metrics was highly variable. If more than one algorithm was compared, only the score of best-performing algorithm is reported in this table.

Table 4.

Machine learning studies for decoding of physiological states from intracranial recordings.

Investigated states	Recording location	Recording modality	Features	Models	Performancea
Upper limb movements
Haddock et al. (2019) Upper limb movements	Primary motor cortex Primary somatosensory cortex	ECoG	BP in beta band (12–30 Hz) Raw signal	LDA SVM Deep NN	Accuracy: 0.79–0.92 (Deep NN)
Xie et al. (2018) Flexion/extension of individual fingers	Frontal/temporal/fronto-temporal	ECoG	Feature extraction via convolutional NN (LSTM) Amplitude modulation in 3 frequency bands (1–200 Hz)	Recurrent NN LARS Random forest	Correlation coefficient: 0.13–0.79 (Recurrent NN)
Shah et al. (2018) Gripping Force	STN	LFP	BP in 10 frequency bands (5–500 Hz) Hjorth parameters Mean raw signal	Wiener cascade model Dynamic NN Kalman filter	Correlation coefficient: Up to 0.79
Tan et al. (2016) Gripping Force	STN	LFP	BP from 3 frequency bands (4–90 Hz)	Linear dynamic model	Correlation coefficient: 0.38–0.94
Motor onset/intention
Khawaldeh et al. (2020) Upper and lower limb movements	STN	LFP	BP from 9 frequency bands (8–500 Hz)	Naïve Bayes classifier	ROC-AUC: 0.8
Ryun et al. (2014) Upper limb movements	Prefrontal area Primary sensorimotor Premotor and supplementary motor	ECoG	BP from patient-specific frequency bands (1–80 Hz)	SVM (linear)	Accuracy: 0.55–0.9 (mean: 0.74)
Swallowing
Hashimoto et al. (2020) Mouth open Water injection Swallowing	Lateral sensorimotor (“orofacial”) cortex	ECoG	Raw signal Band-pass filtered signal (1–200 Hz; 6 bands) Envelope signal BP	Deep learning: AlexNet transfer learning)	Accuracy: 0.77 (raw signal) 0.74 (high gamma BP)
Sleep
Sun et al. (2020) Sleep/wake	Superior frontal gyrus	ECoG	BP (1–40 Hz)	k-means clustering HMM HSMM	Accuracy: 0.85 (HSMM)
Mental fatigue
Yao et al. (2020a) Non-human primates Mental fatigue	Occipital, temporal, frontal cortices and midline structures	ECoG	BP (1–200 Hz) Wavelet entropy Hjorth parameters PAC, PDC, PLI IA (delta), IF (alpha), IA/IF ratio	XGBoost	F1 score: 0.75–0.86
Multiple behavioral states
Golshan et al. (2018a, 2018b) Speech Finger movement Arm movement Rest	STN	LFP	Beta-band time-frequency features (10–30 Hz) Phase-synchronization	Hierarchichal MKL-based SVM	Accuracy: 0.64–0.82

AUC – Area under the curve; ECoG – Electrocorticography; HMM – hidden Markov model; HSMM – hidden semi-Markov model; IA – Instantaneous amplitude; IF – Instantaneous frequency; LARS – Least angle regression; LDA – Linear discriminant analysis; LFP – Local field potential; LSTM – Long short term memory; LVQ – Learning vector quantization; MKL – Multiple-kernel learning; NN – Neural network; PAC – Phase-amplitude coupling; PDC – Partial directed coherence; PLI – Phase locking index; PSD – Power spectrum density; ROC – Receiver operator characteristic; STN – subthalamic nucleus; SVM – Support vector machine; XGBoost – Extreme gradient boosted decision tree.

^aClassification performance is not strictly comparable between studies, as design of the performance metrics was highly variable. If more than one algorithm was compared, only the score of best-performing algorithm is reported in this table.

An intelligent aDBS algorithm should not only be capable of distinguishing few, specific tasks, such as predefined reaching trajectories, but should discriminate between a variety of general behavioral states. The feasibility of successful classification of the actions “button press”, “speech”, “mouth movement”, and “arm movement” was demonstrated using a hierarchical, multiple kernel learning-based SVM classifier (Golshan et al., 2018a, 2018b). However, obtaining training data from a range of possible behavioral states from every single patient undergoing DBS implantation would potentially require hours of training. This would be a burden for patients and medical staff and would require a considerable amount of hospital resources. In our opinion, it is therefore of utmost importance to develop decoding strategies that can generalize predictions across patients. Therefore, each patient would only require a minimal amount of additional training before models can predict pathological and behavioral states. As an example, such across-patient decoding has already been successfully demonstrated for parkinsonian resting tremor (Camara et al., 2015; Hirschmann et al., 2017).

7. Putting it all together: real-time decoding

Real-time decoding implies additional machine learning model constraints for adaptive neuromodulation. An important aspect is to construct a real-time applicable model training and evaluation. For example, when normalization is to be applied, it becomes mandatory to normalize features only using previous training data time segments, and thus avoiding circular model training. An additional constraint lies in feature computation time and thus model inference duration. Multicore processors can use multithreading or pooling to distribute feature extraction modules on multiple cores. In an implanted pulse generator though, energy consumption constraints and memory efficiency become crucial. Therefore, relevant features need to be identified prior to real-time application. Ideally in the future, this process becomes independent of patient individual training. In a preliminary analysis it was successfully shown that movement could be decoded across patients with varying ECoG strip locations, thus patient individual model training may not be necessary in the future (Merk, 2020). In a similar vein, PD tremor has been successfully decoded across patients using hidden-Markov models (Hirschmann et al., 2017). The performance gain and additional effort spent on patient specific training are a tradeoff that needs further investigation. Adaptive machine learning methods were previously proposed for invasive seizure prediction using an active learner based on a Bernoulli-Gaussian mixture model (Karuppiah Ramachandran et al., 2018). Through recent advances in mobile technology, size and efficiency optimized models became a major research topic in machine learning (David et al., 2020; Howard et al., 2017). Impressive first closed-loop embedded hardware algorithms were investigated by Zhu et al. (Zhu et al., 2020b). Power efficient oblique trees, using weight pruning and sharing, showed significant reduction in power consumption and model size for different neural decoding tasks, while keeping performance comparable to gradient boosted trees (Zhu et al., 2020a). To overcome noisy model prediction fluctuations, Kalman filtering can be used to smooth the respective estimate for improved stability of the output prediction.

8. Discussion and practical considerations

Recent advances in machine learning have opened new venues for the development of algorithmic solutions in different areas of healthcare, paving the way for neurotechnological therapies that are adapted to the individual patients’ needs. In this review, we showed that a variety of machine learning models have already been successfully applied in the context of invasive neuromodulation (Castaño-Candamil et al., 2020a; Ferleger et al., 2020; He et al., 2021; Houston et al., 2019; Opri et al., 2020). Fundamental aspects of the development of an intelligent ML-based aDBS device were analyzed in detail.

When working with neurophysiological data for brain signal decoding, the choice of accurate features becomes highly important for the identification of robust and stable biomarkers. Most of the existing works use frequency-domain features to characterize modulation of oscillatory amplitude or coupling in relation to the problem at hand. Statistical features have also been evaluated, of which the Hjorth parameters are the most widely used. Time-domain features such as non-sinusoidal waveform shape asymmetry may be a promising new type of neural feature in parkinsonian patients. Although network connectivity analysis is widely used to characterize different diseases, its usage in the context of invasive neurophysiology-based brain signal decoding remains relatively unexplored. In particular, PAC features seem to be favorable for estimating the therapeutic effects of DBS in PD patients (De Hemptinne et al., 2015) as well as for characterizing parkinsonian symptoms, such as rigidity and bradykinesia (Tsiokos et al., 2017), but PAC is notoriously difficult to estimate in real-time. Similarly, despite the fact that spatial pattern analyses like CSP and SPoC have shown to be powerful and easy to implement feature extraction methods in the area of brain-computer interfaces, they have not yet been applied in the context of aDBS (Peterson et al., 2021). Exploring the use of such spatio-spectral features may help the future development of brain signal decoders for invasive neuromodulation. Feature engineering can help to define optimal feature sets based on thoroughly characterized brain signal biomarkers. It is expected that the better the feature representation is, the lower the complexity of the model architectures needs to be. Thus, it is important that research groups working in the development of aDBS algorithms are working as transparent, open and interdisciplinary as possible.

To construct reliable models for real-life application, care must be taken in how data is treated during the learning process of the ML model. Caveats for model validation, target metric choice and real-time compatibility should be considered. We point out that for avoiding pitfalls in between training and testing a model, every step that comprises the ML architecture should be done by considering online applications. That is, filter design, normalization scheme, feature extraction and decision rule learning should be fully real-time compatible. In addition, care must be taken when working with unbalanced data. The selection of proper data splitting strategies as well as performance indices that are appropriate for such biased data is crucial for avoiding misleading results and interpretations with respect to clinical utility. A description of the different machine learning models already used in the context of invasive neurophysiology, highlighting the advantages and disadvantages, was also provided in the sections above. A special emphasis was placed on interpretability of each described model. An ideal model for the context of aDBS development should be accurate, have low computational complexity during prediction and should be easy to interpret. In this regard, simple models show higher generalization performance and interpretability than more complex models. In addition, simple models are more easily implemented; e.g. linear discriminant analysis or classification and regression trees can be implemented in energy and model size constrained real-time embedded environments (Opri et al., 2020; Rouse et al., 2011; Zhu et al., 2020a). When considering more complex models, such as deep neural networks, it is extremely important to work with large and diverse labelled data-sets. Most of the practical applications in which deep learning has already positioned itself as the best possible ML architecture have used extensive amounts of labelled data. To put this into perspective, machine learning challenges for computer vision routinely use more than 15 million labelled images for training (Krizhevsky et al., 2017). Currently, it is estimated that roughly ~200.000 patients (Lozano et al., 2019) have received DBS treatment, and machine learning based aDBS has been reported in less than 20 cases, usually using recording periods in the range of minutes. Unlike in other ML domains, few datasets are publicly available, hampering not only the evolution of new algorithmic solutions, but also the comparison across different approaches and publications. We therefore encourage the community to create a comprehensive code and data sharing environment. For example, following the publication of an openly available dataset on the Kaggle platform, outstanding model architectures and preprocessing pipelines were proposed for seizure prediction using intracranial EEG recordings (Kuhlmann et al., 2018). We encourage the reproducibility via presenting data and analyses with sufficient transparency, so that experiments can be reproduced and applied beyond the original study. Large datasets and multicohort validation strategies will significantly accelerate clinical machine learning applications.

By utilizing machine learning methods for behavioral state decoding, DBS treatment can be highly personalized. Control parameters can be adapted in a faster and demand-only actuated manner, to reduce side effects due to unnecessary or unwanted stimulation. In addition to traditional pathological biomarker-based DBS, ML driven aDBS may additionally inform stimulation parameters without relying on disease specific activity and may help support aDBS approaches, e.g. using movement decoding for PD, ET, dystonia and other movement disorders.

9. Conclusions and outlook

Machine learning algorithms for designing neural decoding models open a vast field of possibilities for the evolution of aDBS devices. In this review, we analyzed features and machine learning architectures that have been or could in future be applied in the context of invasive neurophysiology-based adaptive neuromodulation. A comparison across methods was performed to provide the reader with guidelines to choose or design a suitable decoding model. In addition, we emphasized that such methods should always be implemented considering online (i.e., real-time) applications, even when offline experiments are conducted. The development of future intelligent aDBS devices strongly depends on multidisciplinary research teams, publicly available datasets, open-source algorithmic solutions and stronger world-wide research collaborations.

Abbreviations:

aDBS

adaptive deep brain stimulation

cDBS

conventional deep brain stimulation

iDBS

intelligent adaptive deep brain stimulation

ML

machine learning