Inferring the shape of data: a probabilistic framework for analysing experiments in the natural sciences

Abstract

A critical step in data analysis for many different types of experiments is the identification of features with theoretically defined shapes in $N$-dimensional datasets; examples of this process include finding peaks in multi-dimensional molecular spectra or emitters in fluorescence microscopy images. Identifying such features involves determining if the overall shape of the data is consistent with an expected shape; however, it is generally unclear how to quantitatively make this determination. In practice, many analysis methods employ subjective, heuristic approaches, which complicates the validation of any ensuing results—especially as the amount and dimensionality of the data increase. Here, we present a probabilistic solution to this problem by using Bayes’ rule to calculate the probability that the data have any one of several potential shapes. This probabilistic approach may be used to objectively compare how well different theories describe a dataset, identify changes between datasets and detect features within data using a corollary method called Bayesian Inference-based Template Search; several proof-of-principle examples are provided. Altogether, this mathematical framework serves as an automated ‘engine’ capable of computationally executing analysis decisions currently made by visual inspection across the sciences.

1. Introduction

Across the physical and life sciences, many experimental techniques rely upon pragmatic data analysis steps where an expert researcher is required to make scientific decisions based on their visual perception of data. This perception involves identifying and recognizing correlations between datapoints that stem from underlying physical processes, which are ideally invariant across experiments; we refer to these correlations as the latent structure of the data. Latent structure manifests visually in what we would colloquially call the ‘shape’ of the data and is the basis for inspection-driven analysis decisions. For example, an expert researcher might have to visually identify a feature of interest by recognizing an expected shape in a plot of their data (e.g. a shoulder on a peak in a molecular spectrum). Alternatively, such a researcher might anticipate the location of an expected feature within their plotted data (e.g. a peak at a specific frequency in a molecular spectrum), but must then decide whether it is actually present at that location. In these types of determinations, the researcher must generate at least two visual models of a phenomenon, manually compare those models with the shape of their experimental data and then choose the model that, in their expert opinion, best describes the data. To be explicit, in the aforementioned first example, the researcher visually compares both the shape of a peak and the shape of a peak with a shoulder with the experimental molecular spectrum. Similarly, in the second example, the researcher visually compares both the shape of a peak and the shape of signal-free background noise with the experimental molecular spectrum.

A key advantage of such expert-driven analyses is the human ability to make accurate, informed decisions about the latent structure of experimental data, even in the absence of a full theoretical description of the phenomenon of interest. For instance, while the spectral line shapes of peaks in molecular spectra arise due to physical processes with well-established theoretical foundations, a full quantum mechanical calculation is generally not required to determine whether a certain peak exists at a particular location, nor whether it has a shoulder. Instead, approximate models of the shape of a peak, guided by a researcher’s physics-based intuition and years of experience, are usually sufficient for the level of analysis required for these problems. Having considered all the models they deem appropriate, the expert researcher then decides which of those models is the best description of their data and, thus, is best supported by the available evidence.

Such researcher-dependent approaches to data analysis create major practical, quantitative and scientific challenges. An obvious difficulty is the time required for manual data processing, which limits a researcher’s output and productivity. Another is simply the learning curve required to perform visual inspection-based analysis tasks—an extensive amount of training is required before an inexperienced researcher can build enough physics-guided intuition to accurately and reliably interpret experimental data. Yet another obstacle is the lack of a quantitative metric for assessing the confidence that one should have in one’s own or someone else’s analysis decisions, especially in cases of conflicting results. The lack of such a quantitative confidence metric makes it similarly difficult to validate or replicate such visual inspection-based analyses. Most importantly, there exist fundamental barriers that inhibit precise communication of the details of these analyses: namely, the intrinsic complexity of describing in writing the exact details of a method performed within one’s mind, and conversely, of understanding the details of such a method solely by reading a description of it. All of these challenges are exacerbated as scientific research fields progress towards more quantitative, data-driven approaches, and as more techniques are developed that yield larger amounts of increasingly more complex data, as is systematically occurring with, for instance, the advent of ultrahigh-throughput methods [1,2].

In contrast to such human-dependent approaches, here we have developed a computational framework designed to automate and imitate the visual inspection-based data analysis steps typically performed by expert researchers, but in a manner that is quantifiable, reproducible and precisely communicable. Inspired by the human ability to visually assess the ‘shape’ of plotted data, our approach is to use probabilistic inference-based model selection [3,4] on technique-specific sets of models to calculate how well the shape of each model, which we call a ‘template’, can quantitatively describe the latent structure of the data. Specifically, we apply Bayes’ rule to the probability expressions, known as evidences, which here characterize the degree to which the models under consideration can explain the observed data in a process known as Bayesian model selection (BMS) [5]. Broadly, advantages of adopting a Bayesian framework have led to the increased usage of Bayesian methods in recent times across the sciences [6]. For instance, in the field of biophysics, and particularly single-molecule studies, the use of Bayesian inference has been transformative due to its intrinsic ability to handle particularly noisy data (reviewed in [5]). However, the difficulty of deriving evidences has historically limited the extension of Bayesian inference to BMS-based analysis approaches [7,8], except in a few specialized cases (e.g. in [9,10]).

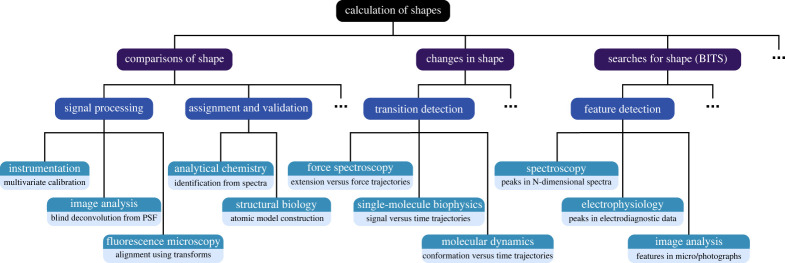
In this work, we create a generalized BMS-based framework using closed-form expressions for evidences that can be adapted by researchers in the physical and life sciences to a variety of different applications with computational ease and efficiency (figure 1). In addition, because each implementation of this framework is defined by the specific set of physics-informed models considered, our approach can be leveraged to create constrained analyses that achieve optimal balances between theoretical precision and computational efficiency. We also harness this framework to create a corollary method, called Bayesian inference-based template search (BITS), which enables us to achieve a large computational speedup when identifying and localizing multiple features of interest within a dataset. Altogether, our probabilistic, BMS-based framework is a radically new method for analysing data that allows researchers to computationally mimic expert-based visual analyses without needing to resort to a subjective, researcher-dependent approach.

Figure 1.

Applications of shape calculation to the physical and life sciences. A graphical representation of our mathematical framework (black), with examples of data analysis methods made possible by it (purple), specific tasks these methods enable (blue) and applications of these tasks in specific techniques in the physical and life sciences (dark cyan) along with the specific problems (light cyan) that the application of our framework to these techniques may address. The given examples are not meant to be exhaustive. (Online version in colour.)

2. Describing the shape of a dataset

In this section, we detail a mathematical framework designed to resemble the process of expert-based visual analysis. This approach uses orientation-preserving affine transformations of a template vector to map the associated model of latent structure onto the experimental data being analysed. The marginal likelihood of the data given a specific template is then calculated regardless of the scaling and translation of this transformation, or the noise present in the data. These marginal likelihoods are computed for a pre-defined set of templates and are then used in BMS to calculate the posterior probabilities for each template. The shape of the data is then optimally described by the template with the highest posterior probability.

(a) . Defining a template

To begin, we consider the problem of specifying a model of the latent structure of a dataset for the purpose of mimicking visual recognition. In our framework, a dataset, $\mathit{y}$, is a tensor whose components are the individual, scalar datapoints. Regardless of the experimental relationships between those datapoints (i.e. the organizational structure of the tensor), for simplicity, we can reshape $\mathit{y}$ into an $N$-dimensional vector $\mathit{y}=[y_1,\dots ,y_N]$, where $y_i$ are the scalar datapoints. One can imagine a dataset $\mathit{y}$ collected using a particular instrument, in a particular location, on a particular day, and by a particular researcher. Altogether, these specific factors might induce systematic differences in $\mathit{y}$ relative to an otherwise equivalent experiment. For example, an optical filter in an instrument might slowly oxidize, which could reduce the intensity of light incident upon the detector and, over a period of months, yield $\mathit{y}$ with different scales (i.e. units). Similarly, overhead lights might be left on accidentally when making an optical measurement, which could increase the background photons incident on the detector and yield $\mathit{y}$ with different relative offsets. Likewise, local vibrations might vary from day to day, which could affect the stability of an instrument and yield $\mathit{y}$ with different amounts of noise. Yet factors such as the scaling, offset or amount of noise in a measurement generally do not alter the underlying physical processes that give rise to the measured data and thus should not affect the latent structure (i.e. the shape) of $\mathit{y}$. Instead, these factors often act as irregularities, or nuisances, that can limit our ability to model the shape of $\mathit{y}$; hence, our use of the term ‘nuisance parameters’ to describe them. With this in mind, we define a template, $\mathit{x}=[x_1,\dots ,x_N]$, as a particular $N$-dimensional vector of scalar quantities, which is related to $\mathit{y}$ through the following transformation:

$$y_i=m{x}_i+b+{\xi }_i\text{for all}\hspace{0.17em}i=1,\dots ,N.$$ 2.1

In this equation, $m$ and $b$ are nuisance parameters representing changes to scale and offset, respectively, $\mathit{\xi }=[{\xi }_1,\dots ,{\xi }_N]$ is a nuisance parameter composed of stochastic terms representing the experimental noise, and $N$ is the number of components in $\mathit{x}$ or $\mathit{y}$. If we recall our definition of shape as correlations within data that derive from fundamental physical processes, we can conceptually understand a template, $\mathit{x}$, as an ideal representation of these correlations, without noise or background. To avoid confusion, we note that our definition of shape is distinct from those that take shape to mean a boundary or segmentation in data [11] and that it is this choice of definition which enables our framework and aligns it with the intuitive visual analyses performed manually by researchers.

It is important to note that the shape of $\mathit{y}$, regardless of any distortions caused by the experimental nuisance parameters described earlier, may often be reasonably described by many different $\mathit{x}$s. Indeed, there are no restrictions on what specific $\mathit{x}$s one may choose as templates. Different $\mathit{x}$s might depend on different levels of theory, the particular details of the experimental set-up and even sample-to-sample variability. For example, the laws of diffraction dictate the point spread function (PSF) that describes the shape of point emissions in a fluorescence microscopy image [12]. However, for a standard microscope, the PSF can be modelled by an Airy disk, a two-dimensional circular Gaussian function or, to incorporate an astigmatism correction, even a two-dimensional elliptical Gaussian function [13]. Each of these models of the PSF provides a distinct, theoretically valid $\mathit{x}$ capable of modelling the shape of $\mathit{y}$ with varying degrees of complexity. Alternatively, one’s $\mathit{x}$s could be empirically derived from data previously recorded in other experiments. In the context of the aforementioned example, an $\mathit{x}$ can be created from fluorescence microscopy images of point emitter-like samples without needing to explicitly invoke a theory of diffraction, and such empirically derived $\mathit{x}$s might even model the latent structure of $\mathit{y}$ more effectively than analytical, theory-derived $\mathit{x}$s. Regardless of the complexity of $\mathit{x}$ or its origin, once formulated, it is directly related to a $\mathit{y}$ by the simple affine transformation given in equation (2.1).

The choice of which $\mathit{x}$ (or set of $\mathit{x}$s) one uses to model the shape of $\mathit{y}$ depends not only on the experimental technique but also on the level of precision required for that particular analysis. When using this mathematical framework to analyse experimental data from the natural sciences, one can invoke prior knowledge of the physics governing the experiment which gave rise to the data to constrain the choice of templates used in the analysis. Thus, while templates with higher complexities (e.g. an Airy disk as a model for a PSF) may be required for certain applications, in other cases, a less complex template (e.g. a two-dimensional Gaussian as model for a PSF) can perform just as effectively while greatly reducing the computational cost of the analysis. The flexibility in choice of templates enabled by our framework can greatly increase the efficiency and effectiveness of an analysis method (see §3); however, determining which of the chosen $\mathit{x}$s, if any, is the optimal template requires that we first compute how well the shape of $\mathit{y}$ is explained by a given $\mathit{x}$.

(b) . Deriving probabilistic expressions for shape

After defining an $\mathit{x}$, we quantify the degree to which it describes the latent structure of $\mathit{y}$, regardless of the nuisance parameters described earlier in equation (2.1). For the $k$th template, ${\mathit{x}}_k$, in a set of templates, $\{\mathit{x}\}=\{{\mathit{x}}_1,\dots ,{\mathit{x}}_K\}$, this means calculating a marginalized likelihood probability called the evidence, $P(\mathit{y}|{\mathit{x}}_k,M_0)$. Here, the conditional $M_0$ represents all of the details of the experiment, previous knowledge about the system and particulars of the analysis method(s)—including which templates have been incorporated into the chosen $\{\mathit{x}\}$. The expression for the evidence of ${\mathit{x}}_k$ is the marginalization of the joint probability, which is given by

$$P(\mathit{y}\hspace{0.17em}|\hspace{0.17em}{\mathit{x}}_k,M_0)=\iiint p(\mathit{y}\hspace{0.17em}|\hspace{0.17em}{\mathit{x}}_k,\mathit{\xi },m,b,M_0)\times p(\mathit{\xi },m,b\hspace{0.17em}|\hspace{0.17em}{M}_0)\hspace{0.17em}\mathrm{d}\mathit{\xi }\hspace{0.17em}\mathrm{d}m\hspace{0.17em}\mathrm{d}b.$$ 2.2

In equation (2.2), $p(\mathit{y}|{\mathit{x}}_k,\mathit{\xi },m,b,M_0)$ is called the likelihood, and it represents the probability density of observing $\mathit{y}$ for a given ${\mathit{x}}_k$ and given values of the nuisance parameters; $p(\mathit{\xi },m,b\hspace{0.17em}|\hspace{0.17em}{M}_0)$ is called the prior, and it represents the joint probability density of those particular nuisance parameter values based on the prior knowledge specified by $M_0$.

In this work, we have used combinations of different likelihoods and priors to derive a set of evidences, expressed in a closed form, that are particularly useful for calculating the shape of data in a variety of experimental situations. For all of the cases presented here, we have assumed in our $M_0$ that ${\xi }_i$ are uncorrelated, such that $⟨{\xi }_i⟩$ = 0 and $⟨{\xi }_i,{\xi }_j⟩$ = ${\tau }^{-1}{\delta }_{ij}$, where $\tau$ is a constant called the precision and ${\delta }_{ij}$ is the Kronecker delta. While this assumption is not a requirement of our approach, this noise model is often experimentally reasonable, and it has allowed us to present analytical solutions to evidence integrals in many general situations (see electronic supplementary materials, §2 for other noise models). Together with equation (2.1), this assumption yields the following likelihood function:

$$p(\mathit{y},|\hspace{0.17em}{\mathit{x}}_k,m,b,\tau ,M_0)=\prod _{i=1}^N{\left(\frac{\tau }{2\pi }\right)}^{1/2}{\mathrm{e}}^{-(\tau /2){(y_i-m{x}_i-b)}^2}.$$ 2.3

Very similar likelihood functions arise with this noise model when $m$ is known to be 0 or 1, and/or $b$ is 0.

Specifying the probability expression for the prior—the second term in the integrand in equation (2.2)—requires that we mathematically represent our previous knowledge of how $m$, $b$ and $\tau$ are distributed in the experiments of interest [3]. In particular, the prior dictates the integration bounds of equation (2.2) by determining the values that are possible for these parameters to assume (i.e. regions where the prior probability is non-zero). For the results derived here, we have used so-called maximum entropy priors, which allow us to encode information and constraints into our prior probability expressions, without dictating their functional form in an ad hoc manner [3]. If we assume in $M_0$ that we only know that $m$, $b$ and $\tau$ are within some range and that we do not know the magnitude of $\tau$ (i.e. the amount of noise we expect), then the corresponding maximum entropy priors are a uniform distribution for $m$ and $b$, and a uniform distribution over the logarithm of $\tau$ (see electronic supplementary materials, §1). If we further assume that $m$, $b$ and $\tau$ are independent, then the corresponding joint prior of these parameters within the given ranges is

$$p(m,b,\tau \hspace{0.17em}|\hspace{0.17em}{M}_0)=\frac{{\tau }^{-1}}{\mathrm{\Delta }m\mathrm{\Delta }b\mathrm{\Delta }(\ln \tau )},$$ 2.4

where the shorthand $\mathrm{\Delta }f\equiv f_{\max }-f_{\min }$ defines the range of a parameter.

To analytically integrate equation (2.2), the integration bounds in the prior must be explicitly defined. We note that a positive transformation of an ${\mathit{x}}_k$ ($m>0$) can have a distinct physical interpretation from a negative transformation ($m<0$). Thus, to differentiate between these two cases and properly model the underlying shape of $\mathit{y}$, we impose that ${\mathit{x}}_k$ and $\mathit{y}$ be oriented in the same direction. This constraint can be encoded into the calculation by only considering orientation-preserving (i.e. positive scaling) affine transforms of the ${\mathit{x}}_k$ in equation (2.1). To explicitly include this information in the prior, and thus in our $M_0$, we therefore use $m_{min}=0$ rather than some $m_{min}<0$. In the case that the negative transformation ($m<0$) is of interest, we note that $-{\mathit{x}}_k$ with $m>0$ is equivalent to ${\mathit{x}}_k$ with $m<0$. Closed-form expressions for the evidence derived using other integration bounds are also provided in the electronic supplementary material. In addition, to keep the prior normalized and avoid using a so-called improper prior, the minimum and maximum values must be chosen such that $\mathrm{\Delta }m$, $\mathrm{\Delta }b$ and $\mathrm{\Delta }\ln \tau$ are not infinite. For the purposes of a tractable integration [14,15], we have used such large negative and positive values that the integration bounds in equation (2.2) can be approximated as $m\in [0,\mathrm{\infty })$, $b\in (-\mathrm{\infty },\mathrm{\infty })$ and $\tau \in [0,\mathrm{\infty })$. While the exact values of the bounds are important and should be chosen judiciously, we note that the resulting prior normalization terms end up cancelling in subsequent steps during BMS (see below). Using the integration bounds discussed earlier, the closed-form probability expression for the evidence calculated using equation (2.2) is

$$\begin{array}{rl}\hspace{0.17em}& P(\mathit{y}\hspace{0.17em}|\hspace{0.17em}{\mathit{x}}_k,M_0)=\frac{\Gamma ((N-2)/2)N^{-N/2}{\pi }^{-((N-2)/2)}}{2\mathrm{\Delta }m\mathrm{\Delta }b\mathrm{\Delta }\ln \tau }{V}_x^{-1/2}\\ \hspace{0.17em}& \hspace{0.17em}\times {(V_y(1-r^2))}^{-(N-2)/2}[1+\frac{r}{|r|}{I}_{r^2}(\frac{1}{2},\frac{N-2}{2})],\end{array}$$ 2.5

where $V_x\equiv ⟨{{\mathit{x}}_k}^2⟩-{⟨{\mathit{x}}_k⟩}^2$, $V_y\equiv ⟨{\mathit{y}}^2⟩-{⟨\mathit{y}⟩}^2$, $r\equiv \left(⟨{\mathit{x}}_k\mathit{y}⟩-⟨{\mathit{x}}_k⟩⟨\mathit{y}⟩\right)/\sqrt{V_x{V}_y}$, $⟨f⟩\equiv (1/N)\sum _i^N{f}_i$ is the arithmetic mean, $\Gamma (x)$ is the gamma function and $I_x(a,b)$ is the regularized incomplete beta function. This evidence is the probability that the shape of $\mathit{y}$ corresponds to a specific template ${\mathit{x}}_k$, regardless of the particular values of the (positive) scale, offset and noise parameters used in the affine transformation that relates ${\mathit{x}}_k$ to $\mathit{y}$ (equation (2.1)). At first glance, the appearance of the term $V_x^{-\frac{1}{2}}$ suggests that two ${\mathit{x}}_k$s that are equivalent up to a multiplicative constant would have different abilities to explain the same $\mathit{y}$. However, that constant must also be accounted for in the prior term $\mathrm{\Delta }{m}^{-1}$, where it can cancel this effect. Thus, choosing the range for $m$ in the prior is intimately related to setting the $V_x$ of the ${\mathit{x}}_k$ and, unless one has a reason to believe different models have different ranges of $m$, the ${\mathit{x}}_k$ within a $\{x\}$ should be normalized such that their $V_x$ are equivalent.

While the evidence expression in equation (2.5) is very general in the sense that it can be used for almost all choices of templates, it is not applicable to the special, ‘null’ case in which a template is absent (i.e. where ${\mathit{x}}_k$ is flat and/or $m$ is only zero). This case is very useful in our approach for validating the presence or absence of a shape in experimental data, as we will show in the following section. The corresponding evidence expression for this case is expressed as follows:

$$P(\mathit{y}\hspace{0.17em}|\hspace{0.17em}{\mathit{x}}_{null},M_0)=\frac{\Gamma ((N-1)/2)N^{-N/2}}{\mathrm{\Delta }b\mathrm{\Delta }\ln \tau }{(\pi V_y)}^{-(N-1)/2},$$ 2.6

where ${\mathit{x}}_{null}$ represents the case that the model lacks a template. This evidence expression represents the probability that the experimental data are featureless (i.e. lacking any latent structure) beyond the presence of a constant background offset and noise, regardless of the exact values of these parameters. Together, the evidence expressions in equations (2.5) and (2.6) enable us to quantitatively express how well the shape of experimental data agrees with candidate templates, independent of extraneous details and nuisance parameters that may change from experiment to experiment.

(c) . Describing the shape of a dataset using BMS

We compare the performance of different templates by using BMS [3–5] to calculate the probability that each ${\mathit{x}}_k$ is the best description of the shape of the data, $\mathit{y}$. This calculation is conditionally dependent on the assumptions in $M_0$, which define the specifics of the analysis method, including the composition of $\{\mathit{x}\}$. Multiple distinct analysis methods can consequently be developed by using different $M_0$s to tailor their effectiveness to individual experimental situations and systems. For any chosen $M_0$, an appropriate template prior probability for ${\mathit{x}}_k$, $P({\mathit{x}}_k|M_0)$, must then be assigned, for example, by (i) using an equal a priori assignment of $K^{-1}$, where $K$ represents the number of templates in $\{\mathit{x}\}$; (ii) learning prior values from separate experiments; or even (iii) using a Dirichlet process or hierarchical Dirichlet process [16] for a non-parametric ‘infinite’ set of templates. Once all of the $P({\mathit{x}}_k|M_0)$ have been assigned, Bayes’ rule can be used to perform BMS and compute the template posterior probability as follows:

$$P({\mathit{x}}_k\hspace{0.17em}|\hspace{0.17em}\mathit{y},M_0)=\frac{P(\mathit{y}\hspace{0.17em}|\hspace{0.17em}{\mathit{x}}_k,M_0)P({\mathit{x}}_k\hspace{0.17em}|\hspace{0.17em}{M}_0)}{\sum _{j=1}^{K}P(\mathit{y}\hspace{0.17em}|\hspace{0.17em}{\mathit{x}}_j,M_0)P({\mathit{x}}_j\hspace{0.17em}|\hspace{0.17em}{M}_0)}.$$ 2.7

This expression represents the probability of an ${\mathit{x}}_k$ given the observed data $\mathit{y}$ and, thus, may be used to identify the ${\mathit{x}}_k$ in $\{\mathit{x}\}$ that most optimally describes the latent structure of $\mathit{y}$ (for a specific choice of $M_0$). Using equation (2.7) is therefore a quantitative means by which the underlying shape of experimental data may be determined. Furthermore, by considering a ‘background’-shaped ${\mathit{x}}_k$ and/or just the presence of noise (i.e. equation (2.6)) in the BMS process, this approach can also validate whether using the most probable ${\mathit{x}}_k$ to describe the shape of $\mathit{y}$ is justified or whether the shape of $\mathit{y}$ can be better explained as just noise in the data. Altogether, this BMS process sets up an objective, quantitative, researcher-independent metric for not only determining the shape of experimental data but also validating such shape assignments.

The shape calculation equations we report earlier describe a relationship between ideal distributions (i.e. ${\mathit{x}}_k$) and noisy signals (i.e. $\mathit{y}$) that is independent of many experimental details which would otherwise complicate the analysis being performed. The only requirements are that both ${\mathit{x}}_k$ and $\mathit{y}$ exist in the same data-space and are vectors of the same size. Practically, however, most templates are generated from some underlying model that exists in a separate ‘model space’ distinct from the data space of ${\mathit{x}}_k$ and $\mathit{y}$. Relating such a model space to data space requires that a set of parameters, $\{\theta \}$, be used to map the model to an ${\mathit{x}}_k$. For example, a model of a three-dimensional object being projected onto a two-dimensional image may use the Euler angles of the object to generate ${\mathit{x}}_k$s with different orientations in the two-dimensional image data space.

Generally, when using such a model to generate ${\mathit{x}}_k$s for identifying the shape of $\mathit{y}$, the template posterior probabilities for an entire group of model-associated ${\mathit{x}}_k$s must be calculated to account for the many possible ways that the single model could have been mapped into data space. Having performed all of those calculations, it is then possible to marginalize out the dependence upon some of the $\{\theta \}$ from the model. In the example mentioned earlier, marginalizing out the Euler angles would yield the posterior probability that the shape of $\mathit{y}$ corresponds to a two-dimensional image of the model, regardless of not knowing the true orientation of the three-dimensional object being projected into the image. Thus, this type of marginalization in data space enables our framework to provide objective measures for shape assignment in model spaces as well. We note that the map between model space and data space used in these shape calculations should be explicitly acknowledged and defined to mitigate unintentional mis-estimations of the weight of particular models in data space during the change of variables. Finally, it is worth mentioning that such model spaces almost always exist for scientific analyses, even if they are only implicitly invoked within $M_0$.

The most complete implementations of these BMS-based shape calculations occur when using $M_0$s that specify every physically appropriate ${\mathit{x}}_k$. However, this approach may not always be theoretically possible or computationally feasible if an effectively infinite number of ${\mathit{x}}_k$s exist. In such situations, it is worth noting that, depending on the precision required by a particular analysis method, the full set of templates may not be required to obtain effective results. Importantly, a major benefit of BMS is that we can determine which ${\mathit{x}}_k$ among a set of approximate templates best describes the shape of $\mathit{y}$, even if none are ‘exact’. In addition, the BMS expression in equation (2.7) can be rearranged into a function of the log difference of evidence expressions (i.e. a Bayes’ factor) between a test ${\mathit{x}}_k$ and an appropriate control ${\mathit{x}}_k$ (or a ‘null’ model), which yields an effective cost function for the direct optimization of a single ${\mathit{x}}_k$ (see electronic supplementary materials, §3). Overall, the most powerful aspect of the BMS-based shape calculations described here is that by considering different $M_0$s, an analysis method can be optimized for completeness (where all appropriate templates are enumerated) or efficiency (where only a test and a control template are considered), or for a trade-off between the two (using only a restricted set of templates), as the situation demands. This flexibility is a large reason why our framework can be effectively adapted to mimic nearly any of the subjective, expert-based analysis methods that it is meant to replace. Furthermore, the ability to easily disseminate the $\{\mathit{x}\}$ used in an analysis means that methods can be readily shared, critiqued and reproduced. Together, these especially powerful aspects of our framework make it extremely straightforward to implement tailor-made, shape-based analysis methods for new experiments and applications.

3. Searching for shapes: BITS

While the practical scientific applications of shape calculations are numerous (see figure 1 and §4), the flexibility of our framework leads to a corollary of this approach that can be used to search for the presence of particular ‘local’ features in the data. Experimental examples of this kind of analysis include finding the location of peaks in molecular spectra, puncta in fluorescence microscopy images or stepping behaviour in time-series. In all of these situations, an underlying physical relationship exists between the datapoints in $\mathit{y}$ (e.g. emission wavelength, Cartesian position on a substrate or measurement time). In the previous section, we considered $\mathit{y}$ as an $N$-dimensional vector in a manner that largely ignored the relationships between datapoints. Because $\mathit{y}$ is a tensor, however, we can reshape it to fundamentally account for these relationships. For instance, if $\mathit{y}$ is a fluorescence microscopy image, then each datapoint might correspond to a pixel of spectral colour $c$ with an associated position ($r_x$, $r_y$ and $r_z$) in the sample space of the experiment. Thus, it would be useful to reshape $\mathit{y}$ from a first-order tensor (i.e. a vector) of $N$ scalar datapoints into a more natural representation as a fourth-order tensor with one dimension each for $c$, $r_x$, $r_y$ and $r_z$. Because $r_x$, $r_y$ and $r_z$ exist in a Euclidean metric space, we can also calculate a distance, $d(y_i,y_j)$, between any two datapoints in this example. With such a distance metric for at least one of the tensor dimensions of $\mathit{y}$, a local neighbourhood around the position of $y_i$ can be defined as the subset of datapoints, ${\mathit{y}}_{(i,\epsilon )}\subset \mathit{y}$, for which $d(y_i,y_j)<\epsilon$, where $\epsilon$ is a specified distance cutoff. Notably, this neighbourhood contains $n\le N$ datapoints and may be orders of magnitude smaller depending on the choice of $\epsilon$. Thus, for a fixed value of $\epsilon$, $\mathit{y}$ can be thought of as a composite of approximately $N$ unique $\epsilon$-neighbourhoods of size $n$ (i.e. distinct subsets ${\mathit{y}}_{(i,\epsilon )}$).

We can then define the local, latent structure of $\mathit{y}$ by performing the BMS-based shape assignment described in §2 separately within each of these unique neighbourhoods using a set of templates, $\{\mathit{x}\}$, where each ${\mathit{x}}_k$ is also of size $n$. Intuitively, this process can be understood as ‘scanning’ a small region through $\mathit{y}$ along the dimensions of the tensor and assessing the shape of the data at each site. Whenever one of the ${\mathit{x}}_k$ is found to be an appropriate description for the data in a particular neighbourhood, a feature (i.e. ${\mathit{x}}_k$) is effectively ‘localized’ at that site. Therefore, we call this local analysis approach ‘Bayesian inference-based template search’ (BITS), because it localizes the templates in $\{\mathit{x}\}$ within $\mathit{y}$ by traversing the unique neighbourhoods of $\mathit{y}$ and determining the latent structure of the data in each using the BMS approach described earlier. As the name BITS suggests, this approach is conceptually similar to traditional template matching calculations (e.g. via normalized cross-correlation [17]), and in fact incredible mathematical similarities, as seen in the $r$ cross-correlation term between ${\mathit{x}}_k$ and $\mathit{y}$ in equation (2.5), have naturally arisen from our probabilistic approach. As such, we believe many strategies used for template matching (e.g. fast Fourier transforms) might be adapted with future work. Regardless, as discussed later, by casting the template matching process into a probabilistic framework BITS enables powerful extensions facilitated by model selection, such as model comparison and automatic feature localization.

We note that each local calculation is technically performed over all $\mathit{y}$ but, by splitting the likelihood into two regions, one within ${\mathit{y}}_{(i,\epsilon )}$ modelled by $\{\mathit{x}\}$ and one without ${\mathit{y}}_{(i,\epsilon )}$ modelled by ${\mathit{x}}_{null}$ (i.e. non-local data are ‘noise’), the evidence contribution from without the local region is the same for each ${\mathit{x}}_k$ and cancels in the Bayes’ factors of equation (2.7). Thus, the entire calculation can be simplified, and only the local region within ${\mathit{y}}_{(i,\epsilon )}$ needs to be addressed. Of course, rather than use the local BITS approach described here, a composite template simultaneously containing all of the features being localized could be used to describe the shape of the entire $\mathit{y}$; however, as we will show, BITS is much more computationally efficient. For instance, a $\mathit{y}$ of size $N$ that contains $R$ unique features of size $n$ that are to be localized with datapoint resolution would require $N^R$ distinct templates be tested. Both constructing each template and calculating the evidence for a template are $\mathcal{O}(N)$, so such a full-sized shape calculation has computational scaling of $\mathcal{O}(N^{R+1})$. Clearly, this approach has severe scaling issues for any number of features. Fortunately, the equivalent BITS calculation that interrogates $N$ localization sites, and where we have chosen $\epsilon$ so that the ${\mathit{x}}_k$ are the size of the features, $n$, has a computational scaling of $\mathcal{O}(nNR)$. In the context of shape-based analyses, template searching with BITS greatly reduces the computational burden of localizing features down from a geometric to a linear scaling.

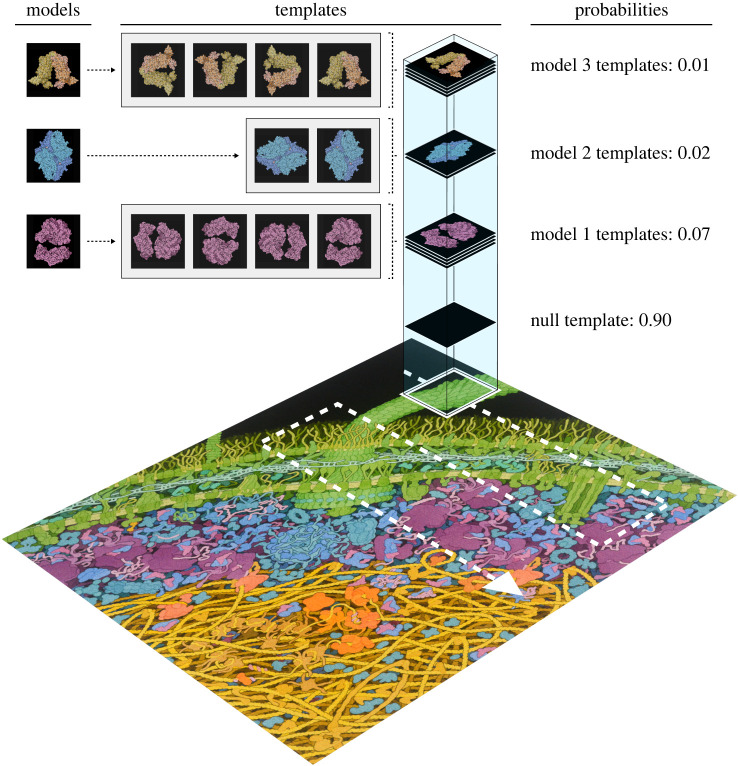
The BITS process is demonstrated in figure 2 with an illustrative example of the analysis of an image of a cellular environment. The data space to be analysed in this example consists of a second-order tensor of pixel intensities where the two tensor dimensions correspond to Cartesian co-ordinates in the cellular environment. While the image is coloured to differentiate and visualize different cellular components with the human eye, we note that, for simplicity, our illustrative example is dealing with the total intensity value of each pixel. Three-dimensional atomic resolution structural models for these molecules are used to generate a corresponding set of two-dimensional ${\mathit{x}}_k$s that represent each biomolecule in a particular orientation in the image of the cellular environment (shown in the figure in grey boxes). Given the number of templates and that the size of these templates is much smaller than the total size of the image, BITS can be used very efficiently in this analysis.

Figure 2.

Illustration of the Bayesian inference-based template search algorithm. An example of a BITS process is shown, where three different biomolecules are searched for in a two-dimensional image of a cellular environment. Different sets of cellular components are coloured differently for illustrative purposes to demonstrate the expected locations of the different biomolecules (green for cell membrane components, purple for translation machinery, blue for enzymes and yellow and orange for transcription and replication machinery). A set of rotational templates (in grey boxes) generated from different models of the biomolecules of interest (coloured as earlier) is scanned through subsections of the image (white arrow), and the probability that each template best matches the local shape of the data in a specific subsection (white box) is calculated and then marginalized into an aggregate probability for each model that is used to identify the local composition of the image. The probability values shown were chosen to illustrate the example case of the null template being identified in the case where the shape of a subsection cannot be explained by any of the model templates. Adapted from illustrations by David S. Goodsell, RCSB Protein Data Bank (DOIs: doi:10.2210/rcsb_pdb/goodsell-gallery-028, doi:10.2210/rcsb_pdb/mom_2000_10, and doi:10.2210/rcsb_pdb/mom_2016_6, doi:10.2210/rcsb_pdb/mom_2003_3). (Online version in colour.)

Along with a null template (${\mathit{x}}_{\mathrm{null}}$), the biomolecular model templates are ‘scanned’ through the image $\mathit{y}$, and the BMS calculation of equation (2.7) is performed on the ${\mathit{y}}_{(i,\epsilon )}$ at each site. The white square on the image shows the specific local neighbourhood ${\mathit{y}}_{(i,\epsilon )}$ currently being interrogated using BMS, and in subsequent steps BMS calculations are performed on the adjacent local neighbourhoods (‘scanning’ order denoted by the white arrow). The biomolecular orientation dependence of the ${\mathit{x}}_k$s is marginalized out of this calculation by combining the template posterior probabilities of the ${\mathit{x}}_k$s derived from the same biomolecular model. This yields the model posterior probability that each biomolecule of interest is localized at a particular position in the image regardless of its orientation. The specific neighbourhood being analysed in figure 2 highlights the advantages of including a ${\mathit{x}}_{null}$ in a BITS analysis. While this region of the image contains some latent structure, we can visually see that it is not explained by any of the biomolecular model templates. Corresponding to this visual analysis, BITS finds that the null template has the highest posterior probability, and hence, no feature is localized. This stipulation, that a feature is only localized if the shape of the data is better explained by a model template than random noise, provides critical protection against over-fitting, which is a distinct advantage of BITS over other template searching methods.

Notably, in figure 2, only a small sample of biomolecular model orientations is used, and we assume that if a particular neighbourhood contains a biomolecule of interest in a similar orientation as one of the chosen templates, there is sufficient overlap of shape between the two for it to be detected in the BMS calculation. The exact amount of similarity required for this correspondence depends only on how well the other templates can account for the local shape of this neighbourhood. Thus, while the number of sampled orientations may need to be optimized for different applications depending on the desired outcome, $\{\mathit{x}\}$ with sparse samples of a model’s orientations may still be used to effectively localize features.

Overall, the BITS algorithm can be understood as a method that quantifies the degree to which the latent structure in the data of each neighbourhood ${\mathit{y}}_{(i,\epsilon )}$ of $\mathit{y}$ is correlated with an ${\mathit{x}}_k$. This correlation is maximized when BITS reaches the ‘true’ location of a feature of interest in the data and the ${\mathit{x}}_k$ is perfectly aligned with the feature. When misaligned by even one datapoint, however, the positive correlation can be negligible, and immediately another ${\mathit{x}}_k$ (e.g. a null template) or even no particular ${\mathit{x}}_k$ can dominate the BMS calculation. The effect of this behaviour is that only the location in $\mathit{y}$ corresponding to the centre of a feature of interest (i.e. perfectly overlapped by ${\mathit{x}}_k$) is identified with a high $P({\mathit{x}}_k|\mathit{y},M_0)$. Interestingly, this means BITS inherently protects against multiple localizations of the same feature while simultaneously facilitating localization of multiple, closely spaced features.

Perhaps the most important and unique aspect of the BITS algorithm is that it enables $\mathit{y}$s acquired under different experimental conditions to be directly compared within a single, common reference frame. Specifically, since BITS uses evidence expressions that are based only upon agreement of an ${\mathit{x}}_k$ with the latent structure of $\mathit{y}$, it is independent of many experimental nuisances that would otherwise obstruct direct comparisons. For example, while different background levels in two experiments can render the use of a common threshold value to localize features completely ineffective, BITS remains invariant under changes in background and thus yields two sets of feature localizations that can be directly compared. Moreover, by setting a pre-defined posterior probability threshold and/or by including a model of the background or simply noise as ${\mathit{x}}_k$s in $\{\mathit{x}\}$, BITS can automatically identify and localize features for a wide range of experimental techniques without human intervention or advanced knowledge about the experimental situation (e.g. exposure times for a detector).

4. Discussion

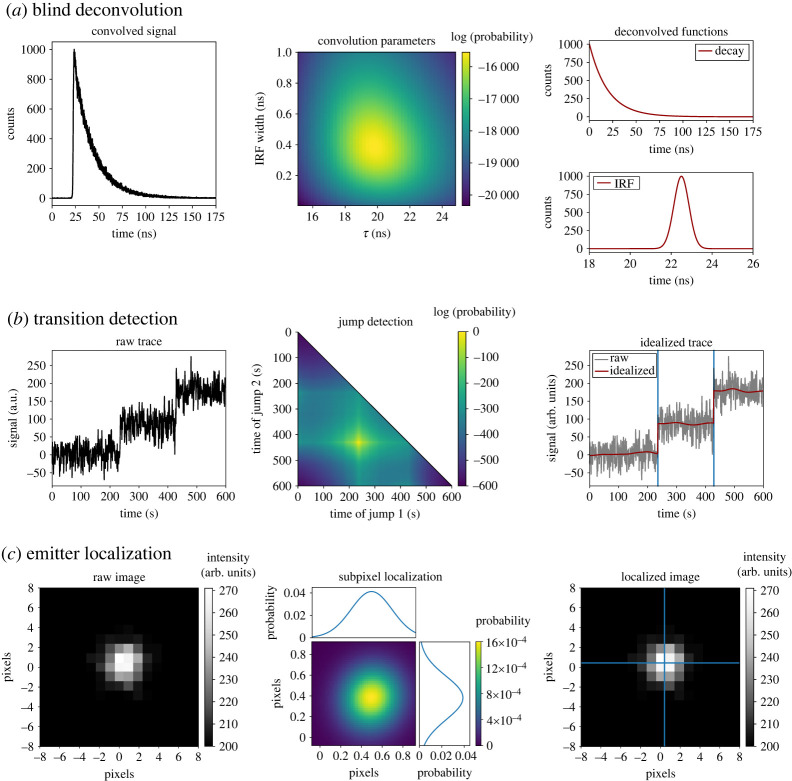
The ability to describe the latent structure of experimental data can readily be leveraged for many different techniques and analyses in the physical and life sciences (figure 1). Here, we consider several examples and briefly demonstrate and discuss some of their implementations. We begin with experiments in which raw data are pre-processed in a manner according to its shape. For instance, in signal processing-based analyses, the shape-based framework presented here can be used to (i) perform multivariate calibration transfer [18] (e.g. in optical spectroscopy techniques) by comparing the shapes of responses for standardized samples across multiple instruments; (ii) perform blind deconvolution [19] (e.g. in atomic force, optical, or electron microscopy) by comparing the convolution of possible instrument response functions and deconvolved signals with the shape of the recorded data (figure 3a); or (iii) to align distinct measurements of the same object or sample (e.g. the same field of view in different colour channels [20] or multiple image planes [21] of a fluorescence microscope) by finding the optimal polynomial transform to create an interpolated measurement that matches the shape of another measurement.

Figure 3.

Examples of analyses based on shape calculations. (a) A fluorescence lifetime dataset (left) may be modelled as a convolution of an exponential decay of unknown lifetime ($\tau$) and a Gaussian instrument response function of unknown width. By comparing shapes of the data with convolved templates, a joint log-probability map of the two unknowns is constructed (middle) and the deconvolved functions corresponding to the parameters with the maximum probability are plotted (right). (b) A signal versus time trajectory (left) with two discontinuous jumps may be compared in shape with a set of templates corresponding to all possible jump times to generate a map of the joint log-probabilities for the times of the jumps (middle). The times corresponding to the maximum probabilities are overlaid (in blue) over the raw signal and the continuous segments identified are idealized (in red) using a Gaussian filter (right). (c) A fluorescence emitter in a microscope image (left) may be modelled as a Gaussian of known width centred at a certain location. By using a subpixel grid to generate such templates with varying centres, a map of the joint probability for the co-ordinates of the emitter is plotted, along with marginalized probabilities for the $x\text{-}\hspace{0.17em}\mathrm{and}\hspace{0.17em}y$-axes (middle). The co-ordinates with the maximum probability are overlaid (in blue) over the raw image (right). (Online version in colour.)

In analytical chemistry experiments that are used to identify the contents of an experimental sample based on the characteristics, or ‘fingerprints’, of known standards, the framework presented here can be used to compare the shape of the signal of an experimental sample against databases of standard experimental and/or theoretical templates of the possible contents. Examples of this kind of analysis include identification of chemicals from characteristic infrared spectra [22], or ${\hspace{0.17em}}^1\mathrm{H}$ nuclear magnetic resonance (NMR) spectra [23], and identification of proteins from fragmentation patterns in mass spectrometry data [24]. Similarly, a shape assignment-based approach would enable the automated identification of sample contents from the noisy measurements typically obtained in analyses involving small sample concentrations. In addition, shape comparisons can be used to construct and validate atomic resolution or near-atomic resolution models in structural biology experiments by comparing the: (i) structure factors from different molecular models to the diffraction pattern for an X-ray crystallography experiment [25], (ii) electrostatic potential maps from different molecular models to the reconstructed density in a cryogenic electron microscopy (cryo-EM) experiment [26], or even (iii) predicted electron scattering patterns from different atomic models to the raw electron microscopy micrographs in a cryo-EM experiment. In fact, in the last example, a similar Bayesian approach has been pioneered by Cossio & Hummer to analyse cryo-EM micrographs [9]. Despite differences in the priors, scaling parameter and specific use of BMS, our generalized shape-based analysis framework otherwise readily maps onto this approach, and could thus be used to develop a specialized method that achieves effectively the same results.

In analyses in which transitions between different signal values need to be identified, our approach can be extended to locate change points by comparing ${\mathit{x}}_k$s with and without a discrete change of any arbitrary magnitude in shape (figure 3b). This could be used to locate changes in the: (i) efficiency of fluorescence resonance energy transfer ($E_{\mathrm{FRET}}$) in the $E_{\mathrm{FRET}}$ versus time trajectories reporting on the (un)folding or conformational dynamics of a biomolecule in single-molecule FRET (smFRET) experiments [27], (ii) extension in the force versus extension or extension versus time trajectories reporting on the (un)folding or conformational dynamics of a biomolecule in single-molecule force spectroscopy experiments [27,28], (iii) position in the position versus time trajectories reporting on the directional stepping of a biomolecular motor in single-molecule fluorescence experiments [29], (iv) conductance in the conductance versus time trajectories reporting on the (un)folding or conformational dynamics of a biomolecule in single-molecule field effect transistor (smFET) experiments [30], or even (v) conformation in the conformation versus time trajectories reporting on (un)folding or conformational dynamics of a biomolecule in molecular dynamics simulations. Indeed, such a BMS-based method to detect transition in time-series data has been pioneered by Ensign & Pande [10]. Despite minimal differences in noise models, our generalized shape-based analysis framework can be mapped onto the approach of Ensign and Pande, thus facilitating the development of a specialized method that can effectively arrive at the same results. This general approach to analysing time-series extends the use of Bayesian inference-based techniques for the detection of change points in a time-dependent signal to any sequential data with arbitrary signal properties, thereby enabling the accurate estimation of kinetics from a wide range of experimental techniques.

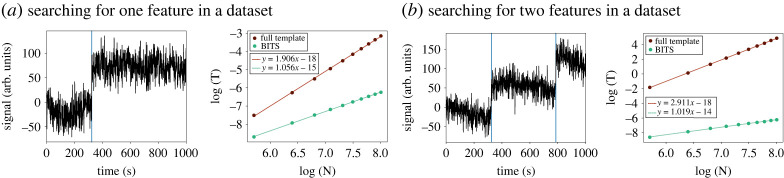
In addition to the full shape-based methods discussed earlier, we expect that BITS is poised to have a large impact on a number of more specialized situations—particularly analyses that require localization of well-defined signals or image features. For example, given a particular spectral line shape (e.g. a Lorentzian function), BITS can be used to find peaks in multi-dimensional NMR spectra [31]. Similarly, BITS can be used to identify particles of interest and their orientations in cryo-EM [32] and cryogenic electron tomography [33] micrographs in a manner similar to that shown in figure 2. This is also readily extended to localizing and identifying individual molecules and molecular structures in atomic force microscopy [34] and super-resolution fluorescence microscopy images [35] (figure 3c). Methods using traditional template matching for such analysis tasks can be easily adapted into our BITS framework, thereby enabling comparison across disparate datasets (e.g. [36,37]). In the case of the analysis of time-series (e.g. single-molecule fluorescence, molecular dynamics), BITS can be used to detect transitions or change points between states, even when those transitions are more diffusive than instantaneous, as is a typical requirement for analysis using hidden Markov models. In addition, as discussed in §3, BITS makes this type of time-series analysis much more efficient than when analysing the shape of a whole time-series at once (figure 4).

Figure 4.

Computational efficiency of full-dataset versus BITS analyses. (a) An example signal versus time trajectory (left) with one discontinuous jump analysed by comparing the shape of the data with templates the size of the entire dataset (full template) and using BITS with a small template encoding a ‘step up’. The logarithm of the computational time, required to perform an analysis, $\tau$, is shown as a function of the logarithm of the length of the signal versus time trajectory, $N$. The linearized curves were fit with a first-order polynomial to yield the computational scaling of each calculation. These values match the predicted scaling for one template ($R=1$) of $\mathcal{O}(N^{R+1}=N^2)$ and $\mathcal{O}(N^1)$, for full template and BITS, respectively. (b) As in ($a$), but with signal versus time trajectories (left) with two discontinuous jumps such as in figure 3b. The computational scaling matches the predicted scaling for two templates ($R=2$) of $\mathcal{O}(N^3)$ and $\mathcal{O}(N^1)$. Together these results demonstrate the linear scaling of BITS with respect to the number of features in a dataset.

The range of examples provided earlier are broad, but not exhaustive. Nonetheless, they highlight the versatility of our approach, and we hope they will inspire others to adopt this framework for their experiments and analysis methods. Although the development, optimization, bench-marking and in-depth discussion of each of the individual scientific applications described earlier is necessarily very specialized, and thus, beyond the scope of the current work, we have created a gallery of illustrative, proof-of-principle examples that are open-source and written in Python to demonstrate and enable the use of our framework; they can be accessed at https://bayes-shape-calc.github.io.

5. Conclusion

To the best of our knowledge, the use of probabilities to determine the latent structure of data as discussed earlier is a radically new approach to analysing experiments in the physical and life sciences. The framework we present here is the quantitative extension of a very intuitive approach to data analysis in which expert researchers visually determine whether their data is the shape that they expect it to be. Rather than develop heuristic approaches to emulate this subjective process, our method provides a quantitative metric based only on probability that is free from human intervention and experimental considerations. Among other things, the ability to determine the shape of data enables researchers to objectively pre-process data; identify fingerprints and validate assignments; detect change points and identify and localize features using BITS (figures 1 and 2). In addition, the shape-based framework we present here can be readily applied to analyse large, high-dimensional datasets that are difficult to visualize and would be nearly impossible to analyse manually. As can be seen from the breadth of potential applications listed earlier (figure 1), the overall methodology described in this work transcends individual fields and techniques and indeed represents a new quantitative lens through which countless experiments in many different areas of the physical and life sciences may be analysed.

Data accessibility

We have provided a clearing house-type website for future method developments using the framework presented here (https://bayes-shape-calc.github.io), through which annotated examples coded in Python can be accessed (https://bayes-shape-calc.github.io/examples). Derivations and additional probability expressions are provided in the electronic supplementary material [38].

Authors' contributions

K.K.R.: formal analysis, investigation, methodology, validation, visualization, writing—original draft, writing—review and editing; A.R.V.: formal analysis, investigation, methodology, validation, visualization, writing—original draft, writing—review and editing; R.L.G.: funding acquisition, methodology, project administration, resources, supervision, writing—original draft, writing—review and editing; C.D.K.: conceptualization, formal analysis, funding acquisition, investigation, methodology, project administration, resources, supervision, validation, writing—original draft, writing—review and editing.

All authors gave final approval for publication and agreed to be held accountable for the work performed therein.

Conflict of interest declaration

The authors declare that they have no competing interests.

Funding

This work was supported by funds to R.L.G. from the National Institutes of Health (NIH) (R01 GM 084288, R01 GM 137608, R01 GM 128239 and R01 GM 136960) and the National Science Foundation (NSF) (CHE 2004016) as well as funds to C.D.K. from the NIH (Training Grant in Molecular Biophysics to Columbia University, T32 GM008281), the Department of Energy (DOE) (Office of Science Graduate Fellowship, DE-AC05-06OR23100) and the NSF (CHE 2137630).