Computational study of biomechanical drivers of renal cystogenesis

Abstract

Renal cystogenesis is the pathological hallmark of autosomal dominant polycystic kidney disease, caused by PKD1 and PKD2 mutations. The formation of renal cysts is a common manifestation in ciliopathies, a group of syndromic disorders caused by mutation of proteins involved in the assembly and function of the primary cilium. Cystogenesis is caused by the derailment of the renal tubular architecture and tissue deformation that eventually leads to the impairment of kidney function. However, the biomechanical imbalance of cytoskeletal forces that are altered in cells with Pkd1 mutations has never been investigated, and its nature and extent remain unknown. In this computational study, we explored the feasibility of various biomechanical drivers of renal cystogenesis by examining several hypothetical mechanisms that may promote morphogenetic markers of cystogenesis. Our objective was to provide physics-based guidance for our formulation of hypotheses and our design of experimental studies investigating the role of biomechanical disequilibrium in cystogenesis. We employed the finite element method to explore the role of (1) wild-type versus mutant cell elastic modulus; (2) contractile stress magnitude in mutant cells; (3) localization and orientation of contractile stress in mutant cells; and (4) sequence of cell contraction and cell proliferation. Our objective was to identify the factors that produce the characteristic tubular cystic growth. Results showed that cystogenesis occurred only when mutant cells contracted along the apical-basal axis, followed or accompanied by cell proliferation, as long as mutant cells had comparable or lower elastic modulus than wild-type cells, with their contractile stresses being significantly greater than their modulus. Results of these simulations allow us to focus future in vitro and in vivo experimental studies on these factors, helping us formulate physics-based hypotheses for renal tubule cystogenesis.

1. Introduction

Renal cystogenesis is pathognomonic of autosomal dominant polycystic kidney disease (ADPKD), the most common genetic disorder of the kidney caused by PKD1 and PKD2 mutations, and a frequent finding in ciliopathies, a group of complex inherited diseases that result from ciliary defects (Braun and Hildebrandt 2017; Anvarian et al. 2019; Cornec-Le Gall et al. 2019; Bergmann et al. 2018). Cystogenesis involves profound changes in the kidney tissue organization and remodeling that are characterized by abnormal cell death and proliferation, alteration of the extracellular matrix (ECM) composition, and protein mislocalization (Harris and Torres 2022).

Epithelial tubule formation, tubulogenesis, is a fundamental morphogenic process of many organs that relies on the ability of the cells to properly reorganize during development and tissue remodeling, and to reconstitute the necessary architecture that supports specific physiological functions. Precise tubule organization depends on epithelial cell polarity, that is the asymmetric segregation of cellular components within the cell (apical-basal polarity) and along the plane of the developing epithelial sheet (planar polarity). Establishment and maintenance of cell and tissue polarity are achieved through interactions with the ECM and the transformation or modulation of biomechanical cues into structural changes (e.g., cytoskeletal and adhesive) and gene regulation. The balance between these forces is particularly important during tissue repair to ensure the re-establishment of the patent organ anatomy.

Renal cystogenesis is associated with abnormalities in the core mechanosensitive machinery of epithelial cells (Smith et al. 2020; Drummond et al. 2018; Gargalionis et al. 2019). Recently, it was suggested that mutations of PKD1 lead to breakdown of a number of parallel mechanobiological signaling pathways, such as Hippo and RhoA, that result in altered cytoskeletal arrangement and focal adhesions organization (Müller and Schermer 2020; Cai et al. 2018; Streets et al. 2020; Nigro et al. 2019). We recently showed that the co-deletion of integrin-β1 (Itgb1^KO), one of the main ECM receptors, in conditional renal Pkd1 knockout (Pkd1^KO) or Ift88 knockout (Ift88^KO) mouse models prevents cystic development (Lee et al. 2015; Yoo et al. 2020), indicating a role for Itgb1 in maintaining tubular morphology. These findings underline the importance of biomechanical forces as determinants of cystic disease onset and progression. Accordingly, we hypothesize that renal tubular abnormalities in ciliopathies are caused by the breakdown of biomechanical equilibrium, whereby balance of forces between intracellular tension, cell-matrix adhesion and cell-cell adhesion is disrupted.

Renal cystogenesis has been studied extensively using transgenic mouse models (Paul and Vanden Heuvel 2014; Ko and Park 2013), with a particular focus on the mutations of Pkd1 that are associated with ADPKD (Cornec-Le Gall et al. 2019; Bergmann et al. 2018), and more recently on ciliary proteins required for cilium assembly (Tsai and Katsanis 2013; Huang and Lipschutz 2014; Gascue et al. 2011; Li et al. 2016; Ma 2021). The Pkd1 gene codes for polycystin-1 (PC1), a protein with complex subcellular localization including all points of cell-cell and cell-ECM contact as well as the cilium (Bergmann et al. 2018; Lee et al. 2011). Cilia are specialized organelles that serve chemical and mechanobiological functions (Nachury and Mick 2019). Ciliary defects produce significant changes both on cytoplasmic microtubules (Berbari et al. 2013; Hua and Ferland 2018) and actin cytoskeleton (Smith et al. 2020; Mirvis et al. 2018; Brucker et al. 2020) in agreement with the role of cilia as biomechanical regulators.

Common to all renal cystic models are the altered deposition of ECM and progressive fibrosis, which contribute to the final organ impairment. Dysregulation of the ECM components dramatically affects renal tubule development (Wallace et al. 2014; Shannon et al. 2006; Wallace et al. 2008). Such aberrant microenvironmental changes are associated with abnormal rearrangement of the intracellular cytoskeleton and altered cellular responses (Herrera et al. 2018), strongly suggesting that the disequilibrium of biomechanical forces may underlay improper tissue organization. Indeed, ample evidence indicates the involvement of PC1 in mechanotransduction through the modulation of various cellular complexes that regulate cell-cell and cell-ECM junctions (Gargalionis et al. 2019; Piperi and Basdra 2015). PC1 functions as regulator of actin contractility in response to extracellular stiffness by reducing YAP activation (Nigro et al. 2019) and prevents cystogenesis at least in part by reducing RhoA and ROCK activity (Streets et al. 2020; Nigro et al. 2019). The dysfunction of PC1 in cystic cells decreases the surface expression of E-cadherin at the adherens junctions (AJs), which, in a ternary complex with β–catenin and α–catenin, would link and rearrange actin microfilaments (Campbell et al. 2017). Along with actin cytoskeletal changes, cells overexpressing PC1 showed weaker and more dynamic junctions that were rapidly reabsorbed as the cell engaged in active migration (Boca et al. 2007). Cell junctions and contractile actin microfilaments generate a network of intercellular contacts along the plane of the epithelium that conjoins the cytoskeleton of each cell and dynamically coordinate tissue-level biomechanical changes in response to environmental conditions (Klompstra et al. 2015; Sluysmans et al. 2017).

Importantly, cadherins and integrins show cross-talk driven by a connected actomyosin network which regulates cellular mechanosensing and signaling responses. Multiprotein complexes associate with integrins and participate in the formation of focal adhesions (FAs), which act as biophysical and biochemical signaling hubs (Geiger and Yamada 2011; Balaban et al. 2001). Forces generated at different cell adhesion points are integrated into the remodeling of the intracellular contractile actin network to define the spatial organization of the cells and the regulation of signaling pathways that control cell polarity, proliferation, differentiation, and movement (Mui et al. 2016; Garcia et al. 2018). All of these biological processes are essential during the maintenance of the tubular structure, which requires cell proliferation and collective migration of differentiated cells in a polarized/directional fashion (Marciano 2017; Bernascone et al. 2017). Alteration of ECM in tubular cystogenesis produces forces that can be channeled through integrins and the interconnected cytoskeleton to exacerbate the abnormal function of the mutant cells, thus triggering a self-reinforcing pathological behavior that culminates with the formation of cysts. To date, however, there has not been a comprehensive study of the biomechanical mechanisms that may control the cystogenic process.

We and others have reported increased expression of integrin-β1 in PC1-defective cells (van Adelsberg 1994; Battini et al. 2006) and that integrin-β1 is active, accounting for the increased adherence and collagen deposition and survival of Pkd1 knockdown cells (Battini et al. 2006). We also showed that co-deletion of the Itgb1 gene (coding for integrin-β1) dramatically reverts the cystic and fibrotic phenotype in the Pkd1^KO mouse model of ADPKD (Lee et al. 2015), indicating a critical role for integrin-β1 during cystogenesis. Importantly, our recent work showed that the ablation of Itgb1 similarly reverses the cystic disease in another ciliary protein mutant, the intraflagellar transport 88 (Ift88) (Yoo et al. 2020), which is also characterized by extensive ECM alteration, further strengthening the universal involvement of integrin-β1 and ECM in the cystic process (Yoo et al. 2020). Overall, this evidence points to profound cytoskeletal changes in PC1 and cilia-defective cells. Our preliminary data indicate that in agreement with their decreased migratory properties, Pkd1 depleted cells produce smaller FAs, while expressing an increased activation of the biomechanical-sensitive Hippo pathway and exhibiting increased contractility. Overall, our findings to date strongly support a role for integrin-β1 in renal tubular cystogenesis via dysregulation of mechanobiological signals. Accordingly, we hypothesize that imbalanced biomechanical forces that affect the spatial dynamics of the actin cytoskeleton drive the cystic phenotype.

The role of mechanical equilibrium in formation and maintenance of structures has been recognized at both the tissue (Savin et al. 2011) and organismal (Chai et al. 2015) scales. These biophysical changes during morphogenesis require epithelial polarization and concerted cell migration. The asymmetric distribution of proteins and the differential lipid composition of the membrane of epithelial cells are supported by dynamic actomyosin cytoskeletal rearrangements (Jewett and Prekeris 2018; Rodriguez-Boulan and Macara 2014) that are controlled by small GTPases of the Rho family (Chan and Nance 2013; Phuyal and Farhan 2019). However, the biomechanical imbalance of cytoskeletal forces that are altered in cells with Pkd1 mutations has never been investigated and its nature and extent remain unknown.

In this computational study, we explored the feasibility of various biomechanical drivers of renal cystogenesis by examining several hypothetical mechanisms that may promote morphogenetic markers of cystogenesis. Our objective was to provide physics-based guidance for our formulation of hypotheses and our design of experimental studies investigating the role of biomechanical disequilibrium in cystogenesis. We employed the finite element method to explore the role of isotropic and anisotropic contraction in the apical and basolateral domains of mutant cells, as well as the role of cell proliferation, to identify a set of conditions that produce the characteristic tubular cystic growth. Such biophysical computational approaches have been shown to be impactful, predictive tools in the study of morphogenic processes and evolutionary principles (Shyer et al. 2013; Savin et al. 2011; Stoddard et al. 2017).

2. Methods

2.1. Mixture framework

To model the breakdown of tubular structures in cystogenesis, we employed the framework of mixture theory as implemented in the NIH-funded open-source finite element software FEBio (febio.org) (Maas et al. 2012, 2017). Mixture theory is a modern framework of continuum mechanics initially formulated in the 60 s and first applied to biomechanics starting in the 80 s (Mow et al. 1980; Oomens et al. 1987; Lai et al. 1991; Huyghe and Janssen 1997; Gu et al. 1998). It formalizes equations of physics (conservation of mass, momentum and energy, and entropy inequality of the second law of thermodynamics) for mixtures of all constituents. In biophysics, these typically include a solvent, any number of neutral or charged solutes, and a porous solid matrix (such as the actin cytoskeleton or the cell membrane). These mixtures may also be reactive, making it possible to model chemical reactions that drive various biological processes (Ateshian 2007), solid matrix remodeling (Ateshian and Ricken 2010; Myers and Ateshian 2014), as well as passive and active transport across biological membranes (Ateshian et al. 2006, 2010) successfully recapitulating the cell osmotic swelling theory of Kedem and Katchalsky (1958; 1961).

Most importantly for this study, this mixture framework is suitable for modeling biological tissue growth by cell division as well as intracellular and extracellular solid matrix deposition (Ateshian et al. 2009, 2012; Myers and Ateshian 2014) and active contraction. While this continuum framework may be used to model individual cells (Albro et al. 2009; Hou et al. 2018), it can also describe the behavior of cell aggregates (such as an epithelium) without explicitly modeling cell boundaries (Azeloglu et al. 2008; Ateshian et al. 2009, 2012). The investigations proposed in this study followed the latter approach, though explicit modeling of individual cells remains an option if needed.

2.2. Modeling assumptions

In this study, we defined biomechanical equilibrium in wild-type (WT) cells as the state when cell elasticity (passive stress from deformation), actomyosin contractile forces and osmotic forces are in balance, in the absence of cell proliferation, causing no significant temporal changes in cell and tubular morphology. For simplicity we modeled WT cells using only passive elasticity starting from a state of rest, with the understanding that internal stresses caused by these various factors cancel each other out. We defined biomechanical disequilibrium as the condition when one or more of these factors evolves beyond its normal homeostatic range, producing a change in tubular morphology.

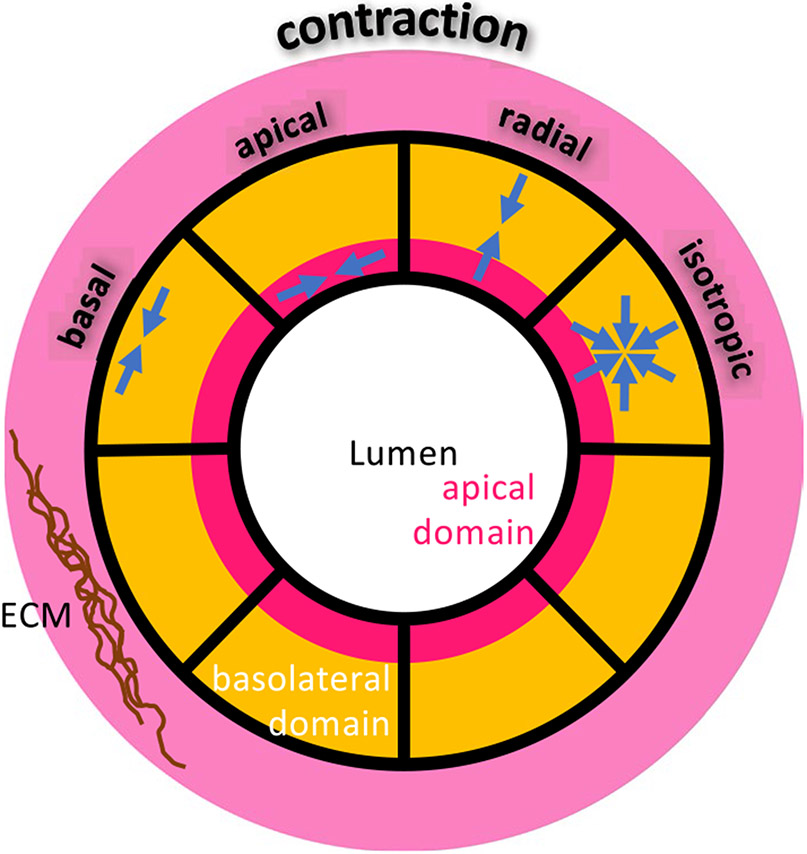
To elucidate biomechanical disequilibrium in cystogenesis, we considered a variety of biomechanical pathways such as active contraction, osmotic effects modulated by passive, facilitated or active transport mechanisms across the cell membrane or within the cell, and cell proliferation (which also involves these other mechanisms, but in a more regulated process). Loss of cell polarity, or alterations in adhesive junctions (AJs) or integrins, could be simulated by altering the distribution of active contraction from apical to basal domains, as well as altering the orientation of the contractile forces in those domains (Fig. 1). Using computational approaches, we explored the role of heterogeneity in material properties, composition, and cell pathophysiology. In particular, cystogenesis is known to be initiated from isolated or small clusters of Pkd1 or Pkd2 mutant cells located along epithelial tubules of the kidney nephron, so we employed models that replicated this initial condition.

Fig. 1.

Schematic illustration of cellular domains and contractile forces in a cross section of a tubule

The generally accepted mechanism of the origin of cystogenesis relies on the two-hit hypothesis, according to which the expression of the phenotype in a heterozygous individual is brought up by a second event such as a somatic mutation or biological context, which can affect the dosage of the normal cystic gene expression, thus manifesting the disease phenotype. These cystic events, whether from genetic and/or environmental insult, appear to be stochastically determined. Early studies focused on the analysis of the normal allele have indicated that cysts are clonal populations with loss of heterozygosity (LOH) (Qian et al. 1996; Pei et al. 1999). The clonal origin suggests that cysts arise from one cystic event, that is from LOH in one original cell. It should be noted, however, that the loss of PC1 function is associated with genomic instability (Battini et al. 2008) and that epithelial cells in ADPKD kidney present variable ploidy and are genetically heterogeneous (Qian et al. 1996; Gogusev et al. 2003). The possible effects of these wider genetic alterations are more difficult to assess and may vary within “ clones” and their biological milieu.

Cystogenesis starts during development and while cysts have been observed in all of the nephron’s segments and in the glomeruli (Ahrabi et al. 2010), the outer medulla and collecting duct epithelium remain particularly prone to cystogenesis (Ahrabi et al. 2010; Wilson 2004). This is likely because proliferation is more active in these areas during the late renal development (Leonhard et al. 2016). Furthermore, kidney damage at different sites along the nephron may significantly induce reparative responses that increase the possibility of cystic transition.

Based on this literature, for our hypothesis-generating computational analyses performed in this study we assumed that the cystic change occurs in one cell as a deviation from its equilibrium state, and we focused on intracellular active contraction and cell proliferation. Based on our prior experimental findings regarding the importance of Itgb1 in the regulation of cyst formation, we assumed that cell contractility increased with increasing concentration of integrin-β1 cell surface receptors, on the assumption that more links would be created between the actin cytoskeleton and extracellular matrix (this is the type of modeling assumption that may be tested experimentally in future studies, if motivated by the outcome of the current investigation). In some scenarios, we divided the cells into two domains, to produce apical contraction or basal (cortical) contraction. In particular, for mutant cells, apical or basal contraction are taken to be transversely isotropic, with contraction in the tangent plane of the lumen or cortex; we also considered isotropic basolateral contraction; and uniaxial apical-basal contraction, along the radial direction of the cylindrical tubule (Fig. 1). In those scenarios, we explored how disruptions in mutant cell contractions within any of these domains (i.e., magnitude and orientation of contractile forces) might affect the propensity toward cystogenesis. We also investigated scenarios where the cytoskeletal stiffness of mutant cells differed from those of healthy cells.

2.3. Constitutive models

The cell protoplasm was modeled using a compressible isotropic elastic neo-Hookean constitutive model as reported by Bonet and Wood (1997). The passive elastic Cauchy stress in this material model is

$${\sigma }^e=\frac{\mu }{J}(\mathbf{B}-\mathbf{I})+\frac{\lambda }{J}(\text{ln}J)\mathbf{I},$$ (1)

where $\mathbf{I}$ is the identity tensor, $J=\text{det}\mathbf{F}$ and $\mathbf{F}$ is the deformation gradient, $\mathbf{B}={\mathbf{F}}^T\cdot \mathbf{F}$ is the left Cauchy-Green tensor, and $\lambda$, $\mu$ are Lamé-like material constants that may be converted to Young’s modulus $E=2\mu (1+v)$ and Poisson’s ratio $v=\frac{1}{2}\lambda ∕(\lambda +\mu )$. A compressible model was adopted to allow mutant cell proliferation in the form of volumetric expansion, as further detailed below.

Cell contraction was modeled as a prescribed active stress ${\sigma }^a$ superposed on the Cauchy stress tensor ${\sigma }^e$ of the neo-Hookean material. For uniaxial contraction along the referential unit vector ${\mathbf{n}}_r$, the active stress was given by ${\sigma }^a=J^{-1}{T}_0\mathbf{n}\otimes \mathbf{n}$, where $\mathbf{n}=\mathbf{F}\cdot {\mathbf{n}}_r$ is the stretched orientation of ${\mathbf{n}}_r$ in the current configuration and $T_0$ is a user-prescribed contractile stress ($T_0\ge 0$ for contraction). For transversely isotropic contraction in the plane normal to the referential direction ${\mathbf{n}}_r$, the active stress was ${\sigma }^a=J^{-1}{T}_0(\mathbf{B}-\mathbf{n}\otimes \mathbf{n})$. For isotropic contraction, the active stress was set to ${\sigma }^a=J^{-1}{T}_0\mathbf{B}$.

Cell proliferation was modeled using the cell growth model described in our earlier study (Ateshian et al. 2012), simplified to the case where cells are not embedded within an ECM. In this framework cell division occurs in conjunction with cell swelling, since daughter cells occupy twice the volume of the parent cell. The swelling mechanism is driven by osmotic forces that drive fluid into the daughter cells as intracellular solid content also doubles in volume. This osmotic swelling effect can be simulated by superposing a swelling pressure $-p\mathbf{I}$ to the passive protoplasmic stress ${\sigma }^e$, where

$$p=RT\left(\frac{c_r}{J-{\phi }_r^s}-c_e\right).$$ (2)

Here, $R$ is the universal gas constant, $T$ is the absolute pressure, ${\phi }_r^s$ is the intracellular solid volume fraction and $c_r$ is the intracellular molar content of membrane-impermeant solutes, both given in the reference configuration (prior to cell proliferation), and $c_e$ is the extracellular osmolarity. Cell growth is modeled by simply increasing the mass of the intracellular solid matrix and membrane-impermeant solute. This is achieved by allowing the parameters ${\phi }_r^s$ and $c_r$ to increase over time as a result of growth.

The total Cauchy stress in proliferating mutant cells was thus evaluated as $\sigma ={\sigma }^e+{\sigma }^a-p\mathbf{I}$, whereas that in wild-type cells was $\sigma ={\sigma }^e$.

2.4. Geometry, mesh, and material properties

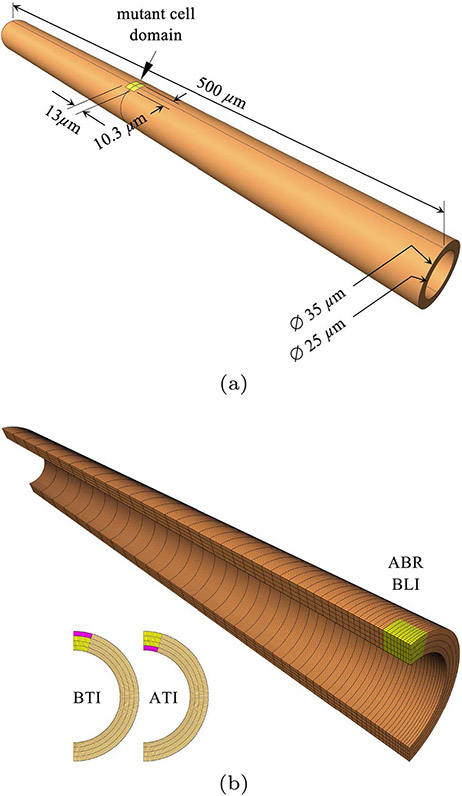
The computational simulations conducted in this study used a three-dimensional model of an epithelial tubule with outer diameter of 35 $\mu \mathrm{m}$ and inner diameter of 25 $\mu \mathrm{m}$, which is representative of the dimensions found in the nephron (diameters varying from 65 $\mu \mathrm{m}$ in the proximal tubule, 15 $\mu \mathrm{m}$ in the intermediate tubule, and 35 $\mu \mathrm{m}$ in the distal tubule). The length of the modeled section was set to 500 $\mu \mathrm{m}$. In all models, a mutant cell domain was located halfway along the tubule length, with an axial length of 13 $\mu \mathrm{m}$, a thickness of 5 $\mu \mathrm{m}$ (spanning the tubule thickness) and a circumferential width of 10.3 $\mu \mathrm{m}$ on the outer tubule surface (Fig. 2a). The apical and basal domains of this mutant cell domain each had a thickness of 1.25 $\mu \mathrm{m}$ starting from the lumen and outer tubule surface, respectively. The remaining finite element domain consisted of WT cells.

Fig. 2.

a Nephron tubule dimensions, showing location and size of initial mutant cell domain (yellow); WT cells occupy the orange domain. b Finite element mesh of quarter-model, with 128 uniformly distributed elements along the circumferential direction, 4 uniformly distributed elements along the radial direction, and 50 non-uniformly distributed elements along the axial direction. This mesh was used for apical-basal radial (ABR) and basolateral isotropic (BLI) contraction (yellow). Insets show mesh partitioning for models that used basal (BTI) and apical (ATI) transversely isotropic contraction (pink). In all cases, cell proliferation was prescribed in the yellow domain only

The tubule was fixed (zero displacements along all three coordinate directions) on both ends. From symmetry considerations, the finite element model used only one quarter of the geometry, with suitably enforced symmetry planes (Fig. 2b). The model included 25,600 hexahedral 8-node elements, with 128 uniformly distributed elements along the circumferential direction, 4 uniformly distributed elements along the radial direction, and 50 non-uniformly distributed elements along the axial direction, with a bias producing a finer mesh in the vicinity of the mutant cell domain and coarser mesh at the fixed end. In particular, the mutant cell domain consisted of 9×12×4 elements along the axial, circumferential and radial directions, respectively (Fig. 2b).

WT cells were modeled using the neo-Hookean material given in (1), with $E^{WT}=1$ kPa and $v^{WT}=0.3$. The value of Young’s modulus for WT cells is approximate, based on reported cell moduli for endothelial cells by Jalali et al. (2015), who reported a range of 0.2 – 1.0 kPa, and for chondrocytes by Koay et al. (2003) and Darling et al. (2006), who reported a range of 0.1 – 1.0 kPa. (The modulus of kidney epithelial cells was determined by Rabinovich et al. (2005), though their reported values appear to be unreasonably large, in the range of 1000 – 5000 kPa.) Mutant cells were modeled as mixtures of a neo-Hookean material, active contraction, and cell proliferation. The neo-Hookean material of mutant cells used $v^{MC}=0$ to accommodate cell proliferation, and $E^{MC}=1$ kPa or $E^{MC}=0.1$ kPa to examine the role of mutant cell stiffness on cystogenesis. Mutant cell contraction was modeled using either uniaxial contraction along the radial (apical-basal) direction, or isotropic (basolateral) contraction, of the entire mutant cell domain. Mutant cell apical and basal contractions were modeled using transversely isotropic contraction in the apical and basal domains, respectively, with the axis of symmetry directed along the radial (apical-basal) direction. In all of these cases, the contractile stress was set to $T_0=0.1$ kPa, 1 kPa or 10 kPa, to explore the influence of contractile stresses on cystogenesis. These values are loosely based on a review of cell traction force microscopy by Schwarz and Soiné (2015), who reported stresses of up to 12.5 kPa exerted on cell substrates due to contraction. We also set $T_0=0$ kPa to turn off contraction in some scenarios. Mutant cell proliferation was modeled by increasing ${\phi }_r$ and $c_r$ in (2) by a factor of 100, either in the entire mutant cell domain (in the case of isotropic and apical-basal contraction) or only in the non-contracting domain (in the case of apical or basal contraction) as shown in Fig. 2b, starting from ${\phi }_r=0.4$ and $c_r=180$ mM in the initial configuration, with $c_e=300$ mM representing ambient osmolarity throughout the analysis.

Finite element analyses were performed where cell contraction was prescribed from time $t=0$ to $t=1$ (time units in these analyses are arbitrary), followed by cell proliferation from time $t=1$ to $t_f=26$. In some scenarios cell contraction and proliferation were turned on simultaneously, spanning the time $t=0$ to $t_f=25$, though cell contraction was still prescribed over the narrower time interval $0\le t\le 1$ on the basis that multifold cell proliferation is a slower process than cell contraction. In other scenarios, the sequence of cell contraction and proliferation was reversed.

2.5. Testing scenarios

The testing scenarios explored in this study included the following four factors: (1) Mutant cell modulus, $E^{MC}$, relative to that of WT, $E^{WT}$. (2) Mutant cell contractile stress $T_0$ relative to modulus $E^{MC}$. (3) Anisotropy and inhomogeneity of mutant cell contraction. (4) Sequence of cell contraction and cell proliferation. The first factor had two levels: $E^{WT}:E^{MC}=1:1$ and $E^{WT}:E^{MC}=10:1$, with $E^{WT}$ remaining unchanged. The second factor had three levels, $E^{MC}=10:1$, 1 : 1, or 0 : 1 (the latter implying no cell contraction). The third factor had four levels: apical-basal contraction in the radial direction (ABR), basolateral isotropic contraction (BLI), apical transversely isotropic contraction (ATI), and basal transversely isotropic contraction (BTI). These contractions occurred in the domains indicated in Fig. 2b. The last factor had three levels: Cell contraction over $0\le t\le 1$ followed by cell proliferation over $1\le t\le 26$ (CCP), cell proliferation over $0\le t\le 25$ followed by cell contraction over $25\le t\le 26$ (CPC), and simultaneous cell contraction over $0\le t\le 1$ and proliferation over $0\le t\le 25$ (SCP). In total, these combinations form 2×3×4×3=72 models. However, since $T_0=0$ implies no contraction and only proliferation, the last factor was not applied to this case, reducing the number of analyzed models to 56. The factors and levels associated with each of these models are summarized in Table 1, where each model is associated with a unique label F####, with # representing the level in each factor.

Table 1.

Summary of the 54 finite element models analyzed in this study. In all cases $E^{WT}=1$ kPa. (a) Models where WT and mutant cells have the same modulus. (b) Models where mutant cells have a modulus ten times smaller than WT cells. ABR: apical-basal uniaxial contraction, BLI: basolateral isotropic contraction, ATI: apical transversely isotropic contraction. CCP: cell contraction then proliferation, CPC: cell proliferation then contraction, SCP: simultaneous contraction and proliferation. Cyst formation (Y=yes, N=no) based on visual inspection of models at final analysis time (Figs. 3 and 4)

$E^{WT}:E^{MC}$	$T_0:E^{MC}$	Contraction	Sequence	Model label	% Completion	Cyst formed
1 : 1	10 : 1	ABR	CCP	F1111	57.3	Y
			CPC	F1112	36.6	N
			SCP	F1113	55.5	Y
		BLI	CCP	F1121	36.8	N
			CPC	F1122	36.6	N
			SCP	F1123	37.2	N
		ATI	CCP	F1131	57.1	N
			CPC	F1132	39.1	N
			SCP	F1133	56.5	N
		BTI	CCP	F1141	53.6	N
			CPC	F1142	38.7	N
			SCP	F1143	51.6	N
	1 : 1	ABR	CCP	F1211	38.3	N
			CPC	F1212	36.6	N
			SCP	F1213	32.6	N
		BLI	CCP	F1221	36.8	N
			CPC	F1222	36.6	N
			SCP	F1223	34.3	N
		ATI	CCP	F1231	70.8	N
			CPC	F1232	39.1	N
			SCP	F1233	69.7	N
		BTI	CCP	F1241	46.7	N
			CPC	F1242	38.7	N
			SCP	F1243	44.6	N
	0 : 1	ABR	SCP	F1313	38.1	N
		BLI	SCP	F1323	38.1	N
		ATI	SCP	F1333	40.6	N
		BTI	SCP	F1343	40.2	N
$E^{WT}:E^{MC}$	$T_0:E^{MC}$	Contraction	Sequence	Model label	% Completion	Cyst formed
10 : 1	10 : 1	ABR	CCP	F2111	100.0	Y
			CPC	F2112	45.9	N
			SCP	F2113	100.0	Y
		BLI	CCP	F2121	37.7	N
			CPC	F2122	45.9	N
			SCP	F2123	35.2	N
		ATI	CCP	F2131	67.5	N
			CPC	F2132	42.4	N
			SCP	F2133	66.2	N
		BTI	CCP	F2141	53.9	N
			CPC	F2142	46.9	N
			SCP	F2143	50.3	N
	1 : 1	ABR	CCP	F2211	47.0	N
			CPC	F2212	45.9	N
			SCP	F2213	48.8	N
		BLI	CCP	F2221	49.0	N
			CPC	F2222	45.9	N
			SCP	F2223	47.0	N
		ATI	CCP	F2231	50.1	N
			CPC	F2232	42.4	N
			SCP	F2233	47.7	N
		BTI	CCP	F2241	49.8	N
			CPC	F2242	46.9	N
			SCP	F2243	49.4	N
	0 : 1	ABR	SCP	F2313	47.6	N
		BLI	SCP	F2323	47.6	N
		ATI	SCP	F2333	44.1	N
		BTI	SCP	F2343	48.7	N

3. Results

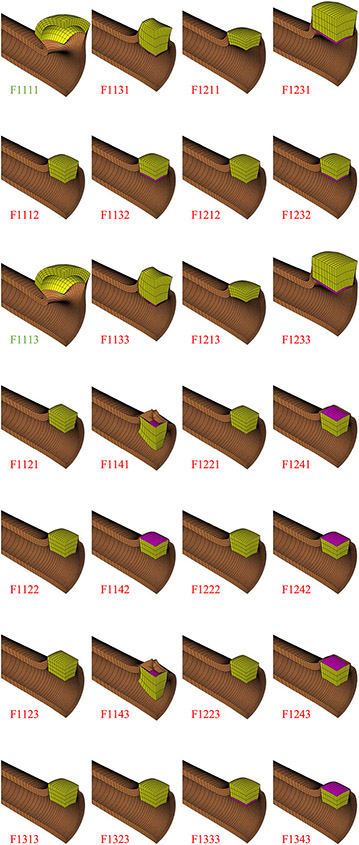
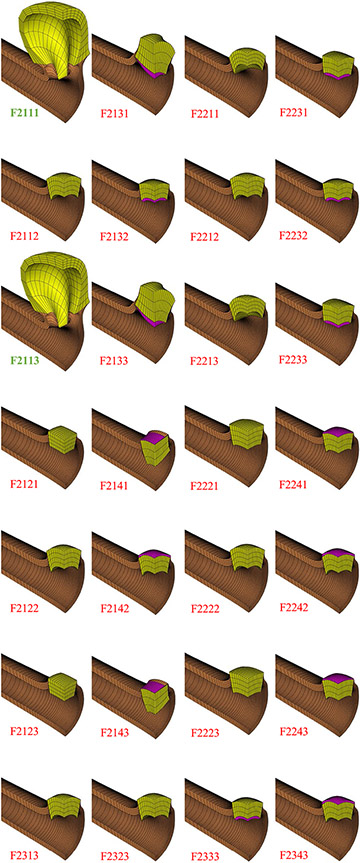
Finite element models for these 56 cases were created and analyzed on FEBioStudio v1.6.1 and executed with FEBio 3.5.1 (febio.org) on a high-performance desktop computer with 128 GB of memory and 18 threads on each of two cores. Models either ran to completion (up to time $t_f=26$ for CCP and CPC cases, or $t_f=25$ for SCP cases) or terminated prematurely at $t_c$ due to excessive element distortion. Elapsed wall clock time for each finite element analysis ranged from 11 min to 95 min. Premature termination ($t_c<t_f$) without evidence of cyst growth was deemed to represent failure of that model to reproduce cystogenesis. Aggregate results for all cases are presented in Table 1 with a graphical representation of finite element models at their final time point given in Figs. 3 and 4.

Fig. 3.

Finite element results for 28 models (F1###). Green labels indicate budding cyst formation, and red labels indicate failure to produce cyst

Fig. 4.

Finite element results for remaining 28 models (F2###). Bold green labels indicate cyst formation, and red labels indicate failure to produce cyst

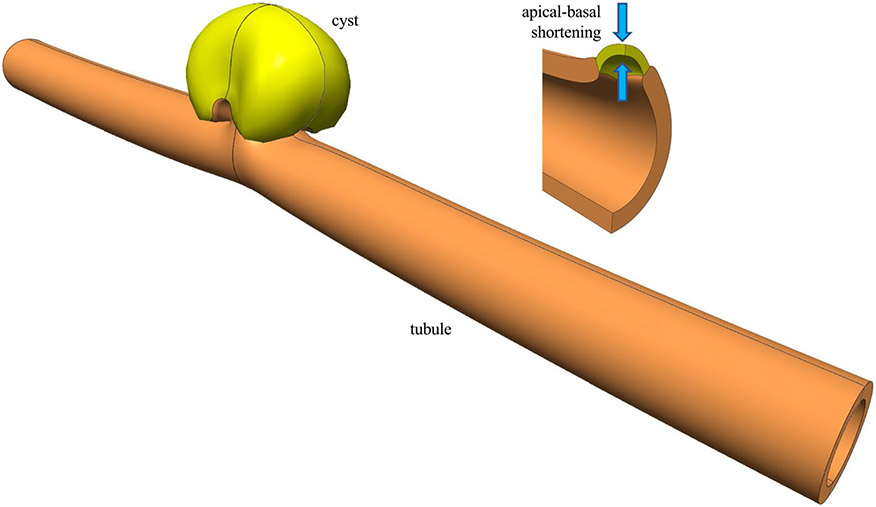
Of the 56 finite element models only two ran to completion, corresponding to models F2111 and F2113 in Table 1b. These models represent the case where mutant cells had a modulus one-tenth that of WT cells, cell contraction had a contractile stress ten times greater than the mutant cell modulus and was uniaxial along the radial (apical-basal) direction, and cell contraction either preceded or accompanied cell proliferation. The final cyst shape is shown in Fig. 4, and an alternative representation of the model results is shown in Fig. 5. The remaining models all failed prematurely, with a percentile completion calculated from $t_c∕t_f$. Cyst formation was observed in the completed models (F2111 and F2113), and budding cyst formation was also found in the F1111 and F1113 models (mutant and WT cells having identical moduli, cell contractile stress ten times greater than mutant cell modulus, contraction along the apical-basal direction, contraction preceding proliferation or progressing simultaneously, Fig. 3).

Fig. 5.

F2111 model showing final cyst shape (at $t_f=26$) with reflections about symmetry planes. Inset shows apical-basal shortening produced by cell contraction (at $t=1$)

No cyst formation was observed when the contractile stress $T_0$ was equal to the mutant cell modulus $E^{MC}$ (F#2## models), nor with isotropic basolateral cell contraction (F##2# models) nor transversely isotropic apical or basal contraction (F##3# and F##4# models). Similarly, no cyst formation was observed when cell proliferation preceded cell contraction (F###2 models) or with only cell proliferation but no contraction (F#3## models).

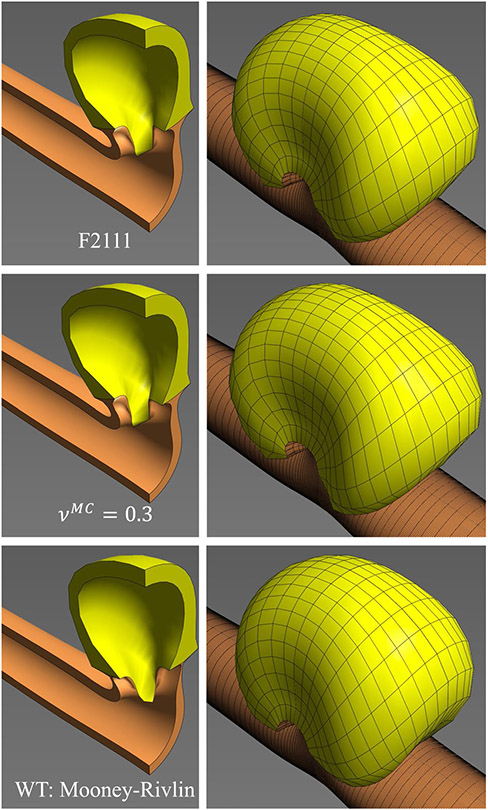
To explore the influence of mutant cell compressibility on cystogenesis, F2111 was re-analyzed with $v^{MC}=0.3$ (instead of $v^{MC}=0$). To explore the influence of WT cell compressibility, their neo-Hookean model was replaced with an incompressible Mooney–Rivlin model with the same Young’s modulus. Both alternative models ran to completion with nearly identical cyst morphologies as F2111 (Fig. 6).

Fig. 6.

Cyst formation observed in the multifactorial study (F2111, top panel) was not sensitive to the choice of Poisson’s ratio for the mutant cells ($v^{MC}=0.3$, middle panel) or the choice of constitutive model for the WT cells (Mooney–Rivlin material, bottom panel)

4. Discussion

The objective of this study was to explore a range of physics-based mechanisms that could explain renal tubule cystogenesis based on the underlying hypothesis that this pathology is triggered by biomechanical disequilibrium. Finite element models were created that accounted for four distinct factors, including disparities in the elastic modulus of WT and mutant cells, a range of contractile stress magnitudes exerted by mutant cells, either isotropically or anisotropically, exclusively within the apical or basal domains or throughout the cell, using three possible sequences for contraction and proliferation. These four factors were motivated by our reading of the literature, as reviewed in the Introduction, observations from our own experimental data (Lee et al. 2011, 2015; Yoo et al. 2020), and the constraints of our modeling approach using a continuum-based finite element formulation (Ateshian et al. 2009, 2012).

The results of these analyses were unambiguous: Among the factors considered in our study, cystogenesis occurred when mutant cells were softer than WT cells; their contractile stress was significantly greater than their elastic modulus; contraction took place along the radial (apical-basal) direction; and contraction either preceded or accompanied proliferation (F2111 and F2113 in Fig. 4). Budding cystogenesis was also observed when mutant cells had a modulus comparable to WT cells (F1111 and F1113 in Fig. 3). For all other factors, including apical or basal constriction, cystogenesis was not observed. The key driving factor was the ratio of active contractile apical-basal stress to passive cell stiffness in the mutant cell(s), $T_0:E^{MC}$; whether the mutant cells had the same stiffness as WT cells, or became softer, they exhibited a characteristic flattening (shortening) when the apical-basal contractile stress was sufficiently elevated to overcome the passive cell stiffness. This flattening caused a small local bulging of the mutant cell and its immediate surroundings, which was sufficient to produce pronounced cystogenesis upon mutant cell proliferation (Fig. 5). Interestingly, cyst-lining epithelia in human and animal models display characteristically flattened cells (Nadasdy et al. 1995; Wilson 2011). In studies of epithelial folding it has been suggested that apical-basal shortening may be driven by an apical microtubule network via a basal polarity shift (Takeda et al. 2018). It is thus noteworthy that the physics-based finite element simulations of this study predict that apical-basal shortening is an essential driving force for cyst formation, which represents a special case of epithelial folding. These computational results are consistent with the expectation that alteration of ECM in tubular cystogenesis can produce forces channeled through integrins and the interconnected cytoskeleton, which exacerbate the abnormal function of the mutant cells, triggering a self-reinforcing pathological behavior that culminates with the formation of cysts.

The dimensions of the “mutant cell domain” shown in Fig. 2 are consistent with the dimensions of a single cell, therefore the model was able to predict cyst formation based on the two-hit hypothesis, taking into consideration the altered equilibrium in one cell upon depletion of PC1 function (the cystic signal) and known effects of PC1 loss such as changes in proliferation and adhesion, in agreement with the reported phenotype of PC1 defective cells (Battini et al. 2006; Aguiari et al. 2008). It has been proposed that a third hit, such as kidney injury, may be involved in cystogenesis of the mature organ (Luyten et al. 2010; Bastos and Onuchic 2011); while this third hit is not necessary, we believe that it may force reparative mechanisms that could require developmental programs relying on PC1 function, thus increasing the odds of heterozygous cells to undergo LOH and become cystic.

Alternative cytoskeletal mechanisms have also been implicated in uniaxial cell contraction. For example, in the Drosophila germband epithelium, it has been shown that planar polarized myosin II can generate contractile stresses in a single direction, perpendicular to the elongation axis, providing an alternative mechanism for uniaxial contraction (Wang et al. 2020).

This study did not explicitly investigate the role of cell-cell adhesion in cystogenesis. Belmonte et al. (2016) performed computational simulations of cyst formation that implicated both cell adhesion and cell proliferation in this process, although these authors found that loss of cell adhesion was required to reproduce cyst morphology. Our modeling approach did not consider individual cells and their potential loss of adhesion, yet we were able to predict cyst formation resulting from apical-basal contraction and cell proliferation. Clearly, computational models can only implicate mechanisms that have been incorporated into the model in order to predict specific outcomes. Nevertheless, these computational models may be very informative because they allow us to include or exclude various hypothesized cystogenesis mechanisms. Indeed, the models of this study suggest that active apical and basal (cortical) contraction are not drivers of cystogenesis.

These models also provide guidance and targets for experimental investigations. In particular, the models of this study have emphasized the importance of mutant cell elastic modulus (cell stiffness) relative to that of WT cells, suggesting that these moduli need to be characterized experimentally, preferably in situ. Our models have also emphasized the importance of characterizing the apical-basal contractile stress magnitude exerted by mutant and WT cells, which may require sophisticated experimental methodologies for extracting those measures in situ. This may be a particularly challenging problem since cell stiffness and cell contractile stress depend significantly on the stiffness of the cell substrate (Discher et al. 2005; Jalali et al. 2015; Schwarz and Soiné 2015), implying that in situ measurements would be preferable compared to cell cultures. If cell mechanics experiments confirm that uniaxial contraction occurs along the apical-basal direction, more detailed investigations of the underlying mechanisms for this contractile stress would need to be investigated, such as the role of the microtubule network and myosin distribution.

Renal tubules are characterized by a luminal space surrounded by polarized epithelial cells. Cell polarization, that is the asymmetric segregation of polarity factors along the axis perpendicular to the adhesion substrate (apical-basal polarity) or parallel to the epithelial sheet (planar cell polarity), is required for the directionality of cellular functions and responses, such as absorption and secretion, cell movement, and proliferation. The maintenance of apical-basal polarity relies on the integration of mechanobiological signals deriving from cell-cell and cell-extracellular matrix (ECM) interactions. Derailment of these concerted exchanges leads to tubular malformations such as tubular dilation, or cystogenesis, and loss of tubule physiological function, which are pathognomonic of polycystic kidney disease. The current computational study is the first of its kind describing how biomechanical imbalance could contribute to cystogenesis. Increasing experimental evidence suggests that mutations in the Pkd1 gene are associated with abnormalities in the core mechanosensitive machinery of epithelial cells (Nigro et al. 2019). Our findings to date indicate that the cystogenesis caused by the deletion of Pkd1 or the ciliary Ift88 gene can be reverted to the normal phenotype by the ablation of integrin-β1, a main ECM receptor. Based on these observations, we hypothesized that the equilibrium of the biomechanical forces generated between intercellular junctions and ECM is essential to establish and maintain tubular integrity.

It would be natural to expect that ECM elasticity would play a role in the mechanical equilibrium of the system, as emphasized in the Introduction to this study. ECM stiffness can be affected by the cell, but it is likely also variable along the nephron and it is unlikely to be present in a significant amount at the onset of cyst formation. In the analysis of this study, we assumed that a stiff ECM would follow the initial cyst formation, not drive it. We note that even in the face of altered substrate elasticity, ECM components cannot generate active forces. In the current exploratory study we focused on the cell’s vectors since the mechanical forces at play, regardless of their origin, would ultimately converge on contractile dynamics intrinsic to the cell, as this is the main “deforming unit” in the generation of the cyst.

The computational simulations presented in this study will guide our future experimental assays, including biophysical, cell biological, and in vivo approaches. Our approach can lead to the identification of novel drug targets that could reverse this unique biophysical disease mechanism, though that would require a better understanding of signaling molecules in normal and diseased renal epithelia, to integrate biological data with physical parameters in the model prediction. For example, most of the current attempts at slowing down the progression of the disease, including the V2 vasopressin receptor antagonist Tolvaptan—the only FDA-approved drug for ADPKD treatment—aim to reduce intracellular cyclic adenosine monophosphate (cAMP), a second messenger associated with growth of cystic cells. cAMP has opposite cell-dependent roles on contraction: it increases contraction in cardiomyocytes and skeletal muscles through the activation of protein kinase A (PKA) and Ca²⁺ channels, and decreases contraction in smooth muscles via the inhibition of myosin light-chain kinase (MLCK). Although higher cAMP levels in cystic cells coincide with the lower stiffness of these cells, the role of cAMP in renal epithelial cells contractility has not been investigated. We plan to run these studies in the future, to get better insights into the underlying causes for increased mutant cell contractility.

It should also be underlined that two stages have been distinguished in the course of ADPKD, one of cyst initiation and one of cyst expansion (Harris et al. 2006), with the former being the main cause of disease severity. While most therapeutic efforts have concentrated on the second stage, this study aimed to dissect the imbalance of mechanical forces in the first stage that allows the deformation of a normal cell into a cystic one, with the underlying idea that regardless of the forces at play, ultimately tubular deformation initiates with the changes in the equilibrium of the cystic cell, which therefore “recapitulates” the contribution of all cellular and extracellular forces.

The computational results presented in this study further suggest that reactive mixture models that reproduce fundamental equations of continuum mechanics are not toys that can be manipulated arbitrarily to produce a desired outcome (cystogenesis in this case). Given realistic geometries, material properties, and composition, they appear to be effective at supporting or rejecting hypothesized mechanisms of pathophysiology. We may now turn our attention to performing experimental measurements with in vitro cell cultures or in vivo conditions to validate the model outcomes, and iteratively refine this back-and-forth process until we establish with high confidence the validity of such hypothesized biomechanical disequilibrium factors. If motivated by experimental findings, our future computational studies may introduce additional modeling capabilities, such as loss of cell-cell adhesion, to investigate alternative hypotheses regarding biomechanical drivers of renal cystogenesis.

Data Availability

The finite element models presented in this study may be downloaded from the FEBioStudio repository, available from https://febio.org (download FEBioStudio from https://febio.org/downloads/, and then follow instructions on how to access the Repository at https://help.febio.org/docs/FEBioStudio-1-7/FSM17-Section-3.10.html).