Decomposition of Disparities in Life Expectancy with Applications to Administrative Health Claims and Registry Data

Abstract

Research shows that geographic disparities in life expectancy between leading and lagging states are increasing over time while racial disparities between Black and White Americans have been going down. In the 65+ age strata morbidity is the most common cause of death, making differences in morbidity and associated adverse health-related outcomes between advantaged and disadvantaged groups an important aspect of disparities in life expectancy at age 65 (LE65). In this study, we used Pollard’s decomposition to evaluate the disease-related contributions to disparities in LE65 for two types of data with distinctly differing structures: population/registry and administrative claims. To do so, we analyzed Pollard’s integral, which is exact by construction, and developed exact analytic solutions for both types of data without the need for numerical integration. The solutions are broadly applicable and easily implemented. Applying these solutions, we found that the largest relative contributions to geographic disparities in LE65 were chronic lower respiratory diseases, circulatory diseases, and lung cancer; and, to racial disparities: arterial hypertension, diabetes mellitus, and cerebrovascular diseases. Overall, the increase in LE65 observed over 1998–2005 and 2010–2017 was primarily due to a reduction in the contributions of acute and chronic ischemic diseases; this was partially offset by increased contributions of diseases of the nervous system including dementia and Alzheimer’s disease.

1. Introduction

Persistent disparities in health outcomes¹ between sex, race/ethnicity, and geographic area-specific subgroups in the United States are an important barrier to improving total life expectancy (LE)². Attempts at reducing such disparities have met with limited success^3-5, and the mechanisms by which health disparities develop and propagate are not fully understood^2,6,7. In the 65+ age strata morbidity is the most common cause of death, making differences in associated adverse health-related outcomes between advantaged and disadvantaged groups an important aspect of disparities in life expectancy at age 65 (LE65). However, isolating the effects of individual diseases/disease groups is not straightforward due to the need to balance estimate accuracy, type and number of methodological assumptions, range of included diseases, and the statistical power of the available data.

Methods of decomposition in demography can provide important insight into the causes of the differences in aggregate measures (such as LE) between well-defined population groups. As we will demonstrate shortly, Pollard’s decomposition^8,9 is the method of choice for representing cause-of-death-specific contributions to disparities in LE^10-12. The difference in LEs for two subpopulations is represented through an integral of age-functions of subpopulation-specific survival functions, LEs, and cause-specific hazard functions. For LE65, the integration is performed over age intervals from 65 to the maximal age in a specific dataset. This means that all functions in the integrand have to be well-defined and computable from available data. This is not trivial for cause-specific hazard functions. Many commonly used data sources report/update information at random age points (e.g., the age and time that a medical insurance claim was submitted to an administrative claim database) or aggregated across a fixed time interval (e.g., calendar-year-specific data on cause-specific mortality aggregated over fixed time periods, usually single-year age groups, in registry datasets). In the first case (administrative data), cause-specific survival functions can be evaluated using the Kaplan-Meier product-limit estimator¹³. This estimator is discontinuous, however, and results in infinite hazards at exact times or ages of death and zero hazards at all other age/time points. Mathematically, this requires us to deal with discontinuous and generalized functions. Although Pollard's decomposition extends (in theory) to discontinuous and generalized functions, numerical integration of such functions is not possible, restricting its use in such applications. In the second case (registry data), cause-specific survival functions and LEs can be evaluated using the life table approach. The life table approach also yields estimates of cause-specific hazards aggregated (or integrated) over discrete age intervals. No comparable life table approach has yet been proposed for cause-of-death decomposition using Pollard’s integral, the result being that practitioners (e.g., ref.¹⁴) continue to use Pollard’s midpoint approximation⁸ (eqn. 14) without considering the associated uncertainties and/or biases.

Pollard’s decomposition is generally applied to aggregated mortality data, allowing the inputs to be obtained from the associated life tables^14,15. Evaluations of Pollard’s decomposition that require assumptions affecting how the input measures are obtained from data, or that use numerical approximations for integration over age-intervals, can introduce bias into the resulting cause-specific decompositions. Systematic biases are generally not considered in such analyses. Pollard’s decomposition has never been applied to administrative data in a way that exploits the additional information provided by having the exact dates of death. In order to address these limitations, we determined how Pollard’s decomposition^8,9 could be adapted for use with administrative claims records and population/registry data. We used a product-limit estimator for left-truncated (or delayed entry) censored administrative data¹⁶ and a life table approach for registry/population data; we developed an exact representation of Pollard’s decomposition for discrete age intervals that does not require numerical integration and does not require an assumption of independence among the causes of death selected for use in the decomposition.

Pollard’s decomposition is exact in continuous time—i.e., the sum of all relative contributions over all causes of death is exactly 1.0, or 100% of the difference in life expectancy. The property of additivity is a major advantage of Pollard’s decomposition; without it, distinguishing small cause-specific contributions to disparities from accumulated uncertainties due to methodological assumptions could be a challenge. The additivity property of Pollard’s decomposition continues to hold exactly in our solutions shown in eqns. (8) and (9), even after applying the multiple operations necessary to solve Pollard’s integral for the two types of data used in this study.

The assumption of independence of cause-specific forces of mortality is not required for our approach; in contrast, independence is required by alternative approaches such as proposed by Beltrán-Sánchez et al.¹². Our method is more broadly applicable because we do not have to limit its use to sets of causes for which independence is a reasonable approximation. This allows us to deal with any specified set of causes without having to consider joint dependence on common risk factors such as diet, exercise, smoking, environmental exposures, etc. Indeed, Mokdad et al.¹⁷ proposed that such variables were not just risk factors but were in fact actual causes for close to half the deaths in the U.S in 2000. This suggests that dependencies between cause-specific contributions to the differences in life expectancy may be explained by common causes that are amenable to behavioral modifications or other forms of intervention. For example, diabetes mellitus, hypertension, and atherosclerosis all increase the risk of death from cerebrovascular disease and cardiovascular disease. The existence of such major dependencies is one reason to further emphasize that Pollard’s decomposition as well as the adaptations performed in this study do not require an assumption of independence of causes of death.

This paper is structured as follows: Section 2.1 provides preliminary results demonstrating that Pollard’s decomposition^8,9 is the method of choice for representing cause-specific contributions to disparities in LE^10-12. Section 2.2 provides a description of our methodological development. Section 2.3 provides the derivation of the explicit formulas for Pollard’s decomposition for administrative and population registry data. Section 3 applies the method to Multiple Cause of Death (MCD) data and Medicare administrative claims, to identify the relative contributions of high-impact morbidities to disparities in LE65 between i) Black and White Americans, ii) the top and bottom eight U.S. states by LE65, and iii) the 1998–2005 and 2010–2017 time-periods. Extensive discussions of methodologic and substantive developments including detailed comparisons of our approach and other decomposition approaches available in the literature, are presented in Section 4. Our conclusions are in Section 5.

2. Methods

2.1. Pollard’s decomposition is the method of choice

Our refinements to Pollard’s decomposition^8,9 are premised on the proposition that Pollard’s decomposition is the method of choice for calculating cause-of-death-specific contributions to differences in LE between two life tables, two populations, or the same population at two time points. Support for this proposition was published in this journal by Beltrán-Sánchez and Soneji¹⁸ who conducted an extensive review of the relevant literature, including prior work by Beltrán-Sánchez et al.¹² that established a close connection between Pollard’s decomposition and cause-elimination life table techniques—the former dealing with observed changes, the latter dealing with hypothetical changes. This close connection is the key to understanding why the Pollard decomposition is the method of choice for the pairwise comparisons noted above.

Our literature review indicated that the close connection between Pollard’s decomposition and the standard cause-elimination methods could have been noted prior to Beltrán-Sánchez’s papers in 2008 and 2011. For example, it could have been noted by Pollard in his 1982 and 1988 papers^8,9. At that time, however, the question of the day was how Pollard’s (1982) method differed from that of Arriaga¹⁹ (1984) whose method was gaining popularity among demographers because it was easy to use. Pollard (1988) resolved the question⁹: the methods were equivalent. Arriaga’s (1984) and later (1989) method^19,20 was a discrete time formulation of Pollard’s continuous time method. This equivalence, combined with the close connection between Pollard’s decomposition and cause-elimination methods, simplifies our presentation substantially and makes our results accessible without dependence on the extensive subsequent literature.

Our development relies on two papers by Makeham^21,22 that extended life table theory to include cause-specific forces of mortality (same as hazard rates) that are additive over any set of independent causes of death. More than three-quarters century later, Greville²³ (1948; p. 288) considered the gain in life expectancy at age $x$ that would occur if deaths from cause $i$ were eliminated under Makeham’s theory. He published the following formula for computing such change:

$$\stackrel{{}_{\circ }}{e}{}_{{}_x}^{{}^{(-i)}}-\stackrel{{}_{\circ }}{e}{}_{{}_x}=\underset{0}{\overset{\infty }{\int }}{}_{{}_t}{p}_{{}_x}{\mu }_{{}_{x+t}}^{{}^i}\stackrel{{}_{\circ }}{e}{}_{{}_{x+t}}^{{}^{(-i)}}dt$$ (1)

where the left side is the difference between the initial LE at age $x$, denoted $\stackrel{{}_{\circ }}{e}{}_{{}_x}$, and the new, higher LE after eliminating deaths from cause $i$, denoted $\stackrel{{}_{\circ }}{e}{}_{{}_x}^{{}^{(-i)}}$, where the superscript ($-i$) is an indexing symbol, not an exponent. The integrand on the right side has three factors. The first is the probability of surviving from age $x$ to age $x+t$ in the initial life table; the second is the force of mortality at age $x+t$ due to cause $i$ in the initial life table; the third is the LE at age $x+t$ in the new life table. By setting $x=0$, one can obtain the formula for the gain in LE at birth due to elimination of deaths from cause $i$. Thus, Greville’s equation (1) can be rewritten as:

$$\stackrel{{}_{\circ }}{e}{}_{{}_0}^{{}^{(-i)}}-\stackrel{{}_{\circ }}{e}{}_{{}_0}=\underset{0}{\overset{\infty }{\int }}{\mu }_{{}_t}^{{}^i}{}_{{}_t}{p}_{{}_0}\stackrel{{}_{\circ }}{e}{}_{{}_t}^{{}^{(-i)}}dt$$ (2)

where the first two factors in the integrand were interchanged.

Pollard⁹ (1988; eqn. (6) presented the following formula for the change in LE at birth between any two life tables, indexed by the superscripts 1 and 2:

$$\stackrel{{}_{\circ }}{e}{}_{{}_0}^{{}^2}-\stackrel{{}_{\circ }}{e}{}_{{}_0}^{{}^1}=\underset{0}{\overset{\infty }{\int }}({\mu }_{{}_t}^{{}^1}-{\mu }_{{}_t}^{{}^2}){}_{{}_t}{p}_{{}_0}^{{}^1}\stackrel{{}_{\circ }}{e}{}_{{}_t}^{{}^2}dt.$$ (3)

Comparing eqns. (2) and (3) term-by-term, one can see that life table 1 corresponds to Greville’s initial life table, and life table 2 corresponds to the life table with deaths from cause $i$ eliminated. The probability of surviving from age 0 to age $t$ is indexed to life table 1; the new, higher LE is indexed to life table 2. The change in the force of mortality at age $t$ between the two life tables corresponds to the force of mortality due to cause $i$ in Greville’s initial life table, i.e., $({\mu }_{{}_t}^{{}^1}-{\mu }_{{}_t}^{{}^2})\leftrightarrow {\mu }_{{}_t}^{{}^i}$. Thus, Greville’s cause-elimination formula (2) and Pollard’s decomposition formula (3) can be matched term-by-term to reveal the formal equivalence between them.

Table 1.

Study diseases/disease groups and associated cause-specific age-adjusted mortality

Disease	ICD-9	ICD-10	Mortality*
Septicemia	038	A40-A41	67
Other Infectious and Parasitic Diseases	001-139	A00-B99	32
Malignant neoplasms of colon, rectum and anus	153-154	C18-C21	94
Malignant neoplasm of pancreas	157	C25	64
Malignant neoplasms of trachea, bronchus and lung	162	C33-C34	276
Malignant neoplasm of breast	174-175	C50	60
Malignant neoplasm of prostate	185	C61	65
Non-solid (leukemias and lymphomas)	200–208	C81-C96	104
Other solid fast progressive	see**	see**	216
Other solid slow progressive	see***	see***	35
Secondary malignant neoplasm	196–198	C77-C79	12
Other non-specified cancers	199	C80, C45, C97	61
In situ, benign uncertain, or unknown neoplasms	210-239	D00-D48	29
Diseases of Blood and Blood Forming Organs	280-289	D50-D89	16
Diabetes mellitus	250	E10-E14	132
Other Endocrine, Nutritional, Metabolic, Immunity	240-279	E00-E89	54
Dementia	290, 294.2	F01, F03	208
Other Mental Disorders	290-319	F01 – F99	12
Alzheimer's disease	331.0	G30	188
Parkinson's disease	332	G20-G21	53
Other Diseases of Nervous System and Sense Organs	320-389	G00-G99, H00-H95	62
Hypertension	401-405	I10-I15	117
Acute myocardial infarction and other acute ischemic	410, 411	I21-I22, I24	275
Atherosclerotic cardiovascular disease, so described	429.2	I25.0	109
All other forms of chronic ischemic heart disease	412-414	I20, I25.1-I25.9	447
Heart failure	428	I50	126
Cerebrovascular diseases	430-434, 436-438	I60-I69	303
Other diseases of Circulatory System	390-459	I00-I99	320
Influenza and Pneumonia	480-488	J09-J18	121
Chronic lower respiratory diseases	490-494, 496	J40-J47	291
Other Diseases of Respiratory System	460-519	J00-J99	104
Diseases of Digestive System	520-579	K00-K95	139
Skin/Subcutaneous/Musculoskeletal/Connective	680-739	L00-L99 M00-M99	33
Renal failure	584-586	N17-N19	89
Other Diseases of Genitourinary System	580-629	N00-N99	42
Signs, Symptoms and Ill-Defined Conditions	780-799	R00-R99	52
Injury and Poisoning	800-999 E800-E999	S00-T88, V00-Y99	125

^*Age adjusted cause-specific mortality rates (per 100,000).

^**ICD-9: 150-152,155, 156, 158, 159 163-165, 170-172, 176, 179, 182, 183, 188, 189, 191, 192, 194, 195, 209; ICD-10: C15-C17, C22-C24, C26, C37-C41, C43, C46-C49, C54-C56, C64-C68, C70-C72, C74-C76

^***ICD-9: 140-149, 160, 161, 173, 180, 181, 184, 186, 187, 190, 193; ICD-10: C00-C14, C30-C32, C44, C51-C53, C57, C58, C60, C62, C63, C69, C73

Greville’s formula (2) represents the increase in LE that would hypothetically occur upon elimination of deaths from cause $i$ ; Pollard’s formula (3) represents the change in LE that actually occurs upon replacement of the force of mortality in life table 1 with the force of mortality in life table 2. This replacement is typically thought of as reductions in the force of mortality at all ages, but this is not required by Pollard’s formula (3); there may be ages where the force of mortality increases.

Moreover, using the additivity of the cause-specific forces of mortality in Makeham’s theory^21,22, Pollard’s decomposition can be rewritten in the form:

$$\stackrel{{}_{\circ }}{e}{}_{{}_0}^{{}^2}-\stackrel{{}_{\circ }}{e}{}_{{}_0}^{{}^1}=\underset{0}{\overset{\infty }{\int }}\sum _{i=1}^I({\mu }_{{}_t}^{{}^{i1}}-{\mu }_{{}_t}^{{}^{i2}}){}_{{}_t}{p}_{{}_0}^{{}^1}\stackrel{{}_{\circ }}{e}{}_{{}_t}^{{}^2}dt.$$ (4)

By setting ${\mu }_{{}_t}^{{}^{i2}}=0$ for some $i$ and ${\mu }_{{}_t}^{{}^{j2}}={\mu }_{{}_t}^{{}^{j1}}$ for all $j\ne i$, one can reproduce the right side of Greville’s formula (2) for elimination of deaths from cause $i$ with $\stackrel{{}_{\circ }}{e}{}_{{}_0}^{{}^2}=\stackrel{{}_{\circ }}{e}{}_{{}_0}^{{}^{(-i)}}$ and $\stackrel{{}_{\circ }}{e}{}_{{}_0}^{{}^1}=\stackrel{{}_{\circ }}{e}{}_{{}_0}$.

The above analysis could have been done in 1982 by Pollard when publishing his paper⁸, or by any reader familiar with Greville²³. Greville’s formula (2) was well-known; it formed the basis of the cause-elimination life tables published by the National Center for Health Statistics beginning with the U.S. Decennial Life Tables for 1959–1961²⁴. Arriaga’s formulas^19,20 were also well-known; they formed the basis of the cause decomposition tables published by the National Center for Health Statistics beginning with calendar years 1984–1989²⁵. The equivalence of Arriaga’s^19,20 and Pollard’s^8,9 formulas were known in 1988 but their relationship to Greville’s formula²³ were not recognized until much later. Arriaga^19,20 made no mention of the concurrent work by Pollard^8,9 or prior work by Greville²³.

Pollard^8,9 further observed that the order of superscripts 1 and 2 used to index the two life tables is arbitrary; they can be interchanged in eqn. (4) to yield, after a change in signs:

$$\stackrel{{}_{\circ }}{e}{}_{{}_0}^{{}^2}-\stackrel{{}_{\circ }}{e}{}_{{}_0}^{{}^1}=\underset{0}{\overset{\infty }{\int }}\sum _{i=1}^I({\mu }_{{}_t}^{{}^{i1}}-{\mu }_{{}_t}^{{}^{i2}}){}_{{}_t}{p}_{{}_0}^{{}^2}\stackrel{{}_{\circ }}{e}{}_{{}_t}^{{}^1}dt,$$ (5)

which, although equal to the formula above, may differ when separated into components that are additive over cause and/or age (i.e., assuming that the integral is separated into age-specific components). Because eqns. (4) and (5) are identities, Pollard recommended they be combined as a convex combination with equal weights. Thus, Pollard’s decomposition has two forms based on the ordering of the life table indexes, 1–2, 2–1, and a third form based on a convex combination of the first two. The convex combination form with equal weights will be used in the present paper for comparisons of life tables for pairs of subpopulations, as recommended by Pollard.

The calculations in the present paper represent discrete-time alternatives to Arriaga’s^19,20 discrete-time formulas; our calculations derive directly from Pollard’s decomposition and, hence, connect directly to Greville’s²³ formulas (1) and (2) and Makeham’s life table theory^21,22 for independent causes of death.

2.1.1. The assumption of independence of cause-specific forces of mortality is not required for Pollard’s decomposition by cause of death in equations (4) and (5).

Greville commented²³ that the independence assumption was required for the cause elimination calculations in eqns. (1) and (2) but independence was not required for the representation of the total force of mortality as a sum of cause-specific forces indexed by i; the only assumption required for additivity was that the set of $I$, $i=1,2,\dots ,I$, causes be mutually exclusive and exhaustive. The same result follows from Gail²⁶ (eqn. 4): the additivity of the cause-specific forces arises solely as a consequence of the chain rule for partial derivatives of multivariable functions. Thus, the additivity over causes in eqns. (4) and (5) applies even if the causes of death are dependent. This is important for our applications because many causes of death above age 65 are chronic degenerative diseases with common risk factors that generate complex forms of dependence that cannot be resolved using available population/registry and administrative claims data.

Makeham²² and Greville²³ used the term “independent” to describe cause-specific forces of mortality that would remain unchanged upon elimination of deaths due to one or more other causes, the implication being that “dependent” cause-specific forces of mortality would allow such changes to occur. Gail²⁶ considered Makeham’s²² use of the term “independent” in the context of competing risk theory and determined that the condition of no change in a given force of mortality upon elimination of deaths due to other causes is slightly weaker than the usual assumption of statistical independence of the multiple theoretical times to death associated with any given set of independent competing risks. The slight difference is of little practical significance given that only the first of the multiple theoretical times to death can actually be observed. Gail²⁶ commented that the use of either form of independence assumption is “always suspect.” Pollard’s decomposition can be formulated without either form of independence assumption making it highly attractive for use in decomposing disparities in LE.

Beltrán-Sánchez et al.¹² (2008) and Beltrán-Sánchez and Soneji¹⁸ (2011) recognized the close connection between Pollard’s decomposition and cause-elimination life table techniques, but they did not mention that Pollard’s decomposition can be performed without the independence assumption. They wrote: “An important limitation in this area of demographic research is the assumption of independence among causes of death.” (Beltrán-Sánchez and Soneji¹⁸, 2011; p. 44). The independence assumption is required only for cause elimination calculations, not for Pollard’s decomposition. Whereas two life tables are observed in Pollard’s formulas (3)-(5), only one is observed in Greville’s formulas (1) and (2). The penalty for the lack of observed information regarding Greville’s second life table is the need for additional assumptions, the simplest of which is independence²⁶.

The impact of assuming independence between causes of death may not be that large in practice. For example, Beltrán-Sánchez et al.¹² developed an alternative decomposition of LE differences based on cause elimination calculations with an explicit independence assumption. Comparisons of their alternative with Pollard’s decomposition led to their conclusion: “Differences are found to be minute between our approach and Pollard’s.” (Beltrán-Sánchez et al.,¹² p. 1327). They found substantially larger differences in comparisons with Arriaga’s approach²⁰. Given the aforementioned equivalence of Arriaga’s²⁰ and Pollard’s⁸ formulas, however, it is highly likely that the differences reported by Beltrán-Sánchez et al.¹² were due to the use of a “1–2” form of Arriaga’s formulas²⁰ rather than the convex-combination form recommended by Pollard⁸. Unlike Pollard⁸ who identified three forms of decomposition consistent with formulas (4) and (5), Arriaga^19,20 published just one form for his decomposition. Preston et al.²⁷ simplified the indexing in Arriaga’s formulas and introduced the “1–2” notation to refer to two different populations in the same way as Pollard did. Once the existence of the different 1–2 and 2–1 forms is taken into account and the discrepancy with Arriaga’s²⁰ approach is explained, it then follows that Beltrán-Sánchez et al.’s¹² results support our conclusion that Pollard’s^8,9 decomposition is the method of choice.

2.2. Pollard’s Decomposition and Cause-Specific Contributions

The approach developed by Pollard^8,9 provides the fundamental decomposition of LE65 which is represented herein as the sum over all cause-of-death-specific contributions:

$$\stackrel{{}_{\circ }}{e}{}_{{}_W}(65)-\stackrel{{}_{\circ }}{e}{}_{{}_B}(65)={\sum }_i\underset{65}{\overset{\infty }{\int }}\left({\mu }_{{}_{iB}}(a)-{\mu }_{{}_{iW}}(a)\right)\frac{\left({\ell }_{{}_B}(a)\stackrel{{}_{\circ }}{e}{}_{{}_W}(a)+{\ell }_{{}_W}(a)\stackrel{{}_{\circ }}{e}{}_{{}_B}(a)\right)}{2}da$$ (6)

where $i$ indexes causes of death, and $\stackrel{{}_{\circ }}{e}{}_{{}_j}(a)$, ${\mu }_{{}_{ij}}(a)$ and ${\ell }_{{}_j}(a)$ are LE, cause-specific force of mortality, and survival function at age $a$ for the groups being compared ($j$ indexes the groups); we use ${\ell }_{{}_j}(a){\equiv }_{{}_{a-65}}{p}_{{}_{65}}^{{}^j}$ to simplify Pollard’s notation in eqns. (3)-(5). Term-by-term comparison shows that eqn. (6) is a convex combination of eqns. (4) and (5) with equal weights, as recommended by Pollard.

We denote the population groups by “$B$” and “$W$” instead of Pollard’s “1–2” to mirror the analysis of race-related disparities between Black and White Americans; but the formula is applicable to any two well-defined groups. We will shift the location of the “$B$” and “$W$” from subscript to superscript freely in the following development, if such shifts simplify the associated equations.

Each individual term in eqn. (6) in the sum over $i$ can be divided by $\stackrel{{}_{\circ }}{e}{}_{{}_W}(65)-\stackrel{{}_{\circ }}{e}{}_{{}_B}(65)\ne 0$ to represent the relative contributions of cause $i$ to the disparities of LE65, with the ratio denoted by $R{C}_{{}_i}$,

$$R{C}_{{}_i}=100\%\cdot \underset{65}{\overset{\infty }{\int }}\left({\mu }_{{}_{iB}}(a)-{\mu }_{{}_{iW}}(a)\right)\frac{\left({\ell }_{{}_B}(a)\stackrel{{}_{\circ }}{e}{}_{{}_W}(a)+{\ell }_{{}_W}(a)\stackrel{{}_{\circ }}{e}{}_{{}_B}(a)\right)}{2\left(\stackrel{{}_{\circ }}{e}{}_{{}_W}(65)-\stackrel{{}_{\circ }}{e}{}_{{}_B}(65)\right)}da,$$ (7)

where ${\sum }_{i}R{C}_{{}_i}=100\%$. The ratios are defined only when the LE65s differ between the two groups (i.e., division by zero is undefined). Moreover, the cause-specific $R{C}_{{}_i}$s may differ in sign, implying that the sum of their absolute values may be substantially greater than 100% and that the differences in LE65s reflect offsetting effects for one or more causes.

Numerical evaluation of integrals always requires approximations. We leverage the specific properties of two types of widely available epidemiological data to evaluate the integral in eqn. (6) without additional assumptions beyond those that are standard for the two types of data. The two types of data are: i) population/registry data (MCD data in our case) where the number of cause-specific deaths and the associated population counts in each age group are known; and ii) administrative claims data (5%-Medicare data in our case) where the age and time at the beginning and end of each individual’s follow-up period and, if deceased, the date and cause of death are known. The standard assumptions for these two types of data are those necessary for life table construction and Kaplan-Meier estimation of group-specific survival functions, respectively.

For population/registry data we evaluate the integral assuming the availability of the numbers of cause-specific deaths between integer ages (i.e., between $x$ and $x+1$, where $x$ is an integer) and observed or estimated exposed-subpopulation counts at exact age $x$. Chiang²⁸ eqn. (23) showed that exposed-population counts at exact age $x$ can be estimated using mid-year population counts for ages between $x$ and $x+1$. The life table calculations provide the age-specific survival functions $l_x^j$ (using $l_x^j\equiv {\ell }_j(x)$) and life expectancies $\stackrel{{}_{\circ }}{e}{}_x^j$ (using $\stackrel{{}_{\circ }}{e}{}_x^j\equiv \stackrel{{}_{\circ }}{e}{}_j(x)$). Pollard’s integral can then be evaluated, yielding the following decomposition (details are presented in Section 2.3):

$$\stackrel{{}_{\circ }}{e}{}_{{}_{65}}^{{}^W}-\stackrel{{}_{\circ }}{e}{}_{{}_{65}}^{{}^B}=\sum _{i=1}^I\sum _{x=65}^{x_1}\left(\frac{{\widehat{\mu }}_{{}_{ix}}^{{}^B}}{{\widehat{\mu }}_{{}_x}^{{}^B}}\left(e^{{}^{{\widehat{\mu }}_{{}_x}^B}}-1\right)-\frac{{\widehat{\mu }}_{{}_{ix}}^{{}^W}}{{\widehat{\mu }}_{{}_x}^{{}^W}}\left(e^{{}^{{\widehat{\mu }}_{{}_x}^W}}-1\right)\right)\times W_{{}_x},$$ (8)

where $W_{{}_x}=\frac{1}{2}\left(l_{{}_{x+1}}^{{}^W}\left(\stackrel{{}_{\circ }}{e}{}_{{}_x}^{{}^B}-({\widehat{a}}_{{}_x}-x)\right)+l_{{}_{x+1}}^{{}^B}\left(\stackrel{{}_{\circ }}{e}{}_{{}_x}^{{}^W}-({\widehat{a}}_{{}_x}-x)\right)\right)$ for $65\le x<x_{{}_1}$, and $W_{{}_{x_{{}_1}}}=\frac{1}{2}(l_{{}_{x_{{}_1}}}^{{}^B}+l_{{}_{x_{{}_1}}}^{{}^W})\frac{(1-q_{{}_{x_{{}_1}}}^{{}^B})(1-q_{{}_{x_{{}_1}}}^{{}^W})}{q_{{}_{x_{{}_1}}}^{{}^B}{q}_{{}_{x_{{}_1}}}^{{}^W}}$. The difference ${\widehat{a}}_{{}_x}-x$ can be set to ½ in the majority of applications.

The total (all-cause) 1-year cumulative hazards are estimated as: ${\widehat{\mu }}_{{}_x}^{{}^B}=\log \left(l_{{}_x}^{{}^B}∕l_{{}_{x+1}}^{{}^B}\right)$ and ${\widehat{\mu }}_{{}_x}^{{}^W}=\log \left(l_{{}_x}^{{}^W}∕l_{{}_{x+1}}^{{}^W}\right)$. Age $x_{{}_1}$ denotes the left bound of the last age group which is open-to-the-right (e.g., the group 100+ if $x_{{}_1}=100$). The total hazard in this group is estimated as ${\widehat{\mu }}_{{}_{x_1}}^{{}^j}=-\log (1-q_{{}_{x_1}}^{{}^j})$, where $q_{{}_{x_1}}^{{}^j}$ denotes the annual probability of death at age $x_{{}_1}$ which is assumed to be constant at age $x_{{}_1}$ and above. It follows from Greville²³ eqn. (5) that if the cause specific hazards are proportional between ages $x$ and $x+1$, then the constant of proportionality for each cause $i$ is equal to the fraction $r_{ix}^j=d_{ix}^j∕d_x^j$, where $d_x^j={\sum }_i{d}_{ix}^j$ are the total and cause-specific number of deaths between ages $x$ and $x+1$, for $65\le x<x_{{}_1}$, or for the last age interval the total and cause-specific number of deaths for age $x_{{}_1}$ and above. The cause-specific one-year cumulative hazards, ${\widehat{\mu }}_{ix}^j$, are estimated using ${\widehat{\mu }}_{ix}^B=r_{ix}^B{\widehat{\mu }}_x^B$ and ${\widehat{\mu }}_{ix}^W=r_{ix}^W{\widehat{\mu }}_x^W$; see Appendix A for proof.

For administrative claims, the product-limit estimates of subpopulation-specific survival functions for left-truncated (or delayed entry) data¹⁶ are constructed using individual follow-up data. Because the product-limit survival functions are constant between exact ages of death, LE65 is easily calculated as the area under the survival function. Pollard’s integral is then represented as a sum of the respective estimates taken at ages of death recorded in the data for one or the other subpopulation:

$$\stackrel{{}_{\circ }}{e}{}_{{}_W}(65)-\stackrel{{}_{\circ }}{e}{}_{{}_B}(65)=\frac{1}{2}\sum _{i=1}^I\sum _{k_i=1}^{K_i}\left(\left(\frac{{\widehat{\mu }}_{{}_{iB}}(a_{{}_{i{k}_i}})}{{\widehat{\mu }}_{{}_B}(a_{{}_{i{k}_i}})}\left(e^{{}^{{\widehat{\mu }}_{{}_B}(a_{{}_{i{k}_i}})}}-1\right)-\frac{{\widehat{\mu }}_{{}_{iW}}(a_{{}_{i{k}_i}})}{{\widehat{\mu }}_{{}_W}(a_{{}_{i{k}_i}})}\left(e^{{}^{{\widehat{\mu }}_{{}_W}(a_{{}_{i{k}_i}})}}-1\right)\right)\left({\ell }_{{}_W}(a_{{}_{i{k}_i+}})\stackrel{{}_{\circ }}{e}{}_{{}_B}(a_{{}_{i{k}_i-}})+{\ell }_{{}_B}(a_{{}_{i{k}_i+}})\stackrel{{}_{\circ }}{e}{}_{{}_W}(a_{{}_{i{k}_i-}})\right)\right)$$ (9)

where $i$ indexes cause of death, $a_{{}_{i{k}_i}}$ represent age at death from cause $i$, and the number of such deaths is $K_{{}_i}$; $\{a_{{}_k}\}$ is the set of ages of death in either or both subpopulations; $a_{{}_{k-}}$ and $a_{{}_{k+}}$ indicate that the left and right limits of the respective functions have to be taken. The product-limit estimator has jump discontinuities of survival functions at these points, so survival functions for $a_{{}_{k-}}$ and $a_{{}_{k+}}$ (and therefore life-expectancies) are not equal but are well-defined at these points. The quantities ${\widehat{\mu }}_{{}_j}(a_{{}_k})$ and ${\widehat{\mu }}_{{}_{ij}}(a_{{}_k})$ denote total and cause-specific cumulative hazards that are estimated as logarithms of the ratios of the respective survival functions at $a_{{}_{k-}}$ and $a_{{}_{k+}}$.

Standard errors and confidence intervals for LE65 and $R{C}_{{}_i}$ are calculated using a simulation strategy^29-31. Although most such approaches provide analytical formulae for the variance in life expectancies, we prefer the version involving Monte Carlo simulations because such an approach allows us to obtain the standard errors and confidence intervals for the cause-specific relative contributions $R{C}_{{}_i}$. Specifically, the number of deaths for an age interval is assumed to be binomially distributed and simulated when a life table is constructed based on the age-specific probability of death and the number of individuals at risk in the input dataset. The standard deviation of the distribution of LEs, simulated multiple times, gives an estimate of the standard error of the life-table-based LE. For our study the standard approach (based on the assumption of a binomial distribution of the number of deaths) was improved in several aspects. First, because there were many different causes of death, the multinomial distribution was used to simulate cause-of-death-specific probabilities of death at each exact age. Technically we used the conditional method to simulate a multinomial draw using a series of binomial draws³². Second, although the standard approach provides for the calculation of standard errors for LE, we also needed standard errors for cause-specific relative contributions $R{C}_{{}_i}$. Therefore, we calculated the $R{C}_{{}_i}$ for each simulated life table and evaluated the standard errors of the $R{C}_{{}_i}$ using their simulated distributions.

2.3. Derivation of Equations (8) and (9)

Formulas (6) and (7) are exact. The sum of the relative contributions ${\sum }_{i}R{C}_{{}_i}$ equals 1 (or 100%). Only the cause-specific hazards ${\mu }_{{}_{ij}}(a)$ depend on $i$, so the sum over $i$ in (6) or (7) results in ${\sum }_i{\mu }_{{}_{ij}}(a)={\mu }_{{}_j}(a)$, where ${\mu }_{{}_j}(a)$ is the total subpopulation-specific hazard function for subpopulation $j$. The integral in the resulting formulas is analytically calculated for two arbitrary ages:

$$\begin{gathered} \underset{a_1}{\overset{a_2}{\int }}({\mu }_{{}_B}(a)-{\mu }_{{}_W}(a))\left({\ell }_{{}_B}(a)\stackrel{{}_{\circ }}{e}{}_{{}_W}(a)+{\ell }_{{}_W}(a)\stackrel{{}_{\circ }}{e}{}_{{}_B}(a)\right)da \\ =\left({\ell }_{{}_B}(a_{{}_1})+{\ell }_{{}_W}(a_{{}_1})\right)\left(\stackrel{{}_{\circ }}{e}{}_{{}_W}(a_{{}_1})-\stackrel{{}_{\circ }}{e}{}_{{}_B}(a_1)\right)-\left({\ell }_{{}_B}(a_{{}_2})+{\ell }_{{}_W}(a_{{}_2})\right)\left(\stackrel{{}_{\circ }}{e}{}_{{}_W}(a_{{}_2})-\stackrel{{}_{\circ }}{e}{}_{{}_B}(a_{{}_2})\right). \end{gathered}$$ (10)

The four-step proof of this statement is (where each line is a step):

$$\begin{gathered} \underset{a_{{}_1}}{\overset{a_{{}_2}}{\int }}({\mu }_{{}_B}(a)-{\mu }_{{}_W}(a))\left({\ell }_{{}_B}(a)\stackrel{{}_{\circ }}{e}{}_{{}_W}(a)+{\ell }_{{}_W}(a)\stackrel{{}_{\circ }}{e}{}_{{}_B}(a)\right)da=\underset{a_{{}_1}}{\overset{a_{{}_2}}{\int }}\frac{{\ell }_{{}_W}^{{}^{\prime }}(a){\ell }_{{}_B}(a)-{\ell }_{{}_B}^{{}^{\prime }}(a){\ell }_{{}_W}(a)}{{\ell }_{{}_B}(a){\ell }_{{}_W}(a)}\left({\ell }_{{}_B}(a)\stackrel{{}_{\circ }}{e}{}_{{}_W}(a)+{\ell }_{{}_W}(a)\stackrel{{}_{\circ }}{e}{}_{{}_B}(a)\right)da \\ =-\underset{a_{{}_1}}{\overset{a_{{}_2}}{\int }}{\ell }_{{}_W}(a)\stackrel{{}_{\circ }}{e}{}_{{}_W}(a)d\left[\frac{{\ell }_{{}_B}(a)}{{\ell }_{{}_W}(a)}\right]+\underset{a_{{}_1}}{\overset{a_{{}_2}}{\int }}{\ell }_{{}_B}(a)\stackrel{{}_{\circ }}{e}{}_{{}_B}(a)d\left[\frac{{\ell }_{{}_W}(a)}{{\ell }_{{}_B}(a)}\right] \\ =-{\ell }_{{}_B}(a)\stackrel{{}_{\circ }}{e}{}_{{}_W}(a){\mid }_{a_{{}_1}}^{{}^{a_2}}-\underset{a_{{}_1}}{\overset{a_{{}_2}}{\int }}{\ell }_{{}_B}(a)da+{\ell }_{{}_W}(a)\stackrel{{}_{\circ }}{e}{}_{{}_B}(a){\mid }_{{}_1}^{{}^{a_2}}+\underset{a_{{}_1}}{\overset{a_{{}_2}}{\int }}{\ell }_{{}_W}(a)da \\ =\left({\ell }_{{}_B}(a_{{}_1})+{\ell }_{{}_W}(a_{{}_1})\right)\left(\stackrel{{}_{\circ }}{e}{}_{{}_W}(a_{{}_1})-\stackrel{{}_{\circ }}{e}{}_{{}_B}(a_{{}_1})\right)-\left({\ell }_{{}_B}(a_{{}_2})+{\ell }_{{}_W}(a_{{}_2})\right)\left(\stackrel{{}_{\circ }}{e}{}_{{}_W}(a_{{}_2})-\stackrel{{}_{\circ }}{e}{}_{{}_B}(a_{{}_2})\right), \end{gathered}$$

where we used i) the equation ${\mu }_{{}_j}(x){\ell }_{{}_j}(x)=-{\ell }_{{}_j}^{{}^{\prime }}(x)$ in step one ($j$ indexes the groups being compared, e.g., $j=B$ or $W$); ii) properties of derivatives of a ratio like ${\left({\ell }_{{}_B}(a)∕{\ell }_{{}_W}(a)\right)}^{\prime }=\left({\ell }_{{}_B}^{{}^{\prime }}(a){\ell }_{{}_W}(a)-{\ell }_{{}_W}^{{}^{\prime }}(a){\ell }_{{}_B}(a)\right)∕{\ell }_W^2(a)$ for step two; iii) integration by parts and the equation ${\ell }_{{}_j}(x)=-{\left({\ell }_{{}_j}(x)\stackrel{{}_{\circ }}{e}{}_{{}_j}(x)\right)}^{\prime }$ that follows from the definition of LE: $\stackrel{{}_{\circ }}{e}{}_{{}_j}(x)=\frac{1}{{\ell }_{{}_j}(x)}{\int }_x^{\infty }{\ell }_{{}_j}(a)da$, for step three; and iv) the equation: $-{\int }_{a_{{}_1}}^{a_{{}_2}}{\ell }_{{}_j}(a)da={\ell }_{{}_j}(a_{{}_2})\stackrel{{}_{\circ }}{e}{}_{{}_j}(a_{{}_2})-{\ell }_{{}_j}(a_{{}_1})\stackrel{{}_{\circ }}{e}{}_{{}_j}(a_{{}_1})$ which also follows from the definition of LE for step four. The result of the integration can be represented as $F(a_{{}_1})-F(a_{{}_2})$ where $F(a)\equiv \left({\ell }_{{}_B}(a)+{\ell }_{{}_W}(a)\right)\left(\stackrel{{}_{\circ }}{e}{}_{{}_W}(a)-\stackrel{{}_{\circ }}{e}{}_{{}_B}(a)\right)$. Pollard’s integral is obtained when $a_{{}_1}=65$ and $a_{{}_2}\to \infty$ because $F(65)=2\left(\stackrel{{}_{\circ }}{e}{}_{{}_W}(65)-\stackrel{{}_{\circ }}{e}{}_{{}_B}(65)\right)$ and $F(\infty )=0$.

An important property of Pollard’s integral is that it is exactly zero if taken over a time interval with no deaths in either subpopulation under comparison. This follows from eqn. (10) because the subpopulation-specific survival functions are constant, and therefore, changes in life expectancies for both subpopulations are equal: $\stackrel{{}_{\circ }}{e}{}_{{}_W}(a_{{}_1})-\stackrel{{}_{\circ }}{e}{}_{{}_W}(a_{{}_2})=\stackrel{{}_{\circ }}{e}{}_{{}_B}(a_{{}_1})-\stackrel{{}_{\circ }}{e}{}_{{}_B}(a_{{}_2})=a_{{}_2}-a_{{}_1}$, and finally, $F(a_{{}_1})=F(a_{{}_2})$. This implies that the entire integration region can be separated into subregions containing and not containing death events and only the former contributes to Pollard’s integral. The area around an event can be chosen to be arbitrarily small. Thus, if all events occurred at different times (from a theoretical point of view this is always true), we can express Pollard’s integral as a sum over all death events as

$$e_{{}_W}^o(65)-e_{{}_B}^o(65)={\sum }_{k=1}^{K}F(a_{k-})-F(a_{k+})$$ (11)

where $a_{{}_{k-}}$ and $a_{{}_{k+}}$ are left and right limits of age $a_{{}_k}$ (i.e., $a_{{}_{k-}}=a_{{}_k}-ϵ$ and $a_{{}_{k+}}=a_{{}_k}-ϵ$, where $ϵ$ is an arbitrary small value or even $ϵ\to 0$), and $k,k=1,\dots ,K$, indexes the sequence numbers of the death events. Each death is associated with a certain cause $i$; hence, we can index each ordered death time by cause as $a_{{}_{i{k}_{{}_i}-}},a_{{}_{i{k}_{{}_i}+}}$, and $a_{{}_{i{k}_{{}_i}}}$. All terms in eqn. (11) can be regrouped by cause, resulting in a decomposition of the disparity in LE in terms of cause-specific contributions:

$$e_{{}_W}^o(65)-e_{{}_B}^o(65)=\sum _{i=1}^I\sum _{k_i=1}^{K_i}F(a_{{}_{i{k}_i-}})-F(a_{{}_{i{k}_i+}})$$ (12)

where $i$ indexes causes of death, $a_{{}_{i{k}_{{}_i}}}$ represent ages of death from cause $i$, and the number of deaths from cause $i$ is $K_i$, where ${\sum }_{i=1}^I{K}_i=K$, the total number of deaths from all causes.

We need to specify the details of this approach for the two types of data used in the present study: i) administrative data, where we have individual follow-up information including initial age, final age of follow-up, an indicator of death/censoring at the final age, and cause of death; and ii) population/registry data where we know the number of deaths by cause and age (or age groups) and the associated exposed-population counts.

2.3.1. Administrative data

The first step of analysis using administrative data is to obtain the product-limit estimates for left-truncated (or delayed entry) data¹⁶ both for total and cause-specific survival functions. The cause-specific survival functions can then be calculated similarly, but ignoring all other causes of death, i.e., treating the other causes as additional “censoring events”. Software to obtain the estimates of such total and cause-specific survival functions is available in all standard statistical packages, e.g., Proc PHREG with BASELINE statement provides such estimates in SAS software³³. The resulting subpopulation-specific total $\left({\ell }_{{}_j}(a)\right)$ and cause-specific $\left({\ell }_{{}_{ij}}(a)\right)$ survival functions then satisfy the equality ${\ell }_{{}_j}(a)={\prod }_{i=1}^I{\ell }_{{}_{ij}}(a)$ for each age $a$. The survival functions obtained using the above product-limit method are constant between events (i.e., times of death) and change only at these time points. This means that subpopulation-specific hazards functions ${\mu }_{{}_B}(a)$ and ${\mu }_{{}_W}(a)$ are zero everywhere except at age-points where deaths occur, i.e., the hazard functions have to be described in terms of the Dirac delta-function. However, the cumulative hazards, i.e., hazard functions integrated over an age interval that includes the age-at-death of a death event ($a_{{}_k}$) are well-defined and can be expressed in terms of logarithms of the ratios of the respective survival functions taken at the age-points just before ($a_{{}_{k-}}$) and just after ($a_{{}_{k+}}$) the death event (e.g., see ref.³⁴). Specifically, the estimates of the total and cause-specific cumulative hazards are: ${\widehat{\mu }}_{{}_j}(a_{{}_k})=\log \left({\ell }_{{}_j}(a_{{}_{k-}})∕{\ell }_{{}_j}(a_{{}_{k+}})\right)$ for total and ${\widehat{\mu }}_{{}_{ij}}(a_{{}_k})=\log \left({\ell }_{{}_{ij}}(a_{{}_{k-}})∕{\ell }_{{}_{ij}}(a_{{}_{k+}})\right)$ for cause-specific cumulative hazards. The equality ${\sum }_i{\widehat{\mu }}_{{}_{ij}}(a_{{}_k})={\widehat{\mu }}_{{}_j}(a_{{}_k})$ is then satisfied exactly, because:

$${\sum }_i{\widehat{\mu }}_{{}_{ij}}(a_{{}_k})={\sum }_i\log \left({\ell }_{{}_{ij}}(a_{{}_{k-}})∕{\ell }_{{}_{ij}}(a_{{}_{k+}})\right)=\log \left({\prod }_i{\ell }_{{}_{ij}}(a_{{}_{k-}})∕{\prod }_i{\ell }_{{}_{ij}}(a_{{}_{k+}})\right)=\log \left({\ell }_{{}_j}(a_{{}_{k-}})∕{\ell }_{{}_j}(a_{{}_{k+}}\right)={\widehat{\mu }}_{{}_j}(a_{{}_k}).$$

As noted above, Pollard’s integral is exactly zero if taken over a time interval with no deaths in either subpopulation under comparison. Therefore, only intervals involving death events contribute to the integral, and Pollard’s integral is represented as a sum of the respective estimates taken at ages of death detected in the data for one of the subpopulations.

If exactly one death occurred in the age interval between $a_{{}_{k-}}$ and $a_{{}_{k+}}$, so that ${\mu }_{{}_j}(a)={\mu }_{{}_{ij}}(a)$, then the integral over the area around the death event from cause $i$ at age $a_{{}_k}$ can be calculated using (10), yielding:

$$\begin{gathered} \underset{a_{k-}}{\overset{a_{k+}}{\int }}({\mu }_{{}_{iB}}(a)-{\mu }_{{}_{iW}}(a))\left({\ell }_{{}_B}(a)\stackrel{{}_{\circ }}{e}{}_{{}_W}(a)+{\ell }_{{}_W}(a)\stackrel{{}_{\circ }}{e}{}_{{}_B}(a)\right)da=F(a_{{}_{k-}})-F(a_{{}_{k+}}) \\ =\left({\ell }_{{}_B}(a_{{}_{k-}})+{\ell }_{{}_W}(a_{{}_{k-}})\right)\left(\stackrel{{}_{\circ }}{e}{}_{{}_W}(a_{{}_{k-}})-\stackrel{{}_{\circ }}{e}{}_{{}_B}(a_{k-})\right)-\left({\ell }_{{}_B}(a_{{}_{k+}})+{\ell }_{{}_W}(a_{{}_{k+}})\right)\left(\stackrel{{}_{\circ }}{e}{}_{{}_W}(a_{{}_{k+}})-\stackrel{{}_{\circ }}{e}{}_{{}_B}(a_{{}_{k+}})\right) \\ ={\ell }_{{}_B}(a_{{}_{k-}})\stackrel{{}_{\circ }}{e}{}_{{}_W}(a_{{}_{k-}})-{\ell }_{{}_W}(a_{{}_{k-}})\stackrel{{}_{\circ }}{e}{}_{{}_B}(a_{{}_{k-}})-{\ell }_{{}_B}(a_{{}_{k+}})\stackrel{{}_{\circ }}{e}{}_{{}_W}(a_{{}_{k+}})+{\ell }_{{}_W}(a_{{}_{k+}})\stackrel{{}_{\circ }}{e}{}_{{}_B}(a_{{}_{k+}}) \end{gathered}$$ (13)

where we used the equalities

$${\ell }_{{}_j}(a_{{}_{k-}})\stackrel{{}_{\circ }}{e}{}_{{}_j}(a_{{}_{k-}})={\ell }_{{}_j}(a_{{}_{k+}})\stackrel{{}_{\circ }}{e}{}_{{}_j}(a_{{}_{k+}})$$ (14)

which are valid for each subpopulation $j$ (e.g., $j=B$ or $W$). The equality holds because both products in the left and right sides of eqn. (14) are equal to ${\int }_{a_{{}_k}}^{\infty }{\ell }_{{}_j}(u)du$. Recall that $a_{{}_{k-}}$ and $a_{{}_{k+}}$ mean that the left and right limits of the respective functions have to be taken. Also recall that we have the freedom to choose any lower and upper integration limit in eqn. (13) and that there is only one age at death ($a_{{}_k}$) inside the integration region. This allows us to choose $a_{{}_{k-}}$ and $a_{{}_{k+}}$ infinitely close to $a_{{}_k}$. Because of the discontinuity of the survival function at the point $a_{{}_k}$, it follows that life expectancy is not continuous at this point either. Recall, however, that the cumulative hazard function is estimated as the logarithm of the ratio of the survival functions at $a_{{}_{k-}}$ and $a_{{}_{k+}}$. It follows that the survival and life expectancy functions can each be expressed in terms of the cumulative hazard function:

$$\begin{gathered} {\ell }_{{}_j}(a_{{}_{k-}})={\ell }_{{}_j}(a_{{}_{k+}})\text{exp}({\widehat{\mu }}_{{}_j}(a_{{}_k})) \\ \stackrel{{}_{\circ }}{e}{}_{{}_j}(a_{{}_{k-}})=\stackrel{{}_{\circ }}{e}{}_{{}_j}(a_{{}_{k+}})\text{exp}(-{\widehat{\mu }}_{{}_j}(a_{{}_k})) \end{gathered}$$ (15)

where the first line of eqn. (10) follows from the definition of the cumulative hazard and the second uses the definition of LE, i.e., $\stackrel{{}_{\circ }}{e}{}_{{}_j}(x)=\frac{1}{{\ell }_{{}_j}(x)}{\int }_x^{\infty }{\ell }_{{}_j}(a)da$, combined with the property that the integral ${\int }_{a_{{}_k}}^{\infty }{\ell }_{{}_j}(u)du$ is a continuous function of age, in which case ${\int }_{a_{{}_{k-}}}^{\infty }{\ell }_{{}_j}(u)du={\int }_{a_{{}_{k+}}}^{\infty }{\ell }_{{}_j}(u)du={\int }_{a_{{}_k}}^{\infty }{\ell }_{{}_j}(u)du$. Multiplication of the first and second lines of eqn. (15) yields eqn. (14), thereby confirming its validity.

Eqn. (15) allows us to express eqn. (13) in terms of ${\ell }_{{}_j}(a_{{}_{k-}})$ and $\stackrel{{}_{\circ }}{e}{}_{{}_j}(a_{{}_{k+}})$:

$$F(a_{{}_{k-}})-F(a_{{}_{k+}})=\left(e^{-{\widehat{\mu }}_{{}_W}(a_{{}_k})}-e^{-{\widehat{\mu }}_{{}_B}(a_{{}_k})}\right)\left({\ell }_{{}_W}(a_{{}_{k-}})\stackrel{{}_{\circ }}{e}{}_{{}_B}(a_{{}_{k+}})+{\ell }_{{}_B}(a_{{}_{k-}})\stackrel{{}_{\circ }}{e}{}_{{}_W}(a_{{}_{k+}})\right),$$ (16)

or, in terms of ${\ell }_{{}_j}(a_{{}_{k+}})$ and $\stackrel{{}_{\circ }}{e}{}_{{}_j}(a_{{}_{k-}})$:

$$F(a_{{}_{k-}})-F(a_{{}_{k+}})=\left(e^{{\widehat{\mu }}_{{}_B}(a_{{}_k})}-e^{{\widehat{\mu }}_{{}_W}(a_{{}_k})}\right)\left({\ell }_{{}_W}(a_{{}_{k+}})\stackrel{{}_{\circ }}{e}{}_{{}_B}(a_{{}_{k-}})+{\ell }_{{}_B}(a_{{}_{k+}})\stackrel{{}_{\circ }}{e}{}_{{}_W}(a_{{}_{k-}})\right).$$ (17)

One more expression involves the difference between ${\ell }_{{}_j}(a_{{}_{k-}})$ and ${\ell }_{{}_j}(a_{{}_{k+}})$ or jump discontinuity, defined as $J_{{}_j}(a_{{}_k})={\ell }_{{}_j}(a_{{}_{k-}})-{\ell }_{{}_j}(a_{{}_{k+}})$:

$$\begin{gathered} J_{{}_j}(a_{{}_k})={\ell }_{{}_j}(a_{{}_{k-}})-{\ell }_{{}_j}(a_{{}_{k+}}): \\ F(a_{{}_{k-}})-F(a_{{}_{k+}})=\left(\frac{J_{{}_B}(a_{{}_k})}{{\ell }_{{}_B}(a_{{}_{k+}})}-\frac{J_{{}_W}(a_{{}_k})}{{\ell }_{{}_W}(a_{{}_{k+}})}\right)\left({\ell }_{{}_W}(a_{{}_{k+}})\stackrel{{}_{\circ }}{e}{}_{{}_B}(a_{{}_{k-}})+{\ell }_{{}_B}(a_{{}_{k+}})\stackrel{{}_{\circ }}{e}{}_{{}_W}(a_{{}_{k-}})\right). \end{gathered}$$ (18)

Eqns. (16), (17), and (18), and the property that the integral over an interval without any deaths is exactly zero, allow us to represent the disparities in LE65 $(\stackrel{{}_{\circ }}{e}{}_{{}_W}(65)-\stackrel{{}_{\circ }}{e}{}_{{}_B}(65))$ as a sum overtimes when deaths occurred:

$$\stackrel{{}_{\circ }}{e}{}_{{}_W}(65)-\stackrel{{}_{\circ }}{e}{}_{{}_B}(65)=\frac{1}{2}{\sum }_k(F(a_{{}_{k-}})-F(a_{{}_{k+}}))=\frac{1}{2}{\sum }_k\left(\left(\frac{J_{{}_B}(a_{{}_k})}{{\ell }_{{}_B}(a_{{}_{k+}})}-\frac{J_{{}_W}(a_{{}_k})}{{\ell }_{{}_W}(a_{{}_{k+}})}\right)\left({\ell }_{{}_W}(a_{{}_{k+}})\stackrel{{}_{\circ }}{e}{}_{{}_B}(a_{{}_{k-}})+{\ell }_{{}_B}(a_{{}_{k+}})\stackrel{{}_{\circ }}{e}{}_{{}_W}(a_{{}_{k-}})\right)\right).$$ (19)

Similar formulas can be obtained using eqns. (16) and (17).

If each term in the sum over $k$ is associated with a certain cause of death, then all terms in (19) can be regrouped to combine all cause-specific terms resulting in decomposition of the disparity in LE in terms of cause-of-death-related contributions:

$$\stackrel{{}_{\circ }}{e}{}_{{}_W}(65)-\stackrel{{}_{\circ }}{e}{}_{{}_B}(65)=\frac{1}{2}\sum _{i=1}^I\sum _{k_i=1}^{K_i}\left(\left(\frac{J_{{}_B}(a_{{}_{i{k}_i}})}{{\ell }_{{}_B}(a_{{}_{i{k}_i+}})}-\frac{J_{{}_W}(a_{{}_{i{k}_i}})}{{\ell }_{{}_W}(a_{{}_{i{k}_i+}})}\right)\left({\ell }_{{}_W}(a_{{}_{i{k}_i+}})\stackrel{{}_{\circ }}{e}{}_{{}_B}(a_{{}_{i{k}_i-}})+{\ell }_{{}_B}(a_{{}_{k_i+}})\stackrel{{}_{\circ }}{e}{}_{{}_W}(a_{{}_{i{k}_i-}})\right)\right)$$ (20)

where $i$ indexes cause of death, $a_{{}_{i{k}_{{}_i}}}$ represent age at death from cause $i$, and the number of such deaths is $K_{{}_i}$.

Eqn. (20) is valid only when no deaths from a different cause occur on the same day, assuming that time of day of each death is not available to break such ties. Because such situations are likely to occur occasionally, a minor modification of eqn. (20) is required. The modification is based on the property that the jump discontinuities $J_{{}_j}(a_{{}_k})$ are proportional to the cause-specific cumulative hazards $J_{{}_j}(a_{{}_k})\to {\sum }_i\frac{{\widehat{\mu }}_{{}_{ij}}(a_{{}_k})}{{\widehat{\mu }}_{{}_j}(a_{{}_k})}{J}_{{}_j}(a_{{}_k})$. This works for one or several deaths from one cause as well as many deaths from different causes, all occurring at exact age $a_{{}_k}$ (i.e., with attained age measured in days since birth). Substituting for $J_{{}_j}(a_{{}_k})$ in eqn. (20), we obtain an expression for disparities in LE valid in the general case, i.e., when multiple deaths with multiple causes can occur at an exact age $a_{{}_k}$:

$$\stackrel{{}_{\circ }}{e}{}_{{}_W}(65)-\stackrel{{}_{\circ }}{e}{}_{{}_B}(65)=\frac{1}{2}\sum _{i=1}^I\sum _{k_i=1}^{K_i}\left(\left(\frac{{\widehat{\mu }}_{{}_{iB}}(a_{{}_{i{k}_i}})}{{\widehat{\mu }}_{{}_B}(a_{{}_{i{k}_i}})}\frac{J_{{}_B}(a_{{}_{i{k}_i}})}{{\ell }_{{}_B}(a_{{}_{i{k}_i+}})}-\frac{{\widehat{\mu }}_{{}_{iW}}(a_{{}_{i{k}_i}})}{{\widehat{\mu }}_{{}_W}(a_{{}_{i{k}_i}})}\frac{J_{{}_W}(a_{{}_{i{k}_i}})}{{\ell }_{{}_W}(a_{{}_{i{k}_i+}})}\right)\left({\ell }_{{}_W}(a_{{}_{i{k}_i+}})\stackrel{{}_{\circ }}{e}{}_{{}_B}(a_{{}_{i{k}_i-}})+{\ell }_{{}_B}(a_{{}_{i{k}_i+}})\stackrel{{}_{\circ }}{e}{}_{{}_W}(a_{{}_{i{k}_i-}})\right)\right),$$ (21)

or, alternatively:

$$\stackrel{{}_{\circ }}{e}{}_{{}_W}(65)-\stackrel{{}_{\circ }}{e}{}_{{}_B}(65)=\frac{1}{2}\sum _{i=1}^I\sum _{k_i=1}^{K_i}\left(\left(\frac{{\widehat{\mu }}_{{}_{iB}}(a_{{}_{i{k}_i}})}{{\widehat{\mu }}_{{}_B}(a_{{}_{i{k}_i}})}\left(e^{{}^{{\widehat{\mu }}_{{}_B}(a_{{}_{i{k}_i}})}}-1\right)-\frac{{\widehat{\mu }}_{{}_{iW}}(a_{{}_{i{k}_i}})}{{\widehat{\mu }}_{{}_W}(a_{{}_{i{k}_i}})}\left(e^{{}^{{\widehat{\mu }}_{{}_W}(a_{{}_{i{k}_i}})}}-1\right)\right)\left({\ell }_{{}_W}(a_{{}_{i{k}_i+}})\stackrel{{}_{\circ }}{e}{}_{{}_B}(a_{{}_{i{k}_i-}})+{\ell }_{{}_B}(a_{{}_{i{k}_i+}})\stackrel{{}_{\circ }}{e}{}_{{}_W}(a_{{}_{i{k}_i-}})\right)\right).$$ (22)

Equation (22) is the final expression for the decomposition of life-expectancy disparities using administrative data; it is the same as eqn. (9). The explicit expressions for the cause-specific relative contributions are:

$$R{C}_{{}_i}=\frac{1}{2}\sum _{k_i=1}^{K_i}\left(\left(\frac{{\widehat{\mu }}_{{}_{iB}}(a_{{}_{i{k}_i}})}{{\widehat{\mu }}_{{}_B}(a_{{}_{i{k}_i}})}\left(e^{{}^{{\widehat{\mu }}_{{}_B}(a_{{}_{i{k}_i}})}}-1\right)-\frac{{\widehat{\mu }}_{{}_{iW}}(a_{{}_{i{k}_i}})}{{\widehat{\mu }}_{{}_W}(a_{{}_{i{k}_i}})}\left(e^{{}^{{\widehat{\mu }}_{{}_W}(a_{{}_{i{k}_i}})}}-1\right)\right)\frac{\left({\ell }_{{}_W}(a_{{}_{i{k}_i+}})\stackrel{{}_{\circ }}{e}{}_{{}_B}(a_{{}_{i{k}_i-}})+{\ell }_{{}_B}(a_{{}_{i{k}_i+}})\stackrel{{}_{\circ }}{e}{}_{{}_W}(a_{{}_{i{k}_i-}})\right)}{\left(\stackrel{{}_{\circ }}{e}{}_{{}_W}(65)-\stackrel{{}_{\circ }}{e}{}_{{}_B}(65)\right)}\right).$$

Because all derivations used to obtain eqn. (22) were exact, and the only actions taken to isolate the contributions of specific causes of death was a regrouping of the terms by combining deaths with the same cause to create the sum over $i$, the property ${\sum }_{i=1}^{I}R{C}_{{}_i}=1$ is exactly satisfied. The $R{C}_{{}_i}$ s may include offsetting effects for one or more causes, in which case some $R{C}_{{}_i}$ s will differ in sign from that of the overall sum.

2.3.2. Population/registry data

In population/registry data, data for integration are usually available in the form of life table functions. We assume that the total and cause-specific survival functions ($l_x^j$ and $l_{ix}^j$) are available for integer ages. We use notation $l_x^j$ and $l_{ix}^j$ in order to underscore that these are life table functions in contrast to the continuous survival functions ${\ell }_{{}_j}(a)$ and ${\ell }_{{}_{ij}}(a)$ that we used in Section 2.1.1. Decomposition of disparities in LE65 can be obtained from eqn. (10) if we consider $a_{{}_1}$ and $a_{{}_2}$ as consecutive integer ages. The integration between the two integer ages is performed as shown in Appendix B.

$$\stackrel{{}_{\circ }}{e}{}_{{}_W}(65)-\stackrel{{}_{\circ }}{e}{}_{{}_B}(65)=\frac{1}{2}\sum _{i=1}^I\sum _{x=65}^{\infty }\left(\left(\frac{{\widehat{\mu }}_{{}_{ix}}^{{}^B}}{{\widehat{\mu }}_{{}_x}^{{}^B}}\left(e^{{\widehat{\mu }}_{{}_x}^{{}^B}}-1\right)-\frac{{\widehat{\mu }}_{{}_{ix}}^{{}^W}}{{\widehat{\mu }}_{{}_x}^{{}^W}}\left(e^{{\widehat{\mu }}_{{}_x}^{{}^W}}-1\right)\right)\left(l_{{}_{x+1}}^{{}^W}\left(\stackrel{{}_{\circ }}{e}{}_{{}_x}^{{}^B}-({\widehat{a}}_{{}_x}-x)\right)+l_{{}_{x+1}}^{{}^B}\left(\stackrel{{}_{\circ }}{e}{}_{{}_W}-({\widehat{a}}_{{}_x}-x)\right)\right)\right),$$ (23)

where the total and cause-specific cumulative hazards are defined as: ${\widehat{\mu }}_{{}_x}^{{}^j}\log \left(l_{{}_x}^{{}^j}∕l_{{}_{x+1}}^{{}^j}\right)$ and ${\widehat{\mu }}_{{}_x}^{{}^{ij}}\log \left(l_{{}_{ix}}^{{}^j}∕l_{{}_{i,x+1}}^{{}^j}\right)$. No specific assumption on the form of the distribution of deaths within an age interval is required. The age ${\widehat{a}}_{{}_x}$ is an effective mean age of death in this interval, which is calculated as weighted sum of the individual ages of death (Appendix B). Equivalently, we can consider the age ${\widehat{a}}_{{}_x}$ as the point at which all deaths in the interval occurred; no specific assumptions are required to do so. In this case, eqn. (23) can be obtained directly from eqn. (22). The assumption that ${\widehat{a}}_{{}_x}-x=1∕2$ can be made for one-year intervals, but it is not necessary for our development.

We need to explicitly demonstrate that the sum over all age intervals, indexed by $x$, results in the difference in life expectancies shown in eqn. (23). The ratios of cause-specific and total cumulative hazards sum to one, after summing over $i$, so we need to deal only with terms derived from eqn. (23) having the following form:

$$\left(\frac{l_{{}_x}^{{}^B}}{l_{{}_{x+1}}^{{}^B}}-\frac{l_{{}_x}^{{}^W}}{l_{{}_{x+1}}^{{}^W}}\right)\left(l_{{}_{x+1}}^{{}^W}\left(\stackrel{{}_{\circ }}{e}{}_{{}_x}^{{}^B}-\frac{1}{2}\right)+l_{{}_{x+1}}^{{}^B}\left(\stackrel{{}_{\circ }}{e}{}_{{}_x}^{{}^W}-\frac{1}{2}\right)\right)=\left(\frac{l_{{}_x}^{{}^B}}{l_{{}_{x+1}}^{{}^B}}-\frac{l_{{}_x}^{{}^W}}{l_{{}_{x+1}}^{{}^W}}\right)\left(l_{{}_{x+1}}^{{}^W}\frac{{\sum }_{y=x}^{\infty }{l}_{{}_{y+1}}^{{}^B}}{l_{{}_x}^{{}^B}}+l_{{}_{x+1}}^{{}^B}\frac{{\sum }_{y=x}^{\infty }{l}_{{}_{y+1}}^{{}^B}}{l_{{}_x}^{{}^W}}\right),$$ (24)

where we used the following expressions for LE in terms of life table functions

$$\stackrel{{}_{\circ }}{e}{}_{{}_x}^{{}^j}=\frac{{\sum }_{y=x}^{\infty }{L}_{{}_y}^{{}^j}}{l_{{}_x}^{{}^j}}={\widehat{a}}_{{}_x}-x+\frac{{\sum }_{y=x}^{\infty }{l}_{{}_{y+1}}^{{}^j}}{l_{{}_x}^{{}^j}}.$$ (25)

That is true when ${\widehat{a}}_{{}_x}-x$ is independent of $x$. The standard expression for LE is obtained using ${\widehat{a}}_{{}_x}-x=1∕2$.

To complete the demonstration, we change the order of summations in the right side of (24) and reintroduce the summation over $x$, starting at $x_{{}_0}=65$:

$$\begin{gathered} \frac{1}{2}{\sum }_{x=x_0}^{\infty }\left(\frac{l_{{}_x}^{{}^B}}{l_{{}_{x+1}}^{{}^B}}-\frac{l_{{}_x}^{{}^W}}{l_{{}_{x+1}}^{{}^W}}\right)\left({\sum }_{y=x}^{\infty }\left(\frac{l_{{}_{x+1}}^{{}^W}{l}_{{}_{y+1}}^{{}^B}}{l_{{}_x}^{{}^B}}+\frac{l_{{}_{x+1}}^{{}^B}{l}_{{}_{y+1}}^{{}^W}}{l_{{}_x}^{{}^W}}\right)\right)=\frac{1}{2}{\sum }_{x=x_0}^{\infty }{\sum }_{y=x}^{\infty }\left(\frac{l_{{}_{x+1}}^{{}^W}{l}_{{}_{y+1}}^{{}^B}}{l_{{}_x}^{{}^B}}+\frac{l_{{}_{x+1}}^{{}^B}{l}_{{}_{y+1}}^{{}^W}}{l_{{}_x}^{{}^W}}\right)\left(\frac{l_{{}_x}^{{}^B}}{l_{{}_{x+1}}^{{}^B}}-\frac{l_{{}_x}^{{}^W}}{l_{{}_{x+1}}^{{}^W}}\right) \\ =\frac{1}{2}{\sum }_{x=x_0}^{\infty }{\sum }_{y=x}^{\infty }\left(\frac{l_{{}_x}^{{}^B}{l}_{{}_{y+1}}^{{}^W}}{l_{{}_x}^{{}^W}}-\frac{l_{{}_x}^{{}^W}{l}_{{}_{y+1}}^{{}^B}}{l_{{}_x}^{{}^B}}+\frac{l_{{}_{x+1}}^{{}^W}{l}_{{}_{y+1}}^{{}^B}}{l_{{}_{x+1}}^{{}^B}}-\frac{l_{{}_{x+1}}^{{}^B}{l}_{{}_{y+1}}^{{}^W}}{l_{{}_{x+1}}^{{}^W}}\right)=\frac{1}{2}{\sum }_{y=x_0}^{\infty }{\sum }_{x=x_0}^y\left(\frac{l_{{}_x}^{{}^B}{l}_{{}_{y+1}}^{{}^W}}{l_{{}_x}^{{}^W}}-\frac{l_{{}_x}^{{}^W}{l}_{{}_{y+1}}^{{}^B}}{l_{{}_x}^{{}^B}}+\frac{l_{{}_{x+1}}^{{}^W}{l}_{{}_{y+1}}^{{}^B}}{l_{{}_{x+1}}^{{}^B}}-\frac{l_{{}_{x+1}}^{{}^B}{l}_{{}_{y+1}}^{{}^W}}{l_{{}_{x+1}}^{{}^W}}\right) \\ =\frac{1}{2}{\sum }_{y=x_0}^{\infty }\left(\frac{l_{{}_{x_0}}^{{}^B}{l}_{{}_{y+1}}^{{}^W}}{l_{{}_{x_0}}^{{}^W}}-\frac{l_{{}_{x_0}}^{{}^W}{l}_{{}_{y+1}}^{{}^B}}{l_{{}_{x_0}}^{{}^B}}+\frac{l_{{}_{y+1}}^{{}^W}{l}_{{}_{y+1}}^{{}^B}}{l_{{}_{y+1}}^{{}^B}}-\frac{l_{{}_{y+1}}^{{}^B}{l}_{{}_{y+1}}^{{}^W}}{l_{{}_{y+1}}^{{}^W}}\right)={\sum }_{y=x_0}^{\infty }\left(l_{{}_{y+1}}^{{}^W}-l_{{}_{y+1}}^{{}^B}\right)=\stackrel{{}_{\circ }}{e}{}_{{}_{x_0}}^{{}^W}-\stackrel{{}_{\circ }}{e}{}_{{}_{x_0}}^{{}^B}, \end{gathered}$$

where, with $x_{{}_0}=65$, the final term is seen to be equal to the first term in eqn. (23). In these calculations $x_{{}_0}$ denotes the left bound of the first age interval (e.g., $x_{{}_0}=65$), so the equation $l_{{}_{x_0}}^{{}^W}=l_{{}_{x_0}}^{{}^B}=1$ was used for consistency with the initialization of the continuous survival functions ${\ell }_{{}_j}(x_{{}_0})=1$. For any other starting age $a$, where $l_{{}_a}^{{}^W}\ne l_{{}_a}^{{}^B}\ne 1$, the result of the above calculation is:

$${\sum }_{x=a}^{\infty }\left(\frac{l_{{}_x}^{{}^B}}{l_{{}_{x+1}}^{{}^B}}-\frac{l_{{}_x}^{{}^W}}{l_{{}_{x+1}}^{{}^W}}\right)\left({\sum }_{y=x}^{\infty }\left(\frac{l_{{}_{x+1}}^{{}^W}{l}_{{}_{y+1}}^{{}^B}}{l_{{}_x}^{{}^B}}+\frac{l_{{}_{x+1}}^{{}^B}{l}_{{}_{y+1}}^{{}^W}}{l_{{}_x}^{{}^W}}\right)\right)=\left(l_{{}_a}^{{}^W}+l_{{}_a}^{{}^B}\right)\left(\stackrel{{}_{\circ }}{e}{}_{{}_a}^{{}^W}-\stackrel{{}_{\circ }}{e}{}_{{}_a}^{{}^B}\right).$$ (26)

This calculation can be repeated for any initial and final interval resulting in:

$${\sum }_{x=a_{{}_1}}^{a_{{}_2}}\left(\frac{l_{{}_x}^{{}^B}}{l_{{}_{x+1}}^{{}^B}}-\frac{l_{{}_x}^{{}^W}}{l_{{}_{x+1}}^{{}^W}}\right)\left({\sum }_{y=x}^{\infty }\left(\frac{l_{{}_{x+1}}^{{}^W}{l}_{{}_{y+1}}^{{}^B}}{l_{{}_x}^{{}^B}}+\frac{l_{{}_{x+1}}^{{}^B}{l}_{{}_{y+1}}^{{}^W}}{l_{{}_x}^{{}^W}}\right)\right)=\left(l_{{}_{a_1}}^{{}^W}+l_{{}_{a_1}}^{{}^B}\right)\left(\stackrel{{}_{\circ }}{e}{}_{{}_{a_1}}^{{}^W}-\stackrel{{}_{\circ }}{e}{}_{{}_{a_1}}^{{}^B}\right)-\left(l_{{}_{a_2+1}}^{{}^W}+l_{{}_{a_2+1}}^{{}^B}\right)\left(\stackrel{{}_{\circ }}{e}{}_{{}_{a_2+1}}^{{}^W}-\stackrel{{}_{\circ }}{e}{}_{{}_{a_2+1}}^{{}^B}\right).$$

The sums in this calculation were treated as follows:

$${\sum }_{x=a_{{}_1}}^{a_{{}_2}}{\sum }_{y=x}^{\infty }\dots \to {\sum }_{y=a_{{}_1}}^{\infty }{\sum }_{x=a_{{}_1}}^{\text{min}(y,a_{{}_2})}\dots \to {\sum }_{y=a_{{}_1}}^{\infty }\left({\sum }_{y=a_{{}_1}}^{\infty }\dots -{\sum }_{y=a_{{}_2}+1}^{\infty }\dots \right).$$

The last age group—with left bound denoted as $x_{{}_1}$—should be chosen such that both $l_{{}_{x_1+1}}^{{}^B}$ and $l_{{}_{x_1+1}}^{{}^W}$ are negligible. In practice, data for life tables contain a last group that is open to the right, e.g., the group 100+ in our study. The total and cause-specific probabilities of death are assumed constant within the last group. The contribution of the last group to the difference in LE65 can be calculated based on eqn. (23) in which all terms starting from $x_{{}_1}$ in the sum over $x$ have to be analytically summed for fixed probabilities of death $q_{{}_{x_1}}^{{}^j}$, where $q_{{}_{x_1}}^{{}^j}=1-\text{exp}(-{\widehat{\mu }}_{{}_{x_1}}^{{}^j})$. Life expectancies for $x\ge x_{{}_1}$ are time independent (i.e., constant) if the probabilities of death are time independent; they are estimated as:

$$\stackrel{{}_{\circ }}{e}{}_{{}_{x_1}}^{{}^j}-({\widehat{a}}_{{}_x}-x)=\frac{{\sum }_{y=x_1}^{\infty }{l}_{{}_{y+1}}^{{}^j}}{l_{{}_{x_1}}^{{}^j}}=\frac{1}{l_{{}_{x_1}}^{{}^j}}{\sum }_{y=x_1}^{\infty }\left(l_{{}_y}^{{}^j}-l_{{}_y}^{{}^j}{q}_{{}_{x_1}}^{{}^j}\right)=\left(1-q_{{}_{x_1}}^{{}^j}\right){\sum }_{y=x_1}^{\infty }(1-q_{{}_{x_1}}^{{}^{\infty }}{)}^{{}^{y-x_1}}=\frac{1}{q_{{}_{x_1}}^{{}^j}}-1.$$ (27)

The survival functions $l_{{}_{x+1}}^{{}^B}$ and $l_{{}_{x+1}}^{{}^W}$ in eqn. (23) are the only functions that change with changing $x$ for $x\ge x_{{}_1}$, and therefore, sums of these functions need to be calculated to evaluate the last-age-group contribution:

$$\sum _{y=x_1}^{\infty }{l}_{{}_{x+1}}^{{}^j}=l_{{}_{x_1}}^{{}^j}\frac{1-q_{{}_{x_1}}^{{}^j}}{q_{{}_{x_1}}^{{}^j}}.$$

Then the last age-group contribution in eqn. (23) is:

$$\frac{1}{2}\sum _{i=1}^I\left(\frac{{\widehat{\mu }}_{{}_{i{x}_1}}^{{}^B}}{{\widehat{\mu }}_{{}_{x_1}}^{{}^B}}\left(\text{exp}({\widehat{\mu }}_{{}_{x_1}}^{{}^B})-1\right)-\frac{{\widehat{\mu }}_{{}_{i{x}_1}}^{{}^W}}{{\widehat{\mu }}_{{}_{x_1}}^{{}^W}}\left(\text{exp}({\widehat{\mu }}_{{}_{x_1}}^{{}^W})-1\right)\right)\left(\frac{(1-q_{{}_{x_1}}^{{}^B})(1-q_{{}_{x_1}}^{{}^W})}{q_{{}_{x_1}}^{{}^B}{q}_{{}_{x_1}}^{{}^W}}\right)(l_{{}_{x_1}}^{{}^B}+l_{{}_{x_1}}^{{}^W}).$$ (28)

Thus, the life-table-based decomposition with $x_{{}_0}$ and $x_{{}_1}$ denoting left bound of the first and last (open-to-the-right) age intervals is:

$$\stackrel{{}_{\circ }}{e}{}_{{}_{x_0}}^{{}^W}-\stackrel{{}_{\circ }}{e}{}_{{}_{x_0}}^{{}^B}=\sum _{i=1}^I\sum _{x=x_0}^{x_1}\left(\frac{{\widehat{\mu }}_{{}_{ix}}^{{}^B}}{{\widehat{\mu }}_{{}_x}^{{}^B}}\left(e^{{\widehat{\mu }}_{{}_x}^{{}^B}}-1\right)-\frac{{\widehat{\mu }}_{{}_{ix}}^{{}^W}}{{\widehat{\mu }}_{{}_x}^{{}^W}}\left(e^{{\widehat{\mu }}_{{}_x}^{{}^W}}-1\right)\right)W_{{}_x},$$ (29)

where

$$W_{{}_x}=\frac{1}{2}\left(l_{{}_{x+1}}^{{}^W}\left(\stackrel{{}_{\circ }}{e}{}_{{}_x}^{{}^B}-({\widehat{a}}_{{}_x}-x)\right)+l_{{}_{x+1}}^{{}^B}\left(\stackrel{{}_{\circ }}{e}{}_{{}_x}^{{}^W}-({\widehat{a}}_{{}_x}-x)\right)\right)\text{for}{x}_0\le x<x_1,$$

and

$$W_{{}_{x_1}}=\frac{1}{2}(l_{{}_{x_1}}^{{}^B}+l_{{}_{x_1}}^{{}^W})\frac{(1-q_{{}_{x_1}}^{{}^B})(1-q_{{}_{x_1}}^{{}^W})}{q_{{}_{x_1}}^{{}^B}{q}_{{}_{x_1}}^{{}^W}}.$$

These quantities correspond to Pollard’s weights in his original notation. The final expression using eqn. (29) with $x_{{}_0}=65$ is shown in eqn. (8).

3. Application

We now apply the new approach to identify cause-specific contributions to disparities in LE65 between i) Black and White subpopulations, ii) U.S. regions leading and lagging the national average in respect to LE65, and iii) two time periods: 1998–2005 and 2010–2017. Leading and lagging U.S. regions were identified by ranking all U.S. states by their LE65 using the Centers for Diseases Control and Prevention (CDC) Wide-ranging OnLine Data for Epidemiologic Research (WONDER)³⁵ and selecting eight with the lowest and eight with the highest LE65 as lagging/leading states, respectively. The lagging states were: Arkansas, Tennessee, Louisiana, Oklahoma, Kentucky, Alabama, Mississippi, and West Virginia. The leading states were: California, New York, Hawaii, Florida, Arizona, Connecticut, Minnesota, and Colorado. We then selected 37 cause groups (Table 1) that cover all possible causes of death that are recorded on death certificates. When an individual cause (e.g., hypertension, heart failure) in a chapter of the International Classification of Disease 10^th Edition (ICD-10) (e.g., disease of the circulatory system) demonstrated rates in excess of 50 per 100,000, it was treated as its own cause group; the remaining diseases in the chapter were combined into an other-cause group (e.g., other diseases of the circulatory system). The total sum of death rates for these 37 cause groups was 4,533/100,000 which was equal to the total age-adjusted death rate obtained from the CDC-Wonder for the study period.

3.1. Data

Two datasets were used in this study. The Multiple Cause of Death database (MCD) provides cause-specific mortality and population counts for the U.S.; the mortality data are derived from death certificates; the mortality and population counts can be aggregated to form race- or geographic-region-specific population strata. The mortality data for each decedent are summarized as a single underlying cause of death, supplemented with up to twenty additional causes, with each cause coded using 4-digit ICD-10 codes; basic demographic data including place of residence, age, race/ethnicity, and sex are also provided. We used the underlying cause of death provided by the CDC-WONDER MCD tool to evaluate race- and geography-specific age-adjusted mortality rates in older adults age 65+ over the 2000–2017 period.

The MCD database is a commonly used source of information for evaluation and analyses of strata-specific LE. However, because of known limitations at ages 65+ (e.g., unavailability of year-specific population counts at ages 85+, erroneous assignment of underlying cause-of-death), another source of data is needed for comparison. Because most legal U.S. residents become eligible for health insurance provided by the Medicare system at age 65, Medicare administrative health insurance claims can serve as an alternative source of information for analyses of LE65. In the present study, a nationally representative sample of 5% of the total Medicare population (5%-Medicare) over the 1991–2017 period was used. The enrollment file provided information on place of residence, age, race, sex and date of all-cause mortality while ICD-9/10 codes in the diagnoses fields of Medicare Part A (facility-based services) or Medicare Part B (professional services) records were used to ascertain morbidity.

Each of the utilized datasets underwent additional processing to make them suitable for the planned analysis. For the MCD data, cause-specific death rates were calculated as the ratio of the number of deaths from a given underlying cause within a given age group to the total mid-year population count within that age group. Our analysis required cause-specific death rates calculated in 36 age groups (single-year age groups from 65 to 99 and the age group 100+ that aggregates all ages above 99) across four population strata (White and Black population, leading and lagging state of residence) for each calendar year of the analysis (2000–2017). The CDC-WONDER provides all necessary data with one exception: population counts by single-year age groups are available only for ages younger than 85 and are aggregated into a single group for ages 85+. Therefore, we used additional information to disaggregate the year-specific population counts in the 85+ age group into single-year age groups for ages 85-99 and a single aggregated group for age 100+. For geographic disparities, we used state-specific life tables from the Human Mortality Database for all years of the analysis (see Akushevich et.al.³⁶, Supplementary Methodologic Remark 1 for methodological details). For racial disparities, we used the Annual Projections of the Resident Population by Age, Sex, Race, and Hispanic Origin, 1999–2100, from the 2000 National Population Projections Datasets³⁷. Reconstructed distributions were smoothed for ages 83–86.

For the 5%-Medicare data, an assigned underlying cause of death was not available. Therefore, we developed a simulation procedure to assign a cause of death from the set of diagnoses associated with each individual decedent. Specifically, we reconstructed individual health trajectories utilizing all 37 cause-specific groups (Table 1) and used them to simulate the cause of death. In the simulation procedure, individual assignment of a cause of death occurred through a random selection of a cause from the lists of health conditions individuals accumulated by the end of their life. Selection of the final cause of death used probabilities proportional to the cause-specific weights, which were iteratively recalculated in such a way as to have the final cause-specific mortality rates equal to those found in the MCD data.

3.2. Results

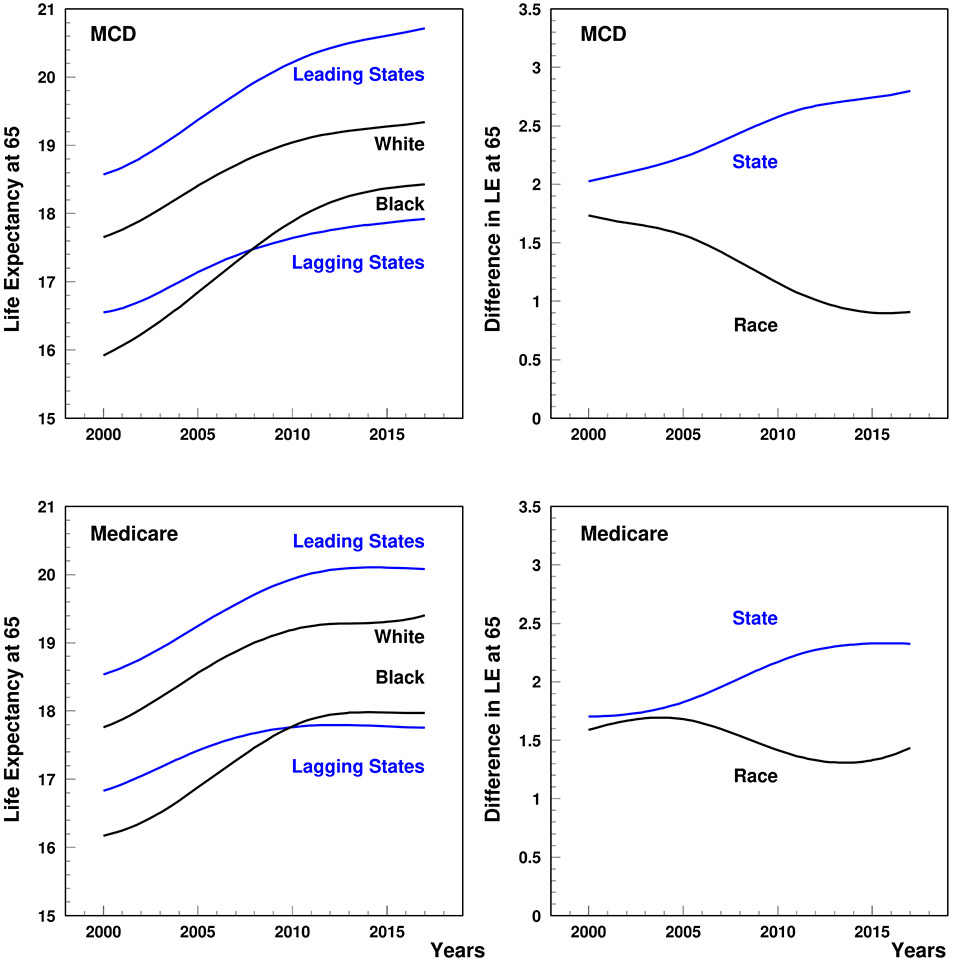
Time-patterns of LE65 for leading and lagging states, the White and Black population, as well as the related differences are shown in Figure 1. Both the size of LE65 and the shapes of the time patterns observed in the MCD and Medicare data were similar. Geographic-related disparities were stronger in their impact on LE65 than race-related disparities over the entire study period. In the 5%-Medicare data, a slow increase in both geographic and race-related disparities can be seen between 2000 and 2005 after which racial disparities decrease sharply until about 2015 while geographic-related disparities continued increasing but at a much higher rate. The MCD data suggest that the decline in racial disparities occurred much sooner than observed in the Medicare data. In general, the MCD data showed much sharper increases in geographic disparities and decreases in racial disparities than the 5%-Medicare data. Even so, both datasets show 2005–2015 as a period of active change.

Figure 1.

Life expectancy at age 65 (left plot) and subpopulation-specific disparities (right plot). State disparities reflect leading states (Hawaii, Florida, Arizona, California, New York, Connecticut, Minnesota, and Colorado) vs, lagging states (Arkansas, Tennessee, Louisiana, Oklahoma, Kentucky, Alabama, Mississippi, and West Virginia). Race disparities reflect White vs. Black. B-splines with two internal nodes in 2005 and 2011 were used to smooth the curves.

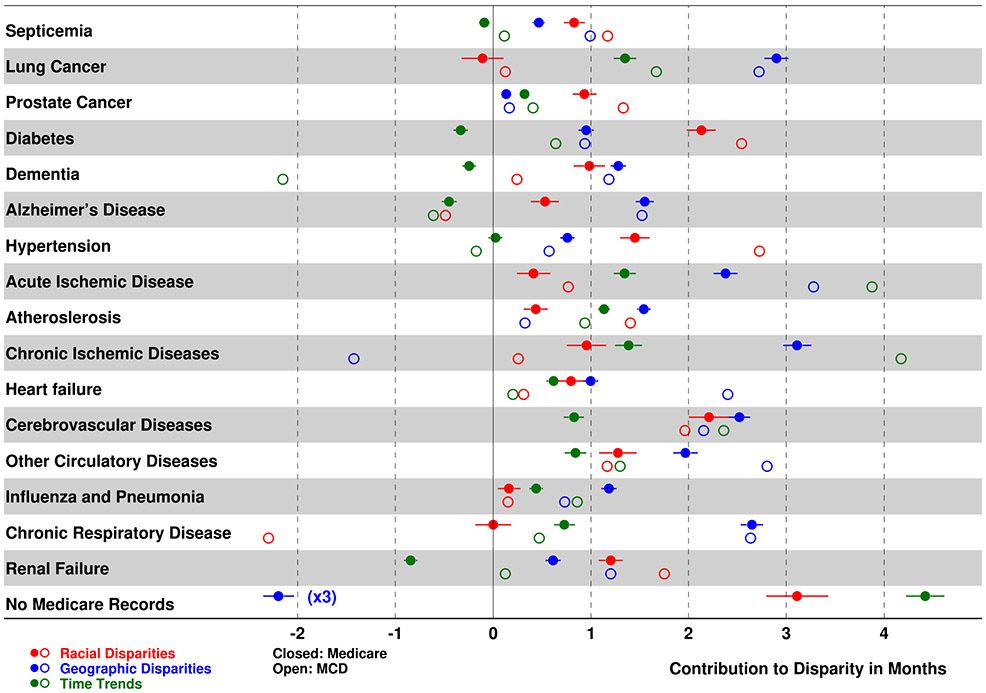
The full set of absolute and relative cause-specific contributions to the differences in life expectancies are shown in Supplementary Tables 1-3. Time trends of the cause-specific contributions are shown in Supplementary Figures 1 and 2. The causes with the largest contributions are shown in Figure 2. A cause was included in Figure 2 if one of its contributions exceeded one month of LE65. The life-table-based cause-specific decomposition was obtained by applying eqn. (8) to the MCD (open circles; all colors), and Medicare-based estimates were obtained on a day-by-day basis using the product-limit form of Pollard’s decomposition using eqn. (9) (closed circles; all colors). Cause-specific contributions for racial (red) and geographic (blue) disparities, as well as the trend of the effect of this condition over time (green) are also shown. In sensitivity analysis, we also obtained Medicare-based estimates on a grouped data basis using the life-table form of Pollard’s decomposition (Supplementary Tables 1-3). The differences between the two Medicare-based estimates were minor; this gives us confidence in the stability of the initial results and allowed us to conclude that the results differed somewhat due to differences in how the respective causes of death were assigned, and possible contributions of individuals without Medicare records available. Standard errors and confidence intervals were evaluated using the life-table approach with simulations based on the multinomial distribution. The last line in Figure 2 presents the contributions to the disparities from the group of individuals without identified Medicare diagnoses for the 37 disease groups included in this study; therefore, a cause of death cannot be assigned for these individuals. Jointly, this group accounts for 10.0% of total available deaths and is not homogenous; it includes four subgroups: i) individuals on Medicare Part C plans that do not contribute claims data to the database (38.9%), ii) individuals eligible for Medicare services but residing outside the U.S. (2.2%), iii) individuals without Medicare service records (38.5%), and iv) individuals with Medicare service records but without diagnoses identified in our algorithms (20.5%). The first two subgroups represent individuals with incomplete data due to a known (entry/exit/duration in this stage is known as well as, in some cases, partial health records, are available) reason; the third – individuals not utilizing the Medicare system for reasons unknown; the last – relatively healthy people. All subgroups contribute to negative geographic disparities (i.e., fractions of membership in leading states for the group shown in Figure 2 are much higher than the fractions in the total sample) and last two subgroups contribute to the positive racial disparities increased time trend in Figure 2. Specifically, the fractions of individuals without a diagnosis are higher for leading states (85.8%) compared to the total group (72.9%) and for the Black subpopulation (10.3% vs. 8.2%). These estimates reflect the observed disparities for the group of individuals without identified Medicare diagnoses in Figure 2.

Figure 2.

The cause-specific contributions to the differences in life expectancy at 65 given by eqns. (8) and (9). Estimates are shown for racial (red), geographic (blue), and time-related (green) disparities using Medicare (closed dots) and Multiple Cause of Death data (open dots). The last line shows disparities for the group of individuals without established diagnoses in Medicare records (the blue point that shows the geographic disparity has to be multiplied by 3 to obtain actual value).

The greatest contributions to racial disparities were observed for arterial hypertension, diabetes mellitus, cerebrovascular diseases, and renal disease. While the majority of causes contributing to LE65 disparities were those with higher rates among the Black population, there were also several causes with substantial contributions to the gap in LE65 whose rates were higher among Whites: chronic respiratory diseases had the greatest contribution in the MCD data and slow progressive cancers in the Medicare data followed by the contribution of Parkinson’s disease in both datasets. The largest relative contributions to geographic disparities in LE65 were from chronic lower respiratory diseases, lung cancer, and circulatory diseases including myocardial infarction, heart failure, and stroke. Chronic ischemic disease had large contributions in both MCD and Medicare data but these contributions were in opposite directions. Circulatory diseases and lung cancer were among the leading causes contributing to increases in LE65 with time. Dementia and Alzheimer’s disease as well as renal disease (in Medicare) had the greatest negative contributions, suppressing LE65 with time.

4. Discussion

We extended Pollard’s decomposition for application to administrative and registry data. We demonstrated that if the continuous-time cause-specific survival functions are estimated using the Kaplan-Meier product-limit estimator, then Pollard’s integral for the difference of life expectancies between two subpopulations can be solved exactly. The analytic formulae for the difference can be specified for administrative data, and then extended to discrete-time registry data. The formulae do not require numerical integration; no parametric assumptions have to be made for the cause-specific hazards and other functions in Pollard’s integrand. An important property of the solutions for Pollard’s integral for registry and administrative data is that the sums of cause-specific contributions in expressions (8) and (9) are exactly 100% of the respective differences in life expectancy. This means that biases of technical or methodological origin do not impact the estimates, or that their contributions mutually cancel out. The new methodology was applied to an exhaustive set of causes of death observed in Multiple Causes of Death and Medicare data, and a series of new results on the racial and geographic disparities as well as their cause-of-death decompositions was presented and discussed.

4.1. Methodologic development: Solving Pollard’s decomposition

Pollard’s decomposition for specific causes of death is given by eqn. (6). To calculate the integral, we need to calculate each function in the integrand at each exact age at death, $a$. Practical applications generally require estimating the required functions from an administrative dataset and, possibly, numerical evaluation of the integral. Medicare data (as well as any other administrative dataset) provide individual measurements including age/time of initial follow-up, age/time of the end of follow-up, and the censoring/death (with a cause) indicator at the end of follow-up. The survival functions can be calculated from such data using the Kaplan-Meier estimator (or its generalization for left-truncated data). To calculate the life expectancy at exact age $a$, the survival function can be integrated from $a$ to infinity. This can be done using a numerical method with specific assumptions concerning the behavior of the survival function after the last observed age at death. The race-specific and cause-specific hazard functions can be evaluated using parametric functions or non-parametric procedures that yield numerical values at each exact age of death and handle multiple deaths with different causes occurring on the same day (usually the smallest time-interval in administrative data). Thus, Pollard’s integral can be numerically calculated under various simplifying assumptions using administrative data with exact ages at death.

Our approach to evaluation for such data of all functions contributing to the integral in eqn. (6) used Kaplan-Meier product-limit estimators for the total and cause-specific survival functions. The survival functions estimated using the Kaplan-Meier approach are discontinuous and the respective instantaneous hazards are equal to zero everywhere except for exact ages at death where the hazards go to infinity. Numerical evaluation of Pollard's integral using such hazard functions is not possible. Instead, we performed the integration analytically, obtaining expressions for the cumulative hazard functions as logarithms of the ratios of the associated survival functions just before and just after each exact age of death. The exact solution for the integral in eqn. (6) is shown in eqn. (9). A remarkable property of this solution is that Pollard’s decomposition is represented as a sum of terms obtained from the Kaplan-Meier estimators for the total and cause-specific survival functions, without numerical integration. Moreover, because the Kaplan-Meier estimator is a maximum likelihood estimator, it follows from Zehna³⁸ that the solution for Pollard’s decomposition in eqn. (9) is likewise a maximum likelihood estimator.

Having solved Pollard’s decomposition for exact ages of death, we then considered the corresponding problem for complete life tables using population/registry data with death recorded using single-year age at last birthday. The expressions for complete life tables were obtained by integration of the expressions for administrative data over each age interval of the life table, using the procedure described in subsection 2.3.2. The expressions in eqns. (8) and (29) reflect the close-out of the life tables at age 100; this can be increased to age 110 or 120 if the life table data are available. The close-out age should be high enough that the impact of the close-out term is negligible. Thus, Pollard’s decomposition can be represented as a sum of terms obtained from the respective life tables for the total and cause-specific survival functions, without numerical integration. Also, given that the life table survival function is a maximum likelihood estimator²⁹, it follows from Zehna³⁸ that the resulting solution for Pollard’s decomposition in eqn. (8) is likewise a maximum likelihood estimator.

Thus, we developed a consistent methodology for solving Pollard’s decomposition for exact ages of death and for grouped ages of death, which are exact in the sense that they do not require numerical integration or parametric models for the cause-specific hazards and other functions in Pollard’s integrand. In addition, methods for generating reliable estimates of standard errors and associated confidence intervals for the cause-specific contributions were also provided. The solutions for Pollard’s decomposition were applied to two types of data that are often used in biodemography for LE evaluation at the national level: i) Medicare administrative claims data, and ii) MCD data with population counts. Each dataset must be analytically extended to be used in these analyses. Population counts for MCD data end at age 84, with the 85+ population represented by an aggregate group. Since this is too imprecise for our study, we applied procedures to distribute population counts aggregated at age 85+ into single-year age groups for ages 85-99 and a single aggregated group for ages 100+. These distributions had to be calculated for each year, had to be race-specific for analyses of racial disparities, and had to be state-specific for analyses of geographic disparities. Medicare data do not contain entries for cause of death. Therefore, we developed a Monte Carlo procedure to assign underlying causes of death for all decedents. The procedure provides equal cause-specific death rates in the 5%-Medicare and MCD data.

The final solutions (8) and (9) for Pollard’s decomposition of LE65 for MCD and Medicare data, respectively, possess the main properties of a decomposition: exact normalization and additivity. The cause-specific contributions to the decomposition related to different causes of death are appropriately normalized, i.e., the sum of the cause-specific relative contributions for each decomposition computed using eqn. (8) and (9) is exactly 1, or 100% of the difference in life expectancy. This property was proved analytically for both types of datasets and was used for additional cross-checks of our analysis software: in our SAS code these sums were exactly 100% for each year of our analysis. Importantly, as long as this property holds, any contribution obtained through Pollard’s integral is directly interpretable regardless of size, i.e., researchers can be equally confident in both large and small cause-specific contributions. The additive property of Pollard’s decomposition holds exactly in our final expressions; even after the multiple operations necessary to apply Pollard’s integral to the two types of data used in this study. For example, this allows us to sum all cancer-related or circulatory-disease-related contributions to obtain the decomposition involving the all-cancer or all circulatory disease groups. The exact normalization will hold in this case. We note that our main decomposition presented by formulae (8) and (9) is valid even in the case when the difference in life expectancies at age 65 is exactly zero. In this purely theoretical scenario, the absolute decomposition shows how effects of causes with positive contributions are exactly compensated by causes with negative contributions. Although relative differences are undefined, the sum of all cause-specific contributions gives zero years exactly.

This study opens potential new avenues for research on the origin of substantial geographic and racial disparities in LE in older U.S. adults. For example, each type of disparity could be expressed using health measures recorded in Medicare data to further identify contributing factors behind the observed time trends and observed disparities. After ranking all causes according to their effects on LE in selected geographic regions, it then becomes feasible to apply partitioning analyses^39-44 to the causes that contribute most to the disparities to assess the extent to which their contributions reflect higher incidence vs. poorer survival. Such analyses are feasible with Medicare data because the longitudinal sub-files for each enrollee beyond age 65 record all covered services before and after onset of each chronic disease allowing measures of incidence, prevalence, and case fatality to be generated and analyzed. Moreover, regression-based approaches, e.g., Oaxaca-Blinder decomposition extended for censored data^45-47, can be used to help understand the role of clinical factors (e.g., screening, effective diagnostic procedures, treatment choice, and treatment adherence), demographic and socioeconomic characteristics, behavioral risks, environmental exposures, as well as access to and quality of available medical care. Ultimately, identification and evaluation of such contributing factors may reveal a role as fundamental drivers of the observed disparities, which could inform the design of strategies to improve public health and the healthcare system⁴⁸.

4.2. Pollard’s decomposition and other methods of cause-specific decomposition of life expectancies.

Two distinct demographic approaches are commonly used to evaluate the cause-specific contributions to the difference in life expectancies for two well-defined subpopulations¹². The first considers each subpopulation separately and estimates the gains in life-expectancy that would occur under the assumption that the causes of death are independent and that the deaths from each cause can be eliminated one at a time, in turn, with the deaths from all other causes retained, i.e., the force of mortality for each selected cause is set to zero for all ages with the forces of mortality for all other causes held unchanged from their initial values⁴⁹. The cause-elimination life expectancy gain for cause $i$ can be computed using Greville’s method²³ as shown in eqn. (2). The difference between the cause-elimination life expectancy gains for cause $i$ in the two subpopulations can then be treated as a measure of the contribution of cause $i$ to the overall life expectancy difference between the two subpopulations. Unfortunately, the contributions are not additive; additional procedures are needed to ensure that the sum of the relative contributions over all causes equals 1. Beltrán-Sánchez et al.¹² developed an alternative decomposition of LE differences based on cause-elimination principles (including the independence assumption) that does not make direct use of the cause-elimination life expectancy gain for cause $i$ in either subpopulation; instead, the underlying cause-specific survival functions in the two subpopulations are used to estimate cause-specific contributions for cause $i$ that are approximately additive for the overall life expectancy difference between the two subpopulations.

The second approach is based on demographic decomposition theory. Pollard’s decomposition belongs to the second approach. The properties of Pollard’s decomposition were discussed in Section 2.1. Pollard’s decomposition is exact by construction and represents the difference in life expectancies for two subpopulations as the sum of cause-specific components. An important property of Pollard’s decomposition is that the assumption of independence of cause-specific forces of mortality is not required. The two approaches, i.e., Beltrán-Sánchez’s decomposition and Pollard’s decomposition, are not equivalent though the respective results are close¹².

Historically, methods for decomposing differences in LE were presented in several mathematically equivalent approaches^8,19,50-52, as demonstrated by Pollard⁹ and Shkolnikov et al.⁵³, although their implementation via various discrete approximations can give rise to different results¹². Several other approaches were presented to further analyze the difference in LE between subpopulations in terms of age and cause-of-death contributions.

Horiuchi et al.⁵⁴ presented a general approach for decomposition of a demographic measure that can be represented as a function of multiple covariates. For example, race-specific LE65 can be considered such a demographic measure, and differences in race-specific LE65s can be represented as functions of age and cause specific mortality rates. Eqn. (5) of ref.⁵⁴ gives the general decomposition formula for an arbitrary demographic measure, and eqns. (9-10) of ref.⁵⁴ give the decomposition formula for differences in life expectancy. Two types of numerical integration are required to represent the difference in LE65 in a form comparable to our eqn. (6): i) integration over age groups, and ii) integration over a linear variable that connects pairs of age-specific mortality rates (e.g., two race-specific mortality rates from lung cancer in age group 65–69). The second integration is specific to Horiuchi’s method and can be performed only under the assumption of a linear relationship between specified covariates (e.g., as in eqn. (11) of ref.⁵⁴). The necessity for this linearity assumption and the two-way numerical integration are limitations of this method that are not present in our approach. Horiuchi reported that an approximation to Pollard’s decomposition (using stepwise replacement⁵⁵) by broad age groups for Japanese females was equivalent to their method when applied on an annual basis over 54 separate calendar years (Table 3 of ref.⁵⁴) and was close when applied across the entire 54-year period (Table 4 of ref.⁵⁴). This equivalence/closeness occurs because our solution of Pollard’s formula in eqn. (8) is an exact solution to Horiuchi’s eqns. (5) and (9)⁵⁴. Horiuchi’s method has been implemented in DemoDecomp R-package⁵⁶ (Decompose Demographic Functions) and used in recent analyses^57,58.

Age decomposition in the general replacement method⁵⁵ was developed based on the idea that the difference between life expectancies can be constructed based on a general algorithm, which includes the stepwise replacement of elements from one vector of age-specific mortality rates by the respective elements of another vector, with the replacements ordered by ascending age. The resulting formula eqn. (3) of ref.⁵⁵) for age decomposition with predetermined age groups is a particular case of our formula (10) that is valid for continuous ages. The cause-of-death decomposition in our approach is then developed based on eqn. (10) using exact methods of calculus for continuous age. Depending on the dataset type, the resulting formulae for continuous age can be reduced to age-interval specific formulae for certain datasets: one day in administrative data and one year in registry data types. In contrast, incorporation of cause-of-death decomposition in the replacement approach requires another set of replacements of age-specific rates with vectors of age- and cause-specific rates. The final effect for a specific cause of death is computed by averaging over all possible combinations of replacements using all other causes.⁵⁹

Another common approach^59-63 is Arriaga’s decomposition¹⁹. Pollard showed⁹ that the age decomposition presented by Arriaga¹⁸ was mathematically equivalent to the "1–2" form of his decomposition. An important difference between our approach and Arriaga's, however, is that our cause-specific decomposition was theoretically derived; Arriaga's formula was an assumed allocation formula that happens to be consistent with Pollard's result. One limitation of Arriaga cause-of-death decomposition is that the calculations may become unstable if the denominator (the difference between the age-specific mortality rates in the two subpopulations being compared) is small relative to the corresponding cause-specific differences. This could happen, for example, if sex differences at some ages were small except for breast and prostate cancers, which could be large but in opposite directions. Our discrete time formula (8) is equivalent to Arriaga's discrete time formula, but: i) ours is easier to interpret given that it can be matched to formula (9) that covers the Kaplan-Meier estimator; and ii) ours does not become unstable for small, or zero, differences between the age-specific mortality rates in the two subpopulations being compared.

A complementary indicator to cause-elimination gains in life expectancy is the average years of life lost prior to some chosen threshold age, which can be evaluated for the age interval between birth (or other fixed age) and any selected upper age limit (e.g., ages 85 or 95). Using this strategy, Andersen et al.⁶⁴ presented a new approach for defining and evaluating life years lost by cause of death, and generating cause-specific decompositions of the differences in restricted (or “temporary”) life expectancy between two subpopulations, where the restricted life expectancy is: ${\int }_0^x\ell (a)da$, assuming $\ell (0)=1$; the higher the value of $x$, the closer the restricted will be to the unrestricted life expectancy. The difference between the restricted life expectancies in any two subpopulations is exactly equal to the difference in their respective life years lost (see page 1135 of ref.⁶⁴), and this difference can be readily decomposed by cause and age. The additivity of the cause-specific forces of mortality implies that the decomposition can be done without assuming that the causes of death are independent (see Gail²⁵ eqn. (4)). The need to choose an upper age limit and use numerical integration are the main limitations of this approach compared to the approach developed in this paper.

A new approach for decomposition of the young adult mortality hump by cause of death was presented in Remund et al.⁶⁵. Under this approach, a non-parametric spline-based model was used to parameterize the age-dependence of the hazard functions. The approach allowed the separation of the trends in the hump from background mortality, yielding multiple insights into the cause-specific structure of the hump in the U.S. The spline-based approach for non-parametric evaluation of the cause-specific hazards could be considered for evaluating Pollard’s integral; however, the error-accumulation from model fitting and the necessity for numerical integration limit the applicability of such an approach when precise estimates are needed. In any case, the property that the sum of all relative cause-specific contributions to the decomposition is exactly 100% of the difference in life expectancy does not hold.

4.3. Differences in time trends of LE65 and its racial and geographic disparities

We found that LE65 in the U.S. increased during the study period for all subpopulations (Figure 1). The increase was more rapid for leading states and for the Black population. The shapes of the time patterns were similar for all study populations as well as for results obtained using MCD and Medicare data. The difference in estimates for LE65 in 2005 and 2015 did not exceed 1% with the exceptions of Blacks (2.12%) and leading states (2.52%) in 2015, for which LE65 was lower in the Medicare data, as well as lagging states (1.63%) in 2005, for which LE65 was lower in the MCD data. A tendency for stagnation in LE65 in later years was seen in the Medicare data. However, even though LE65 increased for all subgroups, notable racial and geographic disparities remained. The geographic disparity in LE65 between leading and lagging states was 2.75 years (2.32 years based on Medicare data) in 2015; this was a 29% increase from its 2005 value of 2.13 years (1.83 based on Medicare data). Over the same time-period the Black/White racial disparity in LE65 decreased by 41% from 1.55 years (1.68 based on Medicare data) in 2005 to 0.91 years (1.33 based on Medicare data) in 2015.

We found that the dynamics of racial and geographic disparities in LE65 demonstrated opposing tendencies. The loss of LE65 associated with racial disparities narrowed between the years 2000 and 2017, predominantly due to increasing LE65 in the Black population. This is consistent with estimates of change in race-specific disparities in life expectancy at birth recently reported by the Global Burden of Diseases Collaboration⁶⁶. Over the same time-period the size of the geographic disparity in LE65 widened, predominantly due to more rapid improvements of LE65 in leading states. Although race-specific differences between age-adjusted mortality between 2005 and 2015 looked similar in leading and lagging states: 913/1077/983 per 100,000 in leading/lagging/all states for the Black and 559/486/497 for the White populations, there were three types of contributions to the time trend in the geographic disparities. A lower difference in mortality for the White population in lagging states provided the main contribution to the overall increase in geographic disparities. The stronger declines in mortality in the Black population of lagging states partly offset the overall widening disparities in LE65 between leading and lagging states. Although the decline in mortality was much larger for the Black population, the contribution of the Black population to the trend in geographic disparities was lower due to the relative size of the Black population in these states (8.5% in leading states and 14.5% in lagging states in 2010). One more contribution to the geographic disparities came from changes in the fraction of the Black population, especially in leading states, e.g., an increase of the fraction from 8.0% in 2005 to 9.0% in 2015 in leading states. Our estimates showed that the effect of such changes in the geographic disparity trend were as large as 7%.

It was reported that the Black-White gap in all-cause mortality (i.e., death rate disparity relative to Whites) narrowed from 33% in 1999 to 16% in 2015⁶⁷. Over a similar time period our findings show a decrease in Black-White disparities in LE65 from 1.70 in 2000 to 0.83 years in 2015. Furthermore, it was reported that the non-Hispanic Black population in 2000–2014 had the greatest increase in LE at birth. Our findings also show that LE65 for Blacks increases sharply over the 2000-2014 period. The magnitude of this growth was much higher than that observed in White individuals which is consistent with a previous finding that non-Hispanic Whites had the lowest increase in LE among all race/ethnicity-related groups^68,69. However, Blacks continue to have higher mortality than Whites at ages < 65⁶⁷ and 60% of the decline in the racial gap in LE at birth in 2000–2010 has been attributed to declining differences in the age at which Black and White individuals die of chronic diseases, with the remaining 40% of the reduction in the LE gap associated with changes in the distribution of causes of death among Blacks and Whites at younger ages (e.g., due to greater declines in HIV/AIDS and perinatal deaths in Blacks, and increasing death rates caused by accidental poisoning—mostly drug related—among Whites)^69-71. A recent study of Medicare beneficiaries aged 65+ supports this rationale by showing that the average decline in LE65 with an additional comorbid condition was higher in the Black population (1.8 years per additional condition) than in the White population (1.7 years), with the Black population being more likely to have 7+ chronic conditions⁷².

Widening disparities in state-specific LE65 across the U.S. have been observed for midlife mortality since the early 1980s⁷³. More recently, persistent geographic inequalities in the risk of death at ages 65–85 have received increasing attention^74,75 with suggestions that the increases in geographic inequality in LE65 in the U.S. over the past three decades have been driven largely by unfavorable dynamics of mortality at older ages⁷⁴. Furthermore, geographic variation in the disparities in LE between Black and White Americans has been documented, suggesting that racial and geographic disparities are intertwined⁷⁶; indeed, there are indications that the narrower racial disparities in LE in certain U.S. states were not due to the Black population living longer but rather to the White population having a shorter LE compared to the national average⁷⁷. Our findings confirmed these tendencies, finding that over time racial disparities decreased but geographic disparities increased. These results were replicable across two distinct data types: Medicare and MCD.

4.4. Causes contributing to racial and geographic disparities in LE65 and the time trend in LE65

Our study showed that trends in the cause-related determinants of racial disparities were characterized by a relatively small number of high-impact contributors with some acting through increased mortality rates in the White population. Lower LE65 in the Black population was associated with death from arterial hypertension (24.4%/9.1% of total 2015 disparity in LE65 using MDS and Medicare data, respectively)), cerebrovascular disease (17.0%/11.0%), diabetes mellitus (21.3%/14.5%), renal disease (16.0%/10.5%), prostate cancer (9.9%/5.9%), and the group of other circulatory diseases (8.0%/7.5%). Disease specific contributions were not identified for LE65 before, however, some of these causes have been previously reported as important determinants of racial disparities in LE at birth. For example, heart disease was found to be a leading contributor that accounted roughly for 25% of the racial gap⁷⁰ with cardiovascular disease in general accounting for 34%⁴⁸ of the racial difference in all-cause mortality. COPD was the only major contributor to Black/White disparities in LE65 that acted through higher mortality rates in the White population^48,78. We note that an important contribution of the Firebaugh study⁷⁰—which utilized the approach of Beltrán-Sánchez et al.¹² to the decomposition of MCD data in order to evaluate the role of age-at-death and incidence of 19 causes in forming the gap in overall LE between Blacks and Whites—was that the decline in Black/White disparities in overall LE was attributable to a reduction in the contribution of age-at-death, largely due to the declining differences in the ages at which Blacks and Whites died of chronic diseases.

In our study trends in cause-related determinants of geographic disparities were characterized by a relatively large number of causes with relatively small individual impacts all acting through increased mortality rates in lagging states. The largest contributions to geographic disparities in LE65 were associated with CVD including acute ischemic heart diseases (7.8%, 7.9%), the other circulatory diseases group (8.4%, 7.4%), and heart failure (8.1%, 3.5%), as well as COPD (10.7%/9.8%), lung cancer (8.7%/9.9%), and Alzheimer’s disease (7.1%/5.3%). The contributions of COPD, Alzheimer’s disease, and arterial hypertension increased over time. Although, not directly comparable due to differences in study design; our results are concordant with several existing studies focused on geographic disparities in cause-specific mortality and LE. For example, MCD-based studies have shown that CVD and smoking-associated diseases were the principal drivers of geographic variations in LE65 which accounted for over 64% of the geographic disparities in changes in LE65 from 2000 to 2016 in the 65+ population^78,79. This effect persisted despite overall declines in CVD mortality in all states⁷⁸. These studies also stressed improvement in smoking-related mortality (lung cancer and respiratory diseases) as being second (following CVD) in contributions to LE65 gain in the U.S.^78,79. Finally, rising mortality from Alzheimer’s disease and other diseases of the mental or nervous systems, including non-Alzheimer’s dementia, has been identified as negative contributors to changes in LE65 among older U.S. adults⁷⁹.

In our study the shapes of the time patterns in LE65 were similar for all subpopulations: LE65 increased over the entire study time-period with the speed of the gains decelerating after 2010. The increase in LE65 between 2005 and 2015 was more than one year for all subpopulations, and Pollard’s approach was then used to decompose this gain into cause-specific contributions for each of the four study groups. Our results showed that the increase in LE65 between 2005 and 2015 was primarily due to (Table 2) reduced mortality from chronic ischemic disease, acute ischemic disease, lung cancer, and cerebrovascular disease. This was offset, in part, by increased mortality from Alzheimer’s disease and dementia. For most causes, the relative contributions to temporal reductions in mortality in Blacks were less than in Whites. We note that approximately 65% of the total gains in LE65 occurred in 2005–2010 and only 35% in 2010–2015 which was consistent with other research^80,81.

Our results are consistent with a comprehensive report on the burden of disease and its patterns in the U.S. states from 1990 to 2016 which also identified wide disparities in the burden of disease at the state level⁸². While the U.S. overall is experiencing improvements in health outcomes, the patterns of health burden at the state level substantially vary across geography, and monitoring location-specific disease trends is essential given the geographic differences in various aspects of health and social policy (e.g., enrollment in the Medicaid program, the use of private insurance companies)⁸³ and the local socioeconomic environment⁸². In this study, we identified a number of exact disease-specific causes, which if targeted, can act to mitigate these tendencies. Although, geographic differences were aggregated at the state-group level, stronger sources of data can now be combined with the methods developed in this study to obtain results specific to smaller localities. Consistency between Medicare and MCD data demonstrated in this study, suggest that high-power Medicare samples can be used for such analysis; though additional linkages to Medicaid claims may be necessary to better reflect socioeconomically disadvantaged individuals, many of whom are also members of other disadvantaged populations.

4.5. Study strengths and limitations

The study has several strengths. Within the same study design, we analyzed the trends of both racial and geographic disparities in LE65 among older U.S. adults over a period spanning 17 years and obtained complementary results from two different large nationally representative datasets. Much of the existing research on disparities in LE is focused on variations in mortality at working ages^82,83. However, unlike working-age individuals, in the 65+ age strata morbidity is the most common cause of death^79,82, making differences in morbidity and associated adverse health-related outcomes between advantaged and disadvantaged groups an important aspect of disparities in LE65. The analysis of individual contributions of discrete diseases to this problem is sub-optimal due to both increasing levels of multi-morbidity in older adults and the inherent relationships between disease trends such as the recent declines in mortality from circulatory disease and certain cancers (lung, colorectal, breast) being partially offset by increases in mortality from other chronic diseases⁸⁴. We used Pollard’s decomposition to evaluate the contributions of 37 cause groups to the size and the time trend in both geographic and racial disparities in LE65 in the U.S.

We also acknowledge the following limitations. An underlying cause of death is not provided in Medicare data, and it may be hard to determine accurately in the MCD data, particularly among the elderly, where multiple mortality-related diseases are likely to be present at the time of death. Involving multiple causes of death (MCD data) in future analyses (e.g., through random assignment of a cause of death from the list of multiple causes) could estimate the sensitivity of our estimates. Furthermore, we developed an approach to assign a cause of death in Medicare records, and these analyses can be repeated when linked cause-of-death data become more widely available for Medicare beneficiaries. Population estimates in the MCD could be biased, especially for minority populations, because of census undercounts, age misreporting, and race misclassification. However, because the MCD and 5%-Medicare results were broadly consistent, this limitation may be of lesser concern. Finally, changes in diagnostic and coding practices have likely affected some of the trends that we have identified in cause-specific mortality. For example, coding changes implemented by the National Center for Health Statistics in 2006 produced an increase in deaths from “unspecified dementia” and “vascular dementia”, and this increase occurred at the expense of anemias, nutritional deficiencies, heart disease, and cerebrovascular disease⁸⁵.

5. Conclusions

Although notable progress has been made in improving the health and well-being of Americans, health inequities between population groups and geographic areas persist representing a major area of policy concern⁷⁸. Using an integral representation of Pollard’s decomposition^8,9 applied to Multiple Cause of Death and Medicare administrative health insurance claims data, this study identified the morbidity-related causes of race and geography-related disparities in LE65; quantified their respective magnitudes to isolate cause-groups with the highest overall impact; and measured the trends in the relative impact of such cause-groups over time. These analyses required methodologic development involving an analytic solution to Pollard’s decomposition to evaluate the cause-specific contributions for administrative and registry data. We demonstrated that if the cause-specific survival functions are estimated using the Kaplan-Meier estimator, then Pollard’s integral for the difference of life expectancies of two subpopulations can be exactly solved. The analytic formulae for the difference were specified for both types of data. They do not require numerical integration; no parametric assumptions for the cause-specific hazards and other functions in Pollard’s integrand have to be made for their derivation. An important property of the expressions (8) and (9) for Pollard’s integral for administrative and registry data is that the sum of all cause-specific contributions is exactly 100% of the difference in life expectancy. This means that biases of technical or methodological origin do not impact our estimates, or that their contributions mutually cancel out. The additivity of the cause-specific contributions arises without the assumption of independence among the selected causes of death. Dependencies between the cause-specific contributions may be due to common risk factors that impact multiple causes.

The developed methodology was applied for an exhaustive set of causes of death observed in Multiple Causes of Death and Medicare data, and a series of new results on the racial and geographic disparities as well as their cause-of-death decompositions were obtained and discussed. We found that the temporal improvement in LE65 was more substantial for the Black than the White population and it was less pronounced in the lagging compared to the leading states. These temporal trends resulted in a narrower LE65 gap between the White and Black populations and a wider gap between the leading and lagging states. Estimates using Medicare data reproduced those obtained using MCD data, though Medicare-based trends were less pronounced. The largest relative contributions to geographic and racial disparities in LE65 were: for geographic—chronic lower respiratory diseases, Alzheimer’s disease, circulatory diseases, lung cancer, and renal failure; for racial—arterial hypertension, diabetes, cerebrovascular diseases, and renal disease. The ranks of the diseases were in agreement between analyses using MCD and Medicare data. Based on the MCD, chronic ischemic diseases for geographic disparities and chronic respiratory diseases for racial disparities were higher in the advantaged groups thereby reducing LE65 disparities, however, these effects were not replicated in the Medicare data. Overall, the increase in LE65 observed in 1998–2005 and 2010–2017 was primarily due to a reduction in the contributions of acute and chronic ischemic diseases, although this was partially offset by increased contributions of diseases of the nervous system, including dementia and Alzheimer’s disease.

Appendix A

Here we demonstrate that if the cause-specific hazard functions are proportional over the interval [$t_{{}_0}$, $t_{{}_1}$], with constant of proportionality $r_{{}_i}(t_{{}_0})$ for cause $i$, then the life-table number of deaths from cause $i$, denoted $d_{{}_i}(t_{{}_0})$, is proportional to the life-table number of deaths from all causes, denoted $d(t_{{}_0})$, where $d(t_{{}_0})={\sum }_{i=1}^I{d}_{{}_i}(t_{{}_0})$, with the same constant of proportionality $r_{{}_i}(t_{{}_0})$. The sum over all such intervals of the life-table number of deaths from all causes is scaled to equal $\ell (0)$, which for simplicity is initialized to $\ell (0)=1$.

Because $\mu (t)={\mu }_1(t)+\dots +{\mu }_I(t)$ and $\ell (t)={\ell }_1(t)\cdot \dots \cdot {\ell }_I(t)$ (see Gail²⁵ eqns. (4) and (5)), the total density of deaths from all causes is:

$$f(t)=\frac{d}{dt}(1-{\ell }_1(t)\cdot \dots \cdot {\ell }_I(t))=f_1(t)\cdot {\ell }_2(t)\cdot \dots \cdot {\ell }_I(t)+\dots +{\ell }_1(t)\cdot \dots \cdot {\ell }_{I-1}(t)\cdot f_I(t).$$

The first term in this sum, $f_1(t)\cdot {\ell }_2(t)\cdot \dots \cdot {\ell }_I(t)=f_1(t)\ell (t)∕{\ell }_1(t)={\mu }_1(t)\ell (t)$, is interpreted as the density of deaths from cause 1; more generally, ${\mu }_i(t)\ell (t)$ is the density of deaths from cause $i$. Therefore, the integrals of these cause-specific densities over the interval [$t_{{}_0}$, $t_{{}_1}$] give the probabilities of death from the specific causes. Hence,

$$d_{{}_i}(t_{{}_0})={\int }_{t_{{}_0}}^{t_{{}_1}}{\mu }_{{}_i}(t)\ell (t)dt=r_{{}_i}(t_{{}_0})\cdot {\int }_{t_{{}_0}}^{t_{{}_1}}\mu (t)\ell (t)dt=r_{{}_i}(t_{{}_0})\cdot {\int }_{t_{{}_0}}^{t_{{}_1}}f(t)dt=r_{{}_i}(t_{{}_0})\cdot d(t_{{}_0}),$$

as required. It follows that the total and cause-specific life-table numbers of deaths are discrete probability functions.

Appendix B

Integration between two integer ages $x$ and $x+1$ starting from (10) and using properties of the integral and approach resulting in (11) allows us to rewrite (10) as

$$\stackrel{{}_{\circ }}{e}{}_{{}_W}(65)-\stackrel{{}_{\circ }}{e}{}_{{}_B}(65)=\frac{1}{2}{\sum }_{x=x_0}^{\infty }\left(F(x)-F(x+1)\right)$$

Consider one time interval [$x$, $x+1$]. We need to sum over all deaths that occurred in this time interval. The contribution for the case of one death is given by (17), so:

$$F(x)-F(x+1)=\sum _{k,x\le a_k<x+1}\left(F(a_{{}_{k-}})-F(a_{{}_{k+}})\right)={\sum }_k\left(e^{{\widehat{\mu }}_{{}_B}(a_{{}_k})}-e^{{\widehat{\mu }}_{{}_W}(a_{{}_k})}\right)\left({\ell }_{{}_W}(a_{{}_{k+}})\stackrel{{}_{\circ }}{e}{}_{{}_B}(a_{{}_{k-}})+{\ell }_{{}_B}(a_{{}_{k-}})\stackrel{{}_{\circ }}{e}{}_{{}_W}(a_{{}_{k-}})\right).$$

We need to prove that

$$F(x)-F(x+1)=\left(\frac{l_{{}_x}^{{}^B}}{l_{{}_{x+1}}^{{}^B}}-\frac{l_{{}_x}^{{}^W}}{l_{{}_{x+1}}^{{}^W}}\right)\left(l_{{}_{x+1}}^{{}^W}\left(\stackrel{{}_{\circ }}{e}{}_{{}_x}^{{}^B}-({\widehat{a}}_{{}_x}-x)\right)+l_{{}_{x+1}}^{{}^B}\left(\stackrel{{}_{\circ }}{e}{}_{{}_x}^{{}^W}-({\widehat{a}}_{{}_x}-x)\right)\right).$$ (30)

To do this we need to use eqn. (15) in the form: ${\ell }_{{}_j}(a_{{}_{k-}})=s_{{}_{kj}}{\ell }_{{}_j}(a_{{}_{k+}})$ and $\stackrel{{}_{\circ }}{e}{}_{{}_j}(a_{{}_{k+}})=s_{{}_{kj}}\stackrel{{}_{\circ }}{e}{}_{{}_j}(a_{{}_{k-}})$, where we define $s_{{}_{jk}}=\text{exp}({\widehat{\mu }}_{{}_j}(a_{{}_k}))$ to simplify formulae. Furthermore, we use relations of survival functions and life expectancies in age points without deaths between them such as: ${\ell }_{{}_j}(a_{{}_{k+}})={\ell }_{{}_j}(a_{{}_{k+1,-}})$ and $\stackrel{{}_{\circ }}{e}{}_{{}_j}(a_{{}_{k-1,+}})=\stackrel{{}_{\circ }}{e}{}_{{}_j}(a_{{}_{k-}})+(a_{{}_k}-a_{{}_{k-1}})$. These equations are sufficient to express all functions through life expectancy at $x$ and all survival functions at $x+1$.

$$\begin{gathered} F(x)-F(x+1)={\sum }_k\left({\ell }_{{}_B}(a_{{}_{k-}})\stackrel{{}_{\circ }}{e}{}_{{}_W}(a_{{}_{k-}})-{\ell }_{{}_W}(a_{{}_{k-}})\stackrel{{}_{\circ }}{e}{}_{{}_B}(a_{{}_{k-}})-{\ell }_{{}_B}(a_{{}_{k+}})\stackrel{{}_{\circ }}{e}{}_{{}_W}(a_{{}_{k+}})+{\ell }_{{}_W}(a_{{}_{k+}})\stackrel{{}_{\circ }}{e}{}_{{}_B}(a_{{}_{k+}})\right) \\ ={\sum }_k\left(s_{{}_{kB}}{\ell }_{{}_B}(a_{{}_{k+}})\stackrel{{}_{\circ }}{e}{}_{{}_W}(a_{{}_{k-}})-s_{{}_{kW}}{\ell }_{{}_W}(a_{{}_{k+}})\stackrel{{}_{\circ }}{e}{}_{{}_B}(a_{{}_{k-}})-s_{{}_{kW}}{\ell }_{{}_B}(a_{{}_{k+}})\stackrel{{}_{\circ }}{e}{}_{{}_W}(a_{{}_{k-}})+s_{{}_{kB}}{\ell }_{{}_W}(a_{{}_{k+}})\stackrel{{}_{\circ }}{e}{}_{{}_B}(a_{{}_{k-}})\right) \\ ={\sum }_k\left((s_{{}_{kB}}-s_{{}_{kW}})({\ell }_{{}_B}(a_{{}_{k+}})\stackrel{{}_{\circ }}{e}{}_{{}_W}(a_{{}_{k-}})-{\ell }_{{}_W}(a_{{}_{k+}})\stackrel{{}_{\circ }}{e}{}_{{}_B}(a_{{}_{k-}}))\right). \end{gathered}$$

Continuing recursively, we can obtain the expression with all functions at bounds. Specifically, for the case of three deaths inside the interval [$x$, $x+1$] we obtain:

$$\begin{gathered} F(x)-F(x+1)=\left(s_{{}_{1B}}{s}_{{}_{2B}}{s}_{{}_{3B}}-s_{{}_{1W}}{s}_{{}_{2W}}{s}_{{}_{3W}}\right)\left({\ell }_{{}_B}(x+1)(\stackrel{{}_{\circ }}{e}{}_{{}_W}(x)+a_1-x)+{\ell }_{{}_W}(x+1)(\stackrel{{}_{\circ }}{e}{}_{{}_B}(x)+a_1-x)\right) \\ -\left(s_{{}_{3B}}-s_{{}_{3W}}\right)\left(a_{{}_3}-a_{{}_2}\right)\left({\ell }_{{}_B}(x+1)+{\ell }_{{}_W}(x+1)\right)-\left(s_{{}_{2B}}{s}_{{}_{3B}}-s_{{}_{2W}}{s}_{{}_{3W}}\right)\left(a_{{}_2}-a_{{}_1}\right)\left({\ell }_{{}_B}(x+1)+{\ell }_{{}_W}(x+1)\right). \end{gathered}$$

Then we introduce $\widehat{a}$ to represent the average age at death:

$$\begin{gathered} F(a_{{}_1})-F(a_{{}_2})=\left(s_{{}_{1B}}{s}_{{}_{2B}}{s}_{{}_{3B}}-s_{{}_{1W}}{S}_{{}_{2W}}{s}_{{}_{3W}}\right)\left({\ell }_{{}_B}(x+1)(\stackrel{{}_{\circ }}{e}{}_{{}_W}(x)-(\widehat{a}-x))+{\ell }_{{}_W}(x+1)(\stackrel{{}_{\circ }}{e}{}_{{}_B}(x)-(\widehat{a}-x))\right) \\ -\left({\ell }_{{}_B}(x+1)+{\ell }_{{}_W}(x+1)\right)\left(\left(s_{{}_{3B}}-s_{{}_{3W}}\right)\left(a_{{}_3}-a_{{}_2}\right)+\left(s_{{}_{2B}}{s}_{{}_{3B}}-s_{{}_{2W}}{s}_{{}_{3W}}\right)\left(a_{{}_2}-a_{{}_1}\right)+\left(s_{{}_{1B}}{s}_{{}_{2B}}{s}_{{}_{3B}}-s_{{}_{1W}}{s}_{{}_{2W}}{s}_{{}_{3W}}\right)(a_{{}_1}-\widehat{a})\right). \end{gathered}$$

Thus,

$$F(a_{{}_1})-F(a_{{}_2})=\left(s_{{}_{1B}}{s}_{{}_{2B}}{s}_{{}_{3B}}-s_{{}_{1W}}{s}_{{}_{2W}}{s}_{{}_{3W}}\right)\left({\ell }_{{}_B}(x+1)(\stackrel{{}_{\circ }}{e}{}_{{}_W}(x)-(\widehat{a}-x))+{\ell }_{{}_W}(x+1)(\stackrel{{}_{\circ }}{e}{}_{{}_B}(x)-(\widehat{a}-x))\right),$$

where $\widehat{a}$ is defined as $\widehat{a}=w_1{a}_1+w_2{a}_2+w_3{a}_3$, with weights:

$$\begin{gathered} w_{{}_1}=1-\frac{s_{{}_{2B}}{s}_{{}_{3B}}-s_{{}_{2W}}{s}_{{}_{3W}}}{s_{{}_{1B}}{s}_{{}_{2B}}{s}_{{}_{3B}}-s_{{}_{1W}}{s}_{{}_{2W}}{s}_{{}_{3W}}} \\ {w}_{{}_2}=\frac{s_{{}_{2B}}{s}_{{}_{3B}}-s_{{}_{2W}}{s}_{{}_{3W}}}{s_{{}_{1B}}{s}_{{}_{2B}}{s}_{{}_{3B}}-s_{{}_{1W}}{s}_{{}_{2W}}{s}_{{}_{3W}}}-\frac{s_{{}_{3B}}-s_{{}_{3W}}}{s_{{}_{1B}}{s}_{{}_{2B}}{s}_{{}_{3B}}-s_{{}_{1W}}{s}_{{}_{2W}}{s}_{{}_{3W}}} \\ {w}_{{}_3}=\frac{s_{{}_{3B}}-s_{{}_{3W}}}{s_{{}_{1B}}{s}_{{}_{2B}}{s}_{{}_{3B}}-s_{{}_{1W}}{s}_{{}_{2W}}{s}_{{}_{3W}}}. \end{gathered}$$

Because $w_1+w_2+w_3=1$, $\widehat{a}$ can be interpreted as a weighted average of ages at death. In addition, because $s_{1j}{s}_{2j}{s}_{3j}={\ell }_{{}_j}(x)∕{\ell }_{{}_j}(x+1)$. eqn. (30) is proven for the case of three deaths in the interval [$x$, $x+1$], as well as for the general case, because it does not depend on the number of deaths except through $\widehat{a}$.

The formula for $\widehat{a}$ in the general case is: $\widehat{a}={\sum }_k{w}_k{a}_k$, with weights:

$$w_{{}_k}=\frac{{\prod }_{k^{\prime }=k}^{K_x}{S}_{B{k}^{\prime }}-{\prod }_{k^{\prime }=k}^{K_x}{S}_{W{k}^{\prime }}}{{\prod }_{k^{\prime }=1}^{K_x}{S}_{B{k}^{\prime }}-{\prod }_{k^{\prime }=1}^{K_x}{S}_{W{k}^{\prime }}}-\frac{{\prod }_{k^{\prime }=k+1}^{K_x}{S}_{B{k}^{\prime }}-{\prod }_{k^{\prime }=k+1}^{K_x}{S}_{W{k}^{\prime }}}{{\prod }_{k^{\prime }=1}^{K_x}{S}_{B{k}^{\prime }}-{\prod }_{k^{\prime }=1}^{K_x}{S}_{W{k}^{\prime }}}.$$

This formula is valid for the first and last age at death (using the convention: ${\prod }_{k=K_x+1}^{K_x}(\cdot )=1$.

The above formulae are valid independently of assumptions on the form of the distribution of ages at death in the age interval. The expressions got $\widehat{a}={\widehat{a}}_{{}_x}$ can be derived for specific cases and under specific assumptions. Assume that the race-specific hazards are time-independent (i.e., constant) for the interval [$x$, $x+1$] and that the number of deaths for each race ($K_{{}_{xW}}$ and $K_{{}_{xB}}$, $K_{{}_x}=K_{{}_{xW}}+K_{{}_{xB}}$) is known. In this case $\widehat{a}$ has to be calculated through $K_{{}_x}$-dimensional integration. For example, if $K_{{}_{xW}}=1$ and $K_{{}_{xB}}=1$, we need to calculate two two-dimensional integrals ${\widehat{a}}_{{}_x}=I_1+I_2$, where:

$$\begin{gathered} I_{{}_1}={\int }_x^{x+1}d{x}_{{}_1}{\int }_x^{x+1}d{x}_{{}_2}{\rho }_{{}_B}(x_{{}_1}){\rho }_{{}_W}(x_{{}_2})\left(x_{{}_1}{w}_{{}_1}^{{}^{BW}}+x_{{}_2}{w}_{{}_2}^{{}^{BW}}\right)I(x_{{}_1}<x_{{}_2}) \\ {I}_{{}_2}={\int }_x^{x+1}d{x}_{{}_1}{\int }_x^{x+1}d{x}_{{}_2}{\rho }_{{}_W}(x_{{}_2}){\rho }_{{}_B}(x_{{}_2})\left(x_{{}_1}{w}_{{}_1}^{{}^{WB}}+x_{{}_2}{w}_{{}_2}^{{}^{WB}}\right)I(x_{{}_1}<x_{{}_2}). \end{gathered}$$

Here $\rho$ denotes the conditional density of age at death for the interval [$x$, $x+1$], i.e.,

$${\rho }_j(y)=\frac{{\mu }_j\text{exp}(-{\mu }_{j}y)}{\text{exp}(-{\mu }_{j}x)-\text{exp}(-{\mu }_j(x+1))}.$$

The weights in this case are:

$$w_{{}_1}^{{}^{BW}}=1-\frac{1-s_{{}_W}}{s_{{}_B}-s_{{}_W}},w_{{}_2}^{{}^{BW}}=\frac{1-s_{{}_W}}{s_{{}_B}-s_{{}_W}},w_{{}_1}^{{}^{WB}}=1-\frac{1-s_{{}_B}}{s_{{}_B}-s_{{}_W}},w_{{}_1}^{{}^{WB}}=\frac{1-s_{{}_B}}{s_{{}_B}-s_{{}_W}}$$

The integrals $I_{{}_1}$ and $I_{{}_2}$ are calculated analytically and can be presented in the form:

$${\widehat{a}}_{{}_x}=x+\frac{1}{2}-\frac{{\mu }_{{}_B}+{\mu }_{{}_W}}{12}+o({\mu }_{{}_B},{\mu }_{{}_W}).$$

The integration for more than two deaths results in:

$${\widehat{a}}_{{}_x}=x+\frac{1}{2}-\frac{K_{{}_{xB}}{\mu }_{{}_B}+K_{{}_{xW}}{\mu }_{{}_W}}{12}+o({\mu }_{{}_B},{\mu }_{{}_W}).$$

The formula for an arbitrary age interval [$a_1$, $a_2$] is:

$${\widehat{a}}_{{}_x}=\frac{a_{{}_1}+a_{{}_2}}{2}-(a_{{}_2}-a_{{}_1}{)}^2\frac{K_{{}_{xB}}{\mu }_{{}_B}+K_{{}_{xW}}{\mu }_{{}_W}}{12}+o({\mu }_{{}_B},{\mu }_{{}_W}).$$

In these illustrations, ${\widehat{a}}_{{}_x}$ is less than halfway between the start and end of the indicated age interval. This property follows from the assumption that the hazard rates are constant over the interval. An assumption of increasing hazard rates is reasonable for human mortality at age 65 and above. The most convenient assumption for such increasing hazard rates is that deaths are uniformly distributed over each interval, with the mean time to death among decedents exactly halfway between the start and end of the interval. The expression ${\widehat{a}}_{{}_x}=x+\frac{1}{2}$ is consistent with this assumption.

Data Availability:

The 5%-Medicare data used in this study cannot be shared publicly due to confidentiality reasons. Please contact the Centers for Medicare and Medicaid Services and/or ResDAC for information on how to obtain the data. The datasets containing the Multiple-Cause-of-Death data analyzed during the current study are available in the CDC Wide-ranging OnLine Data for Epidemiologic Research (WONDER) portal, https://https://wonder.cdc.gov/.