Modeling historic neighborhood deprivation and non-Hodgkin lymphoma risk

Abstract

Many studies have identified associations between neighborhood deprivation and disease, emphasizing the importance of social determinants of health. However, when studying diseases with long latency periods such as cancers, considering the timing of exposures for deprivation becomes more important. In this study, we estimated the associations between neighborhood deprivation indices at several time points and risk of non-Hodgkin lymphoma (NHL) in a population-based case-control study at four study centers – Detroit, Iowa, Los Angeles County, and Seattle (1998-2000). We used the Bayesian index regression model and residential histories to estimate neighborhood deprivation index effects in crude models and adjusted for four chemical mixtures measured in house dust and individual-level covariates. We found that neighborhood deprivation in 1980, approximately twenty years before study entry, provided better model fit than did neighborhood deprivation at 1990 and 2000. We identified several statistically significant associations between neighborhood deprivation in 1980 and NHL risk in Iowa and among long-term (20+ years) residents of Detroit. The most important variables in these indices were median gross rent as a percentage of household income in Iowa and percent of single-parent households with at least one child and median household income in Detroit. Associations remained statistically significant after adjustment for individual-level covariates and chemical mixtures, providing evidence for historic neighborhood deprivation as a risk factor for NHL and motivating future research to uncover the specific carcinogens driving these associations in deprived areas.

Introduction

The exposome is a comprehensive perspective in public health research and is the idea that individuals can derive risk of disease over their life course from a wide set of sources [1]. The exposome consists of three domains or factors, which are internal, specific external, and general external. Internal factors apply exclusively to the individual. Specific external factors also contain an individual component, such as lifestyle factors and environmental or occupational exposures, but also include variable circumstances that are outside of an individual’s immediate control. The general external domain is the broadest and includes socially constructed factors such as socio-economic status (SES) [2]. Analyses of health outcomes that adopt an exposome framework are more powerful than single-exposure analyses because they more accurately model the variety of factors that act on individuals at once [3].

An important component of the general external exposome domain is neighborhood deprivation. This theory holds that continued residence in neighborhoods that are socioeconomically deprived can drive compounding consequences for health over time due to cumulative processes of inequality [4]–[8]. Research on neighborhood effects requires a definition of the neighborhood. Administrative boundaries such as census tracts and block groups are commonly used to define neighborhoods, and particularly so in urban areas [9]. Other conceptualizations including distance from home, town segments, and local resident-mapped regions have also been applied in estimating neighborhood effects in rural areas, but these methods do not allow efficient linkage to data sources such as the U.S. Census Bureau [10]. Several statistical methods have been developed to estimate the effects of neighborhood deprivation on a variety of health outcomes. For example, a deprivation index constructed from a combination of z-scores for neighborhood education, unemployment, and income was shown to be associated with increased body mass index in Finnish children [11]. Additionally, a neighborhood concentrated disadvantage index constructed from principal components analysis (PCA) was associated with increased risk for colorectal cancer among adults in Louisiana [12]. A drawback of the former approach is that it implicitly treats each variable in the index as having equal importance with the outcome, and a drawback of the latter approach is that it constructs indices that are difficult to interpret. Both of these issues were resolved with weighted quantile sum (WQS) regression [13], which estimated the association of the index with an outcome and the importance weights for variables in the index. An application of WQS regression found a statistically significant association between neighborhood SES and colonoscopy screening adherence in Minnesota and Wisconsin [14]. Finally, the Bayesian group index model was built upon WQS regression, enabling estimation of multiple index effects varying in direction and magnitude and avoiding the two-step estimation process with data splitting inherent in WQS regression [15]. This model has been applied in a variety of contexts and has for example identified statistically significant associations between neighborhood deprivation and rates of elevated blood lead levels in ZIP codes across the United States [16], rates of tobacco retail outlet (TRO) sales violations in Virginia [17], cotinine levels in pregnant mothers [18], [19], and rates of TROs and alcohol retail outlets in North Carolina [20].

One potential issue with the construction of neighborhood deprivation indices is determining the optimal timeframe to record neighborhood characteristics. Often, these characteristics are recorded using data from near the time of the outcome. For certain outcomes, such as the rates of TROs in neighborhoods, this may not be an issue. However, for other outcomes such as cancers, there may be a temporal misalignment between the exposures that are measured in the study and those that are truly associated with the outcome. For example, studies have estimated long latencies for bladder cancer (20 to 40 years [21]), non-Hodgkin lymphoma [22], [23], breast cancer (15 and 20 years [24], [25]), and lung cancer (19 to 25 years [26]). Exposures experienced decades before diagnosis for these cancers would therefore be more etiologically relevant than those experienced closer to diagnosis. Few studies have leveraged historical exposure data to estimate its associations with health outcomes that develop cumulatively. One cohort study in Sweden found that cumulative neighborhood deprivation experienced between ages 16 and 43 was associated with statistically significantly greater allostatic load, an outcome that they defined as a sum of health markers including systolic and diastolic blood pressure, triglycerides, and cortisol area under the curve [27]. Findings such as these illustrate how accumulating residence in deprived areas can be associated with adverse health outcomes.

While many studies have demonstrated the connection between neighborhood deprivation and disease, far fewer have considered historic neighborhood deprivation. In this study, we estimate the associations of neighborhood deprivation indices at different time periods, including approximately at study entry and ten and twenty years before, with risk of non-Hodgkin lymphoma (NHL) using data from the National Cancer Institute’s Surveillance, Epidemiology, and End Results (NCI-SEER) case-control study. We estimate the effects of these indices on their own and after adjusting for individual-level covariates and mixtures of chemicals measured inside the home near the time of study entry, some of which have been shown to have statistically significant associations with NHL risk [28]. Our study attempts to uncover the connections between historic neighborhood deprivation and NHL and compare the magnitudes of these associations with those of several chemical mixtures.

Methods

Study Population.

The NCI-SEER study is a population-based case-control study of NHL at four centers in different areas of the United States (Wayne, Macomb, and Oakland Counties, comprising the Detroit study center; the state of Iowa; Los Angeles County; and Snohomish and King Counties, comprising the Seattle study center). The study population has been described in detail previously [29], [30] and included 1,321 cases of NHL aged 20 to 74 years diagnosed between July 1, 1998 and June 30, 2000, at one of the above SEER registries. Population-based controls (1,057) were chosen among the residents of each SEER registry using either random-digit dialing or Medicare eligibility files for controls younger and older than 65 years, respectively. Eligible cases and controls (without a history of NHL or HIV) were matched by age within 5-year groups, race, sex, and study center. Participation rates were 76% and 52% for cases and controls, respectively. The study population in our analysis included participants who were eligible for and participated in dust sampling (had at least half of their carpets/rugs for five years or more, about 57%), had complete chemical analysis results (described below), had good geocoded addresses (street level geocodes) and key covariate data. A summary of the characteristics of the study population is shown in Table 1 by study center.

Table 1.

Characteristics of the NCI-SEER NHL study population included in the analysis (N=1170) by study center.

	Detroit		Iowa		Los Angeles		Seattle
	All	LT	All	LT	All	LT	All	LT
Number of participants	201	99	335	198	292	109	342	81
Cases	127 (63)	64 (65)	188 (56)	106 (54)	168 (58)	63 (58)	182 (53)	47 (58)
Controls	74 (37)	35 (35)	147 (44)	92 (46)	124 (42)	46 (42)	160 (47)	34 (42)
Age (years)	58 (11.4)	56 (12.1)	61 (11.2)	61 (11.7)	59 (11.2)	57 (11.4)	59 (10.8)	56 (12.1)
Sex
Male	114 (57)	54 (55)	177 (53)	105 (53)	165 (57)	63 (58)	171 (50)	45 (56)
Female	87 (43)	45 (45)	158 (47)	93 (47)	127 (43)	46 (42)	171 (50)	36 (44)
Race
White	164 (81)	83 (84)	331 (99)	195 (98)	215 (74)	73 (67)	316 (92)	75 (93)
Non-white	37 (19)	16 (16)	4 (1)	3 (2)	77 (26)	36 (33)	26 (8)	6 (7)
Education
< 12 years	23 (11)	12 (12)	32 (10)	23 (12)	31 (11)	15 (14)	19 (6)	8 (10)
12-15 years	124 (62)	67 (68)	241 (72)	152 (77)	171 (59)	67 (61)	201 (59)	48 (59)
>= 16 years	54 (27)	20 (20)	62 (19)	23 (12)	90 (31)	27 (25)	122 (35)	25 (31)
Unique census tracts
2000	172		260		256		229
1990	168		255		243		218
1980	160		131		234		210
Population in census tracts
2000	3743 (2907, 4889)		3701 (2925, 4608)		5189 (3877, 6422)		4911 (3987, 6087)
1990	3672 (2991, 5030)		3624 (2979, 4613)		5579 (4138, 7075)		5594 (4086, 6947)
1980	4535 (3230, 5709)		4135 (3233, 5470)		4876 (3786, 6478)		5194 (3972, 6384)

Note: Age summarized using mean (standard deviation) and all other demographic variables summarized using count (percent). “LT” denotes long-term residents at a study center whose entire residential history was contained within the geographic bounds of the center. In the United States, < 12 years of education corresponds to less than a high school degree, 12-15 years corresponds to a high school degree and potentially some college, and >= 16 years corresponds to a college degree. Unique census tracts refers to the number of unique tracts among all participants and the population in census tracts is summarized with median (1^st quartile, 3^rd quartile). Some percentages may not sum exactly to one due to rounding.

Study participants completed a calendar detailing their lifetime residential history, which asked them to state the complete address of any of their residences, beginning from birth and including vacation or temporary homes in which they lived for a total of at least two years. Interviewers conducted in-person interviews in which they reviewed the residential history calendar with participants and attempted to resolve any discrepancies or complete missing data in the residential history. Residential addresses were geocoded via matching to street databases in a geographic information system to obtain geographic coordinates [31]. Interviewers recorded global positioning system (GPS) readings outside the interview home to obtain the geographic coordinates for the current residences. Further details on the geocoding process have been described previously [32].

Vacuum cleaner dust was sampled inside the homes of eligible consenting participants, a process which has been described elsewhere [33], [34]. The chemicals were measured using gas chromatography and mass spectrometry [33]. We used the following sets of chemicals: polychlorinated biphenyls (PCBs) (congeners 105, 138, 153, 170, 180); polycyclic aromatic hydrocarbons (PAHs) (benz(a)anthracene, benzo(a)pyrene, benzo(b)fluoranthene, benzo(k)fluoranthene, chrysene, dibenz(ah)anthracene, indeno(1,2,3-cd)pyrene); pesticides (group I) (α-chlordane, γ-chlordane, carbaryl, dichlorodiphenyldichloroethylene (DDE), dichlorodiphenyltrichloroethane (DDT), o-phenylphenol, pentachlorophenol, propoxur); and pesticides (group II) (chlorpyrifos, cis-permethrin, trans-permethrin, 2,4-D, diazinon, dicamba, methoxychlor). We grouped the chemicals in this way for the chemical mixture analysis owing to a previous analysis of chemicals and NHL risk based on univariate associations [35], [36]. The pesticides comprised two distinct groups according to their direction of univariate association with NHL. Some chemical measurements (ranging from 1%-81% depending on the chemical [34], [37]) contained missing values, which were generally due to the chemical concentration falling below the detection limit of its measuring instrument. We then assumed a log-normal distribution for the chemical concentrations and used multiple imputation to replace the missing values to fall in the range of 0 and the detection limit. We generated ten datasets with a fill-in approach, the details of which have been described previously [34], [38], [39], and chose one imputed dataset at random in our analysis.

Historic neighborhood deprivation.

We used data from the United States Census Bureau to estimate neighborhood deprivation indices. We obtained census-tract level estimates from the 2000, 1990, and 1980 Census in order to model deprivation at all these time points. Choosing 2000 for neighborhood deprivation data approximately corresponded to the date of study entry for participants, and 1980 approximated the maximum lag time considered in a spatial analysis of NHL risk using residential histories [23]. For each Census, we obtained a variety of census tract variables for potential inclusion in the neighborhood deprivation index (NDI): median household income, median house value, median year built for housing structures, percent of structures built in 1939 or earlier, median gross rent as a percentage of household income, percent renter, percent in poverty, percent receiving public assistance benefits, percent vacant structures, percent Black, percent Hispanic, percent of residents over 18 without a high school diploma, percent unemployed, percent of single-parent households with at least one child, percent of households having no vehicle, percent of households having no phone, percent of households without complete plumbing facilities, and percent of crowded occupied housing units. We chose this set of variables according to previous analyses of neighborhood deprivation [19], [40], [41] in addition to the component variables in the Area Deprivation Index, a measure that was created by the Health Resources and Services Administration and has been used to represent neighborhood deprivation as well [42]. For median household income, median house value, and median year built for housing structures, we inverted the variable using the formula max(x) – x_i so that all variables would be in the same direction with hypothesized deprivation and based on the observed Spearman correlations. Supplemental Material Figure S1 displays the correlation matrix between all candidate census tract variables for participant locations in 2000. There are frequently high correlations between variables of between 0.6 and 1.0 at each center, which challenges traditional regression methods and necessitates a different approach, as we describe below.

In order to achieve a more parsimonious set of variables in the neighborhood deprivation index, for each SEER study center we only included those variables having positive Spearman correlations with NHL status greater than a threshold (0.03) at that center for two of the three Census periods under consideration. Therefore, the tract-level covariates in the neighborhood deprivation index were allowed to vary for different study centers, allowing the observed correlations and the difference in demographic characteristics between study centers to provide a data-driven way to construct the neighborhood deprivation index at each center. We did this because certain tract-level covariates had no univariate association with NHL status at each center, and including them in the index often led to decreased goodness of fit indicated by the deviance information criterion (DIC), where decreases in DIC values of 5 or more indicate meaningfully better fitting models [43] (Supplemental Material Table S1).

Model Specification.

We used a Bayesian group index model [15] to model the probability that a study participant had NHL at each SEER study center, treating NHL status as a binary response variable Y taking values of 1 and 0 for cases and controls, respectively. Assuming that the response variable Y_i ~ Bernoulli(p_i), where p_i represents the probability of case membership, we specified the following three levels of models according to different forms or functions of the historic neighborhood deprivation and chemical exposure indices. To create the deprivation indices, we intersected a participant’s residential location with the spatial boundaries for census tract(s) at their residence(s) and defined the index using data from the census tract containing each participant’s residence. The models for each study center are written below.

Level 1: Neighborhood deprivation index only

$$log\left(\frac{p_i}{1-p_i}\right)={\beta }_0+\sum _{t=1}^T{\beta }_{1t}\sum _{k=1}^{J_1}{\omega }_{kt}{q}_{ikt}$$

Level 2: Neighborhood deprivation index and chemical exposure indices

$$log\left(\frac{p_i}{1-p_i}\right)={\beta }_0+\sum _{t=1}^T{\beta }_{1t}\sum _{k=1}^{J_1}{\omega }_{kt}{q}_{ikt}+{\beta }_2\sum _{k=1}^{J_2}{w}_{1k}{d}_{i1k}+{\beta }_3\sum _{k=1}^{J_3}{w}_{2k}{d}_{i2k}+{\beta }_4\sum _{k=1}^{J_4}{w}_{3k}{d}_{i3k}+{\beta }_5\sum _{k=1}^{J_5}{w}_{4k}{d}_{i4k}$$

Level 3: Neighborhood deprivation index and chemical exposure indices and individual-level covariates

$$log\left(\frac{p_i}{1-p_i}\right)={\beta }_0+\sum _{t=1}^T{\beta }_{1t}\sum _{k=1}^{J_1}{\omega }_{kt}{q}_{ikt}+{\beta }_2\sum _{k=1}^{J_2}{w}_{1k}{d}_{i1k}+{\beta }_3\sum _{k=1}^{J_3}{w}_{2k}{d}_{i2k}+{\beta }_4\sum _{k=1}^{J_4}{w}_{3k}{d}_{i3k}+{\beta }_5\sum _{k=1}^{J_5}{w}_{4k}{d}_{i4k}+\sum _{b=1}^B{\theta }_b{x}_{ib}$$

In these models, ${\beta }_0$ is an intercept term, and ${\beta }_{1t}$ is the estimated health effect for the t^th neighborhood deprivation index containing $J_1$ exposures, $t=1,\dots ,T$. We specify the number and timing of neighborhood deprivation indices below. Also, $\left[{\beta }_2,\dots ,{\beta }_5\right]$ are the estimated health effects associated with the exposure indices for PCBs, PAHs, Pesticides I, and Pesticides II groups of chemicals containing $\left[J_2,\dots ,J_5\right]$ components measured at one time inside the homes of participants. We adjusted for these owing to their associations with NHL risk in a previous analysis [28] and to permit interpretation of the historic neighborhood deprivation associations in the presence of chemicals measured inside the home. For these indices, the estimated importance weight vectors $\left[{\mathit{W}}_1,{\mathit{W}}_2,{\mathit{W}}_3,{\mathit{W}}_4\right]$ are defined such that the weights $W_{jk}\in \left(0,1\right)$ for all k in the $j^{th}$ index and ${\sum }_k{W}_{jk}=1$. The neighborhood deprivation index importance weights ${\omega }_t$ are defined similarly and represent the importance of variables in the index at the $t^{th}$ timepoint. Additionally, the term $q_{ikt}$ represents the $k^{th}$ quantized exposure in the neighborhood deprivation index at the $t^{th}$ time point for the $i^{th}$ individual, and the terms $d_{ijk}$ represent the $k^{th}$ quantized chemical exposure in the $j^{th}$ chemical index for the $i^{th}$ individual, $j=1,\dots ,4$. We used quantiles (e.g., 0,1,2,3,4) for the exposures to account for different scales of measurement and to limit the effect of outliers [44], [45]. Given this model specification, the coefficients ${\beta }_{1t},{\beta }_2,\dots ,{\beta }_5$ can be interpreted as the change in the log-odds of case membership associated with a one-unit change in the deprivation or chemical indices, which would occur when the quantiles of all components in the index increase by one. Therefore, the odds ratios, which exponentiate these coefficients, represent the association of a one-unit increase in the index with the odds of case membership. Finally, the coefficients for the adjustment covariates $\left[x_{i1},\dots ,x_{iB}\right]$ including race (Black or Other versus referent White), sex (male versus referent female), educational attainment (college degree or high school degree versus referent less than high school degree), and age [23], [28], [35] are given by $\left[{\theta }_1,\dots ,{\theta }_B\right]$. We specified the levels of models in this way to sequentially assess how, if at all, chemical mixtures and individual-level covariates modified the associations between the NDI and NHL risk.

For each of the three model levels (NDI only, NDI plus chemicals, NDI plus chemicals and covariates), we fit a series of seven models that varied in the time-period specification of the neighborhood deprivation index term. For models 1, 2, and 3, we estimated a participant’s neighborhood deprivation index using their residence in 2000, 1990, and 1980, respectively (T = 1). For models 4, 5, and 6, we estimated two neighborhood deprivation indices simultaneously (2000 and 1990, 2000 and 1980, 1990 and 1980, respectively, T = 2), and for model 7, we estimated deprivation indices in all three years simultaneously (T = 3).

Model Fitting.

For prior distributions, all regression parameters ${\beta }_i$ received a noninformative Normal prior with mean 0 and a uniform prior for the standard deviations. When applicable, the coefficients ${\theta }_i$ for the adjustment covariates also received a noninformative Normal prior with mean 0 and a uniform prior for the standard deviations. The importance weights in each index received a Dirichlet prior with parameter vector $\alpha =\left[{\alpha }_1,\dots ,{\alpha }_{J_a}\right]$, where $J_a$, a = 1,2,3,4, denotes the number of components in the index, in order that the importance weights were between 0 and 1 and ${\sum }_{j=1}^{J_a}{W}_{ij}=1$.

We fit models with Just Another Gibbs Sampler (JAGS [46]) in the software R [47], version 4.1.0, using Markov chain Monte Carlo (MCMC) methods. In the MCMC simulations, each model used two chains that each burned in 10,000 iterations and sampled 10,000 observations from the posterior distribution. We assessed convergence of model parameters using the Gelman-Rubin statistic [48], considering a parameter to have converged if its statistic was less than 1.1, using the coda R package [49]. We did not adjust for any multiple testing in our analyses.

Sensitivity analyses.

As a sensitivity analysis to better characterize the historic associations of neighborhood deprivation with risk of NHL diagnosed within the study centers, we restricted the sample at each SEER study center to only include long-term residents whose entire residential history was contained within the geographic bounds of the center (Table 1).

In an additional sensitivity analysis, we assessed the potential for selection bias in the neighborhood deprivation effect estimates arising from nonparticipation among eligible study participants. We used addresses at diagnosis for nonparticipating cases and address at the time of contact of nonparticipating controls. We assigned deprivation index component values using data from the 2000 Census. We fit the NDI Level 1 model (no covariates or chemicals) for each study center to the dataset that also included nonparticipants and compared index effect estimates to those from comparable models in the main analysis. We could not fit models using data from other census years (e.g., 1980, 1990) because residential histories for nonparticipants were unavailable. Additionally, we could not fit models in Level 2 or Level 3 for this sensitivity analysis because there were no chemical dust data for nonparticipants. Finally, we performed another sensitivity analysis that combined participant data from all study centers and used a common set of census tract variables in the NDI in order to assess if our primary findings held when placing additional restrictions on the analysis.

Results

The neighborhood deprivation index (Level 1) models demonstrated consistent positive associations between neighborhood deprivation and NHL in some study centers (Table 2). In Iowa, the neighborhood deprivation index in 1980 was statistically significantly associated with risk for NHL on its own (OR = 1.43, model 3), when including either deprivation in 2000 (OR = 1.41, model 5) or in 1990 (OR = 1.42, model 6), and when including deprivation for both 2000 and 1990 (OR = 1.49, model 7). In these four models for Iowa, median gross rent as a percentage of household income received the majority of the importance weight in the 1980 index, ranging from 0.82 to 0.84 depending on the model. Additionally, of the 12 neighborhood deprivation indices estimated across the seven models and three time periods, there were positive (though not significant) associations with NHL in Detroit for all 12 indices, Los Angeles for 7, and Seattle for 10 of the indices. Across all study centers, modeling historic neighborhood deprivation (1980 and/or 1990) provided a better model fit than did neighborhood deprivation close to diagnosis (2000). At each center, the best-fitting models measured by the DIC included deprivation indices at 1980 in combination with deprivation in 1990 for Detroit and Iowa and with deprivation in 1990 and 2000 for Los Angeles and Seattle, and model goodness of fit improved for the models estimating one deprivation index in 1980 (model 3) compared to one in 2000 (model 1). Certain variables in the NDI received large estimated importance weights, such as median rent as a percentage of household income in Iowa and percent of single parent households with children and percent Hispanic in Detroit. Additionally, cases consistently had higher estimated NDI values than controls across all years and study centers (Supplemental Material Table S2).

Table 2.

Associations with NHL for neighborhood deprivation indices from models with no covariates (Level 1 models).

Center	Model	Neighborhood Deprivation Index			DIC
		2000	1990	1980
Detroit	1	1.22 (0.89, 1.73)	-	-	262.8
	2	-	1.14 (0.82, 1.54)	-	253.9
	3	-	-	1.23 (0.96, 1.64)	243.4
	4	1.17 (0.79, 2.01)	1.04 (0.62, 1.55)	-	252.9
	5	1.02 (0.67, 1.51)	-	1.27 (0.94, 1.97)	242.3
	6	-	1.01 (0.64, 1.47)	1.25 (0.93, 1.95)	242.2
	7	1.02 (0.71, 1.42)	1.23 (0.91, 1.81)	1.22 (0.94, 1.72)	244.4
Iowa	1	1.16 (0.94, 1.45)	-	-	453.7
	2	-	1.13 (0.95, 1.44)	-	444.9
	3	-	-	1.43 (1.17, 1.85)	414.5
	4	1.05 (0.81, 1.36)	1.11 (0.89, 1.50)	-	444.4
	5	1.07 (0.85, 1.38)	-	1.41 (1.12, 1.82)	414.2
	6	-	1.06 (0.87, 1.36)	1.42 (1.15, 1.85)	409.2
	7	0.75 (0.55, 0.97)	1.11 (0.88, 1.41)	1.49 (1.22, 1.92)	412.3
Los Angeles	1	1.01 (0.84, 1.19)	-	-	385.9
	2	-	1.02 (0.85, 1.21)	-	379.7
	3	-	-	0.96 (0.78, 1.17)	353.4
	4	0.96 (0.70, 1.25)	1.06 (0.80, 1.47)	-	372.4
	5	1.04 (0.84, 1.32)	-	0.96 (0.76, 1.17)	345.5
	6	-	1.07 (0.85, 1.40)	0.89 (0.68, 1.14)	346.9
	7	1.01 (0.73, 1.37)	1.09 (0.81, 1.54)	0.91 (0.69, 1.15)	340.3
Seattle	1	1.05 (0.92, 1.22)	-	-	467.2
	2	-	1.06 (0.91, 1.25)	-	440.9
	3	-	-	1.13 (0.97, 1.34)	414.3
	4	0.98 (0.78, 1.20)	1.08 (0.87, 1.38)	-	440.8
	5	1.03 (0.87, 1.23)	-	1.13 (0.96, 1.38)	409.5
	6	-	1.00 (0.82, 1.21)	1.10 (0.92, 1.36)	397.6
	7	1.03 (0.84, 1.27)	0.98 (0.78, 1.23)	1.10 (0.91, 1.36)	397.6

Note: Quantities in the table represent posterior mean and 95% credible interval for the deprivation index odds ratio. Statistically significant associations are presented in bold text. DIC stands for deviance information criterion, where lower values indicate better-fitting models. Models (1, 2, 3, 4, 5, 6, 7) estimated neighborhood deprivation indices in (2000, 1990, 1980, 2000 and 1990, 2000 and 1980, 1990 and 1980, 2000 and 1990 and 1980), respectively.

Many of the elevated associations for neighborhood deprivation persisted in the Level 2 models when adjusting for the four groups of chemicals measured inside the home (Supplemental Material Table S3). In particular, the four statistically significant associations for neighborhood deprivation in 1980 in Iowa not only persisted but became slightly more elevated in magnitude when adjusting for such chemical exposures (OR = 1.47, 1.45, 1.46, 1.53 in models 3, 5, 6, 7). In these four models, median gross rent as a percentage of household income continued to receive the largest weight in the index (0.86 to 0.89 depending on the model). At this level of analysis, historic neighborhood deprivation continued to lead to better model fit than did neighborhood deprivation in 2000. The model that estimated neighborhood deprivation indices in 1980 and 1990 (model 6) was the best or second-best-fitting model at each center according to the DIC values. Additionally, exposure to the first index of pesticides was associated with statistically significantly elevated risk for NHL in Iowa in four models (OR = 1.53, 1.51, 1.52, 1.61 in models 1, 2, 3, 7). Exposure to the second index of pesticides in Iowa had a statistically significant inverse association with NHL in all models, with odds ratios ranging from 0.59 to 0.63.

When adjusting for the individual-level covariates in Level 3, each statistically significant association for historic neighborhood deprivation in Iowa remained (Table 3). The magnitudes of these associations remained relatively unchanged. Additionally, the most important variable in the deprivation index in 1980 continued to be median gross rent as a percentage of household income, receiving importance weights between 0.84 and 0.90 depending on the model. At the other centers, the distribution of importance weight was more uniform between the variables in the deprivation index (Figure 2). In order to further investigate the role of neighborhood deprivation for NHL in Iowa, we mapped the estimated deprivation index for residential locations at each Census period in Iowa (Figure 3), finding that the values of the deprivation index varied across the state and particularly in 1980. For this Census period, participants living in the east-central portion of Iowa near Iowa City generally experienced a lower degree of deprivation, and those living in the southern and southeastern portion of the state generally experienced a higher value of the neighborhood deprivation index. In the Des Moines metropolitan area, considerable variation in neighborhood deprivation existed in different areas of the city, and several participants in the extreme eastern part of the state bordering the Mississippi River experienced high degrees of deprivation. In contrast, the estimated neighborhood deprivation indices in 1990 and in 2000 exhibited less apparent spatial variation. For these more recent Census periods, the degrees of lesser and greater deprivation in the east-central and southern portions of the state respectively were attenuated, and participants near the eastern border of the state experienced high degrees of deprivation to a lesser extent.

Table 3.

Summary of estimated neighborhood deprivation and chemical group index associations, adjusted for individual-level covariates (Level 3 models).

Center	Model	Neighborhood Deprivation			Chemical Group Indices				DIC
		2000	1990	1980	PCBs	PAHs	Pesticides I	Pesticides II
Detroit	1	1.24 (0.84, 2.02)	-	-	1.23 (0.82, 1.83)	0.96 (0.71, 1.28)	0.83 (0.49, 1.27)	1.12 (0.79, 1.78)	257.7
	2	-	1.14 (0.79, 1.69)	-	1.28 (0.87, 1.91)	0.94 (0.69, 1.27)	0.81 (0.46, 1.25)	1.17 (0.77, 1.98)	249.7
	3	-	-	1.33 (0.94, 2.09)	1.17 (0.82, 1.73)	0.93 (0.66, 1.25)	0.86 (0.52, 1.29)	1.15 (0.79, 1.90)	239.1
	4	1.24 (0.79, 2.27)	1.07 (0.65, 1.69)	-	1.20 (0.81, 1.81)	0.95 (0.70, 1.27)	0.83 (0.48, 1.29)	1.20 (0.80, 2.07)	249.9
	5	1.15 (0.70, 1.90)	-	1.36 (0.94, 2.21)	1.15 (0.79, 1.73)	0.94 (0.68, 1.27)	0.87 (0.52, 1.34)	1.19 (0.81, 2.04)	239.0
	6	-	1.08 (0.67, 1.65)	1.34 (0.93, 2.21)	1.16 (0.81, 1.71)	0.92 (0.66, 1.25)	0.89 (0.54, 1.35)	1.17 (0.79, 1.95)	239.7
	7	1.01 (0.70, 1.48)	1.30 (0.93, 1.99)	1.23 (0.92, 1.81)	1.10 (0.78, 1.62)	0.88 (0.63, 1.17)	0.77 (0.44, 1.20)	1.13 (0.77, 1.85)	250.9
Iowa	1	1.07 (0.85, 1.38)	-	-	1.02 (0.81, 1.29)	0.92 (0.72, 1.12)	1.66 (1.09, 1.16)	0.60 (0.39, 0.83)	449.4
	2	-	1.08 (0.88, 1.39)	-	1.02 (0.80, 1.30)	0.91 (0.71, 1.12)	1.66 (1.09, 2.68)	0.63 (0.41, 0.90)	441.2
	3	-	-	1.48 (1.20, 1.89)	1.04 (0.80, 1.36)	0.94 (0.74, 1.17)	1.59 (1.03, 2.63)	0.61 (0.39, 0.90)	411.7
	4	1.02 (0.79, 1.34)	1.07 (0.85, 1.44)	-	1.02 (0.80, 1.31)	0.91 (0.72, 1.13)	1.59 (1.04, 2.56)	0.63 (0.41, 0.92)	441.5
	5	1.03 (0.82, 1.34)	-	1.46 (1.17, 1.89)	1.04 (0.81, 1.39)	0.94 (0.73, 1.17)	1.57 (1.01, 2.59)	0.62 (0.40, 0.92)	412.4
	6	-	1.04 (0.83, 1.32)	1.47 (1.19, 1.94)	1.03 (0.79, 1.38)	0.92 (0.72, 1.15)	1.58 (1.03, 2.57)	0.64 (0.41, 0.98)	407.8
	7	0.76 (0.55, 1.01)	1.15 (0.88, 1.50)	1.54 (1.26, 1.97)	1.04 (0.80, 1.39)	0.94 (0.73, 1.17)	1.70 (1.08, 2.82)	0.55 (0.33, 0.84)	408.2
Los Angeles	1	1.00 (0.82, 1.21)	-	-	1.22 (0.92, 1.70)	1.25 (0.94, 1.67)	0.95 (0.66, 1.38)	0.72 (0.44, 1.10)	388.9
	2	-	1.02 (0.84, 1.27)	-	1.18 (0.89, 1.63)	1.17 (0.90, 1.57)	0.89 (0.60, 1.28)	0.79 (0.50, 1.18)	384.0
	3	-	-	0.95 (0.76, 1.17)	1.18 (0.91, 1.63)	1.18 (0.90, 1.60)	0.86 (0.58, 1.22)	0.82 (0.52, 1.21)	355.5
	4	0.95 (0.66, 1.27)	1.06 (0.78, 1.55)	-	1.22 (0.91, 1.73)	1.18 (0.90, 1.59)	0.89 (0.60, 1.27)	0.79 (0.50, 1.22)	377.2
	5	1.03 (0.82, 1.34)	-	0.95 (0.73, 1.17)	1.25 (0.93, 1.79)	1.15 (0.89, 1.56)	0.88 (0.58, 1.25)	0.80 (0.48, 1.24)	347.5
	6	-	1.06 (0.83, 1.44)	0.89 (0.67, 1.15)	1.17 (0.89, 1.61)	1.13 (0.87, 1.52)	0.85 (0.56, 1.26)	0.84 (0.54, 1.23)	350.0
	7	0.97 (0.75, 1.25)	0.99 (0.81, 1.19)	0.93 (0.75, 1.15)	1.22 (0.93, 1.71)	1.25 (0.95, 1.72)	0.86 (0.57, 1.26)	0.78 (0.48, 1.19)	358.8
Seattle	1	1.02 (0.88, 1.20)	-	-	1.08 (0.85, 1.28)	1.04 (0.85, 1.28)	1.08 (0.79, 1.52)	0.80 (0.52, 1.15)	473.5
	2	-	1.04 (0.88, 1.25)	-	1.07 (0.83, 1.42)	1.07 (0.88, 1.34)	1.11 (0.80, 1.65)	0.75 (0.47, 1.09)	447.8
	3	-	-	1.11 (0.93, 1.34)	1.08 (0.85, 1.41)	1.03 (0.83, 1.29)	1.06 (0.78, 1.51)	0.75 (0.47, 1.08)	417.9
	4	0.97 (0.75, 1.20)	1.07 (0.84, 1.41)	-	1.07 (0.84, 1.41)	1.07 (0.87, 1.34)	1.09 (0.79, 1.58)	0.77 (0.48, 1.11)	447.9
	5	1.03 (0.86, 1.25)	-	1.12 (0.93, 1.38)	1.07 (0.83, 1.40)	1.05 (0.84, 1.32)	1.07 (0.79, 1.53)	0.75 (0.48, 1.10)	413.6
	6	-	0.99 (0.81, 1.22)	1.08 (0.89, 1.35)	1.07 (0.84, 1.41)	1.08 (0.87, 1.37)	1.08 (0.80, 1.54)	0.76 (0.49, 1.12)	401.6
	7	1.05 (0.87, 1.27)	0.81 (0.67, 0.99)	1.18 (0.98, 1.45)	1.09 (0.85, 1.45)	1.03 (0.84, 1.30)	1.04 (0.75, 1.47)	0.83 (0.54, 1.17)	424.5

Note: Quantities in the table represent posterior mean and 95% credible interval for the deprivation index odds ratio. Statistically significant associations are presented in bold text. DIC stands for deviance information criterion, where lower values indicate better-fitting models. Models (1, 2, 3, 4, 5, 6, 7) estimated neighborhood deprivation indices in (2000, 1990, 1980, 2000 and 1990, 2000 and 1980, 1990 and 1980, 2000 and 1990 and 1980), respectively.

Figure 2.

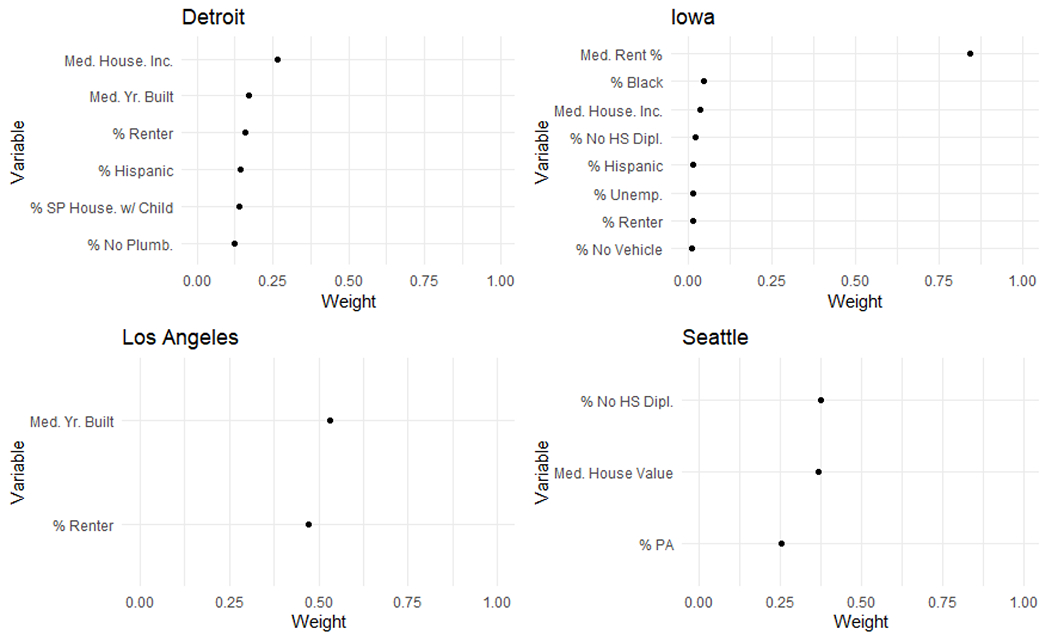
Estimated importance weights in the 1980 deprivation index in the best-fitting models at each study center for Level 3. %PA represents the percent of households in a census tract receiving public assistance income.

Figure 3.

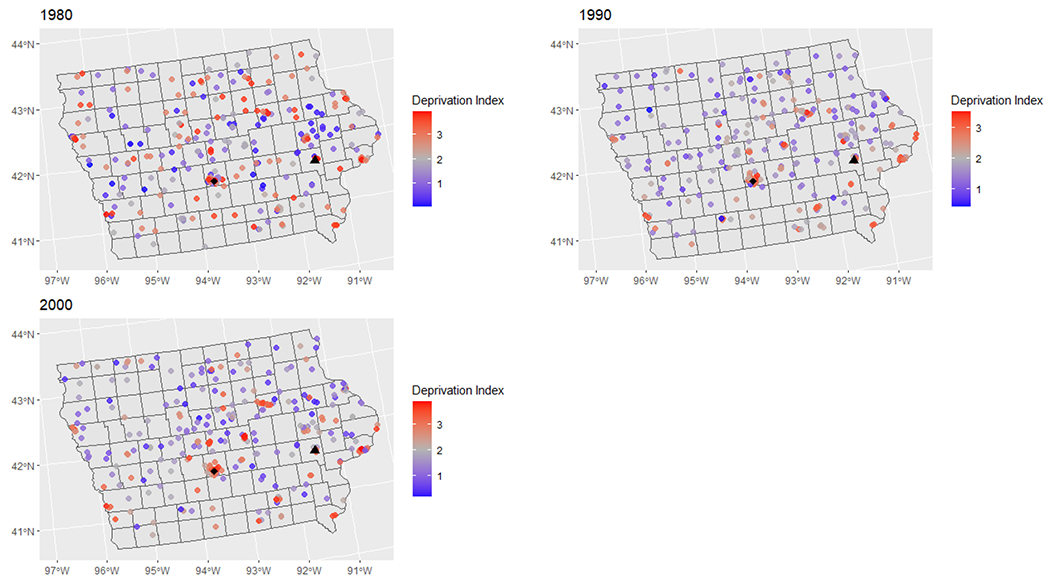
Map of the estimated neighborhood deprivation index in 1980, 1990, and 2000 in Iowa for jittered participant locations at the time of each census.

Note: Red areas represent higher areas of deprivation. Participant locations have been randomly jittered for privacy. The black triangle represents Iowa City and the black diamond represents Des Moines. The Mississippi River forms the eastern border of the state.

Regarding chemical exposure groups, for each model fit in Level 3 in Iowa, there was a positive and statistically significant association for the first chemical index of pesticides, with odds ratios ranging from 1.57 to 1.70, and a negative and statistically significant association for the second index of pesticides, with odds ratios ranging from 0.55 to 0.64. At the other study centers, the best-fitting models from Level 2 were also the best-fitting models in Level 3, demonstrating the stability of the neighborhood deprivation and chemical exposure associations after adjusting for individual-level covariates. Additionally, in the Level 3 models, relative to non-Hispanic Whites, Black race was associated with significantly lower odds of NHL (OR = 0.18, 95% CI (0.05, 0.68)), and in Los Angeles, Other race was associated with significantly greater odds of NHL (OR = 2.84, 95% CI (1.02, 8.59)). However, we note that these estimates are based on relatively few individuals having these characteristics and may not indicate true differences in the likelihood of developing NHL. None of the other covariates were significantly associated with NHL at any center.

For the sensitivity analysis using only long-term residents of each study center, we found that the estimated associations were similar to those described for all residents. In the Level 1 models, there were elevated neighborhood deprivation associations from 1980 in Iowa in models 3, 5, 6, and 7, and statistically significantly elevated associations in models 3 and 7 (Table 4). Additionally, neighborhood deprivation in 1980 was statistically significantly associated with risk for NHL in Detroit in model 3 with OR = 1.62 and 95% CI (1.05, 2.77). There was also a large and nearly statistically significant effect in Detroit with OR = 3.58 and 95% CI (0.95, 17.06). The magnitudes and directions of these associations were largely unchanged when adjusting for exposure to groups of chemicals (Level 2, Table S4) and for individual-level covariates (Level 3, Table 5), and the neighborhood deprivation index in 1980 in Detroit was statistically significantly associated with NHL in every model, with percent single-parent households with at least one child and median household income receiving large importance weights. In the Level 3 models, there were several statistically significant associations for the PAHs chemical index among long-term residents in Seattle, with odds ratios ranging from 1.80 to 2.23. In the best-fitting model at that study center (model 3), benzo(a)pyrene (0.34) and benzo(a)anthracene (0.17), as well as chrysene (0.18), received the majority of the importance weight in the index.

Table 4.

Summary of estimated neighborhood deprivation from Level 1 models fit to data from long-term residents.

Center	Model	Neighborhood Deprivation			DIC
		2000	1990	1980
Detroit	1	1.39 (0.94, 2.37)	-	-	126.9
	2	-	1.30 (0.89, 2.08)	-	123.2
	3	-	-	1.62 (1.05, 2.77)	116.5
	4	1.27 (0.80, 2.33)	1.16 (0.71, 2.00)	-	121.8
	5	1.27 (0.65, 2.37)	-	1.69 (0.99, 3.25)	114.0
	6	-	1.07 (0.62, 1.84)	1.68 (1.01, 3.17)	116.1
	7	1.60 (0.96, 2.98)	0.55 (0.24, 1.06)	1.94 (1.06, 4.02)	113.1
Iowa	1	1.22 (0.96, 1.70)	-	-	270.7
	2	-	1.27 (0.97, 1.89)	-	260.7
	3	-	-	1.47 (1.03, 2.23)	250.4
	4	1.05 (0.71, 1.53)	1.27 (0.90, 2.09)	-	261.6
	5	1.13 (0.86, 1.57)	-	1.42 (0.97, 2.15)	250.4
	6	-	1.22 (0.90, 1.77)	1.39 (0.96, 1.97)	245.4
	7	1.05 (0.80, 1.45)	1.20 (0.89, 1.68)	1.49 (1.03, 2.23)	251.0
Los Angeles	1	1.02 (0.76, 1.36)	-	-	143.2
	2	-	0.99 (0.68, 1.38)	-	136.7
	3	-	-	0.95 (0.69, 1.25)	124.7
	4	0.95 (0.58, 1.47)	1.05 (0.63, 1.79)	-	134.1
	5	1.08 (0.69, 1.72)	-	0.91 (0.59, 1.32)	121.9
	6	-	1.12 (0.68, 1.98)	0.85 (0.49, 1.30)	122.7
	7	1.20 (0.70, 2.25)	0.95 (0.51, 1.79)	0.85 (0.49, 1.35)	119.6
Seattle	1	1.02 (0.74, 1.38)	-	-	111.7
	2	-	1.05 (0.77, 1.42)	-	106.0
	3	-	-	1.12 (0.83, 1.55)	102.1
	4	1.08 (0.71, 1.68)	0.98 (0.64, 1.46)	-	105.5
	5	0.98 (0.67, 1.42)	-	1.13 (0.82, 1.64)	101.6
	6	-	0.93 (0.59, 1.37)	1.17 (0.80, 1.88)	103.4
	7	1.07 (0.69, 1.75)	0.84 (0.46, 1.40)	1.22 (0.82, 2.03)	102.8

Note: Quantities in the table represent posterior mean and 95% credible interval for the deprivation index odds ratio. Significant associations are presented in bold text. DIC stands for deviance information criterion, where lower values indicate better-fitting models. Models (1, 2, 3, 4, 5, 6, 7) estimated neighborhood deprivation indices in (2000, 1990, 1980, 2000 and 1990, 2000 and 1980, 1990 and 1980, 2000 and 1990 and 1980), respectively.

Table 5.

Summary of estimated neighborhood deprivation indices and chemical group index associations from models adjusted for individual-level covariates (Level 3 models) and fit to data from long-term residents.

Center	Model	Neighborhood Deprivation Index			Chemical Group Indices				DIC
		2000	1990	1980	PCBs	PAHs	Pesticides I	Pesticides II
Detroit	1	1.62 (0.88, 3.33)	-	-	1.38 (0.79, 2.82)	1.09 (0.69, 1.80)	0.94 (0.38, 2.28)	0.94 (0.44, 1.88)	126.5
	2	-	1.30 (0.80, 2.52)	-	1.57 (0.84, 3.51)	1.12 (0.70, 1.93)	0.81 (0.31, 1.93)	0.98 (0.43, 2.30)	122.4
	3	-	-	1.95 (1.02, 4.17)	1.67 (0.92, 3.61)	1.18 (0.71, 2.18)	0.86 (0.35, 1.87)	0.99 (0.49, 2.07)	116.2
	4	1.50 (0.74, 3.84)	1.20 (0.58, 2.34)	-	1.47 (0.78, 3.41)	1.13 (0.69, 2.03)	0.82 (0.28, 2.14)	1.01 (0.43, 2.43)	121.2
	5	1.52 (0.65, 3.26)	-	2.02 (1.01, 4.58)	1.52 (0.80, 3.45)	1.20 (0.73, 2.22)	0.89 (0.34, 2.17)	1.06 (0.53, 2.28)	114.3
	6	-	1.10 (0.60, 2.02)	2.08 (1.01, 4.86)	1.82 (0.95, 4.26)	1.20 (0.72, 2.34)	0.76 (0.30, 1.77)	0.98 (0.47, 2.10)	117.3
	7	1.74 (0.87, 4.51)	0.40 (0.14, 0.96)	2.23 (1.07, 5.43)	1.71 (0.92, 3.74)	1.03 (0.60, 1.79)	0.99 (0.43, 2.35)	1.04 (0.44, 2.53)	117.3
Iowa	1	1.26 (0.93, 1.79)	-	-	1.06 (0.79, 1.45)	0.93 (0.69, 1.21)	1.27 (0.83, 2.19)	0.55 (0.33, 0.85)	271.3
	2	-	1.29 (0.94, 1.95)	-	1.05 (0.79, 1.43)	0.92 (0.67, 1.20)	1.22 (0.79, 2.07)	0.61 (0.37, 1.01)	263.7
	3	-	-	1.54 (1.08, 2.30)	1.10 (0.82, 1.52)	0.91 (0.67, 1.21)	1.23 (0.79, 2.14)	0.62 (0.37, 1.03)	254.6
	4	1.09 (0.71, 1.67)	1.25 (0.86, 2.15)	-	1.06 (0.79, 1.44)	0.92 (0.67, 1.21)	1.22 (0.80, 2.06)	0.60 (0.36, 0.99)	264.9
	5	1.15 (0.85, 1.62)	-	1.48 (1.00, 2.23)	1.11 (0.84, 1.55)	0.91 (0.67, 1.20)	1.19 (0.77, 2.02)	0.64 (0.37, 1.06)	256.1
	6	-	1.21 (0.88, 1.79)	1.48 (1.01, 2.15)	1.10 (0.82, 1.56)	0.90 (0.65, 1.19)	1.22 (0.79, 2.07)	0.67 (0.38, 1.12)	250.0
	7	1.03 (0.77, 1.41)	1.23 (0.88, 1.74)	1.45 (0.98, 2.16)	1.13 (0.49, 2.79)	0.80 (0.31, 1.77)	1.35 (0.36, 5.76)	0.26 (0.06, 1.12)	252.2
Los Angeles	1	0.99 (0.69, 1.41)	-	-	1.33 (0.90, 2.11)	1.20 (0.76, 2.01)	0.87 (0.45, 1.57)	0.89 (0.46, 1.59)	151.8
	2	-	0.97 (0.63, 1.58)	-	1.29 (0.86, 2.04)	1.07 (0.69, 1.77)	0.78 (0.40, 1.43)	1.08 (0.57, 2.02)	145.6
	3	-	-	0.93 (0.63, 1.33)	1.31 (0.85, 2.23)	0.96 (0.59, 1.60)	0.76 (0.36, 1.47)	1.14 (0.61, 2.32)	127.8
	4	0.85 (0.45, 1.43)	1.14 (0.63, 2.30)	-	1.29 (0.87, 2.08)	1.10 (0.69, 1.81)	0.75 (0.38, 1.41)	1.11 (0.55, 2.21)	142.6
	5	1.12 (0.63, 2.02)	-	0.89 (0.53, 1.41)	1.32 (0.85, 2.24)	0.94 (0.55, 1.58)	0.76 (0.36, 1.53)	1.15 (0.59, 2.38)	125.3
	6	-	1.43 (0.75, 3.10)	0.73 (0.35, 1.25)	1.24 (0.79, 2.10)	0.92 (0.53, 1.53)	0.64 (0.30, 1.44)	1.24 (0.62, 2.79)	124.9
	7	1.35 (0.91, 2.23)	0.97 (0.63, 1.50)	0.90 (0.59, 1.27)	1.29 (0.84, 2.17)	0.92 (0.53, 1.57)	0.70 (0.33, 1.35)	0.96 (0.47, 1.78)	130.8
Seattle	1	0.93 (0.63, 1.34)	-	-	1.02 (0.61, 1.73)	1.64 (0.99, 2.87)	1.01 (0.48, 2.11)	0.99 (0.47, 2.05)	118.1
	2	-	0.99 (0.67, 1.45)	-	0.88 (0.49, 1.48)	1.92 (1.07, 3.47)	0.86 (0.36, 1.90)	0.90 (0.39, 2.06)	111.4
	3	-	-	1.03 (0.67, 1.60)	0.85 (0.46, 1.45)	1.96 (1.07, 3.64)	0.88 (0.35, 1.89)	0.74 (0.30, 2.03)	106.1
	4	0.96 (0.56, 1.61)	0.97 (0.59, 1.59)	-	0.86 (0.48, 1.49)	1.80 (1.01, 3.33)	0.81 (0.32, 1.79)	0.94 (0.40, 2.26)	112.2
	5	0.90 (0.56, 1.39)	-	1.08 (0.70, 1.75)	0.84 (0.45, 1.43)	1.90 (1.04, 3.57)	0.83 (0.34, 1.82)	0.88 (0.35, 2.31)	107.6
	6	-	0.90 (0.52, 1.48)	1.11 (0.64, 2.04)	0.85 (0.46, 1.45)	1.99 (1.07, 3.85)	0.87 (0.35, 1.92)	0.74 (0.29, 2.10)	107.6
	7	0.94 (0.60, 1.40)	1.01 (0.67, 1.57)	1.05 (0.65, 1.70)	0.85 (0.45, 1.49)	2.23 (1.13, 4.48)	0.95 (0.39, 2.23)	0.91 (0.34, 2.48)	106.2

Note: Quantities in the table represent posterior mean and 95% credible interval for the deprivation index odds ratio. Statistically significant associations are presented in bold text. DIC stands for deviance information criterion, where lower values indicate better-fitting models. Models (1, 2, 3, 4, 5, 6, 7) estimated neighborhood deprivation indices in (2000, 1990, 1980, 2000 and 1990, 2000 and 1980, 1990 and 1980, 2000 and 1990 and 1980), respectively.

The sensitivity analysis of nonparticipation among eligible subjects revealed that nonparticipation likely did not bias the deprivation index effect estimates overall (Supplemental Material Table S5). In Los Angeles and Seattle, the mean odds ratio estimates were within 0.02 of their estimates from the main analysis. In Iowa, the mean odds ratio decreased from 1.16 to 1.02. In Detroit, it decreased from 1.22 to 0.90; however, this study center had the largest number of nonparticipants. While the width of the credible interval shrunk at each study center due to the addition of extra participants, none of the deprivation index effect estimates were statistically significant in this sensitivity analysis when including nonparticipants. Finally, the sensitivity analysis that combined data across study centers and used a standardized set of variables in the NDI lent additional evidence to support our findings (Supplemental Material Table S6). Modeling neighborhood deprivation in 1980 provided the best fit in the one-index models, and modeling NDIs at all three time points provided the best fit overall. Even though the NDI associations were attenuated in this sensitivity analysis, the odds ratio for the 1980 NDI was elevated in all models in which it was included.

Discussion and Conclusion

We estimated associations of neighborhood deprivation indices with NHL risk at a variety of time points, in crude models and after adjusting for individual-level covariates and mixtures of chemicals measured inside the home. In general, we found that modeling historic neighborhood deprivation provided better model fit than did modeling neighborhood deprivation at the time of study entry (2000). Notably, we identified several statistically significant and positive associations between neighborhood deprivation in 1980, approximately 20 years before diagnosis, for NHL in Iowa, where median gross rent as a percentage of household income was the most important variable in the index. Additionally, we found several statistically significant associations between 1980 neighborhood deprivation and NHL among long-term residents in Detroit that increased in magnitude when adjusting for individual-level covariates and exposures to several chemical mixtures. In these indices, percent of single-parent households with at least one child and median household income were often the most important variables in the index. These results demonstrate clear associations between historic neighborhood deprivation and risk for NHL that are not accounted for by specific chemical levels in the homes.

Our results add to the literature surrounding neighborhood deprivation and NHL as ours is the first study to link historic neighborhood deprivation exposures at an etiologically relevant time period with NHL status decades later. Several studies have identified associations between contemporary deprivation and survival among individuals with NHL. A study of NHL cases in Taiwan found a statistically significantly lower hazard for patients living in advantaged neighborhoods compared to those in disadvantaged neighborhoods [50], and a similar study in Denmark found that all-cause mortality was statistically significantly higher in NHL patients with lower educational attainment [51]. While these studies have shown how neighborhood deprivation can influence survival from NHL, our findings illustrate how it may be associated with increased likelihood of NHL incidence. These results can inform cancer prevention and control efforts by focusing identification of carcinogens for NHL in deprived neighborhoods and encouraging screening for NHL among individuals who resided in such neighborhoods.

In our study we used novel analytic methods to connect NHL status with historic neighborhood deprivation using census data from decades prior to diagnosis. This process used geocoded residential histories for NCI-SEER study participants to construct spatially- and temporally-relevant neighborhood deprivation indices. Another analytic strength of our study is its use of the Bayesian index regression model to estimate neighborhood deprivation indices and chemical mixtures. This model has demonstrated better goodness of fit to data than other methods such as factor analysis and principal component analysis [52], [53], which construct indices independently of their association with an outcome variable and are more difficult to interpret. In contrast, the Bayesian index model estimates the importance weights of all variables in the index in a data-driven and interpretable manner. For example, the most important variable in the 1980 deprivation index in Iowa was median rent as a percentage of household income, while other variables such as percent of households with no vehicle received effectively zero weight in the index. An additional strength of our study is its simultaneous modeling of several factors, including neighborhood deprivation, chemical mixtures, and individual-level covariates, for their association with NHL. This choice led to the identification of a statistically significant and positive association between an index of PAHs and NHL among long-term residents of Seattle while adjusting for the other two factors. This finding in the highly urban Seattle metropolitan area where multiple highways increase PAH exposure [54] supports an earlier analysis of data from the NCI-SEER study that identified some elevated risks for NHL among the highest categories of PAH exposure [55]. Our modeling of factors from the internal to general external domains is in line with the exposome philosophy that multiple domains of risk act on individuals at once. This analytical framework is becoming increasingly common in analyses of health outcomes. For example, two recent studies using cohort data from Chicago employed WQS regression, a precursor of the Bayesian index model, and found that NDIs were significantly associated with likelihood of asthma and of forgoing colorectal cancer screening in African American men [56], [57]. These studies and ours illustrate how index regression models can consider mixtures of social environment exposures beyond the chemical exposures for which WQS regression was initially designed [13].

The strengths of our study should be considered in light of its limitations. First, we considered a large initial set of variables for inclusion in the deprivation index at each study center, but we could have considered other variables for the index. Therefore, it is possible that additional neighborhood-level variables influence deprivation and are associated with risk for NHL. Second, we estimated neighborhood deprivation indices using the census tract containing participants’ residences. While this choice reflects a reasonable assumption that individuals spend most of their time in and near their home, it cannot estimate the degree of deprivation that participants experienced for work, school, or other activities that occurred in different census tracts. Additionally, census tracts are larger in rural areas such as much of the Iowa study center, which may make the implicit assumption of homogeneity within a tract more difficult to justify [10]. However, one study found no difference in measured neighborhood deprivation exposure in rural areas using different definitions for the neighborhood, including network and Euclidean distance buffers and other administrative boundaries [9]. Moreover, exposure to chemicals was only measured in the dust of participants’ current residences. It could have been beneficial to have measurements on previous chemical exposures from the previous residences.

In addition, we did not adjust for occupation in our analysis, though a previous study found elevated odds ratios for NHL among workers in certain industries including launderers and ironers, leather and leather products, and roofing and siding [58]. Also, in our sensitivity analysis that combined data across study centers and used a common set of census tract variables, the NDI odds ratios were attenuated. Findings from this analysis supported those of the main analysis, as modeling historic neighborhood deprivation provided considerably better model fit than did neighborhood deprivation at study entry. However, the attenuation was likely attributable to modeling the effects of varying amounts of actual change in the NDI components, given the differing distributions of these components across study centers. For example, an increase of one quantile in median house value would correspond to very different changes in actual house value for participants in the Seattle and Iowa study centers. Another notable factor is that nonparticipation among eligible subjects occurred in this study. This was particularly true among control subjects. We did not have access to demographic characteristics of nonparticipants in our study. However, a previous analysis of nonparticipation in the NHL study found that for cases, nonparticipation was statistically significantly associated with non-White race, lower household income, greater prevalence of multiple-unit housing, and educational attainment, but that socioeconomic and demographic differences between participants and nonparticipants did not result in a substantive bias in risk estimates [59]. An additional comparative spatial analysis of all eligible participants in this study concluded that selection bias did not explain areas of elevated spatial risk detected among participants [23]. However, our sensitivity analysis found only modest changes in the 2000 neighborhood deprivation index effect estimates when adding nonparticipants whose address at study entry was recorded. It is therefore unlikely that selection bias seriously impacted the deprivation index effect estimates in our study. Additionally, a previous study of the spatial variation in risk for NHL did not find substantial changes in the spatial risk surface when using nonparticipant locations [23].

It is important to report that we estimated a few significant negative associations between the NDI and NHL risk. For example, this occurred in Iowa for the 2000 index when estimating NDIs at all three time points, but the association was no longer significant when adjusting for chemical exposures and individual-level covariates. We also found a significant negative association among long-term residents in Detroit for the 1990 index when estimating NDIs at all three time points in Level 3, but we note that this association was based on a subsample of fewer than 100 participants for the long-term residents. Finally, we estimated another significant negative association in Seattle for the 1990 index when estimating NDIs at all three time points in the Level 2 and 3 models. While these few significant negative associations are not necessarily a limitation, they highlight the importance of careful interpretations of study results and the complexities of estimating multiple potentially correlated indices.

Different analytical frameworks and study designs can also permit alternative or additional insights into the relationships under study. In the presence of time-dependent covariates, marginal structural models (MSMs) have emerged as a powerful way to estimate causal effects in epidemiological research. These models use inverse-probability-of-treatment weights to control for confounders in selection of the sample. Attention should be given to the persistence of neighborhood deprivation over time and how using models such as MSMs can estimate causal effects of interest.

Finally, although the NCI-SEER study was conducted in a diverse set of four study centers across the United States, it is possible that associations may vary in magnitude, in timing, or may include different neighborhood-level variables in populations that are geographically or demographically different than those studied. Future research should investigate the role that historic neighborhood deprivation plays for NHL in such different populations. Future research should also consider modeling the trajectory of neighborhood deprivation profiles over time and how continued residence in, moving into, or moving out of deprived neighborhoods is associated with health outcomes.

In conclusion, in this study we identified several associations between historic neighborhood deprivation and NHL in Iowa and Detroit using data from the NCI-SEER study. The neighborhood-level variables driving these associations included median rent as a percentage of household income, percent of single-parent households with at least one child, and median household income. The findings in our study add to our understanding of how neighborhood-level factors are associated with NHL above and beyond individual-level factors, and additional research should study historic neighborhood deprivation and NHL in other populations.

Figure 1.

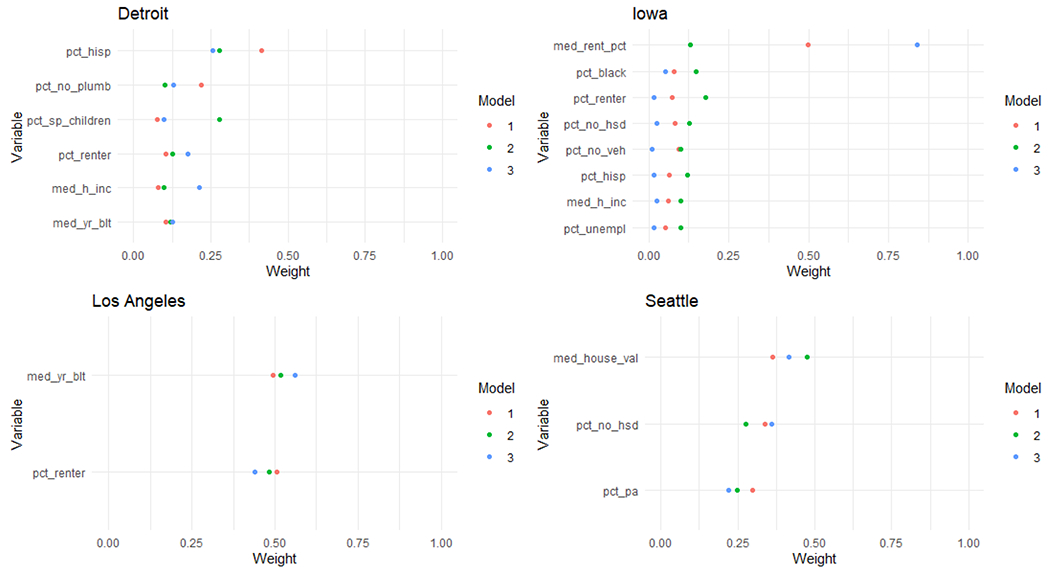
Estimated importance weights in the neighborhood deprivation for all time periods by study center for Level 1. %PA represents the percent of households in a census tract receiving public assistance income.

• Considering historic exposures is necessary for diseases with long latencies.

• We modeled associations of historic neighborhood deprivation & non-Hodgkin lymphoma.

• Such historic deprivation was significantly associated with NHL in Iowa and Detroit.