Effects of low-level air pollution exposures on hospital admission for myocardial infarction using multiple causal models

Abstract

Myocardial infarctions have been associated with PM_2.5, and more recently with NO₂ and O₃, however counterfactual designs have been lacking and argument continues over the extent of confounding control. Here we introduce a doubly robust, counterfactual-based approach that deals with nonlinearity and interactions in associations between confounders and both outcome and exposure, as well as a double negative controls approach that capture omitted confounders.

We used data from over 4 million admissions for myocardial infarction in the US Medicare population between 2000 and 2016 and linked them by ZIP code of residence to high resolution predictions of annual PM_2.5, NO_2, and O₃. We computed the counts of admissions for each ZIP code-year. In the doubly robust approach, we divided each pollutant into deciles, and for each decile, we fitted a gradient boosting machine model to estimate the effects of covariates, including the co-pollutants, on the counts. We used these models to predict, for all ZIP code-years, the expected counts had everyone be exposed in that decile. We also estimated the probability of being in that decile given all covariates, again with a gradient boosting machine, and used inverse probability weights to compute the weighted average rate of MI admission in each decile. In the negative control approach, for each pollutant, we fitted a quasi-Poisson model to estimate the exposure effect, adjusting for covariates including the co-pollutants, and negative exposure and outcome controls to control for unmeasured confounding.

Each 1-μg/m³ increase in annual PM_2.5 increased the admission for MI by 1.37 cases per 10,000 person-years (95% CI: 1.20, 1.54) in the doubly robust approach, and by 0.69 cases (95% CI 0.60, 0.78) using the negative control approach. Elevated risks were seen even below annual PM_2.5 level of 8 μg/m³. Results for NO₂ and O₃ were inconsistent.

1. Introduction

The association of short-term exposure to air pollutants, especially PM_2.5, with myocardial infarctions (MI) is well established and recent studies provide substantial evidence for long-term exposure impacts as well (Madrigano et al., 2013; Zhang et al., 2021; Liao et al., 2021; Yazdi et al., 2021a; Hartiala et al., 2016). NO₂ and O₃ have been less studied for long-term effects on this outcome. Growing realization that multipollutant exposure studies are needed resulted in more studies reporting associations with multiple pollutants simultaneously, although those numbers are still limited. Studies at lower concentrations are still few, and studies making use of causal modeling are also limited. Such studies are important to evaluate current air quality standards and guidelines to determine whether they are adequate to protect public health. Importantly, different causal modeling approaches are subject to different risks of confounding and violations of assumptions, and an examination of several approaches with different confounding risks can provide more assurance that detected associations are causal than any single method.

Few studies have used causal modeling approaches to examine the concentration-response association, and those have focused on generalized propensity scores. Generalized propensity scores are not as robust as categorical propensity scores (Wu et al., 2019). Recent discussion has raised the issue of triangulation, that is using formal methods to make composite judgments based on studies with different potentials for bias. Hence studies of annual exposures to multiple pollutants in large cohorts including exposures below current standards and using such methods would be useful.

Causal inference seeks to determine the contrast between, in the simplest case, two counterfactual events: what would have occurred had the entire population been exposed versus what would have occurred had the entire population not been exposed. Obviously, both counterfactuals cannot be simultaneously observed, and usually neither is observed. Randomized trials seek to obtain valid surrogates for those counterfactuals by treating the outcome in the exposed as a surrogate for what would have occurred had the entire population been exposed, and similarly for the outcome in the unexposed. Since the population was randomized, we assume that the distribution of characteristics of the populations are essentially identical in the exposed and unexposed groups (with sufficient sample size) and therefore accept these as valid surrogates. For observational data, assignment is clearly not random, and causal modeling seeks methods to recover valid surrogates or counterfactuals.

Propensity score methods are a standard approach for making exposure independent of measured population characteristics, and, assuming no unmeasured confounders and several other properties (Stable Unit Treatment Value Assumption-SUTVA), can also provide valid surrogates (Rubin, 1997). For continuous exposures, generalized propensity scores can in principle provide the same, however they are not as robust as propensity scores for a categorical exposure (Imai and van Dyke, 2004). One solution is to divide the continuous exposure into categories, and fit separate propensity scores for each category (Wei et al., 2021). However, propensity score methods do not generate counterfactuals directly. They rely on the assumption that the inverse probability weights make exposure independent of all covariates, and hence that the effect in the people in exposure category k can be assumed to represent a valid substitute for the counterfactual has all participants been exposed in that category. Here we seek to gain insight by using methods with different potential sources of bias and estimate effect sizes using multiple causal models which require different assumptions and have different vulnerabilities to confounding.

First, we recover some robustness by a) dividing each air pollutant into deciles, as just mentioned, and b) by using regression adjustment to directly estimate the counterfactual outcomes for all subjects had they been exposed within each decile of exposure, and then c) additionally applying inverse probability weights to obtain a doubly robust estimate. The idea of regression adjustment is straightforward. Within a category of exposure, we fit a model predicting the outcome based on all the covariates, including other air pollutants. This gives us category specific coefficients of the effect of the covariates on the outcome, conditional on being exposed in that category. If the model fit is unbiased, we can use it to predict the mean outcome had everyone been exposed in that category, by predicting from that model for the entire cohort, and directly estimate the counterfactual. A limitation of this method is the need to assume that the model predicting outcome from covariates is properly specified. We make use of machine learning, which allows for nonlinearities and interactions amongst predictors, to make this assumption more reasonable, and based on different assumptions than a propensity score analysis, which requires correct specification of the model for the exposure. We then add the propensity score for a doubly robust estimate that should be valid if either the model for the outcome or the model for the exposure is correct. Again, we use machine learning to allow for flexibility in that model.

We used the US Medicare cohort between 2000 and 2016. We stratified each air pollutant exposure into deciles. Within each decile, we fit a gradient boosting algorithm predicting the risk of MI based on multiple SES variables, smoking rate, mean BMI, access to care variables, race/ethnicity, exposure to the other pollutants, and calendar year. We then used those 10 models to predict, for the entire cohort, the counterfactual rate of MI hospitalization had everyone been exposed to each decile. We bootstrapped the process 200 times to obtain confidence intervals. We then fit propensity scores estimating the probability of being in each decile given the covariates above and used inverse probability weights to compute the weighted average counterfactual risk had everyone been exposed in that decile.

While this doubly robust model provides considerable assurance that measured confounders have been addressed, it is susceptible to unmeasured confounding. Here we used two additional approaches. First, we used a negative outcome control and a negative exposure control based on the approach described by Tchetgen-Tchetgen (Shi et al., 2020; Miao et al., 2018). Basically, this approach uses the two negative controls to construct an instrumental variable for the omitted confounders, and controls for that variable. The critical assumption here is that the negative controls are truly negative controls, and that the instrument for the omitted confounders is strong enough to correct for bias. The second approach is a generalized difference-in-difference approach which we recently published, and whose results we take for comparison purposes. The critical assumption here is that the time trends in the counts due to unmeasured confounders are the same in all ZIP codes within the same cluster of ZIP codes clustered by socio-economic factors and race/-ethnicity. The key point is that the assumptions of the three different approaches are different, and similarities of results across the methods will imply a robust finding, and vice versa.

2. Data and methods

2.1. Study population

Our cohort comprised all fee-for-service Medicare beneficiaries who were 65 years of age or older, and who lived in the contiguous US between 2000 and 2016. We extracted these data from the Medicare denominator file and the Medicare Provider Analysis and Review (MEDPAR) file, which are available from the Center for Medicare and Medicaid Services. The denominator file contains age, race, sex, Medicaid eligibility, and ZIP code of residence for each beneficiary; and age, Medicaid eligibility, and ZIP code are updated annually. The MEDPAR file provides data on admissions to hospitals, ICD codes for discharge diagnoses, and IDs that match to the denominator files for fee for service participants. Participants entered the cohort on January 1 of the year after enrollment and were followed until they died or the end of the follow-up time (December 31, 2016). During that follow-up we recorded the year of any hospital admissions for a myocardial infarction, and multiple events were allowed per participant, provided they were at least 30 days apart. Medicare used International Classification of Diseases, Ninth Revision (ICD-9) codes through the end of the third quarter of 2015 and then switched to International Classification of Diseases, Tenth Revision (ICD-10). Myocardial infarction admissions were defined as those having ICD-9 codes 410.×0 and 410.×1 and ICD-10 code I21 as the primary discharge code. Individual events were summarized to a count of MIs for each ZIP code for each year. We limited the dataset to zip codes where there were at least 100 beneficiaries. This study has been approved by the Harvard T.H. Chan School of Public Health’s institutional review board.

2.2. Exposure assessment

PM_2.5, O₃, and NO₂ concentrations came from three high-resolution spatiotemporal models, each of which combined estimates from 3 different machine learning algorithms: a neural network, a gradient boosting machine, and a random forest (Di et al., 2019, 2020; Requia et al., 2020). The models used multiple predictors including land use terms, chemical transport model predictions, meteorologic variables, and satellite measurements to estimate daily levels of the pollutants on a scale of 1 km × 1 km. The machine learning models make no assumptions about the functional form of the association between the predictors and the air pollutants and readily incorporate nonlinearities and interactions among predictors. The accuracy of the predictions was assessed using 10-fold cross-validation against measured values at held out monitoring sites across the United States. The resulting R² values for annual average PM_2.5, NO₂, and O₃ respectively were 0.89, 0.84, and 0.86. Grid-cell values were averaged across zip codes. Exposure was assigned based on the residential zip code of the beneficiary in that year. Long-term exposure in our study is defined as the annual concentration for the year of MI admission.

2.3. Covariate assessment

In addition to the individual-level covariates sex, race, age group, and Medicaid eligibility from the Medicare denominator file we used area level data as covariates. From the US Census and the American Community Survey we obtained the following zip code–level socioeconomic and demographic data: proportion of the population >65 years of age living below the poverty line, population density, median value of owner occupied properties, proportion of the population self-reporting as Black, median household income, proportion of housing units occupied by the owner, proportion of the population identified as Hispanic, and the proportion of the population >65 years of age who had not graduated from high school. Census data were available for 2000 and 2010 through 2016. Data for all other years and missing values were obtained using linear interpolation and extrapolation. We used lung cancer hospitalization rates in each zip code as a proxy for pack-years of smoking and derived this from the MEDPAR file. We obtained zip code–level data on mean body mass index and the smoking rate from the Behavioral Risk Factor Surveillance System of the Centers for Disease Control (CDC and Behavioral Risk Factor Surveillance System Control, 2013). Behavioral Risk Factor Surveillance System data were collected at the county level and then linked to zip codes and temporally interpolated using linear regression to fill in missing values.

We obtained data on several access-to-care variables from the Dartmouth Atlas of Health Data (Wennberg and Cooper, 1996). These were the proportion of Medicare beneficiaries with at least 1 hemoglobin A1c test per year; proportion of diabetic beneficiaries who had a lipid panel test in a year; proportion of beneficiaries who had an eye examination in a year; proportion of beneficiaries with at least 1 ambulatory doctor visit in a year; and proportion of female beneficiaries who had a mammogram during a 2-year period. Data were collected at the hospital service area level and linked to the relevant zip code. Missing values were filled in using linear interpolation. We also included distance to hospital as a variable to measure access to health care. The distance to the nearest hospital was calculated from the centroid of the residential zip code of the participant. Hospital locations across the United States were derived from an ESRI dataset. Region of the US was used to control for other regional patterns in health. Observations with missing exposure or covariate information were assumed to be missing at random and were excluded from further analysis. These represented less than 1% of the data.

2.4. Statistical analysis

Method 1.

Each air pollutant was divided into deciles. Separate analyses were conducted for each exposure’s decile. We began by, within each decile of the exposure, fitting a gradient boosting machine predicting the counts of myocardial infarction occurring within each zip code for each year. The predictors included the other two pollutants as continuous exposures, as well as all the covariates delineated above, and an offset term of the log of the population at risk. This produced 10 prediction models, each predicting the expected counts of MI based on covariates, given one was exposed in that decile. For consistency across deciles and pollutants we used the same tuning parameters for each model, choosing 1500 trees, a shrinkage parameter of 0.005, and a depth of 3 for each tree. The gradient boosting machine can incorporate nonlinearities in the relationships between predictors and MI rates, as well as interactions among them.

We then used that model to predict for the entire dataset, based on covariates, the expected counts for MIs in each ZIP code and year, had the entire population been in that exposure decile, and computed the mean of the ratio of those counts to the population at risk to obtain the mean rate in that decile. Applied to each decile, this produces estimates of the counterfactual we wish to estimate. To estimate the uncertainty of this prediction, we bootstrapped the process 200 times. This entire process was repeated for each air pollutant. Using this data we produced two summary results for each pollutant—a plot of the predicted counterfactual rate of MI hospitalization in each decile, with confidence intervals, to see the concentration-response relationship, and a linear regression of the rate in each decile against the mean exposure in that decile, to produce a summary effect assuming linearity.

To better assure confounding was fully accounted for we also computed propensity scores for the probability of being exposed in each decile. These estimated the probability of being exposed in decile k, given all the covariates, including other pollutants. Again, we used a gradient boosting machine to predict the probability of being in exposure decile k to capture nonlinearities and interactions among the predictors. We generated stabilized inverse probability weights from these models. Then, in computing the mean rate of MI in each decile from the predicted counterfactual outcomes for each ZIP code and year, we used the inverse probability weights to compute weighted means. That is, if, given the covariates, there was a high probability that a ZIP code-year would be in that decile, we gave it a lower weight, with higher weights given to ZIP code-years which had lower probabilities of being in that decile of exposure given the covariates. This should provide a doubly robust estimate; that is, unbiased results if either the model predicting the MI rates in each decile or the model predicting the inverse probability weights is correct (Yazdi et al., 2021a).

Method 2.

To motivate this approach, we suppress the covariates. Suppose A is the exposure in the year of the MIs, Z the negative exposure control, for which we will use the exposure in the year after the MI count, Y the outcome, and W the negative outcome control, which we choose to be the counts of MI in the preceding year. Let U be the unmeasured confounder(s). Assume further the usual Poisson model:

$$Log(E(Y))={\beta }_{Y0}+{\beta }_{YA}A+{\beta }_{YU}U.$$ (1)

and

$$Log(E(W))={\beta }_{WY0}+{\beta }_{WU}U$$ (2)

since by hypothesis W does not depend on A.

Further assume that the confounder U is related to A and Z (else it is not a confounder) by

$$E(U)={\beta }_{U0}+{\beta }_{UA}A+{\beta }_{Uz}Z.$$ (3)

Next, consider the model for the negative outcome control. By equation (2), W is a surrogate for U, which by (3) induces an association of W with A and Z. Hence if we regress W on A and Z the predicted W should capture the association of U with A and Z. Essentially, we now have an instrumental variable for U. In addition, if we replace U in (1) by its expectation in the third equation we have

$$log(E(Y))={\beta }_{Y0}+{\beta }_{YA}A+{\beta }_{YU}\left({\beta }_{U0}+{\beta }_{UA}A+{\beta }_{Uz}Z\right)$$

$$=\left({\beta }_{Y0}+{\beta }_{YU}{\beta }_{U0}\right)+\left({\beta }_{YA}+{\beta }_{YU}{\beta }_{UA}\right)A+{\beta }_{YU}{\beta }_{Uz}Z$$

Hence the bias in the estimate of the effect of A is ${\beta }_{YU}{\beta }_{UA}$. If ${\beta }_{\text{UA}}={\beta }_{\text{UZ}}$, then that is precisely the coefficient of Z, the negative control in the outcome regression, and subtracting it from the estimate of the coefficient of A in that model $\left({\beta }_{YA}+{\beta }_{YU}{\beta }_{UA}\right)$ will recover the true unbiased coefficient of A, ${\beta }_{\text{YA}}$. Since in our case Z is the identical variable to A, a year later, this is not an unreasonable assumption. Using these two approaches to control for unmeasured confounding, we can now fit a quasi-Poisson model using both controls for U.

$$\text{log}(E(Y))={\beta }_{Y0}+{\beta }_{YA}A+{\beta }_{Yz}Z+{\beta }_{Yw}PredW+{\beta }_{YC}C$$

where C is measured confounders including the other two pollutants and covariates, and $PredW$ is predicted W given A and Z. The above regression should control for the omitted covariates U if either ${\beta }_{\text{UA}}={\beta }_{\text{UZ}}$ or if U is linearly related to A and Z.

Method 3.

For method 3 we will rely on a previously published difference in differences analysis, and compare those results with method 1 and 2. Specifically we used an extension of the model developed by Schwartz (Schwartz et al., 2021a). In this approach a dummy variable for every ZIP code controls for all slowly varying neighborhood level (and some personal level) covariates, measured or unmeasured, because it removes all contrast across ZIP codes. Confounding is still possible from time varying covariates and is addressed by including the other two pollutants and annual measures of SES, racial composition, smoking, BMI, and access to health care variables. To capture any remaining unmeasured temporally varying confounders, we classified each zip code into one of five clusters whose long-term trends might differ, using Ward’s Hierarchical Cluster Analysis and average values for the following socioeconomic and demographic variables: percent of the population who identify as black, percent of the population who identify as Hispanic, median household income, median house value, the proportion with at least one ambulatory doctor’s visit in a year, percent of the population over 65 living below the poverty line, percentage of the elderly population who did not graduate from high school, smoking rate, population density, and distance of zip code to the nearest hospital. Five clusters were chosen based on an optimization of Euclidean distance and thirty indices in the “NbClust” package in R (Charrad et al., 2014). A separate spline of time was fit in each cluster to capture omitted time varying confounders.

3. Results

Table 1 shows the means and standard deviations of the data. The means of the air pollutants were well below the current US EPA ambient air quality standards. Ten percent of the 65+ population was living in poverty, and 13% was eligible for Medicaid. The population was 56% female. There were roughly 10 myocardial infarctions per ZIP code per year, and on average 1083 participants in each ZIP code-year.

Table 1.

Mean and standard deviations of variables in the analysis.

	Mean (SD)		Mean (SD)
N (ZIP code-years)	435,246	Proportion < High School education	0.28 (0.16)
MI’s per ZIP code-years	9.68 (12.82)	Nearest hospital (km)	11.38 (10.40)
pm25 μg/m3	9.79 (3.13)	Pct Eye exam	67.24 (6.51)
no2 ppb	16.27 (9.11)	Pct LDL test	78.52 (7.22)
ozone ppb	45.28 (5.59)	Pct mammogram	63.82 (7.22)
proportion Black	0.09 (0.17)	Pct owner occupied	73 (15)
Mean bmi (kg/m2)	28.03 (2.39)	Lung Cancer Rate	0.00042 (0.0026)
Proportion Hispanic	0.09 (0.16)	Population density (	1495 (5098)
Median household income $	49336 (21191)	Smoking rate	0.47 (0.07)
Median house value	162466 (139309)	Person-time per ZIP code	1083.20 (1259.96)
Pct A1c exam	83.17 (5.88)	Female proportion	0.56 (0.04)
Pct ambulatory visit	79.25 (6.22)	Medicaid	0.13 (0.10)
Pct in poverty	10 (8)	Other race prop	0.04 (0.09)

3.1. PM2.5

Method 1.

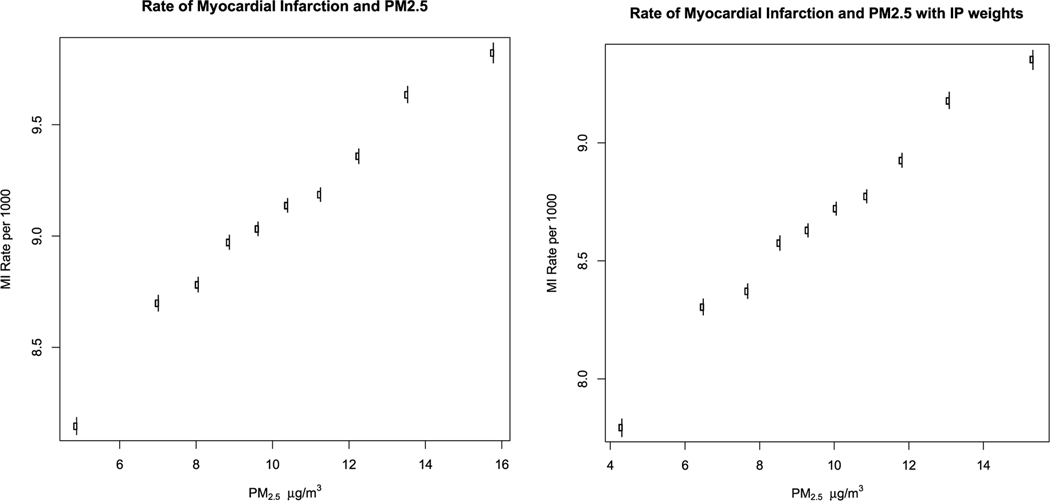
Fig. 1a, below, shows the estimated counterfactual rate of MI in each decile of PM_2.5 concentration, and its 95% confidence interval. It shows a roughly linear association with a suggestion of a steeper slope for concentrations below 10 μg/m³. There is no suggestion of a threshold down to 4.3 μg/m³, the mean concentration in the lowest decile. Each 1 μg/m³ increase in PM_2.5 increased the MI rate by 1.48 cases per 10,000 persons per year (95% CI 1.39, 1.56) in the linear model.

Fig. 1.

Counterfactual rate of myocardial infarction by decile of PM2.5.

Using propensity scores in addition to the estimates of the counterfactual for each decile produced similar results. For PM_2.5 each 1 μg/m³ increase in PM_2.5 increased the MI rate by 1.37 cases per 10,000 per year (95% CI 1.20, 1.54). Fig. 1b shows the estimated counterfactual rate of MI for each decile of PM_2.5, using inverse probability of exposure weights. The rates and confidence intervals for each decile are shown in e=supplemental Table 1.

Method 2.

Using the negative control model, we found that each 1 μg/m³ increase in PM_2.5 increased the MI rate by 0.69 cases per 10,000 per year (95% CI 0.60, 0.78).

Method 3.

In the DID paper of Danesh Yazdi et al. (2022), a 1 μg/m³ increase in PM_2.5 increased the MI rate by 0.74 cases per 10,000 (95% CI 0.55, 0.96).

3.2. O₃

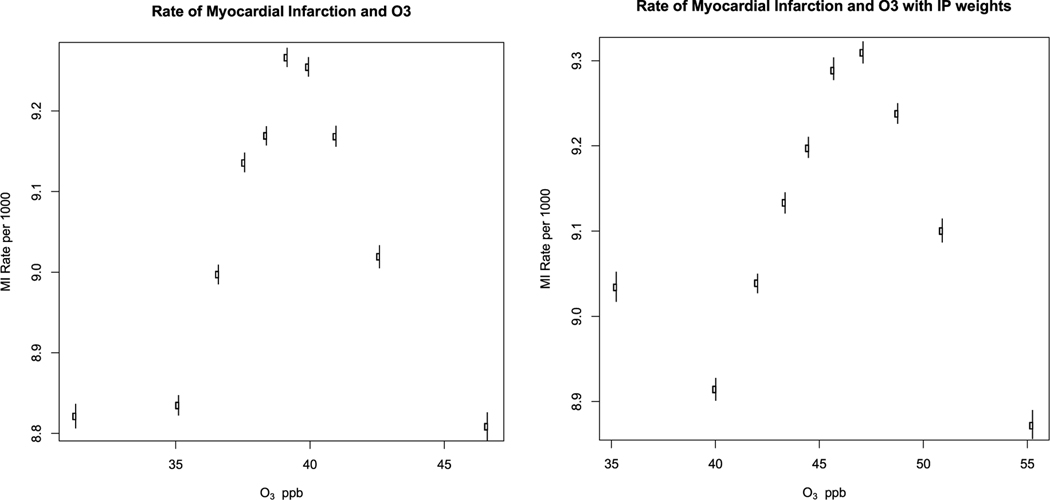
Method 1.

Fig. 2a shows the estimated counterfactual rate of MI for each decile of ozone. The rates increased with increasing ozone up to about 40 ppb, and then decreased with further increases in ozone. In a linear regression, there was no significant association between ozone concentrations and rates of MI (0.06 cases per ppb per 10,000 per year, 95% CI −0.18, 0.304). Using propensity score weights, the effect estimate was 0.01 (95% CI −0.2, 0.2). The plot is shown in Fig. 2b. The rates and confidence intervals for each decile are shown in supplemental Table 1.

Fig. 2.

Counterfactual rate of myocardial infarction by decile of O3.

Method 2.

For each ppb increase in ozone, this method found a 0.048 increase in MI case per 10,000 persons per year, 95% CI (0.017, 0.079).

Method 3.

In the DID paper, a 1 ppb increase in ozone was associated with a 0.22 increase in the MI rate per 10,000 person years (95% CI 0.11, 0.34).

3.3. NO₂

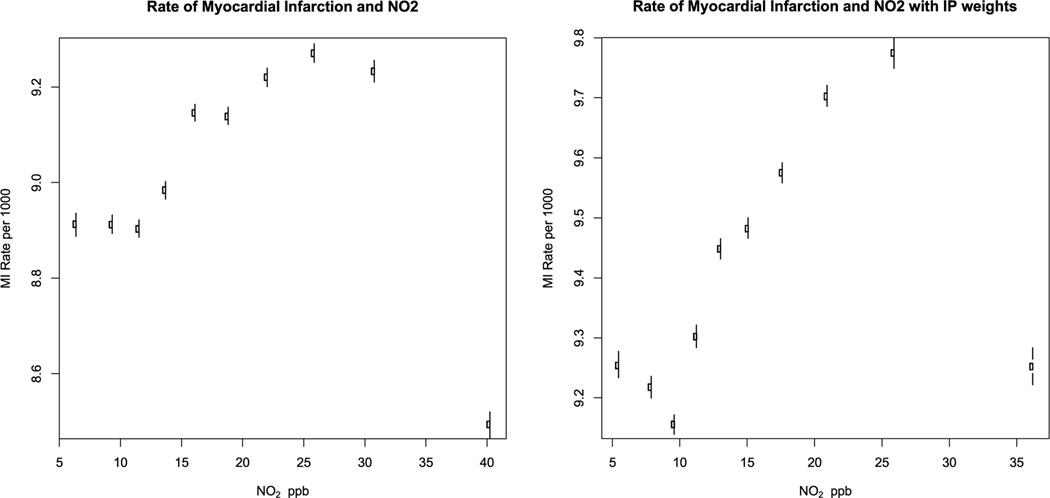
Fig. 3a shows the estimated counterfactual rate of MI for each decile of NO₂. The rates increased up until the eighth decile, and then declined. Using inverse probability weights, the NO₂ effect only declined in the highest decile (Fig. 3b). A linear regression of the rates Vs NO₂ indicating that a 1 ppb increase in NO₂ was associated with a 0.013 (95% CI −0.130, 0.156) case per 10,000 person-year increase in MI rates in the unweighted model and 0.045 (95% CI −0.063, 0.153) with the IP weights. The regression results are shown in Table 2 and the rates and confidence intervals per decile in Supplemental Table 1.

Fig. 3.

Counterfactual rate of myocardial infarction by decile of NO2.

Table 2.

Change in MI rate (per 10,000 persons) with Air Pollution exposure.

Model	PM2.5a (95% CI)	O3b (95% CI)	NO2b (95% CI)
Regression Adjustment	1.48 (0.139, 0.156)	0.06 (−0.18, 0.30)	0.013 (−.013, 0.16)
Plus IPW	1.37 (1.20, 1.54)	0.01 (−0.2, 0.2)	0.093 (−0.05, 0.24)
Negative Controls	0.69 (0.60, 0.78)	0.048 (0.017, 0.079)	0.066 (0.033, 0.008)
Difference in Differences	0.75 (0.55, 0.96)	0.22 (0.11, 0.34)	−0.08 (−0.001, −0.16)

^aPer 1 μg/m³.

^bPer 1 ppb.

Method 2.

For each ppb increase in NO2, we found a 0.066 increase in MI cases per 10,000 person-years (95% CI 0.033, 0.098).

Method 3.

For each ppb increase in NO2, the DID analysis found a −0.08 decrease in MI cases per 10,000 person-years (95% CI −0.001, −0.16).

4. Discussion

Using a doubly robust model we directly estimated the counterfactual rate of myocardial infarction hospitalization by decile of each of three air pollutants. For PM_2.5 we found a very robust effect, with every decile showing significantly higher MI rates than the preceding decile, and a significant linear trend. This included a significant effect at exposures below 8 μg/m³. For NO₂, we found a significant increase in MI rates from the 1st to 9th decile, which then dropped in the highest decile, and the linear trend was not significant. The ozone association was less clear, showing an almost inverted U shape. The advantage of our first approach is that the double robustness means that if either the propensity score model and IP weights or the regression model within deciles of exposure correctly adjusted for confounders then the results are unbiased. Moreover, regression adjustment to directly estimate counterfactual rates for each decile of exposure has not been used previously and provides results from an alternative causal modeling strategy that does not depend on the accuracy of the model for the exposure, which helps evaluate the consistency of the associations across methods. Another advantage of the approach is that we used a very flexible analysis to predict the dependence of MI on covariates within each decile of each exposure, and another flexible one to predict the probability of being in each decile of exposure based on covariates, including the other air pollutants.

Propensity score and regression adjustment models require the assumption of no omitted confounders. We supplemented that approach with our second model, the negative outcome and exposure control model, which can control for omitted confounders as well. As long as the omitted confounder is linearly related to the negative control and true exposure, it can be controlled by this approach. This approach provides some assurance about omitted confounders and relies on different assumptions than previously published causal models. To that, we added the results of our third approach, the modified difference in differences model. This also controls for omitted confounders. In that case, all neighborhood level confounders are controlled for by a dummy variable for each neighborhood, so the assumption of a linear association with outcome is not required for this subset of confounders. Omitted time varying confounders are controlled for by splines of time fit separately for each of 5 clusters of ZIP codes, where clustering was done by race/ethnicity and socioeconomic variables.

The complementarity of the approaches gives greater confidence to the identification of a causal effect if they have similar results. For example, while the DID study required that all unmeasured time varying covariates had the same temporal pattern of association with exposure and outcome within cluster, the negative control model does not, since time variation in omitted confounders is captured by time variation in the negative control exposure and outcome. On the other hand, the DID analysis does not assume the omitted confounder’s association with exposure or outcome is linear. Similarly, the first approach controls for measured covariates if either the regression model for each decile is correct or if the regression model for the probability of exposure being in each decile is correct and uses a very flexible machine learning algorithm to try to ensure a correct model. For PM_2.5 all three approaches showed significant associations with MI, with moderately similar effect sizes. For O₃, methods 2 and 3 found significant associations, but not method 1, so the strength of evidence is weaker. For NO₂ method 1 found an insignificant positive effect, method 2 a significant positive effect, and method 3 a significant negative effect. Methods 2 and 3 provided similar effect size estimates for PM2.5, however the estimate was almost twice as large for method 1. This may either be due to the existence of omitted confounders biasing upward the effect of Method 1, or its superior control for measured confounders (via machine learning) better controlling for negative confounders. For example, the more and finer scale area level SES the ACS study controlled for, the larger the effect size it found. Clearly, further research to validate and refine our approaches is warranted, in order to strengthen the evidence base and improve our understanding of the potential mechanisms.

A key feature of this study was our ability to look at counterfactual effects at low concentrations. For example, we estimate that the difference between the MI rate had the entire population be exposed in the third decile of PM_2.5 (7.7 μg/m³) instead of in the first decile (4.3 μg/m³) would be a yearly increase in the MI rate of 6.4 cases per 10,000 persons per year. Applied to the 62.8 million Medicare participants in 2020, this would imply an increase of 40,000 additional myocardial infarctions per year. In contrast, EPA’s National Contingency Plan (40 C.F.R. § 300.430 (d)(1)) states that the range of acceptable lifetime risks (of developing cancer) for carcinogens should be set between 1 in 10,000 and 1 in a million over a 70-year lifetime. Hence the magnitude of the health burden we see is quite large at concentrations allowed by EPA.

Regarding the NO₂ and O₃ associations, the picture is more mixed. For NO₂, in the doubly robust model, MI risk increases from 10 ppb to 25 ppb, but then fall at the highest annual concentrations. Because the highest decile is a very influential observation, the linear trend regression was not significant. However, due to quenching by NO, those highest NO₂ concentrations are almost invariably associated with quite low O₃ concentrations. When two collinear variables are included in a model, it is common for one coefficient to increase and the other to decrease because of the collinearity. Hence, it is interesting that the effect estimate at the lowest O₃ decile increases and the effect estimate at the highest NO₂ decile decreases compared to the adjacent decile. This higher collinearity at the extremes may explain the anomalous effect estimates in method 1.

Our results add to the growing literature indicating adverse effects of PM_2.5 at concentrations below both the EPA standard of 12 μg/m³ and the previous WHO guidelines of 10 μg/m (; Yazdi et al., 2021b, 2021c; Pinault et al., 2016; Shi et al., 2016; Beelen et al., 2014). The entire NO₂ association takes place at concentrations below the EPA NO₂ annual standard and again, other recent literature has also reported associations in that range (Wei et al., 2021; Ma et al., 2022; Schwartz et al., 2021b; Crouse et al., 2015). Previous results for O₃ have been mixed, as were ours (Yazdi et al., 2021b; Cakmak et al., 2018; Sun et al., 2022; Sommar et al., 2021). In general, studies in North America have reported positive effects of O₃, while studies in Europe have found negative, protective effects. One possible reason is that in the Europe incentives were provided to encourage the purchase of Diesel vehicles resulting in substantially higher NO_x emissions, particularly in urban areas, where slow traffic is likely to drop the exhaust temperature below the 140 °C necessary for the NO_x reduction catalyst to work. In that scenario, high O₃ locations are even more likely to be low NO_x locations, which could result in a protective effect for ozone. However, methods 2 and 3 did provide support for an effect of ozone, and method 1 supports that conclusion for averages below 47 ppb. Although the European and Canadian studies used summer ozone, comparing results based on different exposure windows remains meaningful, as it allows for a comprehensive understanding of the potential health effects of air pollution over varying periods of time.

The strengths of our study are the use of multiple causal modeling methods requiring different assumptions to assess the robustness of the associations. These included regression calibration and inverse probability weighting to provide doubly robust estimates of the effects including direct estimates of the counterfactuals (what would have happened if everyone was exposed in the same decile), the use of machine learning to provide more robust estimates of the associations, the use of three pollutant models to account for potential confounding by other pollutants, the use of an alternative with negative outcome and exposure controls that can capture omitted confounders, and the very large sample sizes that Medicare provides. It also uses exposure models that have very high predictive accuracy. The limitations of the study are that there remain measurement errors in our exposure, including differences between individual exposure and neighborhood exposure. People do not spend all their time at home. However, the National Human Activity Pattern Survey in the U.S. reported that U.S. adults spent 69% of their time at home and 8% of the time immediately outside their home (Klepeis et al., 2001), and for the Medicare population it is likely higher. Also, our definition of a myocardial infarction was based on hospital discharge diagnoses reported to the Center for Medicare and Medicaid Services, and errors are likely in such data. We do not expect those coding error rates to be associated with air pollution, however. Further, the correlated pollutants posed the risk of multicollinearity, which can lead to the statistical inferences being less reliable for the second and third methods. However, the issue of multicollinearity mainly affects the statistical power and not the prediction accuracy of the regression calibration model, thereby alleviating the concerns regarding the first method.

Fig. 1 shows the counterfactual rate of myocardial infarction and 95% confidence intervals in each decile of PM2.5 concentration. Fig. 1a is using regression adjustment and Fig. 1b adds inverse probability weighting.

Fig. 2 shows the counterfactual rate of myocardial infarction and 95% confidence intervals in each decile of O3 concentration. Fig. 2a is using regression adjustment and Fig. 2b adds inverse probability weighting.

Fig. 3 shows the counterfactual rate of myocardial infarction and 95% confidence intervals in each decile of NO2 concentration. Fig. 3a is using regression adjustment and Fig. 3b adds inverse probability weighting.

Data availability

The authors do not have permission to share data.