Automated detection and segmentation of pulmonary embolisms on computed tomography pulmonary angiography (CTPA) using deep learning but without manual outlining

Abstract

We present a novel computer algorithm to automatically detect and segment pulmonary embolisms (PEs) on computed tomography pulmonary angiography (CTPA). This algorithm is based on deep learning but does not require manual outlines of the PE regions. Given a CTPA scan, both intra- and extra-pulmonary arteries were firstly segmented. The arteries were then partitioned into several parts based on size (radius). Adaptive thresholding and constrained morphological operations were used to identify suspicious PE regions within each part. The confidence of a suspicious region to be PE was scored based on its contrast in the arteries. This approach was applied to the publicly available RSNA Pulmonary Embolism CT Dataset (RSNA-PE) to identify three-dimensional (3-D) PE negative and positive image patches, which were used to train a 3-D Recurrent Residual U-Net (R2-Unet) to automatically segment PE. The feasibility of this computer algorithm was validated on an independent test set consisting of 91 CTPA scans acquired from a different medical institute, where the PE regions were manually located and outlined by a thoracic radiologist (>18 years’ experience). An R2-Unet model was also trained and validated on the manual outlines using a 5-fold cross-validation method. The CNN model trained on the high-confident PE regions showed a Dice coefficient of 0.676±0.168 and a false positive rate of 1.86 per CT scan, while the CNN model trained on the manual outlines demonstrated a Dice coefficient of 0.647±0.192 and a false positive rate of 4.20 per CT scan. The former model performed significantly better than the latter model (p<0.01). The promising performance of the developed PE detection and segmentation algorithm suggests the feasibility of training a deep learning network without dedicating significant efforts to manual annotations of the PE regions on CTPA scans.

Graphical Abstract

I. INTRODUCTION

As the third most common cardiovascular condition, pulmonary embolism (PE) is caused by blood clots in the pulmonary arteries. The blood clots often travel from deep veins (e.g., legs) to the lungs and block the blood flow within the lungs. Presentation is heterogeneous and can range from asymptomatic to sudden death. Immediate diagnosis and treatment can reduce the mortality rate from 30% to 8% ¹. In the United States (U.S.), approximately 900,000 people are affected by PE, and 100,000 deaths are related to PE each year ¹. One in four patients with PE dies suddenly without warning. Since the symptoms of PE (e.g., shortness of breath and chest pain) are nonspecific, it may often be misdiagnosed as other heart or lung disorders. Computed tomography pulmonary angiography (CTPA) is often used as the gold standard to diagnose PE ². The utilization of iodinated contrast creates images that enhance the depiction of blood clots in the pulmonary vessels because the clots prevent the contrast agents from filling in the vessels (i.e., a filling defect). However, a CTPA scan is typically formed by hundreds of image slices, making it time-consuming to manually detect PEs ³. Also, it is not easy to accurately quantify the extent of the embolisms to support precision or personalized medicine. As a result, there has been investigative effort dedicated to developing computer algorithms to automate the detection and segmentation of PEs, by which the obstruction level of a PE region and its clot burden can be quantitatively assessed based on its location and extent, making it possible to develop precise and personalized treatment. The challenges for a computer algorithm to automatically detect PEs are caused by the variations of the PE regions in density (i.e., Hounsfield Unit (HU)) and the progressive attenuation of the pulmonary vessels. It is difficult to identify an optimal threshold to reliably identify the PE regions across CTPA scans.

The available algorithms related to the detection and diagnosis of PE can be classified into three stages. From 1990 to 2000, the investigative effort primarily focused on the integration of clinical variables (e.g., symptoms) and/or findings from images (e.g., ventilation-perfusion lung scans) using a neural network to improve the PE assessment ^4-6. From 2000 to 2015, the primary emphasis was on the computerized detection and diagnosis of PE based on CTPA scans. Traditional computer vision algorithms were widely used to extract PE-related image features for different PE from other regions ^7-11. However, the sensitivity of the computer vision algorithms was unsatisfactory and associated with a relatively high false positive rate ^7-12. Recently, the investigative effort has transitioned to deep learning technology, specifically the convolutional neural network (CNN), which does not use explicit handcrafted features. By feeding raw images (e.g., CTPA scans) into a CNN model, the CNN models automatically extract tens of millions of low-level features and abstract them progressively into higher-level features to approximate the predefined targets (e.g., manually segmented PEs). Studies have demonstrated the remarkable performance of CNN models in addressing various image analysis problems ^13-17. However, CNN-based algorithms are data-hungry and require significant effort to manually annotate the images for training the CNN models. As a result, a large number of CNN-related studies only classify CTPA scans as simple negative or positive for PEs ^18-23 because it is less challenging to assign categorical labels to a CT scan than to outline the boundaries of all PEs depicted on CTPA scans. For example, Ma et al. ²³ developed a CNN model recently to classify a CTPA scan into several categories in terms of location (left, right, or central), condition (acute or chronic), and the right-to-left ventricle diameter (RV/LV) ratio. Although categorical classification can efficiently identify patients with PEs, it does not enable quantitative assessment of the extent of PE (e.g., volume and obstruction level). To our knowledge, only limited effort has been dedicated to the automated detection and segmentation of individual PE regions. Yang et al. ²⁴ and Tajbakhsh et al. ²⁵ described two-stage algorithms, which first detected the suspicious PE regions and then reduced the false positive detections based on a two-dimensional (2-D) CNN-based classifier. The former algorithm achieved a sensitivity of 75.4% with two false positives per scan, and the latter demonstrated a sensitivity of around 80% with two false positives per volume. It is unclear why Tajbakhsh et al. reported the false positive rate based on volume instead of per CT scan. Park et al. ²⁶ described a method that required the manual specification of a PE location to segment the PE region using a region-growing operation. Liu et al. ²⁷ described a 2-D CNN model called CAM-Wnet to segment the central embolisms located in the main pulmonary arteries on CTPA images. However, only segmenting the central embolisms limits the practical value of the tool because PE often occurs in the right and/or left lungs. As this study demonstrated, there are also many small PE regions, which definitely should not be ignored for early detection and diagnosis purposes.

We developed a novel algorithm to automatically detect and segment PE regions in a single pass. Our algorithm does not require manually outlined PE regions to train a CNN model. This algorithm uses computer vision methods to first automatically identify suspicious PE regions and assigns a confidence rating. Next, a CNN-based segmentation model is trained using the 3-D image patches associated with these PE regions assigned with high confidence. The publicly available RSNA Pulmonary Embolism CT Dataset (RSNA-PE) ²⁸ was used to develop and test the CNN model. An independent dataset (n=91) with the manually outlined PE regions was used to evaluate the model’s performance. To our knowledge, this is the first study that attempted to automatically detect and segment suspicious PE regions without manual outlining of the PE regions for deep learning.

II. METHODS AND MATERIALS

A. CTPA datasets

Dataset I:

The publicly available Radiological Society of North America (RSNA) CTPA dataset ²⁸ was used to develop and test the CNN models. It includes 7,279 manually annotated CTPA scans with 2211 (30.4%) scans confirmed positive for PE. The manual annotation includes the image slices where the PEs are located, their locations in terms of right/left lung and central PE, acuteness, and quality assurance (QA). This dataset was used to create a pool of negative and positive image patches for training the segmentation model. Among these cases, 157 indeterminate or uncertain cases due to contrast or motion issues were excluded from the study. We split the remaining PE negative and positive cases into two sets at the patient level, namely training and internal validation sets, at a ratio of 9:1 for CNN modeling.

Dataset II:

A second independent dataset consisting of 91 subjects who underwent CTPA scans at Dokuz Eylul University (Izmir, Turkey) with verified PE was also used in this study to validate the developed model. The CTPA scans were acquired using Toshiba Aquilion PRIME with radiopaque contrast with the participants in a supine position and holding their breath at the end inspiration. Images were reconstructed to encompass the entire lung field in a 512×512 pixel matrix. The in-plane pixel dimensions ranged from 0.592 to 0.831 mm, and the image slice thickness ranged from 0.5 to 3.0 mm. The tube voltage was consistently 120 kV, the x-ray tube current ranged from 105 to 469 mA, and the reconstruction kernels included FC08 and FC52. A thoracic radiologist (NSG, >18 years’ experience) reviewed these CT scans and manually outlined the PEs on the series with the maximum number of images using our in-house software, which was designed to facilitate the 3-D outlining of regions of interest depicted on medical image ¹⁴. This outlining software supports various image analysis operations (e.g., region growing, thresholding, freehand sketching, and overlay interpolation). The study related to the second dataset was approved by the Ethics Committee of Dokuz Eylül University School of Medicine (IRB: 2022/14-01).

B. Algorithm overview

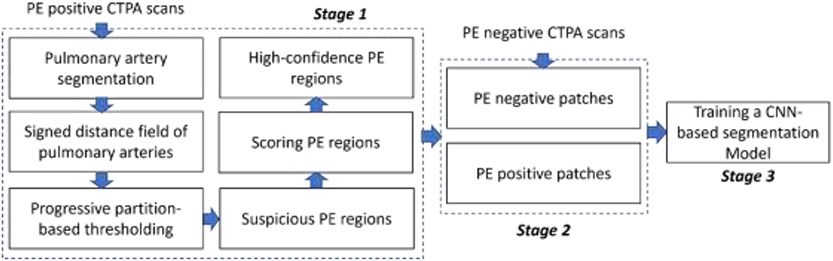
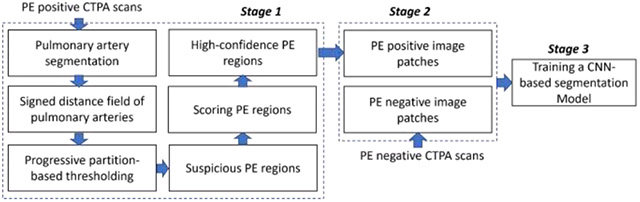
The computer algorithm consists of three stages (Fig. 1): (1) identify regions suspicious for PE and score their confidence level of being a PE based on computer vision methods, (2) randomly generate 3-D paired positive and negative PE image patches in the training and internal validation sets, and (3) train a CNN-based PE segmentation model using the paired image patches. In Stage 1, suspicious PE regions are identified based on whether: (1) PEs are located in the pulmonary arteries and (2) PEs have lower densities compared to their surrounding artery. To increase the data diversity, Stage 2 is performed on the fly during the training of the CNN-based PE segmentation model. The PE negative patches are sampled from the CTPA scans without PE, while the PE positive patches are centered on high-confidence PE regions.

Fig. 1.

Algorithm overview

C. Detection of PE regions with high confidence

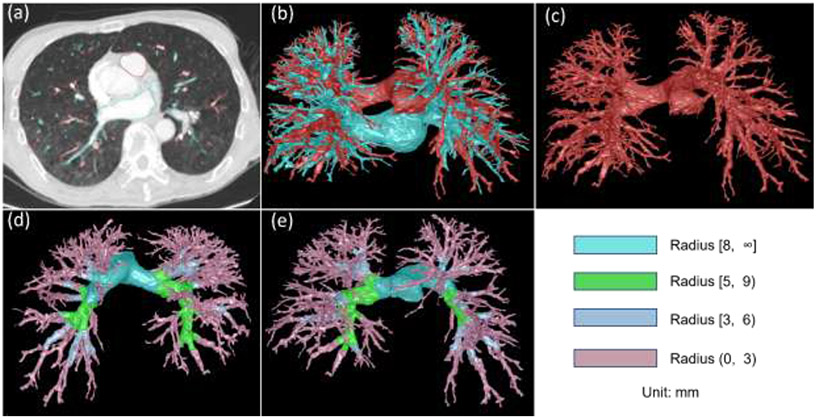
First, intra- and extra-pulmonary arteries on CTPA images are segmented using our recently developed algorithm (Fig. 2) ¹⁴. Compared with available approaches ^29-41, this algorithm does not rely on anatomical knowledge of the lungs (e.g., the proximity of airways and arteries) and demonstrated promising performance to identify lung vessels and differentiate them into lung arteries and veins. Most importantly, this algorithm can identify extra-pulmonary vessels because PE often occurs in the extrapulmonary (main) arteries.

Fig. 2:

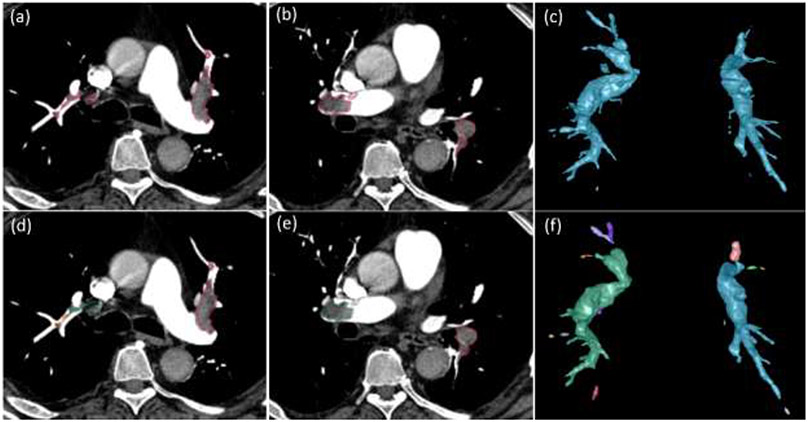
Lung artery and vein segmentation. (a) a CTPA scan where the arteries and veins are segmented and overlayed, (b) 3-D visualization of the segmented pulmonary arteries (red) and veins (green), (c) separate 3-D visualization of the pulmonary arteries, and (d)-(e) the partition of the arteries into four different levels in terms of radius.

Second, the signed distance field of the CT scan was computed with respect to pulmonary arteries using the fast marching method (FMM) ⁴². The distance field values are negative outside the arteries, positive inside the arteries, and zero on the boundaries between the artery and the surrounding regions. Mathematically, given a region denoted as $\mathrm{G}$, its signed distance field can be described by the Eikonal equation (Eq. 1). The FMM provides an efficient solution to numerically solve the Eikonal equation based on a Cartesian grid. A unique characteristic of the FMM is the ability to accurately assess the distance field of small regions (e.g., small vessels).

$$\mid \nabla f\mid =\sqrt{{\left(\frac{\partial f}{\partial x}\right)}^2+{\left(\frac{\partial f}{\partial y}\right)}^2+{\left(\frac{\partial f}{\partial z}\right)}^2}=1\text{subject to}f\mid \partial G=\pi r^2$$ (1)

Where $f_{{}_{{}_{-}}}$ denotes the signed distance from a voxel to the boundary $\partial \mathrm{G}$ formed by the grid points and $\nabla$ denotes the gradient.

Third, the arteries were progressively partitioned into different levels in terms of the artery dimension based on the signed distance field (Fig. 2). In our implementation, the partition was based on four different diameter ranges (unit: mm), including [8, ∞), [5, 9), [3, 6), and (0, 3). This partitioning strategy was to minimize the variation of the artery density in each partition because the density of the arteries on CT images typically varies across their sizes. Overlap between neighboring partitions ensured that potential PEs across two partitions could be fully identified.

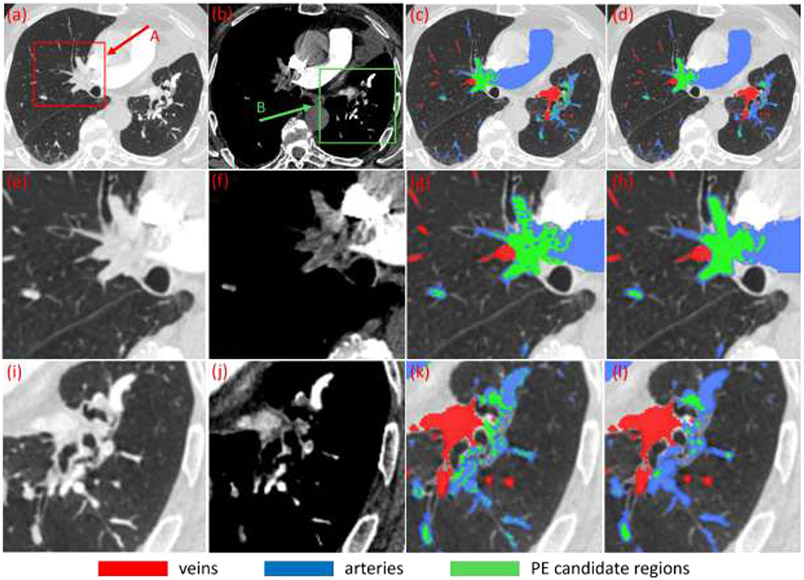
Fourth, the mean density of each partition was computed based on HU value and decreased by a specific HU value (e.g., 50 HU). The computed value is used as the threshold to binarize the corresponding partition region. Since the vessel density decreases towards the vessel boundary, this thresholding operation typically includes “noisy” regions near the walls along with the PEs (Fig.3). To address this issue, an opening morphological operation is performed with the consideration of the distance field. The erosion iteration is performed to remove the regions with small signed distance field values, which limits the erosion to the regions near the vessel wall. The objective of the constrained morphological operation is to avoid the remove small PEs in the center of the vessels. After the opening operation, a series of regions with relatively low density are identified as PE candidates (Fig. 3).

Fig. 3.

Identification of suspicious PE regions based on the thresholding of the partitioned artery regions in a subject. (a)-(b) CT images at different window/level settings, (c) results after thresholding operation, (d) suspicious PE regions (green) after constrained morphological operations, and (e)-(l) local enlargement of the images as indicated by arrow A and B in (a)-(b) and the corresponding results.

Fifth, the contrast level between a suspicious PE region and its surrounding artery region was used to score the confidence of the suspicious region being PE. The arterial region surrounding a suspicious PE is obtained by dilating the PE region to a certain distance (e.g., 5 mm) within the vessel regions. Then, the difference between the mean density of the suspicious PE region and the dilated regions is computed as the contrast level. A higher contrast level indicates a higher confidence of a suspicious region being PE.

D. Generation of PE positive/negative image patches

To avoid the manual confirmation of the PE candidate regions, regions with high confidence for a PE were used to generate the image patches. Suspicious PE regions with a contrast level larger than a specific value (e.g., 75 HU) were treated as high confidence PEs. A unique strength of CT imaging is its ability to characterize various tissues in a standard way, namely Hounsfield Unit (HU). This characteristic makes it possible to use the specific threshold in HU to analyze the images. Given the relatively small dimensions of lung vessels, a threshold of 75 HU typically indicates a conservative contrast to differentiate PE from the surrounding vessels. Based on the voxels forming the high-confidence PE regions, volumetric image patches were sampled. Notably, the volumetric image patches should only contain the high-confidence PE regions; otherwise, the image patches were not used for machine learning. The scaling operation was used to maximize the use of the high-confidence PEs. First, a predefined cubic box is placed on a voxel in the high-confidence PE region. If there are other non-high-confidence PE regions, the cubic box is scaled to a small size to avoid the inclusion of the non-high-confidence PE regions. Thereafter, the image patch based on the scaled cubic box is scaled back to the predefine size and used in the training procedure.

To facilitate unbiased machine learning, PE negative regions were also needed to train the CNN models. There are two ways to identify the PE negative regions. The first way is the simple use of PE negative cases. The limitation is the requirement for verified negative cases. The second way is the use of the regions that have no suspicious PE identifications regardless of their confidence level. The limitation is the potentially biased sampling because the suspicious regions are excluded from machine learning. Given the availability of a large number of PE negative cases in the RSNA-PE dataset, volumetric image patches were randomly sampled from the PE negative cases.

E. Training a CNN-based segmentation model

A state-of-the-art CNN model called R2-Unet ⁴³ was trained to automatically detect and segment the PEs on CTPA images in a single pass. The R2-Unet model uses a residual and recurrent convolution block to replace the traditional consequent convolution block in the U-Net ⁴⁴. The residual component allows the learning of the residual functions with reference to the layer inputs, while the recurrent component makes the learning more robust to the existence of noise. A four-stage U-Net architecture was used in our implementation. The initial number of the convolutional filters was set as 32 and multiplied by 2 in each of the convolutional blocks of the encoder and decoder paths forming the U-Net. The output layer was activated by a sigmoid function to obtain the final predictions of the foreground and the background. The Adam optimizer was used. The Dice coefficient was used as the loss function.

The R2-Unet was trained using paired PE negative/positive volumetric image patches, which were randomly sampled on verified PE negative/positive cases in the RSNA-PE dataset. The size of the volumetric image patches was set at 96×96×96 voxels with an isotropic resolution of 0.8 mm. For the sake of efficiency, the CT images were reconstructed with an isotropic resolution of 0.8×0.8×0.8 mm³ before the sampling. The isotropic resolution was determined based on the in-plane resolution of the CT images and the size of the regions of interest. Various image augmentation operations (e.g., translation, rotation, scaling, noise addition, and blurring) were used during the training to increase the data diversity and thus the reliability of the CNN model ⁴⁵. The initial learning rate was set as 0.001 and reduced by a factor of 0.5 if the validation performance did not increase in three continuous epochs. The training procedure was terminated when the validation loss did not decrease across ten continuous epochs.

F. Performance validation

The performance of the proposed algorithm, which trained the CNN model on the image patches obtained by the computer vision method, was evaluated on the manually outlined PEs in the independent dataset (Dataset II). The Dice coefficient was computed to assess the agreement between the computer segmentation results and the manual outlines. The detection-localization characteristics at the embolism level were estimated in terms of the true-positive fraction (TPF) or sensitivity, which is the proportion of “true” detected PE regions with respect to the total PE regions identified by the radiologist, and the false-positive rate (FPR), which is the average number of FP results per CT scan. A PE region detected by the algorithm was considered as a false positive (FP) if it did not overlap with the radiologist’s manually outlined regions; otherwise, it was considered a true positive (TP). These performance metrics were computed separately based on the location and size of the PEs to clarify the performance of the trained CNN models across different types or sizes of PEs. To facilitate a fair comparison, we trained a second R2Unet model exclusively on the manually annotated cases in the independent test set. We then compared its performance with the model trained on the paired image patches obtained by the computer vision method. Results were also assessed based on PE location as main arteries, right lung, and left lung. Due to the relatively small size of the manually outlined dataset, the 5-fold cross-validation method was used to validate the performance of the second model. We note that the k-fold cross-validation was only performed on the second model for comparison purposes and was not utilized in the development of the proposed algorithm. A paired samples t-test was used to assess the performance difference between the two CNN models. A p-value less than 0.05 was considered statistically significant.

III. RESULTS

In the RSNA-PE dataset, 59.6% (1,317/2,211) of the PE positive cases contained PEs scored by the algorithm as high-confidence (Table 1). The number of cases with high-confidence PEs located in the main arteries, right lung, and left lung were 388, 1068, and 849, respectively. A total of 4,039 high-confident PEs were detected in 1,317 CTPA scans, with 1,107, 1,579, and 1,353 PEs located in the main arteries, right lung, left lung, respectively (Table 2). In the RNA-PE dataset, the average number of PEs per case was 3.07 (±2.21) with a range from 1 to 9. Thirty-five percent (1,426/4,039) of the identified high-confidence PEs were less than 10mm long.

Table 1.

Performance of the computer algorithm to identify high-confidence PE regions in the RSNA-PE dataset (n=7,279).

Case	Count	Cases with high-confidence PEs (%)
PE Positive	2,211	1,317 (59.6%)
PE Negative	4,911	-
Indeterminate	157	-
Central PE	401	388 (96.8%)
Right PE	1,875	1,068 (57.0%)
Left PE	1,544	849 (55.0%)

Table 2.

Characteristics of the manually outlined PE regions in the independent cohort and the high-confident PE regions in the RSNA-PE dataset

	Independent test set (n=91)	RSNA-PE (n=1,317)
Count: total, mean (SD), range	970, 10.66 (6.46), 1–30	4039, 3.07 (2.21), 1–9
Volume (ml): mean (SD)	0.74 (3.02)	1.08 (3.37)
Cross-section radius (mm)*: mean (SD)	1.82 (1.25)	2.06 (1.49)
Length (cm): mean (SD)	2.40 (3.50)	2.97 (3.84)
length (mm): count (%)
(0, 5)	169 (17.4%)	606 (15.0%)
[5, 10)	266 (27.4%)	820 (20.3%)
[10, 20)	235 (24.2%)	1,321 (32.7%)
[20, ∞)	300 (30.9%)	1,292 (32.0%)
Location: count (%)
Central (main artery) PE	193 (19.9%)	1,107 (27.4%)
right PE	419 (43.2%)	1,579 (39.1%)
left PE	358 (36.9%)	1,353 (33.5%)

^*The cross-section radius is the largest distance value of a suspicious PE region.

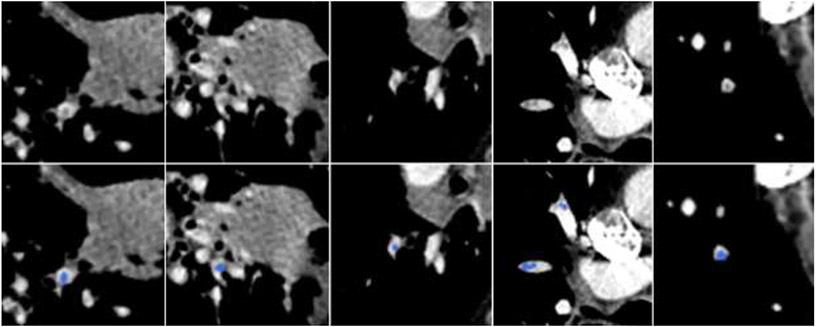
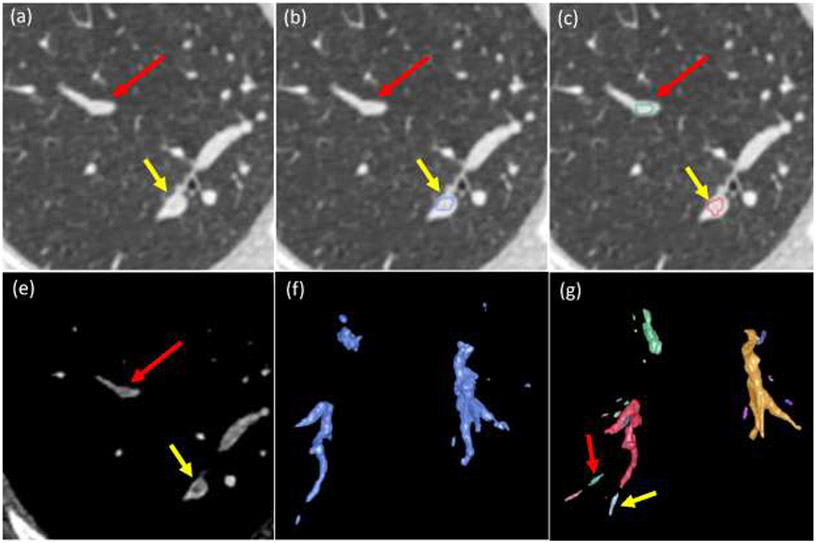
The thoracic radiologist identified and outlined 970 PEs in the independent dataset (n=91), among which 193 were located in the main arteries, 419 in the right lungs, and 358 in the left lungs. Their volume and length distributions were also summarized in Table 3 for a direct comparison with the high-confident PE regions in the RSNA-PE dataset. Forty-five percent of the PEs (435/970) were less than 20 mm long with 17.4% less than 5 mm long. The percentages of the small high-confident PE regions obtained from the RSNA-PE dataset were somewhat higher than those in the independent test set. Some examples of the manually identified small PE regions are shown in Fig. 4.

Table 3:

Performance of the CNN-based models on the independent test set (n=91) with 970 manually outlined PEs.

PE size or location (Length: mm)		Metrics	Model 11	Model 22
Length (mm)	(0,5)	Sensitivity3	0.30 (50/169)	0.32 (54/169)
		False positive rate3	0.76 (69/91)	1.73 (157/91)
	[5,10)	Sensitivity	0.34 (91/266)	0.32 (86/266)
		False positive rate	0.60 (55/91)	1.35 (123/91)
	[10,20)	Sensitivity	0.80 (187/235)	0.61 (143/235)
		False positive rate	0.40 (36/91)	0.87 (79/91)
	[20, ∞)	Sensitivity	0.91 (272/300)	0.90 (269/300)
		False positive rate	0.09 (8/91)	0.25 (23/91)
Location	Central (main artery)	Sensitivity	0.72 (138/193)	0.67 (129/193)
		False positive rate	0.21 (19/91)	0.47 (43/91)
	Right	Sensitivity	0.62 (259/419)	0.55 (230/419)
		False positive rate	0.96 (87/91)	2.18 (198/91)
	Left	Sensitivity	0.57 (203/358)	0.54 (193/358)
		False positive rate	0.68 (62/91)	1.55 (141/91)
All		Dice coefficient4	0.676 (0.168)	0.647 (0.192)
		Sensitivity	0.62 (600/970)	0.57 (552/970)
		False positive rate	1.86 (168/91)	4.20 (382/91)

¹Model 1 was trained on the high-confident PE regions in the RSNA-PE dataset and validated on the manually annotated independent test set.

²Model 2 was trained and validated on the manually annotated independent test set using 5-fold cross-validation.

³Sensitivity and false positive rate (per scan) were computed at the PE level.

⁴Dice coefficient was measured at the voxel level.

Fig. 4.

Small PEs manually outlined by the radiologist in the independent test set. Top row: original CT images. Bottom row: manually outlined PE regions in blue.

Table 4 summarizes the performance of the two CNN models when validated on the same test set. An example in Fig. 5 showed the performance of the trained CNN model in detecting PE regions. The CNN model trained on the high-confident PE regions (Model 1) performed significantly better than the model trained on the manually outlined results (Model 2) in detecting and segmenting PE regions (p<0.01) (Table 3). Model 1 showed a false positive rate of 1.86 per CT scan, while Model 2 had a false positive rate of 4.20 per CT scan. An example in Fig. 6 showed various false positive detections compared to the manual outlines. Performance was poor for detecting small PEs for both models. For the PEs between 10 to 20 mm, Model 1 had significantly higher sensitivity compared to model 2. For the PEs longer than 10 mm, Model 1 had significantly higher sensitivity compared to Model 2 (p<0.01). Both models had a sensitivity of around 0.9 for detecting PEs longer than 20 mm. The typically missed large PEs had a long length but a small radius, as demonstrated by the example in Fig. 7, where the central PE was missed by the CNN models. We made the prototype system based on the algorithm available online to allow anyone to test the system’s performance. The online system can be accessed at the link: http://47.93.0.75:9190/.

Fig. 5.

Performance of the CNN model. Top row: manually outlined PEs. Bottom row: detection and segmentation by the CNN model trained on the high-confidence PE regions.

Fig. 6.

False positive detections. (a) and (e) original CT images at different window/level settings with false positive (red arrow) and true positive (yellow arrow), (b) overlay of the radiologist’s manual outline, (c) overlay of the detection and segmentation by the CNN model, (f) 3-D visualization of the manually outlined PEs, and (g) 3-D visualization of the PE regions detected by the CNN model.

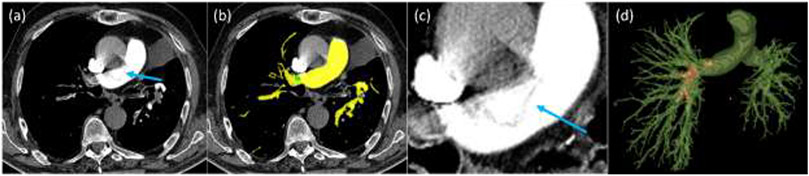
Fig. 7.

A false negative detection of a PE region in the main artery. (a) original CTPA image, (b) automated detection and segmentation of the arteries (yellow) and PE regions (in green), (c) the local enlargement of the false positive detection in the main artery, and (d) 3-D visualization of the segmented arteries and PEs (red).

IV. DISCUSSION

We developed a new computer scheme to automatically detect and segment PEs on CTPA scans. One novelty lies in the strategy of training a CNN model without manually outlining the PE regions. It utilizes computer vision methods to automatically locate high-confidence PE regions and then trains a CNN model based on the image patches located on the identified PE regions. To our knowledge, only a few studies were dedicated to the automated detection and segmentation of PE regions ^{19, 24, 25}. Wittenberg et al. ¹⁹ evaluated the performance of a software system, which was developed by Phillips Healthcare to detect PE, on a dataset of 225 negative and 67 positive cases. At the embolism level, the system had an average 4.7 false positive detection per CT scan. Yang et al. ²⁴ described a two-stage algorithm, which first detected the suspicious PE regions and then reduced the false positive detections based on 2-D CNN-based classifier. Their algorithm demonstrated a sensitivity of 75.4% with two false positives per scan. Tajbakhsh et al.²⁵ used a thresholding method to identify the PE candidate regions and then used 2-D CNN classification model to reduce the false positives. Their algorithm demonstrated a sensitivity of 33% with two false positives per scan. In contrast, our scheme had a sensitivity of 62% and an average 1.86 false positives per CT scan. Our performance is promising, given that a large number of small PEs were taken into account in our analyses.

Another unique characteristic of this study is the verification of whether the legacy of the traditional computer vision technology could be leveraged to facilitate CNN-based deep learning by avoiding the time-consuming manual outlining to generate the ground truth for machine learning. A large number of computer vision algorithms have been developed to detect and segment various diseases and anatomical structures based on medical images; however, their performance is unsatisfactory. The emergence of deep learning technology is rapidly transforming the landscape of medical image analysis, and the image processing methodology is quickly shifting from traditional computer vision technology to deep learning. This shift is primarily caused by the fact that CNN-based deep learning consistently outperforms the traditional computer vision algorithms in medical image analysis. There are arguments about whether the traditional computer vision technique is dying or not. The primary advantage of traditional computer vision algorithms as compared to deep learning is no need for extensive manual outlining of the regions of interest. Although the number of radiological examinations performed in clinical practice is innumerable, the value of the examinations for deep learning is limited without manual annotations or ground truth available. It is extremely desirable to have an approach that can process radiological examinations without the need for extensive manual outlining efforts. Our study compared CNN models developed with and without manual annotation. Although outlines of the PE regions by a single radiologist are inherently associated with some level of bias, our study primarily focuses on the feasibility of the developed annotation-free deep learning strategy. To verify this feasibility, we conducted experiments on an independent dataset collected from a third institution. Our results demonstrate the developed scheme's generalizability to an unrelated population dataset, highlighting its potential applicability to similar problems.

We are aware that the RSNA dataset includes several categories of labels based on location (central, right, and left) and condition (normal, chronic, acute, and both). Previous studies have utilized this labeling system to classify patients or CTPA scans into these categories ^{23, 46-48}. However, in this study, our main focus is on detecting and segmenting PE regions at the voxel level rather than categorizing based on these label categories. We believe that, like many other voxel-level image segmentation tasks, segmenting PE regions is crucial for extracting interpretable image features and has significant clinical implications. For instance, accurate segmentation can help assess the obstruction level of a PE region, which can ultimately aid in developing precise and personalized treatment. Different sizes and/or locations of a PE region could be associated with different clot burdens. The size, shape, location, and extent of a PE region may indicate different clot burdens, making accurate segmentation a crucial factor in clinical decision-making.

There have been a large number of CNN models developed for medical image segmentation, such as nnU-net ⁴⁹. However, our emphasis in this study is not to develop a novel CNN model or to optimize the parameters of an available CNN model like nnU-net but to validate the feasibility of training a CNN model without manual outlines by utilizing traditional computer vision methods and the huge amount of image data in clinical practice to train a CNN-based deep learning model. Hence, we simply used the R2Unet to demonstrate the feasibility of the proposed idea. Based on our previous experiences ⁵⁰, the strength of the R2Unet is its simple implementation and ability to handle relatively fuzzy and small regions of interest (e.g., intramuscular fat ⁵⁰) due to its “recurrent” and “residual” characteristics. When training the CNN models, learning rate, batch size, 3-D image patch size, and image patch resolution can all affect the performance of the trained models. It is difficult to optimize all these parameters. However, we ensured that the CNN models were trained under the same configuration for a fair comparison. In our implementation, the computer vision component is responsible for extracting image patches, while the CNN model component is responsible for machine learning based on the obtained patches. By replacing the specific CNN architecture while retaining the overall framework, our method can be utilized with different CNN models. Therefore, despite the limitation that only a single CNN model (i.e., R2-Unet) was implemented to test the developed method, we anticipate that our method could be adapted to other CNN models.

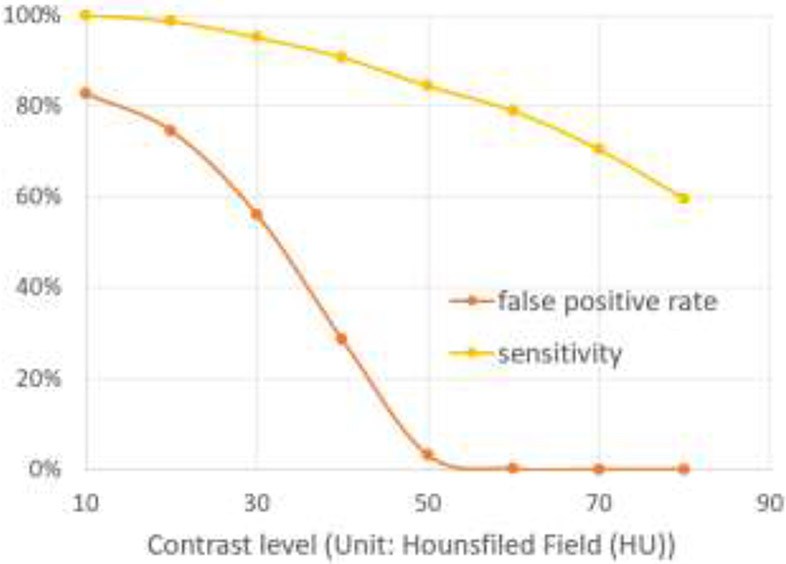
Our approach used the fact that PEs are located in the arteries and appear as low-density regions. We applied a traditional computer vision method to 2,211 PE positive cases in the RSNA-PE dataset and detected 1,317 cases with high-confidence PEs. This suggests a relatively low sensitivity of the traditional computer vision method and demonstrates its inferior reliability compared to CNN-based deep learning. Although the computer vision algorithm missed a large portion of the PE regions, it still reliably detected a certain portion of high-confidence PE regions, which was used to train more reliable CNN models. To determine the confidence level, we used a threshold of 75 HU to distinguish PE from neighboring vessels. To verify the effectiveness of this threshold, we performed an experiment by evaluating the sensitivity and false positive rate (FPR) over a range of thresholds (10-80 HU) using our cohort with manually outlined PE (Fig. 8). FRP is defined as the ratio between false positive detections and all detections. When the threshold was 60 HU, the FRP rate was around 0.1% (only two false positives). When the threshold was 70 HU or larger, there were no false positives. Hence, as we expected, 75 HU is a relatively conservative threshold for our purpose.

Fig. 8.

The impact of the contrast level (unit: HU) on the determination of false positive rate and sensitivity of PE regions.

As our experiments on an independent test set showed, the CNN model trained on the high-confidence PE regions demonstrated a significantly better overall performance (i.e., sensitivity, false positive rate per scan, and Dice coefficient) than the CNN model trained on the manual outlines (p<0.01) (Table 3). This could be attributed to the fact that the former CNN model was trained with 1,317 CT scans with 4,039 PE regions, while the latter CNN model was trained with 91 CT scans with 970 PE regions. Also, the PE-negative cases in the RSNA-PE dataset were also used to train the former CNN model. This advantage benefits directly from utilizing the traditional computer vision method and a relatively large dataset (i.e., RSNA-PE) for identifying high-confident PE regions.

We noticed that the CNN models demonstrated a moderate performance in detecting PE regions located in the main pulmonary arteries. This was primarily caused by the existence of many small PE regions in our independent test dataset (Fig. 4). The dataset with manually annotated PEs contained 17.4% of PE regions with a length less than 5 mm and 27.4% less than 10 mm, indicating the high prevalence of small PEs. The low performance of the CNN models in detecting small PE regions was primarily caused by the challenge of their small size and fuzzy boundaries or low contrast compared to their background (Fig. 4). At this moment, we do not have an approach to effectively address the poor performance in detecting small PE regions. One possible solution is to increase the scale of the dataset to improve the learning of small PEs. Also, the PEs in the main pulmonary arteries only accounts for 19.9% of the PEs in the independent dataset. More PEs are located in the right lung than in the left lung. This fact suggests that only focusing on the PEs located in the central artery and those with large sizes can miss early detection.

While U-Net and its variants are primarily designed for image segmentation, we used a segmentation model (R2Unet) to detect and segment PE regions simultaneously. During the process, the CNN model assigns each voxel in the image a probability of belonging to a specific category or region of interest. However, for CNN-based segmentation tasks, the probability map of the segmentation results often has a value close to 1 for identified regions, and only the voxels near the boundary have low probability values. This “miscalibration” may be caused by the iterative training of the CNN models. Consequently, using the mean probability of a region to characterize the probabilities of identified regions is not reasonable. Therefore, the free-response receiver operating characteristic (FROC) analysis is not a suitable method here to evaluate the detection performance. To mitigate this limitation, we employed two evaluation metrics, namely the Dice coefficient for segmentation performance and a hit criterion, to assess the performance of our approach (Table 3). However, it is important to acknowledge that further research is needed to delve into the underlying reasons for the observed miscalibration. By investigating these causes, we can explore the possibility of incorporating additional performance evaluation methods, such as FROC analysis, to provide a comprehensive assessment of the effectiveness of our proposed algorithm.

The RSNA-PE data was collected from multiple medical institutes and acquired using a variety of imaging protocols. Such data heterogeneity caused by image quality does not affect CNN-based deep learning because various data augmentation operations (e.g., noise addition and image blurring) attenuate the impact of the heterogeneity in image quality. This was verified by the promising performance of the CNN model trained on the RSNA-PE dataset and validated on the independent test dataset. The CNN model proved to be robust to the data heterogeneity in terms of image acquisition protocol or image quality.

V. CONCLUSIONS

We developed and validated a novel strategy to automatically detect and segment PEs depicted on CTPA scans. One unique characteristic is that the CNN-based deep learning model was trained without manually outlined PEs. The underlying idea is to first identify high-confidence PEs in CTPA images using traditional computer vision algorithms and then extract 3-D image patches based on these high-confidence PEs to train a CNN-based segmentation model. A secondary motivation for this study is to utilize the availability of a large image dataset without annotation. Our experiments showed a promising performance of the developed scheme and suggested the feasibility of the proposed idea, which may be applicable to other similar medical image analysis problems.

Highlights.

• A novel strategy to reuse available computed tomography pulmonary angiography (CTPA) scans to train a convolutional neural network for pulmonary embolism (PE) detection and segmentation

• The algorithm uses deep learning but does not require manual outlines of the PE regions.

• The CNN model trained on a large dataset without manual outlining demonstrated a better performance than the same CNN model trained on a small dataset with manual outlining.

• Traditional computer vision algorithms can be leveraged to identify high-confident regions of interest for deep learning.