Abstract
Cardiac function is tightly regulated by the autonomic nervous system (ANS). Activation of the sympathetic nervous system increases cardiac output by increasing heart rate and stroke volume, while parasympathetic nerve stimulation instantly slows heart rate. Importantly, imbalance in autonomic control of the heart has been implicated in the development of arrhythmias and heart failure. Understanding of the mechanisms and effects of autonomic stimulation is a major challenge because synapses in different regions of the heart result in multiple changes to heart function. For example, nerve synapses on the sinoatrial node (SAN) impact pacemaking, while synapses on contractile cells alter contraction and arrhythmia vulnerability. Here, we present a multiscale neurocardiac modeling and simulator tool that predicts the effect of efferent stimulation of the sympathetic and parasympathetic branches of the ANS on the cardiac SAN and ventricular myocardium. The model includes a layered representation of the ANS and reproduces firing properties measured experimentally. Model parameters are derived from experiments and atomistic simulations. The model is a first protoype of a digital twin that is applied to make predictions across all system scales, from subcellular signaling to pacemaker frequency to tissue level responses. We predict conditions under which autonomic imbalance induces proarrhythmia and can be modified to prevent or inhibit arrhythmia. In summary, the multiscale model constitutes a predictive digital twin framework to test and guide high-throughput prediction of novel neuromodulatory therapy.
Keywords: sympathetic nervous system, parasympathetic, autonomic nervous system, cardiac electrophysiology, computationial model, arrhythmia, Digital twins
Graphical Abstract

We present a new multiscale model of autonomic control of cardiac electrophysiology that integrates data from the atomistic, subcellular, cellular and systems scale and predicts the effect of efferent stimulation of the sympathetic and parasympathetic branches of the autonomic nervous system on the cardiac sinoatrial node and ventricular myocardium.
Introduction
“Every affection of the mind that is attended with either pain or pleasure, hope or fear, is the cause of an agitation whose influence extends to the heart.”
William Harvey (1628)
Modulation of peripheral nerve activity holds great promise for treating, preventing, and reversing a host of cardiovascular diseases, including heart failure, hypertension, and heart rhythm disorders (Randall & Ardell, 1985; Zuanetti et al., 1987; Grassi et al., 1998; Grassi, 2007; Grassi et al., 2007; Grassi et al., 2008a; Grassi et al., 2008b; Lahiri et al., 2008; Lopshire et al., 2009; Fukuda et al., 2015). Even though the promise of this approach is well accepted, successful design and implementation of neuromodulatory therapy is limited by the utter paucity of tools that can predict cardiac and vascular responses to peripheral nerve activity. To develop such tools, a comprehensive collaborative effort to map and model complex spatio-temporal subcellular, cellular, and tissue-level responses was needed. Here, we present the first neurocardiac simulator resulting from a collaborative team as part of the NIH Common Fund program “Stimulating Peripheral Activity to Relieve Conditions (SPARC)”.
This computational model we present was built using multiscale data to both inform and validate the model parameters and outputs both within subcellular, cellular and tissue scales as well as across them. To our knowledge, this constitutes the first instance of a digital twin for neurocardiac modulation. The tool can be used to reveal how the autonomic nervous system regulates cardiac function and to predict neuromodulation to prevent or reduce disease. The simulator integrates data from the atomistic (e.g., β-adrenergic receptor – norepinephrine interaction affinities and rates), subcellular (e.g., cAMP dynamics), cellular (e.g., action potential and calcium transient), tissue (e.g., conduction velocity) and system (e.g., pseudo-ECG) scales. The model predicts the effect of efferent stimulation of the sympathetic and parasympathetic branches of the autonomic nervous system (ANS) on the cardiac sinoatrial node (SAN) and ventricular myocardium and accounts for the coupling between them.
Development and application of computational modeling and simulation in the investigation of plausible fundamental cardiac mechanisms and to predict cardiac physiology and pathophysiology has grown dramatically over the last two decades. Indeed, multiple modeling studies have begun to address varying aspects of autonomic cardiac control. As experimental and clinical approaches have become increasingly sophisticated, new data has revealed multiple physiological processes and mechanisms from the protein to the patient. Computational modeling and simulation have kept pace with these developments and a number of important models are now available in the literature and in the public domain.
Computational and mathematical models have also been used to demonstrate functional mechanisms of heart rate variability (Prokhorov et al., 2021) (Karavaev et al., 2019) (von Rosenberg et al., 2019), applied to reveal the dynamics of autonomic control during orthostatic adaptation (Ishbulatov et al., 2020) and shown to capture heart rate control by sympathetic and parasympathetic discharge (Prokhorov et al., 2021) (Warner & Cox, 1962) (Kember et al., 2011) (Kember et al., 2011; Kember et al., 2017). Detailed subcellular models have been utilized to predict the mechanisms of postsynaptic receptor activation following nerve stimulation and to propose likely mechanisms for feedback and feed forward regulation of cardiac electrophysiology and contraction in the SAN and in contractile cells respectively (Castellanos & Godinez, 2015) (Yang & Saucerman, 2012) (Behar et al., 2016) (O’Hara & Rudy, 2012) (Iancu et al., 2007; Iancu et al., 2008).
There have also been numerous atomistic modeling and simulation studies of β-adrenergic receptors (βARs) that link the autonomic nervous system to downstream cellular signaling events and function recently reviewed (e.g., (Ribeiro & Filizola, 2019) (Wang & Miao, 2019; Hilger, 2021)). These studies were enabled in large part by advances in atomic-resolution structural characterization of adrenergic receptors and their complexes with small-molecule ligands as well as regulatory proteins via X-ray crystallography, cryogenic electron microscopy, NMR spectroscopy and other experimental techniques (Kobilka, 2011; Katritch et al., 2013; Thal et al., 2018; Shimada et al., 2021). Exploring atomistic-resolution receptor and ligand conformational dynamics was found to be crucial to provide an accurate description of βAR signaling pathways (Hilger, 2021) but accurately determining ensuing energetic and kinetic quantities was proven to be challenging and requires usage of simplified models, extremely long simulations and/or advanced simulation techniques. This is however essential for elucidation of atomistic simulation derived parameters for functional kinetic modeling of subcellular signaling such as those from Iancu-Harvey (Iancu et al., 2007), Soltis-Saucerman (Soltis & Saucerman, 2010) models as used in our study.
The frequency of activation of pacemaking cells in the SAN, the conduction velocity of action potentials, as well as the strength of EC coupling is tightly regulated by the autonomic nervous system. However, despite the importance of the fundamental connection between the brain and heart, there is still an incomplete understanding of how the autonomic nervous system regulates cardiac function in health and disease (Young et al., 1993; Armour, 2004; Verrier & Antzelevitch, 2004; Olshansky, 2005; Patterson et al., 2007; Tan et al., 2008; Zhou et al., 2008a; Zhou et al., 2008b). Description and prediction of the mechanisms underlying the interaction between nervous system discharge and the resultant emergent cardiac events in a digital twin are needed to allow for identification and specific targeting to prevent and treat arrhythmia provoking conditions by drugs and by direct electrical stimulation (Meng et al., 2017; Hanna et al., 2021).
Methods
Autonomic nervous system (ANS) Network Structure
The structure of the ANS network model is based on the connectivity among various intrathoracic neurons and central neurons that are involved in cardiac regulation as described by Shivkumar et al (Fukuda et al., 2015; Shivkumar et al., 2016) and the corresponding computational models of Kember et al. (Kember et al., 2011; Kember et al., 2017) (see Figure 1). The neural circuit consists of the sympathetic pathway (SNS) and the parasympathetic pathway (PNS). The SNS is comprised of three layers (subnetworks): the central nervous system (CNS), the intrathoracic nervous system (ITNS) and the intrinsic cardiac nervous system (ICNS). Efferent pathways connect the CNS to the ITNS, and the ITNS to a subpopulation of neurons in the ICNS (i.e., the S-ICNS). Afferent pathways connect the S-ICNS with the ITNS. The PNS comprises two layers (subnetworks): the CNS and a subpopulation of neurons in the intrinsic cardiac nervous system (i.e., the P-ICNS), with efferent connections from the CNS to the P-ICNS. The S-ICNS and the P-ICNS are also interconnected. Note that there is no clear delineation between a sympathetic ICNS and a parasympathetic ICNS, and the S-ICNS and the P-ICNS in the model are extensively connected, effectively forming a single sub-network.
Figure 1:
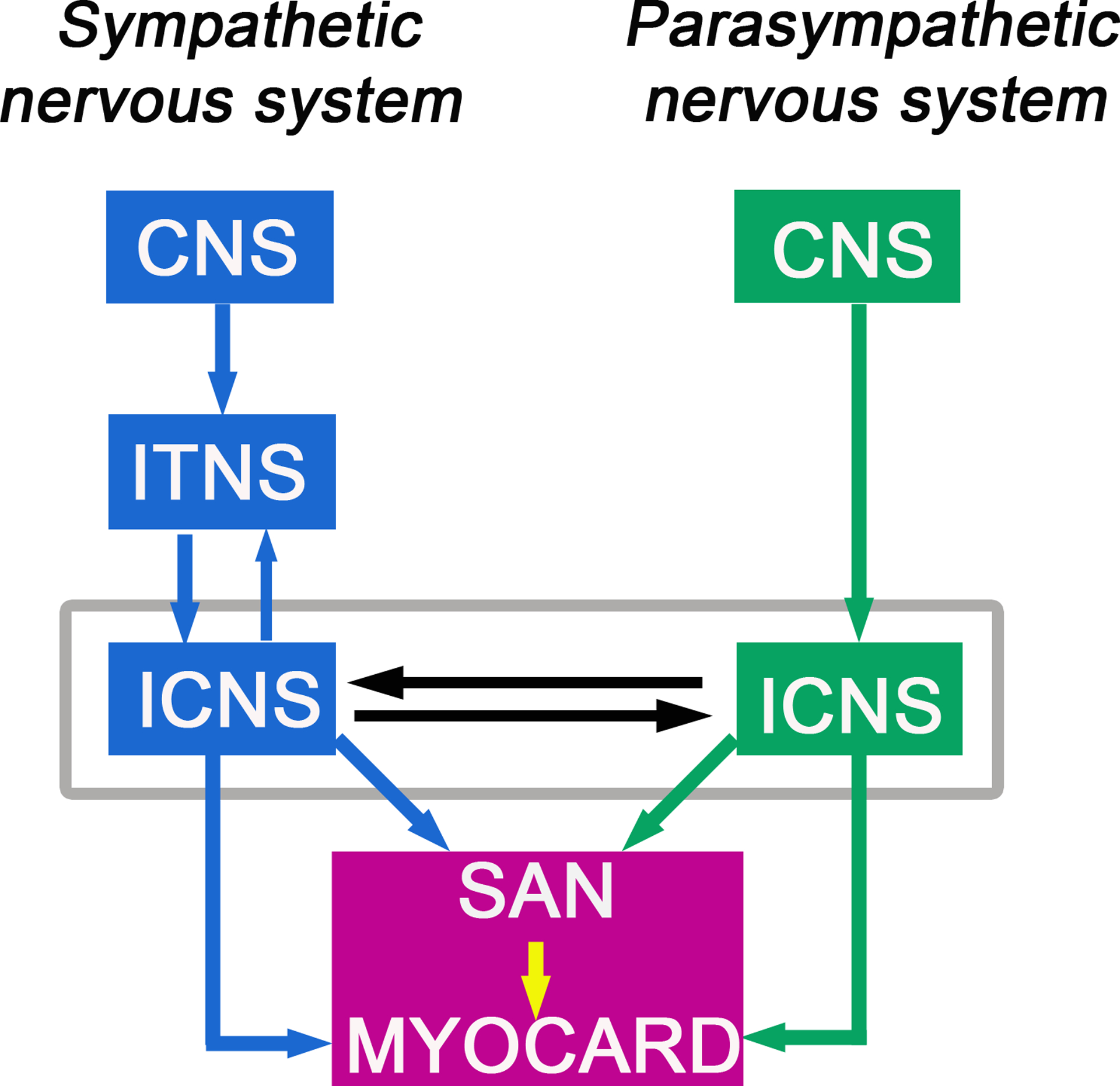
Schematic representation of the connection of sympathetic and parasympathetic nervous system branches to sinoatrial nodal cell representations and ventricular myocyte computational cells. The modular workflow consists of a network layer representation for the sympathetic branch (blue) and the parasympathetic branch (green) of the autonomic nervous system (ANS) that both synapse onto the cardiac sinoatrial node (SAN) as well as on cardiac ventricular myocardium (purple box). The model allows for prediction of efferent sympathetic and parasympathetic signaling and target-organ responses. The model drives spontaneous pacemaker action potentials modulated by the ANS that determine the cardiac ventricular pacing frequency (indicated by the yellow arrow).
ITNS & ICNS Neuronal Dynamics
The ITNS and ICNS sub-networks each contain 50 model neurons. Individual neurons in the ITNS and ICNS are described by a single-compartment conductance-based generalized integrate-and-fire (GIF) model (Jolivet et al., 2004). The subthreshold dynamics of the neurons include a leakage current, a delayed-rectifier potassium current, an M-current (Kwag et al., 2014), and a synaptic current. The equations governing the sub-threshold dynamics of the j-th neuron are
| (1) |
| (2) |
where is time (in ms), is the transmembrane potential (in mV); are the activation variables of the delayed rectifier potassium current and the M-current, respectively; is the input synaptic current into the j-th neuron; is the membrane capacitance, and are the maximal conductances of the leakage, delayed-rectifier potassium, and M-currents, respectively; are the reversal potentials of the leakage and delayed-rectifier potassium and M-currents; are the time-constants for the activation variables, and the function is the subthreshold steady-state activation of the activation variable , given by the equation
When the transmembrane potential of a model neuron reaches a threshold potential (), the neuron fires an action potential and the transmembrane potential is “reset”. Note that, in the GIF model, action potentials are not explicitly modeled. Each action potential can be thought of as an instantaneous spike in membrane potential followed by a brief absolute refractory period (). Following the absolute refractory period, the transmembrane potential is set to a reset potential (), and the sub-threshold dynamics (described above) are resumed. To capture the effect of the action potential on the gating variables, and are updated to include the increase that would occur during a stereotypical spike. Specifically, when , the membrane potential and gating variables are updated to
To model the saturation of the gating variables (i.e., and must be between 0 and 1), the update values for the gating variables, and , are scaled by ,
GIF model parameters where set to elicit similar firing properties of autonomic neurons (Springer et al., 2015) (see Figure 2) and are provided in Table I. Except for the M-current conductance and synaptic conductances, parameters for the neurons were homogeneous; was chosen from a beta distribution with minimum and maximum values taken to approximate values from previous models (Kwag et al., 2014). Synaptic dynamics are described below.
Figure 2:
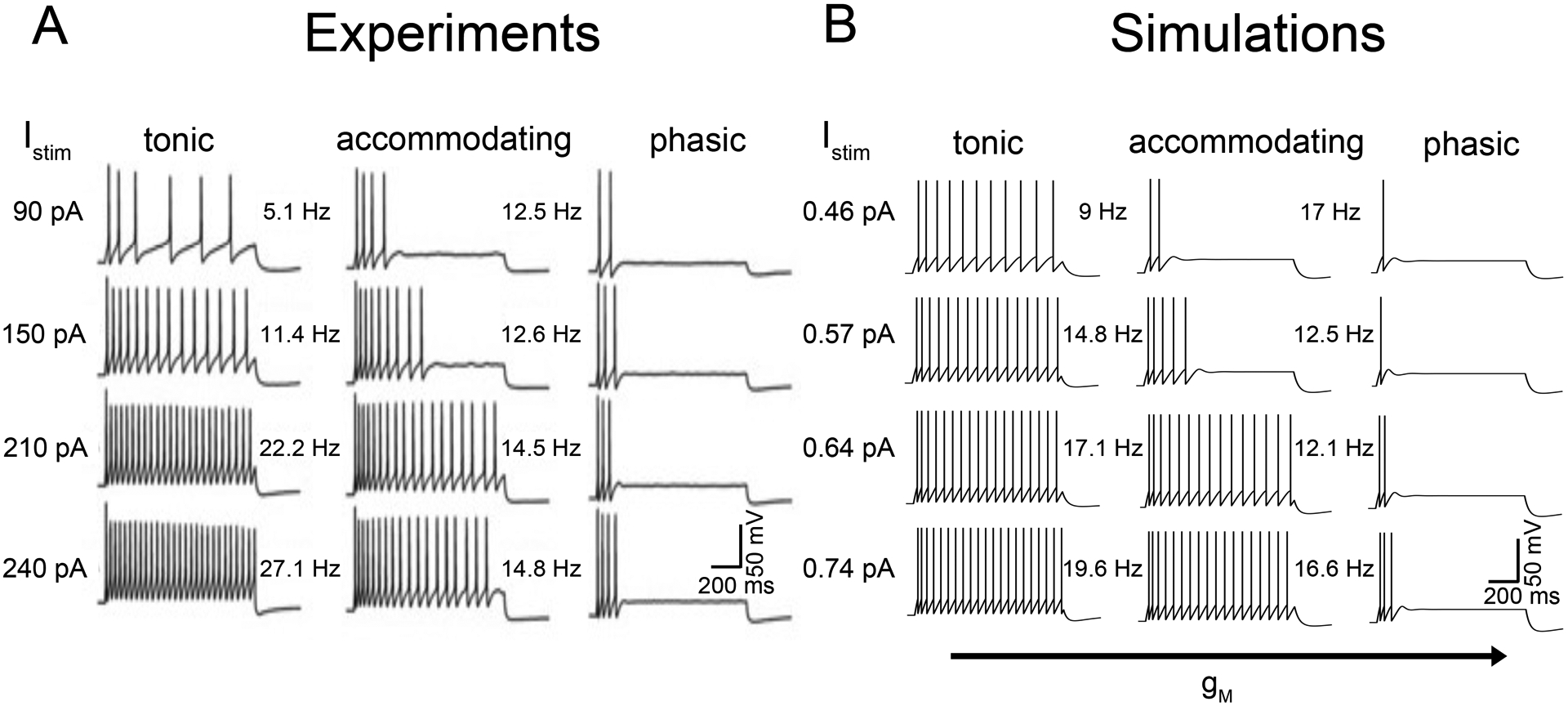
Model generation of three distinct types of neuronal firing dynamics. Shown are examples of A) experimentally recorded current-voltage relationships of neurons in the superior cervical ganglion of adult male rats (Springer et al., 2015) and B) model predicted neuronal firing recorded by using a 1s stimulus with differing stimulus current input amplitude. (A) Experimental recordings indicate that neurons generate at least three types of firing patterns: tonic, accommodating, and phasic. Tonic neurons fired repetitively at frequencies proportional to strength of stimulus. Accommodating neurons adapted and ceased firing at lower stimulus levels. Phasic neurons fired one to four spikes and ceased firing. (B) Model neurons displayed tonic, accommodating, and phasic firing dynamics. Variations in maximal M-current conductance (gM) elicited a change in firing dynamics observed in experiments and indicate a plausible mechanism to explain the firing dynamics in panel A.
Table I:
ANS model parameter values
CNS Neuronal Dynamics
The sympathetic and parasympathetic CNS sub-networks contain 50 model neurons each. Spike times for the individual neurons in the CNS subnetworks are modeled as renewal processes. That is, the firing times of the j-th neuron in the sympathetic and the parasympathetic branches of the CNS are given by Poisson processes with firing rates and and a post-spike absolute refractory period of (Gerstner & Kistler, 2002). In simulations when the SNS is activated, , and when the PNS is activated, ; otherwise they are 0.
Synaptic Dynamics
The synaptic dynamics throughout the neural circuit are modeled as alpha function synapses (Gerstner & Kistler, 2002; Lewis & Rinzel, 2003). It is assumed that, each time a presynaptic neuron fires, there is a stereotypical increase and decrease in the synaptic conductance of the post-synaptic neuron of the form
where sets the maximal conductance, is the rise time constant, and is the decay time constant. When the presynaptic neuron fires multiple times the stereotypical increases and deceases in the post-synaptic conductance adds linearly. Note that is the solution to the linear differential equation
(i.e., the damped harmonic oscillator). Therefore, because the synaptic responses are assumed to add linearly, when the j-th neuron fires at times , its synaptic output is given by
with update conditions
Values of the synaptic time constants () were set to values estimated in (Selyanko et al., 1979; Wheeler et al., 2004).
Network Connectivity
Within the ITNS and ICNS sub-networks of the SNS and within the ICNS sub-networks of the PNS, random recurrent connections from a presynaptic neuron j to a postsynaptic neuron k occur with probability and . Neurons are excitatory with probability and inhibitory with probability . The probability of connection between the S-ICNS and P-ICNS neurons is . In the PNS, efferent connections from CNS neurons to ICNS neurons occur randomly with probability of connection . In the SNS, afferent connections from the ICNS to the ITNS occur with probability . In the SNS, neurons in the ITNS receive efferent input from CNS neurons with probability , and ICNS neurons receive efferent input from ITNS neurons with probability Each neuron in the ITNS that receives efferent input receives it from n+1 random pre-synaptic neurons in each preceding layer (with n = 3), where the n connections are weak, and the 1 connection is strong. This n+1 convergent innervation has been observed in both amphibian sympathetic ganglia (Wheeler et al., 2004) and mammalian sympathetic ganglia (Skok & Ivanov, 1983; Hirst & McLachlan, 1986; Janig & McLachlan, 1992). The random connectivity in the neural circuit inherently generates populations of afferent, efferent, and local circuit neurons (Fukuda et al., 2015; Shivkumar et al., 2016).
To model afferent feedback from the cardiovascular system, each neuron in the ICNS and ITNS receive independent periodically-modulated stochastic input. The input is described by a non-stationary Poisson process with arrival function that determines the firing times of the pre-synaptic neurons, synapsing onto the ITCNS and ICNS neurons. is a piecewise-linear function with a period of 1000 that mimics the shape of the arterial pressure during the cardiac cycle
with time in . The amplitude A of the input to ICNS neurons and ITNS neurons is 0.003 and 0.002 , respectively, so that the subnetworks that are anatomically closer to the heart receive stronger cardiac input (Kember et al., 2011). Note that feedback is applied only in simulations described in Figure 3.
Figure 3:
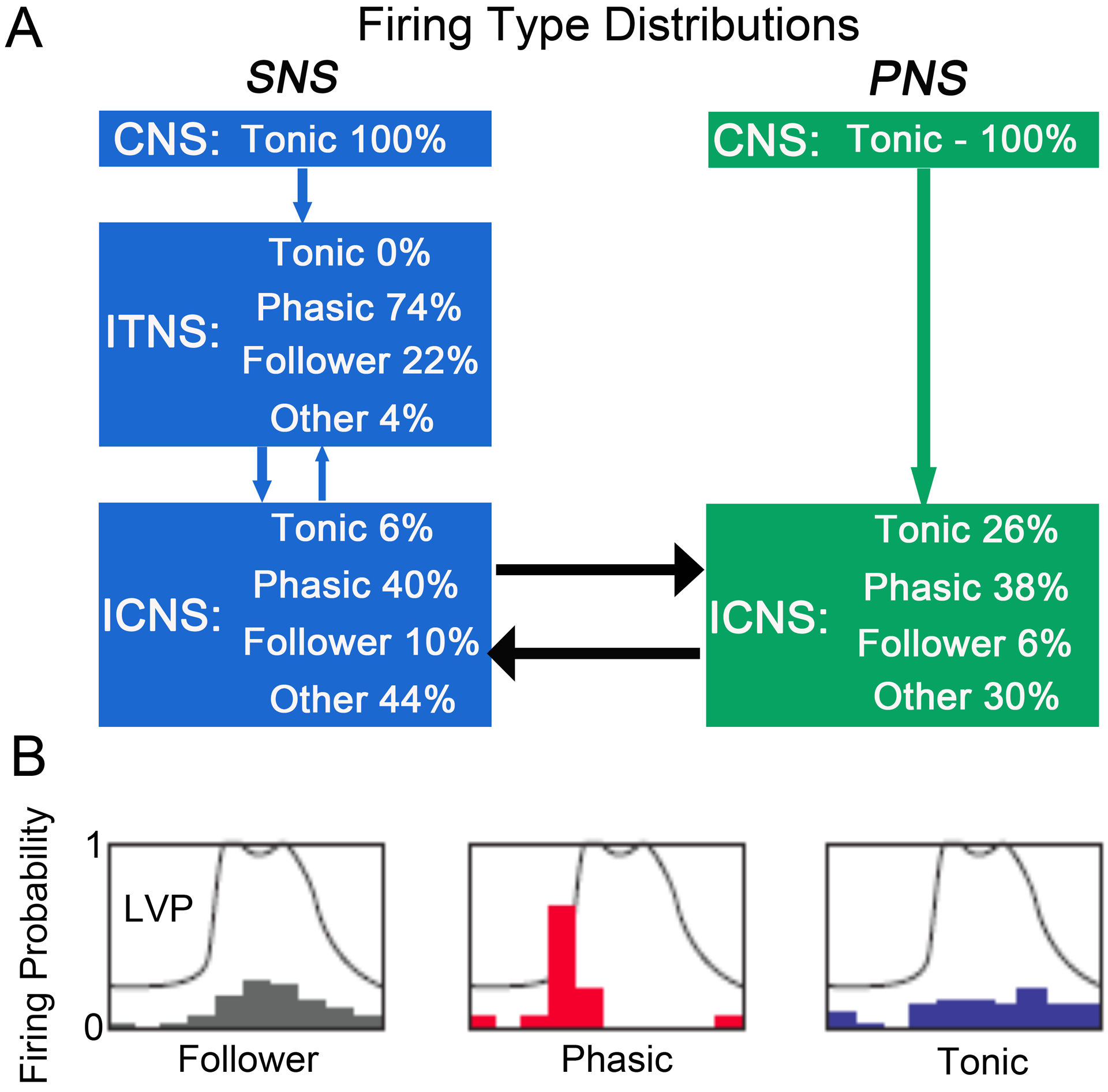
Predicted distribution of firing types in the ANS Layered Network Model. (A) Schematic of the autonomic nervous system layered network model. Each rectangle (CNS, ITNS, ICNS) represents a random network of model generated integrate-and-fire neurons with delayed rectifier potassium, leak, M-type potassium, and synaptic currents. Synaptic currents generate the intra- and inter-network connections. Inter-network connections are represented by arrows. Temporal correlation to left ventricular pressure is used to classify firing types as follower, phasic, or tonic. Distribution of firing types within each network were predicted at steady-state, averaged over seven 60-s simulations. Model generated neuronal firing patters that did not clearly fit into one classification were labeled as “other”. (B) Examples of neural firing relative to cardiac phase in ICNS neurons measured in canine (Beaumont et al., 2013). Probability density of ICNS neuronal firing (i.e., ICNS firing histograms) as a function of the timing within the left ventricular pressure (LVP) cycle (represented as a phase between 0 and 2π). The LVP is indicated by the gray curve.
The synaptic output of the cells is included in the synaptic current of each individual neuron, described by
where and are synaptic weights, and and are the reversal potentials for the synaptic currents between neurons and the network input, respectively. The function f(k) outputs e or i, depending on whether the k-th cell is excitatory or inhibitory. The synaptic weights were drawn randomly from a distribution tuned using the model neurons without an M-current, so the fraction of phasic neurons in the neuronal network approximates those in the experimental data in (Beaumont et al., 2013). These synaptic weights were also used to implement the n+1 convergent efferent innervation protocol in the SNS. The reversal potentials and were chosen to approximate the values represented by nicotinic receptor and GABA receptor activation, respectively.
Functional models of cardiac cells and tissues
Sinoatrial node (SAN) cell model representations: The layered network model of the autonomic nervous system generates both sympathetic and parasympathetic nerve stimulation (SNS and PNS) outputs, which are used as scaling factor inputs for beta-adrenergic stimulation and muscarinic stimulation, respectively in the Behar-Yaniv rabbit SAN model (Behar et al., 2016) to produce spontaneous action potentials that control rates of cardiac pacemaking.
Ventricular cell model representations: We then merged the Iancu-Harvey model of cyclic adenosine monophosphate (cAMP) compartmentation (Iancu et al., 2007; Iancu et al., 2008) to Soltis-Saucerman ventricular cell electrophysiology model (Soltis & Saucerman, 2010) that includes all the relevant components required for a detailed analysis, including accurate cellular electrophysiology, Ca2+ handling (Shannon et al., 2004), and the cAMP-dependent protein kinase (PKA) (Saucerman et al., 2003) and Ca2+/calmodulin-dependent protein kinase (CaMKII) phosphorylation pathways (Soltis & Saucerman, 2010). Pacing frequency was set to the heart rate generated by the Behar-Yaniv SAN model.
One-dimensional Cable
One-dimensional (1D) tissue was simulated as a fiber of 165 cells (1.65cm) (Glukhov et al., 2010) with reflective boundary conditions. Transmural heterogeneity was incorporated into the tissue by a linear decrease to maximal IKr conductance (Myles et al., 2010), corresponding to a linear transition from epicardial to endocardial tissue (Fedida & Giles, 1991). The diffusion coefficient Dx was set to 0.002 cm2/ms to establish a conduction velocity of 61–73 cm/s (epicardium-endocardium in wild-type (WT) conditions) (Brugada et al., 1990).
Norepinephrine (NE) binding affinity to the β-AR
Structural modeling of type 2 β-adrenergic receptor ( β2AR) was performed with ROSETTA software (Yarov-Yarovoy et al., 2006; Bender et al., 2016) using its active-state crystal structure in complex with the stimulatory G protein (PDB ID: 3SN6) as a template. Intracellular loop 3 (ICL3) region missing in the template structure was replaced by a 3-residue linker predicted using Rosetta cyclic coordinate descent (CCD) loop modeling application (Wang et al., 2007). 10,000 decoy structures were generated with top one selected by total score for further simulations. ROSETTALIGAND (Meiler & Baker, 2006; Davis & Baker, 2009) was used for β2AR – cationic (+) and neutral (0) norepinephrine (NE) docking calculations. 50,000 structures were generated with top 10% selected by total score, out of which one with the lowest interfacial score (interaction energy) was chosen. CHARMM-GUI (Jo et al., 2008) was used to prepare β2AR / NE complexes embedded in the palmitoyl-oleoyl-phosphatidylcholine (POPC) lipid bilayer solvated by a 150 mM NaCl aqueous solution. We used CHARMM36m (Huang et al., 2017) protein and C36 lipid (Klauda et al., 2010) force fields, TIP3P water model (Jorgensen et al., 1983) and NE(+) and NE(0) parameters based on CHARMM general force field (CGENFF) (Vanommeslaeghe et al., 2010). The latter were developed using CGNEFF program (Vanommeslaeghe & MacKerell, 2012; Vanommeslaeghe et al., 2012) for initial parameter estimates, which were then optimized through their subsequent fitting to quantum mechanical (QM) reference data using an established protocol (Vanommeslaeghe et al., 2010). All-atom molecular dynamics (MD) simulations were run with NAMD (Phillips et al., 2005) in the NPT ensemble at 310 K and 1 atm pressure. Initial equilibration MD simulations were run for ~52 ns with the first ~2 ns using gradually reduced harmonic restraints on the protein and lipid tail carbon atoms followed by unrestrained 50-ns long MD simulation runs. They were used to start 200 ns long well-tempered metadynamics (Barducci et al., 2008) MD simulations to estimate ligand binding affinities. Distance between centers of mass (COM) of protein α-helical core and NE(+) was used as reaction coordinate R extending to 50 Å in bulk, whereas angle θ between vectors connecting these points and ligand orthosteric binding site was used to restrain sampling within θ≤30° cone as was done in (Provasi et al., 2009; Schneider et al., 2015). Affinities in the form of dissociation constants, Kd, were computed as was done previously (Provasi et al., 2009; Schneider et al., 2015) using equation , where Ω is the solid angle defined by the conical restraint, Rbulk = 50 Å, NA is the Avogadro number, W(R) is free energy profile, k is the Boltzmann constant, and T is absolute temperature. NE Kd value at pH=7.4 was computed from corresponding estimates for NE(+) and NE(0) using Henderson-Hasselbach equation as was done previously (Yang et al., 2020). NE(+) dissociation or “off” rate rfLR was estimated using Kramer’s rate formalism using equation, (Dorairaj & Allen, 2007). Free energy profile from metadynamics MD simulation of the β2AR – NE(+) system was used to estimate activation free energy barrier height (ΔWactivation) and corresponding curvatures at free energy maxima(W″(Rbarrier)) and minima (W″(Rwell)). Diffusion coefficient at the free energy maximum, D(Rbarrier), was estimated using position autocorrelation function from last 20 ns of separate 30 ns long MD simulations with harmonic restraints on the NE(+) position as was done previously (Vorobyov et al., 2014). z component of a distance between COM of protein α-helical core and NE(+) was used as reaction coordinate for diffusion coefficient calculations. NE(+) association or “on” rate was then computed as rfLR / Kd.
In our one-dimensional tissue model, the β-AR binding to ligand equation (2) (Yang & Saucerman, 2012) was used in the Iancu-Harvey model of cAMP compartmentation (Iancu et al., 2007; Iancu et al., 2008). The simulated kinetics and were obtained from molecular dynamics (MD) simulations as described above.
| (3) |
| (4) |
| (5) |
Current density changes in diseased heart
To simulate diseased heart, we modified the current density changes based on heart failure conditions shown in Table III, below. In addition, CaMKII expression is increased in failing human myocardium (Hoch et al., 1999). We simulated CaMKII overexpression (CaMKII-OE) as in Soltis-Saucerman (Soltis & Saucerman, 2010):
Table III:
Current density changes induced in heart failure
| Ionic current | Percentage Change | Species | References |
|---|---|---|---|
| INaL | 10x increase (0.1% → 1%) | Human | (Maltsev & Undrovinas, 2006) |
| Ito,fast | 36% decrease | Human | (Nabauer et al., 1996) |
| IK1 | 25% decrease | Human | (Beuckelmann et al., 1993; Koumi et al., 1995) |
| SR Ca2+-ATPase (SERCA) | 36% decrease | Human | (Hasenfuss et al., 1994) |
| kleak (SR leak) | 3.5-fold increase | Rabbit | (Shannon et al., 2005) |
| INa, leak | 8-fold increase | Rabbit | (Wagner et al., 2011) |
| INaK (Na+/K+-ATPase) | 10% decrease | Human | (Shamraj et al., 1993; Bundgaard & Kjeldsen, 1996; Bossuyt et al., 2005) |
In all simulations, we used a second-order Runga-Kutta method with a time-step of 1/128 ms (~7.5 sec) and included a linear interpolation scheme to compute the spike times between the time steps in the generalized integrate-and-fire (GIF) model (Shelly and Tao, 2001). The interpolation scheme ensures that the method is truly second order, despite the discontinuities due to the fire-and-reset conditions in the GIF formulation.
Code for simulations and analysis was written in C++ and MATLAB 2018a. Code was run on an Apple Mac Pro machine with 2 2.7 GHz 12-Core Intel Xeon processors, and an HP ProLiant DL585 G7 server with a 2.7 GHz 28-core AMD Opteron processor. Code was compiled with the Intel ICC compiler, version 18.0.3. Numerical results were visualized using MATLAB R2018a by The Math Works, Inc. The models used in this paper are available on SPACR Portal (https://sparc.science/datasets/322?type=simulation).
Results
In this study, we endeavored to develop a neurocardiac simulator suite containing modeling tools that will allow for prediction of a range of autonomic effects on cardiovascular function. The model framework is shown schematically in Figure 1 as a modular workflow comprising a network layer representation of the sympathetic branch (blue) and the parasympathetic branch (green) of the autonomic nervous system (ANS) that both synapse onto the cardiac sinoatrial node (SAN) as well as on cardiac ventricular myocardium (purple box). The model allows for the prediction of efferent sympathetic and parasympathetic signaling and model representations of target-organ responses.
We first set out to develop computational models of single neuron action potentials from the three-layer representation of the autonomic nervous system. In Figure 2A, the firing dynamics from experimental recordings of neuronal action potentials measured from the superior cervical ganglion of adult male rats are shown (Springer et al., 2015). An increasing amplitude of current injection applied for 1 s is shown from the top to the bottom panels. Neurons displayed three distinct notable types of firing: tonic, accommodating, and phasic. Tonic neurons fired repetitively at frequencies related to strength of stimulus. Accommodating neurons adapted and demonstrated reduced firing at lower stimulus amplitudes. Phasic neurons fired one to four spikes and then ceased firing. In panel B, a computational model demonstrating comparable firing patterns to experimental measurements. The integrate- and-fire model representation incorporated a range of M-current conductances (gM) in discrete cells (see Table I), which allowed for reproduction of the full range of experimentally observed action potential firing dynamics.
The distribution of neuronal firing resulting from simulation in the ANS layered network model is shown in Figure 3. In panel A, the blue rectangles represent the sympathetic branch (SNS) of the autonomic nervous system with central nervous system input (CNS), the intrathoracic network layer (ITNS), and the intracardiac nervous system layer (ICNS). The parasympathetic branch (PNS) is shown in green with a CNS input layer connected to the ICNS layer, representing the direct vagal connection. Each layer contains a random network of model generated integrate-and-fire neurons with delayed rectifier potassium, leakage, M-type potassium, and synaptic currents. Synaptic currents constitute and generate the intra- and inter-network connections. Inter-network connections are represented by arrows. Within each box, the predicted distribution of firing types from the model network is shown and was noted after the system reaches steady-state firing, averaged over seven 60-s simulations. The distribution of neuronal firing types is classified empirically by comparing firing probability over time relative to the cardiac phase relations (onset of left ventricular pressure) as shown in panel B. Model generated neuronal firing patterns that did not clearly fit into one classification were labelled as “other”. Panel B shows examples of neural firing relative to the phase of the cardiac cycle in ICNS neurons recorded from canines (Beaumont et al., 2013). Temporal correlation to left ventricular pressure was used to classify firing types as follower, phasic, or tonic.
We next set out to model and simulate the impact of sympathetic and parasympathetic stimulation on heart rate shown in Figure 4 left panels. We employed the Behar-Yaniv model of the rabbit SAN as the model incorporates both adrenergic and muscarinic receptor pathways and subcellular signaling events associated with activation of the pathways (Behar et al., 2016). In Figure 4, panel A, the simulated effect of application of SNS stimulation (time course shown middle panel in blue) resulted in an expected increase in heart rate (pink trace in middle panel) over 60 seconds of stimulation. The predicted increase in heart rate shows good agreement when compared to experimental data (black symbols) from (Wang et al., 2019) (n = 4).
Figure 4:
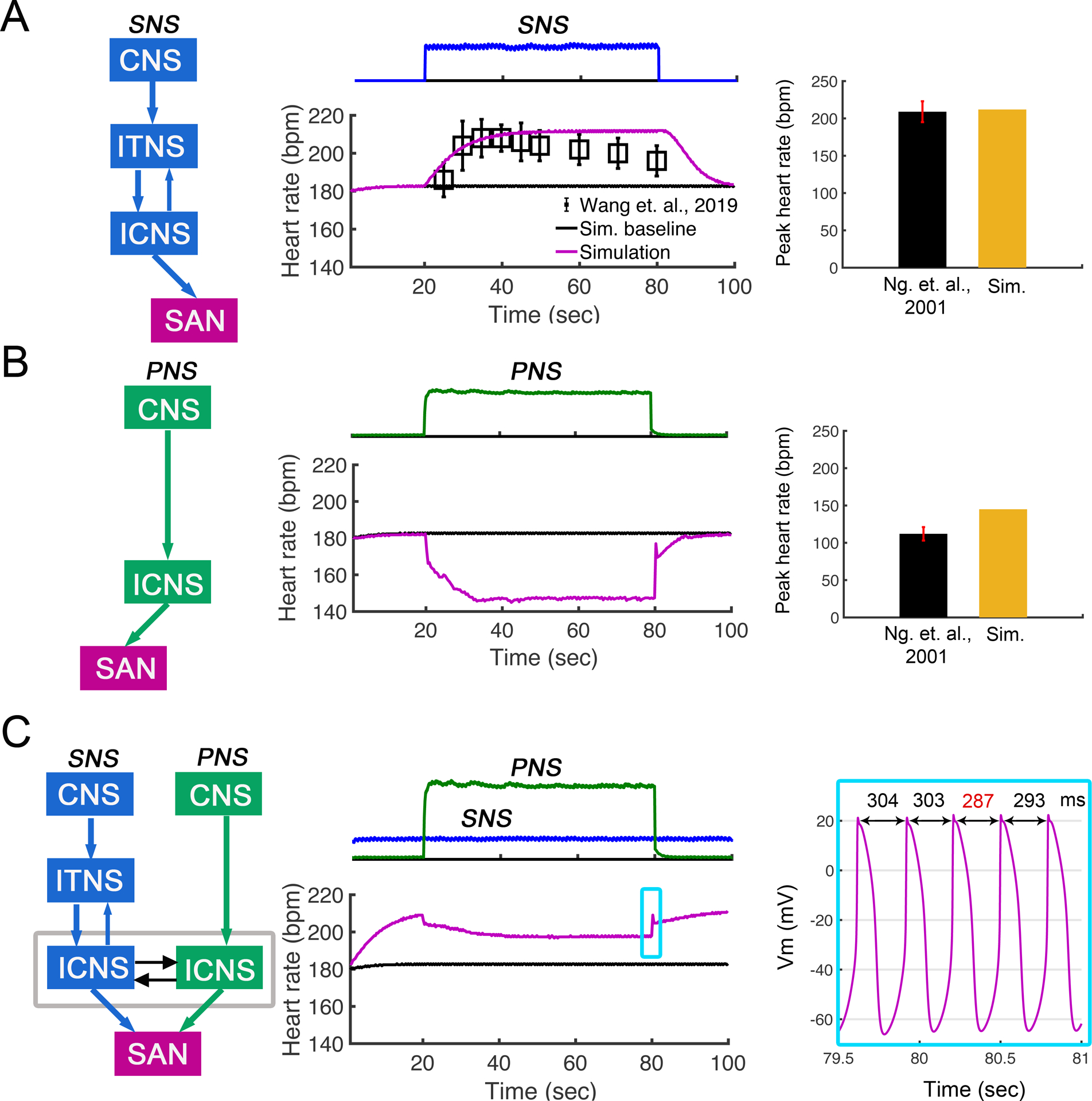
Effects of sympathetic and parasympathetic stimulation on heart rate in the rabbit sinoatrial node (SAN) computational model from Behar et al. (Behar et al., 2016). (A) SNS stimulation (top panel) increased heart rate over 60 seconds of stimulation. Shown in middle panel, change in time of simulated heart rates shows agreement with experimental data from (Wang et al., 2019) (n = 4). Right panel shows simulated peak heart rate during SNS stimulation agrees with experimental data from Ng et. al., 2001. (B) PNS stimulation (top panel) was applied for 60 seconds, and heart rate was predicted to decrease to ~140 bpm. Simulated minimum heart rate during PNS stimulation comparable to experimental data from (Ng et al., 2001) (right panel). (C) Simulation shows effect on heart rate when SNS stimulation was applied continuously and PNS stimulation was applied transiently for 60 s (top panel in C). Heart rate was reduced to ~200 bpm during PNS and then recovered following removal of PNS. AP firing dynamics during removal of PNS are shown in the right panel.
The bar graph in the right panel shows simulated peak heart rate during SNS stimulation agrees with experimental data from Ng et. al., 2001 (Ng et al., 2001). In panel B middle, the application of PNS stimulation (green) resulted in prediction of a rapid reduction in heart rate (pink trace) during 60 s stimulation. The simulated minimum heart rate during PNS stimulation was comparable to experimental data from Ng et. al., 2001 (right panel). In panel C, the application of SNS stimulation followed by PNS stimulation for 60 s in the computational model resulted in a rapid reduction in heart rate upon PNS stimulation, indicating the dominance of the parasympathetic branch to control heart rate. Notably, cessation of PNS stimulation results in immediate heart rate increase from continued stimulation of the sympathetic branch of the ANS. The firing dynamics of SAN action potentials following removal of PNS stimulation are shown in the right panel.
In Figure 5 we show the computational model representation and predicted effects of sympathetic and parasympathetic nerve stimulation (SNS and PNS) on ventricular action potential duration (APD80) and Ca2+ transient (CaT) in the Soltis-Saucerman rabbit model under conditions of constant pacing. To study the impact of the ANS inputs only on the ventricular myocytes (without a change in the pacing frequency), we set pacing cycle length to 320 ms for all simulations. In panel A, the effect of SNS stimulation at a pacing cycle length of 320 ms shows a predicted reduction in the APD80 due to K channel modification (Chen et al., 2014; Wang et al., 2019) and marked increase in CaT over the duration of the stimulation with increased maximum and minimum calcium transient amplitude (green lines in right panels) during the whole stimulation range. The CaT increase is due to β-adrenergic stimulation enhanced intracellular Ca2+ uptake and release. Our simulations show a reduction in the APD80 and CaT when the SNS stimulation ends and then a return to close to baseline. In panel B, the contrasting effect of PNS stimulation at a pacing cycle length of 320 ms is shown. The model predicts that both APD80 (middle panel) and maximum and minimum calcium transient amplitude (green lines in right panels) with PNS stimulation alone was unchanged compared to baseline. Finally, in panel C, we show the predicted effect of constant SNS stimulation, and then application and withdrawal of PNS stimulation after 20 s (during concomitant SNS application). The predicted APD80 and CaT were more complex in this situation, with an initial decrease in both following application of SNS stimulation, and then an increase due to transient application of PNS stimulation.
Figure 5:
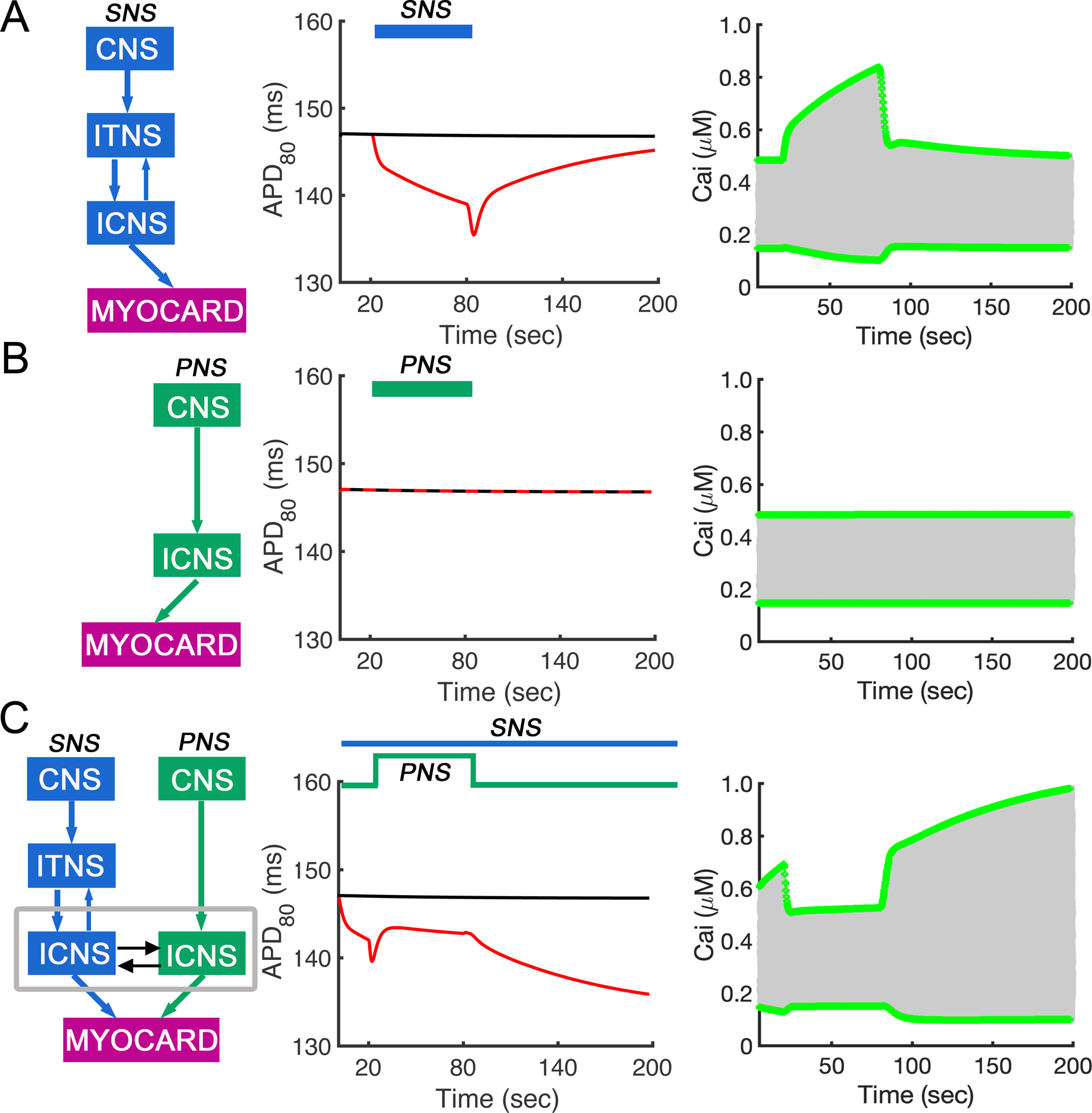
Simulated effects of sympathetic and parasympathetic stimulation on action potential duration (APD80) and Ca2+ transient (CaT) in the rabbit ventricular computational myocyte model during periodic constant pacing. Maximum and minimum amplitude (green lines in right panels) of calcium transients during the whole stimulation range are shown for each case. (A) SNS stimulation was applied at cycle length of 320 ms, and APD80 was decreased. (B) PNS stimulation was applied at cycle length of 320 ms. APD80 was unchanged from baseline. (C) Simulated SNS stimulation was applied throughout the simulation, while PNS stimulation was transiently applied after 20s. The model was paced at cycle length of 320ms. APD80 first decreased due to application of SNS stimulation and then increased after addition of PNS stimulation.
Following the development of the models of sympathetic and parasympathetic branches and the effects of stimulating these branches on both the rabbit SAN alone and the rabbit ventricular model alone, we next set out to combine these models and allow the Behar-Yaniv SAN model to couple to and drive pacing in the Iancu-Soltis-Saucerman ventricular model that is also subject to additional cell-based effects of ANS stimulation (Figure 6). In Panel A, the first combined model representing the impact of SNS stimulation on the SAN and the resulting SAN pacing frequency used to drive ventricular pacing is shown. The time course of the effects of SNS stimulation is shown in the blue trace in the middle panels. The simulated effect of dynamic SAN pacing combined with direct effects of simulated 60 s SNS stimulation on the ventricular APD80 and CaT are shown in the red traces. Experimental data from the Ripplinger Lab (Wang et al., 2019) is also shown in black symbols and demonstrates good agreement with the predicted outputs from the coupled model. The maximum and minimum amplitude (green lines) of calcium transients during the whole stimulation range are shown in the right panels.
Figure 6:

Simulated effects of sympathetic and parasympathetic stimulation on the full coupled cardiac system that includes the autonomic nervous system and sinoatrial node (SAN) cell model coupled to the rabbit ventricular cell model. Pacing frequency was determined by the rate generated by the SAN model. (A) In response to simulated SNS stimulation in the coupled model, predicted effects (red line) on ventricular APD80 agrees with experimental data from Wang et. al., 2019 (black open circle symbols) (n = 4). (B) Simulated PNS stimulation for 60s resulted in a model prediction showing APD80 slightly increased compared to baseline. (C) Shown are predictions where SNS stimulation was applied through the whole simulation, and PNS stimulation was transiently applied between 20 s and 80 s. Model predictions indicate that APD80 was decreased following SNS, and then partially recovered with PNS stimulation. (D) ICaL, IKs and IKr currents during the whole stimulation range for panel C. Maximum and minimum amplitude (green lines) of calcium transients during the whole stimulation range are shown in the right panels for each case.
In Figure 6 panel B, a simulated 60 s stimulation of the parasympathetic branch of the ANS and its impact on both the SAN pacing frequency and the pacing induced changes combined with direct PNS effects on ventricular APD80 and CaT is shown in red. The simulations demonstrate a small increase in APD80 but also a notable effect on CaT (in contrast to PNS effect on a constantly paced ventricular tissue shown in Figure 5, panel B) and discussed above. This suggests that slower pacing from the PNS effect on the SAN leads to a notable increase in ventricular action potential duration and an effect on calcium transient amplitude. Again, the maximum and minimum amplitude (green lines) of calcium transients during the whole stimulation range are shown in the right panels. In contrast to SNS induced increase in the Ca2+ transient, PNS stimulation causes an abrupt decrease in Ca2+ transient amplitude due to ICaL reduction. Our simulations also show that PNS stimulation results in reduction in IKs and IKr due to inhibition of phosphorylation and slower pacing frequency (reverse rate dependence) as shown in Panel D.
Finally, in Figure 6 panel C, SNS stimulation is applied to the SAN resulting in a change in heart rate that drives the pacing frequency in the ventricular cells. During SNS stimulation, a transient PNS stimulus (60 s) is applied as shown in green. The added effect of PNS activation is to slow SAN pacing frequency and consequently the frequency of pacing of the ventricular cells. The pacing effect is combined with and interacts with subcellular signaling events that occur as a result of postsynaptic receptor activation in the ventricular cells. Shown in the middle are predictions where SNS stimulation was applied through the whole simulation, and PNS stimulation was transiently applied between 20 s and 80 s. Model predictions indicate that APD80 was decreased following SNS stimulation, and then partially recovered with PNS stimulation. Maximum and minimum amplitude (green lines) of calcium transients during the whole stimulation range are shown in the right panel. During the SNS stimulation phase that induces a faster pacing rate, a shorter APD ensues as well as marked functional upregulation of the L-type Ca2+ channel from phosphorylation which leads to enhance Ca2+ transient amplitude and increase SR Ca2+-ATPase (SERCA) activity. On the other hand, PNS stimulation was shown to slow rate, increase APD and block the phosphorylation mediated changes intracellular calcium. However, the interplay between the complex signaling events and rate dependence will need further exploration in future studies to identify the parameter spaces that define “imbalance” that may be favorable for arrhythmia formation.
In Figure 7, we demonstrate a multiscale model utilizing the “atom to the rhythm” approach in our recent study shown schematically in the top left (Yang et al., 2020). In this case, molecular dynamics simulations were undertaken using an atomistic structural model of the beta-adrenergic receptor (βAR) in order to predict quantitative estimates of norepinephrine (NE) binding affinity and association/dissociation (“on”/“off”) rates to the βAR (panel A – left). These molecular dynamics simulation derived rates provided us with a reasonable estimate of the time course of beta-adrenergic receptor – norepinephrine binding, with ~97% saturation in a 100 ms range for a nearly saturating ligand concentration of 10 μM. Interestingly, using recently published experimental “on” and “off” rates for norepinephrine – beta-adrenergic receptor interactions resulted (Xu et al., 2021) in substantially slower kinetics and only ~17% receptor saturation at 10 μM ligand concentration in ~1 s and nearly complete receptor saturation only on a ~ 1 hour time scale. We did not see appreciable receptor binding for lower norepinephrine concentrations on a second-long simulation time using that model. On the contrary, using our molecular dynamics simulation derived model we observed gradual decrease of receptor saturation with a longer time course for lower concentrations as expected.
Figure 7:
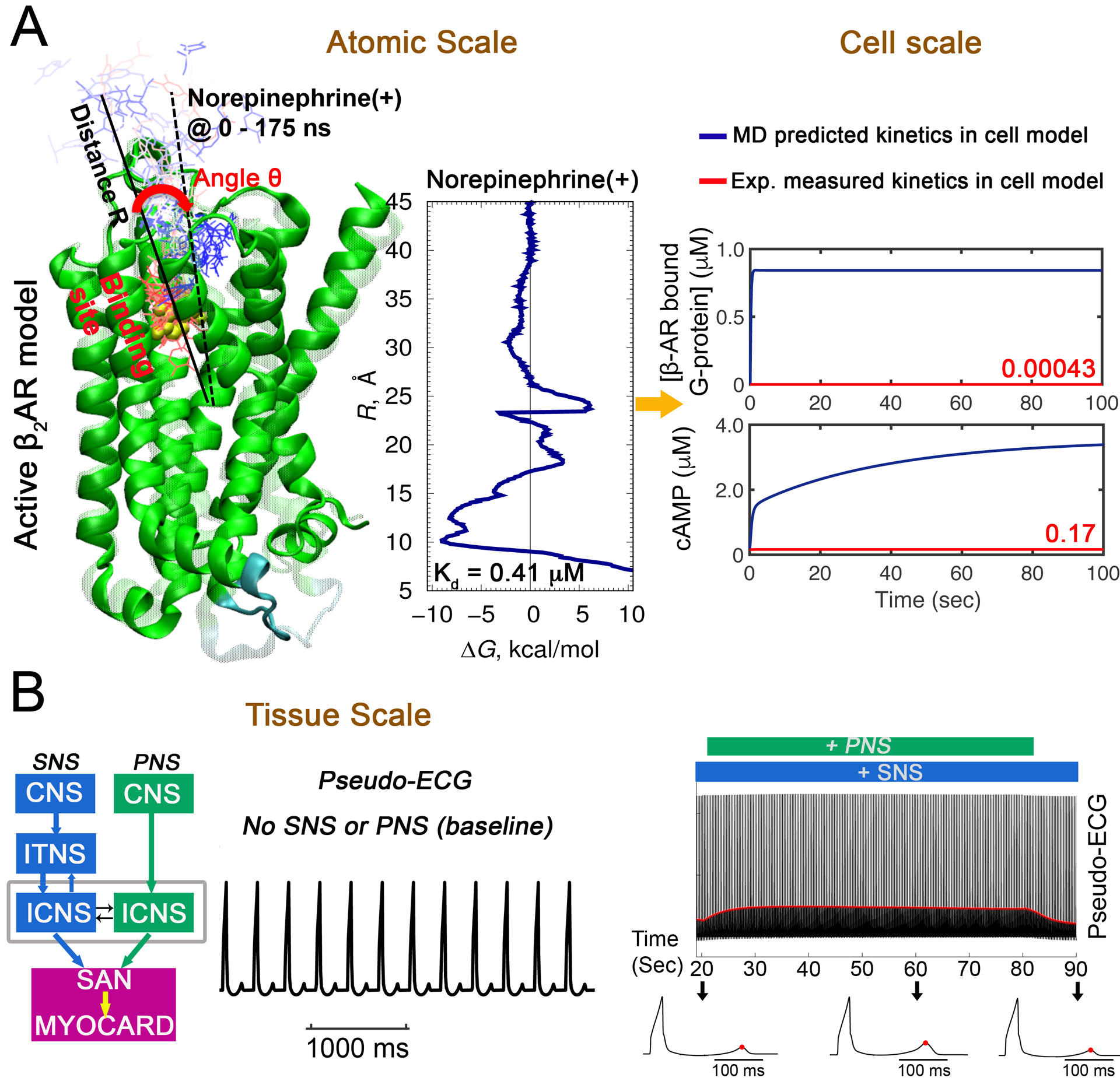
Prediction from atom to the rhythm: A multiscale model to predict effects of sympathetic nerve stimulation (SNS) on sinoatrial node (SAN) cells and the coupled rabbit ventricular cell model. (A) All-atom enhanced sampling molecular dynamics (MD) simulations were used to study cationic norepinephrine (NE) binding (NE progression shown by red to blue thin molecules and their position over time as the molecule moves from binding site) to βAR (green ribbons) to compute the free energy profile as shown on the left of panel A. Predicted affinities and rates of βAR-NE interaction obtained from atomistic MD) simulations were used as parameters in the cell signaling cascade in the SAN and ventricular computational model. Comparison of kinetics from MD (kon = 6.7 μM−1s−1 and koff = 2.7 s−1) and experimental data (kon = 0.0034 μM−1s−1 and koff = 0.0012 s−1, (Xu et al., 2021) for bound βAR and cAMP concentration in cells are shown on right panel. (B) Pacing frequency was set to the rate generated by Behar-Yaniv SAN model. One-dimensional tissue (1.65 cm) simulations in baseline (no SNS or PNS stimulation) for 334 beats. A pseudo-ECG generated from the tissue simulation are shown in the left panel. The right panel shows predictions where SNS stimulation was applied through the whole simulation (100 seconds) along with transient simulated PNS stimulation between 20 s and 80 s. T-wave peaks are indicated by red dots. Three model generated electrograms from 20 s, 60 s and 90 s are shown in the bottom panel.
The molecular dynamics simulation derived rates were then used to populate the function scale model of NE – βAR interaction in the combined Iancu-Soltis-Saucerman ventricular cardiomyocyte model. This new function scale model was then used to make predictions of electrical activity in a one-dimensional cardiac ventricular tissue (1.65 cm in length) in the absence of autonomic input (baseline, middle panel in A) as shown in the computed pseudo-electrocardiograms (pseudo-ECGs) from the tissue in panel A (right). Pacing frequency was set to heart rate generated by Behar-Yaniv SAN model. We then applied a different protocol in B, showing the effect of SNS stimulation (blue) on the computed pseudo-ECG followed by addition of PNS stimulation (green), which was applied in the model simulation between 20 and 80 seconds (SNS was applied for the whole simulated time course of 100 seconds). Again, the changes in pacing frequency are driven by the autonomically mediated changes in the SAN model. The red line indicates the increased amplitude of the T wave during PNS stimulation. Computed electrograms at different time points are shown at the bottom with the peak of the T wave indicated by the red dots. These simulations indicated that T wave amplitude increases during PNS and returns after withdrawal.
In Figure 8, we predict the effect of cessation of SAN input to the ventricular model in the merged multiscale Iancu-Soltis-Saucerman model. Pacing frequency was set to the heart rate generated by SAN model until 415 seconds and then stopped to simulate a sinus pause. In the absence of SNS application and cessation of beating at 415 seconds, the simulated non-diseased (A) and diseased hearts (B) are predicted to have expected normal behavior with no additional electrical or Ca2+ activity following decoupling of the SAN from the ventricular model representation (top row). However, in response to a sympathetic surge as shown in panel (C), even a non-diseased heart generates a single spontaneous AP (red peak in middle) is triggered by a delayed afterdepolarization, following SNS surge and cessation of beating at 415 seconds. In panel (D) simulations in a diseased heart (simulated heart failure) with the same protocol as in panel A predict the emergence of multiple triggered afterdepolarizations.
Figure 8:
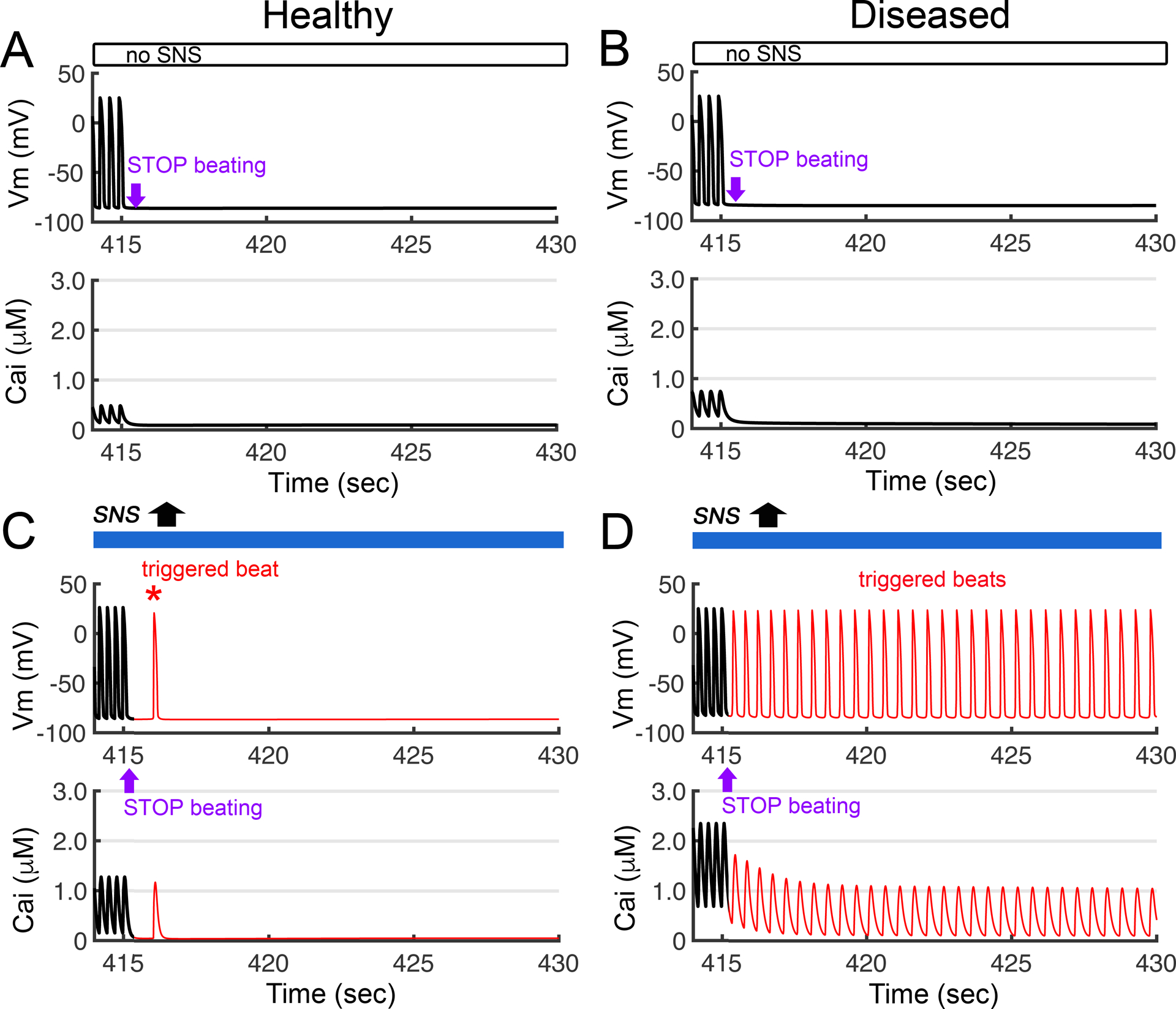
The electrical effects of simulation of transient exposure to a surge of SNS activity in both healthy (non-diseased) and diseased heart tissue models. The prediction shown was made in the ventricular cell model containing the combined Iancu-Soltis-Saucerman model. Pacing frequency was set to heart rate generated by Behar-Yaniv sinoatrial node (SAN) model. The dynamics of the action potential (Vm) are shown in the top panels, and calcium transient (Cai) profiles are shown in the bottom panels. Simulation showing electrical activity in non-diseased (A) and diseased ventricular cells (B) with no SNS stimulation and cessation of beating at 415 seconds. (C) A single spontaneous AP (red peak in middle) is triggered by delayed afterdepolarizations in a non-diseased heart, following SNS surge and cessation of beating at 415 seconds. (D) Simulations in a diseased heart (simulated heart failure) with the same protocol as in panel A result in prediction of emergence of multiple triggered afterdepolarizations.
In Figure 9, we predict the effects of adding parasympathetic nervous system stimulation to the proarrhythmic effects of sympathetic surge shown under the same conditions as in Figure 8. In the setting of overly active sympathetic stimulation in non-diseased heart (blue bar in top of panel A) via the activation of βAR, we applied PNS stimulation (green bar in top of panel A). The dynamics of the single-cell AP and CaT is shown. In (A) PNS stimulation was applied and eliminates the triggered beat in a non-diseased heart that was predicted in Figure 8. In panel (B) a simulation in a diseased heart (simulated heart failure) with the same protocol as in panel A resulted in suppression of triggered activity at 422 s compared to continues firing in Figure 8 with no PNS stimulation.
Figure 9:
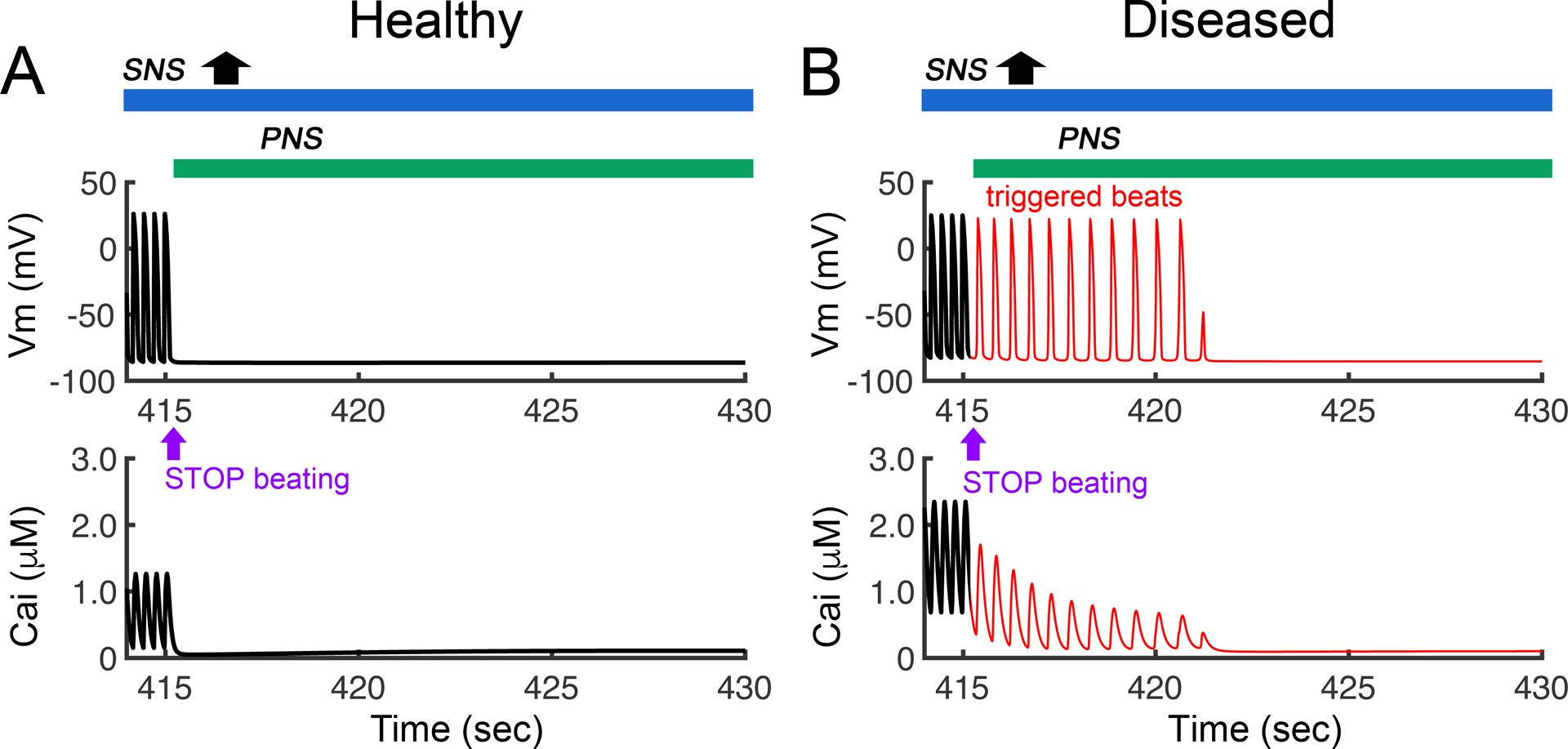
Stimulation of the parasympathetic nervous system stimulation blocks the proarrhythmic effects of sympathetic surge (shown in Figure 8). Shown in a simulation of SNS surge in healthy versus diseased ventricular myocytes in response to SNS surge, but now with the addition of PNS stimulation at = 415 s. (A) PNS stimulation was predicted by the model to eliminate the triggered beat in a non-diseased heart. (B) Simulation of the PNS in a diseased heart (simulated heart failure) with the same protocol as in panel A resulted in suppression of triggered activity at 422 s.
Finally, In Figure 10, we employed the atom to tissue model and tested the case in 1D tissue that included the predicted rates of NE interaction with βAR from our atomistic structural model and simulated the effect of the PNS stimulation on spontaneous beat triggering events. The simulations suggest the triggered activity was initiated and maintained for a much longer period of time in the diseased heart – for about 20 seconds (panel B - top) compared to the observation of a single spontaneous beat in the healthy heart (panel A – top). When PNS stimulation was applied back in the model after termination of pacing, the triggered activity in the diseased heart was discontinued within 5 seconds as shown in panel D (bottom) and was not initiated in the healthy heart condition (panel C – bottom).
Figure 10:
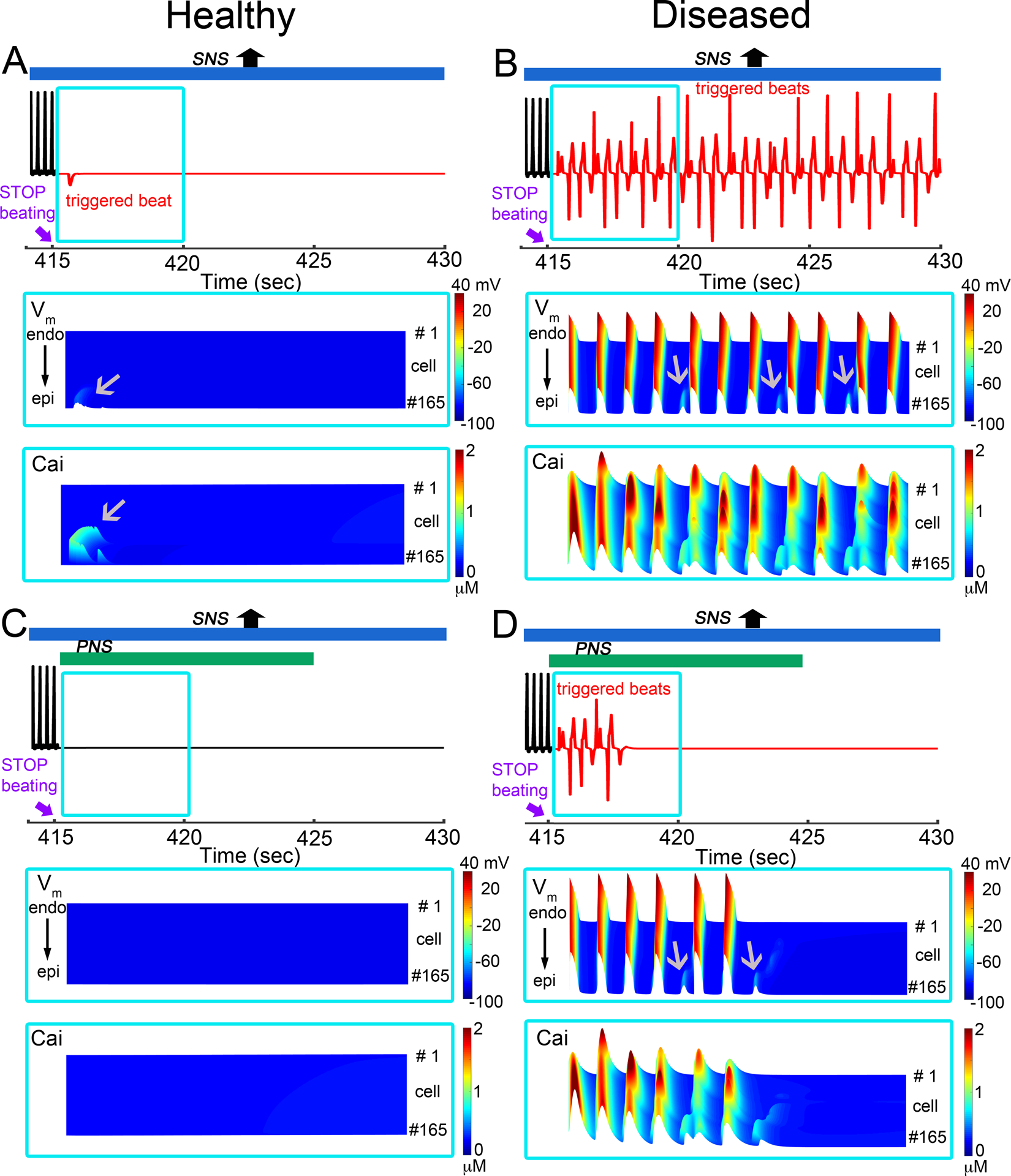
Effects of transient exposure to PNS and SNS surge in simulated healthy (non-diseased) and diseased (simulated heart failure) one-dimensional cardiac tissues using a multiscale model that includes autonomic nerve stimulation on rabbit sinoatrial node (SAN) and ventricular cell models. Pacing frequency was set to heart rate generated by Behar-Yaniv SAN model, and we used predicted rates of βAR – NE interactions obtained from atomic simulations in the functional scale models. One-dimensional tissue (1.65 cm) with SNS was simulated for 1529 beats. For each set of panels, pseudo-ECGs is on top, voltage timecourse and calcium transient between t = 415 s and 420 s are on middle and bottom in blue. (A) Top: In the setting of overly active SNS in a healthy heart model, we ceased application of pacing stimuli at 415 seconds (the 1529th beat). We observed a spontaneous beat (red) that was triggered after cessation of pacing at t = 415 s (top panel). (B) Following the same protocol as in panel A, for diseased heart model, the extensive triggered activity was initiated. (C) With addition of PNS stimulation applied in the non-diseased model after t = 415 s, the triggered beat was suppressed (lower panel in A). (D) With addition of PNS stimulation (bottom panel in B), the triggered activity (red) terminated around 418 seconds in diseased model. Gray arrows indicate triggered action potentials, and Ca2+ transients on space-time representations of one-dimensional tissues.
Discussion
The ultimate purpose of our study is to serve as a digital twin for modeling, simulation and prediction of neuromodulation to treat, reverse and prevent heart disease. As autonomic modulation is increasingly shown to be a powerful tool for cardiac arrhythmia prevention and therapy, new tools to allow finer grained prediction of appropriate interventions are needed and the tool we present represents a critical step in computational modeling and simulation (Kember et al., 2017; Hanna et al., 2018; Liu et al., 2018; Dusi et al., 2021; Dacey et al., 2022; Hadaya et al., 2022; Zhu et al., 2022).
In this study, we set out to advance prediction of the effects of stimulation of the autonomic nervous system on cardiac electrophysiology. To do so, we developed a multiscale digital twin model to capture subcellular, cellular and system scale features of autonomic control of the heart. Some key features of the new modeling and simulation approach include a multi-layered structure of the autonomic nervous system that represents both the sympathetic and parasympathetic branches as shown in Figures 1 and 3. The layers include sparse random intralayer connectivity, synaptic dynamics and conductance based integrate-and-fire cellular dynamics in close agreement with experiment (Springer et al., 2015) as shown in Figure 2.
Another key feature of the neurocardiac computational model is the modeled connection between the autonomic nervous system and both the cardiac pacemaker and contractile cells as shown in Figures 4–6. The result is a dynamic model where modification to pacemaker frequency drives initiation of electrical signals in the contractile cells. Receptor mediated signaling on both pacemaker and contractile cells leads to a cascade of subcellular cardiac signaling processes occurring on multiple time scales that result in predicted functional changes to cardiac electrophysiology in both nodal and contractile cells representations.
We show the predicted effect of application of SNS stimulation resulted in an expected increase in heart rate (pink trace in middle panel) over 60 seconds of stimulation in Figure 4. The predicted increase in heart rate shows good agreement when compared to experimental data (black symbols) from (Wang et al., 2019) (n = 4), but the experimental data shows a decrease in the action potential duration following the peak. There are several possible mechanisms of the HR reduction following the peak increase in the experiment including β1-AR desensitization, depletion of nerve terminals due to persistent high frequency stimulation and/or washout of neurotransmitters and precursors during the experiment. We have recently developed and published a reduced yet detailed computational model of the β1-adrenergic signaling cascade to a system of two differential equations by eliminating extraneous variables and applying quasi-steady state approximation (Meyer et al., 2021). The structure of the reduced model reveals that the large cAMP transients associated with abrupt β1-AR activation are generated by the interplay of production/degradation of cAMP and desensitization/resensitization of β1-ARs. The explicit modeling of desensitization of β1-ARs by PKA is a likely contributing mechanism of the reduction in rate observed in the experimental data. This model is available as a component that can be used in the simulator, but we have not included it in this study.
We demonstrated that we can construct a multimodal model that includes a layered autonomic neural representation connected to nodal and contractile cells with cell signaling dynamics (Figures 4–6). However, a major challenge of extending the model to other receptor mediated signaling events is experimental determination of needed parameters for the model. To begin to overcome this challenge, we set out to determine if we could utilize atomistic-scale approaches to generate some known model parameters that have already been constrained experimentally to allow model validation. A successful example is shown in Figure 7, where we present an extension of the multiscale model from the atom to the rhythm. Such models were previously used in our studies to predict emergent pro-arrhythmia proclivities of small-molecule drugs, blocking cardiac potassium channel encoded by human Ether-à-go-go-Related Gene (hERG) (Yang et al., 2020; DeMarco et al., 2021). There we used all-atom molecular dynamics simulations to predict association and dissociation (“on” and “off”) rates of hERG blocking drugs to the open channel pore. They were computed based on free energy and diffusion coefficient profiles from umbrella sampling molecular dynamics simulations. Those rates were used as parameters of functional kinetic models of state-dependent hERG channel – drug interactions, which were used to reproduce experimental dose response curves and incorporated into cardiac cell and tissue models to predict emergent pro-arrhythmia outcomes (Yang et al., 2020; DeMarco et al., 2021).
In the model pipeline shown in Figure 7, we utilized atomistic scale molecular dynamics simulations to predict the association and dissociation (“on” and “off”) rates of norepinephrine interactions with the beta-adrenergic receptor. Since ligand binding to the adrenergic receptor and other G protein coupled receptors (GPCR) does not follow a linear path (Provasi et al., 2009; Schneider et al., 2015) as a drug binding to the hERG channel pore (Yang et al., 2020; DeMarco et al., 2021), we used a different enhanced sampling molecular dynamics simulation approach, well-tempered metadynamics and estimate dissociation rate using Kramer rate theory formalism based on computed free energy profile and diffusion coefficient at the free energy barrier computed from a separate restrained molecular dynamics simulation. Calculation of diffusion coefficient profiles across an entire reaction coordinate as was done in previous studies (Zhu & Hummer, 2010; Berezhkovskii et al., 2011; Zhu & Hummer, 2012; Setny et al., 2013; Vorobyov et al., 2014; DeMarco et al., 2018; Yang et al., 2020; DeMarco et al., 2021) can help refine computed ligand – receptor “on” and “off” rates and will be explored in our subsequent studies along with other rate computation methods (Pang & Zhou, 2017; Meral et al., 2018; Palacio-Rodriguez et al., 2022; Wang et al., 2023). This methodological shortcoming may contribute to a substantial difference between our MD estimated and substantially slower experimental “on” and “off” rates from a recent study (Xu et al., 2021). Achieving agreement between computed and experimental protein-ligand rates has proven to be a challenging task with results varying by several orders of magnitudes and discrepancies attributed to issues with enhanced sampling methodologies, choice of reaction coordinate(s), force field accuracy, presence of hidden barriers and other MD simulation related factors (Wang et al., 2023) as well as those influencing accuracy of experimental rate measurements using e.g., competitive binding assay (Georgi et al., 2019; Sykes et al., 2019; Hoare, 2021).
Despite these challenges, the molecular dynamics simulation derived rates predicted nearly identical time course of cAMP production compared to the original Soltis-Saucerman and Iancu-Harvey subcellular signaling cardiac myocyte models, where in the latter quasi-steady-state approximation (instantaneous binding of norepinephrine to the receptor) was assumed. This indicates that beta-adrenergic receptor – norepinephrine interaction is not a rate-limiting step for cAMP production in our molecular dynamics informed model. This is also in agreement with our recent model sensitivity study (Meyer et al., 2021), which indicated that production/degradation of cAMP and desensitization/resensitization of βARs are rate-limiting steps for adrenergic stimulation.
Thus, utilizing these predicted rates resulted in what appears to be an effective approach to constrain model parameters through simulation. Indeed, our predicted parameters yielded nearly identical outputs in the multi-scale model compared to those constrained by experimental data alone as shown in Figures 4–6. This gives us some confidence that the approach can be extended to consider multiple conformational states and other types of G protein coupled receptors in future studies and to potentially pursue quantitative investigations into adrenergic receptor binding of different ligands. For example, future studies might allow for comparison between biased agonism versus biased antagonism using a molecular dynamics informed approach similar to the one we use here.
In healthy individuals, the autonomic nervous system plays a critical role in regulating cardiac function, with the parasympathetic nervous system (PNS) primarily responsible for controlling heart rate and the sympathetic nervous system (SNS) regulating both heart rate and contractility. However, chronic cardiac injury can lead to an exaggerated sympathetic response. In Figures 8–10, we explored the potential for activation of the parasympathetic nervous system to suppress arrhythmia triggers induced by an overactive sympathetic nervous system. The simulation is derived from earlier studies suggesting that high sympathetic tone can be combined with muscarinic activation to reduce triggered activity in cardiac tissue (Harvey & Belevych, 2003; Silvani et al., 2016; Meijborg et al., 2020; Mehra et al., 2022). The emergence of arrhythmogenic triggered beats observed in the presence of maximal SNS stimulation was more prominent in a diseased heart model mimicking heart failure condition as shown in panel B of Figure 8. Although we are not able to confirm maximal physiological range of diastolic Ca2+, it is generally accepted that maximal adrenergic stimulation is likely to be a key mechanism contributing to Ca2+ overload conditions as our study suggests. Notably, we also observed a protective role of reapplied parasympathetic stimulation, which substantially reduces triggered beat activity in the diseased heart and eliminates it altogether in the healthy heart as shown in Figures 9 and 10.
Such simulations may be useful to extend and improve understanding underlying molecular mechanisms of vagal nerve stimulation therapies, which are emerging techniques for non-invasive and non-pharmacological arrhythmia treatments (De Ferrari & Schwartz, 2011; Zhang & Mazgalev, 2011; Hanna et al., 2018; Liu et al., 2020). The model parameters can be tuned to be applied in real cases in the absence of drug therapy, or more likely, in combination with therapeutic pharmacology. However, it is important to note that chronic cardiac injury can lead to alterations in autonomic regulation of the heart, including a loss of central vagal drive, which may also require consideration (Francis Stuart et al., 2018). Overall, incorporating the effects of chronic cardiac injury on the autonomic nervous system can be challenging and requires careful consideration of the underlying mechanisms and their potential interactions with experimental conditions.
The present results suggest that antagonism of SNS responses occurring at the myocyte level is one factor that may contribute to the potential for PNS stimulation to attenuate arrhythmogenic responses. However, the interactions between the PNS and SNS are more complex than the steady-state responses reflected in the simulations presented here. For example, dynamic changes in SNS and PNS tone that occur in disease states such as sleep apnea and epilepsy can produce complex temporal responses that may contribute the generation of triggered activity (May et al., 2017; Chadda et al., 2018; Geovanini & Lorenzi-Filho, 2018; Costagliola et al., 2021; Soh et al., 2022). Furthermore, the current models do not account for the changes in presynaptic or postsynaptic signaling mechanisms that are known to occur with myocardial infarction and heart failure. One fundamental experimental and simulation study from Iancu and Harvey demonstrated complex functional responses to activation of the autonomic nervous system arising from the interplay of signaling cascades resulting from stimulation of β1-adrenergic receptors (βAR) and M2 muscarinic receptors (M2R) and resulting compartmentalized cAMP signaling in adult cardiac myocytes (Iancu et al., 2007; Iancu et al., 2008). While it is well known that the M2R plays an important role in parasympathetic regulation of cardiac myocyte function by modulating cAMP production (Harvey & Belevych, 2003) through Gi-dependent inhibition of adenylyl cyclase (AC) activity, Harvey’s group showed the effect muscarinic stimulation has on ventricular myocytes is more complex because M2R stimulation can also activate a stimulatory pathway through stimulation of AC4/7 (Sunahara et al., 1996) (Tang & Gilman, 1992) (Taussig & Gilman, 1995). Modeling and simulation showed that representing cAMP production in different microdomains with different kinetics can account for the experimental observations. We have included these domains in the model presented here to show how complex subcellular signaling manifests during autonomic imbalance.
Furthermore, we still need to learn how to fine-tune vagal nerve stimulation to provide safe and efficacious patient-specific treatment of cardiac arrhythmias resulting from the autonomic imbalance associated with various disease states. This would require an accurate prediction of time-dependent and autonomic nerve stimulus specific responses on heart rate and stroke volume, for which our developed neurocardiac simulator may provide a first framework that can be easily extended and improved to include a variety of new details relevant to new questions (Mehra et al., 2022; Sridharan et al., 2022).
A very important element that will be included in the future state is the the remodeling of the ANS that occurs during a variety of disease states. While we did not address all of these issues in the coarse-grained approach we took to “disease” in this first study, we do recognize its importance as a current limitation and also an important future direction. One important point to emphasize is that the digital twin can be utilized by anyone in the public domain and so critical questions such as how does disease induced remodeling of the nerves modify the predicted effect of neuromodulation? Incoroporating new experimental work by Habecker and others on nerve remodeling will allow the neurocardiac digital twin to predict expected responses to autonomic inputs during disease states based on relevant data (Clyburn et al., 2022a; Clyburn et al., 2022b; Mehra et al., 2022; Sepe et al., 2022). It is important to note that the exact mechanisms underlying some disease induced nerve remodeling and other changes are not fully understood but can be continuously incorporated as new data become available. A full range of parameter regimes can be explored through the digital twin, including the potential effects of changing discharge frequencies, neurotransmitter concentrations and neuropeptide release patterns that are altered during various disease progressions.
In terms of models of cardiac function, there are several approaches that can be taken to incorporate these changes. One approach is to use experimental data to parameterize models that account for altered autonomic input. For example, models can be adjusted to simulate the effects of reduced PNS input on heart rate and contractility, or increased SNS input on contractility. Another approach is to use computational models that incorporate physiological data to simulate the effects of chronic cardiac injury on autonomic regulation. For example, these models can take into account changes in baroreflex sensitivity, which can lead to an exaggerated sympathetic response to changes in blood pressure. It’s important to note that the specific approach taken to incorporate changes in autonomic regulation into models of cardiac function will depend on the research question being addressed and the available data. Overall, however, understanding the effects of chronic cardiac injury on autonomic regulation of the heart is an important area of research, as it has important implications for the development of new therapies for cardiovascular disease. Indeed, these studies comprise the future applications of the digital twin for neurocardiac modulation, which can be modified to include specific elements of an individual or group disease state.
In summary, the developed neurocardiac simulator allows us to directly predict the response of ANS stimulation on heart rhythm through coupled SAN and ventricular cardiac tissue effects in both healthy and disease conditions such as heart failure. It can be used to predict, prevent, and reverse resultant cardiac arrhythmia through precisely targeted parasympathetic and/or sympathetic nervous system stimulations, which is a major goal of our collaborative mutli-scale project supported by NIH Common Fund SPARC initiative. In the future, translation of experimental data on ANS stimulation in animal models to human cardiac electrophysiology (Morotti et al.) can be applied to supplement more scarce human experimental data. Moreover, the digital twin can be made personalized through use of patient-specific induced pluriopotent stem cell derived cardiomyocytes (iPSC-CMs) and translation of their immature phenotype to mature cardiac myocyte electrophysiology and calcium dynamics as we showed recently (Aghasafari et al., 2021).
Supplementary Material
Table II:
Transition rates for β-AR receptor
| Rates | Description | Value | Reference |
|---|---|---|---|
| kf LR | β-AR binding to ligand | 6.7 (μM−1s−1) | MD simulations* |
| kr LR | β-AR binding to ligand | 2.7 (s−1) | MD simulations* |
| kf LRG | Ligand bound β-AR with G-protein | 1000 (μM−1s−1) | (Yang & Saucerman, 2012) |
| kr LRG | Ligand bound β-AR with G-protein | 62 (s−1) | (Yang & Saucerman, 2012) |
| kf RG | Unbound β-AR with G-protein | 1000 (μM−1s−1) | (Iancu et al., 2008) |
| kr RG | Unbound β-AR with G-protein | 8800 (s−1) | (Iancu et al., 2008) |
| k act1Gs | Activation rate for RGs | 0.1 (s−1) | (Iancu et al., 2008) |
| k act2Gs | Activation rate for LRGs | 5 (s−1) | (Iancu et al., 2008) |
Our MD rate estimates have a precision of one order of magnitude based on computed error estimates from 3 separate free energy profiles.
Key points summary.
A multi-layered model representation of the autonomic nervous system that includes sympathetic and parasympathetic branches, each with sparse random intralayer connectivity, synaptic dynamics and conductance based integrate-and-fire neurons generates firing patterns in close agreement with experiment.
A key feature of the neurocardiac computational model is the connection between the autonomic nervous system and both pacemaker and contractile cells, where modification to pacemaker frequency drives initiation of electrical signals in the contractile cells.
We utilized atomistic scale molecular dynamics simulations to predict the association and dissociation rates of norepinephrine with the β-adrenergic receptor.
Multiscale predictions demonstrate how autonomic imbalance may increase proclivity to arrhythmias or be used to terminate arrhythmias.
The model serves as a first step towards a digital twin for predicting neuromodulation to prevent or reduce disease.
Funding
This work was supported by National Institutes of Health Common Fund Grant OT2OD026580 (to C.E.C., L.F.S.), National Heart, Lung, and Blood Institute grants R01HL128537 (C.E.C, L.F.S., I.V.), R01HL152681 (to C.E.C., L.F.S.). American Heart Association Career Development Award grant 19CDA34770101 (to I.V.). UC Davis Department of Physiology and Membrane Biology Research Partnership Fund (to C.E.C. and I.V.) Computer allocations were provided through Extreme Science and Engineering Discovery Environment (XSEDE) grant MCB170095 (to I.V., C.E.C., and K.R.D.), National Center for Supercomputing Applications (NCSA) Blue Waters Broadening Participation Allocation (to C.E.C., I.V., K.R.D.), Texas Advanced Computing Center (TACC) Leadership Resource and Pathways Allocations MCB20010 (I.V., C.E.C., and K.R.D.), Oracle cloud credits award (to I.V., C.E.C.), Pittsburgh Supercomputing Center (PSC) Anton 2 allocations PSCA17085P, MCB160089P, PSCA18077P (to I.V., C.E.C., and K.R.D.). Anton 2 computer time was provided by the Pittsburgh Supercomputing Center (PSC) through Grant R01GM116961 from the National Institutes of Health. The Anton 2 machine (70) at PSC was generously made available by D.E. Shaw Research.
Biography

Dr. Pei-Chi Yang completed her postdoctoral training at Weill Cornell Medicine and University of California, Davis. Her research focuses on development of computational models and methods to reveal the effects of drugs, mutations, hormones, and other interventions on cardiac ion channels. Her goal is to continue to develop and apply new computational modeling and simulation approaches to study how perturbations at multiple system scales can be used to predict arrhythmia vulnerability and potential treatment.
Footnotes
Competing Interests
The authors declare no competing interests.
Data Availability Statement
Molecular dynamics simulation and analysis data file and scripts are available to download from Dryad repository at https://doi.org/10.25338/B87D2J
References:
- Aghasafari P, Yang P-C, Kernik DC, Sakamoto K, Kanda Y, Kurokawa J, Vorobyov I & Clancy CE. (2021). A deep learning algorithm to translate and classify cardiac electrophysiology. Elife 10, e68335. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Armour JA. (2004). Cardiac neuronal hierarchy in health and disease. Am J Physiol Regul Integr Comp Physiol 287, R262–271. [DOI] [PubMed] [Google Scholar]
- Barducci A, Bussi G & Parrinello M. (2008). Well-Tempered Metadynamics: A Smoothly Converging and Tunable Free-Energy Method. Physical Review Letters 100, 020603. [DOI] [PubMed] [Google Scholar]
- Beaumont E, Salavatian S, Southerland EM, Vinet A, Jacquemet V, Armour JA & Ardell JL. (2013). Network interactions within the canine intrinsic cardiac nervous system: implications for reflex control of regional cardiac function. J Physiol 591, 4515–4533. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Behar J, Ganesan A, Zhang J & Yaniv Y. (2016). The Autonomic Nervous System Regulates the Heart Rate through cAMP-PKA Dependent and Independent Coupled-Clock Pacemaker Cell Mechanisms. Front Physiol 7, 419. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bender BJ, Cisneros A 3rd, Duran AM, Finn JA, Fu D, Lokits AD, Mueller BK, Sangha AK, Sauer MF, Sevy AM, Sliwoski G, Sheehan JH, DiMaio F, Meiler J & Moretti R (2016). Protocols for Molecular Modeling with Rosetta3 and RosettaScripts. Biochemistry 55, 4748–4763. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Berezhkovskii AM, Szabo A & Zhou HX. (2011). Diffusion-influenced ligand binding to buried sites in macromolecules and transmembrane channels. J Chem Phys 135, 075103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Beuckelmann DJ, Nabauer M & Erdmann E. (1993). Alterations of K+ currents in isolated human ventricular myocytes from patients with terminal heart failure. Circ Res 73, 379–385. [DOI] [PubMed] [Google Scholar]
- Bossuyt J, Ai X, Moorman JR, Pogwizd SM & Bers DM. (2005). Expression and phosphorylation of the na-pump regulatory subunit phospholemman in heart failure. Circ Res 97, 558–565. [DOI] [PubMed] [Google Scholar]
- Brugada J, Boersma L, Kirchhof C & Allessie M. (1990). [Anisotropy and reentrant ventricular tachycardia: experimental model in the isolated rabbit heart]. Rev Esp Cardiol 43, 558–568. [PubMed] [Google Scholar]
- Bundgaard H & Kjeldsen K. (1996). Human myocardial Na,K-ATPase concentration in heart failure. Mol Cell Biochem 163–164, 277–283. [DOI] [PubMed] [Google Scholar]
- Castellanos P & Godinez R. (2015). Autonomic nervous system regulation of the sinoatrial cell depolarization rate: Unifying computational models. Annu Int Conf IEEE Eng Med Biol Soc 2015, 43–46. [DOI] [PubMed] [Google Scholar]
- Chadda KR, Ajijola OA, Vaseghi M, Shivkumar K, Huang CL & Jeevaratnam K. (2018). Ageing, the autonomic nervous system and arrhythmia: From brain to heart. Ageing Res Rev 48, 40–50. [DOI] [PubMed] [Google Scholar]
- Chen PS, Chen LS, Fishbein MC, Lin SF & Nattel S. (2014). Role of the autonomic nervous system in atrial fibrillation: pathophysiology and therapy. Circ Res 114, 1500–1515. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Clyburn C, Andresen MC, Ingram SL & Habecker BA. (2022a). Untangling Peripheral Sympathetic Neurocircuits. Front Cardiovasc Med 9, 842656. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Clyburn C, Sepe JJ & Habecker BA. (2022b). What gets on the nerves of cardiac patients? Pathophysiological changes in cardiac innervation. J Physiol 600, 451–461. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Costagliola G, Orsini A, Coll M, Brugada R, Parisi P & Striano P. (2021). The brain-heart interaction in epilepsy: implications for diagnosis, therapy, and SUDEP prevention. Ann Clin Transl Neurol 8, 1557–1568. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dacey M, Salahudeen O, Swid MA, Carlson C, Shivkumar K & Ardell JL. (2022). Structural and function organization of intrathoracic extracardiac autonomic projections to the porcine heart: Implications for targeted neuromodulation therapy. Heart Rhythm 19, 975–983. [DOI] [PubMed] [Google Scholar]
- Davis IW & Baker D. (2009). RosettaLigand docking with full ligand and receptor flexibility. J Mol Biol 385, 381–392. [DOI] [PubMed] [Google Scholar]
- De Ferrari GM & Schwartz PJ. (2011). Vagus nerve stimulation: from pre-clinical to clinical application: challenges and future directions. Heart failure reviews 16, 195–203. [DOI] [PubMed] [Google Scholar]
- DeMarco KR, Bekker S, Clancy CE, Noskov SY & Vorobyov I. (2018). Digging into Lipid Membrane Permeation for Cardiac Ion Channel Blocker d-Sotalol with All-Atom Simulations. Front Pharmacol 9, 26. [DOI] [PMC free article] [PubMed] [Google Scholar]
- DeMarco KR, Yang P-C, Singh V, Furutani K, Dawson JRD, Jeng M-T, Fettinger JC, Bekker S, Ngo VA, Noskov SY, Yarov-Yarovoy V, Sack JT, Wulff H, Clancy CE & Vorobyov I. (2021). Molecular determinants of pro-arrhythmia proclivity of d- and l-sotalol via a multi-scale modeling pipeline. Journal of Molecular and Cellular Cardiology 158, 163–177. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dorairaj S & Allen TW. (2007). On the thermodynamic stability of a charged arginine side chain in a transmembrane helix. Proceedings of the National academy of Sciences 104, 4943–4948. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dusi V, Gornbein J, Do DH, Sorg JM, Khakpour H, Krokhaleva Y, Ajijola OA, Macias C, Bradfield JS, Buch E, Fujimura OA, Boyle NG, Yanagawa J, Lee JM, Shivkumar K & Vaseghi M. (2021). Arrhythmic Risk Profile and Outcomes of Patients Undergoing Cardiac Sympathetic Denervation for Recurrent Monomorphic Ventricular Tachycardia After Ablation. J Am Heart Assoc 10, e018371. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fedida D & Giles WR. (1991). Regional variations in action potentials and transient outward current in myocytes isolated from rabbit left ventricle. J Physiol 442, 191–209. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Francis Stuart SD, Wang L, Woodard WR, Ng GA, Habecker BA & Ripplinger CM. (2018). Age-related changes in cardiac electrophysiology and calcium handling in response to sympathetic nerve stimulation. J Physiol 596, 3977–3991. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fukuda K, Kanazawa H, Aizawa Y, Ardell JL & Shivkumar K. (2015). Cardiac innervation and sudden cardiac death. Circ Res 116, 2005–2019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Georgi V, Dubrovskiy A, Steigele S & Fernandez-Montalvan AE. (2019). Considerations for improved performance of competition association assays analysed with the Motulsky-Mahan’s “kinetics of competitive binding” model. Br J Pharmacol 176, 4731–4744. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Geovanini GR & Lorenzi-Filho G. (2018). Cardiac rhythm disorders in obstructive sleep apnea. J Thorac Dis 10, S4221–S4230. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gerstner W & Kistler WM. (2002). Spiking neuron models: Single neurons, populations, plasticity. Cambridge university press. [Google Scholar]
- Glukhov AV, Fedorov VV, Lou Q, Ravikumar VK, Kalish PW, Schuessler RB, Moazami N & Efimov IR. (2010). Transmural dispersion of repolarization in failing and nonfailing human ventricle. Circ Res 106, 981–991. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Grassi G (2007). Adrenergic overdrive as the link among hypertension, obesity, and impaired thermogenesis: lights and shadows. Hypertension 49, 5–6. [DOI] [PubMed] [Google Scholar]
- Grassi G, Bolla G, Quarti-Trevano F, Arenare F, Brambilla G & Mancia G. (2008a). Sympathetic activation in congestive heart failure: reproducibility of neuroadrenergic markers. Eur J Heart Fail 10, 1186–1191. [DOI] [PubMed] [Google Scholar]
- Grassi G, Cattaneo BM, Seravalle G, Lanfranchi A & Mancia G. (1998). Baroreflex control of sympathetic nerve activity in essential and secondary hypertension. Hypertension 31, 68–72. [DOI] [PubMed] [Google Scholar]
- Grassi G, Seravalle G, Quarti-Trevano F, Dell’Oro R, Bombelli M, Cuspidi C, Facchetti R, Bolla G & Mancia G. (2008b). Adrenergic, metabolic, and reflex abnormalities in reverse and extreme dipper hypertensives. Hypertension 52, 925–931. [DOI] [PubMed] [Google Scholar]
- Grassi G, Seravalle G, Trevano FQ, Dell’oro R, Bolla G, Cuspidi C, Arenare F & Mancia G. (2007). Neurogenic abnormalities in masked hypertension. Hypertension 50, 537–542. [DOI] [PubMed] [Google Scholar]
- Hadaya J, Buckley U, Gurel NZ, Chan CA, Swid MA, Bhadra N, Vrabec TL, Hoang JD, Smith C, Shivkumar K & Ardell JL. (2022). Scalable and reversible axonal neuromodulation of the sympathetic chain for cardiac control. Am J Physiol Heart Circ Physiol 322, H105–H115. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hanna P, Buch E, Stavrakis S, Meyer C, Tompkins JD, Ardell JL & Shivkumar K. (2021). Neuroscientific therapies for atrial fibrillation. Cardiovasc Res 117, 1732–1745. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hanna P, Shivkumar K & Ardell JL. (2018). Calming the Nervous Heart: Autonomic Therapies in Heart Failure. Card Fail Rev 4, 92–98. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Harvey RD & Belevych AE. (2003). Muscarinic regulation of cardiac ion channels. British journal of pharmacology 139, 1074–1084. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hasenfuss G, Reinecke H, Studer R, Meyer M, Pieske B, Holtz J, Holubarsch C, Posival H, Just H & Drexler H. (1994). Relation between myocardial function and expression of sarcoplasmic reticulum Ca(2+)-ATPase in failing and nonfailing human myocardium. Circ Res 75, 434–442. [DOI] [PubMed] [Google Scholar]
- Hilger D (2021). The role of structural dynamics in GPCR‐mediated signaling. The FEBS Journal 288, 2461–2489. [DOI] [PubMed] [Google Scholar]
- Hirst GD & McLachlan EM. (1986). Development of dendritic calcium currents in ganglion cells of the rat lower lumbar sympathetic chain. J Physiol 377, 349–368. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hoare SR. (2021). Analyzing kinetic binding data. Assay Guidance Manual [Internet]. [Google Scholar]
- Hoch B, Meyer R, Hetzer R, Krause EG & Karczewski P. (1999). Identification and expression of delta-isoforms of the multifunctional Ca2+/calmodulin-dependent protein kinase in failing and nonfailing human myocardium. Circ Res 84, 713–721. [DOI] [PubMed] [Google Scholar]
- Huang J, Rauscher S, Nawrocki G, Ran T, Feig M, de Groot BL, Grubmüller H & MacKerell AD Jr. (2017). CHARMM36m: an improved force field for folded and intrinsically disordered proteins. Nature methods 14, 71. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Iancu RV, Jones SW & Harvey RD. (2007). Compartmentation of cAMP signaling in cardiac myocytes: a computational study. Biophys J 92, 3317–3331. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Iancu RV, Ramamurthy G, Warrier S, Nikolaev VO, Lohse MJ, Jones SW & Harvey RD. (2008). Cytoplasmic cAMP concentrations in intact cardiac myocytes. Am J Physiol Cell Physiol 295, C414–422. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ishbulatov YM, Karavaev AS, Kiselev AR, Simonyan MA, Prokhorov MD, Ponomarenko VI, Mironov SA, Gridnev VI, Bezruchko BP & Shvartz VA. (2020). Mathematical modeling of the cardiovascular autonomic control in healthy subjects during a passive head-up tilt test. Sci Rep 10, 16525. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Janig W & McLachlan EM. (1992). Characteristics of function-specific pathways in the sympathetic nervous system. Trends Neurosci 15, 475–481. [DOI] [PubMed] [Google Scholar]
- Jo S, Kim T, Iyer VG & Im W. (2008). CHARMM-GUI: a web-based graphical user interface for CHARMM. J Comput Chem 29, 1859–1865. [DOI] [PubMed] [Google Scholar]
- Jolivet R, Lewis TJ & Gerstner W. (2004). Generalized integrate-and-fire models of neuronal activity approximate spike trains of a detailed model to a high degree of accuracy. J Neurophysiol 92, 959–976. [DOI] [PubMed] [Google Scholar]
- Jorgensen WL, Chandrasekhar J, Madura JD, Impey RW & Klein ML. (1983). Comparison of Simple Potential Functions for Simulating Liquid Water. Journal of Chemical Physics 79, 926–935. [Google Scholar]
- Karavaev AS, Ishbulatov YM, Ponomarenko VI, Bezruchko BP, Kiselev AR & Prokhorov MD. (2019). Autonomic control is a source of dynamical chaos in the cardiovascular system. Chaos 29, 121101. [DOI] [PubMed] [Google Scholar]
- Katritch V, Cherezov V & Stevens RC. (2013). Structure-function of the G-protein-coupled receptor superfamily. Annual review of pharmacology and toxicology 53, 531. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kember G, Ardell JL, Shivkumar K & Armour JA. (2017). Recurrent myocardial infarction: Mechanisms of free-floating adaptation and autonomic derangement in networked cardiac neural control. PLoS One 12, e0180194. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kember G, Armour JA & Zamir M. (2011). Neural control of heart rate: the role of neuronal networking. J Theor Biol 277, 41–47. [DOI] [PubMed] [Google Scholar]
- Klauda JB, Venable RM, Freites JA, O’Connor JW, Tobias DJ, Mondragon-Ramirez C, Vorobyov I, MacKerell AD Jr. & Pastor RW. (2010). Update of the CHARMM all-atom additive force field for lipids: validation on six lipid types. J Phys Chem B 114, 7830–7843. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kobilka BK. (2011). Structural insights into adrenergic receptor function and pharmacology. Trends in pharmacological sciences 32, 213–218. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Koumi S, Backer CL & Arentzen CE. (1995). Characterization of inwardly rectifying K+ channel in human cardiac myocytes. Alterations in channel behavior in myocytes isolated from patients with idiopathic dilated cardiomyopathy. Circulation 92, 164–174. [DOI] [PubMed] [Google Scholar]
- Kwag J, Jang HJ, Kim M & Lee S. (2014). M-type potassium conductance controls the emergence of neural phase codes: a combined experimental and neuron modelling study. J R Soc Interface 11. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lahiri MK, Kannankeril PJ & Goldberger JJ. (2008). Assessment of autonomic function in cardiovascular disease: physiological basis and prognostic implications. J Am Coll Cardiol 51, 1725–1733. [DOI] [PubMed] [Google Scholar]
- Lewis TJ & Rinzel J. (2003). Dynamics of spiking neurons connected by both inhibitory and electrical coupling. Journal of computational neuroscience 14, 283–309. [DOI] [PubMed] [Google Scholar]
- Liu C, Jiang H, Yu L & Po SS. (2020). Vagal stimulation and Arrhythmias. Journal of Atrial Fibrillation 13. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu K, Li D, Hao G, McCaffary D, Neely O, Woodward L, Ioannides D, Lu CJ, Brescia M, Zaccolo M, Tandri H, Ajijola OA, Ardell JL, Shivkumar K & Paterson DJ. (2018). Phosphodiesterase 2A as a therapeutic target to restore cardiac neurotransmission during sympathetic hyperactivity. JCI Insight 3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lopshire JC, Zhou X, Dusa C, Ueyama T, Rosenberger J, Courtney N, Ujhelyi M, Mullen T, Das M & Zipes DP. (2009). Spinal cord stimulation improves ventricular function and reduces ventricular arrhythmias in a canine postinfarction heart failure model. Circulation 120, 286–294. [DOI] [PubMed] [Google Scholar]
- Maltsev VA & Undrovinas AI. (2006). A multi-modal composition of the late Na+ current in human ventricular cardiomyocytes. Cardiovasc Res 69, 116–127. [DOI] [PMC free article] [PubMed] [Google Scholar]
- May AM, Van Wagoner DR & Mehra R. (2017). OSA and Cardiac Arrhythmogenesis: Mechanistic Insights. Chest 151, 225–241. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mehra R, Tjurmina OA, Ajijola OA, Arora R, Bolser DC, Chapleau MW, Chen PS, Clancy CE, Delisle BP, Gold MR, Goldberger JJ, Goldstein DS, Habecker BA, Handoko ML, Harvey R, Hummel JP, Hund T, Meyer C, Redline S, Ripplinger CM, Simon MA, Somers VK, Stavrakis S, Taylor-Clark T, Undem BJ, Verrier RL, Zucker IH, Sopko G & Shivkumar K. (2022). Research Opportunities in Autonomic Neural Mechanisms of Cardiopulmonary Regulation: A Report From the National Heart, Lung, and Blood Institute and the National Institutes of Health Office of the Director Workshop. JACC Basic Transl Sci 7, 265–293. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Meijborg VMF, Boukens BJD, Janse MJ, Salavatian S, Dacey MJ, Yoshie K, Opthof T, Swid MA, Hoang JD, Hanna P, Ardell J, Shivkumar K & Coronel R. (2020). Stellate ganglion stimulation causes spatiotemporal changes in ventricular repolarization in pig. Heart Rhythm 17, 795–803. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Meiler J & Baker D. (2006). ROSETTALIGAND: protein-small molecule docking with full side-chain flexibility. Proteins 65, 538–548. [DOI] [PubMed] [Google Scholar]
- Meng L, Tseng CH, Shivkumar K & Ajijola O. (2017). Efficacy of Stellate Ganglion Blockade in Managing Electrical Storm: A Systematic Review. JACC Clin Electrophysiol 3, 942–949. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Meral D, Provasi D & Filizola M. (2018). An efficient strategy to estimate thermodynamics and kinetics of G protein-coupled receptor activation using metadynamics and maximum caliber. J Chem Phys 149, 224101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Meyer EE, Clancy CE & Lewis TJ. (2021). Dynamics of adrenergic signaling in cardiac myocytes and implications for pharmacological treatment. J Theor Biol 519, 110619. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Morotti S, Liu C, Hegyi B, Ni H, Fogli Iseppe A, Wang L, Pritoni M, Ripplinger CM, Bers DM & Edwards AG. Quantitative cross-species translators of cardiac myocyte electrophysiology: Model training, experimental validation, and applications. Science advances 7, eabg0927. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Myles RC, Bernus O, Burton FL, Cobbe SM & Smith GL. (2010). Effect of activation sequence on transmural patterns of repolarization and action potential duration in rabbit ventricular myocardium. Am J Physiol Heart Circ Physiol 299, H1812–1822. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nabauer M, Beuckelmann DJ, Uberfuhr P & Steinbeck G. (1996). Regional differences in current density and rate-dependent properties of the transient outward current in subepicardial and subendocardial myocytes of human left ventricle. Circulation 93, 168–177. [DOI] [PubMed] [Google Scholar]
- Ng GA, Brack KE & Coote JH. (2001). Effects of direct sympathetic and vagus nerve stimulation on the physiology of the whole heart--a novel model of isolated Langendorff perfused rabbit heart with intact dual autonomic innervation. Exp Physiol 86, 319–329. [DOI] [PubMed] [Google Scholar]
- O’Hara T & Rudy Y. (2012). Arrhythmia formation in subclinical (“silent”) long QT syndrome requires multiple insults: quantitative mechanistic study using the KCNQ1 mutation Q357R as example. Heart Rhythm 9, 275–282. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Olshansky B (2005). Interrelationships between the autonomic nervous system and atrial fibrillation. Prog Cardiovasc Dis 48, 57–78. [DOI] [PubMed] [Google Scholar]
- Palacio-Rodriguez K, Vroylandt H, Stelzl LS, Pietrucci F, Hummer G & Cossio P. (2022). Transition Rates and Efficiency of Collective Variables from Time-Dependent Biased Simulations. J Phys Chem Lett 13, 7490–7496. [DOI] [PubMed] [Google Scholar]
- Pang X & Zhou HX. (2017). Rate Constants and Mechanisms of Protein-Ligand Binding. Annu Rev Biophys 46, 105–130. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Patterson E, Jackman WM, Beckman KJ, Lazzara R, Lockwood D, Scherlag BJ, Wu R & Po S. (2007). Spontaneous pulmonary vein firing in man: relationship to tachycardia-pause early afterdepolarizations and triggered arrhythmia in canine pulmonary veins in vitro. J Cardiovasc Electrophysiol 18, 1067–1075. [DOI] [PubMed] [Google Scholar]
- Phillips JC, Braun R, Wang W, Gumbart J, Tajkhorshid E, Villa E, Chipot C, Skeel RD, Kale L & Schulten K. (2005). Scalable molecular dynamics with NAMD. Journal of Computational Chemistry 26, 1781–1802. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Prokhorov MD, Karavaev AS, Ishbulatov YM, Ponomarenko VI, Kiselev AR & Kurths J. (2021). Interbeat interval variability versus frequency modulation of heart rate. Phys Rev E 103, 042404. [DOI] [PubMed] [Google Scholar]
- Provasi D, Bortolato A & Filizola M. (2009). Exploring molecular mechanisms of ligand recognition by opioid receptors with metadynamics. Biochemistry 48, 10020–10029. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Randall WC & Ardell JL. (1985). Selective parasympathectomy of automatic and conductile tissues of the canine heart. Am J Physiol 248, H61–68. [DOI] [PubMed] [Google Scholar]
- Ribeiro JML & Filizola M. (2019). Allostery in G protein-coupled receptors investigated by molecular dynamics simulations. Current opinion in structural biology 55, 121–128. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Saucerman JJ, Brunton LL, Michailova AP & McCulloch AD. (2003). Modeling beta-adrenergic control of cardiac myocyte contractility in silico. J Biol Chem 278, 47997–48003. [DOI] [PubMed] [Google Scholar]
- Schneider S, Provasi D & Filizola M. (2015). The dynamic process of drug–GPCR binding at either orthosteric or allosteric sites evaluated by metadynamics. In G Protein-Coupled Receptors in Drug Discovery, pp. 277–294. Springer. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Selyanko AA, Derkach VA & Skok VI. (1979). Fast excitatory postsynaptic currents in voltage-clamped mammalian sympathetic ganglion neurones. J Auton Nerv Syst 1, 127–137. [DOI] [PubMed] [Google Scholar]
- Sepe JJ, Gardner RT, Blake MR, Brooks DM, Staffenson MA, Betts CB, Sivagnanam S, Larson W, Kumar S, Bayles RG, Jin H, Cohen MS, Coussens LM & Habecker BA. (2022). Therapeutics That Promote Sympathetic Reinnervation Modulate the Inflammatory Response After Myocardial Infarction. JACC Basic Transl Sci 7, 915–930. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Setny P, Baron R, Michael Kekenes-Huskey P, McCammon JA & Dzubiella J. (2013). Solvent fluctuations in hydrophobic cavity-ligand binding kinetics. Proc Natl Acad Sci U S A 110, 1197–1202. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shamraj OI, Grupp IL, Grupp G, Melvin D, Gradoux N, Kremers W, Lingrel JB & De Pover A. (1993). Characterisation of Na/K-ATPase, its isoforms, and the inotropic response to ouabain in isolated failing human hearts. Cardiovasc Res 27, 2229–2237. [DOI] [PubMed] [Google Scholar]
- Shannon TR, Wang F & Bers DM. (2005). Regulation of cardiac sarcoplasmic reticulum Ca release by luminal [Ca] and altered gating assessed with a mathematical model. Biophys J 89, 4096–4110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shannon TR, Wang F, Puglisi J, Weber C & Bers DM. (2004). A mathematical treatment of integrated Ca dynamics within the ventricular myocyte. Biophys J 87, 3351–3371. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shimada I, Ueda T, Kofuku Y, Eddy MT & Wüthrich K. (2021). GPCR drug discovery: integrating solution NMR data with crystal and cryo-EM structures. NMR WITH BIOLOGICAL MACROMOLECULES IN SOLUTION: A Selection of Papers published from 1996 to 2020 by Kurt Wüthrich, 197–220. [Google Scholar]
- Shivkumar K, Ajijola OA, Anand I, Armour JA, Chen PS, Esler M, De Ferrari GM, Fishbein MC, Goldberger JJ, Harper RM, Joyner MJ, Khalsa SS, Kumar R, Lane R, Mahajan A, Po S, Schwartz PJ, Somers VK, Valderrabano M, Vaseghi M & Zipes DP. (2016). Clinical neurocardiology defining the value of neuroscience-based cardiovascular therapeutics. J Physiol 594, 3911–3954. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Silvani A, Calandra-Buonaura G, Dampney RA & Cortelli P. (2016). Brain–heart interactions: physiology and clinical implications. Philosophical Transactions of the Royal Society A: Mathematical, Physical and Engineering Sciences 374, 20150181. [DOI] [PubMed] [Google Scholar]
- Skok VI & Ivanov AY. (1983). What is the ongoing activity of sympathetic neurons? J Auton Nerv Syst 7, 263–270. [DOI] [PubMed] [Google Scholar]
- Soh MS, Bagnall RD, Semsarian C, Scheffer IE, Berkovic SF & Reid CA. (2022). Rare sudden unexpected death in epilepsy SCN5A variants cause changes in channel function implicating cardiac arrhythmia as a cause of death. Epilepsia 63, e57–e62. [DOI] [PubMed] [Google Scholar]
- Soltis AR & Saucerman JJ. (2010). Synergy between CaMKII substrates and β-adrenergic signaling in regulation of cardiac myocyte Ca2+ handling. Biophysical journal 99, 2038–2047. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Springer MG, Kullmann PH & Horn JP. (2015). Virtual leak channels modulate firing dynamics and synaptic integration in rat sympathetic neurons: implications for ganglionic transmission in vivo. The Journal of physiology 593, 803–823. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sridharan A, Bradfield JS, Shivkumar K & Ajijola OA. (2022). Autonomic nervous system and arrhythmias in structural heart disease. Auton Neurosci 243, 103037. [DOI] [PubMed] [Google Scholar]
- Sunahara RK, Dessauer CW & Gilman AG. (1996). Complexity and diversity of mammalian adenylyl cyclases. Annu Rev Pharmacol Toxicol 36, 461–480. [DOI] [PubMed] [Google Scholar]
- Sykes DA, Jain P & Charlton SJ. (2019). Investigating the Influence of Tracer Kinetics on Competition-Kinetic Association Binding Assays: Identifying the Optimal Conditions for Assessing the Kinetics of Low-Affinity Compounds. Mol Pharmacol 96, 378–392. [DOI] [PubMed] [Google Scholar]
- Tan AY, Zhou S, Ogawa M, Song J, Chu M, Li H, Fishbein MC, Lin SF, Chen LS & Chen PS. (2008). Neural mechanisms of paroxysmal atrial fibrillation and paroxysmal atrial tachycardia in ambulatory canines. Circulation 118, 916–925. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tang WJ & Gilman AG. (1992). Adenylyl cyclases. Cell 70, 869–872. [DOI] [PubMed] [Google Scholar]
- Taussig R & Gilman AG. (1995). Mammalian membrane-bound adenylyl cyclases. J Biol Chem 270, 1–4. [DOI] [PubMed] [Google Scholar]
- Thal DM, Vuckovic Z, Draper-Joyce CJ, Liang Y-L, Glukhova A, Christopoulos A & Sexton PM. (2018). Recent advances in the determination of G protein-coupled receptor structures. Current opinion in structural biology 51, 28–34. [DOI] [PubMed] [Google Scholar]
- Vanommeslaeghe K, Hatcher E, Acharya C, Kundu S, Zhong S, Shim J, Darian E, Guvench O, Lopes P, Vorobyov I & MacKerell AD. (2010). CHARMM General Force Field: A Force Field for Drug-Like Molecules Compatible with the CHARMM All-Atom Additive Biological Force Fields. Journal of Computational Chemistry 31, 671–690. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vanommeslaeghe K & MacKerell AD. (2012). Automation of the CHARMM General Force Field (CGenFF) I: Bond Perception and Atom Typing. Journal of Chemical Information and Modeling 52, 3144–3154. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vanommeslaeghe K, Raman EP & MacKerell AD. (2012). Automation of the CHARMM General Force Field (CGenFF) II: Assignment of Bonded Parameters and Partial Atomic Charges. Journal of Chemical Information and Modeling 52, 3155–3168. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Verrier RL & Antzelevitch C. (2004). Autonomic aspects of arrhythmogenesis: the enduring and the new. Curr Opin Cardiol 19, 2–11. [DOI] [PMC free article] [PubMed] [Google Scholar]
- von Rosenberg W, Hoting MO & Mandic DP. (2019). A physiology based model of heart rate variability. Biomed Eng Lett 9, 425–434. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vorobyov I, Olson TE, Kim JH, Koeppe RE Ii, Andersen OS & Allen TW. (2014). Ion-induced defect permeation of lipid membranes. Biophysical journal 106, 586–597. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wagner S, Ruff HM, Weber SL, Bellmann S, Sowa T, Schulte T, Anderson ME, Grandi E, Bers DM, Backs J, Belardinelli L & Maier LS. (2011). Reactive oxygen species-activated Ca/calmodulin kinase IIdelta is required for late I(Na) augmentation leading to cellular Na and Ca overload. Circ Res 108, 555–565. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang C, Bradley P & Baker D. (2007). Protein–protein docking with backbone flexibility. Journal of molecular biology 373, 503–519. [DOI] [PubMed] [Google Scholar]
- Wang J, Do HN, Koirala K & Miao Y. (2023). Predicting Biomolecular Binding Kinetics: A Review. J Chem Theory Comput 19, 2135–2148. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang J & Miao Y. (2019). Recent advances in computational studies of GPCR-G protein interactions. Advances in protein chemistry and structural biology 116, 397–419. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang L, Morotti S, Tapa S, Francis Stuart SD, Jiang Y, Wang Z, Myles RC, Brack KE, Ng GA, Bers DM, Grandi E & Ripplinger CM. (2019). Different paths, same destination: divergent action potential responses produce conserved cardiac fight-or-flight response in mouse and rabbit hearts. J Physiol 597, 3867–3883. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Warner HR & Cox A. (1962). A mathematical model of heart rate control by sympathetic and vagus efferent information. J Appl Physiol 17, 349–355. [DOI] [PubMed] [Google Scholar]
- Wheeler DW, Kullmann PH & Horn JP. (2004). Estimating use-dependent synaptic gain in autonomic ganglia by computational simulation and dynamic-clamp analysis. J Neurophysiol 92, 2659–2671. [DOI] [PubMed] [Google Scholar]
- Xu X, Kaindl J, Clark MJ, Hubner H, Hirata K, Sunahara RK, Gmeiner P, Kobilka BK & Liu X. (2021). Binding pathway determines norepinephrine selectivity for the human beta(1)AR over beta(2)AR. Cell Res 31, 569–579. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yang JH & Saucerman JJ. (2012). Phospholemman is a negative feed-forward regulator of Ca2+ in beta-adrenergic signaling, accelerating beta-adrenergic inotropy. J Mol Cell Cardiol 52, 1048–1055. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yang PC, DeMarco KR, Aghasafari P, Jeng MT, Dawson JR, Bekker S, Noskov S, Yarov-Yarovoy V, Vorobyov I & Clancy CE. (2020). A Computational Pipeline to Predict Cardiotoxicity:From the Atom to the Rhythm. Circ Res 126, 947–964. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yarov-Yarovoy V, Schonbrun J & Baker D. (2006). Multipass membrane protein structure prediction using Rosetta. Proteins 62, 1010–1025. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Young T, Palta M, Dempsey J, Skatrud J, Weber S & Badr S. (1993). The occurrence of sleep-disordered breathing among middle-aged adults. N Engl J Med 328, 1230–1235. [DOI] [PubMed] [Google Scholar]
- Zhang Y & Mazgalev TN. (2011). Arrhythmias and vagus nerve stimulation. Heart failure reviews 16, 147–161. [DOI] [PubMed] [Google Scholar]
- Zhou S, Jung BC, Tan AY, Trang VQ, Gholmieh G, Han SW, Lin SF, Fishbein MC, Chen PS & Chen LS. (2008a). Spontaneous stellate ganglion nerve activity and ventricular arrhythmia in a canine model of sudden death. Heart Rhythm 5, 131–139. [DOI] [PubMed] [Google Scholar]
- Zhou S, Tan AY, Paz O, Ogawa M, Chou CC, Hayashi H, Nihei M, Fishbein MC, Chen LS, Lin SF & Chen PS. (2008b). Antiarrhythmic effects of beta3-adrenergic receptor stimulation in a canine model of ventricular tachycardia. Heart Rhythm 5, 289–297. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhu C, Rajendran PS, Hanna P, Efimov IR, Salama G, Fowlkes CC & Shivkumar K. (2022). High-resolution structure-function mapping of intact hearts reveals altered sympathetic control of infarct border zones. JCI Insight 7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhu F & Hummer G. (2010). Pore opening and closing of a pentameric ligand-gated ion channel. Proc Natl Acad Sci U S A 107, 19814–19819. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhu F & Hummer G. (2012). Theory and simulation of ion conduction in the pentameric GLIC channel. J Chem Theory Comput 8, 3759–3768. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zuanetti G, De Ferrari GM, Priori SG & Schwartz PJ. (1987). Protective effect of vagal stimulation on reperfusion arrhythmias in cats. Circ Res 61, 429–435. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
Molecular dynamics simulation and analysis data file and scripts are available to download from Dryad repository at https://doi.org/10.25338/B87D2J


