Tetra-tert-butyl-s-indacene is a Bond Localized C_2h Structure and a Challenge for Computational Chemistry

Abstract

Whether tetra-tert-butyl-s-indacene is a symmetric D_2h structure or a bond alternating C_2h structure remains a standing puzzle. Close agreement between experimental and computed proton chemical shifts based on minima structures optimized at the M06–2X, ωB97X-D, and M11 levels confirm a bond localized C_2h symmetry, which is consistent with the expected strong antiaromaticity of TtB-s-indacene.

Graphical Abstract

The structure of tetra-tert-butyl-s-indacene is a computational challenge. Highly-correlated methods and popular DFT functionals predict a bond-delocalized D_2h symmetry, but excellent agreement between experimental and computed proton chemical shifts suggests a true C_2h geometry.

Tetra-tert-butyl-s-indacene (TtB-s-indacene) represents one of the first few critical examples of a kinetically trapped antiaromatic compound.^[1,2] It is expected to have a bond localized C_2h structure, resulting from antiaromaticity of the planar, cyclic, 12 π-electron conjugated core, but a large number of experimental and theoretical works indicate a possible bond delocalized D_2h structure.^[3–9] Unsubstituted s-indacene, first prepared in 1963,^[10] decomposes readily and no structural data could be acquired. Hafner later prepared TtB-s-indacene in 1986 showing that while the compound still was sensitive to oxygen and traces of acid in solution, it could be obtained as red needles that were air stable in the solid state.^[1,2] Consistent with its antiaromatic character, ¹H NMR spectra of TtB-s-indacene revealed upfield shifted ring protons compared to those of a non-aromatic methyl-dihydro derivative (Figure 1).

Figure 1.

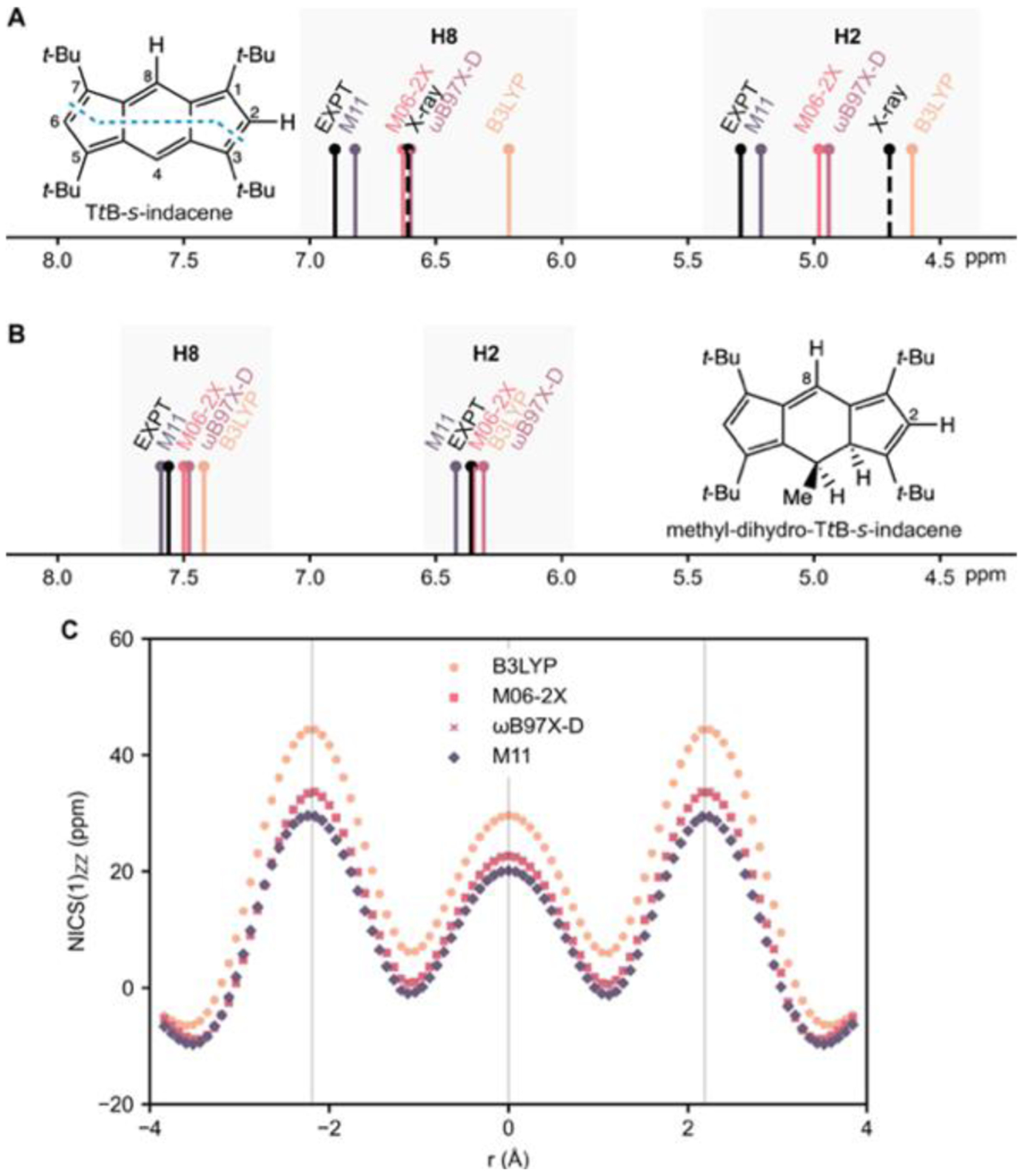
Experimental ¹H NMR (data from reference [2]) and computed proton chemical shifts for H8 and H2 in A) TtB-s-indacene (H8: 6.90 ppm, H2: 5.29 ppm, expt.) and B) methyl-dihydro-TtB-s-indacene (H8: 7.56 ppm, H2: 6.36 ppm, expt.). Proton chemical shifts were computed at B97–2/6–311+G(d,p) for minima geometries optimized at the B3LYP, M06–2X, ωB97X-D and M11/6–311+G(d,p) levels and for a partially optimized X-ray structure (see footnote [e], Table 1). C) NICS-XY-scans for TtB-s-indacene at B97–2/6–311+G(d,p), based B3LYP, M06–2X, ωB97X-D, and M11/6–311+G(d,p) geometries. Note overlapping M06–2X and ωB97X-D scans.

The exact structure of TtB-s-indacene nonetheless was difficult to determine. The presence of four peaks in the ¹³C NMR spectrum at −130 °C for the twelve ring C atoms could point to either a completely delocalized 12 π-electron system or a low energy barrier between two valence isomers. Evidence from X-ray data, both at room temperature and at 100 K, indicated a symmetric D_2h structure,^[2,4] yet the possible roles of residual disorder could not be ruled out. It was suggested that the crystal structure of TtB-s-indacene might be a “frozen transition state structure” resulting from solid-state packing and thus did not necessarily reflect its symmetry as a free molecule. We now show that TtB-s-indacene indeed has a bond localized C_2h structure as expected by its antiaromaticity.

Although early Hückel molecular orbital theory and semiempirical calculations predicted a C_2h structure for unsubstituted s-indacene,^[5,11,12] Koch et al. concluded based on ab initio and density functional theory (DFT) calculations that agreement between the computed D_2h structure of s-indacene and the X-ray structure of TtB-s-indacene must mean that TtB-s-indacene is a “completely delocalized 12 π-electron system”.^[6,7] MP2/6–31G(d) calculations for s-indacene found the C_2h structure to be lower in energy than the D_2h structure by 0.7 kcal/mol, but single point calculations at the CASPT2 level indicated a lower energy D_2h structure by 3.1 kcal/mol.^[6] At the LDA and LDA+BP levels, only a D_2h minimum could be located.^[6] Subsequent studies performed for unsubstituted s-indacene based on various DFT computations were indecisive. B3LYP/6–31G(d) calculations predicted a “quasi-delocalized” structure.^[8] The C_2h structure is a minimum and is 0.1 kcal/mol lower in energy than the D_2h form, which is a transition state structure; however, zero-point energy correction reverses the relative energy, and the D_2h form becomes 0.6 kcal/mol lower. BLYP predicted a bond localized C_2h structure.^[7] Heilbronner and Yang,^[3] and later Salvi et al.,^[5] recognized that TtB-s-indacene exhibits a stronger tendency towards bond delocalization than the parent s-indacene, but neither provided conclusive evidence for a D_2h geometry. Since X-ray structures can be influenced by crystal packing as well as static and dynamic disorders even at low temperatures, agreement with X-ray data does not provide decisive evidence for the structure of TtB-s-indacene. Proton chemical shifts, however, can show large responses even to subtle geometric variations.

Excellent agreement between computed and experimental proton chemical shifts can be found only when the expected geometries are correct. Bühl and Schleyer examined the reported chemical shifts for many boranes, carboranes, and nonclassical carbocations, revealing numerous structural misassignments and finding that computed and experimental proton chemical shifts match only when the assigned geometries were correct.^[13] For example, [18]annulene was expected to have a symmetric D_6h structure for over four decades; however, experimental match to ab initio NMR data identified the correct C₂ symmetry.^[14] Whereas the computed proton chemical shifts of D_6h [18]annulene structures at various DFT levels were in gross disagreement with experiment,^[15,16] the computed averaged proton chemical shifts of C₂ minima geometries of [18]annulene at the KMLYP (outer: 8.9 ppm, inner: −2.5 ppm) and BHLYP (outer: 9.2 ppm, inner: −2.8 ppm) levels matched closely with experiment (outer: 9.3 ppm, inner: −3.0 ppm). Using the same approach, computed proton chemical shifts for a partially optimized X-ray geometry of TtB-s-indacene (H8: 6.61 ppm, H2: 4.70 ppm, black dashed line, see also Table 1, footnote [e]) shows signals far upfield from the reported experimental ¹H NMR shifts (H8: 6.90 ppm, H2: 5.29 ppm, black solid line, Figure 1A).^[1,2] TtB-s-indacene cannot have a symmetric D_2h structure!

Table 1.

Computed C–C bond length difference (Δr), and relative free energies (ΔG_rel) between the C_2h and D_2h structures of TtB-s-indacene at the B3LYP, M06–2X, ωB97X-D, and M11/6–311+G(d,p) levels.

Level	HF[a] (%)	PG[b]	Δr[c] (Å)	ΔErel (kcal/mol)	δ H8[d] (ppm)	δ H2[d] (ppm)
B3LYP	20	C 2h D 2h	– 0	– 0.00	– 6.20	– 4.60
M06–2X	54	C 2h D 2h	0.066 0	0.00 0.30	6.62 6.32	4.97 4.60
ωB97X-D	SR:22 LR:100 ω:0.20	C 2h D 2h	0.069 0	0.00 0.57	6.59 6.26	4.93 4.53
M11	SR:42.8 LR:100 ω:0.25	C 2h D 2h	0.086 0	0.00 1.80	6.81 6.40	5.20 4.67
X-ray[e]	–	D 2h	0.001	–	6.61	4.70

^[a]Short range (SR) and long range (LR) percentages of HF exchange.

^[b]Point Group.

^[c]Δr is the difference between the two C–C bond lengths of the central six-membered ring connected to C4/C8.

^[d]Proton chemical shifts were computed at B97–2/6–311+G(d,p) using the computed chemical shielding for hydrogen in benzene as a reference.

^[e]Based on X-ray crystal structure at 100 K (reference [4]). All ring C–C bonds and the four C–C_t-butyl bonds were fixed to reported X-ray data, all other parameters were optimized at M11/6–311+G(d,p).

Proton chemical shifts computed at B97–2/6–311+G(d,p) for minima geometries of TtB-s-indacene obtained at the B3LYP (H8: 6.20 ppm, H2: 4.60 ppm, D_2h), M06–2X (H8: 6.62 ppm, H2: 4.97 ppm, C_2h), ωB97X-D (H8: 6.59 ppm, H2: 4.93 ppm, C_2h), and M11 (H8: 6.81 ppm, H2: 5.20 ppm, C_2h) levels spread over a range of 0.61 ppm for H8 and 0.60 ppm for H2 (cf. H8: 6.90 ppm, H2: 5.29 ppm, expt., see Figure 1A). Computed proton chemical shifts based on B3LYP-D3 geometries are close to the B3LYP values and are included in the Supporting Information (SI). The M11 structure displays the most bond length alternation (Δr = 0.086 Å, see footnote [c] in Table 1, cf. values for other functionals) and the computed proton chemical shifts match best with experiment. The D_2h minimum geometry of B3LYP (Δr = 0) most closely resembles the X-ray structure of TtB-s-indacene (Δr = 0.001 Å), but the computed proton chemical shifts are significantly upfield shifted and far off from the experimental ¹H NMR data. Accordingly, NICS-XY-scans^[17] computed for the D_2h B3LYP geometry of TtB-s-indacene show a higher paratropicity (more positive NICS values) compared to results obtained with the C_2h minimum geometries of M06–2X, ωB97X-D, and M11 (Figure 1C). Notably, the delocalization errors of B3LYP are less severe for a non-aromatic analogue of TtB-s-indacene. Computed proton chemical shifts for methyl-dihydro-TtB-s-indacene (Figure 1B) show a narrow spread (0.17 ppm for H8 and 0.11 ppm for H2) and the computed proton chemical shifts match better with ¹H NMR data for all functionals: B3LYP (H8: 7.41, H2: 6.40 ppm), M06–2X (H8: 7.49 ppm, H2: 6.34 ppm), ωB97X-D (H8: 7.47 ppm, H2: 6.30 ppm), and M11 (H8: 7.58 ppm, H2: 6.41 ppm) (cf. H8: 7.56 ppm, H2: 6.36 ppm, expt.).

Errors in predicting ¹H NMR shifts based on B3LYP geometries have been reported previously.^[14,18–23] Choi and Kertesz noted that the proton chemical shifts of many higher annulenes, computed using geometries optimized at the B3LYP/6–31G(d) level, disagree with experiment.^[15] Proton chemical shifts computed using B3LYP geometries for a porphyrin nanobelt structure reported by Anderson and Peeks in 2017 matched poorly with experimental ¹H NMR data.^[21–24] The cause of this discrepancy is the large delocalization error of B3LYP.^[25] Functionals like B3LYP have a low percentage of HF exchange at long interelectronic ranges and are prone to overestimating electron delocalization.^[25] Such errors compromise theoretical interpretations of the structures of large annulenes and extended π-conjugated macrocycles. We show here that the delocalization errors of B3LYP apply also to π-expanded antiaromatic systems and worsen for strongly antiaromatic species.

We chose to examine the performance of M06–2X, ωB97X-D, and M11 because they represent a selection of the most commonly used DFT functionals in computational organic chemistry. These functionals are relatively efficient and suitable for studying large sets of expanded π-conjugated systems, and the increasing percentage of HF exchange in this set allows us to scrutinize the importance of long-range electron correlations for properly describing the geometries of antiaromatic compounds.

Besides computed NMR evidence, M06–2X, ωB97X-D, and M11 all predict a C_2h minimum structure for TtB-s-indacene that is, respectively, 0.30, 0.57, and 1.49 kcal/mol lower in relative free energy (ΔG_rel) than the D_2h transition state structure (Table 1). No C_2h minimum structure was found at the B3LYP/6–311+G(d,p) level. Since the barrier to interconverting the two equivalent C_2h structures of TtB-s-indacene is small, dynamic disorder can give rise to a time-averaged D_2h structure for room-temperature experiments and even for low temperature X-ray experiments. Eigenvectors of the imaginary frequencies for the D_2h transition state structure at M06–2X (645i cm^–1), ωB97X-D (688i cm^–1), and M11 (1001i cm^–1) are all substantial and indicate a strong tendency towards ring bond length alternation. CASSCF(12,12)/6–311+G(d,p) calculations based on geometry optimization with an initial C_2h and D_2h symmetry both converged to a bond-alternating C_2h structure. Proton chemical shifts computed at CASSCF(12,12)/6–311G(d,p) for the C_2h structure (H8 = 6.74 ppm, H2 = 5.49 ppm) agreed moderately well with experiment (H8: 6.90 ppm, H2: 5.29 ppm).

Some electron-correlated methods predict a lower energy D_2h minimum for TtB-s-indacene. Single-point energies computed at DLPNO-CCSD(T)/def2-TZVP//M11/6–311+G(d,p) predict a lower energy D_2h vs. C_2h structure (ΔE_rel = 1.01 kcal/mol). Geometry optimizations at MP2/def-TZVP led to a D_2h structure; no C_2h structure was located. MP2/Def2-SVP computations also led to a single D_2h minimum structure; the lowest frequency corresponding to distortion towards C_2h symmetry is 145.9 cm^–1. Computed proton chemical shifts for the MP2/def-TZVP geometry matched poorly with experimental values (H8: 6.63 ppm, cf. 6.90 ppm, expt.; H2: 4.84 ppm, cf. 5.29 ppm, expt.).

Indeed, the structure of TtB-s-indacene is a computational challenge. The small energy difference between the C_2h and D_2h structures are below the accuracy of many of the calculations reported above. Yet, a matched proton chemical shifts value for the C_2h structure provides definitive evidence. TtB-s-indacene may have a “quasi-delocalized” structure^[8] with a competitive D_2h form, but the structure captured by Hafner’s NMR experiments must have a C_2h symmetry.

During the course of this study, Cheng and Tobe et al. reported a series of substituted hexaaryl-s-indacenes with C_2h, D_2h, and C_2v symmetries, as evidenced by X-ray measurements and calculations at the B3LYP level.^[26] We computed the symmetrically substituted hexaxylyl-s-indacene (compound 1f in reference 26) and found that while hexaxylyl-s-indacene exhibits a D_2h s-indacene core at the B3LYP level, minimum geometries at the M06–2X, ωB97X-D, and M11 levels show a C_2h s-indacene core. Computed proton chemical shifts based on M11 geometries give the best match with experiment (Figure 2).

Figure 2.

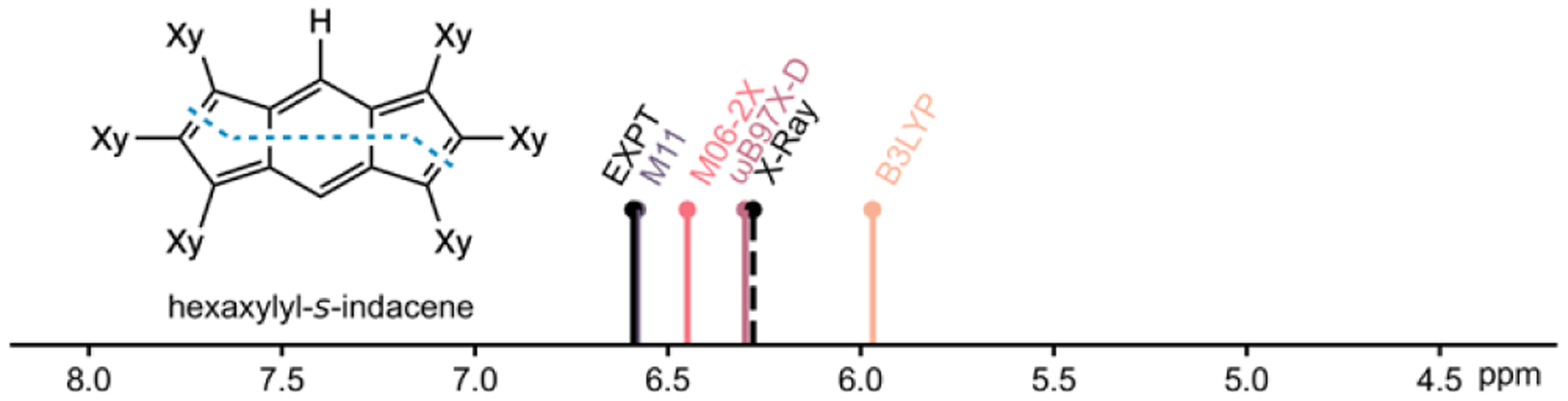
Experimental ¹H NMR and computed proton chemical shifts for hexaxylyl-s-indacene (Xy = 3,5-dimethylphenyl). Proton chemical shifts were computed at B97–2/6–311+G(d,p) for minima geometries optimized at the B3LYP, M06–2X, ωB97X-D and M11/6–311+G(d,p) levels and for a partially optimized X-ray structure.

Some of us recently published a joint experimental and theoretical study of indacenodibenzofurans (IDBFs).^[27] We found that syn-IDBF shows a high degree of paratropicity exceeding that of the parent s-indacene, while anti-IDBF exhibits weaker paratropicity. Indeed, experimental ¹H NMR signals for the hydrogens on the central six-membered ring of syn-IDBF are shifted upfield (H_syn: 5.60 ppm, Figure 3A) compared to those of anti-IDBF (H_anti: 6.15 ppm, Figure 3B). Computed proton chemical shifts reproduce these trends, indicating a more antiaromatic syn-isomer. However, proton chemical shifts based on M11 geometries (H_syn: 5.51 ppm, H_anti: 6.04 ppm) are in much better agreement with experiment than those based on B3LYP geometries (H_syn: 4.74 ppm, H_anti: 5.74 ppm, note greater mismatch for the more antiaromatic syn-isomer) (see Figures 3A–3B and results for M06–2X and ωB97X-D in the SI). These results suggest that M11 geometries most properly capture the degree of bond localization in syn- and anti- IDBF. Note the more bond alternated structures predicted by M11 (Δr_syn = 0.100 Å, r_anti = 0.081 Å) compared to B3LYP geometries (Δr_syn = 0.047 Å, Δr_anti = 0.004 Å).

Figure 3.

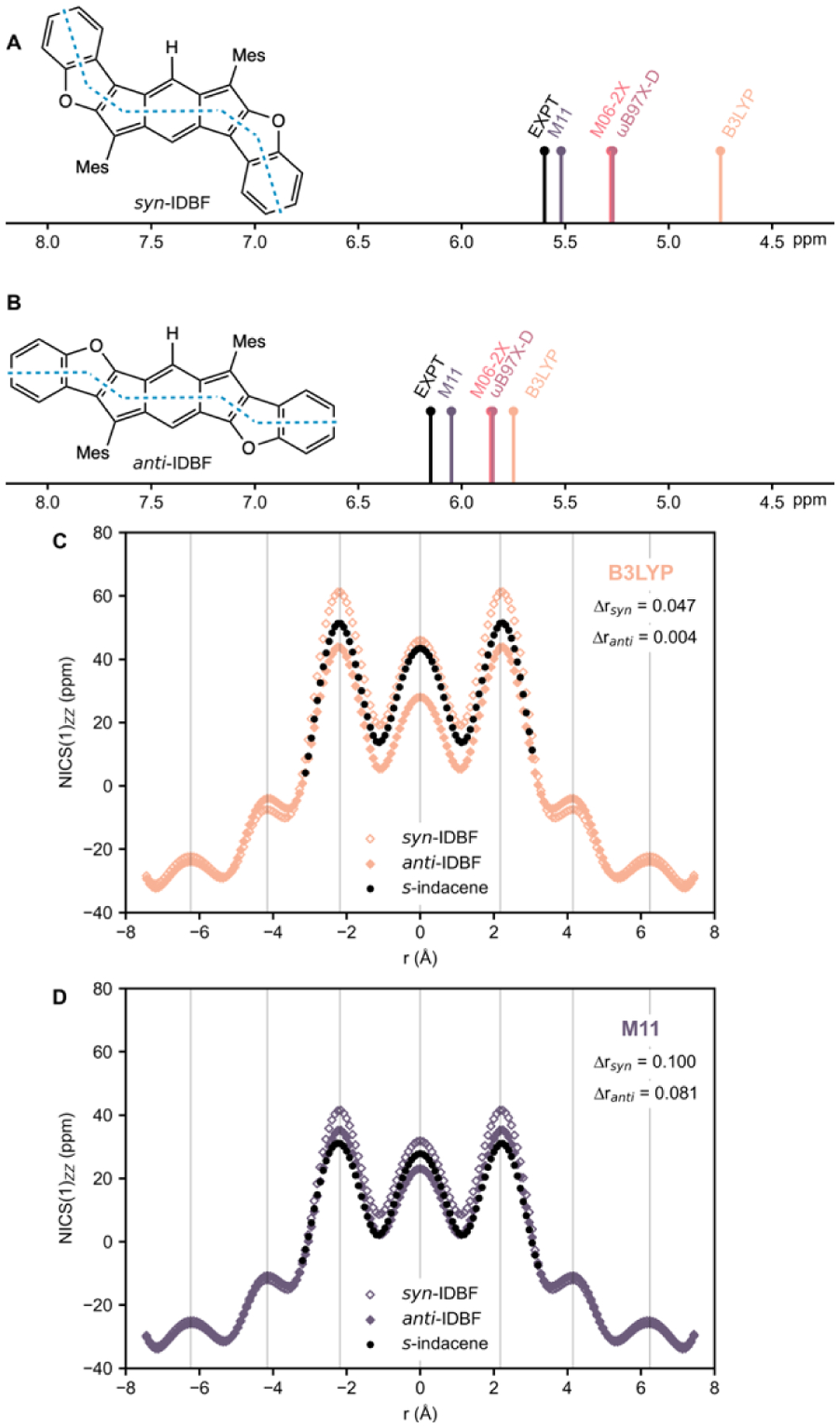
Experimental ¹H NMR (data from reference [27]) and computed proton chemical shifts for the central hydrogens in A) syn-IDBF (H_syn: 5.60 ppm, expt.) and B) anti-IDBF (H_anti: 6.15 ppm, expt.). Computed NICS-XY-scans based on geometries optimized at the C) B3LYP and D) M11 levels. NICS-XY-scans for s-indacene using geometries optimized at the respective levels are included for comparison. Δr values indicate the difference between the two C–C bond lengths connected to C4/C8.

In our previous study, NICS-XY-scans were computed using optimized B3LYP geometries of syn- and anti- IDBF. We now contrast these results to NICS-XY-scans obtained using M11 geometries. Figure 3C reproduces the published results^[27] showing a higher paratropicity for syn-IDBF and a lower paratropicity for anti-IDBF, compared to the parent s-indacene. NICS XY-scans based on M11 geometries (Figure 3D) confirm that syn-IDBF is more antiaromatic than anti-IDBF, but show in contrast to B3LYP results, that anti-IDBF is as antiaromatic as s-indacene based on comparisons of the NICS values at the five membered rings. Computations for indacenodibenzothiophenes (IDBT) and their sulfone analogues (IDBT-sulfone) are included in the SI, and further illustrate the limitations of predicting the ¹H NMR shifts and paratropicities of antiaromatic compounds based alone on B3LYP geometries.

M11 stands out as an especially suitable functional for the study of expanded π-conjugated [4n] antiaromatic systems. Comparisons of experimental ¹H NMR measurements to ab initio NMR calculations for expanded pentalene cores also show that M11 geometries performs the best for describing the degree of bond localization in antiaromatic systems and therefore gives the closest match for proton chemical shifts. Tri-t-butyl-pentalene^[28] shows a clear tendency for bond length alternation and experimental ¹H NMR measurements show highly shielded signals for the equivalent H1 and H3 protons and for H5 (H1/H3_avg: 5.07 ppm, H5: 4.72 ppm, Figure 4A). Computed proton chemical shifts based on M11 geometries (H1/H3_avg: 5.15 ppm, H5: 4.67 ppm) give a closer match with experiment compared to results based on B3LYP geometries (H1/H3_avg: 4.93 ppm, H5: 4.39 ppm). London et al. recently reported a series of substituted benzopentalenes (BP)^[29,30] that can have two unique olefinic protons on the pentalene core. Computed proton chemical shifts for a selected BP structure are shown in Figure 4B. Again, results based on M11 geometries (H1: 5.89 ppm, H5: 6.12 ppm) agree best with experimental ¹H NMR data (H1: 6.12 ppm, H5: 6.36 ppm), while computations based on B3LYP geometries give a poor match (H1: 5.68 ppm, H5: 5.94 ppm).

Figure 4.

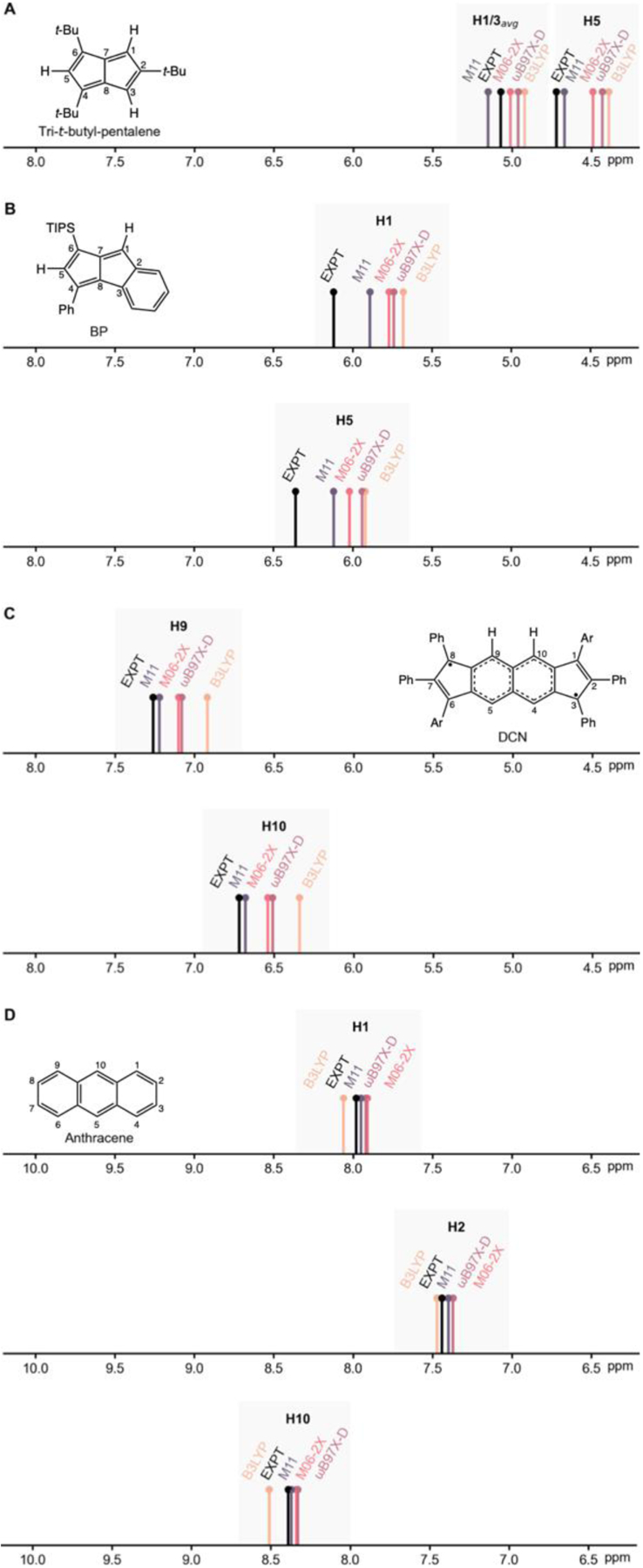
Experimental ¹H NMR and computed proton chemical shifts for: A) H1/H3_avg and H5 in tri-t-butyl-pentalene (H1/H3_avg: 5.07 ppm, H5: 4.72 ppm, expt., reference [28]), B) H1 and H5 in benzopentalene (H1: 6.12 ppm, H5: 6.36 ppm, expt., reference [29]), C) H9 and H10 in DCN (H9: 7.25 ppm, H10: 6.72 ppm, expt., reference [31]), and D) H1, H2, and H10 in anthracene (H1: 7.98 ppm, H2: 7.44 ppm, H10: 8.39 ppm, expt., reference [32]).

Another noteworthy example to examine is the dicyclopenta[b,g]naphthalene (DCN) derivative recently reported by Chi et al.^[31] DCN is a core expanded s-indacene isomer with pronounced open-shell singlet character (y₀ = 0.30). Geometries of DCN were optimized with an unrestricted broken symmetry approach. As shown in Figure 4C, computed chemical shifts at the M11 geometry (H9: 7.23 ppm, H10: 6.68 ppm) match best with experimental ¹H NMR data (H9: 7.25 ppm, H10: 6.72 ppm). B3LYP geometries continue to perform poorly (H9: 6.92 ppm, H10: 6.34 ppm).

In contrast to their antiaromatic congeners, polycyclic aromatic hydrocarbons have bond delocalized π-systems and thus are not subject to the same problems inflicted by use of B3LYP geometries for studying magnetic properties. Computed proton chemical shifts for anthracene, based on geometries optimized at the B3LYP (H1: 8.06 ppm, H2: 7.47 ppm, H10: 8.51 ppm) and M11 (H1: 7.95 ppm, H2: 7.40 ppm, H10: 8.37 ppm) levels both show perfect agreement with experimental data (H1: 7.98 ppm, H2: 7.44 ppm, H10: 8.39 ppm) (Figure 4D).^[32] Results for M06–2X and ωB97X-D are included in the SI.

Polycyclic antiaromatic hydrocarbons like the π-expanded indacenes, indenofluorenes, pentalenes, cyclooctatetraenes, and cyclobutadienes^{[30,31,32–41]} can show bond length alternation, strong paratropicity, and small HOMO–LUMO energy gaps, making them interesting candidates for organic electronics applications.^[35,42–46] Yet, theoretical studies of these emerging antiaromatic species continue to rely largely on computations performed using the B3LYP functional. Herein we have shown that B3LYP geometries poorly capture the bond localizing features of polycyclic antiaromatic systems, and the errors are especially severe for highly antiaromatic systems. Highly electron-correlated methods like MP2 also can give over delocalized geometries for extended antiaromatic π-systems like the TtB-s-indacene.