SUMMARY
Eukaryotic cells tightly control their size, but the relevant aspect of size is unknown in most cases. Fission yeast divide at a threshold cell surface area due in part to the protein kinase Cdr2. We find that fission yeast cells only divide by surface area under a size threshold. Mutants that divide at a larger size shift to volume-based divisions. Diploid cells divide at a larger size than haploid cells but maintain surface area-based divisions, indicating that the size threshold for changing from surface area to volume-based control is set by ploidy. Within this size control system, we found that the mitotic activator Cdc25 accumulates like a volume-based sizer molecule, while the mitotic cyclin Cdc13 accumulates in the nucleus as a timer. We propose an integrated model for cell size control based on multiple signaling pathways that report on distinct aspects of cell size and growth, including cell surface area (Cdr2), cell volume (Cdc25), and time (Cdc13). Combined modeling and experiments show how this system can generate both sizer and adder-like properties.
eTOC Blurb
Miller et al. find that the fission yeast mitotic cyclin Cdc13 accumulates like a molecular timer, while mitotic activator Cdc25 exhibits properties of a volume-based sizer protein. This study reveals an integrated cell size control network and provides insight into how cell cycle signals scale with cell size and growth for cell size control.
INTRODUCTION
Cell size varies widely among different cell types, but most cells control their size within an optimal window for proper function.1-3 Three common strategies for cell size control are timers, adders, and sizers.4,5 Timers act by limiting cell cycle stages to defined periods of time, as often observed in early stages of development.6,7 Adders measure the amount of growth or mass added to a cell during a defined cell cycle stage, as seen in bacteria and mammalian cells.8-10 Sizers work by delaying cell cycle transitions until cells reach a critical size threshold. Sizers have been identified in bacteria, yeast, and animal cells, and they imply the existence of size measuring systems that signal to core cell cycle machinery.11-17 As cells grow, they increase in volume, surface area, mass, and more. For most cell types that exhibit sizer behavior, we do not know which aspect of size is measured, or whether different molecular pathways measure distinct aspects of cell size. Many previous studies have focused on size-dependent changes in an individual protein or pathway, leaving open questions regarding how multiple pathways could converge to generate a robust and dynamic size control system.
The fission yeast Schizosaccharomyces pombe is a strong model system for studies on sizer behavior. These rod-shaped cells grow by linear extension while maintaining a constant cell width.18 Fission yeast cells adjust the amount of growth per cell cycle to compensate for variations in size at birth, such that all cells enter mitosis and divide at a defined and reproducible size.11,12 Historically, cell length has been used as a proxy for cell size in fission yeast studies, but recent work using mutants with altered widths has shown that fission yeast cells divide at a defined surface area, as opposed to volume or length.19,20 This finding raises the question of how cells measure their surface area, and whether other aspects of cell growth and geometry contribute to the overall size control system.
A set of conserved regulatory proteins control mitotic entry and thereby cell size in fission yeast (Figure 1A). The cyclin-dependent kinase Cdk1 (also called Cdc2 in S. pombe) drives mitotic entry in complex with the B-type cyclin Cdc13.21 The protein kinase Wee1 inhibits Cdk1 in small cells by phosphorylating a conserved tyrosine residue.22,23 This inhibition is reversed by the protein phosphatase Cdc25 to promote mitotic entry.24-28
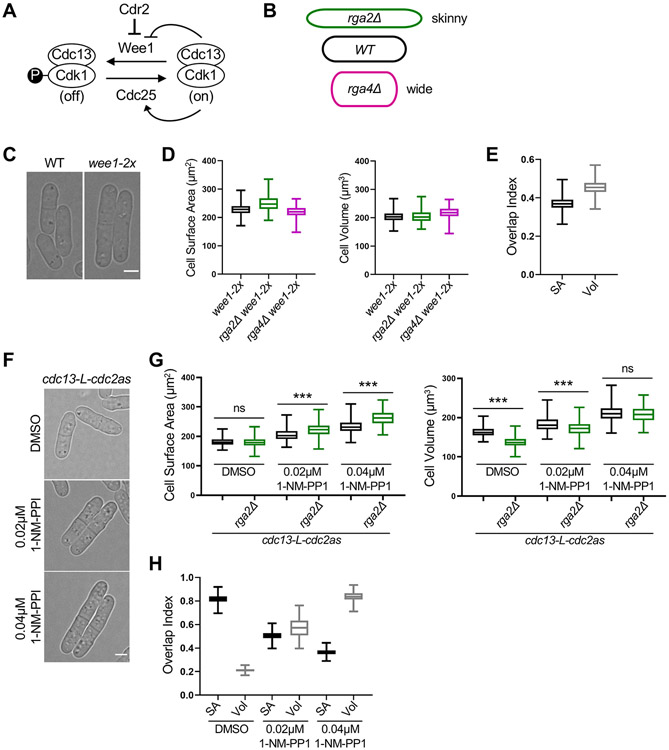
Figure 1. Large cells shift to volume-based division. See also Figure S1 and S2.
(A) Schematic of the pathway regulating mitotic entry and cell size. (B) Cartoon of cell width mutants used to uncouple cell surface area and volume. The colors apply to subsequent graphs in all figures. (C) Brightfield images of wild type (WT) and larger wee1-2x cells. (D) Size of dividing cells for indicated strains plotted by surface area (left) or volume (right). wee1-2x, n=628; wee1-2x rga2Δ, n=227; wee1-2x rga4Δ, n=197. (E) Overlap index analysis for data in panel D. SA, surface area. Vol, volume. (F) Brightfield images of cdc13-L-cdc2as treated with the indicated concentrations of 1-NM-PP1 or DMSO control. cdc13-L-cdc2as: DMSO n=686, 0.02μM 1-NM-PP1 n=424, 0.04μM 1-NM-PP1 n=470; cdc13-L-cdc2as rga2Δ: DMSO n=866, 0.02μM 1-NM-PP1 n=474, 0.04μM 1-NM-PP1 n=486) (G) Size of dividing cells for indicated strains plotted by surface area (left) or volume (right). ns, not significant; ***p<0.0001. (H) Overlap analysis for data in panel G. Graphs show median as a line, quartiles, max, and min. Bars, 4μm. See also Figures S1, and S2.
Within this conserved regulatory module, three mitotic activators have been heavily studied as potential size-measuring systems. First, the protein kinase Cdr2 controls cell size-dependent inhibition of Wee1 at a series of cortical multiprotein structures called “nodes.”29-32 The cortical density of nodes scales with cell surface area and could act as a surface area measurement system.19,20 Indeed, loss of Cdr2 causes cells to divide at an increased size and at a reproducible volume, as opposed to surface area.20,33 However, it is not known if this shift from surface area-based to volume-based size control reflects changes in overall cell size or loss of Cdr2 signaling. A second potential size-measuring system in fission yeast is accumulation of the cyclin Cdc13. Unlike most proteins, the cellular concentration of Cdc13 increases as cells grow, a phenomenon known as ‘superscaling.’ Cdc13 accumulates in the nucleus, where it can complex with Cdk1, and this superscaling has been proposed to act as a primary sensor for the mitotic size control system.34 A third possible size measuring system is superscaling of Cdc25 phosphatase.25,35 A recent study found that Cdc13 and Cdc25 are the only known mitotic regulatory proteins that increase in concentration as cells grow.36 However, it has not been known what aspect of cell size or growth drives accumulation of these mitotic activators.
Here, we studied connections between cell geometry, scaling of mitotic activators, and size control. We show that Cdc13/cyclin accumulates like a molecular timer, as opposed to a sizer. In contrast, Cdc25 accumulates specifically with cell volume, not with surface area or time. Thus, we propose that fission yeast cells have distinct pathways related to cell surface area (Cdr2-Wee1), cell volume (Cdc25), and time (Cdc13/cyclin). By altering cell size and mitotic signaling with previously characterized mutations, we identified conditions where fission yeast cells stop dividing by surface area-based size control and shift to other modes including volume-based size control and adder-like behavior. Our results redefine the fission yeast size control system as a network that integrates multiple pathways, each of which monitors distinct aspects of cell size and growth. Our model has strong implications for mechanisms of size control in other cell types and organisms.
RESULTS
Large cells shift to volume-based size control
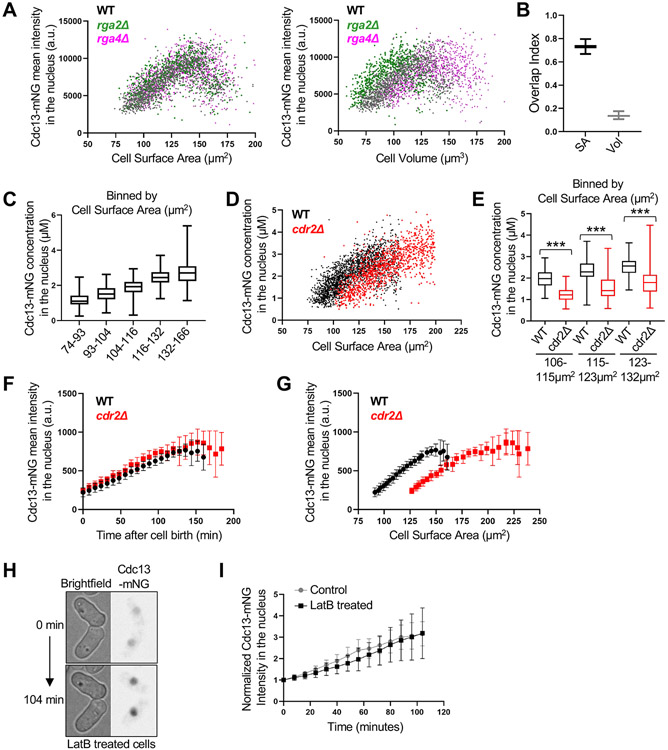
We started our study by asking how changes to overall cell size impact surface area-based size control. We used wide (rga4Δ) and skinny (rga2Δ) mutants to uncouple the scaling of cell surface area, volume, and length, similar to previous work (Figure 1B).19,20,33 designed a semi-automated image analysis pipeline to measure cell geometry (Figure S1A), which confirmed that wild type cells divide at a constant surface area while cdr2Δ cells divide at a constant volume (Figures S1B-S1I). We also generated an “overlap index” to quantify whether sizes were more related by surface area or volume (see Methods). This index confirmed the shift to volume-based divisions for cdr2Δ mutant cells (Figure S1G).
cdr2Δ cells divide at an increased size compared to wild type, so the shift to volume-based divisions could reflect the change in cell size or alternatively the loss of Cdr2 signaling. To distinguish between these possibilities, we tested other large cell size mutants. wee1-2x cells express an extra copy of wee1+. These cells divided larger than wild type but similar to cdr2Δ mutants (Figures 1C and S1L). Combining wee1-2x with wide (rga4Δ) or skinny (rga2Δ) mutants revealed that these enlarged cells also divide at a constant volume, as opposed to surface area (Figures 1D and 1E). This result suggests that large cells switch to volume-based division even with Cdr2 present. As an additional test, we used cells expressing cdc13-L-cdc2as, in which the activity of Cdk1 (i.e. Cdc2) is inhibited by 1-NM-PP1.37 We controlled the size of this strain by adding two different concentrations of 1-NM-PP1, leading to concentration-dependent increases in cell size compared to a DMSO control (Figure S1L). Interestingly, we observed a 1-NM-PP1 concentration-dependent shift towards volume-based division as cell size increased, which was validated by the overlap index (Figures 1G and 1H). We conclude that cells shift from surface area-based division to volume-based division above a certain size threshold.
The shift of cdr2Δ mutants to volume-based division has been suggested to result from loss of surface area-sensing by the Cdr2 pathway,20 but we observed a similar shift for large cells with an intact Cdr2 pathway. These results raise the possibility that the shift is due to increased size, as opposed to a specific role for Cdr2. These possibilities can be distinguished by reducing the size of cdr2Δ mutants. Therefore, we combined cdr2Δ with the previously characterized ppa2Δ and zfs1Δ mutations, which additively reduce cell size.38,39 The resulting triple mutant cdr2Δ ppa2Δ zfs1Δ divided at the same size as wild type cells (Figures 2A and 2B). By combining cdr2Δ ppa2Δ zfs1Δ with wide (rga4Δ) and skinny (rga2Δ) mutants, we found that reducing the size of cdr2Δ mutants shifted cells back to surface area-based divisions (Figure 2C and 2D). The loss of surface area-based divisions in cdr2Δ mutants is largely suppressed by reducing cell size, supporting a model where overall size determines whether cells divide by surface area or by volume. This result indicates that surface-area based size control is not strictly dependent on the Cdr2 pathway as previously suggested,20 but does not rule out Cdr2 acting as a surface area sensor together with additional, redundant systems.
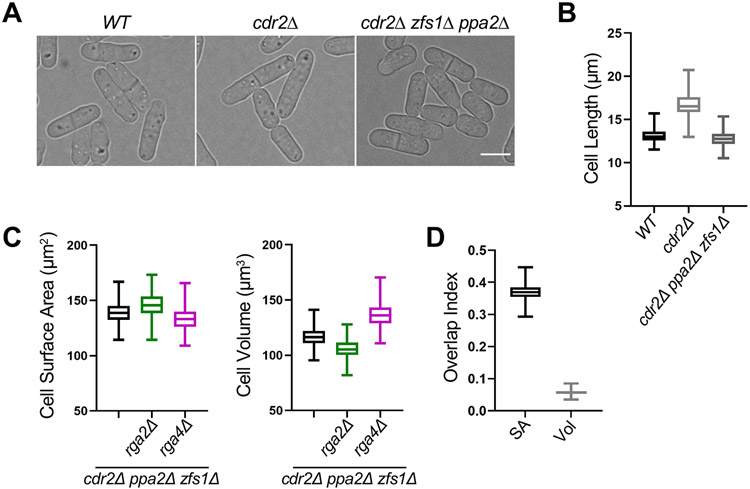
Figure 2. Reducing the size of cdr2Δ cells restores surface area-based divisions. See also Figure S2.
(A) Brightfield images of WT, cdr2Δ, and cdr2Δ zfs1Δ ppa2Δ cells. Bar, 4μm. (B) Cell length at division (μm) of indicated cell types. WT, n=268; cdr2Δ, n=590; and cdr2Δ zfs1Δ ppa2Δ, n=461. (C) Size of dividing cells for indicated strains plotted by surface area (left) or volume (right). cdr2Δ zfs1Δ ppa2Δ, n=461; cdr2Δ zfs1Δ ppa2Δ rga2Δ, n=415; and cdr2Δ zfs1Δ ppa2Δ rga4Δ, n=739. (D) Overlap index analysis for data in panel C. Experiment was repeated in triplicate and representative graphs from one experiment are shown. SA, surface area. Vol, volume. Graphs show median as a line, quartiles, max, and min. See also Figure S2.
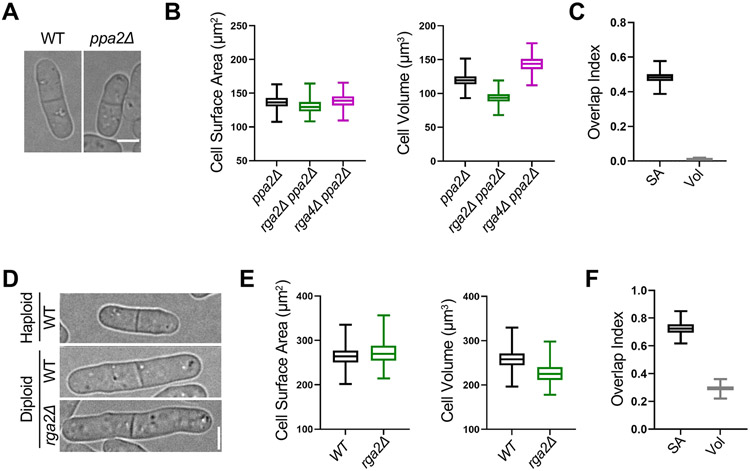
Next, we tested if loss of surface area-based divisions is specific to increased cell size or also occurs when cells divide too small. We examined the small size mutant ppa2Δ, previously shown to divide at a smaller size than wild type cells (Figures 3A and S1L). ppa2+ encodes one of two partially redundant catalytic subunits of the PP2A phosphatase, which counteracts Cdk1 activity.39 We found that ppa2Δ, ppa2Δ rga2Δ, and ppa2Δ rga4Δ all divided at the same surface area, but not at the same volume (Figures 3B and 3C). Therefore, reduced cell size does not cause a shift to volume-based divisions, at least in the ppa2Δ mutant. Rather, this result suggests the shift to volume-based divisions is a specific property of larger cell size.
Figure 3. Small size mutants and diploid cells retain surface area-based divisions. See also Figure S2.
(A) Brightfield images of WT and small ppa2Δ cells. (B) Size of dividing cells for indicated strains plotted by surface area (left) or volume (right). ppa2Δ, n=294; ppa2Δ rga2Δ, n=422; and ppa2Δ rga4Δ, n=365. (C) Overlap index analysis for data in panel B. SA, surface area. Vol, volume. Experiment was repeated in triplicate and representative graphs from one experiment are shown. (D) Brightfield images of indicated strains. (E) Size of dividing cells for indicated strains plotted by surface area (left) or volume (right). WT diploid, n=525 and rga2Δ diploid, n=397. We were unable to generate a rga4Δ diploid. (F) Overlap index analysis for data in panel E. Experiment was repeated in triplicate and representative graphs from one experiment are shown. Graphs show median as a line, quartiles, max, and min. Bars, 4μm. See also Figure S2.
Increased cell size has also been observed to scale with increased ploidy for many cell types and organisms (Figure 3D).1 Our results were obtained in haploid cells, so we hypothesized that genome content could limit the ability of large cells to maintain surface area-based divisions. In support of this model, previous studies have shown that genome content limits transcription in large fission yeast cells,40 and the cytoplasm of budding yeast cells becomes diluted with increased size.17,41 We found that wild type and rga2Δ diploid fission yeast cells divide at an overlapping surface area as opposed to volume, despite increased overall size (Figures 3E and 3F). Therefore, diploid cells use surface area-based divisions similar to haploid cells, despite their increased overall size. This result indicates that the size threshold for shifting from surface area-based to volume-based divisions is set by ploidy.
Cdc25 nuclear accumulation scales with cell volume
We next sought to identify molecular mechanisms that act in cell surface area-based and volume-based size control. Previous work has shown that Cdr2 localization patterns scale with cell surface area and may contribute to cell division at a threshold surface area,19,20 but no volume-based sizer molecules have been identified. Here, we focused on the Cdk1-activating phosphatase Cdc25 and the B-type mitotic cyclin Cdc13. The concentrations of both Cdc25 and Cdc13 increase as cells grow,25,34-36 but it has not been known what aspect of size and/or growth this accumulation reflects. Both Cdc25 and Cdc13 accumulate in the nucleus where Cdk1 activation likely occurs, so we focused on their nuclear concentrations. It is also important to note that the size of the nucleus scales tightly with overall cell size.42,43
As a starting point, we used functional Cdc25-mNG (mNeonGreen) expressed from the endogenous promoter and chromosomal locus. For imaging and segmenting the nucleus, cells also expressed a nuclear localization sequence fused to blue fluorescent protein (BFP-NLS). Cdc25-mNG and BFP-NLS were imaged by confocal microscopy in wild type, wide (rga4Δ), and skinny (rga2Δ) cells. Brightfield imaging of cells was performed to obtain cell dimensions and to segment cells (Figure S1A). To rapidly measure cell geometry and fluorescent protein intensity in thousands of cells, we developed a semi-automated ImageJ/MATLAB image analysis pipeline (Figure S1A). With this pipeline, we confirmed that the whole-cell concentration of both Cdc25 and Cdc13 increases with cell size (Figures S1J and S1K).
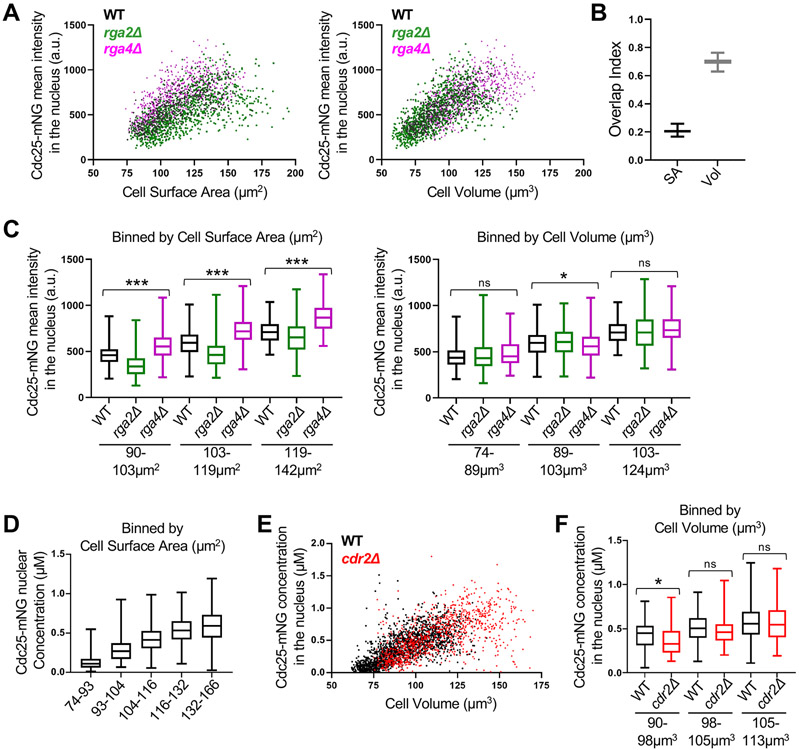
We plotted the mean Cdc25-mNG intensity in the nucleus as a function of cell surface area or cell volume. We observed strong overlap for Cdc25-mNG nuclear concentration in wild type, rga4Δ, and rga2Δ cells when plotted by volume but not by surface area (Figure 4A). We modified our overlap index analysis for bivariate data to quantify the overlap in nuclear concentrations when plotted by surface area or volume (See methods). The index confirmed the strong overlap of Cdc25 concentration in all three strains when plotting by volume (Figure 4B). This result indicates that the nuclear accumulation of Cdc25 scales with cell volume, not with cell surface area. This conclusion was strengthened when we excluded large, potentially mitotic cells (Figure S3A), and compared groups of cells binned by size (Figures 4C and S3D). We also reached the same conclusion quantifying either mean intensity or sum intensity of Cdc25-mNG in the nucleus (Figures S3A-C). In all analyses, Cdc25 nuclear concentration scaled closely with cell volume but not surface area. We conclude that Cdc25 nuclear concentration is a volume-dependent input to the cell size control network.
Figure 4. Cdc25 accumulation in the nucleus scales with cell volume. See also Figure S3 and S6.
(A) Cdc25-mNG nuclear mean intensity in WT, rga2Δ, and rga4Δ single cells plotted either by cell surface area (left) or by cell volume (right) (WT n=502, rga2Δ n=867, and rga4Δ n=684). The same cells are plotted in the two graphs. Experiment was repeated in triplicate and representative graphs from one experiment are shown. See also Figure S3A-C. (B) Overlap index analysis for data in panel A. SA, surface area. Vol, volume. (C) Cdc25 mean intensity in the nucleus for WT, rga2Δ, and rga4Δ cells binned by cell surface area (left) or volume (right). ***p<0.0001; *p<0.03; ns, not significant. n>90 for each strain per bin. Reported p value is the most significant value from pairwise comparisons within each group. (D) The concentration (μM) of nuclear Cdc25-mNG increases with cell size. Cells are binned by cell surface area (n>250 for each size bin). (E) Cdc25-mNG nuclear concentration (μM) in WT and cdr2Δ cells plotted by their cell volume (WT n=1,801; cdr2Δ n=1,037). (F) WT and cdr2Δ cells of the same volume have similar nuclear concentration (μM) of Cdc25 (n>110 per strain). Graphs show median as a line, quartiles, max, and min. *p=0.004; ns, not significant. See also Figures S1, S3, and S6.
We performed three additional experiments to extend this conclusion. First, we calibrated our confocal microscope using proteins of known concentration to measure the molar concentration of Cdc25-mNG in the nucleus (Figure S3E).44 In small cells, Cdc25 was present in the nucleus at levels below 100 nM on average. This concentration steadily increased to over 500 nM for the largest cells, which are close to the size threshold for mitotic entry. Thus, wild type cells enter mitosis when Cdc25 has accumulated to slightly over 500 nM in the nucleus (Figure 4D).
As a second extension, we measured Cdc25-mNG concentration in cdr2Δ cells, which are larger than wild type cells. Consistent with Cdc25 acting as a “sizer” molecule, we measured the same nuclear Cdc25-mNG concentration for wild type and cdr2Δ mutants within a given size bin, and cdr2Δ cells reached a higher level of Cdc25 in the nucleus because they divided at a larger size (Figures 4E and 4F). This result was not specific to the cdr2Δ mutant because we obtained the same result using wee1-2x, a different large mutant (Figure S3F and S3G). Finally, we asked what happens to Cdc25 nuclear concentration when cell growth is inhibited. Treatment of cells with Latrunculin-B (LatB) causes disassembly of the actin cytoskeleton and abolishes cell expansion.19,45 We found that Cdc25-mNG nuclear accumulation plateaued upon treatment of cells with LatB (Figures S3H and S3I). Put together, these results show that Cdc25 accumulates in the nucleus as a volume-dependent sizer molecule. This scaling property is distinct from Cdr2, which accumulates in the cell middle with cell surface area, indicating that cells have at least 2 distinct pathways likely monitoring different aspects of size: cell volume (Cdc25) and cell surface area (Cdr2).
Cdc13 accumulates in the nucleus as a molecular timer
Next, we performed a similar set of experiments for Cdc13-mNG expressed from the endogenous promoter and chromosomal locus. This strain does not exhibit any defects previously suggested for C-terminally tagged constructs (Figures S4A and S4B), and we confirmed key results with an internally tagged Cdc13-sfGFPint strain.46 We imaged Cdc13-mNG and BFP-NLS in wild type, rga4Δ, and rga2Δ strain background and plotted Cdc13-mNG intensity as a function of cell surface area or volume. Nuclear Cdc13 intensity increased with cell size until mitotic entry, when Cdc13 degradation is initiated.34,36 Cdc13-mNG nuclear intensity scaled more closely with cell surface area than with cell volume, indicating a distinct accumulation mechanism from Cdc25 (Figures 5A-B, and S4C-E). The molar concentration of Cdc13 in the nucleus increased from approximately 1 μM in small cells to 3 μM in larger cells (Figure 5C). Surprisingly, nuclear Cdc13-mNG did not show properties of a “sizer” molecule when we compared wild type and cdr2Δ cells, which are larger than wild type. Instead, cdr2Δ mutant and wild type cells had similar Cdc13 nuclear concentrations at birth despite their size differences, while cells in the same size range had different Cdc13 nuclear concentrations (Figure 5D). This conclusion was strengthened by the significant difference in Cdc13-mNG nuclear concentration for wild type versus cdr2Δ for cells binned by size (Figure 5E). To ensure that this result reflects the change in cell size and not Cdr2 activity, we also examined nuclear Cdc13 concentrations in cdc25-degron-DaMP cells, which divide at a larger cell size due to reduced levels of Cdc25. A clear difference in nuclear Cdc13 levels was observed when comparing WT and cdc25-degron-DaMP cells in the same size range (Figure S4F). Together, these results are inconsistent with nuclear accumulation of Cdc13 acting as a sizer mechanism.
Figure 5. Time-based accumulation of mitotic cyclin Cdc13 in the nucleus. See also Figure S4 and S5.
(A) Cdc13-mNG nuclear mean intensity in WT, rga2Δ, and rga4Δ single cells plotted either by cell surface area or by cell volume (WT n=1,166, rga2Δ n=687, and rga4Δ n=1,019). The same cells are plotted in the two graphs. Experiment was repeated two times and representative graphs from one experiment are shown. (B) Overlap index analysis for data in panel A. SA, surface area. Vol, volume. (C) Cdc13-mNG nuclear concentration (μM) in WT cells binned by cell surface area. n>280 for each size bin. Graph shows median as a line, quartiles, max, and min. (D) Cdc13-mNG nuclear concentration (μM) in WT and cdr2Δ cells plotted by cell surface area (WT n=1,950; cdr2Δ n=1,141). (E) Cdc13-mNG concentration (μM) in the nucleus of WT and cdr2Δ cells binned by cell surface area (n>75 for each size bin). ***p<0.0001. Graph shows median as a line, quartiles, max, and min. (F-G) Average Cdc13-mNG mean intensity in the nucleus of single cells from time-lapse imaging WT or cdr2Δ cells. n=10 cells per strain. Error bars indicate SD. Cdc13-mNG nuclear concentration was plotted either by time since cell birth (panel F) or by cell surface area (panel G). (H) Representative time-lapse image of Cdc13-mNG cells upon addition of 100μM Latrunculin B, an actin inhibitor that halts cell growth. (I) Mean nuclear Cdc13-mNG intensity over time from timelapse imaging of cells treated with or without 100μM Latrunculin B. n=10 cells per experiment. Error bars indicate SD. See also Figures S1, S4, and S5.
We considered the alternative hypothesis that Cdc13 accumulates as a “timer” molecule, such that its nuclear concentration reflects time since cell birth as opposed to absolute cell size. Because cells increase in size over time during normal growth conditions, this mechanism could explain accumulation of Cdc13 in our initial experiments as well as in previous studies.34,36 To test this idea, we performed timelapse microscopy of Cdc13-mNG in wild type and cdr2Δ mutant cells (Figure S5A and S5B). For each cell, we plotted Cdc13-mNG nuclear concentration as a function of either cell size or time since cell birth. We observed striking overlap of Cdc13 nuclear concentration in wild type and cdr2Δ cells when plotted as a function of time since cell birth (Figure 5F). In contrast, there was no overlap between these strains when plotted by cell size (Figure 5G), consistent with our static imaging experiment (Figure 5D and 5E). We also confirmed this result using a different large mutant (cdc25-degron-DaMP) and a different version of fluorescently tagged Cdc13 (Cdc13-sfGFPint) (Figures S5C and S5D). These time-lapse experiments were performed in rich media and we obtained similar results when cells were grown in minimal EMM4S media, which leads to a longer cell cycle (Figure S5E and S5F). Additionally, we compared these time-lapse results to Cdc25-mNG in wild type and cdr2Δ mutant cells. In contrast to time-based accumulation of Cdc13, we observed a strong overlap in Cdc25-mNG nuclear intensities when plotted by cell surface area, consistent with Cdc25 nuclear accumulation as a sizer (Figure S6). These combined results are consistent with a model where newborn cells accumulate nuclear Cdc13 over time, regardless of their size.
As a final test of Cdc13 acting as a timer molecule, we stopped cell growth by disrupting the actin cytoskeleton with LatB. If Cdc13 acts as a timer molecule, then we expect Cdc13 nuclear concentration to continue increasing in the absence of cell growth. Alternatively, if Cdc13 acts as a sizer molecule like Cdc25, then its nuclear concentration should plateau in the absence of growth. We found that the nuclear concentration of Cdc13-mNG (and Cdc13-sfGFPint) continued to increase after LatB addition. The rate of this increase was similar to control-treated cells (Figures 5H, 5I, and S5G). Thus, the nuclear accumulation of Cdc13 is time-dependent, not size-dependent. We conclude that Cdc13 has properties of a molecular “timer.”
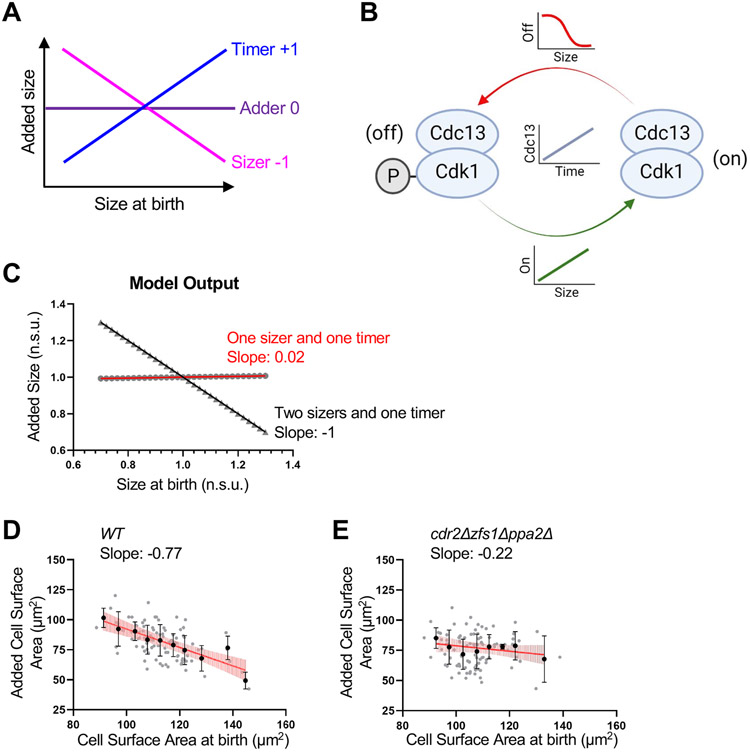
The integrated cell size control network can exhibit sizer and adder behaviors
Cell size homeostasis can be revealed by plotting the birth size of single cells against their size increase during the cell cycle from birth to division (Figure 6A). In these plots, a slope of −1 indicates a sizer mechanism, where cells divide at a fixed target size. A slope of 0 indicates an adder strategy, where cells add a fixed amount of size each division. A slope of +1 suggests timer behavior, where cells grow for a fixed duration of time. Previous work established that fission yeast cells exhibit strong sizer behavior in such experiments with a slope near −1.11,12 Our work combined with previous studies suggests that the fission yeast cell size control system is comprised of at least 3 distinct input signals: cell surface area (Cdr2), cell volume (Cdc25), and time (Cdc13). We formalized this integrated system in a qualitative mathematical model that includes size-dependent activation (Cdc25) and deactivation (Wee1) rates of Cdk1, along with time-dependent accumulation of Cdc13 (Figure 6B, see Methods for additional details). We found that this model is sufficient to recapitulate fission yeast cell size homeostasis with a slope of −1 (Figure 6C). Next, we changed the model to predict the behavior of cells upon loss of one size-dependent input. We altered Cdk1 inhibition (i.e. Wee1 activity) from a size-dependent parameter to a constant, size-independent value. This altered model, consisting of one size-dependent input (Cdc25) and one time-dependent input (Cdc13), qualitatively predicted adder-like behavior based on size-dependent Cdc25 activation and time-dependent Cdc13 activation (Figure 6C). Thus, the model predicts that the underlying biological system shifts from sizer to adder behavior upon loss of cell size-dependent Wee1 inhibition, at least in principle.
Figure 6. Modeling and experiments identify conditions for adder-like cell size homeostasis. See also Figure S7.
(A) Cell size homeostasis graphic showing the expected slope obtained from plotting the birth size of single cells using timer, adder, or sizer strategies against their size increase during the cell cycle. (B) Schematic of model with time-dependent accumulation of Cdc13 and size-dependent activation and inhibition of Cdk1-Cdc13 complex. (C) Size homeostasis plot from model. A model with 2 sizers and 1 timer reveals sizer behavior (Slope of −1). A model with 1 sizer and 1 timer leads to adder behavior (Slope of 0.02). Added size and size at birth are normalized to the mean added size or mean size at birth, respectively. Normalized size units (n.s.u.). Symbols indicate values obtained at specific size at birth. Slope of linear regression displayed. (D-E) Size homeostasis plots of WT (D) and cdr2Δ zfs1Δ ppa2Δ (E) cells. The cell surface area at birth and added surface area for individual cells was determined from timelapse imaging. Plots show data from individual cells (grey circles) and mean cell surface area at birth and added surface area for 5μm2 cell surface area size bins (black circles). Black bars indicate SD. Slope of linear regression line (red) displayed below cell type for each graph. Vertical light red lines along linear regression line indicate 95% confidence of the best-fit line. WT, n=101; cdr2Δ zfs1Δ ppa2Δ, n=100. Size homeostasis experiments were repeated at least 2 times and representative graphs from one experiment are shown. See also Figure S7.
To test this modeling prediction experimentally, we generated cell size homeostasis plots from timelapse microscopy. We measured cell surface area at birth and surface area addition per cell cycle for each cell in a timelapse experiment. Wild type cells exhibited size homeostasis as shown by a slope of −0.77 (Figure 6D), which confirms previous results based on cell length.11,47 To remove size-dependent inhibition of Wee1, we used cdr2Δ zfs1Δ ppa2Δ cells. This strain removes the size-dependent Cdr2 pathway and maintains cells at a similar overall size to wild type (Figure 2B). Remarkably, cdr2Δ zfs1Δ ppa2Δ cells exhibited a slope of −0.22 in cell homeostasis plots, indicating near-adder behavior (Figure 6E). We note that cdr2Δ alone had somewhat weakened size homeostasis (slope of −0.6) compared to wild type (Figure S7). We conclude that cell size homeostasis can occur through the integration of two molecular sizers and one molecular timer in our model. Removing one molecular sizer can shift the system to adder-like behavior, revealing plasticity in the size control system due to multiple input pathways.
DISCUSSION
Our work leads to a new, integrated model for cell size control in fission yeast. We propose that the size control network is comprised of at least three different pathways that monitor distinct aspects of cell growth (Figure 7). First, we have shown that the nuclear concentration of Cdc25 accumulates with cell volume. Second, we found that the nuclear concentration of cyclin Cdc13 increases over time, as opposed to size. Third, previous work has established that Cdr2-Wee1 signaling relates to cell surface area through the spatial density of Cdr2 nodes at the medial cell cortex.19,20 Such an integrated model likely explains why past studies have failed to identify a single “sizer” molecule or pathway in fission yeast.
Figure 7. An integrated model for geometry-based cell size control.
The fission yeast cell size control network integrates multiple signaling pathways that scale with distinct aspects of cell size and growth, including cell volume (Cdc25), time (Cdc13), and cell surface area (Cdr2).
Each of these pathways has been shown to change activity with cell size and growth, but loss of a single pathway does not appear to abolish size homeostasis. Our results do not exclude the possibility of additional pathways and components that monitor other aspects of cell size and growth. For example, we found that reducing the size of cdr2Δ mutant cells restored surface area-based divisions, which suggests that additional pathways act with Cdr2 to monitor cell surface area. Similarly, we do not know how loss of Cdc25 or Cdc13 accumulation might affect sensing of cell volume or time. The pathways that we studied all converge on Cdk1, with both Cdr2-Wee1 and Cdc25 focused on Cdk1-pTyr15. Many mutants alter cell size independently of Cdk1-pTyr15 and could represent more size- and time-dependent pathways in this network.37,38,48 Further, phosphatases that oppose Cdk1 such as PP1 and PP2A could have size-dependent regulation in addition to their known inputs from nutritional availability.49,50
Size control as an adaptable property
We identified two forms of plasticity within the fission yeast mitotic size control system. First, cells divide at a threshold surface area in one size regime but shift to dividing at a threshold volume at larger sizes. This property was initially identified for cdr2Δ mutants,20 but we have shown that it applies as a general size-dependent behavior. This size-dependent shift is likely to involve changes in the balance or integration of the Cdc25, Cdr2, and Cdc13 pathways. Both Cdc25 concentration and Cdr2 localization continue to increase in large cells,35,51 but a quantitative comparison of their scaling properties could reveal mechanisms for the shift to volume-based division. We also identified a role for ploidy in this shift, consistent with well-known links between cell size and genome content. This finding could relate to ploidy-dependent limits on overall transcription rates in large cells, which also exhibit cytoplasmic dilution and signs of senescence.40,41,52
A second form of plasticity in the size control system is the shift from sizer to adder mechanisms for size homeostasis. Size homeostasis plots identify mechanisms that operate across the entire cell cycle and could arise from the combination of multiple pathways. For example, our modeling and experiments identified adder-like behavior upon loss of size-dependent regulation of Wee1, at least for the cdr2Δ ppa2Δ zfs1Δ mutant. According to our model, this adder-like behavior can be explained by a molecular sizer (Cdc25) and a molecular timer (Cdc13). This situation appears related to budding yeast, where separate mechanisms for a G1/S sizer and a S/G2/M timer combine to form a phenomenological adder.53 Both Cdc25 and Cdc13 act on the G2/M transition, meaning that adder-like behavior can arise from the combination of a sizer and a timer that act on the same cell cycle stage.
Additional experiments addressing size homeostasis behavior upon changes in cell width and size might address connections between these two forms of plasticity. For example, we observed a size-dependent shift to volume-based divisions using static images of wide and skinny mutants. Previous work has identified adder-like behavior when large cells are allowed to return to wild type size.11 These results raise the possibility of a volume-dependent adder mechanism for large cells, which could be tested through future studies of rga2Δ and rga4Δ cell width mutants.
Molecular pathways in cell size control
We identified volume-dependent Cdc25 accumulation and time-dependent Cdc13 accumulation in the nucleus as critical pathways in the size control system. Our timelapse microscopy experiments were critical for identification of time-based Cdc13 accumulation in the nucleus. Our conclusion is supported by a recent report that also used timelapse imaging,54 but differs from previous work based on static images.34,55 We note that large-scale changes in cell size can impact Cdc13 levels,34,55 so cell size might contribute to Cdc13 levels even if it accumulates with time during cell cycle progression. Our data do not exclude cell size-dependent regulation of total Cdc13 abundance, with additional regulatory steps generating time-based Cdc13 nuclear accumulation. Identifying the molecular mechanisms for accumulation of Cdc25 and Cdc13 in the whole cell and in the nucleus are important goals for future studies. Disrupting these mechanisms has the potential to reveal how and when the concentrations of Cdc25 and Cdc13 impact size control. Previous work has shown that Cdc25 mRNA levels superscale with cell size,25,35 raising questions about size-dependent loading of transcription factors and RNA PolII at the cdc25+ promoter. cdc13+ mRNA levels do not oscillate during the cell cycle55 and the cdc13+ promoter is not required for superscaling of Cdc13 protein.34 Thus, post-transcriptional mechanisms might predominate in the scaling of Cdc13 levels with cell cycle time.
Beyond protein levels, both Cdc25 and Cdc13 are more concentrated in the nucleus than in the cytoplasm, which highlights the role of nucleocytoplasmic shuttling in cell size control. Mutations in multiple nuclear shuttling factors lead to changes in cell size,56,57 but it is currently unknown if shuttling rates are cell size-dependent or time-dependent for Cdc25, Cdc13 and other proteins in this system. Inside the nucleus, localization to the nucleolus or nucleoplasm could also add further regulation. The molecular mechanisms that control Cdc25 and Cdc13 accumulation and nuclear concentration likely represent additional layers of the integrated cell size control network.
Limitations and broader implications of our study
Our experiments were primarily performed under rich nutrient conditions, but both cell size and growth rate are highly dependent on environmental conditions. This raises the possibility that cells might shift the mode of size control under different growth conditions. Further, environmental stress and nutrient limitation are known to impact signaling by the Cdr2, Cdc25, and Cdc13 pathways.58-63 It will be interesting to learn whether changes to these pathways influence the importance of surface area, volume, and time in the cell size homeostasis network. We also note that we have measured protein concentrations without knowing the added layer of protein activity, such as the catalytic activity of Cdc25 phosphatase. Efforts to measure the specific activity of these proteins from cells of different sizes will extend our understanding of the integrated cell size control system.
Our work exploited the simple geometry of fission yeast to uncover pathways that monitor distinct aspects of cell geometry and growth. Many other eukaryotic cell types exhibit cell size control, but more complex cell shapes complicate attempts to distinguish between cell volume, cell surface area, and other aspects of size. Despite these technical challenges, it will be interesting to learn if a similar integrated system operates in other eukaryotic cell types and organisms. We note that an integrated system opens possibilities for more complex sizing strategies. For example, bacteria have been shown to use the ratio between surface area and volume as a key parameter for size control.64-66 Future work on additional signaling pathways that are modulated as cells grow could lead to new insights in this area.
STAR METHODS
RESOURCE AVAILABILITY
Lead Contact
Further information and requests for resources and reagents should be directed to and will be fulfilled by the Lead Contact, James B. Moseley (james.b.moseley@dartmouth.edu).
Materials Availability
All unique/stable reagents generated in this study are available from the Lead Contact without restriction.
Data and Code Availability
All data reported in this paper will be shared by the lead contact upon request.
All original code has been deposited at GitHub and is publicly available as of the date of publication. DOIs are listed in the key resources table.
Key Resources Table
| REAGENT or RESOURCE | SOURCE | IDENTIFIER |
|---|---|---|
| Antibodies | ||
| anti-Cdc13 antibody | Novus Biologicals | NB200-576 |
| Chemicals, peptides, and recombinant proteins | ||
| 1-NM-PP1 (4-Amino-1-tert-butyl-3-(1’-naphthylmethyl)pyrazolo[3,4-d]pyrimidine) | Toronto Research Chemicals | A603003 |
| Latrunculin B | Abcam | ab144291 |
| Experimental models: Organisms/strains | ||
| S. pombe JM366: WT 972 h- (Alternate name: PN1) | Lab collection | N/A |
| S. pombe JM6972: cdc13-yomNeonGreen::hphR lys3+:ptdh1*:NLS-linker-mTagBFP2:terminatortdh1:kanMX leu1:[pJK148-Pact-yomRuby3-term] h+ | This Study | N/A |
| S. pombe JM7003: rga2Δ::kanMX6 lys3+:ptdh1*:NLS-linker-mTagBFP2:terminatortdh1:kanMX cdc13-yomNeonGreen::hphR leu1:[pJK148-Pact-yomRuby3-term] h- | This Study | N/A |
| S. pombe JM7008: rga4Δ::kanMX6 lys3+:ptdh1*:NLS-linker-mTagBFP2:terminatortdh1:kanMX cdc13-yomNeonGreen::hphR leu1:[pJK148-Pact-yomRuby3-term] | This Study | N/A |
| S. pombe JM7088: cdr2Δ::NAT lys3+:ptdh1*:NLS-linker-mTagBFP2:terminatortdh1:kanMX cdc13-yomNeonGreen::hphR leu1:[pJK148-Pact-yomRuby3-term] h+ | This Study | N/A |
| S. pombe JM7171: lys3+:ptdh1*:NLS-linker-mTagBFP2:terminatortdh1:kanMX cdc25-yomNeonGreen::hphR leu1:[pJK148-Pact-yomRuby3-term] h- | This Study | N/A |
| S. pombe JM7172: rga4Δ::kanMX6 lys3+:ptdh1*:NLS-linker-mTagBFP2:terminatortdh1:kanMX cdc25-yomNeonGreen::hphR leu1:[pJK148-Pact-yomRuby3-term] h- | This Study | N/A |
| S. pombe JM6752: rga2Δ::kanMX6 lys3+:ptdh1*:NLS-linker-mTagBFP2:terminatortdh1:kanMX cdc25-yomNeonGreen::hphR leu1:[pJK148-Pact-yomRuby3-term] h- | This Study | N/A |
| S. pombe JM6753: cdr2Δ::NAT lys3+:ptdh1*:NLS-linker-mTagBFP2:terminatortdh1:kanMX cdc25-yomNeonGreen::hphR leu1:[pJK148-Pact-yomRuby3-term] h- | This Study | N/A |
| S. pombe JM7492: lys3+:ptdh1*:NLS-linker-mTagBFP2:terminatortdh1:kanMX leu1Δ::Pcdc13::cdc13-L-cdc2as::cdc13 3'UTR::ura4+ cdc2Δ::kanMX6 cdc13Δ::natMX6 h+ | This Study | N/A |
| S. pombe JM7490: rga2Δ::kanMX6 lys3+:ptdh1*:NLS-linker-mTagBFP2:terminatortdh1:kanMX leu1Δ::Pcdc13::cdc13-L-cdc2as::cdc13 3'UTR::ura4+ cdc2Δ::kanMX6 cdc13Δ::natMX6 | This Study | N/A |
| S. pombe JM7502: rga4Δ::hphR lys3+:ptdh1*:NLS-linker-mTagBFP2:terminatortdh1:kanMX leu1Δ::Pcdc13::cdc13-L-cdc2as::cdc13 3'UTR::ura4+ cdc2Δ::kanMX6 cdc13Δ::natMX6 | This Study | N/A |
| S. pombe JM7479: lys3+:ptdh1*:NLS-linker-mTagBFP2:terminatortdh1:kanMX leu1-32:[pJK148-Pwee1-wee1-Twee1] h+ | This Study | N/A |
| S. pombe JM7558: lys3+:ptdh1*:NLS-linker-mTagBFP2:terminatortdh1:kanMX leu1-32:[pJK148-Pwee1-wee1-Twee1] rga4Δ::NAT | This Study | N/A |
| S. pombe JM7532: rga2Δ::hphR lys3+:ptdh1*:NLS-linker-mTagBFP2:terminatortdh1:kanMX leu1-32:[pJK148-Pwee1-wee1-Twee1] h+ | This Study | N/A |
| S. pombe JM7503: ppa2Δ::kanMX6 lys3+:ptdh1*:NLS-linker-mTagBFP2:terminatortdh1:kanMX h+ | This Study | N/A |
| S. pombe JM7512: rga4Δ::hphR ppa2Δ::kanMX6 lys3+:ptdh1*:NLS-linker-mTagBFP2:terminatortdh1:kanMX | This Study | N/A |
| S. pombe JM7533: rga2Δ::hphR ppa2Δ::kanMX6 lys3+:ptdh1*:NLS-linker-mTagBFP2:terminatortdh1:kanMX h+ | This Study | N/A |
| S. pombe JM7690: Diploid lys3+:ptdh1*:NLS-linker-mTagBFP2:terminatortdh1:kanMX / pil1-mCherry::natR | This Study | N/A |
| S. pombe JM7674: Diploid rga2Δ::NAT lys3+:ptdh1*:NLS-linker-mTagBFP2:terminatortdh1:kanMX / rga2Δ::hphR lys3+:ptdh1*:NLS-linker-mTagBFP2:terminatortdh1:kanMX | This Study | N/A |
| S. pombe JM7630: cdr2Δ::NAT zfs1Δ::kanMX6 ppa2Δ::kanMX6 lys3+:ptdh1*:NLS-linker-mTagBFP2:terminatortdh1:kanMX | This Study | N/A |
| S. pombe JM7645: cdr2Δ::NAT rga4Δ::hphR zfs1Δ::kanMX6 ppa2Δ::kanMX6 lys3+:ptdh1*:NLS-linker-mTagBFP2:terminatortdh1:kanMX | This Study | N/A |
| S. pombe JM7646: cdr2Δ::NAT rga2Δ::hphR zfs1Δ::kanMX6 ppa2Δ::kanMX6 lys3+:ptdh1*:NLS-linker-mTagBFP2:terminatortdh1:kanMX | This Study | N/A |
| S. pombe JM7627: ppa2Δ::kanMX6 zfs1Δ::kanMX6 | This Study | N/A |
| S. pombe JM7381: cdr2Δ::NAT lys3+:ptdh1*:NLS-linker-mTagBFP2:terminatortdh1:kanMX | Lab collection | Opalko et al.33 |
| S. pombe JM6434: lys3+:ptdh1*:NLS-linker-mTagBFP2:terminatortdh1:kanMX | Martin Lab AV1469 | Vještica et al.67 |
| S. pombe JM6963: cdr2Δ::NAT rga4Δ::kanMX6 lys3+:ptdh1*:NLS-linker-mTagBFP2:terminatortdh1:kanMX cdc25-yomNeonGreen::hphR leu1:[pJK148-Pact-yomRuby3-term] | This Study | N/A |
| S. pombe JM6831: rga2Δ::kanMX6 cdr2Δ::NAT lys3+:ptdh1*:NLS-linker-mTagBFP2:terminatortdh1:kanMX cdc25-yomNeonGreen::hphR leu1:[pJK148-Pact-yomRuby3-term] h- | This Study | N/A |
| S. pombe JM6614: cdc13-mCherry-kanMX | This Study | N/A |
| S. pombe JM7701: cdc13+-internal-sfGFPcp | Hauf lab ST947 | Kamenz et al.46 |
| S. pombe JM6713: cdc13-mNeonGreen-hphR h- | This Study | N/A |
| S. pombe JM5290: cdc25-yomNeonGreen::hphR h+ | This Study | N/A |
| S. pombe JM656: sec8-1 ura4-D18 leu1-32 h+ | Lab collection | N/A |
| S. pombe JM7586: fim1-mNG::hphR h- | This Study | N/A |
| S. pombe JM7588: arp2-mNG::mNG::hphR h- | This Study | N/A |
| S. pombe JM5198: spn1-mNG::hphR h+ | This Study | N/A |
| S. pombe JM5288: mid1-yomNeonGreen::hphR h+ | This Study | N/A |
| S. pombe JM7587: cdc12-mNG::mNG::hphR h- | This Study | N/A |
| S. pombe JM6907: cdc2-mNeonGreen-hphR lys3+:ptdh1*:NLS-linker-mTagBFP2:terminatortdh1:kanMX h- | This Study | N/A |
| S. pombe JM7860: cdc25-yomNeonGreen::hphR leu1-32:[pJK148-Pwee1-wee1-Twee1] lys3+:ptdh1*:NLS-linker-mTagBFP2:terminatortdh1:kanMX | This Study | N/A |
| S. pombe JM7881: cdc25-degron-DAmP::kanMX6 cdc13+-internal-sfGFPcp lys3+:ptdh1*:NLS-linker-mTagBFP2:terminatortdh1:natR | This Study | N/A |
| Software and algorithms | ||
| ImageJ 1.53k | NIH Image | https://imagej.nih.gov/ij/ |
| MATLAB | MathWorks | R2021a |
| RStudio | RStudio PBC | 1.4.1717 |
| Intensity_Size_pombe.m | This Study | https://github.com/millerk89/sizer-timer-pombe |
| cell_geometry_dividing_cells.m | This Study | https://github.com/millerk89/sizer-timer-pombe |
| Overlap_analysis_bivariate_data.nb | This Study | https://github.com/millerk89/sizer-timer-pombe |
| overlap_analysis_size.Rmd | This study | https://github.com/millerk89/sizer-timer-pombe |
| model.Rmd | This study | https://github.com/millerk89/sizer-timer-pombe |
| Other | ||
| Cell Asic ONIX, 3.5 – 5.5 μm Y04C-02 | EMD Millipore | N/A |
| Coverglass-bottom dish | MaTek | P35G-1.5-20C |
| Yokogawa CSU-WI spinning disk | Nikon Instruments | N/A |
| 60× 1.4-NA CFI60 Apochromat Lambda S objective lens | Nikon Instruments | N/A |
| 405-, 488-, and 561-nm laser lines | Nikon Instruments | N/A |
| photometrics Prime BSI camera | Nikon Instruments | N/A |
| Eclipse Ti2 | Nikon Instruments | N/A |
Any additional information required to reanalyze the data reported in this paper is available from the lead contact upon request.
EXPERIMENTAL MODEL AND SUBJECT DETAILS
Schizosaccharomyces pombe strains used in this study are listed in the key resources table. Standard methods were used to grow and culture Schizosaccharomyces pombe cells.68 All gene fusions were expressed from their endogenous promoters at the endogenous chromosomal loci. One-step PCR-based homologous recombination was used for C-terminal tagging or deletion of genes on the chromosome.69 Diploid cells were generated by crossing h− and h+ haploid cells. Diploid cells were confirmed by Phloxin B staining and by the presence of tetrads after isolating single diploid colonies and plating on a MEA4S plate. Diploid cells were imaged immediately after isolating without freezing.
METHODS DETAILS
Microscopy
Analysis of cell geometry and fluorescent protein intensity from static images
Fission yeast cells were grown at 25°C in YE4S medium to logarithmic phase for imaging as previously described.33 Cells were placed in a coverglass-bottom dish (P35G-1.5-20C; MatTek), and covered with a piece of YE4S agar prewarmed to 25°C. Imaging was performed using a spinning disk confocal microscope: Yokogawa CSU-WI (Nikon Software) equipped with a 60× 1.4-NA CFI60 Apochromat Lambda S objective lens (Nikon); 405-, 488-, and 561-nm laser lines; and a photometrics Prime BSI camera on an inverted microscope (Eclipse Ti2; Nikon). Multiple fields of view per cell type were imaged within 1 h at room temperature. Images were captured with 27 z-stacks and 0.2-μm step size.
Microscopy for cell geometry and intensity measurements over time
For imaging Cdc13 or Cdc25 accumulation over time, cells were mounted on a coverglass-bottom dish (P35G-1.5-20C; MatTek) and covered with a piece of YE4S agar prewarmed to 25°C. Images were acquired with 7 z-stacks and 0.5-μm steps every 8 minutes using a spinning disk confocal microscope (described above). For time-lapse imaging Latrunculin B treated cells, 100μM LatB was added to cells prior to their mounting on a coverglass-bottom dish. YE4S agar containing 100μM LatB was used to cover the cells.
For imaging Cdc13 accumulation over time in Figures S5C, S5D, S5E, and S5F, cells were imaged at room temperature in microfluidic flow chambers (Millipore, CellAsic ONIX, 3.5 – 5.5 μm Y04C-02). First, flow chambers were primed by flowing YE4S or EMM4S media for 7 min at 6 psi. Diluted cells were then loaded into chambers and media was flowed at 6 psi for the duration of the experiment. Cells were allowed to acclimate in the chambers for 1 hour prior to imaging. Images were acquired with 7 z-stacks and 0.5-μm steps every 8 minutes using a spinning disk confocal microscope (described above).
Microscopy for cell size homeostasis plots
Cells were imaged at room temperature in microfluidic flow chambers (Millipore, CellAsic ONIX, 3.5 – 5.5 μm Y04C-02) as described above. Brightfield images of cells were acquired with 3 z-stacks and 0.5-μm steps every 8 minutes using a spinning disk confocal microscope (described above). Cell size at birth/division and cell cycle time were analyzed for 2-3 generations of cells. Cell size at division and cell cycle time were consistent for the duration of this imaging period. Size homeostasis experiments were repeated two times for WT and cdr2Δ cells and three times for cdr2Δ zfs1Δ ppa2Δ and zfs1Δ ppa2Δ cells. Representative graphs are shown in Figures 6D, 6E, S7.
Cell and nuclei segmentation
Brightfield images were processed for cell segmentation and cell size analysis using a semi-automated pipeline. First using ImageJ, a smoothing filter and Gaussian blur was applied to each optical section of an image to reduce image noise. Next, global thresholding was performed by selecting a grey value maximum to produce a binary image for each z-section. For consistent segmentation, the same brightfield exposure setting and threshold value was used for all datasets. An optical section outside of the middle focal plane with intact boundary bands around cells was selected for further processing. This section was typically 1-2 μm from the middle focal plane and was chosen to ensure intact boundary bands for downstream processing. The flood fill tool was used (by hand) to generate a black background so that image pixel values in the background were set to 0 and cells in white were 1. Binary images were further processed by morphological erosion and subsequent dilation operators to remove regions between cell clumps for better single-cell segmentation. Images were also processed to remove cells along the edge of the image. The paintbrush tool was used to further separate clumped cells by hand, and the flood fill tool was used to remove any potential imaging artifacts, abnormal cells, or unresolved clumps of cells. The resulting binary image (“cell mask”) was compared with the original medial plane bright-field image and confirmed to be an accurate representation of cell size.20
BFP-NLS images were processed for nuclei segmentation and nuclei size analysis using a semi-automated pipeline. First using ImageJ, a sum projection was created from image z-sections. To reduce image noise, a smoothing filter and Gaussian blur was applied. Next, global thresholding was performed by selecting grey values for the BFP-NLS signal to produce a binary image of nuclei. Images were also processed to remove nuclei along the edge of the image. To correct for uneven BFP illumination across a imaging field, a particle size threshold was applied to nuclei masks to remove nuclei that were abnormally small or large. The resulting binary image (“nuclei mask”) was compared to the original BFP-NLS and Cdc25-mNG or Cdc13-mNG (or sfGFP) images and confirmed to be an accurate representation of nuclear size.
To obtain cell masks of dividing cells, morphological erosion of cell and nuclei masks was initially performed using ImageJ. This is done so that nuclei are not touching the cell border and to better separate clumped cells. To obtain a single image with nuclei overlaid on cells, eroded cell and nuclei masks are processed by a MATLAB code that sets image pixel values in the background and nuclei to 0 and cells in white to 1. Nuclei-overlaid cell images are further processed with a MATLAB code that removes interphase cells and creates a binary mask containing only dividing cells (cells with two nuclei, indicating active division). The paintbrush tool was used to edit clumped cells by hand and the flood fill tool was used to delete any abnormal cells or unresolved clumps of cells. Once binary masks were confirmed to contain only dividing cells, by comparison to original BFP-NLS and brightfield images, images were further processed to remove nuclei so the image pixel values for the whole cell is 1 and processed by morphological dilation to return cells to normal size. This resulting binary image is the mask of dividing cells.
For some time-lapse images (data shown in Figure 5E and F), individual cropped cells are processed like static images with some modifications. To generate cell masks from brightfield time-lapse images, a single z-section outside of the middle focal plane with intact boundary bands around cells was selected for each time-point for further processing. A smoothing filter and Gaussian blur were applied to each image time point to reduce image noise. A sharpening filter was applied to increase contrast of the boundary band around cells, followed by a Sobel edge detector to highlight the sharp change in intensity of the boundary band. Next, global thresholding was performed by selecting a grey value that includes the boundary around cells to produce a binary image for each time point. The flood fill tool was used (by hand) to generate a black background so that image pixel values in the background were set to 0 and cells in white were 1. The paintbrush tool was used to further separate clumped cells by hand or edit cell boundary. The resulting cell mask of each time point was compared with the original brightfield image and confirmed to be an accurate representation of cell size. To create nuclei masks from the BFP-NLS channel for each time point, the same semi-automated pipeline was used to generate nuclei masks (above). Each step in the pipeline was applied to all BFP-NLS image time points.
For time-lapse images in Figures 5I, S3I, S3J, S5, and S6, cell and nuclei segmentation at each time point was performed by hand from brightfield or BFP-NLS images using the polygon selection or oval selection tool in ImageJ.
Cell geometry measurements
The cell width for each strain was manually measured in every experiment from the cell mask in ImageJ using the straight-line tool. Abnormally skinny or wide regions of a cell were avoided when drawing the line by hand. Accuracy in measuring cell width is critical for measurements of cell surface area and volume calculations.70 We found this manual method to be more reproducible than automated approaches. The average cell width divided by 2 (cell radius) was determined for a population of cells (n > 100) (Table S1). We assumed that each cell in a given strain had the same cell radius (average of population) for calculation of cell surface area and volume (Table S2). In MATLAB, the cell length or cell symmetry axis of individual segmented cells (from cell masks) was identified by principal component analysis of the cloud points internal to the cell.20 Cell surface area or volume of individual cells was calculated in MATLAB using the equation for surface area and volume of a cylinder with hemispherical ends, because of the rodlike shape of fission yeast cells (Table S2).
To test the validity of our size measurements and confirm the robustness of our results we also calculated the surface area and volume of cells by rotation of the R(x) function of each single cell around the symmetry axis, which avoids assuming a cylindrical cell shape (as done in Reference 20) (Table S2). We compared cell size results obtained from the rotation method and mean radius of cell population method for all datasets. In all cases, both methods supported the same conclusion. For comparison in Figure S1, we show graphs using both the mean radius method and the rotation method to measure the surface area and volume of wild type and cdr2Δ cells. For simplicity, we show graphs using the mean radius method in all other figures, although the conclusions were also confirmed using the rotation method.
To evaluate the reproducibility of our size measurements we compared the size of WT and cdr2Δ cells obtained from two independent data sets. The mean values for cell surface area and volume were not significantly different from one another and the coefficient of variation values were similar. Cell volume and surface area values from our experiments were also consistent with previously published work.20
For measuring the geometry of cells from time-lapse imaging, the width of each cell was measured from the brightfield image at four time points to obtain an average width per cell. The length of each cell was measured at each timepoint using the straight-line tool or by MATLAB. Cell surface area and volume of individual cells over time was calculated using the equation for surface area and volume of a cylinder with hemispherical ends.
For cell size homeostasis studies, brightfield images were analyzed by hand. In ImageJ, the straight-line tool was used to measure the length and width of each cell at birth and division (determined by the presence of a septa). The cell cycle time from birth to division for each cell was denoted. Cell surface area of individual cells was calculated using the equation for a cylinder with hemispherical ends.
Key experiments were repeated in triplicate and representative graphs from one experiment are shown (Figure 2, 3, 4A, 6E, and S7B). In some cases, such as timelapse imaging of Cdc13 accumulation, we chose to repeat the experiment under different conditions including rich media (Figures 5F-G), minimal media (Figure S5E-F), and a different genetic background (Figures S5C-D). We obtained the same result while varying experimental conditions.
Nuclear size measurements
In MATLAB, the major and minor axis of nuclei (from nuclei mask) was obtained using the regionprops function to return the length (in pixels). To get the actual length, we multiplied the number of pixels by the length in microns represented by one pixel. Volume of nuclei was calculated using the equation for an ellipsoid, assuming two of the three semi-axes are equal in length, similar to previous studies (Table S3).42,43 In our data sets we found that nuclear size scales with cell size as expected. We also obtained nuclear to cytoplasmic volume ratios for WT, rga2Δ, and rga4Δ cells consistent with previous reports (Table S4).42,43
Measurement of fluorescent intensity
Summed intensity projections of z-sections were used for analysis of fluorescent intensity. MATLAB codes were used to measure mean intensity or sum intensity of fluorescent proteins in the cytoplasm, nucleus, or whole cell (as defined by cell and nuclei masks). In supplemental graphs (Figure S3B-C; Figure S4D-E), Cdc25-mNG or Cdc13-mNG values are the sum intensity in the nucleus divided by the nuclear volume for single cells.
For analysis of Cdc13-mNG, Cdc13-sfGFPint, and Cdc25-mNG intensity after treatment with LatB (Figure 5H-I; Figure S3H-J; Figure S5G-H), the lowest intensity value was normalized to 1 and plotted on graphs. Only small daughter cells in interphase prior to mitotic entry were examined in both experimental and control samples.
Calculation of protein concentration (μM) from fluorescent intensities
Molecule counting was performed as described in Wu and Pollard (2005). A standard curve relating fluorescent intensity to concentration (μM) was created by imaging mNG-tagged Fim1, Arp2, Spn1, Mid1, and Cdc12, which have known concentrations. We imaged Cdc13-mNG and Cdc25-mNG in the same genetic background using the same imaging conditions. Cells were grown at 25°C in YE4S medium to logarithmic phase for imaging. Cells were placed on a coverglass-bottom dish and covered with a piece of YE4S agar prewarmed to 25°C. Imaging was performed using a spinning disk confocal microscope (described above). For each strain, images were captured with 27 z-stacks and 0.2-μm steps. Sum projections of all 27 z-stacks were used for analysis. To make the standard curve, mean fluorescent intensity values of mNG-tagged proteins was measured in the whole cell (and nucleus for Cdc13-mG and Cdc25-mNG). Fission yeast cells that do not contain any mNG tagged proteins were also measured and the average intensity value from 100 cells was used for background subtraction. Mean fluorescence values for Fim1, Arp2, Spn1, Mid1, and Cdc12 were then plotted against their known whole cell concentrations (μM) to generate the standard curve. Mean fluorescent intensity of Cdc25-mNG or Cdc13-mNG were plotted against the best-fit line of the standard curve to interpolate the nuclear or whole cell concentration (μM).
Immunoblotting
Cells expressing Cdc13-mNG, Cdc13-mCherry, Cdc13-sfGFPint, or untagged Cdc13 protein were grown in YE4S medium at 25°C or 36.5°C for 5 hours before harvesting. Immunoblot of cell extracts was performed and the presence of Cdc13 was detected using an anti-Cdc13 antibody (Novus Biologicals).
Mathematical Model
In this section, we describe a simple one-dimensional model with the intent of explaining how adder-based cell size control arises in the cdr2Δ genotype. We assume that Cdc13 is expressed proportional to cell size with no active degradation during the cell cycle starting from a zero initial condition. In the context of Cdc13 concentration, this corresponds to a constant synthesis rate and dilution occurring due to an exponential increase in cell size over time. Assuming that activation and deactivation cycles of Cdc13 occur at a much faster time scale than the build of its levels, one can determine the concentration of active Cdc13 from its total intracellular concentration. While there is evidence of Cdc13 itself regulating the deactivation/activation rates forming feedback loops, for simplicity we ignore these feedbacks in this model and consider either constant or size-dependent rates. As the intracellular levels of both total and activated Cdc13 increase during the cell cycle, mitotic entry is assumed to occur based on the active Cdc13 concentration crossing a critical threshold level. Cdc25 and Wee1 are not included as explicit components of the model, but their activities are modeled as activation and deactivation of Cdc13, respectively. We next describe the mathematical model and its analysis.
Let the total intracellular concentration of Cdc13 increase within a cell cycle as per the differential equation
with synthesis rate and dilution rate . As per this model, the Cdc13 level at a given time within the cell cycle is given by the timer-based equation
For an exponential increase in cell size
where is the newborn cell size, the total Cdc13 levels can be rewritten as
In the cdr2Δ background, we assume Cdc13 activation occurs with a rate proportional to size (due to Cdc25 concentration increasing linearly with size), and deactivation occurs at a constant but large rate . These activation and deactivation steps phenomenologically model size-dependent activation by Cdc25 and loss of size-dependent deactivation by Wee1. Assuming fast cycles of activation/deactivation relative to the time scale of cell growth yields the following concentration of activated Cdc13
If mitotic entry is driven by [] reaching a critical threshold , then it is easy to see from the above equation that it will follow an adder-based size control mechanism
where the size added from cell birth to division becomes invariant of .
In Fig. 6, the volume added is plotted as a function of newborn size as it is varied between 0.7 and 1.3, where here 1 unit corresponds to the average newborn size. Given , the cell division size is obtained by solving
which can be rewritten as
assuming and . Note with these parameters when then .
To realize a sizer-based cell size control, we consider a size-dependent deactivation rate that monotonically decreases with increasing . To realize a perfect sizer-based mitotic entry we consider a threshold function that switches from a high to low value when the cell reaches the critical size. More specifically, in Fig. 6 we plot the solution to
considering , when and when .
Model code available at https://github.com/millerk89/sizer-timer-pombe
Quantification and Statistical analysis
For Figure 1G, 4C, 4F, 5E, S3G, S3I, and S3J. Data analysis was performed using Prism 8 (GraphPad Software). A two-tailed Student’s t test was performed to determine statistical differences between two sets of data. An ANOVA was performed to determine statistical differences between sets of data.
Overlap analysis calculations
We adapted the overlap index from previous work.71 We used the overlapping index to compute similarity between cell surface area or volume at division of two yeast strains (data sets). The overlapping index is defined as per
where and are probability densities of the data sets A and B, respectively. Since and are univariate probability densities, the integral is computed over the real domain . This index is computed using the R library overlapping, available at https://cran.r-project.org/package=overlapping. This library estimates the continuous probability densities and via Kernel density estimators and then numerically solves the integral above. The index was bootstrapped 1000 times to compute confidence intervals. We extended the overlapping index to compute similarity between three strains as per
where represents the estimated density of surface area/volume for the strain C dataset. This modification is included in our codes as an explicit R function definition that includes the modification of the code available in https://cran.r-project.org/package=overlapping. We performed comparisons between overlapping index of strains for both surface area and volume probability densities, checking surface area or volume overlapping index by bootstrapping, and counting the number of resampling surface area or volume overlapping index is greater. The p values for all overlap index comparisons of surface area and volume were less than 0.001, indicating a significant difference. An exception is Figure 1H where cells are treated with 0.02μM 1-NM-PP1.
For overlap analysis of bivariate data (Figure 4B and 5B), we first identified a size range that was approximately in common between WT, rga2Δ, and rga4Δ cells, excluding mitotic cells. We calculated the bivariate probability densities for pairs of nuclear Cdc25 concentrations and cell volumes in WT, rga2Δ, and rga4Δ cells. Afterwards, we used these distributions to determine the extended overlapping index.
where represents the pair of nuclear Cdc25 concentration and cell volume values for a given cell. A high value of the overlapping index suggests strong overlap of Cdc25 concentration in all three strains when plotting by volume. We calculated similar bivariate overlapping indexes to evaluate the overlap of Cdc25 nuclear intensities by cell surface area. We performed similar analysis for Cdc13 nuclear accumulation.
Binning analysis
In Figures 4C, 4F, 5E, and S3G we binned the cells by their cell surface area or volume with the same number of cells in each bin using the quantile function included in R.
Supplementary Material
HIGHLIGHTS.
The size and ploidy of fission yeast cells determines their size control strategy.
Mitotic activator Cdc25 exhibits properties of a volume-based sizer molecule.
Mitotic cyclin Cdc13 accumulates in the nucleus dependent on time, not size.
Combined modeling and experiments show conditions for sizer versus adder behavior.
ACKNOWLEDGEMENTS
We thank members of the Moseley laboratory for helpful discussions and comments on the manuscript; as well as the Biomolecular Targeting Core (BioMT) (P20-GM113132) for use of equipment; and Damien Coudreuse, Silke Hauf, and Sophie Martin for sharing yeast strains. This work was funded by grants from the National Institutes of General Medical Sciences (NIGMS) (R01GM099774 and R01GM133856) to J.B.M.
INCLUSION AND DIVERSITY
We support inclusive, diverse, and equitable conduct of research.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
DECLARATION OF INTERESTS
The authors declare no competing interests.
REFERENCES
- 1.Amodeo AA and Skotheim JM (2016). Cell-Size Control. Cold Spring Flarb. Perspect. Biol 8, a019083. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Ginzberg MB, Kafri R and Kirschner M (2015). On being the right (cell) size. Science 348, 1245075. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Dolznig FI, Grebien F, Sauer T, Beug H and Müllner EW (2004). Evidence for a size-sensing mechanism in animal cells. Nat. Cell Biol 6, 899–905. [DOI] [PubMed] [Google Scholar]
- 4.Jun S and Taheri-Araghi S (2015). Cell-size maintenance: universal strategy revealed. Trends Microbiol. 23, 4–6. [DOI] [PubMed] [Google Scholar]
- 5.Facchetti G, Chang F and Floward M (2017). Controlling cell size through sizer mechanisms. Curr. Opin. Syst. Biol 5, 86–92. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Wang P, Flayden S and Masui Y (2000). Transition of the Blastomere Cell Cycle From Cell Size-Independent to Size-Dependent Control at the Midblastula Stage in Xenopus laevis. J. Exp. Zool 287, 128–144. [DOI] [PubMed] [Google Scholar]
- 7.Donnan L and John PC (1983). Cell cycle control by timer and sizer in Chlamydomonas. Nature 304, 630–633. [DOI] [PubMed] [Google Scholar]
- 8.Campos M, Surovtsev IV, Kato S, Paintdakhi A, Beltran B, Ebmeier SE, and Jacobs-Wagner C (2014). A constant size extension drives bacterial cell size homeostasis. Cell 159, 1433–1446. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Taheri-Araghi S, Bradde S, Sauls JT, Hill NS, Levin PA, Paulsson J, Vergassola M, and Jun S (2015). Cell-size control and homeostasis in bacteria. Curr. Biol 25, 385–391. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Varsano G, Wang Y and Wu M (2017). Probing Mammalian Cell Size Homeostasis by Channel-Assisted Cell Reshaping. Cell Rep. 20, 397–410. [DOI] [PubMed] [Google Scholar]
- 11.Fantes PA (1977). Control of cell size and cycle time in Schizosaccharomyces pombe. J. Cell Sci 24, 51–67. [DOI] [PubMed] [Google Scholar]
- 12.Sveiczer A, Novak B and Mitchison JM (1996). The size control of fission yeast revisited. J. Cell Sci 109, 2947–2957. [DOI] [PubMed] [Google Scholar]
- 13.Xie S and Skotheim JM (2020). A G1 Sizer Coordinates Growth and Division in the Mouse Epidermis. Curr. Biol 30, 916–924. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Di Talia S, Skotheim JM, Bean JM, Siggia ED and Cross FR (2007). The effects of molecular noise and size control on variability in the budding yeast cell cycle. Nature 448, 947–951. [DOI] [PubMed] [Google Scholar]
- 15.Turner JJ, Ewald JC and Skotheim JM (2012). Cell size control in yeast. Curr. Biol 22, R350–9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Wallden M, Fange D, Lundius EG, Baltekin Ö and Elf J (2016). The Synchronization of Replication and Division Cycles in Individual E. coli Cells. Cell 166, 729–739. [DOI] [PubMed] [Google Scholar]
- 17.Schmoller KM, Turner JJ, Kõivomägi M and Skotheim JM (2015). Dilution of the cell cycle inhibitor Whi5 controls budding yeast cell size. Nature 526, 268–272. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Mitchison JM and Nurse P (1985). Growth in cell length in the fission yeast Schizosaccharomyces pombe. J. Cell Sci 75, 357–376. [DOI] [PubMed] [Google Scholar]
- 19.Pan KZ, Saunders TE, Flor-Parra I, Howard M and Chang F (2014). Cortical regulation of cell size by a sizer cdr2p. Elife 18, e02040. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Facchetti G, Knapp B, Flor-Parra I, Chang F and Howard M (2019). Reprogramming Cdr2-Dependent Geometry-Based Cell Size Control in Fission Yeast. Curr. Biol 29, 350–358. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Harashima H, Dissmeyer N and Schnittger A (2013). Cell cycle control across the eukaryotic kingdom. Trends Cell Biol. 23, 345–356. [DOI] [PubMed] [Google Scholar]
- 22.Russell P and Nurse P (1987). Negative regulation of mitosis by wee1+, a gene encoding a protein kinase homolog. Cell 49, 559–567. [DOI] [PubMed] [Google Scholar]
- 23.Gould KL and Nurse P (1989). Tyrosine phosphorylation of the fission yeast cdc2+ protein kinase regulates entry into mitosis. Nature 342, 39–45. [DOI] [PubMed] [Google Scholar]
- 24.Russell P and Nurse P (1986). cdc25+ functions as an inducer in the mitotic control of fission yeast. Cell 45, 145–153. [DOI] [PubMed] [Google Scholar]
- 25.Moreno S, Nurse P and Russell P (1990). Regulation of mitosis by cyclic accumulation of p80cdc25 mitotic inducer in fission yeast. Nature 344, 549–552. [DOI] [PubMed] [Google Scholar]
- 26.Gautier J, Solomon MJ, Booher RN, Bazan J, and Kirschner MW (1991). cdc25 is a specific tyrosine phosphatase that directly activates p34cdc2. Cell 67, 197–211. [DOI] [PubMed] [Google Scholar]
- 27.Kumagai A and Dunphy WG (1991). The cdc25 protein controls tyrosine dephosphorylation of the cdc2 protein in a cell-free system. Cell 64, 903–914. [DOI] [PubMed] [Google Scholar]
- 28.Strausfeld U, Labbé JC, Fesquet D, Cavadore JC, Picard A, Sadhu K, Russell P, Dorée M (1991). Dephosphorylation and activation of a p34cdc2/cyclin B complex in vitro by human CDC25 protein. Nature 351, 242–245. [DOI] [PubMed] [Google Scholar]
- 29.Young PG and Fantes PA (1987). Schizosaccharomyces pombe mutants affected in their division response to starvation. J. Cell Sci 88, 295–304. [DOI] [PubMed] [Google Scholar]
- 30.Breeding CS, Fludson J, Balasubramanian MK, Hemmingsen SM, Young PG, and Gould KL (1998). The cdr2(+) gene encodes a regulator of G2/M progression and cytokinesis in Schizosaccharomyces pombe. Mol. Biol. Cell 9, 3399–3415. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Kanoh J and Russell P (1998). The protein kinase Cdr2, related to Nim1/Cdr1 mitotic inducer, regulates the onset of mitosis in fission yeast. Mol. Biol. Cell 9, 3321–3334. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Allard CAH, Opalko HE, Liu KW, Medoh U and Moseley JB (2018). Cell size-dependent regulation of Wee1 localization by Cdr2 cortical nodes. J. Cell Biol 217, 1589–1599. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Opalko HE, Miller KE, Kim HS, Vargas-Garcia CA, Singh A, Keogh MC, and Moseley JB (2022). Arf6 anchors Cdr2 nodes at the cell cortex to control cell size at division. J. Cell Biol 221, e202109152. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Patterson JO, Rees P and Nurse P (2019). Noisy Cell-Size-Correlated Expression of Cyclin B Drives Probabilistic Cell-Size Homeostasis in Fission Yeast. Curr. Biol 29, 1379–1386. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Keifenheim D, Sun XM, D'Souza E, Ohira MJ, Magner M, Mayhew MB, Marguerat S, and Rhind N (2017). Size-Dependent Expression of the Mitotic Activator Cdc25 Suggests a Mechanism of Size Control in Fission Yeast. Curr. Biol 27, 1491–1497. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Curran S, Dey G, Rees P and Nurse P (2022). A quantitative and spatial analysis of cell cycle regulators during the fission yeast cycle. Proc. Natl. Acad. Sci 119, e2206172119. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Coudreuse D and Nurse P (2010). Driving the cell cycle with a minimal CDK control network. Nature 468, 1074–1080. [DOI] [PubMed] [Google Scholar]
- 38.Navarro FJ and Nurse P (2012). A systematic screen reveals new elements acting at the G2/M cell cycle control. Genome Biol. 13, 1–10. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Kinoshita N, Yamano H, Niwa H, Yoshida T and Yanagida M (1993). Negative regulation of mitosis by the fission yeast protein phosphatase ppa2. Genes Dev. 7, 1059–1071. [DOI] [PubMed] [Google Scholar]
- 40.Zhurinsky J, Leonhard K, Watt S, Marguerat S, Bähler J, and Nurse P (2010). A Coordinated Global Control over Cellular Transcription. Curr. Biol 20, 2010–2015. [DOI] [PubMed] [Google Scholar]
- 41.Neurohr GE, Terry RL, Lengefeld J, Bonney M, Brittingham GP, Moretto F, Miettinen TP, Vaites LP, Soares LM, Paulo JA, et al. (2019). Excessive Cell Growth Causes Cytoplasm Dilution And Contributes to Senescence. Cell 176, 1083–1097. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Cantwell H and Nurse P (2019). A homeostatic mechanism rapidly corrects aberrant nucleocytoplasmic ratios maintaining nuclear size in fission yeast. J. Cell Sci 132, jcs235911. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Neumann FR and Nurse P (2007). Nuclear size control in fission yeast. J. Cell Biol 179, 593–600. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Wu JQ and Pollard TD (2005). Counting cytokinesis proteins globally and locally in fission yeast. Science 310, 310–314. [DOI] [PubMed] [Google Scholar]
- 45.Spector I, Shochet NR, Kashman Y and Groweiss A (1983). Latrunculins: Novel Marine Toxins That Disrupt Microfilament Organization in Cultured Cells. Science 219, 493–495. [DOI] [PubMed] [Google Scholar]
- 46.Kamenz J, Mihaljev T, Kubis A, Legewie S and Hauf S (2015). Robust Ordering of Anaphase Events by Adaptive Thresholds and Competing Degradation Pathways. Mol. Cell 60, 446–459. [DOI] [PubMed] [Google Scholar]
- 47.Scotchman E, Kume K, Navarro FJ and Nurse P (2021). Identification of mutants with increased variation in cell size at onset of mitosis in fission yeast. J. Cell Sci 134, jcs251769. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Wood E and Nurse P (2013). Cell Cycle Pom1 and cell size homeostasis in fission yeast. Cell Cycle 12, 3228–3236. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Chica N, Rozalen AE, Perez-Hidalgo L, Rubio A, Novak B, Moreno S (2016). Nutritional Control of Cell Size by the Greatwall-Endosulfine-PP2AB55 Pathway. Curr. Biol 26, 319–330. [DOI] [PubMed] [Google Scholar]
- 50.Martín R, Portantier M, Chica N, Nyquist-Andersen M, Mata J, and Lopez-Aviles S (2017). A PP2A-B55-Mediated Crosstalk between TORC1 and TORC2 Regulates the Differentiation Response in Fission Yeast. Curr. Biol 27, 175–188. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Sayyad WA and Pollard TD (2022). The number of cytokinesis nodes in mitotic fission yeast scales with cell size. Elife 11, e76249. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Lanz MC, Zatulovskiy E, Swaffer MP, Zhang L, Merten I, Zhang S, You DS, Marinov G, McAlpine P, Elias JE, Skotheim JM (2022). Increasing cell size remodels the proteome and promotes senescence. Mol. Cell 82, 3255–3269. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Chandler-Brown D, Schmoller KM, Winetraub Y and Skotheim JM (2017). The Adder Phenomenon Emerges from Independent Control of Pre- and Post-Start Phases of the Budding Yeast Cell Cycle. Curr. Biol 27, 2774–2783. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Sugiyama H, Goto Y, Kondo Y, Coudreuse D and Aoki K (2023). Live-cell imaging provides direct evidence for a threshold in CDK activity at the G2/M transition. bioRxiv 10.1101/2023.03.26.534249. [DOI] [PubMed] [Google Scholar]
- 55.Bashir S, Sun XM, Zhao Y, Martinez-lllescas NG, Gallego-López I, Negron LG, Keifenheim D, Karadimitriou T, Tran T, Pickering M, et al. (2023). Size-Dependent Expression of the Fission Yeast Cdc13 Cyclin is Conferred by Translational Regulation. 10.1101/2023.01.16.524304 [DOI] [Google Scholar]
- 56.Moris N, Shrivastava J, Jeffery L, Li JJ, Hayles J, and Nurse P (2016). A genome-wide screen to identify genes controlling the rate of entry into mitosis in fission yeast. Cell Cycle 15, 3121–3130. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Chua G, Lingner C, Frazer C and Young PG (2002). The sal3(+) gene encodes an importin-beta implicated in the nuclear import of Cdc25 in Schizosaccharomyces pombe. Genetics 162, 689–703. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Lopez-Girona A, Furnari B, Mondesert O and Russell P (1999). Nuclear localization of Cdc25 is regulated by DNA damage and a 14–3-3 protein. Nature 397, 172–175. [DOI] [PubMed] [Google Scholar]
- 59.Lopez-Girona A, Kanoh J and Russell P (2001). Nuclear exclusion of Cdc25 is not required for the DNA damage checkpoint in fission yeast. Curr. Biol 11, 50–54. [DOI] [PubMed] [Google Scholar]
- 60.Kelkar M and Martin SG (2015). PKA antagonizes CLASP-dependent microtubule stabilization to re-localize Pom1 and buffer cell size upon glucose limitation. Nat. Comm 6, 1–13. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Lucena R, Alcaide-Gavilán M, Anastasia SD and Kellogg DR (2017). Wee1 and Cdc25 are controlled by conserved PP2A-dependent mechanisms in fission yeast. Cell Cycle 16, 428–435. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Allard CAH, Opalko HE and Moseley JB (2019). Stable Pom1 clusters form a glucose-modulated concentration gradient that regulates mitotic entry. Elife 8, e46003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Gallardo P, Real-Calderon P, Flor-Parra I, Salas-Pino S and Daga RR (2020). Acute Heat Stress Leads to Reversible Aggregation of Nuclear Proteins into Nucleolar Rings in Fission Yeast. Cell Rep. 33, 108377. [DOI] [PubMed] [Google Scholar]
- 64.Harris LK and Theriot JA (2016). Relative Rates of Surface and Volume Synthesis Set Bacterial Cell Size. Cell 165, 1479–1492. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 65.Harris LK and Theriot JA (2018). Surface Area to Volume Ratio: A Natural Variable for Bacterial Morphogenesis. Trends Microbiol. 26, 815–832. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 66.Ojkic N, Serbanescu D and Banerjee S (2019). Surface-to-volume scaling and aspect ratio preservation in rod-shaped bacteria. Elife 8, e47033. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 67.Vještica A, Marek M, Nkosi PJ, Merlini L, Liu G, Bérard M, Billault-Chaumartin I, and Martin SG (2020). A toolbox of stable integration vectors in the fission yeast Schizosaccharomyces pombe. J. Cell Sci 133, jcs240754. [DOI] [PubMed] [Google Scholar]
- 68.Moreno S, Klar A and Nurse P (1991). Molecular genetic analysis of fission yeast Schizosaccharomyces pombe. Methods Enzymol. 194, 795–823. [DOI] [PubMed] [Google Scholar]
- 69.Bahler J, Wu JQ, Longtine MS, Shah NG, McKenzie A, Steever AB, Wach A, Philippsen P, and Pringle JR (1998). Heterologous modules for efficient and versatile PCR-based gene targeting in Schizosaccharomyces pombe. Yeast 14, 943–951. [DOI] [PubMed] [Google Scholar]
- 70.Facchetti G, Knapp B, Chang F and Howard M (2019). Reassessment of the Basis of Cell Size Control Based on Analysis of Cell-to-Cell Variability. Biophys. J 117, 1728–1738. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 71.Pastore M and Calcagni A (2019). Measuring distribution similarities between samples: A distribution-free overlapping index. Front Psychol. 10, 1089. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
All data reported in this paper will be shared by the lead contact upon request.
All original code has been deposited at GitHub and is publicly available as of the date of publication. DOIs are listed in the key resources table.
Key Resources Table
| REAGENT or RESOURCE | SOURCE | IDENTIFIER |
|---|---|---|
| Antibodies | ||
| anti-Cdc13 antibody | Novus Biologicals | NB200-576 |
| Chemicals, peptides, and recombinant proteins | ||
| 1-NM-PP1 (4-Amino-1-tert-butyl-3-(1’-naphthylmethyl)pyrazolo[3,4-d]pyrimidine) | Toronto Research Chemicals | A603003 |
| Latrunculin B | Abcam | ab144291 |
| Experimental models: Organisms/strains | ||
| S. pombe JM366: WT 972 h- (Alternate name: PN1) | Lab collection | N/A |
| S. pombe JM6972: cdc13-yomNeonGreen::hphR lys3+:ptdh1*:NLS-linker-mTagBFP2:terminatortdh1:kanMX leu1:[pJK148-Pact-yomRuby3-term] h+ | This Study | N/A |
| S. pombe JM7003: rga2Δ::kanMX6 lys3+:ptdh1*:NLS-linker-mTagBFP2:terminatortdh1:kanMX cdc13-yomNeonGreen::hphR leu1:[pJK148-Pact-yomRuby3-term] h- | This Study | N/A |
| S. pombe JM7008: rga4Δ::kanMX6 lys3+:ptdh1*:NLS-linker-mTagBFP2:terminatortdh1:kanMX cdc13-yomNeonGreen::hphR leu1:[pJK148-Pact-yomRuby3-term] | This Study | N/A |
| S. pombe JM7088: cdr2Δ::NAT lys3+:ptdh1*:NLS-linker-mTagBFP2:terminatortdh1:kanMX cdc13-yomNeonGreen::hphR leu1:[pJK148-Pact-yomRuby3-term] h+ | This Study | N/A |
| S. pombe JM7171: lys3+:ptdh1*:NLS-linker-mTagBFP2:terminatortdh1:kanMX cdc25-yomNeonGreen::hphR leu1:[pJK148-Pact-yomRuby3-term] h- | This Study | N/A |
| S. pombe JM7172: rga4Δ::kanMX6 lys3+:ptdh1*:NLS-linker-mTagBFP2:terminatortdh1:kanMX cdc25-yomNeonGreen::hphR leu1:[pJK148-Pact-yomRuby3-term] h- | This Study | N/A |
| S. pombe JM6752: rga2Δ::kanMX6 lys3+:ptdh1*:NLS-linker-mTagBFP2:terminatortdh1:kanMX cdc25-yomNeonGreen::hphR leu1:[pJK148-Pact-yomRuby3-term] h- | This Study | N/A |
| S. pombe JM6753: cdr2Δ::NAT lys3+:ptdh1*:NLS-linker-mTagBFP2:terminatortdh1:kanMX cdc25-yomNeonGreen::hphR leu1:[pJK148-Pact-yomRuby3-term] h- | This Study | N/A |
| S. pombe JM7492: lys3+:ptdh1*:NLS-linker-mTagBFP2:terminatortdh1:kanMX leu1Δ::Pcdc13::cdc13-L-cdc2as::cdc13 3'UTR::ura4+ cdc2Δ::kanMX6 cdc13Δ::natMX6 h+ | This Study | N/A |
| S. pombe JM7490: rga2Δ::kanMX6 lys3+:ptdh1*:NLS-linker-mTagBFP2:terminatortdh1:kanMX leu1Δ::Pcdc13::cdc13-L-cdc2as::cdc13 3'UTR::ura4+ cdc2Δ::kanMX6 cdc13Δ::natMX6 | This Study | N/A |
| S. pombe JM7502: rga4Δ::hphR lys3+:ptdh1*:NLS-linker-mTagBFP2:terminatortdh1:kanMX leu1Δ::Pcdc13::cdc13-L-cdc2as::cdc13 3'UTR::ura4+ cdc2Δ::kanMX6 cdc13Δ::natMX6 | This Study | N/A |
| S. pombe JM7479: lys3+:ptdh1*:NLS-linker-mTagBFP2:terminatortdh1:kanMX leu1-32:[pJK148-Pwee1-wee1-Twee1] h+ | This Study | N/A |
| S. pombe JM7558: lys3+:ptdh1*:NLS-linker-mTagBFP2:terminatortdh1:kanMX leu1-32:[pJK148-Pwee1-wee1-Twee1] rga4Δ::NAT | This Study | N/A |
| S. pombe JM7532: rga2Δ::hphR lys3+:ptdh1*:NLS-linker-mTagBFP2:terminatortdh1:kanMX leu1-32:[pJK148-Pwee1-wee1-Twee1] h+ | This Study | N/A |
| S. pombe JM7503: ppa2Δ::kanMX6 lys3+:ptdh1*:NLS-linker-mTagBFP2:terminatortdh1:kanMX h+ | This Study | N/A |
| S. pombe JM7512: rga4Δ::hphR ppa2Δ::kanMX6 lys3+:ptdh1*:NLS-linker-mTagBFP2:terminatortdh1:kanMX | This Study | N/A |
| S. pombe JM7533: rga2Δ::hphR ppa2Δ::kanMX6 lys3+:ptdh1*:NLS-linker-mTagBFP2:terminatortdh1:kanMX h+ | This Study | N/A |
| S. pombe JM7690: Diploid lys3+:ptdh1*:NLS-linker-mTagBFP2:terminatortdh1:kanMX / pil1-mCherry::natR | This Study | N/A |
| S. pombe JM7674: Diploid rga2Δ::NAT lys3+:ptdh1*:NLS-linker-mTagBFP2:terminatortdh1:kanMX / rga2Δ::hphR lys3+:ptdh1*:NLS-linker-mTagBFP2:terminatortdh1:kanMX | This Study | N/A |
| S. pombe JM7630: cdr2Δ::NAT zfs1Δ::kanMX6 ppa2Δ::kanMX6 lys3+:ptdh1*:NLS-linker-mTagBFP2:terminatortdh1:kanMX | This Study | N/A |
| S. pombe JM7645: cdr2Δ::NAT rga4Δ::hphR zfs1Δ::kanMX6 ppa2Δ::kanMX6 lys3+:ptdh1*:NLS-linker-mTagBFP2:terminatortdh1:kanMX | This Study | N/A |
| S. pombe JM7646: cdr2Δ::NAT rga2Δ::hphR zfs1Δ::kanMX6 ppa2Δ::kanMX6 lys3+:ptdh1*:NLS-linker-mTagBFP2:terminatortdh1:kanMX | This Study | N/A |
| S. pombe JM7627: ppa2Δ::kanMX6 zfs1Δ::kanMX6 | This Study | N/A |
| S. pombe JM7381: cdr2Δ::NAT lys3+:ptdh1*:NLS-linker-mTagBFP2:terminatortdh1:kanMX | Lab collection | Opalko et al.33 |
| S. pombe JM6434: lys3+:ptdh1*:NLS-linker-mTagBFP2:terminatortdh1:kanMX | Martin Lab AV1469 | Vještica et al.67 |
| S. pombe JM6963: cdr2Δ::NAT rga4Δ::kanMX6 lys3+:ptdh1*:NLS-linker-mTagBFP2:terminatortdh1:kanMX cdc25-yomNeonGreen::hphR leu1:[pJK148-Pact-yomRuby3-term] | This Study | N/A |
| S. pombe JM6831: rga2Δ::kanMX6 cdr2Δ::NAT lys3+:ptdh1*:NLS-linker-mTagBFP2:terminatortdh1:kanMX cdc25-yomNeonGreen::hphR leu1:[pJK148-Pact-yomRuby3-term] h- | This Study | N/A |
| S. pombe JM6614: cdc13-mCherry-kanMX | This Study | N/A |
| S. pombe JM7701: cdc13+-internal-sfGFPcp | Hauf lab ST947 | Kamenz et al.46 |
| S. pombe JM6713: cdc13-mNeonGreen-hphR h- | This Study | N/A |
| S. pombe JM5290: cdc25-yomNeonGreen::hphR h+ | This Study | N/A |
| S. pombe JM656: sec8-1 ura4-D18 leu1-32 h+ | Lab collection | N/A |
| S. pombe JM7586: fim1-mNG::hphR h- | This Study | N/A |
| S. pombe JM7588: arp2-mNG::mNG::hphR h- | This Study | N/A |
| S. pombe JM5198: spn1-mNG::hphR h+ | This Study | N/A |
| S. pombe JM5288: mid1-yomNeonGreen::hphR h+ | This Study | N/A |
| S. pombe JM7587: cdc12-mNG::mNG::hphR h- | This Study | N/A |
| S. pombe JM6907: cdc2-mNeonGreen-hphR lys3+:ptdh1*:NLS-linker-mTagBFP2:terminatortdh1:kanMX h- | This Study | N/A |
| S. pombe JM7860: cdc25-yomNeonGreen::hphR leu1-32:[pJK148-Pwee1-wee1-Twee1] lys3+:ptdh1*:NLS-linker-mTagBFP2:terminatortdh1:kanMX | This Study | N/A |
| S. pombe JM7881: cdc25-degron-DAmP::kanMX6 cdc13+-internal-sfGFPcp lys3+:ptdh1*:NLS-linker-mTagBFP2:terminatortdh1:natR | This Study | N/A |
| Software and algorithms | ||
| ImageJ 1.53k | NIH Image | https://imagej.nih.gov/ij/ |
| MATLAB | MathWorks | R2021a |
| RStudio | RStudio PBC | 1.4.1717 |
| Intensity_Size_pombe.m | This Study | https://github.com/millerk89/sizer-timer-pombe |
| cell_geometry_dividing_cells.m | This Study | https://github.com/millerk89/sizer-timer-pombe |
| Overlap_analysis_bivariate_data.nb | This Study | https://github.com/millerk89/sizer-timer-pombe |
| overlap_analysis_size.Rmd | This study | https://github.com/millerk89/sizer-timer-pombe |
| model.Rmd | This study | https://github.com/millerk89/sizer-timer-pombe |
| Other | ||
| Cell Asic ONIX, 3.5 – 5.5 μm Y04C-02 | EMD Millipore | N/A |
| Coverglass-bottom dish | MaTek | P35G-1.5-20C |
| Yokogawa CSU-WI spinning disk | Nikon Instruments | N/A |
| 60× 1.4-NA CFI60 Apochromat Lambda S objective lens | Nikon Instruments | N/A |
| 405-, 488-, and 561-nm laser lines | Nikon Instruments | N/A |
| photometrics Prime BSI camera | Nikon Instruments | N/A |
| Eclipse Ti2 | Nikon Instruments | N/A |
Any additional information required to reanalyze the data reported in this paper is available from the lead contact upon request.