Disentangling local and global climate drivers in the population dynamics of mosquito-borne infections

Abstract

Identifying climate drivers is essential to understand and predict epidemics of mosquito-borne infections whose population dynamics typically exhibit seasonality and multiannual cycles. Which climate covariates to consider varies across studies, from local factors such as temperature to remote drivers such as the El Niño–Southern Oscillation. With partial wavelet coherence, we present a systematic investigation of nonstationary associations between mosquito-borne disease incidence and a given climate factor while controlling for another. Analysis of almost 200 time series of dengue and malaria around the globe at different geographical scales shows a systematic effect of global climate drivers on interannual variability and of local ones on seasonality. This clear separation of time scales of action enhances detection of climate drivers and indicates those best suited for building early-warning systems.

The effects of local and global climate drivers on mosquito-borne diseases have been disentangled using adequate time-scale tools.

INTRODUCTION

Despite continuous control efforts, mosquito-borne diseases, such as malaria, dengue fever, chikungunya, Zika, West Nile fever, and Ross River fever, still pose serious public health threats (1). The number of dengue cases reported to World Health Organization increased about eightfold over the past two decades, from 505,430 cases in 2000 to 5.2 million in 2019 (2). Although malaria mortality decreased by 60% globally from 2000 to 2015 (3), 241 million annual cases were still reported in 2020 worldwide and resulted in an estimated 627,000 deaths (4). Mosquito-borne infections continue to greatly affect life in endemic countries with the persistence of established diseases and the emergence of new ones, substantially reducing population life span (5) and imposing considerable socioeconomic costs (6–7).

Complex dynamic relationships between humans, their population-wide immune landscape, socioeconomic factors, pathogen antigenic diversity, and environmental effects on vectors, all influence outbreaks of mosquito-borne infections (8–10). Despite this complexity, there is a consensus that climate factors, temperature, humidity and rainfall, and their variability are important determinants of mosquito-borne epidemics (11–14). Rainfall is required to establish suitable mosquito habitats for the production of larvae, adequate levels of humidity enable high activity and survival of adult mosquitoes, and temperature affects multiple stages of the mosquito life cycle, biting rates, and pathogen development within the vector, all influencing transmission rates. Thus, climate change is expected to alter the transmission dynamics of these diseases, not only by modifying mean incidence but also by increasing spatial and temporal variability and by allowing invasion by mosquitos of previously unexposed areas with rising temperatures (15–17). Changing patterns can involve not only a general upward trend in incidence but also higher amplitude of outbreaks over time and can be affected by decadal variability in ways that remain poorly understood (18).

In climate-driven population dynamics, multiple time scales are unavoidably at play. The population dynamics of mosquito-borne diseases in regions of recurrent epidemics typically exhibit strong seasonality, as expected from the influence of climate variables on pathogen replication, vector ecology, and human societies. Despite the dominance of seasonality, numerous studies have also highlighted a substantial influence of climate variability, in particular by the El Niño–Southern Oscillation (ENSO) (19). The semiregular El Niño climate cycle centered in the tropical Pacific Ocean drives multiannual climate variability in many parts of the world; it is both influenced by, and influences itself, the global climate. There is evidence, for example, of a relationship between El Niño events and the timing of Ross River virus epidemics in Australia (20), as well as the size of dengue, chikungunya, and malaria outbreaks in several countries (21–28). For dengue, this association can be complex and has been documented as mainly transient (23). The exceptionally high temperatures associated with the 2015–2016 El Niño have been implicated in creating conditions conducive to emergence of the Zika virus (29). Recent evidence on an El Niño influence has been reported for malaria transmission in Hainan, an inland province of Southern China (30).

It is therefore key to understand the effects of climate at different time scales on epidemic patterns of mosquito-borne diseases. In particular, a recurrent open question concerns the link between indirect effects of global climate drivers and the more direct influence of local factors that mediate their regional action and underlie seasonality. Often studies on climate and infectious diseases including vector-borne ones have focused exclusively on one of these two components of climate forcing, but see (23, 27, 31, 32). Some studies have emphasized global drivers as a means to capture through one dominant regional influence the potential myriad pathways that may connect their effect on transmission intensity (22, 28, 33–35). Others have addressed, instead, the local climate modulation of transmission to identify more direct causal pathways (36–39), with interannual variability seen potentially, at least in part, as independent from global drivers.

Here, we propose that the effects of local and global climatic variables on the population dynamics of mosquito-borne infectious diseases can be clearly disentangled and jointly analyzed with an extension of wavelet analysis. We specifically apply partial wavelet coherence (PWC) to determine the nonstationary statistical association between disease incidence and a given climatic variable while controlling for the effects of another. Partial correlation and partial rank correlation are commonly used in Biology in other settings (40), and partial correlation has been extended to partial autocorrelation function for the analysis of time series (41). With the notion of partial correlation recently extended to wavelet coherence (WC) (42, 43), we reanalyze a large number of time series for malaria and dengue, two dominant mosquito-borne disease threats around the globe (17). We specifically consider 197 published time series of incidence (or cases) together with the corresponding local and global climate variables (table S1) for different countries of South Asia, Central and South America, and sub-Saharan Africa. These analyses are also performed at different geographical scales for some countries or regions. Provided that there is sufficient seasonal variability in the disease time series and/or the chosen global climatic variable is adequate, we are always able to conclude that the seasonal and multiannual (2 to 4 years) modes of disease dynamics are significantly associated with local and global climate variables, respectively, with the latter typically exhibiting a more discontinuous pattern. This clear separation of the characteristic temporal scales of action shows that the interannual variability of disease incidence is driven indirectly, although the effect of these remote covariates can, in some cases, be traced to local ones. Local pathways mediating global climate effects are likely to be complex, involving multiple local variables, as they are not typically completely captured by considering a single climate factor. The separation can enhance the identification of the timing and intensity of these interannual effects, which are clearly present in nearly all the disease time series of this large ensemble. Conversely and expectedly, seasonality is the clear result of local climate conditions. These results highlight the importance of considering an adequate set of local and regional climate variables for both a more complete understanding of the population dynamics of mosquito-borne diseases and the incorporation of the most relevant variables in early-warning systems.

RESULTS

For the 197 dengue and malaria time series of incidence (or cases), we first describe the relative importance of seasonal and multiannual variability in the dynamics. We focus first on dengue in Thailand at different spatial scales: the whole country, political regions, and the geographical zones used by the Public Health Department and provinces (see fig. S1 and table S2). Figures S2 to S4 display both the time series and their wavelet power spectrum (see Methods), showing that the seasonal component is always dominant at the larger geographical scales. The percentage of the variance due to this seasonal mode (1 year) is typically higher than that of the multiannual components (2 to 3 years or 3 to 4 years) (table S3). There are some exceptions at the province scale, mainly in Southern Thailand (table S3). Results show that the multiannual component is always present, largely in a discontinuous pattern that depends on the geographical scale (figs. S2 to S4).

Having established the almost universal presence of these two temporal scales of variation, we proceed to examine their association with different climatic variables, local ones such as temperature, rainfall, and humidity, and global ones such as ENSO indices (table S1). Wavelet analysis allows nonstationarity, a characteristic property of these epidemiological time series (23, 25, 36). To quantify the relationship between disease dynamics and climate forcing, we specifically used WC and PWC, an extension of the classical WC. PWC allows the identification of nonstationary statistical associations between two time series, while controlling for the effects of other specified variables (see Methods). We explain in Methods the choice of climate variables in the results we present below, given the large number of possible combinations of local-global covariate pairs.

For Thailand, the WC of dengue incidence with local climatic variables, average temperature (Fig. 1A), or rainfall (fig. S5A) shows a significant statistical association not only for the seasonal mode but also for the 2- to 3-year mode or the 3- to 4-year mode that appears transiently at the end of the 80s, between 1997 and 2005, and the end of the 2000s. WC between incidence and indices of ENSO, whether oceanic Niño index (ONI) (Fig. 1A) or southern oscillation index (SOI) (fig. S5A), reveals significant association not only for the multiannual modes but also, to some extent, for the seasonal mode in a discontinuous way. In contrast, the use of PWC greatly reduces the complexity of these results by showing the respective effects of each driver at a given scale. The seasonal variability appears only significantly associated with local climatic variables, whether mean temperature or rainfall (Fig. 1A and fig. S5A). The multiannual modes observed in WC are no longer significant for the local climatic variables but are now exclusively significant for the global ones (Fig. 1A and fig. S5A). We have illustrated, in these figure panels, specific pairs of local and global variables to emphasize that the result of the separation of time scales of action holds for different choices of local climate factors and for different indices of the same global climate driver of interannual climate variability. This is because local climate factors are at least partially correlated, especially at the seasonal scale, and so are the global indices of a climate phenomenon such as ENSO.

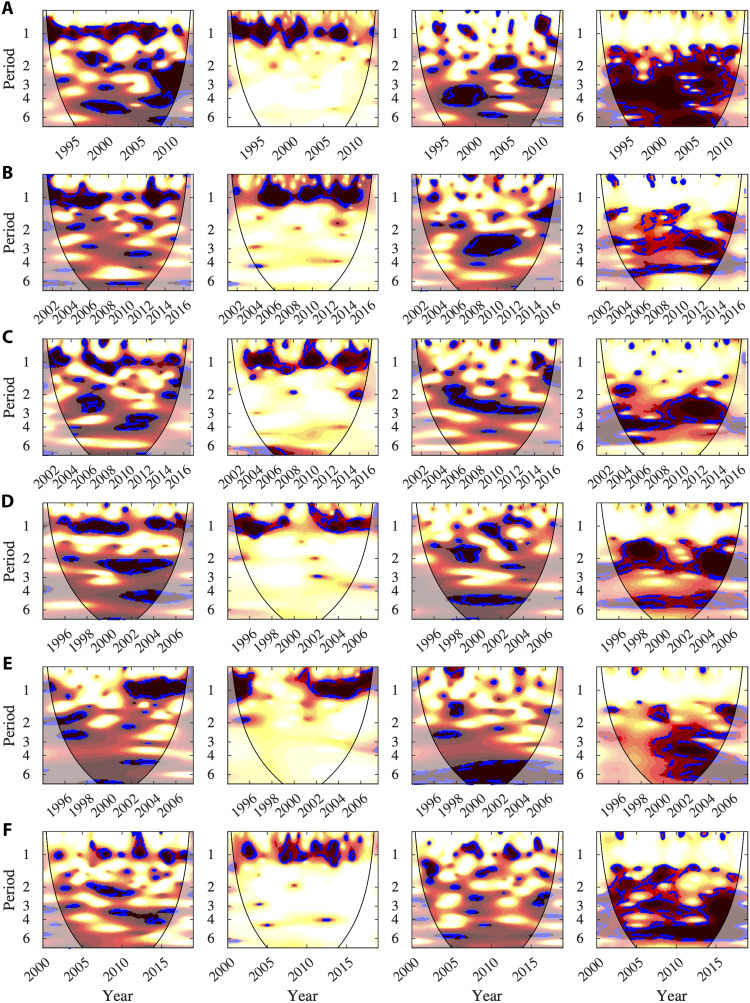
Fig. 1. WC and PWC between dengue in South Asia and local climate or global climate variable.

Each line represents the results of a location. The first column is the WC between incidence and a local climatic variable. The second column is the PWC between incidence and a local climatic variable controlled by a global climatic variable. The third and fourth columns are WC and PWC, respectively, but for global climatic variables. For the coherence, the colors are coded from white (no coherence) to yellow (low coherence) and to dark red (high coherence). The dotted-dashed blue lines show the 95 and 90% significance levels computed on the basis of bootstrapped series that used a Markov model (62). For all the graphs the thin black line is the cone of influence delimiting regions with possible edge effect. (A) Whole Thailand* for mean temperature and ONI. (B) Binh Thuan province (Vietnam) for relative humidity and MEI. (C) Phnom Penh for rainfall and SOI. (D) Singapore for mean daily minimum temperature and ONI. (E) Sri Lanka for maximum rainfall and ONI. (F) Bhopal City (Central India) for maximum temperature and MEI. *For dengue in Thailand, we used have reported cases for dengue fever, dengue hemorragic fever, and dengue shock syndrome. Then, we have added these cases before calculating incidence for each geographical area.

These results also generalize to other dengue datasets in South Asia (Fig. 1) and in Central and South America (Fig. 2) and for different spatial scales. Figure 1 shows the results of WC and PWC for the Binh Thuan province (Vietnam), the city of Phnom Penh (Cambodia), the city of Singapore, one province of Sri Lanka, and Bhopal City (Central India). Note that, for the Colombo province in Sri Lanka, the seasonal mode is for 6 months due to two rainy seasons each year and that, similarly for Bhopal City in India, the 12- and 6-month modes are important. For Central or South America, Fig. 2 shows the results for San Juan (Puerto Rico), two cities of Venezuela, two regions of Peru, and the city of Rio de Janeiro (Brazil). In all cases, the results of PWC highlight that local climate variables are significantly associated with the seasonal mode in dengue dynamics and that the global climate variables are associated with the multiannual modes.

Fig. 2. WC and PWC between dengue and local climate or global climate in Central and South Americas.

The description of the different columns is as in Fig. 1 (see that caption for details). (A) San Juan (Puerto Rico) for mean temperature and the Caribbean Index. (B) Aragua (Venezuela) for rainfall and ONI. (C) Carabobo (Venezuela) for relative humidity and SOI. (D) Peru (jungle region) for minimum temperature and SOI. (E) Peru (coastal region) for maximum temperature and MEI. (F) Rio de Janeiro (Brazil) for maximum mean temperature and tropical southern Atlantic index (TSA).

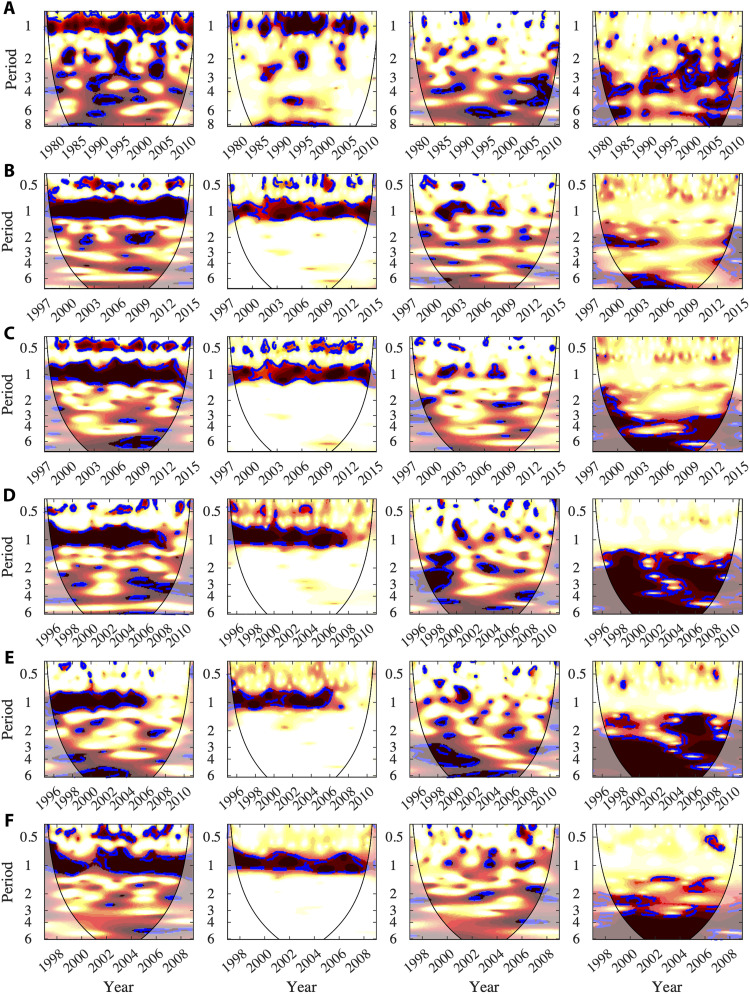
The results obtained for dengue also apply to epidemic malaria. Figure 3 shows results from South Asia. Figure 3 (A to C) displays the results for a rural district, the district of Kutch, and two cities of the semi-arid state of Gujarat in India with different climatic conditions, inland Ahmedabad and coastal and more humid Surat. For similar results in other locations of low transmission, fig. S6 applies the method to time series for highland malaria in East Africa, Kenya, and Ethiopia. For a broader range of malaria transmission intensities, Fig. 3 (D to F) shows results for two provinces of China, the Anhui province and the Hainan island. Malaria is re-emerging in the Anhui Province after a temporary low level of endemicity. Incidence has substantially increased in the north since 2000, while transmission intensity has remained at a relatively low level in the middle and south. The Hainan island used to exhibit endemic malaria, but incidence has declined since 2006 because of successful control efforts. Again, PWC allows a clear separation and localization in the frequency domain of the effects of local and global climatic variables. The seasonal component is associated with local climatic variables, and the multiannual modes exhibit a non-negligible effect of ENSO that could not have been clearly deduced from the WC.

Fig. 3. WC and PWC between malaria and local climate or global climate in Asia.

The description of the different columns is as in Fig. 1 (see that caption for details). (A) Kutch district (Gujarat state, India), incidence of P. falciparum, for rainfall and dipole mode index (DMI). (B) Surat (Gujarat state, India) for relative humidity and SOI. (C) Ahmedabad (Gujarat state, India) for minimum temperature and MEI. (D) Hainan province (Plasmodium vivax) for rainfall and ONI. (E) Hainan province (P. falciparum) for maximum temperature and MEI. (F) Anhui (whole province) for mean temperature and Nino34.

The collected ensemble of datasets allows us to examine more systematically the effect of geographical scale. For the different countries and vector-borne diseases, our findings remain valid at multiple geographical scales and appear therefore largely insensitive to the degree of aggregation of the time series analyzed. Figure S5 illustrates this finding for dengue in Thailand by considering the whole country, political regions, and the capital of Bangkok. Figure S7 shows results for representative geographical zones, and figs. S8 and S9 show results for representative provinces and for both temperature and rainfall, respectively. Figure S10 illustrates results for dengue in selected provinces of Southern Vietnam, and fig. S11 illustrates those of some cities in Brazil. Concerning Brazil, results include the Metropolitan Region of Recife, the major metropolitan area of Northeast Brazil in the state of Pernambuco (fig. S11A), different municipalities of this metropolitan area (fig. S11, B and C), and a number of Brazilian state capitals (fig. S11, D to F). Last, fig. S12 shows results for malaria in some districts of the Anhui province (China), compared to the whole province and illustrating the same and distinct choice of covariates’ pairs. Again, PWC successfully disentangles the effect of different climatic variables at different time scales, and it does so for a range of local climate variables and for various ENSO indices, as well as for other global climatic indices from the Atlantic and Indian Oceans where appropriate. The finding that the separation of time scales of action for local and global climate covariates is valid for different geographical scales and that for a range of climatic variables underscores the effectiveness of PWC.

To summarize results across analyses, we can examine the change in the ratio of mean coherence for the seasonal and multiannual modes as we go from results for WC to those for PWC. Figure 4 shows that PWC enables a considerable increase in the coherence for both local climatic variables for the seasonal mode and global climatic variables for the multiannual mode. Figure S13 shows similar changes than Fig. 4 for the coherence ratios of figs. S5 to S12.

Fig. 4. Ratio of the average coherence computed for the seasonal mode (0.8 to 1.2 years) and for the multiannual mode (2 to 4 years).

These average ratios have been computed for WC or PWC, for both the local climate variables (solid lines) and the global climate variables (dashed lines) for the data used in Fig. 1 (A), Fig. 2 (B), and Fig. 3 (C).

DISCUSSION

We have reanalyzed 197 time series for two major climate-sensitive infectious diseases transmitted by mosquito vectors, malaria and dengue, from regions with recurrent seasonal epidemics in different countries of South Asia, Central and South America, and sub-Saharan Africa, together with their corresponding local and global climatic drivers at different geographical scales. The application of PWC proves to be effective to disentangle the respective effects of different climate drivers acting at different time scales on transmission dynamics, from local variables such as temperature and precipitation to global ones such as ENSO.

Our results add to the growing body of evidence indicating that both local and global climate variables notably affect the transmission dynamics of mosquito-borne disease (16). They go further and show that these effects are consistently time scale dependent (23). We achieve a consistent separation of the temporal scales of action, with local climate variables largely associated with seasonality and global ones to multiannual modes (2 to 4 years) in a more discontinuous interaction. In particular, the multiannual cycles modulating the annual size of seasonal epidemics are completely accounted for by a global climate variable provided one controls for the local seasonal factor. The effect of global drivers and its time localization is also better identified in this way. As a result, a substantial role of a global climate driver is identified in almost all the two hundred time series analyzed, with, in few cases, quite discontinuous areas of significance, for example, in Southern Thailand. Seasonality, as expected, is conversely mostly associated with local climate factors. These findings are general, as they are obtained for different geographical scales and a wide range of local and global climate variables.

The collection of datasets considered also spans a range of transmission intensities, from low transmission rates manifested in intermittent large epidemics (44) to higher values under more endemic conditions with seasonally recurrent outbreaks. Examples of these respective dynamics for dengue are found in a city such as Rio de Janeiro (Brazil) versus the island of Puerto Rico in South America and, more broadly, most of Thailand. Similarly, we have considered low-transmission malaria regions at the edge of the distribution of the disease, in highlands and desert fringes, where considerable interannual variability is known to occur in the size of seasonal epidemics as the result climate forcing (15, 18) and regions in China spanning broader ranges of transmission intensity, also affected by transient intervention efforts (30). We have not pushed the analyses to high-transmission malaria regions, such as those of West Africa, of recurrent seasonal high (asymptomatic) prevalence due to incomplete immunity and high antigenic diversity of the parasite Plasmodium falciparum, as under weak year-to-year variation in prevalence, the question of whether climate variability influences these patterns is not warranted. The open question remains however of whether climate forcing may manifest itself more clearly as intervention efforts move the population dynamics of the disease toward lower transmission intensities and more intermittent epidemics (30).

Our findings imply that ignoring local climate drivers in analyses of these vector-borne diseases will affect not only the understanding of seasonal epidemics as expected but also that of the role of global climate drivers. In the same way, it follows that a local factor such as temperature cannot be the dominant or only factor driving the multiannual components of disease dynamics independently from global climate variability [as analyzed in (45)]. When controlling for the effects of global climate cycles, we find that local climate variables (including temperature) are no longer associated with disease incidence for the multiannual modes, whereas when controlling for the effects of the seasonal variable, the association persists and is even enhanced. There can be some interesting exceptions for specific frequency bands for which a local and a global variables can be correlated and we cannot disentangle their respective effects on the global variability. These exceptions can be identified by careful comparison of the PWC results when controlling respectively for the local and global variables, through the disappearance in both spectra of significant coherence bands for the same frequencies. This situation can be seen for malaria with rainfall and a given global index in Kenya (fig. S6, A and D) for the 1.7- to 2.2-year band.

It also follows that a more systematic consideration of what is known in climate science on the sensitivity of different regions to forcing by global climate variability and, on the predictability of this response, should be extremely valuable to epidemiology. Pathways mediating these effects regionally and locally should be of interest, although our results indicate that these pathways typically involve multiple climate variables and cannot be completely reduced to a single one.

Because our approach is based on wavelet analysis, it is well suited for nonstationary conditions, and it allows us to address large variations in disease dynamic as those observed for malaria in China (30) and in sub-Saharan Africa (35, 36). Nevertheless, our approach necessitates certain requirements of the disease data. These concern the length of the time series of interest and its seasonality. Our method requires the presence of a certain recurrence of the seasonal component, even if for only a part of the observations. Seasonality is a common feature, however, across most of the geographical areas where these diseases persist from year to year. Concerning time series length, requirements are the same as those for the application of Fourier analysis and strongly depend on the observation time step. They are defined for example in Cazelles et al. (46) as a minimum of 30 to 40 data points with significant periodic components smaller than 20 to 25% of the series length. Caution should apply to interpretation of results for the slow time scales close to decadal when the length of the disease record spans one or at most two such long cycles.

In addition, it is well known that wavelet spectra and associated analyses are less reliable close to the boundaries of the time series. Thus, we would not expect to apply these methods to a recently emerged infectious disease for which only a few seasons are available. Another approach would be more suitable at that stage for examining nonstationary correlations with climate variables that are local in time and occur at different temporal scales (47).

To adequately anticipate future mosquito-borne disease outbreaks, we also need to gain a better understanding of how global climate interacts with other exogenous or endogenous drivers. Global oscillations might have not only different effects on local climate but also indirect effects on the ecology of the vector and the behavior of hosts (48). Multiple conditions can interact in complex ways and modulate epidemic size, including those related to climate, the ecology of mosquitoes, the immune status of hosts, and the strain variation of pathogens, e.g., (33, 49). The effects of ENSO on local climate may indirectly influence both the ecology of the vector and the immunity of the host population (33, 45). Immunity provides negative feedbacks whereby increases in transmission due to favorable current and seasonal climatic conditions can impede the spread of the disease through its protective effects (33, 45). Additional factors potentially influencing the population dynamics of mosquito-borne disease include the evolution of the pathogen (50), as well as control efforts, urbanization, and other socioeconomic conditions (51–53). Despite this complexity, identification of local and global climatic drivers remains a fundamental step.

Our results indeed suggest that process-based and statistical models for the population dynamics of these major vector-borne diseases should incorporate both local and global climatic variables. An interesting possibility would be to decompose the observed dynamics into different periodic components (with wavelet decomposition) and to model each periodic component with the suitable exogenous variables. Then, the overall simulated epidemic dynamics would be numerically obtained by summing the reconstructed periodic components. For more mechanistic dynamical models written as extensions of SIR (susceptible-infected-recovered) equations and coupled human-mosquito models, consideration of a single local variable should be generally insufficient to properly capture interannual variability, although exceptions can be identified.

Longer trends due to climate change are expected to alter patterns of seasonal and interannual. Variability and act on the population dynamics of vector-borne infections, especially at the boundaries of their geographical distribution. Rising temperatures are indeed enabling the expansion of mosquito vectors of arboviruses to previously unexposed areas (17, 54, 55) and have been shown to influence epidemic size in highland malaria, where human populations had been protected by the cooling effect of elevation, e.g., (15, 18). Changing patterns in highlands involve not only a general upward trend in incidence from the 1970s to the 1990s but also pronounced increases in the amplitude of outbreaks over these decades. More recent decreases in the size of epidemics at the turn of the 21st century have also been associated with decadal variation in the climate of Ethiopia related to the transient slowdown in global warming. This decadal change in temperatures would have facilitated control efforts at a temporal scale of climate forcing that is not typically investigated in vector-borne infections of other parts of the world (18). Time series analyses based on wavelets are well suited for investigating these changing patterns of variability, and long-term surveillance efforts are invaluable to decipher the interplay of multiple time scales of climate forcing on infectious disease. Although control efforts can decouple climate and health patterns, it is still pertinent to document when this occurs and to understand the effect of control in the context of climate variability. For climate-sensitive diseases, including vector-borne and water-borne ones, we cannot expect to evaluate the effect of control separately from periods of drought, warmer than average seasons, and other anomalous conditions affecting levels of transmission. In addition, control efforts may be reactive intensifying as the result of an increased perception of disease risk, creating an unavoidable link to climate variability in previous seasons (56).

Besides vector-borne diseases, we expect this method to be relevant to water-borne diarrheal diseases such as cholera for which effects of climate variability have been documented (33, 57) and even for respiratory infectious diseases of airborne transmission such as seasonal influenza, syncytial virus diseases, and now coronavirus disease 2019 (COVID-19) (58, 59). The purpose of the proposed method is indeed to contribute to the better exploration of which factors influence population dynamics when multiple time scales of variability are present.

Ultimately, a better understanding of how climate influences the population dynamics of infectious diseases at different time scales and in relation to both local and global forcing is essential to evaluate and design control strategies. This understanding is also important to develop early-warning systems on the basis of efficient environmental variables, and in so doing, to enable timely preventive measures. A valuable starting point is provided by the time series analysis proposed and demonstrated here, which reveals climate-disease associations not only locally in time but also in a way that separates drivers acting on different time scales.

METHODS

Accounting for nonstationarity is recognized as crucial to the analysis of time series in Epidemiology. For this purpose, time-frequency wavelet analysis has been a tool of choice to quantify different periodic components locally in time for a given time series and to examine transient associations with another time series (46, 60, 61). Wavelet analysis is a generalization of windowed Fourier analysis and has been described in detail in our previous papers with applications to both Ecology and Epidemiology (46, 61, 62).

The continuous wavelet transform of a time series x(t) with respect to a chosen mother wavelet is performed as follows:

$$W_x(a,\mathrm{\tau })=\frac{1}{\sqrt{a}}.{\displaystyle {\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}}x(t).{\mathrm{\psi }}^{\ast }\left(\frac{t-\mathrm{\tau }}{a}\right).dt$$

where ψ(·) denotes the mother wavelet, a is the scale of the mother wavelet, t is the time position, and the asterisk * denotes the complex conjugate form. The Morlet wavelet is typically used as the mother wavelet, and in this particular expression, the wavelet scale a is inversely proportional to the central frequency of the wavelet; thus, f ≈ 1/a (46, 61). Then, the wavelet coefficient W_x(a, τ) represents the contribution of the scale a or the period 1/f to the time series at time position τ.

By analogy with Fourier analysis, the wavelet power spectrum can be computed as S_x(f, τ) = ‖W_x(f, τ)‖² to quantify the contribution of different periodic components to the variance along the time axis.

Another interesting quantity is the average variance at each time location, obtained by averaging the frequency components

$$\overline{S_x}(\mathrm{\tau })=\frac{{\mathrm{\sigma }}_x^2.{\mathrm{\pi }}^{1/4}.{\mathrm{\tau }}^{1/2}}{C_{\mathrm{g}}}.{\displaystyle {\int }_0^{\mathrm{\infty }}}{\left(\frac{1}{f}\right)}^{1/2}.{\Vert W_x(f,\mathrm{\tau })\Vert }^2.df$$

where ${\mathrm{\sigma }}_x^2$ is the variance of the time series x(t), C_g is a constant, $C_{\mathrm{g}}={\int }_0^{\mathrm{\infty }}\frac{{\Vert \hat{\mathrm{\psi }}(f)\Vert }^2}{f}.df$, and $\hat{\mathrm{\psi }}(f)$ is the Fourier transform of ψ(f). This quantity, $\overline{S_x}(\mathrm{\tau })$, can also be filtered in a given frequency band, f₁-f₂ and averaged over a considered time period.

With the wavelet transforms at hand, the statistical relationship between two nonstationary time series, x(t) and y(t), can be analyzed with the “wavelet cross-spectrum” and the “WC.” The wavelet cross-spectrum is given by $W_{x,y}(f,\mathrm{\tau })=W_x(f,\mathrm{\tau }).{\mathrm{W}}_y^{\ast }(f,\mathrm{\tau })$, and the WC is defined as the cross-spectrum normalized by the spectrum of each time series

$${WC}_{x,y}(f,\mathrm{\tau })=\frac{\mid ⟨W_{x,y}(f,\mathrm{\tau })⟩\mid }{{\mid ⟨W_x(f,\mathrm{\tau })⟩\mid }^{1/2}.{\mid ⟨W_y(f,t\mathrm{\tau })⟩\mid }^{1/2}}$$

where 〈·〉 denotes a smoothing operator in both time domain and frequency domain. The values of WC_x,y(f, τ) are thus bounded by 0 ≤ WC_x,y(f, τ) ≤ 1. The WC is equal to 1 when the two time series synchronously oscillate at the same frequency, and equal to 0 if x(t) and y(t) are independent.

When there is a link between variable A and variable B, we may wonder whether it is due to another set of variables {C, D, …} that would act on both A and B. To remove the potential effects of {C, D, …}, a common practice is to use partial correlations or partial rank correlations. In the same vein, for controlling the dependence between different signals when analyzing an association between two time series, we use PWC. PWC computes the coherence between two time series after controlling for the effect of other time series. Different authors (42, 63) used an iterative PWC method for computing the coherence between time series x_a(t) and x_b(t) while controlling for the common effect due to x_c(t). This iterative method is not appropriate, however, to analyze series more than three times and gives results that need to be smoothed before interpretation. Thus, in the study of Lara et al. (43), we adapted the inverse PWC method from Fourier analysis (64) to wavelet analysis. This method is based on the inversion of the spectral matrix Σ(f,t) whose elements are the cross-wavelet spectrum for the i and j time series from the n time series analyzed

$$\text{Σ}(f,t)=\left[\begin{array}{cccc}{W}_{11}(f,t)& W_{12}(f,t)& \cdots & W_{1n}(f,t)\\ W_{21}(f,t)& {\mathrm{W}}_{22}(f,t)& \cdots & W_{2n}(f,t)\\ ⋮& ⋮& \ddots & ⋮\\ W_{n1}(f,t)& W_{n2}(f,t)& \cdots & W_{nn}(f,t)\end{array}\right]$$

The PWC between x_j(t) and x_k(t) controlled for all other time series is then defined as

$${\mathrm{PWC}}_{jk\mid (\mathrm{\setminus }jk)}(f,t)={\left(\frac{{\mid S^{jk}(f,t)\mid }^2}{\mid S^{jj}(f,t)\mid .\mid S^{kk}(f,t)\mid }\right)}^{1/2}$$

where S^jk(f, t) is the (j,k) element of the inverse spectral matrix Σ⁻¹(f, t) and (\jk) means all elements except the jth and the kth. PWC_jk∣(\jk)(f, t) captures the frequency-specific and time-localized relationships between time series j and k, by excluding the effects of all other signals.

We analyzed 197 published time series at the different geographical scales and all the local climate time series that were associated with these datasets in the published articles (table S1). We also considered global climate series on the basis of (i) demonstrated effects of a given driver of interannual variability (e.g., ENSO) for regional climate and for documented teleconnections with the infectious disease patterns in the literature and (ii) the plausibility of such an effect given geographical proximity (table S1). For example, the dipole mode index (DMI) was used only for South-East Asian data, the Caribbean Index only for Puerto Rico, and the different global climate indices of the Atlantic for South American datasets.

The number of possible combinations we could present with the assembled dataset is clearly too large (the overall dataset includes 197 disease time series, 724 time series for local climate variables, and 13 time series for global climate drivers; table S1). Thus, although we sought to demonstrate the generality and robustness of the results by analyzing a diversity of “local climate variable–global climate variable” pairs, we had to restrict the number of analyses and results reported. We also had to decide whether to illustrate results for the same or for different covariate pairs when analyzing one region at different spatial resolutions. We relied on the WC results to reduce the number of pairs for the calculation of PWC by considering both redundant and weak effects. Specifically, because the WC results were always close for the different ENSO indices [SOI, ONI, multivariate ENSO index (MEI), and other Nino indices], we presented results for one of these only with no systematic approach to this choice. There can be some particular differences across the spectra with the different global drivers related to the degree of smoothness of the given index, but the overall result on the separation of time scales of action remains unchanged. Thus, the presentation of PWC results for one index was therefore largely representative of those for others. Moreover, in other cases, the effects of a given global driver as seen with WC, for example, those of DMI, were weak, which led us to exclude the specific covariate from consideration. For the plots themselves, we opted for showing first a diversity of local climate variable–global climate variable pairs in initial figures, for the same country or the same continent. We also illustrated the outcome of the analysis for disease data at different spatial resolutions for the region of Thailand and presented results, keeping the chosen pair constant, while also reporting comparisons across figures to another pair.

Supplementary Materials

This PDF file includes:

Tables S1 to S3

Figs. S1 to S13

References