Healthcare Center Clustering for Cox’s Proportional Hazards Model by Fusion Penalty

Summary

There has been growing research interest in developing methodology to evaluate healthcare centers’ performance with respect to patient outcomes. Conventional assessments can be conducted using fixed or random effects models, as seen in provider profiling. We propose a new method, using fusion penalty to cluster healthcare centers with respect to a survival outcome. Without any priori knowledge of the grouping information, the new method provides a desirable data-driven approach for automatically clustering healthcare centers into distinct groups based on their performance. An efficient alternating direction method of multipliers algorithm is developed to implement the proposed method. The validity of our approach is demonstrated through simulation studies, and its practical application is illustrated by analyzing data from the national kidney transplant registry.

1 |. INTRODUCTION

Assessing the comparative performance of healthcare centers (e.g., hospitals, nursing homes, transplant centers, or dialysis facilities) has attracted significant interest over the past decades. The objective is to outline and compare the performance of these centers in order to facilitate improvements through accountability and feedback. This information can aid individuals in selecting the most suitable healthcare facility and also enable stakeholders and payers to identify areas requiring enhancements.

Our motivating example is the national kidney transplant registry data collected by the U.S. Organ Procurement and Transplantation Network (OPTN). Our goal is to evaluate transplant centers based on their five-year post-transplant graft survival rates. For patients with end-stage renal disease, kidney transplantation provides the best opportunity for survival. The Scientific Registry of Organ Recipients (SRTR) commonly utilizes the five-year post-transplant graft survival metric, defined as the time until either death or graft failure within five years following transplantation, for regulatory monitoring of transplant centers^1,2. Consequently, we will employ the five-year post-transplant graft survival to assess the quality of care provided by transplant centers.

Traditionally, profiling methods have been developed to evaluate the quality of care provided by various healthcare centers, using multiple patient outcome quality measures, such as readmission, mortality, and hospitalization. Existing transplant center profiling approaches typically employ inference-based procedures and generate a three-tier system, indicating whether centers perform worse than expected, as expected, or better than expected. Random effects and fixed effects models are two prevalent analytical methods used in profiling^3,4,5,6. However, both models have their drawbacks. For random effects models, healthcare centers on the tails of the distribution tend to have small sample sizes, leading to substantially shrunk estimates towards the population mean^7,8. This may result in reduced sensitivity when classifying healthcare centers in the tail areas, causing the majority of healthcare centers to be classified as expected, despite noticeable heterogeneity⁹. Additionally, misspecification of the random effects distribution can pose challenges in both estimation and inference. In contrast, fixed effects models suffer from a loss of efficiency due to a large number of parameters. Moreover, the simultaneous testing of the null hypothesis for extensive healthcare center effects is computationally demanding.

In order to offer more comprehensive ratings for kidney transplantation, the SRTR has implemented a five-tier rating system^10,11 that indicates whether a transplant center performs better than expected, somewhat better than expected, as expected, somewhat worse than expected, or worse than expected. However, concerns arise regarding the selection of appropriate cutoffs to categorize transplant centers into distinct groups. Furthermore, the decision regarding the total number of tiers is arbitrary.

To tackle the aforementioned challenges, we introduce a new fused effects model¹² designed to automatically identify homogeneous groups of healthcare centers without requiring a priori classification knowledge. We employ Cox’s proportional hazards model¹³ with fusion penalty¹⁴ to cluster transplant centers based on the post-transplant graft survival outcome. Unlike random or fixed effects models, this new method offers a data-driven approach that does not rely on inference tests of statistical significance. Our model can also investigate risk factors associated with post-transplant graft survival. Our method can be considered as an alternative of the latent class model, where we use fusion penalty to “classify” providers into different latent groups.

We employ a local quadratic approximation to the partial likelihood and optimize the penalized partial likelihood with the fusion penalty. Prioritizing clustering accuracy, we opt for the smoothly clipped absolute deviation (SCAD)¹⁵ penalty function over the LASSO penalty¹⁶. Compared to the LASSO, the SCAD penalty is nearly unbiased in identifying groups and enforces a sparser solution more aggressively¹⁷. The alternating direction method of multipliers (ADMM) algorithm can be utilized to implement the estimation, ensuring rapid convergence¹⁸. Due to the information loss during computation, we perform refitting by maximizing the log partial likelihood with the grouped data to obtain accurate parameter estimates.

The remainder of this paper is structured as follows: in Section 2, we outline the penalized Cox’s regression model with fusion penalty for clustering healthcare centers. Section 3 evaluates the performance of our approach through Monte Carlo simulation studies. In Section 4, we demonstrate the proposed method using the kidney transplant data as a practical example. Finally, we summarize our methodology and discuss potential future directions in Section 5.

2 |. METHODS

2. 1 |. Model

We begin by introducing the required notations to formulate our model. For subject $j=1,\dots ,n_i$ from healthcare center $i=1,\dots ,m$, we have data in the format $\left(y_{ij},{\mathbf{x}}_{ij},{\delta }_{ij}\right)$, where the observed time $y_{ij}$ is the minimum of the censoring time $c_{ij}$ and the event time $t_{ij},{\delta }_{ij}=I\left(t_{ij}\le c_{ij}\right)$ is the censoring indicator, and ${\mathbf{x}}_{ij}$ is a $p\times 1$ vector of predictors. The Cox’s proportional hazards model is

$$h_{ij}\left(t\mid {\mathbf{x}}_{ij}\right)=h_0\left(t\right)\text{exp}\left(a_i+{\mathbf{x}}_{ij}^{\text{⊤}}\mathit{\beta }\right),$$ (2.1)

where $h_{ij}\left(t\right)$ is the hazard for patient $j$ of center $i$ at time $t,h_0\left(t\right)$ is a baseline hazard function, $a_i$ is the center-specific effect, and $\mathit{\beta }={\left({\beta }_1,\cdots ,{\beta }_p\right)}^{\text{⊤}}$ is the vector of covariate coefficients. A constraint ${\sum }_{i=1}^m a_i=0$ ensures that all parameters are identifiable. For estimation and inference, we often rely on the partial likelihood, where the unspecified baseline hazards can be canceled out. Patients are assumed to be independent within each healthcare center, i.e., we assume independence of $y_{ij}$ given ${\mathbf{x}}_{ij}$ and $a_i$. The partial likelihood for model (2.1) can be written as

$$L(\mathit{a},\mathit{\beta })=\prod _{i=1}^m \prod _{j=1}^{n_i} {\left[\frac{\text{exp}\left(a_i+{\mathbf{x}}_{ij}^{\text{⊤}}\mathit{\beta }\right)}{\sum _{i^{\prime }=1}^m\sum _{j^{\prime }=1}^{n_{i^{\prime }}}I\left(y_{i^{\prime }{j}^{\prime }}\ge y_{ij}\right)\text{exp}\left(a_{i^{\prime }}+{\mathbf{x}}_{i^{\prime }{j}^{\prime }}^{\text{⊤}}\mathit{\beta }\right)}\right]}^{{\delta }_{ij}},$$ (2.2)

where $\mathit{a}={\left(a_1,\cdots ,a_m\right)}^{\text{⊤}}$. We assume that $a_i$ belongs to one of $K$ groups ${𝒢}_1,\cdots ,{𝒢}_K$, which are mutually exclusive partitions of $\{1,\cdots ,m\}$; and the number of groups is much smaller than that of centers, i.e., $K\ll m$. Moreover, the number of groups and the group membership are unknown in advance.

We utilize the fused SCAD penalty to identify homogeneous center performance and then fuse them as shared parameters to classify groups of healthcare centers. Incorporating the fusion penalty into the partial likelihood (2.2) results in the following optimization problem:

$$\left(\widehat{\mathit{a}},\widehat{\mathit{\beta }}\right)=\text{arg}\text{min}\left[-\ell \left(\mathit{a},\mathit{\beta }\right)+\sum _{1\le i<k\le m}{p}_{\gamma }\left(\left|a_i-a_k\right|,\lambda \right)\right],$$ (2.3)

where $\ell (\mathit{a},\mathit{\beta })$ is the log of the partial likelihood, and $p_{\gamma }(t,\lambda )$ is the SCAD penalty function¹⁵ defined as

$$p_{\gamma }(t,\lambda )=\lambda \underset{0}{\overset{\left|t\right|}{\int }}\text{min}\left\{1,(\gamma -x/\lambda {)}_{+}/(\gamma -1)\right\}dx,$$

with $(x{)}_{+}=x$ if $x>0$ and = 0 otherwise, $\lambda \ge 0$ is a tuning parameter, $\gamma \ge 0$ is a parameter that controls the concavity of the penalty functions. Following Ma et al.,¹⁷ we treat $\gamma$ as a fixed constant.

2. 2 |. Estimation procedure

Note that the penalty function $p_{\gamma }\left(\left|a_i-a_k\right|,\lambda \right)$ cannot be written in the form of addition of separate terms of $p_{\gamma }\left(\left|a_i\right|,\lambda \right)$ and $p_{\gamma }\left(\left|a_k\right|,\lambda \right)$ as in LASSO. Here, we introduce a new set of parameters ${\theta }_{ik}=a_i-a_k$, which are equivalent to the pairwise differences of healthcare center effects. Consequently, the above minimization problem (2.3) can be transformed into the following constraint optimization problem:

$$F_0(\mathit{a},\mathit{\beta },\mathit{\theta })=-\ell (a,\mathit{\beta })+\sum _{i<k}{p}_{\gamma }\left(\left|{\theta }_{ik}\right|,\lambda \right)\text{ subject to }{a}_i-a_k-{\theta }_{ik}=0,$$ (2.4)

where $\mathit{\theta }={\left\{{\theta }_{ik},i<k\right\}}^{\text{⊤}}$. As a result, the alternating direction method of multipliers (ADMM) algorithm can be used to identify the groups in the objective function (2.4). The ADMM algorithm combines the strengths of dual decomposition and augmented Lagrangian methods for constrained optimization. The estimates of the parameters are obtained by the augmented Lagrangian

$$F(\mathit{a},\mathit{\beta },\mathit{\theta },\mathit{v})=F_0(\mathit{a},\mathit{\beta },\mathit{\theta })+\sum _{i<k}{v}_{ik}\left({\theta }_{ik}-a_i+a_k\right)+\frac{\vartheta }{2}\sum _{i<k}{\left({\theta }_{ik}-a_i+a_k\right)}^2,$$ (2.5)

where $\mathit{v}={\left\{v_{ik},i<k\right\}}^{\text{⊤}}$ are Lagrange multipliers, $\vartheta$ is the penalty parameter. We use ADMM to iteratively compute the estimates of $(\mathit{a},\mathit{\beta },\mathit{\theta },\mathit{v})$. For given ${\mathit{\theta }}^{\left(s\right)},{\mathit{v}}^{\left(s\right)}$ at step $s$, the iterations can be specified as follows:

$$\left({\mathit{a}}^{(s+1)},{\mathit{\beta }}^{(s+1)}\right)=\text{arg}\underset{\mathit{a},\mathit{\beta }}{\text{min}}F\left(\mathit{a},\mathit{\beta },{\mathit{\theta }}^{\left(s\right)},{\mathit{v}}^{\left(s\right)}\right),$$ (2.6)

$${\mathit{\theta }}^{(s+1)}=\text{arg}\underset{\mathit{\theta }}{\text{min}}F\left({\mathit{a}}^{\left(s+1\right)},{\mathit{\beta }}^{\left(s+1\right)},\mathit{\theta },{\mathit{v}}^{\left(s\right)}\right),$$ (2.7)

$$v_{ik}^{(s+1)}=v_{ik}^{\left(s\right)}+\vartheta \left(a_i^{(s+1)}-a_k^{(s+1)}-{\theta }_{ik}^{(s+1)}\right).$$ (2.8)

To update $\mathit{a}$ and $\mathit{\beta }$, minimizing (2.6) is equivalent to minimizing

$$f(\mathit{a},\mathit{\beta })=-\ell (\mathit{a},\mathit{\beta })+\frac{\vartheta }{2}\sum _{i<k}{\left(a_i-a_k-{\theta }_{ik}^{\left(s\right)}+{\vartheta }^{-1}{v}_{ik}^{\left(s\right)}\right)}^2+C,$$ (2.9)

where $\mathit{C}$ is the constant independent of $\mathit{a}$ and $\mathit{\beta }$. To solve the optimization problem (2.9), we approximate the nonlinear logpartial likelihood function using a two-term Taylor series expansion. At each iteration, we solve a reweighted least squares problem 19. Specifically, let $\mathbf{y}={\left({\mathbf{y}}_1^{\text{⊤}},\cdots ,{\mathbf{y}}_m^{\text{⊤}}\right)}^{\text{⊤}}$ with ${\mathbf{y}}_i={\left(y_{i1},\cdots ,y_{i{n}_i}\right)}^{\text{⊤}},\mathbf{X}={\left({\mathbf{X}}_1^{\text{⊤}},\cdots ,{\mathbf{X}}_m^{\text{⊤}}\right)}^{\text{⊤}}$ with ${\mathbf{X}}_i={\left({\mathbf{x}}_{i1},\cdots ,{\mathbf{x}}_{i{n}_i}\right)}^{\text{⊤}},\mathbf{A}=\text{diag}\left(1_{n_1},\cdots ,1_{n_m}\right)$ with $1_{n_i}=(1,\cdots ,1{)}^{\text{⊤}}$ being the vector with $n_i$ ones, and $\mathit{\eta }=\mathbf{A}\mathit{a}+\mathbf{X}\mathit{\beta }$. Let ${\ell }^{\prime }\left(\mathit{\eta }\right),{\ell }^{″}\left(\mathit{\eta }\right)$ denote the gradient and Hessian of the log-partial likelihood with respect to $\mathit{\eta }$, respectively. The log-partial likelihood $\ell (\mathit{a},\mathit{\beta })$ can be approximated by the following quadratic form (see the supplementary material)

$$\frac{1}{2}(\mathbf{z}-\mathbf{A}\mathit{a}-\mathbf{X}\mathit{\beta }{)}^{\text{⊤}}{\ell }^{″}(\mathit{\eta }\left)\right(\mathbf{z}-\mathbf{A}\mathit{a}-\mathbf{X}\mathit{\beta })$$

where $\mathbf{z}=\mathit{\eta }-{\ell }^{″}\left(\mathit{\eta }{)}^{-1}{\ell }^{\prime }\right(\mathit{\eta })$ with

$$\begin{gathered} \frac{\partial \ell \left(\mathit{\eta }\right)}{\partial {\eta }_{ij}}={\delta }_{ij}-\text{exp}\left({\eta }_{ij}\right)\sum _{i^{\prime }{j}^{\prime }\in D_{ij}}\frac{1}{\sum _{uv\in R_{i^{\prime }{j}^{\prime }}}\text{exp}\left({\eta }_{uv}\right)}, \\ \frac{{\partial }^2\ell \left(\mathit{\eta }\right)}{\partial {\eta }_{ij}^2}=-\text{exp}\left({\eta }_{ij}\right)\sum _{i^{\prime }{j}^{\prime }\in D_{ij}}\frac{1}{\sum _{uv\in R_{i^{\prime }{j}^{\prime }}}\text{exp}\left({\eta }_{uv}\right)}+\text{exp}\left(2{\eta }_{ij}\right)\sum _{i^{\prime }{j}^{\prime }\in D_{ij}}\frac{1}{{\left\{\sum _{uv\in R_{i^{\prime }}{j}^{\prime }}\text{exp}\left({\eta }_{uv}\right)\right\}}^2}, \end{gathered}$$

where $D_{ij}$ is the set of indices $i^{\prime }{j}^{\prime }$ with $t_{i^{\prime }{j}^{\prime }}<y_{ij}$ (the times for which observation of the $i$ th subject in the $j$ th center is still at risk) and $R_{i^{\prime }{j}^{\prime }}$ is the set of indices $uv$ with $y_{uv}\ge t_{i^{\prime }{j}^{\prime }}$ (those at risk at time $t_{i^{\prime }{j}^{\prime }}$). Since ${\ell }^{″}\left(\mathit{\eta }\right)$ is a full matrix, it requires computation of $O\left(N^2\right)$ elements, we instead replace ${\ell }^{″}\left(\mathit{\eta }\right)$ by a diagonal matrix with the same diagonal elements as ${\ell }^{″}\left(\mathit{\eta }\right)$.^20,21,19 This substitution works well because the diagonal elements of ${\ell }^{″}\left(\mathit{\eta }\right)$ are much larger than the off-diagonal elements. Denote $-{\ell }^{″}\left(\mathit{\eta }\right)$ by $\mathbf{W}.\mathbf{W}$ and $\mathbf{z}$ are computed based on ${\mathit{a}}^{\left(s\right)}$ and ${\mathit{\beta }}^{\left(s\right)}$ at iteration $s$. Equation (2.9) can be rewritten as

$$f(\mathit{a},\mathit{\beta })=\frac{1}{2}(\mathbf{z}-\mathbf{A}\mathit{a}-\mathbf{X}\mathit{\beta }{)}^{\text{⊤}}\mathbf{W}(\mathbf{z}-\mathbf{A}\mathit{a}-\mathbf{X}\mathit{\beta })+\frac{\vartheta }{2}{∥\mathbf{\Delta }\mathit{a}-{\mathit{\theta }}^{\left(s\right)}+{\vartheta }^{-1}{\mathit{v}}^{\left(s\right)}∥}^2+C,$$ (2.10)

where $\mathbf{\Delta }={\left\{\left({\mathbf{e}}_i-{\mathbf{e}}_j\right),i<j\right\}}^{\text{⊤}}$ with ${\mathbf{e}}_i$ being a $m\times 1$ vector whose $i$ th element is 1 and the remaining elements are 0. Thus, for given ${\mathit{\theta }}^{\left(s\right)},{\mathit{v}}^{\left(s\right)}$ at the sth step, we set the derivatives $\partial f(\mathit{a},\mathit{\beta })/\partial \mathit{a}=0$ and $\partial f(\mathit{a},\mathit{\beta })/\partial \mathit{\beta }=0$ to obtain the following updates ${\mathit{a}}^{(s+1)}$ and ${\mathit{\beta }}^{(s+1)}$:

$${\mathit{a}}^{(s+1)}={\left({\mathbf{A}}^{\text{⊤}}{\mathbf{Q}}_x\mathbf{A}+\vartheta {\mathbf{\Delta }}^{\text{⊤}}\mathbf{\Delta }\right)}^{-1}\left[{\mathbf{A}}^{\text{⊤}}{\mathbf{Q}}_x\mathbf{z}+\vartheta {\mathbf{\Delta }}^{\text{⊤}}\left({\mathit{\theta }}^{\left(s\right)}-{\vartheta }^{-1}{\mathit{v}}^{\left(s\right)}\right)\right]$$ (2.11)

where ${\mathbf{Q}}_x=\mathbf{W}-\mathbf{W}\mathbf{X}{\left({\mathbf{X}}^{\text{⊤}}\mathbf{X}\right)}^{-1}{\mathbf{X}}^{\text{⊤}}\mathbf{W}$. We let ${\mathit{a}}^{(s+1)}={\mathit{a}}^{(s+1)}-$ mean $\left({\mathit{a}}^{(s+1)}\right)$ to guarantee that the estimate ${\mathit{a}}^{(s+1)}$ satisfies the constraint ${\sum }_{i=1}^m{a}_i=0$, and

$${\mathit{\beta }}^{(s+1)}={\left({\mathbf{X}}^{\text{⊤}}\mathbf{W}\mathbf{X}\right)}^{-1}{\mathbf{X}}^{\text{⊤}}\mathbf{W}\left(\mathbf{z}-\mathbf{A}{\mathit{a}}^{(s+1)}\right).$$ (2.12)

To update $\theta$, we minimize the function

$$\frac{\vartheta }{2}{\left({\theta }_{ik}-{\pi }_{ik}^{\left(s\right)}\right)}^2+\sum _{i<k}{p}_{\gamma }\left(\left|{\theta }_{ik}\right|,\lambda \right)$$

where ${\pi }_{ik}^{\left(s\right)}=a_i^{\left(s\right)}-a_k^{\left(s\right)}+{\vartheta }^{-1}{v}_{ik}^{\left(s\right)}$. It is worth noting that by using the concave penalties, the objective function $F(\mathit{a},\mathit{\beta },\mathit{\theta },\mathit{v})$ is no longer a convex function. However, it is convex with respect to each ${\theta }_{ik}$ when $\gamma >1/\vartheta +1$ for the SCAD penalty; consequently, given $(\mathit{a},\mathit{\beta },\mathit{v})$, the minimizer of $F(\mathit{a},\mathit{\beta },\mathit{\theta },\mathit{v})$ with respect to ${\theta }_{ik}$ is unique and has a closed-form solution as follows:

$${\theta }_{ik}^{(s+1)}=\left\{\begin{array}{ll}S\left({\pi }_{ik}^{\left(s\right)},\lambda /\vartheta \right)& \left|{\pi }_{ik}^{\left(s\right)}\right|\le \lambda +\lambda /\vartheta ,\\ \frac{S\left({\pi }_{ik}^{\left(s\right)},\gamma \lambda /\left(\right(\gamma -1\left)\vartheta \right)\right)}{1-1/\left(\right(\gamma -1\left)\vartheta \right)}& \lambda +\lambda /\vartheta <\left|{\pi }_{ik}^{\left(s\right)}\right|\le \lambda \gamma ,\\ {\pi }_{ik}^{\left(s\right)}& \left|{\pi }_{ik}^{\left(s\right)}\right|>\lambda \gamma ,\end{array}\right.$$ (2.13)

where $S(x,t)=x(1-t/|x|{)}_{+}$ is a groupwise soft thresholding operator. Finally, the Lagrange multiplier $v_{ik}$ is updated by (2.8). This process is conducted iteratively until the convergence over a grid of values for $\lambda$. The iterative algorithm terminates when primal residuals ${\mathbf{r}}_{\text{primal }}^{(s+1)}=\mathbf{\Delta }{\mathit{a}}^{(s+1)}-{\mathit{\theta }}^{(s+1)}$ and dual residuals ${\mathbf{r}}_{\text{dual }}^{(s+1)}=\vartheta {\mathbf{\Delta }}^{\text{⊤}}\left({\mathit{\theta }}^{(s+1)}-{\mathit{\theta }}^{\left(s\right)}\right)$ are close to zero, i.e., $∥{\mathbf{r}}_{\text{primal }}^{(s+1)}∥<{ϵ}_{\text{primal }}^{(s+1)}$ and $∥{\mathbf{r}}_{\text{dual }}^{(s+1)}∥<{ϵ}_{\text{dual }}^{(s+1)}$, where ${ϵ}_{\text{dual }}^{(s+1)}$ and ${ϵ}_{\text{primal }}^{(s+1)}$ are specified as suggested by Boyd et al.¹⁸ It is important to find appropriate initial values for the ADMM algorithm. In this paper, the initial values ${\mathit{a}}^{\left(0\right)}$ are obtained from the fixed effects Cox model, then we set ${\theta }_{ik}^{\left(0\right)}=a_i^{\left(0\right)}-a_k^{\left(0\right)}$ and ${\mathit{v}}^{\left(0\right)}=0$. If ${\hat{\theta }}_{ik}=0,a_i$ and $a_k$ are classified into the same group. As a result, we obtain $\hat{K}$ estimated groups ${\widehat{𝒢}}_1,\cdots ,{\widehat{𝒢}}_{\hat{K}}$, and set ${\alpha }_k$ to be the common value of $a_i$ ’s from the $k$ th group.

Due to the approximation in the computation, Equation (2.10) does not fully capture parameter information, and the iteration may also lead to a loss in efficiency. Once the groups have been identified, we conduct a refitting step to estimate $\mathit{a}$ and $\mathit{\beta }$ by maximizing the following log-partial likelihood with the grouped information:

$$\ell (\mathit{\alpha },\mathit{\beta })=\sum _{k=1}^{\widehat{K}}\sum _{i={\hat{G}}_k}\sum _{j=1}^{n_i}{\delta }_{ij}\left\{{\alpha }_k+{\mathbf{x}}_{ij}^{\text{⊤}}\mathit{\beta }-\text{log}\left[\sum _{i^{\prime }{j}^{\prime }\in R_{ij},i^{\prime }\in {\widehat{𝒢}}_k}\text{exp}\left({\alpha }_k+{\mathbf{x}}_{i^{\prime }{j}^{\prime }}^{\text{⊤}}\mathit{\beta }\right)\right]\right\},$$ (2.14)

where $\mathit{\alpha }={\left({\alpha }_1,\cdots ,{\alpha }_{\hat{K}}\right)}^{\text{⊤}}$, and ${\mathit{R}}_{ij}$ is the set of indices $i^{\prime }{j}^{\prime }$ with $y_{i^{\prime }{j}^{\prime }}\ge t_{ij}$ (those at risk at time $t_{ij}$). Here rather than the constraint ${\sum }_{i=1}^{\hat{K}}{\alpha }_k=0$ (as for $a_i$ in Section 2.1), we assume that ${\alpha }_{\hat{k}}=0$ to simplify the interpretation, where $\hat{k}=\text{arg}{\text{min}}_{k=1,\cdots ,\hat{K}}\left|{\alpha }_k\right|$. The above procedure can be conveniently implemented using R function coxph, which also provides standard errors and p-values of $\mathit{\alpha }$ and $\mathit{\beta }$.

After obtaining a path of solutions, it becomes essential to choose an optimal tuning parameter $\lambda$ by minimizing the modified Bayesian Information Criterion (BIC) using a grid search.²². The BIC is given by

$$\text{BIC}\left(\lambda \right)=-2\ell \left(\widehat{\mathit{a}}\right(\lambda ),\widehat{\mathit{\beta }}(\lambda \left)\right)+C_N\left(\widehat{K}\right(\lambda )+p)\text{log}N,$$

where $\stackrel{\mathit{ˆ}}{\mathit{a}}\left(\lambda \right),\widehat{\mathit{\beta }}\left(\lambda \right)$ and $\widehat{\mathit{K}}\left(\lambda \right)$ are the estimates of $\mathit{a},\mathit{\beta }$ and $K$ at given $\lambda$, respectively. $\ell \left(\stackrel{\mathit{ˆ}}{\mathit{a}}\right(\lambda ),\widehat{\mathit{\beta }}(\lambda \left)\right)$ is the log-partial likelihood evaluated at $\stackrel{\mathit{ˆ}}{\mathit{a}}\left(\lambda \right)$ and $\stackrel{\mathit{ˆ}}{\mathit{\beta }}\left(\lambda \right),$ $p$ is the dimension of the parameter $\mathit{\beta }$, and $C_N$ is a positive number depending on the total number of observations $N={\sum }_{i=1}^m{n}_i$. If $C_N=1$, the modified BIC reduces to the traditional BIC²³ Following Wang et al^{22, $C_N=\text{log}(\text{log}(N+p\left)\right)$}.

We summarize our method in Algorithm 1 below.

Algorithm 1 ADMM algorithm for healthcare center clustering

Require: Initialize ${\mathit{\theta }}^{\left(0\right)}$ and ${\mathit{v}}^{\left(0\right)}$.

for s = 0,1,2,⋯do

Compute ${\mathit{a}}^{(s+1)}$ using (2.11)

Compute ${\mathit{\beta }}^{(s+1)}$ using (2.12)

Compute ${\mathit{\theta }}^{(s+1)}$ using (2.13)

Compute ${\mathit{v}}^{(s+1)}$ using (2.8)

if the convergence criterion is met, then

Stop and denote the last iteration by $\left(\widehat{\mathit{a}}\right(\lambda ),\widehat{\mathit{\beta }}(\lambda \left)\right)$,

else

s = s + 1.

end if

end for

After identifying the groups, estimate $(\widehat{\mathit{\alpha }},\widehat{\mathit{\beta }})$ using (2.14).

Ensure: Output

3 |. SIMULATION

In this section, we evaluate the finite sample performance of the proposed methods through simulation studies. Conventionally, in Model (2.1), the healthcare center effect $a_i$ is treated as either a random effect or a fixed effect. We compare our fused effects model with SCAD penalty (SCAD) to the random effects model (RE) and fixed effects model (FE). Specifically, we examine the efficiency of estimation and the accuracy of healthcare center classification. We consider two different numbers of centers, $m=50$ and 100, and obtain all simulation results via 100 replicates.

Example 1. To assess the relative performance of different models, we mimic the censoring rate observed in the real-life application of kidney transplant centers in Section 4. We assume that among the $m$ center effects $a_i$ ’s, 10% are set to - 1, representing healthcare centers performing “better than expected,” 10% are set to 1, indicating centers performing “worse than expected,” and the remaining 80% are set to 0, representing centers performing “as expected.” The survival time is generated from the Weibull distribution with scale and shape parameters of 2 and 3, respectively. The censoring time is generated from a uniform distribution $U\left(\mathrm{0,1}\right)$ to achieve approximately a 70% censoring rate, which is close to the real data. The covariates $x_{ij}={\left(x_{i1},x_{i2}\right)}^{\text{⊤}}$ are generated from the multivariate normal distribution with mean 0, variance 1 and an exchangeable correlation $\rho =0.2$. The coefficient $\mathit{\beta }=(\mathrm{2,2}{)}^{\text{⊤}}$. We consider the number of patients in each center $n_i$ ~ Uniform (50,100).

The Rand Index (RI)²⁴ is employed to assess the level of agreement between the estimated partitions and the true partitions. Each pair of observations $a_i$ and $a_k$ falls to one of four categories: (i) true positive (TP) where $a_i$ and $a_k$ from the same group are assigned to the same cluster; (ii) true negative (TN) where $a_i$ and $a_k$ from different groups are assigned to different clusters; (iii) false negative (FN) where $a_i$ and $a_k$ from different groups are assigned to the same cluster; (iv) false positive (FP) where $a_i$ and $a_k$ from the same group are assigned to different clusters. The Rand Index is given by

$$\text{RI}=\frac{\text{TP}+\text{TN}}{\text{TP}+\text{FP}+\text{TN}+\text{FN}}=\frac{\text{TP}+\text{TN}}{\left(\begin{array}{l}\text{N}\\ 2\end{array}\right)}.$$

Intuitively, TP and TN represent agreement between the true group and the estimated cluster, while FP and FN indicate disagreement between the true group and the estimated cluster. RI ranges from 0 to 1, with a larger value indicating a higher degree of agreement.

The top panel of Table 1 presents the mean, median, and standard deviation (SD) of the estimated number of groups $\widehat{K}$, the percentage of $\hat{K}$ equal to the true number of groups (per), and the RI for evaluating the classification accuracy. As expected, the RI and the percentages of correctly classifying centers in comparison to the reference are very close to 1 and improve as $m$ increases. To visually display the distribution of $\widehat{K}$, the histograms of $\widehat{K}$ are depicted in Figure 1

TABLE 1.

The mean, median, and standard deviation (SD) of $\widehat{K}$, the percentage (per) of $\widehat{K}$ equal to the true number of subgroups, and the Rand Index (RI) value by our method with $m=\mathrm{50,100}$ in Examples 1 to 3, respectively.

	m	mean	median	SD	per	RI
Example 1	50	3.08	3.00	0.339	0.91	0.960
	100	3.05	3.00	0.261	0.93	0.969
Example 2	50	8.23	8.00	1.362
	100	9.43	9.00	1.653
Example 3	50	4.06	4.00	0.343	0.91	0.963
	100	4.04	4.00	0.281	0.92	0.970

FIGURE 1.

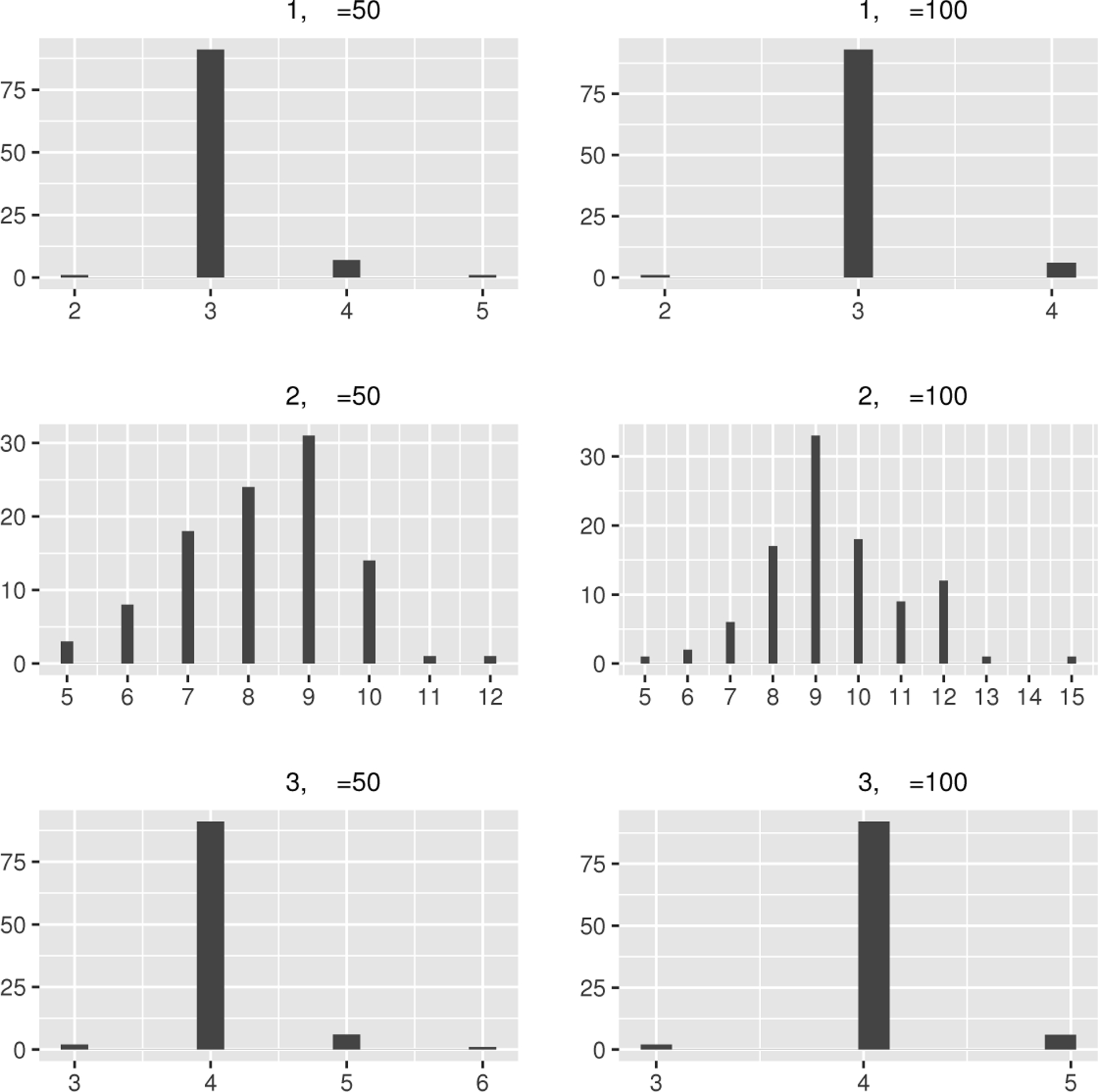
The histograms of $\widehat{K}$ in Example 1–3.

Let ${\widehat{\alpha }}_1,{\widehat{\alpha }}_2$ and ${\widehat{\alpha }}_3$ be the average estimates of center effects from “better than expected”, “as expected”, and “worse than expected” groups, with true values being −1,0 and 1, respectively. The top panel of Table 2 presents the bias, the standard deviation (SD), the standard error (SE), and the coverage probability of 95% confidence intervals (CP) of the estimators ${\widehat{\alpha }}_1$ and ${\widehat{\alpha }}_3$. The estimator ${\widehat{\alpha }}_2$ serves as a reference, such as the national norm. The Oracle estimators are obtained with a priori knowledge of the true grouping information. As not all replications are clustered into three groups by SCAD, we only use the replications with the estimated number of groups equal to three to compute the bias, SD, SE, and CP of ${\widehat{\alpha }}_1$ and ${\widehat{\alpha }}_3$. For the Oracle, the measures are calculated based on all 100 replications. From Table 2. We notice that our method performs very closely to the Oracle, as it can accurately recover the group structure. Evidently, our estimators ${\widehat{\alpha }}_1$ and ${\widehat{\alpha }}_3$ align well with the corresponding true values on average for all cases. The inference is also adequately precise, with a strong correspondence between SD and SE, and the coverage probabilities are near the nominal level of 0.95. All the original estimates of ${\alpha }_1,{\alpha }_2$, and ${\alpha }_3$ without the refitting step are reported in Table S1 of the supplementary material.

TABLE 2.

The bias, standard deviation (SD), standard error (SE), and the coverage probability of 95% confidence intervals (CP) of the estimators in Example 1 and Example 3.

			m=50				m=100
	m	Method	Bias	SD	SE	CP	Bias	SD	SE	CP
Example 1	${\widehat{\alpha }}_1$	SCAD	0.014	0.090	0.113	98.9	0.008	0.070	0.078	97.8
		Oracle	0.009	0.094	0.105	96.0	0.018	0.078	0.074	94.0
	${\widehat{\alpha }}_3$	SCAD	0.028	0.094	0.086	91.5	0.010	0.055	0.061	97.8
		Oracle	0.006	0.094	0.084	92.0	0.006	0.055	0.060	98.0
Example 3	${\widehat{\alpha }}_1$	SCAD	0.009	0.086	0.087	93.4	0.004	0.063	0.062	97.4
		Oracle	0.004	0.082	0.087	95.0	0.002	0.061	0.062	98.0
	${\widehat{\alpha }}_3$	SCAD	0.005	0.069	0.089	97.8	0.019	0.058	0.062	94.8
		Oracle	0.004	0.084	0.086	96.0	0.004	0.059	0.061	94.0
	${\widehat{\alpha }}_4$	SCAD	0.006	0.088	0.085	92.3	0.008	0.057	0.060	93.5
		Oracle	0.009	0.087	0.085	93.0	0.006	0.055	0.060	96.0

We compute the mean squared error (MSE) of $\stackrel{\mathit{ˆ}}{\mathit{a}}$ using the formula ${\sum }_{i=1}^m{\left({\hat{a}}_i-a_i\right)}^2/m$ for each replicated dataset. The top panel of Table 3 presents the MSE of the estimator $\stackrel{\mathit{ˆ}}{\mathit{a}}$, the bias, the standard deviation (SD), the standard error (SE), and the coverage probability of 95% confidence intervals (CP) for the estimators ${\hat{\beta }}_1$ and ${\hat{\beta }}_2$. It is worth mentioning that, in contrast to Table 2, which only displays results for replications with an estimated group count of three, Table 3 includes results for all replicates, regardless of whether the estimated number of groups is three or not. The MSEs of $\stackrel{\mathit{ˆ}}{\mathit{a}}$ from our fused effects model are much smaller than those from the random effects and fixed effects models in all cases. As a result, our method not only accurately classifies centers but also obtains precise estimates of these centers. To graphically visualize the numerical results of Table 3, the boxplots of the MSE of $\stackrel{\mathit{ˆ}}{\mathit{a}}$ are depicted in Figure 2 For the estimators $\stackrel{\mathit{ˆ}}{\mathit{\beta }}$, our method and the random effects model exhibit satisfactory performance, while the fixed effects model yields larger bias.

TABLE 3.

The bias, standard deviation (SD), standard error (SE), and the coverage probability of 95% confidence intervals (CP) of the estimators in Examples 1 to 3.

			$\widehat{a}$	${\widehat{\beta }}_1$				${\widehat{\beta }}_2$
		Method	MSE	Bias	SD	SE	CP	Bias	SD	SE	CP
Example 1	50	SCAD	0.022	0.011	0.043	0.045	95.0	0.012	0.043	0.045	95.0
		FE	0.078	0.029	0.045	0.047	91.0	0.026	0.045	0.047	94.0
		RE	0.189	0.005	0.044	0.046	97.0	0.008	0.044	0.046	95.0
		Oracle	0.002	0.003	0.043	0.046	97.0	0.005	0.043	0.046	94.0
	100	SCAD	0.017	0.002	0.034	0.032	93.0	0.004	0.033	0.032	94.0
		FE	0.074	0.034	0.032	0.033	88.0	0.032	0.034	0.033	87.0
		RE	0.034	0.001	0.032	0.033	95.0	0.001	0.033	0.033	94.0
		Oracle	0.001	0.002	0.032	0.032	95.0	0.001	0.033	0.032	93.0
Example 2	50	SCAD	0.321	0.001	0.032	0.030	93.0	0.002	0.031	0.030	94.0
		FE	1.183	0.002	0.033	0.030	93.0	0.002	0.031	0.030	94.0
		RE	1.810	4e-4	0.032	0.030	94.0	0.003	0.031	0.030	94.0
	100	SCAD	0.242	0.002	0.019	0.021	97.0	0.002	0.022	0.021	93.0
		FE	1.080	0.001	0.020	0.021	98.0	0.003	0.022	0.021	93.0
		RE	0.060	0.001	0.019	0.021	98.0	0.001	0.022	0.021	93.0
Example 3	50	SCAD	0.016	0.004	0.047	0.046	94.0	0.007	0.044	0.046	97.0
		FE	0.079	0.031	0.046	0.047	90.0	0.027	0.045	0.047	92.0
		RE	0.847	0.003	0.045	0.046	96.0	0.006	0.044	0.046	96.0
		Oracle	0.003	9e-5	0.044	0.046	96.0	0.003	0.042	0.046	97.0
	100	SCAD	0.012	0.001	0.033	0.032	94.0	1e-4	0.032	0.032	92.0
		FE	0.077	0.035	0.032	0.033	88.0	0.034	0.033	0.032	89.0
		RE	0.039	0.003	0.032	0.033	94.0	0.001	0.033	0.033	92.0
		Oracle	0.001	0.003	0.032	0.032	94.0	0.002	0.033	0.032	92.0

FIGURE 2.

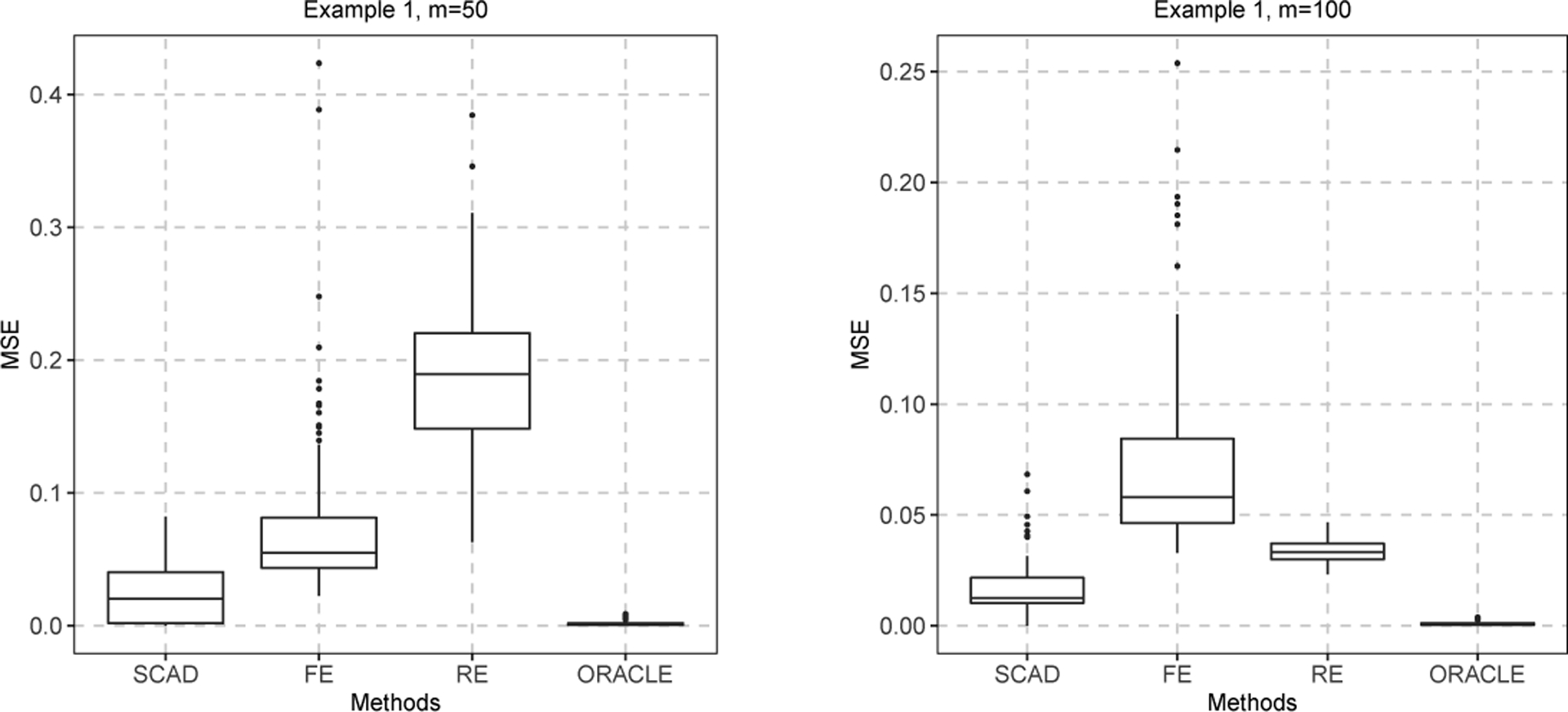
The boxplots of the MSE of $\stackrel{\mathit{ˆ}}{\mathit{a}}$ with $m=50$ and $m=100$ in Example 1.

Example 2. In this example, we generate the covariates $x_{ij}={\left(x_{i1},x_{i2}\right)}^{\text{⊤}}$ from the multivariate normal distribution with mean 0, variance 1, and an exchangeable correlation $\rho =0.2$. The survival time is generated from the Weibull distribution with scale and shape parameters being 2 and 3, respectively. The censoring time is generated from a uniform distribution $U\left(\mathrm{0,1}\right)$ to achieve about a 70% censoring rate. We set the coefficient $\mathit{\beta }=(\mathrm{0.1,0.1}{)}^{\text{⊤}}$, and the number of patients in each center $n_i$ ~ Uniform (50, 100). To demonstrate the robustness of our method, $a_i$ is simulated from the standard normal distribution $N\left(\mathrm{0,1}\right)$. Consequently, the random effects model is the correct model.

The grouping results of ${\widehat{a}}_i$ using our method are presented in the second panel of Table 1 The median of the estimated number of groups $\hat{K}$ is 8 with $m=50$ and 9 with $m=100$. The fusion penalty generally tends to select fewer groups for $m=50$ and more groups for $m=100$. As the number of parameters increases with $m$, the median and the standard deviation of $\widehat{K}$ also grow. To graphically visualize the distribution of $\widehat{K}$, the histograms of $\widehat{K}$ are shown in Figure 1

The second panel of Table 3 presents the mean squared error (MSE) of the estimator $\stackrel{\mathit{ˆ}}{\mathit{a}}$, the bias, the standard deviation (SD), the standard error (SE), and the coverage probability of 95% confidence intervals (CP) for the estimators ${\widehat{\beta }}_1$ and ${\widehat{\beta }}_2$. From Table 3. we observe that the MSE values of $\stackrel{\mathit{ˆ}}{\mathit{a}}$ using our method are smaller than those in the fixed effects model. Moreover, our method outperforms the random effects model when the number of centers is small $(m=50)$, likely due to the shrinkage of the predicted values of $a_i$ ’s in the random effects model. As the number of centers increases, the random effects model performs the best, but our method’s performance is only slightly worse than the random effects model and still much better than the fixed effects model. All methods exhibit similar performance in estimating ${\widehat{\beta }}_1$ and ${\widehat{\beta }}_2$.

Example 3. In this example, we evaluate the performance of the proposed model with four groups. The covariates $x_{ij},\mathit{\beta },n_i,h_0\left(t\right)$, and the censoring time are generated from the same distributions as in Example 1. We assume that among the $m$ center effects $a_i$ ’s, 10% are set to 1 and 10% are set to 2, indicating centers performing at different levels of “worse than expected”; 20% are set to −1.5, signifying centers performing “better than expected”; the remaining 60% are set to 0, indicating centers performing “as expected”.

The grouping results of ${\hat{a}}_i$ using our method are presented in the bottom panel of Table 1, where the medians of $\hat{K}$ over the 100 replicates are 4, which is the true number of subgroups, and the mean values are very close to 4. Furthermore, the RI values and the percentage of correctly selecting the number of subgroups approach 1. Therefore, our methods perform well in cases with an even number of groups. To graphically visualize the distribution of $\widehat{K}$, the histograms of $\widehat{K}$ are shown in Figure 1.

Let ${\widehat{\alpha }}_1,{\widehat{\alpha }}_2,{\widehat{\alpha }}_3$, and ${\widehat{\alpha }}_4$ be the average estimates for the $a_i$ ’s from four groups where the true values are −1.5,0,1, and 2, respectively. The bottom panel of Table 2 presents the bias, the standard deviation (SD), the standard error (SE), and the coverage probability of 95% confidence intervals (CP) for the estimators ${\widehat{\alpha }}_1,{\widehat{\alpha }}_3$, and ${\widehat{\alpha }}_4$. The estimator ${\widehat{\alpha }}_2$, which has the smallest absolute value, is set as the reference. From the bottom panel of Table 2. we can see that the means of ${\widehat{\alpha }}_1,{\widehat{\alpha }}_3$, and ${\widehat{\alpha }}_4$ are close to the true values and the Oracle estimators. We also observe that the SDs of ${\widehat{\alpha }}_1,{\widehat{\alpha }}_3$, and ${\widehat{\alpha }}_4$ are close to the corresponding SEs, resulting in valid coverage probabilities.

The bottom panel of Table 3 reports the MSE of the estimator $\stackrel{\mathit{ˆ}}{\mathit{a}}$, the bias, the standard deviation (SD), the standard error (SE), and the coverage probability of 95% confidence intervals (CP) for the estimators ${\hat{\beta }}_1$ and ${\hat{\beta }}_2$. From the bottom panel of Table 3 we observe that the MSE values of $\hat{a}$ using SCAD are smaller than those of the random effects and fixed effects models. For the estimators $\widehat{\mathit{\beta }}$, our method and the random effects model exhibit satisfactory performance, while the fixed effects model produces larger bias. These results indicate that the proposed method performs well with an even number of groups.

4 ।. APPLICATION

To demonstrate the proposed methods, we conduct an evaluation of kidney transplant centers using the national kidney transplant registry data obtained from the U.S. Organ Procurement and Transplantation Network (https://optn.transplant.hrsa.gov/data/). We limit the study cohort to adult kidney transplant recipients (age ≥ 18) who received a transplant between January 1, 2007, and December 31, 2007. The analysis cohort includes 4198 patients from 60 centers, with the number of patients per center ranging from 50 to 100. In our dataset, out of 4198 patients who received their kidney transplant in 2007, 1137 (27.1%) either died or experienced graft failure within five years after receiving a kidney transplant. All others were censored at five years of follow-up. In our survival analysis, the failure time (termed “graft survival”) $t_{ij}$ is defined as the duration (in years) from transplantation to graft failure or death, whichever occurred first. The censoring time $c_{ij}$ is at the end of the five-year period after the transplantation. Thus, the observed time to event is $y_{ij}=\text{min}\left(t_{ij},c_{ij}\right)$, with a 72.9% censoring rate. We apply our method to investigate the risk factors of five-year graft survival using Cox’s proportional hazards model and assess the performance of centers concerning their graft outcomes.

The study cohort included 15 baseline characteristics of donors and recipients. The characteristics of the study population are as follows: Time on end-stage renal disease (ESRD, reference: <1 years), donor age (reference: 30–45 years old), donor gender (male = 1, female=0), donor body mass index (BMI, reference: normal), donor race (reference: white), donor history of hypertension (DON-HTN, yes=1, no=0), donor meeting expanded criteria (DON-EC, yes=1, no=0), recipient gender (male = 1, female=0), recipient race (reference: white), recipient insulin dependent diabetes (REC-DIAB Type I, yes=1, no=0), recipient non-insulin dependent diabetes (REC-DIAB Type II, yes=1, no=0), recipient age at transplant (REC-AGE, reference: 50–60), recipient body mass index (reference: normal), recipient previous kidney transplant (REC-PREV-KI, yes=1, no=0), recipient total cold ischemia time (REC-COLD-ISCH, > 20 hours = 1,< 20 hours =0).

We use the Akaike Information Criteria (AIC) to assess the performance of three methods. A smaller value of AIC indicates better performance. When treating the center effect $a_i$ as a random intercept, we obtain an AIC of 18501.43. For the fixed effects model, the AIC value is 18535.64. If $a_i$ is estimated by our fused effects model, the 60 centers are classified into 3 groups with an AIC of 18451.24. Our method leads to a significant improvement in model fitting.

Table 4 reports the estimate (Est.), standard error (SE), and p-value of $\stackrel{\mathit{ˆ}}{\mathit{\beta }}$ for testing the significance of the coefficients by our fused effects model with the SCAD penalty (SCAD), the fixed effects model (FE) and the random effects model (RE). Longer time spent in end-stage renal disease, donor age over 60, black donor, donor history of hypertension, black recipient, recipient aged 60 or older at transplant, recipient with non-insulin dependent diabetes, and donor with low body mass index all have a significantly worse effect on five-year graft survival according to all three methods, with p-values less than 0.05. Asian recipients, on the other hand, tended to experience better survival outcomes.

TABLE 4.

The estimates (Est.), standard error (SE), and P-value of $\widehat{\mathit{\beta }}$ in the national kidney transplant study.

Variable	Fused			FE			RE
	Est	SE	P-value	Est	SE	P-value	Est	SE	P-value
Time on ESRD
< 1 years	Ref
1–5 years	0.093	0.041	0.022	0.100	0.041	0.015	0.086	0.041	0.035
> 5 years	0.150	0.040	0.000	0.142	0.042	0.001	0.143	0.041	0.001
Donor age
< 15	−0.063	0.044	0.149	−0.073	0.044	0.098	−0.069	0.044	0.114
15–30	−0.066	0.042	0.113	−0.067	0.042	0.112	−0.075	0.042	0.073
30–45	Ref
45–60	0.073	0.040	0.068	0.076	0.040	0.061	0.075	0.040	0.062
> 60	0.113	0.043	0.009	0.115	0.044	0.009	0.114	0.043	0.009
Donor race
White	Ref
Black	0.066	0.028	0.021	0.072	0.029	0.015	0.071	0.029	0.013
Asian	0.001	0.030	0.987	0.004	0.031	0.908	0.001	0.030	0.969
DON-HTN	0.090	0.035	0.011	0.088	0.036	0.014	0.087	0.035	0.014
DON-EC	−0.003	0.045	0.953	−0.002	0.046	0.973	−0.003	0.046	0.947
Recipient gender	0.048	0.030	0.115	0.053	0.031	0.086	0.053	0.031	0.083
Recipient race
White	Ref
Black	0.079	0.030	0.009	0.090	0.034	0.008	0.091	0.032	0.004
Asian	−0.100	0.037	0.007	−0.105	0.038	0.005	−0.099	0.037	0.008
Recipient BMI
Normal	Ref
Under	0.054	0.029	0.068	0.050	0.030	0.093	0.054	0.030	0.070
Over	0.005	0.037	0.896	0.003	0.038	0.934	−0.001	0.037	0.971
Obesity	0.026	0.037	0.484	0.024	0.038	0.530	0.027	0.037	0.472
REC-PREV-KI	0.046	0.030	0.127	0.038	0.031	0.220	0.053	0.030	0.084
REC-COLD-ISCH	0.006	0.030	0.837	−0.004	0.033	0.895	0.014	0.031	0.662
REC-AGE
18–35	0.050	0.034	0.150	0.055	0.035	0.116	0.045	0.035	0.189
35–50	−0.029	0.038	0.439	−0.025	0.039	0.520	−0.029	0.038	0.449
50–60	Ref
60–70	0.112	0.034	0.001	0.110	0.035	0.001	0.114	0.034	0.001
> 70	0.082	0.030	0.006	0.081	0.030	0.007	0.095	0.030	0.001
REC-DIAB
Type I	0.056	0.029	0.054	0.061	0.030	0.042	0.057	0.030	0.055
Type II	0.075	0.030	0.012	0.071	0.031	0.021	0.075	0.030	0.014
Donor gender	0.005	0.030	0.872	0.007	0.030	0.818	0.005	0.030	0.863
Donor BMI
Normal	Ref
Under	0.104	0.037	0.005	0.108	0.037	0.004	0.103	0.037	0.005
Over	0.037	0.035	0.292	0.036	0.035	0.300	0.034	0.035	0.329
Obesity	−0.008	0.035	0.815	−0.009	0.035	0.798	−0.003	0.035	0.927

Next we utilize the standardized mortality ratio (SMR) as an evaluation measure to assess center-specific survival, defined as the ratio of the observed number of deaths at a given center to the number expected if the center had mortality equal to the population average^25,4. An SMR greater or smaller than 1 indicates that the center’s observed mortality ratio is under-performing or over-performing relative to the population norm, respectively. Let ${\widehat{\alpha }}_k$ be the common value of estimators ${\widehat{a}}_i$ ’s in group $\widehat{{𝒢}_k}$ with $k=\mathrm{1,2},3$. Table 5 reports the estimates ${\widehat{\alpha }}_1$ and ${\widehat{\alpha }}_3$ relative to a reference ${\widehat{\alpha }}_2$ and the number of elements (num.) in each group, standard error (SE), p-value and SMR by our fused effects method. We identify 75.0% (45) of centers as the reference, 10.0% (6) of centers better than the reference and 15.0% (9) of centers worse than the reference. The estimated SMR of better and worse centers are 0.574 and 1.636, respectively.

TABLE 5.

Results of ${\widehat{\alpha }}_i$ in the national kidney transplant study.

	${\widehat{\alpha }}_1$	${\widehat{\alpha }}_2$	${\widehat{\alpha }}_3$
Est	−0.556	ref	0.492
num	6	45	9
SE	0.129	ref	0.073
P-value	<0.001	ref	<0.001
SMR	0.574	1.000	1.636

In our national kidney transplant dataset, we only have a center-specific factor - the numbers of patients within a center (denoted by center size $n_i$). Since center-level confounder, e.g., $n_i$ is not identifiable with the center-specific effect $a_i$, we cannot include $n_i$ directly in our model. Along the lines of He et al.⁴, we instead fit the model $n_i=\beta {\hat{a}}_i+{ϵ}_i$, where ${\hat{a}}_i$ is the estimated center specific effect. The p-value is 0.915, suggesting a minimal correlation between the center-specific effects and the center size. This observation is further supported by the boxplots in Figure 3.

Figure 3.

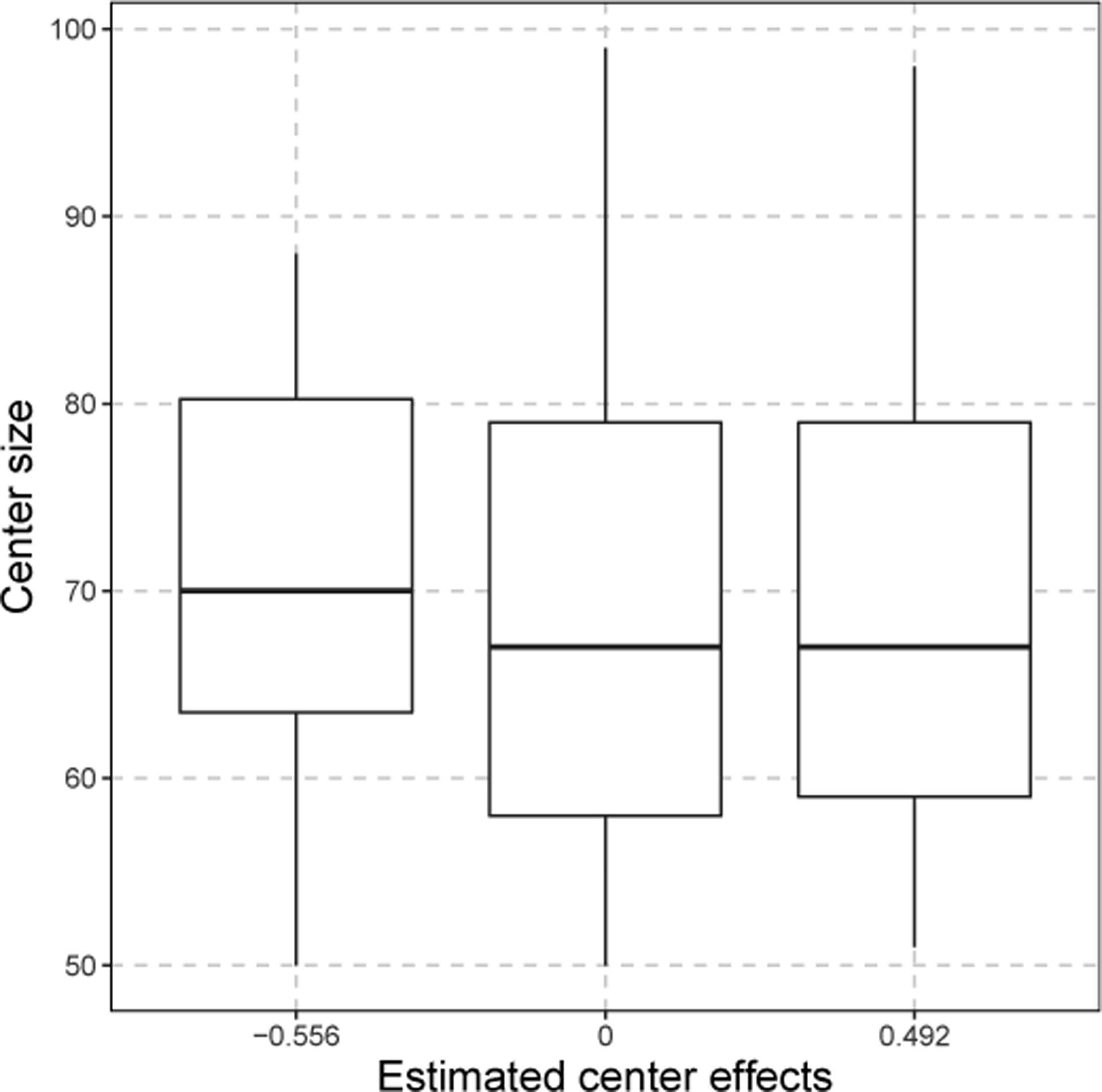
The boxplots of center size from three groups in the national kidney transplant study.

5 |. DISCUSSION

In this study, we proposed an innovative fusion method to assess healthcare centers concerning survival outcomes. Our method proves more efficient than the fixed effects model by using fewer parameters for healthcare centers. Additionally, it outperforms random effects models in identifying healthcare centers with better classification accuracy and lower bias. Through simulation studies, we demonstrated that our method surpasses existing approaches in performance. Our model can be thought as an alternative way to latent class models, as we use fusion penalty to classify different healthcare centers into latent subgroups.

There are several potential extensions for our method. First, when the number of centers is very large, fitting the pairwise fusion penalized Cox model directly becomes computationally demanding. In such cases, we could employ the divide-andconquer strategy²⁶, which typically involves dividing the full sample into multiple subsets, solving the optimization problem for each subset, and combining the subset-specific estimates into a single estimate. Second, our method can be applied to cluster regression coefficients in the Cox’s proportional hazards model when parameters are partially heterogeneous across subgroups. For instance, grouping treatment heterogeneity can enable the provision of precise medical treatments to diverse patient subgroups^27.17.

Finally, it is of interest to consider more sophisticated hierarchical data, e.g., patients clustered within practitioners which are clustered within practices. For this case, a three-level Cox’s proportional hazards model with two fusion effects can be proposed. Let $x_{ijk}$ denote the covariates for patient $k$ nested within doctor $j$ in center $i$, the three-level Cox model can be written as

$$h_{ijk}\left(t\mid {\mathbf{x}}_{ijk}\right)=h_0\left(t\right)\text{exp}\left(a_i+b_{ij}+{\mathbf{x}}_{ijk}^{\text{⊤}}\mathit{\beta }\right),$$

where $a_i$ is the center-specific effect, $b_{ij}$ is the practitioner-specific effect, $h_{ijk}\left(t\right)$ is the hazard for patient $k$ treated by practitioner $j$ in center $i$ at time $t$, and $h_0\left(t\right)$ is a baseline hazard function. We can cluster $a_i$ and $b_{ij}$ by using two fusion penalties. Estimation and inference of this model is of future interest.

DATA AVAILABILITY STATEMENT

Restrictions apply to the availability of these data, which were used under license for this study.