Abstract
Accurate characterization of electrostatic interactions is crucial in molecular simulation. Various methods and programs have been developed to obtain electrostatic parameters for additive or polarizable models to replicate electrostatic properties obtained from experimental measurements or theoretical calculations. Electrostatic potentials (ESPs), a set of physically well-defined observables from quantum mechanical (QM) calculations, are well suited for optimization efforts due to the ease of collecting a large amount of conformation-dependent data. However, a reliable set of QM ESP computed at an appropriate level of theory and atomic basis set is necessary. In addition, despite the recent development of the PyRESP program for electrostatic parameterizations of induced dipole-polarizable models, the time-consuming and error-prone input file preparation process has limited the widespread use of these protocols. This work aims to comprehensively evaluate the quality of QM ESPs derived by eight methods, including wave function methods such as Hartree–Fock (HF), second-order Møller–Plesset (MP2), and coupled cluster-singles and doubles (CCSD), as well as five hybrid density functional theory (DFT) methods, used in conjunction with 13 different basis sets. The highest theory levels CCSD/aug-cc-pV5Z (a5z) and MP2/aug-cc-pV5Z (a5z) were selected as benchmark data over two homemade data sets. The results show that the hybrid DFT method, ωB97X-D, combined with the aug-cc-pVTZ (a3z) basis set, performs well in reproducing ESPs while taking both accuracy and efficiency into consideration. Moreover, a flexible and user-friendly program called PyRESP_GEN was developed to streamline input file preparation. The restraining strengths, along with strategies for polarizable Gaussian multipole (pGM) model parameterizations, were also optimized. These findings and the program presented in this work facilitate the development and application of induced dipole-polarizable models, such as pGM models, for molecular simulations of both chemical and biological significance.
Graphical Abstract
1. INTRODUCTION
The accurate description of electrostatic interactions is crucial for molecular simulations across various fields, including physical, chemical, and complex biological systems.1–4 In classical force fields (FFs), electrostatic interactions are typically represented by fixed partial charges to achieve a balance between efficiency and accuracy, ignoring higher-order multipole effects.5 Despite the limitations of partial charge derivation in systems containing lone-pairs, σ-holes, and π clouds, this remains an active field of research.6–8 Approaches for partial charge derivation can be broadly divided into two categories9 based on how the reference properties are estimated: the first class utilizes experimental data or nonquantum mechanical approaches,10,11 while the second class relies on quantum mechanical (QM) estimation, such as the partition of the electron charge density or wave functions,12–19 that reproduces charge-dependent properties,20–22 interaction energies,23,24 and electrostatic potentials (ESPs).25–27
Different from partitioning electron densities that may incur the ambiguous depiction of molecular dipoles or higher-order moments, methods based on fitting ESPs are physically well-defined since ESP at a certain point is a QM observable and can be calculated readily. As a consequence, fitting ESPs has been selected as the fundamental approach for the development of assisted model building with energy refinement (AMBER) family force fields.28 Although many successes have been achieved, several deficiencies have been observed during their applications, such as ill-defined charges of buried atoms, conformational dependencies, and limited transferability.29–31 To remedy these deficiencies, a restraining term was introduced in the least-squares fitting procedure to achieve more physically reasonable partial charges, particularly for the buried atoms; thus, this approach was later named the restrained electrostatic potential (RESP) method.30,31 Since then, the RESP program has been implemented in AMBER as part of the Antechamber32 program as well as programs developed by others7,33,34 and has been widely applied in the derivation of atomic partial charges,28,35–42 making the strategy highly extendable to cover a broad range of organic compounds and other molecules.
Although the simplicity and efficiency of ESP-based protocols made AMBER force fields popular in biomolecular simulations,43 extensible, and accessible to the broad community, such simple point charge additive force fields could not effectively capture the redistribution of atomic electron density susceptible to the changes of surrounding environments. This drawback mainly comes from the absence of a polarization effect by surrounding molecules and omission of the higher-order multipoles. Consequently, many force fields have been proposed to include higher-order multipoles,9,44,45 such as induced dipoles,46 and by using multipole moment expansion.44,47 Among the induced dipole models, AMOEBA48 and polarizable Gaussian multipole model (pGM)49–51 are two of the models that can reproduce the nonadditive contributions of the electrostatic interactions. A notable difference between pGM and other polarizable methods is that all short-range electrostatic interactions in pGM are handled in a consistent manner where charges and dipoles are represented by s-orbital and p-orbital functions, respectively. Use of Gaussian functions facilitates the screening of short-range interactions, and the notorious “polarization catastrophe” can be avoided automatically. Similar to the work of Elking et al. in their development of Gaussian multipole model (GMM),50 the purpose of pGM is not to represent density but rather to represent the effective ESP near the molecule using Hermite–Gaussian moments. The advantage of the pGM approach is that one can potentially use a minimalist model to implicitly consider some of the higher-order effects, avoiding a large number of terms. In comparison, a density-based approach was utilized in the development of Gaussian electrostatic model (GEM)52 that necessitates the inclusion of nuclear charges. Moreover, buried atoms often exhibit a high degree of uncertainty in charge fitting largely due to the lack of sensitivity of the ESP to their charges.30,31,53 In pGM, however, their contributions to ESP are represented both directly in the form of charges and permanent multipoles and indirectly via short-range induction. Because pGM allows induction between bonded atoms, the ESP can be sensitive to the charges and multipoles of the buried atoms, partially alleviating the “buried atom” problem.
Recently, the accuracy and robustness of pGM models have been evaluated for a range of molecular properties, including interaction energies,6 many-body interaction energies with nonadditive and additive contributions,6 polarizability anisotropy,54 and critically, transferability.55 The simulation infrastructure for pGM is also implemented into the SANDER program and is being ported to PMEMD for parallel and GPU platforms.56–58 A program, PyRESP,7 has been developed for electrostatic parameterization that extends the RESP approach to accommodate both permanent and induced atomic dipoles and has been integrated into the AmberTools package.59 However, the process of generating input files for the program can be tedious and error-prone. The challenge is exacerbated by the inclusion of both permanent and induced dipoles, hindering the widespread application of these methods. Therefore, there is a pressing need for the development of a program that can automatically generate input files for pGM models. Poltype 2 is a similar effort for AMOEBA to automate the parameterization of small molecules for torsion, van der Waals (vdW), atomic multipoles, and formal charges.60
In all of these developments, an efficient QM method that is capable of producing reliable and accurate ESP is a prerequisite. Given the wide range of quantum mechanical methods, a systematic assessment of the accuracy of quantum mechanically calculated ESPs and the methods used to fit charges to these ESPs is needed. In this work, we conduct a comprehensive evaluation of ESPs derived from popular DFT methods, HF theory, second-order Møller–Plesset (MP2), and the coupled cluster-singles and doubles (CCSD) methods, along with different basis sets. We also introduce PyRESP_GEN, a program designed to generate appropriate inputs for charge and dipole fitting programs, complementing the existing programs in Amber (e.g., Antechamber and PyRESP). Different from Poltype 2 mentioned above, PyRESP_GEN only provides input files and all of the electrostatic parameterizations and fitting were done with PyRESP. In addition, we optimized restraint weights and fitting strategies. The PyRESP_GEN program aims to alleviate the burden of tedious input file preparation for researchers, allowing them to focus on more significant aspects such as drug discovery strategies and high-throughput screening. We anticipate that the availability of this program will facilitate the use of pGM models in ESP parameterization, promoting further development and applications.
2. COMPUTATIONAL DETAILS
2.1. Data Set Collection.
A total of 35 small molecules were used in this work, ranging from water (H2O) to methylphosphonic acid (PO3CH5). These molecules were chosen both for their small sizes, which allow the QM calculations to be conducted at high-level (up to CCSD) ab initio methods with extensive basis sets, and for their representation of various biologically relevant building blocks. For example, both neutral (NH3) and charged (NH4+) ammonium were taken into consideration as ammonium can exhibit different charge states depending on the pH and its surrounding environment. In addition, short alkenes and alkanes (C2H4, C2H6, C3H8,C4H10) were included here to mimic the hydrophobic tails of lipid molecules and the side chain of a nonpolar amino acid. Dimethyl disulfide (CH3S2CH3) was included to represent the disulfide bond formed between two cysteine (Cys) residues. Some ringlike molecules, such as benzene (C6H6) and pyrrole (C4NH5), were also incorporated to resemble the side chains of amino or nucleic acids. Finally, N-methylacetamide (NMA) was included to represent the peptide bond. Based on their sizes, these 35 molecules were further classified into two subsets, namely, the SMALL SET (12 molecules) and the LARGE SET (23 molecules). The chemical structures and formulas of all of the molecules are presented in Figure 1, with polar, nonpolar, and charged species shaded in blue, gray, and red, respectively.
Figure 1.
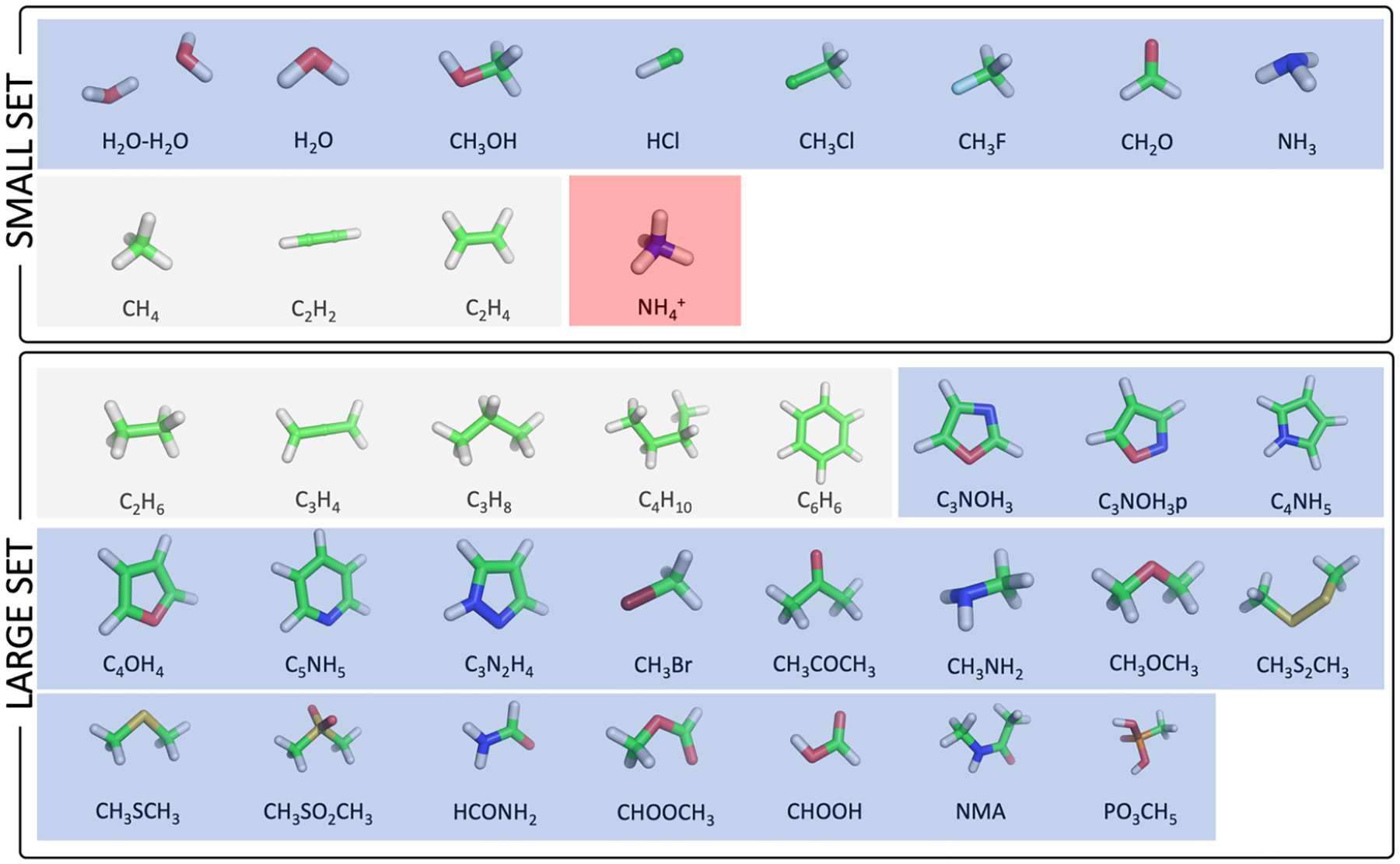
Molecules utilized in this work. The sets of SMALL and LARGE molecules are shown in the upper and lower panels, respectively. For each molecule, the chemical structure together with its corresponding chemical formula is shown. The charged molecule is shaded in red; polar and nonpolar species are in blue and gray, respectively.
2.2. QM Theory Levels.
In this study, we evaluated eight QM methods, namely, Hartree–Fock (HF),61,62 Becke three-parameter exchange and Lee–Yang–Parr correlation (B3LYP),63,64 MN15,65 M06,66 M06–2X,66 second-order Møller–Plesset (MP2),67–70 ωB97X-D,71 and coupled cluster-singles and doubles (CCSD),72–74 combined with 13 different basis sets (specifically, 3–21G (321g), 3–21+G (321pg), 6–31G* (631g), 6–31++G** (631gss), 6–311++G** (6311g), cc-pVDZ (2z), aug-cc-pVDZ (a2z), cc-pVTZ (3z), aug-cc-pVTZ (a3z), cc-pVQZ (4z), aug-cc-pVQZ (a4z), cc-pV5Z (5z), and aug-cc-pV5Z (a5z)). The ESP points were defined according to the Merz–Singh–Kollman scheme26,75 with 6 points per square angstrom and four layers separated by 0.2 Å from each other. All structures were optimized at the MP2 theory level by using 6–311++G** basis sets. All QM computations were conducted using Gaussian 16.76
2.3. ESPs Derived by RESP and pGM Models.
Both the RESP and pGM methods are ESP-based frameworks that aim to reproduce the electrostatic properties calculated at a given QM level. The RESP framework represents molecular ESP by point charges obtained from RESP-fitting. Although pGM models allow any order of multipoles, only zeroth-order (charge) and first-order (dipole) multipoles are implemented in this work. Two pGM variants are implemented. One is the induced dipole model that represents the dipole field by the induced dipoles (μ) only and the other includes both permanent (p) and induced dipoles (μ). These two variants are termed pGM-ind and pGM-perm, respectively, for clarity. The permanent dipole in the pGM-perm model is represented using covalent basis vectors (CBVs).56 The main differences between these methods are the objective functions defined in the least-squares fitting procedure and the estimation of electrostatic potentials at a given point. The objective functions can be written as follows
| (1) |
Here, χ2 denotes the objective function for the whole system, while is the sum of the squared residual for electrostatic potentials, and and are penalties associated with charges and permanent dipoles, respectively. The least-squares fitting for electrostatic potentials is defined as follows
| (2) |
where Vi is the ESP at point i calculated from QM, and is the one calculated from , , and .
In the RESP model, the ESP arises solely from the permanent point charges.31 Therefore, only the first two terms of eq 1, namely, and , are utilized. The electrostatic potential at point i is a sum of contributions from all atoms qj, as defined below where rij is the corresponding distance between point i and atom j
| (3) |
A hyperbolic penalty function was used in the charge fitting30,31 that restrains the charges to small values
| (4) |
where aq represents the restraining strength, bq denotes the “tightness” of the hyperbola and is set to 0.1 in both RESP and PyRESP programs, and qi is the fitted charge at the atomic center i.
However, in the pGM-ind and pGM-perm models, the ESP arises not only from charges but also from induced and permanent dipoles.7,49,56 As a consequence, penalties for both charges (χrstr,q) and permanent (χrstr,p) dipoles are added to the total penalty functions. The induced dipoles can be calculated as
| (5) |
Here, Ei is the electrostatic field generated by all charges and permanent dipoles at position i, αi represents the isotropic polarizability of ith atom, and Tij denotes the dipole–dipole interaction tensor with the following form
| (6) |
where f t and fe are the distance-dependent screening factors,33,77 I is the identity matrix, and x, y, and z are the Cartesian components of the distance vector formed between atoms i and j.
In the pGM-perm model, a hyperbolic penalty function for permanent dipoles is applied to force the dipoles to have small values
| (7) |
In this work, we evaluated the performance of ESPs derived by the RESP method, pGM-ind, and pGM-perm models. In RESP fitting, a two-stage protocol has been a common practice.30,31 In the first stage, equivalence was imposed among chemically equivalent atoms (excluding hydrogen atoms of functional groups −CH2− and −CH3) along with a weak (wk.) hyperbolic restraining strength (aq set to 0.0005 a.u.; see eq 4). In the second stage, the charges obtained from the first stage were held constant, except for methyl (−CH3) and methylene (−CH2−) groups, which were refitted with stronger (st.) hyperbolic restraints (aq = 0.001 a.u.) applied to both hydrogen and carbon atoms while enforcing the equivalence of the methyl and methylene hydrogen atoms. This fitting protocol yielded charges that exhibited better transferability among related functional groups and were more consistent with chemical intuition while preserving the ability to reflect their variability due to local chemical environments.31
For the pGM-ind model, since charges are the only fitting variables, the protocol is identical to the one in RESP, except for the magnitude of the restraining strength. For the pGM-perm model, charges and permanent dipoles were restrained separately. Three strategies were proposed, and their performances were evaluated. In all strategies, the treatment of equivalence and restraining strength for charges are directly borrowed from the RESP protocol. In strategy I, the equivalence of permanent dipoles was enforced at the first stage except those pointing from H to C (H → C) and weak restraints were applied. In the second stage, permanent dipoles derived from the first stage were all fixed, except for those related to functional groups −CH2− and −CH3. In other words, in the second stage, equivalence and refitting were only applied to permanent dipoles H → C and C → H of function groups −CH2− and −CH3. In strategy II, equivalence was enforced in both the first and second stages to all permanent dipoles, including those of H → C and C → H within −CH2− and −CH3. In the second stage, charges and permanent dipoles derived in the first stage were fixed, except those of −CH2− and −CH3 that were then refitted with strong restraint in the second stage. In strategy III, equivalence of charges are enforced to atoms other than −CH2− and −CH3 hydrogens, and the permanent dipoles are equivalenced except those of H → C and C → H in −CH2− and −CH3 that are set to be free in the first stage. The equivalencing of these charges and permanent dipoles is enforced at the second stage, and strong restraints were used.
2.4. PyRESP_GEN Program.
PyRESP_GEN is a flexible and easy-to-use program tailored for preparing input files for the PyRESP program to fit charges for the RESP model or charges and induced/permanent dipoles for the pGM model. The program can be executed through the command line or via the Python application programming interface (API). In order to provide the maximum convenience to users, only an ESP data file generated by the espgen program from the Antechamber suite32 is required. By default, when no additional parameters are specified, the program automatically generates two input files for the first and second stages, respectively. The default restraining strengths for permanent point charges and dipoles are optimized in this work.
The workflow of PyRESP_GEN is presented in Algorithm 1. The primary task of the PyRESP_GEN program is to identify the set of equivalent atoms and bonds as well as classify those that belong to functional groups −CH2− and −CH3. This is accomplished through the following steps: (1) loading coordinates and atom types from the ESP file; (2) generating a distance matrix based on the coordinates; (3) applying a predetermined set of van der Waals radii for elements32 to determine the bonded atom list; (4) identifying functional groups −CH2− and −CH3; (5) cycling through all atoms to find equivalent atoms and bonds; and (6) printing output files according to specified parameters. A comprehensive guide to installation and usage is available at the following website: https://csu1505110121.github.io/tutorial/2023/02/16/pyresp_gen_tutorial.html.

2.5. Metrics for Difference Estimation and Performance Evaluation.
To measure the difference between ESPs derived from distinct QM methods and specific basis sets and evaluate the quality-of-fit to the QM ESPs, following previous work,7,25–27,31,75,78 the root-mean-square error (RMS) and relative root-mean-square (RRMS) errors are utilized in this work, respectively. Here, RMS is in the unit of a.u., while RRMS is dimensionless
| (8) |
| (9) |
When the difference between two different QM methods or basis sets is estimated, Vj and are both QM ESPs at point j derived from these two methods or basis sets, respectively. Superscript ref denotes one of the methods treated as the reference one. For estimating the difference between QM and fitted ESPs, Vj and denote the ESP at point j derived from the fitted and QM methods, respectively. m is the total number of ESP points. The average differences between the QM and fitted dipole and quadrupole moments are
| (10) |
| (11) |
where and μi denote the QM and fitted dipole moments, respectively, and and Qi,m denote component m (m = xx, yy, zz) of the QM and fitted quadrupole moments, respectively, of molecule i. The dipole moment and quadrupole moment are in the units of Debye and Debye angstrom, respectively.
3. RESULTS AND DISCUSSION
3.1. Basis Set Convergence.
Basis set convergence is a well-known issue when estimating molecular properties, such as polarizabilities, charges, and dipole moments.79,80 To assess the impact of basis sets on the accuracy of ESPs, we compared 13 basis sets using eight QM methods. In these comparisons, the CCSD/aug-cc-pV5Z (a5z) and MP2/aug-cc-pV5Z (a5z) were treated as reference methods for the SMALL and LARGE sets of molecules, respectively (as shown in Figure 1, and the detailed data is presented in the Supporting Information).
It is clear that when the basis set size increased from 3–21G (321g) to aug-cc-pV5Z (a5z), the difference among various methods decreased initially and then converged. For example, in the case of the HF method, the average relative RMS difference in the SMALL set initially dropped to 7.51% for aug-cc-pVTZ (a3z) but improved only slightly to 7.18% with augcc-pV5Z (a5z) (left panel of Figure 2 and Table S1). For the LARGE set, the HF method converged slightly earlier at the cc-pVTZ level with an average relative RMS reaching 11.20% and further improved to 10.92% at the aug-cc-pV5Z level (Table S2). Similarly, majority of the DFT methods converged at the aug-cc-pVTZ basis set level for both SMALL and LARGE sets. For example, at the aug-cc-pVTZ level, the errors of the ωB97X-D method reached 1.82 and 3.47% for SMALL and LARGE sets, respectively, and improved to only 1.73 and 3.36% for SMALL and LARGE sets, respectively, at the aug-cc-pV5Z level. For MP2 methods, the relative RMS at the aug-cc-pVTZ level were 1.75 and 1.12% and improved to 1.53% for SMALL set at aug-cc-pV5Z and 0.39% for LARGE set with the aug-cc-pVQZ basis set. Therefore, we conclude that the aug-cc-pVTZ basis set is a reasonable choice, balancing between accuracy and economy.
Figure 2.
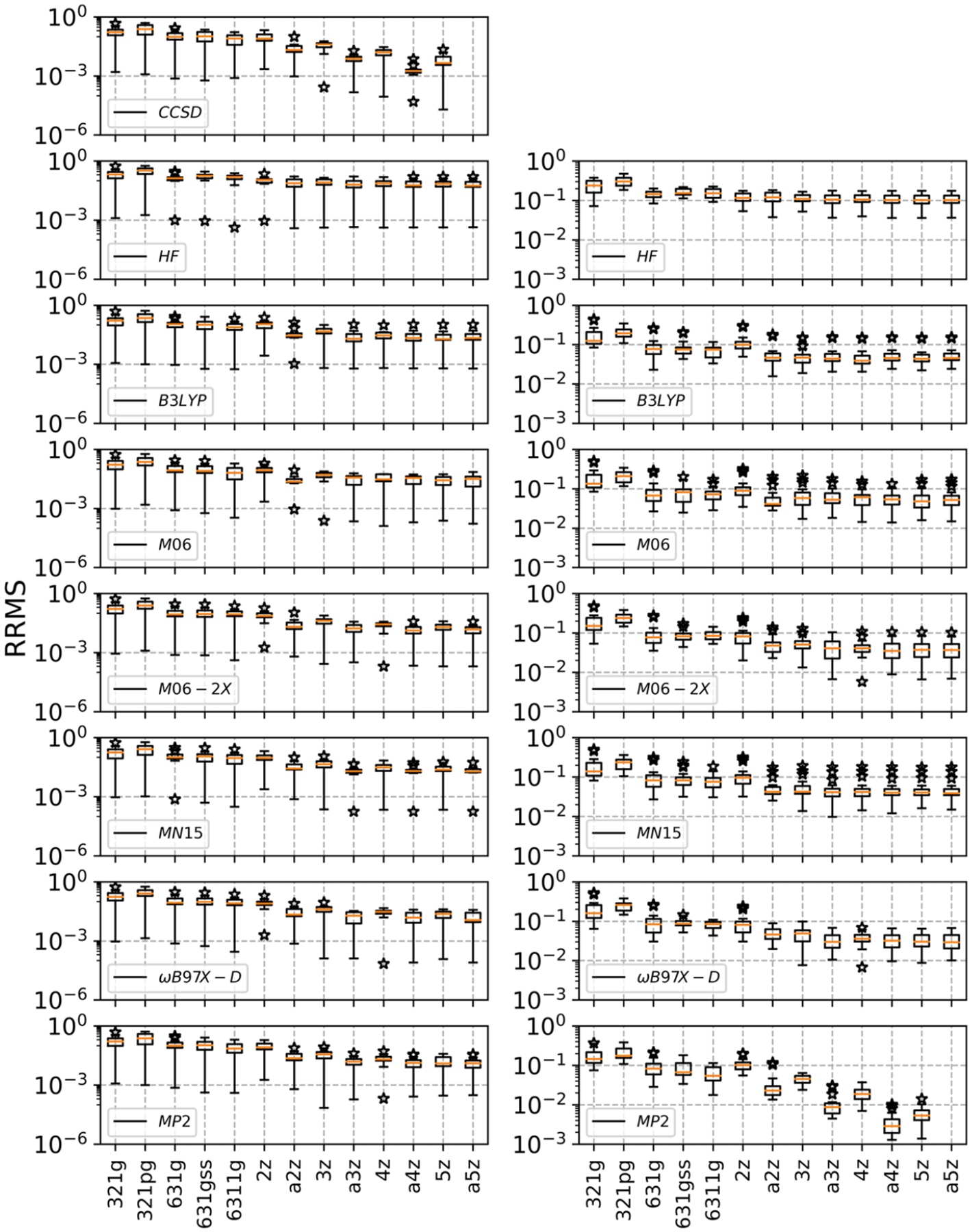
Relative root-mean-square (RRMS) error of the electrostatic potentials (ESPs) between the given and reference methods. The left panel is the result from the SMALL set with the reference method CCSD/aug-cc-pV5Z (a5z), while the right panel refers to the LARGE set with the reference method MP2/aug-cc-pV5Z (a5z). Outliers are marked with a star sign, and median values are shown in orange. The outliers are indicated by “*”, which indicates when the values are outside the range of (Q1−1.5 × IQR) to (Q3 + 1.5 × IQR), where Q1 and Q3 represent the 25 and 75% quartiles, respectively, and IQR denotes the interquartile range between Q3 and Q1. Abbreviations of the basis sets can be found in Section 2.2.
Another clear trend was that for most of the methods examined in this work, augmentation of the basis sets with diffuse functions led to significant improvements. For instance, in the case of the M06–2X method, the value of RRMS with basis sets a2z, a3z, a4z, and a5z was smaller than that with basis sets 2z, 3z, 4z, and 5z, respectively. This could be due to the fact that ESPs are highly related to charge distribution. Therefore, basis sets augmented with diffuse functions are recommended for the effective calculation of electrostatic potentials. In fact, a common observation was that the accuracy of the aug-cc-pVnZ-based combinations was consistently higher than the cc-pV(n + 1)Z-based ones, suggesting that including diffuse functions is superior to solely increasing the zeta (ζ) basis sets. For example, in the SMALL set with reference to CCSD/aug-cc-pV5Z (a5z) (left panel of Figure 2 and Table S1), the difference between aug-cc-pVDZ (a2z) and reference data is 2.78%, which is smaller than that of cc-pVTZ (3z, 3.56%). Similar conclusions can be drawn for the LARGE set with reference to MP2/aug-cc-pV5Z (a5z) (right panel of Figure 2 and Table S2).
Considering both the cost and the accuracy, we suggest that the aug-cc-pVTZ basis set is sufficient for deriving electrostatic potentials for any QM method studied here. From the atomic charge calculation point of view, we can draw the same conclusion that the aug-cc-pVTZ (a3z) basis set is sufficient to achieve converged results. Tables S3–S6 provide a complete list of the atomic charges derived from B3LYP and MP2 theories for both the SMALL and LARGE sets. For example, the average relative RMS differences of the charges obtained from MP2/aug-cc-pVTZ ESP are only 1.02 and 1.20% from those of MP2/aug-cc-pV5Z for the SMALL and LARGE sets, respectively. These charges were obtained directly from the Gaussian outputs and were calculated by fitting to the ESP at the Merz–Singh–Kollman surface.
3.2. Accuracy Estimation among the QM Methods.
In this section, the ESP accuracy of several commonly used QM methods was evaluated and is compared to the CCSD and MP2 methods with the aug-cc-pV5Z basis set as references for the SMALL and LARGE sets, respectively. As expected, the results showed that HF/aug-cc-pV5Z had the poorest accuracy among the examined methods over SMALL set with an average relative error of 7.18%, mainly due to neglect of the electron correlation effect. (Figure 3a and Table S1) The inclusion of electron correlation in the MP2 method resulted in much better accuracy among the SMALL molecule set, and the average relative RMS error was reduced to 1.53% with the augcc-pV5Z basis set. (Table S1) The same observation has been made before in the estimation of dipole moments and polarizabilities.79 As expected, B3LYP, M06, M06–2X, MN15, and ωB97X-D methods outperformed the HF method for both the SMALL and LARGE sets. Among the DFT methods, both ωB97X-D and M06–2X achieved high accuracy for the SMALL set with M06–2X/aug-cc-pV5Z edged out to 1.57%, slightly better than the 1.73% of ωB97X-D/aug-cc-pV5Z, compared to the CCSD/aug-cc-pV5Z method, comparable to the accuracy of MP2/aug-cc-pV5Z (1.53%). The remaining three methods M06, B3LYP, and MN15 all had modest accuracies, and the average relative errors were 3.02, 3.08, and 2.25% for M06, B3LYP, and MN15 methods, respectively, significantly better than the HF/aug-cc-pV5Z whose average relative error was 7.18%, more than double of those from any of the DFT methods with the aug-cc-pV5Z basis set. The high accuracy of the MP2 method renders it often the method of choice in QM calculations. However, poor computational efficiency sometimes makes it prohibitively expensive for large molecules. With a somewhat reduced accuracy, the ωB97X-D method can be an efficient alternative. Compared to MP2/aug-cc-pV5Z for the LARGE molecule set, the average relative RMS errors reached 3.47 and 3.36% with aug-cc-pVTZ and aug-cc-pV5Z basis sets, respectively (Figure 3b and Table S2); both are their respective best compared to other DFT methods with the same basis sets. Another potentially reasonable choice is the M06–2X method. At the aug-cc-pVTZ basis set level, the average relative error was 4.24% and reached 3.98% at the aug-cc-pV5Z level. Given that the ESPs converged well at the aug-cc-pVTZ basis set level, we recommend MP2/aug-cc-pVTZ as the method of choice for calculations of molecular ESP and ωB97X-D/aug-cc-pVTZ as an alternative method.
Figure 3.

Relative root-mean-square (RRMS) error of ESPs derived from different QM methods with respect to different reference methods. Here, reference methods were CCSD/aug-cc-pV5Z and MP2/aug-cc-pV5Z for the SMALL (left) and LARGE (right) sets, respectively. The RRMS is shown here on a logarithmic scale; a linear scale plot can be found in Figure S1.
3.3. Restraining Strength Selection for pGM Models.
Similar to RESP,31 depending on the choices of equivalencing chemically equivalent atoms, the PyRESP fitting is also performed in two stages, as discussed in the Section 2.3. To alleviate the underdetermined character of buried atoms, both charges and permanent dipoles in the PyRESP fitting are restrained by hyperbolic restraining functions.7 In this subsection, we will examine the choices of the restraining strengths and the impact on the fitting quality.
To determine the range of restraining strength that allows the modification of the charges and permanent dipoles without significantly sacrificing the fitting quality, we consider only the first stage of both pGM-ind and pGM-perm models here. The detailed strategy on how to treat the chemically equivalent atoms and permanent dipole moments can be found in Section 2.3. We tested the restraining strength aq in the range from 10−5 to 102 a.u. for the pGM-ind model. For the pGM-perm model, ap was tested in the same range, while aq was held at 0.0005 a.u.
Similar to the observations made by Bayly et al. in their development of the RESP method,31 for the pGM-ind model, as shown in Figure 4a, a sharp transition can be seen when aq is in the range between 0.1 and 1. For comparison, the original RESP model shows an inflection at aq = 1 a.u.,31 which is greater than the one observed here. Thus, the pGM-ind model is more sensitive to the restraining strength than the RESP model. When aq is less than 10−3, no obvious decrease in the accuracy of ESPs is observed, and when aq is greater than 102, the fitting quality stopped deteriorating further. This similar dependence could be attributed to a single parameter dependency of the restraint equation for both RESP and pGM-ind. Such a trend can be observed for both the SMALL and LARGE sets.
Figure 4.
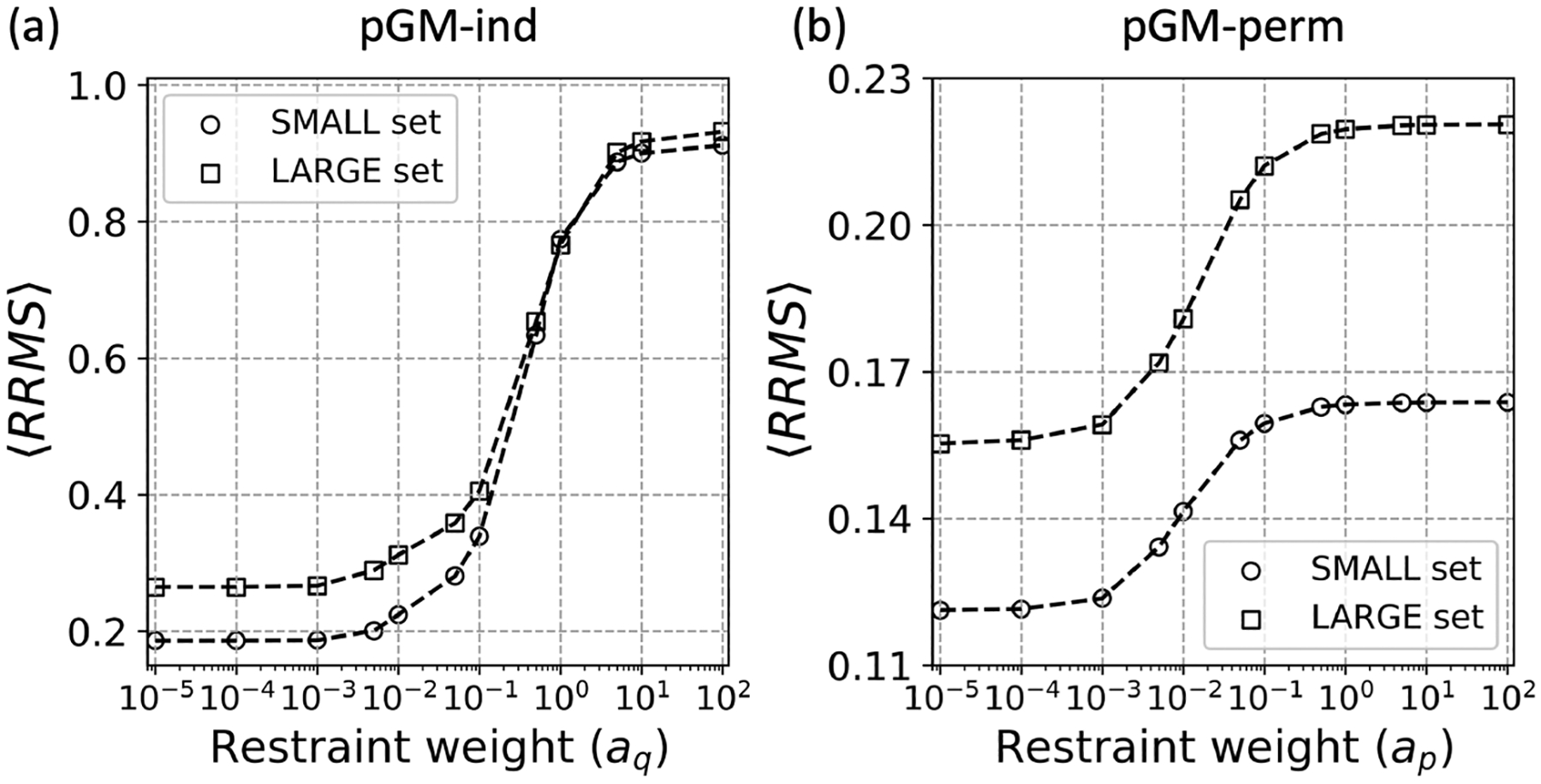
Relative RMS per molecule (〈RRMS〉) as a function of the restraining strength at (a) the permanent point charge of the pGM-ind model (aq in eq 4) and (b) the permanent dipole of the pGM-perm model (ap in eq 7). Reference method and basis sets, namely, CCSD/aug-cc-pV5Z (a5z) and MP2/aug-cc-pV5Z (a5z), are utilized for SMALL (circle point) and LARGE (square point) sets, respectively.
For the pGM-perm model, as depicted in Figure 4b, the inflection point is located around ap = 10−2, more than 1 order of magnitude smaller than that of aq in the pGM-ind model. The plateaus in the pGM-perm model were also reached at much smaller ap values than aq values in the pGM-ind model. A negligible effect is observed when ap is less than 10−4 a.u. However, once the restraining strength exceeds 10−4 a.u., the accuracy of the fitted electrostatic potential starts to deteriorate and levels off toward its limiting value when ap is greater than 1 a.u. Thus, the range of the appropriate restraining strength ap is much smaller than the value of aq. The analysis shows that aq and ap should be treated separately.
In addition, when comparing the 〈RRMS〉 derived from pGM-ind and pGM-perm, we found that the error produced by pGM-perm is about half that of pGM-ind. For example, the 〈RRMS〉 of pGM-perm over the SMALL set is about half of that of the pGM-ind model when ap is below 10−4. While this is not surprising, given the increased number of the fitting parameters, it nevertheless indicates the need to include the permanent dipoles to reproduce accurately the electrostatic potentials in addition to the induced dipoles and monopoles. Given that the error of the pGM-perm model starts to increase when ap is greater than 10−4, we conclude that the range of the appropriate restraining strength ap is between 10−5 and 10−3 for the parameterization of the pGM-perm model.
We tested five distinct restraining strengths (10−5, 5 × 10−5, 10−4, 5 × 10−4, and 10−3) on 10 selected models for first and second stage fittings. The results are listed in Tables 1 and 2. The reference theory levels used were CCSD/aug-cc-pV5Z (a5z) and MP2/aug-cc-pV5Z (a5z) for the SMALL and LARGE sets, respectively. For the pGM-ind model (Table 1), when the restraining strength (aq) at the first stage was fixed at aq = 10−5, increasing aq from 5 × 10−5 to 10−3 at the second stage resulted in a clear trend of reduced fitting quality and the 〈RRMS〉 and Δμ increased from 0.1869 and 0.0742 to 0.1875 and 0.0746, respectively, among the SMALL set and from 0.2797 and 0.1266 to 0.2806 and 0.1293, respectively, among the LARGE set. On the other hand, increasing aq at the first stage while fixing aq at the second stage had almost no impact on the fitting quality. For example, when aq at the second stage was fixed at aq = 10−3, the 〈RRMS〉 remained at 0.1875 and 0.2806 for SMALL and LARGE sets, respectively, when aq at the first stage increased from 10−5 to 10−4. Therefore, the choice of aq at the second stage is comparatively more important to achieving accuracy. Based on these analyses, we conclude that aq can be chosen as 5 × 10−5 and 10−4 for the first and second stages, respectively, which yielded the best accuracy among the tested combinations, as seen in Table 1.
Table 1.
Comparison of Fitting Accuracy for 10 Distinct Restraining Strengths for the pGM-ind Modela
| model | 〈RRMS〉 | 〈Δμ〉d | 〈ΔQxx〉e | 〈ΔQyy〉e | 〈ΔQzz〉e | |
|---|---|---|---|---|---|---|
| 1stb | 2ndc | SMALL SET | ||||
| 10−5 | 5 × 10−5 | 0.1869(0.1230) | 0.0742 | 0.3959 | 0.2974 | 0.3771 |
| 10−5 | 10−4 | 0.1869(0.1230) | 0.0743 | 0.3959 | 0.2974 | 0.3771 |
| 10−5 | 5 × 10−4 | 0.1870(0.1232) | 0.0744 | 0.3960 | 0.2974 | 0.3771 |
| 10−5 | 10−3 | 0.1875(0.1239) | 0.0746 | 0.3961 | 0.2974 | 0.3771 |
| 5 × 10−5 | 10−4 | 0.1869(0.1230) | 0.0742 | 0.3959 | 0.2974 | 0.3771 |
| 5 × 10−5 | 5 × 10−4 | 0.1870(0.1232) | 0.0743 | 0.3960 | 0.2975 | 0.3771 |
| 5 × 10−5 | 10−3 | 0.1875(0.1239) | 0.0745 | 0.3961 | 0.2975 | 0.3772 |
| 10−4 | 5 × 10−4 | 0.1870(0.1232) | 0.0742 | 0.3961 | 0.2976 | 0.3772 |
| 10−4 | 10−3 | 0.1875(0.1239) | 0.0744 | 0.3962 | 0.2976 | 0.3772 |
| 5 × 10−4 | 10−3 | 0.1876(0.1239) | 0.0736 | 0.3965 | 0.2985 | 0.3773 |
| LARGE SET | ||||||
| 10−5 | 5 × 10−5 | 0.2797(0.2109) | 0.1266 | 0.5014 | 0.4324 | 0.4180 |
| 10−5 | 10−4 | 0.2797(0.2109) | 0.1268 | 0.5015 | 0.4324 | 0.4180 |
| 10−5 | 5 × 10−4 | 0.2800(0.2114) | 0.1279 | 0.5022 | 0.4323 | 0.4177 |
| 10−5 | 10−3 | 0.2806(0.2128) | 0.1293 | 0.5030 | 0.4323 | 0.4175 |
| 5 × 10−5 | 10−4 | 0.2797(0.2109) | 0.1265 | 0.5015 | 0.4328 | 0.4180 |
| 5 × 10−5 | 5 × 10−4 | 0.2799(0.2114) | 0.1276 | 0.5022 | 0.4328 | 0.4177 |
| 5 × 10−5 | 10−3 | 0.2806(0.2128) | 0.1291 | 0.5030 | 0.4328 | 0.4175 |
| 10−4 | 5 × 10−4 | 0.2799(0.2114) | 0.1273 | 0.5022 | 0.4333 | 0.4178 |
| 10−4 | 10−3 | 0.2806(0.2129) | 0.1287 | 0.5031 | 0.4333 | 0.4175 |
| 5 × 10−4 | 10−3 | 0.2807(0.2129) | 0.1262 | 0.5036 | 0.4383 | 0.4179 |
Standard deviations are listed in parentheses. The better metrics are shown in bold.
aq restraining strength utilized in the 1st stage.
aq restraining strength utilized in the 2nd stage.
Dipole moment in the unit of Debye.
Quadrupole moment along the principal axes in the unit of Debye angstrom.
Table 2.
Comparison of Fitting Accuracy for 10 Distinct Restraining Strengths for the pGM-perm Modela
| model | 〈RRMS〉 | 〈Δμ〉d | 〈ΔQxx〉e | 〈ΔQyy〉e | 〈ΔQzz〉e | |
|---|---|---|---|---|---|---|
| 1stb | 2ndc | SMALL SET | ||||
| 10−5 | 5 × 10−5 | 0.1238(0.0927) | 0.0620 | 0.2911 | 0.1665 | 0.2231 |
| 10−5 | 10−4 | 0.1238(0.0927) | 0.0620 | 0.2911 | 0.1664 | 0.2231 |
| 10−5 | 5 × 10−4 | 0.1238(0.0927) | 0.0621 | 0.2912 | 0.1662 | 0.2230 |
| 10−5 | 10−3 | 0.1238(0.0926) | 0.0623 | 0.2913 | 0.1659 | 0.2230 |
| 5 × 10−5 | 10−4 | 0.1235(0.0928) | 0.0607 | 0.2908 | 0.1659 | 0.2260 |
| 5 × 10−5 | 5 × 10−4 | 0.1235(0.0928) | 0.0607 | 0.2909 | 0.1657 | 0.2258 |
| 5 × 10−5 | 10−3 | 0.1236(0.0928) | 0.0608 | 0.2910 | 0.1656 | 0.2257 |
| 10−4 | 5 × 10−4 | 0.1236(0.0928) | 0.0606 | 0.2911 | 0.1658 | 0.2270 |
| 10−4 | 10−3 | 0.1236(0.0928) | 0.0606 | 0.2912 | 0.1658 | 0.2269 |
| 5 × 10−4 | 10−3 | 0.1245(0.0925) | 0.0603 | 0.2924 | 0.1668 | 0.2310 |
| 10−5 | 5 × 10−5 | 0.1703(0.1001) | 0.0713 | 0.3247 | 0.2170 | 0.3538 |
| 10−5 | 10−4 | 0.1703(0.1000) | 0.0714 | 0.3246 | 0.2169 | 0.3537 |
| 10−5 | 5 × 10−4 | 0.1703(0.1000) | 0.0723 | 0.3245 | 0.2167 | 0.3530 |
| 10−5 | 10−3 | 0.1705(0.1002) | 0.0734 | 0.3247 | 0.2167 | 0.3523 |
| 5 × 10−5 | 10−4 | 0.1699(0.1001) | 0.0666 | 0.3462 | 0.2165 | 0.3600 |
| 5 × 10−5 | 5 × 10−4 | 0.1699(0.1001) | 0.0669 | 0.3460 | 0.2167 | 0.3595 |
| 5 × 10−5 | 10−3 | 0.1699(0.1002) | 0.0673 | 0.3459 | 0.2170 | 0.3591 |
| 10−4 | 5 × 10−4 | 0.1696(0.1001) | 0.0654 | 0.3488 | 0.2168 | 0.3600 |
| 10−4 | 10−3 | 0.1697(0.1002) | 0.0656 | 0.3485 | 0.2168 | 0.3597 |
| 5 × 10−4 | 10−3 | 0.1706(0.0996) | 0.0697 | 0.3631 | 0.2171 | 0.3728 |
Standard deviations are presented in parentheses. The better metrics are shown in bold.
ap restraining strength utilized in the 1st stage.
ap restraining strength utilized in the 2nd stage.
Dipole moment in the unit of Debye.
Quadrupole moment along the principal axes in the unit of Debye angstrom.
For the pGM-perm model (Table 2), fixing ap at the first stage but changing ap at the second stage has little influence on the accuracy of 〈RRMS〉. When ap is set to 10−5 at the first stage and increased from 5 × 10−5 to 5 × 10−4 at the second stage, the 〈RRMS〉 remained essentially the same at 0.1238 and 0.1703 in the SMALL and LARGE sets, respectively. A slight increase of 〈RRMS〉 was observed when the restraining strength for the second stage exceeds 5 × 10−4, when the accuracy starts to deteriorate, as seen in Figure 4b. On the other hand, fixing ap at the second stage but changing ap at the first stage yielded slightly improved accuracy when ap at the first stage is about ap = 10−4. For example, when the restraining strength for the second stage is set to be 10−3 and the strength for the first stage is increased from 10−5 to 5 × 10−4, the error of 〈RRMS〉 decreases from 0.1705 and 0.0734 to 0.1697 and 0.0656, respectively. However, once the restraining strength for the first stage exceeds 10−4, the error of both 〈RRMS〉 and Δμ increases to 0.1706 and 0.0697, respectively, for the LARGE set. Taking together, we conclude that the optimal combination is ap = 10−4 at the first stage and ap = 5 × 10−4 at the second stage.
3.4. Strategies for the Development of the pGM-perm ESP Model.
In this subsection, we will discuss three strategies for the development of the pGM-perm ESP model as detailed in Section 2.3. We will devote our attention to the treatment of −CH2− and −CH3; therefore, only molecules containing these functional groups were selected. The restraining strength ap was set to be 10−4 and 5 × 10−4 for the first and second fitting stages, respectively. The restraining strength for aq is the same as the one used in the two-stage RESP model (aq = 0.0005 and 0.001 a.u. for the first and second stages, respectively).
The fitting quality and essential electrostatic properties, such as the dipole and quadrupole moments, are listed in Table 3. For the SMALL set, the fitting qualities were similar for all three strategies, with the maximum difference of 〈RRMS〉 being only 6 × 10−4, much smaller than the 〈RRMS〉. This is possible because only four molecules containing −CH2− and −CH3 (i.e., CH3OH, CH3Cl, CH3F, and CH4) were found in the SMALL set (Figure 1). Among the 13 molecules from the LARGE set (i.e., C2H6, C3H8, C4H10, CH3Br, CH3COCH3, CH3NH2, CH3OCH3, CH3S2CH3, CH3SCH3, CH3SO2CH3, HCOOCH3, NMA, and PO3CH5), strategy II demonstrated consistently better fitting quality than the other two, and all of the average errors were consistently smallest. For example, the errors of Qxx, Qyy, and Qzz derived using strategy II were 0.3433, 0.2174, and 0.2167, respectively, which were smaller than those obtained using strategies I and III.
Table 3.
Comparison of the Accuracy Derived from pGM-perm with Different Strategies
| metrics | SMALL SET | LARGE SET | ||||
|---|---|---|---|---|---|---|
| strategy | Ia | IIb | IIIc | Ia | IIb | IIIc |
| 〈RRMS〉 | 0.1265 | 0.1265 | 0.1271 | 0.1808 | 0.1754 | 0.1836 |
| 〈Δμ〉d | 0.0194 | 0.0194 | 0.0196 | 0.1005 | 0.0917 | 0.1182 |
| 〈ΔQxx〉e | 0.1887 | 0.1885 | 0.1938 | 0.3708 | 0.3433 | 0.4038 |
| 〈ΔQyy〉e | 0.1166 | 0.1174 | 0.1300 | 0.2245 | 0.2174 | 0.2418 |
| 〈ΔQzz〉e | 0.1199 | 0.1197 | 0.1070 | 0.2597 | 0.2167 | 0.2758 |
In the 1st stage, for functional groups −CH2− and −CH3, only the C → H permanent dipoles were equivalenced, while H → C dipoles were free to change; in the 2nd stage, equivalences were maintained for both C → H and H → C permanent dipoles.
In both the 1st and 2nd stages, equivalences were maintained for C → H and H → C permanent dipoles.
In the 1st stage, both H → C and dipole C → H permanent dipoles were free; in the 2nd stage, equivalences were maintained for C → H and H → C.
In Debye.
In Debye angstrom.
3.5. Performance Comparison between pGM and the Point Charge RESP Models.
In this section, the performance of pGM-ind, pGM-perm, and point charge RESP models using their optimal restraining strengths are estimated over the SMALL and LARGE sets. Overall, the results indicate that the pGM-perm model performs better than both RESP and pGM-ind models in terms of accuracy, especially for polar molecules (Figure 5 and Tables S7 and S8). As indicated by the median value (colored orange), the inclusion of induced and permanent dipoles in the pGM-perm model helps to capture the electrostatic potentials better than the other models.
Figure 5.
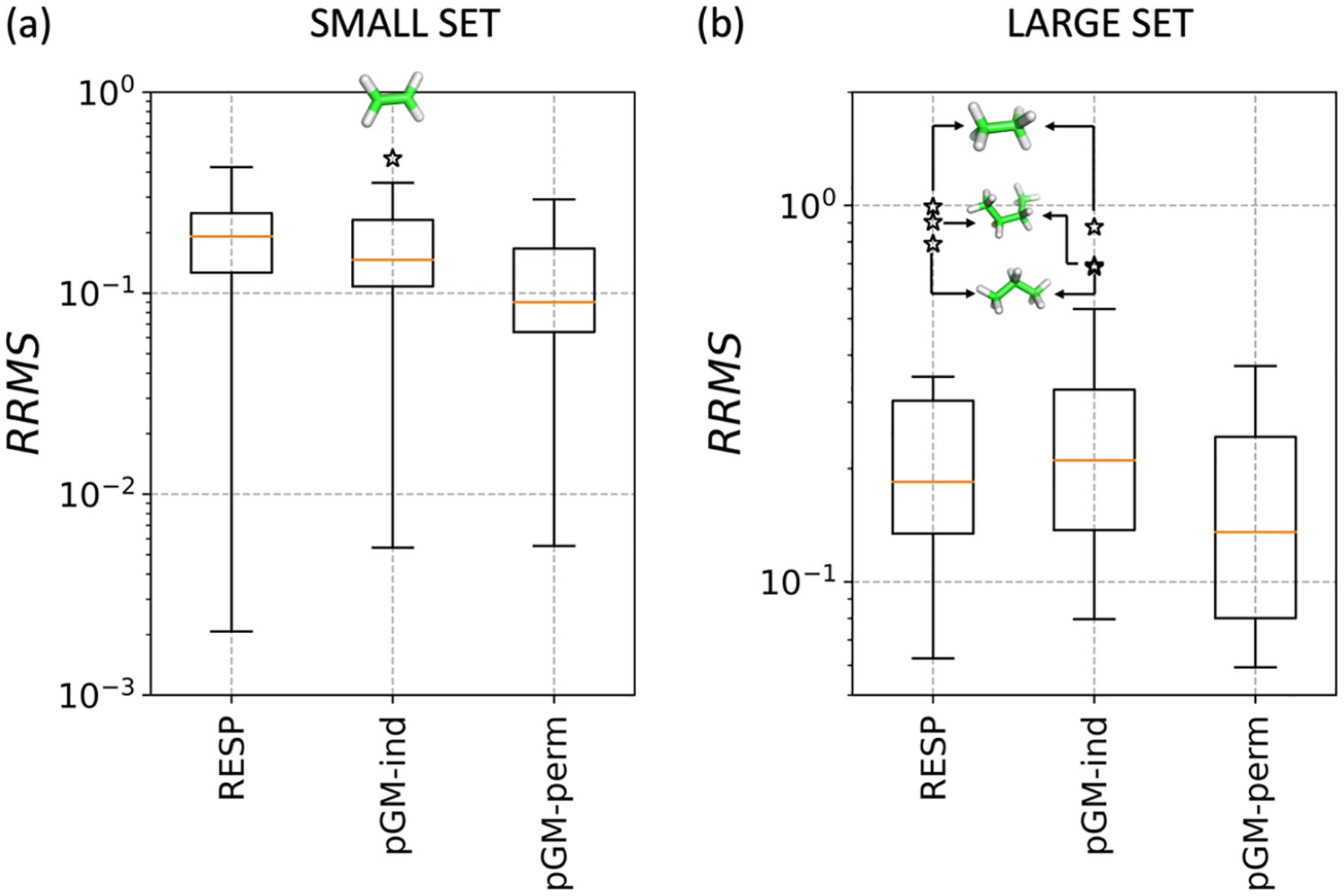
Comparison of the relative root-mean-square (RRMS) errors for multipole fitting to QM ESPs for three models: RESP, pGM-ind, and pGM-perm. For small set (a), QM ESPs are calculated at the CCSD/aug-cc-pV5Z (a5z) level, while for LARGE set (b), QM ESPs are calculated at the MP2/aug-cc-pV5Z (a5z) level. The star signs indicate the outliers, and their chemical structures are shown by the insets.
Among the SMALL set, significant improvements are observed in polar molecules, such as water (H2O) molecule and water dimer (H2O–H2O). However, for nonpolar molecules, such as C2H4, the fitting results derived by RESP and pGM-perm are comparable, while a little decrease of accuracy is observed for the pGM-perm model. Although we are uncertain about the exact cause of such interesting behavior, we speculate that this could be due to the singularity problem associated with the pGM-perm model, which represents the permanent atomic dipoles using the covalent bond vectors.55 Nevertheless, given the fact that nonpolar molecules have much weaker ESP than polar molecules, the absolute error of the nonpolar molecule ESP is rather small (Table S7). Among the LARGE set, RESP and pGM-ind models show comparable accuracy. However, three molecules, namely, C2H6, C3H8, and C4H10, are detected as outliers in these two models due to their nonpolar nature and weak electronegative elements (Figure 5). For other polar molecules, both pGM-ind and pGM-perm models outperform the RESP model. A full list of the root-mean-square (RMS) and relative root-mean-square (RRMS) error values for individual molecules can be found in Tables S7 and S8.
The observation that the RESP method produced some of the largest RRMSs is not surprising, given that it is a monopole-only point charge model. However, the large RRMSs in some cases deserve further scrutiny. For example, in the case of ethane, the RRMS reached close to 100%. Other alkanes also show a large RRMS. Clearly, this shows that alkanes pose significant challenges to the monopole-only point charge models. The reason for such poor behavior lies in both the lack of higher-order multipoles and the poor approximation of point charges. Encouragingly, the pGM-perm models notably improved the fitting. In our view, the improvements show both the need to move beyond the point-type, particularly the point charge-only, models and the need to include higher-order multipoles. Nevertheless, all nucleic and amino acids comprise polar groups and, in some cases, formal charges that have much stronger electrostatic fields than alkanes. Since electrostatic fields of amino acids containing aliphatic side chains are dominated by the polar main-chain peptide group and the aliphatic side chains have relatively weak contributions, the overall RRMS of peptides should be close to those of the polar molecules presented in this study, which has notably lower RRMS compared to alkanes, primarily due to the fact that alkanes have weak electrostatic fields (therefore small denominator in RRMS). For example, all three methods achieved acceptable fitting results for NMA, which closely resembles the main-chain peptide group, and the RRMS ranges from 10.61 to 6.54%, with pGM-perm performing the best (Table S8). In addition, additional restraints were applied throughout the ESP fitting over charge and dipoles; the well-known problem of large charges on the buried atoms should be alleviated. As demonstrated in Table S9, taking molecule NMA as an example, the RESP method together with the pGM-related model lowers the magnitude of charge over atom carbon of the methyl group.
4. CONCLUSIONS
In this work, a comprehensive evaluation of the accuracy of ESPs derived from a variety of quantum mechanical methods combined with various basis sets has been conducted. The augmentation of basis sets with diffuse functions significantly improves the accuracy and is necessary for the quality of ESPs. The polarization-consistent triple-ξ basis set augmented with diffuse functions (aug-cc-pVTZ) is sufficient for accurate ESP calculation. Among the examined quantum mechanical methods, the lowest accuracy is found in HF mainly owing to the neglection of electron correlation. Inclusion of the exact exchange in the exchange–correlation functional is the key to accurate reproduction of ESPs. Calculations using the MP2 method showed that the accuracy of ESPs is comparable to that of CCSD. Given its significant cost advantage over the CCSD method, we recommend MP2/aug-cc-pVTZ as the method of choice in the ESP calculations for biomolecules. Among the DFT methods examined, ωB97X-D shows the best results compared with other hybrid DFT methods, perhaps owing to its inclusion of empirical atom–atom dispersion correlations. Taking the balance between accuracy and efficiency into consideration, method ωB97X-D can serve as the alternative for the QM ESP reproduction when the MP2 method becomes prohibitively expensive.
We present PyRESP_GEN, a utility program that can generate inputs for the charge and dipole fitting program PyRESP to facilitate the process of polarizable force field development. This program is easy to use and flexible. For the pGM-ind and pGM-perm models, we optimized their corresponding restraining strengths. Accuracy comparisons were conducted on the pGM-perm model taking three distinct strategies. The optimized restraining strengths (aq) of the pGM-ind model are smaller than that used in the original RESP protocol, suggesting that the pGM-ind model be more sensitive to the restraining strength than RESP. In addition, the optimized restraining strength (ap) applied to the permanent dipole in the pGM-perm model differs notably from the restraining strength (aq) applied to charges, which further demonstrated the rationality of treating these two restraining strengths separately. With the optimized restraining strengths, the robustness of the pGM-perm model was further validated.
We anticipate that program PyRESP_GEN together with the optimized procedure and strategies provided in this work may promote the dissemination of polarizable force fields by reducing the burden of parameterization for pGM models and pave the way for simulating any organic molecules with pGM models, which could be used in the process of drug design.
Supplementary Material
ACKNOWLEDGMENTS
The authors gratefully acknowledge the research support from NIH (GM79383 to Y.D. and GM130367 to R.L.).
ABBREVIATIONS
- DFT
density functional theory
- RESP
restrained electrostatic potential
- ESPs
electrostatic potentials
- GAFF
general Amber force field
- AMBER
assisted model building with energy refinement
- pGM-ind
polarizable model with induced point dipole
- pGM-perm
polarizable model with induced point dipoles and permanent point dipoles
- 321g
3–21G
- 321pg
3–21+G
- 631g
6–31G*
- 631gss
6–31++G**
- 6311g
6–311++G**
- 2z
cc-pVDZ
- a2z
aug-cc-pVDZ
- 3z
cc-pVTZ
- a3z
aug-cc-pVTZ
- 4z
cc-pVQZ
- a4z
aug-cc-pVQZ
- 5z
cc-pV5Z
- a5z
augcc-pV5Z
- QM
quantum mechanics
- a.u.
atomic unit
Footnotes
Supporting Information
The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.jctc.3c00659.
Relative root-mean-square errors of ESP difference among different QM methods plotted in normal scale (Figure S1); convergence test on RMS and RRMS (Tables S1 and S2); convergence test on atomic charge deviation over SMALL and LARGE sets (Tables S3–S6); full list of RMS and RRMS derived from RESP and pGM methods (Tables S7 and S8); and demonstration of the buried atom problem (Table S9) (PDF)
The authors declare no competing financial interest.
Complete contact information is available at: https://pubs.acs.org/10.1021/acs.jctc.3c00659
Contributor Information
Qiang Zhu, Department of Molecular Biology and Biochemistry, Chemical and Biomolecular Engineering, Materials Science and Engineering, and Biomedical Engineering, University of California, Irvine, Irvine, California 92697, United States;.
Yongxian Wu, Department of Molecular Biology and Biochemistry, Chemical and Biomolecular Engineering, Materials Science and Engineering, and Biomedical Engineering, University of California, Irvine, Irvine, California 92697, United States.
Shiji Zhao, Nurix Therapeutics, Inc., San Francisco, California 94158, United States;.
Piotr Cieplak, SBP Medical Discovery Institute, La Jolla, California 92037, United States;.
Yong Duan, UC Davis Genome Center and Department of Biomedical Engineering, University of California, Davis, Davis, California 95616, United States;.
Ray Luo, Department of Molecular Biology and Biochemistry, Chemical and Biomolecular Engineering, Materials Science and Engineering, and Biomedical Engineering, University of California, Irvine, Irvine, California 92697, United States;.
Data Availability Statement
The source code of PyRESP_GEN can be downloaded from https://github.com/csu1505110121/pyresp_gen.
REFERENCES
- (1).Straatsma TP; McCammon J Computational alchemy. Annu. Rev. Phys. Chem 1992, 43, 407–435. [Google Scholar]
- (2).Allen MP; Tildesley DJ Computer Simulation of Liquids; Oxford University Press, 2017. [Google Scholar]
- (3).Van Gunsteren WF; Bakowies D; Baron R; Chandrasekhar I; Christen M; Daura X; Gee P; Geerke DP; Glättli A; Hünenberger PH; et al. Biomolecular modeling: goals, problems, perspectives. Angew. Chem., Int. Ed 2006, 45, 4064–4092. [DOI] [PubMed] [Google Scholar]
- (4).Marrink SJ; Corradi V; Souza PC; Ingolfsson HI; Tieleman DP; Sansom MS Computational modeling of realistic cell membranes. Chem. Rev 2019, 119, 6184–6226. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (5).Riniker S Fixed-charge atomistic force fields for molecular dynamics simulations in the condensed phase: an overview. J. Chem. Inf. Model 2018, 58, 565–578. [DOI] [PubMed] [Google Scholar]
- (6).Zhao S; Wei H; Cieplak P; Duan Y; Luo R Accurate Reproduction of Quantum Mechanical Many-Body Interactions in Peptide Main-Chain Hydrogen-Bonding Oligomers by the Polarizable Gaussian Multipole Model. J. Chem. Theory Comput 2022, 18, 6172–6188. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (7).Zhao S; Wei H; Cieplak P; Duan Y; Luo R PyRESP: A Program for Electrostatic Parameterizations of Additive and Induced Dipole Polarizable Force Fields. J. Chem. Theory Comput 2022, 18, 3654–3670. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (8).Schauperl M; Nerenberg PS; Jang H; Wang L-P; Bayly CI; Mobley DL; Gilson MK Non-bonded force field model with advanced restrained electrostatic potential charges (RESP2). Commun. Chem 2020, 3 (1), No. 44. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (9).Zhu Q; Ge Y; Li W; Ma J Treating Polarization Effects in Charged and Polar Bio-Molecules Through Variable Electrostatic Parameters. J. Chem. Theory Comput 2023, 19, 396–411. [DOI] [PubMed] [Google Scholar]
- (10).Coppens P Electron density from X-ray diffraction. Annu. Rev. Phys. Chem 1992, 43, 663–692. [Google Scholar]
- (11).Mukherjee G; Patra N; Barua P; Jayaram B A fast empirical GAFF compatible partial atomic charge assignment scheme for modeling interactions of small molecules with biomolecular targets. J. Comput. Chem 2011, 32, 893–907. [DOI] [PubMed] [Google Scholar]
- (12).Mulliken RS Electronic population analysis on LCAO-MO molecular wave functions. I. J. Chem. Phys 1955, 23, 1833–1840. [Google Scholar]
- (13).Baker J Classical chemical concepts from ab initio SCF calculations. Theor. Chim. Acta 1985, 68, 221–229. [Google Scholar]
- (14).Löwdin P-O On the non-orthogonality problem connected with the use of atomic wave functions in the theory of molecules and crystals. J. Chem. Phys 1950, 18, 365–375. [Google Scholar]
- (15).Hirshfeld FL Bonded-atom fragments for describing molecular charge densities. Theor. Chim. Acta 1977, 44, 129–138. [Google Scholar]
- (16).Bultinck P; Van Alsenoy C; Ayers PW; Carbó-Dorca R Critical analysis and extension of the Hirshfeld atoms in molecules. J. Chem. Phys 2007, 126 (14), 144111. [DOI] [PubMed] [Google Scholar]
- (17).Bader RFW; Matta CF Atomic charges are measurable quantum expectation values: a rebuttal of criticisms of QTAIM charges. J. Phys. Chem. A 2004, 108, 8385–8394. [Google Scholar]
- (18).Foster JP; Weinhold F Natural hybrid orbitals. J. Am. Chem. Soc 1980, 102, 7211–7218. [Google Scholar]
- (19).Reed AE; Weinstock RB; Weinhold F Natural population analysis. J. Chem. Phys 1985, 83, 735–746. [Google Scholar]
- (20).Storer JW; Giesen DJ; Cramer CJ; Truhlar DG Class IV charge models: A new semiempirical approach in quantum chemistry. J. Comput.-Aided Mol. Des 1995, 9, 87–110. [DOI] [PubMed] [Google Scholar]
- (21).Li J; Cramer CJ; Truhlar DG MIDI! basis set for silicon, bromine, and iodine. Theor. Chem. Acc 1998, 99, 192–196. [Google Scholar]
- (22).Kelly CP; Cramer CJ; Truhlar DG Accurate partial atomic charges for high-energy molecules using class IV charge models with the MIDI! basis set. Theor. Chem. Acc 2005, 113, 133–151. [Google Scholar]
- (23).Warshel A Electrostatic basis of structure-function correlation in proteins. Acc. Chem. Res 1981, 14, 284–290. [Google Scholar]
- (24).Price SL; Stone A The electrostatic interactions in van der Waals complexes involving aromatic molecules. J. Chem. Phys 1987, 86, 2859–2868. [Google Scholar]
- (25).Cox SR; Williams D Representation of the molecular electrostatic potential by a net atomic charge model. J. Comput. Chem 1981, 2, 304–323. [Google Scholar]
- (26).Singh UC; Kollman PA An approach to computing electrostatic charges for molecules. J. Comput. Chem 1984, 5, 129–145. [Google Scholar]
- (27).Momany FA Determination of partial atomic charges from ab initio molecular electrostatic potentials. Application to formamide, methanol, and formic acid. J. Phys. Chem. A 1978, 82, 592–601. [Google Scholar]
- (28).Cornell WD; Cieplak P; Bayly CI; Gould IR; Merz KM; Ferguson DM; Spellmeyer DC; Fox T; Caldwell JW; Kollman PA A second generation force field for the simulation of proteins, nucleic acids, and organic molecules. J. Am. Chem. Soc 1995, 117, 5179–5197. [Google Scholar]
- (29).Breneman CM; Wiberg KB Determining atom-centered monopoles from molecular electrostatic potentials. The need for high sampling density in formamide conformational analysis. J. Comput. Chem 1990, 11, 361–373. [Google Scholar]
- (30).Cornell WD; Cieplak P; Bayly CI; Kollman PA Application of RESP charges to calculate conformational energies, hydrogen bond energies, and free energies of solvation. J. Am. Chem. Soc 1993, 115, 9620–9631. [Google Scholar]
- (31).Bayly CI; Cieplak P; Cornell W; Kollman PA A well-behaved electrostatic potential based method using charge restraints for deriving atomic charges: the RESP model. J. Phys. Chem. A 1993, 97, 10269–10280. [Google Scholar]
- (32).Wang J; Wang W; Kollman PA; Case DA Automatic atom type and bond type perception in molecular mechanical calculations. J. Mol. Graphics Modell 2006, 25, 247–260. [DOI] [PubMed] [Google Scholar]
- (33).Cieplak P; Dupradeau F-Y; Duan Y; Wang J Polarization effects in molecular mechanical force fields. J. Phys.: Condens. Matter 2009, 21, 333102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (34).Cieplak P; Caldwell J; Kollman P Molecular mechanical models for organic and biological systems going beyond the atom centered two body additive approximation: aqueous solution free energies of methanol and N-methyl acetamide, nucleic acid base, and amide hydrogen bonding and chloroform/water partition coefficients of the nucleic acid bases. J. Comput. Chem 2001, 22, 1048–1057. [Google Scholar]
- (35).Cieplak P; Cornell WD; Bayly C; Kollman PA Application of the multimolecule and multiconformational RESP methodology to biopolymers: Charge derivation for DNA, RNA, and proteins. J. Comput. Chem 1995, 16, 1357–1377. [Google Scholar]
- (36).Wang J; Cieplak P; Kollman PA How well does a restrained electrostatic potential (RESP) model perform in calculating conformational energies of organic and biological molecules? J. Comput. Chem 2000, 21, 1049–1074. [Google Scholar]
- (37).Tian C; Kasavajhala K; Belfon KA; Raguette L; Huang H; Migues AN; Bickel J; Wang Y; Pincay J; Wu Q; Simmerling C ff19SB: Amino-acid-specific protein backbone parameters trained against quantum mechanics energy surfaces in solution. J. Chem. Theory Comput 2020, 16, 528–552. [DOI] [PubMed] [Google Scholar]
- (38).Maier JA; Martinez C; Kasavajhala K; Wickstrom L; Hauser KE; Simmerling C ff14SB: improving the accuracy of protein side chain and backbone parameters from ff99SB. J. Chem. Theory Comput 2015, 11, 3696–3713. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (39).Hornak V; Abel R; Okur A; Strockbine B; Roitberg A; Simmerling C Comparison of multiple Amber force fields and development of improved protein backbone parameters. Proteins: Struct., Funct., Bioinf 2006, 65, 712–725. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (40).Zgarbová M; Sponer J; Jureckč P Z-DNA as a touchstone for additive empirical force fields and a refinement of the alpha/gamma DNA torsions for AMBER. J. Chem. Theory Comput 2021, 17, 6292–6301. [DOI] [PubMed] [Google Scholar]
- (41).Zgarbová M; Sponer J; Otyepka M; Cheatham TE III; Galindo-Murillo R; Jurecka P Refinement of the sugar–phosphate backbone torsion beta for AMBER force fields improves the description of Z-and B-DNA. J. Chem. Theory Comput 2015, 11, 5723–5736. [DOI] [PubMed] [Google Scholar]
- (42).Zgarbová M; Otyepka M; šponer J; Mládek A; Banáš P; Cheatham TE III; Jurecka P Refinement of the Cornell et al. nucleic acids force field based on reference quantum chemical calculations of glycosidic torsion profiles. J. Chem. Theory Comput 2011, 7, 2886–2902. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (43).Salomon-Ferrer R; Case DA; Walker RC An overview of the Amber biomolecular simulation package. Wiley Interdiscip. Rev.: Comput. Mol. Sci 2013, 3, 198–210. [Google Scholar]
- (44).Cardamone S; Hughes TJ; Popelier PL Multipolar electrostatics. Phys. Chem. Chem. Phys 2014, 16, 10367–10387. [DOI] [PubMed] [Google Scholar]
- (45).Warshel A; Kato M; Pisliakov AV Polarizable force fields: history, test cases, and prospects. J. Chem. Theory Comput 2007, 3, 2034–2045. [DOI] [PubMed] [Google Scholar]
- (46).Bedrov D; Piquemal J-P; Borodin O; MacKerell AD Jr.; Roux B; Schröder C Molecular dynamics simulations of ionic liquids and electrolytes using polarizable force fields. Chem. Rev 2019, 119, 7940–7995. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (47).Unke OT; Devereux M; Meuwly M Minimal distributed charges: Multipolar quality at the cost of point charge electrostatics. J. Chem. Phys 2017, 147, 161712. [DOI] [PubMed] [Google Scholar]
- (48).Ponder JW; Wu C; Ren P; Pande VS; Chodera JD; Schnieders MJ; Haque I; Mobley DL; Lambrecht DS; DiStasio RA Jr.; et al. Current status of the AMOEBA polarizable force field. J. Phys. Chem. B 2010, 114, 2549–2564. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (49).Elking D; Darden T; Woods RJ Gaussian induced dipole polarization model. J. Comput. Chem 2007, 28, 1261–1274. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (50).Elking DM; Cisneros GA; Piquemal J-P; Darden TA; Pedersen LG Gaussian multipole model (GMM). J. Chem. Theory Comput 2010, 6, 190–202. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (51).Elking DM; Perera L; Duke R; Darden T; Pedersen LG Atomic forces for geometry-dependent point multipole and Gaussian multipole models. J. Comput. Chem 2010, 31, 2702–2713. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (52).Cisneros GA; Elking D; Piquemal J-P; Darden TA Numerical fitting of molecular properties to Hermite Gaussians. J. Phys. Chem. A 2007, 111, 12049–12056. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (53).Hu H; Lu Z; Yang W Fitting molecular electrostatic potentials from quantum mechanical calculations. J. Chem. Theory Comput 2007, 3, 1004–1013. [DOI] [PubMed] [Google Scholar]
- (54).Wang J; Cieplak P; Luo R; Duan Y Development of polarizable Gaussian model for molecular mechanical calculations I: Atomic polarizability parameterization to reproduce ab initio anisotropy. J. Chem. Theory Comput 2019, 15, 1146–1158. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (55).Zhao S; Cieplak P; Duan Y; Luo R Transferability of the Electrostatic Parameters of the Polarizable Gaussian Multipole Model. J. Chem. Theory Comput 2023, 19, 924–941. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (56).Wei H; Qi R; Wang J; Cieplak P; Duan Y; Luo R Efficient formulation of polarizable Gaussian multipole electrostatics for biomolecular simulations. J. Chem. Phys 2020, 153, 114116. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (57).Wei H; Cieplak P; Duan Y; Luo R Stress tensor and constant pressure simulation for polarizable Gaussian multipole model. J. Chem. Phys 2022, 156, 114114. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (58).Huang Z; Zhao S; Cieplak P; Duan Y; Luo R; Wei H Optimal scheme to achieve energy conservation in induced dipole models. J. Chem. Theory Comput 2023, 19 (15), 5047–5057, DOI: 10.1021/acs.jctc.3c00226. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (59).Case DA; Aktulga HM; Belfon K; Ben-Shalom I; Brozell SR; Cerutti DS; Cheatham TE III; Cruzeiro VWD; Darden TA; Duke RE et al. Amber 2022; University of California, San Francisco, 2022. [Google Scholar]
- (60).Walker B; Liu C; Wait E; Ren P Automation of AMOEBA polarizable force field for small molecules: Poltype 2. J. Comput. Chem 2022, 43, 1530–1542. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (61).Slater JC The self consistent field and the structure of atoms. Phys. Rev 1928, 32, 339. [Google Scholar]
- (62).Hartree DR The wave mechanics of an atom with a non-Coulomb central field. Part I. Theory and methods. Math. Proc. Cambridge Philos. Soc 1928, 24, 89–110. [Google Scholar]
- (63).Lee C; Yang W; Parr RG Development of the Colle-Salvetti correlation-energy formula into a functional of the electron density. Phys. Rev. B 1988, 37, 785. [DOI] [PubMed] [Google Scholar]
- (64).Becke AD Density-functional thermochemistry. III. The role of exact exchange. J. Chem. Phys 1993, 98, 5648–5652. [Google Scholar]
- (65).Yu HS; He X; Li SL; Truhlar DG MN15: A Kohn–Sham global-hybrid exchange–correlation density functional with broad accuracy for multi-reference and single-reference systems and noncovalent interactions. Chem. Sci 2016, 7, 5032–5051. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (66).Zhao Y; Truhlar DG The M06 suite of density functionals for main group thermochemistry, thermochemical kinetics, noncovalent interactions, excited states, and transition elements: two new functionals and systematic testing of four M06-class functionals and 12 other functionals. Theor. Chem. Acc 2008, 120, 215–241. [Google Scholar]
- (67).Frisch MJ; Head-Gordon M; Pople JA A direct MP2 gradient method. Chem. Phys. Lett 1990, 166, 275–280. [Google Scholar]
- (68).Frisch MJ; Head-Gordon M; Pople JA Semi-direct algorithms for the MP2 energy and gradient. Chem. Phys. Lett 1990, 166, 281–289. [Google Scholar]
- (69).Head-Gordon M; Pople JA; Frisch MJ MP2 energy evaluation by direct methods. Chem. Phys. Lett 1988, 153, 503–506. [Google Scholar]
- (70).Head-Gordon M; Head-Gordon T Analytic MP2 frequencies without fifth-order storage. Theory and application to bifurcated hydrogen bonds in the water hexamer. Chem. Phys. Lett 1994, 220, 122–128. [Google Scholar]
- (71).Chai J-D; Head-Gordon M Long-range corrected hybrid density functionals with damped atom–atom dispersion corrections. Phys. Chem. Chem. Phys 2008, 10, 6615–6620. [DOI] [PubMed] [Google Scholar]
- (72).Purvis GD III; Bartlett RJ A full coupled-cluster singles and doubles model: The inclusion of disconnected triples. J. Chem. Phys 1982, 76, 1910–1918. [Google Scholar]
- (73).Scuseria GE; Janssen CL; Schaefer HF Iii An efficient reformulation of the closed-shell coupled cluster single and double excitation (CCSD) equations. J. Chem. Phys 1988, 89, 7382–7387. [Google Scholar]
- (74).Scuseria GE; Schaefer HF III Is coupled cluster singles and doubles (CCSD) more computationally intensive than quadratic configuration interaction (QCISD)? J. Chem. Phys 1989, 90, 3700–3703. [Google Scholar]
- (75).Besler BH; Merz KM Jr.; Kollman PA Atomic charges derived from semiempirical methods. J. Comput. Chem 1990, 11, 431–439. [Google Scholar]
- (76).Frisch MJ; Trucks GW; Schlegel HB; Scuseria GE; Robb MA; Cheeseman JR; Scalmani G; Barone V; Petersson GA; Nakatsuji H; Li X; Caricato M; Marenich AV; Bloino J; Janesko BG; Gomperts R; Mennucci B; Hratchian HP; Ortiz JV; Izmaylov AF; Sonnenberg JL; Williams-Young D; Ding F; Lipparini F; Egidi F; Goings J; Peng B; Petrone A; Henderson T; Ranasinghe D; Zakrzewski VG; Gao J; Rega N; Zheng G; Liang W; Hada M; Ehara M; Toyota K; Fukuda R; Hasegawa J; Ishida M; Nakajima T; Honda Y; Kitao O; Nakai H; Vreven T; Throssell K; Montgomery JA Jr.; Peralta JE; Ogliaro F; Bearpark MJ; Heyd JJ; Brothers EN; Kudin KN; Staroverov VN; Keith TA; Kobayashi R; Normand J; Raghavachari K; Rendell AP; Burant JC; Iyengar SS; Tomasi J; Cossi M; Millam JM; Klene M; Adamo C; Cammi R; Ochterski JW; Martin RL; Morokuma K; Farkas O; Foresman JB; Fox DJ Gaussian16, Revision A.01; Gaussian Inc.: Wallingford CT, 2016. [Google Scholar]
- (77).Applequist J; Carl JR; Fung K-K Atom dipole interaction model for molecular polarizability. Application to polyatomic molecules and determination of atom polarizabilities. J. Am. Chem. Soc 1972, 94, 2952–2960. [Google Scholar]
- (78).Faerman CH; Price SL A transferable distributed multipole model for the electrostatic interactions of peptides and amides. J. Am. Chem. Soc 1990, 112, 4915–4926. [Google Scholar]
- (79).Hickey AL; Rowley CN Benchmarking quantum chemical methods for the calculation of molecular dipole moments and polarizabilities. J. Phys. Chem. A 2014, 118, 3678–3687. [DOI] [PubMed] [Google Scholar]
- (80).Tian L; CHEN F-W Comparison of computational methods for atomic charges. Acta Phys.-Chim. Sin 2012, 28, 1–18. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
The source code of PyRESP_GEN can be downloaded from https://github.com/csu1505110121/pyresp_gen.


