Multifile Partitioning for Record Linkage and Duplicate Detection

Abstract

Merging datafiles containing information on overlapping sets of entities is a challenging task in the absence of unique identifiers, and is further complicated when some entities are duplicated in the datafiles. Most approaches to this problem have focused on linking two files assumed to be free of duplicates, or on detecting which records in a single file are duplicates. However, it is common in practice to encounter scenarios that fit somewhere in between or beyond these two settings. We propose a Bayesian approach for the general setting of multifile record linkage and duplicate detection. We use a novel partition representation to propose a structured prior for partitions that can incorporate prior information about the data collection processes of the datafiles in a flexible manner, and extend previous models for comparison data to accommodate the multifile setting. We also introduce a family of loss functions to derive Bayes estimates of partitions that allow uncertain portions of the partitions to be left unresolved. The performance of our proposed methodology is explored through extensive simulations.

1. Introduction

When information on individuals is collected across multiple datafiles, it is natural to merge these datafiles to harness all available information. This merging requires identifying coreferent records, i.e., records that refer to the same entity, which is not trivial in the absence of unique identifiers. This problem arises in many fields, including public health (Hof et al. 2017), official statistics (Jaro 1989), political science (Enamorado et al. 2019), and human rights (Sadinle 2014, 2017, Ball and Price 2019).

Most approaches in this area have thus far focused on one of two settings. Record linkage has traditionally referred to the setting where the goal is to find coreferent records across two datafiles, where the files are assumed to be free of duplicates. Duplicate detection has traditionally referred to the setting where the goal is to find coreferent records within a single file. In practice, however, it is common to encounter problems that fit somewhere in between or beyond these two settings. For example, we could have multiple datafiles that are all assumed to be free of duplicates, or we might have duplicates in some files but not in others. In these general settings, the data collection processes for the different datafiles possibly introduce different patterns of duplication, measurement error, and missingness into the records. Further, dependencies among these data collection processes determine which specific subsets of files contain records of the same entity. We refer to this general setting as multifile record linkage and duplicate detection.

Traditional approaches to record linkage and duplicate detection have mainly followed the seminal work of Fellegi and Sunter (1969), by modeling comparisons of fields between pairs of records in a mixture model framework (Winkler 1994, Jaro 1989, Larsen and Rubin 2001). These approaches work under, and take advantage of, the intuitive assumption that coreferent records will look similar, and non-coreferent records will look dissimilar. However, these approaches output independent decisions for the coreference status of each pair of records, necessitating the use of ad hoc post-processing steps to reconcile incompatible decisions that ignore the logical constraints of the problem.

Our approach to multifile record linkage and duplicate detection builds on previous Bayesian approaches where the parameter of interest is defined as a partition of the records. These Bayesian approaches have been carried out in two frameworks. In the direct-modeling framework, one directly models the fields of information contained in the records (Matsakis 2010, Tancredi and Liseo 2011, Liseo and Tancredi 2011, Steorts 2015, Steorts et al. 2016, Tancredi et al. 2020, Marchant et al. 2021, Enamorado and Steorts 2020), which requires a custom model for each type of field. While this framework can provide a plausible generative model for the records, it can be difficult to develop custom models for complicated fields like strings, so most approaches are limited to modeling categorical data, with some exceptions (Liseo and Tancredi 2011, Steorts 2015). In the comparison-based framework, following the traditional approaches, one models comparisons of fields between pairs of records (Fortini et al. 2001, Larsen 2005, Sadinle 2014, 2017). By modeling comparisons of fields, instead of the fields directly, a generic modeling approach can be taken for any field type, as long as there is a meaningful measure of similarity for that field type.

Sadinle and Fienberg (2013) generalized Fellegi and Sunter (1969) by linking K > 2 files with no duplicates. However, in addition to inheriting the issues of traditional approaches, their approach does not scale well in the number of files or the file sizes encountered in practice. Steorts et al. (2016) presented a Bayesian approach in the direct-modeling framework for the general setting of multifile record linkage and duplicate detection, which has been extended by Steorts (2015) and Marchant et al. (2021). This approach uses a flat prior on arbitrary labels of partitions, which incorporates unintended prior information.

In light of the shortcomings of existing approaches, we propose an extension of Bayesian comparison-based models that explicitly handles the setting of multifile record linkage and duplicate detection. We first present in Section 2 a parameterization of partitions specific to the context of multifile record linkage and duplicate detection. Building on this parameterization, in Section 3 we construct a structured prior for partitions that can incorporate prior information about the data collection processes of the files in a flexible manner. As a by-product, a family of priors for K-partite matchings is constructed. In Section 4 we construct a likelihood function for comparisons of fields between pairs of records that accommodates possible differences in the datafile collection processes. In Section 5 we present a family of loss functions that we use to derive Bayes estimates of partitions. These loss functions have an abstain option which allow portions of the partition with large amounts of uncertainty to be left unresolved. Finally, we explore the performance of our proposed methodology through simulation studies in Section 6. In the Appendix we present an application of our proposed approach to link three Colombian homicide record systems.

2. Multifile Partitioning

Consider K files X₁, ⋯, X_K, each containing information on possibly overlapping subsets of a population of entities. The goal of multifile record linkage and duplicate detection is to identify the sets of records in X₁, ⋯, X_K that are coreferent, as illustrated in Figure 1. Identifying coreferent records across datafiles represents the goal of record linkage, and identifying coreferent records within each file represents the goal of duplicate detection.

Fig. 1.

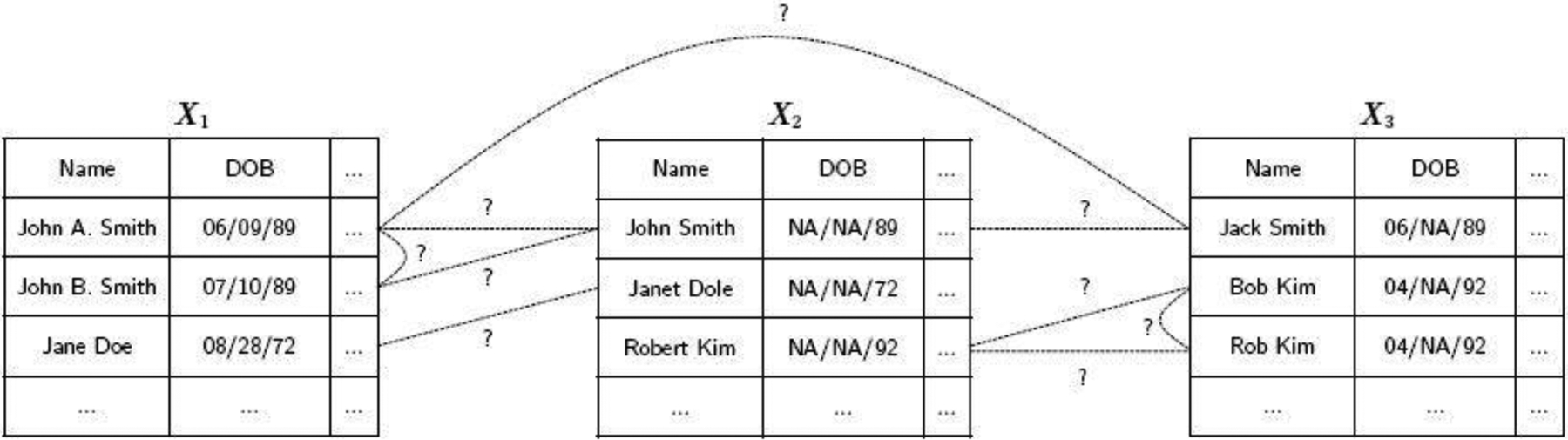
A toy example of the multifile record linkage and duplicate detection problem.

We denote the number of records contained in datafile X_k as r_k, and the total number of records across all files as $r=\sum _{k=1}^K{r}_k$. We label the records in all datafiles in a consecutive order, that is, those in X₁ as R₁ = (1, ⋯, r₁), those in X₂ as R₂ = (r₁ + 1, ⋯, r₁ + r₂), and so on, finally labeling the records in X_K as $R_K=\left(\sum _{k=1}^{K-1}{r}_k+1,\cdots ,r\right)$. We denote [r] = (1, ⋯, r), where it is clear that [r] = (R₁, ⋯, R_K), which represents all the records coming from all datafiles.

Formally, multifile record linkage and duplicate detection is a partitioning problem. A partition of a set is a collection of disjoint subsets, called clusters, whose union is the original set. In this context, the term coreference partition refers to a partition $\mathcal{C}$ of all the records in X₁, ⋯, X_K, or equivalently a partition $\mathcal{C}$ of [r], such that each cluster $c\in \mathcal{C}$ is exclusively composed of all the records generated by a single entity (Matsakis 2010, Sadinle 2014). This implies that there is a one-to-one correspondence between the clusters in $\mathcal{C}$ and the entities represented in at least one of the datafiles. Estimating $\mathcal{C}$ is the goal of multifile record linkage and duplicate detection.

2.1. Multifile Coreference Partitions

In the setting of multifile record linkage and duplicate detection, the datafiles are the product of K data collection processes, which possibly introduce different patterns of duplication, measurement error, and missingness. This indicates that records coming from different datafiles should be treated differently. To take this into account, we introduce the concept of a multifile coreference partition by endowing a coreference partition $\mathcal{C}$ with additional structure to preserve the information on where records come from. Each cluster $c\in \mathcal{C}$ can be decomposed as c = c₁ ∪⋯∪ c_k ∪⋯∪ c_K, where c_k is the subset of records in cluster c that belong to datafile X_k, which leads us to the following definition.

Definition 1. The multifile coreference partition of datafiles X₁, ⋯, X_K is obtained from the coreference partition $\mathcal{C}$ by expressing each cluster $c\in \mathcal{C}$ as a K-tuple (c₁, ⋯, c_K), where c_k represents the records of c that come from datafile X_k.

For simplicity we will continue using the notation $\mathcal{C}$ to denote a multifile coreference partition, although technically this new structure is richer and therefore different from a coreference partition that does not preserve the datafile membership of the records. The multifile representation of partitions is useful for decoupling the features that are important for within-file duplicate detection or for across-files record linkage.

For duplicate detection, the goal is to identify coreferent records within each datafile. This can be phrased as estimating the within-file coreference partition ${\mathcal{C}}_k$ of each datafile X_k. Clearly, these ${\mathcal{C}}_k$ can be obtained from the multifile partition $\mathcal{C}$ by extracting the kth entry of each cluster $c=\left(c_1,\dots ,c_K\right)\in \mathcal{C}$. Two useful summaries of a given within-file partition ${\mathcal{C}}_k$ are the number of within-file clusters $n_k=\left|{\mathcal{C}}_k\right|$, which is the number of unique entities represented in datafile X_k, and the within-file cluster sizes $d_k=\left\{\left|c_k\right|:c_k\in {\mathcal{C}}_k\right\}$, which represent the number of records associated with each entity in datafile X_k.

On the other hand, in record linkage the goal is to identify coreferent records across datafiles. Given the within-file partitions, ${\mathcal{C}}_1,\cdots ,{\mathcal{C}}_K$, the goal can be phrased as identifying which clusters across these partitions represent the same entities. This across-datafiles structure can be formally represented by a K-partite matching. Given K sets V₁, ⋯, V_K, a K-partite matching $\mathcal{M}$ is a collection of subsets from ${\cup }_{k=1}^K{V}_k$ such that each $m\in \mathcal{M}$ contains maximum one element from each V_k. If we think of each V_k as the set of clusters ${\mathcal{C}}_k$ representing the entities in datafile X_k, then it is clear that the goal is to identify the K-partite matching $\mathcal{M}$ that puts together the clusters that refer to the same entities across datafiles. This structure can be extracted from a multifile coreference partition $\mathcal{C}$, given that each element $c=\left(c_1,\dots ,c_K\right)\in \mathcal{C}$ contains the coreferent clusters across all within-file partitions. Indeed, a multifile coreference partition can be thought of as a K-partite matching of within-file coreference partitions.

A useful summary of the across-datafile structure is the amount of entity-overlap between datafiles, represented by the number of clusters $c=\left(c_1,\dots ,c_K\right)\in \mathcal{C}$ with records in specific subsets of the files. We can concisely summarize the entity-overlap of the datafiles through a contingency table. In particular, consider a 2^K contingency table with cells indexed by h ∈ {0, 1}^K and corresponding cell counts n_h. Here, h represents a pattern of inclusion of an entity in the datafiles, where a 1 indicates inclusion and a 0 exclusion. For instance, if K = 3, n₀₁₁ is the number of clusters $c=\left(c_1,c_2,c_3\right)\in \mathcal{C}$ representing entities with records in datafiles 2 and 3 but without records in datafile 1. We let $\mathcal{H}={\{0,1\}}^K\setminus {\left\{0\right\}}^K$ and denote the (incomplete) contingency table of counts as $n={\left\{n_h\right\}}_{h\in \mathcal{H}}$, which we refer to as the overlap table. We ignore the cell {0}^K which would represent entities that are not recorded in any of the K files. This cell is not of interest in this article, although it is the parameter of interest in population size estimation (see e.g. Bird and King 2018).

Example.

To illustrate the concept of a multifile partition, consider two files with five and seven records respectively, so that X₁ contains records 1 – 5 and X₂ contains records 6 – 12. Suppose the coreference partition is {{1,9},{2},{3,8,10,11},{4,5,7},{6},{12}}. The corresponding multifile partition is $\mathcal{C}=\{(\left\{1\right\},\left\{9\right\}),(\left\{2\right\},\varnothing ),(\left\{3\right\},\{8,10,11\}),(\{4,5\},\left\{7\right\}),(\varnothing ,\left\{6\right\}),(\varnothing ,\left\{12\right\})\}$. As illustrated in Figure 2, the within-file partitions can be extracted as ${\mathcal{C}}_1=\left\{\right\{1\},\{2\},\{3\},\{4,5\left\}\right\}$ and ${\mathcal{C}}_2=\left\{\right\{6\},\{7\},\{9\},\{8,10,11\},\{12\left\}\right\}$, and the within-file cluster sizes are d₁ = (1,1,1,2) and d₂ = (1,1,1,3,1). The overlap table in this case is {n₁₁, n₁₀, n₀₁}, indicating that n₁₁ = 3 entities are represented in both datafiles, n₁₀ = 1 entity is represented only in the first datafile, and n₀₁ = 2 entities are represented only in the second datafile. In total, there are $n_1=\left|{\mathcal{C}}_1\right|=n_{11}+n_{10}=4$ unique entities represented in X₁, $n_2=\left|{\mathcal{C}}_2\right|=n_{11}+n_{01}=5$ unique entities represented in X₂, and $n=|\mathcal{C}|=n_{11}+n_{10}+n_{01}=6$ entities among both datafiles.

Fig. 2.

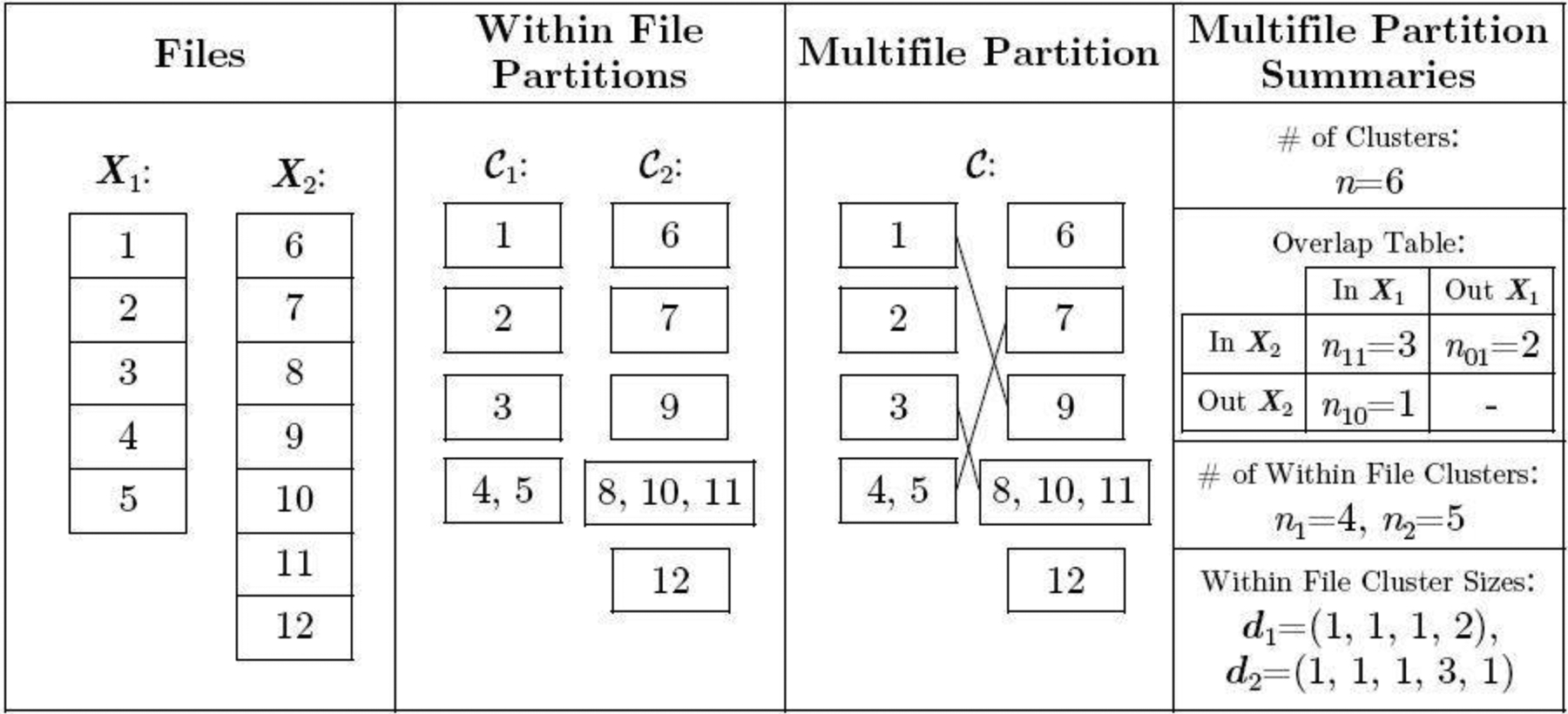
An illustration of a multifile partition of [12], where X₁ contains records 1 – 5 and X₂ contains records 6 – 12.

3. A Structured Prior for Multifile Partitions

Bayesian approaches to multifile record linkage and duplicate detection require prior distributions on multifile coreference partitions. We present a generative process for multifile partitions, building on our representation introduced in Section 2.1. The idea is to generate a multifile partition by first generating summaries that characterize it, as follows:

1. Generate the number of unique entities n represented in the datafiles, which also corresponds to the number of clusters of the multifile partition.

2. Given n, generate an overlap table $n={\left\{n_h\right\}}_{h\in \mathcal{H}}$ so that $n=\sum _{h\in \mathcal{H}}{n}_h$, where $\mathcal{H}={\{0,1\}}^K\setminus {\left\{0\right\}}^K$. From n we can derive the number of entities in datafile X_k as $n_k=\sum _{h\in \mathcal{H}}{h}_k{n}_h$, where h_k is the kth entry of h.

3. For each k = 1, ⋯, K, given n_k, independently generate a set of counts $d_k={\left\{d_{ki}\right\}}_{i=1}^{n_k}$, representing the number of records associated with each entity in file X_k. From d_k, we can derive the number of records in file X_k as ${r^{\prime }}_k=\sum _{i=1}^{n_k}{d}_{ki}$. Index the r′_k records as ${R^{\prime }}_k=\left(\sum _{l=1}^{k-1}{r^{\prime }}_l+1,\cdots ,\sum _{l=1}^k{r^{\prime }}_l\right)$.

4. For each k = 1, ⋯, K, given d_k, induce a within-file partition ${\mathcal{C}}_k$ by randomly allocating R′_k into n_k clusters of sizes $d_{k1},\cdots ,d_{k{n}_k}$.

5. Given the overlap table n and within-file partitions $\left\{{\mathcal{C}}_1,\cdots ,{\mathcal{C}}_K\right\}$, generate a K-partite matching of the within-file partitions by selecting uniformly at random from the set of all K-partite matchings with overlap table n. By definition, the result is a multifile coreference partition.

By parameterizing each step of this generative process, we can construct a prior distribution for multifile partitions, as we now show.

3.1. Parameterizing the Generative Process

Prior for the Number of Entities or Clusters.

In the absence of substantial prior information, we follow a simple choice for the prior on the number of clusters, by taking a uniform distribution over the integers less than some upper bound, U, i.e. $\mathbb{P}(n)=U^{-1}I(n\in \{1,\cdots ,U\})$. In practice, we set U to be the actual number of records across all datafiles r, which is observed. More informative specifications are discussed in Appendix A.

Prior for the Overlap Table.

Conditional on n, we use a Dirichlet-multinomial distribution as our prior on the overlap table $n={\left\{n_h\right\}}_{h\in \mathcal{H}}$. Given a collection of positive hyperparameters for each cell of the overlap table, $\alpha ={\left\{{\alpha }_h\right\}}_{h\in \mathcal{H}}$, and letting ${\alpha }_0=\sum _{h\in \mathcal{H}}{\alpha }_h$, the prior for the overlap table under this choice is $\mathbb{P}(n\mid n)=\left[(n!)\Gamma \left({\alpha }_0\right)/\Gamma \left(n+{\alpha }_0\right)\right]{\prod }_{h\in \mathcal{H}}\left[\Gamma \left(n_h+{\alpha }_h\right)/\left(n_h!\right)\Gamma \left({\alpha }_h\right)\right]$. Due to conjugacy, α can be interpreted as prior cell counts, which can be used to incorporate prior information about the overlap between datafiles. In the absence of substantial prior information, when the number of files is not too large and the overlap table is not expected to be sparse, we recommend setting α = (1, ⋯, 1). In Appendix A we discuss alternative specifications when the overlap table is expected to be sparse.

Prior for the Within-File Cluster Sizes.

Given the number of entities in datafile X_k, $n_k=\sum _{h\in \mathcal{H}}{h}_k{n}_h$, we generate the within-file cluster sizes $d_k={\left\{d_{ki}\right\}}_{i=1}^{n_k}$ assuming that $d_{k1},\cdots ,d_{k{n}_k}\mid n_k\stackrel{iid}{~}{p}_k(\cdot )$. Here p_k (·) represents the probability mass function of a distribution on the positive integers, so that $\mathbb{P}\left(d_k\mid n_k\right)=\prod _{i=1}^{n_k}{p}_k\left(d_{ki}\right)$. We do not expect a priori many duplicates per entity, and therefore we expect the counts in d_k to be mostly ones or to be very small (Miller et al. 2015, Zanella et al. 2016). We therefore use a similar approach to Klami and Jitta (2016), and use distributions truncated to the range {1, ⋯, U_k}, where U_k is a file-specific upper bound on cluster sizes. We further use distributions where prior mass is concentrated at small values. A default specification is to use a Poisson distribution with mean 1 truncated to {1, ⋯, U_k}, i.e. p_k (d_ki) ∝ (d_ki!)^–1 I (d_ki ∈{1, ⋯, U_k}). More informative options could be used for p_k(·) by using any distribution on {1, ⋯, U_k}, where this could vary from file to file if some files were known to have more or less duplication. See Appendix A for more discussion.

Prior for the Within-File Partitions.

Given the within-file cluster sizes d_k, the number of ways of assigning $d_{k1},\cdots ,d_{k{n}_k}$ records to clusters 1, ⋯, n_k, respectively, is given by the multinomial coefficient ${r^{\prime }}_k!/\prod _{i=1}^{n_k}{d}_{ki}!$, with ${r^{\prime }}_k=\sum _{i=1}^{n_k}{d}_{ki}$. However, the ordering of the clusters is irrelevant for constructing the within-file partition ${\mathcal{C}}_k$ of R′_k. There are n_k ! ways of ordering the n_k clusters of ${\mathcal{C}}_k$, which leads to ${r^{\prime }}_k!/\left(n_k!\prod _{i=1}^{n_k}{d}_{ki}!\right)$ partitions of R′_k into clusters of sizes $d_{k1},\cdots ,d_{k{n}_k}$. We then have $\mathbb{P}\left({\mathcal{C}}_k\mid d_k\right)=\left(n_k!/{r^{\prime }}_k!\right)\prod _{i=1}^{n_k}{d}_{ki}!$.

Prior for the K-Partite Matching.

Given the overlap table n and the within-file partitions $\left\{C_1,\cdots ,C_K\right\}$, our prior over K-partite matchings of the within-file partitions is uniform. Thus we just need to count the number of K-partite matchings with overlap table n. This is taken care of by Proposition 1, proven in Appendix A.

Proposition 1. The number of K-partite matchings that have the same overlap table, $n={\left\{n_h\right\}}_{h\in \mathcal{H}}$, is $\prod _{k=1}^K{n}_k!/\prod _{h\in \mathcal{H}}{n}_h!$. Thus $\mathbb{P}\left(\mathcal{C}\mid {\left\{{\mathcal{C}}_k\right\}}_{k=1}^K,n\right)=\prod _{h\in \mathcal{H}}{n}_h!/\prod _{k=1}^K{n}_k!$.

The Structured Prior for Multifile Partitions.

Letting quantities followed by $(\mathcal{C})$ mean they are computable from $\mathcal{C}$, the density of our structured prior for multifile partitions is

$$\begin{gathered} \mathbb{P}(\mathcal{C})=\mathbb{P}(n)\mathbb{P}(n\mid n)\prod _{k=1}^K\left[\mathbb{P}\left(d_k\mid n_k\right)\mathbb{P}\left({\mathcal{C}}_k\mid d_k\right)\right]\mathbb{P}\left(\mathcal{C}\mid {\left\{{\mathcal{C}}_k\right\}}_{k=1}^K,n\right) \\ =\mathbb{P}(n(\mathcal{C}))\frac{n(\mathcal{C})!\Gamma \left({\alpha }_0\right)}{\Gamma \left(n(\mathcal{C})+{\alpha }_0\right)}\prod _{\mathit{h}\in \mathcal{H}}\left[\frac{\Gamma \left(n_{\mathit{h}}(\mathcal{C})+{\alpha }_{\mathit{h}}\right)}{\Gamma \left({\alpha }_{\mathit{h}}\right)}\right]\prod _{k=1}^K\left[\frac{1}{{r^{\prime }}_k(\mathcal{C})!}\prod _{c_k\in {\mathcal{C}}_k}\left|c_k\right|!p_k\left(\left|c_k\right|\right)\right]. \end{gathered}$$ (1)

3.2. Comments and Related Literature

The structured prior for multifile partitions allows us to incorporate prior information about the total number of clusters, the overlap between files, and the amount of duplication in each file. If we restrict the prior for the within-file cluster sizes to be p_k (d_ki) = I (d_ki = 1) for a given datafile X_k, then we enforce the assumption that there are no duplicates in that file. Imposing this restriction for all datafiles leads to the special case of a prior for K-partite matchings, which is of independent interest, as we are not aware of any such constructions outside of the bipartite case (Fortini et al. 2001, Larsen 2005, Sadinle 2017).

Our prior construction, where priors are first placed on interpretable summaries of a partition and then a uniform prior is placed on partitions which have those summaries, mimics the construction of the priors on bipartite matchings of Fortini et al. (2001), Larsen (2005) and Sadinle (2017), and the Kolchin and allelic partition priors of Zanella et al. (2016) and Betancourt, Sosa and Rodríguez (2020). While the Kolchin and allelic partition priors could both be used as priors for multifile partitions, these do not incorporate the datafile membership of records. Using these priors in the multifile setting would imply that the sizes of clusters containing records from only one file have the same prior distribution as the sizes of clusters containing records from two files, which should not be true in general.

Miller et al. (2015) and Zanella et al. (2016) proposed the microclustering property as a desirable requirement for partition priors in the context of duplicate detection: denoting the size of the largest cluster in a partition of [r] by M_r, a prior satisfies the microclustering property if M_r / r → 0 in probability as r →∞. A downside of priors with this property is that they can still allow the size of the largest cluster to go to ∞ as r increases. For this reason Betancourt, Sosa and Rodríguez (2020) introduced the stronger bounded microclustering property, which we believe is more practically important: for any r, M_r is finite with probability 1. Our prior satisfies the bounded microclustering property as $M_r\le \sum _{k=1}^K{U}_k$.

While our parameter of interest is a partition $\mathcal{C}$ of r records, the prior developed in this section is a prior for a partition of a random number of records. In practice we condition on the file sizes, ${\left\{r_k\right\}}_{k=1}^K$, and use the prior $\mathbb{P}\left(\mathcal{C}\mid {\left\{r_k\right\}}_{k=1}^K\right)\propto \mathbb{P}(\mathcal{C})I\left({r^{\prime }}_k(\mathcal{C})=r_k(\mathcal{C})\text{for}\text{all}k\right)$, which alters the interpretation of the prior. A similar problem occurs for the Kolchin partition priors of Zanella et al. (2016). This motivated the exchangeable sequences of clusters priors of Betancourt, Zanella and Steorts (2020), which are similar to Kolchin partition priors, but lead to a directly interpretable prior specification. It would be interesting in future work to see if an analogous prior could be developed for our structured prior for multifile partitions. Despite this limitation, we demonstrate in simulations in Section 6 that incorporating strong prior information into our structured prior for multifile partitions can lead to improved frequentist performance over a default specification.

4. A Model for Comparison Data

We now introduce a comparison-based modeling approach to multifile record linkage and duplicate detection, building on the work of Fellegi and Sunter (1969), Jaro (1989), Winkler (1994), Larsen and Rubin (2001), Fortini et al. (2001), Larsen (2005) and Sadinle (2014, 2017). Working under the intuitive assumption that coreferent records will look similar, and non-coreferent records will look dissimilar, these approaches construct statistical models for comparisons computed between each pair of records.

There are two implications of the multifile setting described in Section 2 that are important to consider when constructing a model for the comparison data. First, models for the comparison data should account for the fact that the distribution of the comparisons between record pairs might potentially change across different pairs of files. For example, if files X_k and X_k′ are not accurate, whereas files X_q and X_q′ are, then the distribution of comparisons between X_k and X_k′ will look very different compared with the distribution of comparisons between X_q and X_q′. Second, the fields available for comparison will vary across pairs of files. For example, files X_k and X_k′ may have collected information on a field that file X_q did not. In this scenario, we would like a model that is able to utilize this extra field when linking X_k and X_k′, even though it is not available in X_q. In this section we introduce a Bayesian comparison-based model that explicitly handles the multifile setting by constructing a likelihood function that models comparisons of fields between different pairs of files separately. The separate models are able to adapt to the level of noise of each file pair, and the maximal number of fields are able to be compared for each file pair.

4.1. Comparison Data

We construct comparison vectors for pairs of records to provide evidence for whether they correspond to the same entity. For k ≤ k′, let ${\mathcal{P}}_{k{k}^{\prime }}=\left\{(i,j):i<j,i\in X_k,j\in X_{k^{\prime }}\right\}$ denote the set of all record pairs between files X_k and X_k′, and let F be the total number of different fields available from the K files. For each file pair (k, k′), k ≤ k′, and record pair $(i,j)\in {\mathcal{P}}_{k{k}^{\prime }}$, we compare each field f = 1, …, F using a similarity measure ${\mathcal{S}}_f(i,j)$, which will depend on the data type of field f. For unstructured categorical fields such as race, ${\mathcal{S}}_f$ can be a binary comparison which checks for agreement. For more structured fields containing strings or numbers, ${\mathcal{S}}_f$ should be able to capture partial agreements. For example, string fields can be compared using a string metric like the Levenshtein edit distance (see e.g. Bilenko et al. 2003), and numeric fields can be compared using absolute differences. Comparison ${\mathcal{S}}_f(i,j)$ will be missing if field f is not recorded in record i or record j, which includes the case where field f is not recorded in datafiles X_k or X_k′.

While we could directly model the similarity measures ${\mathcal{S}}_f(i,j)$, this would require a custom model for each type of comparison, which inherits similar problems to the direct modeling of the fields themselves. Instead, we follow Winkler (1990) and Sadinle (2014, 2017) in dividing the range of ${\mathcal{S}}_f$ into L_f + 1 intervals $I_{f0},I_{f1},\cdots ,I_{f{L}_f}$ that represent varying levels of agreement, with I_f0 representing the highest level of agreement, and $I_{f{L}_f}$ representing the lowest level of agreement. We then let ${\gamma }_{ij}^f=l$ if ${\mathcal{S}}_f(i,j)\in I_{fl}$, where larger values of ${\gamma }_{ij}^f$ represent larger disagreements between records i and j in field f. Finally, we form the comparison vector ${\gamma }_{ij}=\left({\gamma }_{ij}^1,\cdots ,{\gamma }_{ij}^F\right)$. Constructing the comparison data this way allows us to build a generic modeling approach. In particular, extending Fortini et al. (2001), Larsen (2005) and Sadinle (2014, 2017), our model for the comparison data is

$${\gamma }_{ij}\mid \mathcal{C}(i)=\mathcal{C}(j),(i,j)\in {\mathcal{P}}_{k{k}^{\prime }}\stackrel{iid}{~}{\text{M}}_{k{k}^{\prime }}\left(m_{k{k}^{\prime }}\right),$$

$${\gamma }_{ij}\mid \mathcal{C}(i)\ne \mathcal{C}(j),(i,j)\in {\mathcal{P}}_{k{k}^{\prime }}\stackrel{iid}{~}{\cup }_{k{k}^{\prime }}\left(u_{k{k}^{\prime }}\right),$$

where $\mathcal{C}$ is a multifile partition, $\mathcal{C}(i)$ denotes record i’s cluster in $\mathcal{C}$, $\mathcal{C}(i)=\mathcal{C}(j)$ indicates that records i and j are coreferent, M_kk′ (m_kk′) is a model for the comparison data among coreferent record pairs from the file pair X_k and X_k′, U_kk′ (u_kk′) is a model for the comparison data among non-coreferent record pairs from datafile pair X_k and X_k′, and m_kk′ and u_kk′ are vectors of parameters.

In the next section we make two further assumptions that simplify the model parameterization. Before doing so, we note a few limitations of our comparison-based model. First, computing comparison vectors scales quadratically in the number of records. Second, comparison vectors for different record pairs are not actually independent conditional on the partition (see Section 2 of Tancredi and Liseo 2011). Third, modeling discretized comparisons of record fields represents a loss of information. While the first limitation is computational and unavoidable in the absence of blocking (see Appendix B), the other two limitations are inferential. Despite these limitations, we find in Section 6 that the combination of our structured prior for multifile partitions and our comparison-based model can produce linkage estimates with satisfactory frequentist performance.

4.2. Conditional Independence and Missing Data

Under the assumptions that the fields in the comparison vectors are conditionally independent given the multifile partition of the records and that missing comparisons are ignorable (Sadinle 2014, 2017), the likelihood of the observed comparison data, γ^obs, becomes

$$\mathcal{L}\left(\mathcal{C},\Phi \mid {\mathit{\gamma }}^{obs}\right)=\prod _{k\le k^{\prime }}\prod _{f=1}^F\prod _{l=0}^{L_f}{\left(m_{k{k}^{\prime }}^{fl}\right)}^{a_{k{k}^{\prime }}^{fl}(\mathcal{C})}{\left(u_{k{k}^{\prime }}^{fl}\right)}^{b_{k{k}^{\prime }}^{fl}(\mathcal{C})}.$$ (2)

Here $m_{k{k}^{\prime }}^{fl}=\mathbb{P}\left({\gamma }_{ij}^f=l\mid \mathcal{C}(i)=\mathcal{C}(j),(i,j)\in {\mathcal{P}}_{k{k}^{\prime }}\right)$, $u_{k{k}^{\prime }}^{fl}=\mathbb{P}\left({\gamma }_{ij}^f=l\mid \mathcal{C}(i)\ne \mathcal{C}(j),(i,j)\in {\mathcal{P}}_{k{k}^{\prime }}\right)$, $a_{k{k}^{\prime }}^{fl}(\mathcal{C})=\sum _{(i,j)\in {\mathcal{P}}_{k{k}^{\prime }}}{I}_{obs}\left({\gamma }_{ij}^f\right)I\left({\gamma }_{ij}^f=l\right)I(\mathcal{C}(i)=\mathcal{C}(j))$, $b_{k{k}^{\prime }}^{fl}(\mathcal{C})=\sum _{(i,j)\in {\mathcal{P}}_{k{k}^{\prime }}}{I}_{obs}\left({\gamma }_{ij}^f\right)I\left({\gamma }_{ij}^f=l\right)I(\mathcal{C}(i)\ne \mathcal{C}(j))$, I_obs(·) is an indicator of whether its argument was observed, and Φ = (m, u) where m collects all of the $m_{k{k}^{\prime }}^f=\left(m_{k{k}^{\prime }}^{f0},\cdots ,m_{k{k}^{\prime }}^{f{L}_f}\right)$ and u collects all of the $u_{k{k}^{\prime }}^f=\left(u_{k{k}^{\prime }}^{f0},\cdots ,u_{k{k}^{\prime }}^{f{L}_f}\right)$. For a given multifile partition $\mathcal{C}$, $a_{k{k}^{\prime }}^{fl}(\mathcal{C})$ represents the number of record pairs in ${\mathcal{P}}_{k{k}^{\prime }}$ that belong to the same cluster with observed agreement at level l in field f, and $b_{k{k}^{\prime }}^{fl}(\mathcal{C})$ represents the number of record pairs in ${\mathcal{P}}_{k{k}^{\prime }}$ that do not belong to the same cluster with observed agreement at level l in field f.

5. Bayesian Estimation of Multifile Partitions

Bayesian estimation of the multifile coreference partition $\mathcal{C}$ is based on the posterior distribution $p\left(\mathcal{C},\Phi \mid {\gamma }^{obs}\right)\propto \mathbb{P}(\mathcal{C})p(\Phi )\mathcal{L}\left(\mathcal{C},\Phi \mid {\gamma }^{obs}\right)$, where $\mathbb{P}(\mathcal{C})$ is our structured prior for multifile partitions (1), $\mathcal{L}\left(\mathcal{C},\Phi \mid {\gamma }^{obs}\right)$ is the likelihood from our model for comparison data (2), and p(Φ) represents a prior distribution for the Φ = (m, u) model parameters. We now specify this prior p(Φ), outline a Gibbs sampler to sample from $p\left(\mathcal{C},\Phi \mid {\gamma }^{obs}\right)$, and present a strategy to obtain point estimates of the multifile partition $\mathcal{C}$.

5.1. Priors for m and u

We will use independent, conditionally conjugate priors for $m_{k{k}^{\prime }}^f$ and $u_{k{k}^{\prime }}^f$, namely $m_{k{k}^{\prime }}^f~\text{Dirichlet}\left({\mu }_{k{k}^{\prime }}^{f0},\cdots ,{\mu }_{k{k}^{\prime }}^{f{L}_f}\right)$ and $u_{k{k}^{\prime }}^f~\text{Dirichlet}\left(v_{k{k}^{\prime }}^{f0},\cdots ,v_{k{k}^{\prime }}^{f{L}_f}\right)$. In this article we will use a default specification of $\left({\mu }_{k{k}^{\prime }}^{f0},\cdots ,{\mu }_{k{k}^{\prime }}^{f{L}_f}\right)=\left(v_{k{k}^{\prime }}^{f0},\cdots ,v_{k{k}^{\prime }}^{f{L}_f}\right)=(1,\cdots ,1)$. We believe this prior specification is sensible for the u parameters, following the discussion in Section 3.2 of Sadinle (2014), as comparisons amongst non-coreferent records are likely to be highly variable and it is more likely than not that eliciting meaningful priors for them is too difficult. For the m parameters, it might be desirable in certain applications to introduce more information into the prior. For example, one could set ${\mu }_{k{k}^{\prime }}^{f0}>\cdots >{\mu }_{k{k}^{\prime }}^{f{L}_f}$ to incorporate the prior belief that higher levels of agreement should have larger prior probability than lower levels of agreement. Another route would be to use the sequential parameterization of the m parameters, and the associated prior recommendations, described in Sadinle (2014).

5.2. Posterior Sampling

In Appendix B we outline a Gibbs sampler that produces a sequence of samples ${\left\{{\mathcal{C}}^{[t]},{\Phi }^{[t]}\right\}}_{t=1}^T$ from the posterior distribution $p\left(\mathcal{C},\Phi \mid {\gamma }^{obs}\right)$, which we will use to obtain Monte Carlo approximations of posterior expectations involved in the derivation of point estimates $\mathcal{C}$, as presented in the next section. In Appendix B, we discuss the computational complexity of the Gibbs sampler, how computational performance can be improved through the usage of indexing techniques, and the initialization of the Gibbs sampler.

5.3. Point Estimation

In a Bayesian setting, one can obtain a point estimate $\mathcal{C}$ of the multifile partition using the posterior $\mathbb{P}\left(\mathcal{C}\mid {\gamma }^{obs}\right)=\int p\left(\mathcal{C},\Phi \mid {\gamma }^{obs}\right)d\Phi$ and a loss function $L(\mathcal{C},\mathcal{C})$. The Bayes estimate is the multifile partition $\mathcal{C}$ that minimizes the expected posterior loss $\mathbb{E}\left[L(\mathcal{C},\mathcal{C})\mid {\gamma }^{obs}\right]=\sum _{\mathcal{C}}L(\mathcal{C},\mathcal{C})\mathbb{P}\left(\mathcal{C}\mid {\gamma }^{obs}\right)$, although in practice such expectations are approximated using posterior samples. Previous examples of loss functions for partitions included Binder’s loss (Binder 1978) and the variation of information (Meilă 2007), both recently surveyed in Wade and Ghahramani (2018). The quadratic and absolute losses presented in Tancredi and Liseo (2011) are special cases of Binder’s loss, and Steorts et al. (2016) drew connections between their proposed maximal matching sets and the losses of Tancredi and Liseo (2011).

In many applications there may be much uncertainty on the linkage decision for some records in the datafiles. For example, in Figure 1 it is unclear which of the records with last name “Smith” are coreferent. It is thus desirable to leave decisions for some records unresolved, so that the records can be hand-checked during a clerical review, which is common in practice (see e.g. Ball and Price 2019). In the classification literature, leaving some decisions unresolved is done through a reject option (see e.g. Herbei and Wegkamp 2006), which here we will refer to as an abstain option. We will refer to point estimates with and without an abstain option as partial estimates and full estimates, respectively. We now present a family of loss functions for multifile partitions which incorporate an abstain option, building upon the family of loss functions for bipartite matchings presented in Sadinle (2017).

5.3.1. A Family of Loss Functions with an Abstain Option

For the purpose of this section we will represent a multifile partition $\mathcal{C}$ as a vector Z = (Z₁, ⋯, Z_r) of labels, where Z_i ∈{1, …, r}, such that Z_i = Z_j if $\mathcal{C}(i)=\mathcal{C}(j)$. We represent a Bayes estimate here as a vector Z = (Z₁, …, Z_r), where Z_i ∈{1, …, r, A}, with A representing an abstain option intended for records whose linkage decisions are not clear and need further review. We assign different losses to using the abstain option and to different types of matching errors. We propose to compute the overall loss additively, as $L(Z,Z)=\sum _{i=1}^r{L}_i(Z,Z)$. To introduce the expression for the ith-record-specific loss L_i (Z, Z), we use the notation Δ_ij = I (Z_i = Z_j), and likewise ${\widehat{\Delta }}_{ij}=I\left({\widehat{Z}}_i={\widehat{Z}}_j\right)$.

The proposed individual loss for record i is

$$L_i(Z,Z)=\{\begin{array}{ll}{\lambda }_A,\hfill & \text{if}{\widehat{Z}}_i=A,\hfill \\ 0,\hfill & \text{if}{\Delta }_{ij}={\widehat{\Delta }}_{ij}\text{for}\text{all}j\text{where}{\widehat{Z}}_j\ne A,\hfill \\ {\lambda }_{\text{FNM}},\hfill & \text{if}{\widehat{Z}}_i\ne A,\sum _{j\ne i}{\widehat{\Delta }}_{ij}=0,\sum _{j\ne i}{\Delta }_{ij}>0,\hfill \\ {\lambda }_{\text{FM}1},\hfill & \text{if}{\widehat{Z}}_i\ne A,\sum _{j\ne i}{\widehat{\Delta }}_{ij}>0,\sum _{j\ne i}{\Delta }_{ij}=0,\hfill \\ {\lambda }_{\text{FM}2},\hfill & \text{if}{\widehat{Z}}_i\ne A,\sum _{j\ne i}{\widehat{\Delta }}_{ij}>0,\sum _{j\ne i}\left(1-{\widehat{\Delta }}_{ij}\right){\Delta }_{ij}>0.\hfill \end{array}$$ (3)

That is, λ_A represents the loss from abstaining from making a decision; λ_FNM is the loss from a false non-match (FNM) decision, that is, deciding that record i does not match any other record $\left(\sum _{j\ne i}{\widehat{\Delta }}_{ij}=0\right)$ when in fact it does $\left(\sum _{j\ne i}{\Delta }_{ij}>0\right)$; λ_FM1 is the loss from a type 1 false match (FM1) decision, that is, deciding that record i matches other records $\left(\sum _{j\ne i}{\widehat{\Delta }}_{ij}=0\right)$ when it does not actually match any other record $\left(\sum _{j\ne i}{\Delta }_{ij}=0\right)$; and λ_FM2 is the loss from a type 2 false match (FM2), that is, a false match decision when record i is matched to other records $\left(\sum _{j\ne i}{\widehat{\Delta }}_{ij}>0\right)$ but it does not match all of the records it should be matching $\left(\sum _{j\ne i}\left(1-{\widehat{\Delta }}_{ij}\right){\Delta }_{ij}>0\right)$.

The posterior expected loss is $ℝ(Z)=\sum _{i=1}^r\mathbb{E}\left[L_i(Z,Z)\mid {\gamma }^{obs}\right]$, where

$$\mathbb{E}\left[L_i(\mathit{Z},\mathit{Z})\mid {\mathit{\gamma }}^{obs}\right]=\{\begin{array}{ll}{\lambda }_A,\hfill & \text{if}{\widehat{Z}}_i=A,\hfill \\ {\lambda }_{\text{FNM}}\mathbb{P}\left(\sum _{j\ne i}{\Delta }_{ij}>0\mid {\gamma }^{obs}\right),\hfill & \text{if}{\widehat{Z}}_i\ne A,\sum _{j\ne i}{\widehat{\Delta }}_{ij}=0,\hfill \\ {\lambda }_{\text{FM}1}\mathbb{P}\left(\sum _{j\ne i}{\Delta }_{ij}=0\mid {\gamma }^{obs}\right)+{\lambda }_{\text{FM}2}\mathbb{P}\left(\sum _{j\ne i}\left(1-{\widehat{\Delta }}_{ij}\right){\Delta }_{ij}>0\mid {\gamma }^{obs}\right)\hfill & \text{if}{\widehat{Z}}_i\ne A,\sum _{j\ne i}{\widehat{\Delta }}_{ij}>0,\hfill \end{array}$$ (4)

and quantities computed with respect to the posterior distribution, $\mathbb{P}\left(Z\mid {\gamma }^{obs}\right)$, can all be approximated using posterior samples. While this presentation is for general positive losses λ_FNM, λ_FM1, λ_FM2 and λ_A, these only have to be specified up to a proportionality constant (Sadinle 2017). If we do not want to allow the abstain option, then we can set λ_A = ∞ and the derived full estimate Z will have a linkage decision for all records. Although we have been using partition labelings Z, the expressions in (3) and (4) are invariant to different labelings of the same partition. In the two-file case, Sadinle (2017) provided guidance on how to specify the individual losses λ_FNM, λ_FM1, λ_FM2 and λ_A in cases where there is a notion of false matches being worse than false non-matches or vise versa. Sadinle (2017) also gave recommendations for default values of these losses that lead to good frequentist performance in terms not over- or under-matching across repeated samples. In Appendix C, we discuss how our proposed loss function differs from the loss function of Sadinle (2017) and propose a strategy for approximating the Bayes estimate.

6. Simulation Studies

To explore the performance of our proposed approach for linking three duplicate-free files, as in the application to the Colombian homicide record systems of Appendix E, we present two simulation studies under varying scenarios of measurement error and datafile overlap. The two studies correspond to scenarios with equal and unequal measurement error across files, respectively. Both studies present results based on full estimates. In Appendix D we further explore the performance of our proposed approach for linking three files with duplicates, with results based on full and partial estimates.

6.1. General Setup

We start by describing the general characteristics of the simulations. For each of the simulation scenarios we conduct 100 replications, for each of which we generate three files as follows. For each of n = 500 entities, $h\in \mathcal{H}$ is drawn from a categorical distribution with probabilities ${\left\{p_h\right\}}_{h\in \mathcal{H}}$, where h represents the subset of files the entity appears in, and so we change the values of ${\left\{p_h\right\}}_{h\in \mathcal{H}}$ across simulation scenarios to represent varying amounts of file overlap. Files are then created by generating the implied number of records for each entity. In the additional simulations considered in Appendix D, the generated number of records for each entity depends not only on h, but also on the duplication mechanism.

All records are generated using a synthetic data generator developed in Tran et al. (2013), which allows for the incorporation of different forms of measurement error in individual fields, along with dependencies between fields we would expect in applications. The data generator first generates clean records before distorting them to create the observed records. In particular, each observed record will have a fixed number of erroneous fields, where errors selected uniformly at random from a set of field dependent errors displayed in Table 3 of Sadinle (2014) (reproduced in Appendix D), with a maximum of two errors per field. We generate records with seven fields of information: sex, given name, family name, age, occupation, postal code, and phone number.

For each simulation replicate, we construct comparison vectors as given in Table 4 of Sadinle (2014) (reproduced in Appendix D). We use the model for comparison data proposed in Section 4 with flat priors on m and u as discussed in Section 5.1, and the structured prior proposed in Section 3 with a uniform prior on the number of clusters and α = (1, ⋯, 1) as described in Section 3.1. Using the Gibbs sampler presented in Appendix B we obtain 1, 000 samples from the posterior distribution of multifile partitions, and discard the first 100 as burn-in. In Appendix D we discuss convergence of the Gibbs sampler, present running times of the proposed approach, and present an extra simulation exploring the running time of the approach with a larger number of records. We then approximate the Bayes estimate Z for multifile partitions using the loss function described in Section 5.3.1 as described in Appendix C. For full estimates, we use the default values of λ_FNM = λ_FM1 = 1 and λ_FM2 = 2 recommended by Sadinle (2017). In Appendix D we explore alternative specifications of the loss function.

We will assess the performance of the Bayes estimate using precision and recall with respect to the true coreference partition Z. Let $\mathcal{P}$ be the set of all record pairs. Using notation from Section 5.3.1, let $TM(Z,Z)=\sum _{(i,j)\in \mathcal{P}}{\Delta }_{ij}{\widehat{\Delta }}_{ij}$ be the number of true matches (record pairs correctly declared coreferent), $FM(Z,Z)=\sum _{(i,j)\in \mathcal{P}}\left(1-{\Delta }_{ij}\right){\widehat{\Delta }}_{ij}$ be the number of false matches (record pairs incorrectly declared coreferent), and $FNM(Z,Z)=\sum _{(i,j)\in \mathcal{P}}{\Delta }_{ij}\left(1-{\widehat{\Delta }}_{ij}\right)$ the number of false non-matches (record pairs incorrectly declared non-coreferent). Then precision is TM (Z, Z) / [TM (Z, Z) + FM (Z, Z)], the proportion of record pairs declared as coreferent that were truly coreferent, and recall is TM (Z, Z) / [TM (Z, Z) + FNM (Z, Z)], the proportion of record pairs that were truly coreferent that were correctly declared as coreferent. Perfect performance corresponds to precision and recall both being 1. In the simulations, we computed the median, 2nd, and 98th percentiles of these measures over the 100 replicate data sets. Additionally, in Appendix D, we assess the performance of the Bayes estimate when estimating the number of entities, n.

6.2. Duplicate-Free Files, Equal Errors Across Files

In this simulation study we explore the performance of our methodology by varying the number of erroneous fields per record over {1,2,3,5}, and also varying ${\left\{p_h\right\}}_{h\in \mathcal{H}}$, which determines the amount of overlap, over four scenarios:

• High Overlap: p₀₀₁ = p₀₁₀ = p₁₀₀ = 0.4 / 3, p₀₁₁ = p₁₀₁ = p₁₁₀ = 0.15, p₁₁₁ = 0.15,

• Medium Overlap: p₀₀₁ = p₀₁₀ = p₁₀₀ = 0.7 / 3, p₀₁₁ = p₁₀₁ = p₁₁₀ = 0.05, p₁₁₁ = 0.15,

• Low Overlap: p₀₀₁ = p₀₁₀ = p₁₀₀ = 0.8 / 3, p₀₁₁ = p₁₀₁ = p₁₁₀ = 0.05 / 3, p₁₁₁ = 0.15,

• No-Three-File Overlap: p₀₀₁ = p₀₁₀ = p₁₀₀ = 0.55 / 3, p₀₁₁ = p₁₀₁ = p₁₁₀ = 0.15, p₁₁₁ = 0.

These are intended to represent a range of scenarios that could occur in practice. In the high overlap scenario 60% of the entities are expected to be in more than one datafile, in the low overlap scenario 80% of the entities are expected to be represented in a single datafile, and in the no-three-file overlap scenario no entities are represented in all datafiles.

To implement our methodology, in addition to the general set-up described in Section 6.1, we restrict the prior for the within-file cluster sizes so that they have size one with probability one, incorporating the assumption of no-duplication within files (see Section 3.2). Imposing this restriction for all datafiles leads to a prior for tripartite matchings. To illustrate the impact of using our structured prior, we compare with the results obtained using our model for comparison data with a flat prior on tripartite matchings.

The results of the simulation are seen in Figure 3. We see that our proposed approach performs consistently well across different settings, with the exception of the no-three-file overlap setting under high measurement error, where the precision decreases dramatically. The approach using a flat prior on tripartite matchings has poor precision in comparison, and it is particularly low when the amount of overlap is low. This suggests that our structured prior improves upon the flat prior by protecting against over-matching (declaring noncoreferent record pairs as coreferent). In Appendix D we demonstrate how the performance in the no-three-file overlap setting can be improved through the incorporation of an informative prior for the overlap table through α.

Fig. 3.

Performance comparison for simulation with equal measurement error across files. Black lines refer to results under our structured prior, grey lines to results under the flat prior, solid lines show medians, and dashed lines show 2nd and 98th percentiles.

6.3. Duplicate-Free Files, Unequal Errors Across Files

In this simulation study we have different patterns of measurement error across the three files. Rather than each field in each record having a chance of being erroneous according to Table 3 of Sadinle (2014), we will use the following measurement error mechanism to generate the data. For each record in the first file, age is missing, given name has up to seven errors, and all other fields are error free. For each record in the second file, sex and occupation are missing, last name has up to seven errors, and all other fields are error free. For each record in the third file, phone number and postal code have up to seven errors and all other fields are error free. Under this measurement error mechanism, there is enough information in the error free fields to inform pairwise linkage of the files. We further vary ${\left\{p_h\right\}}_{h\in \mathcal{H}}$ over the no-three-file and high overlap settings from Section 6.2.

Our goal in this study is to demonstrate that having both the structured prior for partitions and the separate models for comparison data from each file-pair can lead to better performance than not having these components. We will compare our model as described in Section 6.2 to both our model for comparison data with a flat prior on tripartite matchings (as in Section 6.2) and a simplification of our model for comparison data using a single model for all file-pairs but with our structured prior for partitions.

The results of the simulation are given in Figure 4. We see that our proposed approach outperforms both alternative approaches in both precision and recall in both overlap settings. This suggests that both the structured prior for tripartite matchings and the separate models for comparison data from each file-pair can help improve performance over alternative approaches. We note that in the no-three-file (high) overlap setting the precision of the proposed approach is greater than or equal to the precision of the approach using a single model for all file-pairs in 98 (100) of the 100 replications.

Fig. 4.

Performance comparison for simulation with unequal measurement error across files. “Proposed” refers to our proposed approach, “Single Model” refers to the approach using a single model for all file-pairs and our structured prior for partitions, and “Flat Prior” refers to the approach using our model for comparison data with a flat prior on tripartite matchings. Dots show medians, and bars show 2nd and 98th percentiles.

7. Discussion and Future Work

The methodology proposed in this article makes three contributions. First, the multifile partition parameterization, specific to the context of multifile record linkage and duplicate detection, allows for the construction of our structured prior for partitions, which provides a flexible mechanism for incorporating prior information about the data collection processes of the files. This prior is applicable to any Bayesian approach which requires a prior on partitions, including direct-modeling approaches such as Steorts et al. (2016). We are not aware of any priors for K-partite matchings when K > 2, so we hope our construction will lead to more development in this area. The second contribution is an extension of previous comparison-based models that explicitly handles the multifile setting. Allowing separate models for comparison data from each file pair leads to higher quality linkage. The third is a novel loss function for multifile partitions which can be used to derive Bayes estimates with good frequentist properties. Importantly, the loss function allows for linkage decisions to be left unresolved for records with large matching uncertainty. As with our structured prior on partitions, the loss function is applicable to any Bayesian approach which requires point estimates of partitions, including direct-modeling approaches.

There are a number of directions for future work. One direction is the modeling of dependencies between the comparison fields (see e.g. Larsen and Rubin 2001), which should further improve the quality of the linkage. Another direction is the development of approaches to jointly link records and perform a downstream analysis, thereby propagating the uncertainty from the linkage. See Section 7.2 of Binette and Steorts (2020) for a recent review of such joint models. In this direction, a natural task to consider next is population size estimation, where the linkage of the datafiles plays a central role (Tancredi and Liseo 2011, Tancredi et al. 2020).