Abstract
A common strategy to simulate mixed quantum-classical dynamics is by propagating classical trajectories with mapping variables, often using the Meyer–Miller–Stock–Thoss (MMST) Hamiltonian or the related spin-mapping approach. When mapping the quantum subsystem, the coupled dynamics reduce to a set of equations of motion to integrate. Several numerical algorithms have been proposed, but a thorough performance comparison appears to be lacking. Here, we compare three time-propagation algorithms for the MMST Hamiltonian: the Momentum Integral (MInt) (J. Chem. Phys., 2018, 148, 102326), the Split-Liouvillian (SL) (Chem. Phys., 2017, 482, 124–134), and the algorithm in J. Chem. Phys., 2012, 136, 084101 that we refer to as the Degenerate Eigenvalue (DE) algorithm due to the approximation required during derivation. We analyze the accuracy of individual trajectories, correlation functions, energy conservation, symplecticity, Liouville’s theorem, and the computational cost. We find that the MInt algorithm is the only rigorously symplectic algorithm. However, comparable accuracy at a lower computational cost can be obtained with the SL algorithm. The approximation implicitly made within the DE algorithm conserves energy poorly, even for small timesteps, and thus leads to slightly different results. These results should guide future mapping-variable simulations.
1. Introduction
Theoretical methods for simulating nonadiabatic dynamics are crucial for understanding charge and energy transfer in materials such as organic light-emitting diodes, solar cells, and photosynthetic systems.1−7 Experimental spectroscopic techniques have successfully been developed to probe nonadiabatic processes within photovoltaic materials.8−10 To analyze the complex dynamics observed, accurate and efficient numerical models are of great importance.3,9
Since the 1930s, when Landau and Zener first investigated nonadiabatic dynamics,11,12 accurate calculation of nonadiabatic dynamics has been a challenge due to the large computational expense associated with full-quantum solutions.13−15 This led to the development of approximate classical-like dynamical frameworks, motivated by the classical linear scaling with degrees of freedom (DoF) compared to the exponential scaling of quantum methods.16 Unlike most transformations, discrete quantum DoF do not have an obvious classical counterpart.16 Consequently, approximate methods have been developed to recast the quantum system to look classical whilst retaining some quantum properties, often requiring a compromise between accuracy and cost for large systems.
Many methods exist to incorporate discrete quantum DoF into classical frameworks including Ehrenfest dynamics,17 approximations to the quantum-classical Liouville equation,18−20 the symmetrical quasi-classical windowing method,21 surface hopping,22,23 and mapping methods such as methods inspired by the Meyer–Miller–Stock–Thoss (MMST) mapping24−28 and spin-mapping,29,30 including the mapping approach to surface hopping (MASH).31 The simplest nonadiabatic method, proposed by Mott (1931), evaluates the quantum electronic dynamics along the classical path of the nuclei, known as the “classical path” approach.16,18,19,32 However, this does not include the “back reaction” on the nuclei.16 Surface hopping models, originally developed by Tully and Preston (1971), propagate along one adiabatic surface before “hopping” to another.16,22,23,33,34 “Hopping” is possible at any point along a trajectory, not just where surfaces cross, destroying the state coherence.23,26
In this article, we focus on mapping approaches utilized in various semiclassical methods, where the discrete quantum DoF are mapped onto continuous classical DoF propagated by classical mechanics. The Meyer–Miller mapping developed in 1979,25 and later put on a rigorous footing by Stock and Thoss in 1997,26 constructs a set of classical variables for the discrete electronic DoF and propagates them with the nuclear DoF using an effective Hamiltonian, the MMST Hamiltonian.25,26,35 The electronic dynamics are consistent with the time-dependent Schrödinger equation, and the force exerted on the nuclei is given by the instantaneous values of the electronic variables.25,35 The mapping introduces electronic position and momenta, sometimes expressed as action–angle variables, to describe the nuclear motion on coupled potential energy surfaces.16,26 This approach maps the time-dependent Schrödinger equation for an N-level system to a classical analogue of N-coupled harmonic oscillators following Hamilton’s equations of motion.16,26
The recently derived spin-mapping approach employs a different mapping formalism but gives a Hamiltonian almost identical to that of the MMST methods.29,30,36 The MMST Hamiltonian algorithms compared in this work are thus also applicable to spin-mapping methods. Compared to MMST-based methods, spin-mapping uses a different value of the so-called zero-point energy (ZPE) parameter, introduced by Stock and Müller as a fitting parameter to mitigate ZPE-leakage.37,38 Spin-mapping leads to a ZPE as a function of the number of states, with values close to what was previously found optimal when tuned as a free parameter. A partially linearized spin-mapping method has been found to improve accuracy compared to the fully linearized mapping,39,40 in particular for spectroscopy.41
One application of the MMST Hamiltonian is to calculate dynamical properties at thermal equilibrium by approximating equilibrium time-correlation functions
| 1 |
where the partition function Z is given as
| 2 |
and the quantum Boltzmann operator at inverse
temperature β = 1/kBT is 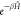 . Semiclassical methods can be used to calculate
quantum time-correlation functions, often by utilizing an “Initial-Value
Representation” (IVR), resulting in a phase-space integral.1,26,42 The semiclassical phase-factor
makes correlation function convergence challenging.1,27,43 Various versions have been developed to
attempt to overcome this, including linearized semiclassical (LSC)-IVR1,27,44−47 and Mixed Quantum-Classical (MQC)-IVR.28,47−51 However, semiclassical methods often fail at describing nuclear
quantum effects.52
. Semiclassical methods can be used to calculate
quantum time-correlation functions, often by utilizing an “Initial-Value
Representation” (IVR), resulting in a phase-space integral.1,26,42 The semiclassical phase-factor
makes correlation function convergence challenging.1,27,43 Various versions have been developed to
attempt to overcome this, including linearized semiclassical (LSC)-IVR1,27,44−47 and Mixed Quantum-Classical (MQC)-IVR.28,47−51 However, semiclassical methods often fail at describing nuclear
quantum effects.52
An alternative method that can capture nuclear quantum effects is to use a ring of multiple classical system replicas (beads) attached by harmonic springs, known as a ring polymer.53−56 While the path-integral representation leads to an exact method for static equilibrium properties, the dynamics of the ring polymer can yield short-time approximations to quantum real-time dynamics through methods such as ring-polymer molecular dynamics (RPMD),53,57−59 centroid molecular dynamics (CMD),60−63 and thermostatted (T)-RPMD.64−66 Specifically, RPMD provides, for a single (adiabatic) potential, an approximation to Kubo-transformed time correlation functions while preserving the Boltzmann distribution and is exact in the short-time and classical limits.58,59,67 The Kubo-transformed correlation functions allow short-time quantum effects to be included, although the long-time quantum coherence effects are neglected. RPMD can be derived from exact quantum dynamics through a series of approximations via Matsubara dynamics,59,68 and RPMD transition-state theory is equivalent to true quantum transition-state theory.67,69−71 Many extensions have been suggested for multiple states, including mean-field RPMD,72 nonadiabatic RPMD (NRPMD), and mapping-variable RPMD (MVRPMD).3,53,54,73−77 As NRPMD utilizes the Meyer–Miller Hamiltonian, the algorithms discussed in this work are directly applicable. However, none of these methods alone fulfils the three important criteria of: replicating Rabi oscillations, preserving the quantum Boltzmann distribution, and reducing to classical dynamics in the adiabatic limit.13,29,78 While a recently developed ellipsoid spin-mapping fulfils all these limits, its mean-field dynamics was found to be often less accurate for short times than the original spin-mapping.78 Further work is still required to find an accurate trajectory-based approach to replicate the true quantum dynamics.
Although mapping Hamiltonians have become increasingly popular for simulating nonadiabatic dynamics, numerical integration of the equations of motion is not straightforward due to coupling between the electronic momenta and nuclear positions. Over the years, various algorithms have been suggested to solve this problem,1−3 but as far as we are aware, there has been no published computational comparison of MMST algorithms to determine their properties and accuracy. To address this, in this paper, we compare the symplectic Momentum Integral (MInt) algorithm by Church et al. (2018), the Split-Liouvillian (SL) algorithm by Richardson et al. (2017), and the algorithm outlined by Kelly et al. (2012), referred to here as the Degenerate Eigenvalue (DE) algorithm.1−3 Other algorithms exist for this problem, such as Runge–Kutta or the Adams–Bashforth Predictor–Corrector algorithm, which are known to be non-symplectic. We note that even though velocity-Verlet is widely considered to be symplectic for classical systems, directly utilizing velocity-Verlet for the MMST Hamiltonian may not result in a symplectic integration scheme. Individual propagation steps of momenta or position are unlikely to correspond to exact sub-Hamiltonian propagation due to the algebraic form of the MMST Hamiltonian and coupling between the nuclear positions and the mapping momenta. To avoid integrating stiff equations of motion, Wang et al. suggested an intelligent canonical transformation.27 However, even with this transformation, these approaches are not ideal for propagating mapping variables and will still require short timesteps. We will not consider these algorithms further and instead focus on algorithms which attempt to propagate the mapping variables exactly for an arbitrary timestep.
We seek to compare the algorithms for the simplest possible system for which they can all be compared on an equal footing and for which there already exists results in the literature for qualitative comparison. To this end, we compute position and state autocorrelation functions for a two-state linear vibronic potential with the MMST Hamiltonian (corresponding to the single-bead limit of NRPMD) using these three algorithms.53 As many of the methods discussed share similar Hamiltonian forms to that of the MMST, including NRPMD, spin-mapping, Ehrenfest, and some surface hopping models, the results are widely applicable and should inform future computational studies using mapping variable methods.
The article is structured as follows. In Section 2, we provide theoretical background for the three algorithms investigated. In Section 3, we investigate the symplecticity, satisfaction of Liouville’s theorem, accuracy of trajectories and correlation functions, computational cost, and energy conservation. We conclude in Section 4.
2. Background Theory
Here, we present the algebraic forms of the three algorithms on an equal footing, such that we can compare properties including the accuracy, symplecticity, and if they satisfy Liouville’s theorem.
Note that a brief theoretical analysis of the MInt and SL algorithms, determining the symplecticity in particular, was previously carried out in the study in ref [1]. We extend the work in ref [1] to a more thorough computational investigation where we compare the algorithmic performance utilizing a model for which there exists results in the literature and include the DE algorithm. As far as we are aware, the symplecticity has not been rigorously determined for the DE algorithm.
2.1. Symplectic Integrators
The Hamiltonian for an N-level electronic system in the diabatic representation is
| 3 |
where the nuclear position
and momenta are x and p, respectively, V(x) is an N × N diabatic electronic potential energy matrix in the basis
of the electronic states, 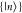 , and μ is a diagonal matrix of nuclear
masses. The classical MMST mapping Hamiltonian in the diabatic representation
is25,26
, and μ is a diagonal matrix of nuclear
masses. The classical MMST mapping Hamiltonian in the diabatic representation
is25,26
| 4 |
where X and P are the electronic position and momenta, respectively. Classical evolution under this Hamiltonian refers to the equations of motion16,26
| 5 |
that constitute a time-dependent Hamiltonian system
| 6 |
where 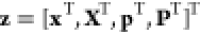 , the ∇z operator
contains the partial derivatives, and J is the structure
matrix
, the ∇z operator
contains the partial derivatives, and J is the structure
matrix
| 7 |
and 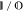 are the identity and zero matrices, respectively.1,25,79 A Hamiltonian integrator is said
to be symplectic if it fulfils the condition1,79,80
are the identity and zero matrices, respectively.1,25,79 A Hamiltonian integrator is said
to be symplectic if it fulfils the condition1,79,80
| 8 |
where M is the monodromy matrix. The monodromy matrix is a matrix of differentials that expresses how the time-evolved phase-space variables depend on the initial phase-space variables81
| 9 |
The monodromy matrix is computed for each timestep and multiplied with the previous timestep matrices to obtain the monodromy matrix for the overall trajectory
| 10 |
If the Hamiltonian is split, H = H1 + H2, then the monodromy matrix is calculated for each timestep according to the algorithmic flow map.79 Calculation of the monodromy matrix is not needed for algorithm propagation, only to determine symplecticity and if the theoretical framework requires it. For example, in some SC-IVR methods, the phase-factor can be calculated using elements of the monodromy matrix, where utilizing a symplectic algorithm can improve the stability, aiding convergence and partially mitigating the “sign” problem.1,82,83
The symplecticity criterion, eq 8, is a much stricter condition than the conservation of volume phase-space (Liouville’s theorem), which only requires the monodromy matrix determinant to be unity.1,80,84 Volume phase-space preservation is a consequence of symplecticity, but this relationship does not necessarily hold the other way around,79i.e., volume phase-space preservation is necessary but not sufficient for symplecticity. Instead, symplectic integrators can arise from exact time-propagation of a Hamiltonian system.79 Splitting the Hamiltonian into sub-evolutions will also result in a symplectic integrator, provided that each sub-evolution is the exact time-propagation of the relevant sub-Hamiltonian.1,79 For example, velocity-Verlet is a classical symplectic algorithm as splitting results in two sub-Hamiltonians that are independent of each other, such that both can be integrated exactly.80 The MMST Hamiltonian contains coupling between the electronic momenta and nuclear position, making symplectic time-evolution of the equations of motion challenging and, in general, results in nonlinear dynamics.1,26 Symplectic integrators are an advantage for Hamiltonian integration as they have little to no energy drift with time and tend to be more stable at long simulation times.1 We also note that the Cayley transform can improve the symplectic stability of algorithms with no additional algorithmic complexity and computational cost, and can be implemented for any path-integral-based scheme.85
2.2. Algorithmic Overview
The MInt algorithm, by Church et al. (2018), was developed to help extend the MQC-IVR method to simulate nonadiabatic dynamics using the MMST mapping.1 The name arose as the MInt algorithm exactly solves the Momentum Integral with time and as we will show, is the only known symplectic algorithm propagating the MMST Hamiltonian.1 The MInt algorithm splits the MMST Hamiltonian into two sub-Hamiltonians, each of which is propagated exactly
| 11a |
| 11b |
| 11c |
The exact evolution of the sub-Hamiltonians results in symplecticity, and the sub-evolution of H1 is split into two half-timesteps to improve the time-order error, such that the algorithm is at least a second-order method.1,79 Hamilton’s equations of motion are obtained for H1 and H2, with the latter being more complicated due to coupling between the nuclear and quantum DoF.1 The MInt algorithm can be used on any Hamiltonian containing a sum of Meyer–Miller-like terms and has algebraically been shown to be symplectic, symmetric, second-order in time, and time-reversible.1 Fortran code of the MInt algorithm is available in the SC-IVR package on the Ananth Group website.86 Recently, the MInt algorithm was utilized by Gardner et al. in NQCDynamics.jl, a Julia package for condensed phase nonadiabatic quantum dynamics.87 To be able to compare the three algorithms on an equal theoretical footing, we use the D5 form of the MInt algorithm where instead H2 is split into two half-timesteps1
| 12 |
where ΨMIntH,Δt is the approximate flow map comprising exact evolutions of the relevant sub-Hamiltonians, ΦH,Δt, and propagation is done from right to left. In our notation, Φ refers to exact evolution and Ψ refers to approximate evolution, which may or may not comprise of exact sub-evolutions, consistent with the notation of Leimkuhler and Reich.79
The SL algorithm, by Richardson et al. (2017), uses the Liouvillian formalism to construct an integrator.3 The Liouvillian operator can be generated from the Hamiltonian using a Poisson bracket
| 13 |
where the solutions to time-evolution are of exponential form.84 We follow the convention in the Matsubara dynamics article59 and by Zwanzig88 and define the Liouvillian to be real with no factor i (the imaginary unit). The MInt algorithm D5 form, eq 12, is equivalent in Liouvillian notation to1
| 14 |
where evolution requires propagation of the
Liouvillians from the right to the left and 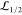 are the Liouvillians of H1/2, respectively. The SL algorithm further symmetrically
splits
are the Liouvillians of H1/2, respectively. The SL algorithm further symmetrically
splits 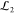 into electronic (el) and nuclear (p) contributions. Hence, the flow map for this algorithm is
into electronic (el) and nuclear (p) contributions. Hence, the flow map for this algorithm is
| 15 |
where
| 16a |
| 16b |
are the electronic and nuclear Liouvillians of H2, respectively, where i is the nuclear index and j is the electronic index.1,3 This uses the approximation
| 17 |
which is valid in the limit Δt → 0.3 Hence, the flow map can also be represented as
| 18 |
where 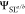 represents the approximate propagation
of H2. Due to symmetric splitting, the
two half-timesteps are not equal and are labeled with the superscripts a for
represents the approximate propagation
of H2. Due to symmetric splitting, the
two half-timesteps are not equal and are labeled with the superscripts a for 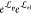 and b for
and b for 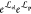 . For an integrator to be symplectic, it
is sufficient but not necessary that the integrator is a sequence
of exact sub-Hamiltonian evolutions. Evolution under Liouvillians
is not guaranteed to be symplectic but will be if each Liouvillian
corresponds to the exact propagation of a Hamiltonian or sub-Hamiltonian.79 For an arbitrary timestep, the splitting of H2 into electronic and nuclear contributions
results in holding the electronic position and momenta constant while
propagating the nuclear momenta. Hence, the propagation of H2 is no longer exact or guaranteed to be symplectic.1 Church et al. (2018) derived
the SL monodromy matrix and using the symplecticity criterion, eq 8, confirmed that the SL
algorithm is not symplectic.1 They stated
that there is likely to be an energy drift associated, but this may
be small if the adiabatic states are close in energy and weakly coupled.1 However, the algebraic proof does not indicate
if the SL algorithm will result in unreasonable dynamics such as a
very large energy drift when compared to the MInt for a given timestep.
. For an integrator to be symplectic, it
is sufficient but not necessary that the integrator is a sequence
of exact sub-Hamiltonian evolutions. Evolution under Liouvillians
is not guaranteed to be symplectic but will be if each Liouvillian
corresponds to the exact propagation of a Hamiltonian or sub-Hamiltonian.79 For an arbitrary timestep, the splitting of H2 into electronic and nuclear contributions
results in holding the electronic position and momenta constant while
propagating the nuclear momenta. Hence, the propagation of H2 is no longer exact or guaranteed to be symplectic.1 Church et al. (2018) derived
the SL monodromy matrix and using the symplecticity criterion, eq 8, confirmed that the SL
algorithm is not symplectic.1 They stated
that there is likely to be an energy drift associated, but this may
be small if the adiabatic states are close in energy and weakly coupled.1 However, the algebraic proof does not indicate
if the SL algorithm will result in unreasonable dynamics such as a
very large energy drift when compared to the MInt for a given timestep.
Kelly et al. (2012) have also developed an integrator that we refer to as the DE algorithm due to the approximation needed to obtain the final algebraic form. The DE algorithm also splits the Hamiltonian into H1 and H2, where the motivation is to enhance stability and minimize the difference between the exact and approximate dynamics.2 The algorithm uses MInt-like equations but makes an implicit approximation equivalent to assuming that the diabatic potential matrix eigenvalues are degenerate,89 simplifying the calculation of the potential matrix derivative and making the DE algorithm unlikely to be symplectic.1,2 The flow map cannot easily be expressed in a Liouvillian form but can be written as
| 19 |
where ΨDE is the approximate DE propagation of H2. The degenerate eigenvalue approximation has previously been utilized in Poisson bracket mapping equation (PBME) simulations of coherent dynamics in photosynthetic systems.90 However, the DE approximation is known to cause the state populations to deviate from the exact results for systems with large energy biases.89
The three algorithms use equivalent propagation equations for the nuclear position, electronic position and momenta, only differing in the nuclear momenta propagation.1−3 The DE algorithm has a similar form to that of the SL algorithm, but the DE algorithm does not hold the electronic position and momenta stationary while propagating the nuclear momenta and has a different diabatic potential matrix differential with respect to the nuclear position.2,3 As far as we are aware, the DE algorithm monodromy matrix has not been algebraically determined or tested for symplecticity and Liouville’s theorem. All three algorithms are derived in the diabatic basis; however, as the Meyer–Miller Hamiltonian is known in the adiabatic basis,91 it may be possible to re-derive the algorithms in the adiabatic basis.
2.3. Propagation of H1
For simplicity, we will consider only one nuclear DoF and two electronic DoF throughout as the generalized multi-dimensional form is known.1−3 All three algorithms propagate H1 in the same way using Hamilton’s equations of motion1−3
| 20 |
where m is the nuclear mass, such that integration provides the propagation equations
| 21a |
| 21b |
We define our monodromy matrix as
 |
22 |
such that the monodromy matrix for the propagation of H1 is a triangular matrix of the form
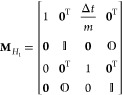 |
23 |
where 0 = [0,0]T and
the determinant is unity, 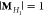 . The propagation of H1 is symplectic for all three algorithms as
. The propagation of H1 is symplectic for all three algorithms as 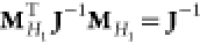 .
.
2.4. Propagation of H2
Here, we present and compare the propagation of H2 for the three algorithms. The diabatic potential matrix is split into a state-independent term, U, and a traceless state-dependent matrix, Ṽ, such that V(x) = U(x)+Ṽ(x). This is as the DE algorithm requires a traceless state-dependent matrix, previously being seen as an advantage as it renders the dynamics invariant to any constant shift of the coupling potential.2,92 This gives
| 24 |
where 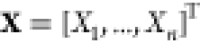 and similarly for P. Although
the splitting of a traceless state-dependent matrix results in
and similarly for P. Although
the splitting of a traceless state-dependent matrix results in 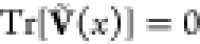 , we have included this term in the derivation
for completeness as the MInt and SL algorithms can be used for any
choice of splitting, likely resulting in a non-zero trace term. The
SL and DE algorithms use approximations to propagate H2, resulting in different, non-exact nuclear momentum
propagation equations.1−3
, we have included this term in the derivation
for completeness as the MInt and SL algorithms can be used for any
choice of splitting, likely resulting in a non-zero trace term. The
SL and DE algorithms use approximations to propagate H2, resulting in different, non-exact nuclear momentum
propagation equations.1−3
The propagation of H2 is split into two half-timesteps that sandwich 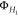 , allowing a fair algorithmic comparison
with the original SL form and the equivalent MInt form. We have swapped
the order of H1 and H2 to test the DE algorithm and in Figures S5 and S6 in the Supporting Information, we show that
this has no effect on the symplecticity or energy conservation.
, allowing a fair algorithmic comparison
with the original SL form and the equivalent MInt form. We have swapped
the order of H1 and H2 to test the DE algorithm and in Figures S5 and S6 in the Supporting Information, we show that
this has no effect on the symplecticity or energy conservation.
2.4.1. The MInt Algorithm
The MInt algorithm exactly propagates H2 with time, taking into account the electronic dependence of the nuclear momentum.1 Using Hamilton’s equations of motion for half a timestep, following the approach of Church et al., we derive propagation equations
| 25a |
| 25b |
where the prime denotes the derivative with
respect to x and the matrix dependence on x has been dropped for notational simplicity. To find solutions
through integration, the MInt algorithm relies on the fact that 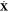 and
and 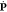 are independent of p but ṗ is dependent on X and P.1 Therefore, solving for
are independent of p but ṗ is dependent on X and P.1 Therefore, solving for 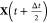 and
and 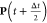 and substituting into eq 25b allows
and substituting into eq 25b allows 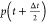 to be found. The electronic position and
momenta are found through integration, resulting in
to be found. The electronic position and
momenta are found through integration, resulting in
| 26 |
which can be recast to be entirely real by
diagonalizing Ṽ into eigenvectors, S, and a diagonal eigenvalue matrix, Λ, such that 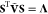 .1 This results
in
.1 This results
in
| 27a |
| 27b |
for the propagation of X and P, where C and D are1
| 28 |
By defining the derivative of the potential
in the adiabatic basis to be 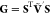 and inserting
and inserting 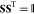 identities into the integration of eq 25b, an intermediate equation
for the propagation of p can be found
identities into the integration of eq 25b, an intermediate equation
for the propagation of p can be found
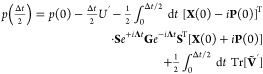 |
29 |
which can be solved by element-wise integration of
| 30 |
Defining
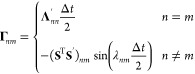 |
31a |
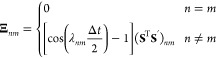 |
31b |
where λnm = (Λ)mm – (Λ)nn , such that
| 32a |
| 32b |
where E is symmetric and F is skew-symmetric. The nuclear propagation, where x is unchanged, is therefore
| 33 |
The extended form for multiple states can
be found in Appendix B of ref [1]. Church et al. have also shown that the MInt algorithm is second-order and exact
in the Δt → 0 limit, deviating on 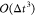 . A higher order of accuracy may be obtained
through a different splitting of H1 and H2.93
. A higher order of accuracy may be obtained
through a different splitting of H1 and H2.93
The MInt monodromy matrix for the propagation of H2 satisfies Liouville’s theorem and can be found by defining
| 34a |
| 34b |
| 34c |
| 34d |
| 34e |
such that the monodromy matrix is1
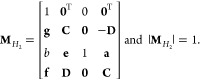 |
35 |
Propagation under H2 is symplectic as 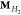 satisfies the symplecticity criterion, eq 8, derived by Church et al. and shown in Appendix A.
As propagation under both H1 and H2 is symplectic, the overall propagation for
the MInt algorithm is symplectic.1,79
satisfies the symplecticity criterion, eq 8, derived by Church et al. and shown in Appendix A.
As propagation under both H1 and H2 is symplectic, the overall propagation for
the MInt algorithm is symplectic.1,79
2.4.2. The SL Algorithm
The SL algorithm propagates H2 using the Liouvillian formalism by splitting further into an electronic and nuclear momentum propagation, where eqs 16a and 16b become1,3
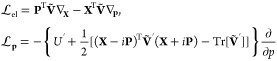 |
36 |
The electronic propagation
resulting from 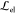 is equivalent to the MInt algorithm, eqs 27a and 27b, and leaves the nuclear variables unchanged.1
is equivalent to the MInt algorithm, eqs 27a and 27b, and leaves the nuclear variables unchanged.1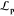 results in the following propagation of p and leaves all other variables unchanged
results in the following propagation of p and leaves all other variables unchanged
| 37 |
The difference between the two algorithms
arises in the nuclear momentum, where due to the SL symmetric propagation
of H2, the electronic variables are always
the half-timestep evolved values for propagation of p.1,3 This algorithm is exact in the Δt → 0 limit, differing on terms of 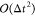 as discussed in Appendix
B.
as discussed in Appendix
B.
The SL monodromy matrices for the propagation of H2 obey Liouville’s theorem and are
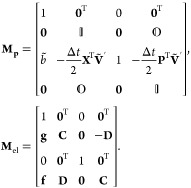 |
38 |
where1
Neither Mp and Mel satisfy the symplecticity criterion individually, seen in Appendix A.1 The combination of Mp and Mel was shown by Church et al. to only be symplectic in the Δt → 0 limit, not for an arbitrary timestep.
2.4.3. The DE Algorithm
The DE algorithm defines Ṽ to be traceless, such that the last term of H2 is ignored.2 Here, we will re-frame the algorithm into a MInt-like form using vector notation and outline the degenerate eigenvalue approximation used. We will also investigate the symplecticity and satisfaction of Liouville’s theorem through defining the monodromy matrix, which as far as we are aware has not been done before.
The electronic Hamiltonian equations are the same as above for the MInt and SL algorithms and solved to provide the same overall propagation equations, eqs 27a and 27b. The nuclear momentum propagation equation is
| 39 |
To solve eq 39, we define an integral, A, that requires the degenerate eigenvalue assumption to arrive at the final form by Kelly et al.(2)
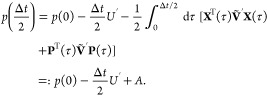 |
40 |
This can be written in a MInt-like form
| 41 |
| 42 |
A transformation is defined into the adiabatic basis using the following overlined variables2
| 43 |
such that, conversion into the adiabatic basis utilizing the decomposition of Ṽ results in
| 44 |
where 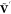 is determined by
is determined by
| 45 |
We can arrive at the form shown by Kelly et al. by making the degenerate eigenvalue approximation,
which appears to be made between eqs C18 and C19 in ref [2]. This approximates that
the eigenvalues are equal, 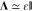 . Kim and Rhee determined that this algorithm
requires assumption of the degenerate limit agreeing with our DE approximation.89 Therefore, the differential of the eigenvalues
can be approximated as
. Kim and Rhee determined that this algorithm
requires assumption of the degenerate limit agreeing with our DE approximation.89 Therefore, the differential of the eigenvalues
can be approximated as 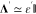 such that the derivative of
such that the derivative of 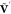 in the adiabatic basis is obtained through
differentiating the identity,
in the adiabatic basis is obtained through
differentiating the identity, 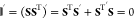
| 46 |
Inserting this into eq 44 results in
| 47 |
Hence, the integral below is obtained
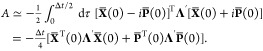 |
48 |
The final form seen in ref
[2] has an additional 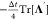 term when written in matrix form, however,
this is just a dummy term. The fact that Ṽ is
traceless requires that the sum of the eigenvalues is zero, therefore, Λ and Λ′ are traceless. The
overall nuclear propagation in the diabatic basis, having made the
DE approximation, is then
term when written in matrix form, however,
this is just a dummy term. The fact that Ṽ is
traceless requires that the sum of the eigenvalues is zero, therefore, Λ and Λ′ are traceless. The
overall nuclear propagation in the diabatic basis, having made the
DE approximation, is then
| 49 |
The DE approximation discards terms to reach eq 49 resulting in the DE algorithm not being exact in the Δt → 0 limit, instead being a zero-order algorithm as derived in Appendix B.
Comparison with the SL and MInt
algorithms can determine whether
the DE algorithm is likely to be symplectic, where the propagation
of x, X and P are equivalent.1−3 It can be seen that in the case where the DE approximation holds
such that, 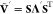 , the propagation of p would
be similar to the SL algorithm. However, the DE algorithm uses the
initial electronic variables when the SL algorithm uses the half-timestep
evolved values. Due to the similarities prior to the DE approximation
being made, the DE algorithm is unlikely to be symplectic. To rigorously
check the symplecticity, we derive the monodromy matrix by defining
, the propagation of p would
be similar to the SL algorithm. However, the DE algorithm uses the
initial electronic variables when the SL algorithm uses the half-timestep
evolved values. Due to the similarities prior to the DE approximation
being made, the DE algorithm is unlikely to be symplectic. To rigorously
check the symplecticity, we derive the monodromy matrix by defining
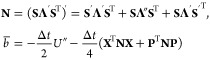 |
such that
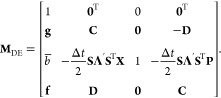 |
50 |
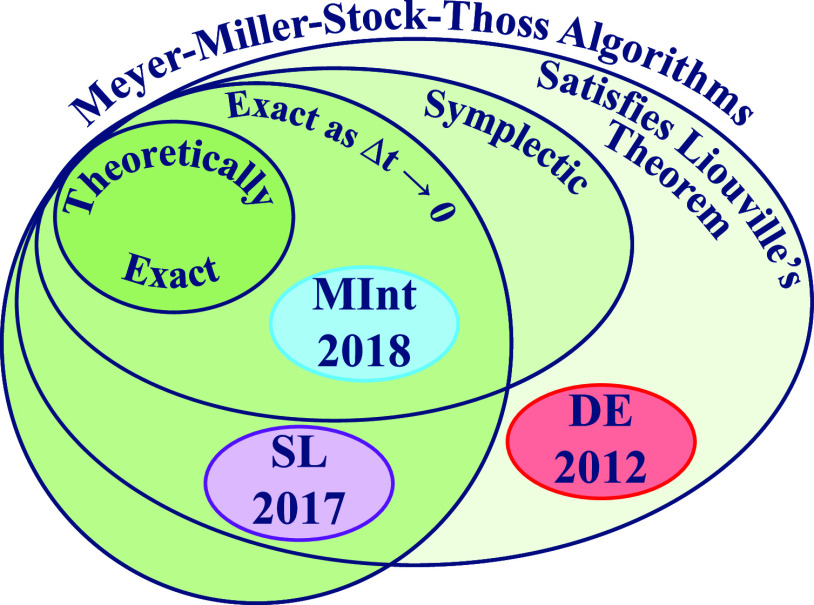
The determinant of MDE can easily be shown to be unity, satisfying Liouville’s theorem. However, the approximate propagation of H2 is not symplectic as MDE does not satisfy the symplecticity criterion, shown in Appendix A. The MInt algorithm is the only algorithm considered here that is both symplectic and satisfies Liouville’s theorem.1
In Table 1 below, we present the theoretical results for easy algorithmic comparison. In Appendix C, we prove that all three algorithms conserve electronic probability.
Table 1. Summary of the Theoretical Results Obtained Here and Ref [1]a.
| Theoretical Results | MInt | SL | DE |
|---|---|---|---|
| H1 propagation | Exact | Exact | Exact |
| H2X/P propagation | Exact | Exact | Exact |
| H2p propagation | Exact | Approx. | Approx. |
| H2 approximation | None | Split into 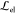 and and 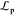
|
Approx. degenerate eigenvalues of V(x) |
| Satisfies Liouville’s theorem | √ | √ | √ |
| Symplectic | √ | × | × |
| Exact in Δt → 0 limit | √ | √ | × |
| Conserves electronic probability | √ | √ | √ |
The H2 electronic propagation for all algorithms is equivalent. The approximations made in the SL and DE algorithms result in inexact nuclear momentum propagation. However, the SL algorithm is exact in the Δt → 0 limit whereas the DE is not.
3. Results and Discussion
The algorithms discussed here have been utilized in the literature but not for the same system to allow direct comparison. We seek to test the algorithms computationally on an equal footing using the same system. Hence, we use a simple two-state linear vibronic potential, also known as a one-dimensional spin-boson model, discussed in this section with the MMST Hamiltonian (corresponding to the single-bead limit of NRPMD) to test the symplecticity, satisfaction of Liouville’s theorem, energy conservation and accuracy of correlation functions. The models defined here also allow qualitative comparison with literature.
3.1. Theoretical Models
To compare the approximate dynamics produced by the MInt, SL and DE algorithms, we use the three potential models introduced in ref [53]. For these models the potential diabatic matrix is
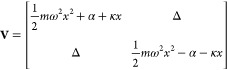 |
51 |
such that splitting to obtain a traceless Ṽ gives
| 52 |
Reduced units are used where m = ℏ = ω = 1, so energy is measured in units of the frequency, ω. The models represent bound potentials, defined in Table 2, where Δ is the electronic coupling, 2α is the energy bias between the potential energy surfaces (the asymmetry) and κ is the vibronic coupling, chosen to be 1. Model 1 represents strong electronic coupling, where the nuclear dynamics occur on a longer timescale than the electronic oscillations and nuclear motion occurs in a mean field of the diabatic surfaces. Model 2 has a strong energy bias and the system is in the inverted Marcus regime. Model 3 is a challenging intermediate regime in which the timescales of the electronic and nuclear dynamics are similar.
Table 2. Values for the Potential Matrix Constants for Models 1–3 from Ref [53].
| Model | α | Δ | Regime |
|---|---|---|---|
| 1 | 0 | 4 | Adiabatic limit |
| 2 | 2 | 1 | Inverted Marcus regime |
| 3 | 0 | 1 | Intermediate regime |
Models 1–3 were utilized to compute correlation functions using the following distribution, ρ, in the N-bead form in refs [3 , (53)]. Here, for simplicity, we use the single-bead form
| 53 |
such that the partition function is
| 54 |
where W = PTMXXTMP and 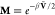 . Note that W is positive
definite for the single bead case. Monte Carlo importance sampling
is utilized as detailed in Appendix D. Time-independent
equilibrium properties are calculated, for example, the population
of state n(3,53)
. Note that W is positive
definite for the single bead case. Monte Carlo importance sampling
is utilized as detailed in Appendix D. Time-independent
equilibrium properties are calculated, for example, the population
of state n(3,53)
| 55 |
The derivation is similar to that of eq C4 in Appendix D by summing over all indices except n,3,53 resulting in
| 56 |
where
| 57 |
This approach for obtaining population information is only valid at t = 0, whereas the electronic populations can be found at time t using3
| 58 |
Correlation functions are calculated through
finding an approximation to eq 1, where for the position auto-correlation function 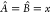 and for the population auto-correlation
function
and for the population auto-correlation
function 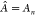 and
and 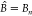
| 59a |
| 59b |
where W(Xi(0), Pi(0)) and initial conditions are sampled from eq D14 for J trajectories. The correlation functions are then averaged over J trajectories
| 60a |
| 60b |
where index i refers to the ith trajectory. We can directly compare the three algorithms and qualitatively compare our results with ref [53]. We sample the same distribution, with our method outlined in Appendix D, as in ref [53]. However, we choose to split the potential matrix such that Ṽ is traceless as the DE algorithm requires this. In ref [53], the matrix was instead split such that the lowest eigenvalue of Ṽ is zero, which in general results in a non-zero trace. To ensure we can compare all three algorithms for the same Hamiltonian, we have used the traceless form leading to small quantitative differences between the results here and in ref [53].
3.2. Algorithmic Properties
First, we consider the symplecticity and conservation of Liouville’s theorem using Model 1. Church et al. determined that the MInt algorithm is symplectic whilst the SL algorithm is not.1 In Appendix A, we algebraically show that the DE algorithm is not symplectic. To numerically determine the symplecticity, we define an error matrix, Er, to be
| 61 |
where for a symplectic integrator the elements of Er, aij, will all be zero.94 The Frobenius Norm is used to track the size of Er
| 62 |
where the matrix size is n × n.94 To average over many trajectories, we weight by W
| 63 |
where i refers to the trajectory index. To determine if Liouville’s theorem is satisfied, we evaluate
| 64 |
which will be zero if it is satisfied.1,80 By squaring the deviation, we ensure no error cancellation when averaging over trajectories. Satisfaction of Liouville’s theorem is quite a “low bar” for an algorithm, as it is equivalent to the Liouvillian associated with the dynamics being divergenceless.95 This can be easily shown for the MInt and SL algorithms but as the DE algorithm cannot easily be expressed in a Liouvillian form, it is still useful to investigate numerically.
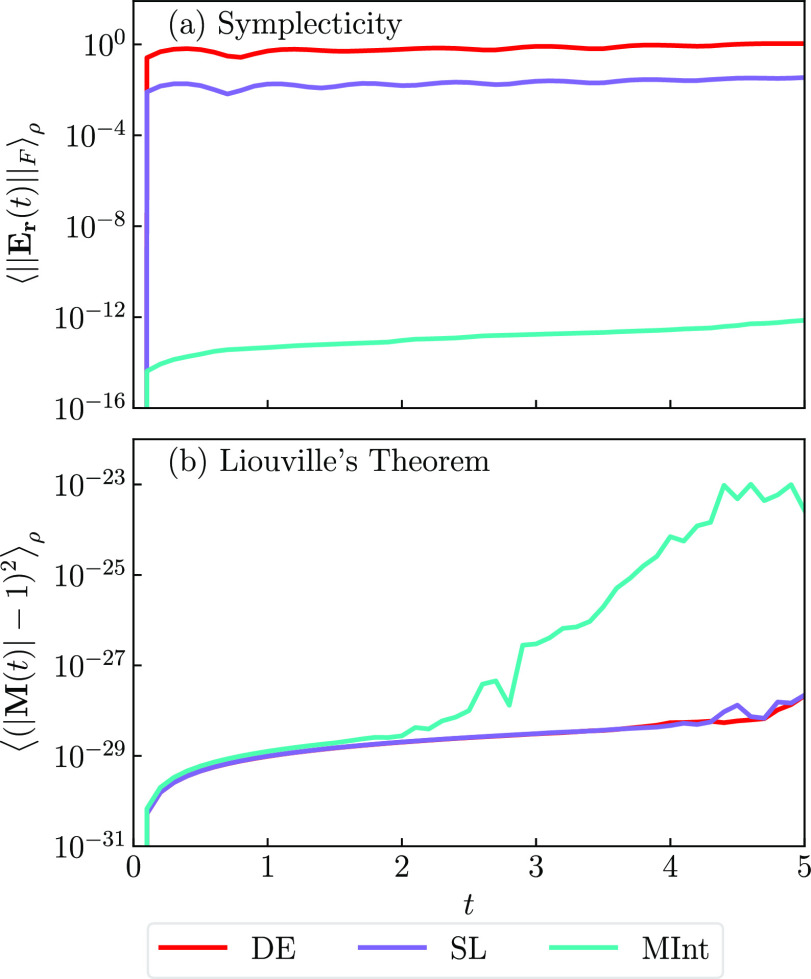
In Figure 1a, the logarithmic plot of ∥Er∥F against time for Model 1 with Δt = 0.1 can be seen. The MInt algorithm (cyan) remains below 10–12 for the entire simulation time and is therefore symplectic, with a small build-up of floating-point errors that arise in numerical calculations, in agreement with the literature.1 The SL algorithm (purple) increases rapidly to around 10–2 and continues to increase indicating that it is not symplectic. The DE algorithm (red) is the least symplectic, being on the order of 1 by the end of the simulation time. In Appendix A, we show the timestep dependence of this error and derive the deviation from symplecticity, using the flow map discussed earlier, to be zero- and second-order for the DE and SL algorithms respectively. Although the SL and DE algorithms are not symplectic, all three algorithms satisfy Liouville’s theorem and conserve volume phase-space, as seen in Figure 1b. We believe that the very slight increase seen for the MInt algorithm is due to additional floating-point error accumulation arising from the more complicated propagation equations.
Figure 1.
(a) The Frobenius Norm of the symplecticity error matrix and (b) the determinant criterion as a function of time using Model 1 and Δt = 0.1, averaged over a million trajectories using the SL (purple), the MInt (cyan) and the DE (red) algorithms. In (a) the MInt algorithm is seen to be symplectic whereas the DE and SL are not, whereas in (b) all algorithms satisfy Liouville’s theorem. Further detail of (a) with respect to a range of timesteps is presented in Figure A1 in Appendix A.
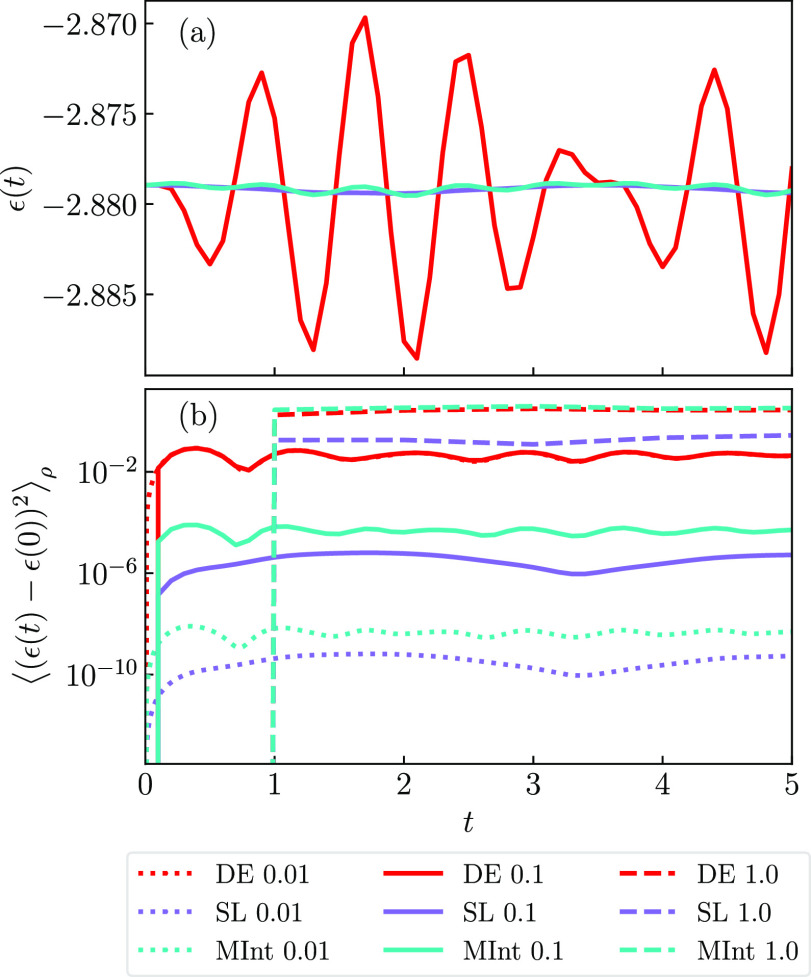
We now look at energy conservation, Figure 2, where (a) depicts the energy of a single trajectory and (b) averages the energy conservation criterion
| 65 |
over trajectories until convergence was observed. We calculate the energy, ε, by evaluating the MMST Hamiltonian, eq 4, at each timestep. Under perfect energy conservation, the criterion should be zero. For a single trajectory, we observe that the DE algorithm has much larger oscillations and does not conserve energy well when compared to the MInt and SL algorithms.
Figure 2.
The energy conservation for Model 1 with (a) a single trajectory and Δt = 0.1 (solid) and (b) averaged using Δt = 0.1 (solid), Δt = 0.01 (dotted) and Δt = 1.0 (dashed) with the SL (purple), the MInt (cyan), and the DE (red) algorithms. The DE algorithm has the worst energy conservation and, for this system, the MInt has slightly worse conservation than the SL. The SL and MInt algorithms show improved energy conservation upon decreasing the timestep, unlike the DE.
In Figure 2b, we
average over many trajectories and consider different timestep sizes.
It is seen that the MInt and SL algorithms are second-order as changing
the timestep by a factor of 10 increases the criterion by ∼104 as expected.79 This agrees with
the algebraic determination of the order by Church et al.(1) However, the DE algorithm remains the
same magnitude for Δt = 0.01 and Δt = 0.1, appearing to not be affected by the smaller timestep.
The very coarse Δt = 1.0 is so large that it
breaks the trends. The DE algorithm’s poor energy conservation
is due to the discarded terms when the DE approximation is made; when
these terms are large, the propagation of the nuclear momentum is
affected significantly, which then affects all other variables through
the propagation equations. The MInt and SL energy conservation is
very similar although the SL algorithm is seen to have the smallest
energy fluctuations throughout and appears to have a longer period
of oscillation for Model 1. This is surprising as one would expect
a symplectic algorithm to have better energy conservation compared
to a non-symplectic algorithm. However, we note that conservation
of energy is not always a good judgement of the algorithm quality.
For a symplectic algorithm, the approximate evolution of the exact
Hamiltonian is equivalent to the exact evolution of an approximate
Hamiltonian that deviates from the exact Hamiltonian on the order
of the algorithm.1,79 Evolution of a symplectic algorithm
results in the energy of the approximate Hamiltonian being exactly
conserved, also described as being on the shell of the shadow Hamiltonian.
For the MInt, this results in the energy being conserved at exponentially
long times with fluctuations on 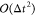 . For Models 2 and 3, we observe that the
MInt and SL algorithms have almost identical energy conservation while
the DE algorithm is worse, seen in Figures S1 and S2 in the Supporting Information.
. For Models 2 and 3, we observe that the
MInt and SL algorithms have almost identical energy conservation while
the DE algorithm is worse, seen in Figures S1 and S2 in the Supporting Information.
3.3. Correlation Functions
The nuclear
position and electronic population autocorrelation functions, eqs 60a and 60b, were calculated for the three models. The fast oscillations
of 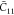 in Figure 3a indicate that the strong electronic coupling is close
to the adiabatic limit and the dynamics tend toward classical evolution
on the lower adiabatic surface as U is approximately
harmonic.53 For Models 2 and 3, the weaker
electronic coupling reduces the electronic oscillation frequency,
producing curves that deviate from the adiabatic result.53 In Model 2, the equilibrium population of the
first electronic state is quickly lost to the lower energy second
state, indicating that the system is almost always on one diabatic
surface. The correlation functions obtained using the MInt and SL
algorithms qualitatively replicate the dynamics expected from the
single-bead calculation in Figure 1 of ref [53] for all models. Comparing
the three algorithms tested in Figure 3 provides the interesting discovery that the DE algorithm
is very accurate for Model 1, despite the lack of energy conservation.
This is likely due to averaging with fast electronic oscillations
providing the correct convergence. However, for the other models,
the DE algorithm predicts the same initial drop in the electronic
population autocorrelation functions as the MInt and SL algorithms
but starts to deviate from the expected behavior after the minima.
The correlation functions have the same shape, indicating a systematic
error that likely arises due to the DE approximation. This assumes
that the off-diagonal elements of
in Figure 3a indicate that the strong electronic coupling is close
to the adiabatic limit and the dynamics tend toward classical evolution
on the lower adiabatic surface as U is approximately
harmonic.53 For Models 2 and 3, the weaker
electronic coupling reduces the electronic oscillation frequency,
producing curves that deviate from the adiabatic result.53 In Model 2, the equilibrium population of the
first electronic state is quickly lost to the lower energy second
state, indicating that the system is almost always on one diabatic
surface. The correlation functions obtained using the MInt and SL
algorithms qualitatively replicate the dynamics expected from the
single-bead calculation in Figure 1 of ref [53] for all models. Comparing
the three algorithms tested in Figure 3 provides the interesting discovery that the DE algorithm
is very accurate for Model 1, despite the lack of energy conservation.
This is likely due to averaging with fast electronic oscillations
providing the correct convergence. However, for the other models,
the DE algorithm predicts the same initial drop in the electronic
population autocorrelation functions as the MInt and SL algorithms
but starts to deviate from the expected behavior after the minima.
The correlation functions have the same shape, indicating a systematic
error that likely arises due to the DE approximation. This assumes
that the off-diagonal elements of 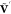 in the adiabatic basis, G,
are zero and that the diagonal elements are equal, which is not the
case for the SL and MInt algorithms.1
in the adiabatic basis, G,
are zero and that the diagonal elements are equal, which is not the
case for the SL and MInt algorithms.1
Figure 3.
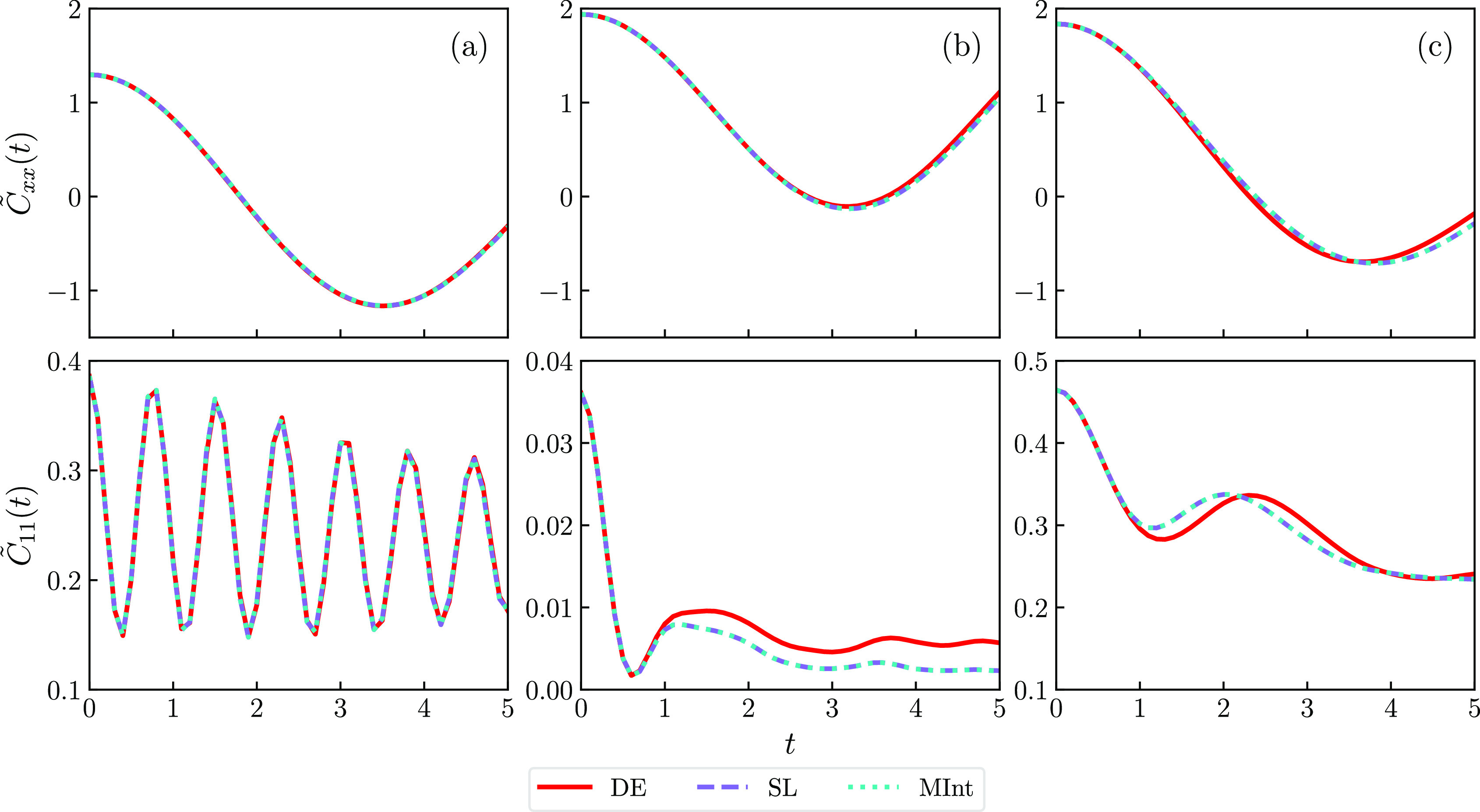
Nuclear
position, 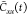 , and electronic population,
, and electronic population, 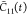 , autocorrelation functions for (a) Model
1, (b) Model 2, and (c) Model 3 using Δt =
0.1 with the DE (red solid), SL (purple dashed), and MInt (cyan dotted)
algorithms. The SL and MInt give identical results, but the DE algorithm
deviates from them in (b, c).
, autocorrelation functions for (a) Model
1, (b) Model 2, and (c) Model 3 using Δt =
0.1 with the DE (red solid), SL (purple dashed), and MInt (cyan dotted)
algorithms. The SL and MInt give identical results, but the DE algorithm
deviates from them in (b, c).
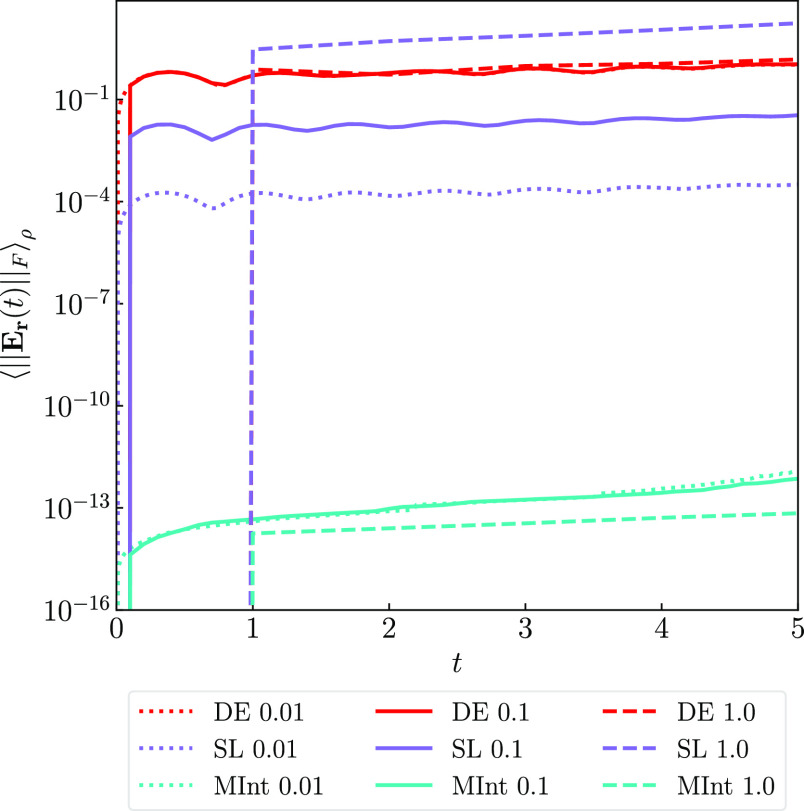
While testing energy conservation, we observed that the DE algorithm has more trajectories with poor energy convergence for models with weaker electronic coupling and was particularly poor in the intermediate regime given by Model 3. The MInt and SL algorithms produce the same correlation functions for all the models tested with small timesteps. When testing different timesteps, as seen in Appendix A, both the MInt and SL algorithms are tolerant of a coarse timestep. For Δt = 1.0, we observe that the MInt and SL correlation functions start to differ, with the MInt being closer to the small timestep results. However, the electronic oscillations are not captured well due to aliasing. The MInt and SL algorithms are limited by the model used rather than the algorithmic accuracy.
In Table 3, we provide an overview of the properties tested. The MInt algorithm is the only symplectic algorithm satisfying the symplecticity criterion, providing exact propagation of H1 and H2.1 The SL and DE algorithms have a non-zero error matrix that increases with time, indicating that neither is symplectic due to the approximations made.1−3,53 The lack of symplecticity may result in an energy drift at long simulation times, although this was not observed within the short simulation time tested here.
Table 3. Summary of the Computational Results, Which Are Consistent with the Theoretical Results in Table 1.
| Computational Results | MInt | SL | DE |
|---|---|---|---|
| Satisfies Liouville’s theorem | √ | √ | √ |
| Symplectic | √ | × | × |
| Energy conservation | good | good | poor |
| Correlation function accuracy | good | good | poor |
The SL algorithm approximates that the electronic
variables can
be held still while the nuclear momentum is propagated.3 The DE algorithm assumes that the eigenvalues
of the potential matrix are equal, such that the potential derivative
in the adiabatic basis is approximated as 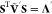 .2 This results
in inaccurate nuclear trajectories that leads to poor energy conservation.
However, all three algorithms obey Liouville’s theorem, preserving
volume phase-space throughout the trajectories. The MInt and SL have
similar energy conservation, where in some cases, the SL has better
energy conservation.1,79 However, as the MInt is symplectic,
it will always fluctuate to the second order, whereas the SL is likely
to drift for long simulation times.
.2 This results
in inaccurate nuclear trajectories that leads to poor energy conservation.
However, all three algorithms obey Liouville’s theorem, preserving
volume phase-space throughout the trajectories. The MInt and SL have
similar energy conservation, where in some cases, the SL has better
energy conservation.1,79 However, as the MInt is symplectic,
it will always fluctuate to the second order, whereas the SL is likely
to drift for long simulation times.
The correlation functions produced for the MInt and SL algorithms are very similar to those computed in ref [53], with the small differences arising from the different choice of splitting the potential. The DE algorithm converges to a different result for models with weaker coupling, being a good approximation only near the adiabatic limit.
Table S1 in the Supporting Information presents timings of the computational algorithms. One should note that in this case, the bottleneck is the evaluation of the algorithm itself rather than the calculation of the potential matrix. When calculating the monodromy matrix, we observed that the SL algorithm has the lowest computational cost followed closely by the MInt, with the DE algorithm taking the longest time to run. Without calculating the monodromy matrix, the SL is significantly faster, and the MInt and DE take similar times to run.
4. Conclusions
In this article, we have tested symplecticity, Liouville’s theorem, energy conservation, and computed correlation functions using the MInt, SL, and DE algorithms for a range of model parameters and timesteps. We find that the computational results agree with our theoretical predictions. If symplecticity is required, for accurate MMST Hamiltonian dynamics with little energy drift, the MInt algorithm should be used. As far as we are aware, the MInt is the only known symplectic algorithm for a general form of the MMST Hamiltonian. However, even though the SL algorithm is not formally symplectic with a finite timestep, it becomes exact in the limit of an infinitesimal timestep. In our tests, it gave comparable accuracy to the MInt algorithm, but at a lower computational cost. We would not recommend the DE algorithm for these models, as it is not exact in the Δt → 0 limit, breaks energy conservation, and introduces errors into the results. This indicates that for the models used here, the degenerate eigenvalue approximation is not valid.
Further work includes integrating the Cayley transform to extend these findings to stable NRPMD simulations.85 Additionally, one can apply the MInt algorithm to related dynamical methods such as forward–backward IVR.51,82 Further development of the MInt algorithm would be of great interest. For example, as the adiabatic form of the Meyer–Miller Hamiltonian is known,91 extension of the MInt algorithm to the adiabatic representation may be possible. Also, one might be able to obtain a higher order of accuracy with the MInt by employing an alternative splitting of H1 and H2.93
Acknowledgments
We thank Gregory S. Ezra and Jiří Vaníček for their helpful comments. TJHH acknowledges a Royal Society University Research Fellowship URF\R1\201502. LEC acknowledges a University College London studentship. JER acknowledges funding from the ETH Hans H. Günthard fellowship.
Appendices A
Symplecticity
The symplecticity criterion can be algebraically determined for the three algorithms, where the MInt and SL have already been derived by Church et al. (2018). It is sufficient to say that under the Hamiltonian splitting into H1 and H2, the symplecticity criterion becomes1,79
| A1 |
For example, following the
method by Church et al.,1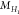 is eq 23 for all three algorithms. This can be derived from
the propagation equations, eqs 21a and 21b, where MXX = Mxx = Mpp = MPP = 1 and
is eq 23 for all three algorithms. This can be derived from
the propagation equations, eqs 21a and 21b, where MXX = Mxx = Mpp = MPP = 1 and
| A2 |
Evaluating the symplecticity criterion results in
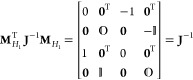 |
A3 |
such that the propagation under H1 is symplectic.1
The symplecticity for H2 is derived separately for all three algorithms due to the different
nuclear propagation equations, where the MInt and SL algorithms had
previously been derived by Church et al.(1) For the MInt algorithm, 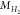 is eq 35 where the symplecticity criterion becomes
is eq 35 where the symplecticity criterion becomes
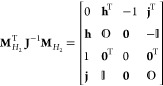 |
A4 |
with
where Church et al.(1) previously determined that h ≡ 0 and j ≡ 0 ∀ X, P.
For the SL algorithm, propagation of H2 is split further into nuclear and electronic contributions for which the monodromy matrices are eq 38. Evaluating the symplecticity criterion for Mp
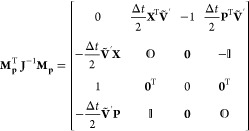 |
A6 |
which will only be symplectic if 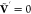 .1 Evaluating
for Mel
.1 Evaluating
for Mel
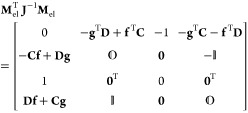 |
A7 |
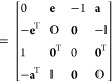 |
where eqs A5a and A5b have been used in conjunction with the fact that h ≡ 0 and j ≡ 0 ∀ X, P.1
Church et al. note that a, e ≠ 0T so evolution under 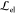 and
and 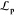 is not symplectic. The combined evolution
under
is not symplectic. The combined evolution
under 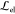 and
and 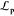 does not provide error cancellation that
restores symplecticity. We find that numerically the difference between
does not provide error cancellation that
restores symplecticity. We find that numerically the difference between 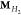 and MelMp is on
and MelMp is on 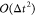 , in agreement with the literature.1 The combination of MpMel also provides the same result.
This means that the propagation of MpMel will be symplectic in the Δt → 0 limit, but it will not be for an arbitrary
timestep.
, in agreement with the literature.1 The combination of MpMel also provides the same result.
This means that the propagation of MpMel will be symplectic in the Δt → 0 limit, but it will not be for an arbitrary
timestep.
For the DE algorithm, the monodromy matrix, MDE, for the approximate propagation of H2 has been derived for the first time as eq 50. Using eqs 34a–34e with h ≡ 0 and j ≡ 0 ∀ X, P, the symplecticity criterion becomes
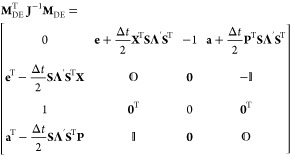 |
A8 |
which will not be symplectic for the same reasoning as for the SL algorithm.
To derive the
order of the difference between 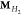 and MDE, following
the approach of Church et al.,1 we define
and MDE, following
the approach of Church et al.,1 we define
| A9a |
| A9b |
such that, the symplecticity criterion will be met if a̅ ≡ a and e̅ ≡ e. Expanding in coefficients of X and P leads to
| A10a |
| A10b |
Rotating to the diabatic basis gives
 |
where Γ and Ξ are given in eqs 31a and 31b. Evaluating element-wise in powers of Δt
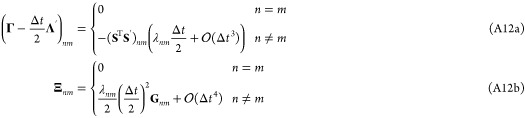 |
Hence, the order of the difference between 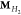 and MDE is
and MDE is 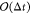 . The SL algorithm, MelMp, is one order higher than
the DE algorithm, MDE, so the symplecticity
is better as seen in Figures 1 and A1.
. The SL algorithm, MelMp, is one order higher than
the DE algorithm, MDE, so the symplecticity
is better as seen in Figures 1 and A1.
Figure A1.
The Frobenius Norm of the error matrix averaged until convergence with the SL (purple), the MInt (cyan), and the DE (red) algorithms using timesteps of Δt = 0.1 (solid), Δt = 0.01 (dotted), and Δt = 1.0 (dashed). The MInt algorithm is seen to be symplectic and does not change with timestep. The SL algorithm is seen to be second-order with respect to time and the DE algorithm is zero-order, in agreement with the theoretical predictions.
We find that, numerically, when considering the
whole propagation
of H using the SL algorithm, the initial difference
in symplecticity between the MInt and SL algorithms scale on 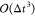 . This is due to some error cancellation
arising from the symmetric splitting of H2. Hence, when propagating for a given length of time, the order is
. This is due to some error cancellation
arising from the symmetric splitting of H2. Hence, when propagating for a given length of time, the order is 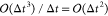 , seen in Figure A1, where changing the timestep by a factor
of 10 results in a change in the symplecticity by ∼102. For the DE algorithm, the initial difference in symplecticity with
the MInt algorithm scales on
, seen in Figure A1, where changing the timestep by a factor
of 10 results in a change in the symplecticity by ∼102. For the DE algorithm, the initial difference in symplecticity with
the MInt algorithm scales on 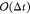 . Therefore, for a given length of time,
the order is
. Therefore, for a given length of time,
the order is 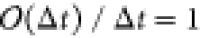 . Figure A1 corroborates this as the DE algorithm appears to be
zero-order for all the timesteps tested. The symplecticity does not
improve with smaller timesteps.
. Figure A1 corroborates this as the DE algorithm appears to be
zero-order for all the timesteps tested. The symplecticity does not
improve with smaller timesteps.
We note that for symplectic methods, i.e., the MInt algorithm, the Er matrix will be smaller for coarser timesteps due to fewer computations where floating point errors accumulate. We see this when comparing the Δt = 1.0 and Δt = 0.1 results for the MInt algorithm. This trend is not seen as clearly for Δt = 0.01 and Δt = 0.1 due to the log scale of the plot, but it is present by the end of the simulation time. In contrast, the Er matrix is typically larger for coarser timesteps for non-symplectic methods as the deviation is an order of Δt, as shown above with the zero- and second-order behaviour of the DE and SL algorithms respectively.
B
Exactness in Δt → 0 Limit
The exact Hamiltonian propagation can be expressed as a Liouvillian with the flow map
| B1 |
| B2 |
The Maclaurin expansion of the exact dynamics is
| B3 |
such that, to obtain the short-time limit,
we truncate the series at 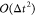 .
.
The MInt algorithm has previously
been proved by Church et al.(1) to deviate from exact dynamics at terms on 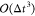 and is at least a second-order method.
The MInt algorithm is therefore exact in the Δt → 0 limit. As all three algorithms have the same propagation
of x, X, and P, the only
step that differs for the SL and DE algorithms is the propagation
of nuclear momentum. Hence, we focus on the deviation of this propagation
from the exact dynamics, where the short-time propagation of p for a whole timestep is
and is at least a second-order method.
The MInt algorithm is therefore exact in the Δt → 0 limit. As all three algorithms have the same propagation
of x, X, and P, the only
step that differs for the SL and DE algorithms is the propagation
of nuclear momentum. Hence, we focus on the deviation of this propagation
from the exact dynamics, where the short-time propagation of p for a whole timestep is
| B4 |
| B5 |
| B6 |
If we stop here, this is the SL propagation
of p, eq 37. The SL algorithm is exact in the short-time limit, deviating
by terms of at least 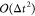 and therefore is at least a first-order
method.
and therefore is at least a first-order
method.
To compare with the DE algorithm, we insert eq 45 into the short time limit in the previous equation, and as the DE requires a traceless Ṽ, we discard the trace term such that
| B7 |
It can be seen that this is equivalent to the DE algorithm, eq 49, if the following terms are discarded
| B8 |
These terms vanish when the DE approximation
is made and are 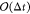 . One might argue that a prior nuclear position
propagation, eqs 21a and 21b, may restore these terms. However,
this would result in Λ′(x) being replaced with Λ′(x + pΔt/m). Using a Taylor expansion, we can show that
. One might argue that a prior nuclear position
propagation, eqs 21a and 21b, may restore these terms. However,
this would result in Λ′(x) being replaced with Λ′(x + pΔt/m). Using a Taylor expansion, we can show that
| B9 |
such that, any correctional terms would be
at least 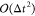 due to the factor of Δt in eq B7. This same
logic holds for X and P. Hence, the DE algorithm
differs from the exact evolution at
due to the factor of Δt in eq B7. This same
logic holds for X and P. Hence, the DE algorithm
differs from the exact evolution at 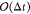 , meaning it is zero-order and is not exact
in the Δt → 0 limit.
, meaning it is zero-order and is not exact
in the Δt → 0 limit.
C
Conservation of Electronic Probability
To prove that all three algorithms conserve electronic probability, we first define
| C1 |
Taking the value at time t
a translation back in time can be achieved with eq 26, resulting in
 |
which is equivalent to eq C2. As all three algorithms propagate eq 26 exactly, this derivation holds and all three algorithms conserve electronic probability.
D
Sampling
Following a similar derivation of the partition function as in refs [3] and [53], the sampling method used in this work is derived. Instead of formulating in the limit of an infinite number of ring-polymer beads, we derive the partition function in the single-bead case. The wavefunctions of the singly excited oscillator (SEO) states are known in the position and momentum bases3
| D1 |
| D2 |
where ⟨n|X⟩ = ⟨X|n⟩* and
likewise for P. The partition function, 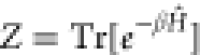 , is expanded as a Trotter product where N = 1 for the one-bead case
, is expanded as a Trotter product where N = 1 for the one-bead case
| D3 |
Inserting the projection operator 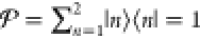 and summing over the two electronic levels
in our model
and summing over the two electronic levels
in our model
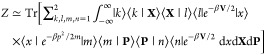 |
D4 |
where the imaginary-time free-particle propagator for N = 1 is3
| D5 |
such that
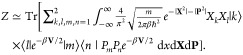 |
D6 |
Separating out the state-independent potential, U
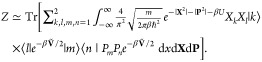 |
D7 |
The sum can be rewritten in matrix notation
| D8 |
where 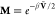 and using the cyclic properties of the
trace
and using the cyclic properties of the
trace
| D9 |
which is a scalar quantity. Using the Gaussian integral identity
| D10 |
such that p can be inserted into the integral
| D11 |
resulting in the probability distribution, ρ, eq 53, where W is positive-definite in the single-bead case as
| D12 |
therefore
| D13 |
This means that 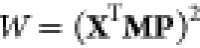 , which will always be positive. We sampled
Gaussian distributions for electronic variables where μ = 0
and
, which will always be positive. We sampled
Gaussian distributions for electronic variables where μ = 0
and 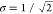 , and classical distributions for nuclear
variables where μx = 0 and
, and classical distributions for nuclear
variables where μx = 0 and 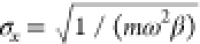 , and μp = 0 and
, and μp = 0 and 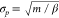 , such that the sampled distribution is
, such that the sampled distribution is
| D14 |
To obtain the required distribution, eq 53, the following relationship is established
| D15 |
Hence, we need to correct calculated observables
to average over the required distribution. We can thus define the
average of an observable over the distribution, 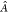 , that may be a function
of initial position and momenta, i.e.,
, that may be a function
of initial position and momenta, i.e., 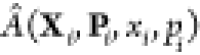 as
as
| D16 |
The integral over the sampled distribution can be replaced with a sum over the number of samples taken, J,
 |
The partition function can be calculated as
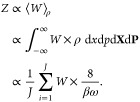 |
D19 |
Supporting Information Available
The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.jctc.3c00709.
Additional energy conservation plots for Models 2 and 3, comparison of correlation functions using different timesteps, and properties of the DE algorithm in the original form (PDF)
Author Present Address
§ Department of Chemistry, University of Oxford, Physical and Theoretical Chemistry Laboratory, South Parks Road, Oxford OX1 3QZ, U.K
The authors declare no competing financial interest.
Supplementary Material
References
- Church M. S.; Hele T. J. H.; Ezra G. S.; Ananth N. Nonadiabatic semiclassical dynamics in the mixed quantum-classical initial value representation. J. Chem. Phys. 2018, 148, 102326. 10.1063/1.5005557. [DOI] [PubMed] [Google Scholar]
- Kelly A.; van Zon R.; Schofield J.; Kapral R. Mapping quantum-classical Liouville equation: Projectors and trajectories. J. Chem. Phys. 2012, 136, 084101. 10.1063/1.3685420. [DOI] [PubMed] [Google Scholar]
- Richardson J. O.; Meyer P.; Pleinert M.-O.; Thoss M. An analysis of nonadiabatic ring-polymer molecular dynamics and its application to vibronic spectra. Chem. Phys. 2017, 482, 124–134. 10.1016/j.chemphys.2016.09.036. [DOI] [Google Scholar]
- Reece S. Y.; Nocera D. G. Proton-Coupled Electron Transfer in Biology: Results from Synergistic Studies in Natural and Model Systems. Annu. Rev. Biochem. 2009, 78, 673–699. 10.1146/annurev.biochem.78.080207.092132. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Domcke W.; Yarkony D. R. Role of Conical Intersections in Molecular Spectroscopy and Photoinduced Chemical Dynamics. Annu. Rev. Phys. Chem. 2012, 63, 325–352. 10.1146/annurev-physchem-032210-103522. [DOI] [PubMed] [Google Scholar]
- Hammes-Schiffer S.; Stuchebrukhov A. A. Theory of coupled electron and proton transfer reactions. Chem. Rev. 2010, 110, 6939–6960. 10.1021/cr1001436. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cheng Y.-C.; Fleming G. R. Dynamics of Light Harvesting in Photosynthesis. Annu. Rev. Phys. Chem. 2009, 60, 241–262. 10.1146/annurev.physchem.040808.090259. [DOI] [PubMed] [Google Scholar]
- De Sio A.; Camargo F. V. d. A.; Winte K.; Sommer E.; Branchi F.; Cerullo G.; Lienau C. Ultrafast relaxation dynamics in a polymer: fullerene blend for organic photovoltaics probed by two-dimensional electronic spectroscopy. Eur. Phys. J. B 2018, 91, 236. 10.1140/epjb/e2018-90216-4. [DOI] [Google Scholar]
- Nguyen X. T.; Timmer D.; Rakita Y.; Cahen D.; Steinhoff A.; Jahnke F.; Lienau C.; De Sio A. Ultrafast Charge Carrier Relaxation in Inorganic Halide Perovskite Single Crystals Probed by Two-Dimensional Electronic Spectroscopy. J. Phys. Chem. Lett. 2019, 10, 5414–5421. 10.1021/acs.jpclett.9b01936. [DOI] [PubMed] [Google Scholar]
- Gaynor J. D.; Petrone A.; Li X.; Khalil M. Mapping Vibronic Couplings in a Solar Cell Dye with Polarization-Selective Two-Dimensional Electronic-Vibrational Spectroscopy. J. Phys. Chem. Lett. 2018, 9, 6289–6295. 10.1021/acs.jpclett.8b02752. [DOI] [PubMed] [Google Scholar]
- Landau L. D. On the Theory of Transfer of Energy at Collisions II. Phys. Z. Sowjetunion 1932, 2, 46. [Google Scholar]
- Zener C. Non-adiabatic crossing of energy levels. Proc. R. Soc. London. Ser. A 1932, 137, 696–702. 10.1098/rspa.1932.0165. [DOI] [Google Scholar]
- Hele T. J.; Ananth N. Deriving the exact nonadiabatic quantum propagator in the mapping variable representation. Faraday Discuss. 2016, 195, 269–289. 10.1039/c6fd00106h. [DOI] [PubMed] [Google Scholar]
- Topaler M.; Makri N. Path integral calculation of quantum nonadiabatic rates in model condensed phase reactions. J. Phys. Chem. 1996, 100, 4430–4436. 10.1021/jp951673k. [DOI] [Google Scholar]
- Beck M. H.; Jäckle A.; Worth G. A.; Meyer H. D. The multiconfiguration time-dependent Hartree (MCTDH) method: A highly efficient algorithm for propagating wavepackets. Phys. Rep. 2000, 324, 1–105. 10.1016/s0370-1573(99)00047-2. [DOI] [Google Scholar]
- Stock G.; Thoss M.. Adv. Chem. Phys.; Rice S. A., Ed.; John Wiley & Sons, 2005; Vol. 131, pp 243–375. [Google Scholar]
- Shalashilin D. V. Multiconfigurational Ehrenfest approach to quantum coherent dynamics in large molecular systems. Faraday Discuss. 2011, 153, 105. 10.1039/c1fd00034a. [DOI] [PubMed] [Google Scholar]
- Kapral R. Progress in the theory of mixed quantum-classical dynamics. Annu. Rev. Phys. Chem. 2006, 57, 129–157. 10.1146/annurev.physchem.57.032905.104702. [DOI] [PubMed] [Google Scholar]
- Donoso A.; Martens C. C. Simulation of Coherent Nonadiabatic Dynamics Using Classical Trajectories. J. Phys. Chem. A 1998, 102, 4291–4300. 10.1021/jp980219o. [DOI] [Google Scholar]
- Kapral R. Surface hopping from the perspective of quantum–classical Liouville dynamics. Chem. Phys. 2016, 481, 77–83. 10.1016/j.chemphys.2016.05.016. [DOI] [Google Scholar]
- Cotton S. J.; Miller W. H. A new symmetrical quasi-classical model for electronically non-adiabatic processes: Application to the case of weak non-adiabatic coupling. J. Chem. Phys. 2016, 145, 144108. 10.1063/1.4963914. [DOI] [PubMed] [Google Scholar]
- Tully J. C.; Preston R. K. Trajectory Surface Hopping Approach to Nonadiabatic Molecular Collisions: The Reaction of H + with D 2. J. Chem. Phys. 1971, 55, 562–572. 10.1063/1.1675788. [DOI] [Google Scholar]
- Tully J. C. Molecular dynamics with electronic transitions. J. Chem. Phys. 1990, 93, 1061–1071. 10.1063/1.459170. [DOI] [Google Scholar]
- Huo P.; Coker D. F. Communication: Partial linearized density matrix dynamics for dissipative, non-adiabatic quantum evolution. J. Chem. Phys. 2011, 135, 201101. 10.1063/1.3664763. [DOI] [PubMed] [Google Scholar]
- Meyer H. D.; Miller W. H. A classical analog for electronic degrees of freedom in nonadiabatic collision processes. J. Chem. Phys. 1979, 70, 3214–3223. 10.1063/1.437910. [DOI] [Google Scholar]
- Stock G.; Thoss M. Semiclassical Description of Nonadiabatic Quantum Dynamics. Phys. Rev. Lett. 1997, 78, 578–581. 10.1103/physrevlett.78.578. [DOI] [PubMed] [Google Scholar]
- Wang H.; Song X.; Chandler D.; Miller W. H. Semiclassical study of electronically nonadiabatic dynamics in the condensed-phase: Spin-boson problem with Debye spectral density. J. Chem. Phys. 1999, 110, 4828–4840. 10.1063/1.478388. [DOI] [Google Scholar]
- Antipov S. V.; Ye Z.; Ananth N. Dynamically consistent method for mixed quantum-classical simulations: A semiclassical approach. J. Chem. Phys. 2015, 142, 184102. 10.1063/1.4919667. [DOI] [PubMed] [Google Scholar]
- Runeson J. E.; Richardson J. O. Spin-mapping approach for nonadiabatic molecular dynamics. J. Chem. Phys. 2019, 151, 044119. 10.1063/1.5100506. [DOI] [PubMed] [Google Scholar]
- Runeson J. E.; Richardson J. O. Generalized spin mapping for quantum-classical dynamics. J. Chem. Phys. 2020, 152, 084110. 10.1063/1.5143412. [DOI] [PubMed] [Google Scholar]
- Mannouch J. R.; Richardson J. O. A mapping approach to surface hopping. J. Chem. Phys. 2023, 158, 104111. 10.1063/5.0139734. [DOI] [PubMed] [Google Scholar]
- Mott N. F. On the Theory of Excitation by Collision with Heavy Particles. Math. Proc. Cambridge Philos. Soc. 1931, 27, 553–560. 10.1017/s0305004100009816. [DOI] [Google Scholar]
- Prezhdo O. V.; Rossky P. J. Mean-field molecular dynamics with surface hopping. J. Chem. Phys. 1997, 107, 825–834. 10.1063/1.474382. [DOI] [Google Scholar]
- Zimmermann T.; Vaníček J. Efficient on-the-fly ab initio semiclassical method for computing time-resolved nonadiabatic electronic spectra with surface hopping or Ehrenfest dynamics. J. Chem. Phys. 2014, 141, 134102. 10.1063/1.4896735. [DOI] [PubMed] [Google Scholar]
- Meyer H.-D.; Miller W. H. Classical models for electronic degrees of freedom: Derivation via spin analogy and application to F → +H2 → F+H2. J. Chem. Phys. 1979, 71, 2156–2169. 10.1063/1.438598. [DOI] [Google Scholar]
- Runeson J. E.; Richardson J. O. Quantum Entanglement from Classical Trajectories. Phys. Rev. Lett. 2021, 127, 250403. 10.1103/physrevlett.127.250403. [DOI] [PubMed] [Google Scholar]
- Müller U.; Stock G. Flow of zero-point energy and exploration of phase space in classical simulations of quantum relaxation dynamics. II. Application to nonadiabatic processes. J. Chem. Phys. 1999, 111, 77–88. 10.1063/1.479255. [DOI] [Google Scholar]
- Stock G.; Müller U. Flow of zero-point energy and exploration of phase space in classical simulations of quantum relaxation dynamics. J. Chem. Phys. 1999, 111, 65–76. 10.1063/1.479254. [DOI] [Google Scholar]
- Mannouch J. R.; Richardson J. O. A partially linearized spin-mapping approach for nonadiabatic dynamics. I. Derivation of the theory. J. Chem. Phys. 2020, 153, 194109. 10.1063/5.0031168. [DOI] [PubMed] [Google Scholar]
- Mannouch J. R.; Richardson J. O. A partially linearized spin-mapping approach for nonadiabatic dynamics. II. Analysis and comparison with related approaches. J. Chem. Phys. 2020, 153, 194110. 10.1063/5.0031173. [DOI] [PubMed] [Google Scholar]
- Mannouch J. R.; Richardson J. O. A partially linearized spin-mapping approach for simulating nonlinear optical spectra. J. Chem. Phys. 2022, 156, 024108. 10.1063/5.0077744. [DOI] [PubMed] [Google Scholar]
- Miller W. H. Classical S Matrix: Numerical Application to Inelastic Collisions. J. Chem. Phys. 1970, 53, 3578–3587. 10.1063/1.1674535. [DOI] [Google Scholar]
- Bonella S.; Coker D. F. A semiclassical limit for the mapping Hamiltonian approach to electronically nonadiabatic dynamics. J. Chem. Phys. 2001, 114, 7778–7789. 10.1063/1.1366331. [DOI] [Google Scholar]
- Wang H.; Sun X.; Miller W. H. Semiclassical approximations for the calculation of thermal rate constants for chemical reactions in complex molecular systems. J. Chem. Phys. 1998, 108, 9726–9736. 10.1063/1.476447. [DOI] [Google Scholar]
- Sun X.; Wang H.; Miller W. H. On the semiclassical description of quantum coherence in thermal rate constants. J. Chem. Phys. 1998, 109, 4190–4200. 10.1063/1.477025. [DOI] [Google Scholar]
- Sun X.; Wang H.; Miller W. H. Semiclassical theory of electronically nonadiabatic dynamics: Results of a linearized approximation to the initial value representation. J. Chem. Phys. 1998, 109, 7064–7074. 10.1063/1.477389. [DOI] [Google Scholar]
- Shi Q.; Geva E. Nonradiative electronic relaxation rate constants from approximations based on linearizing the path-integral forward-backward action. J. Phys. Chem. A 2004, 108, 6109–6116. 10.1021/jp049547g. [DOI] [Google Scholar]
- Liu J. Recent advances in the linearized semiclassical initial value representation/classical Wigner model for the thermal correlation function. Int. J. Quantum Chem. 2015, 115, 657–670. 10.1002/qua.24872. [DOI] [Google Scholar]
- Church M. S.; Antipov S. V.; Ananth N. Validating and implementing modified Filinov phase filtration in semiclassical dynamics. J. Chem. Phys. 2017, 146, 234104. 10.1063/1.4986645. [DOI] [PubMed] [Google Scholar]
- Filinov V. Calculation of the feynman integrals by means of the Monte Carlo method. Nucl. Phys. B 1986, 271, 717–725. 10.1016/s0550-3213(86)80034-7. [DOI] [Google Scholar]
- Thoss M.; Wang H.; Miller W. H. Generalized forward–backward initial value representation for the calculation of correlation functions in complex systems. J. Chem. Phys. 2001, 114, 9220–9235. 10.1063/1.1359242. [DOI] [Google Scholar]
- Ananth N.; Venkataraman C.; Miller W. H. Semiclassical description of electronically nonadiabatic dynamics via the initial value representation. J. Chem. Phys. 2007, 127, 084114. 10.1063/1.2759932. [DOI] [PubMed] [Google Scholar]
- Richardson J. O.; Thoss M. Communication: Nonadiabatic ring-polymer molecular dynamics. J. Chem. Phys. 2013, 139, 031102. 10.1063/1.4816124. [DOI] [PubMed] [Google Scholar]
- Ananth N. Mapping variable ring polymer molecular dynamics: A path-integral based method for nonadiabatic processes. J. Chem. Phys. 2013, 139, 124102. 10.1063/1.4821590. [DOI] [PubMed] [Google Scholar]
- Feynman R. P. Space-Time Approach to Non-Relativistic Quantum Mechanics. Rev. Mod. Phys. 1948, 20, 367–387. 10.1103/revmodphys.20.367. [DOI] [Google Scholar]
- Deymier P. A.; Runge K.; Oh K.-D.; Jabbour G. E.. Springer Ser. Mater. Sci.; Springer, 2016; Vol. 226, pp 13–106. [Google Scholar]
- Habershon S.; Manolopoulos D. E.; Markland T. E.; Miller T. F. III Ring-Polymer Molecular Dynamics: Quantum Effects in Chemical Dynamics from Classical Trajectories in an Extended Phase Space. Annu. Rev. Phys. Chem. 2013, 64, 387–413. 10.1146/annurev-physchem-040412-110122. [DOI] [PubMed] [Google Scholar]
- Craig I. R.; Manolopoulos D. E. Quantum statistics and classical mechanics: Real time correlation functions from ring polymer molecular dynamics. J. Chem. Phys. 2004, 121, 3368–3373. 10.1063/1.1777575. [DOI] [PubMed] [Google Scholar]
- Hele T. J. H.; Willatt M. J.; Muolo A.; Althorpe S. C. Boltzmann-conserving classical dynamics in quantum time-correlation functions: “Matsubara dynamics”. J. Chem. Phys. 2015, 142, 134103. 10.1063/1.4916311. [DOI] [PubMed] [Google Scholar]
- Cao J.; Voth G. A. A new perspective on quantum time correlation functions. J. Chem. Phys. 1993, 99, 10070–10073. 10.1063/1.465512. [DOI] [Google Scholar]
- Cao J.; Voth G. A. The formulation of quantum statistical mechanics based on the Feynman path centroid density. II. Dynamical properties. J. Chem. Phys. 1994, 100, 5106–5117. 10.1063/1.467176. [DOI] [Google Scholar]
- Cao J.; Voth G. A. The formulation of quantum statistical mechanics based on the Feynman path centroid density. III. Phase space formalism and analysis of centroid molecular dynamics. J. Chem. Phys. 1994, 101, 6157–6167. 10.1063/1.468503. [DOI] [Google Scholar]
- Cao J.; Voth G. A. The formulation of quantum statistical mechanics based on the Feynman path centroid density. I. Equilibrium properties. J. Chem. Phys. 1994, 100, 5093–5105. 10.1063/1.467175. [DOI] [Google Scholar]
- Rossi M.; Ceriotti M.; Manolopoulos D. E. How to remove the spurious resonances from ring polymer molecular dynamics. J. Chem. Phys. 2014, 140, 234116. 10.1063/1.4883861. [DOI] [PubMed] [Google Scholar]
- Hele T. J. H. On the relation between thermostatted ring-polymer molecular dynamics and exact quantum dynamics. Mol. Phys. 2016, 114, 1461–1471. 10.1080/00268976.2015.1136003. [DOI] [Google Scholar]
- Hele T. J. H.; Suleimanov Y. V. Should thermostatted ring polymer molecular dynamics be used to calculate thermal reaction rates?. J. Chem. Phys. 2015, 143, 074107. 10.1063/1.4928599. [DOI] [PubMed] [Google Scholar]
- Hele T. J. H.; Althorpe S. C. Derivation of a true (t → 0 + ) quantum transition-state theory. I. Uniqueness and equivalence to ring-polymer molecular dynamics transition-state-theory. J. Chem. Phys. 2013, 138, 084108. 10.1063/1.4792697. [DOI] [PubMed] [Google Scholar]
- Hele T. J. H.; Willatt M. J.; Muolo A.; Althorpe S. C. Communication: Relation of centroid molecular dynamics and ring-polymer molecular dynamics to exact quantum dynamics. J. Chem. Phys. 2015, 142, 191101. 10.1063/1.4921234. [DOI] [PubMed] [Google Scholar]
- Hele T. J. H.Quantum Transition-State Theory. Ph.D. Thesis, University of Cambridge, 2014;. [Google Scholar]
- Hele T. J. H.; Althorpe S. C. On the uniqueness of t → 0 + quantum transition-state theory. J. Chem. Phys. 2013, 139, 084116. 10.1063/1.4819077. [DOI] [PubMed] [Google Scholar]
- Althorpe S. C.; Hele T. J. H. Derivation of a true (t → 0 + ) quantum transition-state theory. II. Recovery of the exact quantum rate in the absence of recrossing. J. Chem. Phys. 2013, 139, 084115. 10.1063/1.4819076. [DOI] [PubMed] [Google Scholar]
- Hele T. J. H.An Electronically Non-Adiabatic Generalization of Ring Polymer Molecular Dynamics. MChem Thesis, University of Oxford, 2011;. [Google Scholar]
- Duke J. R.; Ananth N. Simulating Excited State Dynamics in Systems with Multiple Avoided Crossings Using Mapping Variable Ring Polymer Molecular Dynamics. J. Phys. Chem. Lett. 2015, 6, 4219–4223. 10.1021/acs.jpclett.5b01957. [DOI] [PubMed] [Google Scholar]
- Duke J. R.; Ananth N. Mean field ring polymer molecular dynamics for electronically nonadiabatic reaction rates. Faraday Discuss. 2016, 195, 253–268. 10.1039/c6fd00123h. [DOI] [PubMed] [Google Scholar]
- Chowdhury S. N.; Huo P. Coherent state mapping ring polymer molecular dynamics for non-adiabatic quantum propagations. J. Chem. Phys. 2017, 147, 214109. 10.1063/1.4995616. [DOI] [PubMed] [Google Scholar]
- Chowdhury S. N.; Huo P. Non-adiabatic Matsubara dynamics and non-adiabatic ring-polymer molecular dynamics. J. Chem. Phys. 2021, 154, 124124. 10.1063/5.0042136. [DOI] [PubMed] [Google Scholar]
- Shakib F. A.; Huo P. Ring Polymer Surface Hopping: Incorporating Nuclear Quantum Effects into Nonadiabatic Molecular Dynamics Simulations. J. Phys. Chem. Lett. 2017, 8, 3073–3080. 10.1021/acs.jpclett.7b01343. [DOI] [PubMed] [Google Scholar]
- Amati G.; Runeson J. E.; Richardson J. O. On detailed balance in nonadiabatic dynamics: From spin spheres to equilibrium ellipsoids. J. Chem. Phys. 2023, 158, 064113. 10.1063/5.0137828. [DOI] [PubMed] [Google Scholar]
- Leimkuhler B.; Reich S.. Simulating Hamiltonian Dyn.; Cambridge University Press, 2005. [Google Scholar]
- Hardy D. J.; Okunbor D. I. Qualitative study of the symplectic Störmer–Verlet integrator. J. Chem. Phys. 1995, 102, 8978–8982. 10.1063/1.468951. [DOI] [Google Scholar]
- Irigoyen M.Encycl. Math. Phys.; Elsevier, 2006, pp 624–630. [Google Scholar]
- Malpathak S.; Church M. S.; Ananth N. A Semiclassical Framework for Mixed Quantum Classical Dynamics. J. Phys. Chem. A 2022, 126, 6359–6375. 10.1021/acs.jpca.2c03467. [DOI] [PubMed] [Google Scholar]
- Venkataraman C.; Miller W. H. Chemical reaction rates using the semiclassical Van Vleck initial value representation. J. Chem. Phys. 2007, 126, 094104. 10.1063/1.2567200. [DOI] [PubMed] [Google Scholar]
- Tuckerman M. E.Statistical Mechanics: Theory and Molecular Simulation; Oxford University Press, 2010. [Google Scholar]
- Korol R.; Bou-Rabee N.; Miller T. F. III Cayley modification for strongly stable path-integral and ring-polymer molecular dynamics. J. Chem. Phys. 2019, 151, 124103. 10.1063/1.5120282. [DOI] [PubMed] [Google Scholar]
- Software—Ananth Group. https://ananth.chem.cornell.edu/styleguide/ (accessed on June 23, 2023).
- Gardner J.; Douglas-Gallardo O. A.; Stark W. G.; Westermayr J.; Janke S. M.; Habershon S.; Maurer R. J. NQCDynamics.jl: A Julia package for nonadiabatic quantum classical molecular dynamics in the condensed phase. J. Chem. Phys. 2022, 156, 174801. 10.1063/5.0089436. [DOI] [PubMed] [Google Scholar]
- Zwanzig R.Nonequilibrium Statistical Mechanics; Oxford University Press: New York, 2001; p 222. [Google Scholar]
- Kim H. W.; Rhee Y. M. Improving long time behavior of Poisson bracket mapping equation: A non-Hamiltonian approach. J. Chem. Phys. 2014, 140, 184106. 10.1063/1.4874268. [DOI] [PubMed] [Google Scholar]
- Kelly A.; Rhee Y. M. Mixed Quantum-Classical Description of Excitation Energy Transfer in a Model Fenna–Matthews–Olsen Complex. J. Phys. Chem. Lett. 2011, 2, 808–812. 10.1021/jz200059t. [DOI] [Google Scholar]
- Cotton S. J.; Liang R.; Miller W. H. On the adiabatic representation of Meyer-Miller electronic-nuclear dynamics. J. Chem. Phys. 2017, 147, 64112. 10.1063/1.4995301. [DOI] [PubMed] [Google Scholar]
- Martinez F.; Hanna G. Assessment of approximate solutions of the quantum–classical Liouville equation for dynamics simulations of quantum subsystems embedded in classical environments. Mol. Simul. 2015, 41, 107–122. 10.1080/08927022.2014.923573. [DOI] [Google Scholar]
- Roulet J.; Choi S.; Vaníček J. Efficient geometric integrators for nonadiabatic quantum dynamics. II. The diabatic representation. J. Chem. Phys. 2019, 150, 204113. 10.1063/1.5094046. [DOI] [PubMed] [Google Scholar]
- Ivanov A.; Andrianov S.; Kulabukhova N.; Maier R.; Senichev Y.; Zyuzin D.. Testing of symplectic integrator of spin-orbit motion based on matrix formalism. IPAC 2013 Proc. 4th Int. Part. Accel. Conf., 2013; pp 2582–2584.
- Ezra G. S. On the Statistical Mechanics of Non-Hamiltonian Systems: The Generalized Liouville Equation, Entropy, and Time-Dependent Metrics. J. Math. Chem. 2004, 35, 29–53. 10.1023/b:jomc.0000007811.79716.4d. [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.