Efficient mapping of accurate long reads in minimizer space with mapquik

Abstract

DNA sequencing data continue to progress toward longer reads with increasingly lower sequencing error rates. We focus on the critical problem of mapping, or aligning, low-divergence sequences from long reads (e.g., Pacific Biosciences [PacBio] HiFi) to a reference genome, which poses challenges in terms of accuracy and computational resources when using cutting-edge read mapping approaches that are designed for all types of alignments. A natural idea would be to optimize efficiency with longer seeds to reduce the probability of extraneous matches; however, contiguous exact seeds quickly reach a sensitivity limit. We introduce mapquik, a novel strategy that creates accurate longer seeds by anchoring alignments through matches of k consecutively sampled minimizers ($k$-min-mers) and only indexing $k$-min-mers that occur once in the reference genome, thereby unlocking ultrafast mapping while retaining high sensitivity. We show that mapquik significantly accelerates the seeding and chaining steps—fundamental bottlenecks to read mapping—for both the human and maize genomes with $>96\mathrm{\%}$ sensitivity and near-perfect specificity. On the human genome, for both real and simulated reads, mapquik achieves a $37\times$ speedup over the state-of-the-art tool minimap2, and on the maize genome, mapquik achieves a $410\times$ speedup over minimap2, making mapquik the fastest mapper to date. These accelerations are enabled from not only minimizer-space seeding but also a novel heuristic $\mathcal{O}\left(n\right)$ pseudochaining algorithm, which improves upon the long-standing $\mathcal{O}\left(n\log n\right)$ bound. Minimizer-space computation builds the foundation for achieving real-time analysis of long-read sequencing data.

Recent advances in DNA sequencing enable the rapid production of long reads with low error rates; for example, Pacific Biosciences (PacBio) HiFi reads are 10 to 25 kbp in length with a ≤1% error rate. High-quality long reads have been used to accurately assemble genomes (Kolmogorov et al. 2019; Nurk et al. 2020; Ekim et al. 2021; Bankevich et al. 2022), complete the human genome (Nurk et al. 2022), accurately detect small variants in challenging genomic regions (Olson et al. 2022), and further elucidate the landscape of large structural variants in human genomes (Denti et al. 2023). Critical to these successes are algorithms that perform genomic data analysis, such as reconstructing a reference from reads (genome assembly) (Logsdon et al. 2020), or mapping reads to a reference genome (read mapping) (Alser et al. 2021). With up to hundreds of gigabytes of sequenced data per sample, analysis algorithms need to balance efficiency with high sensitivity and accuracy (the percentage of reads mapped correctly) (Berger and Yu 2023), which is especially critical in rapid sequencing to diagnostics (Galey et al. 2022; Owen et al. 2022).

We recently introduced the concept of minimizer-space computation (Ekim et al. 2021), in which only a small fraction of the sequenced bases is retained as a latent representation of the sequencing data, enabling orders of magnitude improvements in efficiency without loss of accuracy. Minimizers are sequences that are selected under some local or global minimum criteria (Schleimer et al. 2003; Roberts et al. 2004), similar to locally consistent parsing (Şahinalp and Vishkin 1996). We applied the minimizer-space concept to perform genome assembly of long and accurate reads in minutes instead of hours—even for humans, and hypothesized that other types of genome analysis tasks would benefit from it in the future (Ekim et al. 2021). We now pursue the intuition that read mapping would also be amenable to minimizer-space computation, but there are multiple algorithmic challenges to overcome owing to the repetitive nature of genomes, biological variation between samples and references, and sizable input data.

Two cornerstones of read alignment/mapping algorithms—ubiquitous in sequence analysis pipelines—are the seeding and chaining steps, in which each read is locally placed at a homologous location in a reference genome. Seeding is performed by finding pairs of matching seeds, which are snippets of DNA with high-confidence (exact or inexact) matches between a query and a reference genome. Seeds are initial matches that serve as anchoring points of alignments: They allow a challenging instance to be split into a set of easier subinstances by aligning only the shorter intervals between seeds. In the short-read era, state-of-the-art alignment algorithms (e.g., BWA-MEM [Li 2013], Bowtie 2 [Langmead and Salzberg 2012], and CORA [Yörükoğlu et al. 2016; Shajii et al. 2021]) typically relied on finding all possible seeds using a full-text index of the reference genome. For long reads, there has been a recent breakthrough by sampling and indexing only a relatively small number of short potential seeds from the reference genome, which has led to faster and more accurate mapping tools, for example, minimap2 (Li 2018) and Winnowmap2 (Jain et al. 2022b). Chaining consists of finding maximal ordered subsets of seeds that all agree on a certain genomic location (Jain et al. 2022a); seeds often have spurious matches owing to their short lengths.

However, even the most recent long-read alignment tools are bottlenecks in analysis pipelines (Berger and Yu 2023). For instance, the popular minimap2 software requires 12 CPU hours to map a typical PacBio HiFi data set to the human genome, and Winnowmap2 requires 15 CPU days, preventing both real-time analysis of sequencing data (Loose et al. 2016) and efficient reanalysis of previously sequenced data collections (Edgar et al. 2022). A significant part of the minimap2 and Winnowmap2 running times are in their seeding and chaining steps (Kalikar et al. 2022). These state-of-the-art long-read alignment tools are sensitive and accurate, but their underlying seed constructs (k-mers) are tailored to noisy reads. These small seed sizes induce longer computation times owing to the multiple potential mapping locations of seeds that need to be examined and filtered out. Recent advances in short-read alignment methods have shown that 98% of many organism's genomes are nonrepetitive and can be uniquely aligned to with longer seeds (Edgar 2020). Therefore, it seems natural to explore the use of longer seeds also in long reads: This idea is at the heart of our approach.

Here, we provide a highly efficient and accurate read mapping tool for state-of-the-art and low-error long-read data. We introduce mapquik, which instead of using a single minimizer as a seed for a reference sequence (e.g., minimap2) builds accurate longer seeds by anchoring alignments through matches of k consecutively sampled minimizers (k-min-mers). Our approach borrows from natural language processing in which the tokens of the k-mers are the minimizers instead of base pair letters. We asked whether long-read mapping can be sped up by newly substituting k-mer seeds with k-min-mers that occur uniquely in the genome. In this work, we evaluate the extent to which k-min-mers can act as suitable seeds for accurate long-read alignment, as well as the performance of mapquik in making use of them for HiFi-read alignment. Our work represents the promise of unique, inexact seeds, such as k-min-mers, for ultrafast long-read mapping and beyond.

Results

Related work

minimap2 (Li 2018) is a de facto standard for mapping accurate long reads to a reference genome. It applies a seed-and-extend strategy. Specifically, seeds are short k-mer minimizers, namely, sequences of length k that are lexicographically minimal within a window of w consecutive k-mers. The extension step is performed using an optimized implementation of the Needleman–Wunsch algorithm (Needleman and Wunsch 1970) with an affine gap penalty. Several attempts have been made to improve mapping performance compared to minimap2. Mashmap (Jain et al. 2018a) and Mashmap2 (Jain et al. 2018b) compute read-versus-genome and genome-versus-genome mappings without an alignment step and use 5 × less memory than minimap2 at the expense of longer runtime. In very recent work developed concurrently to ours, the aligner BLEND (Fırtına et al. 2023) uses strobemers (Sahlin 2021) and locality-sensitive hashing (inspired by Şahinalp and Vishkin 1996) to speed up minimap2 end-to-end by about 2 ×; however, their seeding approach is integrated into minimap2’s codebase, which is implemented and optimized for exact short seeds (minimizers by Roberts et al. 2004), thus suffering from similar limitations (for the sake of completeness, we compare with BLEND in Results).

Other works have focused on improving the sensitivity and accuracy of minimap2, at the expense of speed. Winnowmap (Jain et al. 2020) and Winnowmap2 (Jain et al. 2022b) use weighted minimizer sampling and minimal confidently alignable substrings to better align in highly repetitive regions, for example, centromeres of chromosomes. Winnowmap2 is around 15 × slower than minimap2 end-to-end, yet uses around 3 × less memory.

In recent years, many research groups focusing on low-level and/or hardware-specific acceleration have proposed ways to accelerate minimap2. mm2-fast (Kalikar et al. 2022), a CPU acceleration of minimap2 developed by Intel, achieved a 1.5 × acceleration over minimap2, end-to-end on HiFi reads. The bulk of the speedup was obtained in the alignment phase, not in the seeding-chaining phase (see Fig. 1 of Kalikar et al. 2022). The domain-specific language Seq was developed to speed up genomic sequence analysis and achieved two orders of magnitude improvement in the homology table reconstruction of the CORA read mapper (Yörükoğlu et al. 2016; Shajii et al. 2021).

Figure 1.

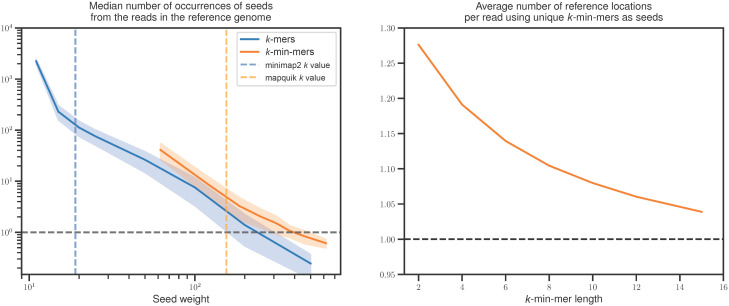
Increased sensitivity and specificity of k-min-mers versus long k-mers. Both panels use the human reference genome CHM13v2.0 and the HG002 DeepConsensus HiFi reads. (Left) Each continuous line indicates the median abundance of read k-mers (darker blue line) and k-min-mers (lighter orange line) in the reference, averaged across all reads (the closer to one, the better). The vertical dashed darker blue line (respectively, the lighter orange line) corresponds to the seed length chosen by minimap2 (respectively, by mapquik). The median is computed from a random subsample of 50,000 HG002 reads. (Right) Average number of reference genome locations indicated by seed matches for each read using k-min-mers (the closer to one, the better). k-min-mer parameters are ℓ = 31, δ = 0.01 with k = 2–10 (left) and 2–15 (right). Regular k-mer lengths are k = 12–500.

There also exist efficient implementations that use specialized hardware. mm2-ax (Sadasivan et al. 2023), a recent GPU acceleration of minimap2 developed by NVIDIA, achieved 2.5 × to 5.4 × acceleration over mm2-fast in the chaining step. Guo et al. (2019) also proposed GPU and FPGA accelerations of minimap2 that, respectively, achieve 7 × and 28 × speedups on the distinct task of detecting pairwise read overlaps. These specialized hardware accelerators are outside the scope of this work. Methods that accelerate short-read alignment, for example, using cloud computing resources (Schatz 2009) or optimized k-mer indexing (Almodaresi et al. 2021), are also not considered here, given that they do not support long reads.

Why use k-min-mers as alignment seeds instead of k-mers?

To motivate why k-min-mers are superior alignment seeds, compared with k-mers, for accurate long reads, we formulate and verify the following two hypotheses: (1) Long exact k-mer seeds are inadequate for accurate long-read alignment owing to lack of sensitivity, whereas (2) k-min-mers are adequate and also offer near-perfect specificity. An empirical analysis on actual HiFi reads with an average error rate of 0.1% over the entire human genome justifies these observations (Fig. 1). In the experiments that follow, we compared Jellyfish (Marçais and Kingsford 2011), DSK (Rizk et al. 2013), rust-mdbg (Ekim et al. 2021), and mapquik. All code and data are available in the mapquik repository (see “Software availability”).

To assess hypothesis 1, we examined the specificity of k-mers and k-min-mers as seeds (Fig. 1, left) by recording their number of occurrences in the CHM13v2.0 as a proxy for the number of potential mapping locations. The x-axis reports the seed weight, which for k-mers corresponds to their length and for k-min-mers corresponds to ℓ × k, namely, the total number of bases in the k-min-mer minimizers. As indicated by the plot, k-mer seeds have either too many matches in the reference (from tens to thousands in the k = 10–100 range) or too few (below one match for k > 300). Notably, minimap2 uses a default k value of 19 for HiFi reads, reflecting that it has to sift through hundreds of false matches for each read on average. On the other hand, k-min-mers have orders-of-magnitude fewer potential matches to examine, on average, one to tens depending on k, owing to their longer lengths being less affected by genomic repetition.

To verify hypothesis 2, we showed that selecting all the k-min-mers that are seen only once in the reference genome is a viable indexing strategy (Fig. 1, right). Indeed, the reads have, on average, 1.05–1.30 candidate reference genome locations when all their k-min-mers are queried on such an index. This finding hints that a read mapping algorithm based on k-min-mers is likely to immediately identify the correct genome location by querying all read k-min-mers, only paying attention to those that occur once in the genome. This algorithm potentially would not even require a subsequent chaining step, given the low number of false matches to remove. This is in stark contrast with existing k-mer-based algorithms, for which colinear chaining removes hundreds of false seed matches per read.

Overview of minimizer-space read mapping with mapquik

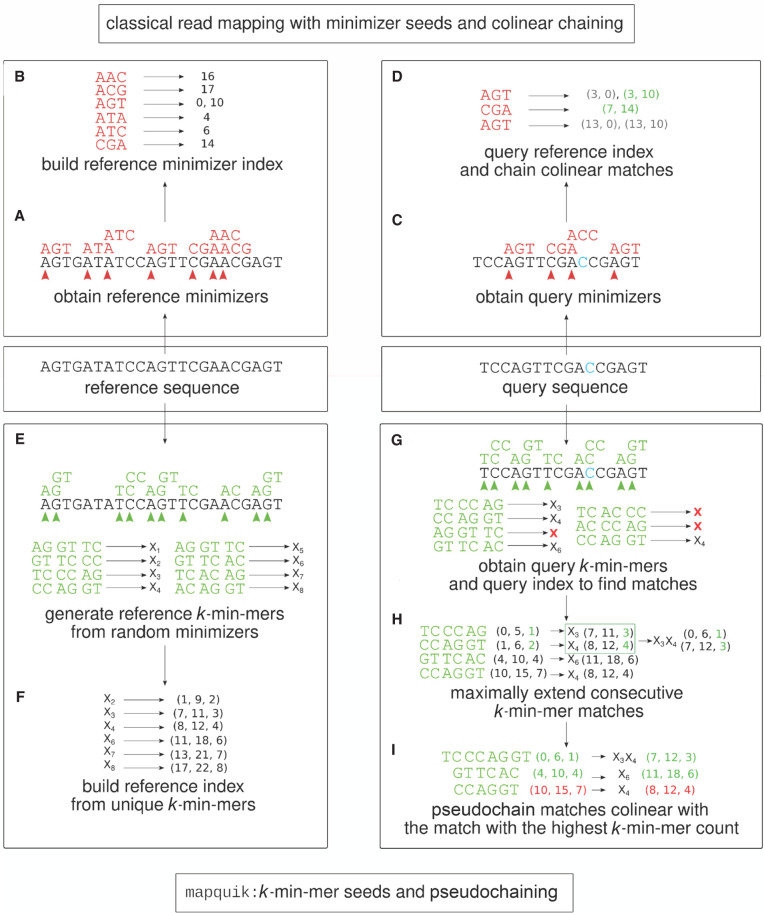
To allow computation in minimizer space (Fig. 2), we here develop mapquik, a read mapper based on k-min-mer seeds. mapquik follows a seed-and-extend strategy used by most read mappers, with two exceptions: (1) Only the k-min-mers that appear exactly once in all reference sequences are indexed (Fig. 2E,F), and (2) unlike a typical colinear chaining procedure that makes use of a dynamic programming formulation (Fig. 2A–D), for example, in minimap2 (Li 2018), a linear-time recursive extension step is performed for each initial k-min-mer match between the query and the reference, followed by a novel, provably linear-time step we call pseudochaining that ensures k-min-mer matches are approximately colinear. Figure 2, G through I, depicts the idea behind our pseudochaining algorithm. Given a set of maximal k-min-mer matches, we chain only the k-min-mer matches that are colinear with the match with the highest score (k-min-mer count). Unlike the DP formulations used in regular colinear chaining, this step can be performed in linear time by identifying the k-min-mer match with the highest score and by checking colinearity with the other matches through a linear scan. Note that the matches in the output chain after this step are not guaranteed to be pairwise colinear; however, thanks to the low number of k-min-mer matches, pseudochaining performs adequately in practice while offering a substantial speedup over classical colinear chaining. The philosophy behind these drastic changes is that mapping long and accurate reads to close reference genomes is “easy enough” that long minimizer-space seeds are sufficient for the vast majority of the reads. The remaining few unmapped reads can, in principle, be fed to a more sensitive, albeit slower, read mapper such as minimap2 or Winnowmap2 (see Discussion).

Figure 2.

Overview of the long-read mapping pipeline using mapquik and comparison with state-of-the-art methods using minimizers as seeds. State-of-the-art read mappers such as minimap2 and Winnowmap2 (top; pink-shaded) build an index for a reference sequence by computing window minimizers (k = 3, w = 5; A) and by storing the positions of the minimizers in the index (B). To map a query sequence using the reference index (top right; nucleotide C in blue denotes a sequencing error), mappers compute the minimizers on the query sequence (C) and find matches between the minimizers of the query and those in the reference index. Once minimizer matches are found, minimap2 and Winnowmap2 perform a colinear chaining step to output a high-scoring set of matches, using dynamic programming (D). In contrast, mapquik (bottom; green-shaded) indexes reference sequences by generating k-min-mers, k consecutive, randomly selected minimizers of length ℓ (k = 3, ℓ = 2; E) and storing only the k-min-mers that appear exactly once in the reference (F). mapquik stores the start and end positions of each k-min-mer, along with the order in which the k-min-mers appear. To map a query sequence using the k-min-mer index, mapquik first obtains matches between the query and the reference index by querying the index with each query k-min-mer (G). k-min-mer matches are extended if the next immediate pair of k-min-mers also match (H). Instead of a colinear chaining step, mapquik performs a linear-time pseudochaining step to locate matches that are colinear with the match with the highest number of k-min-mers (I).

Data sets and mapping evaluation

We used the complete human reference genome CHM13v2.0 for our evaluations. We constructed a simulated data set of long reads with 99% base-level accuracy and 24-kbp mean length using PBSIM (Ono et al. 2013), mimicking HiFi reads at 10 × genome coverage. We also used real HiFi reads for the HG002 individual corrected using DeepConsensus (Baid et al. 2023) at 30 × genome coverage. For maize, we simulated reads from the maize RefSeq genome (GCF_902167145.1) at 30 × coverage using the same protocol as the human simulated reads. mapquik was run with default parameters (k = 5, ℓ = 31, δ = 0.01, β = 4, μ = 11, $\epsilon =2000$); we provide an extensive evaluation of the parameters k, ℓ, and δ in Supplemental Note S8 and Supplemental Figure S3 and of β and μ in Figure 3. All other tools were run with default parameters in HiFi mapping mode. Command lines and versions are given in Supplemental Note S2.

Figure 3.

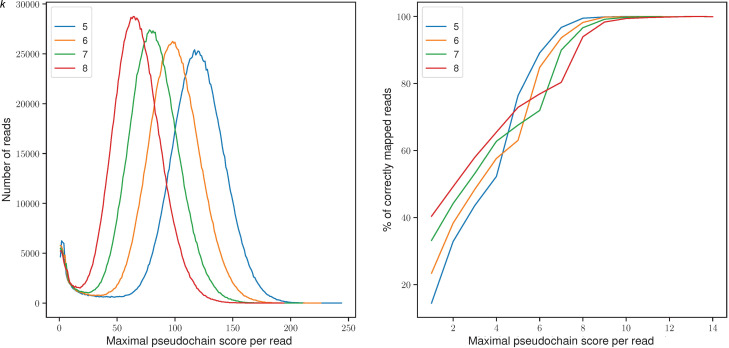
Effect of pseudochain score on mapping accuracy. The x-axis in both subfigures corresponds to the score of the maximal pseudochain per read; on the left, the y-axis denotes the total number of reads with the corresponding maximal pseudochain score; on the right, the percentage of reads that are correctly mapped (assessed by paftools mapeval) with the corresponding maximal pseudochain score. Only the scores below a threshold s, where s denotes the maximum score at which a read was mapped incorrectly, are plotted. The parameters used for mapquik were k = 5–8, ℓ = 31, δ = 0.01.

For simulated reads, we assessed mapping accuracy using the mapeval command of the paftools software distributed in the minimap2 package. A read is considered to be correctly mapped if the intersection between the true and mapped reference intervals is at least 10% of their union. For real reads, we evaluated the concordance between the alignments of minimap2 and mapquik using a custom script (experiments/intersect_pafs.py in the GitHub repository) (Supplemental Code), similar to mapeval. In our evaluation of both the simulated and real data sets, we focus on reads of the highest mapping quality (Q60). Mappers report a mapping quality metric for each read, indicating their confidence that the read is mapped at the right location, as an integer between zero and 60, where 60 corresponds to the highest confidence. Reads with low mapping quality are less frequent and are often removed in downstream applications (e.g., the popular variant-calling pipeline GATK filters out reads with mapQ ≤ 20 by default) (McKenna et al. 2010). With minimap2 results, mapeval reports only two mapping quality groups (Q0 and Q60), with no value between. With mapquik, we report a mapQ of 60 if the output pseudochain has score ≥μ or length ≥β, and zero otherwise.

Mapquik achieves faster and accurate mapping of HiFi reads to the human and maize genomes

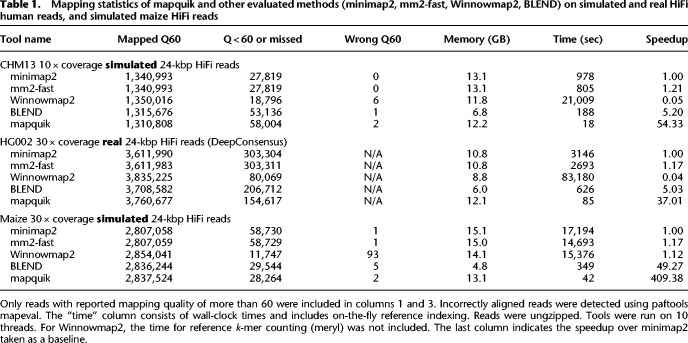
Table 1 shows the enhanced overall performance of mapquik and other evaluated methods (minimap2, mm2-fast, Winnowmap2, and concurrently developed BLEND) on mapping simulated and real PacBio HiFi reads to the human and maize genomes. We show mapquik’s 37 × and 975 × relative speedup over the state-of-the-art mapping methods minimap2 and Winnowmap2, respectively, for both simulated and real HiFi reads from the human genome. We further apply mapquik to mapping simulated HiFi reads from the highly repetitive maize genome and show a 410 × speed-up over minimap2, with no loss of sensitivity nor accuracy.

Table 1.

Mapping statistics of mapquik and other evaluated methods (minimap2, mm2-fast, Winnowmap2, BLEND) on simulated and real HiFi human reads, and simulated maize HiFi reads

On the simulated human data set, mapquik is 54 × faster than minimap2. mapquik maps 95.8% of reads at a mapQ score of 60 (Q60), indicating a high-confidence match, with two errors. In contrast, other mappers map 96.1%–98.6% of reads at Q60 with also no/almost no error. On the real data set from HG002, a similar trend is observed. mapquik outperforms all mappers except Winnowmap2 in terms of percentage of reads mapped (96.1%), as opposed to 92.2%–97.9% for the other tools. The concordance of minimap2 and mapquik mappings is 99.8% on the Q60 reads mapped by minimap2. In Supplemental Table S1, we provide the fraction of the reference genome covered by each tool for all experiments. All mappers required less than 14 GB of memory on the human genome (MashMap2 was not further evaluated as it took more than 13 wall-clock hours on the simulated human data set and does not output mapping quality scores).

A highlight of mapquik is a 410 × mapping speedup compared with minimap2 on the maize genome. Notably, this speedup comes with near-perfect precision for mapquik and no loss of sensitivity, as mapquik reports the second highest number of mapped reads at mapping quality 60 across all tools after Winnowmap2. Of note, Winnowmap2 has a faster performance on maize than the human genome and than that of minimap2 on the maize genome.

We further investigated why some reads were mapped at lower qualities than Q60 or were not mapped at all. Out of 58,004 reads from the simulated human data set that were not mapped at Q60 by mapquik, 94.4% of these reads intersected with centromeric/satellite regions of chromosomes, as reported by BEDTools (Quinlan and Hall 2010) using the chm13v2.0_censat_v2.0.bed annotation from the Telomere-to-Telomere (T2T) Consortium. Thus, the vast majority of reads not aligned at Q60 correspond to challenging genomic regions that would likely have been masked in downstream analyses, making their lack of alignment potentially inconsequential. We hypothesize that similar conclusions hold on real data, but this cannot be ascertained as the true reference interval of each read is not known.

Efficient genome indexing using k-min-mers

Table 2 shows the computing resources necessary to index a human genome for mapquik compared with minimap2, mm2-fast, Winnowmap2, and the concurrently developed BLEND. Although indexes created by the alternative mapping methods to mapquik are different in nature, a similar order of magnitude of numbers of sequences (tens to hundreds of millions) end up being indexed. minimap2 and mm2-fast index positions of windowed minimizers. Those minimizers are different from the (ℓ, δ)-minimizers defined in this article. Winnowmap2 indexes weighted minimizers to increase the accuracy of seeds. BLEND (in HiFi mapping mode) indexes a locality-sensitive seed built from strobemers (Sahlin 2021), which are chains of consecutive windowed minimizers (Roberts et al. 2004), different in nature from k-min-mers.

Table 2.

Indexing a reference human genome using mapquik and other evaluated methods (minimap2, mm2-fast, Winnowmap2, BLEND)

mapquik indexing is 9 × faster than minimap2 and 6 × faster than BLEND. The mapquik seeding strategy provides ultrafast construction of an index that records unique k-min-mer positions across the reference genome. This index is of independent interest, for example, for indexing larger databases such as RefSeq (Li et al. 2021). We anticipate that this index will have other uses beyond long-read mapping, such as large-scale sequence search. We have already shown the usefulness of performing a k-min-mer search in antimicrobial-resistance tracking (Ekim et al. 2021), albeit in earlier work that did not benefit from the speedup of such an index presented here.

Comparison with BLEND

While concurrently developed, we compare with BLEND in Tables 1 and 2 for completeness and show that mapquik achieves a 7 × speedup overall (indexing plus chaining) over BLEND on human data.

Robustness of mapping shorter reads with mapquik

We next asked how mapquik would perform on smaller reads than those offered by HiFi, which are currently available for lengths ranging from 10–25 kbp. Future technologies may also offer long high-accuracy reads, although HiFi is currently the only high-throughput solution available. To determine whether mapquik is also suitable for mapping HiFi reads <24 kbp, we tested mapquik on other data sets with overall shorter reads using both real and simulated data. To assess mapquik’s robustness in mapping reads of varying length, we ran mapquik on real HG002 HiFi 16-kbp length reads from DeepConsensus (Baid et al. 2023), using identical parameters as in the run with 24-kbp read length. mapquik’s performance on 16-kbp reads is similar to that on 24-kbp reads: The running time increased by only 4%; memory usage remains nearly identical; and the concordance with minimap2 remains 99.8%.

To determine if mapquik is still robust to larger variation in read length, we simulated seven samples with 10 × coverage from CHM13, using the same protocol, except that a different average read length is selected for each sample (from 2 kbp–14 kbp, by 2-kbp increments). Supplemental Figure S2 reports that both minimap2 and mapquik map >93% of the reads at Q60 in samples having read lengths of ≥10 kbp, without tuning their parameters. Both minimap2 and mapquik are challenged by read lengths of 2 kbp; with their default HiFi parameters, they respectively map 89% and 27% of the reads at Q60. Note that mapquik maps 63% of the remaining 2-kbp reads at Q0, with a low mapping error rate (1%) as reported by mapeval. We expect mapquik has more difficulty mapping these 2-kbp reads owing to its longer seed weight than minimap2.

Limitations of our study

We evaluated the limitations of our method with respect to several aspects: the choice of k, internal cut-off parameters, and the requirement of having low divergence between the reads and the reference.

As seen in Table 1, mapquik is unable to map some of the reads, mostly in low-complexity regions of the genome, partially because no indexed k-min-mer exists but also because of the lack of a long enough (i.e., high-scoring) pseudochain. We examined the magnitude of the second effect. Figure 3 (left) shows the total number of reads (y-axis) whose highest pseudochain score is given on the x-axis. Read numbers follow approximately a Gaussian distribution, confirming the soundness of filtering out the leftmost tail containing erroneous pseudochains. Figure 3 (right) depicts filtering thresholds by showing the percentage of reads mapped correctly (y-axis) at each pseudochain score per read (x-axis), depending on the choice of k. The monotonically increasing relationship suggests that the pseudochain score is a reliable proxy for evaluating mapping accuracy. Mapping accuracy plateaus around pseudochain scores of nine to 11. In our implementation, we apply a threshold of pseudochain score ≥μ, with μ = 11 by default (Algorithm 3 in Supplemental Note S1).

The mapping performance of mapquik degrades markedly when identity between reads and the reference is <97%, and <1% of the reads are mapped at Q60 for identities <93% (Supplemental Fig. S1). Therefore, mapquik is not suitable for mapping PacBio CLR reads at all and potentially also Oxford Nanopore reads until base-calling consistently reaches identity levels >98%. Remarkably, the mapping error rate at Q60 remains negligible at all identity levels.

Discussion

Our work shows that minimizer-space computation can be successfully applied to read mapping, and overcomes a significant barrier to real-time analysis of sequencing data that simply using longer k-mers or minimizers as seeds cannot. We show for the first time that indexing only the long minimizer-space seeds (k-min-mers) that occur uniquely in the genome is sufficient for sensitive and specific mapping. By leveraging the high specificity of these seeds, we are able to devise a provably $\mathcal{O}\left(n\right)$ time (heuristic) pseudochaining algorithm, which improves upon the subsequent best $\mathcal{O}\left(n\log n\right)$ runtime of all other known colinear chaining methods (Jain et al. 2022a), without loss of performance in practice.

We previously used minimizer-space computation for fast and accurate genome assembly; however, long-read mapping is entirely different as no de Bruijn graph is constructed. This work thus establishes the versatility of k-min-mers in algorithms for biological sequences. As sequencing reads are getting longer and more accurate, we anticipate that our approach will particularly benefit from technological advances: Longer reads will be increasingly easier to map with minimizer-space seeds.

A potential concern with providing a faster alignment method is the loss of sensitivity in “hard-to-map” regions, such as centromeres or structural variant breakpoints. In Supplemental Note S9 and Supplemental Figures S4 and S5, we investigated the missed genomic regions by both minimap2 and mapquik and found that they overlap by >90%. One could partially mitigate this concern by performing a conservative, but fast alignment of reads using mapquik and by remapping the unmapped reads with minimap2 or Winnowmap2 to increase alignment sensitivity while keeping the efficiency of mapquik. Another possible direction would be to use a pangenomic reference to provide more indexable k-min-mers.

Future extensions of this work include implementing base-level alignment, which will allow the design of a complete single-nucleotide variant–calling pipeline, as well as one with structural variant–calling built on top of mapquik. Currently, mapquik is directly usable for quickly finding genomic positions of HiFi reads, which enables many downstream applications such as sorting reads by genome position, separating them by chromosome, filtering nonhuman reads, etc. Because the k-min-mer matches have k exact matches of minimizers of length ℓ, only the regions between minimizers and between neighboring k-min-mer matches would need to be aligned, which potentially lowers both the memory usage and runtime of the alignment step. Another potential improvement to mapquik would be to refine the mapping quality scores, in light of the observations made in Figure 3 that the pseudochain score reliably tracks mapping accuracy. We expect minimizer-space computation to further mitigate challenges in other sequencing data analysis tasks, such as sequence-to-graph alignment, metagenomic binning, and similarity search.

Methods

Although Figure 2 and Algorithm 1 describe the steps of mapquik, we go into more detail below.

Algorithm 1. The mapquik algorithm —

 Input: A collection of reference sequences R and a collection of query sequences Q. We assume global parameters k, ℓ, δ, $\epsilon$, μ, β, f, and φ are predefined.

Output: Query-to-reference mappings S.

 1: function Map(R, Q)

 2: I ← {} $▹$ Empty hash table of reference k-min-mers

 3: L ← {} $▹$ Empty hash table of sequence lengths

 4: S ← {} $▹$ To store mapping results

 5: for r ∈ R do

 6:  X_r ← Extract(r) $▹$ Extract k-min-mers from reference sequence into a list

 7:  L[r_ID] ← |r| $▹$ Store length of r

 8:  for every $x_r^i\in X_r$ do

 9:   if ${\phi }_r^i$ is not a key in I then

10:    $I\left[{\phi }_r^i\right]\leftarrow (r_{\mathrm{ID}},s_r^i,e_r^i,{\pi }_r^i,i_r)$ $▹$ Record the reference ID r_ID and tuple of $x_r^i$

11:   else $I\left[{\phi }_r^i\right]\leftarrow \left(\right)$ $▹$ Assign empty entry

12: for q ∈ Q do

13:  L[q_ID] ← |q| $▹$ Store length of q

14:  X_q ← Extract(q) $▹$ Extract k-min-mers from query sequence into a list

15:  H ← Match(X_q, I, q_ID) $▹$ Generate maximal k-min-mer matches

16:  S [q] ← PseudoChain$(H,q_{\mathrm{ID}},L,\epsilon ,\mu ,\beta )$ $▹$ Create pseudochain from k-min-mer matches

17: return S

Methodological formalization

For a fixed integer ℓ > 1, let $f:{\mathrm{\Sigma }}^{\ell }\mapsto [0,H]$ be a random hash function that maps strings of length ℓ to integers between 0 and H. In practice, we use a 64-bit hash function. Moreover, we require f to be invariant with respect to reverse-complements; namely, an ℓ-mer and its reverse complement map to the same integer. For a density 0 < δ < 1, we define U_ℓ,δ as the set of all ℓ-mers m with f(m) < δ · H. We refer to the elements of U_ℓ,δ as (ℓ, δ)-minimizers. Note that whether an ℓ-mer is a (ℓ, δ)-minimizer does not depend on any sequence besides the ℓ-mer itself.

Let S be a sequence of length ≥ℓ. We define its minimizer-space representation M_S as an ordered list of (ℓ, δ)-minimizers that appear in S. Because the contents of U_ℓ,δ only depend on f, and as long as the same hash function f is used, M_S will always be a subset of U_ℓ,δ. We omit S from the subscript when it is obvious from the context.

Let M be a minimizer-space representation of S, and let k > 0 be a fixed integer parameter. We define a k-min-mer xⁱ of S as an ordered list of k consecutive minimizers in M starting from index i; namely, xⁱ = (m_i, …, m_i+k−1). We denote the ordered list of all k-min-mers (x⁰, …, x^|M|−k) of S as X_S. We omit S from the subscript when it is obvious from the context.

To avoid explicitly storing nucleotide sequences of minimizers, we use a random hash function φ that maps sequences of k ℓ-mers to 64-bit hash values. We define φ so that it is invariant to reversing the order of the k-min-mer; namely, φ(xⁱ) = φ(REV(xⁱ)), where REV(xⁱ) denotes the list of minimizers of xⁱ with the order reversed. This is achieved by hashing xⁱ and REV(xⁱ) and by taking φ(xⁱ) to be the minimum value.

Then, instead of storing X as an ordered list of k-min-mer sequences, we store the ith k-min-mer xⁱ of X as a tuple $(i,{\varphi }^i,s^i,e^i,{\pi }^i)$, where

• i is the rank of xⁱ in X,

• φⁱ = φ(xⁱ),

• sⁱ and eⁱ the nucleotide start and end positions of xⁱ, namely, the start position of minimizer m_i and the end position of minimizer m_i+k−1, respectively, on S, and

• πⁱ a Boolean variable that evaluates to 1 if, in the construction of φ, the hash of REV(xⁱ) was smaller than that of xⁱ, and 0 otherwise.

  We call this the tuple of xⁱ. When the sequence S is not obvious from the context, we add it as a subscript in the above notation, for example, ${\pi }_S^i$. The hash functions f and φ are instantiated before constructing the k-min-mer lists for the input sequences. We consistently use the same functions f and φ when selecting minimizers and consequently building k-min-mer lists for both the reference and query sequences throughout.

Indexing reference sequences

The mapquik index I is a hash table that associates a k-min-mer x to its unique position in the reference genome, whether or not it appears reverse-complemented, and its rank in the list of k-min-mers X. As described in the section “Methodological formalization,” this information is represented by a tuple in the form (r_ID, sⁱ, eⁱ, πⁱ, i). We construct I using a two-pass approach. First, we call the Extract function. It builds the list X by a linear scan through the reference sequence, during which it identifies minimizers and outputs each k consecutive minimizers, together with their hash values. We use the same efficient algorithm as rust-mdbg (Ekim et al. 2021), which runs in $\mathcal{O}\left(\right|X\left|\right)$ time, so we do not include the pseudocode for Extract here. Second, we load every entry of X into a hash table I, indexed by the hash value. In this step, we discard from I any k-min-mer that appears in more than one reference location. Therefore, the hash table holds a single value per distinct k-min-mer key.

Locating and extending query-to-reference k-min-mer matches

Informally, a k-min-mer match is a stretch of k-min-mer seeds that appear consecutively both in the reference and in the query (under the hash function used). Note that all matches are unique, in the sense that all seed k-min-mers appear only once in the genome, by definition. Given a query q and a reference r, we formally define a match as a triple (i, j, c) such that 0 ≤ i ≤ |X_q| − c, 0 ≤ j ≤ |X_r| − c, c ≥ 1, and, for all 0 ≤ c′ < c, ${\phi }_q^{i+c^{\mathrm{\prime }}}={\phi }_r^{j+c^{\mathrm{\prime }}}$. A match (i, j, c) is said to be maximal if it cannot be further extended to the right or left, namely, (1) either i = 0, j = 0, or ${\phi }_q^{i-1}\ne {\phi }_r^{j-1}$ and (2) either i + c = |X_q|, j + c = |X_r|, or ${\phi }_q^{i+c}\ne {\phi }_r^{j+c}$.

For each query q, the mapquik algorithm first builds the list of k-min-mers X_q sorted in increasing order of location (line 14). Then, it runs the Match routine (line 15), which finds all maximal matches between q and the reference. Match works by scanning through X_q and, for each seed x ∈ X_q, using the reference index I to see if x exists in the reference. If it does, then it marks the start of a match and proceeds to extend the match to the right as long as the seeds continue to match. Because we only have to query the index with the hash value of each k-min-mer in X_q, the extension procedure can be performed during a single linear pass over the elements of X_q and thus takes $\mathcal{O}\left(\right|X_q\left|\right)$ time [assuming $\mathcal{O}\left(1\right)$ hashing, look-ups, and insertions]. Care must be taken owing to reverse complements, which can change the direction of matching, but we omit these details. For completeness, the full algorithm (Algorithm 2) and the proof of maximality of k-min-mer matches (Supplemental Note S7) are in the Supplemental Material.

In theory, generating a single 64-bit hash value for each unique k-min-mer could lead to hash collisions and, consequently, lead to false k-min-mer matches. However, because a k-min-mer match can only be extended with a consecutive k-min-mer match, k-min-mers that match an entry in the reference owing to a hash collision are likely to be singletons and get filtered out in the pseudochaining step, with no decrease in final accuracy.

From maximal k-min-mer matches to pseudochains

Recall that k-min-mer matches are extended based solely on whether the next immediate k-min-mer of q matches the next immediate k-min-mer of r. However, k-min-mer matches on q might occur in multiple nonoverlapping positions on r (owing to sequencing errors or biological variation in q); namely, for two matches (i, j, c) and (i′, j′, c′) between q and r, it is not necessarily true that |i − j| = |i′ − j′|.

To output a list of matches that are likely to be true positives while avoiding a computationally expensive dynamic programming procedure, mapquik uses a pseudochaining procedure that finds k-min-mer matches between a query q and a reference r that are gap-bounded colinear but not all pairwise colinear.

Concretely, let h = (i, j, c) and h′ = (i′, j′, c′) be two matches, and consider the coordinates (s_q, e_q, π) and (s_r, e_r, π) of, respectively, the first and last k-min-mers of h, as well as $(s_q^{\mathrm{\prime }},e_q^{\mathrm{\prime }},{\pi }^{\mathrm{\prime }})$ and $(s_r^{\mathrm{\prime }},e_r^{\mathrm{\prime }},{\pi }^{\mathrm{\prime }})$ for the k-min-mers of h′. Let g > 0 be a fixed-integer gap upper bound. We say that h and h′ are gap-bounded colinear if

• the matches are on the same relative strand; namely, π = π′;

• the reference start positions of the matches agree with the order of the matches; namely, if π = 0, $s_r<s_r^{\mathrm{\prime }}$, or if π = 1, $s_r^{\mathrm{\prime }}<s_r$; and

• the length of the gap between the two matches in the query is similar to that on the reference; namely, if π = 0, $\left|({s^{\mathrm{\prime }}}_q-e_q)-({s^{\mathrm{\prime }}}_r-e_r)\right|<g$, or if π = 1, $\left|({s^{\mathrm{\prime }}}_q-e_q)-(s_r-{e^{\mathrm{\prime }}}_r)\right|<g$.

This last gap length difference condition, on top of the traditional definition of colinearity (the first two conditions), ensures that the regions outside the matches are similar in length. A similar parameter ($ϵ$) is used in minimap (Li 2016).

Let H be the list of all maximal k-min-mer matches between a read q and a reference sequence r. We define a pseudochain Ψⁱ as the list of all matches in H that are colinear with the ith match in H; we say that Ψⁱ is anchored at i. Note that even though every match in Ψⁱ is colinear with the ith match in H, it is not necessarily true that every pair of matches in Ψⁱ are pairwise colinear; thus, Ψⁱ does not satisfy the criteria of chains as defined in other works (e.g., Li 2018).

The score of a pseudochain Ψⁱ is the number of matching k-min-mers in Ψⁱ; namely,

$$\mathrm{SCORE}({\mathrm{\Psi }}^i)=\sum _{h\in {\mathrm{\Psi }}^i}c(h),$$

where c(h) denotes the number of matching k-min-mers in match h. Because the maximal matches in Ψⁱ are guaranteed to not share any query k-min-mers because both the start and end locations of each maximal match are distinct, the cumulative sum of the number of matching k-min-mers in each match in Ψⁱ equals the number of total matching k-min-mers in Ψⁱ.

Computing high-scoring pseudochains in linear time

We now introduce a novel algorithm for computing a single high-scoring pseudochain Ψ* for a query q given a list of maximal matches, and prove that it runs in $\mathcal{O}\left(n\right)$ time. The match extension step outputs a hash table H of maximal k-min-mer matches per reference, indexed by their reference identifier. In the pseudochaining step, however, the objective is to output a single list of matches between q and a single reference, even though H might contain matches between q and more than one reference sequence. We first initialize ${\mathrm{\Psi }}^{\ast }=\left[\right]$, and iterate over the key-value tuples in H, processing each list of maximal matches H_q,r for a single reference r one by one. In every iteration, we obtain a candidate pseudochain Ψ_q,r from the list of maximal matches H_q,r by computing the pseudochain anchored at the match in H_q,r with the highest number of matching k-min-mers. After computing Ψ_q,r, we compare its score to that of Ψ*, and replace Ψ* with Ψ_q,r if SCORE(Ψ_q,r) > SCORE(Ψ*). At the end of the loop, Ψ* will be the highest-scoring pseudochain out of all possible candidate pseudochains per reference sequence in H.

Finally, if the pseudochain Ψ* has score ≥μ or length ≥β, where μ and β are user-defined parameters, we retrieve the query and reference coordinates of the region covered by the matches in Ψ*. The final query and reference coordinates for a mapping between query q and reference r are computed by extending the start and end coordinates of the first and last matches in Ψ* to the length of the query. In the Supplemental Material, Algorithm 3 provides a complete description of the pseudochaining procedure, and Algorithm 4 describes the coordinate computation step.

Proof of pseudochaining algorithm's complexity

The complexity of computing pseudochain Ψⁱ for each read q is as follows. Let n be the total number of matches in H. To determine Ψ*, each candidate pseudochain Ψ_q,r for a single reference sequence r needs to be computed. Computing a single pseudochain Ψ_q,r requires determining the match with the highest number of matching k-min-mers and comparing each match in H_q,r to this match, which can both be performed in Θ (|H_q,r|) time. Moreover, every single candidate pseudochain (for every reference in H) needs to be computed to determine Ψ*. Then, the running time of the pseudochaining procedure is $\mathrm{\Theta }\left(\sum _{r\in H}\right|H_{q,r}\left|\right)$. Note that |H_q,r| ≤ n, and the number of reference sequences that appear in H is upper bounded by the total number of reference sequences, which is $\mathcal{O}\left(1\right)$. Hence, the pseudochaining procedure runs in $\mathcal{O}\left(n\right)$ time, where n is the total number of matches in H.

Note that colinear chaining (as implemented by state-of-the-art read mappers) has an asymptotic complexity of $\mathcal{O}\left(n\log n\right)$. We also implemented two alternative heuristics that (1) compute c pseudochains anchored at c matches with the highest number of k-min-mers [thus running in $\mathcal{O}\left(cn\right)$ time], and (2) set c = n and compute all possible pseudochains [thus running in $\mathcal{O}\left(n^2\right)$ time]. However, we observed that the runtime of the $\mathcal{O}\left(n\right)$ pseudochaining procedure is faster in practice: In our tests, the $\mathcal{O}\left(n\right)$ pseudochaining procedure performed $\sim 20\text{\%}-50\text{\%}$ faster than the other heuristics, with little decrease in accuracy.

Software availability

The data and source code are freely available at GitHub (https://github.com/ekimb/mapquik) under the MIT License and as Supplemental Code.

Competing interest statement

The authors declare no competing interests.