Deep learning models predicting TP53 mutations from whole slide images of prostate cancer capture histologic phenotypes associated with stromal composition, lymph node metastasis, and biochemical recurrence, indicating their potential as in silico prognostic biomarkers.
Abstract
In prostate cancer, there is an urgent need for objective prognostic biomarkers that identify the metastatic potential of a tumor at an early stage. While recent analyses indicated TP53 mutations as candidate biomarkers, molecular profiling in a clinical setting is complicated by tumor heterogeneity. Deep learning models that predict the spatial presence of TP53 mutations in whole slide images (WSI) offer the potential to mitigate this issue. To assess the potential of WSIs as proxies for spatially resolved profiling and as biomarkers for aggressive disease, we developed TiDo, a deep learning model that achieves state-of-the-art performance in predicting TP53 mutations from WSIs of primary prostate tumors. In an independent multifocal cohort, the model showed successful generalization at both the patient and lesion level. Analysis of model predictions revealed that false positive (FP) predictions could at least partially be explained by TP53 deletions, suggesting that some FP carry an alteration that leads to the same histological phenotype as TP53 mutations. Comparative expression and histologic cell type analyses identified a TP53-like cellular phenotype triggered by expression of pathways affecting stromal composition. Together, these findings indicate that WSI-based models might not be able to perfectly predict the spatial presence of individual TP53 mutations but they have the potential to elucidate the prognosis of a tumor by depicting a downstream phenotype associated with aggressive disease biomarkers.
Significance:
Deep learning models predicting TP53 mutations from whole slide images of prostate cancer capture histologic phenotypes associated with stromal composition, lymph node metastasis, and biochemical recurrence, indicating their potential as in silico prognostic biomarkers.
Introduction
Prostate cancer is the second leading cause of male cancer-related death in the United States (1) and the fifth leading cause of death worldwide (2). Whereas localized tumors can often be cured by definitive local therapy, advanced tumors represent an incurable disease. Most prostate cancer patients succumb to their disease because of metastatic spread.
In clinical practice, important prognostic factors of prostate cancer include PSA level, clinical T stage, histologic grading (Gleason grade), and the degree of metastatic spread to pelvic lymph nodes (LN). Patients at risk (>5%) of LN metastasis undergo lymph node resection, where lymph nodes are surgically removed and analyzed for metastases. However, LN risk estimation procedures (3–5) are associated with low specificity, and LN resection has high morbidity (6, 7). Furthermore, micrometastases in LN negative (LN−) patients might remain undetected, underestimating a patient's prognosis (8). Therefore, there is an urgent need for an alternative prognostic marker to determine a tumor's metastatic potential and hence prognosis at an early stage.
Over the past years, it has become clear that certain molecular signatures in the primary prostate tumor are associated with aggressive disease biology (9, 10). These signatures have been attributed to both properties of the tumor cells (10–15) and the tumor microenvironment (TME; ref. 16). However, the application of such molecular biomarkers in clinical practice is complicated by the heterogenous nature of prostate tumors. Usually only a sample from the dominant lesion (with highest grade and highest tumor percentage) is profiled. Despite having the highest grade, the dominant lesion does not always correspond to the lesion seeding the metastasis (17). As a result, the biomarker might be missed and the aggressive status of the tumor underestimated.
Profiling multiple lesions per patient (multifocal study) to identify biomarkers would reduce the risk of missing the lesion with the highest metastatic potential, but is in routine too costly and tedious. In contrast, hematoxylin and eosin (H&E)–stained slides are routinely available. They capture rich morphologic information as well as the spatial organization of both tumor cells and TME. In routine practice, the microscopic examination of these samples by expert pathologists is crucial for cancer diagnosis. Efforts to digitize tissue slides and concurrent innovations in machine learning and computer vision have made it possible to computationally analyze digital tissue slides or whole slide images (WSI). Even though WSIs intrinsically offer morphologic rather than molecular information, recent studies have shown the potential of deep learning techniques to extract morphologic features from WSIs that associate with molecular properties (e.g., aneuploidies, genetic alterations, and expression signatures of cancer infiltrating immune cells; refs. 18–27). This indicates that morphologic features contained in WSIs reflect the molecular status of the tumor (28). Hence, deep learning models that predict the spatial presence of molecular features associated with metastatic disease, from WSIs of primary tumors, present potential as a cost-efficient alternative to multifocal molecular profiling (or guide to indicate interesting lesions for sequencing), which is especially desirable in heterogeneous tumors such as prostate cancer.
Recent analyses have indicated TP53 mutations as candidate biomarker for aggressive disease in prostate cancer (9, 10) and findings from previous studies suggest that histologic features from WSIs can be associated to TP53 (23–25). Hence, here, we assess the potential of using WSI-based models as proxy for spatially resolved mutational profiling of TP53 mutations and/or as potential biomarker for aggressive disease in prostate cancer. Hereto, we developed models that predict the presence of TP53 mutations in WSIs of tumor lesions with publicly available data from The Cancer Genome Atlas (TCGA-PRAD) and we illustrated the impact of tumor heterogeneity and data scarcity on model performance. Next, we used an independent multifocal cohort to not only show that our model with state-of-the-art performance generalizes well to an independent dataset, but also that our model can indicate reasonably well the lesion with highest prevalence of TP53 mutations per patient. An in-depth molecular analysis of the prediction results shows how our model captures a TP53-like cellular phenotype that is triggered by expression of pathways affecting stromal composition and that is associated with tumor aggressiveness.
Materials and Methods
Patient cohorts and ethics
For model training, anonymized data from patients with prostate adenocarcinoma (PRAD) were used from the The Cancer Genome Atlas (TCGA) archive (available at https://portal.gdc.cancer.gov).
Our in-house cohort is a single center dataset of primary and matched metastatic tumors of de novo metastatic hormone-sensitive prostate cancer patients that underwent radical prostatectomy with or without pelvic lymph node dissection. Most patients were included in the previously described LoMP1 registry (ClinicalTrials.gov: NCT02138721; refs. 29, 30) or the randomized phase II LoMP2 study (NCT03655886). This study was approved by the Committee for Ethics of Ghent University Hospital (approval #BC-07881). All participants provided written informed consent for retrieval and analysis of archival tissue specimens.
TCGA-PRAD dataset
The TCGA-PRAD dataset contains 449 digital H&E-stained slides from formalin-fixed paraffin-embedded (FFPE) material. The slides originate from 403 unique patients with prostate cancer.
A trained pathologist (K. Van der Eecken) annotated the tumor regions in all images in QuPath (31). Slide annotations were made without any knowledge regarding molecular or clinical features. In the WSI, tumor lesions were marked and graded according to the current Intentional Society of Urological Pathology (ISUP) prostate Cancer guidelines (32). The dominant region was defined as the region(s) with the highest ISUP grade (Gleason grade). In total, 26 slides from 24 patients were discarded due to bad quality. Of these 24 patients, 3 had slides with good quality that were used.
In TCGA, matching sequence data are available for each of the slides. However, it is unclear which exact region on the slide was sampled for sequencing. We here assumed that the region with highest Gleason grade was selected for sequencing. As this region was not yet annotated on the slides, multiple tumor lesions with corresponding Gleason grade were made for a subset of the slides (291). For the remaining slides the dominant lesion was annotated.
Obtaining correct molecular labels for each of the samples (presence versus absence of a TP53 mutation) from the sequence data is not straightforward due to ambiguities in variant calling. To provide reliable labels, we combined (i) the MuTect variant calls available in TCGA and (ii) variant calls we did with Strelka2 (33) on the sequence alignment data (bam files). Variants were annotated with VEP (34). To ensure providing correct labels to the model, we only considered patients for which the two variant callers agreed that a mutation is present, and we discarded 17 patients for which both callers were inconsistent. This resulted in consistent calls for 403 WSIs from 365 unique patients. Of the 365 patients, 31 contain a TP53 mutation. Detailed descriptions of discarded patients, mutation labels as well as annotation masks are available on the project GitHub (https://github.com/mpizurica/WSI_mut/tree/master/code/data_prep/tcga).
We used FACETS (35) to obtain allele specific copy numbers and an estimate of the tumor purity. Copy number data, purity estimates, and somatic variants were used as input for the PyClone algorithm to convert the Variant allele frequency of each somatic SNV to an estimated Cancer Cell Fraction (36). As indels do not have an unambiguously defined VAF, these were not converted to CCF.
Labels for biochemical recurrence were downloaded from UCSC Xena (https://xenabrowser.net/datapages/?dataset=TCGA.PRAD.sampleMap/PRAD_clinicalMatrix&host=https://tcga.xenahubs.net).
Lymph node status data were obtained from the Broad FireBrowse portal (http://gdac.broadinstitute.org/runs/stddata2016_01_28/data/PRAD/20160128/gdac.broadinstitute.org_PRAD.Merge_Clinical.Level_1.2016012800.0.0.tar.gz).
A table providing an overview of the cohort is available in Supplementary Tables S1–S3.
Internal cohort from UZ Ghent
The internal dataset contains TP53 mutation labels and WSIs for 41 patients with de novo hormone sensitive metastatic prostate cancer. In the WSI, tumor lesions were marked and graded (referred to as Gleason grade) as described above. Annotation was revised by two urologic pathologists (K. Van der Eecken and S. Verbeke). For each patient, regions of interest in the radical prostatectomies were chosen based on anatomic location and distinct morphology, including at least the FFPE block with the largest dimensions of the dominant tumor (region with the highest ISUP grade and highest percentage of tumor involvement) plus one to seven additional regions. In addition, metastases measuring ≥2 mm and different areas in their diagnostic PBs were selected. All these samples were subjected to targeted sequencing using a research panel encompassing 73 prostate cancer genes (37).
In total, matched WSI and molecular labels are available for 231 radical prostatectomies (RP), 51 prostate biopsies (PB), and 110 metastatic lymph node samples (MLN). A table with details on the cohort is available in Supplementary Table S4.
TP53 mutations as derived from targeted sequencing were defined present if their variant allele frequency (VAF) ≥ 5%. A threshold of 5% was chosen as the read depth is not sufficient to reliably call mutations at a lower VAF (a read depth of 1650 is recommended for targeted NGS analysis of 3% VAF (38), while the mean RP, PB, and MLN read depths are 622, 361, and 567, respectively with large standard deviations (see Supplementary Fig. S1).
The PyClone algorithm was used to convert the VAF of each somatic SNV to an estimated cancer cell fraction, thereby taking into account copy number data and purity estimates (36). A total of 155 lesions from 35 patients have high tumor purity (≥0.8; RP: 81 lesions from 32 patients, PB: 17 lesions from 8 patients, MLN: 57 lesions from 18 patients) and 37 lesions from 9 patients have low tumor purity (<0.5; RP: 20 lesions from 6 patients, PB: 0 lesions, MLN: 17 lesions from 5 patients).
Image preprocessing
Scanned WSIs, stained with hematoxylin and eosin, were downsampled to ×20 magnification (0.5 μm px−1). Nonoverlapping tiles of 512 × 512 pixels at 0.5 μm px−1 were extracted, consistent with previous studies (24, 25). During training, these tiles were further downsampled to 224 × 224 pixels, conforming the settings used in the pretrained ResNet-18 on ImageNet.
We removed several tiles of bad quality—tiles with >50% background (defined as a brightness of >220/255 pixel intensity) were discarded. In addition, blurred tiles and tiles that contained severe tissue folds were removed based on gradient magnitude derived by the Sobel filter (tiles with gradient magnitude <15, for more than 50% of their pixels were removed). For removing tiles containing pen marks, we made use of filters that detected shades of red, green and blue (implemented by thresholding RGB channels in the image).
To make the model robust against stain variability, we used stain augmentation during training, which we found to outperform Macenko stain normalization (39).
Data splitting
The data we used to develop the models (from TCGA-PRAD) were split in 80% for training and 20% was kept as held-out test set. The training data was further split for three-fold cross-validation. All splits were stratified to ensure consistent class distributions (same percentage of patients with(out) mutation in train/validation/test set), and all tiles and/or slides of a patient were always part of the same set.
We evaluated on the held-out test set only after the models were finalized, that is, all decisions on model architecture and hyperparameters were made on validation set performance. However, because of the small size of the dataset and large class imbalance, this validation set performance varies significantly depending on which patients are assigned to train/validation splits within these three folds. Even the average validation set performance (averaged across three folds of a cross-validation experiment) is not robust: repeating the cross-validation splitting with a different random seed may result in different average validation set performance. For a concrete example, see Supplementary Fig. S2. When calculating the average validation set performance with our models on two different three-fold cross-validation configurations, we sometimes observed significant differences. Because this complicates making decisions on optimal model architectures, we aimed to obtain a more robust validation set performance. Hereto, we repeated the cross-validation split six times with different random seeds (resulting in six configurations) and we report average performance and 95% confidence interval (CI) across these configurations.
After training, to define which of the six cross-validation configurations is best (e.g., BeTiDo from the TiDo models), we chose the configuration that scored best on the following two criteria: (i) best validation/test set performance; (ii) smallest difference in performance between validation and test set (because this means that the estimate of performance is more robust and should indicate better generalization capability). All splits were stratified to ensure consistent class distributions (same percentage of patients with(out) mutation in train/validation/test set), and all tiles and/or slides of a patient were always part of the same set.
Model
In both the tile-level model and the attention-based model, we employ a ResNet-18, pretrained on the ImageNet dataset, for feature extraction. We only keep the convolutional layers and discard the original fully connected layer.
Formally, the tile-level model is trained to make tile-level predictions for each tile tk, given by tk = σ(W1 · zk), with σ the sigmoid function, zk ∈ R512×1 the feature vector extracted by the convolutional layers from the pretrained ResNet-18 and W1 ∈ R1×512 the weights of a fully connected layer we train for classification (bias term not explicitly written for simplicity). To make patient-level predictions for a patient with N tiles, we average tile-level predicted probabilities, resulting in a patient-level probability 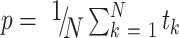 .
.
For the attention module, we used the same architecture as in Lu and colleagues (40), but with fewer parameters as we have less data. First, tile features zk ∈ R512×1 extracted with the pretrained ResNet-18 are transformed into a 256-dimensional vector hk = W1 · zk by trainable weights W1 ∈ R265×512. These are propagated into the attention network, which consists of several fully connected layers that compute the attention weight ak for every tile tk. Formally, the computation consists of two fully connected layers whose weights we represent by U1 ∈ R128×256 and U2 ∈ R128×256 as well as a classification layer with weights W2 ∈ R1×128. The attention weight ak is calculated by Eq. A.
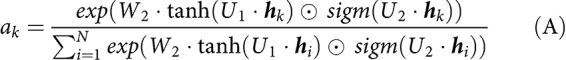 |
The patient-level feature vector hpatient ∈ R256×1 is then calculated by hpatient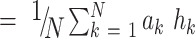 . Finally, we apply a classification layer with weights W3 ∈ R1×256, resulting in the patient-level probability p = σ(W3 · hpatient).
. Finally, we apply a classification layer with weights W3 ∈ R1×256, resulting in the patient-level probability p = σ(W3 · hpatient).
Distribution imbalances
To account for distribution imbalances, we applied different techniques for the two models. To avoid model bias towards patients with many tiles in the tile-level model, we limited the number of tiles per patient in the training set to 500 by random undersampling. Then, to achieve class balance, we further undersampled the tiles of patients without TP53 mutation (ensuring that the patients have an approximately equal number of tiles left). As this method discards a lot of the original available data, we also implemented the option to allow for multiple versions of undersampled datasets to be used in different training epochs (but this did not turn out to make a large difference in training nor model performance).
For the attention-based model, we accounted for class imbalance by using a weighted sampler during training, which equalizes the number of patients with/without mutation in every batch.
Hyperparameters
Concerning hyperparameters, we evaluated several learning rates ∈ [1 × 10−6, 1 × 10−2], batch sizes 2i, i ∈ [0, 10] as well as learning rate schedulers. The optimal configuration was determined based on training convergence and validation set performance. We arrived at a fixed learning rate of 2 × 10−4 for both models. As batch size, we used 512 for tile-level models and 32 for attention-based models. The model parameters were optimized with the Adam optimizer. Finally, all models were trained for at least 30 epochs, with the best model chosen at the epoch with lowest validation cross entropy loss. For TiDo, 50 epochs were necessary to achieve full training convergence.
Model evaluation
Because of our 6-times repeated 3-fold cross-validation, we obtain 18 models for each combination of annotation detail and model type. To report validation/test set performance, consider model mi,j obtained in cross validation configuration i and fold j, with i ∈ [1, 6] and j ∈ [1, 3]. Within each configuration i, we evaluate the three models mi,j on each respective validation fold j, and (after hyperparameter tuning is done) on the external test set. This leads to performances on validation (perf_vali) and test sets (perf_testi) for each of the cross validation configurations i, as given in Eq. B.
 |
Then, we compute the average validation and test performance over the configurations i, which corresponds to our reported value μ. We also compute the standard deviation σ over the six configurations, and use it to compute the 95% CI using μ ± 1.96σ.
Definition true/false positive/negative patients
Throughout the text, we define “extreme” true/false positive/negative (“e” T/F P/N) patients based on the patients with the most extreme predicted probabilities within a certain group. Specifically, eFP are defined as patients without mutation whose predicted probability for a mutation is in the highest quartile (0.75 quantile, 84 patients). Similarly, eTN are defined as patients without mutation whose predicted probability is in the lowest quartile (0.25 quantile, 84 patients). eTP are defined as patients with mutation whose predicted probability is in the upper half quantile (0.5 quantile, 16 patients), as this group is smaller. We chose to define the groups based on these extreme examples, because these are the samples where the model is most confident about, and hence contain the strongest signal for model interpretations.
To relate the number of these “extreme” T/F P/N to the number of T/F P/N at optimal prediction threshold, see Supplementary Table S2. The optimal prediction threshold was defined based on the ROC curve on the validation set (see Supplementary Fig. S3), as the point with closest Euclidean distance to the theoretically optimal point (i.e., the point in the top left corner, where the TPR is 100% and FPR is 0%).
Distance to max CCF
We define the Distance to Max CCF (DMCCF) to evaluate, for a specific patient, how close the CCF of the lesion with highest predicted probability of a TP53 mutation (CCFchosen lesion) is to the lesion with the highest CCF (CCFmax). Specifically, we define the DMCCF for patient i as DMCCF = (CCFmax − CCFchosen lesion for i) where CCF is the derived CCF in percentage ∈ [0%, 100%].
We chose this metric over a rank-based metric (e.g., which would assess whether the model ranks the lesions in the same way as ranked by CCF), because the DMCCF explicitly accounts for the absolute deviation in CCF between the lesion indicated by the model and the true lesion with the highest CCF. This allows to penalize relatively less mispredictions in case two lesions exist with an almost equal TP53 CCF than when the erroneously indicated lesion has a CCF that is truly very different from the lesion with the highest CCF.
Differential gene expression analysis
HTSeq counts were downloaded from UCSC Xena (https://xenabrowser.net/datapages/?dataset=TCGA-PRAD.htseq_counts.tsv&host=https%3A%2F%2Fgdc.xenahubs.net&removeHub=https%3A%2F%2Fxena.treehouse.gi.ucsc.edu%3A443). The differential expression analysis was performed with the most up-to-date version of the limma voom workflow for RNA-seq differential expression analysis (https://ucdavis-bioinformatics-training.github.io/2018-June-RNA-Seq-Workshop/thursday/DE.html). Specifically, genes with low expression level were filtered with the filterByExpr function from the edgeR (41) package, with default parameters. To remove heteroscedasticity from the count data, the voom (42) transformation was used. Then, lmFit from the limma (43) package in R was used to fit the linear model. In the next step, comparisons were made between the two groups of interest and empirical Bayes smoothing of SEs was performed.
Genes were considered significantly differently expressed for FDR adjusted P values ≤ 0.05 and |log(FC)| ≤ 1. The FDR correction was performed with the Benjamini–Hochberg method to compensate for the large number of tests made. Pathway overrepresentations were obtained using the EnrichR tool (44).
Code availability
All methods are implemented using Python and PyTorch. All source code for the model and data preprocessing are available at https://github.com/mpizurica/WSI_mut/.
Detailed annotations of tumor regions with corresponding Gleason Grade for WSIs in TCGA-PRAD are available in https://github.com/mpizurica/WSI_mut/tree/master/code/data_prep/tcga, in the form of color-coded .png masks (see ReadMe file).
Hardware
Training and inference were performed on our local computing cluster using one Tesla V100 with 32GB memory. Training TiDo takes approximately 4 minutes per epoch (includes calculation of validation set performance). For full convergence, TiDo needed to be trained for 50 epochs. Completing one 3-fold cross validation run with a TiDo model, trained for 50 epochs, takes approximately 10 hours in total. In contrast, training the attention-based model (on dominant tumor regions) takes 10 minutes per epoch. In this case, 30 epochs were needed for convergence. A 3-fold cross validation run, trained for 30 epochs, takes 16 hours in total.
Data availability
The dataset used for training in this study (TCGA-PRAD) is publicly available at https://portal.gdc.cancer.gov/repository.
For access to data from our internal cohort, please contact the Department of Pathology from Ghent University Hospital, under supervision of Jo Van Dorpe (jo.vandorpe@ugent.be). All other raw data are available upon request from the corresponding author.
Results
Deep learning on WSIs for predicting TP53 mutation of prostate cancer patients
To assess the feasibility of using WSIs as proxy for spatially resolved mutational profiling, we developed models that predict the presence of TP53 mutations in tumor WSIs. The model architectures in our deep learning workflow (Fig. 1) are based on previous studies (25, 40). For model training, we relied on WSIs and corresponding molecular labels of TP53 available from 365 patients with prostate adenocarcinoma available in TCGA-PRAD.
Figure 1.
Overview of the deep learning workflow. A, Expert-based annotations of tumor regions reveal tumor heterogeneity. Left, regions with different grade are annotated in different colors. Right, enlarged views from four annotated regions with different grade. B, Three types of annotation detail can be evaluated, whether to only include the dominant region, all tumor tissue, or the whole slide. C,N tiles are extracted from the selected annotation and a ResNet-18 model extracts features for individual tiles. Then, either the tile-level or attention-based model is trained to make predictions for the presence of TP53 mutations (trained end-to-end with ResNet). D, Visualizing the tile-level probabilities from the tile-level model or attention weights per tile from the attention-based model on the original WSI gives an indication of the predicted spatial location of TP53 mutations.
A trained pathologist annotated the distinct tumor regions in terms of Gleason grade on the slides. Many samples contain several regions (so called lesions), each with different tumor grades, reflecting tumor heterogeneity (Fig. 1A). As information on the exact lesion selected for sequencing is not available for TCGA-PRAD, we considered the region with highest Gleason grade as the region expected to have been sequenced (in case of multiple lesions in slide with highest grade we considered them all). We refer to this region on the WSI as the dominant region, that is, the region for which we assume the sequencing-based TP53 mutational label to be valid.
To select the best combination of regions to train the model on, we consider three levels of annotation detail, ranging from fine- to coarse-grained: (i) only including tiles derived from the dominant tumor region (the region expected to have been sequenced); (ii) including all tumor tissue; or (iii) using the whole slide that includes both tumor and normal tissue (Fig. 1B).
The images corresponding to the annotated region(s) cannot be directly used as input in deep learning models as typical WSIs can easily supersede 10k × 10k pixels, while the models require inputs of approximately 256 × 256 pixels. Instead, consistent with previous studies (24, 25), we placed a rectangular grid over the image and extract nonoverlapping square tiles from the annotated region(s), which will be used as model input. Subsequently, 20% of the data is kept as held-out test set and the remaining 80% is split for three-fold cross-validation. We repeat the cross-validation split six times (with different random seeds) to more thoroughly evaluate the robustness of the model with respect to specific patients used in train and validation (see Materials and Methods, Supplementary Fig. S2, and Supplementary Table S1 for more details).
We implemented and evaluated two types of state-of-the-art deep learning models. In a first tile-level model (Fig. 1C), which is commonly used in WSI analysis (25, 45), all tiles in the region (dominant region, tumor regions, whole slide) receive the region-level label (label propagation). The model is subsequently trained to make predictions for individual tiles. Afterwards, tile-level predictions are aggregated to obtain predictions on the selected region level. However, this label propagation may lead to noisy labels in case of high molecular heterogeneity combined with coarse annotation detail.
Variations of the second, attention-based model (Fig. 1C) are increasingly used in the state-of-the-art (40, 46) to eliminate the need for detailed annotations. In our case, they can be used to mitigate unreliable labels due to tumor heterogeneity. Namely, given enough training data, these models learn automatically which tiles are relevant to the final prediction. Hereto, an attention weight ai is assigned to every tile ti, which reflects its relative importance to the final prediction.
When the models are trained, the predicted probability or attention weight for a TP53 mutation from respectively the tile-level or attention-based model can be visualized to locate the features spatially on the original WSI (Fig. 1D).
Importance of model type and annotation detail
We examined the impact of model type and annotation detail on prediction performance in TCGA-PRAD. As a baseline, we compared our performance to the state-of-the-art in WSI-based TP53 mutation prediction. Figure 2A shows how the performance of TP53 mutation prediction based on WSIs in prostate cancer relates to models that were trained and validated on other cancer types (23–25).
Figure 2.
TP53 mutation prediction results for TCGA. A, State-of-the-art in TP53 mutation prediction in different studies for different cancer types. B, Impact of annotation detail and model type on TP53 mutation prediction in prostate cancer (TCGA-PRAD). All results are aggregated over the six times repeated cross-validation runs.
Figure 2B compares our performance for TP53 mutation prediction in TCGA-PRAD for varying annotation detail and model type with the state-of-the-art performance of the model developed by Kather and colleagues (25). The best result is achieved by using the tile-level model trained and evaluated on the annotated dominant tumor regions. A patient-level mean validation AUC of 0.71 (95% CI = 0.61–0.82) is achieved over six cross-validation configurations, with a mean test AUC of 0.71 (95% CI = 0.68–0.75). For clarity, we will refer to these models in the text as ‘tile level, trained and evaluated on dominant regions’ (TiDo). Of these six cross-validation runs, the best one achieved a mean patient-level validation AUC of 0.75 and a mean test AUC of 0.71. When specifically talking about the model from this cross-validation run, we will refer to it as Best TiDo (BeTiDo).
Irrespective of the used model type, coarser annotations cause worse performance because tumor heterogeneity may lead to inconsistent labels across tumor regions. As expected, the observed effect becomes more exacerbated as the annotation level becomes more coarse grained. In the tile-level model, there is no way for the model to deal with such noisy labels. Hence, when using all annotated tumor tissue compared to only using the dominant regions, the AUC drops with 6% to 8%. This setting of using all tumor tissue with a tile-level model is comparable with the one reported by Kather and colleagues (25) and hence results in similar performance. When using tiles sampled from the entire whole slide image, the performance further drops significantly (2%–10%).
The attention-based model should be able to cope with these noisy labels, given enough training data. However, this model is trained on region level labels (dominant/tumor/whole slide) instead of on tile level labels. Namely, all tiles from the region are processed at once and only their region-level label guides the training process, during which the model infers tile relevance (Fig. 1C). This means that only ±180 region level labels are used to train the attention-based model of which only ±16 contain a mutation label (∼ 8%). In contrast, thousands of tile-level labels are available for both classes for the tile-level model. Consequently, in case of the attention-based model, the data set is likely too small to achieve training convergence. As a result, it is more sensitive with respect to the specific patients in the train/validation and test sets. The observation that simple, tile-level models outperform the more complicated attention-based models for mutation status prediction from WSIs is consistent with a recent, independent comprehensive study on deep learning pipelines for WSI analysis (47).
Generalization performance of independent cohort at patient and at lesion level
To perform a validation of our best performing model TiDo on an independent dataset, we used a multifocal cohort from Ghent University Hospital (UZ Ghent). The cohort consists of 41 patients diagnosed with de novo hormone-sensitive metastatic prostate cancer, that is, patients for which metastasis was found at the time of diagnosis. In comparison with patients available in TCGA-PRAD, the samples from the in-house cohort have a more aggressive disease state. The cohort is unique in its multifocal set up (see Supplementary Table S4 for details): for each patient, matching primary tumor (both radical prostatectomy or RP and prostate biopsy or PB samples) and lymph node metastases (MLN) were sequenced at multiple regions to account for the tumor heterogeneity (Fig. 3A). This allows validating model predictions at patient level, but also at a more fine-grained region/lesion level.
Figure 3.
Performance evaluation of independent cohort. A, Exemplary slides and tiles for RP (top), PB (middle), and MLN (bottom) samples. The two annotated regions in the RP sample represent two sequenced tumor lesions (same for the two PB and four MLN lesions). B, Generalization performance of model. Red, previously reported performance of TiDo on TCGA-PRAD; purple, generalization performance of TiDo. Results were aggregated over the six times repeated cross-validation.
Figure 3B shows that on this independent UZ Ghent cohort, there is good generalization performance of the TiDo models (across the six times repeated cross-validations) at patient level. In addition, there is also good generalization performance at the more fine-grained lesion level for samples from the primary tumor [RPs (0.65 AUC; 95% CI, 0.63–0.67) and PBs (0.65 AUC; 95% CI, 0.62–0.72)]. Remarkably, the performance on metastatic lymph nodes (MLN; 0.68 AUC; 95% CI, 0.67–0.70) is comparable with the one obtained on primary tumor lesions, indicating that the cellular features (histology) associated with the presence of TP53 in the primary tumor are still present in metastatic tumors.
Association of predictions with TP53 deletions
Although we obtained state-of-the-art performance for TP53 mutation prediction in prostate cancer with our model, we wanted to better understand the potential sources of false positive (FP) and false negative (FN) predictions. We perform this analysis with our BeTiDo model on the TCGA validation and test sets. The confusion matrix (Supplementary Fig. S4) shows that the model clearly makes more FP predictions than FN predictions.
To get insight in the FN predictions, representative tiles of FN obtained with BeTiDo are shown in Fig. 4A. In tiles where a mutation is missed (FN, bottom), artifacts and rare morphologic features often play a role. For example, the second tile is part of a region that was assigned the rare annotation of mucinous adenocarcinoma by the trained pathologist, which explains the odd morphological features in the tile. As another example, in the first and fourth tiles, the inner structure in the cell nuclei (e.g., nucleoli) are almost indiscernible. The same was observed for the FN in the in-house cohort (Supplementary Fig. S5). The relatively few FN can hence be explained by artifacts on the WSIs or rare subtypes.
Figure 4.
Interpretation of model mistakes. A, Mistakenly predicted tiles, predicted to contain a mutation (top) and no mutation (bottom). B, For patients without mutation, predicted probability for patients with (red) and without (blue) deletion in the 0.25 and 0.75 quantile. Patients whose deletion status is unknown are not shown in the figure, but are indicated on top (“?”).
On the other hand, there is a relatively large number of FP. These are cases where a high prediction probability is obtained, despite the absence of a TP53 mutation (Fig. 4A, top). For these samples, visualizing the tiles does not provide an explanation as they look similar to the tiles of TP with no obvious artifacts. In these samples, the tumor cells do not carry a TP53 mutation, but seem to exhibit a phenotype reminiscent of a TP53 mutation. Therefore, we hypothesized that these samples carry an alteration, other than a TP53 mutation, that affects the same downstream phenotypes as observed in the cells triggered by a TP53 mutation.
To find such other alterations, we consider two subsets of equal size within the pool of patients without mutation: one group with most extremely low predicted probabilities (0.25 quantile, “extreme” true negatives or eTN, 84 patients) and the other with most extremely high predicted probabilities (0.75 quantile, “extreme” false positives or eFP, 84 patients), see Materials and Methods and Supplementary Table S2 for more details. This was done to generate a balanced dataset containing samples without TP53 mutations for which the signal derived by our BeTiDo model was most pronounced in being either positive or negative. Note that these representative eTN and eFP is a subset only of the TN and FP in the confusion matrix of Supplementary Fig. S4.
An association analysis using the variant calls in TCGA with the eTN and eFP patients indicated that at least part of these eFP carry TP53 deletions instead of mutations. Indeed, Fig. 4B illustrates that, for patients in TCGA without mutation, patients with a TP53 deletion (in the absence of a TP53 mutation) are statistically more abundant in the eFP than in the eTN (Fisher exact test; P < 0.001). This observation suggests that for some “false” positives (31 out of 84), the model correctly detects a phenotype from the WSI, which in these cases is not caused by a mutation, but rather by a deletion of TP53. This analysis could not be performed for our in-house cohort, because there are not enough patients to reach statistical significance. Having identified this potential source of false positives, we evaluated whether accounting for TP53 deletions could increase model performance. Hereto, we trained a new model, now considering a sample positive if there is a mutation and/or deletion in TP53. The new model, however, did not outperform the model trained solely for TP53 mutations (see Supplementary Note S1).
Given the small sample size compared with the large number of variables (36,822 tested mutations, 24,776 deletions) and the low mutation/deletion rate of aberrations other than TP53, no alterations other than TP53 could be identified as being enriched in the representative eFP as compared with the representative eTN.
Training on TCGA captures both properties of the TME and tumor cells to predict TP53 mutations
If indeed the majority of the FP carry aberrations other than TP53 that converge in the same histopathological phenotype the WSI, we hypothesized that both TP and FP samples must share a common pathway triggered by their TP53 or related aberrations that explain the similarities in their WSI phenotype. To identify such a common downstream pathway, we first compared the gene expression profiles in the TCGA-PRAD data of samples where the BeTiDo model “incorrectly” predicted a mutation (FP) and those where the model correctly predicted no mutation (TN). To define the FP and TN, we again considered “extreme” true negatives or eTN and “extreme” false positives or eFP.
Between eFP and eTN, 30 genes (Supplementary Data S1) involved in processes that relate to extracellular matrix adhesion and collagen fibril organization (Supplementary Data S1) were significantly differentially expressed. The three most significantly differentially expressed genes were NOX4, COL10A1, and ASPN.
If these genes/processes indeed associate with the observed TP53-like phenotype, they should also be differentially expressed between the predicted TP and the TN. As TN, we retained the same group as defined above (eTN). Similarly, for TP, we considered “extreme” true positives or eTP, see Materials and Methods for more details.
Between the eTN and eTP, we found 376 significantly differentially expressed genes (Supplementary Data S1) among which, next to TP53 related processes (mitotic checkpoint), the same extracellular matrix adhesion and collagen related processes (Supplementary Data S1). Of these 376 genes, 21 are indeed contained in the 30 genes that were also differentially expressed between the eFP and eTN. This overlap is significant (P value from hypergeometric t test < 0.0001). These genes hence represent the common downstream pathway shared by the true and false positives. Among those were again NOX4 (now 20th most significant gene), COL10A1 (second most significant gene) and ASPN (9th most significant gene).
Interestingly, all three genes have been associated in literature with cancerous prostate stroma and specifically with Cancer Associated Fibroblasts (CAF). CAFs were shown to be tumor-promoting, promoting immune evasion (48) and related to poor survival in several cancers (49). Specifically, NOX4 was associated with fibroblast to myofibroblast differentiation (49, 50) and was shown to be critical for maintaining immune-suppressive CAF phenotype in tumors (50). In prostate cancer, NOX4-derived ROS would be involved in TGF-β1–induced activation of prostate fibroblasts where TGF-β1 levels positively correlate with prostate cancer risk, rapid disease progression and poor outcome (51). Also COL10A1, a key marker gene for a CAF-phenotype (52), is associated with malignant progression in several cancer types (53, 54). In gastric cancer COL10A1 promotes EMT transition via the TGF-β1–SOX9 axis (53). In addition, ASPN was identified as a biomarker of reactive stroma that correlates with prostate cancer disease progression (55). The authors suggest ASPN expression in stroma may be part of a stromal response in aggressive subtypes.
This analysis shows that processes related to stromal composition, that define the difference between FP and TN, are also present in the TP, and hence likely explain the model predictions. Given the role of the identified genes in stroma, we hypothesized that the difference in stromal composition of the TP53-mutated samples influences model predictions. To assess whether this was true, we analyzed which information in the tiles the model considers to predict TP53 mutations (using TCGA-PRAD as these data were used to train the features used by BeTiDo).
In Fig. 5A, we analyze the predominant cell types within tiles that are most confidently predicted to respectively contain or not contain a TP53 mutation (see also Supplementary Fig. S6 for the cell type analysis per TP/FP/TN). Cell segmentation and type were obtained with a pretrained HoverNet (56) network and regions considered important for model prediction were obtained with GradCam (57). The clearest distinguishing cell types between the two classes are indeed not only tumor cells, but also cells from connective tissue. Overall, tiles predicted to contain a TP53 mutation contain relatively more connective tissue and less tumor cells compared to tiles predicted not to contain the mutation. Regions highlighted in Fig. 5B to be important for a TP53 mutation prediction indeed show that, for samples predicted to contain a TP53 mutation, the model mainly considers cells from connective tissue or tumor cells. These observations are in line with the differential expression analysis on TCGA-PRAD and confirm that the model trained on TCGA-PRAD has learned to extract both features from the tumor cells and also from the TME.
Figure 5.
Predominant cell types in tiles predicted with and without a TP53 mutation. A pretrained network from HoverNet (56) was used to simultaneously detect and classify cells in tiles predicted to (not) contain a TP53 mutation. A, Fraction of detected cell types within tiles for 2,000 tiles that were most confidently predicted to contain a TP53 mutation (left) and not to contain one (right). B, For distinct patients, the tile that was most confidently predicted to contain a mutation. Shown for 10 patients with mutation (top) and 10 patients without mutation (bottom). Regions found to be important for the model prediction are encircled in black [obtained by calculating the contour of GradCam (57) heatmaps on the original tile]. The bar below the plot shows for every tile the fraction of cell types within the black regions (color code same as in A).
Ability of the model to predict the number of cells carrying a TP53 mutation
From the above analysis, we concluded that the model considers both tumor cells and connective tissue cells when making predictions for TP53 mutations. Hence, we hypothesized that only in case of high tumor purity (≥0.8), the predicted probability for a mutation should correlate with the number of cells carrying a TP53 mutation. Namely, in case of low tumor purity (<0.5), the model can still extract features from connective tissue on the WSI impacted by (a possibly low number of) cells with a TP53 mutation. By picking up this signal from the stroma, the model might make a confident prediction of a TP53 mutation while the actual number of cells with TP53 that are available in the sample is low.
For this analysis, we assume that the number of cells carrying a TP53 mutation is reflected by the Cancer Cell Fraction (CCF) of TP53 observed when sequencing the corresponding lesion. Visualizing the predicted probability for a mutation and the TP53 CCF for samples with high purity (Fig. 6A) shows there is indeed a positive correlation (Pearson correlation coefficient 0.33, P < 0.0001) between these two properties, indicating that the model's predictions associate with the number of tumor cells that carry a TP53 mutation. In contrast, for samples with low purity (Fig. 6B) no correlation between the predicted probability for TP53 and the TP53 CCF can be observed. In this case, many samples receive a high probability for a mutation while the TP53 CCF is very low, confirming that the model considered features from the stroma in these samples to make a prediction. The same observations hold for the relation between predicted probability for a mutation and cancer cell fraction in TCGA-PRAD (Supplementary Fig. S7).
Figure 6.
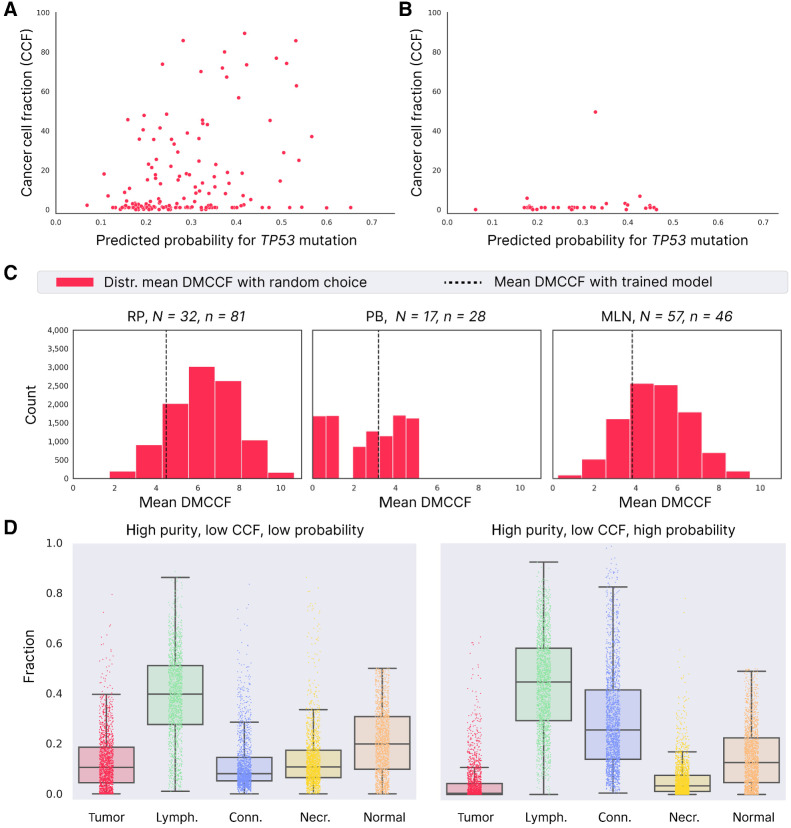
Association between model prediction and TP53 CCF for the UZ Ghent cohort. A, Relation between TP53 CCF (in percentage) and predicted probability for TP53 mutation and for samples with high tumor purity (shown for all RP/PB/MLN samples). B, Same as A for low tumor purity samples. C, Mean DMCCF obtained with random lesion selection (red distribution) compared with trained model (dashed line). N, total number of unique patients; n, total number of lesions. D, Comparison of cell types in tiles with high purity and low CCF, in case the model assigns a low predicted probability (data from 1,000 tiles; left) and high predicted probability (data from 1,000 tiles; right).
Because the predicted probability of a TP53 mutation correlates to the TP53 CCF for samples of high purity, we further assessed whether in this case, the model is able to indicate (within lesions of a particular patient) the lesion with the highest number of TP53 cells. To perform this analysis, we made use of the UZ Ghent multifocal cohort, where multiple lesions were sequenced for the same patient (considering the same samples with tumor purity ≥0.8). Again, we assume that the number of cells carrying a TP53 mutation is reflected by the CCF of TP53. Note that there can be large variability in TP53 CCF for samples in the same patient due to tumor heterogeneity (Supplementary Fig. S8). To evaluate the model's ability to indicate the lesion of interest, we defined the metric “Distance to Max CCF (DMCCF).” The DMCCF for a particular patient represents the distance between (i) the CCF of the lesion with the highest predicted probability and (ii) the CCF of the lesion with the highest CCF (for motivation of this metric, see Materials and Methods). The smaller this distance, the more correctly the model prediction can indicate the lesion with the highest CCF of TP53.
As a baseline, we compared the DMCCF obtained with the model predictions to the ones obtained by randomly selecting a lesion for each patient (repeated 10,000 times). Figure 6C shows that our model outperforms the baseline both for RP and MLN samples, but not for PB. For PB, the worse mean DMCCF of the trained model was caused by an outlier. The median DMCCF that is robust to outliers (Supplementary Fig. S9) shows better performance for the trained model versus random choice. The reason random choice works well for PB samples is because of the small variability in TP53 CCF for PB samples (Supplementary Table S5). As a result, the TP53 CCF of a randomly chosen PB lesion will often not deviate largely from the PB lesion with maximal TP53 CCF. In contrast, the TP53 CCF of RP and MLN samples of a particular patient vary over a larger range (more heterogeneity), and, as desired, our model captures information that allows predicting the lesion with the highest TP53 mutational burden.
These results show that, for samples with high purity, the TiDo model can, to some extent, predict the spatial distribution of cells containing TP53 mutations in the primary tumor. However, even for samples with high purity the correlation is not perfect, especially because of samples with low CCF that receive high predicted probabilities (samples on the right side of the x-axis in Fig. 6A). Visualizing the cell types present in 1,000 such tiles (high purity, low CCF, high predicted probability) and comparing them with 1000 tiles that receive low predicted probabilities (high purity, low CCF, low predicted probability) shows that also in this case, the “mistakes” arise because the model combined features of both connective tissue and the tumor cells (Fig. 6D).
Association of predictions with aggressive disease
Previous results show how our model combines properties of both tumor cells and connective tissue to make predictions. Since TP53 mutations are known to associate with aggressive disease and as the degree of aggressiveness is known to be determined by the interaction of tumor cells with their TME, we wondered to what extent model predictions reflect the aggressiveness of the TP53 containing subpopulations rather than their quantity.
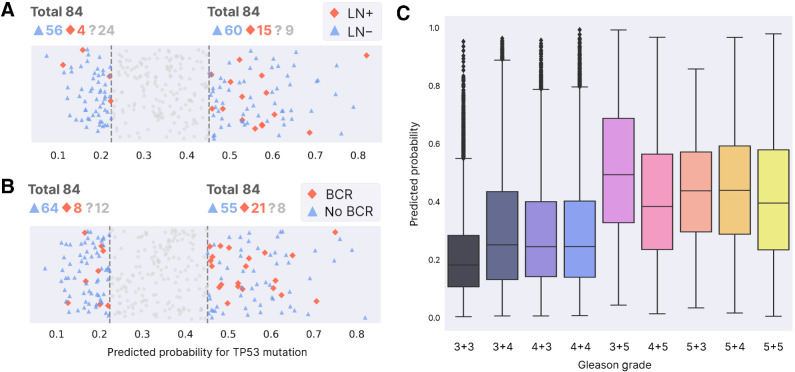
To assess this, we tested whether samples with high predicted probabilities originate more frequently from patients with respectively positive lymph node status (LN+) or biochemical recurrence (BCR). This analysis was performed in TCGA because (in contrast to our in-house cohort) TCGA contains primary prostate tumors from both lymph node positive and negative patients. Patients with LN+ (Supplementary Fig. S10) are indeed statistically more abundant in the quantile with highest predicted probabilities (0.75 quantile) than in the quantile with lowest predicted probabilities (0.25 quantile; Fisher exact P = 0.05). The same is true for BCR (Supplementary Fig. S11, Fisher exact P = 0.02).
To account for the known relation between the presence of TP53 mutations and respectively LN status and BCR, we tested the same enrichment only for patients without TP53 mutation. Figure 7A and B show that indeed, even for patients without mutation, the predictions of our model associate with respectively the patient's LN status and BCR (respectively Fisher exact P = 0.04 and P = 0.01).
Figure 7.
Association with aggressive disease. A, Patients without TP53 mutation that do (red) or do not (blue) have positive lymph node status. The number of patients whose LN status is unknown is shown next to “?” (those samples are not shown in the plot below). The left part are patients with lowest predicted probability for mutation (0.25 quantile, “extreme” true negatives or eTN), while the right side contains patients with highest predicted probability for mutation (0.75 quantile, “extreme” false positives or eFP). See Materials and Methods for motivation and definition of eTN, eFP. B, Same as A, now for biochemical recurrence. C, Tile-level predicted probability for mutation per Gleason grade, with lowest grade on the left.
Furthermore, Fig. 7C shows how overall tiles with lower Gleason grade are generally assigned lower probabilities for TP53 mutation, again indicating that our model's predictions associate with more aggressive disease. However, the plot also shows that many tiles with low grade still receive a high predicted probability for a TP53 mutation, and similarly many tiles with high grade receive a low predicted probability for a mutation. This indicates that the model is considering factors other than the Gleason grade when predicting TP53 mutations (the same observation holds for our in-house cohort see Supplementary Figs. S12 and S13).
To further assess the degree to which our model captures information other than TP53 mutational status or Gleason grade, we built a simple logistic regression model to compare the patient-level performance in predicting LN status and BCR when using all possible combinations of these three features (see Materials and Methods). Supplementary Figures S14 and S15 provide the patient-level performance for respectively LN status and BCR, obtained with Monte-Carlo cross-validations (repeated 100×) on the TCGA dataset (70% of the data was used as train, 30% as test set). These results show a clear association between the probabilities of our model and both proxies of aggressive disease (LN and BCR). Notably, the association of our model predictions with disease aggressiveness is significantly higher than the association observed when using the true TP53 mutation status (P < 0.0001 in both proxies), indicating that our model indeed captures a histopathologic phenotype associated with aggressiveness that is learned by training on a TP53 label, but that can also be present in aggressive samples that have alterations other than TP53.
When used as sole marker (considering only one feature as predictor), our model prediction is still outperformed by the Gleason grade, which, especially for BCR, represents the dominant prediction factor. Particularly, performance for BCR prediction does not increase significantly neither when combining the grade with the true TP53 mutation label nor with the model output. However, for LN status prediction, performance does increase when the Gleason grade is combined with the probabilities predicted by our model (P < 0.01), indicating that our model output offers valuable information on top of the Gleason grade. Notably, the performance obtained by combining these two features (Gleason grade and model output) is one of the three best performing combinations for LN status prediction, reaching equal performance to (i) the combination of Gleason grade and true TP53 mutation status as well as (ii) the performance when including all three features.
Finally, the complementarity of our model predictions versus the Gleason grade also shows from differential gene expression analysis (Supplementary Data S2). The genes that are differentially expressed between high and low grade are mostly enriched in processes that relate to cell cycle and mitosis, both of which also occur in the genes differentially expressed between samples where respectively high and low probabilities have been assigned by our model. In contrast, features related to extracellular matrix organization that are picked up by our model seem not to be discriminative for the distinction between samples based on the Gleason grade.
Discussion
In prostate cancer, there is an urgent need for objective prognostic biomarkers that identify a tumor's metastatic potential and hence a patient's prognosis at an early stage. However, the application of molecular biomarkers is complicated in clinical practice by the heterogeneous nature of prostate cancer. Ideally, multiple lesions should be sequenced to be certain of capturing the biomarker, but this approach is too costly in routine practice.
Deep learning models offer the potential for cost-efficient, spatially resolved profiling of molecular markers. Although previous studies show how these models achieve reasonable performance at patient level, it has not yet been validated whether they can also correctly indicate the region within a heterogenous solid tumor containing a TP53 mutation. In addition, no in-depth assessment has been performed to explain the possible origin of FP or FN predictions, while such interpretations are imperative for model implementation in practice.
As recent analyses indicated TP53 mutations as candidate biomarker for aggressive disease (9, 10), we wanted to assess the potential of using WSI-based models trained on TP53 to serve as proxy for mutational profiling of TP53 mutations and/or as biomarker for aggressive disease. Hereto, we built a state-of-the-art model on TCGA-PRAD for TP53 mutation prediction from WSIs. We found that, to generate a model with optimal performance in the context of scarce data and high heterogeneity, detailed annotations by a trained pathologist are necessary. With the collection of more data in the future, attention-based models present potential to eliminate the need for these detailed annotations.
Our model showed good generalization performance at patient and lesion level on an independent multifocal cohort from UZ Ghent. This allowed showing that our model offers insight into which lesions on the WSI of a patient are likely to contain a TP53 mutation. Although WSI-based models trained on TP53 mutations cannot replace targeted TP53 sequencing yet, when used in combination with targeted sequencing they still offer a cost-efficient alternative to multifocal sequencing.
However, despite being state-of-the-art, the overall performance of the model remains rather low with especially a relative high number of false positive (FP) predictions. Analysis of model predictions revealed that cases where the model predicts a mutation that was not found by sequencing (FP) could at least partially be explained by the presence of TP53 deletions. This suggests that part of the FP consists of samples that carry an alteration other than a TP53 mutation, that affects the same downstream pathways and ultimately histopathologic phenotype as the one observed in the cells triggered by a TP53 mutation. Indeed, by performing comparative expression analysis, we identified in both TP and FP the presence of a common molecular phenotype involved in determining the stromal composition. This observation was also confirmed with histological cell type analysis of the WSIs. Hence, it seems that when making a prediction of a TP53 mutation, our model extracts not only features from tumor cells, but also from stromal cells. This is not surprising, as TP53 mutations have been shown to stimulate secretion of extracellular matrix components and matrix remodeling enzymes, thereby promoting activation of CAFs (58).
Because WSI-based models combine features of both tumor cells and TME, they have a limited capacity to quantitatively predict the number of cells containing a TP53 mutation. They rather seem to predict the degree to which the TP53 containing cells affect the TME and therefore determine the aggressive potential of the tumor. Indeed, the predictive probability assigned to a lesion by our model is associated with proxies of aggressive disease, such as lymph node status and biochemical recurrence. In addition, we could show that by capturing both information from the tumor cells and TME our model is more predictive for aggressive disease than the true TP53 mutational status and complementary to the Gleason grade.
In conclusion, a WSI-based model trained on the molecular label TP53 captures a downstream histopathologic phenotype that is triggered by either TP53 or other, more rare alterations that converge in the same common downstream phenotype. As such, WSI-based models proxy a multigene profiling (or pathway-based profiling) with as additional benefit that the profiling does not only focus on properties of tumor cells, but also of stromal cells. These properties indicate that WSIs might not have the resolution to predict individual mutations such as the presence of TP53, but that by capturing a downstream phenotype of the tumor cells and TME associated with a biomarker such as TP53 (but potentially any other biomarker), they can serve as powerful prognostic biomarkers with spatial resolution.
Supplementary Material
Supplementary Figures, Tables and Notes
Contains 1. significantly differentially expressed genes between eTN and eFP ("FP_TN"), 2. significantly differentially expressed genes between eTN and eTP ("TP_TN"), 3. the pathway overrepresentations for 2-3. ("Reactome_table_FP_TN", "Reactome_table_TP_TN", "MSIGDBHALLMARK_TP_TN", "MSIGDBHALLMARK_FP_TN")
Contains 1. significantly differentially expressed genes between samples with high and low gleason grade ("Gleason_high_low"), 2. the pathway overrepresentations for these genes ("MSigDB_Gleason_HL", "Reactome_Gleason_HL"), 3. the overlapping genes between "Gleason_high_low" and "TP TN" from Suppl. Data 1 ("Gleason_HL_overlap TP_TN"), 4. the pathway overrepresentations for genes from (3) ("reactome_GLHL_TP_TN", "MSigDB_GLHL_TP_TN")
Acknowledgments
The authors thank three anonymous reviewers for their useful remarks. The authors thank Cedric Vandemergel for scanning the histology slides of the UZ Ghent cohort and Pieter-Paul Strybol for technical support. The work was supported by grants of the Fonds Wetenschappelijk Onderzoek-Vlaanderen (FWO 3G045620), UGent BOF [BOF/IOP/2022/045 and 01J06219] and Flanders Innovation & Entrepreneurship (VLAIO, project “ATHENA,” no. HBC.2019.2528). The research was further supported by the National Cancer Institute (NCI) under award: R01 CA260271. The content is solely the responsibility of the authors and does not necessarily represent the official views of the National Institutes of Health. In addition, M. Pizurica was supported by a Fellowship of the Belgian American Educational Foundation and a grant from FWO 1161223N. M. Larmuseau was supported by a grant from FWO 3F013118. L. de Schaetzen van Brienen was supported by an FWO 3S037019. F. Carrillo-Perez was supported by the Spanish Ministry of Sciences, Innovation and Universities under Projects RTI-2018–101674-B-I00 and PID2021–128317OB-I00, the project from Junta de Andalucia P20–00163, and a predoctoral scholarship from the Fulbright Spanish Commission.
The publication costs of this article were defrayed in part by the payment of publication fees. Therefore, and solely to indicate this fact, this article is hereby marked “advertisement” in accordance with 18 USC section 1734.
Footnotes
Note: Supplementary data for this article are available at Cancer Research Online (http://cancerres.aacrjournals.org/).
Authors' Disclosures
M. Pizurica reports grants from FWO and Belgian American Educational Foundation during the conduct of the study. P. Ost reports grants and personal fees from Bayer, Janssen, MSD, AAA, and Novartis outside the submitted work. O. Gevaert reports grants from National Cancer Institute, Saudi Company for AI, Owkin Inc., Roche Molecular Systems, AstraZeneca, Onc.AI Inc., and Melanoma Research Alliance outside the submitted work, as well as a patent for RNA to image synthetic data generator pending to Stanford University and a patent for Methods and systems for learning gene regulatory networks using sparse Gaussian Mixture Models pending to Stanford University. K. Marchal reports grants from FWO and Vlaio during the conduct of the study. No disclosures were reported by the other authors.
Authors' Contributions
M. Pizurica: Conceptualization, data curation, software, formal analysis, validation, investigation, visualization, methodology, writing–original draft, writing–review and editing. M. Larmuseau: Conceptualization, data curation, supervision, funding acquisition, investigation, methodology. K. Van der Eecken: Conceptualization, resources, data curation, validation. L. de Schaetzen van Brienen: Software. F. Carrillo-Perez: Methodology. S. Isphording: Formal analysis. N. Lumen: Resources, writing–review and editing. J. Van Dorpe: Resources, writing–review and editing. P. Ost: Resources, writing–review and editing. S. Verbeke: Resources, writing–review and editing. O. Gevaert: Conceptualization, resources, supervision, funding acquisition, writing–original draft, project administration, writing–review and editing. K. Marchal: Conceptualization, resources, supervision, funding acquisition, writing–original draft, project administration, writing–review and editing.
References
- 1. Siegel RL, Miller KD, Fuchs HE, Jemal A. Cancer statistics, 2022. CA Cancer J Clin 2022;72:7–33. [DOI] [PubMed] [Google Scholar]
- 2. Rawla P. Epidemiology of prostate cancer. World journal of oncology 2019;10:63. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3. Gandaglia G, Fossati N, Zaffuto E, Bandini M, Dell'Oglio P, Bravi CA, et al. Development and internal validation of a novel model to identify the candidates for extended pelvic lymph node dissection in prostate cancer. Eur Urol 2017;72:632–40. [DOI] [PubMed] [Google Scholar]
- 4. Punnen S, Freedland SJ, Presti JC, Aronson WJ, Terris MK, Kane CJ, et al. Multi-institutional validation of the CAPRA-S score to predict disease recurrence and mortality after radical prostatectomy. Eur Urol 2014;65:1171–7. [DOI] [PubMed] [Google Scholar]
- 5. Cagiannos I, Karakiewicz P, Eastham JA, Ohori M, Rabbani F, Gerigk C, et al. A preoperative nomogram identifying decreased risk of positive pelvic lymph nodes in patients with prostate cancer. J Urology 2003;170:1798–803. [DOI] [PubMed] [Google Scholar]
- 6. Lescay H, Abdollah F, Cher ML, Qi J, Linsell S, Miller DC, et al. Pelvic lymph node dissection at robot-assisted radical prostatectomy: Assessing utilization and nodal metastases within a statewide quality improvement consortium. Urol Oncol-Semin Ori 2020;38:198–203. [DOI] [PubMed] [Google Scholar]
- 7. Burkhard FC, Studer UE. The role of lymphadenectomy in high risk prostate cancer. World J Urol 2008;26:231–6. [DOI] [PubMed] [Google Scholar]
- 8. Fujisawa M, Miyake H. Significance of micrometastases in prostate cancer. Surg Oncol 2008;17:247–52. [DOI] [PubMed] [Google Scholar]
- 9. Robinson D, Van Allen EM, Wu Y-M, Schultz N, Lonigro RJ, Mosquera J-M, et al. Integrative clinical genomics of advanced prostate cancer. Cell 2015;161:1215–28. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10. de Schaetzen van Brienen L, Miclotte G, Larmuseau M, Van den Eynden J, Marchal K. Network-based analysis to identify drivers of metastatic prostate cancer using GoNetic. Cancers 2021;13:5291. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11. van Dessel LF, van Riet J, Smits M, Zhu Y, Hamberg P, van der Heijden MS, et al. The genomic landscape of metastatic castration-resistant prostate cancers reveals multiple distinct genotypes with potential clinical impact. Nat Commun 2019;10:1–13. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12. Armenia J, Wankowicz SAM, Liu D, Gao J, Kundra R, Reznik E, et al. The long tail of oncogenic drivers in prostate cancer. Nat Genet 2018;50:645–51. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13. Quigley DA, Dang HX, Zhao SG, Lloyd P, Aggarwal R, Alumkal JJ, et al. Genomic hallmarks and structural variation in metastatic prostate cancer (vol 174, pg 758, 2018). Cell 2018;175:889. [DOI] [PubMed] [Google Scholar]
- 14. Abida W, Cyrta J, Heller G, Prandi D, Armenia J, Coleman I, et al. Genomic correlates of clinical outcome in advanced prostate cancer. Proc Natl Acad Sci 2019;116:11428–36. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15. Alarcón-Zendejas AP, Scavuzzo A, Jiménez-Ríos MA, Álvarez-Gómez RM, Montiel-Manríquez R, Castro-Hernández C, et al. The promising role of new molecular biomarkers in prostate cancer: from coding and non-coding genes to artificial intelligence approaches. Prostate Cancer Prostatic Dis 2022;25:431–43. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16. Calagua C, Ficial M, Jansen CS, Hirz T, Del Balzo L, Wilkinson S, et al. A subset of localized prostate cancer displays an immunogenic phenotype associated with losses of key tumor suppressor GenesImmunogenic prostate cancer and loss of key tumor suppressors. Clin Cancer Res 2021;27:4836–47. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17. Kneppers J, Krijgsman O, Melis M, de Jong J, Peeper DS, Bekers E, et al. Frequent clonal relations between metastases and non-index prostate cancer lesions. Jci Insight 2019;4:e124756. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18. Chen M, Zhang B, Topatana W, Cao J, Zhu H, Juengpanich S, et al. Classification and mutation prediction based on histopathology H&E images in liver cancer using deep learning. Npj Precis Oncol 2020;4:1–7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19. Coudray N, Ocampo PS, Sakellaropoulos T, Narula N, Snuderl M, Fenyö D, et al. Classification and mutation prediction from non–small cell lung cancer histopathology images using deep learning. Nat Med 2018;24:1559–67. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20. Kather JN, Pearson AT, Halama N, Jager D, Krause J, Loosen SH, et al. Deep learning can predict microsatellite instability directly from histology in gastrointestinal cancer. Nat Med 2019;25:1054. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21. Liao H, Long Y, Han R, Wang W, Xu L, Liao M, et al. Deep learning-based classification and mutation prediction from histopathological images of hepatocellular carcinoma. Clin Transl Med 2020;10:e102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22. Bilal M, Raza SEA, Azam A, Graham S, Ilyas M, Cree IA, et al. Novel deep learning algorithm predicts the status of molecular pathways and key mutations in colorectal cancer from routine histology images. medRxiv 2021. [DOI] [PMC free article] [PubMed]
- 23. Noorbakhsh J, Farahmand S, Namburi S, Caruana D, Rimm D, Soltanieh-ha M, et al. Deep learning-based cross-classifications reveal conserved spatial behaviors within tumor histological images. Nat Commun 2020;11:1–14. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24. Fu Y, Jung AW, Torne RV, Gonzalez S, Vohringer H, Shmatko A, et al. Pan-cancer computational histopathology reveals mutations, tumor composition and prognosis. Nat Cancer 2020;1:800. [DOI] [PubMed] [Google Scholar]
- 25. Kather JN, Heij LR, Grabsch HI, Loeffler C, Echle A, Muti HS, et al. Pan-cancer image-based detection of clinically actionable genetic alterations. Nat Cancer 2020;1:789. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26. Jiang S, Zanazzi GJ, Hassanpour S. Predicting prognosis and IDH mutation status for patients with lower-grade gliomas using whole slide images. Sci Rep-Uk 2021;11:16849. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27. Zheng H, Momeni A, Cedoz P-L, Vogel H, Gevaert O. Whole slide images reflect DNA methylation patterns of human tumors. Npj Genom Med 2020;5:1–10. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28. Pietrobon V, Cesano A, Marincola F, Kather JN. Next generation imaging techniques to define immune topographies in solid tumors. Front Immunol 2021;11:604967. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29. Poelaert F, Verbaeys C, Rappe B, Kimpe B, Billiet I, Plancke H, et al. Cytoreductive prostatectomy for metastatic prostate cancer: first lessons learned from the multicentric prospective local treatment of metastatic prostate cancer (LoMP) trial. Urology 2017;106:146–52. [DOI] [PubMed] [Google Scholar]
- 30. Buelens S, Poelaert F, Claeys T, De Bleser E, Dhondt B, Verla W, et al. Multicentre, prospective study on local treatment of metastatic prostate cancer (LoMP study). BJU Int 2022;129:699–707. [DOI] [PubMed] [Google Scholar]
- 31. Bankhead P, Loughrey MB, Fernández JA, Dombrowski Y, McArt DG, Dunne PD, et al. QuPath: Open source software for digital pathology image analysis. Sci Rep-Uk 2017;7:1–7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32. Van Leenders GJLH, Van Der Kwast TH, Grignon DJ, Evans AJ, Kristiansen G, Kweldam CF, et al. The 2019 International Society of Urological Pathology (ISUP) consensus conference on grading of prostatic carcinoma. Am J Surg Pathol 2020;44:e87. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33. Kim S, Scheffler K, Halpern AL, Bekritsky MA, Noh E, Källberg M, et al. Strelka2: fast and accurate calling of germline and somatic variants. Nat Methods 2018;15:591–4. [DOI] [PubMed] [Google Scholar]
- 34. McLaren W, Gil L, Hunt SE, Riat HS, Ritchie GRS, Thormann A, et al. The ensembl variant effect predictor. Genome Biol 2016;17:1–14. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35. Shen R, Seshan VE. FACETS: allele-specific copy number and clonal heterogeneity analysis tool for high-throughput DNA sequencing. Nucleic Acids Res 2016;44:e131–e. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36. Roth A, Khattra J, Yap D, Wan A, Laks E, Biele J, et al. PyClone: statistical inference of clonal population structure in cancer. Nat Methods 2014;11:396–8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37. Wyatt AW, Annala M, Aggarwal R, Beja K, Feng F, Youngren J, et al. Concordance of circulating tumor DNA and matched metastatic tissue biopsy in prostate cancer. J Natl Cancer Inst 2017;109:djx118. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38. Petrackova A, Vasinek M, Sedlarikova L, Dyskova T, Schneiderova P, Novosad T, et al. Standardization of sequencing coverage depth in NGS: recommendation for detection of clonal and subclonal mutations in cancer diagnostics. Front Oncol 2019;9:851. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39. Macenko M, Niethammer M, Marron JS, Borland D, Woosley JT, Guan X, et al. A method for normalizing histology slides for quantitative analysis. 2009;2009. IEEE. p 1107–10. [Google Scholar]
- 40. Lu MY, Williamson DFK, Chen TY, Chen RJ, Barbieri M, Mahmood F. Data-efficient and weakly supervised computational pathology on whole-slide images. Nat Biomed Eng 2021;5:555. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41. Robinson MD, McCarthy DJ, Smyth GK. edgeR: a Bioconductor package for differential expression analysis of digital gene expression data. Bioinformatics 2010;26:139–40. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42. Law CW, Chen Y, Shi W, Smyth GK. voom: Precision weights unlock linear model analysis tools for RNA-seq read counts. Genome Biol 2014;15:1–17. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43. Ritchie ME, Phipson B, Wu DI, Hu Y, Law CW, Shi W, et al. limma powers differential expression analyses for RNA-sequencing and microarray studies. Nucleic Acids Res 2015;43:e47–e. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44. Chen EY, Tan CM, Kou Y, Duan Q, Wang Z, Meirelles GV, et al. Enrichr: interactive and collaborative HTML5 gene list enrichment analysis tool. BMC Bioinf 2013;14:1–14. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45. Nagpal K, Foote D, Liu Y, Chen P-HC, Wulczyn E, Tan F, et al. Development and validation of a deep learning algorithm for improving Gleason scoring of prostate cancer. NPJ digital medicine 2019;2:1–10. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46. Lu MY, Chen TY, Williamson DFK, Zhao M, Shady M, Lipkova J, et al. AI-based pathology predicts origins for cancers of unknown primary. Nature 2021;594:106. [DOI] [PubMed] [Google Scholar]
- 47. Laleh NG, Muti HS, Loeffler CML, Echle A, Saldanha OL, Mahmood F, et al. Benchmarking weakly-supervised deep learning pipelines for whole slide classification in computational pathology. Med Image Anal 2022;79:102474. [DOI] [PubMed] [Google Scholar]
- 48. Ford K, Hanley CJ, Mellone M, Szyndralewiez C, Heitz F, Wiesel P, et al. NOX4 inhibition potentiates immunotherapy by overcoming cancer-associated fibroblast-mediated CD8 T-cell exclusion from tumors. Cancer Res 2020;80:1846–60. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49. Hanley CJ, Mellone M, Ford K, Thirdborough SM, Mellows T, Frampton SJ, et al. Targeting the myofibroblastic cancer-associated fibroblast phenotype through inhibition of NOX4. J Natl Cancer Inst 2018;110:109–20. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50. Sampson N, Koziel R, Zenzmaier C, Bubendorf L, Plas E, Jansen-Dürr P, et al. ROS signaling by NOX4 drives fibroblast-to-myofibroblast differentiation in the diseased prostatic stroma. Mol Endocrinol 2011;25:503–15. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51. Sampson N, Brunner E, Weber A, Puhr M, Schäfer G, Szyndralewiez C, et al. Inhibition of Nox4-dependent ROS signaling attenuates prostate fibroblast activation and abrogates stromal-mediated protumorigenic interactions. Int J Cancer 2018;143:383–95. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52. Luca BA, Steen CB, Matusiak M, Azizi A, Varma S, Zhu C, et al. Atlas of clinically distinct cell states and ecosystems across human solid tumors. Cell 2021;184:5482–96. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53. Li T, Huang H, Shi G, Zhao L, Li T, Zhang Z, et al. TGF-β1-SOX9 axis-inducible COL10A1 promotes invasion and metastasis in gastric cancer via epithelial-to-mesenchymal transition. Cell Death Dis 2018;9:1–18. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54. Liang Y, Xia W, Zhang T, Chen B, Wang H, Song X, et al. Upregulated collagen COL10A1 remodels the extracellular matrix and promotes malignant progression in lung adenocarcinoma. Front Oncol 2020:2597. [DOI] [PMC free article] [PubMed]
- 55. Rochette A, Boufaied N, Scarlata E, Hamel L, Brimo F, Whitaker HC, et al. Asporin is a stromally expressed marker associated with prostate cancer progression. Br J Cancer 2017;116:775–84. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56. Graham S, Vu QD, Raza SEA, Azam A, Tsang YW, Kwak JT, et al. Hover-Net: Simultaneous segmentation and classification of nuclei in multi-tissue histology images. Med Image Anal 2019;58:101563. [DOI] [PubMed] [Google Scholar]
- 57. Gildenblat J., contributors. 2021 Nov 29. PyTorch library for CAM methods. GitHub [cited 2021 Nov 29]. Available fromhttps://github.com/jacobgil/pytorch-grad-cam.
- 58. Capaci V, Mantovani F, Del Sal G. Amplifying tumor–stroma communication: an emerging oncogenic function of mutant p53. Front Oncol 2021:2869. [DOI] [PMC free article] [PubMed]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Supplementary Figures, Tables and Notes
Contains 1. significantly differentially expressed genes between eTN and eFP ("FP_TN"), 2. significantly differentially expressed genes between eTN and eTP ("TP_TN"), 3. the pathway overrepresentations for 2-3. ("Reactome_table_FP_TN", "Reactome_table_TP_TN", "MSIGDBHALLMARK_TP_TN", "MSIGDBHALLMARK_FP_TN")
Contains 1. significantly differentially expressed genes between samples with high and low gleason grade ("Gleason_high_low"), 2. the pathway overrepresentations for these genes ("MSigDB_Gleason_HL", "Reactome_Gleason_HL"), 3. the overlapping genes between "Gleason_high_low" and "TP TN" from Suppl. Data 1 ("Gleason_HL_overlap TP_TN"), 4. the pathway overrepresentations for genes from (3) ("reactome_GLHL_TP_TN", "MSigDB_GLHL_TP_TN")
Data Availability Statement
The dataset used for training in this study (TCGA-PRAD) is publicly available at https://portal.gdc.cancer.gov/repository.
For access to data from our internal cohort, please contact the Department of Pathology from Ghent University Hospital, under supervision of Jo Van Dorpe (jo.vandorpe@ugent.be). All other raw data are available upon request from the corresponding author.




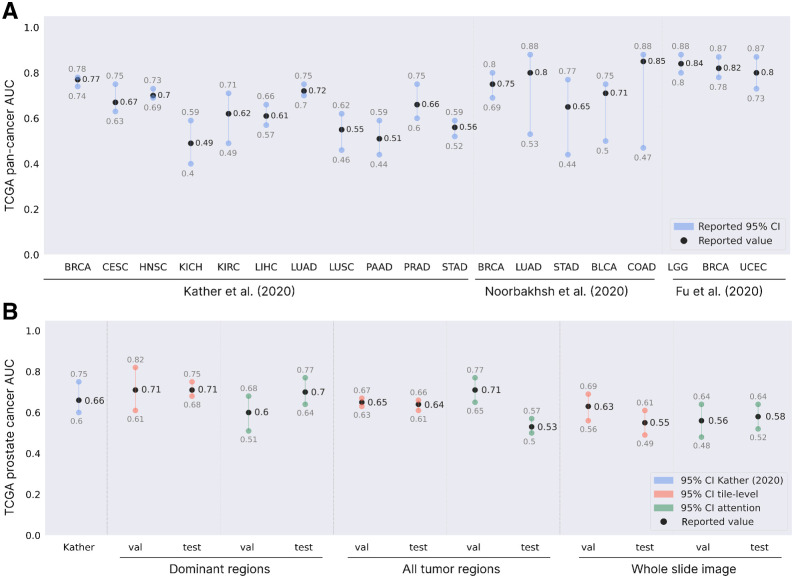
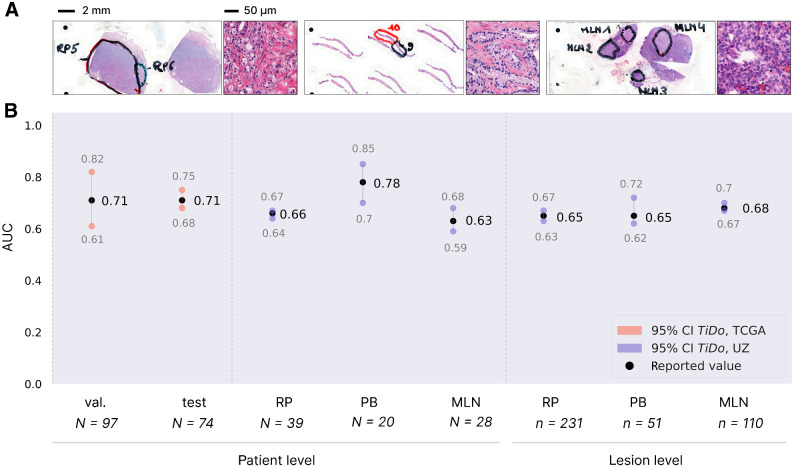
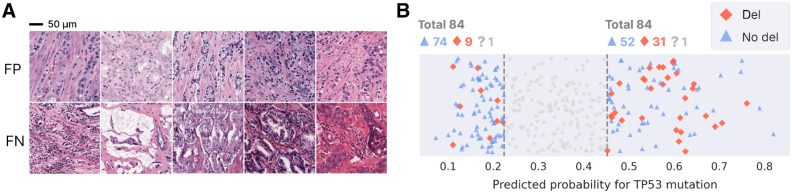
![Figure 5. Predominant cell types in tiles predicted with and without a TP53 mutation. A pretrained network from HoverNet (56) was used to simultaneously detect and classify cells in tiles predicted to (not) contain a TP53 mutation. A, Fraction of detected cell types within tiles for 2,000 tiles that were most confidently predicted to contain a TP53 mutation (left) and not to contain one (right). B, For distinct patients, the tile that was most confidently predicted to contain a mutation. Shown for 10 patients with mutation (top) and 10 patients without mutation (bottom). Regions found to be important for the model prediction are encircled in black [obtained by calculating the contour of GradCam (57) heatmaps on the original tile]. The bar below the plot shows for every tile the fraction of cell types within the black regions (color code same as in A).](https://cdn.ncbi.nlm.nih.gov/pmc/blobs/f12f/10538366/4840ea226cb9/2970fig5.jpg)