Real-Time Passive Acoustic Mapping With Enhanced Spatial Resolution in Neuronavigation-Guided Focused Ultrasound for Blood–Brain Barrier Opening

Abstract—

Objective:

Passive acoustic mapping (PAM) provides the spatial information of acoustic energy emitted from microbubbles during focused ultrasound (FUS), which can be used for safety and efficacy monitoring of blood–brain barrier (BBB) opening. In our previous work with a neuronavigation-guided FUS system, only part of the cavitation signal could be monitored in real time due to the computational burden although full-burst analysis is required to detect transient and stochastic cavitation activity. In addition, the spatial resolution of PAM can be limited for a small-aperture receiving array transducer. For full-burst real-time PAM with enhanced resolution, we developed a parallel processing scheme for coherence-factor-based PAM (CF-PAM) and implemented it onto the neuronavigation-guided FUS system using a co-axial phased-array imaging transducer.

Methods:

Simulation and in-vitro human skull studies were conducted for the performance evaluation of the proposed method in terms of spatial resolution and processing speed. We also carried out real-time cavitation mapping during BBB opening in non-human primates (NHPs).

Results:

CF-PAM with the proposed processing scheme provided better resolution than that of traditional time-exposure-acoustics PAM with a higher processing speed than that of eigenspace-based robust Capon beamformer, which facilitated the full-burst PAM with the integration time of 10 ms at a rate of 2 Hz. In vivo feasibility of PAM with the co-axial imaging transducer was also demonstrated in two NHPs, showing the advantages of using real-time B-mode and full-burst PAM for accurate targeting and safe treatment monitoring.

Significance:

This full-burst PAM with enhanced resolution will facilitate the clinical translation of online cavitation monitoring for safe and efficient BBB opening.

I. Introduction

Focused ultrasound (FUS) can induce cavitation activities of microbubbles and transiently open the blood–brain barrier (BBB) for the targeted drug delivery [1], [2] or immunostimulation [3], [4]. Most transcranial FUS studies in patients were conducted by using an MR-guided FUS system with a hemispherical phased array transducer (ExAblate, InSightec Inc., Israel) [5]–[8] and the treatment requires patients to lie inside the MR scanner throughout the entire therapy session.

Frameless portable FUS systems without MR-guidance have been developed to reduce the cost involved in MRI and the time that also requires the patient to stay still in the scanner [9]–[11]. A clinical study using the NaviFUS system was reported to show the feasibility of BBB opening and immunostimulation [10], [12]. They used a multi-element FUS array, which is smaller than the hemispherical array of ExAblate, with the guidance of the neuronavigation system. Another type of frameless FUS system is a portable neuronavigation-guided system with a single-element FUS transducer and a passive cavitation detector (PCD) [11]. This system was demonstrated by non-human primate (NHP) studies [11], [13] and now two clinical studies are in progress (NCT04118764 and NCT04804709).

Since the BBB opening with microbubble-mediated FUS is based on the linear and nonlinear oscillations of the bubbles, called cavitation, the acoustic emissions from the bubbles during the sonication can be passively detected and analyzed for treatment monitoring. In studies with the MR-guided FUS, cavitation signals from the bubbles were detected by several hydrophones and employed as a feedback control for optimal power calibration [6], [14], [15]. In the portable neuronavigation-guided system, cavitation signals were also detected by a single-element PCD placed at the central opening of the FUS transducer and spectral information of acoustic emissions was provided for safety monitoring [13]. Although they utilized spectral cavitation information, spatially-resolved cavitation maps were not obtained in those studies due to the limited number of sensors.

Spatial information of the microbubble cavitation is important for the safe and efficient treatment as microbubble cavitation can occur outside of the focal region in the brain depending on cerebral vascularity and the brain tissue structures (gyri and sulci and boundaries of ventricles) [16], [17]. Multi-element hemispherical transmit/receive arrays have been developed for MR-guided FUS, and in vivo rat or rabbit studies demonstrated the three-dimensional cavitation mapping capability with harmonic and sub-harmonic microbubble emissions [17]–[20]. The same group also developed a novel patient-specific skull-conformal phased array system [21].

For the frameless clinical FUS system, a study was carried out to demonstrate the feasibility of PAM with a linear array transducer [9]. However, since the imaging array for acoustic mapping was placed onto the temporal bone independently of the FUS transducer, aligning the imaging plane with the focal volume was challenging and not easily translatable to the clinic. Meanwhile, spatial cavitation monitoring would be essential for the neuronavigation-guided FUS because there is no MR thermal imaging or other spatially-resolved monitoring tools. Therefore, PAM in the frameless FUS system needs to be established to adjust or halt the treatment in case substantial off-target cavitation activities are observed.

Cavitation mapping with a linear array transducer generally has a poor spatial resolution because of the small receiving aperture and the uncertainty of the time of cavitation occurrence. Some studies with short-pulse FUS sequences presented that a high axial resolution of PAM can be achieved by utilizing the round trip time of the short pulse [22], [23]. However, long-pulse sequences (i.e., ms-long bursts) are generally employed for BBB opening [10], [24]–[27] and the time-of-flight information cannot be utilized because of the unpredictable cavitation timing during the long pulse. In addition, the point spread function (PSF) of the PAM in a clinical setting is even more compromised because only the low-frequency acoustic signals are detectable through the human skull and the received ultrasound waves are aberrated while propagating the inhomogeneous tissue and skull bone.

Time exposure acoustics (TEA) was first proposed to map the cavitation activity from passively-acquired ultrasonic data with an array transducer[28]. Since then, many studies were carried out to enhance the spatial resolution and the robustness to noise of the cavitation mapping such as robust Capon beamformer (RCB) [29], robust beamforming by linear programming [30], and eigenspace-based RCB (ERCB) [31]. Since coherence factor-based beamforming was suggested for diagnostic ultrasound imaging [32], it has been used for developing various adaptive beamformers [33], [34]. For passive cavitation imaging, phase-coherence-factor-based PAM [35] and sign-coherence-factor-based RCB [36] were suggested. While a simple amplitude-coherence-factor-based PAM was used in a gel phantom study, its performance was not evaluated with other methods [37]. All of those studies were conducted using high-frequency harmonic signals ($>5$ MHz), which are infeasible for transcranial imaging.

In our previous work [9], only a portion (e.g., a few microseconds out of 10 ms) of received data were processed for real-time cavitation monitoring. Although Kamimura et al. suggested the use of sparse matrix multiplication for accelerating the computation, the output was not enough for real-time PAM with the temporal integration of the entire 10-ms long burst [38]. However, Jones et al. demonstrated the importance of both acquiring and processing the full-burst acoustic emission signal during the FUS exposures [20]. In that study, the full-burst sonication-aggregate cavitation maps were generated and showed higher spatial correlation with the damaged volume found in T2*-weighted MRI across multiple animals compared to under-sampled cavitation maps.

In this paper, we developed a real-time cavitation mapping which is capable of full-burst analysis with an enhanced spatial resolution for the neuronavigation-guided FUS system. A diagnostic phased array transducer for cavitation detection was co-aligned with the FUS transducer for the stable registration between the imaging plane and the FUS beam to overcome the challenge of the imaging probe alignment in [9]. A parallel processing scheme of coherence-factor-based PAM (CF-PAM) was developed for enhanced spatial resolution, exploiting the lower complexity of the method compared to other data-adaptive methods. The performance of the method was evaluated and compared with those of TEA- and ERCB-PAM methods. We also investigated the transcranial feasibility of CF-PAM with in vitro human skull experiments and in vivo NHP experiments. A preliminary version of this work has been reported in [39] and this paper expands on in vivo experiments and more extensive performance comparison between methods.

II. Passive Acoustic Mapping

A. Coherence-factor-based Passive Acoustic Mapping

We employed the amplitude CF for enhancing the spatial resolution of PAM. CF is the ratio between the coherent power to the incoherent power of channel signals received by multiple elements, which is equal to 1 when the channel signals are coherent and close to zero when they are incoherent. The CF of channel signals for the pixel $\mathbf{x}$ and the time point $t$ is obtained by

$$C_j(\mathbf{\text{x}},t)\hspace{0.17em}=\hspace{0.17em}\frac{{\left|{\sum }_{i=1}^{N_{\text{E}}}\sqrt{d_i(\mathbf{\text{x}})}{s}_{ij}(t\hspace{0.17em}+\hspace{0.17em}{\tau }_i(\mathbf{\text{x}}))\right|}^2}{N_{\text{E}}{{\sum }_{i=1}^{N_{\text{E}}}\left|\sqrt{d_i(\mathbf{\text{x}})}{s}_{ij}(t\hspace{0.17em}+\hspace{0.17em}{\tau }_i(\mathbf{\text{x}}))\right|}^2},$$ (1)

where $s_{ij}(t)$ is the acoustic signal received by the $i$-th element for the $\text{j}$-th FUS burst ($j\hspace{0.17em}=\hspace{0.17em}1,2, ···,N_{\text{B}}$;$N_{\text{B}}$: number of bursts), $d_i(\mathbf{x})$ is the distance between the pixel $\mathbf{x}$ and the $i$-th element, and ${\tau }_i(\mathbf{x})$ is the round-trip time delay which consists of the transmit delay from the FUS transducer to $\mathbf{x}$ and the receive delay from $\mathbf{x}$ to the $i$-th element, and $N_{\text{E}}$ is the number of transducer elements (i.e., number of channels).

The spatio-temporal cavitation intensity is estimated by employing the CF as a weighting factor as follows:

$$I_j(\mathbf{\text{x}},t)\hspace{0.17em}=\hspace{0.17em}{\left|C_j(\mathbf{\text{x}},t)\hspace{0.17em}\sum _{i=1}^{N_{\text{E}}}\sqrt{d_i(\mathbf{\text{x}})}{s}_{ij}(t\hspace{0.17em}+\hspace{0.17em}{\tau }_i(\mathbf{\text{x}}))\right|}^2.$$ (2)

The cavitation map for the $\text{j}$-th burst is obtained by

$${\Psi }_j(\mathbf{\text{x}})\hspace{0.17em}=\hspace{0.17em}{\int }_0^T{I}_j(\mathbf{\text{x}},t)\hspace{0.17em}dt,\hspace{0.17em}$$ (3)

where $T$ is the integration time which can be the burst length (i.e., 10 ms) for the full-burst integration. In practice, the integration in (3) is converted into the summation over $N_t$ $(=T{f}_s)$ when the signal $s_{ij}(t)$ is sampled by a rate of $f_{\text{s}}$.

B. GPU implementation

Fig. 1(a) shows the parallel processing scheme that we developed for the real-time CF-PAM. It was implemented using NVIDIA compute unified device architecture (CUDA) (Santa Clara, CA). The $n_t$ threads were created in each thread block, and the grid size was $[N_x/n_t]\hspace{0.17em}\times \hspace{0.17em}{N}_z\hspace{0.17em}\times \hspace{0.17em}{N}_t$, where $n_t$ is the maximum number of threads per block, $N_x$ and $N_z$ are the number of pixels of the resultant map in the lateral ($x$) and axial ($z$) directions.

Fig. 1.

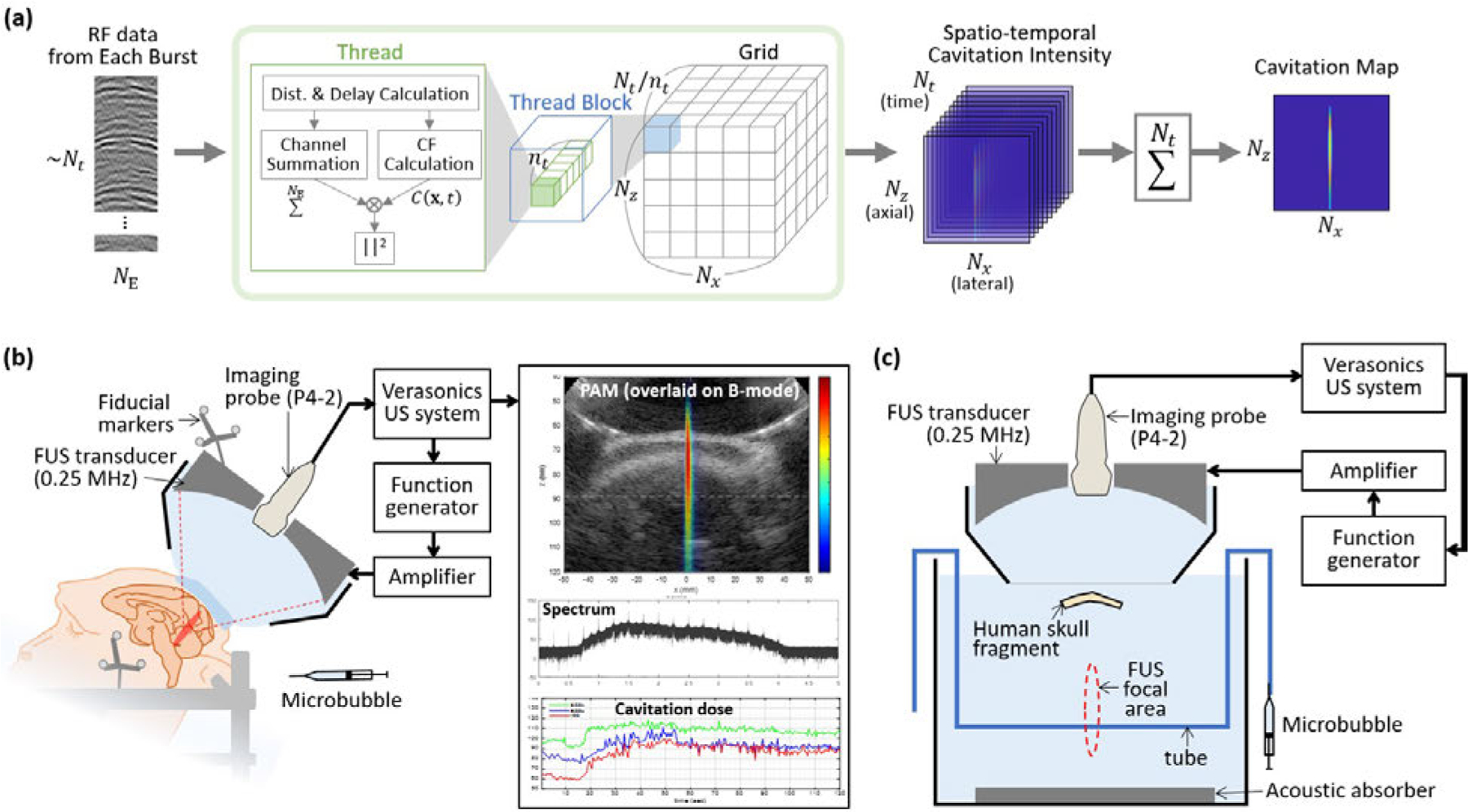
(a) Parallel processing scheme for reconstruction of a cavitation map from the RF channel data acquired in every FUS burst. In each thread block, $n_t$ threads were created where $n_t$ was the maximum number of threads per block. Dimensions of the grid were $[N_x/n_t]\hspace{0.17em}\times \hspace{0.17em}{N}_z\hspace{0.17em}\times \hspace{0.17em}{N}_t$. In each CUDA thread, the intensity at a pixel and a time point was calculated, resulting a spatio-temporal cavitation intensity map $I_j(\mathbf{x},t)$ with a size of $N_x\times \hspace{0.17em}{N}_z\hspace{0.17em}\times \hspace{0.17em}{N}_t$. The final cavitation map ${\mathbf{\Psi }}_j(\mathbf{x})$ for each burst was obtained by summing the results over time. (b) FUS system with cavitation monitoring for the in vivo NHP experiments. During the FUS treatment with the intravenous administration of microbubbles, the cavitation map, spectrum of the cavitation signal, and the cavitation dose were updated after each FUS burst at a rate of 2 Hz. Fiducial markers attached to the transducer and the stereotaxic frame were used for the neuronavigation-guidance targeting. (c) Experimental setup for the in vitro skull experiments. Therapeutic FUS pulses were transmitted from the FUS transducer and the microbubble inside the tube emitted the cavitation signals. The emitted signals were received by the imaging probe through the human skull.

In each CUDA thread, the cavitation intensity at a pixel and a time point was obtained. The distances $d_i(\mathbf{x})$ and time delays ${\tau }_i(\mathbf{x})$ were computed and $s_{ij}(t\hspace{0.17em}+\hspace{0.17em}{\tau }_i(\mathbf{x}))$ was obtained by linear interpolation between the two nearest samples; $s_{\text{intp}}\hspace{0.17em}=\hspace{0.17em}(1\hspace{0.17em}-\hspace{0.17em}\kappa )\hspace{0.17em}·\hspace{0.17em}{s}_{ij}[k]+\kappa \hspace{0.17em}·\hspace{0.17em}{s}_{ij}[k\hspace{0.17em}+\hspace{0.17em}1]$ where $s_{\text{intp}}$ is the interpolated value, $k\hspace{0.17em}+\hspace{0.17em}\kappa$ is the time delay in samples $(={\tau }_i\hspace{0.17em}·\hspace{0.17em}{f}_s)$, and $k$ and $\kappa$ are the integer and fractional numbers. Then, the square of CF-weighted channel sum was computed. Receive apodization window was not applied because the effect was negligible in our case. Since each pixel was computed at each thread, synchronization of threads was not required, which further accelerated the computation. After execution of the GPU kernel, a spatio-temporal cavitation intensity map $I_j(\mathbf{x},t)$ with a size of $N_x\times \hspace{0.17em}{N}_z\hspace{0.17em}\times \hspace{0.17em}{N}_t$ was obtained. The final cavitation map was then obtained by integrating over $N_t$ temporal pixels.

To execute the CUDA code using the Verasonics sequence execution (VSX) software with MATLAB (MathWorks Inc., Natick, MA, USA), MATLAB CUDA Toolkit was used. Before the start of treatment, an initialization function was executed to allocate memory and generate a GPU kernel object using pre-compiled PTX and CUDA codes. During the treatment, immediately after each 10-ms burst, RF channel data were loaded on the global memory of GPU and the parallel processing was executed as an external function to run the GPU kernel for the cavitation map reconstruction. The resultant cavitation map $\Psi (\mathbf{x},\hspace{0.17em}j)$ was updated in a graphic-user interface (GUI) after each burst to serve as a monitoring tool. The data transfer, process, and display were completed within 0.5 s before the next burst started. MATLAB and CUDA codes are available at https://github.com/suabae/pam.

The computational speed of the CF-PAM was compared with those of TEA- and ERCB-PAM [31]. For a fair comparison, TEA and ERCB were also implemented using parallel processing. The formulations and GPU implementations of the TEA and ERCB are presented in Sections 1 and 2 of the Supplementary document. The processing speed was evaluated on an NVIDIA Tesla V100 GPU and an Intel Xeon E5-2698 CPU.

III. FUS System with Cavitation Monitoring

A. FUS Sonication and Cavitation Data Acquisition

Fig. 1(b) shows the frameless FUS system with cavitation monitoring that we suggested in this paper. We used a single-element FUS transducer (H-231, Sonic Concepts, Bothell, WA, USA) with a central opening (outer diameter: 110 mm, innerdiameter: 44 mm, radius of curvature: 110 mm). A phased array imaging transducer (P4-2, center frequency ($f_c$): 2.5 MHz, number of elements: 64; ATL/Philips, Andover, MA, USA) was co-aligned with the FUS transducer through the central opening and was connected to the ultrasound system (Vantage 256, Verasonics Inc., Redmond, WA, USA). The −6 dB width and length of the FUS focus were 6 mm and 49 mm, respectively. The maximum pressure location of the focus relative to the imaging transducer was at $x\hspace{0.17em}=\hspace{0.17em}1$ mm, $z\hspace{0.17em}=\hspace{0.17em}90$ mm in the ultrasound image, which was found from a B-mode image of the hydrophone (HGL-0200, Onda Corp., Sunnyvale, CA, USA) when it was at the pressure maximum point. A therapeutic pulse with a center frequency of 0.25 MHz, a pulse length of 10 ms, and a pulse repetition frequency (PRF) of 2 Hz was used for the FUS sonication. The acoustic signals were recorded by the imaging transducer for slightly longer than 10 ms to account for the round-trip delay, with a sampling rate ($f_{\text{s}}$) of 10 MHz.

B. Online Data Processing

Immediately after every burst, the RF data were transferred to the GPU memory and a spatial cavitation map, spectrum, and doses of the cavitation signal were computed and displayed on the monitor during the treatment as shown in Fig. 1(b). The cavitation map was computed as described in Section II.B. using CF-PAM. We computed the stable cavitation dose with harmonic frequencies (SCDh), stable cavitation dose with ultraharmonic frequencies (SCDu), and inertial cavitation dose (ICD). The 4th to 9th harmonics and ultraharmonics were used for SCDh and SCDu, respectively, and the ICD was computed from the bandwidth of 75 kHz between the harmonic and ultraharmonic frequencies. The equations for the cavitation dose calculation are described in the Supplementary document (Section 3).

IV. SImulations and Experiments

A. Simulation Setup for Spatial Resolution Evaluation

A phased array transducer was assumed to passively receive harmonic signals from one or two cavitation sources. The simulated RF channel data were generated using the software package k-Wave [40] and MATLAB; further information can be found in Section 4 of the Supplementary document. Single cavitation source data were used to reconstruct a point spread function (PSF) and the axial and lateral lengths of the PSF were measured by the full-width half-maximum (FWHM). Source separation capability was quantified from the PAM images with two cavitation sources. Two cavitation sources had a temporal offset ($t_{\text{offset}}$) corresponding to the distance ($d$) between the two sources assuming that the deeper source starts the acoustic emission later than the shallower by $t_{\text{offset}}\hspace{0.17em}=\hspace{0.17em}d/c$, where $c$ is the sound speed. Resolvability was measured as in [41] by the normalized ratio ($A_{\text{ratio}}$) of peak and trough amplitudes which is $A_{\text{ratio}}\hspace{0.17em}=\hspace{0.17em}\text{ (}{A}_{\text{peak}}\hspace{0.17em}-\hspace{0.17em}{A}_{\text{trough}}\text{)/}{A}_{\text{peak}}$ where $A_{\text{peak}}$ is the peak amplitude and $A_{\text{trough}}$ is the minimum amplitude between the two sources. The peak amplitude is taken as the smaller of two peaks.

B. In Vitro Skull Experimental Setup

Fig. 1(c) illustrates the experimental setup for the in vitro skull experiments. A human skull fragment with a thickness range of 5.5–8.5 mm was introduced between the imaging array probe and the cavitation source. The skull fragment was placed on an ultrasonically-transparent membrane at a depth of 60 mm in the B-mode image. The skull was covering the entire aperture of the imaging transducer to obtain the transcranially-detected cavitation signal.

The tube (inner diameter: 0.5 mm) was positioned within the focal area of FUS and in-house made polydisperse microbubbles were injected into the tube [42]. The pressure and the concentration of the microbubbles are presented in Table I The tube was aligned parallel to the array transducer and positioned at the depth of 90 mm with B-mode guidance. The therapeutic pulse (pulse length: 10 ms, center frequency: 0.25 MHz, PRF: 2 Hz) was used to drive the FUS transducer and the cavitation signals from the microbubbles were collected by the imaging probe during the FUS sonication. The received data were used for the reconstruction of cavitation images with TEA-, ERCB-, and CF-PAM to evaluate the methods.

TABLE I.

Acoustic pressure and microbubles used in the experiments

	In vitro human skull	In vivo NHP
Derated Pressure∗	0.1 MPa	0.3 MPa
Microbubble	In-house polydisperse	Definity
MB concentration	5 × 108bubbles/ml	1.2 × 1010bubbles/ml
MB dose	N/A	0.05 ml/kg

^∗We assumed the skull insertion loss of 60% and 50% for in vitro human skull and in vivo NHP experiments, respectively.

C. NHP Experimental Setup

Experiments were performed with two rhesus macaques (NHP 1 and NHP 2; male, 6 years old) as shown in Fig. 1(b). The NHP was sedated with ketamine and dexdomitor (5–8 mg/kg and 0.01 mg/kg, respectively) and maintained under anesthesia with an isoflurane-oxygen mixture and boluses of propofol. The animal was lying in a prone position on the operating table and the transducer was positioned using a robotic arm (UR5e, Universal Robots, Denmark) with the guidance of a neuronavigation system (Brainsight; Rogue Research, Montreal, QC, Canada). The B-mode image was obtained by baseband beamforming for coherent plane wave imaging [43] and used as a supplementary guide for the registration between the ultrasound image and the MRI. A brain target was sonicated for 2 minutes with the therapeutic pulse and a bolus of microbubble was injected at the beginning of the sonication (Table I). During the sonication, the cavitation map, spectrum, and cavitation dose plot were used for real-time monitoring. Post-FUS MRI was obtained to confirm the safety and quantify the BBB opening volume; details can be found in the Supplementary document (Section 5).

To investigate how much the PAM signal spatially correlates with the BBB opened region, the pixel-wise correlation study was performed based on receiver operating characteristic (ROC) and precision-recall (PR) curves. For the pixel-wise analysis, the PAM image and BBB opening mask were resampled with a pixel size of $\text{0}.5\hspace{0.17em}\text{mm }\hspace{0.17em}\times \hspace{0.17em}\text{0}.5\hspace{0.17em}\text{mm}$ in an ROI ($\text{30}\hspace{0.17em}\text{mm}\hspace{0.17em}\times \hspace{0.17em}\text{40}\hspace{0.17em}\text{mm}$) centered at the focus. Only pixels within the brain region were used for the analysis. We evaluated the predictive capability of each pixel in the PAM image for detecting BBB opening and the pixels in the opened region are considered positive. The ratio of the positively labeled pixels to the total number of pixels used for the analysis was approximately 30%.

V. Results

A. Computational Speed

Fig. 2 shows the processing time for reconstruction of a single frame ${\Psi }_j(\mathbf{x})$ when the integration time $T$ is 0.5, 1, 2, 5, and 10 ms. We measured the processing times changing the number of image pixels ($N_x\times \hspace{0.17em}{N}_z$) from 2,000 to 10,000. The average processing time was measured from 20 repeated tests and the error bars denote two standard deviations. Specifically, TEA, ERCB, and CF required 0.22, 47.9, and 0.23 s for the reconstruction of 5,000 pixels and the temporal integration of 10 ms, respectively. ERCB-PAM took approximately 400 times longer execution time in average than those of TEA- or CF-PAM mainly due to the eigenvalue decomposition.In contrast, the processing time required for CF-PAM was very close to that of conventional TEA-PAM regardless of the number of pixels and integration time. For the PRF of 2 Hz, the processing time should be less than 0.5 s and TEA- and CF-PAM were within the limit. In our case, we were able to reconstruct 5,000 pixels with the full-burst integration ($T$=10 ms) using CF-PAM for the real-time monitoring, taking into account the overhead time including the sonication, data transfer, and display.

Fig. 2.

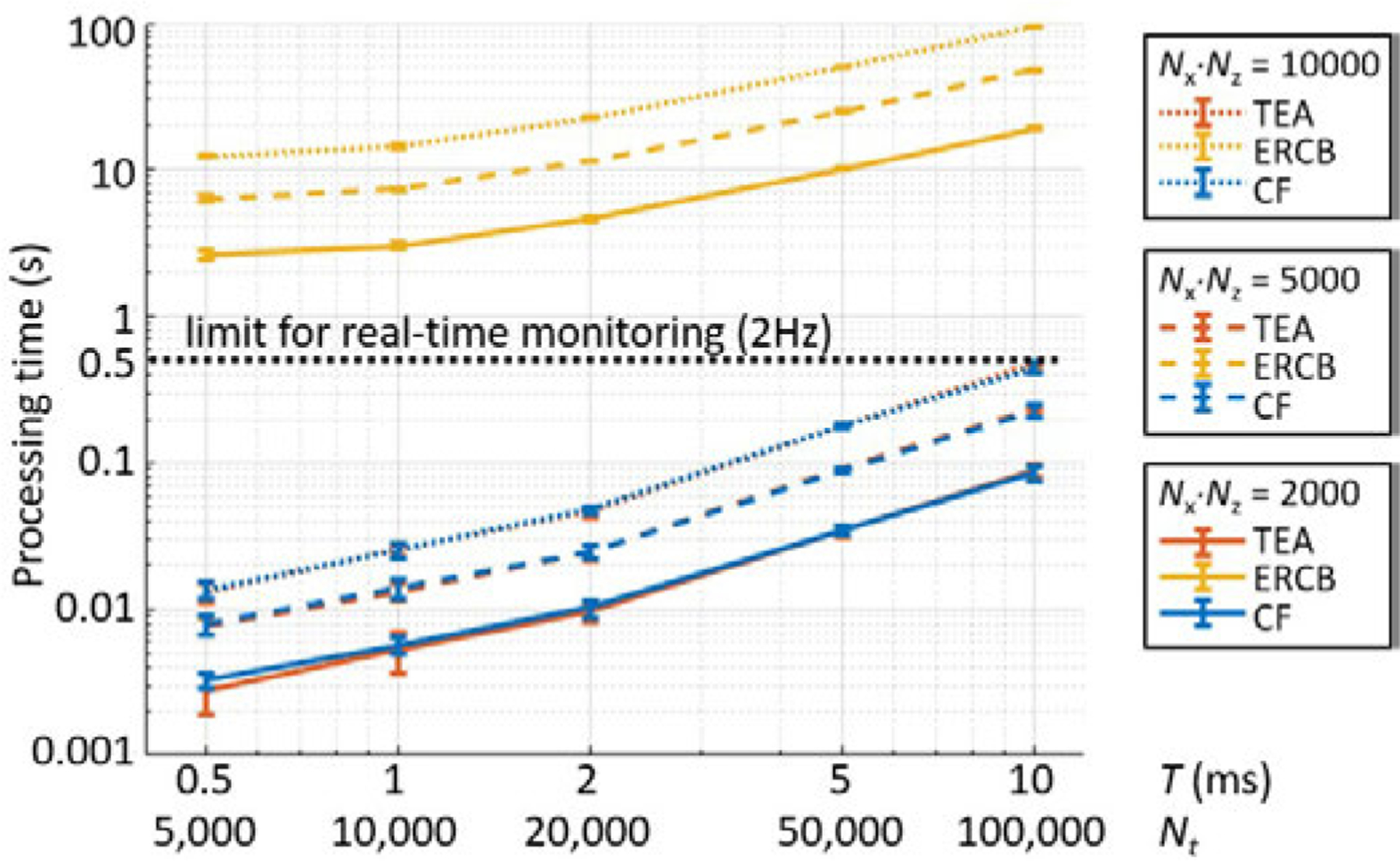
Processing time for reconstruction of a single frame of cavitation map with the number of pixels of $N_x\times \hspace{0.17em}{N}_z$ and the integration time $T$. $N_t$ is the number of time samples to be integrated. The number of channels (i.e., receiving elements, $N_{\mathbf{E}}$) was 64. The average processing time was measured from 20 repeated tests and the error bars denote two standard deviations.

B. Spatial Resolution Evaluation

Using the simulation data, the PSF and the source separation capability of each method were evaluated. Fig. 3(a)–(d) shows the PSFs and their axial length and lateral width when using TEA-PAM, ERCB-PAM, and CF-PAM. The PSF was elongated and the measured FWHM increased as the depth of the cavitation source increased. Compared to the conventional TEA method, ERCB and CF methods provided smaller PSF size throughout all depths. The same trend was found in the off-axis PSF evaluation (Section 6 and Fig. S1 in the Supplementary document); the axial and lateral lengths of the PSF of the CF-PAM were similar to those of ERCB-PAM and shorter than those of CF-PAM.

Fig. 3.

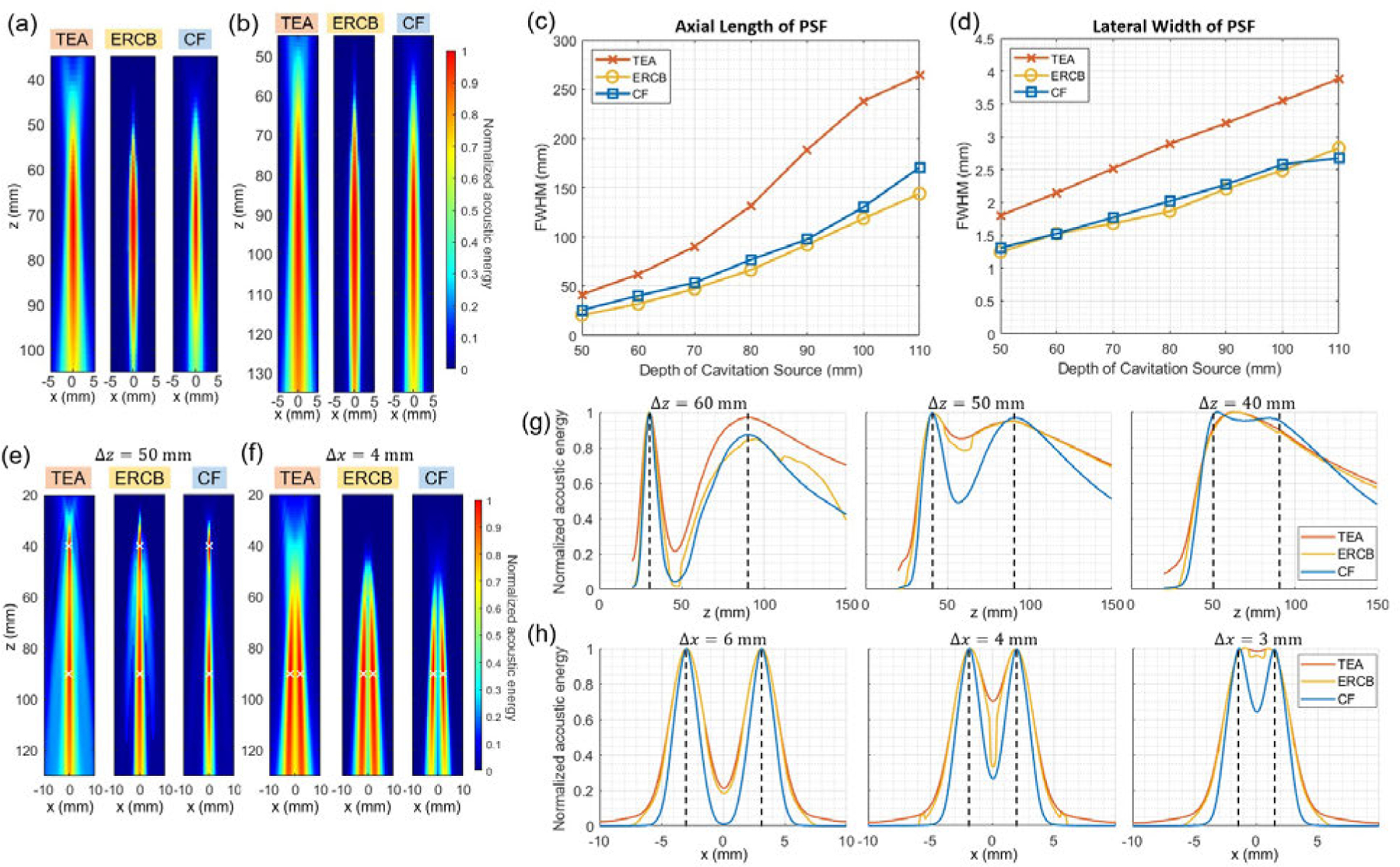
Spatial resolution evaluation results. (a), (b) Point spread functions (PSFs) of TEA-, ERCB-, and CF-PAM obtained from the single cavitation source simulation at the depth ($z$) of (a) 70 mm and (b) 90 mm. (c), (d) Full-width half-maximum (FWHM) of PSFs in (c) the axial and (d) the lateral direction for different depths. (e), (f) Cavitation maps formed by TEA-, ERCB-, and CF-PAM for two cavitation sources with (e) the axial distance of 50 mm and (f) the lateral distance of 4 mm. The source locations are marked with white crosses. (g) Axial profiles of cavitation maps reconstructed by TEA-, ERCB-, and CF-PAM for two sources separated by 60 mm, 50 mm, and 40 mm axially (from left to right). (h) Lateral profile of cavitation maps reconstructed by the three methods for two sources separated by 3 mm, 4 mm, and 6 mm laterally (from left to right). The source locations are marked with black dashed lines in (g) and (h).

Source separation capability was evaluated in the axial dimension (Fig. 3(e) and (g)) and the lateral dimension (Fig. 3(f) and (h)). Overall, the axial resolution was much worse than the lateral resolution mainly due to the long axial tail of PSF resulting from the small aperture of the array transducer relative to the deep imaging depth. As seen in lateral and axial profiles (Fig. 3(g) and (h)), CF-PAM showed the best performance among the three methods for resolving two cavitation sources in both directions. The amplitude ratio of peak to trough ($A_{\text{ratio}}$) for all cases is presented in Table II. Except for the case with $\Delta z$ of 60mm, CF-PAM showed better resolvability than other methods. The parameters used in ERCB-PAM ($\epsilon \hspace{0.17em}=\hspace{0.17em}1$, $\delta \hspace{0.17em}=\hspace{0.17em}0.5$) were chosen by compromising between the spatial resolution and the distortion of image [31].

TABLE II.

Resolvability of Two Cavitation Sources in Axial and Lateral Dimension Measured From FIG. 3(G) and (H)

	Resolvability ($A_{\text{ratio}}$)
$\Delta z$	60 mm	50 mm	40 mm
TEA-PAM	0.78	0.1	0
ERCB-PAM	0.98	0.17	0
CF-PAM	0.95	0.5	0.02
$\Delta x$	6 mm	4 mm	3 mm
TEA-PAM	0.79	0.3	0.02
ERCB-PAM	0.82	0.67	0.04
CF-PAM	0.99	0.73	0.36

C. In Vitro Human Skull Studies

Fig. 4 shows the cavitation images reconstructed by using TEA-, ERCB-, and CF-PAM when the microbubbles in a tube were sonicated by FUS. The human skull fragment and the tube were positioned at $z\hspace{0.17em}=\hspace{0.17em}60$ mm and $z\hspace{0.17em}=\hspace{0.17em}90$ mm, respectively, by the guidance of B-mode image with the imaging transducer. Cavitation data from each sonication were beamformed by TEA-, ERCB-, and CF-PAM, and six representative cavitation maps were shown in Fig. 4. Each cavitation map was normalized to itself.

Fig. 4.

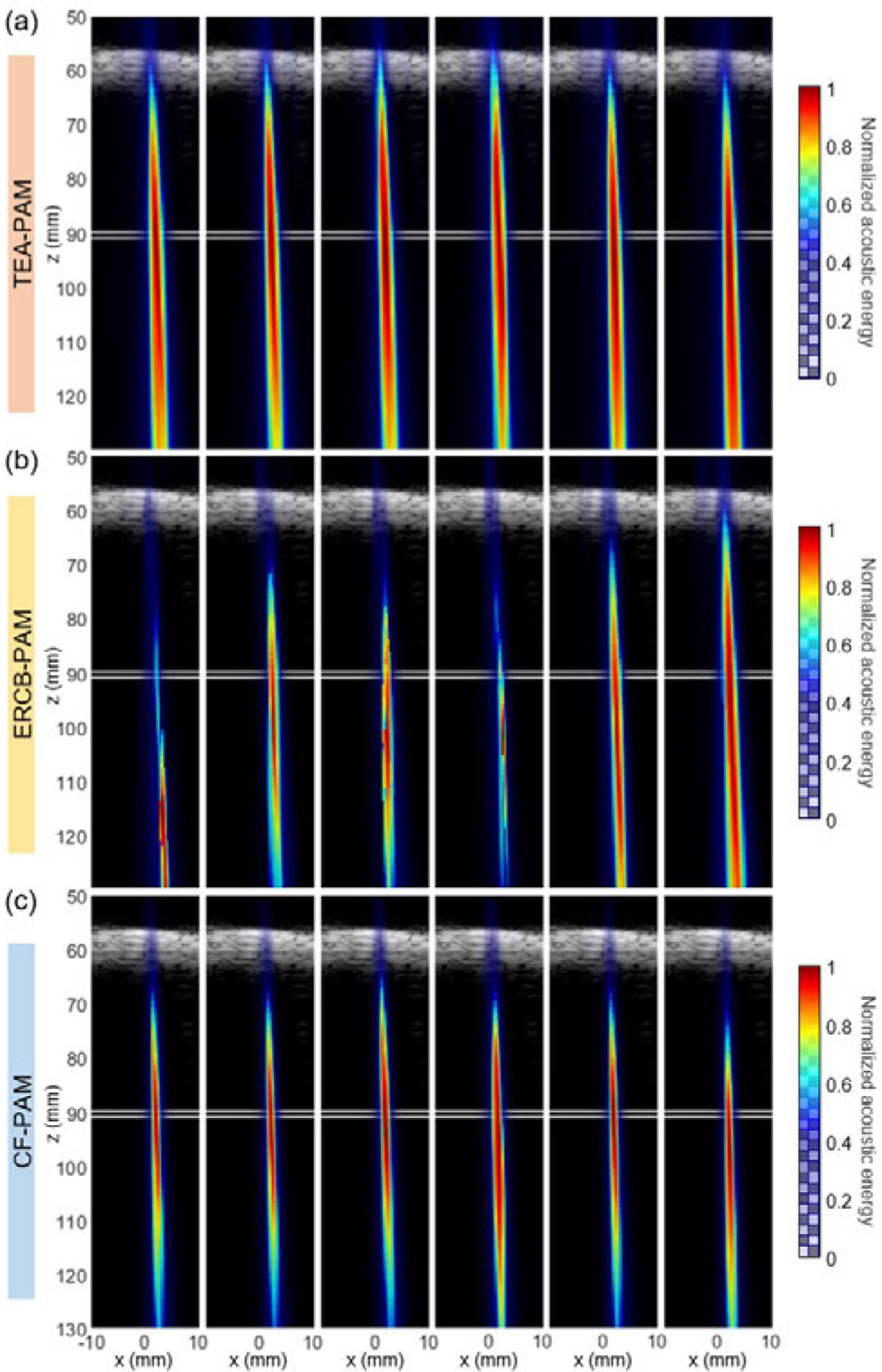
Cavitation map (color) reconstructed by using (a) TEA-, (b) ERCB-, and (c) CF-PAM over time overlaid on the B-mode image (grayscale). Human skull fragment appeared in B-mode image at $z\hspace{0.17em}=\hspace{0.17em}60$ mm. The position of the tube with the microbubbles is indicated by white lines at $z\hspace{0.17em}=\hspace{0.17em}90$ mm.

Strong cavitation signal from the microbubble was detected around the focus ($x\hspace{0.17em}=\hspace{0.17em}1$mm, $z\hspace{0.17em}=\hspace{0.17em}90$mm) through the human skull with a thickness of 5.5–8.5 mm. The results show that the transcranial PAM is feasible with the phased array transducer. However, as the received cavitation data were noisy and the wavefronts were aberrated due to the skull, the spatial resolution of the cavitation map was compromised. Although ERCB-PAM (Fig. 4(b)) provided the better resolution than those of TEA-PAM (Fig. 4(a)), the cavitation signals in the ERCB-PAM maps were shifted and distorted, showing the susceptibility of the method to the noise and aberrations. On the other hand, CF-PAM provided more stable and robust cavitation maps compared to ERCB-PAM and a better spatial resolution than TEA-PAM when the skull fragment was introduced.

Out of 30 bursts, the success rate of cavitation activity localization was measured by counting the number of frames (i.e., bursts) in which the maximum acoustic energy location was within a circle centered at the focus with a radius of 5 mm. CF-PAM and TEA-PAM showed the same success rate of 0.65 while the ERCB-PAM had only 0.39. Although the success rate of the ERCB-PAM could increase with a higher $\epsilon$ that yields less distortion, the degradation of the spatial resolution was unavoidable.

D. In Vivo NHP Studies

In the in vivo NHP experiments, the BBB was successfully opened without any detectable damage in the safety MR scans. Fig. 5 shows the cavitation mapping and BBB opening results in NHPs and videos of real-time cavitation monitoring are available online (MM1 and MM2)¹. Spectrograms in Figs. 5(a) and (d) show harmonic and ultraharmonic signals as well as the broadband inertial cavitation over time. In the cavitation dose graphs, SCDh, SCDu, and ICD increased after the microbubble injection and the saline flush (approximately at 20 s), allowing the cavitation activities distinguishable from the baseline before the injection.

Fig. 5.

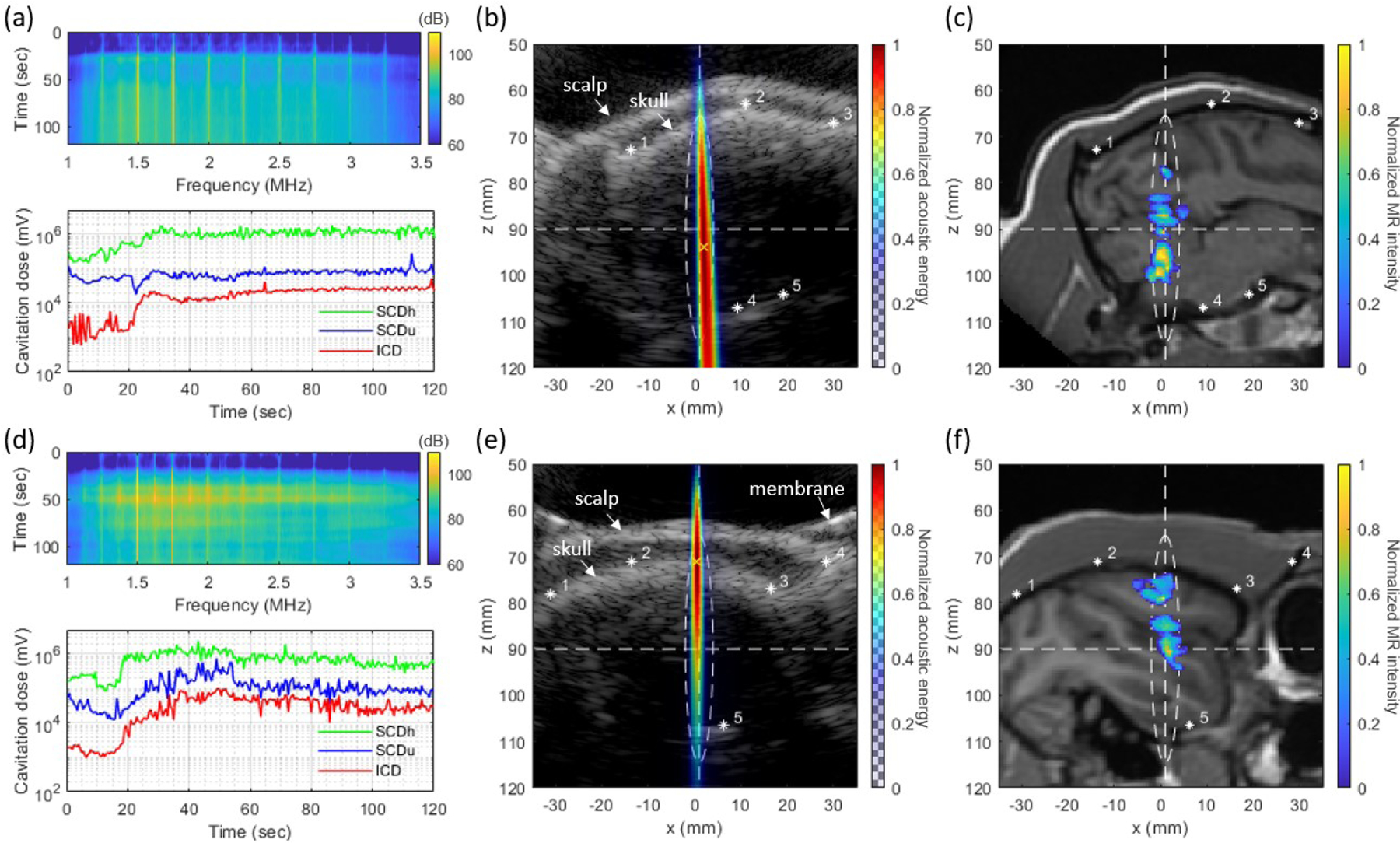
In vivo experiment results of (a)–(c) NHP 1 and (d)–(f) NHP 2. (a), (d) Spectrograms of cavitation signal (top panel) and harmonic (SCDh), ultraharmonic (SCDu) and inertial (ICD) cavitation doses (bottom panel), (b), (e) Cumulative acoustic map reconstructed by CF-PAM (color) overlaid on the B-mode image (grayscale), and (c), (f) BBB opening regions (color) overlaid on T1-weighted MRI (grayscale). Asterisks in (b), (c), (e) and (f) indicate the matching anatomical locations in the B-mode and the MR image. A white-dashed ellipse shows −6 dB focal zone and the white-dashed horizontal and vertical lines are showing the lateral and axial location of FUS focus. Videos of real-time cavitation monitoring are available online (MM1 and MM2).

In Figs. 5(b) and (e), the grayscale B-mode images show the scalp and the skull profiles of the NHP head. The location of focus is indicated by the white-dashed lines and ellipse. The cumulative acoustic maps obtained by averaging the PAM images over all of the 240 bursts are also presented in Figs. 5(b) and (e). Strong acoustic emissions were detected within the focal area in the brain.

The opening volume quantified from the MRI was 154 mm³ and 116 mm³ for NHP 1 and NHP 2, respectively. The ultrasound image (B-mode and PAM) and the MRI were registered as shown in Fig. S2. In Figs. 5(c) and (f), BBB opening region (color) on the slice corresponding to the PAM image slice is overlaid on the T1-weighted MRI for anatomical information. Figs. 5(c) and (f) show that the BBB was opened within the −6 dB focal area.

The distance between the peak location of the PAM and the centroid of the BBB opening region was 3.3 mm and 12.1 mm for NHP 1 and 2, respectively. Fig. 6 shows the pixel-wise ROC and PR analyses between the PAM and the BBB opening. Area under the curve values for ROC plots ($\text{AU}{\text{C}}_{\text{ROC}}$) and for PR plots ($\text{AU}{\text{C}}_{\text{PR}}$) were $\text{AU}{\text{C}}_{\text{ROC}}$ = 0.824, 0.789, and 0.790 and $\text{AU}{\text{C}}_{\text{PR}}$ = 0.641, 0.650, and 0.608 for NHP 1, NHP 2, and the combined case, respectively.

Fig. 6.

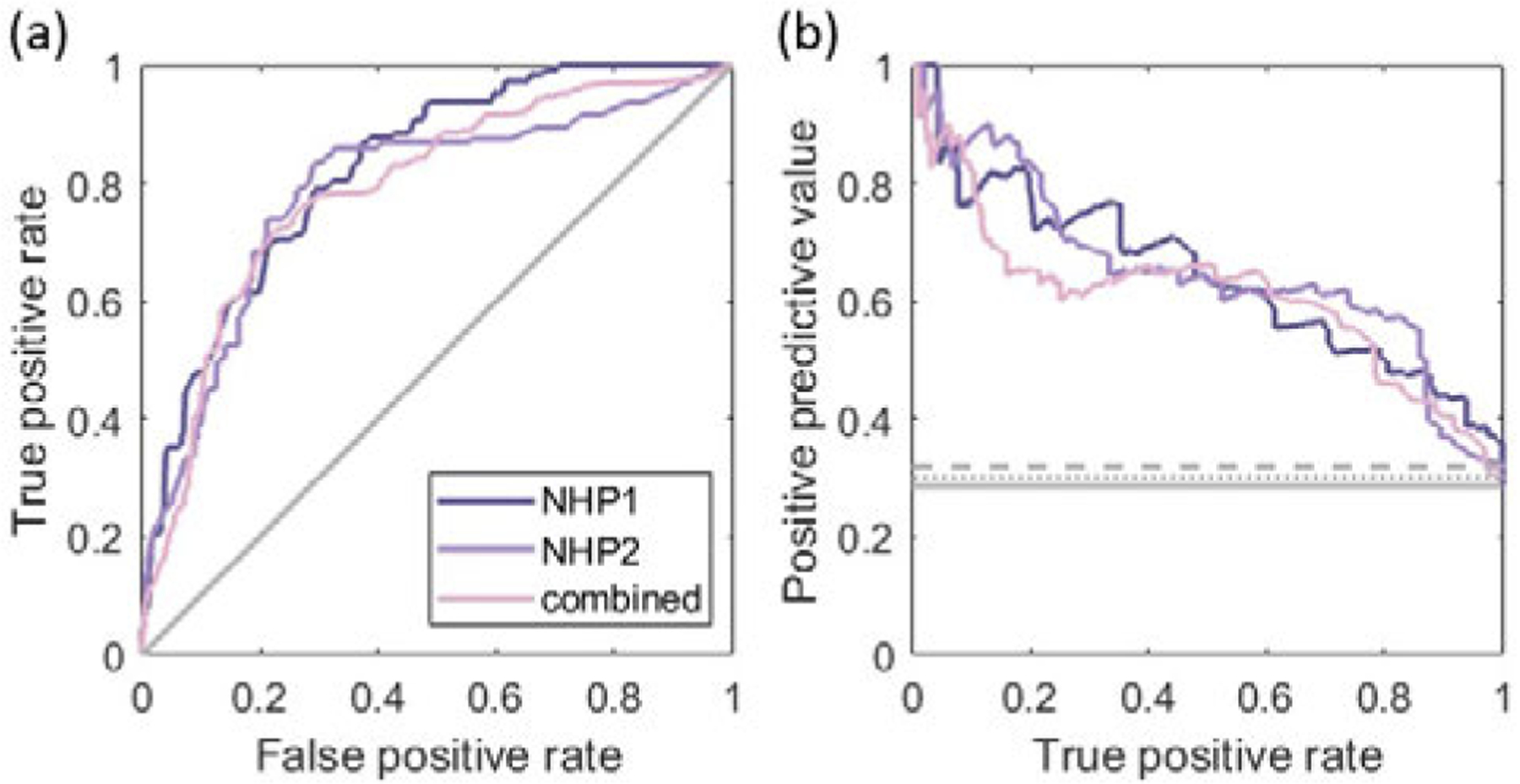
(a) ROC curves and (b) PR curves for pixel-wise binary classification of BBB opening with the PAM intensity based on NHP 1, NHP 2, and combined data sets. The solid gray line represents the ROC curve with a random classifier in (a). PR curves with a random classifier are presented by the solid (NHP 1), dashed (NHP 2), and dotted (combined) gray lines in (b).

VI. Discussion

A. Real-time Implementation of PAM with an enhanced resolution

We developed a parallel processing scheme of CF-PAM for the online monitoring with a better spatial resolution than that of the conventional PAM. Its performance was evaluated and compared with ERCB- and TEA-PAM in terms of the processing speed, the size of PSF, and the resolvability of two adjacent sources.

Compared with TEA-PAM, CF-PAM required a marginal overload for computing the CF as a weighting factor for each spatio-temporal pixel (Fig. 2) while it provided a smaller PSF and a better resolution (Fig. 3). Although ERCB-PAM also yielded a smaller size of PSF and better resolution compared to TEA-PAM, the source separation capability of CF-PAM was better than that of ERCB-PAM (Table I). Compared to ERCB-PAM, CF-PAM was more stable and computationally-efficient without need of parameter optimization.

As well as CF-PAM, TEA and ERCB were also implemented on GPU. While TEA-PAM was fully implemented on GPU, ERCB-PAM was realized by a hybrid approach using multi-core CPU and GPU. In ERCB-PAM [31], the weighting factors were obtained from eigenvalue decomposition for every pixel. When a large number of decompositions are required, multi-core CPU implementation can be more efficient than the GPU implementation because a CPU core is more powerful than a GPU core for such a complex computation [44]. Therefore, the data-adaptive weighting factors were computed using multi-core CPU and other processing steps including covariance matrix calculation and beamforming were parallelized on GPU. In spite of the hybrid approach, the computational complexity of the ERCB-PAM was too high to be completed within a few seconds. A recent study reported the real-time realization of RCB-PAM, which is similar to ERCB-PAM without eigenvalue decomposition, by using frequency-domain beamforming [45].

The proposed parallel processing scheme for PAM exploits a massive number of GPU cores by assigning each spatial-temporal pixel computation to each thread. Compared to our previous GPU realization [38]), the main difference of the proposed scheme herein is on-the-fly calculation of the time delay. Since the same delay values ${\tau }_i(\mathbf{x})$ are used for a spatial location $\mathbf{x}$ across all the temporal points $t$ (see (2) and (3)), the delay calculation for every temporal pixel can be considered redundant. For this reason, the pre-calculated delay lookup tables had been used, and the sparse matrix computation method was developed for processing speed acceleration [38]. However, we found that, the on-the-fly approach was faster than the lookup table approach due to the slow global memory speed of the GPU. Although we also tried to optimize the lookup table approach by using the shared memory which is smaller but faster than the global memory, the overall processing speed was slower than that of the on-the-fly approach because the shared memory is allocated per thread block and the number of threads per block is limited. In addition, the assignment of the thread block along the temporal domain was more efficient than along the spatial domain. This was because of the summation across the temporal pixels afterward.

Although the real-time realization of full-burst CF-PAM with the neuronavigation-guided FUS system was presented for the first time herein, prior studies have been reported on GPU-based full-burst PAM with different FUS setups [17], [20], [21], [30]. Processing time comparison with realizations in other studies can be found in the Supplementary document (Section 7).

B. In Vitro Human Skull Experiments

We tested the CF-PAM and compared with other methods using a human skull fragment. Although we conducted in vivo transcranial NHP experiments, we investigated the human skull effect as well to examine the feasibility of the PAM with a 2.5 MHz imaging transducer through the human skull which is much thicker than the skull of rhesus macaque. The thickness of the human skull fragment used in the experiment was 5.5–8.5 mm whereas the NHP skull thickness was 1–3 mm.

In ERCB-PAM (Fig. 4(b)), the optimization parameters ($\epsilon \hspace{0.17em}=\hspace{0.17em}50$,$\delta \hspace{0.17em}=\hspace{0.17em}0.2$) were chosen more conservatively compared to those for simulation study ($\epsilon \hspace{0.17em}=\hspace{0.17em}1$,$\delta \hspace{0.17em}=\hspace{0.17em}0.5$) because the received cavitation signal through skull was more noisy and aberrated. Although the smaller $\epsilon$ and the larger $\delta$ provided a better spatial resolution, the adverse influence caused distortions and artifacts in the map if the values are too small or too large, as described in [31]. For example, the success rate of cavitation activity localization reduced from 0.39 to 0.17 when the $\epsilon$ decreased from 50 to 30. On the contrary, CF-PAM (Fig. 4(c)) showed more stable cavitation maps with the enhanced spatial resolution and did not require the parameter optimization.

Although a full skull cap was not used in the experiment, the skull fragment was large enough to cover the incident focused beam; the fragment size was $\text{33}\hspace{0.17em}\text{mm}\hspace{0.17em}\times \hspace{0.17em}\text{40}\hspace{0.17em}\text{mm}$ and the distance from the skull to the focus was 30 mm with the F-number of 1.0. In addition, all the paths from the focus to the array elements (aperture size: 20 mm) were crossing the skull fragment to transcranially receive the acoustic emissions from microbubbles.

C. In Vivo NHP Experiments

We performed BBB opening with real-time cavitation monitoring in NHPs. The large FUS focus included the right occipital lobe and cerebellum for NHP 1 Higher cavitation energy was detected from the deeper region ($\text{z}\hspace{0.17em}\text{=}\hspace{0.17em}\text{80}\hspace{0.17em}\text{–}\hspace{0.17em}\text{100}\hspace{0.17em}\text{mm}$) than the near-depth region in the cumulative cavitation map (Fig. 5(b)), which agrees with the fact that BBB was opened mainly in the cerebellum ($\text{z}\hspace{0.17em}\text{=}\hspace{0.17em}\text{85}\hspace{0.17em}\text{–}\hspace{0.17em}\text{100}\hspace{0.17em}\text{mm}$) as shown in Fig. 5(c). For NHP 2, the focus was placed at the right putamen and hippocampus region in the frontal lobe. Within the focus, more cavitation energy was observed at shallow depths (Fig. 5 (e)), which is consistent with the BBB opening region found in the MRI (Fig. 5 (f)). Although the cumulative cavitation map (Fig. 5 (e)) showed the stronger cavitation energy at near depths ($\text{z}\hspace{0.17em}\text{=}\hspace{0.17em}70\hspace{0.17em}\text{–}\hspace{0.17em}9\text{0}\hspace{0.17em}\text{mm}$), the BBB opening region ranged from 80 mm to 100 mm at focus (Fig. 5 (f)). The distance between the peak location of the PAM and the centroid of BBB opening was larger in NHP 2 than NHP 1. This is possibly due to the skull and meninges included within the focus. The complex layers and sinus in conjunction with the high acoustic impedance difference between the skull and the surrounding tissues might have created reverberations of ultrasound waves and strong cavitation activities at the near-skull region.

We showed the ROC and PR analysis of the PAM intensity (i.e., cavitation acoustic energy) for pixel-wise binary classification of BBB opening in two NHPs (Fig. 6). Although we additionally analyzed the correlation using frequency-selective cavitation maps reconstructed, the AUC value was not found to increase (Fig. S3). The AUC values in our study ($\text{AU}{\text{C}}_{\text{ROC}}\hspace{0.17em}=\hspace{0.17em}0.790$ and $\text{AU}{\text{C}}_{\text{PR}}\hspace{0.17em}=\hspace{0.17em}0.641$) were acceptable but comparatively lower than those of other studies that linked the cavitation map with tissue damage in non-thermal brain ablation ($\text{AU}{\text{C}}_{\text{ROC}}\hspace{0.17em}=\hspace{0.17em}0.99\pm 0.01$ and $\text{AU}{\text{C}}_{\text{PR}}\hspace{0.17em}=\hspace{0.17em}0.77\pm 0.07$) [20] or histotripsy ($\text{AU}{\text{C}}_{\text{ROC}}\hspace{0.17em}=\hspace{0.17em}0.934$) [46]. In addition, the PAM–MRI distance for BBB opening in our study (3.3 or 12.1 mm) was larger than the PAM–MRI distance for tissue damage ($0.9\pm 0.6\hspace{0.17em}\text{mm}$) in the brain ablation study [20]. This may be due to the underlying mechanisms, as the FUS-induced change in BBB permeability without tissue damage can involve the increase in various transport mechanisms (e.g., transcellular, paracellular, etc.) [47], [48], while tissue liquefaction or hemorrhage is more likely associated with more destructive mechanical effects of cavitation. Moreover, different transducers and experimental setups across the studies make the direct comparison difficult.

One of the factors that might limit the predictive capability of PAM intensity for BBB opening in our study is that the cavitation threshold for BBB disruption varies across different brain tissues and vessel types. For example, the capillaries are more susceptible to disruption than the bigger vessels which have more endothelial cell layers than capillaries [49] and BBB characteristics vary in different segments of the vessels [50]. The heterogeneity of vessel size and density distribution in brain tissues may induce the different cavitation thresholds for BBB opening across the different brain tissues. Several studies also showed a higher probability of BBB opening in the gray matter than in the white matter [13], [51], [52]. This spatially-variant cavitation threshold might have reduced the correlation between the cavitation energy and the BBB opening distributions. Another factor is the long axial length of the PSF mainly due to the small aperture. The long tail of the PSF of PAM may have contributed to the false positives of the classification. Localization of cavitation [53], [54] or spatial-peak filtering [20] could be used in the future for a better pixel-wise prediction for BBB opening. In addition, the BBB opening volume identified by the contrast-enhanced MR signal includes the diffusion of the contrast agent into the surrounding brain parenchyma after crossing the BBB. As a result, when localizing the cavitation maps to the area of MR contrast enhancement, there may be an increase in the false negative rate of the prediction. In this regard, further studies using the transfer rate ${\text{K}}_{\text{trans}}$ mapping with dynamic contrast-enhanced MRI are warranted [55]. Finally, the MR-ultrasound registration and the phase aberration errors in cavitation mapping might have affected the low correlation between BBB opening and the cavitation map.

In this study, the cavitation dose was calculated by the sum of the array element channel data. However, if the cavitation dose is measured based on the delay-and-summed (i.e., beamformed) data, it would provide more spatially relevant dose information. For example, the spatio-temporal beamformed signal ($A_j(\mathbf{x},t)$) obtained from (2) without the absolute square operation can be used for spectral analysis and dose measurement. A temporal signal can be obtained by spatially integrating $A_j(\mathbf{x},t)$ over the focal area or using the maximum PAM intensity pixel (i.e., $\text{argmax}({\Psi }_j(\mathbf{x}))$) for the given burst $j$ [17].

D. Advantages of the portable FUS system with a co-axial array transducer

The frameless and portable clinical FUS system reduced the complexity of the BBB opening treatment procedure compared to the MR-guided FUS system. As demonstrated in previous studies [13], this portable FUS system is capable of successful BBB opening with neuronavigation-guided targeting and cavitation signal monitoring. This system, however, did not provide spatially-resolved safety monitoring as in MR-guided systems which have thermal imaging. In [9], although an imaging array was used for cavitation mapping, aligning the PAM imaging plane with the FUS focal volume was challenging and not easily translatable to the clinic. Therefore, in this study, we fixed a diagnostic linear array transducer co-axially with the FUS beam for stable alignment.

In addition, the B-mode image obtained by the array can be used for targeting in conjunction with the neuronavigation system since the array was co-aligned with the FUS transducer. The experimentally measured registration error was 5.6±3.6 mm when using the neuronavigation system with the dental imprint platform. B-mode images that show the skin and skull contours, as shown in Figs. 5(b) and (e), were used to reduce the registration errors from the neuronavigation system. After the registration based on the neuronavigation system, the manual fine registration was performed by matching anatomical positions of the B-mode image and the MRI as indicated by asterisks in Figs. 5(b), (c), (e) and (f).

E. Skull-Induced Acoustic Aberration Effect

Due to the complex inner structure and high sound speed of the skull, the received acoustic signals through the skull are distorted and become incoherent across the channels [56]. To compensate for the delay errors in beamforming, phase aberration correction can be performed by using experimentally-measured delay shifts [18] or CT-based phase aberration correction [57], [58]. In our FUS system setup, the incident angle or the time delay shift might not vary substantially across the 64 channels because the array transducer has only a 20-mm aperture size. However, it is still worth investigating the effect of the aberration correction in the future because the frequency band of the acoustic emissions used for PAM (1–3 MHz) was relatively high.

From a computational point of view, if the simulation-based or experiment-based correction factors are employed for the phase aberration correction [18], [59], the use of a large lookup table is unavoidable to compensate for the delay errors of the individual channel and imaging pixel. In this case, the size of the lookup table will be $N_E\hspace{0.17em}\times \hspace{0.17em}{N}_x\hspace{0.17em}\times \hspace{0.17em}{N}_z$, which can slow down the overall computation speed. On the other hand, if the effective sound speed [58] is used for obtaining the correction factor, it could be calculated and used for compensation on the fly with minimal additional computation. Moreover, if a constant compensation factor can be used within a small region of interest [57], [60], instead of using pixel-specific compensation, the computational complexity increase would be marginal. As a frequency-domain beamformer, heterogenous angular spectrum method can be a suitable option for the real-time phase aberration correction [61].

F. Limitations of This Study

In this paper, we only investigated the time-domain beamformers. However, frequency-domain beamformers can be effectively used for frequency-selective cavitation map reconstruction [62]. The frequency-selective maps can provide more in-depth information for treatment monitoring as the harmonic, ultraharmonic, and broadband signal represent different types of microbubble activity. Especially, frequency-domain beamforming can be faster than time-domain beamforming if a limited number of frequency components are used [45], [63], [64]. The angular spectrum method can also be used for accelerating the computational speed [65] and even for compensating the skull-induced aberration [66].

We aimed to enhance the spatial resolution of PAM by incorporating CF and we demonstrated that CF-PAM provides a smaller size of PSF and better source separation capability (Fig. 3). However, improvement in the spatial prediction of BBB opening in NHP was marginal according to the ROC analysis with different PAM algorithms (Fig. S4); $\text{AU}{\text{C}}_{\text{ROC}}$ and $\text{AU}{\text{C}}_{\text{PR}}$ were increased by 1.5% and 3.4% when using CF or ERBC, respectively. This means that both CF-PAM and ERCB-PAM marginally enhanced the correlation between the cavitation map and the bioeffect distribution compared to TEA-PAM, albeit with better PSFs and source separation capability. The minimal improvement might be due to the low spatial resolutions in our experimental setup, regardless of the method used. Despite the smaller PSF, the CF-PAM and ERCB-PAM were still insufficient to distinguish between multiple cavitation sources within the FUS focus while the opening region was heterogeneously distributed within the focus. Additionally, it could be due to the intrinsic limitation of cavitation intensity map for predicting BBB opening.

The resolvable distance between two cavitation sources was much greater in the axial direction than in the lateral direction (Fig. 3). This is because the axial resolution is more affected by the F-number, the ratio of the imaging depth to the aperture size, than the lateral resolution; the theoretical axial PSF length of the PAM is proportional to the squared F-number while the lateral width of PSF is proportional to the F-number [67]. Moreover, low-frequency cavitation signals due to the skull attenuation limited spatial resolution. To overcome these physical limitations, further development of PAM method for enhanced axial resolution should be made, for example, employing a coded FUS signal [68], localizing the acoustic emission by using deconvolution [53] or aperture-domain signal [54], or applying a spatial filter that selects only the spatial-peak pixel [20].

The measured cavitation intensities by TEA-PAM can be converted into the pressure values with physical units to estimate the incident acoustic pressure over the array surface by using the system-dependent calibration factors [63]. This conversion would allow a quantitative comparison of the cavitation dose across different setups or laboratories. Although multiplying the beamformed signal by the CF is not a linear operation, the CF itself is unitless and gives a normalized value from 0 to 1. Consequently, it should not affect the units of the cavitation map theoretically. However, CF is always less than 1 unless all the signals have the same phase/amplitude across the channels, which leads to the cavitation maps with lower intensities overall compared to TEA-PAM. For example, the maximum intensity of TEA-PAM and CF-PAM in Fig. 4 was $1.8\hspace{0.17em}\times {10}^3$ V² and $0.8\hspace{0.17em}\times {10}^3$ V², respectively. Therefore, additional efforts might be required to interpret the intensity of the CF-based cavitation maps for the generalized absolute quantity.

As we used a linear array transducer, two-dimensional PAM was obtained and the out-of-plane acoustic emissions were not detected. Future studies will employ a matrix array transducer that can produce a 3-D volume of cavitation activity for safety monitoring.

VII. Conclusion

We first showed the real-time passive cavitation mapping in the neuronavigation-guided FUS system by using an imaging phased array which is co-axially aligned with the FUS transducer. By comparison studies, CF-PAM was proved to provide higher spatial resolution than TEA-PAM and more robust cavitation mapping than ERCB-PAM when the skull was introduced as an acoustic aberrator. In addition, a parallel processing scheme of CF-PAM was proposed in this paper to enable the real-time cavitation mapping (a PRF of 2 Hz) with the full-burst analysis (0.23 s for 5,000 imaging pixels and 100,000 temporal samples). We also performed transcranial cavitation mapping for in vivo BBB opening in NHPs. The cavitation map showed intermittent acoustic activity outside the focal region but most of the energy was detected near the focus. The cavitation map was spatially correlated with BBB opening region confirmed by contrast-enhanced MRI. This study demonstrates the feasibility of real-time acoustic mapping in BBB opening with a portable FUS system for safe and efficient treatment.