Abstract
Infrared (IR) spectroscopic imaging instruments’ performance can be characterized and optimized by an analysis of their limit of detection (LOD). Here we report a systematic analysis of the LOD for Fourier transform IR (FT-IR) and discrete frequency IR (DFIR) imaging spectrometers. In addition to traditional measurements of sample and blank data, we propose a decision theory perspective to pose the determination of LOD as a binary classification problem under different assumptions of noise uniformity and correlation. We also examine three spectral analysis approaches, namely, absorbance at a single frequency, average of absorbance over selected frequencies and total spectral distance – to suit instruments that acquire discrete or contiguous spectral bandwidths. The analysis is validated by refining the fabrication of a bovine serum albumin protein microarray to provide eight uniform spots from ~2.8 nL of solution for each concentration over a wide range (0.05–10 mg/mL). Using scanning parameters that are typical for each instrument, we estimate a LOD of 0.16 mg/mL and 0.12 mg/mL for widefield and line scanning FT-IR imaging systems, respectively, using the spectral distance approach, and 0.22 mg/mL and 0.15 mg/mL using an optimal set of discrete frequencies. As expected, averaging and the use of post-processing techniques such as minimum noise fraction transformation results in LODs as low as ~0.075 mg/mL that correspond to a spotted protein mass of ~112fg/pixel. We emphasize that these measurements were conducted at typical imaging parameters for each instrument and can be improved using the usual trading rules of IR spectroscopy. This systematic analysis and methodology for determining the LOD can allow for quantitative measures of confidence in imaging an analyte’s concentration and a basis for further improving IR imaging technology.
Keywords: Limit of detection, LOD, chemical imaging, Fourier transform-infrared spectroscopy, FT-IR, binary hypothesis testing, discrete frequency infrared, noise
Introduction
The limit of detection (LOD) is of interest for most analytical measurements. LOD, typically referring to the lowest concentration of a species that can be detected by an instrument in a typical measurement, combines the ideas of sensitivity, resolution and confidence in results.1–4 Formally, the International Organization for Standardization (ISO)5,6 and International Union of Pure and Applied Chemistry (IUPAC) define the LOD as the smallest concentration that can be detected with a specified significance level for the analytical procedure7,8 and can be expressed as
| (1) |
where is the smallest detectable concentration of the analyte, is the mean value of the blank measures and is the standard deviation of the blank measure. is typically estimated from a measured signal, , using a calibration function. Since the absorbance measured in infrared (IR) spectroscopy is linearly related to concentration , the relationship between these quantities is straightforward and the LOD can be estimated from absorption spectra. While blank sample measurements can be used to estimate the detection limit,9–11 with equal to 2 or 3, this practice does not shed light on the confidence in results from a statistical perspective. To combine the concerns of accuracy and confidence, distinguishing the blank measure from the lowest detectable value can be framed as a hypothesis testing problem wherein a measured value is a binary classification problem between detected species and blank. This approach explicitly accounts for both type I and type II () errors. Commonly used factors for , for example, are 3.0 and 3.3 for a presumed type I error of 1.3% and 0.5%, respectively. While this approach is widely applicable and easy to deploy, the underlying assumptions of Gaussian distributions of measured values and the use of linear calibration curves must be carefully validated. In response to possible violations of these conditions, nonparametric approaches have investigated the effects of asymmetric, non-Gaussian blank distributions and nonlinear calibration curves for determining LODs.12 Here, we use both the measured concentration-signal curves as well as a statistical approach to understand the LOD for infrared (IR) imaging spectrometers.
While the detection limits of Fourier transform IR (FT-IR) spectrometers are well known,17–19 recent developments in quantum cascade laser (QCL)-based IR spectroscopy and spectroscopic imaging techniques have led to a renewed interest in detection limits for this new generation of instruments. Emerging bulk spectrometer designs can detect concentrations of proteins as low as 0.0025 mg/mL20 and new records for detection limits are being established by the use of hardware enhancements such as balanced detection20,21 with parts per billion (pbb) level detection of gases.22,23 This progress also bodes well for IR imaging, in which ultrasensitive measurements are made even more challenging due to the signal being recorded from significantly smaller volumes of materials with low light throughput while requiring the use of additional optics and specialized detectors. IR imaging technology has expanded and diversified considerably in recent years with improvements in FT-IR imaging,24–26 new designs to take advantage of synchrotron sources,27–31 surface-enhanced measurements utilizing plasmonic nanorod antennas,32,33 QCL-based imaging instruments,34–43 polarimetric imaging44–48 and the emergence of hybrid techniques such as atomic force microscopy-IR imaging,49,50 and photothermal microscopy.51–61 Since many of these techniques are rapidly developing and their capabilities may not all be geared towards the chemical limit of detection, we focus this study largely on well-established FT-IR and QCL microscopes. These instruments still comprise a majority of those in use and provide representative examples of incoherent and coherent sources for new technologies to compare performance and improve upon. The two classes of instruments also have another important difference, while FT-IR spectrometers measure a continuous spectral bandwidth, discrete frequency IR (DFIR) systems measure specific spectral data points. Given the trade-off between measurement time and signal to noise ratio (S/N), this difference raises important questions. Several attempts have been made to define IR imaging performance. For instance, a detailed theoretical and experimental investigation of LOD in attenuated total reflection sampling focused on pharmaceutical powder mixtures.62 Other studies have focused on the potential of IR imaging for high throughput secondary structure analysis of proteins,63,64 the analysis of small extracted volumes,65 and on related measurements such as S/N, the discussions of which are plentiful.66
Although this extensive body of work relates to the LOD, there is not yet a report on systematically evaluating and optimizing spectral analysis. We address this gap by developing and applying measures for pixel-wise LOD in IR spectroscopic imaging while examining underlying assumptions of data distribution. Aiding characterization, we also evaluate the possibility of using a decision theoretic approach for the LOD as a special case of a classical binary classification problem, given a measurement spanning multiple discrete wavenumbers, we evaluate a statistically viable methodology that can be used to separate between two spectrally different objects. Finally, experiments are reported to relate theoretical predictions to measurements using engineered micro-arrays of bovine serum albumin (BSA).
Formulation of LOD as a Binary Classification Problem
For LOD determination, an average analyte concentration, , is typically estimated from an average measured signal, . Optimization of the measurement and analysis process to achieve the lowest concentration as a LOD then involves maximizing the separation between a signal and a blank . As a binary classification problem,67 the separation parameter, , is a quantitative measure of the ability to separate these classes as
| (2) |
where is the standard deviation in the measurements. In IR spectroscopy, this signal is the measured absorption spectrum that directly relates to concentration via the Beer-Lambert law. Consider the corresponding noise-free spectra and where for are the spectral positions where data are sampled. Then, and are the recorded absorbance, where is the corresponding spectral standard deviations. Note that the ability to separate the two signals is dependent on both maximizing the signal and controlling or reducing noise in spectral analyses. Here, we consider three approaches, namely, using a single wavenumber absorbance, an average absorbance of specified discrete wavenumbers (which may not be contiguous), and a spectral distance to derive and . To generalize the analysis, we will consider the impact of correlated and uncorrelated noise for each of these cases to define . A summary of the analysis approaches and corresponding selection algorithms is provided in Table I and each case is briefly discussed next.
Table I.
Overview of the different approaches and selection algorithms for the evaluation of LOD.
| Approach | Mathematical formulation for | Selection algorithm | Description |
|---|---|---|---|
| Single wavenumber absorbance, SWA | Highest absorbance, SWAH | Selects wavenumber of the highest absorbance. | |
| Best S/N, SWAB | Selects wavenumber that yields the highest S/N value. | ||
| Discrete wavenumber average absorbance, DWA | Highest absorbance, DWAH | Cumulatively adds the absorbance at discrete spectral positions, ordered by decreasing absorbance, to maximize signal. | |
| Best improvement in S/N, DWAB | Adds signal at discrete wavenumbers that yield the maximum improvement of . For uncorrelated, uniform noise, the case of DWAH is recovered. | ||
| Spectral distance analysis, SDA | Full available spectral range, SDA | Using the full recorded spectrum for calculation of spectral distance. |
Single Wavenumber Absorbance (SWA).
It can be shown that is optimized by picking the spectral position, , where the analyte absorption is highest. The optimal separation parameter, , is defined by
| (3) |
Discrete Wavenumber Average Absorbance (DWA).
A wider range of spectral information can be utilized by adding the signal at each spectral position. For uniform and uncorrelated noise, an optimized is then defined as
| (4) |
where denotes the spectral data optimized for the summation. For non-uniform and correlated noise, an optimal can be defined as
| (5) |
Spectral Distance (SDA).
In binary classification, a probabilistic approach compares the likelihood of a spectrum being either part of the sample or the blank. The likelihood of a spectrum being part of the first class is and the likelihood for the second class is . Using a log likelihood ratio approach, this results in the Euclidean spectral distance between blank and sample spectra. For uniform and uncorrelated noise is optimized by
| (6) |
For non-uniform and correlated noise, the Mahalanobis distance formulation provides an equivalent expression68
| (7) |
where denotes the corresponding covariance matrix. The SDA is equivalent to a two class linear discriminant analysis (LDA) approach when the prior probabilities for the sample and blank are equal, with underlying multidimensional normal distributions and , respectively. Two class LDA is known to perform a subspace projection that maximizes class separability, and thus, minimizes the LOD.
Implementation of Selection Algorithms.
For both SWA and DWA, an optimal subset of spectral positions is determined. We propose two greedy algorithms – the first is the simpler one, selecting the spectral positions of highest absorbance from the ranked list. The second is a best improvement selection (Algorithm I, Supplemental Material), which sequentially selects those spectral positions that maximize separation quality. These are indicated in Table I with the subscripts and , respectively. For each of these cases, we consider noise uniformity across the spectral region and correlations in noise magnitude. Under some circumstances, e.g., uniform, uncorrelated noise, the results of SWA for both cases are the same. For the spectral distance approach, we consider the available spectra without qualification.
Methods
Sample Preparation
Bovine serum albumin, a protein with dominant -helix structure and a well-known IR absorption spectrum, was selected as a representative biomolecule. We fabricated a BSA microarray, to facilitate high throughput and consistent sampling, using a picoliter dispensing system.69,70 This platform allows for nanoprinting of highly consistent spot sizes; however, proteins such as BSA exhibit different solubilities and hydrophilicities under different environments, and careful attention to conditions is required for nanoplotting. We tested a range of combinations of deionized water and ethylene glycol and selected a 50–50% mixture as best for optimized spot sizes. BSA (Sigma-Aldrich) was dissolved in this mixture at concentrations of 10, 5, 2, 1, 0.5, 0.2, 0.1, and 0.05 mg/mL. Microarrays were fabricated using Nanoplotter 2001 (Gesim) with a Nano-Tip A-J pipette head (Gesim) that is designed to plot volumes of ~250 pL using piezoelectric pipetting tips that can dispense an accurate volume of a sample solution by applying a predefined voltage. Optimizing parameters, a pulse width of 90 μs and piezo voltage of 105 V was selected. Solutions were prepared immediately before plotting and the spots were plotted in an array with a spatial separation of 704 μm to allow imaging of one BSA spot per frame in our widefield FT-IR imaging instrument. Eight replicate spots for each concentration, each with a volume of ~2.8 nL, were plotted on a clean 25 mm diameter, 2 mm-thick BaF2 substrate (Spectral Systems). For estimation of the actual dispensed volumes, an integrated stroboscope camera-based image recognition software was used. The microarrays were dried under nitrogen until all the liquid evaporated; subsequently, they were kept in a desiccator under vacuum for another 30 min to remove residual ethylene glycol. Taken altogether, our sample preparation procedure allows for the fabrication of a microarray with fairly homogeneous within-spot concentration and minimal coffee-ring effects.
IR Imaging and Data Analysis
The microarrays were imaged with a Cary 620 microscope integrated with a Cary 670 spectrometer (Agilent Technologies). Imaging was performed in a transmission configuration with a 15× objective in standard magnification mode using a liquid nitrogen-cooled 128 × 128 pixels array mercury–cadmium–telluride (MCT) detector with 5.5 μm pixel. Spectral images were acquired in a single frame with spatial size of 704 μm × 704 μm. Spectra were acquired using an undersampling ratio of 4 and a nominal spectral resolution of 8 cm−1 using 64 coadditions. The data were truncated to the detector response region for analysis. A mosaic image of the BSA microarray comprises 8 × 8 frames. For the background, an empty area next to the array was measured using the same spectrometer parameters but with 128 coadditions. We also imaged the microarray using a commercial FT-IR imaging system, Perkin Elmer Spotlight 400 (Perkin Elmer) equipped with a highly sensitive linear MCT detector array. Images were acquired in transmission mode with a nominal spectral resolution of 8 cm−1 and with 8/64 co-additions for 6.25, 25, and 50 μm pixel sizes at line scan of 1 cm/s. A blank area was used for background measurement with 120 scans. Perkin Elmer’s inbuilt atmospheric correction algorithm was utilized to eliminate any interference effects from CO2 and H2O vapor. We also imaged the microarray using a custom-built scanning DFIR imaging system that has been previously described.43,44 Measurements in transmission configuration are enabled by using 0.85/0.71 NA and 12.7 mm EFL lens, and focusing the signal onto a cryogenic single-element MCT detector (MCT-13–0.5PV, InfraRed Associates).
Data evaluation was performed in Python 3.8.5 with functionalities of the Spectral Python package and other custom procedures. A preprocessing step was performed to subtract water vapor absorbance. Next, to reduce noise (and maximize S/N), the images were processed using minimum noise fraction (MNF)71 built in Environment for Visualizing Images Interactive Data Language (ENVI-IDL) as applied previously to IR imaging. The noise characteristics for MNF were estimated using seven empty frames that were imaged (another was used for the frame-wise subtraction and therefore contains no information anymore). The inverse transform was performed using only the first four MNF components, which sums up to 90% of the total sum of the eigenvalues. Before the final evaluation, a linear baseline correction was performed. The same procedure was followed for another data set without MNF correction. After these post-processing steps, we plot the absorbance at 1646 cm−1), which allows visualization of the fabricated protein microarray and allows segmentation of protein and blank regions.
Results and Discussion
Proteins are an important analyte for biomedical IR spectroscopy and imaging. Their amide I and amide II vibrational modes provide strong measurable signals as well as rich information that is suited to our study. An image of the fabricated microarray, obtained by plotting the baseline-corrected absorbance of amide I mode for eight replicates of each concentration of BSA, is shown in Fig. 1a. The fabrication procedure provides for relatively uniform spots and a significant number of pixels from which statistical inferences may be drawn within and across replicates. The format also allows a rapid and straightforward visualization of detection capabilities. Mean sample spectra are shown in Fig. 1b, and used to create the calibration curves. Good spectral quality, with spectra that are relatively free of distortions due to scattering or other optical effects, can be obtained using the microarray. Normalization of the spectra to account for concentration-dependent effects reveals a shift in the amide I peak of approximately 2 cm−1 in lower concentration samples, with insignificant band shape changes. This is expected and likely arises due to decreased hydrogen bonding. While spectral distortion is negligible and not considered further, we do note that more complex mixtures and spatial-morphological variations may introduce significant changes in both band shapes and peak locations. Violin plots of the measurements (Fig. 1c) help in visualization of the variance within the samples and the distribution of the noise associated with measurements around zero. Differences in the distribution are likely from the cumulative effects of drying, concentration dependent evaporation and spreading of droplets. Before undertaking further analysis of this data, we develop our analysis using simulated data and noise models.
Figure 1.
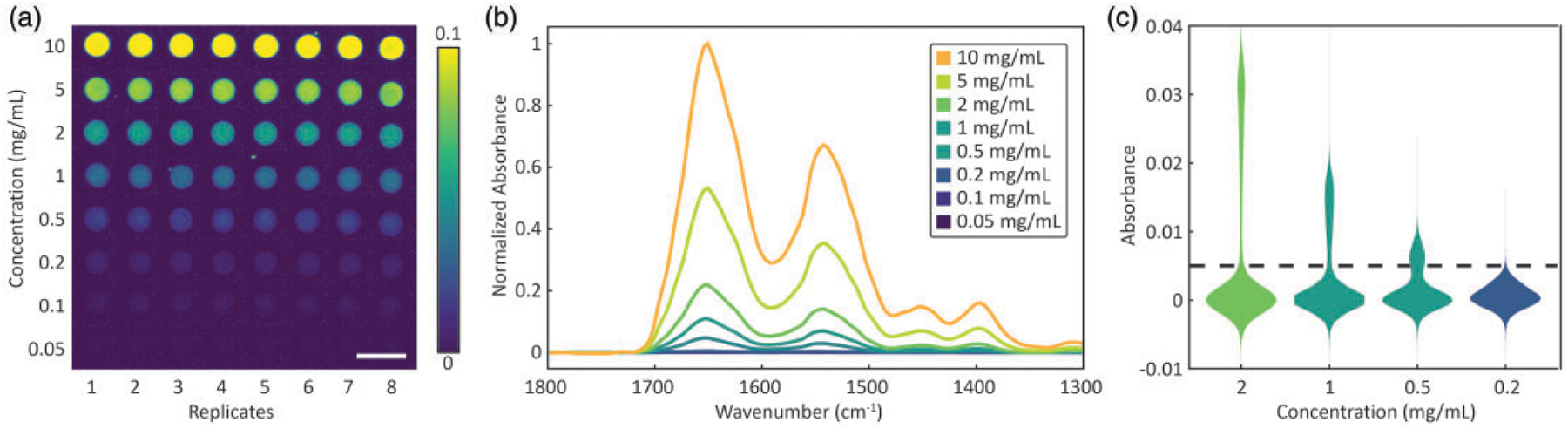
Characterization of the fabricated microarray. (a) Absorbance of the amide 1 (1646 cm−1 vibrational mode used to visualize BSA samples produced from solutions with concentrations from 0.05 to 10 mg/mL in a grid format. Each concentration has eight columns corresponding to eight replicates. Scale bar is 500 μm. (b) Fingerprint region absorption spectra show spectral variation with concentration while (c) violin plots show the underlying distribution of absorbance at 1646 cm−1 of all the pixels from frames with a specific concentration. The two distributions separated by the dashed line correspond to the sample (top) and the blank (bottom), respectively.
Estimation by Simulations
We use the best-fit parametric approximations of recorded data as estimates of and assess the influence of noise on our analysis. The preprocessed spectrum acquired from the 10 mg/mL BSA concentration spot was used for the approximation, as it offers the highest S/N and no significant deviations from other concentrations in band shape or normalized absorbance. Two different models for curve fitting are implemented. The first is the simplest possible model and uses two Gaussian bands, one for amide I and another one for amide II (Fig. 2a). The second model uses nine Gaussian bands to fit the amide I and amide II regions (Fig. 2b) with centers of the bands chosen to correspond to known secondary structures.72 The goodness of fit for each is quantified with a coefficient of determination, R2, showing a good fit with values of 0.989 and 0.999 for the two models, respectively. These different models were considered to simulate slight differences in the sample spectra that could arise from secondary structure changes or the described peak shift from hydrogen bonding effects. Note that our goal here is not to find the precise fit to the BSA spectrum but gauge the effects of various noise models on the LOD prediction.
Figure 2.
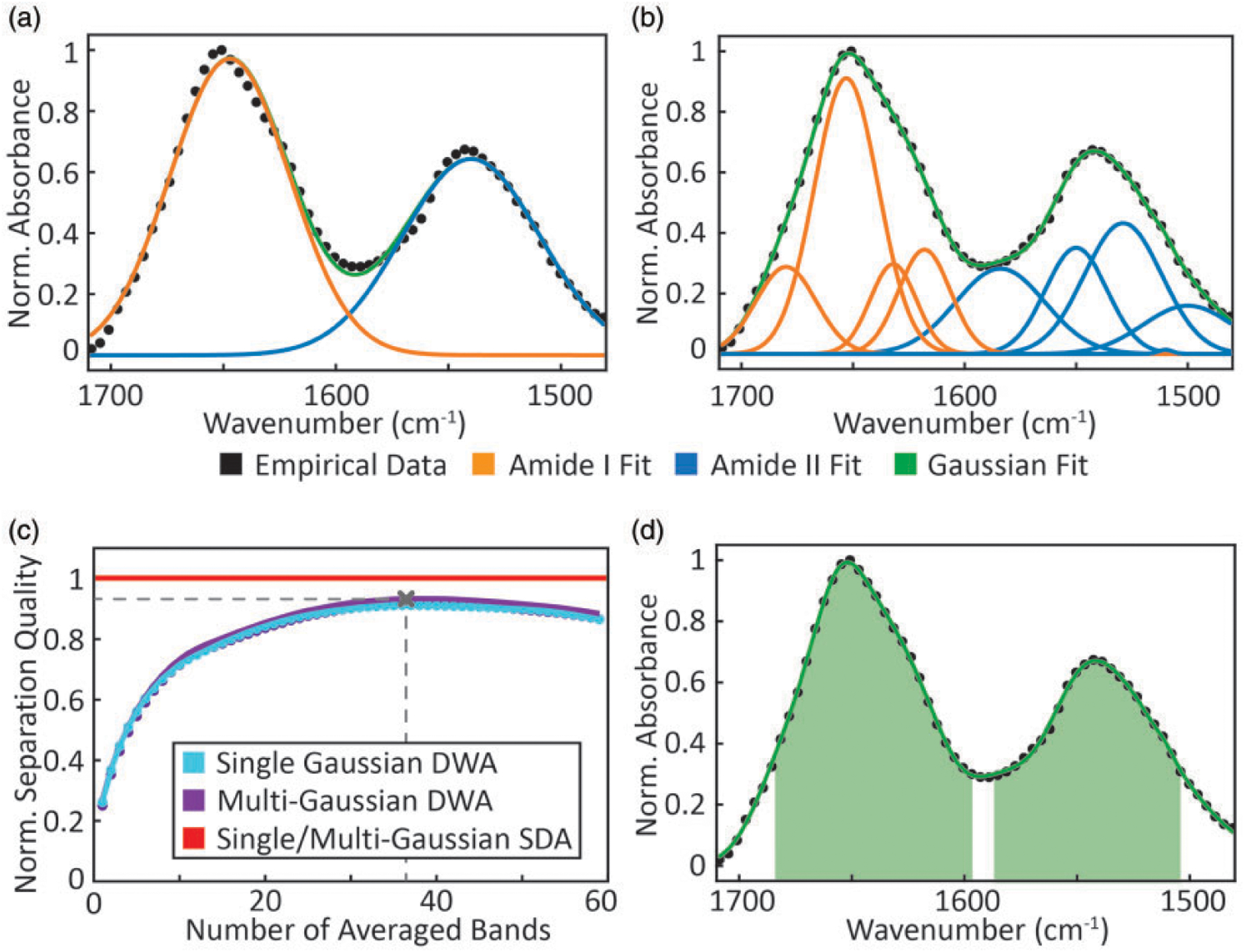
Gaussian fits using (a) a single curve each for amide I and amide II bands and (b) nine curves, with amide I fits shown in orange and amide II fits in blue, respectively. (c) Normalized separation quality with DWA for different spectral subsets: blue showing single Gaussian case, purple showing multiple-Gaussian case and red showing the SDA case in the 1470–1710 cm−1 region. The separation quality predicted by the SDA approach is so similar for both models that only one line is depicted. (d) Selection of discrete wavenumbers that yields the optimal separation quality using DWA.
Uniform and Uncorrelated Noise.
To evaluate the spectral analysis methods in LOD determination, we first consider uniform, uncorrelated noise. A comparison of the analyses is shown in Fig. 2c. Similar results are obtained using SDA and DWA. This similarity implies that minor changes in the band shape, for instance, arising from different secondary structures,73 hydrogen bonding,74,75 or optical effects in IR imaging,76,77 do not severely influence calculations, though it may complicate multicomponent analyses. To easily compare the relative performance of analyses, we normalize each assessment of separation quality to the value obtained using SDA. We observe that for SWA, the normalized separation quality is ~26%, whereas it is ~91% for DWA with the best subset of discrete spectral points. This is expected as the total signal of averaging uncorrelated measures of the same species increases with the cumulative absorbance whereas noise increases proportional to ; thus, the benefits of averaging a spectral bandwidth are realized until . This implies that the optimal averaging range is dependent on band shape and will need to be optimized for specific studies. Here, the optimal averaging subset consists of 37 spectral bands and can be visualized in Fig. 2d. Note that the separation quality is not highly dependent on small changes in the number of spectral bands but is a fairly strong cumulative effect. It is consistent with the expectation that larger bandwidths and higher resolution (for the same S/N) offer both statistical and interpretation advantages that come at a cost defined by the well-known trading rules in IR spectroscopy78 For non-uniform noise sources such as QCLs, the same approach can be used to optimize spectral averaging subsets for the specific case.
Non-Uniform and Correlated Noise.
The presence of non-uniform and correlated noise can be observed in data recorded with a fluctuating background (e.g., from water vapor), from apodization or zero-filling in time domain or from correlated detector responsivity. We model correlated noise by
| (8) |
where . is the uniform noise contribution and denotes the noise term due to water vapor. To compare recorded data to simulations, we set to . Under this assumption, the total noise does not remain constant over the entire spectral region, as shown in Fig. 3, and noise covariance can be calculated as
| (9) |
Figure 3.
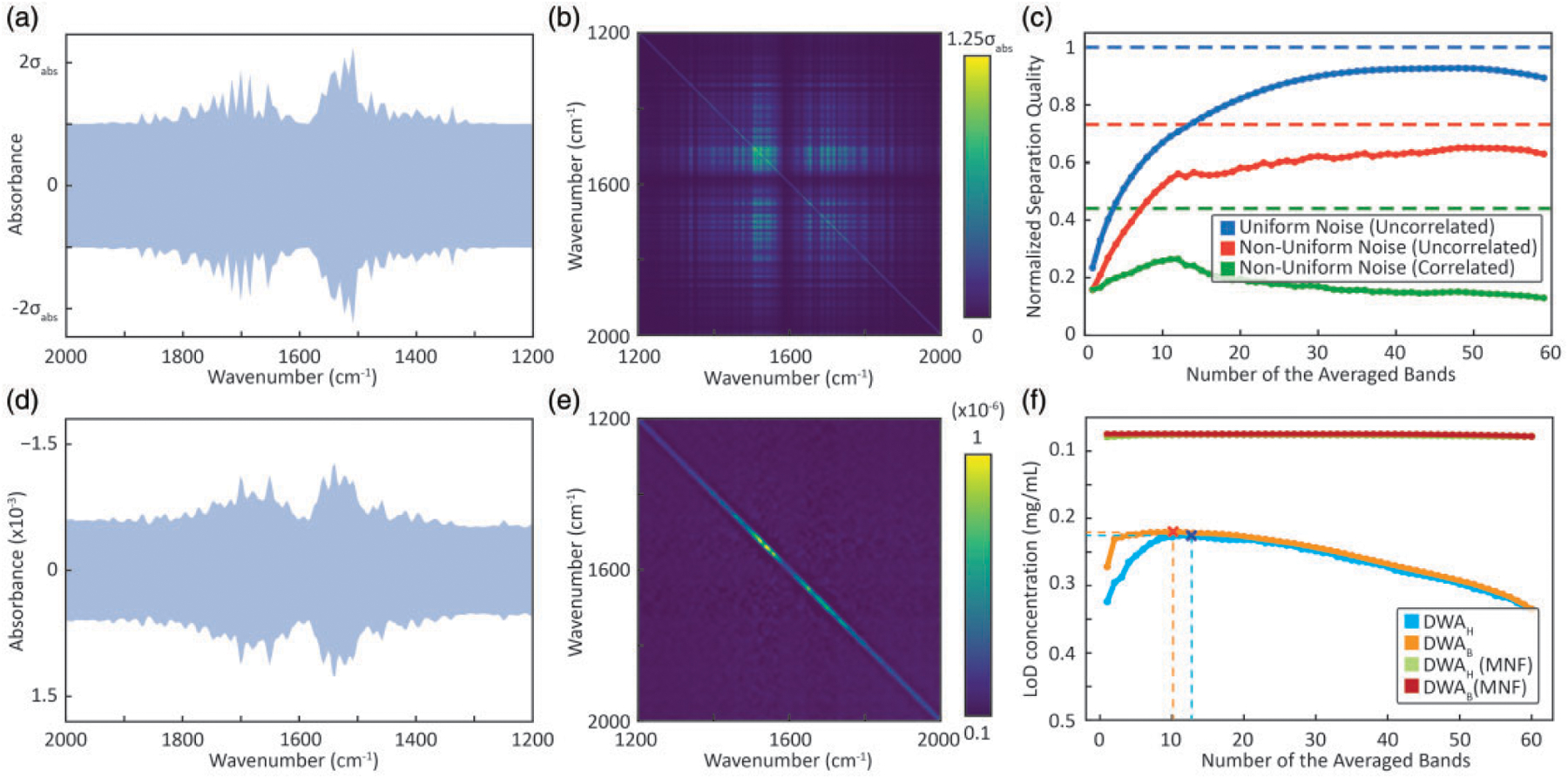
Comparison of simulation with observations. (a) Total simulated noise content in the IR spectra with contributions from non-uniform water vapor absorption and uniform spectral noise. (b) Corresponding estimated noise covariance matrix for the non-uniform and highly correlated spectral noise model. (c) Normalized separation quality for three different cases of simulated noise, namely, uniform (uncorrelated), non-uniform (uncorrelated) and non-uniform (correlated) is shown in bold lines (DWAH. SDA using the log likelihood ratio is shown in dashed lines for the respective cases. (d) Experimental data showing noise effects from water vapor absorption. (e) Noise covariance matrix showing weakly correlated spectral dependence. (f) Estimated LOD concentration plots for two different wavenumber selection methodologies, i.e., highest absorbance (SWAH, DWAH) and best improvement selection (SWAB, DWAB), before and after performing MNF correction on the data. The optimal subset of wavenumbers are marked for both the cases before MNF correction.
The simulated effect of correlated water vapor contributions can be seen in Fig. 3b. The diagonal elements quantify absorbance variance at each spectral position and the off-diagonal elements provide covariances. This visualization allows us to rapidly assess the potential impacts of any correlated perturbations and can serve as a strategy to examine any assumptions of the underlying noise structure. Note the consideration of the noise covariances poses a certain intricacy in calculation of the separation factor using the DWA approach. The time domain interferogram data acquired on FT-IR spectrometers typically undergo a number of signal processing steps that may induce correlation between the spectral measurements in the frequency domain. Apodization and zero-filling, under certain conditions,79 can result in measurements that are correlated as well as change the magnitude of noise. Next, we analyze the effect of noise models on separation quality to compare the performances of SWAH and DWAH approaches and the SDA in Fig. 3c. As expected, uniform and uncorrelated noise shows the best separation quality, with a normalized separation quality of ~100% and ~93%, respectively. Non-uniform noise shows lower separation quality in comparison. For non-uniform, uncorrelated noise, SDA and DWAH both provide a close relative performance of ~73% and ~65%, respectively. For non-uniform correlated noise, a relative performance of only ~44% and ~26% for the SDA and the DWAH approaches is achieved, respectively. Key conclusions from this simulation are that the noise characteristics have significant influence on the LOD, in the worst case leading to a ~fourfold decrease in normalized separation quality. Moreover, the optimal spectral subset for the averaging is highly dependent on correlation and non-uniformity in the spectral noise. Fully uncorrelated noise in measurements is rare, for example, as seen in data recorded from a purged system here and the impact of correlated noise should be considered. This noise model can be applied to analyze other specific situations where the source or detector may have wavelength-dependent characteristics. In particular, non-uniform noise becomes increasingly important for discrete frequency measurements as well.
Experimental Validation
We validate simulations with data acquired from imaging a BSA microarray. We first estimate the blank values for different analysis approaches, followed by predicting the detection limit using a calibration function and validation with the known concentrations of the array.
Estimating Blank Values.
Estimated standard deviation, , were recorded using a blank region of the microarray (7744 pixels), with care to ensure that there were also no contaminating dust or other deposits (Fig. 3d). The spectral region with increased noise level suggests the influence from atmospheric water vapor with noise covariance visualized in Fig. 3e. Aside from the non-uniform standard error at every wavenumber, only a slight correlation in the spectral noise is apparent. While strong spatial atmospheric fluctuations would provide a highly structured noise covariance matrix as simulated in Fig. 3b, the absence of the non-diagonal water vapor related elements in the experimental data of Fig. 3e indicates that the spectrally non-uniform noise might just be due to differential signal attenuation by atmospheric species. Unsurprisingly, purging the instrument will lead to lower variation and lower noise but the analysis here shows that the typical measurement noise is impacted by atmospheric contributions in a well-purged instrument.
Estimating the LOD Concentration.
We first develop a calibration curve using absorbance at high concentrations (10, 5, 2, and 1 mg/mL) since the impact of noise is smaller. Lower concentrations are used for validation, since those are closer to the limits of the instrument. The standard deviation for each concentration is computed using all pixels from the eight replicates. The LOD is first calculated using the simple threshold of . We report our measurements in concentrations as they are intuitively understandable and commonly adopted; however, a mass LOD can also be calculated. It is also important to emphasize that we do not aim to describe means to maximize the analyte concentration through sample preparation techniques such as a longer path length or pre-concentrating the solution, but we discuss approaches to strategically and efficiently analyze the data.
First, we use SWA to calculate the LOD. The optimal wavenumbers picked by SWAH and SWAB are 1646 cm−1 and 1654 cm−1, yielding LODs of 0.32 mg/mL and 0.27 mg/mL (Fig. 3f), respectively. The DWAH and DWAB procedures choose 13 and 10 discrete wavenumbers (dashed lines in Fig. 3f) with LODs of 0.22 mg/mL using both the methods. Interestingly, the DWAB selection provides a significantly lower LOD for a small number of selected wavenumbers, but overall, this did not result in better LOD in the best selected subset. We assess use of SDA by first averaging all the pixels from the 10 mg/mL spots, which gives us an estimation of . An LOD of 0.16 mg/mL is estimated from these data as the concentration where the Mahalanobis distance of the class spectra equals three. For the calculation of the Mahalanobis distance, it is necessary to compute the inverse of the noise covariance matrix, which becomes an increasingly complex problem for highly correlated noise with resulting multicollinearity. This problem is typically resolved by regularized computation of approximate pseudoinverse of such matrices.
Denoising techniques in post-processing have been used to improve data quality80,81 and are expected to result in an improved LOD. The MNF transform has been used previously as an effective means to reduce noise. Even though these techniques result in spectra that are visually more appealing they cannot alter the inherent uncertainty of the spectral information. Water vapor correction performed before MNF transformation is recommended. So that the variance of water vapor does not affect the principal components used for spectral reconstruction. The alternate approach is compared in Fig. S1 (Supplemental Material). The net result of MNF treated data is that the LOD is 0.079 mg/mL for SWA and only slightly affected by averaging, resulting in a LOD of 0.075 mg/mL for the best subset from DWAB. Surprisingly, the LOD predicted using DWAB or SWAB after MNF correction is lower than that achieved using SDA. Methods such as principal component analysis (PCA) or MNF already exploit the entire spectral information during the projection onto the lower-dimensional sub-space. The concentration-signal LOD curves before and after MNF are shown in Fig. 4. The classification results with these approaches, using a decision boundary is depicted in Fig. S2. We also calculate the mass equivalent for LOD of 0.075 mg/mL and it corresponds to 216 pg of mass spotted for spot volume of 2.7 nL. Assuming each spot size spans approximately 1928 pixels, the mass spotted per pixel is 112fg/pixel, which also corresponds to 1.7 amol of BSA per pixel. While the linear relation between concentration and absorbance is strictly valid for the integrated band area, in the depicted LOD curves, the concentration is derived. Differences in the slope of the curves arise, from the dependence of the slope on the average absorbance of the subset.
Figure 4.
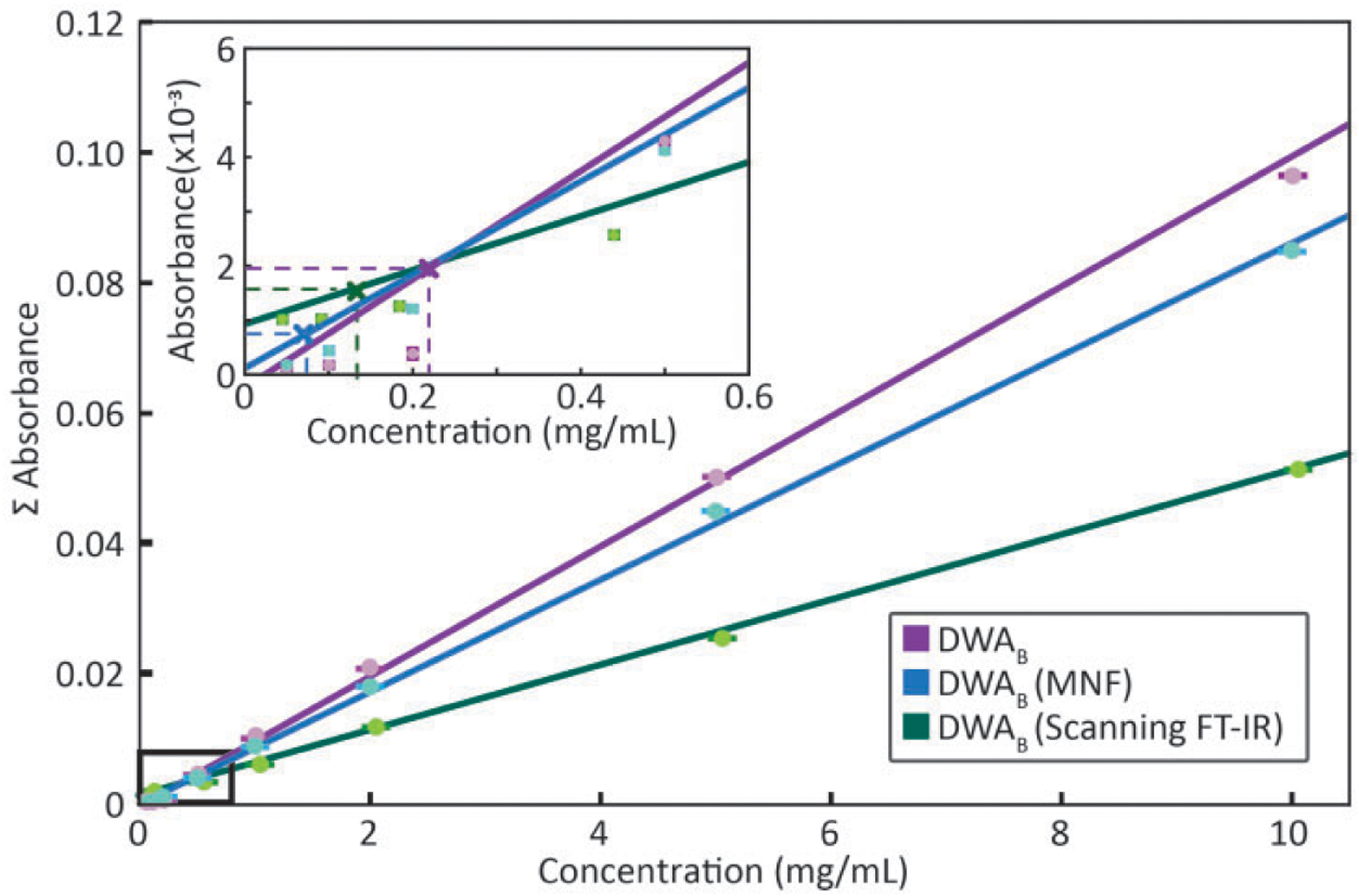
Comparison of concentration-signal curves obtained with DWAB before and after MNF correction for a widefield FT-IR imaging spectrometer. Also shown are data obtained with DWAB for representative imaging spectrometer, namely, a line-scanning FT-IR system. Inset plot shows magnified region near the detection limits. LOD can be interpreted as the x-intercept of the vertical lines projected from the calibration curve such that the horizontal lines correspond to three times the standard deviation (99.73% confidence level) in the blank absorbance distribution for the chosen metric.
Statistical Validation.
In addition to single pixel measures, we compare the distributions (blank and standard) to expected distributions (Fig. 5) from a model of Gaussian noise for both SWAH (Fig. 5a) and DWAB (Fig. 5b). While data follows the predicted distributions at low concentration, a broadening is seen for higher concentrations that likely arises from within-spot heterogeneity in thickness. SDA is based on decision theory such that likelihood function or spectral distance between the sample and blank classes, is maximized with an assumed noise model. Thus a spectral distance of zero implies equal likelihood of a spectrum being a part of the sample class or the blank class . For the MNF transformed data, the distributions of the blank and sample measurements using SWAH (Fig. 5d) show that the separations indicate an improved LOD. Thus, having a good understanding of the system noise characteristics helps us in pushing the detection limits beyond those calculated from recorded data.
Figure 5.
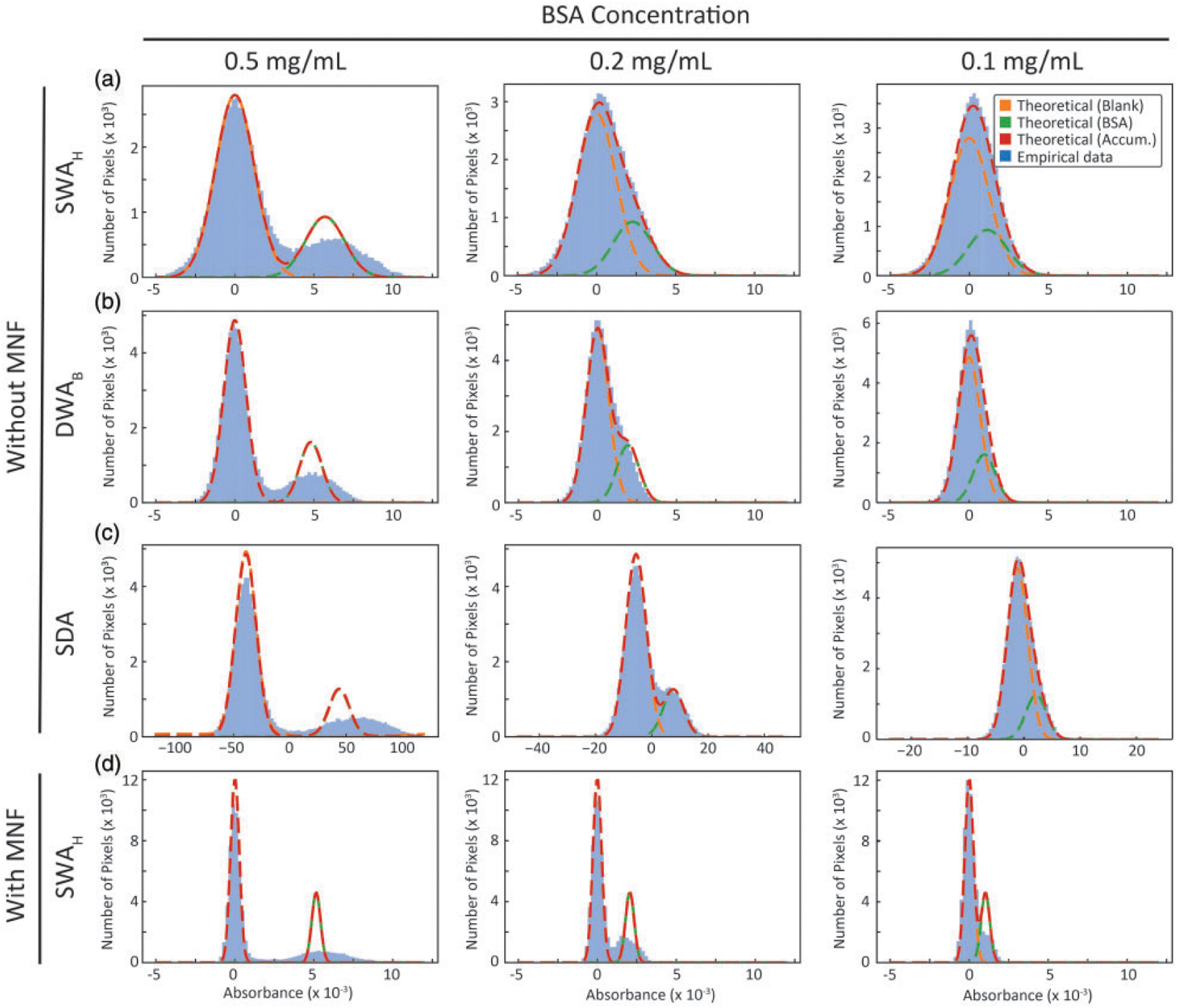
Histogram of the intensity value distributions for three different cases of BSA concentrations shown in different columns. Rows correspond to various methods, namely, (a) SWAH, (b) DWAB with the best subset, (c) SDA, all without any MNF correction, and (d) SWAH case with MNF correction. Gaussian fits for theoretical blank and sample distributions, and cumulative predicted distribution is projected on the empirical data. Increased standard deviation in the sample distributions is caused by within spot concentration irregularities.
The noise model that best describes experimental FT-IR data is non-uniform and correlated, which should be assumed for LOD optimizations. With DFIR imaging becoming more popular, the noise characteristics of each instrument should be considered while remembering that a poor choice of the set of discrete frequencies to scan may result in an inferior performance. In general, non-uniform and correlated noise in laser sources inspires us to consider covariance matrices for the characterization of noise, because of their comprehensiveness in comparison to simple metrics like root mean square error or peak-to-peak noise. In practical applications, further, a 100% line of FT-IR data is not comparable to a 100% line from DFIR data. Apodization and other signal processing techniques in FT-IR data will transfer a fraction of the noise into covariance that cannot be visualized simply by a 100% line. Further, comparisons of different spectral selection procedures further indicates that not all the spectral information is necessary to reach an excellent LOD and DFIR instruments cannot automatically be considered inferior in performance. Similarly, wide bandwidth FT-IR spectroscopy may not always be superior. DFIR systems, where the imaging time is directly proportional to the number of frequencies imaged, hardware innovations such as balanced detection, and optimal frequency selection all provide yet untapped opportunities improve the detection limits of DFIR systems.
As representative examples, we compare the performances of two instruments, first, a line scanning FT-IR instrument equipped with a linear array. The predicted LOD is 0.12 mg/mL for the smallest pixel size at typical scanning parameters and 0.008 mg/mL for the representative DFIR system. While we have presented typical performance for several imaging systems, the trading rules of IR spectroscopy78 should be carefully considered in comparisons of performance. Notably, the scan times for widefield staring systems are larger though the number of pixels acquired is also larger. Normalizing for pixel rate, while accounting for pixel size and at constant S/N, is a better comparison of relative performance. Obviously, the predicted LOD depends significantly on the pixel sizes and acquisition times (co-additions). Our goal was not to compare performance of systems but to show that a reasonably low LOD could be obtained by modern IR imaging instrument. This LOD is obviously poorer than state of the art bulk spectral measurements by several orders of magnitude, which cannot provide spatially resolved data and typically measure orders of magnitude larger volume of material, as well as those methods specifically designed to provide ultrasensitive measurements, such as using plasmonic substrates to provide signals from small, localized volumes. However, for unenhanced measurements within spatially heterogeneous structures, IR imaging easily provides measurements in the biomedically relevant physiologic range of mM to μM concentrations.
Conclusion
This study undertakes a quantitative characterization of the detection ability of typical measurements in IR imaging. We propose methods to analyze FT-IR and DFIR data and consider suitable spectral analyses with a simultaneous consideration of noise. The typical IR imaging measurement was found to have a LOD in the mg/mL range for typical measurements, which can be improved by invoking the trading rules of spectroscopy. The effects of correlated and non-uniform noise characteristics on measurements is observed and recommended for IR imaging data. We also demonstrate that minor changes in the band shape have only a negligible influence on separation quality. While comparing different spectral analysis methods, calculating spectral distances is not necessarily preferable to simple averaging. Finally, post-processing techniques can improve the LOD to less than 100 μg/mL. This study provides a means to characterize and optimize LOD calculations for IR imaging, while providing experimental validation using a BSA microarray to represent typical biomedical samples. These methods can be useful in assessing and optimizing the performance of existing and emerging IR imaging instruments.
Supplementary Material
Acknowledgements
The authors would like to thank Prof. Bernhard Lendl for inspiring this study and support. L.L., Marshall Plan Fellow, acknowledges financial support through the COMET Centre CHASE, funded within the COMET (Competence Centers for Excellent Technologies) program by the BMK, the BMDW and the Federal Provinces of Upper Austria and Vienna. The COMET program is managed by the Austrian Research Promotion Agency (FFG). We would also like to thank Kevin Yeh, Max Tetrick and Craig Richard for discussions and valuable comments. Last, we appreciate Holger Pils for his kind support in using the Nanoplotter.
Funding
The author(s) disclosed receipt of the following financial support for the research, authorship, and/or publication of this article: This work was supported by the National Institutes of Health (grant numbers R01EB009745, R01GM142172).
Footnotes
Declaration of Conflicting Interests
The author(s) declared no potential conflicts of interest with respect to the research, authorship, and/or publication of this article.
Supplemental Material
All supplemental material mentioned in the text is available in the online version of the journal.
References
- 1.Currie LA. “Limits for Qualitative Detection and Quantitative Determination. Application to Radiochemistry”. Anal. Chem 1968. 40(3): 586–593. doi: 10.1021/ac60259a007. [DOI] [Google Scholar]
- 2.Currie LA. “Detection and Quantification Limits: Origins and Historical Overview”. Anal. Chim. Acta 1999. 391(2): 127–134. doi: 10.1016/S0003-2670(99)00105-1. [DOI] [Google Scholar]
- 3.Loock HP, Wentzell PD. “Detection Limits of Chemical Sensors: Applications and Misapplications”. Sens. Actuators, B 2012. 173: 157–163. doi: 10.1016/j.snb.2012.06.071. [DOI] [Google Scholar]
- 4.Allegrini F, Olivieri AC. “IUPAC-Consistent Approach to the Limit of Detection in Partial Least-Squares Calibration”. Anal. Chem 2014. 86(I5): 7858–7866. doi: 10.1021/ac501786u. [DOI] [PubMed] [Google Scholar]
- 5.International Organization for Standardization (ISO). “ISO 11843 1:1997. Capability of Detection–Part 1: Terms and Definitions”. Geneva: International Organization for Standardization, 1997. https://www.iso.org/standard//096.html [accessed 12 October 202I]. [Google Scholar]
- 6.International Organization for Standardization (ISO). “ISO 11843 2:2000. Capability of Detection–Part 2: Methodology in the Linear Calibration Case”. Geneva: International Organization for Standardization, 2000. https://www.iso.org/standard/20186.html [accessed 12 October 202I]. [Google Scholar]
- 7.Alañón Molina A, Murillo Pulgarín J, Martínez Ferreras F. “Nomenclature, Symbols, Units and Their Usage in Spectrochemical Analysis. 2. Data Interpretation”. Spectrochim. Acta, Part B 1978. 33: 242–245. [Google Scholar]
- 8.Armbruster DA, Pry T. “Limit of Blank, Limit of Detection and Limit of Quantitation”. Clin. Biochem. Rev 2008. 29(Suppl 1): S49. [PMC free article] [PubMed] [Google Scholar]
- 9.Kaiser H. “Zur Definition der Nachweisgrenze, der Garantiegrenze und der Dabei Benutzten Begriffe”. Anal. Bioanal. Chem 1966. 216(1): 80–94. doi: 10.1007/BF00515298. [DOI] [Google Scholar]
- 10.Wing J, Wahlgren MA. “Detection Sensitivities in Nuclear Activation with an Isotopic Fast-Neutron Source”. Anal. Chem 1967. 39(1): 85–89. [Google Scholar]
- 11..Hubaux A, Vos G. “Decision and Detection Limits for Calibration Curves”. Anal. Chem 1970. 42(8): 849–855. doi: 10.1021/ac60290a013. [DOI] [Google Scholar]
- 12.Linnet K, Kondratovich M. “Partly Nonparametric Approach for Determining the Limit of Detection”. Clin. Chem 2004. 50(4): 732–740. doi: 10.1373/clinchem.2003.029983. [DOI] [PubMed] [Google Scholar]
- 13.Tittel FK, Richter D, Fried A. “Mid-Infrared Laser Applications in Spectroscopy”. In: Sorokina IT, Vodopyanov KL, editors. Solid-State Mid-Infrared Laser Sources. London, UK: Springer Nature, 2003. Vol. 89. Pp. 458–529. doi: 10.1007/3-540-36491-9_11. [DOI] [Google Scholar]
- 14.Willer U, Saraji M, Khorsandi A, Geiser P, Schade W. “Near-and Mid-Infrared Laser Monitoring of Industrial Processes, Environment and Security Applications”. Opt. Lasers. Eng 2006. 44(7): 699–710. doi: 10.1016/j.optlaseng.2005.04.015. [DOI] [Google Scholar]
- 15.Hodgkinson J, Tatam RP. “Optical Gas Sensing: A Review”. Meas. Sci. Technol 2012. 24(1): 012004. doi: 10.1088/0957-0233/24/1/012004. [DOI] [Google Scholar]
- 16.Moser H, Pölz W, Waclawek JP, Ofner J, Lendl B. “Implementation of a Quantum Cascade Laser-Based Gas Sensor Prototype for Sub-PPMV H2S Measurements in a Petrochemical Process Gas Stream”. Anal. Bioanal. Chem 2017. 409(3): 729–739. doi: 10.1007/s00216016-9923-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Chan KLA, Kazarian SG. “Detection of Trace Materials with Fourier Transform Infrared Spectroscopy Using a Multi-Channel Detector”. Analyst (Cambridge, UK). 2006. 131(1): 126–131. doi: 10.1039/b511243e. [DOI] [PubMed] [Google Scholar]
- 18.Baldassarre M, Barth A. “Pushing the Detection Limit of Infrared Spectroscopy for Structural Analysis of Dilute Protein Samples”. Analyst (Cambridge, UK). 2014. 139(21): 5393–5399. doi: 10.1039/C4AN00918E. [DOI] [PubMed] [Google Scholar]
- 19.Gonzalvez A, Garrigues S, de la Guardia M, Armenta S. “The Ways to the Trace Level Analysis in Infrared Spectroscopy”. Anal. Methods 2011. 3(1): 43–52. doi: 10.1039/COAY00437E. [DOI] [PubMed] [Google Scholar]
- 20.Akhgar CK, Ramer G, Zbik M, Trajnerowicz A, Pawluczyk J, et al. “The Next Generation of IR Spectroscopy: EC-QCL-Based Mid-IR Transmission Spectroscopy of Proteins with Balanced Detection”. Anal. Chem 2020. 92(14): 9901–9907. doi: 10.1021/acs.analchem.0c01406. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21..Freitag S, Baer M, Buntzoll L, Ramer G, Schwaighofer A, et al. “Polarimetric Balanced Detection: Background-Free Mid-IR Evanescent Field Laser Spectroscopy for Low-Noise, Long-Term Stable Chemical Sensing”. ACS Sens. 2020. 6(1): 35–42. doi: 10.1021/acssensors.0c01342. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Pinto D, Moser H, Waclawek JP, Russo SD, Patimisco P, et al. “Parts-Per-Billion Detection of Carbon Monoxide: A Comparison Between Quartz-Enhanced Photoacoustic and Photothermal Spectroscopy”. Photoacoustics. 2021. 22: 100244. doi: 10.1016/j.pacs.2021.100244. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Waclawek JP, Moser H, Lendl B. “Balanced-Detection Interferometric Cavity-Assisted Photothermal Spectroscopy Employing an All-Fiber-Coupled Probe Laser Configuration”. Opt. Express 2021. 29(5): 7794–7808. doi: 10.1364/OE.416536. [DOI] [PubMed] [Google Scholar]
- 24.Nasse MJ, Walsh MJ, Mattson EC, Reininger R, Kajdacsy-Balla A, et al. “High-Resolution Fourier-Transform Infrared Chemical Imaging with Multiple Synchrotron Beams”. Nat. Methods 2011. 8(5): 413–416. doi: 10.1038/nmeth.1585. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Kazarian SG, Chan KLA. “ATR-FTIR Spectroscopic Imaging: Recent Advances and Applications to Biological Systems”. Analyst. (Cambridge, UK) 2013. 138(7): 1940–1951. doi: 10.1039/c3an36865c. [DOI] [PubMed] [Google Scholar]
- 26.Reddy RK, Walsh MJ, Schulmerich MV, Carney PS, Bhargava R. “High-Definition Infrared Spectroscopic Imaging”. Appl. Spectrosc 2013. 67(1): 93–105. doi: 10.1366/11-06568. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Carr G, Miller L, Dumas P. “Synchrotron Radiation as a Source for Infrared Microspectroscopic Imaging with 2D Multi-Element Detection”. In: Moss David, editor. Biomedical Applications of Synchrotron Infrared Microspectroscopy: A Practical Approach. Cambridge, UK: Royal Society of Chemistry, 2010. Chap. 7, Pp. 226–259. doi: 10.1039/978|849731997-00226. [DOI] [Google Scholar]
- 28.Hirschmugl CJ, Gough KM. “Fourier Transform Infrared Spectrochemical Imaging: Review of Design and Applications With a Focal Plane Array and Multiple Beam Synchrotron Radiation Source”. Appl. Spectrosc 2012. 66(5): 475–491. doi: 10.1366/12-06629. [DOI] [PubMed] [Google Scholar]
- 29.Chan KLA, Altharawi A, Fale P, Song CL, Kazarian SG, et al. “Transmission Fourier Transform Infrared Spectroscopic Imaging, Mapping, and Synchrotron Scanning Microscopy with Zinc Sulfide Hemispheres on Living Mammalian Cells at Sub-Cellular Resolution”. Appl. Spectrosc 2020. 74(5): 544–552. doi: 10.1177/0003702819898275. [DOI] [PubMed] [Google Scholar]
- 30.Kalkhoran MA, Fitzpatrick A, Winter AD, Kelley CS, Warrick E, et al. “Characterization of Double-Deformable-Mirror Adaptive Optics for IR Beam Shaping in Hyperspectral Imaging”. Proc. SPIE 11351, Unconventional Optical Imaging 11. 2020. 13511A. doi: 10.1117/12.2554162. [DOI] [Google Scholar]
- 31..Michaelian KH, Frogley MD, Cinque G, Quaroni L. “Infrared Spectra of Micro-Structured Samples with Microphotoacoustic Spectroscopy and Synchrotron Radiation”. Analyst (Cambridge, UK). 2020. 145(4): 1483–1490. doi: 10.1039/C9ANO1281H. [DOI] [PubMed] [Google Scholar]
- 32.John-Herpin A, Tittl A, Altug H. “Quantifying the limits of detection of surface-enhanced infrared spectroscopy with grating order-coupled nanogap antennas”. ACS Photonics. 2018. 5(10): 4117–4124. doi: 10.1021/acsphotonics.8b00847. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Mayerhöfer TG, Popp J. “Periodic array-based substrates for surface-enhanced infrared spectroscopy”. Nanophotonics. 2018. 7(1): 39–79. doi: 10.1515/nanoph-2017-0005. [DOI] [Google Scholar]
- 34.Guo B, Wang Y, Peng C, Luo G, Le HQ. “Multi-Wavelength Mid-Infrared Micro-Spectral Imaging Using Semiconductor Lasers”. Appl. Spectrosc 2003. 57(7): 811–822. [DOI] [PubMed] [Google Scholar]
- 35.Kole MR, Reddy RK, Schulmerich MV, Gelber MK, Bhargava R. “Discrete Frequency Infrared Microspectroscopy and Imaging with a Tunable Quantum Cascade Laser”. Anal. Chem 2012. 84(23): 10366–10372. doi: 10.1021/ac30253f. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Bassan P, Weida MJ, Rowlette J, Gardner P. “Large Scale Infrared Imaging of Tissue Micro Arrays (TMAs) Using a Tunable Quantum Cascade Laser (QCL) Based Microscope”. Analyst (Cambridge, UK). 2014. 139(16): 3856–3859. doi: 10.1039/c4an00638k. [DOI] [PubMed] [Google Scholar]
- 37.Kröger N, Egl A, Engel M, Gretz N, Haase K, et al. “Quantum Cascade Laser-Based Hyperspectral Imaging of Biological Tissue”. J. Biomed. Opt 2014. 19(11): 111607. doi: 10.1117/1.JBO.19.11.111607. [DOI] [PubMed] [Google Scholar]
- 38.Yeh K, Kenkel S, Liu J-N, Bhargava R. “Fast Infrared Chemical Imaging with a Quantum Cascade Laser”. Anal. Chem 2015. 87(1): 485–493. doi: 10.1021/ac5027513. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Tiwari S, Raman J, Reddy V, Ghetler A, Tella RP, et al. “Towards Translation of Discrete Frequency Infrared Spectroscopic Imaging for Digital Histopathology of Clinical Biopsy Samples”. Anal. Chem 2016. 88(20): 10183–10190. doi: 10.1021/acs.analchem.6b02754. [DOI] [PubMed] [Google Scholar]
- 40.Kuepper C, Kallenbach-Thieltges A, Juette H, Tannapfel A, Großerueschkamp F, et al. “Quantum Cascade Laser-Based Infrared Microscopy for Label-Free and Automated Cancer Classification in Tissue Sections”. Sci. Rep 2018. 8(1): 7717. doi: 10.1038/s41598018-26098-w. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41..Mittal S, Yeh K, Leslie LS, Kenkel S, Kajdacsy-Balla A, et al. “Simultaneous Cancer and Tumor Microenvironment Subtyping Using Confocal Infrared Microscopy for All-Digital Molecular Histopathology”. Proc. Natl. Acad. Sci. U.S.A 2018. 115(25): E5651–E5660. doi: 10.1073/pnas.1719551115. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Ran S, Berisha S, Mankar R, Shih WC, Mayerich D. “Mitigating Fringing in Discrete Frequency Infrared Imaging Using Time-Delayed Integration”. Biomed. Opt. Express 2018. 9(2): 832–843. doi: 10.1364/BOE.9.000832. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Yeh K, Lee D, Bhargava R. “Multicolor Discrete Frequency Infrared Spectroscopic Imaging”. Anal. Chem 2019. 91(3): 2177–2185. doi: 10.1021/acs.analchem.8b04749. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Phal YD, Yeh K, Bhargava R. “Concurrent Vibrational Circular Dichroism Measurements with Infrared Spectroscopic Imaging”. Anal. Chem 2020. 93(3): 1294–1303. doi: 10.1021/acs.analchem.0c00323. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Phal YD, Yeh K, Bhargava R. “Polarimetric Infrared Spectroscopic Imaging Using Quantum Cascade Lasers”. Proc. SPIE 11252, Advanced Chemical Microscopy for Life Science and Translational Medicine. 2020. II252: 36–45. doi: 10.1117/12.2544392. [DOI] [Google Scholar]
- 46.Phal YD, Yeh K, Bhargava R. “Mid-IR laser-based polarimetric imaging for polymeric and biological applications”. Proc. SPIE II656, Advanced Chemical Microscopy for Life Science and Translational Medicine. 2021. 1165619. doi: 10.1117/12.2579099. [DOI] [Google Scholar]
- 47.Phal YD, Yeh K, Bhargava R. “Discrete Frequency Infrared Vibrational Circular Dichroism Spectroscopy & Imaging”. Biophotonics Congress 2021, OSA Technical Digest (Optical Society of America). 2021. Paper NW3C.I. [Google Scholar]
- 48.Phal YD, Yeh K, Bhargava R. “Design Considerations for Discrete Frequency Infrared Microscopy Systems”. Appl. Spectrosc 2021. 1–26. 75(9): 1067–1092. doi: 10.1177/00037028211013372. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Lahiri B, Holland G, Centrone A. “Chemical Imaging Beyond the Diffraction Limit: Experimental Validation of the PTIR Technique”. Small. 2013. 9(3): 439–445. doi: 10.1002/smll.201200788. [DOI] [PubMed] [Google Scholar]
- 50.Dazzi A, Prater CB. “AFM-IR: Technology and Applications in Nanoscale Infrared Spectroscopy and Chemical Imaging”. Chem. Rev (Washington, DC, U.S.). 2017. 117(7): 5146–5173. doi: 10.1021/acs.chemrev.6b00448. [DOI] [PubMed] [Google Scholar]
- 51..Furstenberg R, Kendziora CA, Papantonakis MR, Nguyen V, McGill R. “Chemical Imaging using Infrared Photothermal Microspectroscopy”. Proc. SPIE 8374, Next-Generation Spectroscopic Technologies. 2012. 837411. doi: 10.1117/12.919574. [DOI] [Google Scholar]
- 52.Mërtiri A, Jeys T, Liberman V, Hong M, Mertz J, et al. “Mid-Infrared Photothermal Heterodyne Spectroscopy in a Liquid Crystal Using a Quantum Cascade Laser”. Appl. Phys. Lett 2012. 101 (4): 044101. doi: 10.1063/1.4737942. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Totachawattana A, Liu H, Mertiri A, Hong MK, Erramilli S, et al. “Vibrational Mid-Infrared Photothermal Spectroscopy Using a Fiber Laser Probe: Asymptotic Limit in Signal-to-Baseline Contrast”. Opt. Lett 2016. 41(1): 179–182. doi: 10.1364/OL.41.000179. [DOI] [PubMed] [Google Scholar]
- 54.Zhang D, Li C, Zhang C, Slipchenko MN, Eakins G, et al. “Depth-Resolved Mid-Infrared Photothermal Imaging of Living Cells and Organisms with Submicrometer Spatial Resolution”. Sci. Adv 2016. 2(9): e1600521. doi: 10.1126/sciadv.1600521. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Fu P, Chen T, Zhu H, Xu C, Chen M, et al. “Pushing the Resolution of Infrared Imaging by Mid Infrared Photothermal Microscopy”. Proc. SPIE 11549, Advanced Optical Imaging Technologies III. 2020. 115490P. doi: 10.1117/12.2575306. [DOI] [Google Scholar]
- 56.Klementieva O, Sandt C, Martinsson I, Kansiz M, Gouras GK, et al. “Super-Resolution Infrared Imaging of Polymorphic Amyloid Aggregates Directly in Neurons”. Adv. Sci 2020. 7(6): 1903004. doi: 10.1002/advs.201903004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Samolis PD, Sander MY. “Phase-Sensitive Lock-In Detection for High-Contrast Mid-Infrared Photothermal Imaging with Sub-Diffraction Limited Resolution”. Opt. Express 2019. 27(3): 2643–2655. doi: 10.1364/OE.27.002643. [DOI] [PubMed] [Google Scholar]
- 58.Tamamitsu M, Toda K, Horisaki R, Ideguchi T. “Quantitative Phase Imaging With Molecular Vibrational Sensitivity”. Opt. Lett 2019. 44(15): 3729–3732. doi: 10.1364/OL.44.003729. [DOI] [PubMed] [Google Scholar]
- 59.Pavlovetc IM, Aleshire K, Hartland GV, Kuno M. “Approaches to Mid-Infrared, Super-Resolution Imaging and Spectroscopy”. Phys. Chem. Chem. Phys 2020. 22(8): 4313–4325. doi: 10.1039/C9CP058I5]. [DOI] [PubMed] [Google Scholar]
- 60.Pavlovetc IM, Podshivaylov EA, Chatterjee R, Hartland GV, Frantsuzov PA, et al. “Infrared Photothermal Heterodyne Imaging: Contrast Mechanism and Detection Limits”. J. Appl. Phys (Melville, NY, U.S.). 2020. 127(16): 165101. doi: 10.1063/1.5142277. [DOI] [Google Scholar]
- 61..Schnell M, Mittal S, Falahkheirkhah K, Mittal A, Yeh K, et al. “All-Digital Histopathology by Infrared-Optical Hybrid Microscopy”. Proc. Natl. Acad. Sci. U.S.A 2020. 117(7): 3388–3396. doi: 10.1073/pnas.1912400117. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Lanzarotta A. “Approximating the Detection Limit of an Infrared Spectroscopic Imaging Microscope Operating in an Attenuated Total Reflection (ATR) Modality: Theoretical and Empirical Results for an Instrument Using a Linear Array Detector and a 1.5 Millimeter Germanium Hemisphere Internal Reflection Element”. Appl. Spectrosc 2015. 69(2): 205–214. doi: 10.1366/14-07538. [DOI] [PubMed] [Google Scholar]
- 63.De Meutter J, Derfoufi KM, Goormaghtigh E. “Analysis of Protein Microarrays by FTIR Imaging”. Biomed. Spectrosc. Imaging 2016. 5(2): 145–154. doi: 10.3233/BSI-160137. [DOI] [Google Scholar]
- 64.De Meutter J, Goormaghtigh E. “FTIR Imaging of Protein Microarrays for High Throughput Secondary Structure Determination”. Anal. Chem 2021. 93(8): 3733–3741. doi: 10.1021/acs.analchem.0c03677. [DOI] [PubMed] [Google Scholar]
- 65.Park K, Lee J, Bhargava R, King WP. “Routine Femtogram-Level Chemical Analyses Using Vibrational Spectroscopy and Self-Cleaning Scanning Probe Microscopy Tips”. Anal. Chem 2008. 80(9): 3221–3228. doi: 10.1021/ac702423c. [DOI] [PubMed] [Google Scholar]
- 66.Snively C, Koenig J. “Characterizing the Performance of a Fast FT-IR Imaging Spectrometer”. Appl. Spectrosc 1999. 53(2): 170–177. [Google Scholar]
- 67.Ortiz MC, Sarabia LA, Sánchez MS. “Tutorial on Evaluation of Type I and Type II Errors in Chemical Analyses: From the Analytical Detection to Authentication of Products and Process Control”. Anal. Chim. Acta 2010. 674(2): 123–142. doi: 10.1016/j.aca.2010.06.026. [DOI] [PubMed] [Google Scholar]
- 68.Manolakis D, Shaw G. “Detection Algorithms for Hyperspectral Imaging Applications”. IEEE Signal Process. Mag 2002. 19(1): 29–43. doi: 10.1109/79.974724. [DOI] [Google Scholar]
- 69.Haberkorn M, Frank J, Harasek M, Nilsson J, Laurell T, et al. “Flow-Through Picoliter Dispenser: A New Approach for Solvent Elimination in FT-IR Spectroscopy”. Appl. Spectrosc 2002. 56(7): 902–908. doi: 10.1366/000370202760171581. [DOI] [Google Scholar]
- 70.Surowiec I, Baena JR, Frank J, Laurell T, Nilsson J, et al. “FlowThrough Microdispenser for Interfacing μ-HPLC to Raman and Mid-IR Spectroscopic Detection”. J. Chromatogr. A 2005. 1080(2): 132–139. doi: 10.1016/j.chroma.2005.04.082. [DOI] [PubMed] [Google Scholar]
- 71.Green AA, Berman M, Switzer P, Craig MD. “A Transformation for Ordering Multispectral Data in Terms of Image Quality with Implications for Noise Removal”. IEEE Trans. Geosci. Remote Sens 1988. 26(1): 65–74. doi: 10.1109/36.3001. [DOI] [Google Scholar]
- 72.Kong J, Yu S. “Fourier Transform Infrared Spectroscopic Analysis of Protein Secondary Structures”. Acta Biochim. Biophys. Sin 2007. 39(8): 549–559. doi: 10.1111/j.1745-7270.2007.00320.x. [DOI] [PubMed] [Google Scholar]
- 73.Barth A. “Infrared Spectroscopy of Proteins”. Biochim. Biophys. Acta, Bioenerg 2007. 1767(9): 1073–1101. doi: 10.1016/j.bbabio.2007.06.004. [DOI] [PubMed] [Google Scholar]
- 74.Zhang H, Bhagwagar DE, Graf JF, Painter PC, Coleman MM. “The Effect of Hydrogen Bonding on the Phase Behaviour of Ternary Polymer Blends”. Polymer. 1994. 35(25): 5379–5397. doi: 10.1016/S0032-3861(05)80001-1. [DOI] [Google Scholar]
- 75.Coleman MM, Painter PC. “Hydrogen Bonded Polymer Blends”. Prog. Polym. Sci 1995. 20(1): 1–59. doi: 10.1016/0079-6700(94)00038-4. [DOI] [Google Scholar]
- 76.Davis BJ, Carney PS, Bhargava R. “Theory of Mid-Infrared Absorption Microspectroscopy: I. Homogeneous Samples”. Anal. Chem 2010. 82(9): 3474–3486. doi: 10.1021/ac902067p. [DOI] [PubMed] [Google Scholar]
- 77.Davis BJ, Carney PS, Bhargava R. “Theory of Mid-Infrared Absorption Microspectroscopy: II. Heterogeneous Samples”. Anal. Chem 2010. 82(9): 3487–3499. doi: 10.1021/ac902068e. [DOI] [PubMed] [Google Scholar]
- 78.Giffiths PR, De Haseth JA. In: Winefordner JD, editor. Fourier Transform Infrared Spectrometry. Hoboken, NJ: John Wiley and Sons, Inc., 2007. 2nd. ed. doi: 10.1016/0022-2364(73)90076-0. [DOI] [Google Scholar]
- 79.Bartholdi E, Ernst RR. “Fourier Spectroscopy and the Causality Principle”. J. Magn. Reson 1973. 11(1): 9–19. doi: 10.1016/00222364(73)90076-0. [DOI] [Google Scholar]
- 80.Bhargava R, Ribar T, Koenig JL. “Towards Faster FT-IR Imaging by Reducing Noise”. Appl. Spectrosc 1999. 53(11): 1313–1322. [Google Scholar]
- 81..Bhargava R, Wang SQ, Koenig JL. “Route to Higher Fidelity FT-IR Imaging”. Appl. Spectrosc 2000. 54(4): 486–495. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


