Abstract
A low-cost ($120 NZD, $75 USD), low-power (1-year battery life), portable, and programmable syringe pump design is presented, which offers an alternative to high-cost commercial devices with limited battery life. Contrary to typical motor-driven syringe pumps, the design utilizes a compression spring coupled with a clockwork escapement mechanism to advance the syringe plunger. Full control over flow-rate and discrete (bolus) deliveries is achieved through actuation of a clockwork escapement using programmable, low-power electronics. The escapement mechanism allows the syringe plunger to advance a fixed linear distance, delivering a dose size of 0.001 ml in the configuration presented. The modular pump assembly is easily reconfigured for different applications by interchanging components to alter the minimum dose size. Testing to IEC 60601-2-24(2012), the average error of the clockwork syringe pump was 8.0%, 4.0%, and 1.9% for 0.001 ml, 0.002 ml, and 0.01 ml volumes, respectively. An overall mean error of 1.0% was recorded for a flow-rate of 0.01 ml h−1. Compared to a commercial insulin pump, the clockwork pump demonstrated reduced variability but greater average error due to consistent over-delivery. Further development of the design and/or manufacture should yield a device with similar performance to a commercial pump.
Keywords: Escapement, Spring-driven, Programmable, Micro-litre pump, Insulin pump
Graphical abstract
belowfloat
- NZD
New Zealand Dollar
- USD
United States Dollar
- IEC
International Electrotechnical Commission
- ISO
International Organization for Standardization
- ANSI
American National Standards Institute
- AGMA
American Gear Manufacturers Association
- CAD
Computer-Aided Design
- EDM
Electrical Discharge Machining
- PCB
Printed Circuit Board
- SPI
Serial Peripheral Interface
- ID
Internal Diameter
- OD
Outer Diameter
- CSII
Continuous Subcutaneous Insulin Infusion
| Specifications table | |
| Hardware name | Low-cost, low-power, clockwork syringe pump |
| Subject area |
Mechanical Engineering Biomedical Engineering Medical devices |
| Hardware type |
Mechanically-driven syringe pump Low-cost device for controlled insulin delivery |
| Closest commercial analog |
Syringe pump Insulin pump |
| Open source license | Creative Commons Attribution - ShareAlike 4.0 International (CC BY-SA 4.0) |
| Cost of hardware | $120 NZD ($75 USD) |
| Source file repository | https://doi.org/10.17605/osf.io/j24f6 |
1. Hardware in context
Syringe pumps control the movement of fluid by mechanically advancing (or retracting) a syringe plunger. Large, externally-powered syringe pumps are commonly used in laboratory applications, and for delivering medication in acute and intensive care scenarios. Devices for medication delivery require very small delivery volumes with low variability. Extension of technologies with small delivery capability to portable applications is hampered by high power consumption, or prohibitive expense. For example, syringe pumps are used for continuous subcutaneous insulin infusion (CSII) in diabetes outpatient care via insulin pumps [1], [2], [3], [4]. Insulin pumps present an extreme case for portable syringe pump devices in terms of size, while also requiring small, precise volumes to be delivered.
A significant limitation of syringe pumps is cost. In New Zealand, insulin pumps cost between $7000–10,000 NZD ($4400–$6250 USD). In addition to large upfront cost, they are not typically able to be repaired or serviced. For relatively simple hardware – a motor-driven leadscrew which advances a plunger – this cost is very high. For insulin pumps in particular, pump cost prevents more universal uptake of CSII, which is regarded the gold-standard for glucose control and diabetes outpatient care [5].
One further common problem with motor-driven syringe pumps is a large electrical energy requirement, as all energy to deliver fluid must be provided by an electrical power source. For portable devices, this energy requirement results in either large, inconvenient batteries, or limited battery life. Commercially available insulin pumps, for example, require batteries to be changed approximately every 1–4 weeks.
The device presented here provides a portable, low-cost, low-power, and programmable syringe pump. It achieves great generalizability through configurable components, but is intended for eventual use as an insulin pump. The design operates using a spring-driven clockwork mechanism with electrical actuation, which lends itself to long battery life, as electrical energy is only used for dose control, rather than to advance the plunger. Flow-rate and bolus dose functionality are provided, and can be modified via program. Cost is minimized through selection of off-the-shelf components for a total bill of materials of $120 NZD ($75 USD), depending on access to mechanical and electronic workshops. The modular design enables users to easily perform repairs or modifications, increasing potential application in low-resource regions.
There are currently many open-source syringe pump designs suitable for a wide-range of research applications. These designs address issues of commercial pumps, including cost, compatibility, and lack of customizability. The design developed by [6] offers similar performance to a commercial syringe pump for 5% of the cost. It fits any size syringe, and is controlled using a web-interface. Similar open-source devices include a design targeting fluid delivery for behavioural neuroscience [7], a touch-screen controlled device for life science applications [8], a dual-syringe device for chemistry lab use [9], and a generic syringe pump constructed predominately by re-purposing an open-source 3D printer [10]. While inexpensive, easy to build, and customizable for different lab-based research applications, the designs all operate using a motor-driven leadscrew to advance a syringe plunger, and are powered using an external power source. None change the drive mechanism to meet other criteria. Therefore, the devices are not appropriate for field-based use, insulin therapy, or other applications where a highly portable, self-powered device is required.
An open-source insulin pump design developed by [11] is portable, and powered by an AAA battery. However, the design also operates using a motor-driven leadscrew, which limits battery life to the 1–4 weeks of commercial insulin pumps. The clockwork design presented here is differentiated from other open-sourced designs by its unique spring-driven, escapement-controlled actuation mechanism. It will enable a significantly longer, 1 year battery life (estimated). However, compared to this open-source insulin pump, the presented configuration of the clockwork pump cannot achieve the same delivery resolution, with a minimum dose size of 0.001 ml, compared to 0.25 10-3 ml (4 smaller) achieved by the open-source insulin pump [12].
Portable and mechanical pump designs can also be found in literature, including a device for microfluidic applications, which utilizes a compression spring to drive fluid stored in a cartridge [13]. Flow control is achieved using passive valves in a microfluidic chip. Another pump targeted at portable microfluidics advances the syringe plunger using a rack and pinion configuration, powered by a helical spring [14]. Flow-rate is controlled using a clockwork escapement actuated by a balance spring. Both designs operate without electronics (no battery or external power required). As a result, these devices are highly portable, reliable, and well-suited for continuous-flow applications. However, as dose timing is not controlled electrically, these pumps cannot be programmed for different flow-rates, or deliver discrete doses requested by the user, rendering them incompatible with insulin therapy or many other applications requiring variable dosing over time. In contrast to other open-source syringe pumps, the design presented here offers a small, portable, low-cost, and low-power device, which can be programmed for different flow-rates and/or discrete deliveries.
2. Hardware description
The clockwork pump is a modular, cylindrical syringe pump, which displaces fluid from a reservoir using a spring-driven plunger. The plunger is attached to a threaded nut, which back-drives a leadscrew, inducing rotation. Dose volume is controlled using a clockwork escapement mechanism which prevents uncontrolled release of the gear train [15]. The escapement consists of an oscillating component (pallet) and a club-toothed gear (escape wheel), as shown in Fig. 1. The escape wheel is connected through a 60:1 gearbox to the leadscrew. Free rotation of the escape wheel is interrupted by the pallet, which is coupled to a low-power actuator with an inbuilt spring-return mechanism. Each activation of the actuator allows the escape wheel to rotate 1/15th of a revolution, enabling the plunger to advance 9 µm, displacing a 0.001 ml discrete dose from the reservoir.
Fig. 1.

Escape wheel and pallet used for dosage control in the clockwork pump.
As the force provided by the spring to the plunger decreases as the plunger advances (as the spring decompresses), the achievable pumping pressure linearly decreases from peak pressure at the fully retracted plunger position (maximum spring compression) to minimum pressure at the fully extended plunger position (minimum spring compression). For the presented design, the pressure range is 175 kPa to 50 kPa, which is considered suitable for initial testing and development of a device targeting insulin therapy. However, the achievable pressure range can easily be altered for a different pumping application by varying the stiffness of the spring. The method used to select a spring with adequate stiffness for insulin therapy is outlined in Section 7.4, and can be adapted for any pumping application with a given minimum (or maximum) pressure requirement.
Provided the required pumping pressure for a given application can be met by the minimum achievable pressure of the pump, the dose delivered each actuation across the entire working range of the plunger will remain constant at 0.001 ml. A constant dose size is achieved as the escapement mechanism restrains the lead-screw to a fixed rotation each actuation, so greater spring force does not result in larger lead-screw rotations or subsequent linear plunger movement. Therefore, pump accuracy is independent from plunger position, provided the spring force can generate sufficient pumping pressure.
As the pump is intended for eventual use as an insulin pump, the device must be capable of providing both pseudo-continuous flow-rates, and one-off ‘bolus’ doses. In insulin therapy, the continuous flow-rate provides a background level of insulin to manage blood sugar levels between meals, and boluses are additional doses programmed by a user to compensate for meals, or to correct blood sugar levels. The presented pump design can provide modifiable flow-rates, and deliver bolus doses when connected to an external controller. The current device does not have Bluetooth connectivity or a built-in button, so a user cannot directly program a bolus dose.
Flow-rates are achieved by repeated activations of the low-power actuator at set intervals, controlled by an on-board micro-controller. Flow-rate is governed by the interval between each 0.001 ml dose (cycle time), which can be modified by program. The minimum achievable flow-rate is a function of the per-actuation dose volume, and the maximum acceptable cycle time for a certain application. If a cycle time of 1 h is considered acceptable, the minimum hourly flow-rate is 0.001 ml h−1. The maximum flow-rate is governed by the minimum possible cycle time (approximately 100 ms), allowing a flow-rate of 36 ml h−1. The practicality of the maximum flow-rate is limited in the current design by the reservoir volume of 3 ml, allowing the flow-rate to be sustained for only 5 min before the reservoir is depleted. With all flow-rates comprised of the same 0.001 ml individual increments, flow-rate is unaffected by plunger position. Pump accuracy is also not impacted by flow-rate.
Bolus deliveries of various size are possible through repeated activations of the actuator at a cycle time of 100 ms, providing rapid delivery. The minimum possible bolus size is 0.001 ml. The maximum possible bolus size depends on the period of time the dose must be delivered in. If an arbitrary period of 10 s is adopted, a maximum bolus size of 0.1 ml could be requested. Flow-rate and bolus accuracy are both tested to IEC standard in Section 7.1.
There is a significant difference between this design and current commercial, and open-source syringe pump designs. Other designs typically rotate a leadscrew (and advance a plunger) using a motor. The force required to deliver the fluid must be provided solely by the motor, which results in a greater electrical power requirement compared to this clockwork design. It is estimated the novel spring-based drive mechanism will offer a battery life of approximately 1 year, powered by two CR1632 cells, offering improvement over current devices. In addition, the pump can be built for $120 NZD ($75 USD), which represents a cost reduction compared to a commercial insulin pump. The current prototype is lightweight and portable, weighing 106 g, and measuring 20 mm in diameter and 120 mm in length.
The clockwork pump is also highly configurable for different applications. The leadscrew, gearbox, and reservoir can be changed to alter the pumping resolution. The design is modular, consisting of 6 separate sub-assemblies, which can be replaced or redesigned without impacting other sub-assemblies. Although the design is well-suited for medical applications, it is a prototype, and does not meet the safety requirements required for medical device certification. The pumping mechanism and design analysis presented will be useful to researchers who wish to further develop the concept for a wide variety of applications.
The clockwork pump:
-
•
Enables manufacture of a syringe pump for $120 NZD ($75 USD), with battery life of 1 year;
-
•
Provides a highly customizable design;
-
•
Allows for easy and inexpensive repair, and continued development; and
-
•
Provides researchers with a novel pumping concept able to be developed for medical applications, including insulin therapy.
3. Design file summary
The design files are all available at https://doi.org/10.17605/osf.io/j24f6. The file locations specified in Table 1 are relative to the base of this directory.
Table 1.
List of design files.
| Design filename | File type | Open source license | File location |
|---|---|---|---|
| Leadscrew_Housing | SLDPRT | CC BY-SA 4.0 | physical/ |
| Gearbox_Connector | SLDPRT | CC BY-SA 4.0 | physical/ |
| Gearbox_Housing | SLDPRT | CC BY-SA 4.0 | physical/ |
| Escapement_Support | SLDPRT | CC BY-SA 4.0 | physical/ |
| Escape_Wheel | SLDPRT | CC BY-SA 4.0 | physical/ |
| Escape_Wheel | DXF | CC BY-SA 4.0 | physical/ |
| Pallet | SLDPRT | CC BY-SA 4.0 | physical/ |
| Pallet | DXF | CC BY-SA 4.0 | physical/ |
| Actuator_Support | SLDPRT | CC BY-SA 4.0 | physical/ |
| Pallet_Lever | SLDPRT | CC BY-SA 4.0 | physical/ |
| Pallet_Lever | DXF | CC BY-SA 4.0 | physical/ |
| Motor_Mount | SLDPRT | CC BY-SA 4.0 | physical/ |
| Electronic_Housing | SLDPRT | CC BY-SA 4.0 | physical/ |
| Plunger | SLDPRT | CC BY-SA 4.0 | physical/ |
| Reservoir_Housing | SLDPRT | CC BY-SA 4.0 | physical/ |
| Spring_Housing | SLDPRT | CC BY-SA 4.0 | physical/ |
| b1 | KiCAD project | CC BY-SA 4.0 | electrical and software/ |
| b2 | KiCAD project | CC BY-SA 4.0 | electrical and software/ |
| continuousDelivery | Arduino | CC BY-SA 4.0 | electrical and software/ |
3.1. CAD files
Physical design was completed in SolidWorks. CAD files for all components to manufacture are provided as SolidWorks Part files (SLDPRT). Component drawings for manufactured components are included in https://doi.org/10.17605/osf.io/j24f6 located under component drawings. DXF files for the escape wheel, pallet, and pallet lever are included in place of drawings, as these components are wire-cut.
3.2. Electronics and software
PCB design was performed in KiCAD. Local library files are included for both the schematics and PCB footprints. Production files for PCB B1 and PCB B2 are provided in b1.zip and b2.zip, respectively. There is minimal software included as only the pump hardware is presented here. An Arduino script providing slow, continuous administration – continuousDelivery.ino – is included only, but can be expanded for any type of basic control [16].
4. Bill of materials
Manufactured and purchased components are listed in Table 2, Table 3 respectively. The total device cost is $123 NZD ($75 USD). A detailed bill of materials with all components, and relevant details is provided in https://doi.org/10.17605/osf.io/j24f6. All subsequent references to component numbers are consistent with the identification numbers in Table 2, Table 3.
Table 2.
Components to manufacture, with all costs in NZD.
| No. | Part | Assembly | Material | Cost(NZD) |
|---|---|---|---|---|
| 1 | Leadscrew housing | Leadscrew | Aluminium round bar | $2.21 |
| 2 | Gearbox connector | Gearbox | Aluminium round bar | $2.21 |
| 3 | Gearbox housing | Gearbox | Aluminium round bar | $2.21 |
| 4 | Escapement support | Escapement | Brass round bar | $0.80 |
| 5 | Escape wheel | Escapement | Brass sheet | $2.82 |
| 6 | Pallet | Escapement | Brass sheet | $2.82 |
| 7 | Actuator support | Escapement | Brass round bar | $0.80 |
| 8 | Pallet lever | Escapement | Brass sheet | $2.82 |
| 9 | Motor mount | Actuator | Aluminium round bar | $2.21 |
| 10 | Electronics housing | Actuator | Aluminium round bar | $2.21 |
| 11 | Plunger | Reservoir | Aluminium round bar | $2.21 |
| 12 | Reservoir housing | Reservoir | Aluminium round bar | $2.21 |
| 13 | Spring housing | Reservoir | Aluminium round bar | $2.21 |
| Total | $27.74 | |||
Table 3.
Components to purchase, with all costs in NZD.
| No. | Part | Assembly | Number | Unit cost (NZD) | Total cost(NZD) |
|---|---|---|---|---|---|
| 14 | Ball bearing | Leadscrew | 1 | $2.30 | $2.30 |
| 15 | Thrust bearing | Leadscrew | 1 | $3.20 | $3.20 |
| 16 | Leadscrew | Leadscrew | 1 | $4.95 | $4.95 |
| 17 | Circlip | Leadscrew | 1 | $0.30 | $0.30 |
| 18 | One-way bearing | Gearbox | 1 | $4.50 | $4.50 |
| 19 | Gearbox | Gearbox | 1 | $15.50 | $15.50 |
| 20 | Pallet shaft | Escapement | 1 | $1.50 | $1.50 |
| 21 | Miniature shutter motor | Actuator | 1 | $4.60 | $4.60 |
| 22 | M1.6 × 16 mm socket screw | Actuator | 2 | $0.16 | $0.32 |
| 23 | M1.6 × 5.5 mm spacer | Actuator | 2 | $2.23 | $4.45 |
| 24 | M1.6 × 14 mm socket screw | Electronics | 2 | $0.18 | $0.36 |
| 25 | M1.6 × 10 mm spacer | Electronics | 2 | $2.23 | $4.45 |
| 26 | PCB B1 | Electronics | 1 | $0.65 | $0.65 |
| 27 | PCB B2 | Electronics | 1 | $0.65 | $0.65 |
| 28 | 2 Pos cable | Electronics | 1 | $1.22 | $1.22 |
| 39 | 3 Pos cable | Electronics | 1 | $1.26 | $1.26 |
| 30 | CR1632 battery | Electronics | 2 | $3.02 | $6.04 |
| NA | PCB components | Electronics | 1 | $10.49 | $10.49 |
| 31 | Leadscrew nut | Reservoir | 1 | $1.95 | $1.95 |
| 32 | 3 mlreservoir | Reservoir | 1 | $5.90 | $5.90 |
| 33 | Infusion set | Reservoir | 1 | $15.30 | $15.30 |
| 34 | Compression spring | Reservoir | 1 | $2.50 | $2.50 |
| 35 | M2.5 × 3 mm grub screw | Multiple | 6 | $0.55 | $3.30 |
| Total | $95.69 | ||||
5. Build instructions
5.1. Overview of build process
Four key steps are required for the manufacture and assembly of the pump: manufacture of machined components; modification of purchased components; population of PCBs; and construction and integration of sub-assemblies. The six pump sub-assemblies are shown in Fig. 2, and identified in Table 4. The tools and equipment required for all manufacture, modification, and assembly tasks are listed in Table 5.
Fig. 2.
Breakdown of the 6 sub-assemblies in the clockwork pump.
Table 4.
Component list for 6 key pump sub-assemblies.
| Identifier | Sub-assembly | Components |
|---|---|---|
| A | Reservoir | 11, 12, 13, 31, 32, 33, 34 |
| B | Leadscrew | 1, 14, 15, 16, 17 |
| C | Gearbox | 2, 3, 18, 19, 35 |
| D | Escapement | 4, 5, 6, 7, 8, 19, 20 |
| E | Actuator | 9, 21, 22, 23, 35 |
| F | Electronics | 10, 24, 25, 26, 27, 28, 29, 30 |
Table 5.
Tools and equipment required for component manufacture, modification, and assembly.
| Tools/equipment | Required for |
|---|---|
| Mill, lathe | Manufacture and modification of multiple components |
| Tap/die | Manufacture and modification of multiple components |
| Broaching tool | Manufacture of spring housing |
| Wire EDM | Manufacture of escape wheel, pallet, and pallet lever |
| Saw | Modification of pinion and pallet shafts |
| Scalpel | Modification of shutter motor |
| Screwdrivers | Modification of gearbox |
| Soldering iron | Modification of shutter motor |
| Vice/press | Assembly of leadscrew and gearbox sub-assemblies |
| Pliers | Assembly of leadscrew sub-assembly |
| Hex keys | Assembly of gearbox, actuator, electronics, and reservoir sub-assemblies |
| Kapton tape | Assembly of electronics sub-assembly |
| SMT P & P machine | Assembly of PCB B1 and PCB B2 |
| Loctite | Assembly of escapement and reservoir sub-assemblies |
5.2. Manufacture of machined components
Manufacture components in Table 2 using the component drawings. The escape wheel, pallet, and pallet lever require wire EDM for manufacture. DXF files for these components are provided in https://doi.org/10.17605/osf.io/j24f6. Required tooling and equipment are listed in Table 5. For ease of manufacture, multiple components can be machined from the same stock. Table 6 provides material dimensions enabling all components to be fabricated. Individual part dimensions and possible material suppliers are provided in the detailed bill of materials.
Table 6.
Pre-manufacture material dimensions for fabrication of all pump components.
| Material | Dimensions | Components |
|---|---|---|
| Aluminium round bar | 20 mmOD × 300 mm | 1, 2, 3, 9, 10, 11, 12, 13 |
| Brass round bar | 16 mmOD × 30 mm | 4, 7 |
| Brass sheet | 30 mm × 30 mm × 1.2 mm | 5, 6, 8 |
5.3. Population of PCBs
Populate the PCBs in accordance with the KiCad project files. Table 7 specifies the PCB components required. More detail, including supplier links, is provided in the detailed bill of materials, including non-essential components. A solder paste stencil and a pick and place machine – manual or automatic – greatly assist the PCB population process.
Table 7.
PCB component list.
| Component | Board | Number | Unit cost (NZD) | Total cost (NZD) |
|---|---|---|---|---|
| Contact spring | B1, B2 | 7 | $ 0.50 | $3.50 |
| 2 Pos connector header | B1 | 1 | $ 0.48 | $0.48 |
| 3 Pos connector header | B1, B2 | 2 | $ 0.69 | $1.38 |
| 10 kΩresistor | B1 | 1 | $ 0.27 | $0.27 |
| 8 VN-Channel mosfet | B1 | 1 | $ 0.53 | $0.53 |
| Linear voltage regulator | B2 | 1 | $ 1.15 | $1.15 |
| 0.1 µFcapacitor | B2 | 3 | $ 0.10 | $0.30 |
| ATTiny 441 IC MCU | B2 | 1 | $ 1.36 | $1.36 |
| 6 Pos connector header | B2 | 1 | $ 0.69 | $0.69 |
5.4. Modification of off-the-shelf components
Instructions for modifying the purchased components are listed in Table 8. The two modification steps for the shutter motor (using components 21 and 28) are shown separately in Fig. 3, Fig. 3.
Table 8.
| Component(s) | Modification |
|---|---|
| 16 | Use the leadscrew modification drawing to turn a shoulder and groove onto the leadscrew shaft, and cut to length. |
| 19 + 20 | Cut the pallet shaft and gearbox pinion shaft down to 10 mm . |
| 21 + 28 | |
| a Using a scalpel, remove one of the two actuator lever arms. Remove the hook at the end of the remaining arm. | |
| b Using a scalpel, cut the flex circuit from the shutter motor, trimming the edges so they do not extend out from the motor body. Cut the connections off one end of the 2 position cable, and solder to the exposed wires of the 460 Ω coil. | |
| 23 | Cut two 5.5 mm sections from the brass tube. Ensure the exposed ends are flat. |
| 25 | Cut two 10 mm sections from the brass tube. Ensure the exposed ends are flat. |
| 31 | Use the leadscrew nut modification drawing to turn down the flange of the nut, and drill and tap two holes for grub screws. |
Fig. 3.
(a) Removal of actuator arm and hook (b) Removal of flex circuit and connection of 2 position cable.
5.5. Assembly
5.5.1. Leadscrew sub-assembly
Graphical instructions for assembling the leadscrew sub-assembly (sub-assembly B as identified in Fig. 2) are provided in Fig. 4. Each assembly step is detailed in Table 9. Components are numbered with reference to Table 2, Table 3.
Fig. 4.
Graphical build instructions for the leadscrew sub-assembly.
Table 9.
| Step | Instruction |
|---|---|
| 1 | Press the ball bearing (14) into the leadscrew housing (1) using a vice or press. |
| 2 | Press the clearance washer (larger ID) of the thrust bearing (15) into the housing using a vice or press. A piece of rod or tube will be required to press on the surface of the washer. Ensure the washer is orientated so the grooves are exposed. |
| 3 | Insert the leadscrew (16) into the housing so that ball bearing sits against the shoulder of the leadscrew. |
| 4 | Insert the ball cage onto the leadscrew shaft, followed by the remaining thrust washer (grooves facing inwards). Using pliers, place the circlip (17) onto the shaft. Push the circlip down the shaft using spare tube to seat it in the shaft groove. |
5.5.2. Gearbox sub-assembly
Graphical instructions for assembling and integrating the gearbox sub-assembly (sub-assembly C as identified in Fig. 2) are provided in Fig. 5. Each assembly step is detailed in Table 10. Components are numbered with reference to Table 2, Table 3.
Fig. 5.
Graphical build and integration instructions for the gearbox sub-assembly.
Table 10.
Assembly and integration instructions for the gearbox sub-assembly. Component numbering per Tables 2–3.
| Step | Instruction |
|---|---|
| 1 | Press the one-way bearing (18) into the leadscrew-gearbox connector (2) using a vice or press. Ensure the bearing is orientated so the leadscrew can rotate freely in the direction indicated in step 4 of Fig. 5, but lock in the opposite direction. |
| 2 | Insert the shaft of the gearbox (19) into the connector so that the connector sits up against the flange of the gearbox. Insert grub screws (35) into the threaded holes, and tighten onto the shaft using a 1.5 mm hex key. |
| 3 | Press the gearbox and connector into the gearbox housing (3) so that back plate of the gearbox sits on the bottom face of the rectangular cut-out. |
| 4 | Integrate the leadscrew and gearbox sub-assemblies by pushing the one-way bearing onto the leadscrew shaft, and screwing the housing components together. |
5.5.3. Escapement sub-assembly
Graphical instructions for assembling the escapement sub-assembly (sub-assembly D as identified in Fig. 2) are provided in Fig. 6. Each assembly step is detailed in Table 11. Components are numbered with reference to Table 2, Table 3.
Fig. 6.
Graphical build instructions for the escapement sub-assembly.
Table 11.
| Step | Instruction |
|---|---|
| 1 | Insert the pinion shaft (19) into the escapement support plate (4) as far as possible. Push the escape wheel (5) onto the shaft so that the wheel sits against the plate. Ensure the wheel is attached in the orientation shown. Use Loctite to secure the wheel to the shaft. |
| 2 | Position the pallet (6) 1 mm from the end of the pallet shaft (20), and secure with Loctite. Insert the pallet shaft into the escapement support plate in the orientation shown. |
| 3 | Push the escapement support plate and the actuator support plate (7) together. |
| 4 | Attach the pallet lever arm (8) to the pallet shaft so the lever sits 1 mm from the actuator support plate. Secure the connection with Loctite. |
5.5.4. Actuator sub-assembly
Graphical instructions for assembling and integrating the actuator sub-assembly (sub-assembly E as identified in Fig. 2) are provided in Fig. 7. Each assembly step is detailed in Table 12. Components are numbered with reference to Table 2, Table 3.
Fig. 7.
Graphical build and integration instructions for the actuator sub-assembly.
Table 12.
Assembly and integration instructions for the actuator sub-assembly. Component numbering per Tables 2–3.
| Step | Instruction |
|---|---|
| 1 | Press the motor mount (9) onto the shutter motor (21) so that the mount sits against the flange of the motor. Insert grub screws (35) into the threaded holes, and tighten onto the motor using a 1.5 mm hex key. |
| 2 | Insert M1.6 × 16 mm socket screws (22) into the clearance holes of the mount, and place a 5.5 mm spacer (23) onto each of the screws. |
| 3 | Insert the socket screws into the clearance holes of the escapement sub-assembly. Ensure the pin of the motor arm sits inside the slot of the pallet lever arm (see detail view). The motor may need to rotated in the mount for proper alignment. |
| 4 | To integrate the actuator and escapement with the gearbox and leadscrew assemblies, insert the socket screws into the threaded holes of the gearbox housing and tighten using a 1.5 mm hex key. |
5.5.5. Electronics sub-assembly
Graphical instructions for assembling and integrating the electronics sub-assembly (sub-assembly F as identified in Fig. 2) are provided in Fig. 8. Each assembly step is detailed in Table 13. Components are numbered with reference to Table 2, Table 3.
Fig. 8.
Graphical build and integration instructions for electronics sub-assembly.
Table 13.
Assembly and integration instructions for the electronics sub-assembly. Component numbering per Tables 2–3.
| Step | Instruction |
|---|---|
| 1 | Insert the M1.6 × 14 mm socket screws (24) through the B1 board (26) so that the head of the screws sits on the battery contact side of the board. Place a 10 mm spacer (25) onto each of the screws. Insert the screws into the threaded holes of the actuator motor mount and tighten using a 1.5 mm hex key. |
| 2 | Insert the motor cable into the two-pin connector of B1 (26). Connect B2 (27) to B1 using the 3 pin connector cable. Ensure the battery contacts of B2 face B1. |
| 3 | Insert two CR1632 batteries (cylindrical sides wrapped in Kapton tape) between the two boards, with the negative terminal of the battery against the black board. |
| 4 | Screw the electronics housing (10) onto the gearbox housing. If the internal shoulder in the electronics housing does not apply gentle pressure to B2 (27), create a spacer to ensure good contact pressure. |
5.5.6. Reservoir and plunger sub-assembly
Graphical instructions for assembling and integrating the reservoir and plunger sub-assembly (sub-assembly A as identified in Fig. 2) are provided in Fig. 9. Each assembly step is detailed in Table 14. Components are numbered with reference to Table 2, Table 3.
Fig. 9.
Graphical build and integration instructions for the reservoir and plunger sub-assembly.
Table 14.
Assembly and integration instructions for the reservoir and plunger sub-assembly. Component numbering per Tables 2–3.
| Step | Instruction |
|---|---|
| 1 | Secure the plunger (11) to the base of the leadscrew nut (31) using Loctite. Insert M2 grub screws (35) into the threaded holes and tighten using a 1.5 mm hex key until the flat of the grub screw extends 1 mm from the surface of the flange. Secure the grub screws in place using Loctite. |
| 2 | Fill the reservoir (32) and connect the infusion set (33) as per the manufacturer’s instructions. Insert the reservoir into the reservoir housing (12) and lock the infusion set to the housing using the threaded fitting. |
| 3 | Place the compression spring (34) over the leadscrew. Screw the spring housing (13) onto the leadscrew housing. Thread the plunger onto the leadscrew, ensuring the grub screws sit in the internal slots of the spring housing. Press the plunger down as far as it will go. |
| 4 | Screw the reservoir housing onto the spring housing. |
6. Operation instructions
6.1. Loading and programming procedure
After assembling the pump, the following procedure should be used to program, load, and prime the pump. Software is provided only to configure continuous, un-changing delivery. Behaviour can be adapted to specific needs, including real-time changes, by incorporating Bluetooth communication, or a physical button mounted to the device. SPI and other peripherals are broken out from the rear of B2 (27) to enable significant customization.
Users should be aware the current design is a proof-of-concept prototype, and has not been proven to meet the requirements to act as an in-vivo medical device.
-
1.
Input the desired rate of continuous infusion into the code (continuousDelivery.ino).
-
2.
Program the ATTiny441 using a suitable programmer, for example an Arduino Nano configured as an in-system programmer. The pinout for the programming header can be seen in Fig. 10.
-
3.
Load the pump by pushing on the plunger until the spring is fully compressed.
-
4.
Fill the reservoir with the desired fluid using a syringe or vial, so that the rubber plunger of the reservoir sits flush with the end of the reservoir. Connect the infusion set to the reservoir, as per the manufacturer’s instructions.
-
5.
Insert the reservoir into the reservoir housing, as shown in Section 5.5.6.
-
6.
Place the free end of the infusion set into a beaker. Screw the reservoir housing onto the spring housing. The pump plunger will engage with the reservoir plunger as the housing components are connected. Fluid will be flushed through the infusion line into the beaker, priming the infusion line.
Fig. 10.
Pinout of the programming header on B2 (27).
6.2. Operational safety hazards
Potential safety hazards during operation of the device along with measures to mitigate the risk are listed in Table 15.
Table 15.
Operational risks, and measures to mitigate risk.
| Hazard | Potential cause | Mitigation |
|---|---|---|
| Injury from spring decompression | Uncontrolled release of compressed spring and plunger during loading. | Follow assembly instructions, ensure the escapement and one-way bearing lock the screw, and ensure the grub screws are installed securely in the plunger. |
| Injury from needle | Contact with the exposed needle of the infusion set. | Follow manufacturer’s instructions for handling infusion sets and cover exposed needle with a sheath when the pump is not in use. |
| Injury from sharp edges on manufactured components | Burrs or rough surfaces on pump housings could cause injury when loading and handling the pump. | De-burr all components after manufacture and ensure there are no exposed sharp edges. |
7. Validation and characterization
7.1. Accuracy testing to IEC 60601-2-24(2012)
The accuracy of the clockwork pump was assessed according to the test settings and evaluation methods provided in IEC 60601-2-24(2012), an international standard outlining safety and performance requirements for infusion pumps [17]. The IEC compliant testing set-up is shown in Fig. 11. The pump delivers the testing fluid through an infusion set, and a 18 gauge needle into a beaker of water. The change in mass of the beaker during testing is measured using an analytical balance (readability of 0.01 mg), and correlated to the volume delivered by the pump.
Fig. 11.
Testing setup to IEC 60601-2-24.
The flow-rate and bolus accuracy of the clockwork pump were individually assessed to clauses 201.12.103 and 201.12.105 of the IEC standard. To benchmark the clockwork pump against a commercial syringe pump, a Medtronic 640G insulin pump (Medtronic Inc; Northridge, CA, USA) was tested using the same test set-up and protocol. Specific test parameters and results for the flow-rate and bolus tests are presented in Sections 7.1.1, and 7.1.2 respectively.
The IEC standard does not provide guidelines for quantifying measurement uncertainty. Therefore, the United States Pharmacopeia methodology was used to estimate both repeatability and accuracy contributions to the measurement uncertainty of the balance [18]. Measurement uncertainty arising from repeatability error can be estimated using the balance repeatability, , a safety factor of 2, and the minimum weight to be measured, .
| (1) |
Balance repeatability is defined as the standard deviation of at least 10 repeated measurements of a test weight. The repeatability of the balance used for assessing the clockwork pump was found to be 0.014 mg. The minimum weight to be measured is 1 mg, corresponding to the minimum volume displaced by the pump (0.001 ml).
In addition to repeatability error, accuracy error of the balance was assessed from 15 repeated measurements of a test weight with mass greater than 5% of the balance capacity (repeatability errors dominate near limit of balance capacity) [18]. With a 20 g test weight, the average accuracy error was found to be 3.4 10-3% of the measured weight, which is negligible. The combined measurement uncertainty arising from the balance is therefore considered to be 3% of the minimum measured weight, or .
Aside from measurement uncertainties associated with the balance, experimental factors could introduce error. Potential sources of error are listed in Table 16 along with steps taken to mitigate their impact. With a factor of safety of 2 placed on measurement uncertainty, and sources of experimental error effectively controlled, the uncertainty for each individual measurement is conservatively estimated as .
Table 16.
Sources of experimental error and mitigation strategies.
| Source | Description and mitigation steps |
|---|---|
| Change in ambient test conditions | Changes in temperature and humidity in the laboratory used for testing could impact results, including the density of the testing solution (and recorded mass). Temperature and relative humidity were measured every 5 min over a period of 24 h to quantify the fluctuations in ambient conditions over the length of a flow-rate test. The average temperature was measured as 20.4 ° C , with variation 2 ° C . The average relative humidity was 58.3%, with variation 13.5%. As the water used for testing was left to equilibrate to room temperature, volume was calculated using the density of water at 20.4 ° C . The variation on calculated volume due to temperature changes (2 ° C ) is 0.05%, and thus considered negligible. |
| External vibration | External vibrations could have significant impact on the performance of the balance, by introducing loads which interfere with the weight measurement mechanism. Therefore, the balance was placed on an active vibration isolating table (Vibraplane, Boston, MA, USA). |
| Eccentric loading of balance | If the load is not centred on the weighing pan, eccentricity error could impact the measurement. To reduce potential eccentricity error, the beaker was centred on the weighing pan. The level of the balance was also monitored throughout testing. |
| Evaporation | Evaporation of water from the beaker could impact the measured mass, which is of particular concern in flow-rate tests which run for 24 h . To reduce likelihood of evaporation, a 1.5 mm layer of paraffin oil was placed on top of the water in the weighing beaker. The use of paraffin oil is common in studies investigating the accuracy of commercial insulin pumps, and is proven to improve test accuracy [19], [20], [21], [22]. |
| Air in testing solution | Air in the testing solution would impact the measured mass. A testing solution of ISO 3696:1987 class 3 water was used, as per the IEC standard. The water was de-gassed to reduce bubble formation, and limit the resulting variation in mass. |
| Siphoning effects | Siphoning effects could occur if the pump is not vertically aligned with the cannula tip. As shown in Fig. 11, an adjustable table was used to ensure the pump centre-line was level with the cannula tip. |
| Blockage in the infusion line | If a blockage developed in the infusion line, the test would be compromised. As per the IEC standard, a new infusion set was used for every flow-rate test. Frequent changes of the infusion line limits the chance of blockages developing. |
7.1.1. Flow-rate accuracy
Flow-rate testing was carried out in accordance with clause 201.12.103 of the IEC standard. An intermediate flow-rate rate was assessed over an analysis period of 24 h, with a sampling interval of 15 min. To enable comparison to a commercial pump (insulin pump), a flow-rate of 0.01 ml h−1 was selected, as it is considered an intermediate rate for insulin therapy [20]. The maximum positive and negative percentage errors on flow ( and respectively) were calculated for six discrete sliding observation windows (15 min, 60 min, 150 min, 330 min, 570 min, and 930 min) and plotted as ‘trumpet’ curves, the standard specified method for presenting flow-rate accuracy data. Trumpet plots for the commercial and clockwork pumps are presented in Fig. 12, Fig. 12, respectively.
Fig. 12.
(a) Trumpet curve plot for the commercial insulin pump at a flow-rate of 0.01 ml h−1 (b) Trumpet curve plot for the clockwork pump at a flow-rate of 0.01 ml h−1.
The flow-rate is calculated from the total recorded mass in each observation window. The largest relative measurement uncertainty will occur for the 15 min observation window, due to the smallest recorded mass (2.5 mg). The relative uncertainty on the measurement for the 15 min window is . For larger observation windows, the recorded mass is greater, and the relative uncertainty decreases. Due to hardware differences between the two pumps, the number of doses each device delivers over the hour to provide a given flow-rate differ. The clockwork pump delivers 10 individual doses (cycle time of 6 min) while the commercial device delivers 20 (cycle time of 3 min). Clause 201.12.103 the standard does not specify a required cycle time (or individual dose size) for any given flow-rate.
The maximum positive and negative flow errors for the commercial device at an observation window of 15 min are 7.8% and −5.8% respectively. The clockwork pump presents greater error for the same observation window duration, with maximum flow errors of 16.7% and −11.8%. As shown in Fig. 12, Fig. 12, error decreases as the observation window widens, which is an expected result due to greater averaging within the window. At the standard based 930 min observation window, the two pumps demonstrate similar error range with 0.7% to −0.2% for the commercial device compared to 3.1% to 2.2% for the clockwork pump. The commercial pump delivers 20 doses per hour compared to 10 for the clockwork pump, so the results are averaged across a greater range of individual doses, which yields smaller error.
and remain symmetrical about the set rate for the commercial pump, which indicates similar positive and negative error across the entire test, which averages out to an insignificant overall mean error of −0.5%. The clockwork pump consistently over-delivers throughout the test. As a result, becomes positive, due to the small systemic bias in the current prototype, as shown in the 930 min observation window, resulting in a larger overall mean error of 1.0%. Overall, accuracy testing of the clockwork pump prototype produced promising results. While the clockwork pump mean error is greater than the commercial pump, further development and manufacture of the design should yield a device with very similar performance. The results validate the novel pumping concept, proving adequate accuracy can be obtained.
7.1.2. Bolus accuracy
Bolus testing was conducted to the protocol outlined in clause 201.12.105 of the IEC standard by measuring the mass displaced by 25 successive bolus deliveries for each bolus volume tested. The minimum setting for the pump was tested, which for the clockwork pump is 0.001 ml. Two other volumes were also tested, 0.002 ml, and 0.01 ml. The standard does not specify a settling time between measurements, so a 2 min period was implemented to ensure consistency across experiments. Testing found a 2 min period was adequate to achieve a stable reading. The uncertainty of each measurement is . For measurements of 0.001 ml, 0.002 ml, and 0.01 ml boluses, the relative uncertainty is , , and respectively.
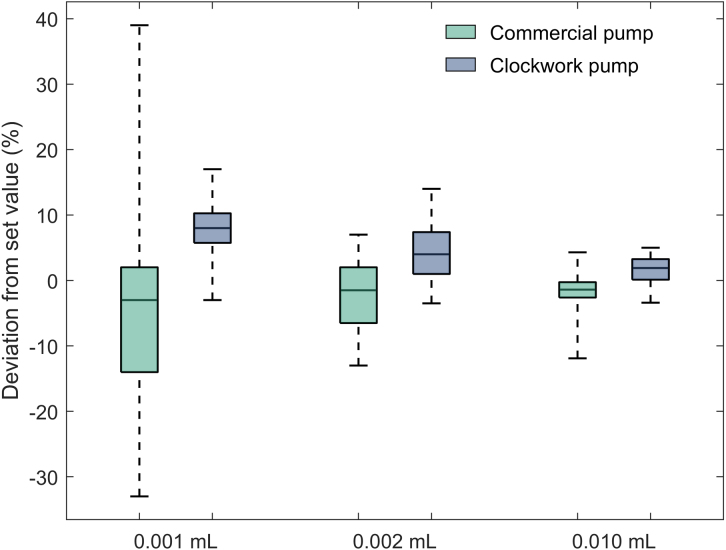
Bolus accuracy, presented as relative deviation from the set value (expressed as a percent) for all bolus volumes and pumps tested is shown in boxplots in Fig. 13. The vertical lines on the boxplot indicate the maximum negative deviation and maximum positive deviation from the set value from the series of 25 boluses. The upper and lower limits of the box indicate the upper and lower quartiles of deviation, and the middle line separating the box represents the median deviation. For dose sizes of 0.001 ml and 0.002 ml, the clockwork pump demonstrates improved consistency compared to the commercial device with decreased interquartile ranges (4.5% and 6.4% compared to 16.0% and 8.5%, respectively). The overall range for the commercial device at a volume of 0.001 ml is also significantly greater than the clockwork pump (72% compared to 20%). For a dose size of 0.01 ml, the clockwork pump interquartile range is slightly greater than the commercial device (3.1% compared to 2.9%). However, the overall range is lower (8.4% compared to 16.2%), which indicates similar consistency. The larger relative interquartile range associated with 0.002 ml compared to 0.001 ml for the clockwork pump is an unexpected result, but can likely be attributed to the small sample size (25) specified in the standard. Further testing is required to better quantify pump performance.
Fig. 13.
Box plot comparing bolus accuracy of commercial insulin pump (Medtronic 640G) to the clockwork pump.
Despite exhibiting improved or similar consistency to the commercial device, the median error for the clockwork pump is greater than the commercial device across all three bolus volumes (8.0%, 4.0%, and 1.9% compared to −3.0%, −1.5% and −1.4% for 0.001 ml, 0.002 ml, 0.01 ml volumes respectively). Low variability with a consistent positive median error indicates a systemic error, such as a slightly different gear ratio, or leadscrew pitch than expected. Systematic errors can be eliminated with further development and testing, and/or more precise fabrication.
7.2. Theoretical pump resolution
The linear distance the plunger travels per actuation, , can be calculated using the gear ratio, , number of teeth on the escape wheel, , and the lead of the leadscrew, . The theoretical volume displaced from the reservoir is then found using the reservoir inner diameter, :
| (2) |
| (3) |
The minimum resolution of the pump can easily be adjusted by altering the leadscrew lead, gear ratio, number of escape wheel teeth, or the diameter of the reservoir. Note for fine leads, the screw becomes self-locking, and cannot be back-driven. Section 7.4 presents the method to estimate the minimum lead required to ensure the screw can be back-driven. Increasing the gear ratio also increases the torque required to rotate the escape wheel, and thus, the spring force required. The number of escape wheel teeth and the reservoir diameter can be changed without significantly altering the spring force and torques. If the reservoir inner diameter was reduced by half to 6 mm, the minimum delivery of the pump would decrease to 2.5 10-4 ml.
7.3. Torque measurement
The torque to rotate the escape gear through the gearbox, and the torque required to actuate the pallet of the escapement were measured. For both cases, a mass at the end of a lever was used to find the force, and torque required to initiate rotation. The test apparatus for escape wheel rotation and pallet rotation are shown in Fig. 14, Fig. 14, respectively. Washers were used as the mass, and were incrementally added to the end of the 3D-printed lever, until rotation occurred. Using the force ( and ) and known lever length ( and ), the torques and were calculated:
| (4) |
| (5) |
Fig. 14.
(a) Apparatus for the measurement of escape wheel starting torque (b) Apparatus for the measurement of pallet actuation torque.
7.4. Spring validation and calculation of forces, torques and pressures
To select a spring suitable for insulin delivery, a minimum required spring stiffness was calculated. The stiffness of various off-the-shelf springs were estimated, and a spring meeting the required stiffness selected. The minimum and maximum plunger force, and achievable pumping pressure, were then calculated along with the maximum generated leadscrew torque. Table 17 lists the variable definitions and values required for all calculations.
Table 17.
Variable definitions, values, and source for validating spring selection.
| Variable | Definition | Value | Source |
|---|---|---|---|
| Mean screw diameter | 7 10-3 m | Leadscrew property | |
| Thread angle | 15° | Leadscrew property | |
| Leadscrew lead | 8 10-3 m | Leadscrew property | |
| Starting friction of brass nut | 0.30 | Tabulated value [23] | |
| Escapement starting torque | 5.4 10-4 N m | Measured (see Section 7.3) | |
| Force to deliver 1.0 10-6 l in 1 s | 0.8 N | Estimated (see Appendix) | |
| Factor of safety | 1.5 | Design parameter | |
| Minimum spring compression | 12.0 10-3 m | Design parameter | |
| Maximum spring compression | 40.0 10-3 m | Design parameter | |
| Spring wire diameter | 1 10-3 m | Spring property | |
| Shear modulus | 79.3 109 N m−2 | Tabulated value for steel [24] | |
| Mean spring diameter | 13 10-3 m | Spring property | |
| Number of active spring coils | 9 | Spring property | |
| Cross-sectional area of reservoir | 1.13 10-4 m2 | Reservoir property |
7.4.1. Required spring stiffness
The selected spring must provide sufficient axial force across the entire working range of the plunger to back-drive the leadscrew and generate adequate pressure to deliver fluid. To ensure the selected spring meets the force requirements for successful operation of the pump, a condition for back-driving involving all forces and torques present in the system must be established. Back-driving will occur when , where is the lowering torque [23]. The lowering torque is the torque required to rotate the lead-screw so the plunger is advanced in the same direction as the load (spring force). A negative indicates the load will advance the plunger, and drive fluid from the reservoir through rotation of the screw without any external effort (back-driving).
As shown in Fig. 15, the spring force driving the plunger, , is opposed by the delivery force, . Rotation of the leadscrew is also opposed by the starting torque of the escape wheel, . Note, the delivery force depends on the pumping application. A value of appropriate for initial testing and development of the device as an insulin pump was estimated, with details provided in Appendix. To adapt the design for another application, should be measured, or calculated from a minimum or maximum pressure requirement.
Fig. 15.
Free body diagram of leadscrew and plunger.
An equation for in terms of , and can be formed:
| (6) |
Where all variable definitions, values, and sources are listed in Table 17. The minimum spring force required for back-driving is found by rearranging Eq. (6) and setting :
| (7) |
The spring stiffness required to ensure adequate spring force is provided across the entire working range of the spring, , can be found using Hooke’s law:
| (8) |
7.4.2. Validation of selected spring
To find a suitable spring, a variety of compression springs 50 mm in length with varying wire diameters, , and mean spring diameters, , were found. The spring stiffness for each spring was estimated using a strain energy approach, and the spring which most closely matched the required stiffness identified [25]. Estimation of the spring stiffness for the closest matching spring is presented:
| (9) |
As , the spring will provide adequate force across the entire working range of the plunger to back-drive the leadscrew and ensure all fluid in the reservoir can be delivered.
7.4.3. Minimum and maximum spring forces and pumping pressure
The minimum and maximum axial forces acting on the plunger, and , can be calculated using the minimum and maximum spring compression of the chosen spring:
| (10) |
| (11) |
The minimum and maximum pressure applied to the fluid in the reservoir by the plunger can then be calculated using and , and the internal cross-sectional area of the fluid reservoir.
| (12) |
| (13) |
7.4.4. Maximum leadscrew torque
Maximum torque experienced by the leadscrew, , must be known to assess the suitability of the one-way bearing. can be substituted for in Eq. (6) to find a maximum leadscrew torque of 2.8 10-3 N m.
7.5. Battery-life estimate
To estimate pump battery life, use as an insulin pump is considered, where a delivery requirement of up to 1 ml per day can be expected. All variables, values, and sources of values required for the battery life estimate are listed in Table 18. The average electromagnet current required to deliver 1 ml per day, , can be calculated:
| (14) |
The average on-board processor current required to deliver the required daily dose, , can be calculated:
| (15) |
The pump battery life, , can be then be estimated:
| (16) |
was used as the peak current is greater than the peak pulse current stated within the battery datasheet [27].
Table 18.
Variable definitions, values, and source for battery life estimate.
| Variable | Definition | Value | Source |
|---|---|---|---|
| Electromagnetic actuation time | 40 ms | Design parameter | |
| Number of actuations per day | 1000 | Design parameter | |
| Time in day | 86.4 106 ms | – | |
| Electromagnet coil current | 12.2 mA | Measured steady-state current | |
| Processor active time | 24 000 ms | Design parameter | |
| Processor active current | 0.2 mA | Product data-sheet [26] | |
| Processor idle time | 24 700 ms | Design parameter | |
| Processor idle current | 0.03 mA | Product data-sheet [26] | |
| Processor sleep time | 86.35 106 ms | Design parameter | |
| Processor sleep current | 0.0013 mA | Product data-sheet [26] | |
| Battery capacity | 130 mA h | Product data-sheet [27] | |
| Factor of safety | 2 | Selected parameter |
7.6. Failure considerations
7.6.1. Circlip failure
The circlip transfers the axial spring load to the thrust bearing. To assess the load bearing capacity of the circlip, an MTS Criterion (MTS Systems Corporation, MN, USA) tensometer was used to apply an axial load directly onto a circlip sitting in the groove of a test shaft. As shown in Fig. 16(a), the test shaft was attached to the bottom jaw of the tensometer. A 4.05 mm ID aluminium tube was attached to the top jaw so the load could be applied directly to the circlip. The load was applied with a set crosshead movement of 1 mm min−1.
Fig. 16.
(a) Apparatus for circlip testing (b) Load cell readout with circlip failure load indicated.
The load cell readout is presented in Fig. 16(b), and shows a peak load of 423 N, before failure (indicated by a reduction in applied load). The factor of safety on circlip failure is calculated using the circlip failure load, , and the maximum spring force:
| (17) |
7.6.2. One-way bearing failure
The factor of safety on one-way bearing failure is calculated by comparing the maximum leadscrew torque to the bearing manufacturer’s published torque limit. The torque limit (0.34 N m) represents the maximum torque that can be applied to the bearing without slippage, for a lifetime of 1 million locking cycles, which occur when reloading the pump [28].
| (18) |
7.6.3. Gear failure
The tangential load applied to the input gear of the gearbox by the leadscrew, , can be estimated using the maximum torque, , and the pitch diameter of the gear, :
| (19) |
It is suggested the approach for estimating gear contact and bending stress outlined in the ANSI/AGMA 2001-D04 standard is followed [29]. The standard provides methodology for rating the pitting resistance and bending strength of spur and helical involute gear pairs, and accounts for fatigue loading. Due to the complexity of the calculations and unknown characteristics of the current gearbox, including material hardness and surface condition, the analysis is not presented here. If the design is further developed for applications where gearbox failure would have severe consequences, it is essential a fatigue-based gear analysis is conducted to ensure the selected gearbox can safely support the load for the pump lifetime.
7.7. Design limitations
Limitations of the clockwork pump design are identified in Table 19, along with potential implications.
Table 19.
Design limitations and implications.
| Limitation | Description and implication |
|---|---|
| No fail-safe mechanism | If the escapement is decoupled from the leadscrew, there is currently no mechanism to prevent the delivery of all fluid in the reservoir. The escapement could become decoupled if the one-way bearing fails, the gearbox shaft slips in the gearbox connector, the gearbox fails, or the escape wheel slips on its shaft. |
| Excess spring force | As the compression spring is selected to provide sufficient force to back-drive the leadscrew when the plunger is at the minimum spring compression position, there is excess spring force at all other plunger positions. Extra spring force places greater load on key components such as the gearbox, increasing wear and reducing pump life. |
| Variable pumping pressure | Achievable pressure decreases from 175 kPa at maximum spring compression to 50 kPa at minimum spring compression. The large pressure drop is a limitation as if the required pressure exceeds the achievable pressure at any stage of delivery, the pump will fail to deliver. The pump will also not be suitable for a situation which must provide a constant pressure throughout pump operation. |
| Unsupported axial load | Only the axial load in the pumping direction is supported by the thrust bearing. The axial force on the leadscrew when loading the pump is currently supported by the gearbox connector and gearbox, which places unnecessary load on these components. |
| Limited pumping resolution | Although the pumping resolution of the design can be modified easily, it is unlikely that the resolution achieved by motor driven pumps with high gearing can be matched. For the majority of applications, the resolution achievable with the clockwork pump will be adequate. |
8. Conclusion
A design for low-cost, low-power, portable, and programmable syringe pump is presented. The device is highly customizable, but is intended for eventual use as an insulin pump. The pump design is made accessible through construction from off-the-shelf or readily manufactured components. The flow-rate and bolus delivery accuracy of the device are similar to a commercial insulin pump. The testing results validate the novel pumping mechanism which utilizes a clockwork mechanism to achieve low-power delivery of fluid from the reservoir, showing it can compete with motor-driven devices. A systematic error in the current prototype was identified, with the pump consistently over-delivering. Further development of the design and incorporation of higher precision hardware will likely rectify the issue. Bluetooth control of the device will be included in future design iterations, allowing the user to alter flow-rates, and select bolus doses real-time, using a mobile phone.
Human and animal rights
No human or animal studies were conducted in the design of this work.
Declaration of competing interest
None.
Acknowledgements
Funding
This work was supported by the NZ National Science Challenge 7, Science for Technology and Innovation (2019-S3-CRS), and the University of Canterbury Doctoral Scholarship programme . The authors would also like to thank CANTEC Ltd, Christchurch, New Zealand, for offering workshop tools, equipment, and expertise during the design and development of this project.
Biography

Francis Pooke obtained a Bachelor of Mechanical Engineering with First Class Honors from the University of Canterbury, New Zealand, in 2021. He is currently completing his doctoral studies, where his focus is on medical devices, and providing accessible care to all.
Appendix.
To obtain a realistic estimate of the delivery force, , during operation of the device as an insulin pump, a simple energy balance was performed. A requirement for the pump to deliver 0.001 ml over a period of 1 s was established. While arbitrary, the dose size and delivery time-frame were deemed reasonable for initial development of a pump targeting insulin therapy. As the infusion line is 0.7 m long, a height difference between the pump and the delivery point of 0.7 m was selected, to represent the situation requiring greatest pumping pressure. The variables, values, and value sources used for all calculations are included in Table 20.
The linear distance each 0.001 ml dose travels through the infusion line, and fluid velocity required to deliver the dose over a period of 1 s can be calculated:
| (20) |
| (21) |
Table 20.
Variable definitions, values, and source for estimating delivery force.
| Variable | Definition | Value | Source |
|---|---|---|---|
| Dose volume | 1.0 10-9 m3 | Reservoir property | |
| Cross-sectional area of infusion line | 1.12 10-7 m2 | Infusion line property | |
| Time to deliver dose | 1 s | Selected time period | |
| Density of water | 997 kg m−3 | Reference value | |
| Acceleration due to gravity | 9.81 m s−2 | Reference value | |
| Height difference | 0.7 m | Length of infusion line | |
| Cross-sectional area of reservoir | 1.13 10-4 m2 | Infusion line property |
The delivery force, can then be estimated using a simple energy balance:
| (22) |
References
- 1.Stephens E., Riddle M. Evolving approaches to intensive insulin therapy in type 1 diabetes: multiple daily injections, insulin pumps and new methods of monitoring. Rev. Endocr. Metab. Disord. 2003;4(4):325–334. doi: 10.1023/A:1027345927676. [DOI] [PubMed] [Google Scholar]
- 2.Ziegler R., Waldenmaier D., Kamecke U., Mende J., Haug C., Freckmann G. Accuracy assessment of bolus and basal rate delivery of different insulin pump systems used in insulin pump therapy of children and adolescents. Pediatr. Diabetes. 2020;21(4):649–656. doi: 10.1111/pedi.12993. [DOI] [PubMed] [Google Scholar]
- 3.Ziegler R., Oliver N., Waldenmaier D., Mende J., Haug C., Freckmann G. Evaluation of the accuracy of current tubeless pumps for continuous subcutaneous insulin infusion. Diabetes Technol. Therapeut. 2021;23(5):350–357. doi: 10.1089/dia.2020.0525. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Pickup J., Keen H. Continuous subcutaneous insulin infusion at 25 years: Evidence base for the expanding use of insulin pump therapy in type 1 diabetes. Diabetes Care. 2002;25(3):593–598. doi: 10.2337/diacare.25.3.593. [DOI] [PubMed] [Google Scholar]
- 5.Holder-Pearson L., Chase J.G. Socio-economic inequity: diabetes in New Zealand. Front. Med. 2022;9 doi: 10.3389/fmed.2022.756223. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Wijnen B., Hunt E.J., Anzalone G.C., Pearce J.M. Open-source syringe pump library. PLoS One. 2014;9(9) doi: 10.1371/journal.pone.0107216. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Amarante L.M., Newport J., Mitchell M., Wilson J., Laubach M. An open source syringe pump controller for fluid delivery of multiple volumes. eNeuro. 2019;6(5) doi: 10.1523/ENEURO.0240-19.2019. ENEURO.0240–19.2019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Garcia V.E., Liu J., DeRisi J.L. Low-cost touchscreen driven programmable dual syringe pump for life science applications. HardwareX. 2018;4 doi: 10.1016/j.ohx.2018.e00027. [DOI] [Google Scholar]
- 9.Cubberley M.S., Hess W.A. An inexpensive programmable dual-syringe pump for the chemistry laboratory. J. Chem. Educ. 2017;94(1):72–74. doi: 10.1021/acs.jchemed.6b00598. [DOI] [Google Scholar]
- 10.Baas S., Saggiomo V. Ender3 3D printer kit transformed into open, programmable syringe pump set. HardwareX. 2021;10 doi: 10.1016/j.ohx.2021.e00219. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Payne M., Pooke F., Holder-Pearson L., Chase J., Bock M., Campbell J., Knopp J. Bench-side dose accuracy of an open-source ultra-low-cost insulin-pump, with testing conducted to IEC 60601-2-24. J. Diabetes Sci. Technol. 2022 doi: 10.1177/19322968221142316. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Payne M., Pooke F., Fulton H., Shaw H., Coulson T., Knopp D., Holder-Pearson L., Campbell J., Chase J. Design of an open source ultra low cost insulin pump. HardwareX. 2022;12 doi: 10.1016/j.ohx.2022.e00375. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Zhang X., Xia K., Ji A. A portable plug-and-play syringe pump using passive valves for microfluidic applications. Sensors Actuators B. 2020;304 doi: 10.1016/j.snb.2019.127331. [DOI] [Google Scholar]
- 14.Han W., Kim S., Shin S., Yang S.Y., Choi S., Shin J.H. Wind-up precision pump for portable microfluidics. Sensors Actuators B. 2021;347 doi: 10.1016/j.snb.2021.130592. [DOI] [Google Scholar]
- 15.Headrick M.V. 1997. Clock and Watch Escapement Mechanics. [Google Scholar]
- 16.Payne M., Pooke F., Chase J.G., Campbell J., Holder-Pearson L., Knopp J. The separation of insulin pump hardware and software - a novel and low-cost approach to insulin pump design. IFAC-PapersOnLine. 2021;54(15):502–507. doi: 10.1016/j.ifacol.2021.10.306. [DOI] [Google Scholar]
- 17.International Electrotechnical Commission M. 2012. IEC 60601-2-24:2012. [Google Scholar]
- 18.M. Toledo, WP_USP41_Weighing_EN.Pdf, White Paper, 2019.
- 19.Jahn L.G., Capurro J.J., Levy B.L. Comparative dose accuracy of durable and patch insulin infusion pumps. J. Diabetes Sci. Technol. 2013;7(4):1011–1020. doi: 10.1177/193229681300700425. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Kamecke U., Waldenmaier D., Haug C., Ziegler R., Freckmann G. Establishing methods to determine clinically relevant bolus and basal rate delivery accuracy of insulin pumps. J. Diabetes Sci. Technol. 2019;13(1):60–67. doi: 10.1177/1932296818788349. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Borot S., Franc S., Cristante J., Penfornis A., Benhamou P.-Y., Guerci B., Hanaire H., Renard E., Reznik Y., Simon C., Charpentier G., Diabeloop Study Group Accuracy of a new patch pump based on a microelectromechanical system (MEMS) compared to other commercially available insulin pumps: Results of the first in vitro and in vivo studies. J. Diabetes Sci. Technol. 2014;8(6):1133–1141. doi: 10.1177/1932296814543946. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Girardot S., Jacquemier P., Mousin F., Rendekeu C., Hardy S., Riveline J.-P. All insulin pumps are not equivalent: a bench test assessment for several basal rates. Diabetes Technol. Therapeut. 2020;22(6):476–483. doi: 10.1089/dia.2019.0486. [DOI] [PubMed] [Google Scholar]
- 23.Deutschman A.D., Michels W.J., Wilson C.E. Macmillan; 1975. Machine Design; Theory and Practice. [Google Scholar]
- 24.Engineering Toolbox A.D. 2005. Modulus of rigidity. https://www.engineeringtoolbox.com/modulus-rigidity-d_946.html. [Google Scholar]
- 25.Budynas R., Nisbett K. McGraw-Hill Education; 2010. Shigley’s Mechanical Engineering Design. [Google Scholar]
- 26.Atmel R. 2014. ATtiny441-ATtiny841_Datasheet.pdf. http://ww1.microchip.com/downloads/en/DeviceDoc/Atmel-8495-8-bit-AVR-Microcontrollers-ATtiny441-ATtiny841_Datasheet.pdf. [Google Scholar]
- 27.Energizer R. 2020. Cr1632.pdf. https://data.energizer.com/pdfs/cr1632.pdf. [Google Scholar]
- 28.Boca bearings R. 2018. One-Way-Bearing-Catalog.pdf. https://www.bocabearings.com/Files/Images/drawings/One-Way-Bearing-Catalog.pdf. [Google Scholar]
- 29.ANSI/AGMA R. 2001. ANSI/AGMA 2001-D04 - Fundamental Rating Factors and calculation methods for involute spur and helical gear teeth. https://webstore.ansi.org/Standards/AGMA/ANSIAGMA2001D04?source=preview. [Google Scholar]