Thin-Film Rheology and Tribology of Imidazolium Ionic Liquids

Abstract

Ionic liquids (ILs) are organic molten salts with low-temperature melting points that hold promise as next-generation environmentally friendly boundary lubricants. This work examines the relationship between tribological and rheological behavior of thin films of five imidazolium ILs using a surface force apparatus to elucidate lubrication mechanisms. When confined to films of a few nanometers, the rheological properties change drastically as a function of the number of confined ion layers; not only the viscosity increases by several orders of magnitude but ILs can also undergo a transition from Newtonian to viscoelastic fluid and to an elastic solid. This behavior can be justified by the confinement-induced formation of supramolecular clusters with long relaxation times. The quantized friction coefficient is explained from the perspective of the strain relaxation via diffusion of these supramolecular clusters, where higher friction correlates with longer relaxation times. A deviation from this behavior is observed only for 1-ethyl-3-methylimidazolium ethylsulfate ([C₂C₁Im][EtSO₄]), characterized by strong hydrogen bonding; this is hypothesized to restrict the reorganization of the confined IL into clusters and hinder (visco)elastic behavior, which is consistent with the smallest friction coefficient measured for this IL. We also investigate the contrasting influence of traces of water on the thin-film rheology and tribology of a hydrophobic IL, 1-ethyl-3-methylimidazolium tris(pentafluoroethyl)trifluorophosphate, [C₂C₁Im][FAP], and a hydrophilic IL, [C₂C₁Im][EtSO₄]. [C₂C₁Im][EtSO₄] remains Newtonian under both dry and humid conditions and provides the best lubrication, while [C₂C₁Im][FAP], characterized by a prominent solid-like behavior under both conditions, is a poor lubricant. The results of this study may inspire molecular designs to enable efficient IL lubrication.

Introduction

Since the pioneering work by Ye et al.,¹ the application of ionic liquids (ILs) for lubrication has gained broad interest.²⁻⁴ ILs display remarkable stability against harsh tribological conditions, such as high pressure and heat, and possess great chemical tunability to tailor for specific working environments.⁵ Furthermore, the ionic nature of ILs opens up the possibility of electrotunable lubrication, where the friction coefficient in a lubricated contact can be controlled by external voltages.^6,7 Importantly, water is ubiquitous and unpreventable in many industrial applications, and hence, ensuring efficient lubrication in the presence of water traces is a need for many real-world applications of IL lubricants.

ILs can adsorb strongly on solid surfaces through electrostatic, van der Waals, hydrogen bonding, and other forces (see ref (4) and references herein). A key aspect originating from the strong ion–ion correlations in ILs is that ion adsorption generally leads to overscreening of the surface charge, which sets off alternating layering of counterions and co-ions away from a surface.⁸ These ion layers can be discerned from surface force data, where steps in the structural force result from the squeeze-out of ion layers.⁹ The layering of ILs between surfaces influences the lubrication mechanisms. For example, a stepwise increase of pull-off force and friction coefficient (often referred to as “quantized” friction coefficient) has been observed when the number of IL layers confined between the surfaces is reduced.¹⁰ At high pressure, when IL films thin down to just a few layers, the relative strength of interlayer interactions and ion–surface interactions determines the location of the slippage plane.¹¹ Molecular dynamics (MD) simulations¹² have shown that the shift of the slippage plane from the solid/liquid interface to the interior of the film (upon an increase in surface potential in that cited work) leads to a notable decrease in the friction coefficient. Intralayer ion packing and interactions also govern the stability of IL films under shearing, thus affecting the friction coefficient.¹³

The investigation of the dependence of friction on velocity in single-asperity contacts lubricated by ILs has revealed intricate mechanisms.¹⁴ Depending on the load and water content, friction can increase, decrease, or remain constant with sliding velocity. This was explained through the strength and dynamics of the interionic interactions via a stress-assisted thermally activated slip model. More recently, friction measurements on stainless steel have revealed that friction and the degree of interfacial structure are inversely correlated.¹⁵ This means that more ordered (structured) films lead to higher energy dissipation because stronger interlayer bonds need to be broken at the slip plane compared to disordered films. Intralayer ion ordering and surface structure also determine the commensurability of an adsorbed ion layer with its confining surfaces, which can lead to either high friction or superlubricity at the solid/IL slippage plane.¹⁶ Many studies have revealed that friction is generally system-specific (e.g., specific to the types of ILs and surfaces and the physicochemical state of surfaces). Such molecular specificity can be traced to the different molecular structure, dynamics, and interactions of IL films confined between the sliding surfaces when different ions are used.^13,17−21 For example, Perkin’s group investigated thin films of dry 1-decyl-1-methylpyrrolidinium bis[(trifluoromethane)sulfonyl]imide (abbrev. [C₁₀C₁Pyrr][TFSI]).²² Here, a monolayer on each surface led to high friction, which was associated with the location of the shear plane at the alkyl–alkyl plane. In contrast, a bilayer on each surface led to a low friction, which was associated with the location of the shear plane at the ionic interface. In the presence of water, the shear planes remained unchanged, but water increased the friction coefficient. As discussed later, we provide an alternative explanation for the increase in friction with the decrease in the number of layers and for the influence of the water molecules, which is not based on the location of the shear plane but on the rheological behavior of the confined ILs.

Various nanomechanical methods have provided insight into the slowdown of the dynamic properties of ILs at interfaces.²³⁻²⁵ Using the so-called dynamic surface forces apparatus, reciprocal shear revealed an order-of-magnitude increase in shear stress with decreasing film thickness for an imidazolium IL, 1-butyl-3-methylimidazolium hexafluorophosphate, abbrev. [C₄C₁Im][PF₆].²⁶ Kurihara and colleagues investigated two ILs with the same cation and different anion, specifically 1-butyl-3-methylimidazolium bis[(trifluoromethane)sulfonyl]imide (abbrev. [C₄C₁Im][TFSI]) and 1-butyl-3-methylimidazolium tetrafluoroborate (abbrev. [C₄C₁Im][BF₄]) confined between silica surfaces.²⁷ Surface force apparatus (SFA)-based resonance shear measurements revealed that the viscosities of the two confined ILs were 1–3 orders of magnitude higher than that of the bulk ILs. In situ X-ray diffraction (XRD) measurements on the two same systems revealed that [C₄C₁Im][TFSI] formed a checkerboard-like structure, and [C₄C₁Im][BF₄] formed alternating layers of anions and cations.²⁸ Molecular dynamics (MD) simulations¹³ indicated that the shape of the IL molecules was the key parameter to determine the two different layering structures and the dynamical properties at the molecular level. Larger and more irregular molecular fluctuations were observed for [C₄C₁Im][TFSI]. In contrast, the smaller anion [BF₄] led to smaller oscillations as the layers slid on top of each other in a laminar fashion. Separate MD simulations have shown that the shear force across a thin film of 1,3-dimethylimidazolium bis(trifluoromethanesulfonyl)amide ([C₁C₁Im][TFSI]) can be justified by the increase of its viscosity.^29,30 Despite the significant gained knowledge, these studies did not inform about the relationship between the quantized friction coefficient and the rheological behavior.

All of this has motivated our interest in studying the relationship between thin-film rheology and tribology of imidazolium ILs experimentally using a surface forces apparatus. Although it is accepted that thin-film lubrication is undermined by the rheological properties of the lubricant under nanoconfinement, there is no thorough understanding of how the rheological behavior of IL thin films can be used to inform the performance of ILs in thin-film lubrication. We have examined the relationship between tribological and rheological behavior of IL thin films for five different ILs, 1-ethyl-3-methylimidazolium bis(trifluoromethylsulfonyl)imide (abbrev. [C₂C₁Im][TFSI]), 1-butyl-3-methylimidazolium bis(trifluoromethylsulfonyl)imide (abbrev. [C₄C₁Im][TFSI]), 1-hexyl-3-methylimidazolium bis(trifluoromethylsulfonyl)imide (abbrev. [C₆C₁Im][TFSI]), 1-ethyl-3-methylimidazolium ethylsulfate (abbrev. [C₂C₁Im][EtSO₄]), and 1-ethyl-3-methylimidazolium tris(pentafluoroethyl)trifluorophosphate (abbrev. [C₂C₁Im][FAP]). This selection allows us to identify the role of the cation by comparing results obtained with [C₂C₁Im][TFSI], [C₄C₁Im][TFSI], and [C₆C₁Im][TFSI] and to determine the effect of the anion by examining the results for [C₂C₁Im][TFSI], [C₂C₁Im][FAP], and [C₂C₁Im][EtSO₄]. In addition, we investigate the influence of traces of water on the thin-film rheology and tribology of two ILs, a hydrophobic IL, [C₂C₁Im][FAP], and a hydrophilic IL, [C₂C₁Im][EtSO₄]. To the best of our knowledge, the effects of the molecular structure and water on the relation between tribological and rheological behavior of IL thin films have not been experimentally investigated before. The results from this study not only extend our knowledge of the different mechanisms underlying thin-film lubrication by ILs but also help establish principles for the molecular design of efficient lubricants.

Results

An extended surface force apparatus (SFA) was used to measure the normal force between mica surfaces first in the dry ILs at 25 °C. The SFA cell was continuously purged with dry nitrogen, which led to a relative humidity smaller than 3% RH. We label this condition as dry or 0% RH in the following; see details in Materials and Methods section. An example is shown in Figure 1a for [C₆C₁Im][TFSI]. The steps in the force–distance curves at ∼1.5 and ∼10 mN/m indicate that the ions are arranged in layers between the two surfaces. In this case, each layer is composed of two bilayers of cations, with the alkyl chains facing each other, and of anions.³¹ The force measurements are in good agreement with reported SFA results (see review⁴ and references herein).

Figure 1.

Thin-film rheology and tribology for dry [C₆C₁Im][TFSI]. (a) Surface forces; the colored lines indicate the investigated film thicknesses D₀ and D_+Δ. (b) Friction as a function of sliding velocity at three different surface separations, D₀ ∼ 2 and D_+Δ ∼ 3 and 4 nm; the corresponding applied loads are 0.46, 0.23, and 0.044 mN, respectively. (c) Representative lateral force at 15 μm/s as a function of time for a film thickness D₀ = 2 nm; the top plot shows the results for a single friction loop. (d) Effective viscosity η_eff as a function of strain rate for IL films with two different film thicknesses (D₀ ∼ 2 nm and D_+Δ ∼ 4 nm). The red and blue solid lines show the fits of Eyring′s model for shear thinning, which deviates from the experimental results at D₀ at large strain rates. G′ and G″ are shown in Figure S1a (in Supporting Information). Bulk viscosity = 0.081 Pa·s.³² Error bars are shown in plots of friction force, effective viscosity, storage, and loss moduli (see the SI). However, they are often smaller than the marker size, and hence, not always visible. No error bars are shown in surface force measurements but results from various measurements are shown in the same plot to visualize the variability across experiments. This also applies to Figures 2–5. (a, d) Reprinted (adapted) with permission from ref (34). Copyright 2022 American Chemical Society.

Rheological and tribological measurements were performed at various film thicknesses (D). The minimum film thickness is labeled as D₀. A maximum force of 100 mN/m was applied in each experiment, which led to slightly different values for D₀ for each IL. The measurements were also carried out when more IL layers were confined between the mica surfaces. In this work, the layer thickness is labeled as Δ, and hence, the corresponding film thicknesses are labeled as D_+Δ, if the film has one more layer than at D₀, D_+2Δ, if the film has two more layers than at D₀, and D_+3Δ, and if the film has three more layers than at D₀. Please see the exact film thickness of rheological and tribological measurements in Figures 1a, 2a, 3a, 4a, and 5a for each of the ILs investigated accordingly.

Figure 2.

Thin-film rheology and tribology for dry [C₄C₁Im][TFSI]. (a) Surface forces; the colored lines indicate the investigated film thicknesses in tribological measurements. (b) Friction as a function of sliding velocity at three different surface separations, D₀ = 1.5, D_+Δ = 3, and D_+2Δ = 5 nm; the corresponding applied loads are 2.2, 0.11, and 0.02 mN, respectively. (c) Lateral force as a function of time while one surface slides at 15 and 150 nm/s for a film thickness of D₀ = 1.5 nm. Representative friction loops for D_+Δ = 3 and D_+2Δ = 5 nm are shown in Figure S2. (d) Effective viscosity η_eff as a function of strain rate for IL films with two different thicknesses (D₀ ∼ 1.5 nm, D_+Δ∼ 2 nm, and D_+2Δ ∼ 5 nm). The gray and blue solid lines show the fits of Eyring′s model. The dashed line in panel (d) results from the detection limit of shear stress; see the Materials and Methods section. The data points with less intense (semitransparent) colors are those close to the detection limit. This also applies to the plots of the effective viscosity in Figures 3–6. G′ and G″ are shown in Figure S1b. Bulk viscosity = 0.061 Pa·s.³² (a, d) Reprinted (adapted) with permission from ref (34). Copyright 2022 American Chemical Society.

Figure 3.

Thin-film rheology and tribology for dry [C₂C₁Im][TFSI]. (a) Surface forces. (b) Friction as a function of sliding velocity at two different surface separations, D₀ = 2.5 and D_+Δ = 3.5 nm; the corresponding applied loads are 0.23 and 0.69 mN, respectively. (c) Lateral force as a function of time while sliding at 15 nm/s for a film thickness D₀ = 2.5 nm. (d) Effective viscosity η_eff as a function of strain rate for IL films with two different thicknesses (D₀ ∼ 2 nm and D_+Δ ∼ 3 nm). G′ and G″ are shown in Figure S1c. Bulk viscosity = 0.033 Pa·s.³² (a, d) Reprinted (adapted) with permission from ref (34). Copyright 2022 American Chemical Society.

Figure 4.

Thin-film rheology and tribology for dry [C₂C₁Im][EtSO₄] at 0 and 35% RH. (a) Surface forces. (b, f) Friction as a function of sliding velocity at selected film thicknesses: (b) D₀= 2 nm, D_+Δ = 3 nm at loads of 1.3 and 0.4 mN, respectively, for the dry IL, and (f) D₀ = 0.8, D_+Δ = 3 nm and D_+2Δ = 5 nm at the applied loads of 0.026, 0.26, and 1.8 mN, respectively, for the IL equilibrated at 35%RH. (d, e) Lateral force as a function of time while sliding at 300 nm/s for a film thickness D₀ at 0 and 35% RH. The noise is of the same order of magnitude as the variation of the lateral force. (c, g) Effective viscosity η_eff as a function of strain rate for IL films with two different thicknesses (D₀ and D_+Δ) at (c), 0% RH and (g), 35% RH. G′ and G″ are shown in Figure S1d. Bulk viscosity = 0.115 Pa·s.⁴⁰ The water content in the bulk IL at 35% RH is 1.51 water-to-IL mole ratio (12.56 vol %). (a, c) Reprinted (adapted) with permission from ref (34). Copyright 2022 American Chemical Society.

Figure 5.

Thin-film rheology and tribology for dry [C₂C₁Im][FAP] at 0 and 18, and 35% RH. (a) Surface forces with film thickness for the rheological measurements and molecular structure of [C₂C₁Im][FAP]. (b, d) G′ (solid markers), and G″ (hollow markers) as a function of frequency. (c, e) Effective viscosity η_eff as a function of strain rate. Investigated film thicknesses: (b, c) D₀ = 2 nm, D_+Δ = 3 nm for the dry IL, (d, e), D_+Δ = 2 nm for the IL equilibrated at 35% RH and D₀ = 0.8, and D_+3Δ = 4 nm for the IL equilibrated at 18% RH. Bulk viscosity = 0.071 Pa·s.⁴¹ The water content in the bulk IL at 18 and 35% RH is 0.03 ± 0.01 and 0.08 ± 0.05 water-to-IL mole ratio, respectively. (a–c) Reprinted (adapted) with permission from ref (34). Copyright 2022 American Chemical Society.

Influence of the Cation

The experimental results for dry [C₆C₁Im][TFSI], [C₄C₁Im][TFSI], and [C₂C₁Im TFSI], in equilibrium with dry nitrogen, are summarized in Figures 1–3 and S1. In the case of [C₆C₁Im][TFSI], three film thicknesses were selected for friction force measurements (Figure 1a): D₀ ∼ 2 nm, D_+Δ ∼ 3 nm, and D_+Δ ∼ 4 nm. Friction measurements were conducted by laterally moving one surface at a distance of 15 μm at various sliding velocities (V); see Figure 1b. A representative friction loop at D₀ is displayed in Figure 1c (top). The lateral motion yields an increase in the lateral force until a plateau is achieved, which indicates the commencement of sliding. Sliding is smooth at the investigated conditions for this IL. Reducing the film thickness from 4 to 3 nm leads only to a small increase in friction, whereas an abrupt rise in friction is measured after an IL layer is squeezed out (D₀). Here, friction decreases with velocity at slow sliding velocities and increases with velocity above a threshold value (V_c = 300 nm/s). The increase of friction with velocity is sublinear (∼V^m, m < 1) at the three investigated film thickness, with power exponents m equal to 0.51, 0.55, and 0.22, respectively. These results point at a change of the lubricity of [C₆C₁Im][TFSI] when the film thickness changes from D_+Δ to D₀, whereas compressing the film from D_+Δ = 3 to 4 nm only leads to a minor change of friction. Importantly, the friction loops at D₀ evolve with time, with the first friction loop providing the highest lateral force and then decreasing until they remain stable (Figure 1c, bottom). This suggests that the IL ions in the nanoconfined films rearrange upon shear until the film structure becomes stable.

We define a friction coefficient as the change of friction (F) divided by the change of normal load (L) at a sufficiently slow velocity at which the variation of friction with velocity is small. At a sliding velocity of 150 nm/s, the friction coefficient increases from 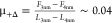to 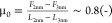, i.e., by 1 order of magnitude upon squeezing out one layer from D_+Δ to D₀. An increase in the friction coefficient with the decrease in the number of confined layers was reported before for ILs and labeled as “quantized” friction.¹⁰

The dynamic properties of thin films can be investigated with an SFA by applying an oscillatory shear stress; see previous studies of polymer melts.³³ These measurements provide G′ (storage modulus) and G″ (loss modulus), which characterize the rheological properties of the confined IL film.³⁴ That is, G′ represents the elastic behavior of a material, indicating its ability to store energy. G″ represents the viscous behavior of a material, indicating its ability to dissipate energy when subjected to oscillatory shear stress; in other words, it measures the material’s resistance to flow. We also report the effective viscosity, which can be calculated with G′ and G″ according to η_eff = (G′² + G″²)^0.5/ω, where ω is the angular frequency. Eyring’s model^35,36 is used to describe shear-thinning behavior. Based on this model, shear thinning originates from the shear-promoted flow, as the work done by the applied shear stress reduces the energy barrier that needs to be surpassed for the flow unit to move to the next equilibrium location. Eyring’s model gives the following expression for the viscosity

1

where t_rel = 1/γ̇_E is the characteristic relaxation time, γ̇_E is the critical shear rate for the onset of shear thinning, and V_act is the shear-activation volume, which decreases the energy barrier by σV_act, σ being the shear stress. The relaxation time t_rel is related to the molecular relaxation time involved in the shear response. We use eq 1 to fit the measured effective viscosity.

Figure 1d shows the effective viscosity of the thin film, η_eff, as a function of the strain rate, γ̇. When [C₆C₁Im][TFSI] is confined to films with a thickness D_+Δ, the effective viscosity decreases with an increase in strain rate, which indicates shear thinning of this IL. The solid blue line gives the fit of Eyring′s model to the experimental data. Note that the shear-thinning behavior of films with thickness D_+Δ is consistent with the sublinear increase of friction with velocity (∼V^0.51 and ∼ V^0.54) based on the standard equation for Couette flow. This is discussed later in detail.

An abrupt jump of the effective viscosity is observed upon the squeeze out of one layer from D_+Δ to D₀, which coincides with the sudden increase in friction. Shear thinning is also observed at D₀ but only at strain rates <2000 s^–1, while the effective viscosity at higher strain rates follows η_eff ∼ γ̇^–1, which points at the solid-like behavior of this IL.³³ Indeed, frequency-sweep oscillatory-shear rheology in the range from 0.01 to 20 Hz (Figure S1a) demonstrates that this IL behaves as a viscoelastic fluid at frequencies smaller than ν₀ = 3 Hz (G′ < G″), while above ν₀, [C₆C₁Im][TFSI] exhibits a solid-like behavior (G′ > G″). The cross-over frequency ν₀ is determined at the frequency at which G′ = G″. At ν₀, the relaxation time scale is τ₀ ∼ 1/(2πν₀) = 1/ω₀ = 0.095 s. With more layers confined between the two mica surfaces (D_+Δ and thicker films), [C₆C₁Im][TFSI] behaves predominantly as a viscous liquid.

Figure 2 summarizes the results for [C₄C₁Im][TFSI]. The selected film thicknesses are D₀ and D_+2Δ (Figure 2a,b). The friction force at D₀ ∼ 1.5 nm is much higher than that measured at D_+2Δ ∼ 3 and D_+2Δ ∼ 5 nm. Friction increases sublinearly with sliding velocity at D_+2Δ, as in the case of [C₆C₁Im][TFSI]. At D₀, the friction force decreases with increasing sliding velocity at velocities smaller than ∼150 nm/s while exhibiting remarkable stiction and stick–slip (Figure 2c). Stick–slip reflects the intermittent relative motion between the surfaces, alternating between periods of no motion (when the surfaces “stick” together) and rapid sliding (“slip”). Such behavior can have various origins^37,38 like a transition from solid-like (stick) to liquid-like (slip) state of the confined IL or a mechanical instability resulting from the decrease in friction with the increase in velocity. At higher sliding velocities, the motion of the surfaces is smooth, friction first increases, and then, it remains constant with velocity. The latter is likely because the friction force achieves the detection limit of our device (∼2 mN). Note that the origin of the stick–slip could be explained by both the phase transition model and the velocity-dependent friction model. In comparison, the friction loops at D_+2Δ show smooth sliding and no appreciable static friction (Figure S2). The estimated friction coefficient increases from 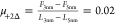to 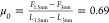(-) (values estimated at 500 nm/s), and hence, it is smaller than that for [C₆C₁Im][TFSI].

Three film thicknesses were selected for rheological measurements: D_+2Δ = 5 nm, D_+Δ = 2 nm, and D₀ = 1.5 nm (Figure 2d). The dashed line represents the detection limit of the instrument, and hence, we only consider data to the right of this line; see the Materials and Methods section. The semitransparent markers are thus neglected here; see our previous work for more information about these data.³⁴ Above a strain rate of ∼100 s^–1, the effective viscosity η_eff for films with thicknesses D_+2Δ and D_+Δ exhibits a Newtonian plateau before the onset of shear thinning. The solid blue and gray lines show the satisfactory fit of Eyring′s model to η_eff. The behavior is similar for thin films D_+2Δ and D_+Δ, yielding η_eff ∝ γ̇^–0.27 and η_eff ∝ γ̇^–0.33 at the highest strain rates, respectively. At D₀, the effective viscosity of dry [C₄C₁Im][TFSI] follows the order η_eff ∝ γ̇^–1. G′ at D₀ is large and remains constant with frequency, while the loss modulus is immeasurably small (G′ ≫ G″), indicating the prominent solid-like behavior of the thin film (Figure S1b). This IL film is a viscoelastic fluid at D_+Δ (G′ < G″, G′ ∼ ω^1.36, and G″ ∼ ω^0.83) in the range of investigated frequencies. A cross-over between G′ and G″ is determined by extrapolation at ν₀ = 15.87 Hz, which leads to a relaxation time of τ₀ = 0.01 s. The rheological behavior at D_+2Δ is characteristic of a viscous fluid. This example demonstrates that thin films of [C₄C₁Im][TFSI] can retain their viscous characteristics or become viscoelastic or even elastic, depending on the film thickness.

Importantly, the sublinear relation between friction force and sliding velocity provided by films with thicknesses of D_+Δ and D_+2Δ is consistent with the shear-thinning behavior revealed by rheology. The stick–slip response and the much higher friction force at D₀ correlate with the presence of an elastic (solid-like) film in rheological measurements.

Figure 3 summarizes the results for [C₂C₁Im][TFSI]. The tribological measurements were performed at D_+Δ = 3.5 and D₀ = 2.5 nm (Figure 3a). As shown in Figure 3b, friction is small but the increase in friction with the decrease in the number of confined IL layers is still evident. The friction coefficient is 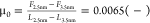at 150 nm/s and hence smaller than when lubricated by [C₄C₁Im][TFSI] and [C₆C₁Im][TFSI]. Under all conditions, the sliding is smooth (Figure 3c).

Above V_c ∼ 5 μm/s, a weak increase of friction with sliding velocity is observed, while below V_c, a nonmonotonic trend is observed for both film thicknesses D₀ and D_+Δ. The error bars are large, and the variation of friction is close to the detection limit of the device (±10 μN), though. Nevertheless, a nonmonotonic velocity dependence of friction was also measured for this IL by colloidal probe AFM, i.e., with a silica colloid sliding on the mica surface,¹⁴ which supports these results. The decreasing trend of friction with sliding velocity was associated with the relaxation times for bond formation/rupture at the shear plane, as previously proposed for shearing surfactant-bearing surfaces in an aqueous solution.³⁹

The effective viscosity achieves a Newtonian plateau in the range of measurable strain rates (Figure 3d). The viscosity value of the plateau is smaller at D_+Δ compared to D₀ (∼13 vs ∼49 Pa·s). In the range where friction increases with velocity, we note a close-to-linear relationship between friction and velocity (Figure 3b), which agrees with the Newtonian plateaus. Figure S1c shows G′ and G″ from frequency-sweep oscillatory-shear rheology. At D₀, the behavior is that of a viscoelastic fluid (G″ > G′, G′ ∼ ω^1.66, and G″ ∼ ω^1.02). The frequency at the cross-over between G′ and G″ is determined by extrapolation to be ν₀ ∼ 91 Hz, yielding a relaxation time of τ₀ = 0.002 s. That is, the solid-like behavior is expected to set in at higher frequencies compared to [C₄C₁Im ][TFSI] and [C₆C₁Im][TFSI]. With one more confined layer, at D_+Δ, the confined IL exhibits purely viscous behavior.

Influence of the Anion

The effect of the anion on thin-film tribology and rheology was investigated by comparing the results of dry [C₂C₁Im][EtSO₄], [C₂C₁Im][TFSI], and [C₂C₁Im][FAP]; cf. Figures 3, 4 and 5. As described next, [C₂C₁Im][EtSO₄] and [C₂C₁Im][FAP] exhibit contrasting nanorheological behavior, while the behavior of [C₂C₁Im][TFSI] is intermediate.

Thin-film tribological and rheological measurements for [C₂C₁Im][EtSO₄] were carried out at D_+Δ = 3 nm and D₀ = 2 nm (Figure 4a–c). Friction is close to the precision of the instrument for the two investigated film thicknesses (Figure 4b). The error bars are similar in magnitude to the change in friction with velocity, and hence, it is not possible to evaluate the velocity dependence of friction with precision. But the solid lines represent a linear increase in friction with velocity to guide the eye. The friction loops demonstrate smooth sliding at all conditions (Figure 4d). The estimated coefficient of friction at 150 nm/s is , and hence, a bit smaller than that for [C₂C₁Im][TFSI].

A Newtonian plateau (∼18 Pa·s) was observed for [C₂C₁Im][EtSO₄] at D₀ (Figure 4c). Note that the plateau value at D₀ is smaller than that for [C₂C₁Im][TFSI] (∼49 mPa·s), although the bulk viscosity of the former is much greater (116 vs 33 mPa·s). Interestingly, the effective viscosity of [C₂C₁Im][EtSO₄] at D_+Δ was observed to increase with the strain rate. We speculate that the shear-strengthening behavior is related to the small decrease in the film thickness (∼2 Å) measured during rheological measurements (see Figure S3). Such a variation was observed only at D_+Δ, while the film thickness remained constant during the oscillatory shear at D₀. Because this small variation of D_+Δ is smaller than the size of a single ion layer, it might be related to a subtle reorganization of the ions while shearing. Based on G′ and G″ (Figure S1d), [C₂C₁Im][EtSO₄] remains a viscous liquid at both investigated conditions, D_+Δ = 3 nm and D₀ = 2 nm; recall that [C₂C₁Im][TFSI] behaves as a viscoelastic fluid at D₀.

Thin-film rheological measurements were carried out for dry [C₂C₁Im][FAP] at D_+Δ = 3 nm and D₀ = 2 nm (Figure 5a). In contrast to the results for [C₂C₁Im][TFSI] and [C₂C₁Im][EtSO₄], [C₂C₁Im][FAP] exhibits prominent solid-like behavior. Figure 5b shows G′ and G″ for [C₂C₁Im][FAP] at 0% RH. At D₀, the IL is a viscoelastic liquid below ν₀ = 1.13 Hz (τ₀ = 0.141 s), while it exhibits predominantly elastic behavior (G′ > G″) above ν₀. At D_+Δ, the scaling relations of the moduli are slightly different, G′ ∼ ω^1.9 and G″ ∼ ω^0.73, and the cross-over between G″ and G′ is determined to occur at ν₀ ∼ 25 Hz by extrapolation (τ₀ ∼ 0.006 s), leading to a solid-like behavior at higher frequencies compared to D₀. Longer relaxation times with a decrease in the number of layers has also been reported for a molecular liquid under confinement³³ and associated with the more prominent solid-like behavior.

Figure 5c shows much higher values for the effective viscosity of [C₂C₁Im][FAP] at D_+Δ = 3 nm and D₀ = 2 nm compared to [C₂C₁Im][EtSO₄] and [C₂C₁Im][TFSI], without any correlation to their respective bulk viscosities (71 vs 115 vs 33 mPa·s). The effective viscosity at D₀ = 2 nm decreases significantly from ∼4528 Pa·s with strain rate, reflecting the shear-thinning behavior of this IL. However, at strain rates larger than ∼10³ s^–1, η_eff ∼ γ^–1, which is characteristic of the solid-like behavior of the dry IL. At D_+Δ ∼ 3 nm, there is a plateau of the effective viscosity at ∼627 Pa·s, until the onset of shear thinning, which remains up to much higher strain rates than at D₀. Red and blue solid lines display the fits of Eyring′s model to the effective viscosity.

Tribological measurements were conducted with dry [C₂C₁Im][FAP] by SFA and reported by us earlier.^42,43 In that work, we showed irregular stick–slip and very high friction at D₀, which was hypothesized to be associated with the cooperative response of the confined molecules in the thin films and their solid-like behavior. Here, we demonstrate the prominent solid-like behavior of thin films of this IL in rheological measurements. The estimated friction coefficient is μ₀ ∼ 0.71 (-) and hence much higher than when the mica surfaces are lubricated by [C₂C₁Im][EtSO₄] and [C₂C₁Im][TFSI]. We also note that tribological experiments often failed due to contamination. We believe that the failure of these experiments is likely related to the solid-like behavior of this IL, which led to wear of the mica surfaces.

Influence of Water

The influence of the water uptake on thin-film rheology and tribology was investigated for [C₂C₁Im][EtSO₄] and [C₂C₁Im][FAP]. The presence of water in the thin films leads to a change in refractive index, which can be roughly estimated according to⁴⁴

2

where n is the measured refractive index of the mixture of IL and water, n₀ = 1.374 is the refractive index of dry, n_w = 1.337 is the refractive index of water, and ϕ is the volume fraction of water in the thin film. The refractive index was measured in thin films with a thickness between 10 and 50 nm, and it is 1.374 ± 0.005 and 1.372 ± 0.003 at 0 and 35% RH for this IL, respectively; hence, the difference is not statistically significant; see Figure S4. Equation 2 yields a water content ϕ of ∼0.057, which is close to the water content in the bulk IL. A precise estimation of the water content is not possible in films with a thickness of <10 nm due to the large variation of the refractive index. Nonetheless, it seems to be a bit smaller for the IL equilibrated with 35% RH than for the dry IL, which points toward the presence of more water close to the mica surface.

Figure 5e compares the effective viscosity of [C₂C₁Im][FAP] at two different RH conditions. For D_+Δ = 2 nm at 35% RH, the plateau viscosity is significantly smaller compared to the dry IL (1489 vs 4528 Pa·s) and the shear thinning remains up to higher strain rates compared to dry conditions (3000 vs 600 s^–1), but a solid-like behavior (η_eff ∝ γ^–1) is still achieved. A small decrease in the film thickness (∼2 Å) happened during rheological measurements (Figure S5). Measurements at D_+2Δ were not possible in equilibrium with 35% RH, because one IL layer was always spontaneously squeezed out during the oscillatory shear. It has been shown²¹ that increasing the water content above a threshold in hydrophobic ILs leads to phase separation between water and the IL in the confined thin film, which leads to a significant attraction (capillary force) between the mica surfaces and to the spontaneous squeeze out of the IL. This could justify the spontaneous drainage of the IL layer during rheological measurements.

To reduce the water content, the IL was equilibrated with humid air at 18% RH (water content ∼0.03 ± 0.01 wt %), which enabled the investigation of two more film thicknesses, D₀ = 0.8 nm and D_+3Δ = 5 nm. While the IL at D₀ exhibits a solid-like behavior, it remains a viscous fluid at D_+3Δ with shear-thinning behavior within the range of investigated strain rates. Figure 5d displays the storage and loss modulus. At D₀, the humid IL exhibits predominantly solid-like behavior (G′ > G″, G″ ∼ 0 at 0.06 Hz and above), while it is a viscous liquid at D_+3Δ (G′ < G″, G′ ∼ 0). The behavior at D_+Δ (35% RH) is intermediate; the IL is viscoelastic (G″ ∼ ω^0.85 and G″ ∼ ω^0.79) and above ν₀ = 3.5 Hz (τ₀ ∼ 0.045 s), the behavior becomes solid-like (G′ > G″, G″ ∼ 0). This also happens for the dry IL in a film of 2 nm in thickness but at a smaller frequency. Hence, the presence of water mitigates the solid-like behavior of this IL. Our previous friction and pull-off force measurements in equilibrium with air at 37% RH⁴² demonstrated the poor lubricious properties of [C₂C₁Im][FAP] at D < 2 nm, with a friction coefficient μ₀ ∼ 0.75, and an increase in adhesion compared to the dry condition.

At 35% RH, the equilibrium water content in [C₂C₁Im][EtSO₄] is 1.51 water-to-IL mole ratio (12.56 vol %) in the bulk and, hence, much higher than that in [C₂C₁Im][FAP]. The refractive index also increases upon equilibration with air at 35% RH; it is 1.488 at 0% RH vs 1.468 at 35% RH for films with thickness ranging between 20 and 100 nm (Figure S6). Equation 2 yields a volume fraction of water of ϕ ∼ 13.2 vol %, in satisfactory agreement with the bulk value. At smaller surface separations, there is a variation of the refractive index but the noise increases, which is common to molecular liquids with an interfacial layered structure, making it impossible to determine the water content.

Three different film thicknesses were selected for tribological measurements with [C₂C₁Im][EtSO₄] at 35% RH; D₀ = 0.8 nm, D_+Δ = 3, and D_+2Δ = 5 nm. Figure 4f shows a very small variation of friction with velocity at D_+Δ = 3 nm and D_+2Δ = 5 nm, but note the decrease of friction with an increase in velocity. At D₀, there is a statistically significant nonmonotonic change of friction with velocity; friction decreases with velocity below V₀ ∼ 1 μm/s and it increases linearly above V₀. Interestingly, the friction coefficient drops from 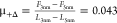(-) to 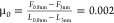(-); these values are estimated at 150 nm/s. This is against the expected trend for the quantized friction coefficient. We believe that this drop could result from the enrichment of water at the hydrophilic contact as the film thickness decreases.²¹

The rheological behavior of [C₂C₁Im][EtSO₄] equilibrated at 35% RH was investigated at D_+Δ = 2 nm and D₀ = 0.8 nm. Similar to the dry IL, this thin film exhibits a purely viscous behavior upon nanoconfinement: G′ becomes negligible, and G″ increases with frequency, with G″ ∼ ω^0.85 at D₀ and D_+Δ nm, respectively (Figure S7). Interestingly, while G″ of the dry IL increases with a decrease in film thickness, the reverse trend is observed for the IL equilibrated at 35% RH. Similarly, the effective viscosity is smaller at D₀ compared to the values at D_+Δ (Figure 4g) while remaining smaller than that of the dry IL (Figure 4c). As revealed by the refractive index measurements, water is present in the confined fluid film, and the water content varies with film thickness.²¹ Hence, it is possible that the decrease in viscosity (as well as G′ and G″, and friction coefficient) with the decrease in film thickness reflects the enrichment of water closer to the mica surface. Interestingly, the effective viscosity increases with strain rate at both D_+Δ = 2 nm and D₀ = 0.8 nm but more significantly at D_+Δ. It is speculated that the shear thickening could be related to a subtle rearrangement of the ions under dynamic conditions. The physics in this case is further complicated due to the presence of water and ions.

Discussion

The comparison between thin-film rheology and tribology allows us to identify characteristics of the lubrication mediated by ILs. If two planar surfaces are separated a distance D by a Newtonian fluid with viscosity η, the shear or friction force F while sliding at velocity V is given by the standard equation for Couette flow

3

where A = πa² is the contact area and a is the contact radius (∼7 μm in these experiments). This is approximately the geometry of our SFA experiments, as the glue underneath the mica surfaces deforms under applied load, which flattens the curved surfaces and more so with an increase in load. Our results demonstrate that the rheological characteristics of the thin films strongly deviate from the bulk rheological properties since all ILs are Newtonian liquids. Changing either the cation [C_nC₁Im]⁺ (n = 2, 4, and 6) or the anion ([TFSI]⁻, [FAP]⁻, and [EtSO₄]⁻) can cause a transition from a Newtonian viscous behavior to viscoelastic or even to an elastic behavior of the thin film at specific film thicknesses and shear frequencies or strain rates. In eq 3, we thus substitute η by the effective viscosity η_eff of the thin films and use the modified equation to relate rheological and tribological characteristics of the thin films, i.e.,

4

This is the same approach that was applied by Luengo et al. to polymer melts.³³ Tribological measurements reveal the variation of friction with sliding velocity for the investigated dry ILs, which indeed qualitatively reflects the influence of the effective viscosity. For example, the shear-thinning behavior of [C₄C₁Im][TFSI] and [C₆C₁Im][TFSI] (η_eff ∼ γ̇^–n, n > 0) justifies the sublinear relationship between friction and velocity (F ∼ (V/D)^m, m < 1) based on eq 4. A solid-like behavior (η_eff ∼ γ^–1) correlates with the prominent jump of the friction force and a decrease of the scaling exponent m. For instance, this happens with [C₆C₁Im][TFSI], with F ∼ (V/D)^0.22 at D₀. The more prominent solid-like behavior of [C₂C₁Im][FAP] announces the worse lubrication performance of this IL. Indeed, the stick–slip and the wear of mica in multiple attempts are consistent with the poor lubricious behavior of [C₂C₁Im][FAP]. Stick–slip was also measured for [C₄C₁Im][TFSI] at D₀ = 1.5 nm, for which the rheological measurements demonstrate that G′ ≫ G″ (Figure S1b), supporting the suggested relation between solid-like behavior and stick–slip of the thin film.⁴⁵ In contrast, the lubrication provided by [C₂C₁Im][TFSI] and [C₂C₁Im][EtSO₄] is much more efficient, which correlates with their more viscous (less elastic) behavior and their smaller effective viscosity. It also appears that friction increases quasi-linearly with sliding velocity, which is consistent with the close-to-Newtonian behavior of the thin films. Nonetheless, the friction force is close to the precision of the instrument, and hence, this conclusion needs to be considered with caution.

To quantitatively demonstrate the relationship between the rheological and tribological properties of the thin films, we use the values of the effective viscosity at the plateaus to calculate the friction force with eq 4. We thus estimate the friction force F at V = 10 μm/s with following values for η_eff: ∼ 20 and 10 Pa·s for dry [C₂C₁Im][EtSO₄] at D₀ = 2 nm and D_+Δ = 3 nm yields F = 15.4 and 5.1 μN, respectively; ∼ 49 and 20 Pa·s for [C₂C₁Im][TFSI] at D₀ = 2.5 nm and D_+Δ = 3.5 nm yields F = 30.2 and 8.8 μN, respectively; ∼314 and 200 Pa·s for [C₄C₁Im][TFSI] at D_+Δ = 2 nm and D_+2Δ = 5 nm yields F = 161 and 61.6 μN, respectively; 283 Pa·s at D_+Δ = 4 nm for [C₆C₁Im][TFSI] yields 109 μN; and 239 Pa·s at D_+Δ = 3 nm for [C₂C₁Im][FAP] yields 122 μN. This is in qualitative agreement with the experimental results, supporting that the thin-film rheology of ILs determines their lubricious performance. Nonetheless, this simplified approach overestimates the friction force for [C₆C₁Im][TFSI], [C₄C₁Im][TFSI], and [C₂C₁Im][FAP] at D₀, characterized by the solid-like behavior, pointing out the limitation of this viscous model.

Figure 6a shows the estimated friction coefficients, and Figure 6b displays the relaxation time, τ₀. A larger relaxation time reflects a more significant solid-like behavior, which is enhanced with the length of the alkyl chain in [C_nC₁Im]⁺, and it is more significant for the [FAP]⁻ anion, followed by [TFSI]⁻ and [EtSO₄]⁻ when paired with [C₂C₁Im]⁺. Overall, greater friction coefficients are obtained for the ILs/film thicknesses with longer relaxation times. This suggests that insufficient relaxation of shear strain within the confined IL film is key for determining an increase in friction. Although the relaxation time increases when IL layers are squeezed out, the variation of the friction coefficient can be more complex, as reflected in the decrease in friction coefficient for [C₂C₁Im][EtSO₄] at 35% RH, and discussed later.

Figure 6.

Comparison of thin-film rheology and tribology of imidazolium ILs: friction coefficient, relaxation time, and master curves for G′ and G″. Color legend for all plots: red for 0% RH and blue for 18 and 35% RH. (a) Friction coefficient. The solid bars give the friction coefficient μ₀, whereas the dashed bars give the friction coefficient for the transition to μ_+Δ. (b) Characteristic relaxation time scale, τ₀ = 1/ω₀, at the cross point between G′ and G″ for the selected ILs at D₀ (solid bar) and D_+Δ (dashed bars). (c) Master curve for G′ and G″.

In our previous work,³⁴ we investigated the nanorheological behavior of dry [C₆C₁Im][TFSI], [C₄C₁Im][TFSI], [C₂C₁Im][TFSI], and [C₂C₁Im][FAP]. A master curve for G′ and G″ as a function of the Deborah number, i.e., D_h = ωτ₀, displays the rheological commonalities of the thin films, i.e., the confinement-induced viscoelastic fluid behavior (time scale > τ₀, D_h < 1) and the transition to a solid-like behavior at high frequencies (time scale < τ₀, D_h > 1). This conceptual model is extended here to the effect of water (Figure 6c). The master curve captures the behavior of [C₂C₁Im][FAP] at 35% RH well.

Thin films (D∼2 nm) of the investigated ILs, except [C₂C₁Im][EtSO₄], exhibit a behavior close to the terminal-zone rheology (G″ ∼ ω, G′ ∼ ω², G′ < G″) at D_h < 1, i.e., at long time scales (>τ₀). This implies that the flow units can relax within the experimentally relevant time scale. Using the relaxation time scale, τ₀ = 1/ω₀, it is possible to roughly estimate the dimensions of the structural flow units. Assuming that translational diffusion is the main mechanism for relaxation upon shear,⁴⁶ the diffusion coefficient is related to the relaxation time by a²/4τ₀, where a is the size of the structural unit. By additionally using the Stokes–Einstein relation, the size of the structural units is given by

where k_B is Boltzmann constant and T is the absolute temperature. The assumed value for η₀ is determined in the plateau region (49, 314, 2840, and 4150 Pa·s for dry [C₂C₁Im][TFSI], [C₄C₁Im][TFSI], [C₆C₁Im][TFSI], and [C₂C₁Im][FAP] at D₀, respectively; see Figures 1–5). This yields a ∼ 3.5–3.6 nm for the dry ILs at D₀ = 2 nm and a ∼ 3.2 nm at D_+Δ = 3 nm for dry [C₂C₁Im][FAP]. The size is larger than an ion pair, and hence, it implies that confinement-induced supramolecular clusters form and are responsible for the viscoelastic behavior of the thin films.

For [C₂C₁Im][FAP] equilibrated at 35% RH (D_+Δ= 2 nm), the plateau occurs at ∼1489 Pa·s and a is 1.9 nm. This suggests that the presence of water reduces the size of the ionic clusters in films of equal thickness, and the relaxation time is significantly reduced 0.141 s (D₀ = 2 nm) vs 0.007 s (D_+Δ = 2 nm) for dry and wet [C₂C₁Im][FAP], respectively. Note that we are comparing D₀ and D_+Δ (both equal to 2 nm) because we remove one more layer in equilibrium with humid air. The calculation of a is not possible at D₀ = 0.8 nm (18% RH) because of the absence of a plateau in the effective viscosity. The relaxation time τ₀ is 0.79 s, and hence, it is quite large. Note that the friction coefficient remains high for the humid [C₂C₁Im][FAP] at D₀ (Figure 6a), and hence, the correlation between the friction coefficient and relaxation time is still valid in the presence of water.

We find a deviation from the master curve for dry [C₂C₁Im][EtSO₄] since this IL remains a Newtonian liquid upon confinement to films with a thickness of D₀ = 2 nm and despite its high bulk viscosity compared to the other ILs. In our previous work,³⁴ we hypothesized that the prominent hydrogen bond network prevented the ions from rearranging into clusters upon nanoconfinement and helped maintain the viscous behavior. In contrast, the enhanced solid-like behavior induced by the drainage of ion layers was attributed to enhanced interionic interactions like electrostatic, steric, and solvophobic interactions, promoting the formation of clusters. Here, we have found that thin films of [C₂C₁Im][EtSO₄] in equilibrium with humid air also remain viscous fluid, the effective viscosity being smaller compared to the dry IL. As inferred from IR spectroscopy,²⁰ water hydrogen bonds with the anion and cation at mole ratios of water to IL larger than 1.5 is present in the thin films based on the refractive index. Hence, it is possible that hydrogen bonding restricts the rearrangement of the water molecules and ions and the formation of clusters that are responsible for the viscoelastic and elastic behavior of the confined ILs. On the other hand, the anomalous behavior observed for the friction coefficient and the effective viscosity in the case of humid [C₂C₁Im][EtSO₄], i.e., the removal of a layer leads to a decrease in the effective viscosity and friction coefficient, is intriguing. We believe that this reflects the higher volume fraction of water with a decrease in the film thickness in a hydrophilic contact, but this warrants further investigation.

It is important to emphasize that previous studies with a surface forces apparatus (or balance) attributed the quantized friction of ILs to a change of the shear plane.²² This relation between the location of the shear plane and friction was also inferred from MD simulations.¹² We provide an alternative or complementary explanation that relates the tribological properties to the rheological behavior of the IL thin films. That is, the IL compositions that lead to the more solid-like behavior yield higher friction coefficients. Based on our work, the formation of supramolecular clusters and the solid-like behavior are promoted by longer alkyl chains in imidazolium (and presumably other) cations and by bulkier anions (compare [FAP]⁻ to [TFSI]⁻ and [EtSO₄]⁻). We also propose that hydrogen bonding could play an important role in determining the dynamic properties of the IL films. Furthermore, the presence of water at hydrophilic contacts can alter cluster size, relaxation times, and Newtonian viscosity. As shown for a hydrophilic and a hydrophobic IL, i.e., [C₂C₁Im][EtSO₄] and [C₂C₁Im][FAP], water can both enhance and mitigate the liquid-like response and thereby can decrease and increase the friction coefficient, respectively.

Previous studies show that stabilization of colloidal dispersions results from viscous and solvation forces.⁴⁷⁻⁵⁰ Viscous stabilization results from the slow diffusion of particles in ILs, while solvation stabilization is due to interfacial layering. Hereby, it has also been reported that ion specificity can play an important role in the adsorption process and thereby in particle stability.⁵¹ Thus, the insight into the structure–dynamics relationship of IL thin films and ion specificity provided by this study may be also relevant to explain the stability of particle dispersions in ILs.

It is well recognized that ILs are promising boundary lubricants because of their ability to form strongly surface-bound and robust boundary layers. In addition, ILs exhibit many physical properties that are desirable in lubrication, such as negligible volatility, nonflammability, and high thermal stability. And their tunable response to external electrical stimuli makes them ideal for the dynamic control of friction. This work has advanced our understanding of mechanisms underlying lubrication by ILs, and how their molecular structure and water traces can significantly influence their performance. Importantly, ILs often involve concerns regarding their toxicity, biodegradability, and potential accumulation in the environment. As the world transitions toward greener practices, the design of environmentally friendly ILs with targeted lubricious properties is crucial in advancing sustainable technologies. Among others, halogen-free ionic liquids are inherently less toxic and more environmentally benign than their halogenated counterparts and are expected to lead to less corrosive wear than their halogenated counterparts. Recent research is addressing this challenge (e.g., by studying amino acid-based ionic liquids^52,53). Future studies should investigate the relation between thin-film rheology and tribology arising from these more complex molecular structures.

Conclusions

Through combined thin-film rheology and tribology studies using an SFA, we study the mechanisms underlying IL boundary lubrication. The quantized friction coefficient as a function of the number of confined layers is related to the rheological behavior of the thin films, which significantly deviates from the bulk rheology. The rheological characteristics of the IL thin films can transition from Newtonian to viscoelastic fluid behavior and to a solid-like response, depending on the molecular structure of the IL and the film thickness. A correlation is found between the relaxation time scale and the friction coefficient, with a higher coefficient being associated with the solid-like rheology of the thin films. Both the cation and anion can significantly influence this transition. For instance, with the same [C₂C₁Im]⁺ cation, the bulkiest anion, [FAP]⁻, promotes the solid-like behavior, whereas [EtSO₄]⁻ is able to maintain a Newtonian behavior under nanoconfinement and to provide efficient lubrication. With the [TFSI]⁻ anion, increasing the length of the alkyl chain in [C_nC₁Im]⁺ promotes the solid-like behavior and therefore increases the friction coefficient.

We have also studied the influence of water on the thin-film rheology and tribology of two ILs, [C₂C₁Im][FAP] (hydrophobic) and [C₂C₁Im][EtSO₄] (hydrophilic), and found that water can have opposite effects. For thin films of [C₂C₁Im][FAP] of similar thickness (∼2 nm), the presence of water near the mica surface results in smaller flow units, reduced effective viscosity, and smaller relaxation times, which is reflected in a decrease in friction coefficient. However, the solid-like behavior is still maintained in the presence of water in thinner films, which concurs with very high friction coefficients. Thin films of [C₂C₁Im][EtSO₄] remain Newtonian upon significant water uptake but with smaller viscosity compared to the dry IL, leading to a smaller friction coefficient.

Materials and Methods

All chemicals including ILs were purchased from Millipore Sigma and aliquots of ∼500 μL were dried in vials under vacuum at 50 °C for 48 h before use.

Surface Force Apparatus

The mica surfaces were prepared by manually cleaving Optical grade #1 mica (S&J Trading, NY) into 1 by 1 cm sheets and back-coated with 40 nm silver using an E-beam evaporator. Two mica sheets of the same thickness (3–6 μm) were glued to transparent glass disks with a radius of curvature R of 2 cm using Epon 1004 F epoxy glue. The precise thickness of the mica surfaces was determined by multiple beam interferometry when the two surfaces were in adhesive contact in a N₂ atmosphere. Rheological and friction measurements of the thin films were conducted under a constant N₂ flow. The relative humidity was monitored with a humidity sensor (SHT75, Sensirion, Switzerland). Under the constant nitrogen flow, the relative humidity was smaller than 3% RH. This is referred to as the dry condition or 0% RH. The system was also equilibrated at 18 and 35% relative humidity (RH) with selected ILs, which was controlled through the ratio of dry and water-saturated N₂ flow. All measurements were conducted at 25 ± 0.04 °C.

After equilibrating the system overnight in dry nitrogen (∼12 h), the surface force between the mica surfaces was measured to determine the layered structure of the IL thin films.

Thin-Film Rheology

The surface was then brought to the selected surface separation, and when the drift was smaller than 0.02 nm/s, friction force and rheological measurements were conducted. A maximum force of ∼100 mN/m was applied in all measurements. The surface separations (D₀, D_+Δ, D_+2Δ, etc.) were selected so that a different number of layers was sandwiched between the two mica surfaces.

Rheological measurements were performed following the protocol reported before.³⁴ Briefly, one of the springs was driven by a piezoelectric motor (P-754, Physik Instrumente, Germany) with a sinusoidal trajectory (z) of constant amplitude equal to 1 μm and frequency in the range of 0.01–20 Hz in the lateral direction. During the motion, the spring deflected (δ), so that the motion of the surface was (z – δ). Hence, the strain applied to the IL was determined as (z – δ)/D, where D is the thickness of the thin film. The lateral deflection of the spring was determined by a home-built transducer consisting of four strain gauges (FLK-1–11–3LJCT, Texas Measurements, College Station, TX) configured into a full Wheatstone bridge. The voltage output was read by a data acquisition system (Pacific Instrument, Concord, CA) that was synchronized with a piezoelectric motor. The resonance frequency of the device is ∼30–40 Hz, which limits the maximum experimental frequency.

The raw data was filtered and analyzed using a homemade MATLAB code to extract the signal of the target frequency and obtain the amplitude of the wave and the phase change with respect to the input wave. The storage modulus (G′) and the loss modulus (G″) were calculated with the known input amplitude, and the measured phase shift and amplitude of the sinusoidal deflection, using the predetermined conversion factors, and the geometrical information on the contact region were measured by scanning the spectrometer around the point of the closest approach (PCA). See details about the method in ref (34). In the present work, the conversion factor of voltage to force is K′ = 0.0256 N/mV. The dashed lines in the plots of the effective viscosity were determined as σ/γ̇, with shear stress σ = K′V_min/A = 25 kPa, where V_min is the precision of the strain gauges, roughly 0.00015 mV, and A is the area of contact. The data points close to the dashed line are those close to the detection limit, and hence, they are less reliable. These data points are not discussed here and are not shown in plots of storage modulus (G′) and the loss modulus (G″).

Thin-Film Tribology

Friction force measurements were conducted at sliding velocities between 30 nm/s and 150 μm/s and a constant sliding distance of 15 μm. The friction force was calculated as F = (F₁ – F₂)/2, F₁ and F₂ being the lateral force upon sliding in one and the opposite direction, respectively. Lateral forces were measured by the strain gauges glued to the springs, as described earlier. At least three friction loops were measured at low velocity (<150 nm/s), and at least ten loops were measured at higher velocities. The friction force was calculated as the average over the loops. The error bars give the standard deviation.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acsami.3c10018.

• File includes a plot with storage and loss modulus of [C₆C₁Im][TFSI], [C₄C₁Im][TFSI], [C₂C₁Im][TFSI] and [C₂C₁Im][EtSO₄]; lateral force during tribological measurements at a sliding velocity of ∼15 μm/s for [C₄C₁Im][TFSI]; change in surface separation D (film thickness) during the nanorheological measurements with dry [C₂C₁Im][EtSO₄] at 0% RH; refractive index of thin films of [C₂C₁Im][FAP] and [C₂C₁Im][EtSO₄] at 0 and 35% RH, respectively; change in film thickness of [C₂C₁Im][FAP] at 35% RH, and storage and loss modulus of [C₂C₁Im][EtSO₄] equilibrated with humid air at 35% RH (PDF)

Author Contributions

^§ X.Z. and M.H. contributed equally to this work. This manuscript was written through contributions of all authors. All authors have given approval to the final version of the manuscript.

This material is based upon work supported by the National Science Foundation Grant CBET No. 1916609 (to R.M.E-M.).

The authors declare no competing financial interest.