Contractile ring composition dictates kinetics of in silico contractility

Abstract

Constriction kinetics of the cytokinetic ring are expected to depend on dynamic adjustment of contractile ring composition, but the impact of ring component abundance dynamics on ring constriction is understudied. Computational models generally assume that contractile networks maintain constant total amounts of components, which is not always true. To test how compositional dynamics affect constriction kinetics, we first measured F-actin, non-muscle myosin II, septin, and anillin during Caenorhabditis elegans zygotic mitosis. A custom microfluidic device that positioned the cell with the division plane parallel to a light sheet allowed even illumination of the cytokinetic ring. Measured component abundances were implemented in a three-dimensional agent-based model of a membrane-associated contractile ring. With constant network component amounts, constriction completed with biologically unrealistic kinetics. However, imposing the measured changes in component quantities allowed this model to elicit realistic constriction kinetics. Simulated networks were more sensitive to changes in motor and filament amounts than those of crosslinkers and tethers. Our findings highlight the importance of network composition for actomyosin contraction kinetics.

Significance

We created a microfluidic device compatible with high-numerical-aperture light-sheet microscopy to measure cytokinetic ring component abundance during cytokinesis in the Caenorhabditis elegans zygote. Implementing measured dynamics into our three-dimensional agent-based model of a contractile ring elicited biologically realistic kinetics. This work enhances our understanding of factors that affect contractile force generation during cytokinesis, and highlights the importance of component abundance for proper constriction kinetics. Of specific importance to constriction is motor filament abundance, which directly leads to more accurate representation of biological kinetics.

Introduction

In animal cell cytokinesis, one cell is physically separated into two by a plasma membrane furrow drawn in by a dynamic cytoskeletal contractile ring. The contractile ring is rich in actin filaments (F-actin), non-muscle myosin II (NMMII) filaments, and other structural components, including non-motoring crosslinkers such as anillin, and other scaffold proteins, including septins. The anaphase spindle initiates a Rho signaling cascade that concentrates contractile ring components at the equatorial cortex (1,2,3) first as a loose isotropic mesh that reorganizes into a tight circumferentially aligned cord, which closes the cytoplasmic connection between daughter cells (4,5,6,7). The two nascent cells become topologically distinct when the intercellular midbody bridge is severed during abscission. Accurate genomic inheritance requires complex regulation of cytokinesis, from initial placement of the assembling actomyosin structure (8,9), to proper regulation of constriction dynamics and irreversible completion (10,11). As the contractile ring constricts, the abundance of structural components changes due to continued recruitment, compaction, disassembly, depolymerization, inhibition, and other processes. Early electron microscopic studies of cytokinetic rings suggested that the overall density of the cortical cytoskeleton was constant throughout ring closure (12). More recently, changes in the density of several contractile ring components have been reported: for NMMII (13,14,15,16,17), F-actin (14,16,17), septin (13,17), and anillin (13,14,15). In the fission yeast Schizosaccharomyces pombe, the density of these, and other, components first increases as the contractile ring matures and then decreases in the latter half of constriction (14). In Caenorhabditis elegans blastomere cytokinesis, although changes are less pronounced, an increase in overall density is visible late in division (13), and, in zygotic division, evidence exists for exponential increase in density of both NMMII and anillin throughout cytokinesis (15). These studies suggest that the overall composition of the contractile ring can change throughout constriction, with components exhibiting differential changes in density that would result in different ratios between them (13,14,17). However, in some cases, multiple contractile ring components exhibit parallel changes in abundance, suggesting consistent composition and the potential for contractile units (15). Dynamic differences in ring composition could account for variations in constriction kinetics and overall cytokinesis timing among different cell types and species. We expected that, beyond the “parts list” of conserved, essential structural components, the dynamic abundance of these components affects cytokinetic ring dynamics. Indeed, the abundance of NMMII motors and non-motor crosslinkers has a non-linear effect on contractile ring dynamics (6,18,19), further highlighting the importance of contractile ring composition and its dynamics for constriction kinetics.

Computer models are powerful tools for evaluating the potential consequences of measured changes in actomyosin ring composition. Although it comes with its own set of limitations, the ability to model with high spatial and temporal resolution serves as a complementary approach for cell biology where microscopy can suffer from resolution limits. Two-dimensional agent-based models have successfully captured how changes in crosslinker density affect the contractility of an isotropic network (20) and isotropic rings (6,18), but differences between ring organization in vivo and in silico (isotropic versus sarcomeric) (13,21) may limit the relevance of these simulations. Agent-based models of cytokinesis were used to predict and describe physical concepts that drive contractile ring formation (7,22) and general mechanisms of actomyosin contraction (23,24,25,26), although these models do not generally incorporate changes in contractile ring composition. Some active gel models of cytokinesis have incorporated contractile ring compositional changes by varying actomyosin concentration temporally (27,28), although these do not consider more complex variation in contractile ring distribution or the changes in relative amounts of actin, myosin, and non-motoring crosslinkers beyond the simple actomyosin variation.

We chose the mitotic cytokinetic rings of the C. elegans zygote as the biological model for our simulation, because 1) its evolution is stereotyped and well-characterized, 2) its contraction is a cell-autonomous event, 3) fluorescent CRISPR transgenes with endogenous expression are readily availability, 4) it can be imaged in toto using live single-plane illumination microscopy, and 5) it can be resistant to phototoxic damage under certain long-term imaging conditions (29). Previous C. elegans zygote imaging methods relied on imaging of the contractile ring in profile view and were subject to reconstruction artifacts, anisotropic resolution, and depth penetration issues. Fission yeast and HeLa cells were previously manipulated into miniature wells (16) to place the contractile ring parallel to the focal plane, such that confocal acquisition could be reduced to a few z sections rather than a full cell volume. Such en face imaging reduces artifacts and permits higher temporal resolution.

Here, we performed en face imaging with a custom-built microfluidic chip based on a staging device (30), combined with high-resolution light-sheet microscopy (31), further illuminating the contractile ring from the side with a light sheet, which allowed isotropic spatial resolution and minimal reconstruction or depth artifacts. We measured the dynamic composition of contractile rings, specifically changes of NMMII, F-actin, anillin, and septin throughout cytokinesis. We implemented these measurements in a three-dimensional (3D) agent-based model that consists of actin-like filaments, NMMII-like motor filaments, non-motor crosslinkers, and tethers that link the network to a deformable surface that represents the plasma membrane. Contractile ring constriction is physically resisted by several extrinsic factors, including membrane resistance to deformation, resistance from the flanking cortex, and cytoplasmic viscosity. To help account for these dampening factors, we built a simple geometric description of a dividing C. elegans zygote based on a numerical solution of published viscoelastic models (32). This model revealed that constriction kinetics better reflect measured biological kinetics when composition changes are considered. With constant composition, simulations failed to recapitulate our biological measurements of cytokinetic kinetics. We further identify specific contractile ring components, NMMII and F-actin filaments, as particularly important for dictating constriction kinetics.

Materials and methods

Generation of microfluidic chip template by photolithography

Microfabrication of microfluidic imaging traps was performed at University of North Carolina (UNC) under the guidance of Dr. Matthew DiSalvo and Dr. Nancy Allbritton. Chamber design was adapted from an embryo trap originally made for high-throughput embryo sorting (30), but with altered channel dimensions to trap embryos in a vertical orientation instead of a horizontal orientation (orthogonal versus parallel to the focal plane, respectively; Fig. 1 A). Modifications were made to trap width and channel size to ensure proper flow for trapping and suction. Once finalized, the design was printed on glass (FrontRange Photomask), which was used as a mask for photolithography (Fig. 1 A; Fig. S1 C).

Figure 1.

Live imaging of C. elegans zygotic contractile rings. (A) Left: graphical representation of custom microfluidic trap on a 25 × 60-mm coverslip (black) with a second coverslip approximately perpendicular to the imaging plane (black; green arrow). Center: microfluidic trap design showing the inlet and outlet channels and four trap features; scale bar, 2 mm. Right: representative C. elegans embryo standing upright in trap cup; scale bar, 30 μm. (B) Left: time-lapse series of the contractile ring in a C. elegans zygote expressing fluorescently tagged NMMII (NMY-2::GFP). Right: normalized mean pixel intensity plot of the contractile ring of a representative cell expressing NMY-2::GFP. Dotted red line is the best-fit line. (C) Left: time-lapse series of contractile ring in a C. elegans zygote expressing a fluorescent F-actin reporter transgene (mKate::LifeAct). Right: normalized mean pixel intensity plot of the contractile ring of a representative cell expressing mKate::LifeAct. Dotted purple line is the best-fit line. (D) Left: time-lapse series of contractile ring in a C. elegans zygote expressing a fluorescently tagged anillin (mNeonGreen::ANI-1). Right: normalized mean pixel intensity plot of the contractile ring of a representative cell expressing mNeonGreen::ANI-1. Dotted blue line is the best-fit exponential curve. (E) Left: time-lapse series of contractile ring in a C. elegans zygote expressing a fluorescently-tagged septin UNC-59::GFP. Right: normalized mean pixel intensity plot of the contractile ring of a representative cell expressing UNC-59::GFP. Dotted green line is the best-fit exponential curve. (F) Plot of cytokinetic ring constriction speed (originally peaking at 0.54% starting ring size per second; normalized so maximum speed is 1.0) in the C. elegans zygote. Gray area around the solid black line represents the mean ± standard deviation. n = 23. Scale bars, 15 μm. Time-lapse frames show both approximate time from imaging onset (bottom; seconds) and approximate closure percentage (top; %).

For template creation, a large, 50 × 75-mm glass slide was first cleaned thoroughly with 99% isopropanol (IPA) and air dried using nitrogen gas. The cleaned slide was then placed in a plasma chamber for 3–5 min in order to clean the top layer of the glass surface and improve deposition of the photoreactive resin (photoresist 1002F-50) (33). The glass slide was then placed, and vacuum sealed, onto a minicentrifuge and an aliquot of photoresist approximately 1 inch in diameter was placed at the center of the slide (over the vacuum-sealed pedestal). The slide was then spun at 200 rpm for 10 s to spread out the bulk and then at 1890 rpm for 30 s to create a uniform coating of photoresist 80–100 μm thick.

Following this initial coating, the photoresist hardened while the slide incubated at 95°C for 1 h, protected from dust or other debris. After incubation, the patterned photomask was carefully placed onto the photoresist and the slide was exposed to 260 mJ UV light (∼300 nm) at 450 mW power. Following exposure, the photomask was carefully removed from the slide and the slide was incubated for an additional 30 min at 95°C.

Next, the glass slide was washed on an orbital shaker with fresh resin solvent for 90 s and rinsed with used solvent for 30 s, ensuring even coverage across the whole slide surface. Finally, the slide was washed twice with IPA for 15 s and briefly air dried. After washing off uncured photoresist, the slide was examined for proper feature retention with a stereoscope at 10× magnification. If successful, the slide was then incubated overnight at 95°C for 30 min then at 120°C overnight to fully cure and harden.

Next, the slide was silanized with trichloro(octyl)silane (Sigma-Aldrich) overnight in a chamber under vacuum in order to reduce adhesion of polydimethylsiloxane (PDMS; Sylgard 184, Corning) to the finished template. Finished slides were kept in a vacuum chamber for up to 1 month without need for re-silanization.

PDMS casting of microfluidic devices

To image C. elegans zygotes on the Mizar Tilt system (31), it was necessary for PDMS microfluidic chips to have enough thickness such that a glass coverslip could be securely affixed to the side of the PDMS, orthogonal to the imaging surface coverslip (the two coverslips being the entry point for the light sheet, and against which the embryo rests, respectively; Fig. 1 A). Thus, PDMS of the desired thickness, which was about 10 mm, was cast in an aluminum chamber within which we could place a template, lithograph side up. Proper Tilt imaging with minimal scattering of the illumination light sheet requires that the light sheet enter the sample chamber roughly parallel to the imaging plane, through a nearly orthogonal, flat, and flawless surface. We therefore designed the casting chamber to have mirror-finished interior surfaces with a slight tilt (2.3° offset from orthogonal); this resulted in a nearly flawless lateral PDMS surface onto which a coverslip was later affixed. For ease of microfluidic chip removal, the casting chamber was made to be easily disassembled.

For casting, the back surface of a glass template was lightly coated in vacuum grease and carefully centered onto the bottom of the casting chamber bottom panel. The casting chamber was then assembled with care to ensure that the template slide did not shift. Uncured PDMS was then poured slowly into the chamber to the desired height and degassed under vacuum for 3–5 min. After degassing, the PDMS was cured in an incubator for 2 h at 90°C. Our templates were constructed to produce six microfluidic chips per casting; 10 min prior to removing the cast PDMS from incubation, six 60 × 25-mm coverslips along with six 22 × 22-mm coverslips (all #2) were prepared for binding to the PDMS. All coverslips were carefully washed with 100% ethanol and allowed to air dry. Dry coverslips were placed in a plasma chamber for 3 min for surface cleaning, all coverslips were then placed, same side up, into an airtight container for temporary storage.

All steps involving preparation of hardened PDMS into fully finished microfluidic chips with coverslips were performed in a laminar flow hood to avoid contamination with dust. The PDMS casting was removed from the incubator and the casting chamber was carefully disassembled. The hardened PDMS was then carefully removed from the template and care was taken to avoid contact between dust or debris and the bottom or side PDMS surfaces, which were nearly flawlessly mirror finished, and to which coverslips would be affixed. The six microfluidic chips were then cut apart using a new disposable scalpel. A 1.5-mm biopsy punch was used to create the inlet and outlet channels from the PDMS. Finally, a 22 × 22-mm coverslip was carefully placed, plasma-cleaned side toward the PDMS, onto the angled lateral surface of each chip, and a 60 × 25-mm coverslip was similarly placed onto the bottom surface of the PDMS with the PDMS chip roughly centered on the slide. The casting chamber created a small lip of PDMS because the bottom surface of the chamber is roughly 1.5 mm larger than the template glass slide on all sides. Thus, each PDMS chip had a lip of 1.5-mm width by ∼1-mm thickness, which allowed for proper placement of the bottom coverslip without impinging on the vertical coverslip. Once both coverslips were placed on all microfluidic chips, assembled chips were carefully placed at 60°C for 3 h to cement coverslips to the PDMS. Completed devices were stored in airtight containers for several months, protected from dust before and after being used for imaging, and could be reused dozens of times, flushing with distilled water after every use.

C. elegans strains and maintenance

The following C. elegans strains were used for the live cell imaging:

SWG007: GFP-NMMII heavy chain; LifeAct F-actin probe tagged with mKate, a red fluorescent protein.

(nmy-2(cp8 [nmy-2::GFP unc-119+]) I; gesIs001 [Lifeact:: mKate2]) (5)

NK2228: GFP-septin.

(unc-59(qy88[unc-59:GFP-C1:3xflag:AID + loxP])) (34).

MDX87: GFP-septin; mKate-anillin

(unc-59(qy88[unc-59::GFP-C1::3xflag::AID + loxP]); Si57[pEZ152; pani-1:mkate2::ANI-1; cb-unc-119(+)]IV). This strain resulted from a cross of NK2228 with ZAN103.

MDX29: mNeonGreen-anillin

(ani-1(mon7[mNeonGreenˆ3xFlag:ani-1]) III).

MDX82: LifeAct F-actin probe tagged with mKate; GFP-tagged utrophin CH-domain-based F-actin probe.

(unc-119(ed3) III; ltIs81 [Ppie-1::gfp-TEV-Stag::ani-2; unc-119 (+)];gesIs001 [Lifeact:: mKate2]; mgSi3[tb-unc-119(+) pie-1>gfp:utrophin] II.; unc-119 (+)] III; ltIs37 [pAA64; pie-1/mCHERRY::his-58; unc-119 (+)] IV). This strain was made by crossing SWG001 (5) with JCC719 (35).

C. elegans strains were maintained as previously described (36).

Dissection and embryo staging

L4 hermaphrodites were grown overnight at 25°C. The following day, two to four gravid adults were placed on a watch glass with autoclave-sterilized M9 buffer (22 mM KH₂PO₄, 42 mM Na₂HPO₄, 85 mM NaCl, 1 mM MgSO₄). Following an initial cleaning in the M9, worms were dissected with 20-gauge needles and eggs were pooled at the center of the watch glass. Using a hand-drawn fine-capillary tube and mouth aspirator, zygotes in which pronuclei had met or that were in pseudocleavage as identified with a stereoscope were aspirated and placed directly into the inlet channel of a microfabricated PDMS imaging chip. A 20-mL syringe full of M9 was then attached to the inlet channel via microfluidic tubing and a flat-head needle. A syringe-controlled flow of M9 through the microfluidic chip for zygote trapping provided a liquid well to maintain fluid pressure and ensure zygotes stayed trapped in the imaging channels. A small volume of M9 was then slowly pushed through the microfluidic chip while observing through a dissection microscope to check for flow-through of worm zygotes. If zygotes were observed to be caught in an imaging cup, flow was immediately stopped; if zygotes flowed through without becoming trapped, flow was reversed and flow-through was repeated more slowly. Zygotes trapped in an angled or horizontal position (long axis horizontal) were coaxed to stand up vertically (long axis vertical) via quick, short pulses of forward and reverse flow. After trapping zygotes in a vertical orientation, the microfluidic imaging chamber and attached syringe were carefully placed on the stage of an inverted microscope for time-lapse imaging.

Imaging on Mizar Tilt

Microfluidic chips were placed directly onto a Nikon Ti Eclipse inverted microscope (Nikon Instruments) with a Mizar Tilt modular light sheet (Mizar) (31). A 10× air objective (Nikon Instruments) was used to locate zygotes in the imaging chip; a 60× planApo oil immersion objective (Nikon Instruments) with an N.A of 1.42 was used for acquisition along with a Prime 95B CMOS camera (Photometrics). Micromanager was used to operate the microscope body, shuttering system (Sutter), and light-sheet box. Modular power lasers (Coherent) at wavelengths of 488 and 594 nm were used for imaging; zygotes were located via brightfield. Zygotes were scanned in the Z dimension to check for pronucleus (or metaphase plate) location in order to verify correct staging and orientation. Zygotes were only imaged and analyzed if their contractile rings formed close to on plane or on plane with the imaging light sheet. Once a properly aligned zygote was identified, it was observed via light sheet in order to approximate the range in Z over which the contractile ring was likely to form based on the absence of cytoplasmic signal at the location of the pronuclei or based on enrichment of the cortical fluorescent signal (Fig. 1 A and B). Immediately on detection of the contractile ring, a time lapse with z stack acquisition (11–25 optical sections, 200 nm apart) was initiated. Imaging was continuous with 150-ms exposures, resulting in timesteps of approximately 3–7 s. We used an OBIS laser module with a 150-mW 561-nm laser at 40% power for red flours and a 150mW 488nm laser at 25% power for green flours.

Image pre-processing

All image pre-processing was performed in FIJI (ImageJ). Image sequences were trimmed in x, y, z, and time to contain only the contractile ring. The resultant 4D images (XYZT) were then z projected (FIJI > Image > Stacks > Z Project) for maximum signal intensity in the z dimension for all time points, resulting in a 3D stack which contained 2D projections for each time point (XYT).

For segmentation of contractile ring signal, we also generated a minimum-intensity projection from the original 4D stack (XYZT). The resulting 3D stack was minimum intensity projected again, to generate a 2D image of the minimum signal for each XY pixel over all Z and T dimensions. This 2D image was then subtracted from each time point in the maximum intensity projection time series. The “result” stack (XYT; maximum intensity minus minimum-minimum intensity) and the original maximum-intensity projection stack (XYT) were saved for processing through a custom pipeline to segment contractile ring signal, report signal intensity and calculate contractile ring kinetics.

Contractile ring measurements

Custom code was adapted to segment the contractile ring in end-on orientation throughout cytokinesis (37,38). Processed stacks were segmented by a neural network that fits a polygon to the shape of the contractile ring and digitizes the resulting shapes into a binary stack with the same pixel and temporal dimensions as the input. These ring stacks are then exported as TIFFs and further processed in FIJI (Fig. S1 D, third panel).

Ring stacks were first dilated (FIJI > Process > Binary > Dilate) to thicken the ring masks to be six to eight pixels thick (Fig. S1 D, fourth panel). For each frame of the maximum-intensity projection stack, the corresponding frame of the mask was used to select the ring region from where average pixel intensity, Feret’s diameter, area, and perimeter were measured. For each maximum-intensity projection stack, the average pixel intensity of the background was also measured in a 10 × 10-pixel region of interest in the cytoplasmic signal away from the contractile ring. The background measurement was taken for each time point in the series and subtracted from the average contractile ring pixel intensity for the corresponding time point.

The relative amounts of several contractile ring components throughout cytokinesis were quantified as a function of percentage closure with respect to initial cell radius (Fig. S1 A and B):

$$C=100\ast \left(1-\frac{r_t}{r_0}\right)\text{,}$$ (1)

where r_t is the radius (or half of the ring diameter; herein the diameter along the major axis of the mask shape) of the contractile ring at the current time point and r₀ is the initial radius estimate (Fig. S1 B). Component fluorescence intensity for a given cell was normalized to its value at 50% ring closure.

Biological data from all imaged strains were pooled to generate our in vivo contraction dynamics estimates. First, each individual cell’s speed curve was generated from a second-degree polynomial fit of its speed over percentage closure. Each curve was then normalized to its own internal maximum speed (such that all curves reached a peak speed of 1.0). All cell data were then averaged to generate a mean fit of speed over percentage closure for all points between 0% (fully open) and 100% (fully constricted). For each averaged speed, the standard deviation was calculated and the mean speed plus/minus the standard deviation was reported.

Calculating relative fold change from normalized intensity curves

To generate population-averaged normalized fluorescence intensity curves, linear regressions were used on the normalized intensity for actin and myosin markers and on the log of the normalized intensity for septin and anillin markers. The fitted lines for all cells from each strain were then averaged together to generate the average over the entire dataset obtained for that strain, for myosin, F-actin, septin, and anillin. This procedure allowed us to interpolate the measured intensities, exceeding the temporal resolution of our image acquisition (intervals of 3–7 s; see section “imaging on Mizar Tilt”). Note that, for septin and anillin, linear fits were exponentiated to derive the final fit.

Population-averaged fluorescence intensity curves served as proxies for the estimated density of each contractile ring component during constriction. We assumed that the contractile ring width stayed roughly constant after constriction begins; therefore, we multiplied the estimated normalized density of ring components by the perimeter of the contractile ring. This served as an estimate of the contractile ring area and provided an estimated amount of each ring component for each time point throughout constriction. The resulting normalized density curves relate to the relative, not absolute, change in protein amount for each contractile ring component (Fig. S3). These final curves were used to estimate component amounts in our contractile ring simulations as discussed in point 2 in section “Cytosim agent-based software modifications.”

Base model description

Our agent-based models of cytokinesis were built within Cytosim (www.cytosim.org), an open-source stochastics physics engine used to simulate cytoskeletal networks. The base Cytosim code can be found on Gitlab (Gitlab: https://gitlab.com/f.nedelec/cytosim). Significant modifications were, however, needed to run our specific simulations (discussed in the next section), for which code is available on Gitlab (Gitlab: https://gitlab.com/CortesLab/cytosimCR).

Contractile ring simulations were run in 3D (discussed below) and included agents representing the main molecular components of animal cytokinetic rings (Table S2) interacting with an outer cylinder of variable radius, representing the plasma membrane of a constricting cell.

F-actin was simulated as a treadmilling filament initially 500 ± 200 nm in length, exhibiting stable treadmilling where the plus (barbed) end assembly and minus (pointed) end disassembly both occur at 10 nm/s. Actin filament length has not been measured in C. elegans; estimates from S. pombe suggest a range from 500 nm to 2.5 μm in length (14, 39). We selected 500-nm-long filaments as filaments shorter than 500 nm resulted in slower constriction and longer filaments resulted in more variability in constriction (Fig. S5 E). Septin, a crosslinker and membrane tether in the contractile ring, was simulated as a 100-nm-long filament with 10 evenly spaced actin-binding components (herein, binding domains are referred to as couples). Anillin, a scaffold protein, was simulated as a 40-nm-long filament with two actin-binding couples and one motor-binding couple affixed on the filament backbone. A final simple crosslinker was simulated as a short, 20-nm-long filament bearing two actin-binding couples. NMMII, the crosslinking motor implicated in driving cytokinesis, was simulated as a bipolar filament ensemble (40) as characterized through electron microscopy (41,42,43,44). Each ensemble consisted of 30 motors, with 15 motors bound to either end of a single 300-nm-long filament. Each motor binds and unbinds actin-like filaments independently as force is exerted across the spring-like linker. Motors had an unloaded speed of 150 nm/s, and lower speeds under load as demonstrated in vitro and in vivo (41,42,44,45,46).

The model included steric interactions between all filamentous components. The steric range was 10 nm for all filaments, to match the diameter of actin filaments; thus, component segments within 10 nm sterically repelled one another (47).

Simple component turnover was necessary to avoid rupture and collapse of simulated rings (Fig. S5 A–D), as observed in simulations of a membrane-anchored model of the fission yeast cytokinetic ring (26). In our simulations, every 1–2 s, one agent of each component type was randomly selected and removed from the simulation and replaced by a new one, placed somewhere at random within 100 nm of the space surface.

The simplest 3D simulated contractile ring was constructed as a ring-shaped meshwork of isotropic filaments and filament binders confined within a static viscous space. The simulated contractile ring was 10-fold smaller in cross-sectional area than the C. elegans zygote to decrease computation load and time. The simplest simulations estimated functional amounts for each of four ring components (filaments, motor ensembles, crosslinkers, and tethers) based on measured maximum protein abundance in the fission yeast cytokinetic ring (14).

Cytosim agent-based software modifications

A sample configuration file to run a simulation with the modifications detailed below can be found within our Gitlab repository, titled “cytokinesis_ring.cym" (Gitlab: cytokinesis_ring.cym). Modifications made to the Cytosim base code for this work are as follows:

• 1.We previously coded and tested a more physically realistic model of motor unbinding based on force in Cytosim (40). Here, we implemented our previously characterized fully discretized model of NMMII motor ensembles with subunits exhibiting catch-slip unbinding dynamics and composed of 15 motors on either side of a 300-nm-long semi-rigid filament. The choice to simulate motor ensembles with this degree of biophysical complexity is justified in part by recent reports that the mechanosensitivity of crosslinkers is important for both maintaining stable contractile ring structure (48) and generating suitable connectivity and force (6,18,19). The unbinding of all other filament binders in our simulations was described by a simple Kramer’s theory relationship where bond lifetime decreases exponentially with applied force (slip bond).
• 2.Default Cytosim allows users to set event codes to add or remove specific amounts of any component in a time-dependent manner. However, we needed to change to component abundance as a function of contractile ring size, and not time. Thus, an algorithm was added to automatically update the amounts of contractile ring components based on the radius of the deformable bounding space. Component fold-changes (see section “Cytosim agent-based software modifications”) were converted to component count by estimating a maximum amount for each component based on measurements from fission yeast (14,39). At every time step (1 ms) Cytosim calculated the total amount of each component from the radius of the virtual cell given the normalized fold-change functions known for each component. A user-defined “adjust” function (Supplemental File 1) added or removed members of that component class at random in the whole user-defined space, for removal, or in a specified sub-region, for addition, until the expected amount calculated by the fold-change function was reached. The implementation used a timer generated at random from an exponential distribution, to mimic the noise present in vivo.
• 3.The cylindrical bounding space representing the plasma membrane could change radius but remained cylindrical throughout the simulation. Dimension change was driven by the forces generated by the associated network, similarly to a previous study (49). In short, the rate of radius change was set proportionally to the force exerted.

The cylinder symmetric around the z axis (herein referred to as the cell) consisted of three surfaces: two discs parallel to the xy plane, defined by a radius R and separated along the z axis by a length L, and one cylindrical surface, of matching length, and circumference 2φR. Simulated components were constrained in Z ∈ [−L/2, L/2]. Along the cylindrical surface, however, components were not rigidly contained and were instead confined to be either within or on the surface through an energy potential, characterized by a scalar stiffness parameter. Moreover, components slightly outside the cylinder and internalized surface-confined components exerted forces on the cylinder. Components added to the system were set only near the cylindrical surface and inside the cylinder.

Forces were transmitted to the cylinder by cytoskeleton-like components through their interactions defined by the potential associated with the cylindrical surface. Applying the force potential to actin-like filaments and septin-like tethers was sufficient to tether the entire contractile network near the surface, because these components are connected to the rest of the network via motors and non-motor crosslinkers. For any component point subjected to the confinement force potential, its radial displacement was used to calculate a resultant radial force. This force could be directed either inward or outward (contractile or expansile; Fig.S2 C). Septin-like tethers were confined on the space surface along all of their points, allowing them to exert both inward and outward force on the space. Actin-like filaments were confined in two ways. First, their plus ends were confined to the cylindrical surface, also allowing them to exert either inward or outward force on the surface. Second, all other actin-like filament vertices were confined inside the surface, allowing them to exert only outward forces. All other components were only confined inside, thus allowing them to contribute only outward forces as a result of either expansile motion in the contractile ring or crowding of components.

Forces acting on the cell’s cylindrical surface were calculated for every confined vertex. At every time point, the inward or outward offset of each vertex was calculated by first projecting to the closest point onto the surface. The offset, x, was calculated as the difference between the vertex and its projection (Fig. S2 C), resulting in a vector that is in a radial direction in the xy plane (the x and y components are equal, and the Z component of the force is zero). The associated force is Hookean with zero resting length:

$$F_C=kx\text{,}$$ (2)

given the confinement stiffness, k. The total radial force, $F_R$, is the sum of the radial component of all forces calculated for all confined vertices in the simulated system. The radial component is a scalar that has the same magnitude as $F_C$, positive for outward-directed force and negative for inward-directed force:

$$F_R=\sum _1^i{F}_C^i\text{,}$$ (3)

• 4.To establish the equations governing the radius $R$, mathematical estimations of the forces involved in membrane deformation during cytokinesis (32) were adapted to Cytosim, creating a custom simulation space class where the radius of the cylinder could change under tension. Using simple geometric descriptors of whole-cell shape as division progresses, and assuming constant total volume, the surface area S is calculated as a function of $R$, and $x$, the non-overlapping length from the center of one hemisphere to the division plane, was calculated. Assuming that the energy involved in surface deformation is affected by surface tension, $T$, the energy of deformation, $E\text{,}$ of the cell at any given radius was calculated as the following:

$$E=TS\left(R,x\right)\text{.}$$ (4)

The force of membrane deformation could then be estimated as the following:

$$F_D=-\frac{dE}{dR}\text{.}$$ (5)

The resultant deformation force was added to the force exerted on the space by contractile ring components:

$$F\left(t\right)=F_R+F_D\text{.}$$ (6)

The change in radius, dR, for each time point was then calculated by multiplying $F\left(t\right)$ by a constant, $\alpha$, representing the dampening factors mentioned above:

$$dR=\alpha F\left(t\right)\text{.}$$ (7)

An α value was chosen such that the overall time for simulation constriction scaled with biological data

Finally, the change in radius was added to the current radius at the end of each time step, τ, to calculate a new radius, $R_{t+\tau }$, for the following time point:

$$R_{t+\tau }=R_t+dR\text{.}$$ (8)

• 5.The adjust function described in point 2 in section “Cytosim agent-based software modifications” could work by incorporating new components into the simulation right under the circumferential surface of the cell. However, because this cell must be wide to simulate the initially wide contractile ring, seeding new components anywhere along its surface resulted in some components never being incorporated into the active contractile ring. We therefore restricted nucleation to a band of width of 2 μm, and thickness of 700 nm. This "equatorial" seeding better reproduced the incorporation of components into the mature contractile ring.

Measuring contraction kinetics of simulations

The “report” functionality of Cytosim generates numerical data from saved simulations. A new addition to this is the reporting of the radius of the dynamic cylinder space into a comma-separated value (CSV) format. Our simulations report out the radius every 10 ms, and this temporal resolution is much higher than that achieved via live cell imaging of ring constriction (6,13,50,51). The reported radius was used to calculate the percentage closure (see section “contractile ring measurements” for description) of the space and the relative speed of constriction at each time point. Speed data were smoothed using a moving mean method with a sliding window of 30 frames (3 s), similar to how biological data were treated (6).

Estimation of component coverage in dynamic cylinder space simulations

Contractile ring coverage and distribution of motor agents was estimated from color images generated with a 100-ms time interval. These images represented the cell as seen from the z axis, where it appeared as a circle (Fig. S5 C and D), akin to a maximum-intensity projection. The images were imported into FIJI (ImageJ) as a time stack and the red, green, and blue channels were split into three 16-bit gray-scale stacks: one corresponding to the motors and the other two representing other components that were ignored for this analysis. The motor image stacks were down-sampled to 8-bit gray-scale stacks, which were then segmented by thresholding to create binary masks for all time points using the default thresholding algorithm in FIJI (FIJI > Process > Binary > Make Binary). Mask stacks were thickened slightly to fill small holes using binary erosion (FIJI > Process > Binary > Erode). Using the Points from Mask (FIJI > Edit > Selection > Points from Mask) and Fit Circle (FIJI > Edit > Selection > Fit Circle) functions, best-fit circles were generated for all time points and thickened into 1-pixel-thick bands using the Make Band functionality (FIJI > Edit > Selection > Make Band). The resultant band regions of interest (ROIs) were then used to measure the mean pixel intensity from the motor mask stack. If the distribution of motor agents along the simulated ring space were 100%, the ROI generated from the circle fitting would be expected to read all pixel values as 255 (maximum for an 8-bit image). Therefore, the standard for 100% coverage would be a mean pixel intensity of 255. Actual distribution was thus calculated as the following:

$$G=100\left(\frac{{motor}_{mean}}{255}\right)\text{,}$$ (9)

where ${motor}_{mean}$ is the mean pixel intensity of the motor component image ROI. A visual representation of this same analysis was generated by projecting the two-dimensional view of each individual component type over time. Using this temporal projection, large gaps were made apparent in simulations with inconsistent distribution of contractile ring components.

Five-Dimensional metric analysis

To quantify the ring contraction kinetics, we defined five metrics: maximum speed, inflection point (percentage closure at which maximum speed occurs), maximum acceleration, maximum deceleration, and the ratio between acceleration and deceleration (as a metric of the skew of the kinetics curve; Fig. S1 E). Metrics were normalized to the biological dataset. Speed had previously been normalized for each individual biological sample to its own internal maximum, so the average maximum speed for 23 measured cells was 1.0 with a standard deviation of zero. All other metrics were measured from the individual standardized speed curve for each cell, and the average is reported along with its standard deviation. The five normalized metrics are displayed in pentagonal plots. By virtue of the normalization with respect to the biological sample, a simulation that perfectly recapitulated the biology would be represented by a regular pentagon (all radii are 1.0).

Maximum speed served as the scaling metric between biological data and the simulation data. The gradient of the smoothed speed curve was taken to calculate the peak acceleration and peak deceleration of each simulation. The maximum speed and inflection point (closure percentage where peak speed was reached) were also tabulated for each simulation. For each simulated configuration, 30 simulations were run to calculate mean and standard deviation data for each of the above-mentioned metrics. For speed and acceleration/deceleration, data from simulations in which all contractile ring component abundances were modulated were set to 1.0 and the scaling factor between its true maximum speed (∼0.054 μm/s) and 1.0 was used to scale speed and acceleration/deceleration from other simulation conditions. Inflection point, which reported the percentage closure at which maximum speed occurred, was not affected by scaling of the y values of the curve, nor was the slope between acceleration and deceleration, since both are scaled by the same factor.

We then generated the pentagons as the following:

$$x_i=a_i\cos \left(i\theta \right);y_i=a_i\sin \left(i\theta \right)\text{,}$$ (10)

with $i\in \left\{0...4\right\}$ and θ = 2φ/5 (Fig. S1 D). The area of the pentagon was then calculated by breaking it down into five triangles with individual areas:

$$A_i=a_i{a}_{i+1}\sin \left(\theta \right)/2\text{,}$$ (11)

Where $a_i$ and $a_{i+1}$ are the lengths of the sides of the triangles, with $a_5=a_0$ (Fig. S1 F). The area of the pentagon shape is then:

$$A=\sum _{i=0}^4{A}_i\text{.}$$ (12)

All simulation datasets were analyzed to yield the five metrics from the smoothed speed curve of each individual simulation. These metrics were then averaged for each dataset; thus, for the simulation, standard deviations were reported for all five metrics. The vertices for each simulated dataset pentagon were calculated as before, using the ratio between the simulated condition and the biological data as r (Fig. S1 F). For each comparison, the simulation pentagon was plotted over the biological standard. The Δr for each metric was reported to show the fold increase (or decrease when negative) of each metric. The ΔA was reported to show the total relative difference of each simulated dataset from the biological standard. Very small ΔA suggested simulations very similar to the biological data, whereas large ΔA suggested simulations very dissimilar from the biological data.

Results

Abundance dynamics measurements from C. elegans zygotic division

The compositional dynamics of contractile rings have been measured for some components in some cell types (13,14,15,16), but a systematic study has not been undertaken in an animal system. We therefore first measured contractile ring composition changes throughout C. elegans zygotic division. To generate data with high spatiotemporal resolution and with minimal reconstruction or imaging artifacts, we imaged the zygotic contractile ring en face using custom-made PDMS microfluidic devices, which were designed based on similar devices that immobilize C. elegans embryos in a horizontal orientation (30). Our device trapped dissected zygotes in an upright position and allowed us to illuminate the contractile ring with a Mizar Tilt lateral-excitation light-sheet system (31). We imaged cytokinesis in zygotes expressing endogenously expressed fluorescent markers for NMMII (NMY-2::GFP; Video S1), F-actin (mKate::LifeAct; Video S2), anillin (mNeonGreen::ANI-1; Video S3), and septin (UNC-59::GFP; Video S4). The z stacks were acquired from the onset of furrowing through the end of constriction. Maximum-intensity projections through the thickness of the contractile ring revealed differences among markers for normalized ring intensity dynamics throughout cytokinesis (Fig. 1 B–E, B′–E′). NMMII (n = 10) and F-actin (n = 12) markers increased in normalized intensity in a linear fashion as cytokinesis progressed (Fig. 1B′, C′). Septin (n = 15) and anillin (n = 14), on the other hand, increased exponentially in normalized intensity (Fig. 1 D′, E′). Normalized intensity measurements provided an estimate of the relative density changes for each of the four measured contractile ring components (Fig. 1 B–Eʺ). Relative density changes described composition changes per unit area of the contractile ring as opposed to describing changes in whole contractile ring composition. Thus, we multiplied the density curves by contractile ring perimeter (derived from radius measurements) to estimate total fold change of each contractile ring component (Fig. S3 A–D, A′–D′; section “calculating relative fold change from normalized intensity curves”). Since the absolute amount of any component in the C. elegans zygote cytokinetic ring has not been measured, we estimated maximum protein amounts for each component using measurements of total amounts on the S. pombe contractile ring (14, 39). For each ring component, we normalized our estimated fold change to these maximum values, resulting in an estimated amount of each ring component throughout cytokinesis (Fig. S3 A–Dʹ) combining C. elegans and S. pombe measurements. These data were then used to set the amount of each of the four simulated agents as a function of the cylinder’s radius at every time point of the simulation (Fig. S4 F and G).

Video S1. Timelapse of NMMII on the contractile ring, related to Figure 1B

Maximum intensity projection of a 4-dimensional stack showing NMMII (NMY-2::GFP) on the zygotic contractile ring during constriction. Scale bar (bottom right) = 15 μm. Imaging was performed using a microfluidic imaging chip on a Mizar TILT, collecting a full stack every ∼3 seconds. Movie shows 12 frames per second.

Video S2. Timelapse of F-actin reporter on the contractile ring, related to Figure 1C

Maximum intensity projection of a 4-dimensional stack showing an F-actin reporter (mKate::LifeAct) on the zygotic contractile ring during constriction. Scale bar (bottom right) = 15 μm. Imaging was performed using a microfluidic imaging chip on a Mizar TILT, collecting a full stack every ∼3.5 seconds. Movie shows 10 frames per second.

Video S3. Timelapse of anillin on the contractile ring, related to Figure 1D

Maximum intensity projection of a 4-dimensional stack showing anillin (mNeonGreen::ANI-1) on the zygotic contractile ring during constriction. Scale bar (bottom right) = 15 μm. Imaging was performed using a microfluidic imaging chip on a Mizar TILT, collecting a full stack every ∼4 seconds. Movie shows 9 frames per second.

Video S4. Timelapse of septin on the contractile ring, related to Figure 1E

Maximum intensity projection of a 4-dimensional stack showing septin (UNC-59::GFP) on the zygotic contractile ring during constriction. Scale bar (bottom right) = 15 μm. Imaging was performed using a microfluidic imaging chip on a Mizar TILT, collecting a full stack every ∼3 seconds. Movie shows 12 frames per second.

Multi-dimensional analysis of C. elegans contraction kinetics

To next compare in vitro and in silico closure kinetics, we pooled the imaging data together to estimate the average closure kinetics curve from our biological dataset (Fig. 1 F, B, n = 27). We characterized ring closure with five metrics: normalized maximum speed, percentage closure at maximum speed, peak acceleration, peak deceleration, and the ratio between acceleration and deceleration (as a measure of the symmetry of the kinetics curve). These measurements of our biological data were assembled into a pentagon wherein the value of each parameter in vivo was normalized to 1.0 (Fig. S1 E). Zygote ring contraction speed increased until 47% closure (Fig. S1 E; Table S1), at which point it reached approximately 0.5%/s (normalized to 1.0 below). Acceleration and deceleration rates were indistinguishable at 7.9 × 10⁻³%/s²); the ratio of acceleration to deceleration was 1.0 (Table S1). The shape of the pentagon displays the five metrics (Fig. S1 E), and its area served to score our different conditions.

Simulated contractile rings with C. elegans abundance dynamics recapitulate biological constriction kinetics

Generic simulations of contractile rings incorporate actin-like filaments, various configurations of motors, and non-motor crosslinkers (18, 23, 24). Some published simulations incorporate a change in total actomyosin throughout constriction represented as a net change in contractile force generation (28); however, these models generally assume, and impose, uniform distribution of actomyosin along the furrow (circular symmetry) and ignore other components of the contractile ring. To test the impact of measured changes in ring composition on contraction kinetics, we simulated a 3D contractile network tethered to a deformable space (Fig. 2 A and B; Fig. S2 A). Such models have been implemented successfully for fission yeast cytokinesis (26), but without implementation of protein abundance dynamics. We adapted a variable-radius cylindrical space in Cytosim to represent the plasma membrane (49) and used a simple geometric approximation of cell deformation throughout cytokinesis to estimate a surface tension-based resistance to deformation of the membrane (32). We estimated the membrane tension and cytoplasmic viscosity of the C. elegans zygote based on measurements of other cytokinesis in zygotes of other species (52,53,54). Within this framework, we further added an algorithm to change contractile ring component abundance in real time to match total protein amounts estimated from measured density changes in live cells (Figs. S3 and S4). Our algorithm removed components at random from anywhere in the simulation space or added them uniformly in the space proximal to the deformable surface at each time point, according to instantaneous contractile ring size (see section “PDMS casting of microfluidic devices”). In this way, we simulated the changes in the composition of contractile ring components (Fig. S4 Aʹ–Dʹ). Furthermore, we implemented each of the four contractile ring components as filaments, made up of points connected by springs, with permanently attached “domains” that can bind other components. In this way, we simulated NMMII-like motor ensemble with 30 discrete filament-binding motors in a bipolar arrangement. This approach also allowed us to simulate anillin-like crosslinkers with multiple types of binding interactions as anillin has been shown to interact with both F-actin and NMMII filaments (55).

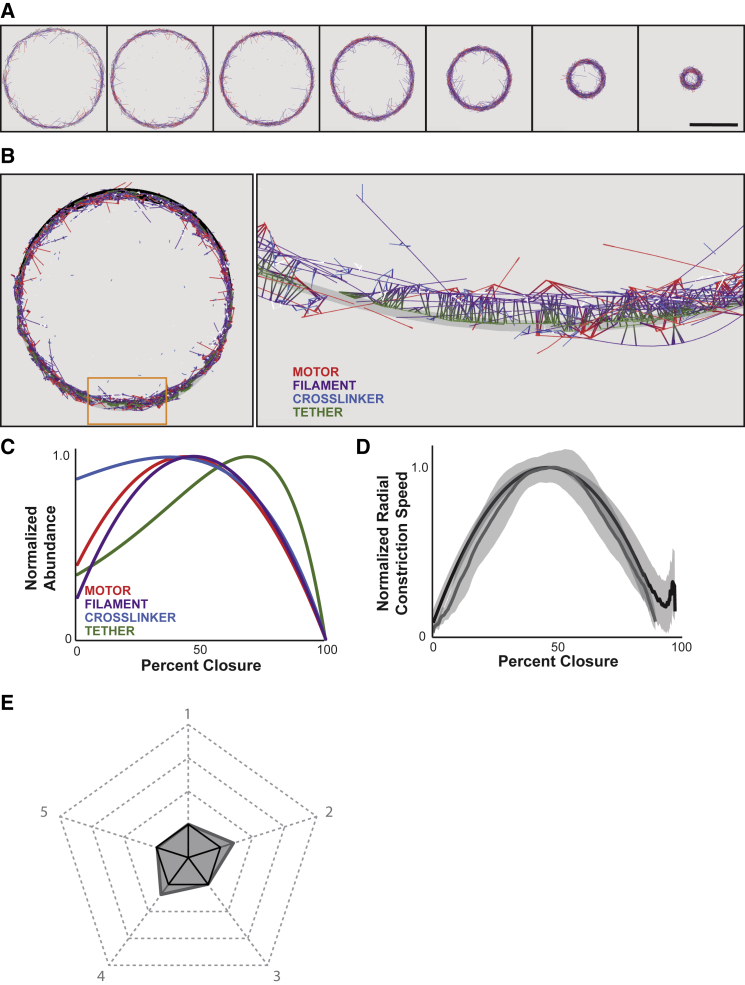
Figure 2.

Simulated contractile rings with biologically informed abundance dynamics exhibit realistic closure kinetics. (A) Time series from a representative 3D simulation viewed as a two-dimensional projection, showing the four main simulated contractile ring components. Dynamic space is tethered to the contractile ring trailing (outside) edge. (B) Left: full view of a representative simulated contractile ring with dynamic ring space shown in black. Right: magnified view of orange-rectangle region in (A); dynamic space is shown as a gray surface. Tether components (green) are tightly associated with the gray surface. All other components associate with the deformable space indirectly through association with the tethering component, except for the filaments (purple), whose plus ends are also tethered directly to the surface. (C) Normalized abundance of four main simulated contractile ring components as a function of constriction of the dynamic space. (D) Average constriction dynamics curve of simulated contractile ring (gray line) and C. elegans zygotic cytokinetic ring (black line). Gray areas, mean ± standard deviation. n = 30. (E) Pentagon generated from the five contractile metrics measured (gray) compared with the biological standard metrics (black solid pentagon). Scale bar, 15 μm.

We first tested the effects of modulating all four major contractile ring components (Fig. 2 A, C; Video S5). All simulations with biological abundance dynamics closed completely with reproducible kinetics (30/30; Fig. 2 A, D; Video S6). Ring closure kinetics quantitatively resembled our cell biological measurements. To compare simulated and biological kinetics, we normalized the average closure curve so that the normalized maximum contractile speed was 1.00. This maximum speed occurred at 46% closure, which was statistically indistinguishable from the biological standard (Table S1). Peak acceleration and deceleration were comparable, at 1.1 × 10⁻²%/s², and the ratio between them was 1.0 (Fig. 2 D and E; Table S1). Comparing these five metrics via our pentagon plot revealed a 30% higher composite score for these simulations, compared with our biological data (Fig. 2 E; Table S1). The increase in composite score was attributed mostly to higher peak acceleration and deceleration of the simulated contractile rings. However, the ratio between these two, along with the normalized maximum speed and the point at which maximum speed occur, were all strikingly similar to biological measurements.

Video S5. Rotating view of agent-based simulation of dynamic component abundance on the contractile ring, related to Figure 2

Movie shows a representative simulation of the contractile ring where all four main ring components, motors (red), filaments (purple), tethers (green), and crosslinkers (blue; legend on bottom right) have modulated abundance. Rotation at 0% and ∼25% closure shows how components can be visualized in 3D. The dynamic deformable space is shown in blue.

Video S6. Orthogonal view of agent-based simulation of dynamic component abundance on the contractile ring, related to Figure 2

Movie shows a representative simulation of the contractile ring where all four main ring components, motors (red), filaments (purple), tethers (green), and crosslinkers (blue; legend on bottom right) have modulated abundance. The dynamic deformable space is not visible from this perspective.

It was not clear whether the prescribed component dynamics were responsible for biologically realistic ring closure kinetics or whether it was simply important that the correct abundance of components was reached at some point in the simulations. To test the latter hypothesis, we next simulated ring closure with component abundance invariably set to the maximum amount calculated from biological data (Fig. 3 B). In this condition, simulated rings consistently closed beyond 90% (30/30, Fig. 3 A, C; Video S7). However, these rings lacked resemblance to biological constriction kinetics. First, for simulations with constant component abundance, normalized maximum speed was significantly higher than for simulations with all component dynamics (the “simulation standard”) and the biological standard, at 1.20 (which would translate to approximately 0.6%/s). Normalized maximum speed was reached significantly earlier than either standard as well, at 27% closure. Acceleration and deceleration were also higher than in the biological dataset, at 3.3 × 10⁻²%/s² and 1.1 × 10⁻²%/s², respectively; the ratio between these two metrics was also higher than with the biological data at 3.0 (Fig. 3 C and D; Table S1). Overall, these changes resulted in a 320% increase in the area of the parameter pentagon compared with the biological standard (Fig. 3 D; Table S1). Altogether, this suggested that, although simulations with constant component abundance could generate robust constriction, abundance dynamics were important for recapitulating the constriction kinetics of C. elegans zygote cytokinesis.

Figure 3.

Simulated contractile rings with no abundance dynamics do not exhibit realistic kinetics. (A) Time series from a representative 3D simulation viewed as a two-dimensional projection, showing the four main components of the simulated contractile ring and dynamic space. (B) Normalized abundance over closure for all four components (constant throughout closure). (C) Plot of average constriction dynamics curve of simulated division (gray line) versus the curve from the biological dataset (black line). Gray areas, mean ± standard deviation. n = 30. (D) Pentagon generated from the five contractile metrics measured (gray) compared with the biological standard metrics (black solid pentagon). Scale bar, 15 μm.

Video S7. Orthogonal view of agent-based simulation of static component abundance on the contractile ring, related to Figure 3

Movie shows a representative simulation of the contractile ring where all four main ring components, motors (red), filaments (purple), tethers (green), and crosslinkers (blue; legend on bottom right) have preset static abundance. The dynamic deformable space is not visible from this perspective.

The dynamics of motor and filament composition are important for biologically realistic constriction kinetics

While all four contractile ring components simulated here are phylogenetically conserved and essential for normal contractile kinetics in vivo, the effects of their loss of function vary quantitatively. NMMII motoring is inconsistently necessary for successful constriction (56,57), and depletion of actin regulator Arp2/3, anillin, or septin all result in successful but uncharacteristically concentric division of the C. elegans zygote (58). Thus, we next explored how changing composition of each contractile ring component individually affected constriction kinetics. We simulated rings in which the abundances of all components but one were set to the maximal amounts, whereas the altered component was allowed to change in abundance to match biological data (Fig. 4 A–D).

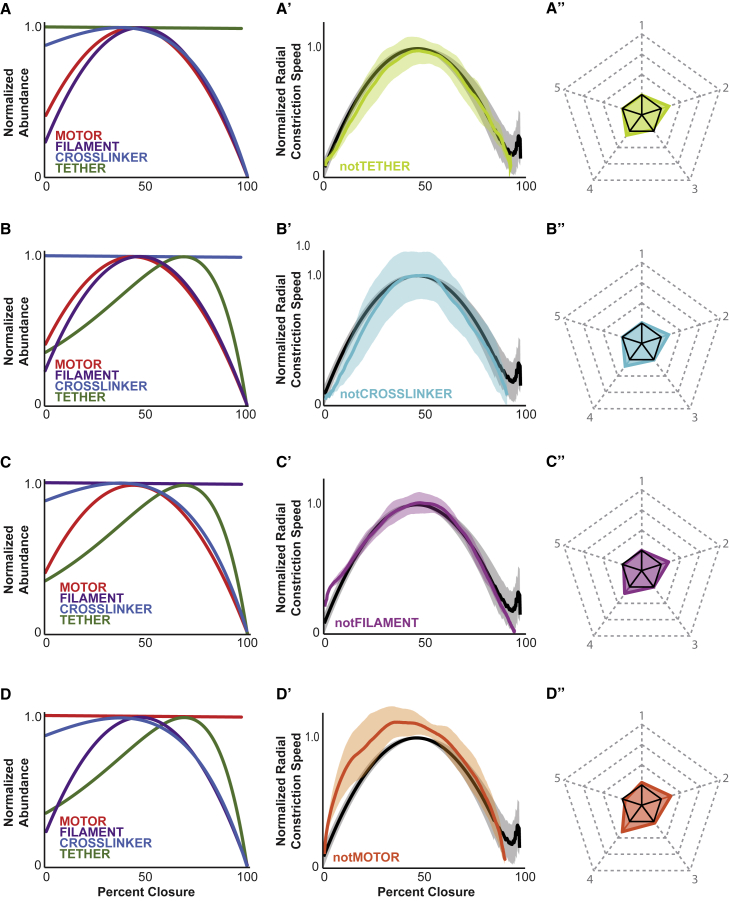
Figure 4.

Implementing abundance dynamics of different ring components has distinct effects on constriction. (A–D) Normalized component abundance over closure input for simulations with conditions in which each of the four main simulated ring components was individually dynamic. (A) Only tether is dynamic. (B) Only non-motor crosslinker is dynamic. (C) Only F-actin-like filament is dynamic. (D) Only motor ensemble is dynamic. (Aʹ–Dʹ) Plots of average constriction dynamics curves of simulated divisions (correspondingly colored curves) versus the curve from the biological dataset (black line; Aʹ–Dʹ) and the simulated dataset with no change in composition (light gray in A’, B’). Lighter-colored areas around solid curves represent the mean ± standard deviation. (Aʺ–Dʺ) Pentagons generated from the five contractile metrics measured from each simulation setup (color matched) compared with the biological standard metrics (black solid pentagon). n = 30 for all.

We began with adjustment of the tether component, representing septin in our model, alone (Fig. 4 A). These contractile rings constricted the dynamic space fully (30/30) but did not exhibit biological kinetics (Fig. 4 Aʹ). The average constriction curve for these simulations was very similar to that of simulations with no composition changes (Fig. 4 Aʹ); the parameter pentagon was similarly 310% larger than the biological standard (Fig. 4 Aʺ; Table S1). Specifically, normalized maximum speed was significantly higher than in the biological and simulation standards, at 1.26, and occurred abnormally early, at 28% closure. Acceleration and deceleration were likewise higher at 3.3 × 10⁻²%/s² and 1.2 × 10⁻²%/s² respectively, and the ratio between them was 2.761. Overall, the pentagon area-based composite score was 310% higher than for the biological data (Table S1).

Likewise, for simulations in which the abundance of the non-motoring crosslinker component, which represented anillin, alone were adjusted (Fig. 4 B), the contractile rings constricted the dynamic space (30/30) with non-biological kinetics (Fig. 4 Bʹ). Just as with the simulations with no composition changes, non-motor crosslinker changes alone resulted in a statistically faster normalized maximum constriction speed, of 1.21, which occurred earlier than in the biological or simulation standards, at 25% closure. These simulations also exhibited higher acceleration and deceleration (3.3 × 10⁻²%/s² and 1.1 × 10⁻²%/s² respectively; Fig. 4 Bʺ; Table S1). The composite score for these was 330% higher than that of the biological standard, comparable with that seen following adjusting tethers alone, and simulations with no composition changes.

Next, we simulated rings in which only the abundance of the actin-like filament changed (Fig. 4 C). These simulations successfully constricted beyond 90% closure (30/30) and closely recapitulated the constriction kinetics of our biological dataset (Fig. 4 Cʹ). Overall, the normalized maximum speed was close but statistically distinguishable from the biological and simulation standards at 1.07. Its occurrence at 45% closure, on the other hand, was indistinguishable from both standards (Table S1). Acceleration and deceleration were 1.2 × 10⁻²%/s² and 1.1 × 10⁻²%/s², respectively (Table S1). The ratio between acceleration and deceleration was 1.1, which was statistically different from the biological standard but not the simulation standard (Table S1). The parameter pentagon for simulations in which the abundance of only the actin-like filaments was modulated was only 40% larger than the biological standard and 10% larger than the simulations standard (Fig. 4 Cʺ; Table S1).

Finally, we simulated contractile rings in which only the motor ensemble abundance was modulated (Fig. 4 D), and 30/30 of these simulations successfully constricted the dynamic space beyond 90% closure. Their contractile kinetics closely matched the kinetics of the biological and simulation standards (Fig. 4 Dʹ, Dʺ). The normalized maximum speed was statistically different from both standards, at 0.95; maximum speed occurred at 44% closure, which was different from the biological standard but not the simulation standard (Table S1). Similarly, acceleration and deceleration were 1.3 × 10⁻²%/s² and 1.2 × 10⁻²%/s² respectively (Table S1). For these simulations, the ratio between acceleration and deceleration was 1.1 (Table S1). Altogether, the parameter pentagon for these simulations was only 10% larger than the biological data (Fig. 4 Cʺ; Table S1).

Omitting abundance dynamics of ring components has distinct effects on constriction

Our data suggested motor and filament abundance dynamics are sufficient to generate more accurate constriction kinetics. We next tested whether they are necessary to generate such accuracy. Since tether and crosslinker abundance dynamics did not influence constriction kinetics in our previous simulations, we set up simulations wherein all components but tethers (Fig. 5 A) or all components but crosslinkers (Fig. 5 B) were modulated as a baseline. Omission of the abundance dynamics of either component alone resulted in constriction kinetics similar to the biological data (Fig. 5 Aʹ, Bʹ), and an overall composite score 30% above the biological dataset, which was indistinguishable from the simulation standard (Fig. 5 Aʺ, Bʺ; Table S1). Next, we ran simulations where all components were modulated except for filaments (Fig. 5 C) or motors (Fig. 5 D). Only simulations with static motor abundance were worse at recapitulating biological kinetics with a 50% increase in composite score (Fig. 5 Dʺ, Dʺ; Table S1). Altogether, these results suggested that the dynamic abundance of motor ensembles specifically is of key importance for realistic constriction kinetics.

Figure 5.

Omitting abundance dynamics of different ring components has distinct effects on constriction. (A–D) Normalized component abundance over closure input for simulations with conditions in which dynamics of each of the four main ring components was individually omitted. (A) All components dynamic except tethers. (B) All components dynamic except crosslinkers. (C) All components dynamic except F-actin-like filaments. (D) All components dynamic except motor ensembles. (Aʹ–Dʹ) Plots of average constriction dynamics curves of simulated divisions (correspondingly colored curves) versus the curve from the biological dataset (black line). Lighter-colored areas around solid curves, mean ± standard deviation. (Aʺ–Dʺ) Pentagons generated from the five contractile metrics measured from each simulation setup (color matched) compared with the biological standard metrics (black solid pentagon). Closure dynamics graphs include the curve generated from image data as a standard for comparison (black curve); lighter-colored areas represent the mean ± standard deviation. Solid black pentagons, biological standard. n = 30 for all.

Motoring activity or fast filament treadmilling is required for realistic constriction kinetics

NMMII motor complexes contribute several activities to actomyosin network kinetics, including crosslinking, bundling, and translocating F-actin (41,42,43,44,45). All these activities could underlie the importance of implementing myosin component abundance for accurate constriction kinetics. Thus, we next tested whether motoring activity was necessary for this effect by simulating contractile rings bearing myosin-like complexes with no motoring activity. Myosin-like components were unchanged except that their motoring speed was set to 0 nm/s; this ensured that fiber binding dynamics were unaltered but that the myosin-like components did not directly generate force representing the power stroke. These simulations were run with all component composition changes (Fig. 6 A). Under these conditions, filament networks were contractile but constricted approximately 16-fold slower than networks in which myosin-like complexes were active motors (Table S1). Constriction speed remained consistent over time and simulated rings did not close past 45% (20/20) during the simulation time that allowed all other simulated rings to close (Fig. 6 A). Previous biological and in silico work reported contractility in the absence of NMMII (or simulated myosin) translocation. One possible explanation for this observation is that faster F-actin treadmilling can generate force through Brownian ratcheting and persistent attachment of end-bound myosin (23, 24). We tested this possibility by simulating contractile rings with motor-dead myosin-like components as before, and increased filament treadmilling fivefold. Under these conditions, the contractile rings constricted fully (30/30) with kinetics comparable with our biological measurements. The normalized maximum speed was statistically different from both biological and simulation standards, at approximately 1.14, but occurred at a point indistinguishable from the simulation standard, at 44% closure (Fig. 6 B–Bʺ; Table S1). Thus, as in the in vivo and other simulation regimes, the absence of motor activity can be compensated for by filament treadmilling and crosslinker end-tracking.

Figure 6.

Motor activity or fast filament treadmilling is necessary for normal contraction dynamics in silico. (A and B) Dynamic abundance of all components was implemented in simulations. (Aʹ) Graph of average constriction dynamics of simulations with motor-dead motor ensembles. (Bʹ) Graph of average constriction dynamics of simulations with motor-dead motor ensembles and fast-treadmilling F-actin-like filaments. (Aʺ and Bʺ) Pentagon showing comparison of five constriction metrics with the biological standard. Closure dynamics graphs include the curve generated from image data as a standard for comparison (black curve); lighter-colored areas represent the mean ± standard deviation. Solid black pentagons, biological standard. n = 30 for all.

Switching abundance of motors with crosslinkers changes contraction kinetics

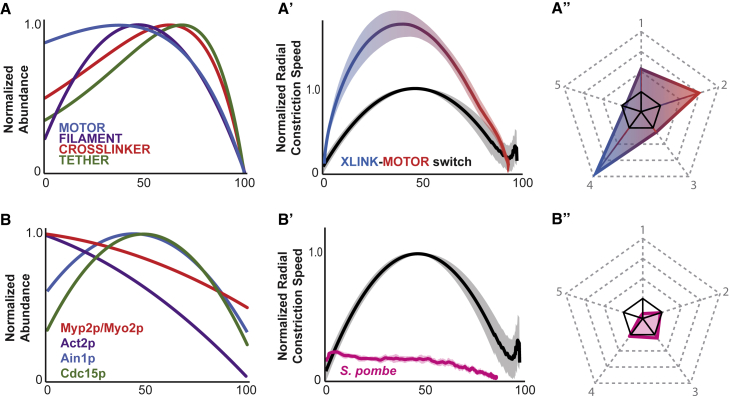
While myosin and F-actin abundance increased in a linear fashion unlike anillin and septin, whose abundance changed exponentially (Fig. 1 B–E), the dynamic density curves of all four components shared the characteristics of accumulating to a single peak during the middle third of ring constriction, followed by loss of components (Fig. S3 Aʹ–Dʹ). To test the importance of the measured abundance dynamics for each component to in silico contractile ring constriction kinetics, we swapped the abundance dynamics of motor components (linear change) with crosslinkers (exponential change; Fig. 7A). These simulated rings constricted successfully (30/30) but exhibited drastically altered constriction metrics (Fig. 7 Aʹ, Aʺ). Normalized maximum constriction speed was 2.1-fold faster than our biological or simulation standards, and was reached at 39% closure, much earlier than either the biological standard or the simulation standard (Table S1). Acceleration and deceleration were both markedly faster than both our biological measurements and the simulations lacking abundance dynamics at 3.0 × 10⁻²%/s² and 2.4 × 10⁻²%/s² respectively (Table S1). In conclusion, myosin abundance dynamics measured in the C. elegans zygote were crucial for simulating contractile ring constriction with realistic kinetics.

Figure 7.

Altered abundance dynamics affect simulated contractile ring contraction. (A–Aʺ) Effects of switching motor and crosslinker abundance dynamics in simulations. (A) Graph of normalized abundance showing that all components were allowed to change abundance but motors and crosslinkers now have switched their respective curves. (Aʹ) Graph of average constriction dynamics of simulations from (A). (Aʺ) Pentagon showing comparison of five constriction metrics with the biological standard. (B–Bʺ) Effects of swapping out C. elegans abundance dynamics with approximations of fission yeast abundance dynamics. (B) Graph of normalized abundance showing that all components were allowed to change abundance but with alternate dynamics calculated from fission yeast literature. (Bʹ) Graph of average constriction dynamics of simulations from (B). (Bʺ) Pentagon showing comparison of five constriction metrics with the biological standard. All closure dynamics graphs include the curve generated from image data as a standard for comparison (black curve); lighter-colored areas represent the mean ± standard deviation. Pentagon plots include the biological standard in solid black.

Implementing S. pombe composition alters constriction kinetics

A limitation of our approach is that we combined measurements from multiple species. However, different species exhibit distinct cytokinetic dynamics and their maximum closure speed occurs at different times. In the case of S. pombe, absolute amounts of ring components have been measured at several time points, thus allowing us to estimate amount as a function of time and test the impact of the measured abundances on network dynamics. To do so, we fitted the experimental fission yeast time point measurements to polynomial curves (14). We implemented the resulting estimated normalized component abundance curves for S. pombe NMMII (Myp2p/Myo2p), F-actin (Act2p), non-motor crosslinker alpha-actinin (Ain1p), and membrane tether (Cdc15p) (14,46; Fig. 7 B) in our model. The simulated ring contracted with a speed of 0.15%/s, which remained roughly constant until 50% closure and decreased steadily afterward (Fig. 7 B′). Importantly, the simulated closure kinetics are in agreement with observations S. pombe contractile rings close several-fold more slowly than C. elegans contractile rings (16).

Discussion

Ring composition as a predictor of constriction kinetics

Here we report that incorporating changes in global composition into simulations of the contractile ring throughout its constriction lead to more realistic constriction kinetics. This is noteworthy considering that the variations in abundance and constrictions were both measured in the same cell type. Although our simulation parameters were compiled from published studies on a range of cell types (14,42,44,46,59), incorporating the measurements from the C. elegans zygote dramatically improved the resemblance between the simulated contraction and the kinetics measured in the same cells. Moreover, by swapping our component dynamics measurements from the C. elegans zygote with those made in S. pombe (14, 39) we observed constriction kinetics more closely resembling those of fission yeast cytokinesis (Fig. 7 B–Bʺ). These results highlight the importance of accurately representing the contractile ring composition in any simulation of the actomyosin contractile ring aiming to reproduce biological closure dynamics. The effects of global composition highlight an important void in the field: mesoscale composition and the effects of mesoscopic differences in composition on mesoscale kinetics and global constriction kinetics. Future work will compare simulated ring ultrastructure with local compositional changes in vivo, such as dynamics of contractile units, as have been reported in cells (16,21,60).

Motors and filaments are the backbone of contractility

The components contributing most prominently to simulated constriction kinetics were those representing F-actin and NMMII, rather than the components emulating tethers and non-motoring crosslinkers. In fact, simulating proper contractile ring composition of either filament or motor alone was sufficient to yield the biological constriction kinetics. The effectiveness of modulation of actin-like filaments likely stems from their significant role as a substrate on which motors and crosslinkers bind and generate forces. In vitro, F-actin can also generate force directly via treadmilling since some crosslinkers can associate persistently with depolymerizing ends (44). Therefore, the abundance of biological and simulated filaments directly relates to network contractility. Similarly, modulation of motor abundance is likely important due to the several contributions of multimeric NMMII motor ensembles to actomyosin network architecture and direct force generation. In silico, as well as in vivo, contraction speed is substantially affected by changing the number of active motors present on the contractile ring (6, 57). Furthermore, because NMMII filaments likely have 10–30 motor pairs, they contribute substantially to network connectivity. We previously showed that discretely simulating the motor domains that comprise ensembles optimized contractile ring constriction, unlike coarse-graining the collection of motor subunits as a single entity (40). It is worth noting that our current simulations do not account for motor-binding cooperativity; all motor domains bind and unbind independently even if they are part of the same ensemble. We previously compared the effects of motors ensemble subunit cooperativity and observed more realistic network dynamics in the absence of cooperativity (40, 61). It is interesting that, in the case of cooperative motor domain binding, increased biological accuracy did not translate into increased realism of network behavior. Finally, in our simulations, even motor-dead motor complexes increase contractility of treadmilling actin filaments by being strong end-binders (44). Here, motor components were simulated with binding and unbinding rates informed by NMMII binding dynamics measurements (44, 46) and with persistent binding of ends such that they consistently track shrinking ends until their internal dynamics dictated unbinding. Therefore, if biological NMMII motors are indeed strong end-binders, we would expect their abundance to have profound effects on constriction kinetics regardless of motoring activity, as has been shown with partial global depletions by RNAi (6).

Our in silico results with motor-dead components highlight two regimes under which biological constriction can occur. First, with slower actin filament treadmilling, motoring activity was necessary to generate sufficient circumferential contraction to drive radial constriction. In this regime, loss of motor activity resulted in very slow contraction and constriction, which were roughly 16-fold slower than constriction with motoring activity unaffected (Fig. 5 C′, Cʺ). In these simulations, constriction was driven by a Brownian ratchet mechanism where motors bound to depolymerizing filament ends indirectly generated constriction through the active shrinking of the filament end. However, because treadmilling was slow in these simulations, constriction did not reach 30% closure within 300 s of simulated time, far slower than C. elegans zygotic division. This observation is partly in line with the necessity of motoring as has been reported in C. elegans (57). The second regime, where actin treadmilling is far faster and therefore motoring activity becomes dispensable for constriction kinetics, was also explored in our simulation work. With five-fold faster filament treadmilling, simulations with motor-dead components were almost indistinguishable from our simulations with motor activity and slower filament treadmilling (Fig. 5ʹDʹ, Dʺ). Here again, constriction was driven by filament shortening, but now, with faster treadmilling and therefore faster filament end shortening, constriction was able to generate enough radial force to constrict the deformable dynamic space. Our work suggests that systems where motoring activity is dispensable should have faster actin treadmilling or filament shrinking than systems where motoring activity is necessary for constriction to proceed as normal.

It is worth noting that, although modulating levels of both motors and filaments profoundly affected contractile kinetics, modulating either alone was sufficient for recapitulating biological kinetics in our simulations. Furthermore, in simulations where the amounts of all components except for motors or filaments were allowed to change, we saw that motors were more necessary for accurate kinetics than filaments. Altogether, these data suggest that the contributions from motor and filament components to constriction are partially redundant, but ring kinetics are slightly more sensitive to motor tuning than filament tuning, all other things being equal. This suggests that molecular motors contribute more to contraction than filament shortening does, although motors also contribute to connectivity by crosslinking filaments. It is possible that, with further fine-tuning of the model and the biological data, these possibilities could be tested.

Modulation of tethers and non-motor crosslinker composition, on the other hand, had very little effect on overall constriction kinetics. This is unsurprising as these components did not directly contribute to force generation and provided less connectivity, per component, than motors to actin-like filaments (maximum of 2 (crosslinker) or 10 (tether) versus up to 30 (motor)). Similarly, since they are smaller than motors and filaments, non-motor crosslinkers and tethers likely also play less of a role in the deceleration phase of constriction, when network compaction and curvature slow contraction.

Simulation advancements in this work

Simulations of contractile rings have advanced our understanding of contractility. However, whether contractile networks have been represented as active gels (28,32) or nematic active gels (5,27,58), or modeled as discretized agents in ring formation (22,62) and constriction (6,18,20,23,24,26,40), it has been generally assumed that the amount of contractile ring components, and thus global composition of the whole apparatus, remains unchanged throughout the process under study. In addition, contractile networks have largely been modeled independent of their relevant bounding space, such as the plasma membrane, in vivo.

Here, we increased the realism of simulations by incorporating a simplified approximation of membrane deformation energetics derived from the simplified representation of the geometry of a cell as it constricts at its equator. This derivation, although simplistic and requiring several assumptions, is in general agreement with the kinetics described by the active gel models (27,28). We paired this with a deformable space in Cytosim, which can interact with confined filaments and changes in shape in response to forces from filament networks (49). The result was a cylinder of variable radius whose resistance to deformation was dependent on radius (as a proxy to contractile ring radius). Finally, we advanced the field by incorporating adaptive component adjustments into simulations of actomyosin constriction. By pairing the expected amount of network components to the size of the deformable space, we generated simulations that self-regulate, adding or removing some amount of each component type to match user-defined functions dependent on the dimensions of the bounding space. We set these functions to reflect our in vivo measurements; future work will involve incorporating measurements from other cell types or biological contexts and help make predictions about specific conditions such as temporal depletions or over-expressions.

Closing remarks

Our work represents an increase in the realism of simulating contractile rings, but the implications of our findings are somewhat limited due to the paucity of measurements of key parameters that are presently inferred or estimated. For example, although we measured ring component abundance in C. elegans, the biophysical measurements that informed and constrained our simulations originated from work with a variety of animal cell types and with fission yeast. Our ability to closely recapitulate C. elegans zygotic division constriction kinetics highlights the universality of the mechanisms that give rise to cytokinesis, but biophysical measurements of NMMII and other proteins from C. elegans will strengthen the predictive power of our simulations. Second, we used a simple geometric model to approximate the force resisting ring constriction in the capsuloid zygote. This model estimated membrane tension of the C. elegans zygote, based on reasonable approximations from the literature (52,53) but did not take into account the likely differences in mechanical properties of the cytokinetic ring and the flanking cortex to which it is extensively coupled. It will be interesting to make and compare measurements of the cortical stiffness of the C. elegans cortex and contractile ring with those of other cell types. Furthermore, some actin crosslinkers, such as alpha-actinin, have been observed to exhibit catch or catch-slip dynamics (63,64), whereas others may exhibit slip bonding (65,66,67). Since increased mechanosensitivity associated with catch-slip behavior increases the robustness of contractile networks (48), future work should continue to explore incorporation of catch-slip dynamics into contractile network simulations.

Author contributions

A.S.M. was primarily responsible for funding acquisition, supervision, and project administration. P.S.M. contributed to funding acquisition and project supervision. D.B.C. and A.S.M. together conceptualized the research. D.B.C. performed all aspects of the research including the data acquisition, methodology development, software modification, data curation, data validation, and visualization. F.J.N. provided supervision and validation for in silico work performed with Cytosim. D.B.C., A.S.M., and F.J.N. together reviewed and edited the manuscript for content and composition.

Editor: Dimitrios Vavylonis.

Supporting citations

References (68,69,70) appear in the Supporting Material.