From cells to form: A roadmap to study shape emergence in vivo

Abstract

Organogenesis arises from the collective arrangement of cells into progressively 3D-shaped tissue. The acquisition of a correctly shaped organ is then the result of a complex interplay between molecular cues, responsible for differentiation and patterning, and the mechanical properties of the system, which generate the necessary forces that drive correct shape emergence. Nowadays, technological advances in the fields of microscopy, molecular biology, and computer science are making it possible to see and record such complex interactions in incredible, unforeseen detail within the global context of the developing embryo. A quantitative and interdisciplinary perspective of developmental biology becomes then necessary for a comprehensive understanding of morphogenesis. Here, we provide a roadmap to quantify the events that lead to morphogenesis from imaging to image analysis, quantification, and modeling, focusing on the discrete cellular and tissue shape changes, as well as their mechanical properties.

Significance

How individual cell behaviors are converted into collective movement of epithelia, leading to organ formation, has been one of the central questions in developmental biology. Advances in light microscopy, molecular biology, and computational power are revolutionizing this field, giving us impressive multiscale, three-dimensional information about morphogenesis. With this explosive increase in information, quantifying morphogenetic processes becomes essential, bringing objectivity to the experimental results and facilitating the connection between experimental biology and theoretical physics. In this review, we provide a roadmap for studying and quantifying in three-dimensional the events (both at the cell and tissue level) that lead to shape emergence, from imaging to image analysis, quantification and modeling, using light microscopy.

Introduction

Organogenesis is a multistep process during which an organ is formed from the coordination of discrete events: cell migration, cell intercalation, cell proliferation, and cell deformation. Such events are tightly coordinated at the genetic and biophysical level to ensure correct organ form and function. Understanding organ development and shape acquisition requires the investigation of these discrete cellular events, how they are coordinated, and how they influence and are influenced by the biophysical and molecular properties of the tissue in which they are integrated.

How individual cell behaviors are converted into collective movement of epithelia has been one of the central questions in developmental biology, being an object of intense study since the beginning of the 20th century (1,2,3). Still today, the interplay of complex morphogenetic processes across scales remains a central subject of study in developmental biology. Indeed, advances in light microscopy, molecular biology, and computational power are revolutionizing this field, giving us impressive multiscale, three-dimensional information about morphogenesis. It has become possible to record complex morphogenetic movements of deep tissues in vivo over extended periods of time and at single-cell resolution, and to quantify these arrangements at an unprecedented scale. The field is also more open to studying “nontraditional” model organisms, thus bringing new perspectives to the area and forging connections to evo-devo studies (4,5,6). With this explosive increase in information, quantifying morphogenetic processes becomes essential, bringing objectivity to the experimental results and facilitating the connection between experimental biology and theoretical physics.

Focusing on the discrete cellular events and the mechanical properties of cells and tissues, we survey technological tools that, by using light microscopy, allow quantifying the events that lead to shape emergence during morphogenesis, from imaging and quantitative analysis to computational modeling.

We begin by describing how to extract shape and quantify morphological changes before moving on to the quantification and perturbation of mechanical properties. We then finish with an introduction to theoretical modeling and how to integrate discrete cell and tissue biomechanical information into a comprehensive understanding of shape emergence and morphogenesis. Ultimately, our goal is to give the reader a roadmap to successfully navigate this highly interdisciplinary and, potentially, collaborative environment.

Quantifying cell and tissue shape changes

When studying shape and form, it is important to dissociate their components into discrete steps. Indeed, shape quantification’s primary goal is to decompose shape information into simpler pieces, such as geometrical and topological information. Here, we find it important to clarify these concepts: geometry refers to the study of aspects of shape that are permitted to vary continuously. Lengths, areas, volumes, angles, curvatures, distances, etc., are all manifestly geometric quantities for this reason. And since continuously varying quantities allow for derivatives, the rates of change of all these quantities are also clearly defined and understandable. As a result, geometry is local. Topology, on the other hand, is the study of those aspects of shape that remain once geometry is accounted for—quantities that are discretized or quantized and that may only vary in finite steps of fixed size. Counting quantities, such as the number of particles or the number of holes in a surface are common examples, but anything that can only change discontinuously qualifies here, from the charge of a topological defect in an orientational pattern to the neighborhood network in an epithelial sheet. As small, localized changes in a system can never produce these jump-like discontinuous shifts in quantities, topology can be considered global. In sum, during morphogenesis, we can find, on the one hand, the global topological modifications that the developing organ is going through. On the other, the geometric progression and variation of the cells or tissue over time.

Here, we give an overview of the workflow typically in place to extract these parameters from 4D images, automatically or semi-automatically, and examples of open-source programs available, either standalone or as plugins to use within ImageJ2/FIJI (7,8) or Napari (9). While this is a nonexhaustive overview of tools available, many other resources can be found online, such as specific workflows (10), teaching materials (NEUBIAS training schools (11)), and image analysis resources catalog (BioImage Informatics Index (http://biii.eu/)). We also refer the reader to a review and guide of the most used bioimage analysis tools (12).

Imaging

The first step toward quantification is the imaging of the relevant process. Whether we need to count cell nuclei, measure the volume of a cell or its velocity, or measure cell surface curvature changes, the imaging and experimental setup might be different. For example, while studying nuclear deformations requires a high Z resolution and voxel size, counting nuclei to measure cell density or to track cell position over time may not require such a high level of detail. It is therefore important to consider the scientific question and which parameters one needs to target since it will help plan the experiments and subsequent analysis workflow.

Recent advances in microscopy have made it relatively easy to acquire high-resolution images at high frame rates, with reduced phototoxicity, thus allowing for long-term imaging of biological processes. This comes at the cost of producing image files that can reach a few terabytes in size, accompanied by the problem of long image processing times, requiring high-performance workstations (or remote servers) and a considerable amount of data storage. This issue—how to best handle, store, and keep track of big data—is becoming increasingly discussed (12). However, having a clear idea of the needs and the minimal requirements to attain them should always be the first step.

Image processing

After acquisition of the image, it is often necessary to improve or correct the fluorescence signal of interest—deconvolve, register, remove background, denoising, or increase contrast of membrane signal—are a few examples. This will help the computer to correctly process the image and identify its components.

There are several ways to improve signal and signal/noise ratio, but probably the most common is through digital filtering and background correction. Filters are numerical operations produced on the image, meaning they change pixel values according to the neighboring pixels. Depending on the filter used, this will result in, for example, a smoother image or an image with enhanced edges. Given that a new image is created (with different pixel values), filtered data sets may no longer be suitable for certain data analyses requiring fluorescence intensity measurements (for example, protein or mRNA levels).

More recently, several algorithms that employ deep learning for image-processing tasks have come to the forefront. They typically target the improvement of signal/noise ratio (Noise2Void, Noise2Self (13,14)), the restoration of image signal from very weak intensities (CARE (15)) or the prediction of boundary geometry (3DUnet (16)). Deep learning is becoming a highly valuable tool for imaging reconstruction (17,18) and allows researchers to gain insight from weakly labeled data sets. Such advantage ultimately allows imaging with less laser power and/or at a higher frame rate, thus decreasing the potential for phototoxicity and its interference with normal cellular processes (19). For example, image restoration using CARE allowed tracking of photoreceptors in vivo to reveal that their migration pattern is crucial for proper retinal morphogenesis (20). Despite the major advantages, applying deep learning algorithms poses new questions regarding the veracity of the processed image, since quality assessment can be tricky.

Besides filtering, image representation can also be changed. For example, 2D cartographic projections of 3D surfaces, besides reducing data size, can aid further steps in image analysis and feature extraction. For example, tissue cartography has been used to quantify cell movement and shape changes in Drosophila embryogenesis (21,22,23,24).

Segmentation

Segmentation refers to the process of separating an image into different components or segments. It can be of two types: instance segmentation, where individual objects, within a given class, are identified (region1 = nuclei1; region2 = nuclei2 …) (Fig. 1 A); and semantic segmentation, where each pixel is classified and associated with a label (region1 = nuclei pixels, region2 = cell membrane pixels). Image segmentation can be the most challenging part of the image analysis workflow, and failures in correct segmentation may create errors in proceeding with data extraction. This step relies on having the most appropriate imaging parameters and the best-fit processing workflow. Even though several algorithms for automatic segmentation exist (Table 1), they are often relatively specific for a certain type of element (for example, cells versus nuclei) or a certain imaging technique, thus not fully compatible with the high heterogeneity of biological contexts. Fortunately, many segmentation algorithms are open-source, thus allowing them to be changed and adapted to other data sets. For this reason, segmentation tools are continuously evolving. In Table 1 we present a (non-exhaustive) list of recent open-source tools for automated or semi-automated 3D segmentation.

Figure 1.

Examples of image analysis sequences to quantify parameters related with retina morphogenesis in zebrafish. (A) Imaged nuclei were automatically segmented with StarDist (25). From this segmentation, nuclei volume information was extracted and represented as a color code. Scale bar 50μm (B) Outline of the retina detected by the Kappa (26) plugin to fit a Bezier curve and calculate curvature over time. (C) Schematic of a zebrafish embryo at 24 h postfertilization. Dashed lines feature the retina.

Table 1.

Common open source software for 3D segmentation

Software	Standalone application	Interface	Scriptable	Programming language	Plugin	Method	Type of segmentation	Requires training dataset	Requires GPU	Most suitable for
CellPose (27)	yes	GUI, command line	yes	Python3	yes	DL	instance	not necessarily	not necessarily	LM and HM –
										cells and nuclei
CellProfiler (28)	yes	GUI, command line	creates and saves CellProfiler pipelines	–	–	image thresholding	–	no	no	LM and HM –
										cells, nuclei, and organelles
EmbedSeg (29)	–	–	yes	Python3	no	DL	instance	yes	yes	LM and HM –
										organisms, cells, nuclei, and organelles
Ilastik (30)	yes	GUI	creates protocols	–	no	ML, DL	semantic	yesa	no	LM, EM, HM –
									(only for DL)	cells, nuclei, and organelles
Labkit (31)	no	GUI	no	–	yes	ML	semantic	yesa	no	LM, HM –
										cells, nuclei, and organelles
LimeSeg (32)	no	GUI	no	–	yes	oriented particle-based surfel	–	yesa	yes	LM –
										membranes
PlantSeg (33)	yes	GUI, command line	yes	Python3	no	DL	instance	no	yes	LM –
										membranes
StarDist-3D (25)	–	–	yes	Python3	yes	DL	instance	yes	yes	LM, HM –
										star-convex-shaped objects (e.g., nuclei)
Zelda (34)	no	GUI	creates protocols	–	yes	image thresholding	–	no	no	LM, HM –
										cells, nuclei, and organelles
CLIJ2, CLIJ2-assistantb (35)	no	GUI	yes	ImageJ Macro, Python3 (py-clesperanto), JavaScript (clicy), MATLAB (clatlab)	yes	image thresholding, ML	–	–	yes	LM, EM, HM –
										cells, nuclei, and organelles

GUI, graphical user interface; EM, electron microscopy; HM, histochemical methods; LM, light microscopy; ML, machine learning; DL, deep learning.

^aThe data set is generated during the workflow using the labeling tools incorporated in the software.

^bCLIJ2 is a library for image processing that can be installed in FIJI, Icy, and MATLAB. The implementation for Python is named pyclesperanto.

Tracking

While segmentation identifies objects within an image, it is not able to make a correspondence between the same object over time. To analyze morphogenesis over time, it is crucial to track the objects over time. Tracking is, therefore, crucial to infer properties such as strain rate of cells and tissues through analysis of velocity and displacement (inference from cell geometry and behavior) or to analyze the directionality of cell movement (36,37). Examples of open-source tracking algorithms include TrackMate (38), Mastodon, and Elephant (4). Alongside segmentation, tracking algorithms are constantly evolving for better prediction and to make them as generally applicable as possible (39). Still, tracking performance will depend on segmentation performance and on data set behavior over time: objects with big shifts in position are more challenging to track.

Feature extraction

The process of quantifying the properties of objects is often referred to as feature extraction. Most of the features of the segmented objects can be extracted from the image viewer or segmentation software, or can be obtained through small scripts in, for example, Python, MATLAB, or R. Certain measurements may need specific plugins or packages. Curvature, for example, can be extracted with LimeSeg (32) or Kappa (26) plugins for FIJI (Fig.1 B). Having a triangular mesh of an object instead of a binary mask (the typical segmentation output) will potentially facilitate specific feature extraction using, for example, PyMesh, a geometry processing library for Python or Vedo. Special tools also exist for Fiji and Napari for investigating the properties of cells in a tissue context (40).

Infer mechanical properties

The technology available to quantify the mechanical properties of cells and tissues has rapidly advanced in recent years. Several tools allow for direct determination of the mechanical properties of cells and tissues: micropipette aspiration (41,42,43), microplates (44,45), or atomic force microscopy (46,47,48), are a few examples. Such tools allowed great advances in our knowledge of cells and tissue mechanics and their contributions to morphogenesis (reviewed in (49)). Since these tools require contact manipulation of the sample, however, there are challenges to their application to in vivo contexts. For this reason, here we focus on tools that, by using light microscopy, allow either the quantification or inference of mechanical properties in deep tissues in vivo.

Inference from cell geometry and behavior

Within an epithelium, cell-cell contacts display a certain typical angle that is then subject to deviations upon force loading or other changes to the equilibrium state. Geometric force inference uses these deviations and, by fitting a dynamic model of cell mechanics, infers the effectively applied force (50,51,52,53) However, it accounts only for the balance between intracellular pressure and cortical tensions; thus, it can be a limited technique when studying in vivo systems. Ogita et al. used image-based force inference to show how junction remodeling and resistance to pulling are controlled during Drosophila development (50). In a more global context, Bhattacharya et al. calculated strain maps from the analysis of cells’ velocity fields during zebrafish gastrulation. This allowed the identification of areas submitted to compaction and expansion and how those were affected by molecular inhibitors of morphogenesis (37). Analysis of cell flow fields also allows one to infer tissue fluidity changes during morphogenesis, as seen during zebrafish axis elongation (54).

Molecular sensors

Förster resonance energy transfer (FRET) tension biosensors are genetically encoded proteins consisting of a deformable, flagelliform linker attached on both sides by opposite domains of the same protein, which are per se tagged with a donor and an acceptor fluorophore, or an FRET pair. Stretching of the linker (and thus increasing the distance of the FRET pair) upon loading, leads to changes in signal intensity and FRET index.

This technique allows the measurement of force load at the molecular scale, and thereby the detection of the few picoNewtons experienced by individual proteins in cells. Measurements within embryos are possible since the sensors are genetically encoded and the signal is detected through imaging (examples (55,56,57)). The list of molecules studied through this technique is growing and includes cell adhesion proteins and cytoskeleton and nucleoskeleton proteins (Table 2).

Table 2.

Examples of molecular tension sensors

Vinculin	LaCroix et al. (58); Grashoff et al. (59)
Talin	Austen et al. (60)
Paxillin	Shao et al. (61)
Integrin	Tan et al. (62)
Lima1	Hirano et al. (56)
Cadherin	Lagendijk et al. (57)
Desmoplakin	Price et al. (63)
Nesprin	Déjardin et al. (64)

The properties of the linker dictate the force load that can be detected (65). Proper quantification of force load through tension sensors requires advanced data analysis and careful experimentation. Often it is safer to use fluorescence lifetime imaging microscopy to calculate FRET efficiencies since it removes potential noise from differential instrument settings or variations in protein concentration. While it is not easy to perform those measurements, several protocols and reviews for data analysis and for the creation of new tension sensors have been published (66,67).

Droplets and compressible beads

This technique consists in the insertion of a deformable (fluorescent) material within the developing tissue. The deformations imposed on the insert by the surrounding tissues are then imaged and quantified. Having prior knowledge of the mechanical properties of the insert, it is then possible to quantify the forces that arise from the tissue acting on the insert, and thus the forces that are involved in the morphogenetic process.

Currently, two types of inserts are available: biocompatible fluorinated oil droplets (68), magnetically responsive ferrofluid microdroplets (69), and hydrogel fluorescent beads, including polyacrylamide (70,71,72), alginate hydrogels (73), and polyethylene glycol (74). The latter further includes FRET donors and acceptors, used to report local deformations as stress shifts. Both types of probes have been successfully applied in live embryos but with some differences. While oil droplets can be injected at the region of interest, hydrogel beads need to be delivered at very early stages of embryogenesis and allowed to spread randomly through the embryo. Hydrogel beads are compressible and can measure both isotropic and anisotropic stresses; oil droplets are instead incompressible, therefore, only anisotropic stresses can be measured. The specific properties of the droplets or beads will vary with their material composition and size. Therefore, careful control of manufacturing and characterization before insertion is essential (reviewed in (75)).

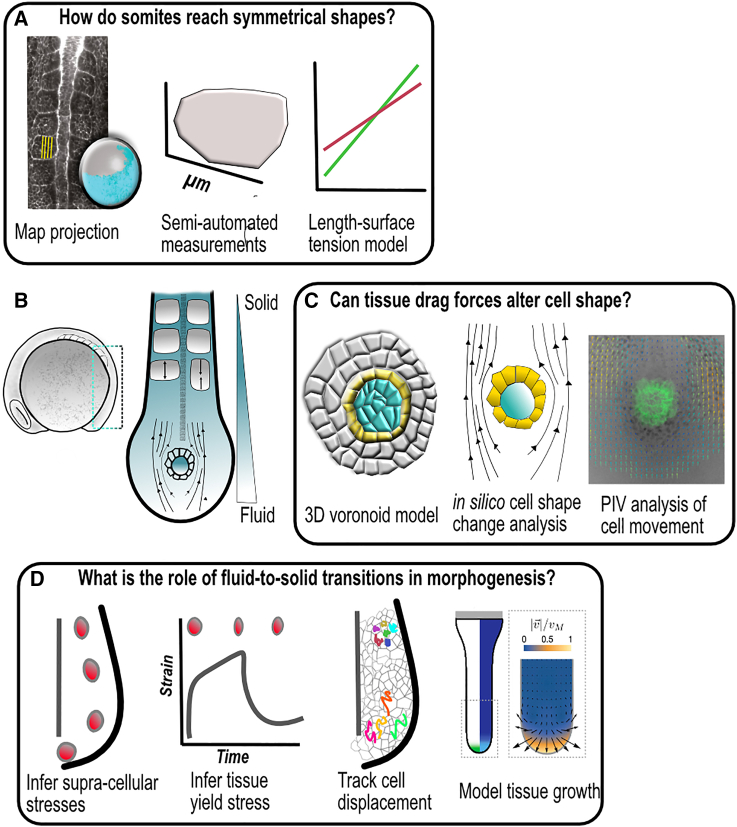
Droplets were used for the direct quantification of cell-generated forces in developing embryonic tissues, allowing the characterization of tissue viscoelasticity within the zebrafish developing tailbud. Such measurements, together with analysis of cell movement, showed that zebrafish body elongation relies on a tissue jamming transition from fluid to solid-like behavior (Fig. 2 D) (68,69,78).

Figure 2.

(A) To understand how somites can reach a symmetrical shape during zebrafish somitogenesis, Naganathan et al. use advanced techniques of image analysis to project 3D imaged data in 2D. Such projection allowed for semi-automated measurements of somite shape parameters in control and disrupted conditions. At the end, with the help of a model of surface length versus tension, the authors propose that somite length adjustment relies on somite surface tension ((76) reproduced with permission from SNCSC). (B) Schematics of a zebrafish embryo at 13 h postfertilization, with emphasis on tailbud growth, merging the knowledge gathered by the three works. (C) On a bottom-up approach Sanematsu et al. built a 3D Voronoi model of the Kupffer’s vesicle, the zebrafish left-right organizer. This model is used to test how drag forces generated by the vesicle’s movement can drive cell shape changes. The predictions are then tested through analysis of cell movement ((77) reproduced with permission from Elsevier). (D) The introduction and manipulation of magnetic beads in the zebrafish tailbud allowed measurement of the tissue yield stress. Together with cell tracking, Mongera et al. conclude that a jamming transition from fluid to solid-like behavior occurs from the progenitor zone to the presomitc mesoderm. Such a transition sustains a unidirectional extension of the tailbud, as confirmed by the theoretical model ((78) reproduced with permission from SNCSC).

Optical tweezers

The ability to move small objects using optical forces was first demonstrated by Ashkin and co-workers (79,80), who used infrared laser beams to manipulate bacteria and viruses. Optical tweezers were subsequently developed to trap, manipulate, and probe target objects in biological systems. The optical properties of the highly focused laser beam allow the manipulation of objects from 100 nm to 10 μm, such as nanospheres, organelles, or small organisms. The optical forces are proportional to small displacements of the particle and depend on its shape, size, and refractive index. After proper calibration, it becomes possible to quantify the mechanical properties of the particle surroundings, such as stiffness and viscoelasticity (81).

The refinement of this technique through modifications of the light shape and improvement of the calibration method has allowed an increasing number of potential applications, including the quantification of mechanical properties during morphogenesis in vivo. Examples include the microrheological characterization of the extracellular matrix in zebrafish (82) or the mechanical characterization of cell contacts in Drosophila embryos (83). On the downside, calibration of the probe is time-consuming and may become prohibitive in the context of a fast-developing tissue. The need for calibration can potentially be overcome, however, by splitting the laser in multiple spots and trapping several probes at once. This has been achieved by using holograms—holographic optical tweezers, or HOTs (84) —which have been applied in zebrafish larvae (85). A relative readout of viscoelastic properties can then be calculated by measuring the differences in mechanical properties at each location.

Laser ablation

Existing tensions within a tissue can also be inferred relative to the tissue material properties by analyzing its reaction upon sudden release of tensile stresses. A focused laser beam (typically UV) can deliver intense energy to a small region, which can be used to precisely sever tissues or cell membranes. Quantification of the recoil time of the displaced areas allows one to calculate the relative magnitudes and directions of tensions and ultimately build mechanical models with tension maps (86,87).

This is a rather simple and flexible technique, given that a suitable, properly calibrated, laser is provided. The recoil reaction happens in the order of milliseconds after laser ablation; therefore, it must be imaged at a high frame rate to ensure proper quantification. It is one of the most used techniques when studying mechanical properties during morphogenesis, with several examples in vertebrate and invertebrate model systems (88,89,90,91,92,93).

Perturbation of cells’ and tissues’ mechanical properties

Cell and tissue mechanical properties emerge from a combination of various players. Many of these properties can be attributed to cytoskeleton composition and arrangement variations. Therefore, many tools that interfere with mechanical components focus on disrupting cytoskeletal components: microfilaments, intermediate filaments, and microtubules.

Generally, these tools are either: pharmacological compounds that interfere with protein structure or block its activity; changes in genetic expression, and thus protein level (morpholinos, mutants, transgenes, siRNA, mRNA); and changes in protein dynamics (genetically encoded dominant negative forms or light-sensitive proteins). In addition, instruments used to probe mechanical properties, such as atomic force microscopy and laser ablation, can be applied to modify them.

It can be challenging, however, to confirm the modification of the mechanical properties. Therefore, it is important to set appropriate controls, either by directly measuring such changes or by combining in vivo and controlled ex vivo approaches (94).

As before, we will focus on tools that rely on light microscopy to, potentially, modify mechanical properties in cells and tissues.

Disruption using optogenetics

Optogenetics uses light to modify the properties of genetically encoded proteins, allowing control of protein dynamics.

Currently, there are several optogenetics systems, which can be grouped into: photosensitive gated channels (neuronal optogenetic system); light-induced dimerization, where light-inducible conformational changes in a protein lead to higher affinity with its binding partner, which can be used to recruit proteins to a given location; photo-caging, with light-induced unfolding, which leads to protein activation or exposure of specific motifs, which can be used to modify protein activity (reviewed in (95,96)).

Optogenetics allows control of protein activity in both space and time: on one hand, the genetically encoded protein can be expressed only in the tissue of interest by using specific promoters; on the other hand, the researcher is explicitly in control of the time of the photoswitch. This spatiotemporal control makes optogenetics one of the most promising techniques for precise studies of morphogenesis. As an example, Mitchell et al., using optogenetics to modify actin activity, were able to show that folding of the Drosophila midgut during development is dependent on the contraction of the surrounding muscle. In combination with high-end image analysis of cell shape changes, they were able to precisely connect such out-of-plane contractions with the midgut cell shape changes that lead to its folding (97) (Fig. 3 A).

Figure 3.

(A) Using advanced frameworks of image cartography and single-cell segmentation, Mitchell et al. were able to determine that the folds appearing in the Drosophila gut are a result of a convergent extension pattern driven by cell shape changes. Such shape changes are promoted by out-of-plane contraction of the surrounding muscle. This is confirmed by induction of muscle contractility using optogenetic tools. The authors went further and were able to link muscle contraction with calcium spikes generated in areas where specific hox genes are present, thus directly linking gene expression with cell shape (and tissue shape) changes (adapted from (97)). (B) Schematic of a Drosophila embryo depicting the midgut in blue. (C) Schematic of a Drosophila follicle showing the extracellular matrix (in green) surrounding the cells. (D) Also using cartography projections of 3D data into 2D, Chen et al. show that follicle elongation is dependent on the reorientation of elongated cells, regulated by mechanical cues from the extracellular matrix (adapted from (23)).

Tissue depth (which affects light diffraction) and differential protein dynamics can undermine the application of this technique in whole organisms. Indeed, optogenetics have been applied mostly in cell culture, organoids (98), or during Drosophila (99,100) embryogenesis and, to a lesser extent, in zebrafish embryogenesis (101,102). Examples of optogenetic tools include the Gef2/RhoA CRY2 and the OptoMYPT systems to control actin contractility (99,103), the photoactivatable RAc1 (104), the π-EB1 to control microtubule dynamics (105), OptoShroom3 to control shroom3 activity and apical constriction (98), and OptoYAP to control YAP localization and activity (102). Given the significant potential of this technique, optogenetic systems continue to mature with new tools appearing frequently. The web site Optobase.org keeps track of the latest novelties in this area.

Optochemical disruption

Another method of using light to interfere with cytoskeleton structure is by using synthetic photosensitive molecules. These small, cell-permeable molecules can affect, for example, the activity of ion channels, enzymes, or cytoskeleton components, in an irreversible or reversible manner (reviewed in (106)). Given the small size of these compounds, it is, in principle, possible to use them at the organismal level, given that they penetrate the tissue/organ of interest.

Few examples of photoswitchable drugs that affect the cytoskeleton include optojaps, for disruption of actin filaments (107,108), azobenzene-based microtubule stabilizers (109), microtubule-depolymerizing SBTubs (110), and photoactivatable cytochalasin D (111).

Theoretical approaches to morphogenesis

Measurements of morphological changes per se might not be sufficient to explain the dynamics of tissues and of the myriad of cells during morphogenesis. Combining experimental results with theoretical modeling of shape changes gives a new perspective on the analyzed process, helping to interpret and validate experimental results. Computational models can further explore the parameter spaces and make predictions of tissue behavior upon disruption of specific parameters. Thus, experimentation and theory should evolve side by side in constant feedback.

Here, we give an overview of the several approaches to computational models and in which conditions they can be used to model morphogenesis. Readers further interested in the interplay between imaging data and computational modeling, and related terminology, concepts, and models, are referred to (112). The choice of a model will partially depend on which scale (subcellular versus tissue) one is focused on in the study of a particular scientific question (113,114). But, given the complex multiscale event that is the shaping of an organ, it remains an area of active theoretical research to understand precisely how these different potential models relate to each other.

Cell-based models

Cell-based models represent the tissues as collections of interacting cells to capture how changes at the cellular levels are propagated throughout the tissue and may result in global deformations or flows. Defining each cell explicitly also allows us to include the cell’s internal biological state as well as topological events such as neighbor exchanges, cell divisions, or cell death. Several such approaches have been developed, ranging from the cellular Potts model (115), which uses Monte Carlo simulations to represent cell boundary fluctuations on a fixed lattice, to lattice-free models investigating vertex or cell center dynamics.

In vertex models, cells are represented by polygons defined by vertices at which three or more cells meet. Since the neighbors are mechanically coupled, the movement of each vertex is influenced by forces exerted by all of the cells that are connected to it. The forces, in turn, result from each cell tending to change shape in a way to maintain its preferred volume and minimize surface area. Additional terms can also be added to include, for example, external forces acting on a vertex or preferred membrane curvatures (116). Similarly, in the field of membrane computing, scientists model tissues as interconnected cells spanning a graph exchanging information via chemical signals through membranes (117). In contrast, in the Voronoi models, a cell is defined in relation to its center, which moves in response to the forces. This allows for an effective way to model cell motility, but it is no longer possible to specify cell volumes.

Vertex and Voronoi models have been used to study many phenomena, including epithelial sheet deformations (118), cell shape changes (77,119) (Fig. 2 C), jamming transitions (120,121), and even the usage of mechanical properties as an error correction mechanism (122).

The main strength of cell-based models lies in their ability to bridge the scales between events at the cellular level and their effect on the tissue scale. They are also very flexible, allowing one to include biochemical events and feedback loops between cell surroundings and their mechanical properties. However, this flexibility also means that this class of models has many parameters, which makes the comparison between different models difficult since the same event can be implemented in many ways.

Continuum models

In contrast to cell-based models, continuum models reflect statistics over individual cells to represent tissues as homogeneous materials. Such models can be built by explicit coarse graining over the individual cells, or from first principles such as symmetry considerations. This is analogous to bulk descriptions of fluids or solids where the interactions between individual particles give rise to the effective material parameters such as viscosity or elasticity. In addition, features such as individual cell stiffness, frequency of neighbor exchange, and cell alignment further modify the macroscale behavior and so determine which theoretical model best describes the investigated tissue (reviewed in (123,124)). As an example, depending on how easily the neighbors are exchanged, tissue behavior will be more solid- or liquid-like (125). On short timescales, of the order of seconds, soft tissues behave like viscoelastic solids, which deform when a force is applied and quickly recover the initial shape once the force is removed (126,127,128). Such behavior can be modeled using two main parameters—Young’s modulus and dynamic viscosity. In contrast, on longer timescales, when neighbor exchange becomes relevant, tissues behave in a more fluid-like manner—the deformations persist, and tissues seem to flow as the cells rearrange (44,127).

However, recently more unusual materials have been advanced as candidates to describe tissue behavior in continuum theories, such as the shape programmable hydrogels (129) and liquid crystal solids (130). Liquid crystal elastomers, for example, are composed of aligned, elongated polymers cross-linked into an elastomer. This alignment can be increased or reduced in reaction to certain stimuli, leading to anisotropic shape change of the whole material, which in some cases can lead to shape establishment (131,132,133). A similar shape change can be observed in tissues where a change in the alignment of cells can trigger shape change. In such cases, tissue can be modeled as a viscoelastic solid with a pattern of spontaneous strain, whose relaxation leads to deformations.

Probably the most important difference between nonliving materials and tissues is that tissues exist out of equilibrium. The individual cells transduce free energy into motion or shape changes that can give rise to large-scale deformations. This contribution is considered in models that treat tissue using the soft active matter formalism (134,135), where, in addition to the material properties, additional terms such as force generation by cytoskeleton (136) or cell division (137) are included. The active matter models have successfully represented phenomena such as collective cell migration (138), tissue spreading (139), or tissue invagination (140).

The relative strength of the continuum models is that they have much fewer parameters than cell-based models. These parameters can be often measured more easily than the ones required for cell-based models, since they concern more high-level tissue properties, such as tissue density, average cell density, or alignment. On the other hand, these models can only describe systems whose mechanical properties are constant—once an appropriate model representing the tissue is chosen it is usually difficult to change it to account for how bulk mechanical forces change cell properties (124,141).

Conclusions

We have presented here a roadmap for a systems approach to the study of morphogenesis and shape emergence in vivo, from image analysis to theoretical modeling. We hope this review can serve as a guide for those starting the challenging but exciting task of studying shape emergence.

It has become increasingly clear that understanding complex shape emergence is necessarily a highly interdisciplinary undertaking. As such, it stands to greatly benefit from a comprehensive, collaborative approach bringing together three separate poles of expertise: image analysis, (wet lab) biology, and biophysics. It is then beneficial for a project to start by laying out the challenges and possibilities at all three fronts, kickstarting natural, collaborative feedback among the different experts, that, critically, should continue throughout the project (142).

Interdisciplinary approaches to developmental biology are not new, of course. Still, with the rapid recent technological advances, there are now more than ever new opportunities to bring interdisciplinarity to bear on new problems and with new constellations of expertise. The benefit to all sides is clear. Applying physical approaches and physical thinking to the problem of understanding developmental processes brings new perspectives and the possibility of a much deeper understanding of biology.

Author contributions

Planning of review outline, A.P.R.; writing – original draft, A.P.R., L.C.F., A.S., and C.D.M.; writing – review & and editing, A.P.R. and C.D.M.; retina curvature images, A.P.R.; nuclei segmentation images, L.C.F.

Editor: Meyer Jackson.