Abstract
Upon vascular injury, platelets form a hemostatic plug by binding to the subendothelium and to each other. Platelet-to-matrix binding is initially mediated by von Willebrand factor (VWF) and platelet-to-platelet binding is mediated mainly by fibrinogen and VWF. After binding, the actin cytoskeleton of a platelet drives its contraction, generating traction forces that are important to the cessation of bleeding. Our understanding of the relationship between adhesive environment, F-actin morphology, and traction forces is limited. Here, we examined F-actin morphology of platelets attached to surfaces coated with fibrinogen and VWF. We identified distinct F-actin patterns induced by these protein coatings and found that these patterns were identifiable into three classifications via machine learning: solid, nodular, and hollow. We observed that traction forces for platelets were significantly higher on VWF than on fibrinogen coatings and these forces varied by F-actin pattern. In addition, we analyzed the F-actin orientation in platelets and noted that their filaments were more circumferential when on fibrinogen coatings and having a hollow F-actin pattern, while they were more radial on VWF and having a solid F-actin pattern. Finally, we noted that subcellular localization of traction forces corresponded to protein coating and F-actin pattern: VWF-bound, solid platelets had higher forces at their central region while fibrinogen-bound, hollow platelets had higher forces at their periphery. These distinct F-actin patterns on fibrinogen and VWF and their differences in F-actin orientation, force magnitude, and force localization could have implications in hemostasis, thrombus architecture, and venous versus arterial thrombosis.
Significance
Impaired platelet contraction is associated with bleeding and enhanced platelet contraction may be associated with thrombosis, implicating platelet traction forces as an important component of hemostasis. F-actin drives the generation of traction forces, but a direct connection between F-actin structure and force localization has been limited by methodologies that do not permit the simultaneous measurement of subcellular forces and immunofluorescent stains. Here, we used our recently developed black dots technique to connect adhesive environment, platelet F-actin pattern, F-actin filament orientation, force magnitude, and force subcellular localization. Relationships between protein stimuli and F-actin structure and function may be important in hemostasis, thrombosis, and thrombus architecture.
Introduction
Platelets bind to adhesive ligands and undergo a change in shape to support the formation of a hemostatic plug. Typically, unactivated platelets are discoids that are 2–5 μm in diameter (1). Upon engaging surface-immobilized matrix proteins, they flatten and spread in area fivefold (2,3). During the process of spreading, the actin cytoskeleton of platelets forms filamentous structures that associate with myosin to form actomyosin filaments that generate traction forces (4). This process is critical for stable adhesion (5,6,7), but there are differences in platelet spreading depending on the adhesive environment (8,9,10,11).
On fibrinogen, a blood protein that mediates platelet-to-platelet interactions through integrin αIIbβ3, early-bound platelets form punctate actin nodules, which are structures similar to podosomes observed in many cell types (12,13). Actin nodules are thought to play a role in platelet-to-platelet adhesion and their absence may be associated with excessive bleeding (14). As platelets spread on fibrinogen, their actin nodules rearrange into filamentous actin (F-actin) at their periphery, with a prominent absence of F-actin in their central region (11,14,15,16). The alignment and orientation of F-actin are thought to be indicators of integrin activation and contractile function in platelets (11,17). Notably, individual platelets produce traction forces in the range of tens to hundreds of nanonewtons when on fibrinogen-coated surfaces (2,18,19,20,21,22,23). The strength of these forces correlate with the formation of F-actin, while impairment of these forces is associated with bleeding disorders (7,20).
Platelets spreading and contracting on von Willebrand factor (VWF), a blood protein that mediates platelet binding to sites of damage at the vessel wall and to other platelets, has been less well- characterized. Platelets bind initially to VWF via their glycoprotein Ib-IX-V complex and then, once activated, via their integrin αIIbβ3 (24). Platelets bound to a VWF-coated surface without other agonists have an F-actin morphology that is notably different than on fibrinogen, wherein there is 1) an absence of actin nodules in early spreading and 2) F-actin is more abundant in their central region than at their periphery (25,26,27). On VWF, individual platelets produce traction forces that are similar to, if not greater than, on fibrinogen (23,26,27). Distinctly, higher traction forces correlate with the distribution of F-actin throughout the platelet (27).
The description and characterization of F-actin patterns in platelets on fibrinogen have led to understanding the dynamics of platelet spreading (3,11) and how the actin cytoskeleton is altered in diseased states (11,14). While some previous studies have conducted spreading and contraction assays on VWF (13,25,26,27,28) and published images of platelet F-actin with patterns distinct from those observed on fibrinogen (25,26,27), differences in F-actin morphology between VWF and fibrinogen have not been directly compared or discussed in the literature, to our knowledge. One study that measured the traction forces of platelets on fibrinogen or VWF found that platelets on VWF produced nearly twice as much force as on fibrinogen (23). While an interesting result, this study was focused on platelet storage and noted this difference without applying statistical tests to this observation, accounting for spread area, or investigating F-actin structure.
Here, we report that the morphology of F-actin in platelets seeded onto surfaces coated with fibrinogen or VWF had distinct patterns based on the protein coating. We verified these F-actin patterns using a machine learning approach. Furthermore, we use black dots (27) to measure F-actin and traction forces and found that platelets produced more force on VWF than on fibrinogen. In addition, after categorization of F-actin patterns using machine learning, we found that the strength of traction forces for platelets was dependent on protein and F-actin pattern. Finally, after enhancing spatial resolution of forces obtainable with the black dots, we measured platelet traction forces with immunofluorescent stains on the subcellular scale for the first time. We observed that force localization qualitatively corresponded with the ends of F-actin fibers and that traction forces were significantly more peripheral on fibrinogen than on VWF.
Materials and methods
Blood collection and platelet seeding
With approval from the University of Washington Institutional Review Board, blood was collected from healthy, volunteer human subjects who gave informed consent. Whole blood was collected via venipuncture into BD Vacutainer tubes containing acid citrate dextrose A solution. The blood was loaded into a swinging-bucket centrifuge and spun at 200 × g for 20 min to separate platelet-rich plasma and hematocrit. Platelet-rich plasma was transferred to a fresh tube and centrifuged at 1000 × g for 10 min to pellet the platelets. The platelet pellet was washed (i.e., resuspended) in CGS buffer (120 mM NaCl [JT Baker, Phillipsburg, NJ], 30 mM glucose [ACROS Organics, Geel, Belgium], and 13 mM sodium citrate [Fisher Scientific, Waltham, MA] [pH 7.0]). Platelets were centrifuged again at 1000 × g for 10 min to pellet the platelets. All centrifugations were conducted in a Beckman Coulter Allegra X-22R centrifuge at room temperature on relatively slow acceleration (setting 4 out of 10) and nearly no brake (deceleration 1 out of 10). Washed platelets were resuspended in Tyrode’s buffer (10 mm HEPES [Fisher Scientific], 138 mM NaCl [JT Baker], 5.5 mM glucose [ACROS Organics], 12 mM NaHCO3 (Sigma, St. Louis, MO), 0.36 mM Na2HPO4 [Sigma], 2.9 mM KCl [VWR, Radnor, PA], 0.4 mM MgCl2 [Fisher Scientific], 0.8 mM CaCl2 [VWR] [pH 7.5]). Both CGS and Tyrode’s buffer were filtered using a 0.22 μm filter before use.
Substrate protein treatment
On the day of the platelet experiment, human VWF (Haematologic Technologies, Essex Junction, VT) or human fibrinogen (Sigma) were incubated on ethanol-cleaned glass coverslips or black dots substrates for 1–2 h. VWF and fibrinogen were, respectively, diluted to 5 μg/mL and 1 mg/mL, because these are the approximate concentrations in human blood (i.e., approximately half of the concentration of each in plasma) (29,30). Glass coverslips were then blocked with 1% bovine serum albumin (Sigma) for 2 h. VWF, fibrinogen, and bovine serum albumin were diluted in phosphate-buffered saline (PBS) (1× without calcium or magnesium, Life Technologies, Carlsbad, CA.) Additional details are included in the supporting material.
Platelet seeding, fixing, and staining
Washed platelets were seeded onto glass coverslips or black dots and allowed to bind over 10 min. Substrates were gently dipped in PBS to remove unbound platelets. Glass coverslips and black dots were then submerged in Tyrode’s buffer for an additional 30 or 80 min, respectively, allowing time for platelets to spread and contract. All assays were conducted in the absence of additional biochemical agonists such as thrombin, ristocetin, and botrocetin that could affect F-actin morphology. After the incubation, platelets were fixed with 4% paraformaldehyde (Electron Microscopy Sciences, Hatfield, PA) for 20 min, permeabilized with 0.1% Triton X-100 (Thermo Scientific) for 20 min, and blocked with 10% goat serum (Gibco, Billings, MT) for 1 h. They were then stained for F-actin with phalloidin-Alexa Fluor 488 (1:500 dilution in 10% goat serum, Invitrogen, Waltham, MA) and for glycoprotein Ib (GPIb) with a CD42b monoclonal antibody, clone SZ2 (1:100 dilution in 10% goat serum, Life Technologies) and an Alexa 647 goat anti-mouse IgG secondary antibody (1:200 dilution in 10% goat serum, Life Technologies). All stains were incubated for 1 h. After primary antibody staining and after secondary antibody staining, the substrates were rinsed with PBS three times for 5 min each time to wash away any unbound stain. Samples were mounted with Fluoromount-G mounting medium (Life Technologies). All substrate treatment, platelet seeding, fixing, and staining steps were conducted at room temperature.
Imaging by confocal microscopy and structured illumination microscopy
Samples were imaged by confocal microscopy on a Nikon A1R with a 60× oil objective. Super-resolution images were collected with a Zeiss Elyra 7 with lattice structured illumination microscopy and a 63× oil objective.
F-actin morphology classification and machine learning
F-actin morphology of each platelet was manually assigned as nodular, hollow, or solid. Nodular morphology was defined by containing more than one punctate F-actin assembly, hollow morphology was defined by F-actin being localized at the platelet periphery with absent F-actin in the platelet center, and solid morphology was defined by centralized and/or homogenously spread F-actin. If platelets exhibited features of multiple categories or if it was unclear which category best represented the platelet, the platelet morphology was deemed indeterminate.
Manually assessed data were used to train a machine learning model to classify platelet F-actin pattern in high yield without sample-to-sample bias. To build the platelet image classifier, we used deep learning in the form of a convolutional neural network (ConvNet). We used Python 3.8.10 using TensorFlow 2.7.0 to apply transfer learning to the existing ConvNet InceptionV3, which is a model that has previously been shown to perform image classification using ImageNet data with 1000 classes (31). We modified the model by replacing the last 1000-class layer with a 3-class layer representing the three F-actin patterns. A set of 1597 manually classified platelet F-actin images was split into a training set (80% of images) and a validation set (20% of images). Each image was cropped, reshaped, normalized, and contrast adjusted. The model was trained over 200 epochs and fine-tuned over another 200 epochs. Model performance was evaluated by predicting the classes of the validation images. Ultimately, of the 318 validation images, the model correctly predicted 93.7%, incorrectly predicted 0.94%, and assigned 5.35% as indeterminate. More details of the machine learning methodology are included in the supporting material.
Black dots manufacturing
As described previously (27), microcontact printing was used to deposit a fluorescent surface with a pattern of nonfluorescent circles onto a flexible, polydimethylsiloxane (PDMS) surface. In brief, a PDMS microcontact printing stamp was created by casting Sylgard 184 (base and curing agent prepared at a 10:1 ratio by weight, Dow Corning, Midland, MI) onto a silicon master structure with an array of circular features arranged in an orthogonal lattice. Fluorescent bovine serum albumin (2.5 μg/mL of Alexa Fluor 594-conjugated, Life Technologies) was pipetted onto the surface of the PDMS stamps and allowed to adsorb for 40 min. A plasma-treated polyvinyl alcohol film (Sigma) was used to transfer the fluorescent pattern from the stamp to the flexible PDMS substrate, which was done by incubating the polyvinyl alcohol film on the PDMS stamp for 20 min and then transferring it to the flexible PDMS substrate and incubating for 20 min. The flexible PDMS substrate had a Young’s modulus of 13.5 kPa and was manufactured by mixing 95% of Sylgard 527 (A and B components prepared at a 1:1 ratio by weight, Dow Corning) and 5% of Sylgard 184 (base and curing agent prepared at a 10:1 ratio by weight). This microcontact printing process resulted in a flexible substrate with a contiguous fluorescent coating containing an orthogonal array of 1 μm diameter nonfluorescent circles spaced 2 μm apart center-to-center.
Black dots analysis
Single-platelet forces were calculated from displacements of the black dot centroids using regularized Fourier transform traction cytometry, as described previously (27). Total force for a single platelet was calculated by summing the force magnitudes from each dot beneath a cell. The platelet boundary and its area were determined in MATLAB (MathWorks, Natick, MA) by thresholding and shape filling the F-actin image.
In addition to measuring total platelet force from the displacements of black dot centroids, we measured higher-resolution forces by fitting ellipses to the deformed black dots and applying a Bayesian approach by maximizing model evidence (hyperparameter posterior distribution given data) with probabilistic priors for regularization, global force balance, and constraint of force exertion within the cell boundary. Black dot image intensity was normalized and regions without substrate deformation were assigned as reference regions. An ellipse was fitted to each black dot to obtain the shapes of both deformed dots and reference dots. Displacements of the black dots were measured from the undeformed circles to the vertices of the deformed ellipses. The Boussinesq Green’s function in the Bayesian framework was used to relate displacements to traction stresses.
Filament orientation and radial order quantification
We quantified F-actin filament orientation and radial order as described previously (11). Fluorescence images of platelets labeled for F-actin were filtered, normalized, and binarized to create F-actin masks. Local orientation of F-actin filaments was found by detecting the second-order gradient using 5 × 5 Sobel kernels. Orientation of F-actin filaments was determined from the local orientation and F-actin masks. The output angle was plotted based on a rainbow-colored color wheel and an overall alignment value (between 0 and 1) was calculated for each platelet. Radial order was calculated from the filament orientation relative to the centroid of the cell. The output was plotted on a blue (circumferential) to red (radial) scale and an overall radial order was calculated (between 0 and 1) for each platelet. The MATLAB code, sample images, and a detailed user guide is available online (11).
Statistics
A Pearson’s chi-squared test was used to compare frequencies of F-actin morphologies (Figs. 1 C and 3 C). A two-tailed, paired t-test was used to compare the average platelet force per donor on fibrinogen versus VWF (Fig. 3 E). An analysis of covariance was used to examine relationships between force and area (Fig. 3 F), filament orientation (Fig. 4 D), and radial order (Fig. 4 G). An unpaired, two-tailed t-test was used to compare two-group F-actin data (Fig. 4, B and E). An ANOVA and Tukey’s post hoc test was used to compare all multigroup data (Figs. 3 G, 4 C, F, and 6 B, C). Asterisks (∗) indicate p values <0.05.
Figure 1.
F-actin morphologies in platelets are distinct on fibrinogen- and VWF-treated coverslips. (A) After spreading on fibrinogen (FBN)-coated coverslips, platelet F-actin is commonly hollow (purple arrow) and nodular (blue arrow) while on VWF-coated coverslips (B), these morphologies were rare and, instead, platelets predominantly had solid (red arrow) F-actin patterns. (C) Manual quantification of n = 4304 platelets (2157 on FBN and 2147 on VWF) from 10 experiments showed that, on FBN, 24% were nodular (blue), 54% were hollow (purple), 15% were solid (red), and 6% were indeterminate (gray). In contrast, 2% were hollow F-actin structure, 95% were solid, and 3% were indeterminate on VWF. When tested with a Pearson’s chi-squared test, these frequencies are significantly different (p < 0.0001). Between experiments, differences in morphology trended similarly (Table S1). (D–F) These hollow (D), nodular (E), and solid (F) F-actin patterns were further characterized in super-resolution using SIM. D–F are on the same scale. To see this figure in color, go online.
Figure 3.
Total platelet forces are protein and F-actin pattern dependent with significantly higher forces on VWF. Platelets labeled for F-actin (white on monochromatic image, cyan on colorized image) on (A) fibrinogen (FBN)-coated or (B) VWF-coated black dots substrates for traction force measurements. In the colorized images, F-actin is cyan, glycoprotein Ib is yellow, and black dot array is magenta. (C) Frequencies of F-actin patterns on FBN- or VWF-treated black dots were determined via machine learning. When tested with a Pearson’s chi-squared test, these frequencies are significantly different (p < 0.0001). (D) Inset: white box from (B). The dots underneath a platelet are deformed by forces generated by the platelet. Forces (cyan arrows) were calculated from the displacement of the dots from their undeformed centroids (white dot). Cell boundary is shown in white in the middle and right panels. (E) Force is significantly higher on VWF (p = 0.0104 when tested with a paired t-test). Black dots indicate the mean per donor (n = 4) and colored dots indicate the value per cell (n = 146 on FBN and 134 on VWF). (F) Platelets on VWF produced more force per area than platelets on FBN. The best fit line of VWF (red) has a slope of 0.415 and an intercept of 11.9. The best fit line of FBN (blue) has a slope of 0.348 and an intercept of 1.87. Dotted lines are the 95% confidence interval. These intercepts are significantly different (p = 0.0002) when tested with an analysis of covariance. (G) Force per platelet was both protein and F-actin pattern dependent. Hollow platelets on VWF produced more traction force than hollow platelets on FBN (p = 0.0036 when tested with an ANOVA and Tukey’s post hoc test). In addition, indeterminate platelets produced more force on VWF than FBN (p = 0.0296). VWF-bound solid platelets produced significantly more force than FBN-bound hollow platelets (p < 0.0001). Finally, FBN-bound hollow platelets produced significantly more force than FBN-bound nodular platelets (p < 0.0001). Error bars represent standard deviation. Note that F-actin patterns making up less than 3% of platelets were not plotted, which included solid platelets on FBN and nodular platelets on VWF. To see this figure in color, go online.
Figure 4.
Radial order of F-actin filaments varies by protein and by F-actin pattern. (A) For platelets with F-actin patterns identified by machine learning, filament orientation and radial order were quantified. (B and C) Filament orientation did not vary between FBN and VWF (B) or by F-actin pattern (C). (D) The relationship between filament orientation and force for FBN and VWF had slopes of −0.303 and −4.82, respectively, which were not significantly different from each other or from zero. However, these relationships on FBN and VWF had y-intercepts of 18.6 and 33.1, which were significantly different (p < 0.0001) when tested with an analysis of covariance. (E) Radial order was significantly higher on VWF-bound platelets, indicating that actin fibers were oriented more radially on VWF and more circumferentially on FBN (p < 0.0001 when tested with an unpaired, two-tailed t-test). (F) Radial order also significantly varied between F-actin patterns. Solid platelets on VWF had significantly higher radial order than FBN-bound hollow platelets (p < 0.0001), VWF-bound hollow platelets (p = 0.0197), and VWF-bound indeterminate platelets (p = 0.0041) when tested with an ANOVA and Tukey’s post hoc test. (G) The relationship between radial order and force for FBN and VWF had slopes of 8.86 and −22.8, respectively, which were not significantly different from each other (p = 0.138) or from zero. However, these relationships on FBN and VWF had y-intercepts of 15.5 and 41.2, which were significantly different (p < 0.0001) when tested with an analysis of covariance. Thin lines in D and G indicate 95% confidence intervals. Error bars in B, C, E, and F represent standard deviation. To see this figure in color, go online.
Figure 6.
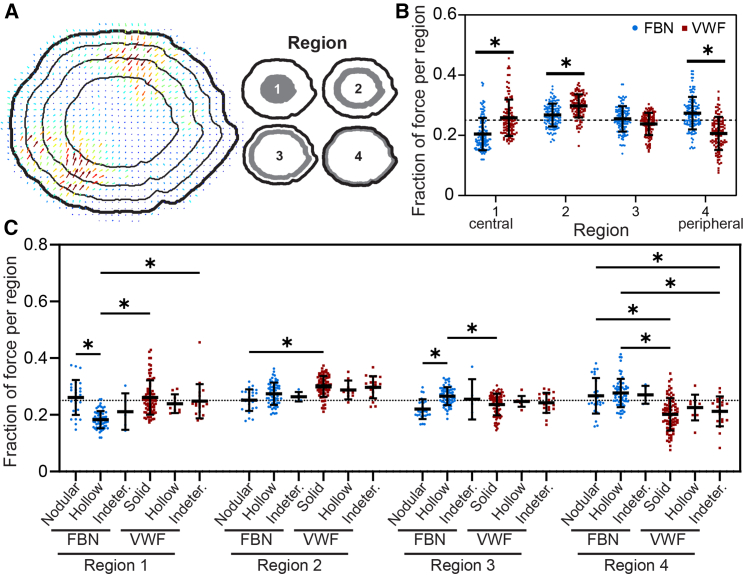
Platelet subcellular forces are significantly more peripheral on fibrinogen and more central on VWF. (A and B) When separating the cell into four regions of equal area, we found that forces are significantly more peripheral on FBN (p < 0.0001 for region 4 when tested with an ANOVA and Tukey’s post hoc) and significantly more central on VWF (p < 0.0001 for regions 1 and 2). The representative image in A is a VWF-bound platelet and its fraction of force in regions 1, 2, 3, and 4 is, respectively, 0.275, 0.300, 0.247, and 0.178. The horizontal dotted line at y = 0.250 indicates the expected fraction of force in each of the equal-area regions if forces were distributed randomly. (C) We next examined regional force localization by machine learning-assigned F-actin pattern. VWF-bound solid and indeterminate platelets had a significantly higher fraction of force than FBN-bound, hollow platelets in region 1 (p < 0.0001 and p < 0.0001, respectively, when tested with an ANOVA and Tukey’s post hoc). FBN-bound nodular platelets also had a higher fraction of force than FBN-bound hollow platelets in region 1 (p < 0.0001). In region 2, VWF-bound solid platelets had a significantly higher fraction of force than FBN-bound nodular platelets (p = 0.0007). In region 3, FBN-bound, hollow platelets had a significantly higher fraction of force than VWF-bound solid (p = 0.0295) and FBN-bound nodular (p = 0.0045). In the most peripheral region (region 4), FBN-bound hollow platelets had a significantly higher fraction of force than VWF-bound solid platelets (p < 0.0001) and VWF-bound indeterminate platelets (p < 0.0001). In addition, FBN-bound nodular platelets had a higher fraction of force than VWF-bound indeterminate platelets (p = 0.0168) and VWF-bound solid platelets (p < 0.0001) in region 4. The horizontal dotted line at y = 0.250 indicates the fraction of force expected if forces were randomly distributed. Therefore, compared with if randomly distributed, values above this dotted line indicate more force per region and values below indicate less force per region. Error bars represent standard deviation. Note that the sample platelet in A is a VWF-bound solid pattern platelet in Fig. 5, A–C and D (right). To see this figure in color, go online.
Results
After seeding human platelets isolated from whole blood onto fibrinogen- or VWF-coated coverslips and allowing them to spread, we observed distinct patterns in the F-actin morphology in individual platelets (Fig. 1, A and B). On fibrinogen, the majority of platelets had F-actin arranged along the periphery of the cell and with a prominent absence of F-actin in the center, which we classified as hollow platelets (Fig. 1 A, purple arrow). In contrast, on VWF, hollow platelets were rare and, instead, most platelets had F-actin that spanned the central region of their spread area, which we classified as solid platelets (Fig. 1 B, red arrow). In addition, we observed that a portion of platelets on fibrinogen coatings had punctate nodules of F-actin, which we classified as nodular platelets (Fig. 1 A, blue arrow). Across 10 distinct experiments, nodular platelets were rarely observed on VWF coatings (Fig. 1 B). Furthermore, we classified a platelet as indeterminate if its F-actin morphology displayed features of two or more other classifications or if it was unclear which pattern best represented it. By quantifying the distribution of these four classifications of platelets by their F-actin morphology, we found that the matrix coatings had distributions that were significantly different (p < 0.0001 by Pearson’s chi-squared test) (Fig. 1 C). Platelets seeded onto blocked coverslips without fibrinogen or VWF did not spread, indicating that the adhesion is matrix coating specific (Fig. S1). We characterized these F-actin patterns further with super-resolution images obtained by structured illumination microscopy (SIM) (Figs. 1, D–F and S2). Our SIM images of hollow and nodular (Fig. 1, D and E) platelets resembled fibrinogen-bound platelets previously characterized in super-resolution (11,14). In contrast, our SIM images of VWF-bound solid platelets showed an F-actin pattern distinct from hollow and nodular patterns wherein actin filaments pass through the center of the platelet.
To ensure that an identical criterion was applied to each platelet and to reduce analysis time in future experiments, the manual classifications of F-actin morphology were used to train and assess a machine learning model in the form of a convolutional neural network (Fig. 2), which is a machine learning technique commonly used for image classification. Convolutional neural networks use spatial convolution kernels to extract localized features and shapes in images; they have been widely used for classification of faces, scenes, and cells (32,33). In total, 1597 manually classified platelets were used, of which 318 platelets were randomly selected to serve as the validation group for assessing the accuracy of the machine learning model. We found that the accuracy increased with each instance of training (i.e., epoch) (Fig. 2 A). Specifically, the machine learning model correctly predicted 93.7% of the platelet classification, incorrectly predicted 0.94%, and assigned 5.35% as indeterminate due to the prediction scores of the model being insufficiently low (Figs. 2 B and S3). As expected, the model assigned platelets into distinct groups based on F-actin pattern (Fig. 2 C). In addition, model-assigned indeterminate platelets showed features of multiple patterns. For instance, some had features that resembled both nodular and hollow patterns. Thus, the accuracy of the machine learning model and the machine learning-based identification of indeterminate platelets provides a measure of confidence in the model.
Figure 2.
Distinct F-actin morphologies on fibrinogen and VWF are identifiable via machine learning. (A) Training the machine learning model resulted in over 90% accuracy after 200 epochs and over 95% accuracy after fine-tuning. (B) The machine learning model confusion matrix represents the accuracy of the model wherein the dark green cross section represents the number of cells that the manual assessment agrees with the machine learning predictions (C) Representative images are shown for machine learning-assigned F-actin patterns. To see this figure in color, go online.
F-actin couples with myosin to drive platelet contraction. We previously found that F-actin dispersion, which is the distribution of F-actin throughout the spread area of a platelet, significantly contributes to the magnitude of its traction forces (27). Here, we investigated whether the distinct F-actin patterns on VWF and fibrinogen result in differences in force generation (Fig. 3). To measure single-platelet forces, we utilized our “black dots” approach. Black dots are a flexible, silicone elastomer substrate with a fluorescent coating and a pattern of nonfluorescent circular dots. We used this technique because it is compatible with immunofluorescent staining and does not significantly constrain cell shape or spreading, making it possible to compare the F-actin morphology of individual platelets with their traction forces. F-actin patterns for platelets seeded onto fibrinogen- or VWF-coated black dots were assessed using the machine learning model. The resulting distributions of platelet classification were distinct for matrix coating (Fig. 3 C, p < 0.0001 by Pearson’s chi-squared test) and consistent with distributions observed on coverslips (Fig. 1 C). With the black dots technique, the traction forces generated by an individual platelet (Fig. 3 D, left) displace the black dot pattern (Fig. 3 D, middle), from which the magnitude and direction of its traction forces can be obtained (blue arrows in Fig. 3 D, right). Total force per platelet is calculated by summing the magnitude of the force vectors at each dot under a platelet. From assessing the total force for individual platelets from four unique blood donors and 279 total cells, platelet forces were significantly higher on VWF than on fibrinogen (p = 0.0104 when average platelet force per donor was tested by paired, two-tailed t-test). By examining the relationship between single-platelet force and spread area, we found that platelets with the same spread area produced higher forces on VWF than on fibrinogen (Figs. 3 F and S4, p = 0.0002 when tested with an analysis of covariance). This indicates that, despite the well-established correlation between spread area and force (2,21,27), this observed difference in force generation is not simply a consequence of differences in spread area. Interestingly, the magnitude of force that platelets produce is affected by both protein and F-actin pattern (Fig. 3 G). In particular, hollow and indeterminate platelets produced significantly more force when seeded on VWF than on fibrinogen (p = 0.0036 and p = 0.0296, respectively, by ANOVA with Tukey’s post hoc test). In addition, VWF-bound solid platelets, which are the most common F-actin pattern on VWF, produce significantly more force than fibrinogen-bound hollow platelets (p < 0.0001), which are the most common F-actin pattern on fibrinogen. When comparing fibrinogen-bound platelets, hollow platelets produced more force than nodular platelets (p < 0.0001), which we expected given that nodular platelets have less developed F-actin. For VWF-bound platelets, solid, hollow, and indeterminate platelets did not produce significantly different forces. Due to insufficient sample size, platelets that made up less than 3% of a population were not plotted by pattern.
To further characterize the connection between F-actin morphologies and force for platelets on fibrinogen or VWF coatings, we analyzed the orientation and radial order of F-actin, as described previously (11) (Fig. 4 A). F-actin images were binarized, resulting in an F-actin mask (Fig. 4 A, left two panels). From these, the orientation of filaments was measured, resulting in images with filaments colorized by angle (Fig. 4 A, rainbow images) and a value per platelet indicating the extent of overall F-actin alignment within a cell wherein 0 is isotropic and 1 is fully aligned (Fig. 4 A, rainbow images). We found that filament orientation did not vary significantly for platelets seeded on fibrinogen versus VWF (Fig. 4 B) and that mean filament orientation was similar to values previously reported for fibrinogen-coated substrates of similar stiffness (11). We did not find differences in filament orientation by pattern for platelets classified by machine learning (Fig. 4 C). When relating filament orientation to platelet force, we found no correlation (i.e., slopes are not significantly different from zero, Fig. 4 D), perhaps because our platelet force technique measures forces in all directions, making it independent of filament orientation. Nonetheless, the relationship between filament orientation and force on fibrinogen and VWF had significantly different intercepts (p < 0.0001 by an analysis of covariance), indicating that, for platelets of the same filament orientation, platelets on VWF produced more force.
Next, we measured the radial order of F-actin for platelets on VWF or fibrinogen coatings (Fig. 4 A, red/blue images), which is a measure of fiber orientation relative to the geometric centroid of a platelet wherein the radial order is 0 if F-actin structures are circumferential (i.e., oriented parallel to the perimeter of a circular cell) and 1 if they are radial (i.e., oriented from the platelet centroid to the boundary). We found that fibers were significantly more radial on VWF-bound platelets compared with fibrinogen-bound platelets (p < 0.0001 by t-test, Fig. 4 E). Strikingly, radial orientation varied by F-actin classification pattern. Fibrinogen-bound platelets classified by machine learning as hollow had significantly more circumferential fibers than VWF-bound platelets classified as solid (p < 0.0001 by ANOVA and Tukey’s post hoc, Fig. 4 F). When comparing VWF-bound platelets, solid platelets had significantly higher radial order than those with hollow or indeterminate classification (p = 0.0197 and 0.0041 by ANOVA and Tukey’s post hoc, Fig. 4 F). Like the relationship between filament orientation and force, we found no significant relationship between radial order and force (Fig. 4 G). However, for platelets with the same radial order, those on VWF produced more force (p < 0.0001 by an analysis of covariance). Taken together, this indicates that the differences in radial order observed in platelets on fibrinogen versus VWF do not account for differences in platelet force generation. Note that, because filament orientation and radial order are measures designed to quantify filament structures, we did not apply the image analysis to nodular platelets that lack visible filaments.
In addition, we examined whether F-actin patterns reflect subcellular distributions of traction forces. To increase the spatial resolution of the platelet forces, we improved the computational analysis by fitting ellipsoids to the distorted image of each black dot (Fig. 5 A). Originally, we had identified the outline of each black dot in the array (Fig. 5 B, cyan shapes), determined its geometric centroid from those outlines (Fig. 5 B, red dots), and calculated its displacement vector (Fig. 5 B, white arrows). To enhance the resolution, we fitted ellipses to the fluorescent black dots (Fig. 5 C, cyan ellipses), identified the vertices of the ellipses (Fig. 5 C, red dots), and calculated four displacement vectors (Fig. 5 C, white arrows) per black dot. These higher-resolution displacements combined with a Bayesian approach by maximizing model evidence with probabilistic priors for regularization, global force balance, and constraint of force exertion within the cell boundary result in high-resolution platelet traction forces with immunofluorescent stains (Fig. 5 D, more examples in Fig. S5, A and B). As expected, platelet forces calculated with the ellipse method correlated with the centroid method (Fig. S5 C) without increasing noise (Figs. S6 and S7). Qualitatively, the localization of these traction forces corresponded to the F-actin patterns, where the highest forces localized at the ends of F-actin fibers (Fig. 5 D, more examples in Fig. S5, A and B).
Figure 5.
Platelet subcellular forces correspond with F-actin patterns. (A) For a representative fluorescently labeled platelet (F-actin, bottom) on black dots (top), (B) force per platelet was calculated by finding the outline of the fluorescent black dot pattern (cyan shapes, left image), determining the centroid of those outlines (red dots, left image), and calculating the centroid displacement (white arrows, right image) from the undeformed grid. (C) To enhance the resolution to better characterize subcellular localization of traction forces, ellipses were fit to the fluorescent black dot pattern (cyan ellipses, left image), finding the vertices of the ellipses (red dots, left image), and calculating the vertex displacement (white arrows, right image) from the undeformed grid. This results in fourfold higher-resolution displacements. (D) These higher-resolution displacements combined with a Bayesian approach result in high-resolution platelet traction forces with immunofluorescent stains. Qualitatively, the localization of these traction forces corresponded to the F-actin patterns, wherein the highest forces localized at the ends of F-actin fibers. To see this figure in color, go online.
To analyze the forces spatially, we separated each platelet into four regions (Fig. 6 A for regions of equal area, Fig. S8 for regions of equal radius) based on proximity to the platelet centroid. We found that the fraction of force in the central areas (regions 1 and 2) was significantly higher on VWF than on fibrinogen (p < 0.0001 by ANOVA and Tukey’s post hoc) (Fig. 6 B). In contrast, the fraction of force at the periphery (region 4) was significantly higher on fibrinogen than on VWF (p < 0.0001) (Fig. 6 B). This difference corresponds to the F-actin patterns most prevalent on each protein. VWF-bound, solid platelets exerted a significantly higher fraction of force centrally (region 1) and a significantly lower fraction of force peripherally (region 4) than fibrinogen-bound hollow platelets (p < 0.0001, Fig. 6 C). These data indicate that localization of platelet forces was both protein and F-actin pattern dependent.
Discussion
We examined the F-actin patterns of platelets on fibrinogen and VWF and observed distinct patterns that are identifiable by machine learning. Our data agree with previous studies that observed nodular and hollow platelet F-actin patterns on fibrinogen (11,13,14,15,16), yet we found that these morphologies were almost completely absent on VWF. Instead, platelets on VWF had an inverse F-actin distribution, with F-actin localized in the platelet center. In addition to differences in F-actin structure on fibrinogen versus VWF, we observed differences in function, wherein platelets on VWF produced more force than platelets on fibrinogen, even when accounting for spread area. In addition, hollow fibrinogen-bound platelets generated less force than hollow VWF-bound platelets but more force than nodular fibrinogen-bound platelets, indicating that platelet forces are both protein- and F-actin pattern-dependent. Nodular platelets’ reduced forces align with the previous finding that treatment with inhibitors of contraction increases the fraction of nodular platelets on fibrinogen (13). Because black dots enable simultaneous visualization of immunofluorescent stains and measurement of single-cell forces (34), we were able to covisualize F-actin and force generation on the subcellular scale, finding that platelet F-actin structure corresponded with force localization. This builds on previous work that observed modest correlations between total platelet force and F-actin intensity (20) or F-actin dispersion (27), but could not measure the localization of subcellular forces. In addition, we found that F-actin patterns induced by VWF resulted in forces localized significantly more centrally while patterns induced by fibrinogen resulted in forces localized significantly more peripherally.
While the mechanism of these differences in F-actin pattern and traction forces was not investigated in this work, we postulate that it could be due to differences in receptor engagement or protein structure. Fibrinogen and VWF both contain the RGD adhesive motif that engages integrin αIIbβ3 (35), while VWF also has its A1 domain that binds to platelet GPIb (35,36,37). GPIb-A1 binding can trigger signaling pathways that mediate F-actin formation and activate integrins (38,39,40). Previously, we have found that, when GPIb is blocked, platelets on VWF have reduced traction forces (26). However, because this reduction in force is accompanied by an approximately proportional reduction in area (26), these previous findings do not explain the reduced force irrespective of area observed on fibrinogen versus VWF (Fig. 3 F). Another potential difference in platelet receptor engagement on these matrix proteins includes glycoprotein VI (GPVI), which binds to fibrinogen and mediates platelet activation (17). Platelets that lack GPVI have impaired spreading on fibrinogen (17). However, because GPVI-deficient platelets on fibrinogen appear to predominantly form nodular F-actin patterns (17), a lack of GPVI engagement is likely not the sole mediator of the solid F-actin patterns observed on VWF. Given that GPIb and GPVI associate with each other on the platelet surface (41), it is also possible that these receptors have synergistic roles in the organization of F-actin and generation of traction forces. While the mechanism remains unclear, these differences in F-actin patterns and traction forces could be mediated by receptor engagement of unique adhesive motifs on VWF versus fibrinogen, receptor association with actin cross-linkers (e.g., filamin A), and/or other signaling responses downstream of these receptors’ activation (e.g., intracellular calcium release, granule secretion, inside-out signaling). In addition, VWF is a large, fibrillar protein and fibrinogen is a smaller protein converted to fibrillar fibrin by thrombin. Because platelet shape and granule secretion are modulated by nanotopography (42), the difference in biophysical cues by different protein structures could play a role. Investigation of the complex responses of platelets to stimuli resulting in these distinct F-actin patterns warrants future study.
Distinct F-actin patterns, contraction magnitudes, and subcellular localization of forces observed on fibrinogen versus VWF could have implications in hemostasis and thrombus architecture due to the unique role of VWF in tethering platelets to the subendothelial matrix as the first step of platelet plug formation (36,37). It is possible that, toward cessation of bleeding, it is advantageous for the earliest bound platelets to be hypercontractile and that actin fibers formed through the center of the platelet enable maximal forces. In addition, these F-actin structural and functional differences could be important in clots of different protein content and protein organization, such as the fibrin(ogen)-rich outer shell observed in acute ischemic stroke thrombi (43) and the distribution of VWF within a thrombi that is associated with stroke etiology and revascularization outcome (44).
Beyond the study of platelets, we see this study as a connection between advanced computational techniques (machine learning, fiber alignment quantifications), cellular structural characterizations (super-resolution microscopy of immunofluorescence-stained cellular components), and cellular functional measurements (single-cell and subcellular measurement of force generation). We anticipate that the combination of these computational and experimental techniques will be complementary in the association of cellular structure and function, characterization of biological heterogeneity, and investigation of biological mechanisms.
Author contributions
M.Y.M. performed the blood collection, experiments, total platelet force analysis, filament analysis, and statistics. K.M.B. performed the machine learning methodology in consultation with K.M. A.K. performed the subcellular force analysis with guidance from J.C.d.Á. J.C. and J.L. provided helpful experimental design and feedback. L.M.R. and F.R.M. assisted with optimization experiments and analysis. M.Y.M., W.E.T., and N.J.S. designed the experiments, interpreted the data, and wrote the manuscript. All authors reviewed the manuscript.
Acknowledgments
This work was supported by the National Institutes of Health (HL147462, HL007093, EB001650, HL145262, 5R01HD092216-03, 1R01AI167943-01A1, and 2R01GM084227) and the National Science Foundation (CMMI-1824792 and CBET-1706436/1706571). Imaging in this study was conducted in the Lynn & Mike Garvey Imaging Core. The machine learning training was performed using the University of Washington’s high-performance computing cluster Hyak. We also thank Tom Mikolyuk for his involvement in the early stages of the machine learning project.
Declaration of interests
N.J.S. is a cofounder, board member, and has equity in Stasys Medical Corporation. He is also a scientific advisor and has equity in Curi Bio, Inc.
Editor: Guy Genin.
Footnotes
Twitter: @Molly_Mollica
Supporting material can be found online at https://doi.org/10.1016/j.bpj.2023.07.006.
Contributor Information
Molly Y. Mollica, Email: mollica@umbc.edu.
Nathan J. Sniadecki, Email: nsniadec@uw.edu.
Supporting material
References
- 1.White J.G. Platelets. Elsevier; 2007. Platelet structure; pp. 45–73. [Google Scholar]
- 2.Hanke J., Probst D., et al. Köster S. Dynamics of force generation by spreading platelets. Soft Matter. 2018;14:6571–6581. doi: 10.1039/c8sm00895g. [DOI] [PubMed] [Google Scholar]
- 3.Paknikar A.K., Eltzner B., Köster S. Direct characterization of cytoskeletal reorganization during blood platelet spreading. Prog. Biophys. Mol. Biol. 2019;144:166–176. doi: 10.1016/j.pbiomolbio.2018.05.001. [DOI] [PubMed] [Google Scholar]
- 4.Cohen I. The contractile system of blood platelets and its function. Methods Achiev. Exp. Pathol. 1979;9:40–86. [PubMed] [Google Scholar]
- 5.Ono A., Westein E., et al. Jackson S.P. Identification of a fibrin-independent platelet contractile mechanism regulating primary hemostasis and thrombus growth. Blood. 2008;112:90–99. doi: 10.1182/blood-2007-12-127001. [DOI] [PubMed] [Google Scholar]
- 6.Feghhi S., Sniadecki N.J. Mechanobiology of platelets: Techniques to study the role of fluid flow and platelet retraction forces at the micro- and nano-scale. Int. J. Mol. Sci. 2011;12:9009–9030. doi: 10.3390/ijms12129009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Williams E.K., Oshinowo O., et al. Myers D.R. Feeling the force: Measurements of platelet contraction and their diagnostic implications. Semin. Thromb. Hemost. 2019;45:285–296. doi: 10.1055/s-0038-1676315. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Lee D., Fong K.P., et al. Hammer D.A. Differential dynamics of platelet contact and spreading. Biophys. J. 2012;102:472–482. doi: 10.1016/j.bpj.2011.10.056. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Zarka R., Horev M.B., et al. Geiger B. Differential modulation of platelet adhesion and spreading by adhesive ligand density. Nano Lett. 2019;19:1418–1427. doi: 10.1021/acs.nanolett.8b03513. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Horev M.B., Zabary Y., et al. Geiger B. Differential dynamics of early stages of platelet adhesion and spreading on collagen IV- and fibrinogen-coated surfaces. F1000Research. 2020;9:ISF-449. doi: 10.12688/f1000research.23598.1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Lickert S., Sorrentino S., et al. Schoen I. Morphometric analysis of spread platelets identifies integrin αIIbβ3-specific contractile phenotype. Sci. Rep. 2018;8:5428. doi: 10.1038/s41598-018-23684-w. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Linder S., Kopp P. Podosomes at a glance. J. Cell Sci. 2005;118:2079–2082. doi: 10.1242/jcs.02390. [DOI] [PubMed] [Google Scholar]
- 13.Calaminus S.D.J., Thomas S., et al. Watson S.P. Identification of a novel, actin-rich structure, the actin nodule, in the early stages of platelet spreading. J. Thromb. Haemost. 2008;6:1944–1952. doi: 10.1111/j.1538-7836.2008.03141.x. [DOI] [PubMed] [Google Scholar]
- 14.Poulter N.S., Pollitt A.Y., et al. Thomas S.G. Platelet actin nodules are podosome-like structures dependent on Wiskott-Aldrich syndrome protein and ARP2/3 complex. Nat. Commun. 2015;6:7254. doi: 10.1038/ncomms8254. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Thomas S.G. Platelets. Elsevier; 2019. The structure of resting and activated platelets; pp. 47–77. [Google Scholar]
- 16.Hagmann J. Pattern formation and handedness in the cytoskeleton of human platelets. Proc. Natl. Acad. Sci. USA. 1993;90:3280–3283. doi: 10.1073/pnas.90.8.3280. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Mangin P.H., Onselaer M.B., et al. Watson S.P. Immobilized fibrinogen activates human platelets through glycoprotein VI. Haematologica. 2018;103:898–907. doi: 10.3324/haematol.2017.182972. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Lam W.A., Chaudhuri O., et al. Fletcher D.A. Mechanics and contraction dynamics of single platelets and implications for clot stiffening. Nat. Mater. 2011;10:61–66. doi: 10.1038/nmat2903. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Schwarz Henriques S., Sandmann R., et al. Köster S. Force field evolution during human blood platelet activation. J. Cell Sci. 2012;125:3914–3920. doi: 10.1242/jcs.108126. [DOI] [PubMed] [Google Scholar]
- 20.Myers D.R., Qiu Y., et al. Lam W.A. Single-platelet nanomechanics measured by high-throughput cytometry. Nat. Mater. 2017;16:230–235. doi: 10.1038/nmat4772. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Hanke J., Ranke C., et al. Köster S. Human blood platelets contract in perpendicular direction to shear flow. Soft Matter. 2019;15:2009–2019. doi: 10.1039/c8sm02136h. [DOI] [PubMed] [Google Scholar]
- 22.Oshinowo O., Copeland R., et al. Lam W.A. Significant differences in single-platelet biophysics exist across species but attenuate during clot formation key points. Blood Adv. 2021;5:432–437. doi: 10.1182/bloodadvances.2020003755. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Miles J., Bailey S.L., et al. Stolla M. Storage temperature determines platelet GPVI levels and function in mice and humans. Blood Adv. 2021;5:3839–3849. doi: 10.1182/bloodadvances.2021004692. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Jackson S.P., Mistry N., Yuan Y. Platelets and the injured vessel wall - “Rolling into action.” Focus on glycoprotein Ib/V/IX and the platelet cytoskeleton. Trends Cardiovasc. Med. 2000;10:192–197. doi: 10.1016/s1050-1738(00)00062-1. [DOI] [PubMed] [Google Scholar]
- 25.Yuan Y., Kulkarni S., et al. Jackson S.P. The von Willebrand factor-glycoprotein Ib/V/IX interaction induces actin polymerization and cytoskeletal reorganization in rolling platelets and glycoprotein Ib/V/IX-transfected cells. J. Biol. Chem. 1999;274:36241–36251. doi: 10.1074/jbc.274.51.36241. [DOI] [PubMed] [Google Scholar]
- 26.Feghhi S., Munday A.D., et al. Sniadecki N.J. Glycoprotein Ib-IX-V complex transmits cytoskeletal forces that enhance platelet adhesion. Biophys. J. 2016;111:601–608. doi: 10.1016/j.bpj.2016.06.023. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Beussman K.M., Mollica M.Y., et al. Sniadecki N.J. Black dots: High-yield traction force microscopy reveals structural factors contributing to platelet forces. Acta Biomater. 2021;163:302–311. doi: 10.1016/j.actbio.2021.11.013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.McCarty O.J.T., Calaminus S.D.J., et al. Watson S.P. von Willebrand factor mediates platelet spreading through glycoprotein Ib and alpha(IIb)beta3 in the presence of botrocetin and ristocetin, respectively. J. Thromb. Haemost. 2006;4:1367–1378. doi: 10.1111/j.1538-7836.2006.01966.x. [DOI] [PubMed] [Google Scholar]
- 29.Lavin M., O’donnell J.S. How I treat low von Willebrand factor levels? Blood. 2019;133:795–804. doi: 10.1182/blood-2018-10-844936. [DOI] [PubMed] [Google Scholar]
- 30.Fernández K.S., De Alarcón P.A. Von Willebrand disease: range of the disease, and management. Curr Pediatr Rep. 2014;2:60–70. [Google Scholar]
- 31.Szegedy C., Vanhoucke V., et al. Shlens J. Proceedings of IEEE Conference on Computer Vision and Pattern Recognition (CVPR) 2016. Rethinking the inception architecture for computer vision; pp. 2818–2826. [Google Scholar]
- 32.Al-Saffar A.A.M., Tao H., Talab M.A. 2017 International Conference on Radar, Antenna, Microwave, Electronics, and Telecommunications (ICRAMET) 2017. Review of deep convolution neural network in image classification. [Google Scholar]
- 33.Oei R.W., Hou G., et al. Yang Y. Convolutional neural network for cell classification using microscope images of intracellular actin networks. PLoS One. 2019;14:e0213626. doi: 10.1371/journal.pone.0213626. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Obenaus A.M., Mollica M.Y., Sniadecki N.J. (De)form and function: measuring cellular forces with deformable materials and deformable structures. Adv. Healthc. Mater. 2020;9:1–16. doi: 10.1002/adhm.201901454. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Varga-Szabo D., Pleines I., Nieswandt B. Cell adhesion mechanisms in platelets. Arter. Thromb. Vasc. Biol. 2008;28:403–412. doi: 10.1161/ATVBAHA.107.150474. [DOI] [PubMed] [Google Scholar]
- 36.Quach M.E., Li R. Structure-function of platelet glycoprotein Ib-IX. J. Thromb. Haemost. 2020;18:3131–3141. doi: 10.1111/jth.15035. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Springer T.A. von Willebrand factor, Jedi knight of the bloodstream. Blood. 2014;124:1412–1425. doi: 10.1182/blood-2014-05-378638. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Ju L., Chen Y., et al. Zhu C. Cooperative unfolding of distinctive mechanoreceptor domains transduces force into signals. Elife. 2016;5 doi: 10.7554/eLife.15447. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Du X. Signaling and regulation of the platelet glycoprotein Ib-IX-V complex. Curr. Opin. Hematol. 2007;14:262–269. doi: 10.1097/MOH.0b013e3280dce51a. [DOI] [PubMed] [Google Scholar]
- 40.Zaffran Y., Meyer S.C., et al. Fox J.E. Signaling across the platelet adhesion receptor glycoprotein Ib-IX induces α(IIb)β3 activation both in platelets and a transfected Chinese hamster ovary cell system. J. Biol. Chem. 2000;275:16779–16787. doi: 10.1074/jbc.275.22.16779. [DOI] [PubMed] [Google Scholar]
- 41.Arthur J.F., Gardiner E.E., et al. Berndt M.C. Glycoprotein VI is associated with GPIb-IX-V on the membrane of resting and activated platelets. Thromb. Haemost. 2005;93:716–723. doi: 10.1160/TH04-09-0584. [DOI] [PubMed] [Google Scholar]
- 42.Kenny M., Stamboroski S., et al. Schoen I. Nanofiber topographies enhance platelet-fibrinogen scaffold interactions. Adv. Healthc. Mater. 2022;11:e2200249. doi: 10.1002/adhm.202200249. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Di Meglio L., Desilles J.-P., et al. Mazighi M. Acute ischemic stroke thrombi have an outer shell that impairs fibrinolysis. Neurology. 2019;93:e1686–e1698. doi: 10.1212/WNL.0000000000008395. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Mereuta O.M., Abbasi M., et al. Brinjikji W. Correlation of von Willebrand factor and platelets with acute ischemic stroke etiology and revascularization outcome: an immunohistochemical study. J. Neurointerv. Surg. 2023;15:488–494. doi: 10.1136/neurintsurg-2022-018645. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.