G-actin diffusion is insufficient to achieve F-actin assembly in fast-treadmilling protrusions

Abstract

To generate forces that drive migration of a eukaryotic cell, arrays of actin filaments (F-actin) are assembled at the cell’s leading membrane edge. To maintain cell propulsion and respond to dynamic external cues, actin filaments must be disassembled to regenerate the actin monomers (G-actin), and transport of G-actin from sites of disassembly back to the leading edge completes the treadmilling cycle and limits the flux of F-actin assembly. Whether or not molecular diffusion is sufficient for G-actin transport has been a long-standing topic of debate, in part because the dynamic nature of cell motility and migration hinders the estimation of transport parameters. In this work, we applied an experimental system in which cells adopt an approximately constant and symmetrical shape; they cannot migrate but exhibit fast, steady treadmilling in the thin region protruding from the cell. Using fluorescence recovery after photobleaching, we quantified the relative concentrations and corresponding fluxes of F- and G-actin in this system. In conjunction with mathematical modeling, constrained by measured features of each region of interest, this approach revealed that diffusion alone cannot account for the transport of G-actin to the leading edge. Although G-actin diffusion and vectorial transport might vary with position in the protruding region, good agreement with the fluorescence recovery after photobleaching measurements was achieved by a model with constant G-actin diffusivity ∼2 μm²/s and anterograde G-actin velocity less than 1 μm/s.

Significance

Regulation of the actin cytoskeleton is central to understanding force generation in migrating cells. This process is inherently dynamic, stochastic, and associated with cell shape changes, complexities that hamper estimation of physicochemical parameters such as those characterizing actin monomer transport. To address this, we employed a strategy that compels cells to adopt a steady-state, protruding region; with this experimental system, together with programmed photobleaching and mathematical analysis thereof, we found that monomer transport by diffusion alone (as commonly assumed) cannot explain the data.

Introduction

In mammalian cells, dynamic polymerization of actin filament networks is critical for cell motility, vesicular trafficking, and the formation of specialized protrusions such as lamellipodia, filopodia, and dendritic spines (1). While much is known about the biochemical and biophysical basis for actin polymerization and depolymerization, several important aspects of this process, such as the recycling of actin monomers from zones of depolymerization to areas of polymerization, are poorly understood. Actin filaments within lamellipodial protrusions constitute a prototypical recycling actin network that has been extensively studied with both experimental and theoretical approaches (2,3,4), yet there remains a gap between understanding of actin dynamics in reconstituted assays versus intact cells.

In lamellipodial protrusions, actin filament (F-actin) assembly and disassembly tend to be spatially separated, with monomer (G-actin) incorporation largely occurring at the leading membrane edge and disassembly occurring some distance away. F-actin polymerization occurs on free barbed ends of filaments and is facilitated by both actin polymerases, such as Ena/VASP proteins and formins, as well as by de novo nucleation via activation of the Arp2/3 complex (5). Disassembly of actin networks is driven by ADF/cofilin proteins that sever filaments and enhance depolymerization (6). In addition, actin filament breakage by the force of nonmuscle myosin II (NMII) contributes to filament disassembly (7). These assembly and disassembly reactions have been studied intensively, to the extent that a quantitative understanding has been established (2,3). In solution, with well-mixed components, it is readily determined how rates of F-actin assembly/disassembly are related to G-actin concentration. In actively migrating cells, however, those relationships are difficult to characterize, in part because 1) “working” filaments acting to push the membrane forward are subject to force-dependent feedbacks (3,8,9,10) and 2) such regions stochastically advance and retract. How actin monomers relocate from the rear to the front of the actin network to complete the “treadmilling” cycle in lamellipodia is incompletely understood.

Two mechanisms have been considered for actin monomer recycling to the front of the network at the leading edge: diffusion and some form of vectorial transport. Several experimental and theoretical studies have concluded that diffusion alone is sufficient to account for actin monomer movement from the zone of depolymerization to the front of the network for repolymerization (11,12). Others have concluded that advective fluid flow and active, motor-driven transport also contribute. The bulk flow hypothesis postulates that contraction and disassembly of the actin network by NMII produces an osmotic pressure gradient that manifests as an advective flow from rear to front (13). Other work suggests that the unconventional myosin motor, Myo1c, may be responsible for actin monomer anterograde transport (14). Despite such attempts to characterize G-actin transport from the site(s) of depolymerization back to the leading edge, the question of whether or not G-actin diffusion is sufficient to account for the flux of F-actin assembly remains unclear.

A significant barrier to resolving this question is the difficulty of comparing results from disparate cellular contexts. In particular, some lamellipodia are dynamic, displaying cycles of protrusion and retraction that alter cell shape. The complexity of leading-edge morphodynamics is inherently interesting, but it confounds analysis of actin dynamics in terms of local rates of actin polymerization and depolymerization. In addition, as lamellipodia engage the substrate over which they protrude, adhesion receptors such as integrins form attachments to adhesive, extracellular matrix-associated ligands such as fibronectin (Fn), which are naturally found in the extracellular matrix during fibroblast invasion of wounded tissue (15). The adhesive bonds mediate both physical actin network clutching (facilitating protrusion) and activation of signaling pathways that tune actin polymerization/depolymerization kinetics.

To analyze the flux of G-actin incorporated into filaments at the leading edge, an ideal experimental system would show negligible shape change over time, while supporting rapid and persistent actin polymerization and depolymerization (treadmilling); this scenario dramatically simplifies mathematical modeling of the actin dynamics. To achieve this, we reasoned that F-actin polymerization ought to be unfettered by adhesive interactions with the underlying substrate. Here, we introduce just such a model system. Analyses of fluorescence recovery after photobleaching (FRAP) experiments were designed, in conjunction with modeling predictions, to more accurately define the mode(s) of actin monomer transport to the cell periphery.

Materials and methods

Fn surface patterning

Single-cell micropatterning was performed essentially as described (16), with minor modifications. Microscope cover glasses (Marienfeld Superior 25 mm, No. 1.5H; Paul Marienfeld GmbH & Co. KG, Germany) were cleaned with 70% ethanol and dried with an air hose before plasma cleaning for 90 s (high power with PDC-32G Basic Plasma Cleaner; Harrick Plasma, Ithaca, NY). After plasma cleaning, cover glasses were incubated with a 0.1 mg/mL solution of PLL-g-PEG (SuSoS AG, Dübendorf, Switzerland) in 15 mM HEPES (pH 7.4) for at least 30 min up to overnight at room temperature. Cover glasses were then rinsed with water and dried shortly before surface patterning.

Surface patterning was achieved using a chrome photomask on a quartz substrate (Photo Sciences, Torrance, CA) with arrays of square and triangle microfeatures (30 μm edges) and circles (30 μm diameter). The patterned shapes allow deep UV light to locally irradiate and desorb the PLL-g-PEG coating in discrete shapes and regions, amenable to subsequent Fn coating and cell attachment.

The chrome side of the photomask was first illuminated with deep UV for 3 min (UVO-Cleaner, Model 24; Jelight, Irvine, CA), and then 5 μL of water was added on the chrome side over the desired photopatterning region as a buffer before gently pressing down the PLL-g-PEG-coated cover glass against the photomask, oriented with the PLL-g-PEG-coated side down against the photomask. The photomask with the attached cover glass(es) was then illuminated again with deep UV, this time inverting the photomask so that the light passed through the quartz side first to the chrome side with the cover glass affixed below. After this second illumination, the chrome side of the mask was flooded with water to allow the gentle detachment and flow of the cover glass(es) to the edge of the mask for careful retrieval with plastic forceps. After another gentle wash with water, the cover glasses were secured in imaging chambers (Attofluor A-7816; Thermo Scientific, Waltham, MA) and coated with a solution of 20 μg/mL human Fn (Corning, Corning, NY) in PBS for 20 min at room temperature. A final wash with PBS was performed before adding cells and imaging.

Live-cell imaging

Cells used for capturing live cell micrographs of actin dynamics are from a diploid clonal population of mouse dermal fibroblasts (JR20) that were stably expressing GFP-β-actin via lentiviral transduction, and were cultured and imaged in high glucose DMEM (Gibco; Thermo Scientific, Waltham, MA) supplemented with 10% FBS (MedSupply Partners, Atlanta, GA) and GlutaMAX (Gibco) at 37°C with 5% CO₂. JR20s were lifted from culture dishes using 0.25% Trypsin-EDTA (Gibco), and approximately 22,500 cells were seeded in imaging chambers with surface-patterned cover glasses. After allowing the cells to settle onto the Fn patterns for 30 min, the imaging/culture medium was gently pipetted up and down and replaced with fresh medium to remove a portion of the unattached cells.

Images were captured starting 45 min after seeding cells with a Zeiss LSM800 confocal microscope using a Plan-Apochromat 63×/1.4 NA oil objective with a 1.7 μm optical section. Images were collected at 512 × 512 pixels with 16 bits per pixel, typically using 0.2% laser power of a 10 mW, 488 nm laser. For closely monitoring individual protrusions, 22.5 × 22.5 μm regions with a 0.04 μm pixel size were collected, while whole-cell time lapse movies typically encompassed a 67.6 × 67.6 μm region with a 0.13 μm pixel size. For the visualization of actin polymerization and retrograde flow rates, discrete regions near the edge of protrusions were bleached (100% power of 10 mW 488 laser, 1.03 μs pixel dwell time, 4 iterations) and subsequently monitored at approximately 1 s per frame, with additional bleaches occurring every 60 frames. For cytochalasin D (CytoD) wash-in experiments, time lapse movies were paused for roughly 20 s for the addition of 200 μL of 5 μM CytoD to the 800 μL of cells and medium already present in the imaging dish (giving a 1 μM working concentration). Bleaching of post-CytoD leading-edge actin was performed with similar settings as above.

Image quantification and presentation

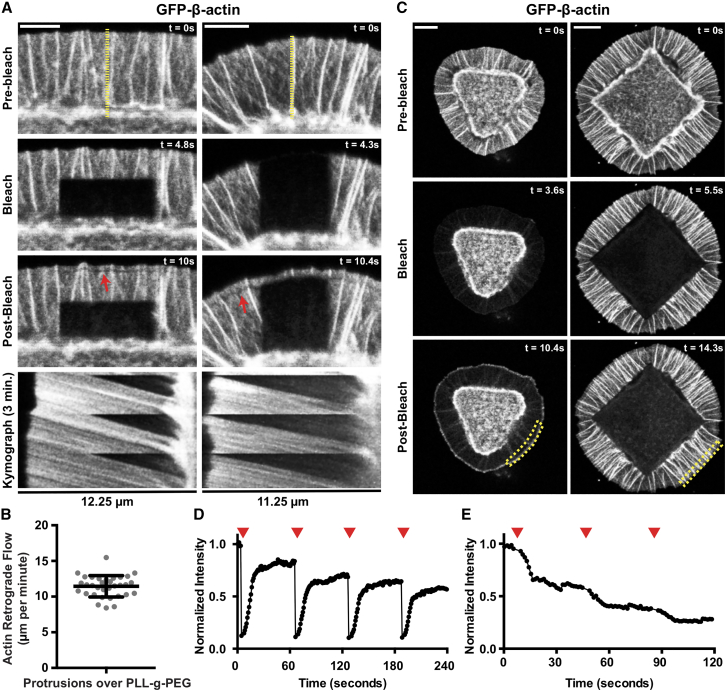
The Fiji distribution of ImageJ was used to extract and measure the relevant metrics from live-cell imaging data. For the measurement of retrograde flow rates, kymographs were generated from 5-pixel-wide line scans over regions of leading cell edges labeled with GFP-actin during sequential bleaching every 60 frames (∼1.0 s per frame). The slope of the line from the leading edge of the protrusion to the interface between bleached and unbleached actin incorporated into the filamentous actin network after the bleach could be easily visualized in these kymographs and used to accurately calculate retrograde flow rates at an approximately steady state. For the measurements of leading-edge GFP-actin intensity shown in Fig. 2, an approximately 10 μm long (along the periphery of the spillover) and 1 μm wide (from the edge toward/into the cell body) region of interest was manually drawn for intensity measurements in this region.

Figure 2.

Bleached and unbleached GFP-actin are incorporated into F-actin structures at the leading edge of spillover protrusions. (A) Still images and associated kymographs from a time lapse series of micrographs of JR20s expressing GFP-actin that were plated as detailed in Fig. 1A, focused on regions between the edge of a Fn attachment site and the edge of a cell protrusion as different regions of the protrusion are photobleached. Yellow lines show the regions the kymographs below were generated from, and red arrows signify where GFP-actin was bleached and then incorporated into the treadmilling actin filaments at the leading edge. Scale bars, 5 μm. (B) Graph of the retrograde flow rate of GFP-actin in spillover protrusions measured from kymographs like those shown in (A). Bars represent the mean ± standard deviation (n = 33 protrusions from 3 independent experiments). (C) Still images from a time lapse series of micrographs of JR20s expressing GFP-actin that were plated as detailed in Fig. 1A and bleached throughout the entire protrusive area (left column) or cell body over the Fn attachment site (right column) every 60 frames. Yellow regions indicate areas measured for intensity traces shown in (D and E). Scale bar, 10 μm. (D) Trace of the normalized GFP-actin intensity over time in the region indicated by the yellow dotted outline in the bottom-left panel of (C). Red arrows mark photobleaching events of the entire protrusive spillover region of the cell. (E) Trace of the normalized GFP-actin intensity over time in the region indicated by the yellow dotted outline in the bottom-right panel of (C). Red arrows mark photobleaching events of the entire region of the cell that sits over the square Fn attachment cell-adhesive pattern. To see this figure in color, go online.

Raw single-plane images were copied from Fiji, and the Despeckle and Gaussian Blur (radius: 0.5 pixels) filters were applied in Photoshop (Adobe). Multiplane image stacks were viewed as 3D reconstructions in Imaris (Oxford Instruments, Abingdon, Oxfordshire, UK). Figures were assembled, arranged, and labeled in Illustrator (Adobe), and graphs were generated with Prism (GraphPad, San Diego, CA). Prism was also used to fit one-phase exponential curves to leading edge GFP-actin FRAP data after CytoD treatment, yielding estimated plateau and half-life values. Recovery curves that could not be fit with a one-phase exponential curve were disregarded as outliers (2 out of 17 cells assessed).

For full-span FRAP experiments that were compared with simulation predictions (Figs. 3 and 5), MATLAB (The MathWorks, Natick, MA) was used for image processing. Image stacks were background subtracted, segmented, and cropped. Crop dimensions were determined by first using the bleach region of interest coordinates (extracted from the image metadata) to identify the position of interest, and the crop width was set by subtracting ∼0.5 μm from each of the left and right edges. The crop length was set to include both the leading and adhesive edges. For each cropped image matrix in the time series, the intensity values were smoothed with a moving average smoothing filter applied across the length of the image (traversing the spillover protrusion from the leading edge to the adhesive edge). Then, for each column (y value) of each image matrix, the leading-edge position was estimated as the maximum value in the column, and positions x were aligned relative to that pixel. Pixel intensities for each column were normalized by the mean of the prebleach intensities of the leading-edge pixel and its 10 nearest neighbors (spanning ∼0.5 μm), averaged also temporally over the 5 images just before bleaching. Finally, a single fluorescence profile for each image was obtained by averaging across the aligned, normalized columns.

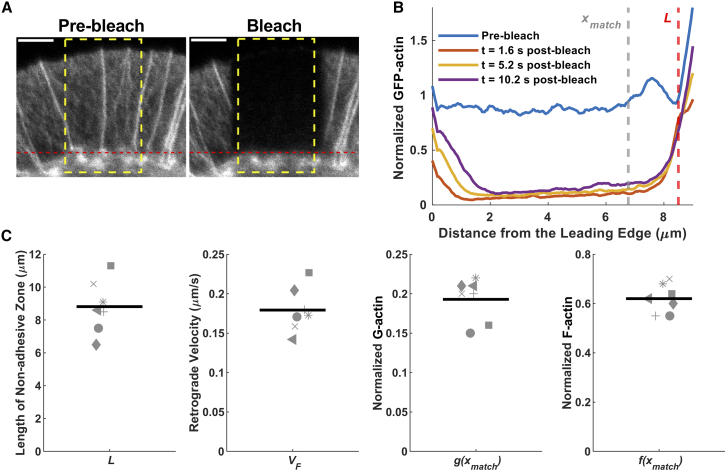
Figure 3.

Experimental inputs that constrain parameterization of quantitative models. (A) For a cohort of seven cells, the full span of the nonadhesive region was rapidly bleached. For each cell, the span of region L was estimated from the prebleach image (red dashed lines). The spatial profiles of GFP-actin fluorescence pre- and postbleach were averaged across most of the width of the bleached area (yellow dashed rectangle). F-Actin retrograde flow velocity, V_F, was estimated from the associated kymograph. Scale bar, 3 μm. (B) Plot of the spatial profiles of GFP-actin fluorescence pre- and postbleach. At a suitable distance from the leading edge, x = x_match, the normalized, prebleach fluorescence was attributed to the sum of F- and G-actin [f(x_match) + g(x_match)], whereas the normalized fluorescence ∼5 s postbleach was attributed to G-actin [g(x_match)]. (C) The four experimental estimates for each cell in the cohort (each with a unique symbol) are plotted. To see this figure in color, go online.

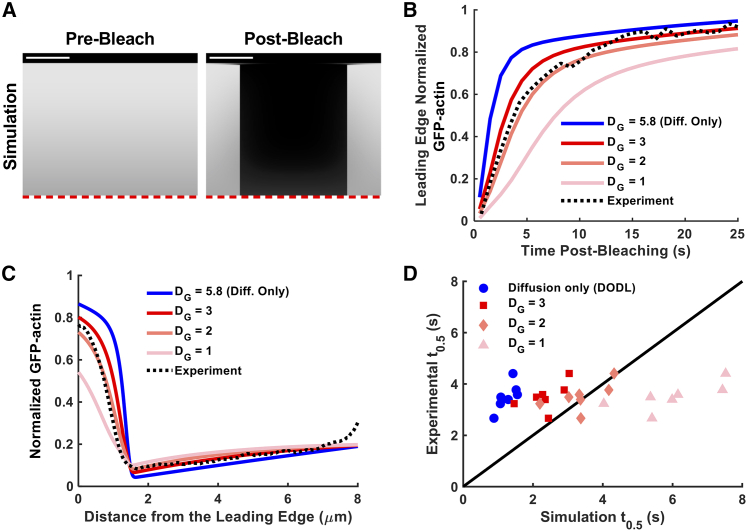
Figure 5.

Model-guided analysis of FRAP experiments consistently rules out anterograde transport of G-actin by diffusion only. (A) Two-dimensional model simulations were parameterized to yield a prebleach steady-state actin profile comparable with the corresponding movie. The spatiotemporal bleaching protocol was replicated as closely as possible accounting for bleach area, bleach duration, and associated equipment processing time. Scale bar, 3 μm. (B) Graph of the fluorescence recovery of GFP-actin at the leading edge for the representative movie shown in (A) along with the corresponding model predictions for different parameterizations of G-actin diffusion and anterograde velocity. (C) Graph of the spatial profile of GFP-actin spanning the spillover protrusion at time = 2^∗t_0.5 postphotobleaching for the representative movie shown in (A) and the corresponding model simulations. (D) Graph of the experimental t_0.5 values, for each of the movies in the cohort (n = 7), plotted against the corresponding predictions of t_0.5 values from simulations with different parameterizations of G-actin diffusion and anterograde velocity. To see this figure in color, go online.

Model of actin transport at steady state

Here, we examine a domain corresponding to the nonadhesive region, with spatial coordinate x (μm) measured from the leading edge and spatial coordinate y parallel to the leading edge; the z dimension, measured across the height of the domain, is considered thin, and so all concentrations are considered averages over the height. As with other continuum models of actin dynamics, and consistent with the analysis of fluorescence image data, F- and G-actin are homogenized into a single, fluid medium/phase. The basic model assumption is that the system is at (quasi-) steady state. The reader is referred to Text S1, section 1, in which we derive the general steady-state relationships, with full consideration of all states of G-, F-, and membrane-bound actin, and of direct versus polymerase-mediated F-actin elongation.

To model the steady-state conservation of F-actin (concentration F) and of G-actin (concentration G) at any point within the nonadhesive region, the y dimension may be considered semi-infinite, and so the steady-state problem is one-dimensional (1D). For F-actin, net retrograde transport is balanced by net disassembly, considering local rates of depolymerization, r_depol, and polymerization, r_pol. The forms of these rate terms will be specified, but for now we show what general results may be derived.

$$\frac{\partial F}{\partial t}=-\frac{\partial N_F}{\partial x}-r_{depol}+r_{pol}=0$$

$$N_F=V_{F}F$$

N_F(x) is the flux of F-actin, and V_F(x) is the retrograde flow velocity (which points in the positive x-direction). For G-actin,

$$\frac{\partial G}{\partial t}=-\frac{\partial N_G}{\partial x}+r_{depol}-r_{pol}=0$$

N_G(x) is the flux of F-actin. With conservation of total actin in 1D, we obtain flux matching conditions.

$${N_F|}_{x=0}=-{N_G|}_{x=0}=N_{pol}$$

$$N_F\left(x\right)=-N_G\left(x\right)=N\left(x\right)$$

Except where noted otherwise, we assume that all states of G-actin have the same transport parameters, with

$$N_G=-D_G\frac{dG}{dx}-V_{G}G$$

D_G(x) is the effective diffusivity of G-actin in the domain, and V_G(x) is the anterograde velocity (which points in the negative x-direction); both are potentially position dependent.

To proceed further, we need to assume the forms of V_F(x), r_depol(x), r_pol(x), D_G(x), and V_G(x). Supported by empirical measurements for this system, we take

$$V_F\left(x\right)\approx \mathrm{c}\mathrm{o}\mathrm{n}\mathrm{s}\mathrm{t}\mathrm{a}\mathrm{n}\mathrm{t}$$

And, consistent with previous modeling work (17,18,19,20), we considered first-order turnover of F-actin,

$$r_{depol}\left(x\right)=k_{depol}F\left(x\right)$$

After photobleaching, we do not observe structured recovery of fluorescence throughout the bleached region, and therefore for our system we take

$$r_{pol}\approx 0$$

With these specifications, and the boundary condition F(0) = F₀

$$F\left(x\right)=F_0\exp \left(-\frac{k_{depol}}{V_F}x\right)$$

$$N\left(x\right)=D_G\frac{dG}{dx}+V_{G}G=V_{F}F$$

As for the G-actin transport parameters, we considered two distinct cases. In the first, we assume that D_G and V_G are constants, with values D_G(c) and V_G(c), respectively. With the boundary condition G(0) = G₀, the solution in this case is

$$G\left(x\right)=\alpha F_0\exp \left(-\frac{k_{depol}}{V_F}x\right)+\left(G_0-\alpha F_0\right)\exp \left(-\frac{V_{G\left(c\right)}}{D_{G\left(c\right)}}x\right)\text{;}$$

$$\alpha =\frac{V_F}{V_{G\left(c\right)}-D_{G\left(c\right)}\frac{k_{depol}}{V_F}}$$

In the limit of V_G(c) = 0, the equation above reduces to

$$G\left(x\right)=G_0+\frac{{V_F}^2{F}_0}{k_{depol}{D}_{G\left(c\right)}}\left[1-\exp \left(-\frac{k_{depol}}{V_F}x\right)\right]$$

An even more specific limit, referred to as diffusion-only, diffusion-limited (DODL) takes the above equation with G₀ = 0 and names D_G(c) as D_G,DODL(c).

The second case we examined was DODL but with nonconstant diffusivity, D_G,DODL(x). With the assumption that D_G,DODL(x) is a smoothly increasing or decreasing function (G-actin diffusion is slower or faster as molecules approach the leading edge),

$$D_{G,DODL}\left(x\right)=D_{G,0}+\left(D_{G,\infty }-D_{G,0}\right)\left(1-e^{-x/\lambda L}\right)$$

Here, D_G,0 and D_G,∞ are the values of D_G,DODL(x) at and far from the leading edge, respectively, L is the measured span of the nonadhesive region, and dimensionless λ characterizes the slope of the function. In the analyses performed, λ = 0.3 was used.

Model parameterization from experimental inputs

The F-actin retrograde flow velocity, V_F, was estimated from the experimental kymograph as described above. Background-subtracted fluorescence intensities were expressed as a fraction of the total GFP-actin intensity at the leading edge, prebleach. Accordingly, in the model, normalized concentrations are

$$f\left(x\right)=\frac{F\left(x\right)}{F_0+G_0};g\left(x\right)=\frac{G\left(x\right)}{F_0+G_0}$$

To determine sets of model parameter values consistent with a particular FRAP experiment, the normalized pre- and postbleach fluorescence intensities were quantified some distance x_match from the leading edge (close to the interface between the nonadhesive and adhesive zones). The postbleach intensity was measured a short time (∼5–10 s) after bleaching such that the G-actin fluorescence had stabilized. Thus, f(x_match) and g(x_match) were estimated. Based on the estimated values of V_F and f(x_match), the value of k_depol was estimated. The value of D_G,DODL(c) was estimated as follows.

$$D_{G,DODL\left(c\right)}=\frac{V_{F}L}{g\left(x_{match}\right)}\left[\frac{1-f\left(x_{match}\right)}{-\ln f\left(x_{match}\right)}\right]$$

To identify combinations of D_G(c), V_G(c), and g₀ as scenarios consistent with estimable quantities, values of D_G(c) and g₀ were assumed, and the value of V_G(c) was determined by matching the estimated value of g(x_match). For the case of nonconstant D_G,DODL(x), the value of D_G,0 was assumed, and the value of D_G,∞ was determined by matching the estimated value of g(x_match).

FRAP predictions

We refer to f_un(x,y,t) and g_un(x,y,t) as the normalized concentrations of unbleached (fluorescent) F-actin and G-actin, respectively. They are initialized according to the steady-state f(x) and g(x) profiles established in the previous sections. Contained within the domain, there is a defined region in which bleaching occurs with first-order rate constant k_bleach(x,y,t); its time dependence reflects that bleaching is turned on and off at specified times. The conservation equation and boundary condition for f_un are

$$\frac{\partial f_{un}}{\partial t}=-k_{bleach}{f}_{un}-V_F\frac{\partial f_{un}}{\partial x}-k_{depol}{f}_{un}\text{;}$$

$$f_{un}\left(0,y,t\right)=\left[\frac{f\left(0\right)}{g\left(0\right)}\right]g_{un}\left(0,y,t\right)$$

The boundary condition effectively assumes that actin polymerization at the leading edge is in pseudoequilibrium with the local G-actin concentration; this is to say that all G-actin at the leading edge is equally polymerizable, and that the lifetimes of G-actin interactions with polymerases, mediated by profilin, are short. The latter assumption is readily justified, considering that measured off-rates of profilin-mediated interactions are quite fast (21,22), and measured elongation rates for the processive polymerases are ∼10–1000 monomers/s (8,23) (further analysis provided in Text S1, section 2). The singularity introduced when g(0) = 0 is avoided by using a small but nonzero value. For g_un,

$$\frac{\partial g_{un}}{\partial t}=-k_{bleach}{g}_{un}+\nabla ·\left(D_G\nabla g_{un}\right)+V_G\frac{\partial g_{un}}{\partial x}+k_{depol}{f}_{un}\text{;}$$

$${\left(D_G\frac{\partial g_{un}}{\partial x}+V_G{g}_{un}\right)|}_{x=0}=V_F\left[\frac{f\left(0\right)}{g\left(0\right)}\right]g_{un}\left(0,y,t\right)\text{;}$$

$$g_{un}\left(L,y,t\right)=g\left(L\right)\text{;}$$

$${\frac{\partial g_{un}}{\partial y}|}_{y=0}={\frac{\partial g_{un}}{\partial y}|}_{y=W}=0$$

The boundary condition at x = L, the interface between nonadhesive and adhesive regions, assumes a constant value, calculated from the prebleach steady state equation for g(x). The justification for this is that the rear of the bleach zone backs up to the bulk of the cell volume and to a concentrated depot of disassembling F-actin. This assumption is critically assessed through ancillary simulations (Text S1, section 3 and Fig. S1).

Models with two G-actin species

In the models described above, states of G-actin are lumped together with respect to both transport properties and leading-edge polymerizability. To address the possibilities of diffusion-only scenarios with those assumptions relaxed, we formulated models with two G-actin species. The steady-state and FRAP equations for these models are presented and analyzed in Text S1, sections 4 and 5.

Model implementation

FRAP protocols were simulated by solving the partial differential equations in the VCell software environment (24), with the fully implicit finite volume (variable time step) solver. Not shown in the conservation equation for f_un is a very slow diffusion term, added to promote numerical stability (D_F = 1 × 10⁻⁵ μm²/s), along with the arbitrary boundary condition, f_un(L,y,t) = f(L). For preliminary, 1D simulations, the length of the spillover region was 10 μm, and the full-bleach FRAP protocol was simulated with a bleaching rate constant of 200 s⁻¹ and a duration of 0.1 s, comparable with experiments. For 2D simulations matched to experiments, the rectangular geometry was 20 μm wide, and the length was chosen to match the span of the particular nonadhesive region. The bleached region and bleach duration were parameterized to match the experimental bleaching protocol of each experiment, and the simulation results were analyzed in the same fashion as the experiment. To mitigate “numerical diffusion,” which arises when transport of some species is dominated by advection (25), fine meshes were employed, and control simulations confirmed that the contribution of numerical diffusion was acceptably low. For 1D simulations, we used a mesh size of Δx = 5 × 10⁻⁵ μm and a maximum time step of 0.1 s. For 2D simulations, we elected to mesh the geometry with Δx ≤ 0.0028 μm and Δy = 0.1 μm, which was sufficient to ensure a second-order accurate discretization for G-actin in our cohort of simulations. The primary simulations may be accessed in VCell under user name, ra_mb_jb_jmh.

Results

A simplified system to interrogate actin dynamics in protrusions

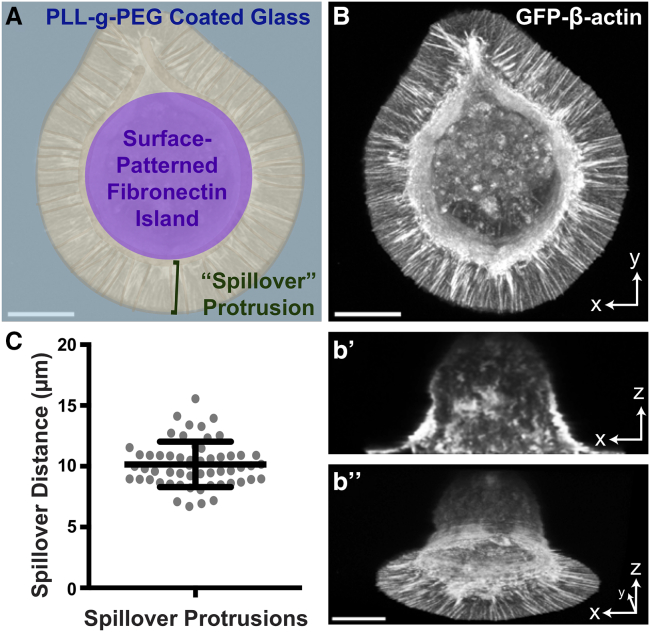
To examine the dynamics of G-actin diffusion and F-actin retrograde flow in cell protrusions that adopt reproducible shapes, we used surface micropatterning of Fn islands on microscope cover glasses that are surrounded by nonadhesive PLL-g-PEG. A variety of shapes were tested, including squares with 30 μm edges, triangles with 30 μm edges, and circles with 30 μm diameters. On shapes of this size, JR20 mouse dermal fibroblasts (26) attach to and fill the Fn patterns. Interestingly, these cells make protrusions of a relatively uniform radial length that “spill over” the edge of the original pattern (Fig. 1 A). These spillover protrusions are flat, with a nearly uniform thickness, and they are filled with a mixture of bundled F-actin microspikes and actin filament mesh as visualized by expression of GFP-actin (Fig. 1 B). Measurements of the spillover protrusion distance from the adhesive boundary show an average of about 10 μm, with a standard deviation of less than 2 μm (Fig. 1 C). Thus, spillover protrusions are highly consistent from cell to cell despite apparent heterogeneity in the cell population when plated on evenly coated Fn substrates. This provides us with large, relatively uniform regions to monitor actin polymerization and recycling dynamics.

Figure 1.

Fibroblasts extend flat, roughly uniform, and steady-state protrusions over PLL-g-PEG from surface-patterned Fn attachment sites. (A) Schematic of cell-plating conditions for the analysis of actin dynamics in steady-state “spillover” protrusions over PLL-g-PEG-coated glass surfaces from surface patterned Fn attachment sites. (B) GFP-actin stably expressed in JR20 cells (mouse dermal fibroblasts) that has been plated as schematized in (A) was visualized and captured in a series of images along the Z-plane, displayed as a maximum intensity projection. A cross section from the Z-stack projected in (B) is shown in (b’), and a pseudo side view of a 3D reconstruction is shown in (b”). Scale bars, 10 μm. (C) Graph of the approximate average cell protrusion distance outward from the edge of micropatterned Fn shapes in JR20s stably expressing GFP-actin. Bars represent the mean ± standard deviation (n = 56 protrusions from 3 independent experiments). To see this figure in color, go online.

Monitoring spillover protrusions over time show that they are quite stable, with very little fluctuation in protrusion distance and infrequent retraction events (Fig. 2 A). To assess various dynamic behaviors of GFP-actin, we bleached different regions of the spillover protrusions, either at discrete regions behind the leading edge or sections that span the full distance of the spillover, from the leading edge to the outer boundary of the Fn attachment site (Fig. 2 A; Videos S1 and S2). This allows for the visualization and measurement of the retrograde flow rates of the treadmilling actin network, which, under these circumstances, averages 11.4 μm/min (Fig. 2 B). This actin polymerization rate is considerably faster than the 3.6 μm/min observed when this cell line is plated on evenly coated 10 μg/mL Fn-coated glass (26), suggesting that there is significantly less resistance to the retrograde flow here, or clutching, and that the polymerization rate may be nearing the maximum rate for these cells. An additional, telling feature of these bleaching experiments is the almost immediate appearance of a thin, dark band in the F-actin network. This band is both preceded and followed by unbleached actin populations (Fig. 2 A, red arrows), indicating that bleached G-actin is rapidly incorporated in F-actin arrays at the leading edge.

Video S1. Supplemental movie for Fig. 2A

Spillover protrusion labeled with GFP-actin bleached at a discrete region between the leading edge and the fibronectin attachment zone. Scale bar, 5 μm, and time stamp is in MM:SS format.

Video S2. Supplemental movie for Fig. 2A

Spillover protrusion labeled with GFP-actin bleached in a wide stripe running all the way from the leading edge to the fibronectin attachment zone. Scale bar, 5 μm, and time stamp is in MM:SS format.

In addition to bleaching discrete regions of spillover protrusions, we also bleached all the GFP-actin either contained in the spillover protrusion or in the cell body above the patterned Fn adhesive zone (Fig. 2 C; Videos S3 and S4). Monitoring the intensity of GFP-actin along the furthest edge of the spillover protrusion over time while repeatedly bleaching either the spillover or adhesive zone show that there is strong recovery when the spillover is bleached, with a loss of roughly 10–15% of the maximum intensity per each bleaching event (Fig. 2 D). However, when the cell body over the adhesive zone is bleached instead, there is a continuous, dramatic decrease in intensity at the periphery of the spillover protrusion, with the mean intensity trending downward after each bleach and shallowing out around a 30–40% loss with each bleach (Fig. 2 E). Thus, it appears as if most of the actin being incorporated into the F-actin network of the spillover protrusion at any given time originates from the cell body rather than the spillover being a more self-contained structure with significant local recycling. This characterization is similar to what has been reported for cells plated under more standard conditions (12), but quite different from characteristics ascribed to other cellular contexts for which local actin polymerization is considered substantial (27,28).

Video S3. Supplemental movie for Fig. 2C

JR20 Fibroblast expressing GFP-actin plated on a triangle micropatterned Fn island and bleached all throughout the spillover protrusion zone. Scale bar, 10 μm, and time stamp is in MM:SS format.

Video S4. Supplemental movie for Fig. 2C

JR20 Fibroblast expressing GFP-actin plated on a square micropatterned Fn island and bleached all throughout the cell body at and above the Fn attachment site. Scale bar, 10 μm, and time stamp is in MM:SS format.

Experimental inputs constrain a model of steady-state actin dynamics and FRAP predictions

The representative kymographs shown in Fig. 2 A and the associated movies show several consistent and telling features of our system.

• 1)Averaging out the small fluctuations, the polymerization and depolymerization of F-actin in the protrusion are approximately at steady state.
• 2)Retrograde flow of F-actin exhibits constant velocity across the nonadhesive region.
• 3)FRAP near the back end of the bleached area approaches a plateau within ∼5 s, to a fluorescence intensity that is much lower than the prebleach intensity and lacking discernible structure/texture. We therefore attribute this early recovery to the restoration of unbleached G-actin into the region, with no evidence of local actin polymerization.
• 4)The F-actin structures in the nonadhesive region exhibit variable but consistently modest decreases in intensity (depolymerization) as they flow from the leading edge. Once they arrive at the interface with the adhesive region, the F-actin is compacted in a dense structure, where most of its disassembly must occur.

For each of seven cells that were photobleached in a consistent manner, with the bleached region spanning the spillover protrusion (Fig. 3 A), we estimated four quantities: the span of the nonadhesive region, L; the constant velocity of F-actin retrograde flow, V_F; and the intensities attributable to G- and F-actin at a distance x_match from the leading edge, close to the back of the bleached region (g(x_match) and f(x_match), respectively), normalized by the prebleach intensity at the leading edge (Fig. 3 B). Among the cells in the cohort, the estimated values of those quantities are reasonably consistent (Fig. 3 C).

The four experimental inputs constrain the parameterization of a basic mathematical model of actin dynamics at steady state (materials and methods and Fig. 4 A), as manifest prebleach. The steady-state nature of the system permits dramatic simplification of the model, such that most molecular details related to actin regulation do not need to be specified or assumed (materials and methods and Text S1). With just one other key assumption—that all G-actin at the leading edge is equally polymerizable—any set of G-actin transport parameters that matches the measurable constraints yields a prediction of the dynamics observed during any FRAP protocol, which can be compared with the corresponding experiment. Principally, we sought to determine whether or not diffusion alone can explain the flux of G-actin. As an alternative, we considered the addition of anterograde, vectorial transport of G-actin to demonstrate how the recovery kinetics are affected (Fig. 4 A). We also considered model variations with certain assumptions relaxed.

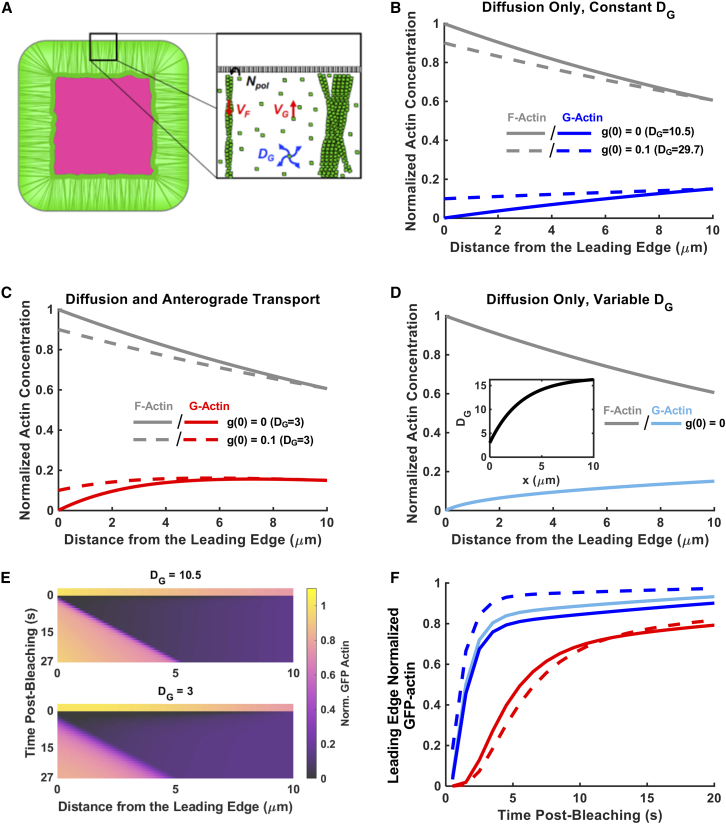
Figure 4.

Model predictions of FRAP experiments demonstrate that G-actin transport to the leading edge by diffusion only is distinguishable from transport aided by anterograde drift. (A) Model schematic illustrating G-actin transport and polymerization in the “spillover” protrusion. (B–D) Spatial profiles of actin species (normalized by the total actin concentration at the leading edge) in the spillover protrusion at steady state for transport of G-actin to the leading edge by diffusion-only with constant diffusivity (B), diffusion (constant diffusivity) plus constant anterograde velocity (C), and diffusion-only with variable diffusivity that increases from the leading edge (D_G(0) = 3) rearward (D). (E) Kymographs of FRAP simulations where the entire span of the spillover is bleached for the constant diffusion-only (top) and diffusion aided by anterograde drift (bottom) cases. The G-actin concentration at the leading edge is ∼0 for the simulations shown. (F) Predictions of leading-edge FRAP of GFP-actin, normalized to the GFP-actin concentration at the leading edge at steady state, after a simulated full-bleach protocol. Graphs show simulations for normalized G-actin concentration at the leading edge equal to ∼0 (solid curves) and 0.1 (dashed curves). Units for D_G are μm²/s. To see this figure in color, go online.

To develop intuition about this modeling approach and its predictions, simple 1D model simulations were performed. As a baseline scenario, with which others will be compared, we considered the hypothetical assumptions that G-actin transport is by diffusion only and that the rate of F-actin polymerization is limited by the diffusion of G-actin (g(0) = 0). Hereafter, we refer to this pair of assumptions as diffusion-only, diffusion-limited (DODL). If we further assume for now that the G-actin diffusivity is constant, and taking typical, measurable values for our experimental system (L = 10 μm; V_F = 0.2 μm/s; g(L) = 0.15; f(L) = 0.60), the corresponding value of the G-actin diffusivity, D_G,DODL(c), would need to be equal to 10.5 μm²/s to match the flux of F-actin polymerization at the leading edge (Fig. 4 B). An alternative scenario is to assume diffusion only, with constant diffusivity D_G(c), but allow nonzero polymerizable G-actin concentration at the leading edge (g(0) > 0). For example, this would be the case if capture of polymerizable G-actin were rate-limiting. Given the same measurable constraints, the estimated value of D_G(c) for such a scenario is always greater than D_G,DODL(c). For example, with an assumption that g(0) = 0.1, the value of the diffusivity D_G(c) would need to be 29.7 μm²/s to match the flux (Fig. 4 B).

Adding constant anterograde velocity (agnostic of mechanism) as another contribution to G-actin transport, under the same experimental constraints, allows the same flux to be achieved with a lower G-actin diffusivity (Fig. 4 C). For the same measurable inputs as above, transport-limited polymerization (g(0) = 0), and a diffusivity value of D_G(c) = 3 μm²/s, a G-actin anterograde velocity of V_G(c) = 0.89 μm/s is required, and this estimate only increases by 0.2% when g(0) = 0.1 (Fig. 4 C). This is because advective flux does not depend on the concentration gradient, and, in these scenarios, advection contributes much more than diffusion throughout most of the domain (Péclet number Pe ≈ 3). We also considered the possibility of DODL with position-dependent diffusivity, D_G,DODL(x). With D_G,DODL(0) set to 3 μm²/s and the other parameters set to match experimental inputs, the G-actin profile is similar to the case of constant diffusivity plus advection (Fig. 4 D).

With the model parameterized, one can predict associated outcomes of FRAP experiments. With regard to modeling, the simplest protocol to interpret is the photobleaching of the entire nonadhesive zone. The corresponding 1D model was used to predict the recovery of unbleached actin for each of the five scenarios outlined above (Figs. 4 E, S1, and S2). The simulations predict distinct rates of recovery at the leading edge, assessed in terms of t_0.5, defined as the postbleach time at which leading-edge actin fluorescence had recovered to half of its prebleach value (Fig. 4 F). For our five example scenarios, the predicted t_0.5 values are: DODL (constant diffusivity): 1.7 s; diffusion-only, g(0) = 0.1: 1.2 s; D_G(c) = 3 μm²/s, g(0) = 0: 5.6 s; D_G(c) = 3 μm²/s, g(0) = 0.1: 6.6 s; and DODL (variable diffusivity) with D_G,DODL(0) = 3 μm²/s: 1.5 s. For a given flux, reducing the diffusivity by allowing advection yields substantially slower recovery. In contrast, allowing variable diffusivity only slightly affects leading-edge recovery relative to the constant diffusivity case; this was true for other variable-diffusivity scenarios with either increasing or decreasing D_G,DODL(x) (Fig. S3). Analysis of the DODL scenarios, based on the leading eigenvalue of the related Dirichlet problem (29), explains this finding; a recent mathematical analysis of the variable-diffusivity scenario (30) was key to helping us understand this result (see also Text S1, section 6).

As an addendum to this analysis, we also examined diffusion-only scenarios with two distinct G-actin states, relaxing the assumptions that G-actin states may be lumped with respect to transport properties and polymerizability (Text S1, sections 4 and 5). In one such scenario, we considered the possibility that a slowly diffusing pool of polymerizable actin is fed by rapid and spatially focused conversion from a fast-diffusing state, rather than by vectorial transport. Although such a scheme successfully flattens the steady-state G-actin gradient far from the leading edge, leading-edge FRAP is comparable with that of the simple DODL model (Fig. S4). In a second scenario, we considered that the two G-actin species have equal diffusivities, but conversion from a nonpolymerizing to a polymerizable state occurs at a modest frequency. Nevertheless, leading-edge FRAP is likewise comparable with that of the simple DODL model (Fig. S5).

Analysis of FRAP experiments consistently rules out G-actin transport by diffusion only

In the previous section, we showed how modeling can be used to test the common assumption that G-actin is transported by diffusion only. If the t_0.5 of leading-edge FRAP substantially exceeds that of the DODL prediction, constrained by flux-defining inputs from the particular experiment, it indicates that another transport mechanism is assisting diffusion. Here, we show the results of this test applied to the aforementioned cohort of seven cells (Fig. 5).

For each cell in the cohort, a rectangular zone containing a section of the leading-edge contour was selected and rapidly bleached. Experimental inputs were estimated to yield the prebleach, steady-state actin profile; this served as the initial condition for 2D simulations in which the position and dimensions of the bleach zone and the bleaching time were recreated as precisely as possible (Fig. 5 A). Scenarios corresponding to DODL (constant diffusivity) and various combinations of constant G-actin diffusivity and anterograde flow velocity were simulated, and the simulations were analyzed in the same fashion as for the corresponding experiment to construct leading-edge recovery profiles (Fig. 5 B). The representative cell showed recovery (t_0.5 = 3.8 s) that was ∼2.5-fold slower than the DODL (constant diffusivity) scenario; the recovery was reasonably consistent with a lower constant diffusivity and advection added (D_G(c) = 2 μm²/s and V_G(c) = 0.55 μm/s). For this cell, comparison of the total actin intensity profiles, quantified at a postbleach time approximately equal to 2^∗t_0.5, likewise shows the best agreement with the D_G(c) = 2 μm²/s scenario (Fig. 5 C). This finding was consistent for all of the cells in the cohort (Fig. 5 D). The ratios of t_0.5 (experimental) to t_0.5 (DODL simulation) ranged from 2.3 to 3.2, and spatial profiles were also compared (Fig. S6). We conclude that the assumption that G-actin transport is by diffusion alone grossly and consistently fails to predict the arrival of unbleached G-actin in our system.

Whether after photobleaching the full or partial span of the nonadhesive region, we saw rapid incorporation of bleached actin into F-actin, manifest as a thin, dark band extending out beyond the lateral boundaries of the bleached area (Fig. 2 A). Simulated FRAP predictions are qualitatively consistent with those observations, and they indicate certain quantitative differences between DODL versus diffusion plus advection scenarios (Fig. S7); however, various methods devised to quantify those features from experimental time series proved to be insufficiently robust.

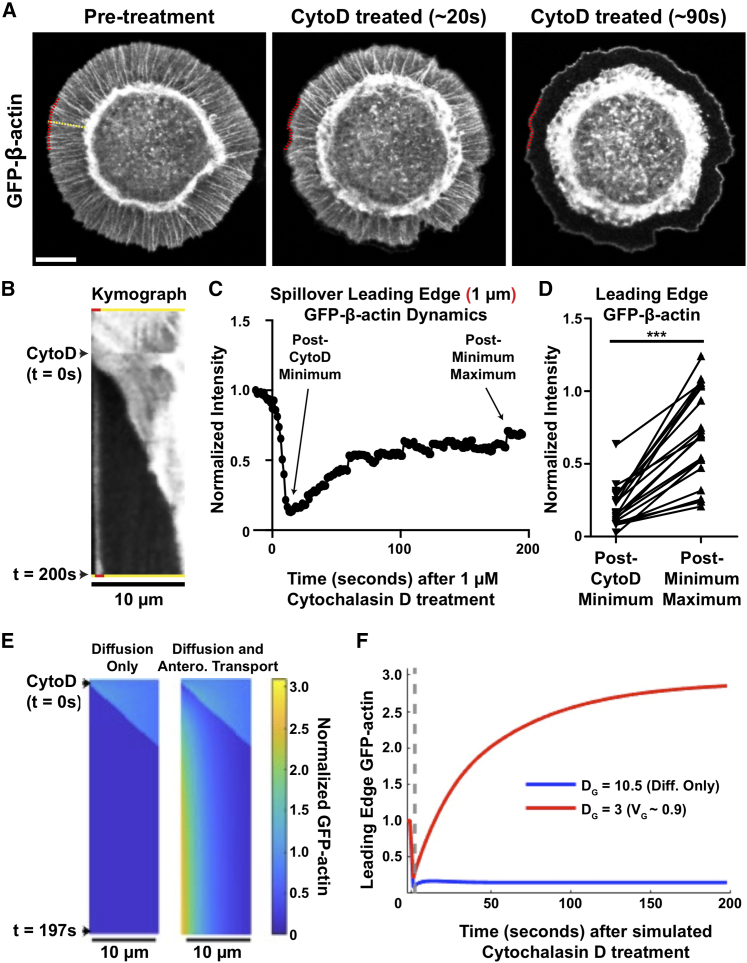
Inhibition of actin polymerization elicits accumulation of G-actin at the leading edge

Our modeling efforts suggest a possible vectorial transport mechanism contributing to the supply of actin monomers for actin polymerization at the leading edge. Thus, one might predict an accumulation or enrichment of G-actin at the leading edge upon the stalling of F-actin polymerization in our experimental model. To test this prediction, we treated cells plated on the Fn micropatterns with CytoD (1 μM) to abruptly halt F-actin polymerization by blocking barbed end elongation, and we monitored the changes in the GFP-actin intensity in the spillover region. CytoD treatment stalled F-actin polymerization, resulting in withdrawal and condensation of the F-actin network, leading to a large drop in GFP-actin intensity at the leading edge; shortly thereafter, a thin (∼1 μm) band of GFP-actin signal appeared there (Fig. 6 A; Video S5). Kymographs show that this signal was stationary with respect to the leading edge and increased in intensity with time over the course of ∼1 min (Fig. 6, B and C). Every treated cell showed such recovery of the leading-edge intensity (Fig. 6 D). When leading-edge regions of CytoD-treated cells were photobleached, FRAP was near-complete (∼85% mean mobile fraction), with kinetics that were consistent with the prior appearance of the GFP-actin band (∼50 s mean half-time) (Fig. S8). The CytoD-induced effects were simulated, under DODL and diffusion plus vectorial transport scenarios, by assuming that the fluxes at the leading edge suddenly vanish. Consistent with the experimental observations, G-actin is predicted to accumulate at the boundary, with a timescale of ∼1 min, when advection is included; in contrast, such a gradient of G-actin cannot be established if its transport is by diffusion only (Fig. 6, E and F).

Figure 6.

GFP-actin accumulates at the very leading edge of spillover protrusions upon inhibition of F-actin polymerization. (A) Still images of a JR20 Fibroblast expressing GFP-actin and plated on micropatterned Fn island as detailed in Fig. 1A before and after treatment with 1 μM cytochalasin D (CytoD). The dashed yellow line is representative of a region kymographs were generated from, and the dashed red line marks the ∼1 μm distal-most region of spillover protrusion that intensity measurements were taken from. Scale bar, 10 μm. (B) Kymograph of a spillover protrusion labeled with GFP-actin in the cell shown in (A), with the distal-most region marked by the red rectangles at the top and bottom of the kymograph. (C) Quantification of spillover leading edge GFP-actin intensity before and after 1 μM CytoD treatment of the cell shown in (A) normalized to the intensity ∼13 s pretreatment (10 frames). (D) Minimum GFP-actin intensity at the edge of spillover protrusions after 1 μM CytoD treatment with a connecting line to the maximum GFP-actin intensity that accumulates in the same roughly 10 × 1 μm region a short time afterward. Each pair of measurements comes from a single cell plated on a unique micropatterned coverslip (n = 20 cells across 5 independent experiments). p < 0.0001 (paired t-test). (E and F) In 1D simulations parameterized as in Fig. 4, B and C, with g(0) ≈ 0, CytoD treatment was mimicked by switching the leading-edge boundary conditions to zero flux. Simulated kymographs (E) and leading-edge kinetics (F) of GFP-actin intensity are shown. To see this figure in color, go online.

Video S5. Supplemental movie for Fig. 6A

JR20 Fibroblast expressing GFP-actin plated on a circle micropatterned Fn island and treated with 1 μM between frames marked with 00:36 and 00:37. Scale bar, 10 μm and time stamp is in MM:SS format (there was a ∼1–20 s pause between 00:36 and 00:37 for drug wash in, which is not shown/accounted for in the time stamp).

Discussion

Cell migration is a dynamic process involving both biochemical (signal transduction and actin dynamics) and mechanical (cell adhesion/traction, membrane protrusion, and contractility) subprocesses. Leading-edge motility and cell shape changes are stochastic and unpredictable, reflecting nonlinearities that have been attributed to positive and negative feedback loops and excitability (26,31,32,33,34). This makes cell migration a rich yet challenging phenomenon to study. To reduce complexity, an informative approach to study actin dynamics in particular has been to isolate the effects of certain interactions among purified proteins. The hope is that the knowledge gained from such careful measurements may be stitched together in a conceptual and mathematical modeling framework (32,33,34).

Here, we describe an experimental system that presents a compromise between observing dynamics as they occur in cells and measuring kinetics in a simplified system. By limiting the area of adhesive contact between a cell and the substratum, the cell’s lamellipodium is forced to spill over into the nonadhesive area, with a morphology that is remarkably steady and consistent in dimensions. In this region, actin polymerization is ∼3 times faster than measured in the same cell line when randomly migrating, which might be attributed to the lack of adhesion complexes that would otherwise clutch the network and resist/dissipate retrograde flow (35), and to reduced mechanical load on elongating barbed ends at the approximately stationary boundary. Accordingly, the retrograde flow velocity is approximately constant as F-actin travels from the leading edge to the nonadhesive/adhesive interface; along the way, actin depolymerization is modest, and so the bulk of the F-actin is disassembled at the interface, where it is seized by myosin II. Therefore, most actin monomers must traverse the full span of the nonadhesive region before reincorporation into F-actin.

The combination of fast actin polymerization and low G-/F-actin ratio per volume within the nonadhesive region led us to question whether or not the required G-actin flux is achieved by diffusion alone in our system. Within the thin lamellipodial protrusion, the F-actin mesh impedes macromolecular transport, with excluded volume and nonspecific interaction effects contributing (36,37,38). Indeed, our robust estimates of the minimum G-actin diffusivity required are at the high end of the range of published estimates (∼1–10 μm²/s) (11,12,13,39,40,41,42,43). Through design, analysis, and simulation of FRAP experiments, we found that the assumption that G-actin is transported by diffusion only grossly and consistently fails to predict recovery. This was the case even when G-actin diffusivity was allowed to vary with position, potentially due to gradients of F-actin mesh porosity and/or of G-actin interactions (both specific and nonspecific), or when two states of G-actin with different diffusivities or propensities to polymerize were simulated. By comparison, a G-actin transport model with diffusivity ≈2 μm²/s and constant anterograde velocity less than 1 μm/s yielded good agreement. To explain this, we consider that, at early times postbleach, there is a steep, positive gradient of unbleached G-actin and an almost-as-steep, negative gradient of bleached G-actin in the x-direction. These sum to maintain the relatively modest, positive gradient of G-actin overall. Therefore, at early times postbleach, the flux of unbleached G-actin is much greater than at steady state and dominated by diffusion. Slowing down the diffusion is the key to slowing down FRAP, while adding anterograde, vectorial transport allows the steady-state flux to be achieved.

While we are currently not in a position to speculate on the precise nature of vectorial G-actin transport, related discussions in the literature have centered on motor-driven transport and bulk fluid flow as ways to enhance G-actin transport in lamellipodia. With regard to the action of motors, anterograde transport of G-actin has been attributed to direct interaction with Myo1c (14), but it is presently unclear whether this interaction can account for the inferred magnitude of the velocity. On the other hand, the bulk fluid flow concept is related to the hypothesis that actin disassembly by myosin II can generate a significant gradient in osmotic pressure (13,44,45,46), with water leaking out of the cell courtesy of aquaporin channels (46,47,48). The anterograde velocity cited above corresponds to an estimated, overall volumetric flow rate of ∼10 fL/s. With an estimated rate of ∼10⁹ water molecules per channel per second, such a flow rate might be achieved by only a few hundred aquaporin molecules.

Acute disruption of F-actin barbed end elongation by CytoD led to the expected retrograde withdrawal of the F-actin network from the spillover protrusion, but also later led to the appearance of a stationary band of GFP-actin intensity at the extreme leading edge of the protrusion. We postulate that this GFP-actin fluorescence represents G-actin that has accumulated at the leading edge in a futile manner, without barbed ends on which to polymerize. While this result is consistent with vectorial transport contributing to G-actin recycling, it is important to interpret this result carefully. For example, treatment with CytoD causes substantial rearrangements of all F-actin networks in the cell, and this could disrupt or alter some of the aforementioned mechanisms of bulk transport, such as myosin-based contractility. Another possibility worth considering is that stalled actin polymerases such as formins or Ena/VASP proteins may concentrate monomeric GFP-actin at the leading edge upon CytoD treatment. Future experiments and modeling will tackle these and other possibilities.

To the extent that bulk fluid flow contributes significantly to G-actin transport, two conjectures arise. The first is that asymmetries of the cell geometry and of the osmotic pressure would render the assumption of a constant, unidirectional flow implausible. Complex, multidirectional flow should be expected. The second is that the constrained adhesion drives the enrichment of actomyosin at the nonadhesive/adhesive interface that, in turn, drives bulk flow. If so, it would be fair to ask how such an osmotic pressure gradient might differ across experimental contexts, depending on the spatial organization of myosin II activity. More generally, the broad variety of cell migration/actin-based motility phenotypes displayed by different cell types presents an inherent limitation of any experimental system in this field.

Related to the above, we also acknowledge certain limitations of the mathematical modeling and model-based analysis presented here. The model used to directly compare with experimental data invokes certain simplifying assumptions, which were explored through ancillary simulations and specific variations of the model. We critically evaluated assumptions concerning the boundary conditions used for FRAP predictions and considered two distinct pools of G-actin (12). Although none of these variations substantially alter the prediction of leading-edge FRAP when G-actin transport is by diffusion only, refinements of the model should be considered when additional evidence or the experimental context warrants. Another model assumption, based on experimental observations in fibroblasts, was to neglect local reincorporation of actin into filaments at sites other than the leading edge; this is noteworthy because it stands in direct contrast with indications from other studies (27,28,43). Although local polymerization no doubt occurs at some rate in our system, the observed patterns of FRAP in the bleached region support our assumption. If actin were somehow reincorporated at a substantial rate but without perceptible image texture, the consequence would be an overestimation of the relative G-actin concentration distal from the leading edge; some of the measured intensity attributed to G-actin would be in the form of F-actin. In that case, the value of the diffusivity that matches the required steady-state flux for a diffusion-only scenario would need to be higher, contributing to a faster leading-edge FRAP.

The experimental and modeling framework established here can be used to evaluate and make quantitative predictions for future experimental approaches, as well as to explore other biological questions concerning actin network dynamics. Previous studies have used photoconvertible actin probes (12) or tagged, but nonpolymerizable actin mutant proteins (14) to test the mechanisms of G-actin transport, and it will be useful in future work to compare those approaches with the FRAP approach in our system. The spillover protrusion system is ripe to explore other aspects of actin filament network dynamics such as the relative contributions of branched versus unbranched actin polymerization, the role of NMII in network turnover, and the roles of profilin and other actin monomer binding proteins in transport and polymerization/depolymerization.

Author contributions

R.A. designed research, performed research, analyzed data, and wrote and edited the paper. M.T.B. designed research, performed research, analyzed data, and wrote and edited the paper. J.E.B. was responsible for conceptualization, research design, supervision, funding acquisition, and wrote and edited the paper. J.M.H. was responsible for conceptualization, research design, data analysis, supervision, funding acquisition, and wrote and edited the paper.

Editor: Alex Mogilner.