Abstract
Multi-channel electroencephalography (EEG) is used to capture features associated with motor imagery (MI) based brain-computer interface (BCI) with a wide spatial coverage across the scalp. However, redundant EEG channels are not conducive to improving BCI performance. Therefore, removing irrelevant channels can help improve the classification performance of BCI systems. We present a new method for identifying relevant EEG channels. Our method is based on the assumption that useful channels share related information and that this can be measured by inter-channel connectivity. Specifically, we treat all candidate EEG channels as a graph and define channel selection as the problem of node classification on a graph. Then we design a graph convolutional neural network (GCN) model for channels classification. Channels are selected based on the outputs of our GCN model. We evaluate our proposed GCN-based channel selection (GCN-CS) method on three MI datasets. On three datasets, GCN-CS achieves performance improvements by reducing the number of channels. Specifically, we achieve classification accuracies of 79.76% on Dataset 1, 89.14% on Dataset 2 and 87.96% on Dataset 3, which outperform competing methods significantly.
Keywords: Brain-computer interface(BCI), Motor imagery(MI), Graph convolutional neural network (GCN), Channel selection
Introduction
Brain-computer interfaces (BCIs) are a communication technology in which the brain interacts directly with the outside environment without the need for any muscle movement (Huang et al. 2016). A BCI system contains four basic steps: brain signals acquisition, signal processing, external device control, and feedback. BCIs have been used to control a wide range of external devices including examples such as assistive devices for rehabilitation, vehicle control, and games (Zuo et al. 2019). There are a variety of non-invasive and invasive methods available to record bioelectrical signals from brain activity. Of these methods, the electroencephalography (EEG) is the most widely-research due to its advantages of being non-invasive, low cost, and highly portable (Huang et al. 2017; Zhang et al. 2021).
Motor imagery-based BCI systems can work without the need for a stimulus and play an important role in many applications, including movement assistance for individuals with Parkinson’s disease, amyotrophic lateral sclerosis (ALS) and post-stroke rehabilitation (Mirelman et al. 2013; Shahid et al. 2010; Miao et al. 2019). Indeed, motor imagery-based BCIs have an important application within the field of medical rehabilitation (Carrasco and Cantalapiedra 2016; Khan et al. 2020; Frolov et al. 2017). When humans perform motor imagery tasks, such as imaging limb movement, event-related desynchronization (ERD) and event-related synchronization (ERS) can be observed in the EEG (Pfurtscheller and Neuper 1997). These signals are expressed as localized reductions and intensification of EEG band power within specific frequency bands throughout the task period (Pfurtscheller 2000; Pfurtscheller and Lopes da Silva 1999).
The brain regions which contain the most discriminative information about MI vary from person to person (Xiao et al. 2021). Therefore, multi-channel EEG recording is widely used in MI-based BCI systems in order to provide coverage of a sufficiently large area of the scalp to ensure good measurement of the ERD/S. Indeed, multi-channel EEG data is widely considered to be necessary for effective BCI performance because more channels theoretically provide more information about underlying brain activity. However, multi-channel EEG also results in a large degree of data redundancy. Consequently, task-irrelevant data and noise make EEG classification more challenging (Baig et al. 2020). As a result, channel selection strategies are widely used to increase the performance of MI-based BCI.
EEG channel selection is often based on empirical knowledge of underlying brain activity and manual selection of channels (McFarland et al. 2000). However, manual selection methods bring great challenges to the reliability of the BCI system. Consequently, for MI-based BCI, a variety of automatic EEG channel selection algorithms have been developed. These automatic methods can be divided into wrapper and filter based methods. In general, wrapper based channel selection is combined with a specific classifier, and the selection policy contains validation strategies. For example, Wang et al. (2020) designed a weight update strategy for EEG channel selection based on the canonical correlation analysis (CCA), which updated weight based on cross-validation from the Support Vector Machine (SVM) classifier and selected channels according to the weight after each iteration. An evolutionary computation approach is commonly used with wrapper based channel selection methods, such as genetic algorithms (GAs) (Sun et al. 2020; He et al. 2013) and artificial bee colony algorithms (Miao et al. 2018). For example, Qiu et al. (2016) designed a wrapper channel selection method by modifying the sequential floating forward selection algorithm.
Compared with wrapper methods, filter based channel selection approaches cost less computing time because filter methods do not require verification with a classifier. A number of channel selection methods have been developed based on the filter strategy. For instance, mutual information was used to determine the weight of an EEG channel that was chosen based on its weight value (Lan et al. 2007). In filter techniques, a method called CSP-rank, which utilizes the projection matrix calculated by the common spatial pattern (CSP) algorithm to sort and select EEG channels, had been verified in chronic stroke patients (Tam et al. 2011). Jin et al. (2020) proposed a channel selection scheme that was based on the bispectrum feature coupled with the F score. However, most previous studies focused on the univariant features in a single channel to develop channel selection strategies. These methods ignore the relationships between brain regions, a lacuna which we investigate.
Functional connectivity is an effective tool for feature extraction in neuroscience (Luo et al. 2021). Studies show that the functional connectivity of brain regions has been explored for its utility in representing brain activities (Nentwich et al. 2020) and aiding BCI control (Daly et al. 2012). Neural units can be regarded as single neurons, neuronal populations, or brain areas (Friston 1994; Stam et al. 2007). The neural interconnection between different EEG channels is embedded to characterize the activity of the brain (Sargolzaei et al. 2015; Chang et al. 2021).
We suggest that brain connectivity between pairs of channels can be used to assist the estimation of the importance of EEG channels in motor imagery tasks. Thus, in this study, we regard channel selection in BCI as a node classification problem. Combining neurophysiologic knowledge and graph data, we propose a GCN model for utilizing the characteristics of connectivity between EEG channels and estimating the importance of each channel.
In summary, this work makes the following main contributions:
Unlike traditional channel selection methods, where the main purpose is to mine the criterion in univariate sequence, we utilize the connections between EEG channels to develop a filter based EEG channel selection method.
A node classification problem for EEG channel selection has been developed. We also designed a GCN architecture for classifying effective channels and redundant channels.
The rest part of the paper is organized as follows. Section 2 introduces preliminary knowledge and our method. Sections 3 and 4 show the result and discussion. Section 5 presents the conclusion of this study.
Methods
Preliminaries
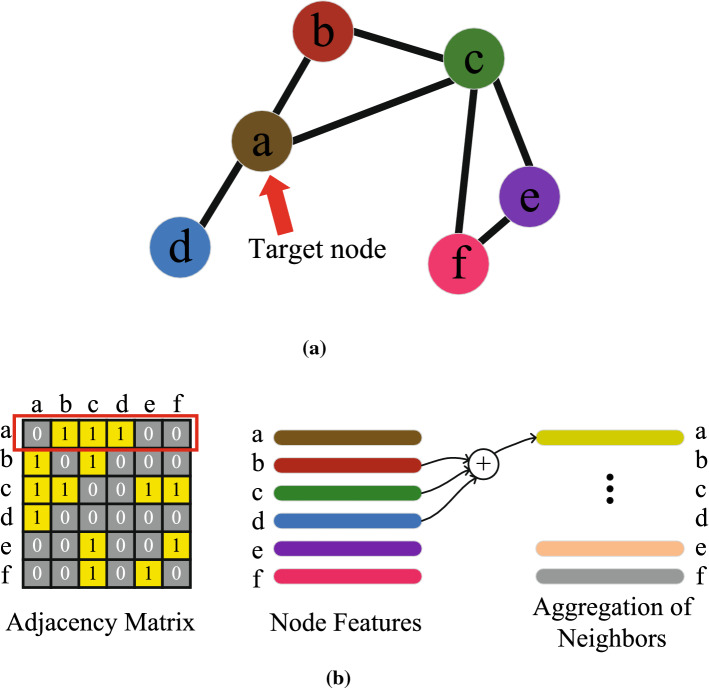
A graph with n nodes can be defined as G(V, E) with denoting the set of nodes and m edges denoted by . A graph that contains n nodes can be represented by an adjacency matrix , where represents the weight from the node to node in a weighted graph. Additionally, in a non-weighted graph, the adjacency matrix A contains only two elements , where if there is a connection from the node to node , otherwise , as shown in Fig. 1a.
Fig. 1.
Illustration of the aggregation function of a GCN layer
In the graph, the Laplacian matrix is used in a wide range of applications (Spielman 2007). The graph Laplacian matrix L is defined as , where is the degree matrix of the graph G and the symmetric normalized version of graph Laplacian is (Shuman et al. 2013):
| 1 |
Spectral graph theory has been proposed based on the graph structural data (Erb 2021). With the Laplacian matrix, the graph filter and graph convolution have been developed (Xu et al. 2021). The signals on the graph’s nodes can be represented as , and , where is the value at the node. The graph Fourier transform is defined as (Shuman et al. 2013): , where is the Fourier domain of the graph signal. U is the eigenvector matrix and is defined as a Fourier basis such that , where denotes the eigenvalues present in the diagonal matrix. Therefore, the inverse graph Fourier transform is .
Graph convolutional neural networks model
As the graph Fourier transform is defined above, the convolution operator between signal g and f on graph data can be defined in the Fourier domain with the Hadamard product in the graph’s spectral domain (Wu et al. 2021). Additionally, the spectral graph convolutions can be seen as the graph’s filter whose parameters are free :
| 2 |
According to the theory of the graph filter (Xu et al. 2021), it is defined as: , where . The parameter denotes the set of Fourier coefficients, and it can be trained in a neural network. The advancement of graph convolutional neural networks (GCN) has marked a significant milestone in the development of methods to estimate node importance (Kipf and Welling 2016). In the study of Kipf and Welling (2016), the authors used the truncated Chebyshev polynomials to approximate the graph’s filter and the GCN layer is designed as :
| 3 |
where is the input of the layer, are the free parameters of the GCN layer, is the output of the layer, , , . When at the first GCN layer, n is the number of nodes and k is the dimension of the feature. The Eq. (3) can be abbreviated as ,where which is described as an information propagation model on a graph. We use this model for embedding the graph data of the EEG.
GCN-based channel selection method
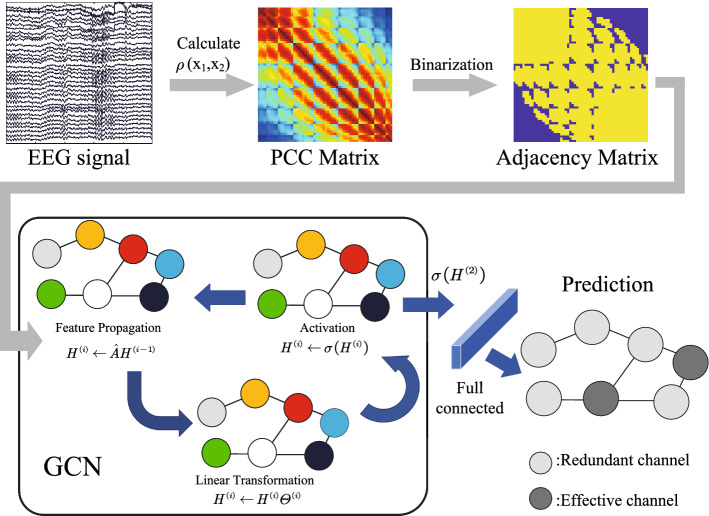
We propose a channel selection technique based on an integration of graph convolutional neural networks (GCN) and neuroscientific expertise. The proposed framework is shown in Fig. 2.
Fig. 2.
Illustration of the GCN-CS framework
Construction of graph data
In our study, each EEG channel is regarded as a node, and the set of all channels is regarded as a graph.
To construct the graph model of the data, in this study, the Pearson correlation coefficient (PCC) is used to quantify the connectivity between all pairs of EEG channels during the period of motor imagery epoch. The PCC is defined as:
| 4 |
where and are the two observed EEG time series from a pair of EEG channels, is the mean of the time series x. In our problem, the whole time series from each channel during the motor imagery period can be regarded as variables. Therefore, linear dependence between two EEG channels can be calculated. Since the PCC between two variables is symmetric as , the representation of the entire EEG channel is defined as:
| 5 |
where , NC is the number of channels. Then, a weighted adjacency matrix W is constructed. In practice, there is a very small chance of because there are coupling relationships between all brain regions (Gonuguntla et al. 2016). Various strategies have been proposed to set a threshold to construct a brain network (Garrison et al. 2015). The application of such thresholds can help to maximize the separation of signals and noise between assumed real and false links between pairs of channels within the network.
Therefore, we set the threshold by calculating the median value as the threshold in each channel. Consequently, the adjacency matrix A is defined as a binary matrix:
| 6 |
where the operator denotes calculating the median of all elements in W, denotes the element in the row and column of A.
The matrix A is symmetric and , which means the graph is undirected and has unweighted edges. When the PCC value that is greater than the threshold this indicates a strong coupling exists between time series from the corresponding pair of channels, as shown in Fig. 1. Setting the median PCC as the threshold allow us to generate a sparse adjacency matrix A in which we retain half of the edges. Therefore, the strongest 50% coupling connections will be retained which indicates the information flow way that exists between channels.
Framework of the GCN-CS model
In terms of the GCN layer, we use the modified adjacency matrix in the study of Kipf and Welling (2016). Then the GCN layer with activation function can be defined as :
| 7 |
where is the modified adjacency matrix, is the output of the layer, is the input data of the layer, are the free parameters of the network, is the activation function and the ReLU activation function is used in this study. denotes the node features in this study. As the input of the GCN, commonly the identity matrix I is used to present the nodes’ location. In this study, each column of the identity matrix is different from the other, which indicates that the location of each channel is unique and different.
The product of and aggregates the node features through linear combination. In the example illustrated in Fig. 1, a graph with 6 channels and 7 edges is shown. In the adjacency matrix, yellow squares indicate that a communication exists between the and the channel. On the contrary, grey squares indicate that there is no meaningful communication way between the and the channel. The corresponding column of yellow squares in the first row of the adjacency matrix indicates the neighbors of channel ‘a’. As shown in Fig. 1b, the matrix product of the adjacency matrix and channel feature matrix, which is , indicates the aggregation of channel features as Fig. 1b shows the aggregation of channel ‘a’.
As shown in Fig. 2, we use two GCN layers for EEG channel embedding, one fully connected layer for the fusion of the GCN’s output, and a softmax layer for classification. The detailed parameters of the proposed GCN model can be seen in Table 1, and in the figure indicates the output of the second GCN layer.
Table 1.
Parameters of the GCN model (C is the number of EEG channels)
| Module | Parameters |
|---|---|
| GCN layer | |
| GCN layer | |
| Full connected | 4 |
| Softmax | 2 classes |
Tagging and training tasks for channel classification
After building the adjacency matrix for EEG channels, we tag some channels as effective channels or redundant channels. In terms of brain activity, various researchers have suggested that specific areas of the brain show the differences between different motor imagery tasks. Based on widely reported neuroscience knowledge, the EEG channels C3 and C4 in the 10-20 system for EEG placement are most often selected because these channels allow good discrimination between different motor imagery tasks (Pfurtscheller and Lopes da Silva 1999; Gaur et al. 2015; Yang et al. 2017).
To make the model effective, the tagging task is done according to neurophysiologic knowledge. We label channels C3, C4,and Cz as the effective channels at the left hand, right hand, and foot imagery classification for the reason that these three channels are seen as the motor cortex related channels. Additionally, we label three channels on the frontal lobe as redundant channels.
With the help of the free parameters and spectral graph theory, the loss function of graph neural networks can be designed as , is a set of nodes that have labels, is the matrix of labels, loss(*) denotes the cross entropy loss function, and is the output of the graph convolutional networks at node. When using the GCN for channel classification, the goal is to learn the parameter matrix in networks by minimizing the loss function. The trained GCN network has the ability to output the probability of labels for the unlabeled EEG channels. Therefore, we use the output of the GCN model to select EEG channels.
Feature extraction
Various feature extraction methods for BCI systems have been developed. In the field of MI-based BCI systems, the common spatial pattern (CSP) algorithm has been extensively used. CSP aims to find projections that maximize the separation of two classes (Ramoser et al. 2000). Specifically, CSP builds a filter by maximizing the variance of projected data from one class while minimizing the variance of the other class. Suppose that , where NC is the number of channels and T is the length of the time series. Then the covariance matrix of class y is calculated as follows:
| 8 |
where the operator denotes the trace of the input matrix. Consequently, the objective function can be formulated as the Rayleigh quotient:
| 9 |
The solution to this problem is the Lagrange multiplier method. And the Rayleigh quotient is amounted to solve the generalized eigenvalue problem such that and is a symmetric positive definite matrix. Then we have the following solution:
| 10 |
Hence, 2m eigenvectors corresponding to the m smallest and the m largest eigenvalues of , are obtained as the spatial filters , resulting in . To make the features similar to Gaussian distribution, the feature vector of filter is transformed by logarithmic transformation:
| 11 |
where is the row of the matrix Z.
Classification
In this article, we use the Linear Discriminant Analysis (LDA) for the classification of the motor imagery task, taking the features that are constructed above. Suppose the dataset that contains n samples: where is the feature vector, y is the label of . Consider a two classes classification task, the class label of LDA is defined as . The mean and the covariance of the features are calculated in feature space. LDA tries to project the feature data to maximize the variance of the two classes while minimizing the variance of features in the same category (Fisher 1936).
| 12 |
where and are the metrics of the intra-class variance and inter-class variance. The solution of the LDA classifier is efficient and there are no adjustable parameters.
Results
Dataset description
In this study, three datasets were used to verify the effectiveness of the proposed channel selection method. All datasets came from the public BCI competition dataset series.
Dataset 1 came from the part I of the BCI Competition IV (Zhang et al. 2012). All the EEG data was recorded at 1000 Hz. We downsampled the data to 100 Hz. The dataset contained EEG from 7 participants and was recorded via 59 channels. Since the EEG data of participants ‘c’, ‘d’ and ‘e’ was artificially generated, we only used the EEG from participants ‘a’, ‘b’, ‘f’, and ‘g’. Each participant was asked to complete 200 trials of two classes of motor imagery tasks. In the experiment, arrows pointing left, right, and down were displayed, participants performed the motor imagery tasks corresponding to these cues (left hand, right hand, and foot motor imagery). The execution time of motor imagination was 4 s. More details of this dataset can be found on the following website: http://www.bbci.de/competition/iv/.
Dataset 2 came from the BCI competition III, IVa part (Blankertz et al. 2006). This dataset recorded EEG from 118 channels, which were set at positions in the 10–20 EEG systems. Three motor imagery tasks were used: left hand, right hand, and right foot imagery. However, only the EEG data for right hand and right foot motor imagery were provided. This data set consisted of data from 5 healthy participants (labeled: aa, al, av, aw, ay), 280 trials were recorded per participant. The visual cues were shown for 3.5 s in each trial, during which the participants performed the motor imagery. Then the period for participants to relax was randomly drawn from between 1.75 to 2.25 s. In this study, we downsampled the data to 100 Hz. More details of this dataset can be found on the following website: http://www.bbci.de/competition/iii/.
Dataset 3 came from the IIIa part of the BCI Competition III (Blankertz et al. 2006). All the EEG data were recorded from 3 subjects with 250 Hz sampling rate. A set of 60 EEG channels were used to record the EEG during the experiment. The participants were labeled as k3, k6, and l1. In the experiment, the beginning of the trial was a black screen for the first 2 s. Then the cross symbol “+” was displayed from 2 s, this remained on screen for one second. An arrow to up, right, down, or left was then displayed from 3 to 7 s, to indicate the motor imagery tasks tongue, right hand, foot, or left hand. The participants were asked to perform the corresponding imagery task until the arrow disappeared. In this study, we used the trials during which participants attempted left and right hand motor imagery to verify the proposed method. More details of this dataset can be found on the following website: http://www.bbci.de/competition/iii/.
Data preprocessing
EEG signals are first preprocessed via the Butterworth filter and band-pass filtered from 8 to 30 Hz. The setup of the Butterworth filter is aimed at cancelling the high-frequency noise such as the power line noise and retaining the information of the brain activity related to motor imagery.
Experiment results
The proposed GCN-based channel selection method (GCN-CS) is applied to the above-mentioned datasets. To illustrate the effectiveness of the proposed channel selection method, we compared the average accuracies of the full channels and the selected channels in the MI-based BCI.
Table 2 shows the result between all EEG channels and the selected EEG channels via the proposed channel selection method. A tenfold cross-validation method is used to train the method and calculate the accuracy. The mean accuracy of the chosen channel combination is higher than that achieved when all EEG channels are used. Additionally, the proposed channel selection method improved the BCI performance for each participant in the dataset.
Table 2.
Ten-fold cross-validation classification results (%) of the GCN-CS method on the three datasets
| aa | al | av | aw | ay | a | b | f | g | k3 | k6 | l1 | p | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| AC | 76.07 | 97.14 | 63.93 | 83.57 | 90.36 | 70.50 | 54.00 | 64.50 | 93.00 | 90.56 | 57.50 | 90.00 | - |
| GCN-CS | 83.21 | 98.93 | 74.64 | 95.00 | 93.93 | 85.00 | 64.00 | 75.55 | 94.50 | 93.89 | 75.00 | 95.00 | < 0.05 |
A Wilcoxon Signed Rank Test (Rey and Neuhäuser 2011) is also used to assess the results. This reveals that the GCN-CS method significantly outperformed the use of all channels (AC) ().
With the cancelling of redundant channels, the number of channels is reduced while the average classification accuracy is increased. For participants ‘av’ and ‘aw’, the reduction of EEG channels can increase the classification accuracy by over 8 percent. As an example, the accuracy of participant ’a’ increased to 85.00% from 70.50%, while the accuracy of participant ’b’ improved by about 10 percent, increasing from 54.00 to 64.00%.
Comparisons
The classification accuracy achieved by using the GCN-based channels selection method is compared with the other channel selection methods.
For motor imagery tasks, the traditional method used EEG data from only three channels (3C-CSP), called C3, Cz, and C4. This strategy was founded on neurophysiologic findings indicating the left primary motor cortex (C3), right primary motor cortex (C4), and center primary motor cortex (Cz) were the best locations for MI task classification (Hu et al. 2014). Additionally, the CSP feature extraction method was attempted to aid classification.
The CSP-rank (Tam et al. 2011) method was based on sorting the absolute values of the CSP filter coefficients in the filters which were produced by the CSP algorithm. CSP-rank used the eigenvectors that corresponded to the largest and smallest eigenvalues respectively to construct spatial filters which generate features with two dimensions from the EEG data. The filter’s coefficient of a particular EEG channel corresponded to the importance of the channel.
The Sparse common spatial pattern (SCSP) (Arvaneh et al. 2011) method added the ratio of L1-norm and L2-norm as a constraint on the CSP objective function. Then the spatial filters obtained by the new objective function were used for ranking the channels.
Table 3 shows that GCN-CS achieves the highest average accuracy compared with other methods on three datasets. The boldface denotes the highest accuracy of the subject. Moreover, GCN-CS uses fewer channels and achieves over 6 percent higher accuracy than SCSP. Except for participants ’ay’ and ’g’, GCN-CS has the best performance over participants. For three datasets, our method achieves the highest average accuracies.
Table 3.
Comparison of the highest classification accuracies among the proposed method and other reported channel selection methods from data from three datasets
| Participants | Methods | |||||||
|---|---|---|---|---|---|---|---|---|
| 3C-CSP | CSP-rank | SCSP | GCN-CS | |||||
| Acc (%) | Num | Acc (%) | Num | Acc (%) | Num | Acc (%) | Num | |
| k3 | 80.00 | 3 | 93.33 | 16 | 93.33 | 33 | 93.89 | 33 |
| k6 | 57.50 | 3 | 65.00 | 30 | 71.66 | 11 | 75.00 | 11 |
| l1 | 81.67 | 3 | 92.50 | 12 | 91.66 | 58 | 95.00 | 16 |
| Mean | 73.06 | 83.61 | 85.55 | 87.96 | ||||
| a | 74.00 | 3 | 83.00 | 16 | 82.50 | 12 | 85.00 | 19 |
| b | 60.00 | 3 | 57.00 | 38 | 57.00 | 30 | 64.00 | 12 |
| f | 62.50 | 3 | 66.50 | 6 | 74.50 | 17 | 75.55 | 8 |
| g | 89.00 | 3 | 95.00 | 51 | 95.50 | 52 | 94.50 | 48 |
| Mean | 71.38 | 75.38 | 77.38 | 79.76 | ||||
| aa | 61.43 | 3 | 81.43 | 46 | 80.36 | 45 | 83.21 | 20 |
| al | 87.50 | 3 | 98.57 | 57 | 97.86 | 54 | 98.93 | 37 |
| av | 58.21 | 3 | 54.29 | 30 | 65.71 | 52 | 74.64 | 6 |
| aw | 74.29 | 3 | 90.00 | 32 | 88.21 | 74 | 95.00 | 51 |
| ay | 85.00 | 3 | 94.30 | 55 | 93.21 | 101 | 93.93 | 20 |
| Mean | 73.29 | 83.72 | 85.07 | 89.14 | ||||
| p-value | < 0.05 | < 0.05 | < 0.05 | – | ||||
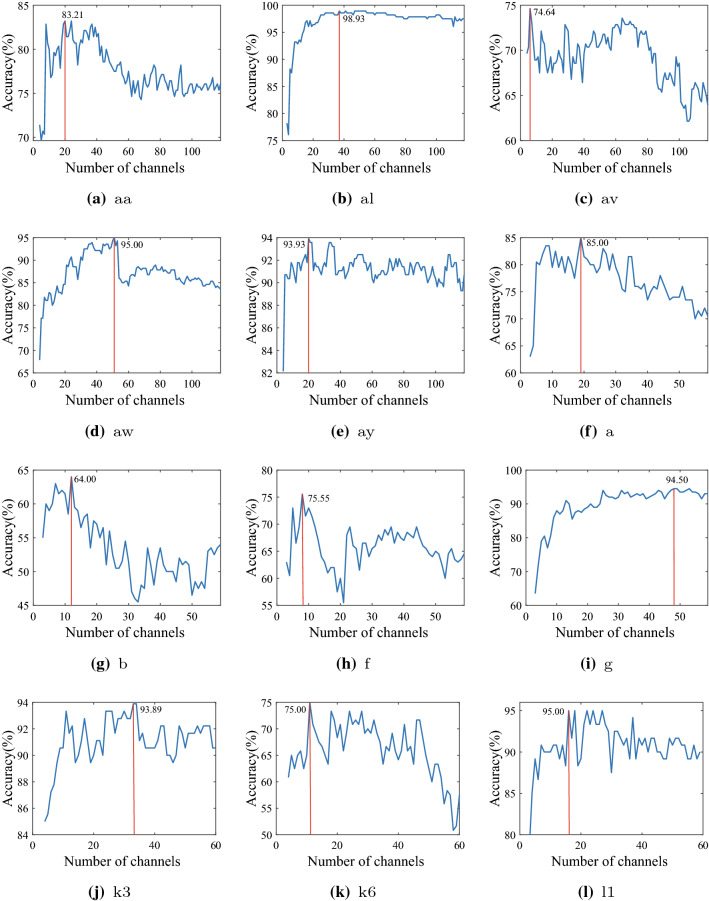
We rank the channels by scores of importance and select a specific number of important channels for classification. Figure 3 shows the relationship between the number of channels selected and the average accuracies achieved. The red line marks the best classification accuracy and the corresponding number of channels. As the number of channels increases, the accuracy of the classification first rises and then decreases with the increase in the number of channels. The accuracies peak at about 15 channels on Dataset 1 and about 30 channels on Dataset 2. The effectiveness of the proposed method in removing redundant information can be seen in Fig. 3. Mostly, around two-thirds of redundant channels can be found, which deteriorates the feature separability. With GCN-CS method, higher classification accuracies are achieved with less EEG channels.
Fig. 3.
The performance of our proposed channel selection method in terms of number of channels selected compared to classification accuracy
For participant ‘aw’, Fig. 3(d) shows that classification accuracy peaks at over 90% within 30 channels but obtains an accuracy of less than 85% when all channels are used. A sharp decline in accuracy at around 50 channels can be seen, which indicates that the addition of redundant channels brings a reduction in classification accuracy. For all participants, Fig. 3 shows that a decline can be seen, which indicates that the GCN-CS method ranks the importance of each EEG channel effectively.
Our results suggest that some EEG channels are not conducive to the performance of BCI. If redundant EEG channels are fed into the classifier, classification performance may decline. Our proposed method can be used to remove the redundant channels and improve the performance of MI-based BCI systems.
Map of selected channels
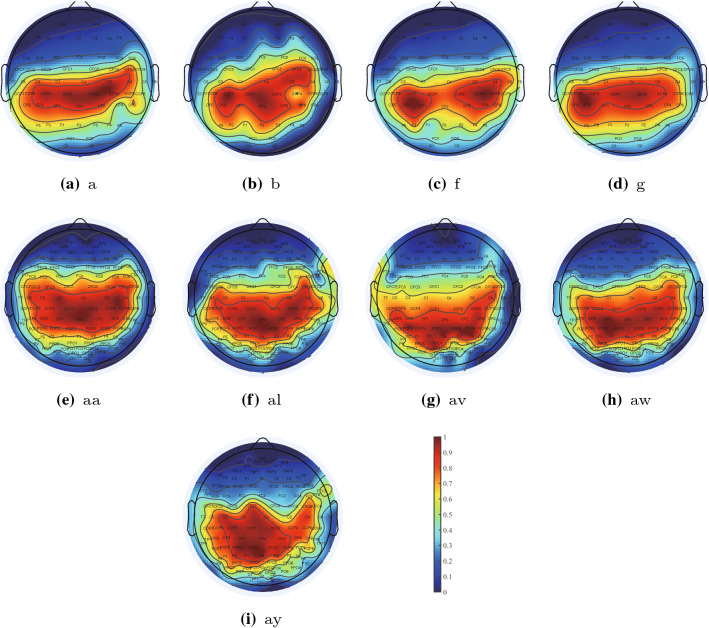
The outputs of the proposed GCN model can be seen as the evaluation scores of the contributions of channels to classification. We use MATLAB with the EEGLAB toolbox (Delorme and Makeig 2004) to plot the topography for each participant. In our study, the evaluation score of each channel is calculated by the rank of the outputs from the GCN model. For 10-fold cross-validation, we get ten scores for a participant and illustrate the topography with the average values for each participant.
The maps of the selected channels for Dataset 1 and Dataset 2 are shown in Fig. 5. Based on the ranking of channels, we calculate the percentile ranking of each participant to help visualize the evaluation scores. Since we used ten folds cross-validation, we calculated average of the scores and the distribution of the channels’ average scores is shown in Fig. 5. The color red denotes high evaluation scores, whereas the color blue denotes low evaluation scores. As can be seen, all of the participants have certain commonalities. High-scoring areas are seen on the left primary motor cortex and center primary motor cortex, which is located around the C3, C4 and Cz channels. In addition, low-scoring areas are seen in the area of the frontal lobe. The similarities of the maps of channels suggest that the proposed GCN-CS method is a promising tool for distinguishing the essential regions in multi-channel EEG data.
Fig. 5.
Topography of average scores of EEG channels on Dataset 1 and Dataset 2. Higher scores indicate that the channel is more important in this study
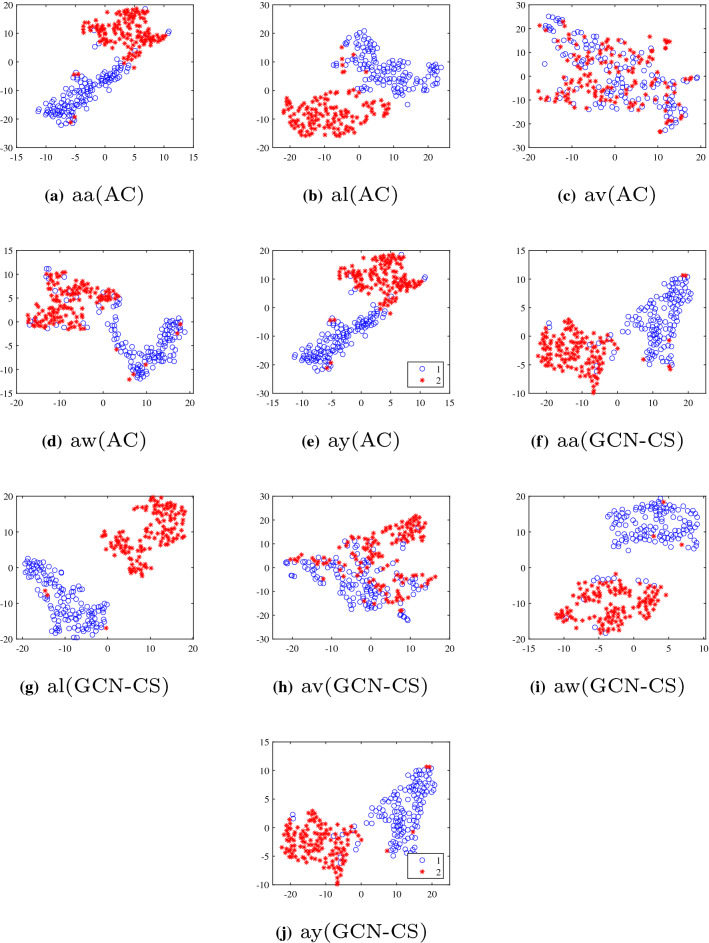
Additionally, we use the T-SNE method (Van der Maaten and Hinton 2008) for illustrating the feature distribution. As Fig. 4 shows, we embed the CSP features of all channels and selected channels on Dataset 2. The separability of selected channels is more apparent than that achieved when all channels are used. For participant ’av’, after applying GCN-CS, Table 2 shows an over 8% improvement is obtained, and a more significant degree of separability can be seen in Fig. 4h. Similarities can also be seen in other participants. The results show that removing the redundant EEG channels can enhance the separability of the features and help improve classification performance.
Fig. 4.
Comparison of feature distributions (AC: all channels scheme. GCN-CS: proposed channel selection scheme)
Discussion
Rationality of GCN in channel selection
Most MI-BCI researches focus on the univariant information available in single-channels to develop channel selection methods. For instance, Tam et al. (2011) use the CSP algorithm to set a criterion, which is calculated with the discriminative information in individual channels, to evaluate the importance of each channel. However, this kind of criteria for channel selection is restricted to univariant information and ignores connectivity between brain regions.
Graph data has great advantages in representing the interaction of brain regions. All the EEG channels form a network and each channel is regarded as a node in the network. Then, the statistical relationships between channels can be easily quantified, and the connectivity is regarded as an edge in the network.
Effectiveness of GCN-CS model
It is uncertain whether the connectivity of the networks can be used to select channels in BCI systems. This study regards channel selection as the node classification problem in the EEG network. We quantify the statistical relationship between EEG channels with the Pearson correlation coefficient. We then use binarization for retaining half of the edges. Then, we build the graph and use our proposed GCN model to learn and predict the channels with a few labels.
The performance improvement brought by removing redundant channels is verified in our method, which is shown in Table 2 and Fig. 3. Our method can estimate the importance of the EEG channels in MI tasks and remove the redundant EEG channels to improve the classification performance.
Our comparison results, in which we compare our method with traditional methods, are given in Table 3. With the introduction of the GCN model, our method achieves high performance in MI-based BCI systems. Moreover, our proposed method is a promising tool to reveal the brain regions which are highly relevant to the motor imagery task.
The channel selection GCN model proposed in this paper is different from the model used for classification. Additionally, the scale of the graph in this study is less than 200. Therefore, the model designed in this paper does not need a lot of iterative training, and the training time can be completed in a few seconds which is superior to most wrapper-based methods.
Challenges and future work
There still exist some limitations in our method. Firstly, the tagging task is only based on neurophysiologic knowledge. Only channels C3, C4, and Cz can be labeled as effective channels. Additionally, the number of labeled channels in the MI task is small and limited. Second, the method for quantifying the connectivity between channels is the Pearson correlation coefficient. Thus, only linear relationships between EEG channels are considered, which ignores the complex nonlinear relationship that also exists between EEG channels. Thirdly, it is hard to conclude how many channels are most helpful for improving the BCI performance because the difference between the training dataset and the online dataset can affect the performance, such as covariate shift. But we can seek the number of selected channels from Fig. 3, which shows that 15–25 channels can work effectively.
To address these issues, we will experiment with information theory and other quantification methods for connectivity. In the future, we will design a new tagging method based on information theory, which has the potential to help identify channels more effectively. We will also explore the used use of nonlinear quantification methods for connectivity to improve performance. In addition, we might add mutual information to optimize the number of selected channels in future work.
Conclusion
In this study, we proposed a novel EEG channel selection method based on graph convolutional neural networks. Channel selection in MI-based BCI is regarded as a node classification problem. All the scalp electrodes are regarded as nodes, and the edges between electrode pairs are calculated according to the Pearson correlation coefficient. We remove half of the edges to generate a graph for EEG channels, which retains the coupling relationships between the most important pairs of channels. Then, we design a GCN model for classifying the resulting features. The weight values of predicted labels are used to sort the channels. Experimental results suggest that high classification accuracy can be obtained by using the LDA classifier to classify features extracted by CSP from the selected channels. In sum, the proposed GCN-CS method is a promising tool for increasing the performance of motor imagery-based BCI systems.
Acknowledgements
This work was supported by the Grant National Natural Science Foundation of China under Grant 62176090; in part by Shanghai Municipal Science and Technology Major Project under Grant 2021SHZDZX, in part by the Program of Introducing Talents of Discipline to Universities through the 111 Project under Grant B17017; in part by the ShuGuang Project supported by the Shanghai Municipal Education Commission and the Shanghai Education Development Foundation under Grant 19SG25; in part by the Ministry of Education and Science of the Russian Federation under Grant 14.756.31.0001, and in part by the Polish National Science Center under Grant UMO-2016/20/W/NZ4/00354.
Footnotes
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
References
- Arvaneh M, Guan C, Ang KK, et al. Optimizing the channel selection and classification accuracy in EEG-based BCI. IEEE Trans Biomed Eng. 2011;58(6):1865–1873. doi: 10.1109/TBME.2011.2131142. [DOI] [PubMed] [Google Scholar]
- Baig MZ, Aslam N, Shum HPH. Filtering techniques for channel selection in motor imagery EEG applications: a survey. Artif Intell Rev. 2020;53(2):1207–1232. doi: 10.1007/s10462-019-09694-8. [DOI] [Google Scholar]
- Blankertz B, Muller KR, Krusienski D, et al. The BCI competition III: validating alternative approaches to actual BCI problems. IEEE Trans Neural Syst Rehabil Eng. 2006;14(2):153–159. doi: 10.1109/TNSRE.2006.875642. [DOI] [PubMed] [Google Scholar]
- Carrasco DG, Cantalapiedra JA. Effectiveness of motor imagery or mental practice in functional recovery after stroke: a systematic review. Neurología (English Edition) 2016;31(1):43–52. doi: 10.1016/j.nrleng.2013.02.008. [DOI] [PubMed] [Google Scholar]
- Chang W, Huang W, Yan G, et al (2021) EEG based graph network analysis for motor imagery task. In: 2021 6th international conference on computational intelligence and applications (ICCIA), pp 185–189. 10.1109/ICCIA52886.2021.00043
- Daly I, Nasuto SJ, Warwick K. Brain computer interface control via functional connectivity dynamics. Pattern Recogn. 2012;45(6):2123–2136. doi: 10.1016/j.patcog.2011.04.034. [DOI] [Google Scholar]
- Delorme A, Makeig S. EEGLAB: an open source toolbox for analysis of single-trial EEG dynamics including independent component analysis. J Neurosci Methods. 2004;134(1):9–21. doi: 10.1016/j.jneumeth.2003.10.009. [DOI] [PubMed] [Google Scholar]
- Erb W. Shapes of uncertainty in spectral graph theory. IEEE Trans Inf Theory. 2021;67(2):1291–1307. doi: 10.1109/TIT.2020.3039310. [DOI] [Google Scholar]
- Fisher RA. The use of multiple measurements in taxonomic problems. Ann Eugen. 1936;7(2):179–188. doi: 10.1111/j.1469-1809.1936.tb02137.x. [DOI] [Google Scholar]
- Friston KJ. Functional and effective connectivity in neuroimaging: a synthesis. Hum Brain Mapp. 1994;2(1–2):56–78. doi: 10.1002/hbm.460020107. [DOI] [Google Scholar]
- Frolov AA, Mokienko O, Lyukmanov R, et al. Post-stroke rehabilitation training with a motor-imagery-based brain-computer interface (BCI)-controlled hand exoskeleton: A randomized controlled multicenter trial. Front Neurosci. 2017;11:400. doi: 10.3389/fnins.2017.00400. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Garrison KA, Scheinost D, Finn ES, et al. The (in)stability of functional brain network measures across thresholds. Neuroimage. 2015;118:651–661. doi: 10.1016/j.neuroimage.2015.05.046. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gaur P, Pachori RB, Wang H, et al (2015) An empirical mode decomposition based filtering method for classification of motor-imagery EEG signals for enhancing brain-computer interface. In: 2015 International joint conference on neural networks (IJCNN), pp 1–7. 10.1109/IJCNN.2015.7280754
- Gonuguntla V, Wang Y, Veluvolu KC. Event-related functional network identification: application to EEG classification. IEEE J Sel Top Signal Process. 2016;10(7):1284–1294. doi: 10.1109/jstsp.2016.2602007. [DOI] [Google Scholar]
- He L, Hu Y, Li Y, et al. Channel selection by Rayleigh coefficient maximization based genetic algorithm for classifying single-trial motor imagery EEG. Neurocomputing. 2013;121:423–433. doi: 10.1016/j.neucom.2013.05.005. [DOI] [Google Scholar]
- Hu S, Wang H, Zhang J, et al (2014) Causality from Cz to C3/C4 or between C3 and C4 revealed by granger causality and new causality during motor imagery. In: 2014 International joint conference on neural networks (IJCNN), pp 3178–3185. 10.1109/IJCNN.2014.6889769
- Huang M, Daly I, Jin J, et al. An exploration of spatial auditory BCI paradigms with different sounds: music notes versus beeps. Cogn Neurodyn. 2016;10(3):201–209. doi: 10.1007/s11571-016-9377-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Huang M, Jin J, Zhang Y, et al. Usage of drip drops as stimuli in an auditory p300 BCI paradigm. Cogn Neurodyn. 2017;12(1):85–94. doi: 10.1007/s11571-017-9456-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jin J, Liu C, Daly I, et al. Bispectrum-based channel selection for motor imagery based brain-computer interfacing. IEEE Trans Neural Syst Rehabil Eng. 2020;28(10):2153–2163. doi: 10.1109/TNSRE.2020.3020975. [DOI] [PubMed] [Google Scholar]
- Khan MA, Das R, Iversen HK, et al. Review on motor imagery based BCI systems for upper limb post-stroke neurorehabilitation: From designing to application. Comput Biol Med. 2020;123(103):843. doi: 10.1016/j.compbiomed.2020.103843. [DOI] [PubMed] [Google Scholar]
- Kipf T, Welling M (2016) Semi-supervised classification with graph convolutional networks. arXiv:1609.02907
- Lan T, Erdogmus D, Adami A, et al. Channel selection and feature projection for cognitive load estimation using ambulatory EEG. Comput Intell Neurosci. 2007;074:895. doi: 10.1155/2007/74895. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Luo C, Li F, Li P, et al. A survey of brain network analysis by electroencephalographic signals. Cogn Neurodyn. 2021;16(1):17–41. doi: 10.1007/s11571-021-09689-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Van der Maaten L, Hinton G. Visualizing data using t-SNE. J Mach Learn Res. 2008;9(11):2579–2605. [Google Scholar]
- McFarland DJ, Miner LA, Vaughan TM, et al. Mu and beta rhythm topographies during motor imagery and actual movements. Brain Topogr. 2000;12(3):177–186. doi: 10.1023/A:1023437823106. [DOI] [PubMed] [Google Scholar]
- Miao M, Wang A, Liu F. Application of artificial bee colony algorithm in feature optimization for motor imagery EEG classification. Neural Comput Appl. 2018;30(12):3677–3691. doi: 10.1007/s00521-017-2950-7. [DOI] [Google Scholar]
- Miao Y, Yin E, Allison BZ, et al. An ERP-based BCI with peripheral stimuli: validation with ALS patients. Cogn Neurodyn. 2019;14(1):21–33. doi: 10.1007/s11571-019-09541-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mirelman A, Maidan I, Deutsch JE. Virtual reality and motor imagery: Promising tools for assessment and therapy in Parkinson’s disease. Mov Disord. 2013;28(11):1597–1608. doi: 10.1002/mds.25670. [DOI] [PubMed] [Google Scholar]
- Nentwich M, Ai L, Madsen J, et al. Functional connectivity of EEG is subject-specific, associated with phenotype, and different from fMRI. Neuroimage. 2020;218(117):001. doi: 10.1016/j.neuroimage.2020.117001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pfurtscheller G (2000) Chapter 26 spatiotemporal ERD/ERS patterns during voluntary movement and motor imagery. In: Ambler Z, Nevšímalová S, Kadaňka Z, et al (eds) Clinical neurophysiology at the beginning of the 21st century, supplements to clinical neurophysiology, vol 53. pp 196–198. 10.1016/s1567-424x(09)70157-6 [DOI] [PubMed]
- Pfurtscheller G, Lopes da Silva F. Event-related EEG/MEG synchronization and desynchronization: basic principles. Clin Neurophysiol. 1999;110(11):1842–1857. doi: 10.1016/s1388-2457(99)00141-8. [DOI] [PubMed] [Google Scholar]
- Pfurtscheller G, Neuper C. Motor imagery activates primary sensorimotor area in humans. Neurosci Lett. 1997;239(2):65–68. doi: 10.1016/s0304-3940(97)00889-6. [DOI] [PubMed] [Google Scholar]
- Qiu Z, Jin J, Lam HK, et al. Improved SFFS method for channel selection in motor imagery based BCI. Neurocomputing. 2016;207:519–527. doi: 10.1016/j.neucom.2016.05.035. [DOI] [Google Scholar]
- Ramoser H, Muller-Gerking J, Pfurtscheller G. Optimal spatial filtering of single trial EEG during imagined hand movement. IEEE Trans Rehabil Eng. 2000;8(4):441–446. doi: 10.1109/86.895946. [DOI] [PubMed] [Google Scholar]
- Rey D, Neuhäuser M (2011) Wilcoxon-signed-rank test, Springer, Berlin, Heidelberg, pp 1658–1659. 10.1007/978-3-642-04898-2_616
- Sargolzaei S, Cabrerizo M, Goryawala M, et al. Scalp EEG brain functional connectivity networks in pediatric epilepsy. Comput Biol Med. 2015;56:158–166. doi: 10.1016/j.compbiomed.2014.10.018. [DOI] [PubMed] [Google Scholar]
- Shahid S, Sinha RK, Prasad G. Mu and beta rhythm modulations in motor imagery related post-stroke EEG: a study under BCI framework for post-stroke rehabilitation. BMC Neurosci. 2010;11(1):127. doi: 10.1186/1471-2202-11-S1-P127. [DOI] [Google Scholar]
- Shuman DI, Narang SK, Frossard P, et al. The emerging field of signal processing on graphs: Extending high-dimensional data analysis to networks and other irregular domains. IEEE Signal Process Mag. 2013;30(3):83–98. doi: 10.1109/msp.2012.2235192. [DOI] [Google Scholar]
- Spielman DA (2007) Spectral graph theory and its applications. In: 48th Annual IEEE symposium on foundations of computer science (FOCS’07), pp 29–38. 10.1109/FOCS.2007.56
- Stam CJ, Nolte G, Daffertshofer A. Phase lag index: assessment of functional connectivity from multi channel EEG and MEG with diminished bias from common sources. Hum Brain Mapp. 2007;28(11):1178–1193. doi: 10.1002/hbm.20346. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sun H, Jin J, Kong W, et al. Novel channel selection method based on position priori weighted permutation entropy and binary gravity search algorithm. Cogn Neurodyn. 2020;15(1):141–156. doi: 10.1007/s11571-020-09608-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tam WK, Ke Z, Tong KY (2011) Performance of common spatial pattern under a smaller set of EEG electrodes in brain-computer interface on chronic stroke patients: A multi-session dataset study. In: 2011 Annual international conference of the ieee engineering in medicine and biology society. IEEE, pp 6344–6347. 10.1109/IEMBS.2011.6091566 [DOI] [PubMed]
- Wang Q, Cao T, Liu D, et al. A motor-imagery channel-selection method based on SVM-CCA-CS. Meas Sci Technol. 2020;32(3):035701. doi: 10.1088/1361-6501/abc205. [DOI] [Google Scholar]
- Wu Z, Pan S, Chen F, et al. A comprehensive survey on graph neural networks. IEEE Trans Neural Netw Learn Syst. 2021;32(1):4–24. doi: 10.1109/TNNLS.2020.2978386. [DOI] [PubMed] [Google Scholar]
- Xiao R, Huang Y, Xu R, et al. Coefficient-of-variation-based channel selection with a new testing framework for MI-based BCI. Cogn Neurodyn. 2021;16(4):791–803. doi: 10.1007/s11571-021-09752-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Xu M, Fu P, Liu B, et al. Multi-stream attention-aware graph convolution network for video salient object detection. IEEE Trans Image Process. 2021;30:4183–4197. doi: 10.1109/TIP.2021.3070200. [DOI] [PubMed] [Google Scholar]
- Yang Y, Chevallier S, Wiart J, et al. Subject-specific time-frequency selection for multi-class motor imagery-based BCIs using few Laplacian EEG channels. Biomed Signal Process Control. 2017;38:302–311. doi: 10.1016/j.bspc.2017.06.016. [DOI] [Google Scholar]
- Zhang H, Guan C, Ang KK, et al. BCI competition IV—data set I: Learning discriminative patterns for self-paced EEG-based motor imagery detection. Front Neurosci. 2012;6:7. doi: 10.3389/fnins.2012.00007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang X, Jin J, Li S, et al. Evaluation of color modulation in visual p300-speller using new stimulus patterns. Cogn Neurodyn. 2021;15(5):873–886. doi: 10.1007/s11571-021-09669-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zuo C, Jin J, Yin E, et al. Novel hybrid brain-computer interface system based on motor imagery and p300. Cogn Neurodyn. 2019;14(2):253–265. doi: 10.1007/s11571-019-09560-x. [DOI] [PMC free article] [PubMed] [Google Scholar]