Feature hypergraph representation learning on spatial-temporal correlations for EEG emotion recognition

Abstract

Electroencephalogram(EEG) becomes popular in emotion recognition for its capability of selectively reflecting the real emotional states. Existing graph-based methods have made primary progress in representing pairwise spatial relationships, but leaving higher-order relationships among EEG channels and higher-order relationships inside EEG series. Constructing a hypergraph is a general way of representing higher-order relations. In this paper, we propose a spatial-temporal hypergraph convolutional network(STHGCN) to capture higher-order relationships that existed in EEG recordings. STHGCN is a two-block hypergraph convolutional network, in which feature hypergraphs are constructed over the spectrum, space, and time domains, to explore spatial and temporal correlations under specific emotional states, namely the correlations of EEG channels and the dynamic relationships of temporal stamps. What’s more, a self-attention mechanism is combined with the hypergraph convolutional network to initialize and update the relationships of EEG series. The experimental results demonstrate that constructed feature hypergraphs can effectively capture the correlations among valuable EEG channels and the correlations inside valuable EEG series, leading to the best emotion recognition accuracy among the graph methods. In addition, compared with other competitive methods, the proposed method achieves state-of-art results on SEED and SEED-IV datasets.

Introduction

EEG-based connectivity patterns can be used for classifying different mental states. Graph-based models have been proposed to describe pairwise relationships within multichannel EEG recordings. For example, Zhang et al. (2019) proposed a graph-based hierarchical model to classify movement intention based on the relationships among EEG signals and their spatial information. However, in real scenarios, the state of a channel being activated may be related to multiple channels, which means that there is a higher-order relationship among the channels. Current graph-based methods neglect the complex higher-order correlations existed in EEG recordings, and are incapable of depicting such set-like relations.

It is worth noting that EEG is a non-stationary signal, and its statistics related to brain regions vary with time. However, the relationship between EEG timing samples is still under investigation. In order to tackle the above challenges, we model the higher-order interdependence of EEG features as hypergraphs to extract two different types of EEG relations. To verify the effective of the idea, we apply the model to EEG-based emotion recognition.

Emotion recognition is a technique for capturing human emotional states, which is vital in human-computer interaction. Typically, two types of signals can be utilized for emotion recognition. One is non-physiological signals, which are easily controlled by humans and are biased when people try to hide them. By contrast, physiological signals are difficult to be disguised and are helpful to obtaining real emotions, like electroencephalogram(EEG) signals, electrocardiogram(ECG) signals, electromyography(EMG), etc. This discovery inspired researchers to use physiological signals for emotion recognition. Among them, EEG signals are a direct response to brain activity belonging to the central nervous system so that real emotions can be captured more objectively and reliably. Also, their acquisition costs are low, making them the most commonly used physiological signals in emotion recognition.

Traditional machine learning methods, such as SVM (Wang et al. 2011; Zheng and Lu 2015), KNN (Bahari and Janghorbani 2013), etc., are used for emotion recognition at the beginning. However, traditional machine learning can not fully extract emotional features existed in EEG recordings. Methods based on convolutional neural networks(CNN)(Lotfi and Akbarzadeh-T 2014; Li et al. 2020; Deng et al. 2021) can make up for the shortcomings of traditional machine learning methods, improve the accuracy of emotion recognition. With the development of graph neural networks, graph-based methods (Feng et al. 2019; Zhong et al. 2020; Zhonget al. 2020) are also applied to EEG emotion recognition. Since these methods consider relationships between EEG channels, they have achieved more accurate recognition results. Till now, higher-order relationships of EEG recordings are not extracted and utilized in obtaining more accurate emotion recognition results.

To fill this gap, we propose a spatial-temporal hypergraph convolutional network named STHGCN, a hypergraph-based architecture for extracting higher-order EEG relations related to emotion recognition in spatial and temporal domains. The STHGCN consists of a spatial block and a temporal block. Each block is composed of a Feature Extraction Layer and a Hypergraph convolutional Layer(3.2). A Fusion layer to fuse the spatial and temporal dependencies in EEG features is added after two blocks 3.3. Through experiments on EEG recordings in two datasets, SEED, SEED-IV 4.1, we show that STHGCN outperforms most state-of-the-art methods in terms of both accuracy and standard variance 5.1. Lastly, we perform an hypergraph visualization and ablation study (5.2, 5.3) to contextualize each component’s effectiveness and pave the future directions towards combining hypergraphs and EEG correlations extraction 6 . The code will be available on GitHub(https://github.com/lmenghang/STHGNN.git)

The main contributions of the paper are as follows:

We use feature hypergraph representation learning for EEG emotion recognition for the first time, propose a parallel spatial-temporal hypergraph convolution structure, and capture the higher-order correlations of EEG signals for better feature extraction.

To capture the higher-order correlations among EEG channels, we construct the hypergraph of EEG channels by combining two kinds of correlations of EEG recordings in spatial and spectral domains, and updated the hypergraph automatically via STHGCN.

To capture the higher-order correlations inside the EEG series, we construct and update the hypergraph of the EEG series via designing a self-attention modal with learnable parameters.

Extensive experiments are conducted on two benchmark datasets. The experimental results show that our STHGCN consistently outperforms all state-of-the-art models.

Related work

Hypergraph learning

Hypergraph learning has made progress in problems where relations among data points extend beyond pairwise interactions, owing to its ability to extract patterns from higher-order relationships, and reduce information loss. With the popularity of deep learning, many methods of combining hypergraphs with neural networks have emerged. The earliest ones are the hypergraph neural network proposed by Feng et al. (2019) and the hypergraph convolutional network proposed by Yadati et al. (2019). Dynamic hypergraph convolutional neural network (Jiang et al. 2019) uses KNN and K-Means to dynamically update the hypergraph structure, improving the ability to capture data relationships and can extract local and global relationships of data. In order to better apply the graph learning strategy to hypergraphs, Huang and Yang (2011) proposed UniGNN, which not only solved the over-smoothing problem of deep hypergraph convolutions but also proved that hypergraphs have powerful representation capabilities. The addition of the attention mechanism also greatly improves the representation ability of the hypergraph. For example, Bai et al. (2021) used the attention mechanism to dynamically update the weights of hyperedges in a hypergraph.

There are a few studies combining hypergraph learning with prediction tasks, such as session-based recommendation (Xia et al. 2021), classification problems across biological networks (Lugo-Martinez and Radivojac 2017), stock selection (Sawhney et al. 2021), etc. However, there is no research bridging hypergraph neural networks and EEG-based emotion recognization, and we are the first to fill this gap.

Contemporary methods in EEG-based emotion recognition

EEG recordings consists of emotional features in different domains, like the time domain, space domain, and frequency domain. Paper (Deng et al. 2021; Ding et al. 2021; Wang et al. 2022) considered both temporal and spatial features and use them for EEG-based emotion recognition. Deng et al. (2021) linearly combined the capsule network with LSTM. TSception (Ding et al. 2021) used multi-scale 1D convolutional kernels to dynamically learn temporal features of EEG signals, and multiple 1D convolutions to globally learn spatial features of brain hemispheres. Wang et al. (2022) used Transformer to extract emotional features from EEG signals, which is based on the spatio-temporal self-attention mechanism. Recently, some methods consider emotional features in the spectral domain. LEDPatNet19 (Tuncer et al. 2021) proposed a multilevel hand-crafted feature generation network to better extract emotion-related EEG features. SST-EmotionNet (Jia et al. 2020) combines spectral, temporal, and topological features to construct two sets of 3D feature maps, which are input into the proposed network for extracting temporal-spatial features and spatial-spectral features. The idea of the method proposed by Shen et al. (2020) is to combine frequency, time, and topological features to form a 4D emotion feature representation. Xiao et al. (2022) used the attention mechanism to further utilize emotion-related EEG features. The above studies verify that EEG signals possess complementarity among the spectral-spatial-temporal emotional features.

Neurological studies have shown that emotional response is closely related to the cerebral cortex of the human brain, which is a 3D spatial structure and is not completely symmetrical between the left and right hemispheres (Lotfi and Akbarzadeh-T 2014). Thus, many studies have focused on capturing the relationships between channels to improve the accuracy of recognizing emotion. Due to the discrepancy of the cerebral cortex, Li et al. (2020) employed four directed recurrent neural networks(RNN) to keep the intrinsic spatial dependence, and captured the discrepancy information between two hemispheres for final classification. And Bagherzadeh et al. (2022) analyze effective brain connectivity to extract relationships among EEG channels. Graph-based methods are more capable of modeling inter-channel relationships, which help learn the representation of spatial relationships in EEG recordings. Feng et al. (2019) adopted a dynamical graph convolutional neural network (DGCNN) to extract more discriminative spatial features for emotion recognition. RGNN (Zhong et al. 2020) considered the biological topology among different brain regions to capture both local and global relations among different EEG channels. LGGNet (Zhonget al. 2020) also considered the local and global relationships between EEG channels, and obtains the global relationship by integrating the local relationships of the four functional brain regions. Utilizing the symmetry of the left and right hemispheres of the brain, and the symmetry of the upper and lower hemispheres of the brain, SFE-Net (Deng et al. 2021) performed data increments based on this, achieving a higher classification accuracy.

Since the cerebral cortex has a 3D structure, and the EEG signal is essentially a time sequence, the relationship of EEG recordings exists not only in the spatial domain, but also in the temporal domain. Similarly, emotion-related EEG features also have relationships in both temporal and spatial domains. Only considering spatial relationships is not enough to accurately represent EEG emotional features. However, it is still challenging to make full use of features in different domains to generate discriminative relationship representations for different emotions.

Method

In this section, we first introduce the notions and definitions used throughout this paper, and then we show how EEG recordings is modeled as a hypergraph. After that, we present our spatial-temporal hypergraph convolutional network for EEG-based Emotion Recognition. Finally, we show the way to optimize STHGCN.

Notations and definitions

Let $X^T=(S_1,S_2,\cdots ,S_T)\in R^{C\times T}$ denotes an EEG signal sample containing T timesteps, where C is the number of electrods. Each sample at a timestep t is represented as a set $S_t=(s_t^1,s_t^2,\cdots ,s_t^E,)\in R^E$ and $s_t^e(1\le e\le E)$ represents the EEG signal of an anonymous electrodes collected at the timestep t. $S_t$ of all timesteps are used to construct incidence matrix $M^T\in R^{T\times N}$. $M^T$ and $X^T$ are then transformed into temporal hypergraph $G^T$, where N is the number of hyperedges in $G^T$. Similarly, Let $X^E=({\mathcal{T}}_1,{\mathcal{T}}_2,\cdots ,{\mathcal{T}}_C)\in R^{T\times C}$ denotes an EEG signal sample containing C electrods, where T is the number of timesteps, $X^E$ is the transpose of $X^T$. Each sample at electrods c is represented as a set ${\mathcal{T}}_c=(t_c^1,t_c^2,\cdots ,t_c^E,)\in R^E$ and $t_c^t(1\le t\le T)$ represents the EEG signal of electrode c collected at an anonymous time. ${\mathcal{T}}_c$ of all electrodes are used to construct incidence matrix $M^E\in R^{C\times N^{\prime }}$. $M^E$ and $X^E$ are then transformed into channelwise hypergraph $G^E$, where $N^{\prime }$ is the number of hyperedges in $G^E$. The task of EEG-based emotion recognition is to predict the emotion label Y for any given hypergraph sets, $G^T$ and $G^E$.

Definition 1

(Hypergraph) Let $G=(V,E)$ denotes a hypergraph, where V is a set containing C unique vertices and E is a set containing N hyperedges. Each hyperedge $ϵ\in E$ contains two or more vertices and is assigned a positive weight $W_{ϵϵ}$, all the weights formulate a diagonal matrix $W\in R^{N\times N}$. The hypergraph can be represented by an incidence matrix $H\in R^{C\times N}$ where $H_{iϵ}=1$ if the hyperedge $ϵ\in E$ contains a vertex $v_i\in V$, otherwise $H_{iϵ}=0$. For each vertex and hyperedge, their degree $D_{\mathit{ii}}$ and $B_{ϵϵ}$ are respectively defined as $D_{\mathit{ii}}={\sum }_{ϵ=1}^N{W}_{ϵϵ}{H}_{iϵ}$, $B_{ϵϵ}={\sum }_{i=1}^C{H}_{iϵ}$. D and B are diagonal matrics.

Definition 2

(Hypergraph Convolution) Let $X^l\in R^{C\times F(l)}$, where F is the demension of vertex features. Hypergraph laplacian is defined as $▵=I-B^{-1/2}HW{H}^T{D}^{-1}{B}^{-1/2}$. To learn the interdependence among vertices, the hypergraph convolution update rule, an information transfer way from vertex to edge, and then from edge to vertex, is defined as,

$$\begin{array}{c}\hfill X^{l+1}=\sigma (B^{-1/2}HW{H}^T{D}^{-1}{B}^{-1/2}{X}^l{W}_l)\end{array}$$

where $\sigma (·)$ is an active function. $W_l\in R^{F(l)\times F(l+1)}$ is a learnable matrix. D and B are degree matrixes for normalization.

Spatial-temporal hypergraph

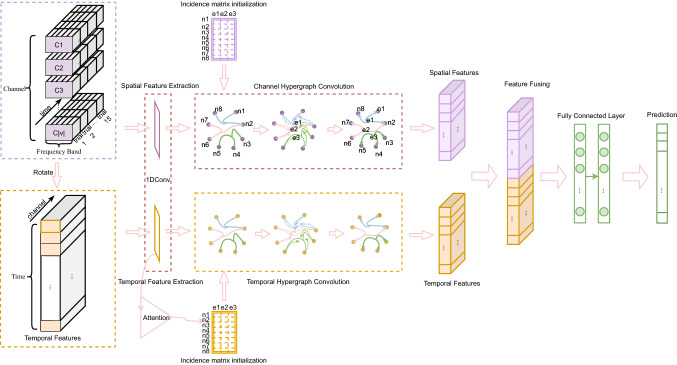
The overall stucture of the spatial-temporal hypergraph convolutional network (STHGCN) is illustrated in Fig. 1. The proposed STHGCN is used to decode EEG signals and extract spatial relationships of EEG channels and dynamic relationships of EEG series. It consists of a spatial block and a temporal block, which are independent but have a similiar network structure. The input of spatial block is original EEG recordings with constructed hypergraph containing spatial and spectral relations of EEG channels. The input of temporal block is rotated EEG recordings. The hypergraph containing temporal relations of EEG series was constructed via a self-attention mechanism in temporal block. In the end, the captured spatial and temporal features are fused for classification.

Fig. 1.

Architecture of STHGCN for emotion recognition. STHGCN is composed of a spatial block and a temporal block which share a similar structure. C denotes EEG channels. n and e denote nodes and edges of hypergraph

Hypergraph construction

Spatial Hypergraph Construction To capture the beyond pairwise relations between channels in EEG-based emotion recognition, we adopt a hypergraph $G^E=(V,E)$ to represent each EEG channel $c\in C$ as a node $v\in V$ and the subset of their relations as a hyperedge $ϵ\in E$. We inject domain knowledge by initializing spatial and spectral hyperedges among channels based on two types of relations: spatial correlations and spectral coherences.

Spatial Hyperedges: Electrods adjacent in space, usually produce a time series with similar variation trends. To leverage this finding, we define relations between EEG channels using Pearson correlation coefficient. Formally, we construct a hyperedge $epsilo{n}_1\in E_1$ that connects EEG signals having the same or similar shapes and increasing/decreasing simultaneously and proportionally.

Spectral Hyperedges: Similarly, we construct a hyperedge $epsilo{n}_2\in E_2$ that connects EEG signals whose trends can be described using same or similar linear systems, using spectral coherence coefficient. We combine these two kind of relations among channels of EEG recordings as hyperedges $E=E_1\cup E2$ to construct the hypergraph $G^E$, equivalently denoted by an incidence matrix $M^c\in R^{\mid V\mid \times \mid E\mid }$, with entries $h(v,ϵ)$ defined as:

$$\begin{array}{c}\hfill h(v,ϵ)=\left\{\begin{array}{cc}1,\hfill & v\in ϵ\hfill \\ 0,\hfill & v\notin ϵ\hfill \end{array}\right)\end{array}$$

The degree of each vertex v is obtained using a function d(v), and stored in a diagonal matrix $D_v\in R^{\mid V\mid \times \mid V\mid }$ as:

$$\begin{array}{c}\hfill d(v)=\sum _{ϵ\in E}w(ϵ)h(v,ϵ)\end{array}$$

$w(ϵ)$ represents the weight of hyperedge $ϵ$ which is set to 1 at initialization. The degree of each hyperedge $ϵ$ is obtained using a function $d(ϵ)$, and stored in a diagonal matrix $D_E\in R^{\mid E\mid \times \mid E\mid }$ as:

$$\begin{array}{c}\hfill d(ϵ)=\sum _{v\in V}h(v,ϵ)\end{array}$$

Temporal hypergraph construction To capture the beyond pairwise relations between timesteps in EEG-based emotion recognition, we adopt a hypergraph $G^T=(V,E)$ to represent each timestep $t\in T$ as a node $v\in V$ and the subset of their relations $r\in R$ as a hyperedge $ϵ\in E$. We inject time domain knowledge by constructing hyperedges among timesteps based on relations captured by self-attention mechanism. Time Hyperedges: The importance of different timesteps inside an EEG sequence for identifying emotions are different. Relations among timesteps in an EEG sequence is exploring the intra-correlation of EEG recordings, which could help marking significant period with more information of an EEG sequence. The self-attention mechanism has the ability to screen important information and can give more attention to the time period that is more important in emotion recognition. Herein is used to construct the incidence matrix $H\in R^{\mid E\mid \times \mid E\mid }$ of hypergraph .

The temporal hypergraph construction flowchart are shown in Fig. 2. As illustrated, the EEG recordings is organized as 3D sequences, containing spatial, spectral and temporal information. We first let each node represent a timestep, containing spatial and spectral features. Incidence matrix is initialized with zero. Then, self-attention mechanism is adopted to model the relationship between timesteps. And incidence matrix is constructed according to this. Finally node features and incidence matrix are combined to construct the temporal hypergraph.

Fig. 2.

The temporal hypergraph construction flowchart. n and e denote nodes and edges of the constructed hypergraph

The differences of emotion are presented in the degree of activation of different frequency bands, timesteps, and brain regions. There are some stable and discriminative patterns of higher-order relationships inside time series and among brain regions for each emotion state. Therefore, it is important to extract relations of EEG recordings in these specific patterns for emotion recognition.

Spatial hypergraph convolution

First, to learn the interdependence among EEG channels, we use a hypergraph convolution on the hypergraph $G^E$. We first define a single hypergraph convolution $SConv(·)$, where the input to the hypergraph convolution layer is a matrix of EEG emotional features $X_E^{(l)}\in R^{C\times T}$. The hypergraph convolution layer updates $X_E^{(l)}$ to new features $X_E^{(l+1)}$, using their relationships represented in hypergraph $G^E$. Following (Jiang et al. 2019, we define the hypergraph Laplacian as $▵=I-D_V^{-1/2}HW{D}_e^{-1}{H}^T{D}_V^{-1/2}$ resulting in the hypergraph convolution update rule as:

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill X_E^{(l+1)}& =SConv(X^{(l)},H,\mathrm{\Theta })\hfill \\ \hfill & =ELU(D_V^{-1/2}HW{D}_e^{-1}{H}^T{D}_V^{-1/2}{X}_E^{(l)}\mathrm{\Theta })\hfill \end{array}\end{array}$$ 1

$\mathrm{\Theta }\in R^{T\times T}$ is learnable parameters, $ELU(·)$ is exponential linear unit activation. We set $W=I$ for initialization. Then, a 1D spatial CNN is used to better represent spatial features of EEG signals for feature fusion.

Temporal hypergraph convolution

To learn the interdependence between EEG channels, we use a hypergraph convolution on the hypergraph $G^T$, We first define a single hypergraph convolution $TConv(·)$, where the input to the hypergraph convolution layer is a matrix of EEG emotional features $X_T^{(l)}\in R^{T\times C}$. The hypergraph convolution layer updates $X_T^{(l)}$ to new features $X_T^{(l+1)}$ using the same strategy with $SConv(·)$. Then, a 1D temporal CNN is used to better represent temporal features of EEG signals for feature fusion.

Learning to predict and network optimization

We employ spatial and temporal hypergraph convolution concurrently to obtain spatial and temporal representations of EEG recordings respectively. Then, these two representations are concatenated. And label prediction is implemented through two fully-connected layer with softmax activation.

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill \widehat{I}& =softmax(W_{f2}\times (W_{f1}\hfill \\ \hfill & \times [SConv(·),TConv(·)]+b_1)+b_2)\hfill \end{array}\end{array}$$ 2

where $W_{f1}$, $W_{f2}$, $b_1$ and $b_2$ are learnable parameters. In this paper, the classification cross entropy is used as loss function, which is defined as follow:

$$\begin{array}{c}\hfill L=-\sum _{i=1}^N\sum _{k=1}^M{y}_{\mathit{ik}}log(p(\widehat{y_{\mathit{ik}}}))\end{array}$$

where $y_{\mathit{ik}}$ is a binary indicator meaning the label of sample i is k, $p(\widehat{y_{\mathit{ik}}})$ represents the probability that label prediction of sample i is right.

Experiment setup

Datasets

We validate our model on SEED (Zheng and Lu 2015) SEED-IV (Zheng et al. 2018) datasets.

SEED contains three different states of emotions, namely positive, negative, and neutral. EEG recordings were collected from fifteen participants while they were watching stimulus videos. The participants were asked to give feedback immediately after each experiment. Experiments are designed for each participant on three sessions with each session using 15 video clips repeatedly. The EEG series of 62 channels were recorded by an EEG cap and down-sampled into 200Hz. Emotion-related features are pre-computed over different frequency bands for each EEG sample in each channel.

SEED-IV contains four different states of emotions, namely happy, sad, fear, and neutral. Similiar to SEED, the experiment consists of 15 participants and the EEG recordings contains 62 channels. Three experiments are designed for each participant on three sessions, and 24 stimuli video clips in each session are different. DE feature is pre-computed over five frequency bands for each EEG sample in each channel.

Training step

We implement the STHGCN on NVIDIA RTX 3080 GPU. In the training process, we use the RAdam optimizer with learning rate $1e-3$ with multi-step decay to $1e-7$. The training epoch is set to 600 and the batch size is 32. For each experiment, we randomly shuffle the samples and use 5-fold cross validation.

Evaluation metrics

To show the performance of the proposed method, we compare it with several latest methods on SEED and SEED-IV datasets, including graph methods, like DGCNN, RGNN, and some other SOTA models. We use the recognition accuracy to show the performance of the proposed model. Also, the standard deviation, reflecting the degree of dispersion of a dataset, is adopted to verify the robustness of the proposed model.

Results and analysis

Comparison with baselines

We compare our model with baseline models on SEED and SEED-IV datasets. The left part of Table 1 presents the average recognition accuracy and the standard deviation of these models for EEG based emotion recognition on SEED dataset. The proposed STHGCN achieves the state-of-the-art performance on the SEED dataset. Obviously, deep learning models outperform the traditional SVM. DGCNN only considers the spatial relationship of EEG channels, and employs graph convolution to extract spatial information. BiHDM uses two directional RNNs to extract spatial information of EEG signals, reaching 93.12$\%$ on classification accuracy. R2G-STNN extracts spatial information by hierarchically learning improtant information from local to global.

Table 1.

The performance comparison of the state-of-the-art models on the SEED and SEED-IV dataset

Model	SEED		SEED-IV
	ACC($\%$)	STD($\%$)	ACC($\%$)	STD($\%$)
SVMWang et al. (2011)	83.99	9.72	56.61	20.05
DBNZheng and Lu (2015)	86.08	8.34	66.77	7.38
DGCNNSong et al. (2018)	90.40	8.49	69.88	16.29
BiDANNLi et al. (2018)	92.38	7.04	70.29	12.63
BiHDMLi et al. (2020)	93.12	6.06	74.35	14.09
R2G-STNNLi et al. (2019)	93.38	5.96	68.51	12.37
RGNNZhong et al. (2020)	94.24	5.95	79.37	10.54
4D-CRNNShen et al. (2020)	94.74	2.32	81.27	11.62
SST-EmotionNetJia et al. (2020)	96.02	2.17	84.92	6.66
EeTWang et al. (2022)	96.28	4.39	83.27	8.37
STHGCN	97.51	2.01	85.99	7.33

4D-CRNN represents EEG recordings in spatial, spectral and temporal domain achieving 94.74$\%$. SST-EmotionNet takes the complementarity of spatial, spectral and temporal information into consideration, achieves better performance with an accuracy of 96.02$\%$. Adopting transformer structure, EeT achieves the accuracy of 96.28$\%$, demonstrating the effectiveness of updated transformer with ‘joint attention’. Different from the fomer methods, STHGCN adopts feature hypergraph to construct the dynamic relationship inside EEG series and the spatial relationship among EEG channels, which enables our model to comprehensively capture valuable features from EEG signals for emotion recognition. Compared with the baseline models, the accuracy of our model is further improved. In addition, the left map of Fig. 3 shows the confusion graph of our model on SEED dataset. The results indicate that positive emotion is slightly easier to recognize for STHGCN than negative and neutral emotion.

Fig. 3.

Confusion map of STHGCN. The left graph is on SEED and the right graph is on SEED-IV

The right part of Table 1 presents the performance of all models on the SEED-IV dataset. The proposed STHGCN achieves the state-of-the-art performance on the SEED-IV dataset. For the four-category classification task, DBN achieved an accurracy of 66.77$\%$, and the graph-based network DGCNN and RGNN further improve the accuracy to 69.88$\%$ and 79.37$\%$, respectively. BiDANN and BiHDM fully utilize the bi-hemispheric discrepancy of EEG recordings to achieve 70.29$\%$ and 74.35$\%$ repectively. SST-EmotionNet and EeT add attention mechanism to learn emotion features from different domains, achieving 84.92$\%$ and 83.27$\%$ respectively. STHGCN focuses on modeling channelwise and dynamical relationship of EEG recordings. Compared with the baseline models, the accuracy of our model is further improved to 85.99$\%$. In addition, the confusion graph is shown in the right of Fig. 3. The confusion graph presents that STHGCN does well in the recognition on happy and neutral emotion. Sad and fear emotion may be more confused than happy and neutral emotion. The recognition accuracy of fear emotion was 68%, 15% easily confused with sad emotion, and 11% neutral emotion. We infer that the extracted relation patterns among EEG channels for fear emotions are not so unique and share some similarities with sadness and neutral emotions.

We can deduce from the above experiments that deep learning models outperform traditional ones, considering different domain information of EEG signals can improve the performance on emotion recognition, and fear emotion is more confused comparing to happy, sad and neutral.

Higher-order relationships in EEG recordings

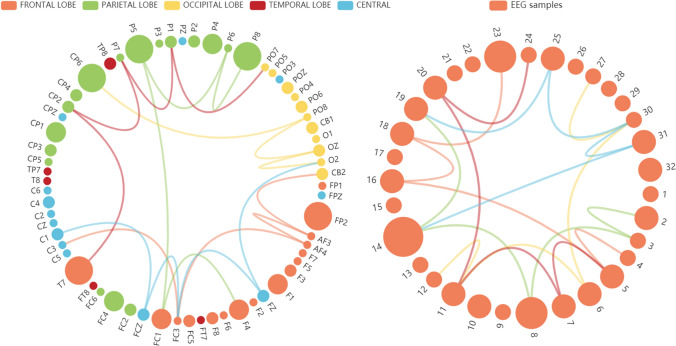
The left hypergraph in Fig. 4 illustrates correlations among EEG channels with different dot colors representing different brain regions and different curve colors representing different hyperedges. The size of dots illustrates the importance of EEG channels. Conceptually, if a channel appears in more hyperedges, it is relative with more channels, which means that the channel is more important. And a hyperedge with a higher weight illustrates a stronger connection among channels linked by it. It is clear from Fig. 4 that important channels are most on the frontal lobe and parietal lobe, indicating that these regions are strongly related to the emotion processing in the brain. As we can see, the relationships extracted by hypergraph indicating that local connections and global connections are both valuable for emotion recognition. Through the experiment, we note that modeling inter-channel dependence through spatial correlation as hyperedges drastically supports valuable channels selection. And more importantly, hypergraphs effectively capture higher-order relations among EEG channels.

Fig. 4.

Five strongest higher-order channel correlations and temporal correlations captured by Hypergraph. The left graph is obtained by spatial hypergraph convolutional network. The right graph is obtained by temporal hypergraph convolutional network

The right hypergraph in Fig. 4 illustrates correlations inside EEG series with different dot colors representing different timesteps and different curve colors representing different hyperedges. The size of dots illustrates the importance of timesteps. We have tested different lengths of EEG series and adopted 32 as the best choice. We depict that periodicity maybe is existed in EEG series. Conceptually, if a stamp appears in more hyperedges, it is relative with more timesteps, which means that the stamp is more important. And a hyperedge with a higher weight illustrates a stronger connection of timesteps linked by it. It is clear from Fig. 4 that important samples which contribute more on emotion recognition are selected to give higher weight. Through the experiment, we note that modeling dependence inside EEG series through temporal correlation pays more attention to valuable samples. And hypergraph effectively capture higher-order relations inside EEG series.

Model component ablation study

Ablation studies on two blocks

We conduct ablation studies on two blocks: spatial block and temporal block. Table 2 presents that the two-block structure outperforms the single-block structure(only with spatial block or temporal block). For example, the accuracy of two-block structure increases by 15.75$\%$ and 2.40$\%$ than the model only with spatial block or temporal block. The results show that two-block structure effectively uses the spatial-spectral features to construct channelwise hypergraph, uses temporal features to construct temporal hypergraph, and finally improves the classification accuracy. What’s more, the variant model only with spatial block has a worse performance than the one only with temporal block. It indicates the importance of finding dynamic correlations of EEG signals.

Table 2.

The performance comparison of variant models on the SEED dataset

Model	ACC($\%$)	STD($\%$)
SHGCN	81.76	5.58
THGCN	95.11	4.88
STHGCN	97.51	2.01

On the effectiveness of hypergraphs

Most existing graph-based models ignore higher-order relationships, only focus on pairwise patterns of EEG channel correlations. And graph methods left dynamical relationship inside EEG series behind. These limit the accuracy of emotion recognition. To study the effectiveness of hypergraphs, we use identity matrix to replace incidence matrix of each hypergraph, without modeling correlations of spatial relationships, temporal relationships of EEG recordings. That is, no hyperedge exists. As shown in Table 3, hyperedges play an important role in emotion recognition. We observe that the accuracy decreases as we remove hyperedges representing correlations of EEG channels and relationships of EEG series, and performs the worst after all hyperedges are removed. Especially when hyperedges representing temporal relationships are removed, the accuracy drops from 97.51$\%$ to 94.69$\%$.

Table 3.

The performance comparison of variant hypergraphs on the SEED dataset

Model	ACC($\%$)	STD($\%$)
STHGCN	97.51	2.01
-Spatial	95.68	3.08
-Temporal	94.69	4.73
-Spatial, -Temporal	94.36	4.74

Conclusion and future

In this paper, we propose the STHGCN model for EEG emotion recognition. STHGCN first explores dependencies among EEG channels via channel hypergraph and captures dynamic correlations via temporal hypergraph. Previous studies based on the graph method exist a problem that they could only extract dependencies between two EEG channels, ignoring the higher-order dependencies among multiple EEG channels, which can be solved by proposed spatial hypergraph convolution. Then, temporal hypergraph convolution with a self-attention modal is proposed to capture dynamic correlations of EEG recordings. Moreover, to learn spatial and temporal relationships of EEG recordings accurately, the hypergraph is updated automatically through hypergraph convolution. Through ablative and qualitative experiments on SEED and SEED-IV, we probe the effectiveness of STHGCN, having better performance than all baselines.

Discussion

Recently, more graph-based methods in EEG recordings representation are proposed for their ability to extract relations between pairwise EEG channels. However, the higher-order relationship among EEG channels and the higher-order relationship among EEG series have not been explored. To fill this gap, our study constructs feature hypergraphs for the first time to extract higher-order relationships in temporal and spatial for EEG-based emotion recognition. Similarly, Different higher-order relation patterns may exist in EEG recordings in different cognitive functions. For example, Zhang et al. (2019) have used the graph method to extract spatial relations for movement intention detection. Thus, extracting spatial and temporal relations could help classify different mental states for different downstream tasks based on EEG.

The results of the proposed model show that higher-order relationships in space and time exist in EEG recordings. And our analysis shows that the valuable channels are distributed mostly in the frontal and parietal lobes. This result is consistent with empirical evidence that the frontal and parietal lobes are related to emotion. The former study did not involve the relation of EEG time series. And our analysis shows that it is worth paying more attention to.

Our model mainly focuses on the spatial relationship among channels, which may be too fine-grained for emotion recognition and prone to high variance between subjects. In the future, we aim to explore the relationship among different brain regions using a hypergraph to confirm our conjecture and reduce the impact of individual differences. Our work is only tested on datasets based on a discrete emotion model, which limits the extendency of our model and the explanation of the result. In the future, we aim to test the effectiveness of hypergraphs on datasets based on emotion dimensional models.

Data Availibility Statement

The datasets analysed during the current study are available in the SEED repository,https://bcmi.sjtu.edu.cn/~seed/index.html.

Declarations

Conflicts of interest

All authors certify that they have no affiliations with or involvement in any organization or entity with any financial interest or non-financial interest in the subject matter or materials discussed in this manuscript.