Influence of Charges Deposited on Membranes of Human Hyperdirect Pathway Axons on Depolarization During Subthalamic Deep Brain Stimulation

Abstract

Objective.

The motor hyperdirect pathway (HDP) is a key target in the treatment of Parkinson’s disease with deep brain stimulation (DBS). Biophysical models of HDP DBS have been used to explore the mechanisms of stimulation. Built upon finite element method (FEM) volume conductor solutions, such models are limited by a resolution mismatch, where the volume conductor is modeled at the macro scale, while the neural elements are at the micro scale. New techniques are needed to better integrate volume conductor models with neuron models.

Approach.

We simulated subthalamic DBS of the human HDP using finely meshed axon models to calculate surface charge deposition on insulting membranes of nonmyelinated axons. We converted the corresponding double layer extracellular problem to a single layer problem and applied the well-conditioned charge-based boundary element fast multipole method (BEM-FMM) with unconstrained numerical spatial resolution. Commonly used simplified estimations of membrane depolarization were compared with more realistic solutions.

Main result.

Neither centerline potential nor estimates of axon recruitment were impacted by the estimation method used except at axon bifurcations and hemispherical terminations. Local estimates of axon polarization were often much higher at bifurcations and terminations than at any other place along the axon and terminal arbor. Local average estimates of terminal electric field are higher by 10–20%.

Significance.

Biophysical models of action potential initiation in the HDP suggest that axon terminations are often the lowest threshold elements for activation. The results of this study reinforce that hypothesis and suggest that this phenomenon is even more pronounced than previously realized.

1. Introduction

Multiscale modeling of deep brain stimulation (DBS) [1],[2],[3] is an active area of research. The motor hyperdirect pathway (HDP) [4], which directly connects the motor cortex to the subthalamic nucleus (STN), is considered a key target in the treatment of Parkinson’s disease symptoms with deep brain stimulation (DBS). Recently, biophysical models of the human HDP have been used to explore the therapeutic mechanisms of subthalamic DBS [1],[5]. However, comparison of clinical and model-predicted thresholds for evoked potentials implies that model detail remain insufficient for precise prediction of pathway recruitment [6],[7],[8].

Oversimplified axonal anatomy and branching might explain much of the prediction error [8]. Heterogeneous charge deposition and voltage-gated channel distribution on variegated membrane surfaces, such as at bifurcations and terminals, may partly explain lingering errors in predictions of axon recruitment in response to extracellular electric fields. Built upon finite element method (FEM) volume conductor solutions, models of DBS pathway recruitment are often limited by a resolution mismatch which ignores local charge deposition on neuronal membranes. Further, FEM models, which can accurately estimate charge deposition on anatomically realistic axons at the micron-scale, are computationally expensive [9],[10]. Lastly, the spatial derivative of the external macroscopic electric field is frequently used as an estimator of neuronal recruitment (activating function), ignoring the effect of unique neuronal geometry on membrane polarization (cf., for example, [11],[12]).

However, accurate high-resolution implementation of membrane surface charges might alter estimates of neuronal recruitment, particularly where axons bifurcate and terminate [13],[14],[3]. This could be especially true for the HDP, which emits an axon collateral that terminates in the STN with multiple bifurcations [15],[16],[17]. From quasi-electrostatic theory, both terminations and bifurcations are natural targets for strong charge accumulation and thus for the strong electric current induction within axons.

Estimation of induced charges on complex neuronal membrane surfaces presents a challenging numerical problem which classic finite element methods struggle to solve [9],[10]. A layer of electric dipoles, known as the double layer, forms across the thin membranes. Modeling this phenomenon accurately in three dimensions and at multiple scales is a challenging task. However, when dealing with an insulating membrane at the end of initial polarization [23],[29],[21],[22], it is feasible to describe the extracellular solution using an equivalent single layer of charges. This allows for the direct application of the recently developed charge-based boundary element fast multipole method (BEM-FMM) formulation [18],[19],[20], which possesses inherent capabilities for multiscale modeling due to an unconstrained spatial numerical resolution. BEM-FMM enables micron-scale numerical solution of extracellular fields for axon models which are up to 100 mm (~20 mm in this study) long and 1 μm thin with multiple bifurcations and terminations in an external electric field induced by active DBS contacts. Accurate mesh models of HDP axon membrane surfaces can be composed of several millions of triangular facets, each with the size of 0.2 μm or so. This leads to a scale ratio of 20 mm/0.2 μm or 100,000:1, which is inappropriate for traditional finite element method solvers.

In the present study, modeling was used to compare the recruitment solutions with and without membranes, respectively, i.e., in an otherwise homogeneous volume conductor. To quantify the differences in the neuronal recruitment, we computed all three quantities – extracellular potential, electric field, and activating function [32],[33],[34] – at the axonal centerline after averaging over its gross-section. Special attention was paid to the effect of bifurcation and termination on estimates of membrane depolarization. The results of this study include data obtained from the first 60 axons of HDP as referenced in [1], with 40 axons being retained for analysis. Additionally, data for various axonal diameters have also been included in the study.

The sensitivity of axon terminals to electric fields and the role of terminal membrane potential have been recognized for decades [24],[25],[26],[27],[28],[3] with a number of important conclusions about higher (up to four times) susceptibility to polarization for different stimulation modalities. The effect of bifurcations was investigated too [3]. The primary insight of the present study is that traditional volume conductor methods used in these references might still somewhat underestimate the electric field and severely underestimate the activating function at neuronal bifurcations as well as terminations and may, therefore, lead to underestimations of axon recruitment in models of subthalamic DBS.

2. Materials and Methods

2.1. Creating 2-manifold membrane surfaces for axons collaterals from a graph

Initially, every axon is represented by an arbitrary graph of simply interconnected spatial nodes. The graph includes (i) nodes in 3D; (ii) edges or segments with 2 points each; (iii) axon radii for every edge and; (iv) any other labeled edge properties. An example of nodes and edges of a graph is shown in Fig. 1a. As a first processing step, the graph is automatically refined by edge split to have the edge length less than or equal to, let’s say, the anticipated axonal diameter. This operation illustrated in Fig. 1b is necessary for a good-quality mesh. Next, all contiguous oriented paths of the nodes - graph centerlines (different colors, 6 in Fig. 1c) – are automatically identified. Every such path has two termination nodes. Every termination node is either a physical termination, or a bifurcation, trifurcation, etc. node. After that, a tubular open triangular surface mesh is automatically created for every path using the method of a moving cross-section (or extrusion along a curved 3D path) shown in Fig. 2a and applicable to any cross-sectional shape.

Fig. 1.

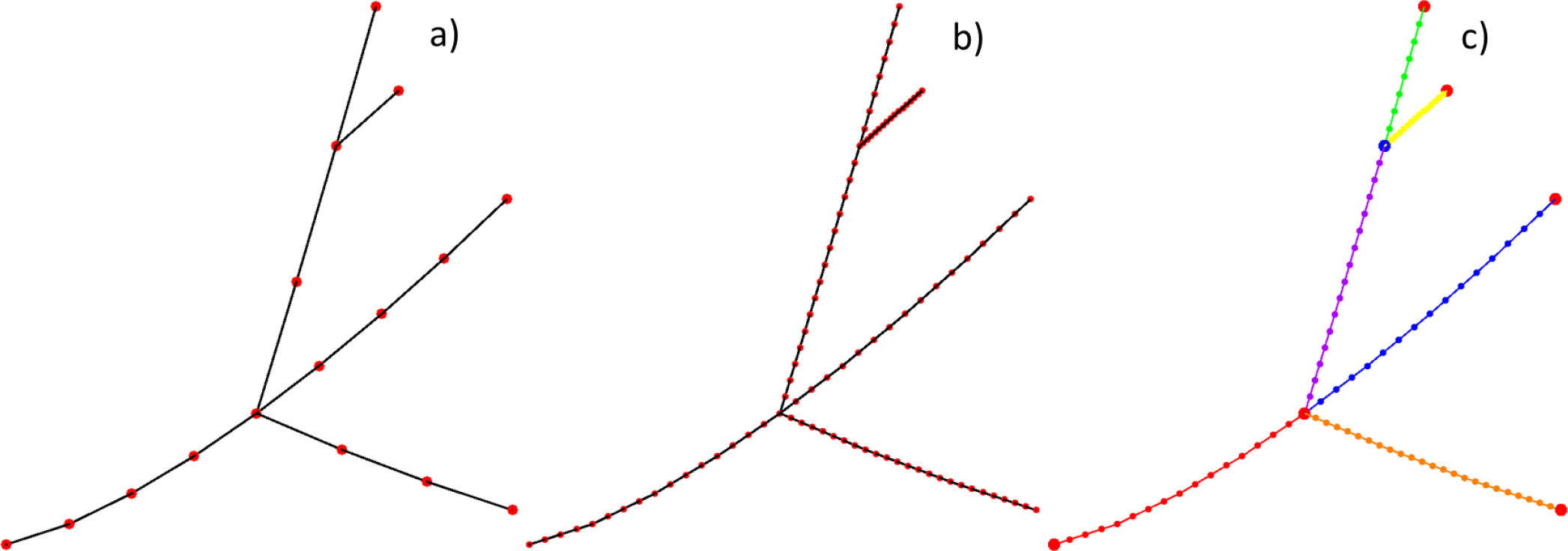
a) Initial graph – a set of nodes, segments or edges, and segment properties (e.g., a radius). b) Graph refined by edge split following segmental properties. c) Contiguous oriented paths of the nodes - graph centerlines (different colors, 6 here). Every path has two termination nodes. Every termination node is either a physical termination, or a bifurcation, trifurcation, etc. node.

Fig. 2.

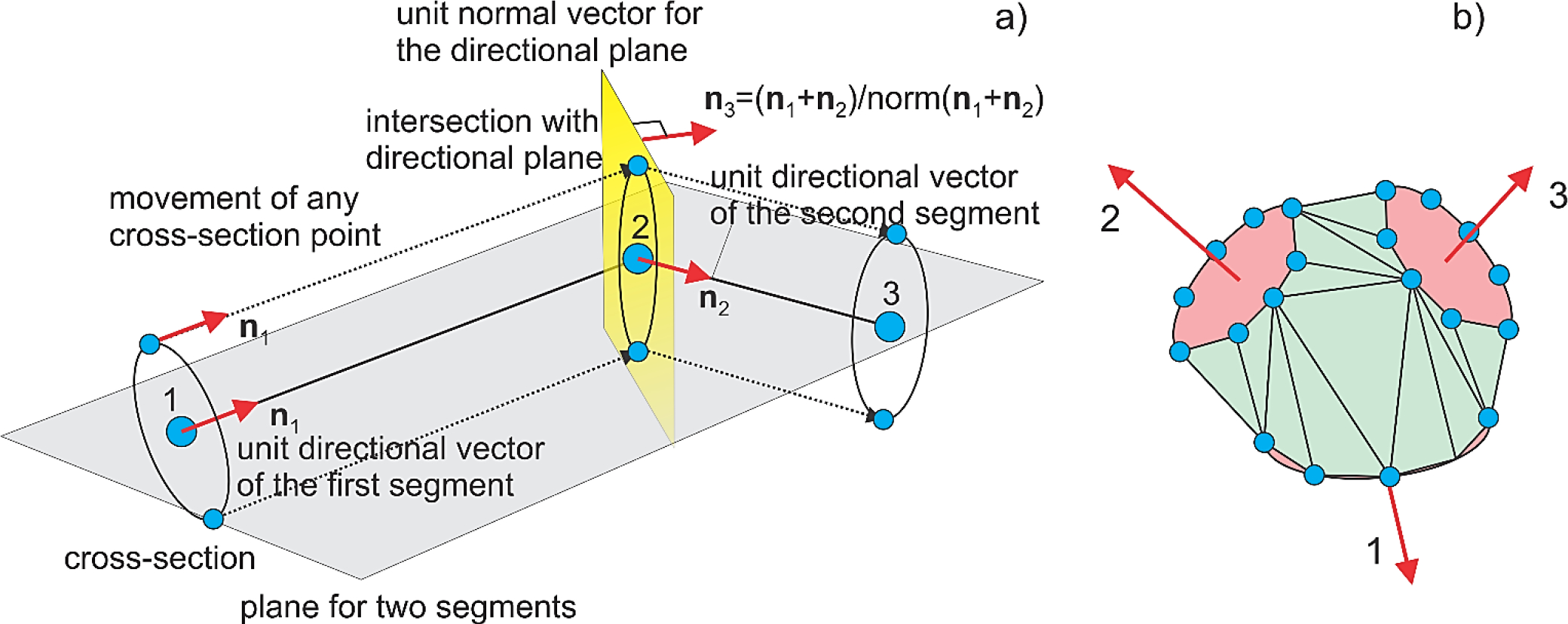
a) Method of a moving cross-section (or extrusion along a curved 3D path) used to create a tubular surface mesh. The key is a directional plane shown in yellow in a) that is formed for every two adjacent segments. This plane is used to add the new cross-section. b) Convex-hull mesh formed from three adjacent cross-sections of a bifurcation fork. The cross-sections are selected by checking the condition of no unused(inner) nodes. Facets belonging to the cross-sections have been subtracted.

The open tubular meshes are automatically joined together via special junction meshes (Fig. 2b). The junction mesh is based on the nodes of termination rings for every tubular mesh entering the given fork. It is a convex-hull mesh but without caps. The termination rings are chosen in such a way that the resulting junction mesh is manifold. This is done by selecting either the last ring, or the second last ring, etc. for every tube. An illustration of a complete watertight 2-manifold graph mesh for a graph from Fig. 1a is given in Fig. 3. The termination cap (Fig. 3c) can be either flat or hemispherical (used in this study). The corresponding mesh generator is available online.

Fig. 3.

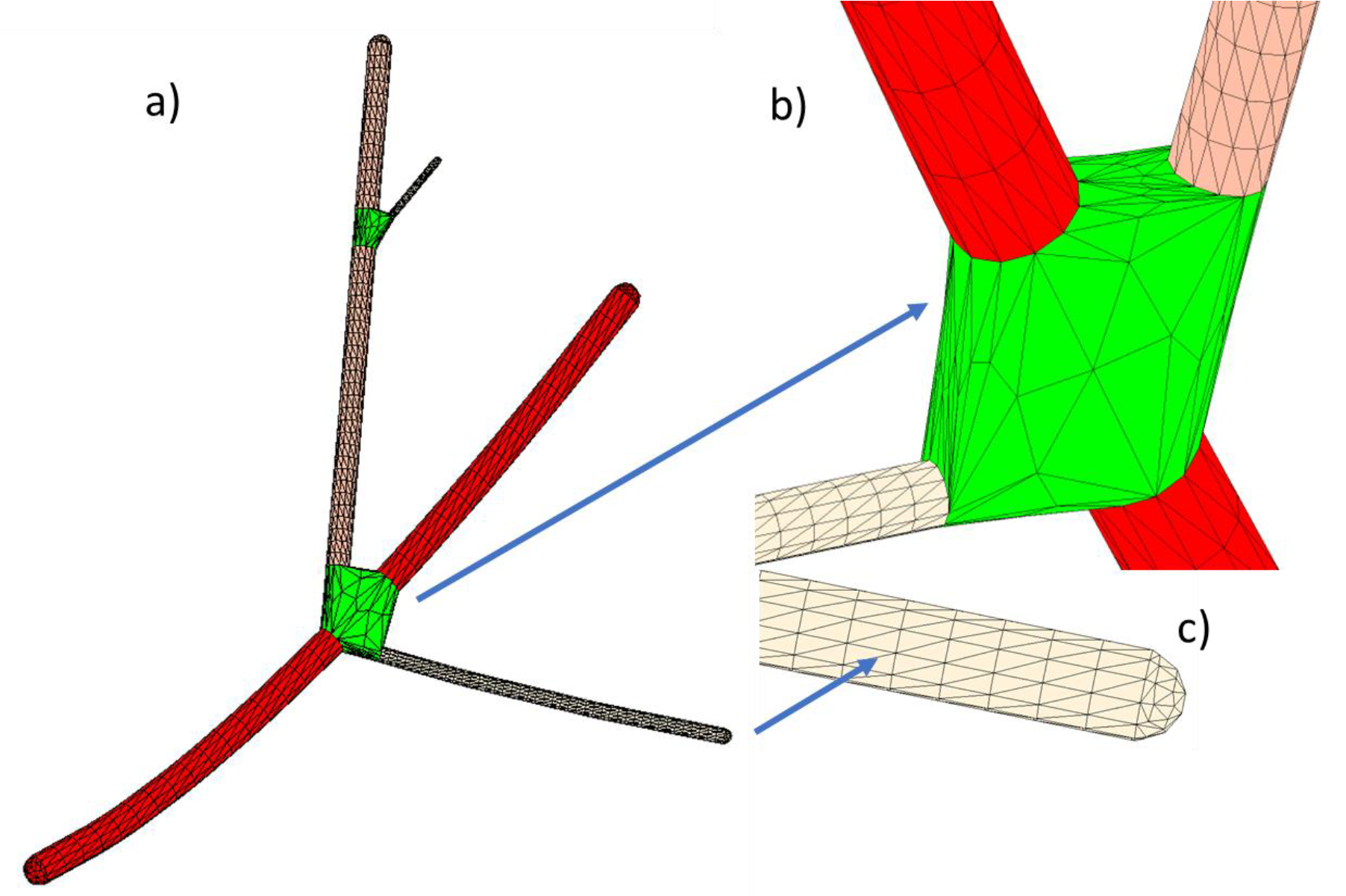
a) Illustration of a complete watertight 2-manifold graph mesh for a graph from Fig. 1. b) Junction (trifurcation) topology. c) Termination topology (can be either flat or hemispherical).

2.2. Constructing models for HDP axons and DBS lead

The HDP graph topology adapted from Ref. [1] follows Fig. 4a. The STN volume is omitted to better visualize the collaterals. Fig. 4a displays 60 axons of cortical pyramidal motor neurons that have an axon collateral which terminates in the STN. They were chosen from ~8,000 arborized motor axons of Ref. [1]. Every such axon will have exactly two bifurcations shown in Fig. 4b. There, we follow Hack’s (or classic) stream (or level) order also depicted in Fig. 4b. There, the root axon (red) has Hack’s level 1; the next-level axon (green) has Hack’s level 2, the last-level axon (blue) has Hack’s level 3. We consider only non-myelinated axons in this study.

Fig. 4.

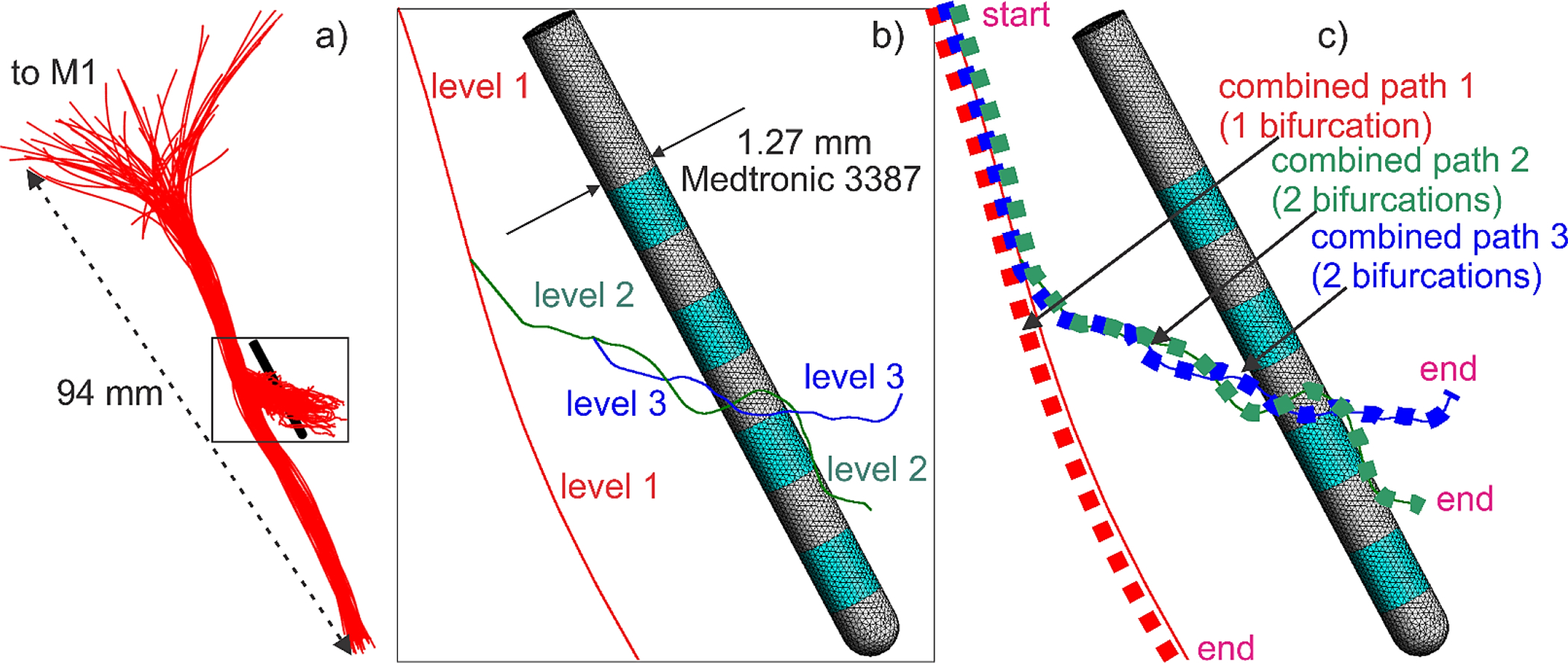
a) Initial HDP graphs with 60 axons. b) Axon #1 with two bifurcation points and three centerline paths. Hack’s level 1 is red; Hack’s level 2 is green; Hack’s level 3 is blue. c) Three continuous combined centerline paths for evaluating the potential, the field, and the field derivative along the path for a typical axon (axon #1). Start and end terminals (for Table 1 and Table B1) are shown.

Fig. 5 displays assembly of 60 axonal membrane meshes all at once with some intermediate zooming steps a) through g). The overall zoom from Fig. 5a to Fig. 5g is 4,000:1. Following data of [35],[36], three sets of axonal diameters were investigated: i) 2μm (level 1), 2μm (level 2), 2μm (level 3); ii) 2μm (level 1), 1μm (level 2), 1μm (level 3) and; iii) 1μm (level 1), 1μm (level 2), 1μm (level 3). It should be noted that non-myelinated axons are even thinner than the myelinated ones. The membrane mesh for every axon contains ~0,7 million facets (~2.8 million after refinement). A Medtronic 3387 DBS lead was constructed following dimensions of Ref. [38] – cf. Fig. 4b. Outermost contacts 0 and 3 were driven with the current of ± 1 mA (the cathode contact 0 is on the bottom), which corresponds to a bipolar electrode excitation. We were looking for an instantaneous idealized-amplitude electric-field field estimation. This means that no cumulative charge deposition due to pulse width or capacitive charging have been considered.

Fig. 5.

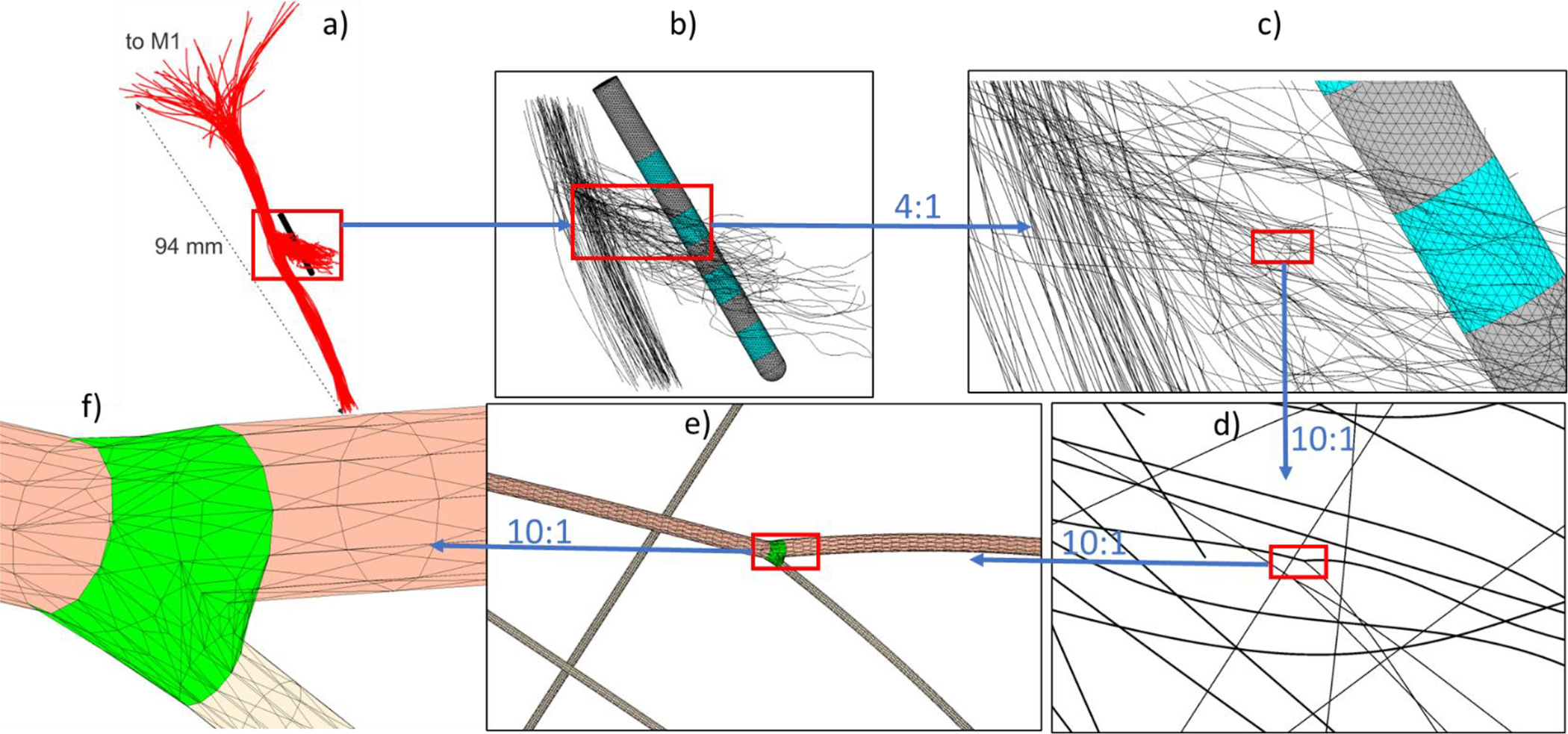
Assembly of 60 axonal meshes all at once with intermediate zooming steps a) through f). The overall zoom from a) to f) is 4,000:1. Average triangle sizes for a 1 μm thick axon in f) are approaching 0.2 μm after mesh refinement via barycentric triangle subdivision.

2.3. Axon model at the end of initial polarization [21]

Consider a simplified axonal model in the form of a thin membrane with surface capacitance $C_{\mathrm{m}}$, enclosing an intracellular volume with intracellular resistivity $r_{\mathrm{i}}$ (being significantly smaller than an extracellular resistivity), and with a typical dimension $d_c$ (the axonal radius). When a primary electric field is applied, the membrane capacitance will be locally charged (or discharged). This very fast charging process – called initial polarization [21],[22] – proceeds with the cellular time constant ${\tau }_{\mathrm{c}}=\left(d_{\mathrm{c}}{r}_{\mathrm{i}}\right)C_{\mathrm{m}}$. Estimating $d_{\mathrm{c}}~1\mu \mathrm{m}$ as well as $r_{\mathrm{i}}~100\mathrm{\Omega }\mathrm{c}\mathrm{m},C_{\mathrm{m}}~1\mu F/{\mathrm{c}\mathrm{m}}^2$ [30],[9] confirms that ${\tau }_{\mathrm{c}}<1\mu s$ [21]. During the fast initial polarization, the ionic currents are still very small and can be neglected compared to the capacitive currents [21],[22],[23],[29]. Our main interest lies in obtaining a “steady-state” solution at the end of the initial polarization. A detailed asymptotic analysis of the coupled membrane equations [21] at the end of the initial polarization states that

1. the membrane itself becomes non-conducting (insulating) since the capacitive membrane current density, $i_{\mathrm{m}}=C_{\mathrm{m}}\partial {\phi }_{\mathrm{m}}/\partial t$ (${\phi }_{\mathrm{m}}$ is the transmembrane potential), approaches zero while the ionic current density is still negligibly small and;

2. the conducting intracellular space becomes strictly equipotential, ${\phi }_{\text{inside}}=const$, with a constant resting potential [21] since no electric current within a closed cell volume isolated by the nonconducting membrane can exist in a conservative (curl-free) field.

Thus, the axon (cell) model becomes a non-conducting charged membrane separating the intra- and extracellular conducting spaces, respectively. This is a steady-state DC conduction model.

2.4. Steady-state solution at the end of initial polarization

The steady-state DC conduction model is applied here, which possesses three main features [21]:

1. the solution for the extracellular potential ${\phi }_{\mathrm{e}}$ only uses the boundary condition of zero transverse current at the (outer) membrane surface. It is decoupled from the intracellular solution. Such a solution coincides with the potential ${\varphi }_{\mathrm{e}}$ for a completely non-conducting axon (cell). This fact follows from the uniqueness of the solution for the exterior Neumann problem;

2. the solution for the intracellular potential ${\phi }_{\mathrm{i}}$ is trivial, meaning that ${\phi }_{\mathrm{i}}=const$;

3. the solution for the transmembrane potential is ${\phi }_{\mathrm{m}}={\phi }_{\mathrm{i}}-{\varphi }_{\mathrm{e}}$.

At first glance, an alternative approach is to keep the intracellular space conducting, assign a very small yet finite membrane thickness corresponding to its surface capacitance $C_{\mathrm{m}}$, and then solve the coupled problem. This “direct” thin-membrane solution is very difficult numerically since it is characterized by both a double-layer (dipolar) charge density and a single-layer (monopolar) charge density deposited on the membrane. However, it is equivalent to the simpler solution described above which only needs the single-layer charge density. Appendix A illustrates this fact via two complete analytical thin-membrane solutions: for a sphere and a cylinder, respectively. In both cases, the extracellular potential and the deposited double-layer charge density $p_{\text{shell}}$ are automatically obtained from the simpler solution as ${\phi }_{\mathrm{e}}={\varphi }_{\mathrm{e}}$ and $p_{\text{shell}}={\epsilon }_0{\varphi }_{\mathrm{e}}$.

2.5. Value of steady-state solution at the end of initial polarization

First, the extracellular solution with the insulating membrane serves as an initial condition to the problem governing the subsequent neuronal activation – evolution of membrane potential – that proceeds with a much larger membrane time constant [21]. When the physiological state of the cell changes, the transmembrane currents are indeed no longer zero.

Second, an accurate bi-domain modeling indicates that currents flowing across the cell membrane have only a small effect on the usually large extracellular space [21],[9]. Therefore, the extracellular solution with the insulating membrane may also serve as an approximate solution for the extracellular potential, field, and activating function during the entire time course.

2.6. Computing steady-state solution at the end of initial polarization via BEM-FMM

The recently developed charge-based boundary element fast multipole method (BEM-FMM) [18],[19],[20] enables us to solve the extracellular problem shown in Fig. 5 either for an individual axon or for all axons simultaneously. We use the model of non-conducting axons with the single-layer charge density, which is equivalent to the model of the insulating membrane for the extracellular solution. In contrast to FEM, BEM-FMM could be ideal for this kind of problem since it does not require meshing the large extracellular space (including the DBS lead and the axon(s)) at micrometer scale. It operates with the induced charge density residing at the membranes and solves a well-conditioned Fredholm equation of the second kind. The detailed formulation can be found in Supplement to Ref. [18]. For a single axon with 1 million facets, BEM-FMM reaches a relative residual of 10⁻¹² in ~30 sec using a 2.6 GHz multicore machine. Solution accuracy is controlled by mesh refinement. The corresponding computer code (MATLAB) is available online.

2.7. Computing “effective” potentials and fields at axon centerlines

The 1D cable equation (cf. [31],[32],[33],[34]) uses the potential or the corresponding activating function, $f\left(z\right)=d^2{\varphi }_{\mathrm{e}}/d{z}^2=-d{E}_{\mathrm{z}}/dz$ [32],[33],[34], of the collinear extracellular field on the axonal centerline $z$ when the axon itself is not physically existent. However, a 3D extracellular solution schematically shown in Fig. 6 predicts significant field variations across the axonal perimeter. To derive a comparable metric from the 3D solution and obtain an “effective” collinear field $E_{\mathrm{z}}$ on the centerline, some averaging over the cross-section must be made as illustrated in Fig. 6. The simplest way to do this is again to obtain the collinear electric field at the axonal centerline from the extracellular solution with the entirely non-conducting interior.

Fig. 6.

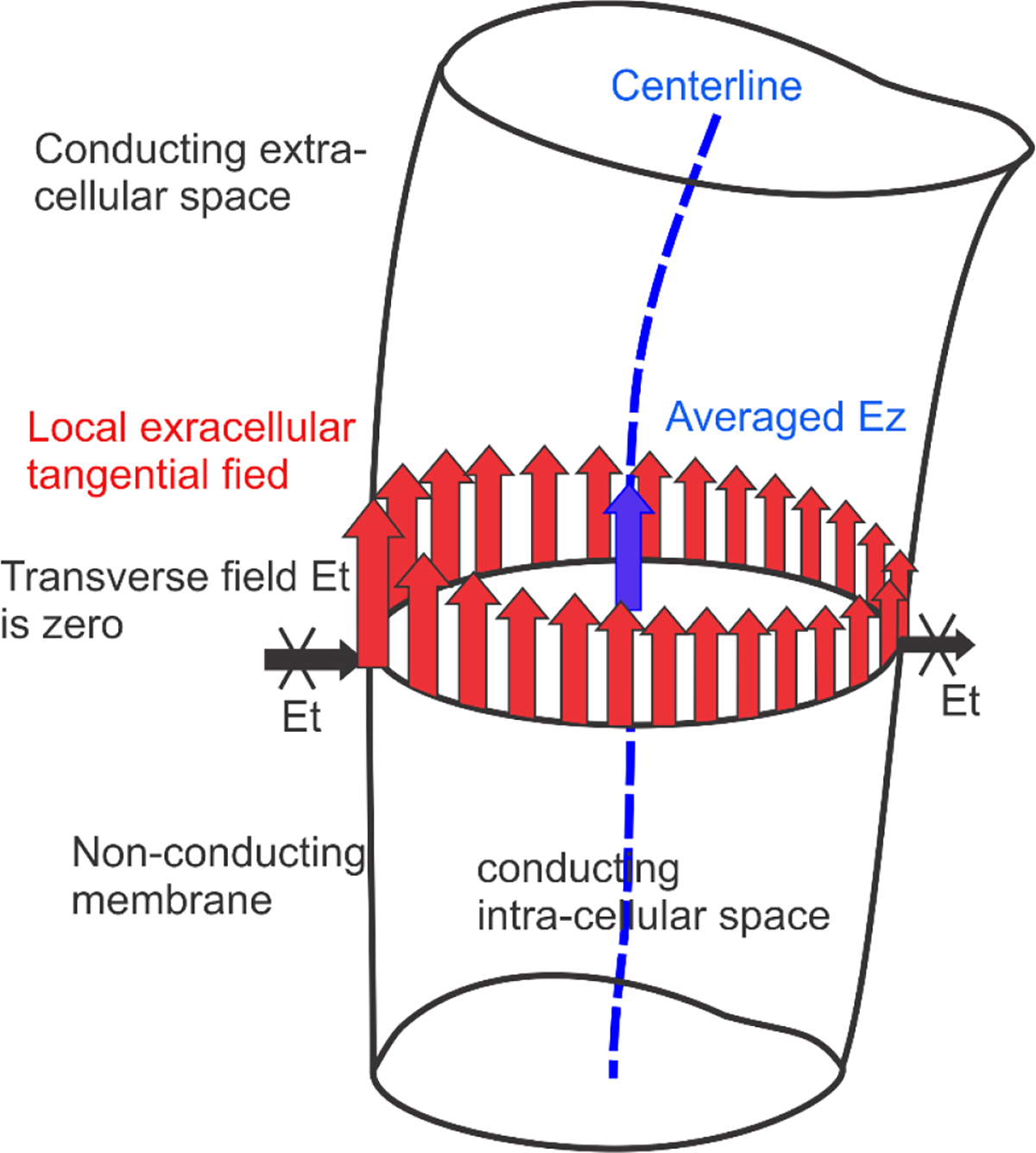
Schematic of computing averaged $E_{\mathrm{z}}$ (blue color) of the extracellular field at the axonal centerline. Non-uniform extracellular tangential electric field for a certain cross-section is shown in red. Extracellular transverse electric field $E_{\mathrm{t}}$ is zero (for more discussion on transverse fields refer to [40],[41],[42]). The averaged $E_{\mathrm{z}}$ is obtained as a collinear field at the centerline computed from the decoupled extracellular problem.

2.8. Segmentation resolution of $\mathit{f}\left(\mathit{z}\right)$

For non-myelinated axons, the segmentation resolution of $f\left(z\right)$ can be made arbitrarily fine while for myelinated fibers, the segmentation resolution is naturally given by the nodes of Ranvier [32]. For modeling purposes, we considered a fine numerical resolution on the order of 1 μm. However, for practical purposes, we also obtained averaged values $f\left(z\right)$ over an interval of 1 mm i.e., reduce the segmentation resolution to 1 mm. This averaging allowed us to derive meaningful quantitative estimates for otherwise microscopic spiking effects at the terminations and bifurcations.

3. Results

3.1. Behavior of potential, centerline field, and activating function along axonal centerlines

All results below are given for the extracellular resistivity $r_{\mathrm{e}}=400\mathrm{\Omega }\mathrm{c}\mathrm{m}$ (conductivity of 0.25 S/m) and for the outermost contacts 0 and 3 of the Medtronic 3387 DBS lead in Fig. 4 driven with the current of ± 1 mA. Electrode 0 (bottom) is a cathode. Typical field behavior is illustrated in Fig. 7 with axonal thicknesses of 2 μm, 1, μm, and 1 μm for Hack’s levels 1, 2, and 3 (cf. Fig. 4b). The data for $d{E}_{\mathrm{z}}/dz$ were downsampled using a spline interpolation and then sampled back to reduce a high-frequency noise. No averaging or filtering of any other kind has been made.

Fig. 7.

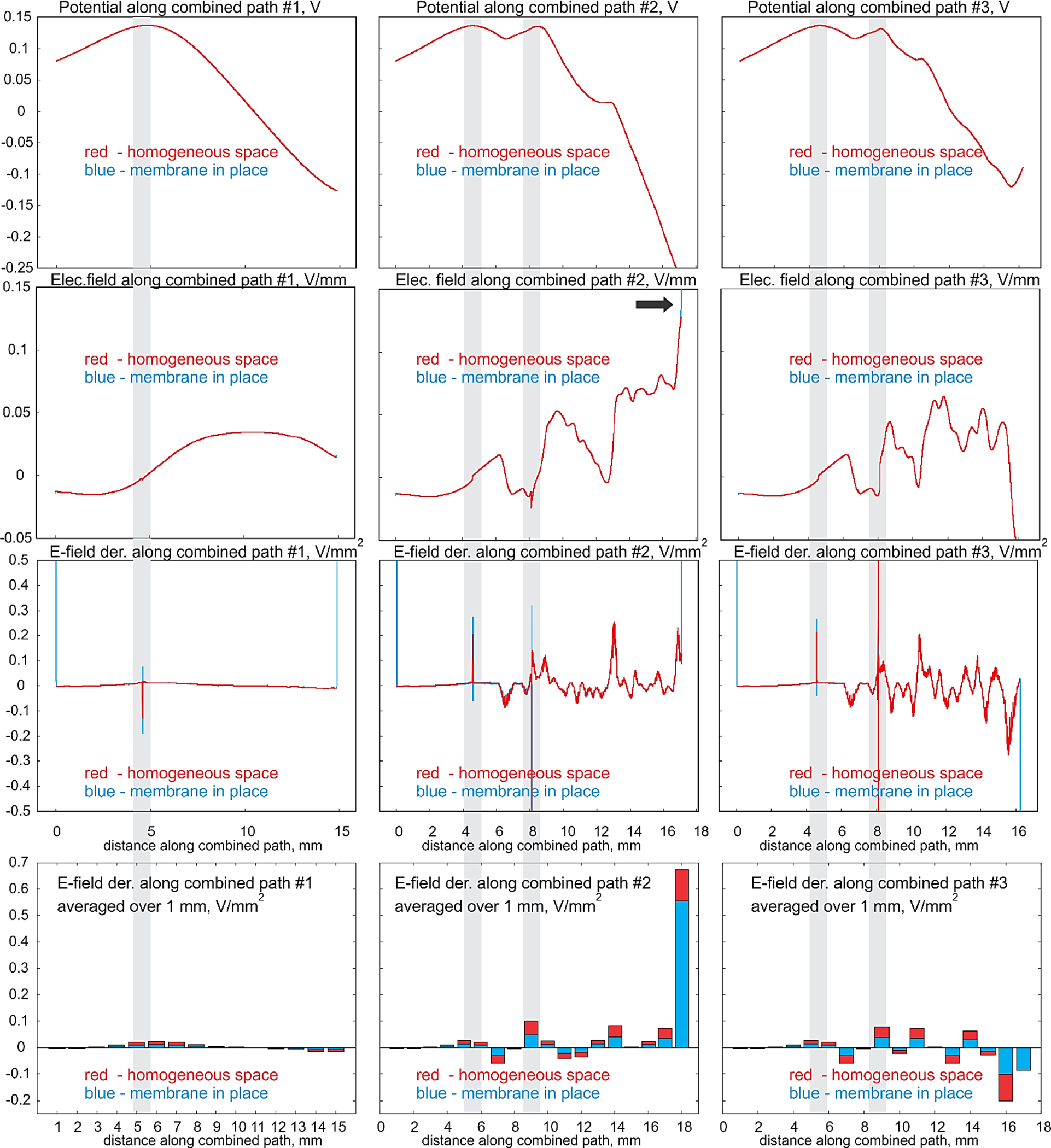
First row – electric potential (V); second row – collinear electric field (V/mm); third row – collinear field derivative along the path or (negative) activating function (V/mm²) for axon #1. Three columns correspond to the three continuous combined centerline paths from Fig. 4b,c. Red color – computations for the homogeneous space; blue color – computations with the membrane. The last row is the bar plot for the activating function averaged over a 1 mm centerline interval. Grey strips indicate bifurcation nodes; termination nodes are located at both ends of the curves.

First row of Fig. 7 shows the extracellular electric potential ${\varphi }_{\mathrm{e}}$ (V), second row – the collinear (averaged) electric field $E_{\mathrm{z}}$ (V/mm), third row –the field derivative $d{E}_{\mathrm{z}}/dz$ along the path or the (negative) activating function (V/mm²) for axon #1. Three columns correspond to the three continuous combined centerline paths from Fig. 4b,c. The red color indicates computations for the homogeneous space; the blue color – computations with the membrane. The last row is the bar plot for the activating function averaged over a 1 mm centerline interval as described in Section 2.8. The grey strips indicate the bifurcation nodes; the termination nodes are located at both ends of the respective curves.

3.2. Behavior of extracellular potential and tangential extracellular field at the membrane surface

Fig. 8 Illustrates maps of the extracellular potential and the extracellular field at the membrane surface of axon #1. There, the computations for a 2 μm thick axon were projected to the corresponding tubular surface with a much larger diameter of 200 μm; this is done for visualization purposes only. Fig. 8a shows the extracellular electric potential (or the transmembrane potential to within an additive constant) at the end of initial polarization for axon #1 while Fig. 8b shows the magnitude of extracellular tangential electric field.

Fig. 8.

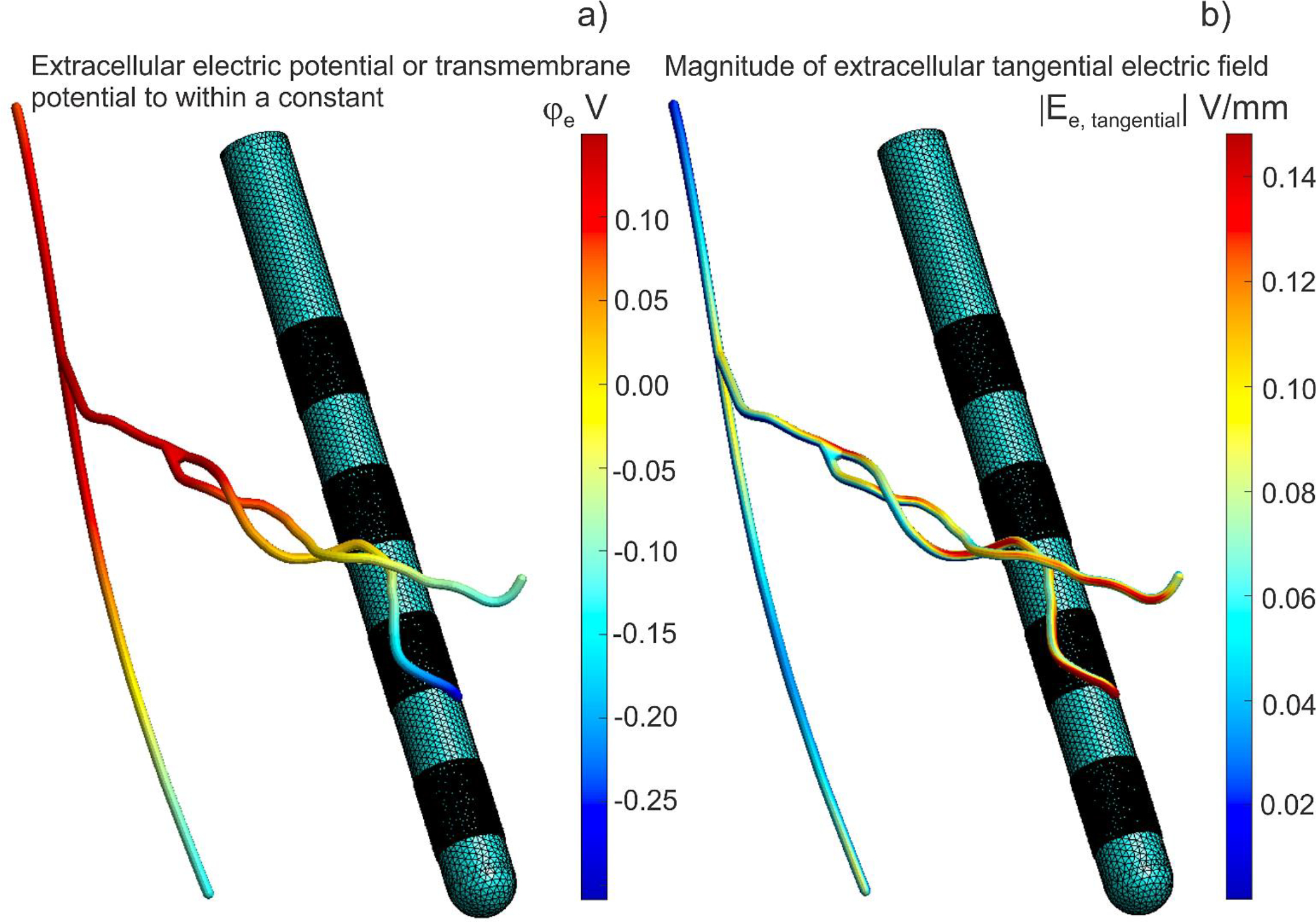
Computations for a 2 μm thick axon #1 were projected onto the corresponding tubular surface with a much larger diameter of 200 μm for visualization purposes only. Electrode 0 (bottom) is a cathode, electrode 3 (top) is an anode at 1 mA of the net current. a) Extracellular electric potential at the end of initial polarization for axon #1. The transmembrane potential is this value minus the axon resting potential. The transmembrane potential is simultaneously the double layer dipole density to within a multiplicative constant – the dielectric permittivity. b) Magnitude of extracellular electric field at the end of initial polarization for axon #1.

3.3. Quantitative estimates

Table 1 reports average relative percent differences for electric potential, longitudinal electric field, and the line derivative of the longitudinal field (activating function) distributions along the three combined axonal centerlines, with and without the membranes (in a completely homogeneous geometry), for the 60-axon bundle in Fig. 4a. Only 40 axons which have exactly three continuous combined centerline paths illustrated in Fig. 4b,c were finally retained. Relative signed (membrane solution vs. the homogeneous solution) $E_z$ differences at the terminations were computed at the center of the hemispherical closing cap. The corresponding standard deviations are shown by subscripts.

Table 1.

Average relative difference percentages (between solutions for insulating membrane vs. homogeneous space) for electric potential, longitudinal electric field, and line derivative of the longitudinal field (the activating function) distributions along axon centerlines for the 60-axon bundle in Fig. 4a. Only 40 axons, which have exactly three continuous combined centerline paths illustrated in Fig. 4b,c, were retained. Relative signed $\left|E_z\right|$ differences at the terminations were computed at the center of the hemispherical closing cap. The corresponding standard deviations are shown by superscripts.

Testing case	Combined path #1	Combined path #2	Combined path #3
Axons diam.	Hack’s level 1 – 2 μm	Hack’s level 2 – 1 μm	Hack’s level 3 – 1 μm
Rel. potential ${\varphi }_{\mathrm{e}}$ diff. (L2 norm)	0.005% 0.001%	0.003% 0.001%	0.003% 0.001%
Rel. $E_{\mathrm{z}}$ diff. (L2 norm)	0.2% 0.1%	0.5% .0.2%	0.5% 0.4%
Rel. $d{E}_{\mathrm{z}}/dz$ diff. (L2 norm)	112% 63%	106% 80%	87% 92%
Rel. $\left|E_{\mathrm{z}}\right|$ diff. at start termination	+16.1% .0.2%	+16.4% 0.5%	+16.4% 0.5%
Rel. $\left|E_{\mathrm{z}}\right|$ diff. at end termination	+16.1% 0.2%	+16.0% 0.3%	+14.9% 0.3%
The same results for the refined axonal meshes (1:4 barycentric triangle subdivision)
Rel. potential ${\varphi }_{\mathrm{e}}$ diff. (L2 norm)	0.005% 0.001%	0.003% 0.001%	0.003% 0.001%
Rel. $E_{\text{z}}$ diff. (L2 norm)	0.2% 0.1%	0.5% 0.2%	0.5% 0.4%
Rel. $d{E}_{\mathrm{z}}/dz$ diff. (L2 norm)	112% 63%	106% 81%	85% 90%
Rel. $\left|E_{\mathrm{z}}\right|$ diff. at start termination	+16.1% .0.1%	+16.4% 0.3%	+16.4% 0.8%
Rel. $\left|E_{\mathrm{z}}\right|$ diff. at end termination	+16.1% 0.3%	+16.0% 0.3%	+15.0% 0.7%

Similar results for axons with thicknesses of 1 μm, 1, μm, and 1 μm as well as 2 μm, 2, μm, and 2 μm, respectively, corresponding to Hack’s levels 1, 2, and 3 and are given in Table B1 of Appendix B.

4. Discussion

4.1. Perturbations of centerline electric potential are negligibly small

It follows from Fig. 7 as well as from Table 1 (and Table B1 of Appendix B) that explicitly modeling the effect of membrane surfaces led to vanishingly small relative differences for the centerline electric potential with respect to the solution for the homogeneous space. This fact is valid for all combined paths, irrespective of how close they are to the DBS electrodes. Therefore, these variations could likely be neglected when the potential values are fed into NEURON models [39]. Further reinforcing this observation, Fig. 8a demonstrates that the extracellular potential remains consistent across neural cross-sections with a high degree of accuracy.

4.2. Perturbations of centerline electric field are negligibly small except for local variations at terminations

It follows from Table 1 (and Table 1B of Appendix B) that that the average relative variations in the one-dimensional collinear electric field along the centerlines caused by nonconducting membranes are also quite small as compared to the homogeneous case. However, local relative $\left|E_{\mathrm{z}}\right|$ values at the centers of the termination hemispherical caps are higher by 10–20% on average. In certain instances where the axonal centerline aligns parallel to the DBS field, there is an approximate 50% increase. A similar tendency was observed when the electric field was averaged over a terminating centerline path of 3 diameters in length. Fig. 8b also shows that the extracellular tangential electric field at the membrane surface can be very different from the (averaged) collinear centerline field.

4.3. Perturbations of activation function are quite small except for extremely large spikes at bifurcations and terminations

It is seen in Fig. 7 that the variations in the one-dimensional activating function along the centerlines caused by nonconducting membranes are also quite small as compared to the homogeneous case everywhere except bifurcations and terminations. Similarly, these variations could likely be neglected everywhere except bifurcations and terminations.

On the other hand, variations of the one-dimensional activating function close to both the bifurcation and the termination nodes may be very large as Fig. 7 shows. They are very local and only span several axonal diameters. These variations are due to the strong induced membrane surface charges whose coaxial fields do not cancel out at the axonal centerline as is expected, for example, for straight infinite non-conducting cylinders in a homogeneous space.

The local variations of the activating function close to the bifurcations and terminations are so huge that they very substantially (by up to 100%) distort an integral measure of the activating function over the entire axonal branch path – its L² norm. This is shown in Table 1 and Table B1 of Appendix B. Such a behavior is typical for a mathematical delta function that has an infinite peak at one point. The definition implies that the delta function value is zero everywhere except at the point, but its integral over the entire real line containing this point is equal to one [43].

4.4. Effect of arbor diameter

By comparing Table 1 and Table B1 of Appendix B one can see that the effect of the axonal diameter does not have a well-defined influence on the results. The obtained error and deviation estimates are approximately of the same order.

4.5. Implication for the solution of cable equation

The delta-function like behavior of the terminal/bifurcation corrections may result in a development of a lumped circuit model in the form of a current clamp or a voltage clamp that can be used in the cable equation (e.g., NEURON models) [39]. The strength of the source will be a function of the angle(s) between the arbor direction(s) and the field direction at the termination(bifurcation). Yet another alternative solution might be to modify the terminal values of the extracellular electric potential $V_e$ sampled with the resolution of approximately 1 mm. To comply with the terminal values of the activating function from Fig. 7, the equality $f\left(z\right)=\left({\varphi }_{\mathrm{e},\mathrm{n}+1}-2{\varphi }_{\mathrm{e},\mathrm{n}}+{\varphi }_{\mathrm{e},\mathrm{n}-1}\right)/d{z}^2$ could be applied while redefining the last value, ${\varphi }_{\mathrm{e},\mathrm{n}+1}$, accordingly, using $dz=1\mathrm{m}\mathrm{m}$.

4.6. Constraints and limitations of the study

The present study is limited in the following ways:

1. the effect of myelin, although this simplification is likely reasonable for the task of estimating surface potential under the assumption of initial polarization since we aren’t modeling actively conducting axons;

2. a potentially significant effect of rapidly varying non-circular axonal cross-sections which is frequently simplified away in histology-based or non-invasive primate neuroimaging;

3. the approximation of initial polarization and is that of the insulating membrane.

The latter approximation implies that the extracellular currents have little effect on the extracellular solution. Alternative approaches and the corresponding modifications of $f\left(z\right)$ for the transverse electric field can be found in Refs. [40],[41],[42],[9].

While the axonal models from Bingham & McIntyre, 2022 [1] used in this study are closely modeled after 3D histological tracings from Coude et al., 2018 [44], which indicate little to no tapering and comparable parent/child diameters across bifurcations, the true parent/child diameter ratios remain unknown. The impact of parent/child diameter ratios on charge deposition and membrane polarization remains a question of interest for future studies.

4.7. Software availability

The manuscript is supplemented with (i) a standalone MATLAB code which generates a manifold mesh containing terminations and bifurcations for a generic axonal graph, as described in Sections 2.1 and 2.2 and; (ii) a standalone MATLAB code implementing the BEM-FMM for the computation of extracellular fields and centerline fields. The default example demonstrates the generation of the mesh and computations for axon #1, accommodating various axonal radii [45].

5. Conclusion

For HDP axonal arbors subject to DBS activation, the effect of explicitly modeling membrane surfaces and the resulting charge deposition suggests that voltage hyperintensities emerge at axon terminations and bifurcations. At these micron-scale structures, the activating function may be very large, behaving similar to the mathematical delta function, and the centerline electric field may increase too. This insight may offer a way to describe the effect of physical bifurcations and terminations of the arbor as distinct point processes. Further work is required to understand the role of bifurcations and terminals on axon recruitment and to develop robust approaches to simulating this behavior.

Appendix A. Analytical Solutions for Thin Spherical and Cylindrical Shells with a Conducting Medium Inside Immersed in a Conducting Fluid – Formation of Double and Single Charge Layers

This Appendix provides an illustration of the main features of the steady state extracellular solution, as described in the Materials and Methods section. Two examples are provided: analytical solutions for a thin spherical and cylindrical non-conducting shell in a uniform external electric field. The shell, representing a simplified model of a cell/axon, consists of a conducting homogeneous cytoplasm internally, a non-conducting membrane with a thickness of $\mathrm{\Delta }$ (where $\epsilon \mathrm{\Delta }$ represents the membrane capacitance per unit area, with $\epsilon$ denoting the dielectric permittivity), and a homogeneous extracellular space.

A general analytical steady-state conduction solution for a spherical shell in an external field was obtained by J. C. Maxwell [1]. The description of the steady-state (at the end of initial polarization) and transient transmembrane voltages induced on spherical cells was derived by H. P. Schwan more than six decades ago [2] (see also see Refs. [3],[4]). This Appendix provides a simplified derivation for thin non-conducting shells explaining the formation of single and double layers of charges at the thin membrane shell in a steady state.

The thin-membrane solution given below is characterized by a double-layer (dipolar) charge density and a single-layer (monopolar) charge density deposited on the membrane. The presence of both layers is necessary to assure the condition of the equipotential intracellular space (no electric field inside). This condition is valid for an arbitrary applied extracellular field since no electric current within a closed cell volume isolated by the nonconducting membrane can exist in a conservative (curl-free) field. The zero electric field inside the shell can be achieved thanks to both a discontinuity of its normal component across the single layer [5] as well as a discontinuity of its tangential component across the double layer [5].

Next, we are placing emphasis on the equivalence between the complete insulting membrane-based extracellular solution and a simpler extracellular solution for the entire non-conducting cell (e.g., the non-conducting sphere or the cylinder). The latter solution only requires a single layer of charge. However, this simple extracellular solution for the non-conducting cell still allows us to find the most critical parameter – the transmembrane potential – since a constant resting intracellular potential can be postulated. It also allows us to find the dipolar charge density in the leading order.

Multiple helpful analytical solutions for simple cell geometries can be found in [6],[7],[8],[9],[10],[11] including those . The double layer theory is given, for example, in Ref. [5]. The solution given below is a mathematical abstraction; for a more detailed biophysical analysis of the membrane composition and operation please refer to [2],[12],[13],[4] and other sources.

A1. Solution for three separate domains

An analytical solution can be readily obtained for a spherical shell of outer radius $R$ and inner radius $R_1$ having shell conductivity, ${\sigma }_s$, and placed in a uniform primary electric field, ${\mathit{E}}^{\text{pri}}$. The extracellular medium possesses a constant conductivity ${\sigma }_e$ while the intracellular medium possesses a constant conductivity ${\sigma }_i$ as shown in Fig. A1. The primary or incident field is given by $E_z^{\mathrm{p}\mathrm{r}\mathrm{i}}=E_0=const$ or $E_r^{\mathrm{p}\mathrm{r}\mathrm{i}}=E_{0}cos\theta$ and the primary potential is given by ${\phi }^{\text{pri}}=-E_{0}rcos\theta$ when the spherical coordinate system with the elevation angle of zero at zenith is used (Fig. A1).

Fig. A1.

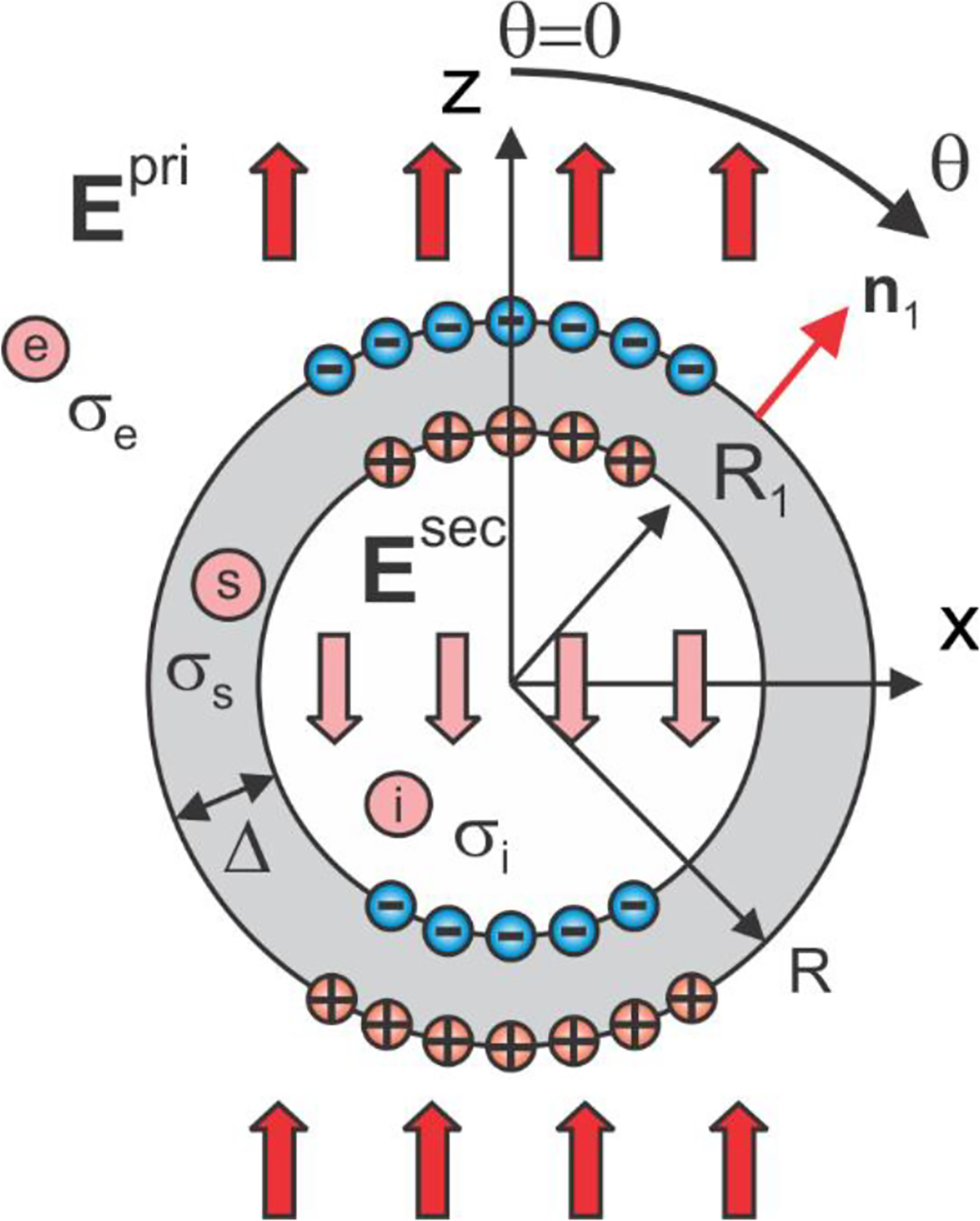
Two-layer conducting sphere in an external electric field. The sum of the primary and the secondary field in the intracellular space is zero.

A solution for a secondary or induced scalar electric potential ${\phi }^s$ and a secondary electric field ${\mathit{E}}^s$ due to the induced surface charges (cf. Fig. A1) can be obtained via three expansions each of which satisfies Laplace equation in three dimensions,

$$\begin{gathered} {\phi }_{\text{inside}}^S=arcos\theta ,{\phi }_{\text{outside}}^s=\frac{b}{r^2}cos\theta ,{\phi }_{\text{shell}}^S=crcos\theta +\frac{d}{r^2}cos\theta \\ {E}_{r,\text{inside}}^s=-acos\theta ,E_{r,\text{outside}}^s=2\frac{b}{r^3}cos\theta ,E_{r,\text{shell}}^s=-ccos\theta +2\frac{d}{r^3}cos\theta \end{gathered}$$ (1)

We are using notations ${\phi }_{\text{inside/outside}}^S$ instead of standard ${\phi }_{\mathrm{i}/\mathrm{e}}^S$ to better distinguish between multiple dual formulae. The four unknown constants $a,b,c,d$ are found from four boundary conditions for the total electric potential ${\phi }^{\text{pri}}+{\phi }^{\text{s}}$ (the potential continuity) and the total electric field ${\mathit{E}}^{\text{pri}}+{\mathit{E}}^{\mathrm{s}}$ (continuity of the normal current density across the boundaries). Since the potential ${\phi }^{\text{pri}}$ is already continuous, one obtains

$$\begin{array}{l}{\phi }_{\text{inside}}^S={\phi }_{\text{shell}}^{S}atr=R_1,\\ {\phi }_{\text{outside}}^S={\phi }_{\text{shell}}^{S}atr=R,\\ {\sigma }_i\left\{E_{0}cos\theta -\frac{\partial {\phi }_{\text{inside}}^S}{\partial r}\right\}={\sigma }_s\left\{E_{0}cos\theta -\frac{\partial {\phi }_{shell}^S}{\partial r}\right\}atr=R_1,\\ {\sigma }_s\left\{E_{0}cos\theta -\partial {\phi }_{\text{shell}}^s/\partial r\right\}={\sigma }_e\left\{E_{0}cos\theta -\partial {\varphi }_{\text{outside}}^s/\partial r\right\}atr=R\end{array}$$ (2)

We now assume that ${\sigma }_s=0$. From 3^rd Eq. (2), we immediately obtain that $a=E_0$ so that the field of the induced charges cancels the primary field inside the shell and the total field inside the shell is exactly zero. This is to be expected since no current can flow within a closed volume in a conservative (curl-free) field. The interior or intracellular volume thus becomes equipotential (at a resting potential). After substituting Eqs. (1), the boundary conditions given by Eqs. (2) yield

$$\begin{gathered} a{R}_1=c{R}_1+d/R_1^2 \\ b/R^2=cR+d/R^2 \\ a=E_0 \\ b=-0.5R^3{E}_0 \end{gathered}$$ (3)

One can see that the final solution will not depend on the conductivities or their ratio. The first two equations (3) yield a system of two equations in the following form:

$$\begin{gathered} E_0{R}_1=c{R}_1+d/R_1^2 \\ -0.5E_{0}R=cR+d/R^2 \end{gathered}$$ (4)

and the remaining constants are found as

$$c=-0.5E_0-\frac{d}{R^3}=-E_0\frac{\frac{1}{2}{R}^3+R_1^3}{R^3-R_1^3},d=+\frac{3}{2}{E}_0\frac{R^3{R}_1^3}{R^3-R_1^3}$$ (5)

Now assume that $R_1=R-\mathrm{\Delta }$ and that $\frac{\mathrm{\Delta }}{R}\ll 1$ is a small parameter (the thin-shell condition). One can employ several binomial series expansions to obtain a closed-form result. To the leading and the second order of approximation, one has

$$\begin{gathered} R_1^3=R^3\left(1-\frac{3\mathrm{\Delta }}{R}\right);\frac{R^3}{R^3-R_1^3}=\frac{1}{3}\frac{R}{\mathrm{\Delta }}+\frac{1}{3} \\ c=-\frac{1}{2}{E}_0\frac{R}{\mathrm{\Delta }}+\frac{1}{2}{E}_0 \\ d=+\frac{1}{2}{E}_0\frac{R^4}{\mathrm{\Delta }}-E_0{R}^3 \end{gathered}$$ (6)

Thus, the electric field within the non-conducting thin shell is very high and it approaches infinity when the shell thickness $\mathrm{\Delta }$ approaches zero.

A2. Potential, field, and charge density at the outer boundary of the shell

Using Eqs. (3) and (6), the extracellular potential, the extracellular field just outside, and the charge density $\rho \left(\mathit{r}\right)$ at the outer boundary of the shell are obtained from Eqs. (1) in the following form (to compute the charge density we would also need the electric field $E_{r\text{,shell}}\left(R\right)$ just inside the outer boundary of the shell):

$$\begin{gathered} {\phi }_{\text{outside}}(R)={\phi }^{\mathrm{p}\mathrm{r}\mathrm{i}}+{\phi }_{\text{outside}}^s=-\frac{3}{2}{E}_{0}R\mathit{cos}\theta \text{(exact}\text{result)} \\ {E}_{r,\text{outside}}(R)=E_r^{\mathrm{p}\mathrm{r}\mathrm{i}}+E_{r,\text{outside}}^s=0\text{(exact}\text{result)} \\ {E}_{r,\text{shell}}\left(R\right)=-ccos\theta +2\frac{d}{R^3}cos\theta =+\frac{3}{2}{E}_0\frac{R}{\mathrm{\Delta }}cos\theta -\frac{5}{2}{E}_{0}cos\theta \\ {\rho }_{\text{outer}}(R)=\frac{{\sigma }_s-{\sigma }_e}{{\sigma }_e}{\epsilon }_0{E}_{r,\text{shell}}(R)=-\frac{3}{2}{\epsilon }_0{E}_0\frac{R}{\mathrm{\Delta }}cos\theta +\frac{5}{2}{\epsilon }_0{E}_{0}cos\theta \end{gathered}$$ (7)

where ${\epsilon }_0$ is the permittivity of vacuum. The charge density is obtained following Eq. (12) of [14] (cf. also [15], Eq. (5)).

A3. Potential and charge density at the inner boundary of the shell

Similarly, the intracellular potential and the charge density $\rho \left(\mathit{r}\right)$ (cf. 15, Eq. (5)) at the inner boundary of the shell are obtained in the following form (to compute the charge density we would also need the electric field $E_{r,\text{shell}}\left(R_1\right)$ just outside the inner boundary of the shell):

$$\begin{gathered} {\phi }_{\text{inside}}\left(R_1\right)={\phi }^{\text{pri}}+{\phi }_{\text{inside}}^S=0\text{(exact}\text{result},\text{valid}\text{to}\text{within}\text{a}\text{constant)} \\ {E}_{r,\text{shell}}\left(R_1\right)=-ccos\theta +2\frac{d}{R_1^3}cos\theta =+\frac{3}{2}{E}_0\frac{R}{\mathrm{\Delta }}cos\theta +\frac{1}{2}{E}_{0}cos\theta \\ {\rho }_{\text{inner}}\left(R_1\right)=\frac{{\sigma }_i-{\sigma }_s}{{\sigma }_i}{\epsilon }_0{E}_{r,\text{shell}}\left(R_1\right)=+\frac{3}{2}{\epsilon }_0{E}_0\frac{R}{\mathrm{\Delta }}cos\theta +\frac{1}{2}{\epsilon }_0{E}_{0}cos\theta \end{gathered}$$ (8)

to the leading and the second order of approximation. The charge density is again obtained following Eq. (12) of [14] (cf. also [15], Eq. (5)).

A4. Transmembrane potential

A combination of Eqs. (7) and (8) for the extracellular and intracellular potentials, respectively, also allows us to find the transmembrane potential (defined to within a constant), ${\phi }_{\mathrm{m}}={\phi }_{\text{inside}}^S-{\phi }_{\text{outside}}=+\frac{3}{2}{E}_{0}Rcos\theta$, This is the exact (not asymptotic) result and the original (steady-state) Schwan’s equation [2].

A5. Double and single layers formed across the thin shell and transmembrane potential

Together, both charge densities ${\rho }_{\text{outer}}(R)$ and ${\rho }_{\text{inner}}\left(R_1\right)$, which are “almost” equal to each other in magnitude but have the opposite signs when $\mathrm{\Delta }\to 0,R\to R_1$, form a double layer – a layer of electric dipoles – with the surface dipole moment density per unit area, $p_{\text{shell}}$, given by

$$p_{\text{shell}}\equiv \frac{\mathrm{\Delta }\left({\rho }_{outer}-{\rho }_{inner}\right)}{2}=-\frac{3}{2}{\epsilon }_0{E}_{0}Rcos\theta +2{\epsilon }_0{E}_0\mathrm{\Delta }cos\theta$$ (9a)

as well as a single layer with the surface charge density given by

$${\rho }_{\text{shell}}\equiv {\rho }_{outer}+{\rho }_{inner}=+3E_{0}cos\theta$$ (9b)

The net charge on the membrane is zero.

A6. Solution for non-conducting sphere with a single layer of charges

In this case, only constants $a,b$ in Eqs. (1) are retained for the secondary or induced electric potential ${\varphi }^s$ and,

$$\begin{gathered} {\varphi }_{\text{inside}}^S=arcos\theta ,{\varphi }_{\text{outside}}^S=\frac{b}{r^2}cos\theta \\ {E}_{r,\text{inside}}^s=-acos\theta ,E_{r,\text{outside}}^s=2\frac{b}{r^3}cos\theta \end{gathered}$$ (10)

From the boundary conditions, one has

$$a=-0.5E_0,b=-0.5R^3{E}_0$$ (11)

The extracellular potential $\varphi$, the extracellular field just outside, and the charge density ${\rho }_{noncond}\left(\mathit{r}\right)$ at the boundary of the nonconducting sphere are obtained in the following form:

$$\begin{gathered} {\varphi }_{\text{outside}}={\phi }^{\mathrm{p}\mathrm{r}\mathrm{i}}+{\varphi }_{\text{outside}}^s=-\frac{3}{2}{E}_{0}Rcos\theta \\ {E}_{r,\text{outside}}=E_r^{\mathrm{p}\mathrm{r}\mathrm{i}}+E_{r,\text{outside}}^s=0 \\ {E}_{r,\text{inside}}=\frac{3}{2}{E}_{0}cos\theta \\ {\rho }_{noncond}=\frac{{\sigma }_i-{\sigma }_e}{{\sigma }_e}{\epsilon }_0{E}_{r,\text{inside}}=-\frac{3}{2}{\epsilon }_0{E}_{0}cos\theta \end{gathered}$$ (12)

The solutions for the extracellular potential and the extracellular electric field from Eqs (12) indeed coincide with the extracellular thin-shell solutions from Eqs. (7). Hence, the equivalence of the two solutions is demonstrated.

A7. Expression of transmembrane potential and double layer density using the solution for non-conducting sphere (cell)

It follows from Eqs. (7), (8), (12) that, to the leading order of magnitude, the transmembrane potential ${\phi }_{\mathrm{m}}$ and the actual double layer density $p_{\text{shell}}$ of the thin-shell solution can be directly expressed through the extracellular potential $\varphi$ of the simplified solution for the entirely non-conducting sphere (cell) in the form:

$$\begin{gathered} {\phi }_{\mathrm{m}}={\phi }_{\text{inside}}-{\phi }_{\text{outside}}=const-{\varphi }_{\text{outside}} \\ {p}_{\text{shell}}={\epsilon }_0{\varphi }_{\text{outside}} \end{gathered}$$ (13)

Eqs. (13) is valid for any geometry, not necessarily spherical. This is because the equivalence of the two extracellular solutions follows from the uniqueness of a solution for the exterior Neumann problem with the zero normal field just outside the nonconducting membrane of any shape.

A8. Solution for the cylindrical shell in a transverse field

The same Fig. A1 can be reused to represent a cross-section of the cylindrical shell. The primary or incident field is again given by $E_z^{\mathrm{p}\mathrm{r}\mathrm{i}}=E_0=const$ or $E_r^{\mathrm{p}\mathrm{r}\mathrm{i}}=E_{0}cos\theta$ and the primary potential is given by ${\phi }^{\text{pri}}=-E_{0}rcos\theta$ when the cylindrical coordinate system with the polar angle of zero at the positive direction of the z-axis is used (Fig. A1).By analogy with Eqs. (1), a solution for the secondary or induced scalar electric potential ${\phi }^S$ and the secondary electric field ${\mathit{E}}^s$ due to the induced surface charges (cf. Fig. A1) can be again obtained via three expansions each of which now satisfies Laplace equation in two dimensions,

$$\begin{gathered} {\phi }_{\text{inside}}^S=arcos\theta ,{\phi }_{\text{outside}}^S=\frac{b}{r}cos\theta ,{\phi }_{\text{shell}}^S=crcos\theta +\frac{d}{r}cos\theta \\ {E}_{r,\text{inside}}^s=-acos\theta ,E_{r,\text{outside}}^s=\frac{b}{r^2}cos\theta ,E_{r,\text{shell}}^s=-ccos\theta +\frac{d}{r^2}cos\theta \end{gathered}$$ (14)

The four unknown constants $a,b,c,d$ are found from four boundary conditions Eqs. (2) for the total electric potential ${\phi }^{\text{pri}}+{\phi }^{\mathrm{s}}$ (the potential continuity) and the total electric field ${\mathit{E}}^{\text{pri}}+{\mathit{E}}^{\mathrm{s}}$. We again assume that ${\sigma }_s=0$. From 3^rd Eq. (2), we immediately obtain that $a=E_0$ so that the field of the induced charges cancels the primary field inside the shell and the total field inside the shell is exactly zero. This is to be expected since no current can flow within a closed volume in a conservative (curl free) field. The interior or intracellular volume thus becomes equipotential (at a resting potential). After substituting Eqs. (14), the boundary conditions given by Eqs. (2) yield

$$\begin{gathered} a{R}_1=c{R}_1+d/R_1 \\ b/R=cR+d/R \\ a=E_0 \\ b=-R^2{E}_0 \end{gathered}$$ (15)

The final solution will not depend on the conductivities or their ratio. The first two equations (15) yield a system of two equations in the following form:

$$\begin{gathered} E_0{R}_1=c{R}_1+d/R_1 \\ -E_{0}R=cR+d/R \end{gathered}$$ (16)

and the remaining constants are found as

$$c=-E_0\frac{R^2+R_1^2}{R^2-R_1^2},d=2E_0\frac{R^2{R}_1^2}{R^2-R_1^2}$$ (17)

Assuming that $R_1=R-\mathrm{\Delta }$ and that $\frac{\mathrm{\Delta }}{R}\ll 1$ is a small parameter (the thin-shell condition), one can employ several binomial series expansions to obtain a closed-form result. To the leading and the second order of approximation, one has

$$\begin{gathered} R_1^2=R^2\left(1-\frac{2\mathrm{\Delta }}{R}\right);\frac{R^2}{R^2-R_1^2}=\frac{1}{2}\frac{R}{\mathrm{\Delta }}+\frac{1}{4} \\ c=-E_0\frac{R}{\mathrm{\Delta }}+\frac{1}{2}{E}_0 \\ d=+E_0\frac{R^3}{\mathrm{\Delta }}-\frac{3}{2}{E}_0{R}^2 \end{gathered}$$ (18)

Thus, the electric field within the non-conducting thin shell is very high and it approaches infinity when the shell thickness approaches zero.

A9. Potential, field, and charge density at the outer boundary of the shell

Using Eqs. (15) and (18), the extracellular potential, the extracellular field just outside, and the charge density $\rho \left(\mathit{r}\right)$ (cf. [15], Eq. (5)) at the outer boundary of the shell are obtained from Eqs. (14) in the following form (to compute the charge density we would also need the electric field $E_{r,\text{shell}}(R)$ just inside the outer boundary of the shell):

$$\begin{gathered} {\phi }_{\text{outside}}(R)={\phi }^{\mathrm{p}\mathrm{r}\mathrm{i}}+{\phi }_{\text{outside}}^s=-2E_{0}Rcos\theta \text{(exact}\text{result)} \\ {E}_{r,\text{outside}}(R)=E_r^{\mathrm{p}\mathrm{r}\mathrm{i}}+E_{r,\text{outside}}^s=0\text{(exact}\text{result)} \\ {E}_{r,\text{shell}}\left(R\right)=-ccos\theta +\frac{d}{R^2}cos\theta =+2E_0\frac{R}{\mathrm{\Delta }}cos\theta -2E_{0}cos\theta \\ {\rho }_{\text{outer}}(R)=\frac{{\sigma }_s-{\sigma }_e}{{\sigma }_e}{\epsilon }_0{E}_{r,\text{shell}}(R)=-2{\epsilon }_0{E}_0\frac{R}{\mathrm{\Delta }}cos\theta +2{\epsilon }_0{E}_{0}cos\theta \end{gathered}$$ (19)

where ${\epsilon }_0$ is the permittivity of vacuum. The charge density is again obtained following Eq. (12) of [14] (cf. also [15], Eq. (5)).

A10. Potential and charge density at the inner boundary of the shell

The intracellular potential and the charge density $\rho \left(\mathit{r}\right)$ at the inner boundary of the shell are obtained in the following form (to compute the charge density we would also need the electric field $E_{r,\text{shell}}\left(R_1\right)$ just outside the inner boundary of the shell):

$$\begin{gathered} {\phi }_{\text{inside}}\left(R_1\right)={\phi }^{\text{pri}}+{\phi }_{\text{inside}}^S=0\text{(exact}\text{result},\text{valid}\text{to}\text{within}\text{a}\text{constant)} \\ {E}_{r,\text{shell}}\left(R_1\right)=-ccos\theta +\frac{d}{R_1^2}cos\theta =+2E_0\frac{R}{\mathrm{\Delta }}cos\theta \\ {\rho }_{\text{inner}}\left(R_1\right)=\frac{{\sigma }_i-{\sigma }_s}{{\sigma }_i}{\epsilon }_0{E}_{r,\text{shell}}\left(R_1\right)=+2{\epsilon }_0{E}_0\frac{R}{\mathrm{\Delta }}cos\theta \end{gathered}$$ (20)

to the leading and the second order of approximation (the terms of the second order cancel out).

A11. Transmembrane potential

A combination of Eqs.(19) and (20) for the extracellular and intracellular potentials, respectively, also allows us to find the transmembrane potential (defined to within a constant), ${\phi }_{\mathrm{m}}={\phi }_{\text{inside}}^S-{\phi }_{\text{outside}}=+2E_{0}Rcos\theta$. This is the exact (not asymptotic) result.

A12. Double and single layers formed across the thin shell and transmembrane potential

Together, both charge densities ${\rho }_{\text{outer}}(R)$ and ${\rho }_{\text{inner}}\left(R_1\right)$, which are “almost” equal to each other in magnitude but have the opposite signs when $\mathrm{\Delta }\to 0,R\to R_1$, form a double layer – a layer of electric dipoles – with the surface dipole moment density per unit area, $p_{\text{shell}}$, given by

$$p_{\text{shell}}\equiv \frac{\mathrm{\Delta }\left({\rho }_{\text{outer}}-{\rho }_{inner}\right)}{2}=-2{\epsilon }_0{E}_{0}Rcos\theta +{\epsilon }_0{E}_0\mathrm{\Delta }cos\theta$$ (21a)

as well as a single layer with the surface charge density given by

$${\rho }_{\text{shell}}\equiv {\rho }_{\text{outer}}+{\rho }_{inner}=+2{\epsilon }_0{E}_{0}cos\theta$$ (21b)

The net charge of the membrane is zero.

A13. Solution for non-conducting cylinder with a single layer of charges

In this case, only constants $a,b$ in Eqs. (14) are retained for the secondary or induced electric potential ${\varphi }^s$ and,

$$\begin{gathered} {\varphi }_{\text{inside}}^S=arcos\theta ,{\varphi }_{\text{outside}}^S=\frac{b}{r}cos\theta \\ {E}_{r,\text{inside}}^s=-acos\theta ,E_{r,\text{outside}}^s=2\frac{b}{r^2}cos\theta \end{gathered}$$ (22)

From the boundary conditions, one has

$$a=-E_0,b=-R^2{E}_0$$ (23)

The extracellular potential $\varphi$, the extracellular field just outside, and the charge density ${\rho }_{noncond}\left(\mathit{r}\right)$ (cf. [15], Eq. (5)) at the boundary of the nonconducting cylinder are obtained in the following form:

$$\begin{gathered} {\varphi }_{\text{outside}}={\phi }^{\text{pri}}+{\varphi }_{\text{outside}}^s=-2E_{0}Rcos\theta \\ {E}_{r,\text{outside}}=E_r^{\text{pri}}+E_{r,\text{outside}}^s=0 \\ {E}_{r,\text{inside}}=2E_0\mathrm{c}\mathrm{o}\mathrm{s}\theta \\ {\rho }_{noncond}=\frac{{\sigma }_i-{\sigma }_e}{{\sigma }_e}{\epsilon }_0{E}_{r,\text{inside}}=-2{\epsilon }_0{E}_{0}cos\theta \end{gathered}$$ (24)

The solutions for the extracellular potential and the extracellular electric field from Eqs (24) coincide with the extracellular thin-shell solutions from Eqs. (19). Hence, the equivalence of the two solutions is demonstrated again.

A14. Expression of transmembrane potential and double layer density using the solution for non-conducting cylinder (cell)

It follows from Eqs. (19), (20), (24) that, to the leading order of magnitude, the transmembrane potential ${\phi }_{\mathrm{m}}$ and the actual double layer density $p_{\text{shell}}$ of the thin-shell solution can be directly expressed through the extracellular potential $\varphi$ of the simplified solution for the entirely non-conducting cylinder (cell) in the form:

$$\begin{gathered} {\phi }_{\mathrm{m}}={\phi }_{\text{inside}}-{\phi }_{\text{outside}}=\text{const}-{\varphi }_{\text{outside}} \\ {p}_{\text{shell}}={\epsilon }_0{\varphi }_{\text{outside}} \end{gathered}$$ (25)

Eqs. (25) is valid for any geometry, not necessarily spherical. This is because the equivalence of the two extracellular solutions follows from the uniqueness of a solution for the exterior Neumann problem with the zero normal field just outside the nonconducting membrane of any shape.

Appendix B. Results for thicknesses of 1 μm, 1, μm, and 1 μm as well as 2 μm, 2, μm, and 2 μm corresponding to Hack’s levels 1, 2, and 3

Table B1.

The same centerline results as in Table 1 of the main text, but for different axonal diameter combinations.

Testing case	Combined path #1	Combined path #2	Combined path #3
Axons diam.	Hack’s level 1 – 1 μm	Hack’s level 2 – 1 μm	Hack’s level 3 – 1 μm
Rel. potential ${\varphi }_e$ diff. (L2 norm)	0.005% 0.001%	0.003% 0.001%	0.003% 0.001%
Rel. $E_z$ diff. (L2 norm)	0.2% 0.1%	0.3% 0.3%	0.4% 0.3%
Rel. $d{E}_z/dz$ diff. (L2 norm)	41% 30%	54% 47%	69% 74%
Rel. $\left|E_z\right|$ diff. at start termination	+3% 1%	+3% 1%	+3% 1%
Rel. $\left|E_z\right|$ diff. at end termination	+3% 1%	+21% 0.5%	+7% 30%
Axons diam.	Hack’s level 1 – 2 μm	Hack’s level 2 – 2 μm	Hack’s level 3 – 2 μm
Rel. potential ${\varphi }_e$ diff. (L2 norm)	0.005% 0.001%	0.003% 0.001%	0.003% 0.001%
Rel. $E_z$ diff. (L2 norm)	0.2% 0.2%	0.5% .0.3%	0.6% 0.4%
Rel. $d{E}_z/dz$ diff. (L2 norm)	98% 62%	92% 70%	99% 110%
Rel. $\left|E_z\right|$ diff. at start termination	+13% 1.5%	+13% 1.5	+13% 1.5
Rel. $\left|E_z\right|$ diff. at end termination	+13% 0.6%	+19% 8%	+6% 35%