An automated pipeline for obtaining labeled ICA‐templates corresponding to functional brain systems

Abstract

The complexity of our actions and thinking is likely reflected in functional brain networks. Independent component analysis (ICA) is a popular data‐driven method to compute group differences between such networks. A common way to investigate network differences is based on ICA maps which are generated from study‐specific samples. However, this approach limits the generalizability and reproducibility of the results. Alternatively, network ICA templates can be used, but up to date, few such templates exist and are limited in terms of the functional systems they cover. Here, we propose a simple two‐step procedure to obtain ICA‐templates corresponding to functional brain systems of the researcher's choice: In step 1, the functional system of interest needs to be defined by means of a statistical parameter map (input), which one can generate with open‐source software such as NeuroSynth or BrainMap. In step 2, that map is correlated to group‐ICA maps provided by the Human Connectome Project (HCP), which is based on a large sample size and uses high quality and standardized acquisition procedures. The HCP‐provided ICA‐map with the highest correlation to the input map is then used as an ICA template representing the functional system of interest, for example, for subsequent analyses such as dual regression. We provide a toolbox to complete step 2 of the suggested procedure and demonstrate the usage of our pipeline by producing an ICA templates that corresponds to “motor function” and nine additional brain functional systems resulting in an ICA maps with excellent alignment with the gray matter/white matter boundaries of the brain. Our toolbox generates data in two different file formats: volumetric‐based (NIFTI) and combined surface/volumetric files (CIFTI). Compared to 10 existing templates, our procedure output component maps with systematically stronger contribution of gray matter to the ICA z‐values compared to white matter voxels in 9/10 cases by at least a factor of 2. The toolbox allows users to investigate functional networks of interest, which will enhance interpretability, reproducibility, and standardization of research investigating functional brain networks.

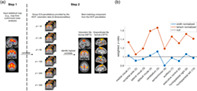
We propose a strategy to identify customized ICA‐templates for neuroimaging analyses based on matching a statistical brain map (e.g., functionally‐labeled) to the best matching group‐ICA component from the Human Connectome Project (a). This method yielded systematically stronger contribution of gray matter versus white matter voxels in 9/10 demo cases (b).

1. INTRODUCTION

Functional magnetic resonance imaging at rest (resting‐state fMRI or rs‐fMRI) has revealed consistent patterns of statistical associations, so‐called networks of functional connectivity (FC), between certain sets of regions in the human brain (Biswal et al., 1995; M. D. Fox & Raichle, 2007; Smith et al., 2009). In this context, (spatial) independent component analysis (ICA) has become a widely adopted multivariate data‐driven analysis method, which attempts to identify spatially independent components (i.e., statistical parameter maps). In brain imaging, this allows to cluster brain regions with similar functional response patterns into groups and can hence be regarded as a measure of FC (Calhoun et al., 2009; Hyvärinen, 1999). In the last two decades, studies using rs‐fMRI have reported a consistent set of large‐scale resting‐state networks whose functions have become research topics in cognitive and clinical neurosciences (Damoiseaux et al., 2006; Raichle et al., 2001; Yeo et al., 2011).

In order to compare ICA components from rs‐fMRI on the group level (e.g., patients vs. controls) one needs to obtain subject‐wise component maps that represent corresponding networks. Performing single‐subject ICA and subsequently computing group statistics on matched components seems impractical since, for example, due to individual noise, some component one finds in some subjects can be split into or across multiple components in other subjects. Instead, a common practice is to use a template (a collection of spatial components that one assumes to be common to the entire set of subjects) and map the template back to individual subjects in order to compute group comparisons on these subject‐wise component maps.

There are two major strategies for choosing a template. The first strategy is to derive the template from the data at hand (within‐sample template) or from an independent dataset (independent‐sample template) by performing an ICA on the concatenated data of all subjects in that sample. The second strategy is to use an atlas‐template available in the literature (e.g., Smith et al., 2009) or to create a customized template.

The advantage of deriving a within‐sample template is that since the resulting template is optimized for the sample of subjects in the study it provides optimal statistical sensitivity in group analyses. However, since the results of group‐ICA decompositions can look different in terms of dimensionality and topology of spatial components depending on factors such as acquisition parameters, group size, and preprocessing strategies, it may become difficult to compare the results of different studies that follow this strategy.

Using an atlas‐template may yield slightly less sensitive group analyses compared to using a within‐sample or an independent‐sample template, but atlas‐templates have the great advantage of referring to consistent spatial components across studies, for which there may even exist commonly accepted labels in the task‐domain. To date, few such functionally labeled atlas templates exist. One of the few exceptions was published by Smith et al. (2009). The authors pointed out a striking similarity in the spatial structure between group‐ICA maps they identified in 36 healthy participants and task‐based statistical parameter maps drawn from meta‐analyses of 1687 fMRI studies that investigated different perceptual, cognitive, and motor‐tasks in overall 29,671 subjects. The authors labeled the identified group‐ICA maps pertinent to the task‐based statistical parameter maps of highest correspondence, yielding labeled components such as the “sensorimotor,” the “lateral visual,” or the “executive control” network. In total, their publicly available template1 contains 10 components and has been widely used either for providing a standardized visualization of results, or as the basis for group comparisons (Castellazzi et al., 2018; Pflanz et al., 2015; Rane et al., 2014; Rubin et al., 2017).

In terms of standardization, it is beneficial or even necessary for the cognitive and clinical neurosciences to use common functionally labeled templates to compute network differences as opposed to calculating study‐specific group‐ICA maps. However, studies that investigate different functional systems may require different network templates targeting specific functional systems of interest, which may not all be covered by the 10 functional systems put forth by (Smith et al., 2009). Therefore, a pipeline which allows one to flexibly generate ICA‐based templates that capture customizable task‐related or functional domains is highly desirable. Such maps should be as spatially accurate (e.g., alignment with gray‐matter/white‐matter boundary) as possible in order to yield high sensitivity and specificity (Bodurka et al., 2007) and cover all relevant brain areas.

Here, we describe a standardized and automatized procedure to obtain such high‐quality ICA‐templates that correspond to functional systems of the researcher's choice. To this aim, we propose combining information from fMRI meta‐analyses with high‐resolution ICA‐maps from the Human Connectome Project (HCP, www.humanconnectome.org; Van Essen et al., 2013; Marcus et al., 2011), which provides a large dataset with excellent spatial resolution and high‐quality alignment between whole‐brain functional and structural data. Creating customized HCP‐templates follows a simple and fast two‐step procedure (Figure 1): In step 1, the user defines an “input” statistical brain map, for example, identified from already available meta‐analyses databases (such as NeuroSynth or Brainmap, see section “Pipeline” below), which in step 2 is correlated with the complete set of the 690 ICA component maps from the HCP (https://www.humanconnectome.org/storage/app/media/documentation/s1200/HCP1200‐DenseConnectome+PTN+Appendix‐July2017.pdf) to find the best matching HCP‐component map for the functional system of interest. Importantly, our pipeline allows one to generate ICA templates in two different file formats: the volumetric and commonly‐used NIFTI file format (Neuroimaging Informatics Technology Initiative, https://NIFTI.nimh.nih.gov/NIFTI-2), as well as the emerging CIFTI file format (Connectivity Informatics Technology Initiative, https://www.nitrc.org/projects/CIFTI/). The latter combines cortical data rendered on the surface with volumetric data of subcortical structures and the cerebellum (Marcus et al., 2011). To illustrate the proposed methodology, we create a labeled template for the term “motor function.” We compare that resulting ICA‐component from our pipeline to an existing ICA‐template corresponding to motor function from Smith et al. (2009). Furthermore, we create an updated template atlas based on the original atlas by Smith et al. (2009) and discuss potential benefits of the updated atlas.

FIGURE 1.

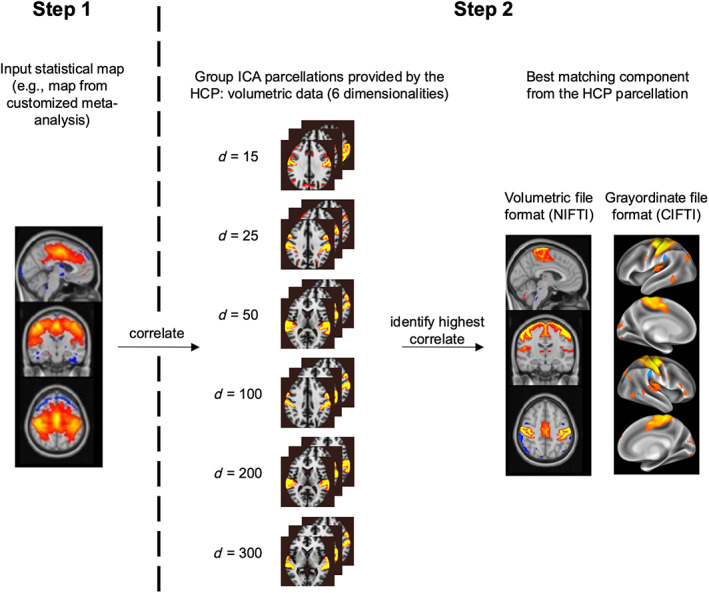
Overview of the proposed strategy to identify customized ICA‐templates of maximal correspondence to user‐specified functional systems. In step 1 (left panel), the user defines a functional system of interest and provides a brain statistical map representing that functional system as input. Such map can be generated with existing open‐access software such as NeuroSynth and BrainMap. In step 2, that input map is correlated to 690 group‐ICA maps (independent component analysis) provided by the Human Connectome Project (HCP). The HCP provides ICA maps for different target numbers of ICA components (“dimensionalities,” abbreviated with d in the figure), such that we consider all of these dimensionalities within our pipeline (middle panel). That HCP‐component with the highest correlation value to the input template is selected as “best match” (output ICA‐template). Within our pipeline, the output is provided in two different file formats: volumetric space (NIFTI), as well as a combined surface/volumetric file format (CIFTI) (right panel), which is also provided by the HCP.

2. METHODS

2.1. Subjects and preprocessing by the Human Connectome Project Consortium

Our pipeline is based on a subset of 1003 subjects (534 females, age range of 22–35 years) from the Human Connectome Project's (HCP) 1200 Subjects Release (https://db.humanconnectome.org/data/projects/HCP_1200), who completed four resting‐state fMRI runs (14.4 min each, resulting in 4800 total timepoints per subject at a TR of 0.72 s). All of the data were fully preprocessed by the HCP consortium and the cleaned data has been made publicly available (for the preprocessing procedure, see [Fischl, 2012; Glasser et al., 2013; Jenkinson et al., 2002; Jenkinson et al., 2012; Smith et al., 2013], including artifact removal with ICA‐FIX [Griffanti et al., 2014; Salimi‐Khorshidi et al., 2014]). The preprocessed data were used for group‐ICA parcellation in CIFTI space based on FSL's MELODIC tool. Note that the ICA‐decomposition using different dimensionalities (including 15, 25, 50, 100, 200, and 300 dimensions, see below) was also performed by the HCP consortium and the resulting maps have been made publicly available. We have chosen to use the HCP maps to enhance the standardization, reproducibility, and transparency of our pipeline. In brief, ICA decomposition was performed by the HCP consortium as follows (cf., also the HCP1200 documentation on higher level rs‐fMRI connectivity analyses at https://www.humanconnectome.org/storage/app/media/documentation/s1200/HCP1200-DenseConnectome+PTN+Appendix-July2017.pdf; the component maps are made available within the HCP database under the name “HCP1200 Parcellation + Timeseries + Netmats (PTN)”).

Our pipeline is based on a subset of 1003 subjects (534 females, age range of 22–35 years) from the Human Connectome Project's (HCP) 1200 Subjects Release (https://db.humanconnectome.org/data/projects/HCP_1200), who completed four resting‐state fMRI runs (14.4 min each, resulting in 4800 total timepoints per subject at a TR of 0.72 s). All of the data were fully preprocessed by the HCP consortium and the cleaned data has been made publicly available (for the preprocessing procedure, see [Fischl, 2012; Glasser et al., 2013; Jenkinson et al., 2002; Jenkinson et al., 2012; Smith et al., 2013], including artifact removal with ICA‐FIX [Griffanti et al., 2014; Salimi‐Khorshidi et al., 2014]). The preprocessed data were used for group‐ICA parcellation in CIFTI space based on FSL's MELODIC tool. Note that the ICA‐decomposition using different dimensionalities (including 15, 25, 50, 100, 200, and 300 dimensions, see below) was also performed by the HCP consortium and the resulting maps have been made publicly available. We have chosen to use the HCP maps to enhance the standardization, reproducibility, and transparency of our pipeline. In brief, ICA decomposition was performed by the HCP consortium as follows (cf., also the HCP1200 documentation on higher level rs‐fMRI connectivity analyses at https://www.humanconnectome.org/storage/app/media/documentation/s1200/HCP1200‐DenseConnectome+PTN+Appendix‐July2017.pdf; the component maps are made available within the HCP database under the name “HCP1200 Parcellation + Timeseries + Netmats (PTN)”).

First, inter‐subject registration of the cortex was performed the Multimodal Surface Matching algorithm (“MSMAll”; Glasser et al., 2016; Robinson et al., 2014). Then, each data set was demeaned and variance‐normalized (Beckmann & Smith, 2004). Next, group principal component analysis (PCA) was run using the tool MELODIC's Incremental Group‐PCA (MIGP). The MIGP output comprised the top 4500 weighted spatial eigenvectors, that is, eigenmaps, from a group‐averaged PCA, which is a close approximation to concatenating the timeseries data from all subjects and subsequently performing PCA (Smith et al., 2014). Each of the MIGP group‐eigenmaps was then input into FSL's MELODIC tool for spatial group‐ICA. ICA was run for six different numbers of output components (referred to as “dimensionalities”), with 15, 25, 50, 100, 200, and 300 components, respectively (Beckmann & Smith, 2004; Hyvärinen, 1999), whereby a higher number of dimensions typically outputs component maps with fewer significant areas. Those operations were performed in grayordinate, that is, “CIFTI,” space (surface vertices plus subcortical grey matter voxels, [Glasser et al., 2013]), but moreover, voxel‐based NIFTI versions (normalized to volumetric MNI152 2 mm space) of each component were generated and released. To note, as with any ICA, these maps are not binary; rather they provide weight values of how strongly each grayordinate (CIFTI)/voxel (NIFTI) belongs to a component. Thus, every grayordinate/voxel is part of each component, but to varying degrees, meaning that such ICA maps do overlap.

2.2. Pipeline

The purpose of our pipeline is to find the best matching ICA component map from the HCP‐ 1200‐Subjects‐Release to any spatial map in MNI‐space (statistical parameter map or mask) provided as input. Our pipeline is designed to run in Matlab (The Mathworks, Natick, MA). Input brain maps can be provided both in NIFTI or CIFTI file formats. Likewise, the user can choose either of the two data formats as output format of the best‐matching ICA‐template, independent of the input format. In our code, we make use of other Matlab‐based tools, including parts of CoSMoMVPA (Oosterhof et al., 2016) to manipulate NIFTI files and HCP's Workbench software (Marcus et al., 2011) to manipulate CIFTI files. With these tools, data of either file format can be read into Matlab. Within Matlab, the brain map is represented as a vector of length n, where n is the respective number of brainvoxels (in case NIFTI was chosen as the file format) or grayordinates (in case CIFTI was chosen as the file format). These vectors are then Pearson‐correlated to all of the 690 HCP's ICA‐templates, which we provide in matrix representation within our toolbox (note that we provide six sets of matrix representations, corresponding to the six ICA‐dimensionalities provided by the HCP, each in two versions NIFTI and CIFTI). The input vector is Pearson‐correlated to all rows of all six HCP matrices, and the matrix and row indices of the highest correlate are stored and used to extract the vector representing the “best‐matching” group ICA‐template, with which we then generate the output image in the desired output format (NIFTI/CIFTI).

To generate customized high‐quality ICA‐templates that correspond to functional systems of interest, we propose a two‐step‐procedure (Figure 1). First, the user provides a statistical brain map that corresponds to the functional label of choice (“input”), for example, generated from fMRI meta‐analyses, as previously suggested (Smith et al., 2009). Databases, such as NeuroSynth (Yarkoni et al., 2011, www.neurosynth.org) or BrainMap (Fox & Lancaster, 2002; Laird et al., 2005): www.brainmap.org), synthesize results from thousands of fMRI studies and allow users to automatically conduct meta‐analyses based on a search term of interest. These tools provide statistical brain maps (in MNI152 2 mm space, i.e., NIFTI files) which correspond to the user's query. For example, searching for “fear” outputs a brain map in MNI space with highest values in the amygdalae. The second step is to identify the HCP‐component which best matches such an input map as described above, that is, for a given input statistical brain map, Pearson's correlations to all of the 690 HCP‐provided ICA templates are calculated and the HCP map with the highest Pearson correlation is chosen as the ‘labeled HCP‐component’.

While the user can generate the input for step 1 with already available and validated software such as NeuroSynth, we provide a Matlab toolbox to conduct step 2 (https://osf.io/mek47/). Our toolbox provides the labeled HCP‐component in NIFTI and CIFTI format as well as the HCP‐component number and dimensionality and its correlation with the input‐map.

2.3. Demo 1: Generating an ICA‐template corresponding to “motor function”

Below, we demonstrate the results from our pipeline when applied with the term “motor function,” as an example for a commonly investigated system in the neurosciences. We entered the search term “motor function” into the meta‐analysis tool from NeuroSynth (https://neurosynth.org/analyses/terms/) and submitted the resulting parameter map to our pipeline, which yielded the labeled HCP‐component template for motor function, which we subsequently compare to one of the few existing labeled ICA‐templates corresponding to motor function (Smith et al., 2009). Spatial ICA component maps contain a weight (z‐value) for every voxel. We argue, that in functional MRI a functional component should be located in gray‐, but not in white matter (WM). Hence, gray matter (GM) voxels should exhibit higher z‐values than WM voxels. We contrast the spatial alignment with respect to GM and WM between the two “template versions” by comparing their z‐weighted GM/WM ratios (zwr) as,

$$\mathit{zwr}=\frac{\sum \left|z\left(i\right)\right|p_{\mathit{GM}}\left(i\right)}{\sum \left|z\left(i\right)\right|p_{\mathit{WM}}\left(i\right)}*\frac{\sum p_{\mathit{WM}}\left(i\right)}{\sum p_{\mathit{GM}}\left(i\right)}$$ (1)

with, z(i) the ICA z‐value of voxel I, p _GM (i) the prior tissue probability of voxel i belonging to GM, and p _WM (i) the prior tissue probability of voxel i belonging to WM.

The first term represents the sum of each voxels' absolute ICA z‐values multiplied with the voxel's probability to belong to GM divided by the voxel's probability to belong to WM. The term on the right corrects the expression by the ratio of the probabilities that voxels belong to white or GM, and thereby centers zwr at 1 (GM and WM have the same strength of ICA‐z components). A zwr >1 indicates that GM contains stronger ICA component loadings than WM, whereas a zwr < 1 indicates that WM contains stronger ICA loadings than GM. Thus, greater values indicate greater weighting of GM and higher dissociation from WM, which is desirable for BOLD imaging (Bodurka et al., 2007). Probabilities of voxels belonging to white or GM were taken from tissue‐prior maps provided with fsl (avg152T1_gray and avg152T1_white). Computations were conducted within Matlab. To illustrate that different file formats are compatible and can be produced with our pipeline, we also show the corresponding CIFTI‐version of the “motor function” ICA‐template created with our framework. We display the results using FSLeyes for NIFTI‐files (FMRIB Software Library image viewer, https://zenodo.org/record/3403671) and the Connectome Workbench Viewer for CIFTI‐files (Marcus et al., 2011, 2013).

2.4. Demo 2: Generating ICA‐templates corresponding the “brain's functional architecture during activation and rest”

To generalize the usage of our pipeline beyond motor function, we compared all of the 10 ICA components published by Smith et al. (2009) to the corresponding templates generated with our pipeline (instead of contrasting only the “motor function” template as in the previous section). To identify the best‐matching IC from the HCP parcellation for each of the 10 Smith‐templates, we proceeded as described above (i.e., we ran a correlation analysis for each of the 10 Smith‐templates with all of the 690 HCP's component maps in volumetric MNI 2 mm space and chose that HCP component with the highest Pearson correlation value to the original template as a new version of that template, see Figure 3). To quantify the expected gain of our method, we used Equation 1 to calculate for each component a statistic that expresses a ratio of how high the ICA z‐values in GM voxels are with respect to those in WM voxels and compared that metric between the 10 components published by Smith et al. (2009) and our updated version of the templates (as shown in Figure 3): If z‐values in GM exceed those of WM this ratio becomes larger than one. Although studies reporting functional networks within the WM are becoming increasingly available (Huang et al., 2020; Peer et al., 2017), the majority of coherent stable networks corresponding to distinct functions including vision, language, and other cognitive and motor functional domains were reported in the GM (Biswal et al., 1995; Buckner et al., 2008; Fox & Greicius, 2010; Fox & Raichle, 2007; Gonzalez‐Castillo et al., 2014; Lee et al., 2013; Raichle et al., 2001; Zhang & Raichle, 2010). We, therefore, conclude that an atlas whose driving components are stronger represented in GM than in WM will be more sensitive to actual cortical processes when used in dual regression analyses.

FIGURE 3.

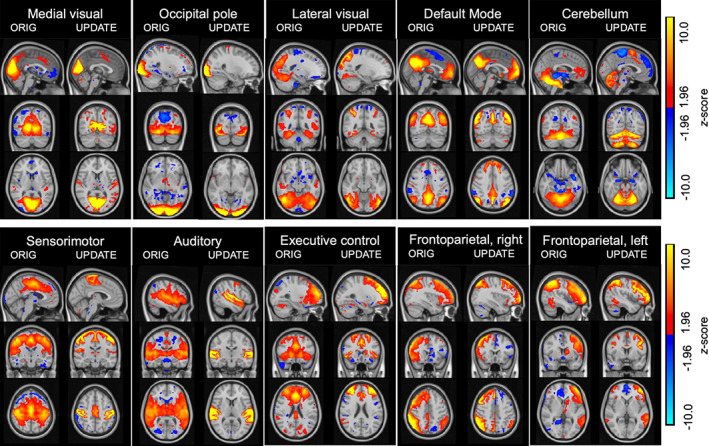
Comparison between the original templates by Smith et al. (2009) (left panels) and the results from our proposed procedure that selects the maximally correlated component map from the HCP dataset (right panels), displayed on the anatomical standard image by the Montreal Neurological Institute (MNI152) in 2 mm voxel‐resolution. We show z‐scored maps of each version for comparability. The side‐by‐side visual comparisons show that the maps generated with our template yield high alignment with the MNI‐template as well as the distinction between gray‐/white matter boundaries. (Display range: z = 1.96–10, negative and positive).

3. RESULTS

3.1. Demo 1: Generating an ICA‐template corresponding to “motor function”

The meta‐analysis ran on the term “motor function” in NeuroSynth yielded a statistical brain map comprised of 74 studies investigating motor function in MNI152 2 mm space (Figure 2a). We used that map as an input to our pipeline to generate a high‐quality ICA‐template corresponding to “motor function” (Figure 2b). The side‐by‐side visual comparison between the input and output maps demonstrates the high spatial accuracy of our output ICA‐template in terms of alignment with the gray and WM, while capturing the functionally relevant anatomical brain regions defined by the input map. To further illustrate that high spatial accuracy, we show one of the few existing labeled ICA‐templates corresponding to motor function (Smith et al., 2009) alongside our template, in Figure 2c. To compare the spatial alignment of the input brain statistical map to each of the ICA template versions with the cortical sheet, we calculated the respective z‐weighted GM/WM ratios (zwr) and found that the version created using the current pipeline yielded a ratio of 1.2609, indicating that ICA‐z components in GM were about 25% stronger than in WM. The existing template yielded a ratio of 0.8044 indicating that its ICA components in WM were actually stronger than in GM. These numbers are backed by visually inspecting the topography of the two templates (see panels b and c in Figure 2). While the best matching component found by our pipeline shows excellent alignment with the cortical sheet, the component from the published template appears shifted in the z‐axis, actually missing the most dorsal aspect of motor cortex and clearly leaking into WM.

FIGURE 2.

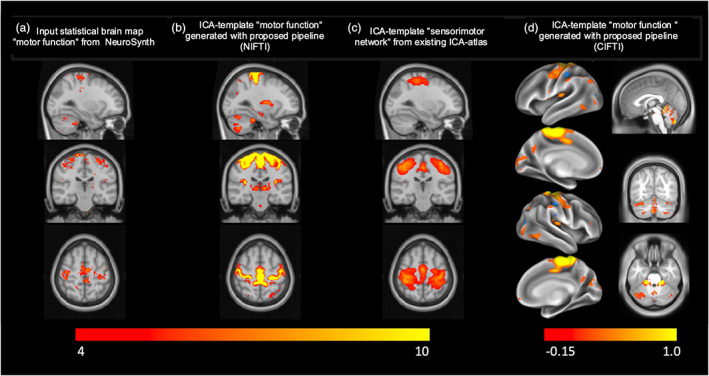
Illustration of the results from our pipeline. To generate an ICA‐template which corresponds to motor function, we started by entering the search term “motor function” into the meta‐analyses tool from NeuroSynth (neurosynth.org), which generated the statistical brain map displayed in (a) from 74 studies investigating motor function. We used this map with our pipeline and obtained the ICA‐template shown in (b). Note the high spatial accuracy of our resulting ICA‐template in terms of alignment with the gray matter/white matter boundaries, while capturing the functionally relevant anatomical brain regions defined by the input map. To further illustrate that high spatial accuracy, we additionally show one of the few existing labeled ICA‐templates corresponding to motor function (Smith et al., 2009). Additionally, we show the CIFTI‐version of our resulting ICA‐template (d), projected on the surface (left column in d) and volumetrically for the subcortex and cerebellum (right column in d). Brain maps in a–c are displayed on the MNI152 2 mm template at voxel location 59, 51, 64 (color map range [4–10]). Brain map in D is displayed on CIFTI Grayordinates standard space, projected on the surface (left column in d) and volumetrically in subcortex/cerebellum at voxel location 0, −65, −27 (right column in d) (display ranges in d: [−0.15; 0.1]; color map range in absolute percent, positive, and negative: [2; 98]).

3.2. Demo 2: Generating ICA‐templates corresponding the “brain's functional architecture during activation and rest”

Visual comparison between the original Smith‐templates and the volumetric version of our identified components qualitatively shows good spatial agreement between the two atlases (Figure 3; left columns show the original templates, right columns our updated versions). In Table 1, we provide the Pearson correlation values between each pair of the template versions. This indicates that the general concept of the Smith‐templates is maintained within our templates. However, it becomes evident in Figure 3 that spatial alignment with the borders of the MNI152 template is superior in the updated compared to the original version. Particularly strong examples are components 4 (default mode), 5 (cerebellum), 6 (sensorimotor), and 7 (auditory). In Figure 4, we display the z‐weighted gray–white‐matter ratio (see Equation 1) for both the original 10 components published by Smith et al. (blue) and our updated version of the templates (red) and complement those findings with the exact values in Table 2: While the original atlas of Smith et al does not exhibit systematically stronger contribution of GM to the ICA‐z values compared to WM voxels (notice that the blue line oscillates around values of 1) our procedure yields component maps that substantially outperform the original atlas on 9 of the 10 components by at least a factor of 2.

TABLE 1.

Overview of the best‐matching ICA map from the HCP parcellations to the original templates (from Smith et al., 2009).

Component label from the Smith et al. (2009) ICA	Best match of the HCP's 1200 subject's release ICA	Correlation value (Pearson's r)
Medial visual areas	15‐component parcellation: IC 2	0.5927
Occipital pole	15‐component parcellation: IC 3	0.6982
Lateral visual areas	25‐component parcellation: IC 4	0.6262
Default mode network	25‐component parcellation: IC 2	0.5761
Cerebellum	25‐component parcellation: IC 22	0.3417
Sensorimotor network	25‐component parcellation: IC 13	0.3846
Auditory network	50‐component parcellation: IC 38	0.4798
Executive control network	100‐component parcellation: IC 26	0.4234
Frontoparietal network, right	15‐component parcellation: IC 7	0.6249
Frontoparietal network, left	15‐component parcellation: IC 5	0.6192

FIGURE 4.

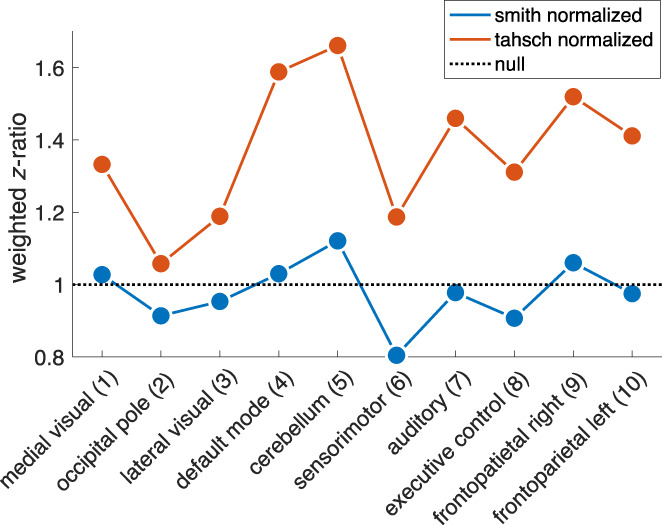
To demonstrate the expected gain of our method, we calculated a statistic that expresses per component a ratio of how high the ICA z‐values in gray matter voxels are with respect to those in white matter voxels and compared that metric between the 10 components published by Smith et al., 2009 (blue line/dots) and “our” version of the templates as shown in Figure 3 (here depicted as red line/dots; “tahsch” refers to the authors' names, “Tahedl/Schwarzbach”). The metric was calculated as follows: First, we added all ICA‐values within gray matter voxels and normalized that sum by the probability of a voxel being in gray matter (based on the gray‐/white matter tissue priors provided by FSL). We repeated that procedure for the white matter and calculated the ratio of (normalized) gray vs. white matter sums. The dotted line denotes the outcome of our procedure for a null‐component map in which z‐values in gray and white matter have the same amplitude, that is, such a map yield a ratio of 1. If z‐values in gray matter exceed those of white matter this ratio becomes larger than one. We argue that an atlas whose driving components are stronger represented in gray matter than in white matter will be more sensitive to actual cortical processes. Note that the original template oscillates around ratios of 1 whereas our updated templates yield ratios of 1.51–2.93 (see Table 1).

TABLE 2.

Weighted z‐ratio for original and updated component maps.

Component	z(GM/WM)—org	z(GM/WM)–updated	Delta(org–updated)	Gain (org/updated)
Medial visual (1)	1.13	2.33	1.20	2.06
Occipital pole (2)	0.95	1.51	0.55	1.58
Lateral visual (3)	1.14	2.57	1.43	2.26
Default mode (4)	1.22	2.93	1.71	2.40
Cerebellum (5)	0.99	2.34	1.35	2.37
Sensorimotor (6)	0.92	2.10	1.18	2.28
Auditory (7)	0.98	2.37	1.38	2.40
Executive control (8)	1.04	2.31	1.27	2.23
Frontoparietal right (9)	1.27	2.92	1.65	2.29
Frontoparietal left (10)	1.20	3.10	1.90	2.58

Abbreviation: org, original (component map).

4. CONCLUSIONS

Here, we have proposed a standardized method to obtain labeled ICA‐templates from the high‐quality HCP database which correspond to research‐specific brain functions. Within this framework, the user provides a statistical brain map that represents a chosen functional system, for example, by making use of already available software which allows users to conduct automatized meta‐analyses provided by large databases such as NeuroSynth and BrainMap. Within our framework, this map is subsequently correlated to 690 group‐ICA maps from the HCP, generated from more than 1000 subjects and acquired with standardized resting‐state fMRI data. We suggest using that HCP group‐ICA map with the highest correspondence to the input statistical map as an ICA‐template for the functional system of interest for subsequent analyses such as dual regression.

Due to the high quality of the underlying HCP‐data the templates, which are generated using that strategy, exhibit excellent accurate spatial alignment with the GM/WM boundaries of the MNI‐template, likely enhancing the sensitivity of BOLD‐analyses within GM (Bodurka et al., 2007) based on these templates. This aspect is highlighted when comparing the statistical maps in Figure 2b,c that contrast the HCP‐based template for “motor function” with the existing “sensorimotor” component of Smith et al., 2009, with the latter one showing a systematic deviation from the cortical sheet. We report similar observations when extending the comparisons to the entire set of 10 components of the original atlas by Smith et al. (2009) (Figures 3 and 4 and Table 2). Thus, next to ease‐of use of our pipeline for creating customized templates as volumetric NIFTI‐files as well as combined surface/volumetric CIFTI files we consider high‐quality alignment and large sample size an important advantage of using HCP‐data when generating customized templates for the purpose of conducting group comparisons based on labeled ICA components. We provide our toolbox for public download on OSF (https://osf.io/mek47/).

5. LIMITATIONS/OUTLOOK

One limitation of our method is that the ICA‐templates which can be generated within our framework are limited to the 690 components provided by the HCP. Although the pipeline will identify a relative best‐matching ICA‐template for many brain functions, there will be brain functions our method cannot account for. Since our pipeline will however always output the best‐matching ICA‐template of the input map to the HCP data, users should be aware that better matching algorithms than correlation may exist and that there is no commonly agreed critical correlation‐threshold that ensures that an ICA component truthfully captures the functional system in question. Users should at least visually inspect the results before deciding to accept a functional label for an ICA template and use it with their analyses.

Note that in this work, we have suggested to generate the input map for brain functional maps of interest. However, the input can be any statistical brain map; for example, alternatively, gene expression maps might be used, which are now available for the MRI research community in MNI space thanks to the work from the Allen Brain Institute (Hawrylycz et al., 2012). Thus, ICA templates corresponding to the gene expression from a specific genetic might be investigated rather than brain functions, which offers new exciting opportunities for innovative research questions. However, such experimental approaches are yet to be tested and validated.

Our project uses the HCP data as to create an atlas template for ICA. However, while HCP is a valuable and widely used resource, it is still limited in demographic range. Such sampling bias attenuates out‐of sample performance of brain‐behavior prediction models, for example when it comes to data from different ethnicities (Li et al., 2022). The degree to which one may observe population‐dependent systematic differences in core resting‐state networks is an empirical question outside the scope of the current paper. Nevertheless, maps from our updated atlas may provide a high‐quality reference to which future studies can compare data from other ethnicities or age groups using comparable up‐to date acquisition protocols in terms of TR, resolution and scan‐duration and using the published processing pipelines from the HCP‐consortium (Glasser et al., 2013).

To conclude, we have provided a framework to generate high‐quality ICA‐templates that can be linked to statistical parameter maps, which allows to address research questions investigating specific functional systems. Such parameter maps that correspond to brain functional systems can be retrieved from automatized meta‐analyses from existing external software, and our own toolbox can then be used to identify the best matching ICA‐component from the high‐quality and sizeable HCP data. We believe that this approach has the potential to enhance power, sensitivity, reproducibility, and interpretability of studies investigating coherence changes in functionally defined brain networks.

AUTHOR CONTRIBUTIONS

Marlene Tahedl and Jens V. Schwarzbach developed the idea for the toolbox. Marlene Tahedl wrote the code for the toolbox, ran the analyses, and provided the initial draft. Marlene Tahedl and Jens V. Schwarzbach reviewed and agreed on the final version of the manuscript.

FUNDING INFORMATION

Marlene Tahedl is supported by a Walter‐Benjamin Postdoc Stipend from the Deutsche Forschungsgemeinschaft (DFG, TA 1902/1‐1). Jens V. Schwarzbach is supported by the DFG (FOR 2858, SCHW 1925/2‐1).

CONFLICT OF INTEREST STATEMENT

The authors declare no conflicts of interest.

Tahedl, M. , & Schwarzbach, J. V. (2023). An automated pipeline for obtaining labeled ICA‐templates corresponding to functional brain systems. Human Brain Mapping, 44(16), 5202–5211. 10.1002/hbm.26435

DATA AVAILABILITY STATEMENT

The data that support the findings of this study are openly available in Human Connectome Project at https://db.humanconnectome.org/app/template/Login.vm;jsessionid=67986192BF654DD982A67A67FCB5A432.