A general image misalignment correction method for tomography experiments

Summary

Tomography experiments generate three-dimensional (3D) reconstructed slices from a series of two-dimensional (2D) projection images. However, the mechanical system generates joint offsets that result in unaligned 2D projections. This misalignment affects the reconstructed images and reduces their actual spatial resolution. In this study, we present a novel method called outer contour-based misalignment correction (OCMC) for correcting image misalignments in tomography. We use the sample’s outer contour structure as auxiliary information to estimate the extent of misalignment in each image. This method is generic and can be used with various tomography imaging techniques. We validated our method with five datasets collected from different samples and across various tomography techniques. The OCMC method demonstrated significant advantages in terms alignment accuracy and time efficiency. As an end-to-end correction method, OCMC can be easily integrated into an online tomography data processing pipeline and facilitate feedback control in future synchrotron tomography experiments.

Graphical abstract

Highlights

• •A novel tomography alignment method based on the outer contour structure
• •Significant advantages in terms of alignment accuracy and time efficiency
• •Integration into the real-time data processing pipeline of tomography is possible

Analytical method in materials science; Materials characterization techniques

Introduction

Tomography experiments are a powerful approach for investigating the three-dimensional (3D) structure of matter across many fields^{1,2,3,4,5,6,7} such as biology, medical diagnosis, materials science, and industrial inspection. Recent advancements in scanning transmission X-ray microscopy (STXM), ptychography, and electron microscopy (EM), has vastly improved the resolution of two-dimensional (2D) projection images over the past decade, reaching nano and atomic scale.^8,9,10 Despite these gains in 2D projection image resolution, motion artifacts caused by joint offsets, such as mechanical vibrations and positional errors limit the actual resolution of 3D reconstructed slices.^11,12,13 This is because the axis origin of spatial frequency information changes for the same projected object at different projection angles, leading to a loss of details in slices after reconstruction via the Fourier slice theorem. However, accurate and efficient correction of joint misalignment in nanometer domain tends to be technically challenging. Furthermore, as tomography experiments heading toward dynamic and serial characterization in next generation synchrotron beamlines, achieving real-time reconstruction and instantaneous feature extraction is vital for decision-making in data acquisition to capture critical sample states.^14,15 However, the significant time required to align joint offsets presents a bottleneck for real-time reconstruction. As data volume grows, this issue becomes increasingly pressing, highlighting the necessity for an end-to-end image alignment method that is highly computationally efficient and can be easily incorporated into a fully automated tomography data processing pipeline.

At present, there are three main approaches for image alignment: feature marking-based methods,^16,17,18 feature matching-based methods,^{19,20,21,22,23,24} and iterative reprojection-based methods.^25,26,27,28 Among them, feature marker-based methods are considered to be straightforward and effective. However, they require manual addition of feature markers during the sample preparation process and picking of feature point in the projection images. This can increase the complexity of the process and affect the quality of imaging. Moreover, with an increasing number of projection images, these methods are limited by the amount of labor required and the accuracy of feature point extraction, which makes real-time correction and reconstruction unfeasible. Feature matching-based methods are currently evolving from traditional methods such as scale-invariant feature transform (SIFT)^19,20 and center of mass (CM)²¹ to deep learning feature matching methods.^23,24 While traditional methods rely on geometric relations or feature operators, the accuracy of these methods can be influenced by the environment and impurities surrounding the sample. In contrast, deep learning feature extraction methods are accurate and efficient, aided by the graphic processing unit (GPU). However, tracking features of a wide variety of samples requires large AI models and huge training dataset that have yet to be created. Iterative reprojection-based methods have proven to be highly accurate and widely applicable. Yet achieving high-precision output necessitates multiple iterations along with appropriate reconstruction algorithms and hyperparameters. Selecting the optimal parameters can be challenging, particularly for parameters that cannot be precisely determined such as the position of the rotational axis²³ in the presence of mechanical vibrations. Furthermore, the computational complexity of iterative reprojection-based methods increases significantly with an increasing number of projection images for higher resolution, resulting in a significant time overhead. Additionally, these methods require the acquisition process to be completed before any correction can be performed, posing difficulties in achieving real-time correction.

We introduce a novel and general method called outer contour-based misalignment correction (OCMC) for correcting misalignments in tomography experiments. This approach achieves high accuracy in alignment while only requires light computation. OCMC relies exclusively on the sample’s outer contour information to select the best correction method for each image, ensuring consistent alignment of the outer contour structure to achieve globally optimal misalignment correction of all images. The accuracy of correction is proportional to the complexity of the sample structure and the amount of information available. OCMC is theoretically capable of correcting misalignments for arbitrary samples and is not limited to any specific tomography methodology. The computational complexity of OCMC is O(n) where n is the number of projection images. Also, our method allows images to be corrected during the acquisition process, eliminating the need to wait for image acquisition to complete.

To assess the effectiveness of OCMC, a quantitative analysis was performed on two microbial sample datasets that were simulated through back-projection. Multiple sources of instability, such as positioning offset, rotational axis offset, and jitter, were individually corrected. Subsequently, the offsets were jointly corrected to determine the overall effectiveness of the method. The correction performance was evaluated by reducing the MSE of offsets by several orders of magnitude, demonstrating the effectiveness of OCMC even with large irregular offsets. The versatility of OCMC was also demonstrated by applying it to correct raw projection images of nanoscale X-ray computed tomography (Nano-CT), 3D X-ray fluorescence tomography (3D-XRF), and electron tomography (ET). In these cases, the joint offsets were unknown, and significant improvements in contrast and detail of the reconstructed slices were observed. In addition, the time consumption of OCMC was evaluated at different resolutions and projection numbers. It was discovered that OCMC, in combination with parallelized processing, achieves faster correction. With its “correction during acquisition” capability, OCMC can process the data stream in batch, enabling real-time correction.

Results

Workflow of OCMC

The fundamental concept behind the OCMC algorithm is to use the unchanging outer contour structure (OCS) of the sample to align projection images throughout the entire tomography process. The correction workflow consists of three key steps: initialization, coarse alignment, and fine alignment, as shown in Figure 1A. The algorithm employs a 3D reference model and iteratively updates it to search for the actual OCS of the sample. The basic updating process for a specific projection image is illustrated in Figure 1B. During this process, an OCS model corresponding to the jth image in a tomography stack is formed by stretching the aligned OCS image along its normal direction. The OCS model is then rotated by an angle theta and combined with the reference model. The overlapping volume of the two models is extracted as the updated reference model using a method called common volume extraction (CVE). This updating process is performed throughout the entire alignment workflow. It is important to note that theta is generally arbitrary during the two alignment stages but tends to be around 90° in the initialization step. Figure 2A depicts the reference model creation process that takes place during the initialization step of the OCMC algorithm. The initialization step is a crucial aspect of the OCMC algorithm, with two objectives: segmentation and positioning. The segmentation process involves extracting the OCS images for all projection images (the detailed process is elaborated in the method details subsection on segmentation). The positioning process aims to generate a rough 3D model using two OCS images positioned at the center of field of view (CoV), approximately 90° apart in projection angle. Initially, an OCS image (typically the first acquired image used as default) is selected, and the center of its bounding box (CoB) is moved to the CoV. An updating operation is then applied to the cubic-shaped reference model using the newly positioned OCS. This operation creates a reference model located in the CoV, and the projection angle corresponding to this OCS is defined as the initial angle. In the next step, another OCS image collected at a projection angle approximately orthogonal to the initial angle is aligned horizontally with the CoV and moved to an optimal position, where it has the maximum intersection area with the back-projected rectangle from the previous reference model. The reference model is then updated again using the newly positioned OCS and is ready for the following coarse alignment process.

Figure 1.

Concept of OCMC

(A) The steps of OCMC workflow: initialization, coarse alignment, and fine alignment.

(B) Schematic of updating process. The newly corrected OCS image is stretched and stacked with the old reference model, and their common volume becomes the new reference model.

Figure 2.

Procedure of OCMC

(A) Schematic of initialization process. The OCS images are extracted and the spatial position of the reference model is determined by two OCS images with orthogonal imaging angles.

(B) Schematic of the coarse alignment and fine alignment process. The OCS images are updated with a larger step size in the coarse alignment, while in the fine alignment the OCS images are updated at a step size of 1 and a filter module is added.

During the coarse alignment step, the OCMC algorithm cycles through the projection images at a specific step size (Δj) to align them to the most recently updated reference model. This process is illustrated in Figure 2B. Initially, Δj can be set to a large value, so that only a few projection images spreading across the entire angular scanning range are selected for alignment. The extracted OCS images from the selected projections are sequentially aligned to their current optimal positions. The optimal position for moving the jth OCS is determined based on its maximum intersection area with the back-projected OCS from the latest reference model at the same projection angle. The latest corrected jth OCS is then immediately used to update the most recent reference model. It is important to note that certain OCSs may have multiple optimal correction positions, which are temporarily skipped by the algorithm. The process is then repeated with Δj halved at each new iteration. Additionally, OCS images that were aligned in previous iterations and have only one optimal position are skipped in new iterations.

The OCMC algorithm concludes with a fine misalignment correction procedure, where all remaining OCSs are aligned. This step consists of two separate loops. In the first loop, the algorithm performs the same alignment and updating operation as in the coarse alignment step but with a smaller step size (Δj = 1) for the entire dataset. For OCSs with multiple optimal correction positions, a filter function is utilized in the second loop to obtain the average of these positions. This refinement process aims to improve the remaining misalignments. It’s worth noting that the second loop may not be necessary if the sample exhibits a complex OCS.

To enhance the efficiency of the misalignment correction process, the OCMC algorithm incorporates parallel computing techniques (detailed process is elaborated in the method details subsection on parallel correction pipelines). Additionally, a batch image selection strategy is employed (detailed process is elaborated in the method details subsection on batch selection strategy) to enable real-time correction during image acquisition. By starting the OCMC operation during the image acquisition process, the efficiency of misalignment correction is further improved.

Validation on simulation data

To evaluate the effectiveness of the OCMC algorithm, we conducted a comprehensive assessment on two different datasets: dataset A, which was a measurement on a sternaspis scutata specimen,²⁹ and dataset B, which was a measurement on the owenia fusiformis specimen.³⁰ We intentionally introduced various offset sources, such as positioning offset, rotational axis offset, and jitter, to examine the algorithm’s performance. These datasets were chosen due to their distinct morphological characteristics, providing a test of the algorithm’s generality.

To quantify the improvement achieved by the OCMC, we compared the MSE of the offsets before and after corrections, defined as follows:

$$MSE=\frac{{\sum }_{i=1}^n{\left(O_i-C_i\right)}^2}{n}$$ (Equation 1)

where n is the number of projection images, O_i is the summation of all offsets for one projection image, and C_i is the amount of correction for one projection image.

To correct the joint offsets by using OCMC, it is crucial to determine the spatial position of the sample, which serves as the positioning point. In the absence of jitter, the sample can be considered to rotate on a perfect reference circle (Figures S1A and S1B). For any sample position, there is a horizontal distance Δd and a vertical distance Δz between the center of the sample and the reference point, both contributing to the positioning offset (Figure S1A). Correcting the positioning offset may not be necessary in the absence of jitter, but with jitter it is crucial before reconstruction. Furthermore, correcting the positioning offset enables image cropping, which reduces the reconstruction volume and speeds up real-time processing. When the rotational axis offset is present, the center of reference circle deviates from the CoV (Figure S1B). As shown in Figure S1B, Δd can be decomposed into two orthogonal offsets Δx and Δy. Thus, using the initial acquisition position as the standard offset, the positioning offset can be expressed as (Δx, Δy, Δz). In the presence of jitter, the reference circle becomes an irregular shape (Figure S1C).

In order to confirm the error of OCMC in moving the spatial position of the sample, we designed a positioning offset correction experiment. For dataset A, we set the positioning offset to (3.5, −3.5, 1) without any rotational axis offset or jitter. As shown in Figures 3A and 3B, the OCMC algorithm accurately determined the required movement, which is in good agreement with the input positioning offset. However, we did observe a small difference between the corrected value and the ground truth due to rounding errors at the sub-pixel level, as image movements are measured in pixels. The impact of this corrected value was assessed using MSE, resulting in 0.43 horizontally and 0 vertically for dataset A. As the positioning error was caused by sample repositioning, we referred to it as the positioning error. It is worth noting that this error depends on the detection method and may be challenging to completely eliminate in simulation tests. In subsequent evaluations, we retained this offset and simply subtracted the positioning error for evaluation purposes.

Figure 3.

Validation results of simulated data

(A and B) Correction curves for positioning errors of dataset A.

(C–F) Correction curves for horizontal (C and D) and vertical (E and F) jitter of dataset A.

(J–G) Correction curves for horizontal (J and H) and vertical (I and G) joint offsets of dataset A.

(K–N) Correction curves for horizontal (K and L) and vertical (M and N) joint offsets of dataset B.

(O) Histogram of time-consumption for offline correction and online correction of simulated datasets.

In addition, the alignment of the CoR is an important goal of the algorithm to facilitate the subsequent reconstruction process. For dataset A, we introduced a rotational axis offset of 44 pixels along with a positioning offset of (3.5, −3.5, 1) without any jitter. After executing the OCMC algorithm and eliminating the positioning error, we measured the corrected values for each projection image, a CoR offset of 44 pixels. The MSE was found to be 0 (Table S1 indicating a precise correction of the rotational axis. This process is user-friendly as it eliminates the need for manual examination of the center of rotation axis of the jittered projections. The OCMC algorithm automatically corrects the CoR to the CoV with high accuracy, thus facilitating 3D reconstruction.

Finally, jitter, attributed from mechanical vibration, temperature shift, and other factors, introduces complex positional errors with an irregular pattern, as shown in Figure S1C. We simulated jitter by introducing random offset values ranging from −20 to 20 pixels in both horizontal and vertical directions for each projection image. For dataset A, with a positioning offset of (3.5, −3.5, 1) and no rotational axis offset, we applied random jitter. After applying OCMC alignment and eliminating the positioning error, the resulting jitter was largely corrected, as illustrated in Figures 3C–3F. The horizontal and vertical MSE were calculated and found to be 0.22 and 0, respectively (Table S1). This demonstrates the OCMC algorithm’s success in correcting each offset individually. It is worth noting that the alignment of the positioning offset had a larger MSE due to sub-pixel errors during the rotation process, which is the primary error source of the OCMC algorithm.

To assess the general applicability and effectiveness of OCMC in correcting mixed offsets, we conducted simulation experiments on datasets A and B, which had combined offsets. Dataset A was configured with a positioning offset of (3.5, −3.5, 1), an axis offset of 44 pixels, and random horizontal and vertical jitter values ranging from −20 to 20 pixels. Dataset B had a positioning offset of (2, −2, 1), an axis offset of 32 pixels, and random horizontal and vertical jitter values ranging from −20 to 20 pixels. Figures 3I–3G and 3K–3N depict the results, demonstrating that OCMC achieved high accuracy in correcting both horizontal and vertical offsets. The horizontal offset was relatively large due to the positioning error. The horizontal and vertical MSEs for the combined offset of datasets A and B were 0.62, 0.0, 0.31, and 0.0, respectively, as presented in Table S1. This evaluation indicates that OCMC effectively corrects joint offsets and shows good generality across different datasets.

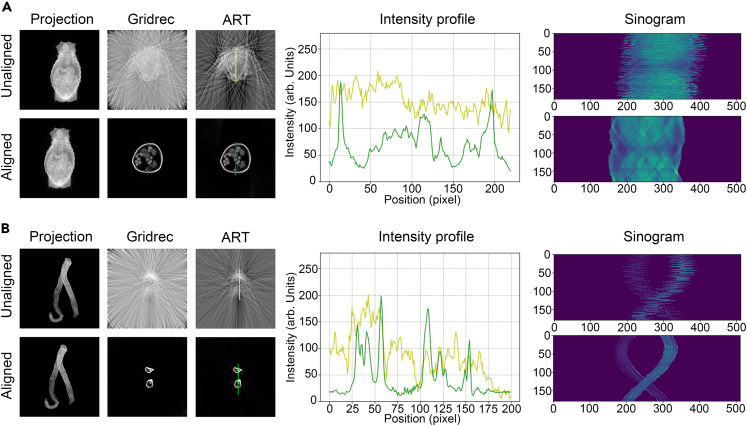
For a more intuitive comparison, we visually assessed the reconstructed images of two samples before and after OCMC alignment. TomoPy³¹ was employed to reconstruct the projection images using Fourier Grid Reconstruction algorithm (Gridrec) and Algebraic Reconstruction Technique (ART). The results presented in Figures 4 and S3 unequivocally illustrate that the alignment significantly enhanced the details of the reconstructed slices of the samples. Moreover, the intensity profile on the same position of the slice after reconstruction demonstrates improved image contrast and sharpness.

Figure 4.

Correction of simulated data

(A) The projection images, reconstructed slices using Gridrec and ART methods, intensity profiles and sinograms of dataset A before and after correction.

(B) The projection images, reconstructed slices using Gridrec and ART methods, intensity profiles and sinograms of dataset B before and after correction. The intensity profiles are acquired from the location of the yellow and green straight lines in the reconstructed slices using ART method. The reconstructed slices have been contrast-enhanced to facilitate the observation of details.

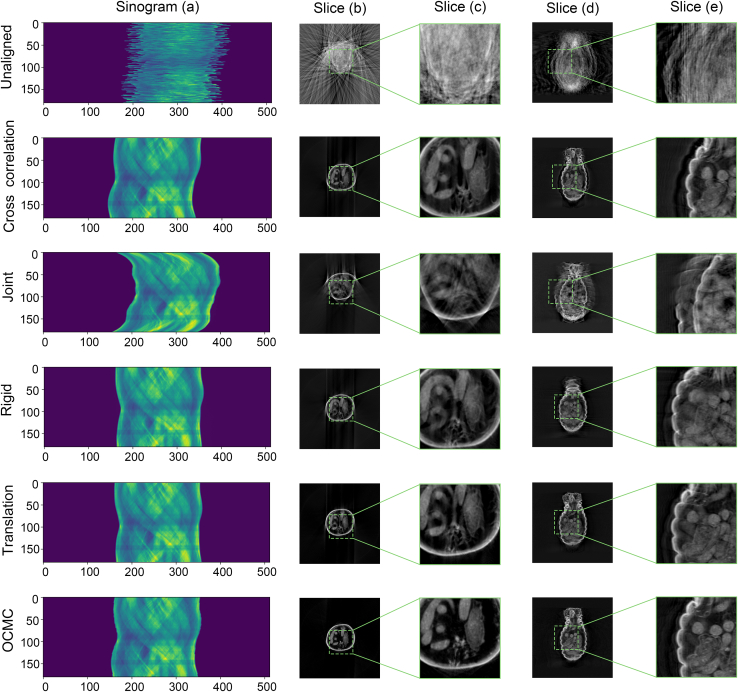
To compare the effectiveness of the proposed OCMC with that of other correction methods, we conducted a joint misalignment correction test using dataset A. We compared OCMC with the cross-correction method, the joint correction method²⁵ integrated in TomoPy, rigid correction, and translation correction methods provided by StackReg.³² It is important to note that the other methods do not correct the position of the rotational axis.

Typically, the first image of the tomography stacks is considered as the reference without offset, and all the other images are aligned to it. To ensure a fair comparison, we removed the joint offset of the first image from dataset A for all methods. The corrected results obtained from the various methods were compared and presented in Figure 5. The sinogram demonstrates the effective correction by all methods. However, the reconstructed slices obtained from the sinogram corrected by OCMC exhibit the finest details. They are superior to other results, where significant artifacts (Figure 5) are present due to the uncorrected offset of rotational axis.

Figure 5.

Comparison of different correction algorithms with OCMC

(A–E) The sinograms (A), different slices (B and D) of reconstruction volume using ART algorithm and the corresponding enlarged images (C and E). The reconstructed slices have been contrast-enhanced to facilitate the observation of details.

To remove the impact of the rotation axis offset, we manually aligned it before reconstruction and selected translation correction method, which provides relatively good reconstruction detail, for a comparison. Reconstruction from OCMC still exhibits details closer to the ground truth (GT) (the detailed process is elaborated in the method details subsection on methods comparison and Figure S2), indicating a better alignment. The joint correction results presented in Figure 5 were obtained after 10 iterations, which took approximately 10 h. Given the large joint offset we set, finding the optimal point is a time-consuming task. With more iterations, an even better result may be achieved.

Validation on experimental data

We proceeded to assess the versatility of OCMC by validating its performance on real raw tomography image stacks that naturally contain joint offsets. To this end, we selected three experimental methods of tomography, full-field tomography, scanning tomography, and ET, to serve as representatives for the validation.

Full-field tomography is a widely used imaging method for tomography experiments, where a series of snapshots of the whole sample are taken with a camera. Nano-CT is the high-resolution version of the technique with a magnifying lens. The raw image stack of nano-CT often suffers from significant misalignments due to the stringent requirement on position accuracy. To assess the performance of OCMC on this imaging technique, we conducted a test on the experimental dataset of a Lithium Nickel Cobalt Manganese Oxide (NMC) battery cathode particle (dataset C) from TomoBank.³³ The dataset was collected using nano-CT setup with a target resolution of approximately 30 nm and unknown joint offsets in the projection images. The tomography stack consisted of 180 projection images with a size of 1024∗1024 pixels. OCMC took approximately 17 min to correct the dataset. The uncorrected and OCMC-corrected projection images were reconstructed using Gridrec and ART with Shepp-Logan, Cosine, and Parzen filters. The resulting reconstructed NMC particle regions were then compared.

Figures 6 and S3 show that the reconstructed slices from unaligned dataset exhibited coarser details and had smoother intensity profiles, while those from aligned dataset depicted finer details, more distinct sample boundaries, and sharper intensity curves.

Figure 6.

Correction of Nano-CT data

It shows the projection images, reconstructed slices, intensity profile and sinogram before and after correction by OCMC. The reconstructed slices have been contrast-enhanced to facilitate the observation of details. The intensity profiles are acquired from the location of the yellow and green straight lines on the raw reconstructed slices using the ART reconstruction method.

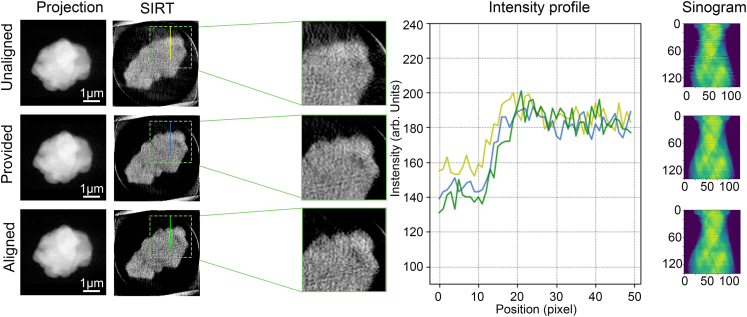
Scanning tomography is another important category of tomography technique that employs a small probe to perform raster scan on the sample and acquire the projection images of different modalities. The image resolution is usually determined by the probe size, scan step size and the overall system stability. To assess the ability of OCMC to correct misalignments in scanning microscopy images, we tested it on a 3D-XRF dataset (dataset D) of a particle collected at the hard X-ray nanoprobe beamline of Brookhaven National Laboratory (BNL). This tomography stack was collected with a probe size of 40 nm and comprises 141 projection images with a size of 125∗100 pixels. OCMC completed the alignment of all images within a minute. Following the alignment, we used the simultaneous algebraic reconstruction technique (SIRT) to perform the reconstruction. The unaligned and aligned sinograms in conjunction with the reconstructed slices obtained from them were compared (Figures 7 and S3). Again, OCMC correctly aligned the image stack and led to an improved reconstruction with enhanced level of detail, sample boundary visibility, and intensity profile sharpness.

Figure 7.

Correction of 3D-XRF data

It shows the projection images, reconstructed slices, intensity profile and sinogram before and after correction. The reconstructed slices have been contrast-enhanced to facilitate the observation of details. The intensity profiles are acquired from the location of the yellow, blue and green straight lines on the raw reconstructed slices using the SIRT reconstruction method (200 iterations).

ET is a transmission electron microscopy-based technique, where 2D projection images of a sample at a series of tilting angles, typically less than 180°, are captured. This high-resolution method is suitable for investigating nanoscale 3D structures, such as organelles and larger protein complexes. To evaluate the performance of OCMC correction in this sparse-angle tomography, we applied the correction to the raw image data of SARS-CoV-2 particles which were taken with ET (dataset E)³⁴ with a resolution of 0.64 nm. The tomography stack comprised 131 projection images, each containing 2048∗2048 pixels. OCMC correction took 40 min due to the large volume of data. Reconstructions based on raw (unaligned) OCMC corrected, and aligned, projection images from the authors were obtained using SIRT according to the processing metadata. For comparison, we selected slices from the same location. As depicted in Figures 8 and S3, OCMC correction led to an improved reconstruction where the clarity and contrast were enhanced and the membrane structure of the SARS-CoV-2 particle was more visible.

Figure 8.

Correction of ET data

It shows the projection images, reconstructed slices, intensity profile and sinogram before and after correction. The reconstructed slices have been contrast-enhanced to facilitate the observation of details. The intensity profiles are acquired from the location of the yellow and green straight lines on the raw reconstructed slices using the SIRT reconstruction method (15 iterations).

Computation efficiency and real-time correction

We conducted an efficiency test on a Windows computing platform with Intel(R) Xeon(R) Gold 6130 CPU @2.10 GHz. Dataset A was used to generate three different sizes of projection images (the detailed process is elaborated in the method details subsection on generation of simulation data): datasets A1 (180∗512∗512), A2 (360∗512∗512), and A3 (180∗1024∗1024). We performed offline correction on datasets A1 (A1¹), A2 (A2) and A3 (A3¹) and online correction on A1 (A1², A1³) and A3 (A3²). Simulated data acquisition time was set to 3 s per image for A1³ and 10 s for A1² and A3². The results in Table S1 show that OCMC achieves accurate corrections for all datasets. Through our analysis, we found that the time consumption of the OCMC method is closely related to both the number and size of the acquired images. Specifically, when comparing the correction of A1¹ and A2, we observed a linear increase in time consumption from 5 to 10 min with an increase in the number of images. However, when comparing the correction of A1¹ and A3¹, the increase in time consumption is less pronounced, rising from 10 to 16 min due to the correction strategy. This increment in time is negligible when compared to the iterative reprojection-based methods. To further support our findings, we conducted a 3D reconstruction of dataset A3 using the filtered back-projection (FBP) algorithm, which took approximately 116 s for one iteration. Compared to the time required for iterative reprojection-based methods to achieve satisfying results, which amounts to approximately 5800 s after 50 iterations even without taking into account the reprojection time, OCMC correction only took 972 s and is nearly 6-fold faster.

Furthermore, we analyzed the computational complexity of OCMC and found that it is mainly dependent on the size of the input data, as each projection image only needs to be aligned once. As a result, the computational complexity of OCMC is O(n). On the other hand, the joint alignment algorithm provided by TomoPy requires a large number of iterations and has a computational complexity of O(mn), where m is the number of alignment iterations (each containing a reconstruction and a back-projection) and n is the number of projection images. Because of that, OCMC is much more computationally efficient.

We also conducted a simulation experiment to evaluate the real-time correction capability of OCMC in tomography. We emulated three scenarios: A3², A1², and A1³, which differ in image resolution, acquisition time, and rotation step. During the simulation, OCMC correction was started in the middle of the acquisition, and all images were processed using the batch selection strategy. The results, as presented in Figure 3O, show that the correction of all images was completed approximately 323, 45, and 57 s after the completion of the acquisition for experiments A3², A1², and A1³, respectively. Consequently, for experiments with fast acquisition and real-time processing requirement, it is necessary to scaling down the image size in order to accelerate the alignment process.

Discussion

In order to tackle the challenge of accurately and efficiently correcting misalignment in tomography projection images with high-precision, and to achieve real-time correction during data acquisition, we have introduced a general alignment method for correcting joint offsets. In our study, we have observed that our method achieves exceptional alignment accuracy by leveraging the structural information of the sample’s outer contour. Even when environmental factors like noise and impurities affect the sample segmentation, our method can still produce excellent correction results. However, for samples with weak boundary features, additional methods such as traditional gamma enhancement or neural network-based enhancement may be required to improve the accuracy of the outer contour detection. Therefore, one of our future objectives is to optimize our method to address cases where outer contour information is absent or inadequate. Moreover, our current method has limitations in correcting samples that are either completely out of the field of view or cannot be segmented into a single part within the field of view. To overcome these limitations, we plan to explore and develop further capabilities of OCMC. As an end-to-end correction method, OCMC is capable of aligning image stacks on-the-fly, making it a promising candidate for integration into highly automatic real-time data processing pipelines.^35,36 Such integration is crucial for achieving feedback control³⁷ in future synchrotron tomography experiments.

Conclusions

In summary, we introduce a novel alignment method for tomography datasets that utilizes the sample’s OCS to correct joint offsets between projection images. This method has demonstrated high effectiveness in correcting misalignment in both simulated and experimental datasets obtained from various imaging techniques. Furthermore, the proposed method can be integrated into the data acquisition pipeline, enabling real-time data processing.

Looking ahead, we plan to explore machine learning methods to automate the outer contour extraction process. With that improvement, we can increase the applicability of OCMC algorithms to handle other weak-contrast imaging modalities.

Limitations of the study

Several limitations of our study exist. First, for samples with weak boundary features, we suggest that additional enhancement methods should be required to improve the accuracy of the outer contour detection. Second, when correcting samples that are either completely out of the field of view or cannot be segmented into a single part within the field of view, the lack of boundary information will result in a reduction in alignment accuracy.

STAR★Methods

Key resources table

REAGENT or RESOURCE	SOURCE	IDENTIFIER
Deposited Data
Sternaspis scutate dataset	Zenodo	https://zenodo.org/record/6275179#.YyLaSXZByUl
Owenia fusiformis dataset	Zenodo	https://zenodo.org/record/5222921#.YyLcPnZByUm
NMC dataset (Nano-CT)	TomoBank	https://tomobank.readthedocs.io/en/latest/source/data/docs.data.XANES.html
NMC dataset (3D-XRF)	Brookhaven National Laboratory	N/A
SARS-CoV-2 particles dataset	Zenodo	https://zenodo.org/record/3985103#.Y4gFRBRByUk
Software and algorithms
python 3.9.12	Python	https://www.python.org/
pytorch 1.8.2	Pytorch	https://pytorch.org/
Numpy 1.23.0	Numpy	https://numpy.org
Pillow 9.1.1	Pillow	https://python-pillow.org
Scikit-image 0.19.3	Scikit-image	https://scikit-image.org
Opencv-python 4.5.5.64	OpenCV	https://opencv.org
Tomopy 1.11.0	Tomopy	https://tomopy.readthedocs.io/en/stable/index.html
StackReg	EPFL	https://bigwww.epfl.ch/thevenaz/stackreg/
Other
Source code	Github	https://github.com/sampleAlign/alignment

Resource availability

Lead contact

Further information and requests for resources should be directed to and will be fulfilled by the lead contact, Yi Zhang (zhangyi88@ihep.ac.cn).

Materials availability

This study did not generate new materials.

Method details

Segmentation

For datasets A and D, we utilized the grayscale threshold segmentation method to directly extract the OCS structure. For datasets B and E, we applied a linear transformation image enhancement method to enhance the contrast of the projection images and subsequently used grayscale threshold segmentation to extract the OCS images. In the case of dataset C, the presence of a capillary background in the battery particle projection images influenced the segmentation process. Therefore, we first identified the portions that solely contain capillary above and below the projection image and generated an interpolated image utilizing the Fast Marching Method (FFM).³⁸ By removing the interpolated images from the original projection images, we obtained background-subtracted projection images. Similarly, we employed a linear transformation image enhancement method to enhance the contrast of the projection images and used grayscale threshold segmentation to extract the OCS images.

During the segmentation process, we endeavored to select a threshold that would satisfy the height consistency of the segmented OCS images. However, despite our efforts, an error of approximately 5 pixels persisted. An optimal segmentation, which is expected to reduce the correction error of OCMC, remains challenging to attain. Notably, we observed that deep learning segmentation methods are well-suited for this task, as they can significantly enhance segmentation accuracy compared to traditional methods. Therefore, integrating deep learning-based segmentation methods into our segmentation module is an ongoing area of research for future work.

Parallel correction pipelines

In order to improve the efficiency of OCMC, we have implemented multiple correction pipelines for parallel processing during the second loop of coarse alignment. The corrected images are grouped together, with a default grouping size of three, to form a correction pipeline for the images within that range. The group size is adjustable, with a single channel being created if it is set equal to the total number of image acquisitions. This parallel processing strategy has proven effective in significantly reducing the correction time of the OCMC algorithm, allowing for more rapid and efficient correction of large datasets.

Batch selection strategy

To enable real-time OCMC correction during online data acquisition, we employ a batch selection strategy that optimizes the pipeline for both time and accuracy. Specifically, immediately following acquisition of the 90° range of images, coarse and fine alignment correction pipelines are activated in parallel to quickly correct the images in this range. During subsequent image acquisition, the OCMC verifies the acquired images to identify batches of at least three images that can be coarsely and finely aligned. The batch size can be adjusted depending on the specific requirements of the experiment. To further improve the speed of correction, optimization steps are removed for high resolution images after internal model rotation, which may result in a slightly higher MSE but saves approximately 50% of the time required for correction. These approaches enable real-time OCMC correction with fast processing times, making it suitable for various tomography experiments.

Generation of simulation data

To enhance computational efficiency and facilitate comparison, we employed a normalization approach on dataset A and dataset B. This involved the normalization of raw projection images obtained through Radon transformation, wherein each image was uniformly normalized at a 1° rotation step, generating a total of 180 images. Subsequently, the projection images were zero-padded to form square images, which were then downscaled to 512∗512 pixels. As a result of this normalization process, each dataset assumed the shape of 180∗512∗512.

To assess the effectiveness of OCMC, we constructed three datasets: A1, A2, and A3, which were generated with distinct image resolutions and rotation steps. Specifically, dataset A1 comprised 180 images with a 1° rotation step and an image resolution of 512∗512 pixels; dataset A2 comprised 360 images with a 0.5° rotation step and an image resolution of 512∗512 pixels, while dataset A3 comprised 180 images with a 1° rotation step and an image resolution of 1024∗1024 pixels. After construction, dataset A1 had the shape of 180∗512∗512, dataset A2 had the shape of 360∗512∗512, and dataset A3 had the shape of 180∗1024∗1024.

Output and data mapping

As OCMC is a rectification of OCS images, the resulting output requires mapping back to the initial projection images. Thus, we record the horizontal and vertical offset pixel values for each OCS image and subsequently utilize these values to identify and translate the corresponding original projection images.

Methods comparison

The rotational axis of the translation-corrected image was calibrated manually before initiating the reconstruction process. Subsequently, we compared the reconstructed slices derived from the corrected image after OCMC and ground truth (GT), as shown in Figure S2. Upon close examination of the bottom left section, we observed that the OCMC-corrected reconstructed slice exhibited superior detail and was more similar to the GT.

Implementation details

The alignment algorithm is comprised of distinct modules, whereby the OCS extraction module is fully decoupled, thereby enabling the utilization of diverse methods. Moreover, the initialization module for sample positioning can be adjusted as desired. Our configuration was set to the CoV for computational convenience. The coarse and fine alignment steps are likewise adjustable and can be tailored to specific requirements.

Published: September 15, 2023

Data and code availability

• •This study did not generate new data and mainly uses publicly available datasets. Detailed descriptions are listed in the key resources table.
• •All original code has been deposited at Github and is publicly available as of the date of publication. The URL is listed in the key resources table.
• •Any additional information required to reanalyze the data reported in this paper is available from the lead contact upon request.