Enzyme-constrained metabolic model and in silico metabolic engineering of Clostridium ljungdahlii for the development of sustainable production processes

Abstract

Constraint-based genome-scale models (GEMs) of microorganisms provide a powerful tool for predicting and analyzing microbial phenotypes as well as for understanding how these are affected by genetic and environmental perturbations. Recently, MATLAB and Python-based tools have been developed to incorporate enzymatic constraints into GEMs. These constraints enhance phenotype predictions by accounting for the enzyme cost of catalyzed model´s reactions, thereby reducing the space of possible metabolic flux distributions. In this study, enzymatic constraints were added to an existing GEM of Clostridium ljungdahlii, a model acetogenic bacterium, by including its enzyme turnover numbers (k_cats) and molecular masses, using the Python-based AutoPACMEN approach. When compared to the metabolic model iHN637, the enzyme cost-constrained model (ec_iHN637) obtained in our study showed an improved predictive ability of growth rate and product profile. The model ec_iHN637 was then employed to perform in silico metabolic engineering of C. ljungdahlii, by using the OptKnock computational framework to identify knockouts to enhance the production of desired fermentation products. The in silico metabolic engineering was geared towards increasing the production of fermentation products by C. ljungdahlii, with a focus on the utilization of synthesis gas and CO₂. This resulted in different engineering strategies for overproduction of valuable metabolites under different feeding conditions, without redundant knockouts for different products. Importantly, the results of the in silico engineering results indicated that the mixotrophic growth of C. ljungdahlii is a promising approach to coupling improved cell growth and acetate and ethanol productivity with net CO₂ fixation.

Graphical Abstract

Highlights

• •Enzyme-constrained model for Clostridium ljungdahlii was developed.
• •Improved prediction accuracy of the proposed model over original metabolic model.
• •New model used to predict optimal reaction knockouts for metabolite overproduction.
• •C. ljungdahlii mixotrophic fermentation may yield acetic acid, ethanol, and fix CO₂.

1. Introduction

The widespread adverse impacts of human caused climate change has made necessary a global effort for accelerating the reduction of anthropogenic greenhouse gas emissions [1]. As the main greenhouse emitted gas, CO₂ reduction is the main target of most of the strategies to counteract climate warming; the main processes for the capture of CO₂ typically are grouped as carbon capture and storage (CCS) and carbon capture and utilization (CCU) strategies, depending on the fate of the CO₂ [2]. In CCU strategies hold great potential as recaptured CO₂ is utilized as a feedstock for chemical, biochemical, and electrochemical processes to produce materials and chemicals. This approach can play a significant role in the development of a circular economy, allowing potential carbon-negative products. In biologically mediated CCU, biological systems are utilized to capture and utilize CO₂ present at the emission source, or in the atmosphere, to be introduced in the metabolism of autotrophic bacteria, algae, or archaea [3]. Among autotrophic microorganisms, acetogenic bacteria, or acetogens are particularly interesting for potential industrial applications, employing an energetically efficient CO₂ fixating pathway, the reductive acetyl-CoA pathway, or Wood-Ljungdahl pathway (WLP)[4], [5]. In this pathway, 2 moles of CO₂ are converted to one mole of acetyl-CoA, utilizing H₂ as an electron donor[6]. The acetyl-CoA is then typically converted to acetic acid through phosphotransacetylase and acetate kinase, allowing to recover one mole of ATP per mole of acetic acid produced by phosphorylation at the substrate level [6]. Despite the promising potential of these microorganisms for industrial applications, their use has been hindered by their slow growth and low productivity when grown autotrophically, particularly without the presence of CO. Until now, Lanzatech has been the only company developing a gas fermentation process with acetogens reaching commercial scale, successfully producing ethanol from syngas fermentation [7]. However, CO-rich syngas fermentation results in CO₂ emissions, coming from the oxidation of CO to CO₂; recently, a breakthrough has been described in a publication reporting the development of a gas fermentation process by an engineered Clostridium autoethanogenum strain, resulting in carbon-negative production of acetone and isopropanol [8].

Clostridium ljungdahlii is one of the most studied acetogen, known for its ability to convert different gaseous substrates, CO₂, H₂, and CO [9] through the Wood-Ljungdahl pathway, making it a promising candidate for conversion of synthesis gas into valuable chemicals. Moreover, C. ljungdahlii has been proven to be able to grow mixotrophically when fed with fructose, reconverting the CO₂-produced glycolysis through the Wood-Ljungdahl pathway [10]. Supplementation of an organic carbon source, resulting in a mixotrophic growth, is an interesting approach to boost the growth and productivity of acetogens, typically low during autotrophic growth, particularly in the case of a syngas composition poor in CO [11], [12]. Moreover, if enough H₂ is supplemented in the gas phase during mixotrophic growth, fixation of exogenous CO₂, not produced in glycolysis, is possible [10], [13].

Native products of C. ljungdahlii are mainly acetic acid (HAc) and ethanol (EtOH) with the possibility to also produce small amounts of 2,3-butanediol (BDO) and lactic acid (LAc) [9], [11], [14]. Moreover, many attempts to broaden the product range of this specie have been performed over the last years, by insertion of heterologous biosynthetic pathways [15], to produce acetone, isopropanol, butyrate, butanol, and many other valuable chemicals. Industrial utilization of strains engineered for the production of longer chains and reduced chemicals may be strongly affected by the reduced growth rate caused by the energetic burden coming from the production of these products.

Genome-scale models (GEM) are mathematical representations of a metabolic network of a microorganism, reconstructed from the genome annotation of the microbe, utilizing a gene-protein-reaction stoichiometry association [16]. By utilizing computational tools such as Flux Balance Analysis (FBA), and Flux Variability Analysis (FVA), it is possible to constraint the uptake of nutrients and compute the outputs of the cell (growth rate and metabolites secretion) by maximizing an objective function, usually biomass production, under the hypothesis that this is the main biological objective of the microorganism [17]. The stoichiometries of the model´s reactions, ensuring to maintain closed mass balances, impose a constraint on the fluxes of metabolites in the cell´s metabolic network, allowing to identify a space of fluxes distributions allowing growth of the cell. Through optimization by FBA, the optimal flux distribution for maximization (or minimization) of the objective function is found [17]. Among the many utilizations of genome-scale models, there is the possibility to identify optimal genetic manipulations to produce a desired metabolite, by simulations of the growth of the strains in case of knock-out, additions of heterologous pathways, up- or down-regulation of gene expressions [18].

In the last decade, many strategies have been developed to improve the accuracy of metabolic models in the simulations of microbial growth. These strategies aim at including providing additional constraints to the model, such as thermodynamic, enzymatic, or kinetic constraints, in order to reduce the space of possible fluxes and improve the predictive ability of the model [19]. The introduction of additional constraints allows a better description of the microorganisms’ physiology, accounting for other biological processes inside the cell, other than the sole network of metabolic reactions [19]. In the approach defined as Metabolic and gene Expression models (ME-models), genome-scale models are integrated with reactions accounting for macromolecular processes such as protein synthesis and transcriptional regulation, allowing to accurately predict gene expression levels and predict the maximum feasible growth rate without explicit constraining the substrate uptake rates [20], [21]. Models constructed taking into account reaction kinetics can reach a very high fidelity of metabolic fluxes predictions, and successfully predict cell growth in a dynamic environment, accounting for the changes in nutrients and metabolite concentrations in complex environments [22], [23]. A strong limitation in these approaches is the great amount of specific biological information needed for the parametrization of the models, which is not available for most microorganisms. Moreover, the computational effort required for the simulating growth of the microbe can be extremely challenging, due to the presence of non-linear expressions and processes taking place at radically different time scales [24].

The addition of constraints on the total amount of enzymes in the cell, following strategies such as MOMENT [25], short MOMENT [26], and GECKO [27] and ECMpy [28] has also the potential to increase the predictive ability of the simulated growth of the microorganism, utilizing readily available data as turnover rates (k_cat) and molecular weights (MW), without resulting in computationally demanding models, and allowing to utilize linear programming tools as for metabolic-only models.

The use of computational tools for synthetic biology may offer the possibility to better understand acetogens´ metabolism, and guide towards possible metabolic engineering strategies to transform them into production hosts. A metabolic model was published in 2013 for C. ljungdahlii [29], represented the first genome-scale model available for an acetogenic bacterium, allowing to characterize the nitrate reduction pathway of this strain and clarify the role of flavin-based electron bifurcation. A ME model published in 2019 then allowed to describe the overflow metabolism of C. ljungdahlii, predicted gene expression of the bacterium in different conditions, and predicted the positive effect of Nickel availability on the growth rate [30].

The objective of the present study was to generate an enzyme-constrained model of C. ljungdahlii, by adding constraints on the total allocation of metabolic enzymes to the original model published by Nagarajan et al. [29], with the goal of improving its predictive capability. The performance of the model was evaluated using in vivo data sourced from both the existing literature and generated in our lab from the cultivation of the strain under mixotrophic conditions. Subsequently, the generated model was employed to predict optimal metabolic engineering strategies for enhancing the production of metabolites of interest under two different growth scenarios. The first scenario considered was syngas fermentation, which has been the most explored application of the strain. The second scenario was mixotrophic growth, which has recently been proposed as a potential strategy to overcome the energetic limitations in the growth of acetogenic bacteria [31], [32].

2. Materials and methods

2.1. Addition of annotations to the original model

The C. ljungdahlii DSM 13528 metabolic model iHN637 [29] was used as the initial model for the construction of the enzyme-constrained model of the acetogen following the AutoPACMEN method [26]. The SBML (XML) file of the model iHN637 was downloaded from the BiGG Models [33] database. The model iHN637 has 698 metabolites, 785 reactions, and 637 genes; the report generated by the testing with MEMOTE [34] evidenced an overall high quality of the model, having a total score of 90%. The benchmark provided by MEMOTE is based on the consistency of the model and the quality of annotations. The very high consistency score (Fig. 1) indicates that mass and charge are well balanced, while the low score for gene annotations is because gene annotations are present only for the NCBI database. Before proceeding with the addition of the enzyme constraints, it was needed to update the model with the addition of UniProt IDs annotations and missing EC numbers, as these annotations are used in the AutoPACMEN workflow to retrieve the molecular weights of enzymes and the turnover numbers (k_cat) of reactions.

Fig. 1.

Model scores by MEMOTE. Score for each model category evaluated by MEMOTE in the original model (iHN637) and the updated version (iHN637_v2).

Gene annotations of UniProt IDs were added to the iHN637 model by using the UniProt ID Mapping tool on the UniProt website [35]. The 670 GI numbers (ncbigi gene annotation) provided in the original model were mapped to 1096 results, indicating a non-bijective correspondence between GI numbers and UniProt IDs, as some GI numbers were associated to multiple UniProt IDs belonging to different strains. Addition of the Uniprot IDs annotations increased the score for gene annotations from 36.6% to 43%; the score remained low as it is calculated considering also gene annotations for other databases; for the scope of the study, addition of Uniprot IDs was sufficient for the successive steps of the workflow.

The MEMOTE report indicated that 71% of the reactions in the model were assigned EC numbers (ec-code), while 228 reactions were not annotated. Most of these unannotated reactions were metabolite exchange reactions, typically not associated with EC numbers [36]. However, some of the reactions lacking the EC number were enzyme-catalyzed reactions, and for these, a manual search was conducted on the BRENDA Enzyme Database [37] to identify the corresponding EC number. The addition of the EC_numbers slightly increased the score for reaction annotations.

The retrieved UniProt IDs and the missing EC numbers were added to the XML file, and the updated model was analyzed by MEMOTE, to have a comprehensive overview and compare with the original version.

2.2. Background of short MOMENT (sMOMENT) model construction

Standard metabolic models are defined by a stoichiometric matrix, where each column corresponds to a reaction and each row corresponds to a metabolite, and a flux vector under steady state mass balance [17]:

$$\mathit{Sv}=0$$ (1)

where each flux is constrained by a lower and upper bound:

$${\alpha }_i\le v_i\le {\beta }_i$$ (1)

The short MOMENT method is characterized by the addition to the stoichiometric matrix of a pseudo metabolite (i.e. an additional row), containing the enzymatic cost (c) of each reaction, which for each reaction i was calculated as:

$$c_i=-\frac{{\mathit{MW}}_i}{k_{\mathit{cat},i}}$$ (3)

A pseudo reaction is also added as a new column of the matrix, whose coefficients are 0 for all the metabolites except for thepseudo metabolite pool, for which it is 1.

The associated flux of this pseudo reaction was then constrained by an upper bond, the protein pool P, measuring the upper limit of metabolic enzymes mass in the cell [26]. The model, thus, was constrained allowing only a limited maximum mass of enzymes in the cell, which could be directly determined experimentally or derived by fitting experimental growth data to simulation results.

2.3. Generation of enzyme-constrained model

After the model update, it was possible to proceed with application of AutoPACMEN workflow for the generation of the enzyme-constrained model [26]. The AutoPACMEN package was downloaded from GitHub and installed, then the steps indicated by the authors were followed with few modifications for the addition of enzyme constraints:

• 1.The BiGG metabolite text file was downloaded from the BiGG website [33] and converted to the JSON format.
• 2.The BRENDA database text file was downloaded from the BRENDA Enzyme database website [37] and converted to the JSON format.
• 3.The BRENDA JSON file was parsed to retrieve the EC numbers present in the updated model; the associated k_cat was then saved into a new JSON file.
• 4.All the EC numbers in the model were searched in the SABIO-RK database [38] and saved into a JSON file.
• 5.The JSON files from BRENDA and SABIO-RK were merged into a combined JSON database.
• 6.The model reactions were mapped to their turnover numbers using the EC numbers.
• 7.The molecular weights of model proteins were calculated from their aminoacidic sequence, and mapped to their Uniprot ID.
• 8.The XLSX files for setting protein pool, enzyme concentrations, and enzyme stoichiometries were created [25]. The format of enzyme stoichiometries was modified to make them available for the successive step.
• 9.The enzyme-constrained model was created using the “create_smoment_model_reaction_wise_with_sbml” function.

2.4. Model calibration

To improve their prediction capability, genome scale models need calibration of their parameters, in particular the upper limit of the protein pool and the turnover numbers.

The initial value of the protein pool was set to 0.095 g/gCDW, which was the value used to constrain the Escherichia coli enzyme constrained model iJO1366 * [26]. Then it was iteratively adjusted, to improve model simulation agreement with experimentally determined growth rates. In this phase, however, it was not possible to obtain a univocal value of protein pool that could allow good predictions of both autotrophic and heterotrophic growth. In fact, different enzyme pools had to be used to simulate different growth modes, resulting either in overestimation of autotrophic growth rates or underestimation of heterotrophic growth rates, as can be seen in Fig. 2. Thus, it was needed to first adjust the turnover rates.

Fig. 2.

Comparisons of model performance against experimental values at two different enzyme pool upper bounds, 0.03 g/gCDW (top figure) and 0.05 g/gCDW (bottom figure). Respectively, the first was giving a good fit for autotrophic growth with strong underestimation of the heterotrophic growth, the latter gave a good fit of growth rates on fructose with overestimation of autotrophic growth.

The choice of the k_cats to be adjusted has been carried out differently in previous studies, choosing reactions with high impact on simulation results [26] or reactions with high enzyme usage [28]. In this case, we chose to select for calibration the reaction’s main high fluxes carrying reactions for different conditions (Table 1). For this reason, FBA simulations were performed using the EC model in different growth conditions, autotrophic and heterotrophic, constraining the substrates (CO and fructose) uptake rates respectively to 40 mmol/gCDW/h and 1.8 mmol/gCDW/h, which are fluxes close to experimental values measured for this strain. The main reactions identified were mainly glycolysis and WLP reactions. It has been previously demonstrated that in vivo determined k_cats should be preferred, when available, to in vitro determined values, which are available on databases as BRENDA and SABIO-RK, used in autopacmen workflow [39]. In this case, it was possible to find in literature in vivo measured apparent turnover rates of Clostridium autoethanogenum, an acetogenic species closely related to C. ljungdahlii [40].

Table 1.

Updated turnover rates.

Reaction	kcat assigned (s-1)	New kcat (s-1)
CODH4	1787.21	73.85
CODH_ACS	250.79	70.71
FTHFLi	286.36	29.45
MTHFC_TG_reverse	896.68	48.16
ACKr_TG_reverse	1536.86	43.88
R_ALCD2x_TG_reverse	368.84	16.33
PTAr_TG_forward	1661.54	19.91
FRNDPR2r_TG_forward	Not assigned	15.15
MTHFR5_TG_forward	Not assigned	24.39
FDH7_TG_forward	Not assigned	84.75

Thus, the selection of the turnover numbers to be adjusted was done by comparing, for the high fluxes carrying reactions, the k_cats assigned by autopacmen with the in vivo values, and to in silico turnover numbers calculated using DLKcat, a Python-based deep learning tool able to predict the turnover rate of an enzyme based on its aminoacidic sequence and substrate [41]. Reactions selected for the calibration were those for which the previously assigned k_cat had strong deviations from the in vivo and the in silico value; for each of them, the k_cat was then substituted with the highest turnover number among the in silico and in vivo value. In Table 1 are indicated the reactions selected for k_cat calibration. In can be observed that in most cases, this step consisted in decreasing the turnover numbers of Wood-Ljungdahl Pathway related reaction. This may seem in contrast with what is usually observed during calibration of constrained models, in which the main issue is represented by avoiding over-constraining of the model [28], [42]. However, this step allowed to reduce the overestimation of the strain metabolism during autotrophic growth, which characterized the original model and the first version of the updated model.

Then, it was possible to find an optimal value of the protein pool. Initially, a manual adjustment was performed to identify a range around the optimal protein pool value, starting again from the value of 0.095 g/gCDW. The optimal protein pool was then selected as the value minimizing the error with respect to experimental values using [26]:

$$E_{\mathit{norm}}=‖\frac{{\mu }_{\mathit{sim}}-{\mu }_{\exp }}{{\mu }_{\exp }}‖$$ (4)

2.5. Evaluation of prediction accuracy

The prediction accuracy of the generated enzyme-constrained model was evaluated by measuring the Pearson correlation coefficient, and by linear regression.

The experimental product profiles in the different conditions were also compared to the predictions by iHN637 and ec_iHN637.

2.6. Simulations

Simulations of the bacterium steady-state growth, by Flux balance analysis (FBA), were carried out using Cobrapy [43]. For computational design of metabolic interventions, it was used the package StrainDesign [44].

2.7. Bacterial growth conditions

C. ljungdahlii mixotrophic cultivations were carried out to retrieve data about growth rate, uptake, and secretion fluxes during simultaneous CO₂, H₂, and fructose consumption. This information is not available in the literature and was considered important for the determination of model performance.

C. ljungdahlii (DSM 13528) was ordered from the Leibniz Institute DSMZ – German Collection of Microorganisms and Cell Cultures GmbH [45]. The bacterium was grown anaerobically in 125 mL serum bottles containing 42 mL of modified DSM 879 medium [46], at 37 °C. In all cultivation experiments, the use of NaHCO₃ was avoided, and MES 50 mM was used as buffer; Sodium sulfide nonahydrate (Na₂S x 9 H₂O) was substituted by doubling the amount of Cysteine hydrochloride monohydrate (L-Cys HCl x H₂O) suggested in the medium recipe DSM 879. The gas mixture of 80% N₂: 20% CO₂ indicated in the medium recipe was also substituted by a mixture of 80% H₂: 20% CO₂. All bottles were pressurized once, before the start of the fermentation experiments, to a pressure of 2.5 bar. Two different fructose concentrations were tested, 5 g/L and 10 g/L. All experiments were performed in triplicates and compared to negative controls. The bottles were inoculated using 3 mL of inoculum from cultures in the mid-exponential growth phase (OD₆₀₀ 0.5–0.8) Samples were collected shortly after inoculation and then every 24 h of the culture for determination of OD₆₀₀, pH, and metabolites concentrations. Before each sampling, the internal pressure of the bottles was measured, using a manometer connected to a needle, puncturing the butyl stopper of each bottle.

2.8. Detection of metabolites by HPLC

For the detection of metabolites of interest (fructose, acetic acid, ethanol), samples were centrifuged for 10 min at 4 °C, and filtrated with 0.22 µm syringe filters. The filtrated samples were analyzed using a Dionex Ultimate 3000 high-performance liquid chromatograph UHPLC+ focused system (Dionex Softron GmbH, Germering, Germany) equipped with a Bio-Rad Aminex HPX 87-H column, at 60 °C, using mM H₂SO₄ as mobile phase at a flowrate of 0.6 mL/min.

3. Results

3.1. The enzyme-constrained model ec_iHN637

The original model, iHN637, is characterized by a total of 785 reactions, and 698 metabolites [29]. In the enzyme-constrained model ec_iHN637, the number of reactions was increased to 956, due to the splitting of enzyme-catalyzed reversible reactions and the addition of the protein pool pseudo-reaction, while the number of metabolites was increased to 699 with the addition of the protein pool pseudo-metabolite.

Starting from 0.095 g/gCDW, the protein pool was manually decreased and an ideal range between 0.072 and 0.080 g/gCDW was identified. The final value of the protein pool was then set to 0.078 g/gCDW by minimizing the normalized error.

3.2. Evaluation of model growth rate prediction performance

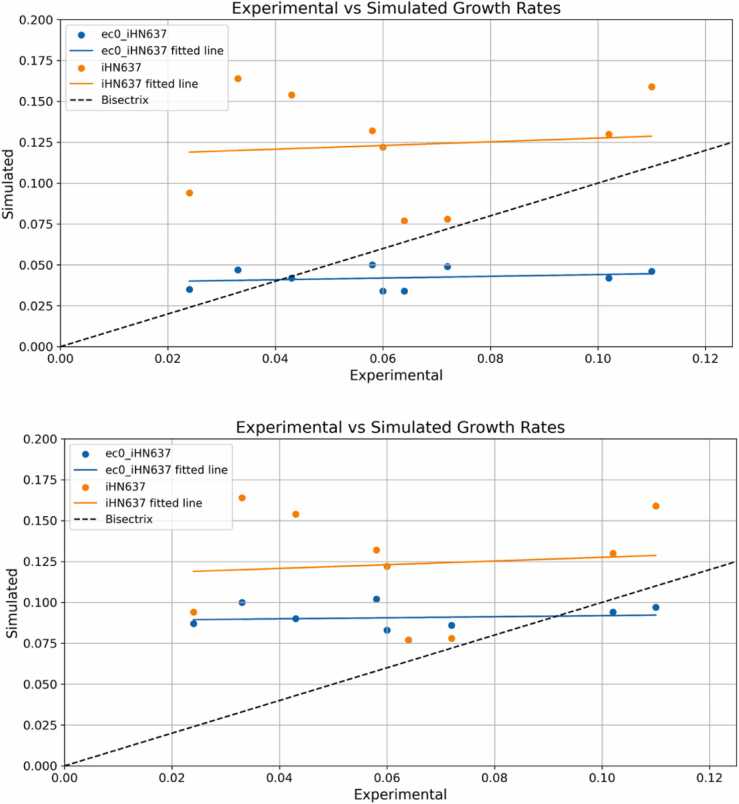
The model performance was compared to the original metabolic model, iHN637, by evaluating the ability to predict growth rate, constraining the model with uptake rates obtained from the literature. Fig. 3 presents a comparison of the 2 models, showing that the prediction ability of growth rates was increased in the enzyme-constrained model. The plot was generated by comparing experimentally determined growth rates and simulated growth rates, from simulations in which only the uptake rates of substrates (CO₂, H₂, fructose, and CO) were used as constraints.

Fig. 3.

Models’ predictions accuracies. Comparison of accuracy of growth rate prediction between the original model iHN637 and the enzyme constrained ec_iHN637. When only one simulated value corresponds to an experimental one, the prediction by the original and the enzyme-constrained model were corresponding.

The data in Table 2 were used as constraints for the FBA simulations. The mean normalized error decreased from 1.42 for the original model to 0.37 in the enzyme-constrained model, with standard deviations equal to 1.41 and 0.59, respectively. The good correlation of the EC model with the in vivo growth rates was also evidenced by the results of Pearson’s r, which was increased to 0.750 (p = 0.020), compared with the value of 0.096 (p = 0.803) for the original model. The result can be also compared to those obtained by the ME-model iJL965-ME, published in 2019, that had a Pearson´s r equal to 0.68 with a p value of 0.14 [30].

Table 2.

Substrate fluxes constrained for FBA simulations for evaluation of the accuracy of growth rate prediction by the models.

Constrained Fluxes	Uptake rates [mmol/gCDW/h]	Growth rate [h-1]	Source
H2, CO	-7.724, − 40.132	0.043	[11]
H2	-79.5	0.033	[12]
H2, CO2	-46.630, − 21.765	0.024	[11]
CO	-38.5	0.058	[12]
CO	-35.878	0.060	[11]
Fructose	-1.88	0.72	[29]
Fructose, CO2	-0.672, − 15.861	0.110	[This study]
Fructose, CO2	-0.615, − 16.480	0.102	[This study]
Fructose, CO2	-0.507, − 8.785	0.064	[This study]

3.3. Effect of enzyme constraints and prediction of product fluxes

To visualize the effects of enzymatic constraints on the predictions of the model, the growth rates and production rates of acetate and ethanol were plotted for both the original model and the enzyme-constrained model (Fig. 4, Fig. 5).

Fig. 4.

Growth rate (a), acetate, and ethanol production (b) trends at increasing CO-specific uptake rates for growth on sole CO as substrate.

Fig. 5.

Growth rate (a), acetate, and ethanol production (b), and CO₂ emissions (c) trends at increasing CO-specific uptake rates for growth on syngas (CO+H₂).

Growth on CO as substrate was simulated in the range 0–50 mmol/gCDW/h, considering that the experimental uptake rates found in the literature were 38.5 and 35.9 mmol/gCDW/h for the cases of growth on sole CO, while for the case of syngas fermentation an average uptake flux of 40.132 was reported [11], [12]. Moreover, the maximum specific uptake rate of CO by C. ljungdahlii has been determined to be 34.4 mmol/gCDW/h utilizing a kinetic model [47].

For the iHN637 model, a continuous linear correlation was observed between the CO-specific uptake and the predicted growth rate during growth on CO. On the contrary, the ec_iHN637 model predicted a critical point, occurring between 20 and 30 mmol/gCDW/h, at which the enzyme pool reached its upper limit, interrupting the linear relationship between growth rate and CO uptake. The behavior is an effect of the introduction of the enzyme constraint in the model. Consequently, the iHN637 model did not forecast the onset of ethanol production when the model was constrained solely with uptake fluxes. Instead, Flux Balance Analysis (FBA) simulation predicted a steadily increasing production of acetate. In metabolic models, indeed, alternative fermentation products are not predicted, unless additional constraints are provided, on the secretion fluxes or the redox fluxes [30]. In the ec_iHN637, when the critical CO uptake flux was reached, the beginning of ethanol production was predicted as an overflow metabolism strategy to balance reducing equivalents. Despite the prediction of ethanol as the main fermentation product, comparing the results to the experimental values, the predictions by the ec_iHN637 model was still underestimating the ethanol production rate in the case of CO growth, and overestimating it in the case of syngas fermentation. In one of the experimental sources, also BDO and lactate production were observed [11], but none of the models was able to predict their secretion.

When the modes were used to simulate growth on syngas at different CO uptakes, leaving unconstrained the hydrogen uptake flux, the model iHN637 predicted a linear increase of growth rate at increasing uptake fluxes of CO (Fig. 5). In the enzyme constrained model, instead, a first interruption of the linear relationship was observed at 14 mmol/gCDW/h. In correspondence of this point, the model predicted a decrease of ethanol productivity and the start of emissions of CO₂. In the original model, instead, the absence of enzyme limitations allowed the model to predict continuous increase of the growth and ethanol production, without emissions of CO₂, as all the carbon was directed into the metabolic pathways for production of biomass and ethanol. At CO uptake of 29 mmol/gCDW/h, the predictions by ec_iHN637 had showed another inflection point, corresponding to a decrease of growth rate and an increase of ethanol production. When compared to experimental points derived from literature [11], [48], the enzyme constrained model showed again improved capability of predicting growth rate and exchange fluxes with respect to the original model.

When the model was constrained with CO₂ and fructose uptake, the range 25–80 mmol/gCDW/h of H₂ uptake rates was analyzed to simulate the mixotrophic conditions, with a minimum CO₂ uptake of 15.861 mmol/gCDW/h (Fig. 6).

Fig. 6.

Growth rates (a) and product fluxes (b) under mixotrophic growth. Growth rate, acetate, and ethanol production trend at increasing specific uptake rates of H₂.

In this scenario, the experimental values were not included in the graphs, since the experimental H₂ uptake flux was not known. The outcomes indicated that in this case, the two models, ec_iHN637 and iHN637, demonstrated less divergence in their trends compared to the case with CO, particularly concerning acetate and ethanol production. A notable difference, however, was seen in the maximum growth rate predictions at different H₂ uptake rates: the ec_iHN637 model predicted a maximum growth rate at 33.58 mmol/gCDW/h, while the iHN637 model predicted it at 48.34 mmol/gCDW/h. Thus, when the model was constrained without specifying the (unknown) H₂ uptake flux, the iHN637 model predicted a growth rate of 0.114 h^-1 while in ec_iHN637 it was limited by the additional constraint to 0.094 h^-1, compared to an experimental value of 0.110. While the original iHN637 model's prediction was closer to the experimental value in this context, the divergence in product secretion rates was significant. The enzyme-constrained model was able to predict that acetate was nearly the sole secreted product, with a flux equal to 7.67 mmol/gCDW/h, compared to an experimental value of 6.79 mmol/gCDW/h. The model iHN637 predicted instead ethanol to be the only fermentation product, with a secretion rate equal to 7.47 mmol/gCDW/h, largely deviating from the experimental value of 0.0035 mmol/gCDW/h. The specific rate of ethanol production predicted by ec_iHN637 was equal to 0.245 mmol/gCDW/h.

3.4. In silico metabolic engineering

The new model was then used to predict potential genetic engineering to target and improve the secretion of metabolites of interest, from the perspective of an industrial application of the bacterium. The in silico engineering experiments were carried out constraining the model with substrate uptake fluxes simulating syngas fermentation and H₂-enhanced mixotrophy scenarios, as these are of particular interest for future industrial applications of the microorganism. It was decided to focus only on native products of C. ljungdahlii, since introduction of heterologous pathway for production of other metabolites (butyrate, butanol, acetone) would result in a strong burden for the cell. Production of native metabolites was thus considered a more feasible and realistic scenario.

3.4.1. Metabolic engineering using syngas as substrate

Syngas can be derived by the gasification of many different carbon-rich sources, including biomass [49], and its composition is influenced by feedstock characteristics and process conditions applied during gasification. In the present study, the model was constrained with the substrate fluxes from Hermann M. et al. [11] for syngas growth scenario, which were derived by the exponential growth of a batch culture C. ljungdahlii cultivated using a substrate with the following composition: 55% CO, 30% H₂, 5% CO_2, 10% Ar. A 25% possible variability of each constraint was also considered for the OptKnock simulations, in order to account for some variability of uptake rates when compared to other sources in literature [47], [50] and possible minor adjustments of some fluxes.

The growth rate predicted by the FBA simulation in this condition was 0.068 h^-1, with an ethanol secretion flux of 4.83 mmol/gCDW/h, and CO₂ emission of 17.48 mmol/gCDW/h.

For OptFlux prediction of optimal knockouts, some parameters must be specified:

• •The minimum growth rate to be reached by the mutant strains generated was set to 0.034 h^-1, half of the wild-type case.
• •The minimum secretion flux for the desired product was different for each product.
• •The maximum number of genetic interventions was limited to 3.

For the case of syngas fermentation, acetate overproduction was not considered, as any attempt to overproduce acetate would result in low acetate flux and negatively affected growth rates. Since the wild-type C. ljungdahlii grown using syngas as substrate was already producing mainly ethanol, production of a less reduced end product, such as acetic acid, would have negative effects on the growth of the bacterium, because of the impossibility to keep the redox state of the cell. Therefore, it was chosen to focus only on ethanol, lactate, and BDO production.

3.4.1.1. Ethanol production

For ethanol, the lower bound of ethanol secretion was set to 5.00 mmol/gCDW/h. The highest increase of ethanol secretion was reached when the number of knockouts was set to 3: the deletion of the reactions ACALD, PTAr, and LDH resulted in a 17.4% increase of the ethanol flux to 5.67 mmol/gCDW/h, with a growth rate reduced to 0.047 h^-1. No other products were predicted in the simulations (Table 3).

Tablee 3.

Knockout strategies for overproduction of Ethanol, Lactate and 2,3 Butanediol on syngas predicted by OptKnock with 1, 2, and 3 deletions, compared to wild type. In parenthesis is reported the % variation with respect to the wild type.

Desired product	Target reactions	Growth rate (h-1)	Product flux (mmol/gCDW/h)	CO2 emission flux (mmol/gCDW/h)
Ethanol	Wild type	0.068	4.83	17.48
	KAS15	0.052 (−23.5%)	5.07 (+5.0%)	17.62 (+0.8%)
	KAS15, RNDR1	0.050 (−26.5%)	5.13 (+6.2%)	17.65 (+1.0%)
	ACALD, PTAr, LDH	0.047 (−30.9%)	5.67 (+17.4%)	19.61 (+12.2%)
Lactate	Wild type	0.068	0	17.48
	ACALD, ACKr	0.048 (- 29.4%)	5.77	14.31 (−18.1%)
	ACALD, ACKr, GLUDy	0.045 (−33.8%)	5.91	14.59 (−16.5%)
2,3 Butanediol	Wild type	0.068	0	17.48
	LDH, ACKr, ALCD2x	0.036 (−47.1%)	3.50	20.82 (+19.1%)

For all the predicted phenotypes displayed, there was an important trade-off between increased ethanol production and growth rate decrease which impacts the economy of such process when commercialized in industry. This is particularly relevant also if compared with results from previous OptKnock simulations on the original model iHN637 [50], in which predicted engineering strategies for iHN637 resulted in doubled ethanol flux compared to the wild-type, with a growth rate higher than 0.05 h^-1. In the present case, considering enzyme constraints to the model strongly inhibited the redirection of carbon and reducing equivalents towards ethanol production. Considering the analysis, it could be inferred that the wild-type strain is already optimized for ethanol production in the chosen scenario, given that ethanol is its sole product. Consequently, any potential improvement in its performance would likely stem from engineering strategies that enable the strain to enhance its uptake fluxes.

3.4.1.2. Lactate production

For lactate production, the minimum secretion rate was set to 5.00 mmol/gCDW/h. OptKnock was not able to predict any possible engineering strategy to increase the lactate secretion over this threshold with only one knockout, so only the results for the cases of two and three deletions are shown. In both cases, lactate was the only product predicted (Table 3).

In this case, the deletion strategies predicted by OptKnock resulted in lactate production not observed in the wild type, with a 33.8% decrease in growth rate for the case of 3 deletions, and a slightly lower decrease of 29.4% in the case of 2 deletions. The suggested strategy aims at the interruption of the pathways responsible for acetate, by deletion of the Acetate kinase (ACKr) and ethanol production, by deletion of the acetaldehyde dehydrogenase (ACALD). The FBA simulations for the mutant strains also showed decreased CO₂ emission fluxes, due to the increased need for carbon atoms for lactate production.

3.4.1.3. BDO production

For 2,3-butanediol production a minimum secretion flux of 3 mmol/gCDW/h was considered, as no mutant with fewer than 3 knockouts could reach higher thresholds (Table 3).

BDO production was predicted only for the case of 3 reaction knockouts, and as for other products, it was predicted to be the sole secretion by the cell, together with CO₂, in the simulated phenotype. The growth rate was strongly affected, with a 47.1% decrease, which brings the mutant growth rate very close to the threshold set for the strain. This was also the product for which the highest CO₂ fluxes were produced, as a result of the higher number of reducing equivalents needed for its production.

3.4.2. Metabolic engineering in mixotrophic growth

To simulate mixotrophic growth in OptKnock, the uptake fluxes of fructose, hydrogen, and carbon dioxide were constrained using values obtained for one of the mixotrophic cultures utilized in this study: 0.672 mmol/gCDW/h for fructose uptake, 33.6 mmol/gCDW/h for H₂ uptake, value that was obtained from previous FBA simulations.

The CO₂ flux was not constrained in order to be able to predict increases in CO₂ fixation that could result in some engineering strategies. The CO₂ uptake, however, is strongly correlated to electron availability, limited by the constraint on the maximum uptake of H₂, thus only moderate increases of CO₂ fixation could be predicted.

For the case of mixotrophic growth, only the overproduction of acetate and ethanol was considered, since no metabolic engineering strategy predicted by OptFlux was able to predict significant production of lactate and BDO while simultaneously utilizing H₂, CO₂, and fructose at the specified substrate uptakes.

The growth rate predicted by the FBA simulation in this condition was 0.093 h^-1, with acetate as the main product (6.92 mmol/gCDW/h) and ethanol secretion flux of 0.76 mmol/gCDW/h; in this case, CO₂ was consumed at a rate equal to 15.36 mmol/gCDW/h.

The OptFlux simulations were carried out as for the previous case with syngas, only increasing the constraint of minimal growth rate to 0.047 h^-1, half of the wild type.

3.4.2.1. Acetate production

For acetate overproduction, a minimum acetate secretion flux of 8 mmol/gCDW/h was used to constrain OptKnock. Some possible engineering strategies were identified with 1, 2, or 3 deletions, for increasing the specific flux of acetate, but in all cases, the increased secretion fluxes (22.3%, 25.6% and 29.9% respectively for 1, 2, and 3 deletions) also corresponded to strongly decreased growth rates (19.3%, 26.9% and 49.5%). The CO₂ fixation fluxes were also predicted to slightly increase, as a result of the increased availability of reducing equivalents generated by the reduced biomass formation (Table 4).

Table 4.

Knockout strategies for overproduction of acetate and ethanol in mixotrophic growth predicted by OptKnock with 1,2, and 3 deletions, compared to wild type. In parenthesis is reported the % variation with respect to the wild type.

Desired product	Target reactions	Growth rate (h-1)	Product flux (mmol/gCDW/h)	CO2 fixation flux (mmol/gCDW/h)
Acetate	Wild type	0.093	6.92	15.36
	FRNDPR2r	0.075 (−19.3%)	8.51 (+23.0%)	16.24 (+5.7%)
	FBA, FRNDPR2r	0.068 (−26.9%)	8.69 (+25.6%)	16.30 (+6.1%)
	GHMT2r, ENO, FRNDPR2r	0.052 (−49.5%)	8.99 (+29.9%)	16.27 (+6.9%)
Ethanol	Wild type	0.93	0.76	15.36
	ACKr	0.053 (−43.0%)	6.04 (+695%)	10.36 (−32.6%)
	GLUDy, ACKr	0.049 (−47.3%)	6.11 (+704%)	10.32 (−32.8%)
	PSP_L, GLUDy, ACKr	0.047 (−49.7%)	6.14 (+708%)	10.30 (−32.9%)

3.4.2.2. Ethanol production

For ethanol overproduction, the minimum secretion flux was set to 6 mmol/gCDW/h (Table 4). Also, for ethanol production, it was possible to reach the desired minimum rate of production considering only 1 deletion. The growth rate was strongly affected by the switch of production from acetogenic to solventogenic, for the reduced ATP gain caused by deletions of a key enzyme for acetate production, ACKr. Moreover, the CO₂ fixation was also strongly decreased with respect to the wild-type and acetate-producing strains, as a result of the decreased availability of reducing equivalents, which were diverted towards ethanol formation.

4. Discussion

Inclusion of enzyme constraints in metabolic models of microorganisms has been shown to strongly increase the ability to predict both wild-type and mutant phenotypes [24], [26], [42], [51], [52], thanks to the restriction of the flux distribution space. In the case of C. ljungdahlii introduction of enzyme constraints by sMOMENT workflow resulted in an improved performance in the prediction of growth rate and main secretion fluxes of the cell. In particular, the limitation in the maximum amount of metabolic enzyme present in the cells allowed to avoid overestimations of growth rates when compared to experimentally obtained values, for all the conditions tested. Also, the prediction of the product profile was much closer to actual values, with prediction of overflow metabolism during growth on CO, and the secretion of acetate as the main end product in mixotrophic conditions, differently from the original metabolic model. Further improvements in the prediction ability of the model can be reached by improvement of the k_cats data utilized for the calculation of the enzyme costs. Availability of high-quality turnover rates data is indeed the key parameter in the construction of enzyme-constrained models [39], but for most of the strains, it is not possible to retrieve publicly available specific data. In the present study, most of the utilized enzymes were taken from web databases, BRENDA and SABIO-RK, where mainly in vitro k_cats are available. Generation of strain-specific in vivo turnover rates, by coupling of FBA and proteomics, could further increase the prediction ability of the model [53], [54]. In vivo inferred values of turnover rates available for C. autoethanogenum [40] were already used in the calibration of the present model.

An important application of metabolic models is the prediction of metabolic engineering interventions to improve the production of a desired metabolite, under specified growth conditions. Utilization of OptKnock through the StrainDesign package available on GitHub [44], [55] allowed to design in silico mutant strains for potential syngas fermentation to ethanol, lactate, and BDO, which are native products of C. ljungdahlii. Despite many attempts to genetically engineer this strain aimed at the production of non-native metabolites by the introduction of heterologous pathways [10], [15], these products were not included in the analysis, as enzyme kinetics were not available, and, most importantly, the introduction of heterologous pathways may represent too great a burden for the growth of these bacteria.

With respect to previous in silico analysis of possible mutant C. ljungdahlii strains, utilization of an enzyme constrained model did not result in redundant engineering strategies for overproduction of different metabolites [50]. The enzyme constrained model provided more reliable predictions of the growth rate and production fluxes with respect to the original model, and the performance of the generated overproducing mutants was negatively affected, due to the lower growth rates predicted by the enzyme-constrained model. In many cases, low increases in production fluxes corresponded to strong effects on the growth rate, which would discourage the application of the strain for industrial production. Mixotrophic metabolism of C. ljungdahlii, however, may offer some solutions to improve the metabolism of the strain, as already suggested in the literature [10], [31], [32]. In particular, when the model was constrained with experimental uptake fluxes, the mutants generated in mixotrophic conditions were able to produce acetate and ethanol while converting exogenous CO₂. Moreover, comparing the ethanol overproducing strains in syngas fermentation and mixotrophy, the latter were able to secrete higher fluxes, at higher growth rates, and simultaneously converting CO₂.

5. Conclusions

Recent developments in computational tools for synthetic biology may provide a great opportunity to improve the knowledge of acetogenic metabolism and to simulate potential metabolic engineering strategies to increase their industrial potential. An enzyme-constrained model for in silico simulation of C. ljungdahlii was generated utilizing the short MOMENT approach, resulting in a model with enhanced prediction capacity for the microbial phenotype under all conditions where experimental values were either retrieved from literature or generated in the lab. This model was subsequently utilized to simulate knockout strategies aimed at increasing the production of valuable native metabolites, using the OptKnock computational framework. In the context of syngas fermentation, strains engineered for overproduction of ethanol and BDO demonstrated a reduced growth rate and an increased CO₂ emission per gram of cell dry weight. For lactic acid production, growth rate was negatively affected but CO₂ emissions were reduced with respect to the wild type. Simulated knockouts in the mixotrophic growth of C. ljungdahlii did not yield strains capable of producing lactic acid and BDO, given the parameters applied to OptKnock. However, this solution appears promising to produce acetic acid or ethanol, leading to higher growth rates and net uptake of CO₂ instead of emission. The practical feasibility of these strategies will need to be validated in vivo.

Author Agreement

We certify that all authors have seen and approved the final version of the manuscript being submitted. We also confirm that this is an original work that has not been published previously and that is not under consideration for publication elsewhere. All the authors agreed that this manuscript should be submitted to Computational and Structural Biotechnology Journal. If accepted for publication, it will not be published elsewhere in the same form, in English or any other language, including electronically, without the consent of the copyright holder.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Appendix A. Supplementary material

Supplementary material

.