Topic Modeling Based Classification of Clinical Reports

Abstract

Electronic health records (EHRs) contain important clinical information about patients. Some of these data are in the form of free text and require preprocessing to be able to used in automated systems. Efficient and effective use of this data could be vital to the speed and quality of health care. As a case study, we analyzed classification of CT imaging reports into binary categories. In addition to regular text classification, we utilized topic modeling of the entire dataset in various ways. Topic modeling of the corpora provides interpretable themes that exist in these reports. Representing reports according to their topic distributions is more compact than bag-of-words representation and can be processed faster than raw text in subsequent automated processes. A binary topic model was also built as an unsupervised classification approach with the assumption that each topic corresponds to a class. And, finally an aggregate topic classifier was built where reports are classified based on a single discriminative topic that is determined from the training dataset. Our proposed topic based classifier system is shown to be competitive with existing text classification techniques and provides a more efficient and interpretable representation.

1. Introduction

Large amounts of medical data are now stored as electronic health records (EHRs). Some of these data are in the form of free text and they need to be processed and coded for better utilization in automatic or semi-automatic systems. One possible utilization is to support clinical decision-making, such as recommending the need for a certain medical test while avoiding intrusive tests or medical costs. This type of automated analysis of patient reports can help medical professionals make clinical decisions much faster with more confidence by providing predicted outcomes. In this study, we developed several topic modeling based classification systems for clinical reports.

Topic modeling is an unsupervised technique that can automatically identify themes from a given set of documents and find topic distributions of each document. Representing reports according to their topic distributions is more compact and can be processed faster than raw text in subsequent automated processing. It has previously been shown that the biomedical concepts can be well represented as noun phrases (Huang et al., 2005) and nouns, compared to other parts of speech, tend to specialize into topics (Griffiths et al., 2004). Therefore, topic model output of patient reports could contain very useful clinical information.

2. Background

This study utilized prospective patient data previously collected for a traumatic orbital fracture project (Yadav et al., 2012). Staff radiologists dictated each CT report and the outcome of acute orbital fracture was extracted by a trained data abstractor. Among the 3,705 reports, 3,242 had negative outcome while 463 had positive. A random subset of 507 CT reports were double-coded, and inter-rater analysis revealed excellent agreement between the data abstractor and study physician, with Cohen’s kappa of 0.97.

2.1. Bag-of-Words (BoW) Representation

Text data need to be converted to a suitable format for automated processing. One way of doing this is bag-of-words (BoW) representation where each document becomes a vector of its words/tokens.

The entries in this matrix could be binary stating the existence or absence of a word in a document or it could be weighted such as number of times a word exists in a document.

2.2. Topic Modeling

Topic modeling is an unsupervised learning algorithm that can automatically discover themes of a document collection. Several techniques can be used for this purpose such as Latent Semantic Analysis (LSA) (Deerwester et al., 1990), Probabilistic Latent Semantic Analysis (PLSA) (Hofmann, 1999), and Latent Dirichlet Allocation (LDA) (Blei et al., 2003). LSA is a way of representing hidden semantic structure of a term-document matrix where rows are documents and columns are words/tokens (Deerwester et al., 1990) based on Singular Value Decomposition (SVD). One of the problems of LSA is that each word is treated as having the same meaning due to the word being represented as a single point; therefore in this representation, polysemes of words cannot be differentiated. Also, the final output of LSA, which consists of axes in Euclidean space, is not interpretable or descriptive (Hofmann, 2001).

PLSA is considered probabilistic version of LSA where an unobserved class variable z_k ∈ {z₁, …, z_K} is associated with each occurrence of a word in a particular document (Hofmann, 1999). These classes/topics are then inferred from the input text collection. PLSA solves the polysemy problem; however it is not considered a fully generative model of documents and it is known to be overfitting (Blei et al., 2003). The number of parameters grows linearly with the number of documents.

LDA, first defined by (Blei et al., 2003), defines topic as a distribution over a fixed vocabulary, where each document can exhibit them with different proportions. For each document, LDA generates the words in a two-step process:

1. Randomly choose a distribution over topics.

2. For each word in the document:

   1. Randomly choose a topic from the distribution over topics.
   2. Randomly choose a word from the corresponding distribution over the vocabulary.

The probability of generating the word w_j from document d_i can be calculated as below:

$$P(w_j/d_i;\theta ,\phi )=\sum _{k=1}^{K}P(w_j/z_k;{\phi }_z)P(z_k/d_i;{\theta }_d)$$

where θ is sampled from a Dirichlet distribution for each document d_i and φ is sampled from a Dirichlet distribution for each topic z_k. Either sampling methods such as Gibbs Sampling (Griffiths and Steyvers, 2004) or optimization methods such as variational Bayes approximation (Asuncion et al., 2009) can be used to train a topic model based on LDA. LDA performs better than PLSA for small datasets since it avoids overfitting and it supports polysemy (Blei et al., 2003). It is also considered a fully generative system for documents in contrast to PLSA.

2.3. Text Classification

Text classification is a supervised learning algorithm where documents’ categories are learned from pre-labeled set of documents. Support vector machines (SVM) is a popular classification algorithm that attempts to find a decision boundary between classes that is the farthest from any point in the training dataset. Given labeled training data (x_t, y_t), t = 1, …, N where x_t ∈ R^M and y_t ∈ {1, −1}, SVM tries to find a separating hyperplane with the maximum margin (Platt, 1998).

2.3.1. Evaluation

Once the classifier is built, its performance is evaluated on training dataset. Its effectiveness is then measured in the remaining unseen documents in the testing set. To evaluate the classification performance, precision, recall, and F-score measures are typically used (Manning et al., 2008).

3. Related Work

For text classification, topic modeling techniques have been utilized in various ways. In (Zhang et al., 2008), it is used as a keyword selection mechanism by selecting the top words from topics based on their entropy. In our study, we removed the most frequent and infrequent words to have a manageable vocabulary size but we did not utilize topic model output for this purpose. (Sarioglu et al., 2012) and (Sriurai, 2011) compare BoW representation to topic model representation for classification using varying and fixed number of topics respectively. This is similar to our topic vector classification results with SVM, however (Sriurai, 2011) uses a fixed number of topics, whereas we evaluated different number of topics since typically this is not known in advance. In (Banerjee, 2008), topics are used as additional features to BoW features for the purpose of classification. In our approaches, we used topic vector representation as an alternative to BoW and not additional. This way, we can achieve great dimension reduction. Finally, (Chen et al., 2011) developed a resampling approach based on topic modeling when the class distributions are not balanced. In this study, resampling approaches are also utilized to compare skewed dataset results to datasets with equal class distributions; however, we used randomized resampling approaches for this purpose.

4. Experiments

Figure 1 shows the three approaches of using topic model of clinical reports to classify them and they are explained below.

Figure 1:

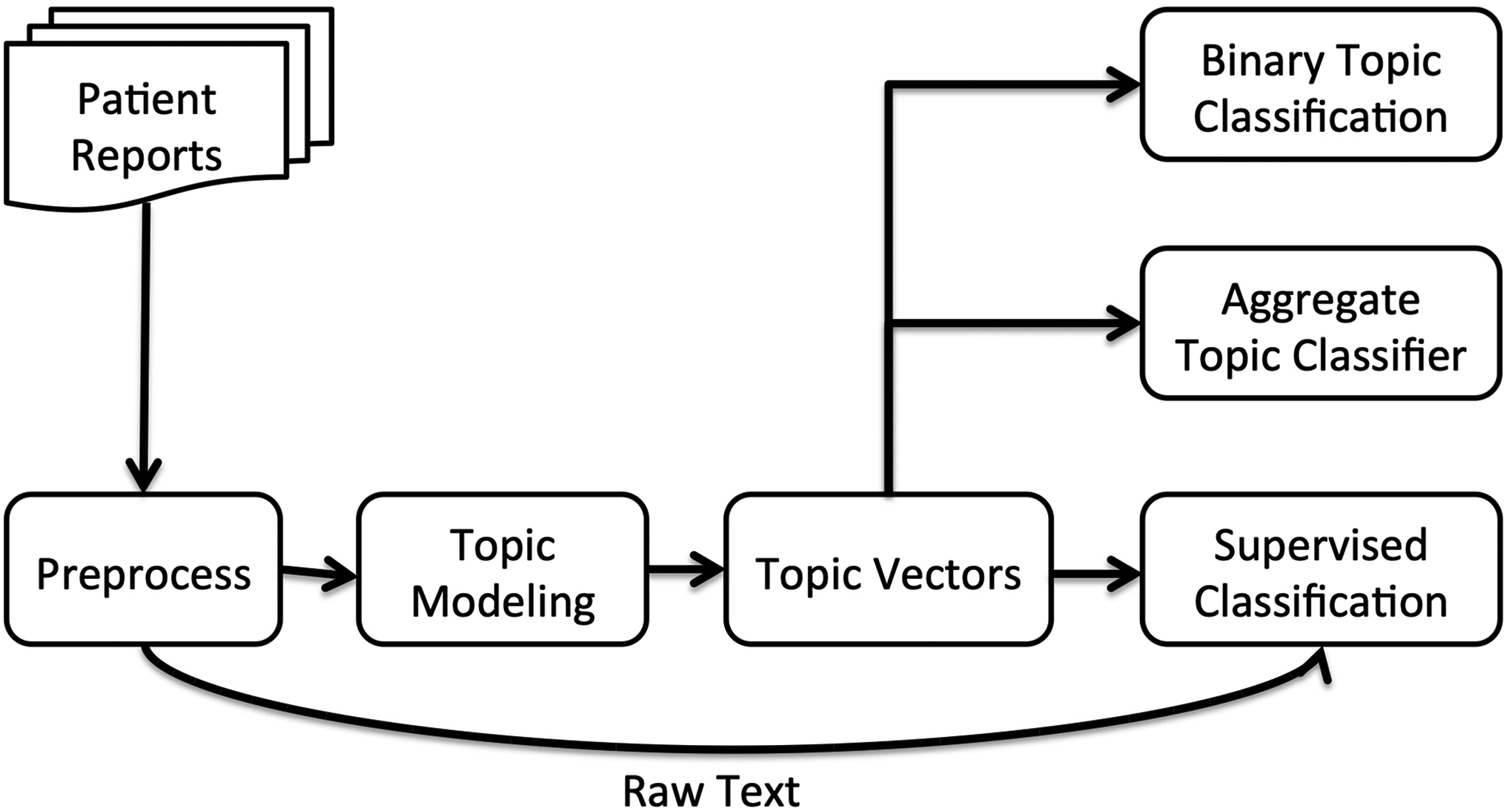
System overview

4.1. Preprocessing

During preprocessing, all protected health information were removed to meet Institutional Review Board requirements. Medical record numbers from each report were replaced by observation numbers, which are sequence numbers that are automatically assigned to each report. Frequent words were also removed from the vocabulary to prevent it from getting too big. In addition, these frequent words typically do not add much information; most of them were stop words such as is, am, are, the, of, at, and.

4.2. Topic Modeling

LDA was chosen to generate the topic models of clinical reports due to its being a generative probabilistic system for documents and its robustness to overfitting. Stanford Topic Modeling Toolbox (TMT)¹ was used to conduct the experiments which is an open source software that provides ways to train and infer topic models for text data.

4.3. Topic Vectors

Topic modeling of reports produces a topic distribution for each report which can be used to represent them as topic vectors. This is an alternative representation to BoW where terms are replaced with topics and entries for each report show the probability of a specific topic for that report. This representation is more compact than BoW as the vocabulary for a text collection usually has thousands of entries whereas a topic model is typically built with a maximum of hundreds of topics.

4.4. Supervised Classification

SVM was chosen as the classification algorithm as it was shown that it performs well in text classification tasks (Joachims, 1998; Yang and Liu, 1999) and it is robust to overfitting (Sebastiani, 2002). Weka was used to conduct classification which is a collection of machine learning algorithms for data mining tasks written in Java (Hall et al., 2009). It uses attribute relationship file format (ARFF) to store data in which each line represents a document followed by its assigned class. Accordingly, the raw text of the reports and topic vectors are compiled into individual files with their corresponding outcomes in ARFF and then classified with SVM.

4.5. Aggregate Topic Classifier (ATC)

With this approach, a representative topic vector for each class was composed by averaging their corresponding topic distributions in the training dataset. A discriminative topic was then chosen so that the difference between positive and negative representative vectors is maximum. The reports in the test datasets were then classified by analyzing the values of this topic and a threshold was chosen to determine the predicted class. This threshold could be chosen automatically based on class distributions if the dataset is skewed or cross validation methods can be applied to pick a threshold that gives the best classification performance in a validation dataset. This approach is called Aggregate Topic Classifier (ATC) since training labels were utilized in an aggregate fashion using an average function and not individually.

4.6. Binary Topic Classification (BTC)

Topic modeling of the data with two topics was also analyzed as an unsupervised classification technique. In this approach, binary topics were assumed to correspond to the binary classes. After topic model was learned, the topic with the higher probability was assigned as the predicted class for each document. If the dataset is skewed, which topic corresponds to which class was found out by checking predicted class proportions. For datasets with equal class distributions, each of the possible assignments were checked and the one with the better classification performance was chosen.

5. Results

Classification results using ATC and SVM are shown in Figures 2, 3, and 4 for precision, recall, and f-score respectively. They are each divided into five sections to show the result of using different training/testing proportions. These training and test datasets were randomized and stratified to make sure each subset is a good representation of the original dataset. For ATC, we evaluated different quantile points: 75, 80, 82, 85, 87 as threshold and picked the one that gives the best classification performance. These were chosen as candidates based on the positive class ratio of original dataset of 12%. Best classification performance was achieved with 15 topics for ATC and 100 topics for SVM. For smaller number of topics, ATC performed better than SVM. As number of topics increased, it got harder to find a very discriminative single topic and therefore ATC’s performance got worse whereas SVM’s performance got better as it got more information with more number of topics. However, using topic vectors to represent reports still provided great dimension reduction as raw text of the reports had 1,296 terms and made the subsequent classification with SVM faster. Finally, different training and test set proportions did not have much effect on both of ATC’s and SVM’s performance. This could be considered a good outcome as using only 25% of data for training would be sufficient to build an accurate classifier. We analyzed the performance of classification using binary topics with three datasets: original, undersampled, and oversampled. In the undersampled dataset, excess amount of negative cases were removed and the resulting dataset consisted of 463 documents for each class. For oversampled dataset, positive cases were oversampled while keeping the total number of documents the same. This approach produced a dataset consisting of 1,895 positive and 1,810 negative cases. With the original dataset, we could see the performance on a highly skewed real dataset and with the resampled datasets, we could see the performance on data with equal class distributions. Classification results using this approach are summarized in Table 2. As a baseline, a trivial rejector/zero rule classifier was used. This classifier simply predicted the majority class. Balanced datasets performed better compared to skewed original dataset using this approach. This is also due to the fact that skewed dataset had a higher baseline compared to the undersampled and oversampled datasets. In Table 3, the best performance of each technique for the original dataset is summarized. Although BTC performed better than baseline for datasets with equal class distribution, for the original skewed dataset, it got worse results than the baseline. ATC, on the other hand, got comparable results with SVM using both topic vectors and raw text. In addition, ATC used fewer number of topics than SVM for its best performance.

Figure 2:

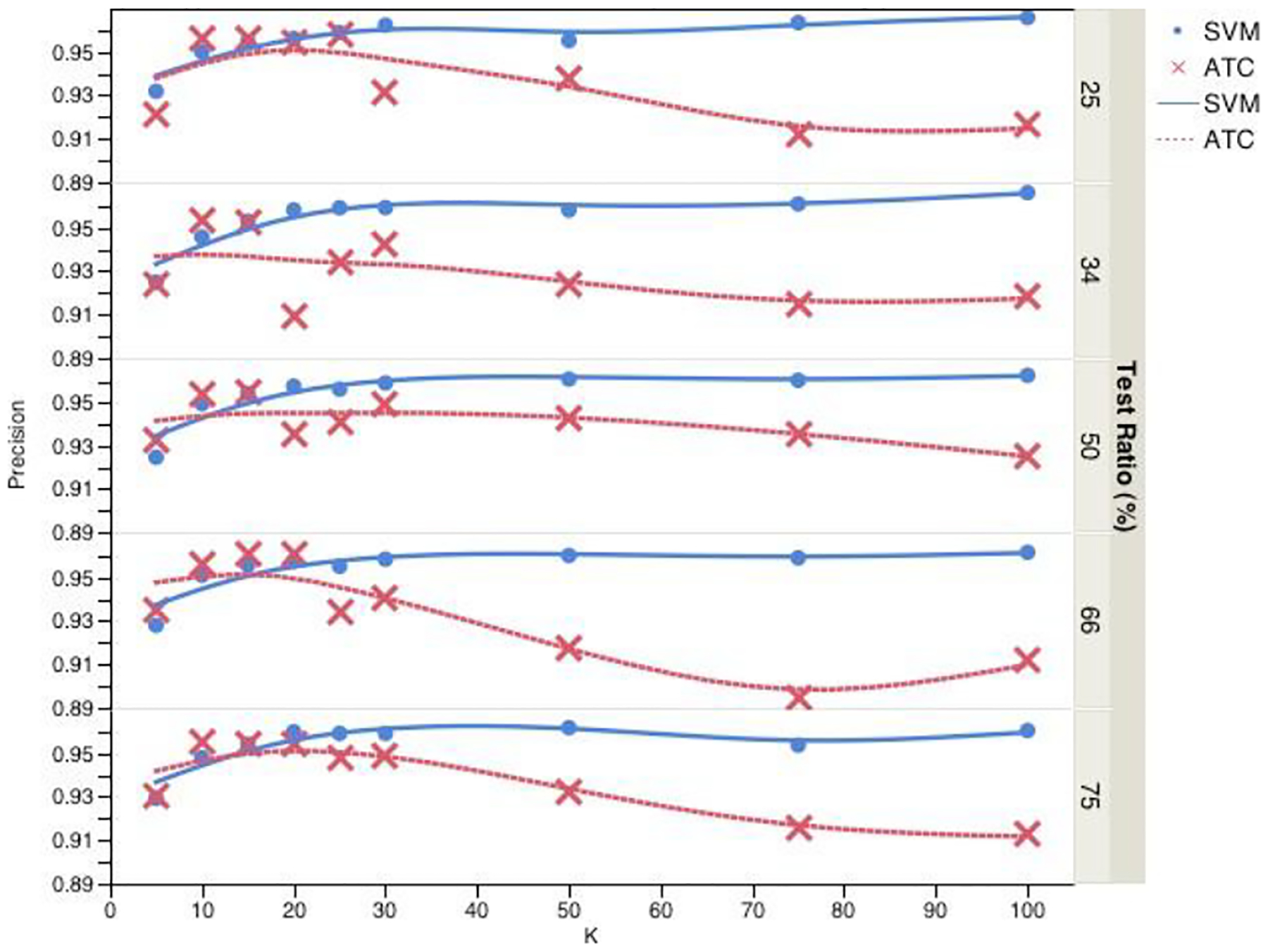
Precision

Figure 3:

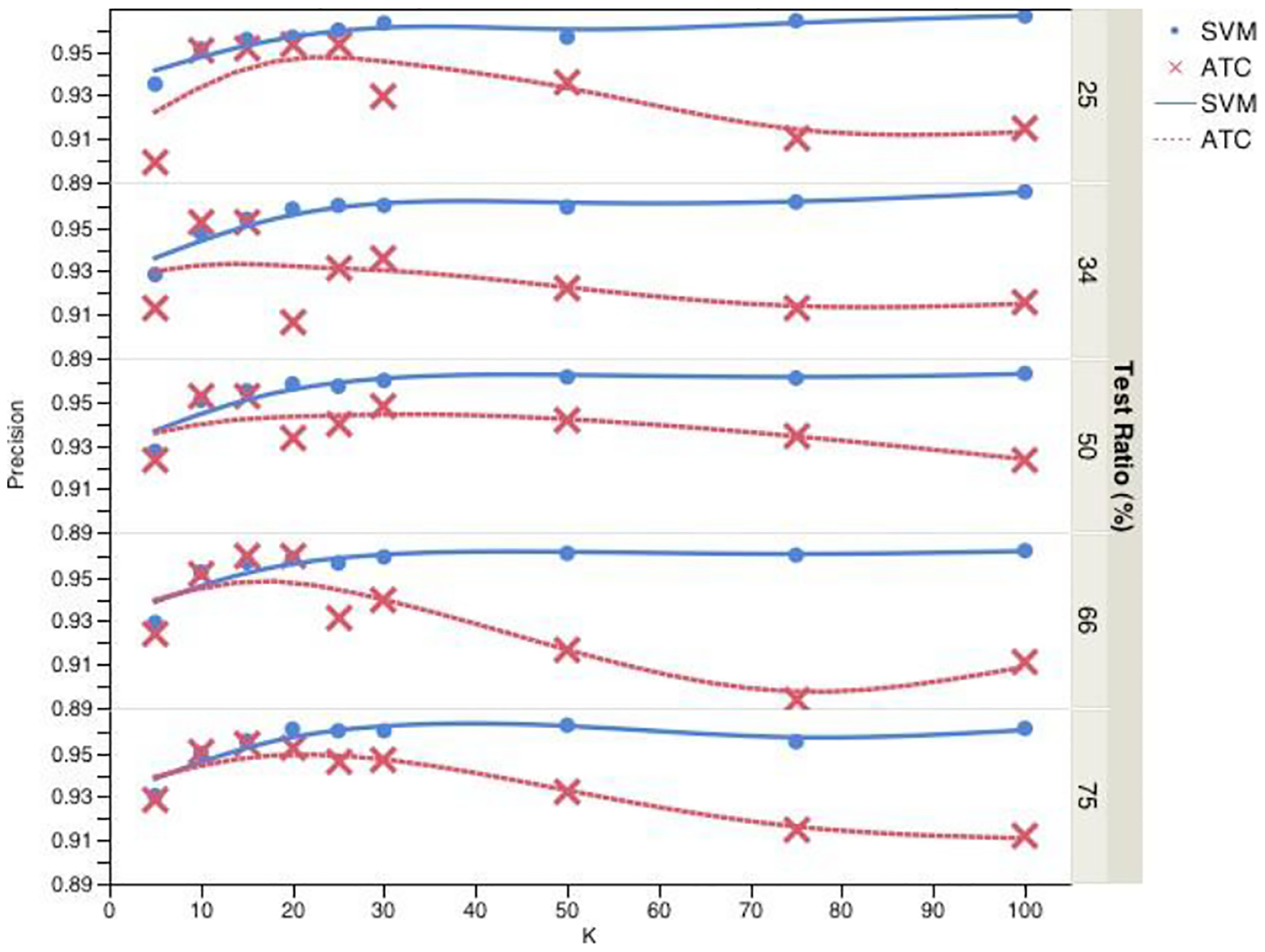
Recall

Figure 4:

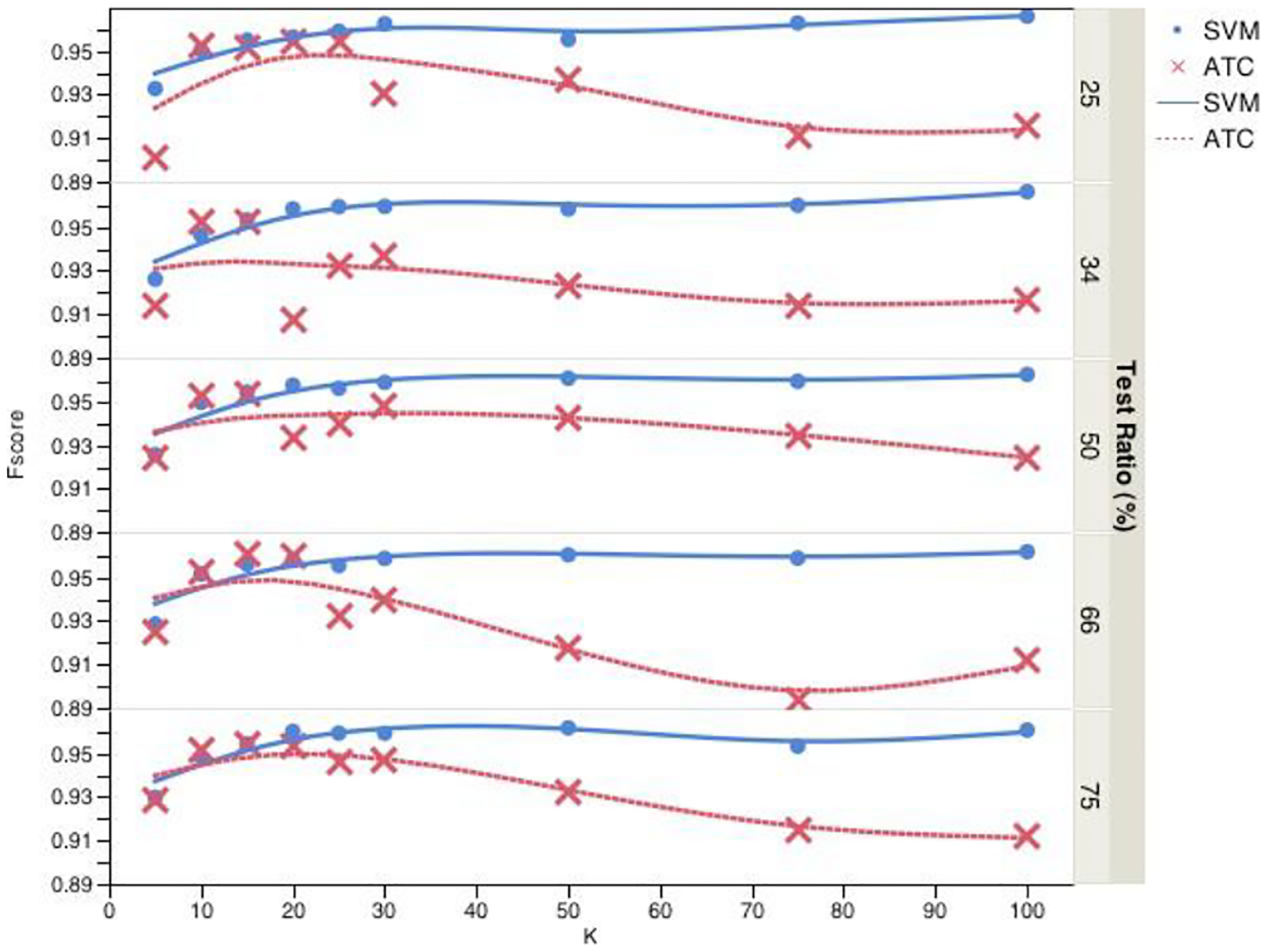
F-Score

Table 2:

Binary Topic Classification Results

Dataset	Algorithm	Precision	Recall	F-score
Original	Baseline	76.6	87.5	81.7
	BTC	88.6	73.4	77.7
Undersampled	Baseline	49.6	49.7	47.6
	BTC	84.4	84.2	84.2
Oversampled	Baseline	26.2	51.1	34.6
	BTC	83.4	82.5	82.5

Table 3:

Overall classification performance

Algorithm	Precision	Recall	F-score
Baseline	76.6	87.5	81.7
BTC	88.6	73.4	77.7
ATC	96.1	96.0	96.1
Topic vectors	96.6	96.7	96.6
Raw Text	96.4	96.3	96.3

6. Conclusion

In this study, topic modeling of clinical reports are utilized in different ways with the end goal of classification. Firstly, bag-of-words representation is replaced with topic vectors which provide good dimensionality reduction and still get comparable classification performance. In aggregate topic classifier, representative topic vectors for positive and negative classes are composed and used as a guide to classify the reports in the test dataset. This approach was competitive with classification with SVM using raw text and topic vectors. In addition, it required few topics to get the best performance. And finally, in the unsupervised setting, binary topic models are built for each dataset with the assumption that each topic corresponds to a class. For datasets with equal class distribution, this approach showed improvement over baseline approaches.

Table 1:

Classification performance using ATC and SVM

K	Dimension Reduction (%)	Train-Test (%)	ATC			SVM
			Precision	Recall	F-score	Precision	Recall	F-score
5	99.61	75 – 25	92.15	89.96	90.11	93.19	93.52	93.28
		66 – 34	92.40	91.26	91.37	92.50	92.85	92.62
		50 – 50	93.24	92.37	92.44	92.48	92.76	92.59
		34 – 66	93.50	92.43	92.50	92.80	92.92	92.86
		25 – 75	93.03	92.84	92.87	92.93	93.06	92.99
10	99.23	75 – 25	95.65	95.03	95.23	95.01	95.14	95.05
		66 – 34	95.38	95.23	95.30	94.58	94.76	94.64
		50 – 50	95.38	95.29	95.33	94.98	95.14	95.03
		34 – 66	95.61	95.13	95.26	95.11	95.26	95.16
		25 – 75	95.53	95.07	95.20	94.81	95.00	94.85
15	98.84	75 – 25	95.61	95.14	95.18	95.48	95.57	95.51
		66 – 34	95.26	95.23	95.24	95.31	95.39	95.34
		50 – 50	95.49	95.35	95.41	95.46	95.57	95.49
		34 – 66	96.07	96.03	96.05	95.58	95.71	95.61
		25 – 75	95.47	95.43	95.45	95.42	95.57	95.45
20	98.46	75 – 25	95.45	95.36	95.40	95.62	95.68	95.65
		66 – 34	90.89	90.62	90.75	95.83	95.87	95.85
		50 – 50	93.59	93.35	93.40	95.79	95.90	95.82
		34 – 66	96.07	95.95	95.97	95.77	95.87	95.80
		25 – 75	95.40	95.28	95.30	96.00	96.11	96.02
25	98.07	75 – 25	95.85	95.36	95.44	95.89	96.00	95.92
		66 – 34	93.37	93.16	93.26	95.92	96.03	95.95
		50 – 50	94.10	94.00	94.05	95.65	95.79	95.68
		34 – 66	93.38	93.17	93.20	95.52	95.66	95.55
		25 – 75	94.79	94.56	94.59	95.92	96.04	95.94
30	97.69	75 – 25	93.12	92.98	93.04	96.23	96.33	96.26
		66 – 34	94.21	93.64	93.73	95.93	96.03	95.96
		50 – 50	94.95	94.86	94.90	95.94	96.06	95.95
		34 – 66	94.05	93.95	94.00	95.85	95.95	95.88
		25 – 75	94.86	94.71	94.73	95.92	96.04	95.94
50	96.14	75 – 25	93.75	93.63	93.69	95.53	95.68	95.54
		66 – 34	92.44	92.21	92.32	95.82	95.95	95.84
		50 – 50	94.32	94.21	94.26	96.12	96.22	96.15
		34 – 66	91.78	91.70	91.74	96.02	96.11	96.04
		25 – 75	93.26	93.20	93.22	96.19	96.29	96.18
75	94.21	75 – 25	91.21	91.04	91.12	96.35	96.44	96.30
		66 – 34	91.51	91.26	91.37	96.10	96.19	96.01
		50 – 50	93.57	93.46	93.51	96.07	96.17	96.00
		34 – 66	89.43	89.33	89.38	95.91	96.03	95.89
		25 – 75	91.54	91.47	91.50	95.38	95.54	95.34
100	92.28	75 – 25	91.63	91.47	91.55	96.59	96.65	96.61
		66 – 34	91.82	91.57	91.69	96.62	96.66	96.64
		50 – 50	92.51	92.37	92.44	96.30	96.38	96.32
		34 – 66	91.21	91.12	91.17	96.16	96.24	96.19
		25 – 75	91.26	91.18	91.22	96.05	96.15	96.08