Fluoroscopy-Guided Robotic System for Transforaminal Lumbar Epidural Injections

Abstract

We present an autonomous robotic spine needle injection system using fluoroscopic image-based navigation. Our system includes patient-specific planning, intra-operative image-based 2D/3D registration and navigation, and automatic robot-guided needle injection. We performed intensive simulation studies to validate the registration accuracy. We achieved a mean spine vertebrae registration error of 0.8 ± 0.3 mm, 0.9 ± 0.7 degrees, mean injection device registration error of 0.2 ± 0.6 mm, 1.2 ± 1.3 degrees, in translation and rotation, respectively. We then conducted cadaveric studies comparing our system to an experienced clinician’s free-hand injections. We achieved a mean needle tip translational error of 5.1 ± 2.4 mm and needle orientation error of 3.6 ± 1.9 degrees for robotic injections, compared to 7.6 ± 2.8 mm and 9.9 ± 4.7 degrees for clinician’s free-hand injections, respectively. During injections, all needle tips were placed within the defined safety zones for this application. The results suggest the feasibility of using our image-guided robotic injection system for spinal orthopedic applications.

I. Introduction

Transforaminal epidural steroid injection in the lumbar spine (TLESI) is a common non-surgical treatment for lower back pain or sciatica. Globally, between 60–80% of people are estimated to experience lower back pain in their lifetime and it is among the top causes of adult disability [1], [2]. Efficacy of treatment is reported as 84%, with adequate targeting of the injection site thought to be critical to successful treatment [3].

Epidural injection in the lumbar spine is typically performed by a clinician using fluoroscopy. The clinician will acquire several images before and during manual insertion of the needle. When satisfied with needle placement, the clinician will inject a steroid and remove the needle. Several injections at different levels of the spine may be performed in sequence. The clinical effect of TLESI is related to the diffused pattern of the injected steroid agent. However, failure injections may cause damage to the vessels or nerves, which can result in symptoms of spinal nerve pricking or more complicated issues [4], [5]. Previous studies have suggested that injections through the safety triangle allow the steroid to be injected more effectively and safely [6]. In this work, we used the defined safety triangle as the clinical requirement of successful injections, which combines the conventional safe triangle, located under the inferior aspect of the pedicle [4], and the Kambin’s triangle [6], defined as a right triangle region over the dorsolateral disc.

Given the importance of accurate targeting and the proximity to critical anatomy, robotic systems have been considered in the literature as a tool to perform these injections. Various imaging technologies have been used for guidance of these systems including MRI [7], [8], [9], [10], ultrasound [11], [12], and cone-beam CT [13]. However, MRI and CT machines are expensive, and are not commonly available in the orthopedic operating rooms. Furthermore, these 3D imaging modalities - MRI in particular - can greatly prolong the surgical procedure. Ultrasound data are often noisy and it can be complicated to extract contextual information. Thus, ultrasound-guided needle injection requires longer scanning time and is limited in reconstruction accuracy [11]. Often additional sensing modalities are needed along with ultrasound, such as force sensing [12].

In contrast, fluoroscopic imaging is fast and low-cost. In particular, C-arm X-ray machines are widely used in orthopedic operating rooms. X-ray imaging presents deep-seated anatomical structures with high resolution. A general disadvantage of fluoroscopy is that it adds to the radiation exposure of the patient and surgeon. However, in current practice, orthopaedic surgeons always use fluoroscopy for verification to gain “direct” visualization of the anatomy. As such, the use of fluroroscopy for navigation is intended to replace its use for these manual verification images, resulting in similar radiation exposure compared to a conventional procedure.

Fluoroscopic guided needle placement has been studied [14], [15], [16]. These approaches either require custom-designed markers to calibrate the robot end effector to the patient anatomy or the surgeon’s supervision to verify the needle placement accuracy. Fiducial-free navigation has drawn attention in image-guided surgical interventions [17], [18], [19], [20]. Fiducial-free navigation does not put markers on the patient’s body, which is less invasive and simplifies the procedures. Poses of the anatomy relative to the surgical tool are estimated using purely image information. Different clinical applications have different algorithmic designs for fiducial-free navigation, such as automatic pelvic landmark detection [21], multi-modality registration [22], etc. Gao et al. proposed a fiducial-free registration pipeline for femoroplasty, which uses the multi-view pelvis registration to initialize and constrain the femur registration [19]. In this work, the pose estimation of the spine vertebrae has additional challenges compared to the hip, because the vertebrae are smaller in size and have multiple components, which deforms the shape of the spine. To the best of our knowledge, there has been no research published on using fiducial-free image-based 2D/3D registration for autonomous spine needle injection.

Here, we present a robotic system for transforaminal spine injection using only 2D fluoroscopic images for navigation. The contribution of the paper includes:

1. A customized module for TLESI needle trajectory planning;

2. A joint injection device registration method to accurately estimate the multi-view C-arm geometry;

3. A vertebrae-by-vertebrae 2D/3D registration pipeline for intra-operative spine vertebrae pose estimation;

4. System calibration and integration, followed by testing of the full automatic navigation pipeline.

We present the results of testing the system with a series of simulations and cadaveric studies, and compare the robot performance with an expert clinician’s manual injection.

II. Methodology

Our robotic injection platform performs planning, registration and navigation, automatic injection, and post-operative analysis (Fig. 1). The intra-operative pose of the injection device relative to the spine vertebrae is estimated using X-ray image-based 2D/3D registration. The multiple C-arm view geometry is firstly estimated using the proposed joint injection device registration. Then, both the spine and the injection device are registered using the multi-view X-ray images. Specially, we register the spine in a vertebrae-by-vertebrae fashion due to the spine shape deformation. We introduce the system setup, registration methods, and evaluation in the following sections.

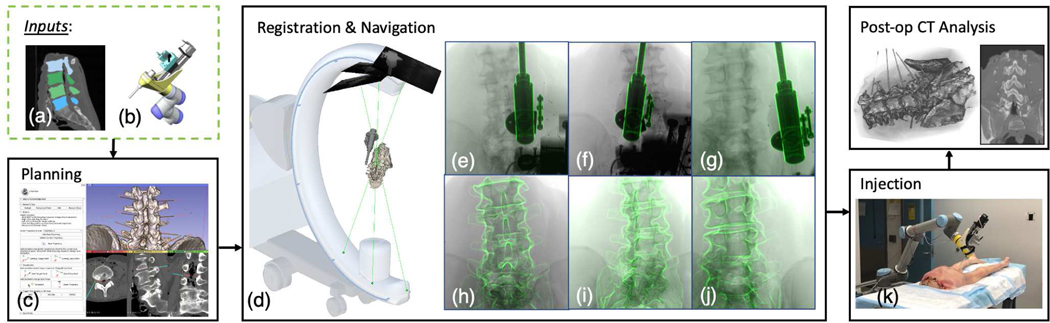
Fig. 1:

Overall pipeline of our robotic needle injection system. Inputs include (a) patient-specific CT scan and spine vertebrae segmentation, (b) an injection device model. The planning module shows (c) the surgeon’s interface to annotate needle injection trajectories and an example display of the planned trajectories on the CT segmentation. Multi-view registration presents: (d) multi-view C-arm X-ray projection geometries. The source-to-detector center projection line is rendered in green and the detector planes are rendered as squares. The needle injector guide and the spine anatomy are rendered using the registration pose. (e)(f)(g) Registration overlay images of the needle injector guide. The outlines of the reprojected injection device are overlayed in green. (h)(i)(j) Registration overlay images of the cadaveric spine vertebraes. We present an actual cadaveric needle injection image in (k).

A. Pre-operative Injection Planning

Needle targets and trajectories were planned in a custom-designed module in 3D Slicer [23]. Pre-procedure lower torso CT scans were acquired. The CT images were rendered in the module with the standard coronal, sagittal, and transverse slice views as well as a 3D volume of the bony anatomy, segmented automatically by Slicer’s built-in volume renderer. Needle target and entry points could be picked on any of the four views. A model needle was rendered in the 3D view according to the trajectory defined by the mentioned points and the needle projection was displayed on each slice view. Users had the option to switch to a “down-trajectory” view where the coronal view was replaced with a view perpendicular to the needle trajectory and the other two slice views were reformatted to provide views orthogonal to the down-trajectory view. These views, together with 3D rendering, provided opportunities to determine the amount of clearance between the planned needle trajectory and bone outline. This module is provided in github¹. An example screenshot of the surgeon’s interface is presented in Fig. 1(c).

B. System Setup and Calibration

The robotic system’s end effector consisted of a custom-designed automated injection unit, attached to a 6-DOF UR-10 (Universal Robots, Odense, Denmark). The injection unit consists of a supporter shell, a linear stage, a load cell and a gauge with a cylinder guide (Fig. 2). This device was developed for the application of femoroplasty, which requires both drilling and injection [19]. In this work, we mainly used this device as a syringe holder. A custom-designed attachment between the syringe and needle was constructed to allow for the robotic system to leave a needle behind after placement with minimal perturbation and to allow for repeatable reloading of needles with minimal positional deviation. (Fig. 2). The syringe mount consisted of a plug with a female Luer lock and a receptacle with a male Luer lock, for which the receptacle was screwed onto the syringe and the needle was screwed into the plug. The mating tapers on each Luer lock connection ensured concentricity between needles, while the linear degree of freedom between the plug and receptacle, when unlocked, allowed for precise adjustment of the needles’ axial position, to ensure that the length from the tip of the needle to the base of the injection device was consistent between trials. The forward kinematic accuracy of the robot is insufficient for this task. This insufficiency is further amplified by the weight of the injection unit and long operating reach needed to perform injections on both sides of the specimen spine from L2 to the sacrum from a single position at the bed-side. To ameliorate these inaccuracies, an NDI Polaris (Northern Digital Inc., Waterloo, Ontario, Canada) system was used to achieve closed-loop position control of the robotic system.

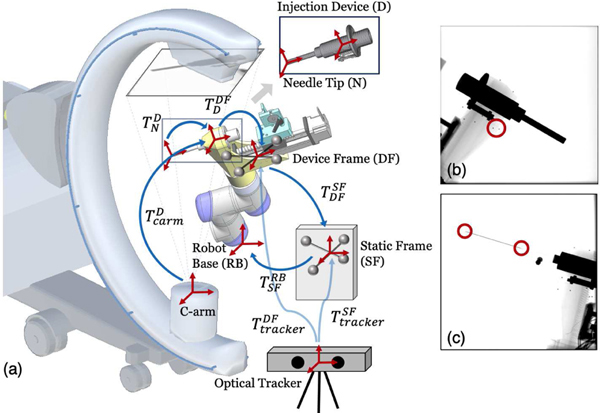
Fig. 2:

Picture of robotic injection system setup including C-arm, UR-10, optical tracker, injection device and a cadaveric specimen. Bottom left: Picture of the injection device unit model. Bottom right:Picture of the syringe mount.

Our robotic injection system was navigated using pose estimations from X-ray image-based 2D/3D registration. An accurate calibration of the device registration model to the robot kinematic chain is required for automatic robot positioning and injection. To achieve closed-loop navigation, several calibrations were required: hand-eye calibration of the optical frame, hand-eye calibration of the injection device and needle calibration (Fig. 3).

Fig. 3:

(a) System calibration scheme. Coordinate frames are marked as red cross arrows. Key transformations are shown in blue arrows. The 3D model of injection device for 2D/3D registration is illustrated on top. (b) An example X-ray image used for hand-eye calibration. Example BBs are marked in a red circle. (c) An example X-ray image used for needle calibration. The needle tip and base points are marked in red circles.

1). Hand-eye Calibration of the Device Frame:

A hand-eye calibration was performed to determine the location of the optical tracker body on the injector unit (DF) relative to the robot’s base coordinate frame (RB). This allows for real-time estimation of the manipulator Jacobian J_m associated with movement of the injector attached to the base robot. The calibration was performed using the well-established method of moving the robot to 60 configurations within the region of its workspace in which the injections would occur, recording the robot’s forward kinematics and the optical tracker body location $\left(T_{DF}^{SF}\right)$, and using these measurements to solve an AX = XB problem to find $T_{SF}^{RB}$ in Fig. 3(a).

2). Hand-eye Calibration of the Injection Device:

Another hand-eye calibration was conducted to compute the transformation of the injection device model frame (D) to the optical tracker unit (DF). This is necessary to integrate the registration pose estimation to the closed-loop control. Metallic BBs were glued to the surface of the injection device and their 3D positions were extracted in the model. At different robot configurations, X-ray images of the injection device were acquired. 2D BB locations are easily detected on the images and were manually annotated (Fig. 3(b)). The rigid pose of the injection device $\left(T_{Carm}^D\right)$ was estimated by solving a PnP problem. This also results in an AX = XB problem to find $T_D^{DF}$ in Fig. 3(a). These two hand-eye calibration processes only need to occur if the injector is removed and reattached to the robot.

3). Needle Calibration:

As the positional accuracy of the needle tip is of greatest importance, a one-time calibration was also completed to determine the location and direction of the needle tip relative to the marker body on the injector. Ten X-ray images were taken with the injector and the needle in the view of the image. The needle tip and BB markers attached to the surface of the injector were annotated in each image (Fig. 3(c)). These annotations were used when solving the optimization of the 3D location of the needle tip relative to the injector’s coordinate frame, which is described in Section III-A.

To this end, the chain of transformation is well established that connects the C-arm frame, the injection device model, the optical marker units and the robot base frame. These calibration results are used to navigate the injector to the planning trajectories once the registration is complete.

C. Intra-operative Registration and Navigation

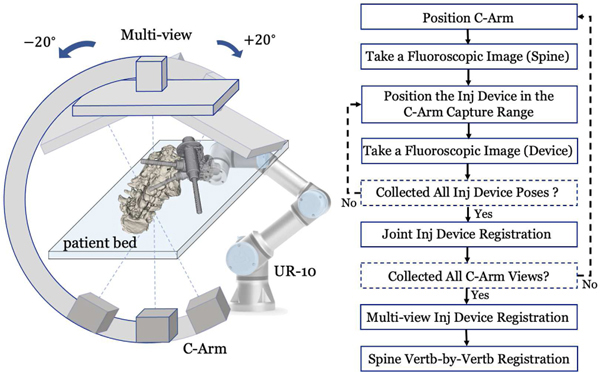
Intra-operative pose estimation of the injection device and the spine vertebrae was achieved using multi-view X-ray image-based 2D/3D registration. The patient remained stationary during the registration phase. The robot base was fixed relative to the patient bed. The C-arm was positioned at multiple geometric views with separate angles of ±20°. At each C-arm view, we first took a fluoroscopic image of the spine. Then, we positioned the robotic injection device at varied configurations above the patient anatomy and within the C-arm capture range. Fluoroscopic images of the injection device were taken for each injection device pose. These images were used for joint injection device registration to estimate the C-arm view geometry. These robot configurations were saved and kept the same while the C-arm was positioned at different views. This data acquisition workflow is illustrated in Fig. 4. The acquired fluoroscopic images were used for multi-view injection device registration and multi-view spine vertebrae registration, which are described in the following sections.

Fig. 4:

Multi-view Registration Workflow. Left: Illustration of collecting multi-view C-arm images. The spine anatomy is rendered on the patient bed. Various configurations of the injection device are presented. Right: A workflow chart detailing the data acquisition and registration steps.

1). Joint Injection Device Registration:

Intensity-based 2D/3D registration of the injection device was performed at each C-arm view. It optimizes a similarity metric between the target X-ray image and a digitally reconstructed radiograph (DRR) image simulated from the 3D injection device model (V ^D). Because single-view 2D/3D registration has severe ambiguity [20], we proposed a joint injection device registration by optimizing various robot configurations together. Given J tracker observations $T_{D{F}_1}^{SF}$, $T_{D{F}_2}^{SF},\dots ,T_{D{F}_J}^{SF}$, the hand-eye calibration matrix $T_{ID}^{DF}$, the injection device poses in the static frame are $T_{I{D}_j}^{SF}=T_{ID}^{DF}\cdot T_{D{F}_j}^{SF}$, $j\in \{1,\dots ,J\}$. We used the first pose as reference and the rest of the poses can be computed relative to the reference pose using $T_{I{D}_0}^{I{D}_j}=T_{ID}^{DF}\cdot T_{D{F}_j}^{SF}\cdot {\left(T_{D{F}_0}^{SF}\right)}^{-1}\cdot {\left(T_{ID}^{DF}\right)}^{-1}$. Given an X-ray image $I_k^{D_j}$ (the k^th C-arm view and the j^th injection device pose), a DRR operator ($𝓟$), a similarity metric ($𝓢$), the joint 2D/3D registration estimates the injection device pose ($T_{Car{m}_k}^{I{D}_0}$) by solving the following optimization problem:

$$\underset{T_{Car{m}_k}^{I{D}_0}\in SE(3)}{\min }\sum _{j=1}^J𝓢\left(I_k^{D_j},𝓟\left(V^D;T_{Car{m}_k}^{I{D}_0},T_{ID}^{DF},T_{D{F}_j}^{SF}\right)\right).$$ (1)

The similarity metric ($𝓢$) was chosen to be patch-based normalized gradient cross correlation (Grad-NCC) [24]. The 2D X-ray image was downsampled 4 times in each dimension. The optimization strategy was selected as “Covariance Matrix Adaptation: Evolutionary Search” (CMA-ES) due to its robustness to local minima [25]. The registration gives an accurate injection device pose estimation at each C-arm view ($T_{Car{m}_k}^{I{D}_0}$).

2). Multi-view Injection Device Registration:

Because the injection device pose was the same when we changed the C-arm view, it then functioned as a fiducial to estimate the multi-view C-arm geometry. Given the first C-arm view as reference, poses of the rest C-arm views can be calculated using $T_{Car{m}_0}^{Car{m}_k}={\left(T_{Car{m}_k}^{I{D}_0}\right)}^{-1}\cdot T_{Car{m}_0}^{I{D}_0}$, $k\in \{1,\dots ,K\}$, where K is the total number of C-arm views. We then performed a multi-view injection device registration to estimate the reference injection device pose in the reference C-arm view ($T_{Car{m}_0}^{I{D}_0}$) by solving the optimization:

$$\underset{T_{Car{m}_0}^{I{D}_0}\in SE(3)}{\min }\sum _{k=1}^K𝓢\left(I_k^{D_0},𝓟\left(V^D;T_{Car{m}_0}^{I{D}_0},T_{Car{m}_0}^{Car{m}_k}\right)\right).$$ (2)

We used the same similarity metric, image processing and optimization strategy as introduced in the joint injection device registration. $T_{Car{m}_0}^{I{D}_0}$ derived from multi-view registration further refined the result of joint registration under single-view. The multi-view C-arm geometries ($T_{Car{m}_0}^{Car{m}_k}$) were also used for multi-view spine vertebrae registration.

3). Spine Vertebrae-by-Vertebrae Registration:

We proposed this vertebrae-by-vertebrae registration to compensate the intra-operative spine vertebrae shape difference from the pre-operative CT scans. The spine vertebrae ($V_m^S$, $m\in \left\{\mathrm{1..}M\right\}$, where M is the total number of vertebrae for registration) were segmented from the pre-operative CT scans using an automated method [26]. Intra-operative pose estimation of each individual spine vertebrae ($T_{Car{m}_0}^{v_m}$) was achieved following a coarse-to-fine manner. Firstly, a single-view rigid 2D/3D registration was performed using the first C-arm view X-ray image and the rigid vertebrae segmentation from the pre-operative CT scans. Given the X-ray image $I_0^S$ (the first C-arm view X-ray image for spine registration), a DRR operator ($𝓟$), a similarity metric ($𝓢$), the single-view 2D/3D registration estimated the pose of rigid spine vertebrae ($T_{Car{m}_0}^v$) by solving the following optimization problem:

$$\underset{T_{Car{m}_0}^v\in SE(3)}{\min }𝓢\left(I_0^S,𝓟\left(\sum _{m=1}^M{V}_m^S;T_{Car{m}_0}^v\right)\right).$$ (3)

Because of the shape difference and the ambiguity of single-view 2D/3D registration, $T_{Car{m}_0}^v$ solved from equation 3 is prone to be less accurate. A precise intra-operative vertebrae pose estimation was achieved by performing multi-view vertebra-by-vertebra 2D/3D registration. The pose of each individual vertebra was optimized independently. The multiple C-arm geometries ($T_{Car{m}_0}^{Car{m}_k}$) were estimated from the joint injection device registration. The registration was initialized by $T_{Carm}^v$ and estimates deformable spine vertebrae poses ($T_{Car{m}_0}^{v_m},m\in \left\{\mathrm{1..}M\right\}$) by solving the optimization:

$$\underset{T_{Car{m}_0}^{v_m}\in SE(3)}{\min }\sum _{k=1}^K𝓢\left(I_k^S,𝓟\left(\sum _{m=1}^M{V}_m;T_{Car{m}_0}^{v_m},T_{Car{m}_0}^{Car{m}_k}\right)\right).$$ (4)

The registration setup and optimization strategies in both single-view and multi-view spine registrations were the same as intensity-based injection device registration. Multi-view spine vertebrae registration functioned as an accurate local search of each vertebra component of the deformable spine object. The vertebrae pose estimation ($T_{Car{m}_0}^{v_m}$) and the injection device pose estimation ($T_{Car{m}_0}^{I{D}_0}$) were both in the reference C-arm frame. Their relative pose can be computed using $T_{I{D}_0}^{v_m}={\left(T_{Car{m}_0}^{I{D}_0}\right)}^{-1}\cdot T_{Car{m}_0}^{v_m}$, $m\in \left\{\mathrm{1..}M\right\}$, was used to update the injection plan of each nearby vertebra and navigate the robot to the injection position.

The target trajectory consisting of an entry point and a target point for the needle injection was transformed into the optical marker coordinate frame on the injector (DF) using the system calibration matrices. We first controlled the robot to a start position, which was a straight line extension of the target needle path above the skin entry point. Next, the needle injector was moved along the straight line to reach the target point. To ensure smooth motion, joint velocities $\dot{\theta }$ were commanded to the robot. These velocities were chosen by $\dot{\theta }=J_m^{-1}\cdot v$, where v represents the instantaneous linear and angular velocities that would produce a straight-line Cartesian path from the start to goal positions. This is the desired method of movement for needle insertion. The pose of the injector relative to a base marker was measured using the optical tracker. Once the needle reached the target point, the needle head was manually detached from the syringe mount. Then the robot was moved back to the start position to finish this injection.

D. Post-op Evaluation

We took post-operative CT scans and manually annotated the needle tip and base positions from the CT images. We reported the metrics of target point error, needle orientation error, and needle tip position relative the safety zone of this application. Considering the spine shape mismatch of the post-operative and pre-operative CT scans, we performed a 3D/3D registration of each vertebra from post-op to pre-op CT. The annotated needle point positions were transformed to the pre-operative CT frame for comparison.

The annotation of the safety zone was performed on pre-operative CT scans under the instruction of experienced surgeons. We followed the definitions of both [4] and [6] to manually annotate the Kambin triangle safety zone. In [4], the safety triangle is the inferior aspect of the pedicle and above the traversing nerve root. In [6], the Kambin triangle is defined by the hypotenuse, base, and height. The hypotenuse is the exiting nerve; the base is the caudad vertebral body; and the height is the traversing nerve root. Our safety zone is a combination of both these definitions. The safety zone for each injection trajectory target was manually segmented in 3D Slicer. We checked the needle tip positions relative to these safety zones in the post-operative CT scans as part of the evaluation.

III. Experiments and Results

In the following section, we report our system calibration and verification using simulation and cadaveric experiments. For system calibration, we first performed needle and hand-eye calibration. For our navigation system verification, we then performed simulation studies and cadaveric experiments. Lower torso CT scan images of a male cadaveric specimen were acquired for fluoroscopic simulation and spine vertebrae registration. The CT voxel spacing was resampled to 1.0 mm isotropic. Vertebrae S1, L2, L3, L4 and L5 were segmented. The X-ray simulation environment was set up to approximate a Siemens CIOS Fusion C-Arm, which has image dimensions of 1536 × 1536, isotropic pixel spacing of 0.194 mm/pixel, a source-to-detector distance of 1020 mm, and a principal point at the center of the image. We simulated X-ray images in this environment with known groundtruth poses using xreg² and tested our proposed multi-view registration pipeline.

A. System Calibration

We pre-operatively calibrated the needle base and tip positions in the injection device model frame using an example needle attached to the syringe mount. Six X-ray images were taken with variant C-arm poses. 2D needle tip, base ($x_k^{tip}$, $x_k^{base}$, $k\in \{1,\dots ,6\}$) and metallic BB positions were manually annotated in each X-ray image (Fig. 3 (c)). The C-arm pose (${\left(T_{Carm}^D\right)}_k^{pnp}$, $k\in \{1,\dots ,6\}$) was estimated by solving the PnP problem using corresponding 2D and 3D BBs on the injection device. Using the projector operator ($𝓟$), the 3D needle tip and base positions ($p_D^{tip}$, $p_D^{base}$) were estimated by solving the following optimization:

$$\underset{p_D^{tip,base}\in {ℝ}^3}{\min }\sum _{k=1}^K\left(x_k^{tip,base},𝓟\left(p_D^{tip,base},{\left(T_{Carm}^D\right)}_k^{pnp}\right)\right).$$ (5)

The optimization was performed using brute force local search starting from a manual initialization point. We report the residual 2D error by calculating the l₂ difference of the annotated needle tip and base points ($x^{tip,base}$) and the reprojected points ($𝓟\left(p_D^{tip,base},{\left(T_{Carm}^D\right)}_k^{pnp}\right)$) on each X-ray image. the mean 2D needle tip and base point errors were 0.6±0.5 mm and 0.6 ± 0.4 mm, respectively.

We moved the robotic injection device to 30 variant configurations for injection device hand-eye calibration, while the C-arm was fixed static. At each configuration, we took an X-ray image and solved the injection device pose $T_{Carm}^D$. After solving the AX = XB problem to find $T_D^{DF}$, we reported the calibration accuracy by calculating the injection device tip position difference between the PnP estimation (${\left(T_{Carm}^D\right)}_i^{pnp}$) and estimation using the chain of calibration transformations:

$${\left(T_{Carm}^D\right)}_i^{cali}={\left(T_D^{DF}\right)}^{-1}\cdot {\left(T_{DF}^{SF}\right)}_i^{-1}\cdot T_{DF}^{SF}\cdot T_D^{DF}\cdot {\left(T_{Carm}^D\right)}_0,$$ (6)

where i is the index of the calibration frame and ${\left(T_{Carm}^D\right)}_0$ is our reference pose corresponding to the first calibration frame. The hand-eye calibration error was calculated as the mean l₂ difference of the estimated needle tip point in the injector model ($p_D^{tip}$) between these two pose estimations: $\Vert \left({\left(T_{Carm}^D\right)}_i^{cali}-{\left(T_{Carm}^D\right)}_i^{pnp}\right)\cdot p_D^{tip}\Vert$. The mean error was 2.5 ± 1.6 mm.

In order to quantify the precision of the injection module, we performed a system testing experiment by adding weight load to the tip of injection device and monitoring its shape deflection. Two optical fiducial markers were used for this testing: one was attached to the injection device tip, and the other one was the injection device marker itself. We applied increasing weight loads on the injection module tip uniformly from 0 to 2 kg. An NDI Polaris system was used to monitor the pose transformation of the two fiducial markers. We calculated the positional deviation of the tip marker relative to the injection device marker. We observed a mean relative deviation of 0.14 ± 0.08 mm, and a maximum relative deviation of 0.29 mm.

B. Simulation Study

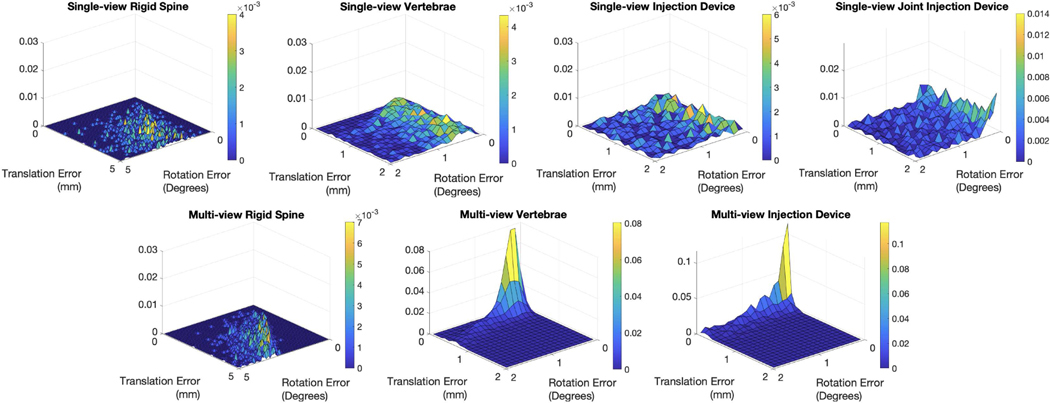
We tested the registration performance under various settings, including single-view and multi-view C-arm geometries, rigid spine and deformable spine, etc. 1,000 simulation studies were performed with randomized poses of the injection device and the spine for each registration workflow. To simulate the intra-operative spine shape difference from the pre-operative CT scans, we applied random rotation change to the consecutive vertebrae CT segmentations. Fig. 6 (a)(b) presents an example of this simulated spine deformation, which is mentioned in the supplemental video. This deformed spine model was used to perform rigid spine registration and initialize the vertebrae pose in deformable spine registration. We defined the reference frame of the injection device model at the center of the injector tube. Reference frames of spine vertebrae were manually annotated at the center of each individual vertebra in the pre-operative CT scan. Thus, the registration poses, such as $T_{Carm}^{ID}$, $T_{Carm}^v$ as defined in Section II-C refer to the rigid transformations from the simulated C-arm source to these reference frames. We report the registration accuracy based on our simulated “groundtruth” poses of the objects using $\delta T_{Carm}^{obj}={\left(T_{Carm}^{obj}\right)}_{gt}\cdot {\left(T_{Carm}^{obj}\right)}_{regi}^{-1}$, $obj\in \{ID,v\}$, where gt and regi refer to ground truth and registration estimation, respectively. We described the detailed simulation setup in the following subsections. Numeric results and statistical plots are presented in Table I and Fig. 5.

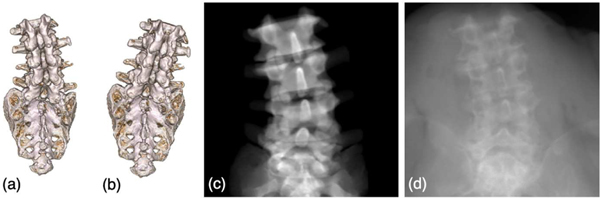
Fig. 6:

(a) Rendered vertebrae segmentation from pre-operative CT scans. (b) An example of randomly simulated spine shape. (c) An example DRR image of the spine vertebrae. (d) An example simulation X-ray image.

TABLE I:

Mean Registration Error in Simulation Study

		Translation Error (mm)	Rotation Error (degrees)
Single-View	Rigid Spine	4.8 ± 2.4	2.8 ± 1.7
	Vertb-by-Vertb	3.5 ± 2.9	1.1 ± 1.9
	Inj Device	2.2 ± 1.6	1.6 ± 1.4
	Joint Inj Device	1.7 ± 1.2	0.9 ± 0.9
Multi-View	Rigid Spine	3.7 ± 1.6	2.9 ± 1.2
	Vertb-by-Vertb	3.7 ± 1.6	0.9 ± 0.7
	Inj Device	3.7 ± 1.6	1.2 ± 1.3

Note: Vertb is short for vertebrae. Inj is short for injection.

Fig. 5:

Normalized 2D histograms of registration pose error ($\delta T_{Carm}^{ID}$, $\delta T_{Carm}^v$) reported in joint magnitudes of translation and rotation.

1). Single-view Registration:

We performed 2D/3D registration workflows of rigid spine, deformable spine and injection device by simulating single-view X-ray images. We also tested the proposed joint injection device registration by simulating three variant robot configurations under single-view C-arm geometry. These three device poses are jointly registered using the simulated relative robot configurations. For every registration running, uniformly sampled rotations from −5 to 5 degrees in all three axes were applied to the vertebrae segmentations. Random initializations of the spine and injection device were uniformly sampled including translation from 0 to 10 mm and rotation from −10 to 10 degrees. Table I summarizes the magnitudes of translation and rotation errors. The vertebrae error is computed as a mean error of vertebra S1, L2, L3, L4 and L5. We achieved a mean translation error of 3.5±2.9 mm and a mean rotation error of 1.1±1.9 degrees using vertebra-by-vertebra registration. The single injection device registration errors were 2.2 ± 1.6 mm and 1.6 ± 1.4 degrees, respectively. We achieved lower errors using joint injection device registration, which were 1.7 ± 1.2 mm and 0.9 ± 0.9 degrees, respectively.

2). Multi-view Registration:

Three multiple C-arm pose geometries were estimated with a uniformly sampled random separation angle between 20 and 25 degrees for the two side views. The three registration workflows tested in single-view were performed with the same settings under this multi-view setup. Both the vertebrae and the injection device registration accuracy was improved. The mean vertebra registration error was 0.8 ± 0.3 mm and 0.9 ± 0.7 degrees in translation and rotation respectively, and the injection device registration error was 0.2 ± 0.6 mm and 1.2 ± 1.3 degrees, respectively. Joint histogram of the translation and rotation errors are presented in Fig. 5. From the plots, we clearly observed the multi-view vertebrae and injection device registration has the best error distribution with the cluster close to zero errors.

C. Cadaver Study

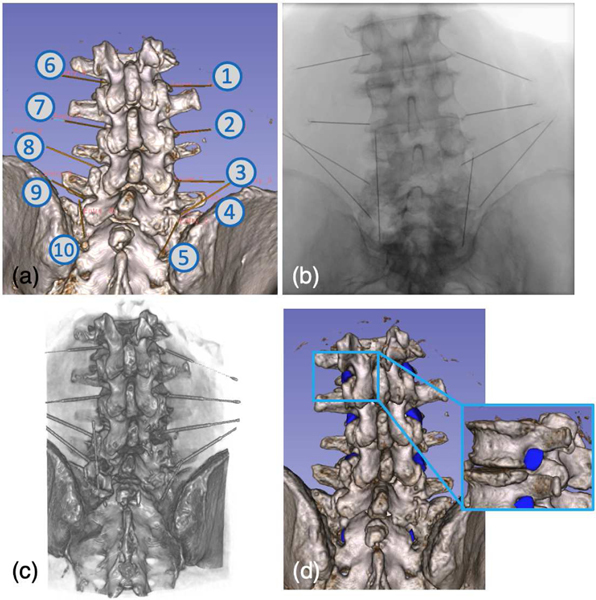
An injection plan on this specimen was made by an expert clinician who also performed the procedure according to this plan, allowing for comparison of performance to the robotic injection (Fig. 7 (a)). Ten injections were simulated via needle placement at five targets on each side of the specimen. Targets were the epidural spaces L2/3, L3/4, L4/5, L5/S1, and the first sacral foramen (Fig. 7) on each side. The target points were planned at the center of each safety zone.

Fig. 7:

(a) Screenshot of planning trajectories. (b) An example X-ray image taken after the robotic needle injections. (c) Rendering of the Post-operative CT scans. (d) Illustration of the manually labeled safety zones.

We performed needle injection with our robotic system according to this plan under X-ray image-based navigation. The registration workflow was initialized using the PnP solutions from eight corresponding 2D and 3D anatomical landmarks. 3D landmarks were annotated pre-operatively on the CT scans. 2D landmarks were annotated intra-operatively after taking the registration X-rays. For the purpose of needle placement validation in this study, a small deviation from the proposed clinical workflow was performed in which needles were left within the specimen after placement. This allowed for acquisition of a post-procedure CT to directly evaluate the needle targeting performance relative to the cadaveric anatomy with high fidelity. After the post-operative CT scan was taken, needles were removed and the needle placement was repeated by the expert clinician as his normal operation, using fluoroscopy as needed and another post-procedure CT was taken for evaluation. Fig. 7 presents rendering of the post-operative CT scan and an X-ray image taken after the robotic injection.

We reported the needle injection performance using three metrics: needle tip error, needle orientation error, and safety zone. The needle tip error is calculated as the l₂ distance between the planned trajectory target point and the injected needle tip point after registering vertebrae from post-operative CT to pre-operative CT. The orientation error was measured as the angle between trajectory vectors pointing along the long axis of the needle in its measured and planned positions. The results are summarized in Table. II. Our robotic needle injection achieved a mean needle tip error of 5.1 ± 2.4 mm and mean orientation error of 3.6 ± 1.9 degrees, compared to the clinical expert’s performance of 7.6 ± 2.8 mm and 9.9 ± 4.7 mm, respectively. The manually annotated safety zones in the post-operative CT scans are illustrated in Fig. 7 (d). All the injected needle tips, including both the robotic and clinician’s injections, were within the safety zones.

TABLE II:

Cadaveric Needle Injection Accuracy

ID	Needle Tip Error (mm)		Orientation Error (degrees)
	Robot	Surgeon	Robot	Surgeon
1	3.1	9.5	5.1	5.8
2	6.1	11.4	1.9	8.3
3	7.0	6.2	2.4	13.2
4	7.1	12.3	4.6	7.0
5	4.4	6.9	2.1	9.3
6	1.5	8.5	1.6	8.6
7	5.1	3.3	2.6	7.1
8	8.0	7.0	5.5	20.9
9	1.6	5.3	3.0	13.5
10	6.9	5.6	7.4	5.5
Mean	5.1 ± 2.4	7.6 ± 2.8	3.6 ± 1.9	9.9 ± 4.7

IV. Discussion

Our robotic needle injection system is fiducial-free, using purely image information to close the registration loop, automatically position the needle injector to the planned trajectory and execute the injection. The robotic needle injection was navigated using multi-view X-ray 2D/3D registration. For this application, our simulation study has shown that multi-view registration is significantly more accurate and stable than single-view registration in all the ablation registration workflows (Table. I). This is because multi-view projection geometries fundamentally improve the natural ambiguity of single-view registration. In this work, the multi-view C-arm projection geometries are estimated using the proposed joint injection device registration. In simulation, we have shown that this method is superior than single injection device registration in accuracy: the mean errors decreased from 2.2 mm, 1.6 degrees to 1.7 mm, 0.9 degrees in translation and rotation, respectively. This is because the joint registration of multiple injection device poses balances the ambiguity of single-view single object registration. The injection device was positioned close to the C-arm rotation center so that the C-arm detector can be rotated to large side angles while maintaining both the injection device and the spine vertebrae within the capture range. During the cadaveric experiment, the C-arm views were separate around 40–50 degrees. Large C-arm multi-view separation provides more image information from the side, which makes the multi-view registration more accurate. This change helps with registering the spine vertebrae which are small in size.

Our specially designed vertebra-by-vertebra registration solves the problem of spine shape deformation between pre-operative CT scan and intra-operative patient pose. In simulation, the mean multi-view registration error decreased from 3.7±1.6 mm, 2.9±1.2 degrees to 0.8±0.3 mm, 0.9±0.7 degrees in translation and rotation, using pre-operative rigid spine segmentation compared to multiple vertebrae. This registration algorithm decomposes the multi-component spine bone anatomy into automatically segmented rigid vertebrae pieces. The intra-operative spine shape can be reconstructed using the 2D/3D registration pose estimations. Accurate spine pose estimation is critical to the success of image-based navigation for this application.

Our cadaver study experiments show the feasibility of using our system for transformaminal lumber epidural injections. Our comparison study with an expert clinician’s manual injection using the same plan presents clear improvements in both translation and orientation accuracy: mean needle tip translation error of 5.1 ± 2.4 mm and 7.6 ± 2.8, mean needle orientation error of 3.6 ± 1.9 degrees and 9.9 ± 4.7 degrees, corresponding to the robot and clinician’s performance, respectively. The maximum needle tip translation and needle orientation errors of robot injection are 8.0 mm and 7.4 degrees, respectively. The experienced clinician’s performance showed corresponding maximum errors of 12.3 mm and 20.9 degrees, respectively. The standard deviation of both translation and orientation errors of robot injection are lower than those of the clinician’s injection. We also evaluated the performance using the defined safety zone for this application. Both the robotic and clinician’s injected needle tips laid inside the safety zones. Although the expert clinician’s injection tip error and orientation error are larger, this manual injection’s accuracy is still sufficient for this application. However, the robotic performance of higher accuracy and stability demonstrates potential reduction of the risk of violating the safety zone.

We also looked at the individual contributions of errors due to hand-eye calibration and registration. The needle tip error due to registration as compared to planning was 2.8±2.6 mm. The needle tip error resulting from hand-eye calibration was 2.5 ± 1.6 mm (Section. III-A). Our system testing result shows that the injection module tip precision is within the magnitude of 0.3 mm. This suggests that the potential needle tip deflection due to the relatively large distance between the tip and injection module is not significant. The other factor affecting the overall error is that we performed calibration only for one needle and did not repeat for successive injections with different needles. Calibrations after changing each needle may also help to reduce the reported translation error. The above system error investigation suggests that this non-purpose-built injection unit does not introduce significant system error due to its mechanical design. An improved injection device with smaller body, lighter mass and more rigid material would perform better.

One common concern of the fluoroscopic navigation system is the excessive radiation exposure to the patient. Our approach requires ten to twelve X-rays to register the patient to our injection device. Considering X-rays are commonly used in the clinician’s manual injections to check the needle position, this amount of radiation is acceptable for this procedure. Our pipeline is designed to be fully automated, however, our current implementation required a few manual annotations from the clinician to initialize the registration. Future work would consider automating the intra-operative landmark detection to further simplify the workflow, similar to our work reported in [21], [27].

In this study, needle steering was neglected. This is a widely studied topic, and such functionality could be added in future work and may improve results. The decision to not consider needle steering was made as 1) the focus of this work was on the novel application of the registration techniques used to the spine and correction via needle steering could mask inaccuracies of the registration. 2) The relatively large injection target area does not necessitate sub-millimeter accuracy. 3) The use of stiff low gauge needles in this application limits bending in soft tissue, reducing both the need for, and the effect of needle steering. We are aware that there are some studies of the clinical effects of spinal screw fixation [28] and needle steering [29], [30]. We want to emphasize that the clinical requirement of TLESI is positioning the needle tip within the safety triangle zone as introduced in Section I. Requirements of screw placement are more strict compared to our application. Based on our experiment results, deflection of the needle does not affect our accuracy to go outside the safety zone.

The current methodology design requires the patient to be stationary during the registration procedure without dealing with the potential patient’s motion before or during the needle injection. In the future, we plan to take more intermediate fluoroscopic images during the needle injection phase to verify the registration pose estimation. If the trajectory is detected to be off with respect to the plan, the needle can be moved out and redo the injection using the updated registration. We also plan to study modeling the needle steering behavior during insertion by performing more phantom study with soft tissue.

V. Conclusion

In this paper, we present a fluoroscopy-guided robotic spine needle injection system. We show the workflows of using multi-view X-ray image 2D/3D registration to estimate the intra-operative pose of the injection device and the spine vertebrae. We performed system calibration to integrate the registration estimations to the planning trajectories. The registration results were used to navigate the robotic injector to perform automatic needle injections. Our system was tested with both simulation and cadaveric studies, and involved comparison to an experienced clinician’s manual injections. The results demonstrated the high accuracy and stability of the proposed image-guided robotic needle injection.