Accurate age prediction from blood using a small set of DNA methylation sites and a cohort-based machine learning algorithm

Summary

Chronological age prediction from DNA methylation sheds light on human aging, health, and lifespan. Current clocks are mostly based on linear models and rely upon hundreds of sites across the genome. Here, we present GP-age, an epigenetic non-linear cohort-based clock for blood, based upon 11,910 methylomes. Using 30 CpG sites alone, GP-age outperforms state-of-the-art models, with a median accuracy of ∼2 years on held-out blood samples, for both array and sequencing-based data. We show that aging-related changes occur at multiple neighboring CpGs, with implications for using fragment-level analysis of sequencing data in aging research. By training three independent clocks, we show enrichment of donors with consistent deviation between predicted and actual age, suggesting individual rates of biological aging. Overall, we provide a compact yet accurate alternative to array-based clocks for blood, with applications in longitudinal aging research, forensic profiling, and monitoring epigenetic processes in transplantation medicine and cancer.

Graphical abstract

Highlights

• •AI-based analysis of 11,910 blood methylomes from donors aged 0–103 years
• •Identification of 80 age-associated DNA methylation sites
• •Non-linear non-parametric cohort-based regression models predict age from ≥10 CpG sites
• •Median prediction accuracy of 2.1 years from 30 sites, using arrays or NGS data

Motivation

Epigenetic clocks predict age from DNA methylation and are a valuable tool in the research of human aging, with additional applications in forensic profiling, disease monitoring, and lifespan prediction. Most existing epigenetic clocks are based on linear models and require hundreds of methylation sites. However, non-linear patterns of methylation changes across aging are observed for many CpG sites. Here, we present a compact epigenetic clock for blood, which outperforms state-of-the-art models using only 30 CpG sites. We also demonstrate the applicability of our clock to sequencing-based data, with far-reaching implications for a better understanding of epigenetic aging.

Using an extensive set of genome-wide DNA methylation samples, Varshavsky et al. train an AI-based model to predict chronological age from blood using few CpG sites, achieving a robust prediction accuracy of 2.1 years from 30 CpGs. Deviations between predicted and chronological age provide evidence of accelerated aging.

Introduction

DNA methylation is a stable epigenetic mark robustly maintained throughout life. Yet few CpG sites across the genome show gradual gain or loss of methylation during aging. Seminal studies by Hannum and colleagues¹ and by Horvath,² following earlier research of epigenetic changes with age,^3,4,5,6,7,8 demonstrated how such age-related changes could be used for chronological age prediction. These foundational studies used Illumina DNA methylation arrays, and integrated the methylation levels at a predefined set of 71 or 353 CpG sites (respectively) across the genome in a linear regression model to predict age, yielding impressive predictions. Intriguingly, these models assumed linear change of methylation with age,¹ but observed faster changes in DNA methylation levels until the age of 20 years, after which methylation levels were assumed to change at a constant rate throughout adulthood.²

The molecular mechanisms of aging are yet to be fully uncovered, and the factors that drive changes in DNA methylation with age are not completely understood. These changes may either be consistent and predictable, such as alterations in DNA methylation as a result of accumulating stress,⁹ or spontaneous and unpredictable, such as under-performance of the DNA methylation maintenance system after DNA replication.¹⁰ More recent studies suggested that T and NK cell activation could serve as a driver of change of the epigenetic landscape.^11,12

Epigenetic clocks are a valuable tool in the research of human aging and the genetic and environmental factors that influence it.¹³ In addition to opening a unique window for research opportunities, the prediction of chronological age from methylation data may have applications in multiple fields, such as analysis of DNA samples from crime scenes; indication of poor health and all-cause mortality prediction using an “age acceleration” metric, defined as the difference between chronological and predicted age^14,15,16,17; identification of early graft-versus-host disease in organ transplant recipients¹⁸; and more.

New and improved epigenetic clocks for chronological age prediction have been developed in recent years, using alternative sets of age-correlated CpG sites, informative of age. Most clocks were developed as a linear model based on the Illumina 450K BeadChip platform, some using hundreds of CpG sites,^19,20 and others using only a few CpGs.^21,22 Few non-linear models were introduced, including those using neural networks.^23,24,25 The high cost of the Illumina BeadChip platforms, compared with targeted sequencing via targeted-PCR or capture panels, hinders accessible use of such chronological age predictors, and thus several less-accurate clocks trained on small pyrosequencing datasets with few CpG sites were also proposed, mostly for forensic applications.^{22,26,27,28,29} Additionally, developments in single-cell DNA methylation assays recently led to novel epigenetic clocks for mice.^30,31 As these data are extremely sparse, typically with a whole-genome coverage of 0.25x per cell, estimating the methylation level of individual CpG sites is almost impossible and alternative approaches based on multiple CpG sites were developed in these works.^30,31

In addition to chronological age predictors, the field of biological age prediction recently gained much attention. These models integrate DNA methylation data with additional clinical biomarkers to predict an individual’s healthspan and lifespan, including their risk for mortality, physical functioning, cognitive performance, and more.^17,32,33 While these models provide a broader view on health and aging, they do not serve the same purpose as chronological age predictors, and are limited to a small number of donors for which multi-omics integrative data were collected, as well as detailed clinical information.

In this work, we present GP-age, a non-parametric cohort-based epigenetic clock for chronological age prediction from blood samples, based on Gaussian process regression (GPR) models. We collected a large cohort of 11,910 human blood methylomes, measured for healthy individuals at a wide variety of ages, and identified a compact set of age-related CpGs. Given a query blood sample, the methylation levels at these sites are compared against the training cohort, and the ages of similar samples are integrated to predict age. As we show, using only 10 to 30 carefully selected CpGs, GP-age outperforms larger state-of-the-art models. Finally, we demonstrate the applicability of GP-age to studying aging using methylation arrays or targeted sequencing data, providing an accessible and accurate alternative to current clocks and opening new avenues for the study of epigenetic changes at multiple neighboring age-related CpG sites.

Results

A dataset of 11,910 blood-derived methylomes of healthy donors across various ages

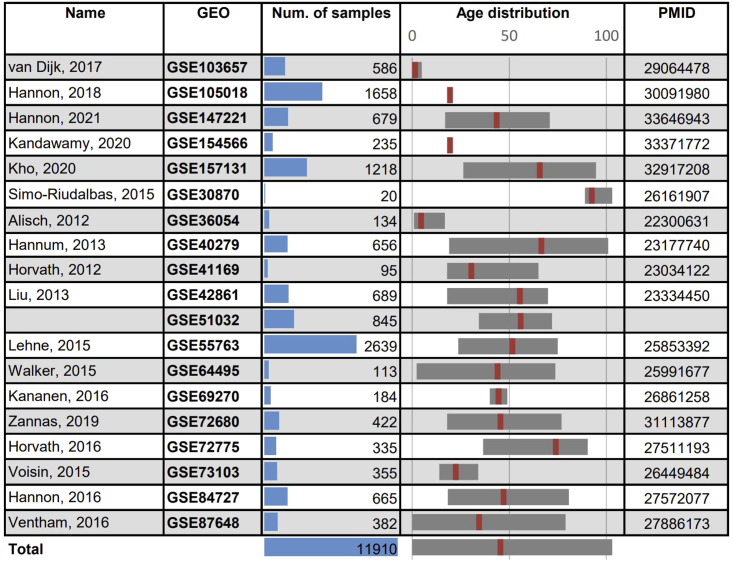
We assembled a large dataset of publicly available blood-derived methylomes from 19 genome-wide methylation array studies, obtained from blood samples in a variety of ages and scenarios.^{1,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51}

Overall, our data contains 11,910 blood methylomes, from donors aged 0–103 years (Figure 1). One of these studies,⁵⁰ a large dataset (n = 665) that spans a wide range of ages, was selected as a held-out independent validation set, to unbiasedly assess our prediction results. Importantly, this database was not included in the training of previously published epigenetic clocks, allowing a direct and unbiased comparison between GP-age and other state-of-the-art models.^1,2,19

Figure 1.

Description of datasets

A total 11,910 blood methylomes were collected from 19 studies. Shown are publication names, GEO accessions, number of samples per dataset, age ranges (median age marked in red), and PMID numbers.

Samples from all other studies were randomly split into a training set cohort (70%, total of n = 7,860 samples) and a held-out test set cohort (30%, n = 3,385 samples). The train and the test sets show similar age distributions across all datasets. All methylomes were used as published, following their original preprocessing and normalization by various methods.^{1,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50}

Selection of age-associated CpG sites

We aimed to identify a set of CpG sites that are highly informative of age. For this, we calculated the correlations between chronological age and methylation levels in train set samples across datasets. Spearman rank correlation was specifically used to not assume linearity (as in Pearson correlation). Other measures (e.g., mutual information) were also tested, but did not reveal additional non-monotonic sites, informative of age.

To avoid age-related sites that change at a slow rate, therefore relying on accurate estimations of DNA methylation levels and thus requiring deep sequencing depth, we preferred CpG sites whose overall methylation gain/loss during adulthood is above 20% (Figure 2E; STAR Methods). It should be emphasized that samples from the held-out validation set (GSE84727) were strictly excluded from these feature selection processes.

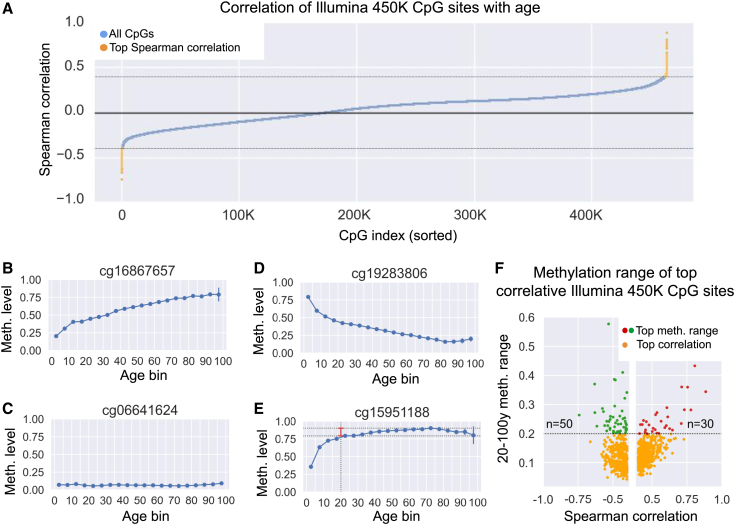
Figure 2.

Selection of the age set CpG sites for GP-age

(A) Shown are Spearman correlation coefficients for all CpGs from the BeadChip 450K array (blue dots) calculated across training samples ≥20 years old. A total of 964 CpGs with absolute Spearman coefficients ρ ≥ 0.4 were selected for further analysis (yellow dots).

(B–E) Example of average methylation levels across aging, for four CpG sites. For each 5-year bin, shown are the average methylation levels (blue dots; vertical bars show 95% confidence intervals, CI). Dashed lines and red vertical bar (E) mark the 20–100 years methylation range. CpGs with low methylation range (i.e., flat slopes) offer limited age-predictive value and are not included in our age set (e.g., cg06641624 [C], cg15951188 [E]). Conversely, dynamic sites (e.g., cg16867657 [B], cg19283806 [D]) offer high predictive value. (B) A CpG with positive age correlation: Spearman ρ = 0.88, meth. range = 0.34. (C) A non-age-correlated CpG: Spearman ρ = −0.01, meth. range = 0.04. (D) A CpG with negative correlation: ρ = −0.74, range = 0.26. (E) Age-correlated CpG (ρ = 0.4) with meth. range = 0.11 (not selected).

(F) Comparison of correlation (x axis) vs. the methylation range (y axis). CpGs with range ≥0.2 are shown in red (ρ ≥ 0.4, n = 30 CpGs) or green (ρ ≤ −0.4, n = 50 CpGs). Eighty of 964 age-correlated CpGs were selected.

Specifically, we analyzed the train set samples across all 485,512 BeadChip 450K array CpGs, retained CpGs with ≤20% of missing values across samples, and calculated their correlation with age (Figure 2). CpG sites with absolute Spearman correlation ≥0.4 were selected for further analysis (all showing FDR-corrected p values ≤1e-200). We then computed the methylation range for each CpG, defined as the difference between maximum and minimum methylation values in adulthood, and removed CpGs with span ≤20% (Figure 2E). Overall, our feature selection stages concluded in 80 age-related CpG sites (Figure 2F). These CpG sites are indicative of age and are robust to sequencing noise (STAR Methods). Selecting alternative thresholds (at each stage of our selection process) did not greatly change the results below.

Aiming to develop a compact model applicable to targeted multiplex bisulfite PCR sequencing, we wished to further reduce the number of CpG sites used. For this, we clustered the candidate CpG sites by their methylation levels across samples to k = 30 clusters, and selected the most age-correlated CpG from each cluster (STAR Methods). Intuitively, CpGs from the same cluster show similar methylation patterns, and therefore contribute little additional information.

Gaussian process regression models

We then integrated the k = 30 CpG sites into a non-parametric cohort-based Bayesian age predictor, based on GPR models (Figure 3A). This is a flexible class of models, estimating the probability distributions over a continuous feature (e.g., chronological age) across multiple (possibly infinite) functions that fit the input data. Unlike parametric regression models (e.g., linear regression models, which assume a constant rate in methylation changes), GPs do not define priors over the parameters of a given set of functions, but rather a distribution over multidimensional functions that are not explicitly defined.⁵² Moreover, as these basis functions are not limited to linear functions, they do not require that non-linear corrections, such as Horvath’s mAge transformation,² be applied in the preprocessing step.

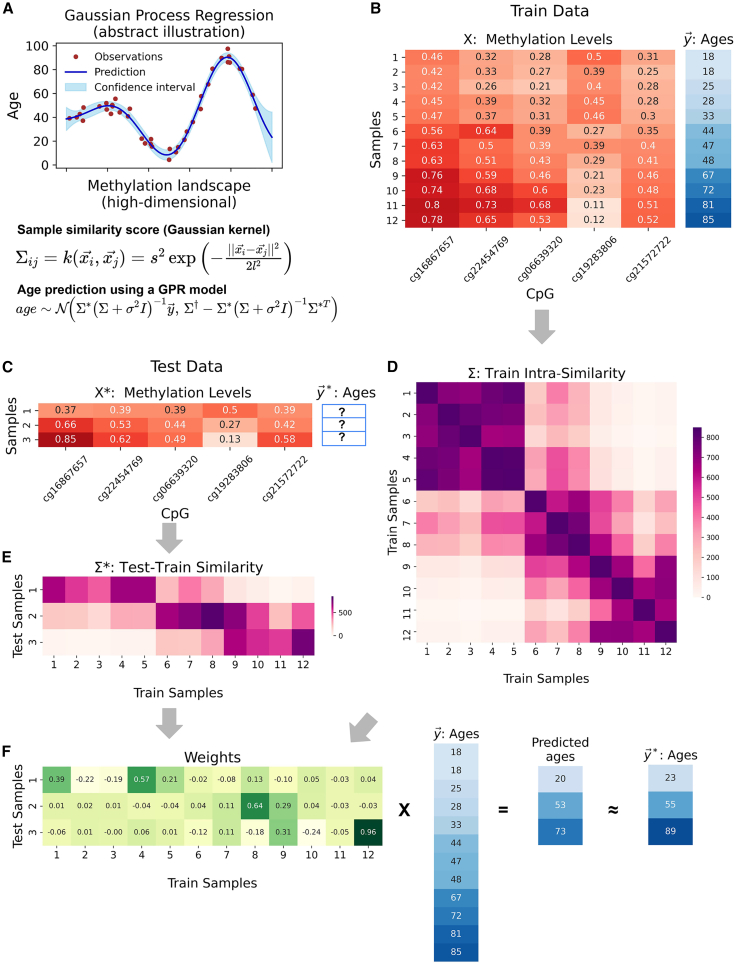
Figure 3.

Gaussian process regression model

(A) Abstract visualization of a GPR. Shown are example observations (red dots), along with the predictions (blue line) and confidence intervals (light blue strip) of the Gaussian process, which is a distribution over possible regression functions from the methylation vectors to chronological age. The Gaussian kernel defining the GP and the distribution of age predictions is shown below.

(B–F) Toy example of age prediction for three samples based on five CpG sites and a cohort of 12 training samples (from real data). (B) Shown is a cohort of 12 train samples, containing methylation levels of five CpG sites, along with the donor ages. (C) Three test samples (methylation vectors over the same five CpG sites) are shown. The chronological ages of the samples are unknown. (D) The cohort intra-similarity matrix, as calculated with the optimized Gaussian kernel function. (E) The similarity matrix between the test and the train set samples, as calculated with an optimized Gaussian kernel function. (F) The weights assigned to each cohort sample by each test sample are shown, with the resulting final prediction along the real ages of the test samples.

In practice, it is easier to think of GP models in their dual representation: Gaussian kernels are used to measure the similarity across the DNA methylation patterns of train set cohort samples, resulting in the intra-similarity covariance matrix. Given test set samples, the model calculates their similarities to each of the train set samples, which are normalized by the covariance matrix. This results in a weight matrix that associates each test sample to train set samples that show similar methylation patterns. Finally, these samples are weighted and combined to predict the age of each test sample (Figures 3B–3F).

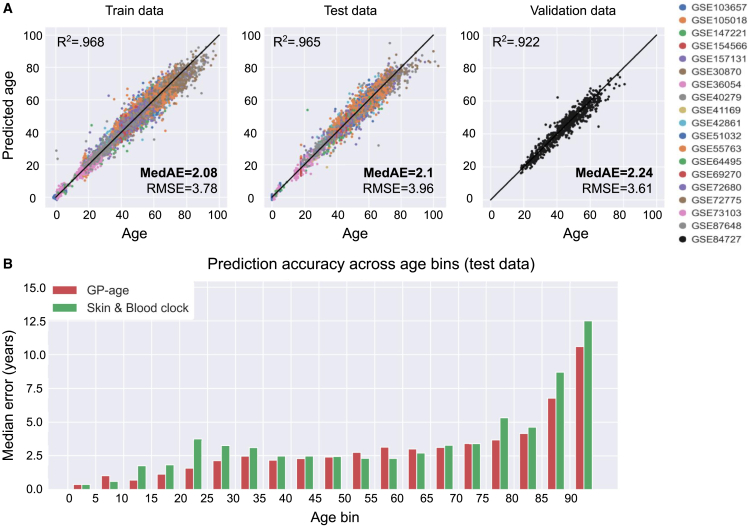
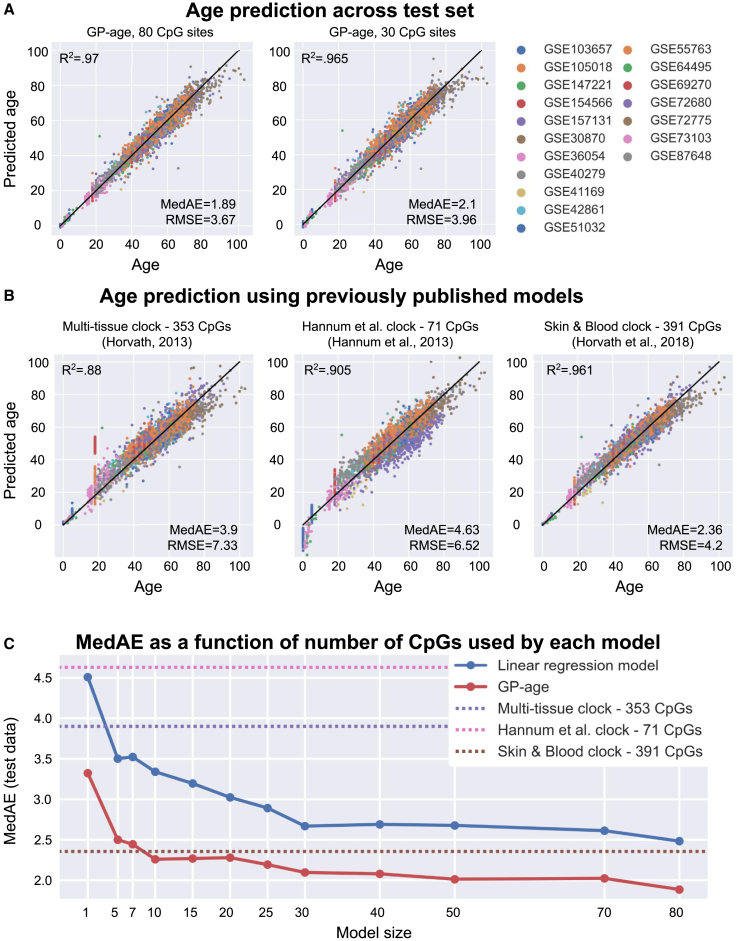
The accuracy of our age prediction model, GP-age, was evaluated by computing the root-mean-square error (RMSE), which provides a good estimator for the standard deviation of prediction errors. For direct comparison with previous works, we also calculated the median absolute error (MedAE) in years. First, we evaluated the accuracy of the predictions of GP-age with 30 CpGs on the train (7,860 samples from 18 datasets) and held-out test samples (3,385 samples from 18 datasets), resulting in MedAEs of 2.08 and 2.10 years, respectively (Figure 4A). RMSE estimations were also very similar between the two sets (3.78 years, train; 3.96 years, test), suggesting that the regression model did not overfit. Importantly, similar accuracy was achieved for the held-out validation set (665 samples from GSE84727), with a median error of 2.24 years, and RMSE of 3.61 years (Figure 4A). Repeating this procedure with other held-out datasets showed similar results (Figures S1 and S2). In agreement with previous works,^1,27,53 the prediction accuracy of GP-age decreases as age increases, as demonstrated by measuring the average prediction error across 5-year bins (Figures 4B and S3).

Figure 4.

Prediction accuracy of GP-age with 30 CpGs

(A) Chronological age vs. predicted age of GP-age with 30 CpGs, across train, test, and validation (GSE84727) set samples, yielding a median error of ∼2.1 years, and an RMSE of ∼4 years, across different datasets (colors). Coefficient of determination R² between prediction and age, RMSE, and MedAE are shown.

(B) The median error of GP-age with 30 CpGs (red) and the Skin&Blood (green) methylation clocks across different 5-year bins of donor ages.

Comparison with state-of-the-art age prediction methods

We next turned to analyze chronological age predictions of the test cohorts using published state-of-the-art models, including the 353-CpG multi-tissue clock,² the 71-CpG methylation clock by Hannum et al.,¹ and the 391-CpG Skin&Blood clock.¹⁹ As Figures 5B and 5C show, these models achieve median errors of 3.9, 4.63, and 2.36 years, respectively, compared with a 2.1-year error by the 30-CpG GP-age model, or a 1.89-year error by the 80-CpG GP-age model. GP-age also outperforms these models on the independent validation set, with a median error of 2.24 years, compared with 6.01, 3.01, and 7.24 years, respectively (Figure S4C). It should be noted that GP-age is more accurate than the Skin&Blood model on young samples (aged 10 through 35) as well as older ones (70 through 95), and is similarly accurate on samples aged 40–45 (Figures 4B, S3, and S5).

Figure 5.

Prediction accuracy of GP-age of different sizes and of state-of-the-art models

(A) Age vs. age prediction across test set samples. MedAE of GP-age is ∼2 years and RMSE is <4 years across the different datasets (colors). Increasing the size of the model increases its accuracy. Black line: y = x.

(B) Age vs. age prediction by previously published models across test set samples. Predictions are less accurate than GP-age across different datasets. Color legend is the same as in (A).

(C) Using only 30 CpG sites, GP-age (red) is more accurate than previously published models (horizontal dotted lines), and simpler models trained on the same set of CpG sites (linear regression model in blue). Increasing the model size increases the accuracy.

Other models, including Vidal-Bralo et al.,²¹ were also compared with GP-age, and were shown to be less accurate (Figure S6). Unlike most previous models, the clock by Zhang et al.²⁰ was trained on an impressively large dataset (∼13K samples), including the Lothian Birth Cohorts data.^54,55 While our results show that GP-age offers higher accuracy than all these models, including Zhang et al. (514 CpGs, MedAE ≥8 years) it is possible that this model is tailored to older samples and will be more suitable when applied to special age distributions. Additional chronological age predictors that use 1,000 CpGs or more were not compared, as they are outside the scope of this manuscript.^20,23,24,25

Model complexity vs. accuracy

Next, we wished to study how the number of CpGs in the GPR models affects their predictive power. Different model sizes were tested by clustering to k clusters and choosing the most age-correlated CpG from each cluster (STAR Methods). We therefore examined a range of models varying from the full model of k = 80 CpG sites, to the single CpG model at k = 1. Remarkably, a GPR model with a single CpG (ELOVL2) achieves a MedAE of 3.3 years, whereas a model with k = 10 CpGs outperforms all state-of-the-art models, with a median error of 2.26 years. Overall, the 30-CpG GP-age model allows an optimal tradeoff between prediction accuracy (2.1 years) and compactness, and is comparable to the k = 50 and k = 70 models (Figure 5C), as well as the full k = 80 CpGs model (1.89 years). Similar results are reported when using the RMSE and MeanAE metrics (Figure S5), and on the held-out validation cohort (Figure S7).

To ensure statistical stability, we applied 10 stratified 4-fold cross-validation runs for each value of k, resulting in an estimated error of <0.01 for the reported MedAE for each model. In addition to estimating RMSE and median error (50^th percentile of predictions), we also estimated the prediction errors at the 25th, 75th, and 90th percentiles of samples (Table S1). Across all percentiles, GP-age consistently outperforms all other models.

Comparison with non-GPR models and alternations of the feature selection processes

Finally, we compared the GP models of different sizes with linear regression models, similar to the ones used by previously published clocks (Figure 5C, blue). For all model sizes, linear models were consistently less accurate than the non-linear cohort-based model, while using the exact same sets of CpGs. For example, using the set of 80 CpGs sites we selected, a linear regression model with elastic net regularization (as used by Horvath’s multi-tissue clock and other models) achieves a MedAE of ∼2.5 years, similar to that of the Skin&Blood linear model (391 CpG sites). These predictions are outperformed by our cohort-based non-parametric GP-age model, which obtains a median error of 1.89 years, using the same set CpG sites. Similar trends were obtained for other sets of CpGs (Figure 5C, blue), with or without Horvath’s non-linear age transformation (mAge).²

Additionally, we trained a non-linear generalized additive model (GAM), where age-related changes in DNA methylation are modeled using a non-parametric spline (for each CpG site), and are later integrated into a linear additive model. Intriguingly, these models outperformed all linear regression models, but were generally less accurate than the cohort-based GP-age models (using the same training and test data, based on the same sets of age-related CpG sites). Specifically, the GAM model shows a median error of 2.19 years (RMSE of 4.17 years) compared with a median error of 2.1 years (RMSE of 3.89 years) by GP-age.

To demonstrate the advantage of clustering, where a single representative CpG is selected from each group of highly correlated sites, we also compared the GP-age models with a GPR model trained on the top-k age-correlated CpG sites (without clustering). For all values of k ≤ 30 CpGs, the clustering-aware sets outperform the top-k sets (Figure S8).

Retraining GP-age with the validation set

After observing similar prediction accuracy on held-out test data and three independent validation sets (Figures 4A, S2, and S4), we hypothesized that the model is general enough and invariant of different dataset normalizations, and thus combined all 19 datasets for an improved GP-age model. Samples were partitioned into test (30%, n = 3,573) and train (70%, n = 8,337) sets, and GP-age models trained as described above. Overall, we identified 1,034 age-correlated CpGs (|⍴| ≥ 0.4, Table S2), 71 of which with methylation range ≥0.2. These were clustered, and updated sets of CpGs were selected (Table S3). Intriguingly, for k = 30, 27 of the 30 CpGs overlap with the previously selected model, supporting the robustness of the feature selection process. Overall, this model resulted in a median train error of 2.06 years (RMSE = 3.74), and a median test error of 2.10 years (RMSE = 3.89), using 30 CpGs. Downstream analyses (on held-out test data or external samples), were all performed using these full GP-age models.

Consistent prediction errors may reflect biological age

To detect consistent prediction errors that may reflect differences between chronological and biological age, we trained three independent GPR models. For this, the 71 age-correlated CpGs were split into three independent groups of 19, 33, and 22 CpGs, selected from disjoint sets of chromosomes, and three independent GPR models were trained (Table S3). The three models show MedAEs of 2.45, 2.42, and 2.75 years, respectively, on held-out test data. Importantly, the models are as correlated with age as they are with each other (Figure S9).

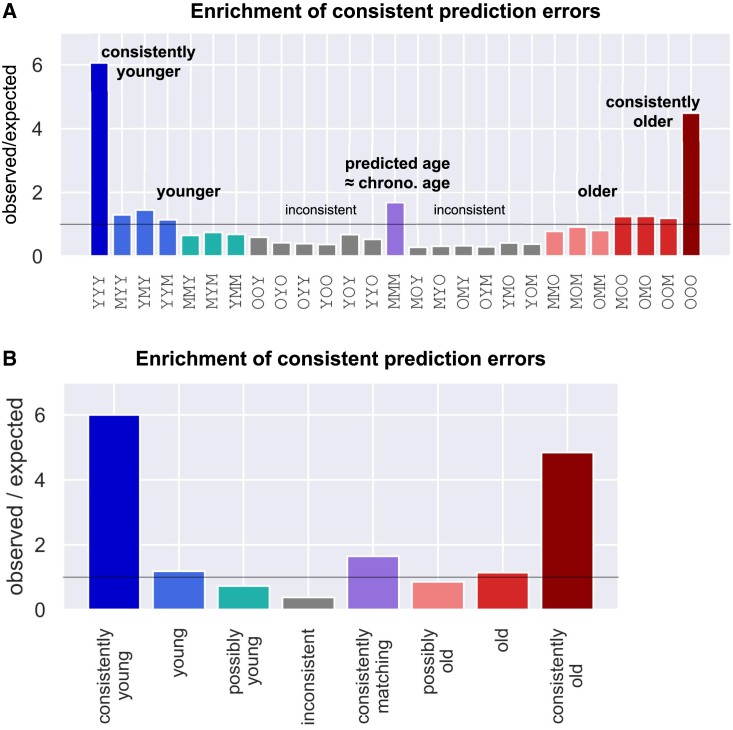
We next analyzed the pattern of prediction errors across these three independent clocks, and focused on prediction errors larger than the MedAE of each model (Figure 6). Intriguingly, 8.5% of donors were predicted to be younger than their chronological age by all three models, a 6-fold enrichment compared with only 1.4% that are expected under a null error model (binomial p value ≤ 2e-133). Similarly, 7.5% of samples are consistently predicted as older, a 4.5-fold enrichment compared with the 1.7% expected (pvalue ≤ 2e-88). Statistically significant enrichment was also observed for donors consistently predicted to match their chronological age (21% observed, 12.5% expected, p value ≤ 3e-46). No enrichment was observed for donors with mixed predictions (Figure 6). These results suggest that most donors (83%) who are predicted to be younger than their age by all three clocks cannot be explained by the background model. Similarly, 77% of the donors consistently predicted as older may reflect a true deviation between their chronological and biological ages.

Figure 6.

Consistent prediction errors across independent GPR models suggest biological variance

(A) Three independent GP-age models were trained using CpGs from different chromosomes, and applied to test set donors. Epigenetic age was then compared with chronological age, and deviations greater than the median absolute error (per clock) were marked. Blue bar (left) reflects a 6.06-fold enrichment of donors consistently predicted as younger (8.5% of test samples, compared with 1.4% expected by random). Similarly, the burgundy bar (right) reflects 4.48-fold enrichment for consistently older samples (7.5% compared with 1.7%), and lilac bar (center) reflects a 1.68-fold enrichment for consistently accurate predictions by all three clocks (21% compared with the expected 12.5%). Other bars correspond to inconsistent predictions.

(B) Same as (A), after binning of similar patterns: “young” and “old” bins contain cases where one clock matches chronological age, whereas the other two clocks consistently deviate; “possibly young” and “possibly old” bins for two age-matching clocks and one younger/older prediction; and the under-represented class of “inconsistent” for other combinations.

Methylation trends of clock CpG sites

To better understand the age-related dynamics of the 71 CpG sites in GP-age, we divided the CpG sites into those gaining methylation over age (n = 33) and those losing methylation (n = 38). Intriguingly, while both positively and negatively age-correlated sites were identified, we observed a small enrichment for CpG sites that gain methylation with age (Figure S10A). Accordingly, when training two separate models, the epigenetic clock that uses positively correlated (“gaining”) sites shows a higher accuracy than the one based on negatively correlated ones (“losing”) (Figures S10B and S11), with median errors of 2.54 and 3.45 years, respectively. Interestingly, the gap between the two clocks becomes smaller when the ELOVL2 CpG site cg16867657 is excluded from the positive set, leading to a median error of 2.83 years. These results suggest that age-related changes in DNA methylation involve both hyper- and hypo-methylation.

Accurate age predictions from whole-genome bisulfite sequencing data

Encouraged by these results, we wished to establish our 30-CpG epigenetic clock in sequence-based DNA methylation data from blood, in addition to methylation array data as previously shown. Unlike methylation arrays, whole-genome bisulfite sequencing (WGBS) methylation data are relatively shallow with typically no more than 30 sequenced reads (fragments) covering each CpG (30x). Yet, neighboring CpG sites are also sequenced and could be an additional source of data, at least in genomic regions with block-like methylation patterns.^56,57,58,59 We therefore turned to test the performance of GP-age on such data, which could pave the way for capture panels or targeted-PCR sequencing-based epigenetic clocks.

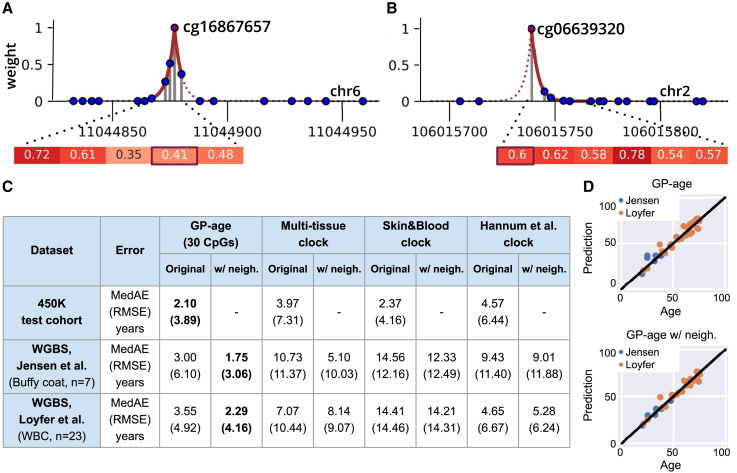
GP-age with 30 CpG sites was applied to two blood WGBS datasets. Initially, average methylation was calculated at k = 30 CpGs of the GP-age model, and age was directly predicted. As Figure 7 shows, this resulted in a median error of 3.0 years (RMSE = 6.10) on buffy coat methylomes sequenced by Jensen et al. at 29x depth from n = 7 donors aged 20–47.⁶⁰ We also applied GP-age to a set of n = 23 deeply sequenced (83x) leukocyte methylomes of donors aged 21–75, recently published by us,⁵⁹ resulting in a median error of 3.55 years (RMSE = 4.92).

Figure 7.

Weighted average of neighboring CpG sites in WGBS data

(A and B) Each target CpG expanded to include neighboring CpG sites, using a predefined segmentation of the human genome into consecutive sets of methylation blocks, concordantly methylated across all cell types,⁵⁹ typically with fewer than 20 CpGs per block. A Laplace kernel (red line) was used to assign decaying weights for neighboring CpGs, based on their distance from the target CpG (solid red line). Methylation levels of CpG sites in the neighborhood are shown below.

(C) RMSE and MedAE errors of GP-age and reference models (with and without neighbors), across datasets. The lowest error for each dataset is marked in bold.

(D) Age prediction across the two sequencing datasets. Top: Using a single CpG resolution methylation level for each CpG from the age set. Bottom: Using a Laplace kernel for a methylation level estimation by a weighted average of methylation levels of neighboring CpGs.

Encouraged by these results, we wished to incorporate the methylation values of neighboring CpG sites to compensate for the relatively low coverage of the data. For this, we segmented the human genome (hg19) into homogeneous methylation blocks,⁵⁹ and averaged the target CpG with surrounding sites (typically less than 10–20 such sites), weighted using an exponentially decaying Laplace kernel, based on their distance from the target CpG (STAR Methods). The resulting average was then used as a noise-reduced approximation for the methylation level of each target CpG. As Figure 7 shows, this further improved GP-age’s predictions on WGBS datasets, yielding a median error of 1.75 years on the Jensen et al. dataset,⁶⁰ and 2.29 years on the Loyfer et al. dataset.⁵⁹ The difference in accuracy between the two datasets could be explained by the different ages in the two datasets (Figures S12B–12D). This again is consistent with the previously reported decrease in the accuracy of epigenetic clocks as age increases.

Notably, previously published array-based methylation age models^1,2,19 all showed higher errors of 5–15 years for the two datasets (Figure 7C). We reason that this is partly due to age-correlated CpG sites that do not change greatly overall (low methylation range), and are therefore hard to approximate at WGBS sequencing depths. Other age prediction models used pyrosequencing data^22,27,29,61 at few CpG sites, mostly for forensic use. GP-age with 30 CpGs outperforms these models as well (Figure S12A).

Discussion

In this article we present GP-age, a non-parametric cohort-based chronological age prediction model, and compare it with previously published state-of-the-art models. While other epigenetic clocks were developed for different tissues, or as multi-tissue predictors, in this work we focus on whole blood, as it is easily accessible. Future work may be to apply a similar method to develop GP-based epigenetic clocks for other tissues and organisms.

GP-age uses a cohort of 11,910 blood methylomes, measured using Illumina BeadChip 450K/EPIC methylation arrays. These are made available as a resource to the methylation age community. Samples from various cohorts were merged, and split into test and train sets. Sets of non-redundant age-correlated CpGs were then selected. In this cross-cohort analysis, we specifically did not renormalize samples from different datasets, so CpG sites with batch differences were implicitly selected against. We then trained a non-parametric GPR model, which uses these CpGs to compare a query sample against the train set cohort, find similar methylomes, and predict the query age based on train set ages and intra-cohort dependencies.

As we show, A 30-CpG GP-age model achieves a MedAE of 2.1 years across 3,573 held-out test samples, outperforming state-of-the-art methods (on the same data). An even more compact model, consisting of only 10 CpGs, is comparable to state-of-the-art clocks with a median error of 2.26. Similar results were achieved on parallel GP-age models, for which one of the datasets was considered as a validation set, and its samples were excluded from feature selection and model training (Figures 4A and S2, showing three different such validation sets).

Depending on the desired model size and accuracy, 10-, 30-, or 71-CpG GP-age models are suggested for age prediction, as these models provide a good tradeoff between compactness and accuracy. As we further show, the model is also applicable to next-generation sequencing data, where a Laplace kernel is used to augment the methylation levels of the age prediction CpGs by their neighboring CpGs. This resulted in a similar prediction accuracy of ∼2 years.

It shall be noted that previous studies presented highly compact chronological epigenetic clocks, sometimes involving as few as three CpGs. Nonetheless, these compact models presented inferior accuracy, with MedAEs of 5–21 years on our Illumina 450K and sequencing data.^{21,22,26,27,28,61} Conversely, we provide an epigenetic clock that is more accurate than commonly used models,^1,2,19 and at the same time compact enough to allow direct measurement using multiplex targeted-PCR, making these models simpler and more accessible compared with DNA methylation arrays.

Overall, GP-age predictions of chronological age outperform current state-of-the-art models while using fewer CpG sites, thus opening the way for various applications in aging, forensics, transplantations, or more, using low-cost capture-based or targeted-PCR sequencing data. Previous models assume linear change of methylation with age, and utilize linear regression models for age prediction. As we show, implementation of linear models similar to those used by Horvath^2,19 and Hannum et al.¹ that were trained and evaluated on the same data as GP-age, were found to be less accurate than GP-age (Figure 5). Interestingly, using other non-linear models, such as k-nearest neighbors (KNN) and GAM, resulted in epigenetic clocks that are more accurate than the linear regression models, emphasizing the importance of the relaxation of the linearity assumption, but slightly less accurate than GP-age.

These results were achieved by three independent means. First, we selected a set of CpG sites whose average methylation changes with age. As we showed, using these sites to train a linear regression model, similar to the ones used by Horvath^2,19 and Hannum et al.,¹ already achieves a MedAE of 2.70 years. The compactness of the model is achieved by selecting one representative from each cluster of correlated CpG sites, thus minimizing similarities between model CpGs. Second, we assembled a large training cohort that allows cohort-based models to identify similar methylomes for each query set. Third, GPR models add accuracy by not being limited to a fixed number of neighbors (as in KNN), and use intra-cohort similarities to further determine how these samples are weighed. Thus, through a more complex assignment of weights to the training set samples, GP-age utilizes more information from the cohort, resulting in higher accuracy.

Several of the CpG sites that were automatically selected by our model are known to be associated with age-related genes or have been previously included in epigenetic clocks. Most notable is ELOVL2,^1,62,63 single-handedly providing a MedAE of 3.3 years in our cohort-based algorithm. Intriguingly, exclusion of ELOVL2 resulted in a median error of 2.49 years using a GP-age model with 10 sites (and 2.28 years using 30 sites). Additional genes were previously associated with aging, including FHL2,^1,19,62,63 OTUD7A,^1,63 CCDC102B,^1,63 TRIM59,^1,19,64 RASSF5,⁶⁵ GRM2,⁶⁶ ZEB2,^67,68 Zyg11A,⁶³ TP73,⁶⁹ IGSF11,⁷⁰ MARCH11,⁷¹ SORBS1,⁶⁶ ANKRD11,⁷² and EDARADD.^1,2,19,73 The remaining CpGs, including cg20816447 (CC2D2A), cg06155229 (PMPCB), cg06619077 (PDZK1IP1), cg19991948 (TIAL1), cg22078805 (FAM171A2), and cg17621438 (RNF180), were not, to the best of our knowledge, previously associated with aging and should be further studied. It shall be noted that similar to other studies of methylation clocks, our method for CpG selection relies on high correlation with age. Future research might shed light on the causative role of these CpGs.

The set of CpG sites used by GP-age consists of both methylation-gaining and methylation-losing sites. Intriguingly, a GPR model that uses only methylation-gaining CpGs predicts age better than a GPR model that uses only methylation-losing CpGs (Figures S10 and S11). This observation is still valid when the ELOVL2 CpG is excluded, and raises questions regarding the biochemical processes that underlie the changes of the epigenetic landscape with age.

Age prediction errors across multiple samples are often summarized as the MedAE, which could be somewhat different from the RMSE. While the median error provides an upper bound of the error for half the samples (regardless of the other half), the RMSE score provides the standard deviation of predictions across all samples. The differences between RMSE and MedAE scores are observed in the prediction statistics of both the array-based models (Figure 7C) and the targeted-PCR-based models (Figure S12A). For GP-age and the array-based models, these differences are partially explained by the lower accuracy achieved for older ages (Figure 4B), in agreement with previous studies.^1,27,53 Importantly, GP-age outperformed state-of-the-art models in both measures.

We show that both GP-age and the Skin&Blood clocks are more accurate on younger samples, with the highest improvement by GP-age achieved on ages 10–45 and 70–95 (Figure 4B). Importantly, specific models explicitly trained on target age groups did not improve the prediction accuracy. Similarly, female- or male-only clocks have not obtained higher accuracy on held-out test data (data not shown). These results suggest that the methylation clock presented here reflects universal processes involved in aging.

GP-age also showed increased accuracy when predicting age from next-generation sequencing data. Here we augment this information by incorporating neighboring CpGs, with their importance decaying exponentially the farther they are from the target CpG site (Figure 7). This, combined with the small set of CpGs, suggests that GP-age could be used to predict chronological age from blood samples using sequencing data, including genomic DNA enriched by hybrid-capture panels for specific age-related regions, or even multiplex targeted-PCR data, which are more accessible than methylation arrays, and with shorter turnaround time.

As we show, methylation arrays provide extensive information regarding the methylation landscape of a given sample, but for the purposes of chronological age estimation, a small set of CpGs suffices. Future research should validate GP-age on targeted-PCR data. Notably, GP-age shows higher accuracy than forensic age prediction models^22,27,29,61 when tested on identical sequencing data. Additionally, the developing field of single-cell DNA methylation, as well as single-cell epigenetic clocks recently published for mouse models,^30,31 raises interesting questions regarding age prediction from such data, often spanning the entire genome at an extremely low sequencing depth of 0.25x or less, per cell. We hypothesize that non-linear cohort-based GPR models could be applied to such datasets, but this will require much larger sets of age-correlated genome regions, as well as a considerably larger training set of human donors with single-cell DNA methylation data.

Notably, the improved predictions in WGBS samples using information from neighboring CpG sites suggests that aging-related epigenetic changes occur—at least for some genomic loci—at DNA methylation blocks,^56,59 rather than at isolated independent CpGs (as may seem from DNA methylation array data). Further, this raises questions regarding the underlying processes of epigenetic aging. A possible research direction may be the examination of the recruitment of methylases and demethylases to specific loci, their dynamics, their processivity across neighboring sites, and how these change with age.

Most importantly, we show that NGS data targeted at ∼30 genomic regions, at a sequencing depth of 30x, can accurately predict age with a median error below 2 years. This implies that ∼1,000 sequenced DNA molecules at regions carefully selected and targeted, are enough for accurate age prediction.

The use of GP-age could involve a variety of applications, including forensic profiling, transplantation medicine, and health monitoring. While the models presented here were trained and tested on blood-derived methylomes from healthy humans, future works could further expand this approach to other species, tissues, or clinical conditions. Most importantly, its unique simplicity and shorter turnaround times could facilitate longitudinal studies that will shed light on the molecular processes underpinning human aging.

Limitations of the study

Here, we analyze blood-derived DNA methylation data to predict chronological age. As previously reported,^2,19,21 changes in age-correlated CpGs also reflect gradual changes in the cellular composition of the blood. We therefore used cell-type-specific differentially methylated markers and applied computational deconvolution to infer the relative abundance of various cell types in the blood. Indeed, the cellular composition slightly changes across different age groups, but in a much smaller magnitude that cannot explain the dramatic changes in methylation (STAR Methods; Figure S13). Future studies based on sorted cells could further improve age prediction by learning cell-type-specific methylation clocks for various common blood cells.

In this work, we focused on prediction of chronological age, and deviations between predicted and chronological age are assumed to reflect a biological signal of “accelerated” aging. Alternatively, such deviations could arise from prediction inaccuracies. To test that, we trained three independent clocks and showed that coordinated prediction errors across the three models are common, suggesting a relation to biological age (Figure 6). Thus, although GP-age was not trained as a biological age predictor per se,^32,33 the high availability of DNA methylation data (e.g., the large cohort presented here) opens opportunities to directly study the molecular mechanisms of aging, as well as variation across individuals, which could not be conveniently addressed using current biological age clocks or datasets that involve additional biochemical features. With the given data, future studies could focus on training a multi-system biological age clock, predicting the biological age of various tissues and pathways from DNA methylation data.

GP-age uses non-linear GPR models, where predictions are done by comparing the query with a cohort of annotated samples. Other, more compact, non-linear regression models were also tested here, including GAM, where non-linear CpG-specific splines are trained and integrated into a linear additive model. Unlike Horvath’s fixed mAge transformation, such splines reflect CpG-specific accelerated changes in DNA methylation across different ages, and could shed light on various mechanisms involved in age-related changes for specific genes.

STAR★Methods

Key resources table

REAGENT or RESOURCE	SOURCE	IDENTIFIER
Deposited data
GP-age: code, models, algorithm, data	https://github.com/mirivar/GP-age	https://doi.org/10.5281/zenodo.8167201
DNA methylation data from blood: 19 datasets, 11,910 samples from 450K/EPIC platforms, annotated with age.	GEO	GSE207605
Whole-genome DNA methylation (Jensen et al.)60	dbGaP	phs000846
Whole-genome DNA methylation (Loyfer et al.)59	EGA	EGAS00001006791
Software and algorithms
GP-age: code, models, algorithm, data	https://github.com/mirivar/GP-age	https://doi.org/10.5281/zenodo.8167201

Resource availability

Lead contact

Further information and requests should be directed to Tommy Kaplan: tommy@cs.huji.ac.il.

Materials availability

This study did not generate new unique reagents.

Method details

Illumina BeadChip array dataset

We assembled a large whole-blood DNA methylation dataset by combining 11,910 blood-derived methylomes from 19 publicly available individual datasets, measured on the Illumina 450K or EPIC array platforms (Figure 1). All donors included in our dataset were healthy, with ages spanning the range of 0–103 years with a median of 43 years 51.8% of the samples are from male donors, and generally most datasets used by this study are sex-balanced, except for GSE51032 (78% female); Kho, 2020; Liu, 2013; and Zannas, 2019 (all at 71% female); Lehne, 2015 (67% male); Horvath, 2012; Hannon, 2016; and Hannon, 2021 (all at 71%–72% male). The partition into the train and test sets was performed randomly, with 30% of the assembled dataset (3,573 samples, median age of 43 years) assigned for test and held-out, and the remaining 70% (8,337 samples, median age of 44 years) were used for feature selection and model training. For the initial analysis, one dataset (GSE84727) was held-out and used for validation. Normalized beta values from the original datasets were downloaded from GEO and used without additional normalization or batch correction, to facilitate use of the GP-age model by future datasets. Missing values of each CpG site were imputed with the average beta value of that CpG across other samples, using SimpleImputer from the python package scikit-learn⁷⁴ (version 0.24.2).

CpG feature selection

Low-quality CpG sites, with >20% of missing values across train samples, were removed. The Spearman correlation between methylation levels and age was calculated independently for each CpG site from the Illumina 450K platform, across train samples. For a more robust correlation estimation, in order to avoid outlier effect by young (<20 years) samples, datasets including exclusively young donors (GSE154566, GSE105018, GSE36054 and GSE103657) were excluded from correlation analysis (Figure S1). Overall, 964 CpG sites showed an absolute Spearman ρ ≥ 0.4 (or 1,034 sites across all 19 datasets, including GSE84727), and were retained for downstream analysis.

Next, the range of methylation levels was calculated for each CpG independently by calculating the methylation average in adults (≥20) in 5-year bins, and calculating the difference between the maximal and minimal values. CpGs sites with range <0.2 were excluded, yielding a set of 71 candidates (when the validation set GSE84727 was included; 80 when not). These were clustered using the spectral clustering algorithm by Ng, Jordan and Weiss,⁷⁵ with k∊{1,5,7,10,15,20,25,30,40,50,70,80} clusters, and the top correlated CpG was selected from each cluster. For most analyses, we used k = 30, but k = 10 and k = 80 are also reported.

Gaussian Process regression

A Gaussian Process regression (GPR) model was developed to predict the age of donors given their methylome. GPR is a flexible non-parametric Bayesian approach for regression. In our model, the inputs are blood-derived methylomes over k = 30 CpG sites, and the outputs are the ages of the donors. The model was trained using the python GPy package (version 1.10.0),⁷⁶ with the default hyper-parameters adjustments.

A Gaussian Process (GP) is a probability distribution over possible functions that fit a set of points. Formally, it is a collection of random variables, any finite number of which have a joint Gaussian distribution.⁵² Given a finite set of input points:

$$X=\left\{{\overrightarrow{x}}_1..,{\overrightarrow{x}}_n\right\}\subseteq {\mathbb{R}}^d$$

a mean function:

$$m:{\mathbb{R}}^d\to \mathbb{R}$$

and a covariance function:

$$k:{\mathrm{ℝ}}^d\times {\mathrm{ℝ}}^d\to \mathrm{ℝ}$$

a GP $f$ can be written as:

$$f\left(\overrightarrow{x}\right)\backsim GP\left(m\left(\overrightarrow{x}\right),k\left(\overrightarrow{x},\overrightarrow{x^{\prime }}\right)\right)$$

if the outputs $\overrightarrow{f}={\left(f\left({\overrightarrow{x}}_1\right),..f\left({\overrightarrow{x}}_N\right)\right)}^T$ have a Gaussian distribution described by: $\overrightarrow{f}\backsim N\left(\overrightarrow{\mu },Ʃ\right)$, where $\overrightarrow{\mu }=m{\left({\overrightarrow{x}}_1..,{\overrightarrow{x}}_N\right)}^T$ and ${Ʃ}_{i,j}=k\left({\overrightarrow{x}}_i,{\overrightarrow{x}}_j\right)$. The mean function is usually assumed to be the zero function, and the covariance function is a kernel function chosen based on assumptions about the function to be modeled. In our modeling, we used the commonly used RBF kernel function, defined as:

$$k\left({\overrightarrow{x}}_i,{\overrightarrow{x}}_j\right)=s^2\mathit{exp}\left(-\frac{\parallel {\overrightarrow{x}}_i-{\overrightarrow{x}}_j{\parallel }^2}{{2l}^2}\right)$$

where $s^2$ is the variance hyper-parameter, and $l$ is the length-scale hyper-parameter which controls the smoothness of the modeled function, or how fast it can vary.

In summary, with noise-free observations, the training data comprises of input-output pairs such as:

$$\left\{\left({\overrightarrow{x}}_1,f_i\right):i=1,\dots ,N\right\}$$

where the inputs are $X=\left\{{\overrightarrow{x}}_1..,{\overrightarrow{x}}_n\right\}\subseteq {\mathbb{R}}^d$ and the outputs are distributed according to a normal distribution: $\overrightarrow{f}\backsim N\left(0,Ʃ\right),\overrightarrow{f}ϵ{\mathrm{ℝ}}^N$.

Often, the output variables are assumed to further include some additive Gaussian noise η. In which cases the training data can be written as:

$$\left\{\left({\overrightarrow{x}}_1,y_i\right):i=1,\dots ,N\right\}$$

whereas $y_i=f\left({\overrightarrow{x}}_i\right)+\eta$, with $\eta \backsim N\left(0,{\sigma }^2\right)$. Under these assumptions, where the noise is independent and of equal variances, and outputs could be written as $\overrightarrow{y}=N\left(0,Ʃ+{\sigma }^{2}I\right)$.

To fit a GP for a regression task, the hyper-parameters of the model $\theta =\left(s^2,l,{\sigma }^2\right)$ are optimized with respect to the training data. If the mean of the GP is set to zero, Python’s GPy package estimates the hyper-parameters by minimizing their negative log marginal likelihood:

$$\mathrm{l}\mathrm{n}P\left(\overrightarrow{y}|\theta \right)=-\frac{N}{2}\ln 2\pi -\frac{\ln |Ʃ+{\sigma }^{2}I|}{2}-\frac{{\overrightarrow{y}}^T{\left(Ʃ+{\sigma }^{2}I\right)}^{{-1}_{\overrightarrow{y}}}}{2}$$

Given a test point $\overrightarrow{x_0^{\ast }}$, its output distribution is defined by $f\left(\overrightarrow{x_0^{\ast }}\right)|\overrightarrow{x_0^{\ast }},X,\overrightarrow{y}$, and can be analytically derived. From the definition of a Gaussian process, the finite set $f_1,..f_N,f_0^{\ast }$ are jointly distributed as:

$$\left[\begin{array}{c}\overrightarrow{f}\\ f_0^{\ast }\end{array}\right]⃒\left[\begin{array}{c}\overrightarrow{y}\\ \overrightarrow{x_0^{\ast }}\end{array}\right]\backsim N\left(0,\left[\begin{array}{cc}Ʃ& {\overrightarrow{k}}^{\ast }\\ {{\overrightarrow{k}}^{\ast }}^T& k\left(\overrightarrow{x_0^{\ast }},\overrightarrow{x_0^{\ast }}\right)\end{array}\right]\right)$$

where

$$f_0^{\ast }≔f\left(\overrightarrow{x_0^{\ast }}\right),{\overrightarrow{k}}^{\ast }≔\left(k\left({\overrightarrow{x}}_1,\overrightarrow{x_0^{\ast }}\right)\right),\dots ,{\left(k\left({\overrightarrow{x}}_1,\overrightarrow{x_0^{\ast }}\right)\right)}^T\text{.}$$

Adding the Gaussian noise to the observations, the finite set $y_{1,..}{y}_{N,}{f}^{\ast }$ are jointly distributed as:

$$\left[\begin{array}{c}\overrightarrow{y}\\ f_0^{\ast }\end{array}\right]⃒\left[\begin{array}{c}\overrightarrow{y}\\ x_0^{\ast }\end{array}\right]\backsim N\left(0,\left[\begin{array}{cc}Ʃ+{\sigma }^{2}I& {\overrightarrow{k}}^{\ast }\\ {{\overrightarrow{k}}^{\ast }}^T& k\left(\overrightarrow{x_0^{\ast }},\overrightarrow{x_0^{\ast }}\right)\end{array}\right]\right)$$

Conditioning the joint Gaussian prior distribution on the observations gives the following conditional distribution:

$$f_0^{\ast }|\overrightarrow{x_0^{\ast }},X,\overrightarrow{y}\backsim N\left({{\overrightarrow{k}}^{\ast }}^T{\left(Ʃ+{\sigma }^{2}I\right)}^{-1}\overrightarrow{y},k\left({\overrightarrow{x}}^{\ast },{\overrightarrow{x}}^{\ast }\right)-{{\overrightarrow{k}}^{\ast }}^T{\left(Ʃ+{\sigma }^{2}I\right)}^{-1}{\overrightarrow{k}}^{\ast }\right)$$

For a set of new samples, instead of a single test sample:

$$X^{\ast }=\left\{\overrightarrow{x_1^{\ast }}..,\overrightarrow{x_M^{\ast }}\right\}\subseteq {\mathbb{R}}^d$$

a prediction can be made by taking the mean of the well-defined conditional distribution:

$${\overrightarrow{f}}^{\ast }|X^{\ast },X,\overrightarrow{y}\backsim N\left({Ʃ}^{\ast }{\left(Ʃ+{\sigma }^{2}I\right)}^{-1}\overrightarrow{y},{Ʃ}^{†}-{Ʃ}^{\ast }{\left(Ʃ+{\sigma }^{2}I\right)}^{-1}{{Ʃ}^{\ast }}^T\right)$$

where

$${\overrightarrow{f}}^{\ast }≔f\left(\overrightarrow{x_1^{\ast }}..,\overrightarrow{x_M^{\ast }}\right),{Ʃ}_{i,j}^{\ast }=k\left(\overrightarrow{x_i^{\ast }},{\overrightarrow{x}}_j\right),{Ʃ}_{i,j}^{†}≔k\left(\overrightarrow{x_i^{\ast }}..,\overrightarrow{x_j^{\ast }}\right)$$

Thus, given the training data, the distribution of predictions of a new point or set of points is given by a closed analytical form. In our model, the inputs are methylation vectors, and the outputs are the donor ages. The mean of the distribution can be used as the final prediction of the regression model.

It shall be noted that the mean term of the conditional distribution of the new output variable derived from the joint Gaussian distribution could be viewed as a weighted sum of the train set ages (Figure 3). Here, the weights are based on the covariance between the input sample and the train data samples, then multiplied by the inverse of the covariance of the train set cohort data (with Gaussian noise added). Intuitively, this procedure gives higher weights to train set samples with methylomes similar to the query, but penalizes train set samples that are similar to each other, as they do not provide additional information. That way, the GP builds a non-linear relationship between input vectors and output variables.

Comparison to previously published 450K-based models

Previously published chronological age predictors^1,2,19 were tested on our test set using the R methylclock package (v 0.7.7).⁷⁷ An intercept of −5.5 was added to the Hannum et al. clock, for calibration. The Zhang et al. clock²⁰ was tested with their provided code, and the Vidal-Bralo et al. clock²¹ was tested with a linear regression model using their published coefficients.

Training of other regression models

Using the same CpG sites as of GP-age, we trained linear regression models and KNN models for chronological age predictions. The models were trained with LinearRegression (default parameters) and KNeighborsRegressor (n_neighbors = 3, p = 1, weights = ’uniform’) from the python package scikit-learn (version 0.24.2),⁷⁴ accordingly.

Stratified 4-fold cross validation

To check the robustness of GP-age, we performed 10 repetitions of stratified 4-fold leave-one-out cross validation. The samples were divided by binning the donor ages into 5-year bins, and in each repetition, each bin was divided into four subgroups. A single subgroup was retained for validation each time, resulting in four different models for each repetition. The errors across repetitions of cross validations were logged. The mean error and its 95% confidence interval were calculated, using a t-distribution with n-1 degrees of freedom.

Independent models and coordination of prediction errors

The 71 age-correlated CpGs were divided into three groups, such that the CpGs in each group are from distinct chromosomes. Three GP-age models were then learned, from the training samples, as described above. The median absolute error was then determined for each clock, as well as the percent of training samples with a greater positive error (over-estimation, ‘O’, average of ∼26% of training samples across three clocks), or a greater negative error (under-estimation, ‘Y’, average of ∼24% across three clocks). These percentages were used to estimate the expected frequency of each prediction error pattern across three clocks. Binomial distribution was used to estimate the statistical significance of enrichment at specific patterns (OOO, YYY).

Blood deconvolution

All 11,910 methylomes were deconvoluted using our previously published human DNA methylation atlas⁵⁸ (https://github.com/nloyfer/meth_atlas), including seven blood cell types. Proportions of each cell type were then grouped across samples in 5-year bins.

WGBS data for validation

Two WGBS datasets have been used in our study. First, we used a dataset published by Jensen et al.⁶⁰ in their study of cell-free DNA in pregnant women. The dataset contains, along with other samples, the methylation levels of 7 samples isolated from maternal buffy coat cells, collected from female donors aged 20–47 (mean age 31.4, median 32 years). Bam files were downloaded from dbGaP (accession number phs000846), and analyzed by wgbstools using the bam_to_pat function.⁷⁸ Second, we analyzed a dataset published by us,⁵⁹ including 23 WGBS white blood cells samples from healthy donors (EGA, EGAS00001006791). The samples include 21 female donors (aged 21–75 years old, mean age 56, median 58), and 2 male donors (60, 72 years old).

Testing on WGBS

Single CpG resolution of WGBS dataset was obtained with wgbstools, a computational suite we recently developed,⁷⁸ using the beta_to_450K function which calculates the average methylation levels of each CpG. These were then analyzed by GP-age for age prediction. We also augmented the methylation level estimation at each target CpG $x$ by considering neighboring CpGs $x_i$ within the same DNA methylation block,⁵⁹ and averaging their methylation levels using an exponentially decaying Laplace kernel:

$$w_i=\exp \left(-\frac{|x-x_i|}{d}\right)$$

with $d$ being a parameter controlling the length scale of effect of CpG neighbors. Here, we used $d$ = 3.

Quantification and statistical analysis

For robustness, GP-age was trained on DNA methylation data collected from 11,910 methylomes, including fresh and dried samples of whole blood or leukocytes, obtained from donors aged 0–103 years, from 19 datasets (preprocessed using various methods and normalizations). The model was tested on held-out samples, either from the same datasets or from held-out validation datasets, resulting with similar accuracy. Prediction errors were measured (in years) across different age groups, using root mean squared errors (RMSE), and using absolute errors at the median (MAE) or at other percentiles (25%, 75%, 90%). Age-specific and sex-specific models were also examined, with similar accuracy as the general GP-age model. We also trained and compared three independent clocks, each based on CpGs from different chromosomes.

Published: August 28, 2023

Supplemental information

Table S2. List of 1,034 age-correlative CpG sites, related to STAR Methods

Sites are sorted by their absolute value Spearman correlation with age, and their correlation p value, correlation q value, and methylation range are listed.

Table S3. List of 71 CpG sites with a Spearman correlation and methylation range over the defined ratios, related to STAR Methods

Sites are sorted by their absolute Spearman correlation coefficient. Also shown are methylation range and neighboring genes, as well as the cluster number and whether the CpG site was included in the final list of 30 “age set” CpG sites. Last column lists, for each CpG, in which of three independent clocks it was included.

Data and code availability

• •The data analyzed in this study were deposited at Gene Expression Omnibus (GEO) under accession GSE207605.
• •A standalone implementation for age prediction from array methylomes is available at https://github.com/mirivar/GP-age or from the lead contact. An archival DOI is provided in the key resources table.
• •Any other information needed to reanalyze the data in this paper is available from the lead contact upon request.