Abstract
During breast-conserving surgeries, it remains challenging to accomplish adequate surgical margins. We investigated different numbers of fibers for fiber-optic diffuse reflectance spectroscopy to differentiate tumorous breast tissue from healthy tissue ex vivo up to 2 mm from the margin. Using a machine-learning classification model, the optimal performance was obtained using at least three emitting fibers (Matthew’s correlation coefficient (MCC) of 0.73), which was significantly higher compared to the performance of using a single-emitting fiber (MCC of 0.48). The percentage of correctly classified tumor locations varied from 75% to 100% depending on the tumor percentage, the tumor-margin distance and the number of fibers.
1. Introduction
The aim of breast-conserving surgery (BCS) is to completely resect the tumor with a small margin of healthy breast tissue. In this way, a surgeon balances the endpoint of removing all tumor tissue, and the endpoint of achieving an optimal cosmetic result. To evaluate whether the tumor is completely removed or not, the surgical margin status of the specimen is determined after surgery. In the most commonly used ’radial’, pathological margin assessment technique, the margins are evaluated by inking the surface of the specimen and examining the distance between the ink on the edge and the boundary of the tumor in the surgical specimen [1,2]. Margin assessment is important since the presence of positive resection margins is one of the key determinants associated with ipsilateral breast tumor recurrence and hampers long-term survival [3–9].
Although the surgical margin status is extremely relevant to the outcome of BCS patients, there is a lack of consensus worldwide on a standardized definition of a ’positive’ margin for both invasive carcinoma (IC) and ductal carcinoma in situ (DCIS) [10–14], it varies substantially across countries. For instance, in the USA a re-excision for IC is recommended as soon as the ink on the margin is in contact with tumor cells during radial margin assessment, in accordance with the SSO-ASTRO guidelines [15]. In the Netherlands, a re-excision is recommended when the tumor cells reach the inked margin over a trajectory of more than 4 mm [16]. For DCIS, guidelines on an adequate margin vary from no DCIS cells on the resection surface to no DCIS cells within 2 mm from the resection edge [10]. The range in definition contributes to the large difference in reported positive margins worldwide, which varies from 9% to 36% for invasive breast cancer and from 4% to 23% for DCIS [10].
In case of a positive surgical margin, a patient would need additional treatment in the form of radiotherapy or a re-excision (i.e. repeat breast conserving surgery or mastectomy), with a potential risk for increased morbidity [3,17], unsatisfactory cosmetic outcome [18–20], decreased quality of life [21–23] and increased health care costs [24,25]. Therefore, the complete removal of breast tumors during primary surgery is essential.
On the other hand, extensive resections with negative margins may result in worse cosmetic outcomes. Studies have reported unsatisfactory cosmetic results in up to 40% of patients undergoing BCS [26,27]. According to multiple studies, specimen volume in relation to breast volume is a statistically significant determinant of a poor cosmetic outcome [28–31]. Various studies have determined that in many cases of BCS, the resected volume varies from 1.5 to 5.0 times the optimum resection volume, which is defined as the tumor volume plus an arbitrarily chosen margin of healthy breast tissue [32–34]. A poor cosmetic outcome leads to an increased risk of depression, anxiety, self-esteem issues, and a decreased quality of life [22,23,35]. Thus, it is important for breast cancer surgeons to excise as little healthy breast tissue as possible.
To balance the goals of complete tumor removal and a satisfactory cosmetic outcome, surgeons mainly rely on visual and tactile feedback. Discriminating healthy tissue from tumor tissue can be extremely challenging based on these types of feedback. Therefore, an accurate method for real-time intraoperative breast cancer margin assessment is needed. Many imaging techniques, such as ultrasound [36,37], fluorescence imaging [38], Raman spectroscopy [39], optical coherence tomography [40,41], radiofrequency spectroscopy [42] and photoacoustic tomography [43] are being investigated as a margin assessment tool. However, these techniques have not been incorporated into surgical practice due to various reasons including diagnostic inaccuracy, lack of speed, complicated user experience, high operator dependence, high costs, and/or inability to perform over the entire margin [44–46].
Fiber-optic diffuse reflectance spectroscopy (DRS) is a non-invasive, optical technique that could be used to study the structural and biochemical composition of tissue, based on the interaction of the tissue with different wavelengths of light. Light from a broadband light source is sent into the tissue through an emitting fiber, where it undergoes several interactions such as scattering and absorption, and part of the light will be reflected back. This reflected light is collected by a receiving fiber. The distance between an emitting and a receiving fiber is approximately equivalent to the measurement depth [47]. DRS spectra contain information concerning the absorption and scattering properties of the illuminated tissue. This could be applied to distinguish different tissue types and thus potentially delineate cancerous tissue during surgery. A previous study of our research group has proven that the absorption of fat compared to water in the near-infrared (NIR) wavelength band has a sensitivity and specificity of 100% in discriminating pure tumorous breast tissue from pure healthy tissue in sliced ex vivo breast cancer specimens [48].
Despite the promising results, a crucial issue to achieve the envisioned application of DRS has not been resolved yet. It involves the lack of data concerning the diagnostic accuracy of DRS on the actual resection margins of breast tissue. Measuring the resection margin is more challenging compared to measuring on the sliced specimen as used in previous studies. The DRS measurements on breast lumpectomy specimens could be acquired from locations with inhomogeneous composition. It has been shown by de Boer et al. that the accuracy of DRS classification models tested on sliced specimen locations with a mixture of tissue types, is dependent on the percentage of tumor cells in these locations [49]. It was shown that a lower percentage of tumor cells leads to a worse tissue classification performance with a high chance of missing the tumor presence [49]. This is important, since single-emitting fiber DRS is a point-based measurement method covering a small tissue volume. Therefore, DRS using a single emitting fiber might lead to missing tumorous tissue in a particular region. Furthermore, it would necessitate many measurements to cover a larger area, which could be time-consuming.
In order to overcome this obstacle, we developed a multi-fiber-optic probe that enabled collecting more optical information from one measurement location as compared to the earlier used probe. In this way, multiple spectra could be collected from different tissue volumes at the same measurement locations, which could be used for tissue classification. To the best of our knowledge, this is the first study investigating whether the number of optical fibers has an influence on the accuracy of DRS for detecting different tumor volumes at various depths when measuring on the surgical margin. Although researchers have performed DRS measurements on breast tissue using probes with multiple fibers [50–55], it has never been investigated how the number of fibers affects the accuracy of margin assessment. This study will provide new insights into this relationship, which could enable sampling information from a larger tissue area using the same probe tip size. A larger probe tip area provides the advantage of covering a larger tissue area, while giving the disadvantage of an uncertainty regarding the exact location where a particular DRS signal was measured. A larger number of fibers offers the advantage of sampling more information from the same probe tip area, while giving the disadvantage of a larger data acquisition time. We have tried to balance the size of the probe tip to the number of fibers, in which we tried to sample as much information from a tissue area as possible while maintaining an acceptable data acquisition time. Therefore, this work will contribute to the understanding of how the classification performance of DRS combined with a machine learning models depends on the numbers of fibers at a certain probe tip area.
In this study, we have taken the next step toward the use of optical spectroscopy for intraoperative margin assessment by improving the reliability and resolving the earlier-mentioned uncertainties. The first aim of this study was to investigate the optimum number of optical fibers to distinguish tumorous breast tissue from healthy breast tissue. The second goal was to investigate how the classification accuracy of this optimum number of fibers is affected by various tumor percentages and various distances of the tumor to the margin. In order to meet these goals, we have conducted DRS measurements with our custom-made probe on ex vivo lumpectomy specimens. Subsequently, we have trained several machine learning algorithms on data sets based on a different number of fibers, where the labels are assigned based on different ratios of tumor and healthy tissue. Furthermore, we analyzed the classification performance of each model on a test set, which was not used for training the models. After obtaining the optimal number of fibers, we evaluated the classification performance of detecting tumor volumes in various percentages. Lastly, the best-performing models were further evaluated by analyzing the correctly classified tumor locations at different distances from the tumor to the margin.
2. Materials and methods
2.1. Diffuse reflectance spectroscopy setup
The experimental DRS device consisted of 5 identical light sources, a fiber-optic DRS probe, two spectrometers, and in-house developed MATLAB software to collect and save data. The light sources were halogen broadband light sources (Avantes, AvaLight-HAL, 360 – 2500 ) with integrated shutters. A custom-designed DRS probe was used, as described below. The setup contained one spectrometer covering a visible wavelength range of 200 to 1160 (Avantes, AVASPEC-HS2048XL-EVO) and one covering a near-infrared wavelength range of 900 to 1750 (Avantes, AVASPECNIR256-1.7-RS). All spectra were calibrated using a similar method as described in [49,56,57].
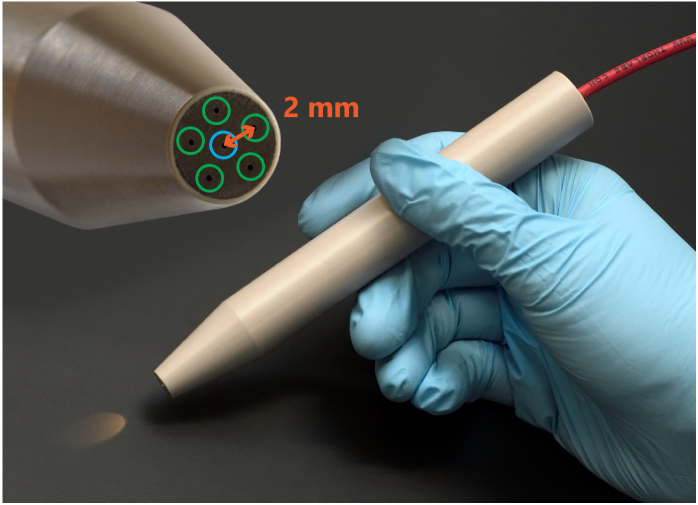
For this study, we developed a multi-fiber-optic probe with 5 identical emitting fibers positioned in a circle around one central receiving fiber as illustrated in Fig. 1. All emitting fibers had an equal source-detector fiber distance of 2.0 .
Fig. 1.
Handheld DRS probe. In the upper left corner, the distal probe tip is displayed, with a circular configuration of 5 emitting fibers around 1 central receiving fiber, and a distance of 2 mm between each emitting fiber and the receiving fiber.
2.2. Study design
This ex vivo study was conducted from 2019 to 2022 at the Netherlands Cancer Institute-Antoni van Leeuwenhoek hospital (NKI-AvL) after approval of the study protocol by the Institutional Review Board (IRBm20-077). During this period, patients with invasive breast carcinoma and/or ductal carcinoma in situ who were scheduled for surgery, were included. According to the medical research involving human subjects act, no written consent was required. In total, 100 breast lumpectomy specimens were obtained from 100 female patients who had undergone BCS.
2.3. Data acquisition
Immediately after surgical excision, we collected the specimen from the surgical team and proceeded with DRS measurements after an estimated time gap of a few minutes. We have aimed to maintain this time gap as consistent as possible throughout all measurements. After specimen collection, approximately 3 to 5 locations on the margin of each lumpectomy specimen were selected as measurement locations. At each location, 3 consecutive DRS point measurements were performed with an acquisition time of a few seconds per measurement. Throughout all measurements, the probe was lightly pressured against the tissue surface area and it was ensured that the entire surface of the probe tip was in contact with the tissue at all times. Due to limitations in the number of measurement locations on each specimen and in order to avoid significant imbalance in our data set, we have used ultrasound imaging on some specimens to localize areas with the smallest distance from the tumor to the resection margin.
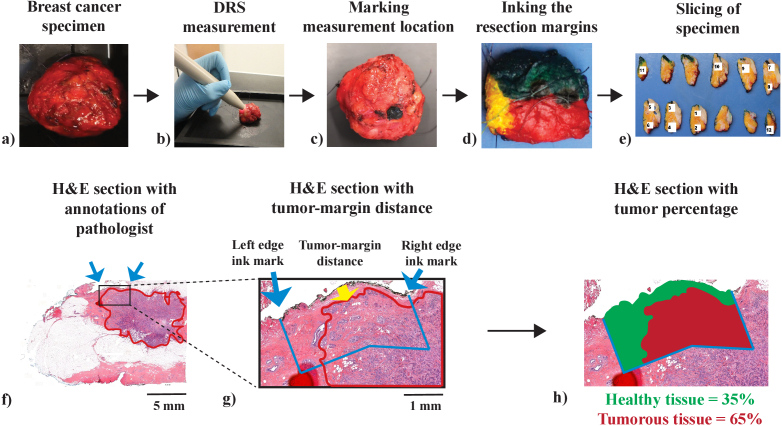
After acquiring DRS, each measurement location on the tissue was marked with black pathology ink, approximately equaling the size of the probe tip. Afterward, the specimen was brought to the pathology department, where the resection margins were inked, the whole specimen was frozen, and sliced in a bread-loafed manner. During this process, it was made sure the specimen was sliced at the ink marks. Then the specimen was processed in a standardized manner. An overview of the data acquisition process is shown in Fig. 2
Fig. 2.
Overview of the data acquisition method, with a) specimen collection after surgery, b) point-based DRS measurement, c) marking the measurement location with black pathology ink, and d) standard processing by the pathology department, including coloring and slicing the specimen. Schematic overview of the method for determining the tumor percentage and the tumor-margin distance of each measured tissue location in the corresponding histopathology section. In f) the original H&E section with the annotated borders of the lesion in red, and g) the magnified image of the measured tissue location, recognizable due to the black ink along the margin. The yellow arrow (g) indicates the tumor-margin distance, determined by measuring the perpendicular distance from the surgical surface to the tumor in the middle of this region. Lastly, the percentage of tumorous tissue and healthy breast tissue was determined over a depth of 2 at this particular marked region, indicated by the blue box (h).
The pathology H&E sections of all measurement locations were digitized and examined by a general pathologist with a high level of experience in breast pathology, who precisely annotated all tumor areas of IC and DCIS in the images. The healthy tissue areas, which consisted of connective and fat tissue, were identified by thresholding the green channel of the H&E sections as described in [58]. The percentage of IC and DCIS based on the annotations of the pathologist and the percentage of healthy tissue based on the thresholding was determined up to 2 underneath the black ink marks. These percentages formed the labels (ground truth) of the data set. Hereafter, the sum of IC and DCIS percentage scores will be referred to as ’tumor percentage’. It is important to emphasize that the tumor percentages indicate the area of tumor tissue in a box of 2 wide from the margin and do not entail actual percentages of tumor cells. The area percentages of all tissue types were exactly determined using image processing tools in MATLAB. Furthermore, the perpendicular distance of the tumor to the margin at the middle of the black ink mark was determined. Hereafter, this distance will be referred to as the ’tumor-margin distance’. Figure 2 gives an overview of the method for determining the tumor percentage and the tumor-margin distance of each measured tissue location in the corresponding histopathology section.
The data analysis consisted of several steps to build tissue classification models and evaluate their accuracy. In the following subsections, each step is explained in more detail. All data analyses were performed using MATLAB (2022a, MathWorks Inc., Natick, Massachusetts, United States).
2.4. Data preprocessing
2.4.1. Spectrum normalization
After data acquisition, the three consecutive optical spectra of each measurement location were averaged and the spectra from the visual and near-infrared wavelength ranges were stitched together to form one continuous spectrum. Furthermore, data up to 400 and after 1600 were eliminated as these parts of the spectrum have a low signal-to-noise ratio. To correct for intensity differences, all spectra were normalized using multiplicative scatter correction (MSC) [59], where the spectra are corrected in such a manner that they are as close as possible to the mean of the data set.
2.4.2. Feature extraction
Each normalized spectrum consists of the reflection intensities at 1200 different wavelengths. During previous research of our group, it was found that the visual wavelength range is principally influenced by absorption through blood, while the near-infrared wavelength range is principally influenced by absorption through fat and water [48]. Furthermore, it was demonstrated that the fat fraction in combination with the total volume of fat and water provided optimal discrimination between tumorous breast tissue and healthy breast tissue, when measuring on slices of BCS specimens or biopsies [48,49,60]. All reflection intensities represent 1200 features, that could be used for training the model. In order to avoid overfitting, we have applied feature extraction. In this process, we quantified and extracted a set of spectral features in the near-infrared wavelength range, as described by de Boer et al.[49]. These features included the slopes of spectra between designated wavelengths, the maximum difference between the slope and the spectrum, the corresponding wavelength at the point of maximum difference, and the inflection points left and right of the point of maximum difference [49]. This yielded a total of 80 features per fiber.
2.5. Data set preparation
2.5.1. Random fiber selection and mixture
The next step was to build 5 different data sets using features from a different number of fibers (1-5) with a random combination. The first data set contained all features from 1 randomly selected fiber for each measurement location, the second data set contained a combination of all features of 2 randomly selected fibers for each measurement location, and so on. In our study, we tried to sample as much information from the probe tip area as possible, using different numbers of fibers. Therefore, when using 2, 3 or 4 fibers, we always selected random fibers in opposing directions, instead of adjacent fibers. In this way, the fibers would cover the largest tissue area possible and we would always maintain the same illumination-collection geometry for a particular number of fibers. Using a combination of all features of all fibers would result in 400 features per measurement location. The 5 different data sets were used to investigate the impact of the number of fibers in assessing surgical margins.
2.5.2. Labeling
Thereafter, multiple data sets were built from the 5 earlier built data sets, by labeling each measurement location as ’healthy tissue’ or ’tumorous tissue’ according to different definitions of the labels. The definition was based on various cut-off (threshold) points for the tumor percentage and a constant cut-off point of 2.0 for the distance to the margin, for each data set. The threshold points for tumor percentage (TTP) were incrementally increased 5%, up to the maximum TTP of 40% which still enabled training a model with sufficient tumor-labeled data. Any measurement location was labeled as tumorous tissue if it had 1) a tumor percentage equal to or above the chosen TTP and 2) a distance to the tumor less than 2.0 . Otherwise, the measurement location was labeled as healthy tissue. Thus eventually, all data sets contained the same number of measurement locations, but with a different distribution of tumor labels and healthy labels.
2.5.3. Feature selection
The following step was the implementation of feature reduction using a minimum redundancy maximum relevance (MRMR) feature selection algorithm [61], in order to prevent the algorithm from overfitting. This iterative algorithm selects features during each iteration that correlate the strongest with the response variable while being minimally redundant compared to the set of already selected features. Using the outcome of this algorithm, the optimum feature subsets were selected based on a cut-off point of of a quantified score of the importance of each feature. The feature selection was performed for each fiber combination data set individually.
2.6. Classification
2.6.1. RUSBoost model
The subsequent step was building a model with an ensemble random under sampling boosting tree (RUSBoost) as a classifier to distinguish tumorous tissue from healthy tissue [62]. We used this particular classifier since it has a higher classification performance on imbalanced data sets compared to other classification models [63]. The RUSBoost model mitigates the problem of imbalance by using 1) random under sampling [64] and 2) boosting [65]. Random under sampling means that in our case the algorithm randomly removes measurements from the majority class of healthy tissue until the desired class ratio is achieved at each iteration of the algorithm [62]. Boosting in our case means that the model iteratively builds an ensemble of models, where eventually all constructed models have a weighted vote to classify new data [62].
2.6.2. Cross-validation
We used iterative 5-fold cross-validation to classify the measurement locations. Each cross-validation process was repeated 20 times, with a different distribution of the patients over the folds during each of the 20 repetitions. To avoid bias, the data from each patient were randomly assigned to either the training set or the test set during each iteration, but never both. This analysis was executed for each of the data sets.
2.6.3. Performance evaluation
The following metrics averaged over 20 iterations were calculated: Matthews Correlation Coefficient (MCC), sensitivity, and specificity. The is a metric that is less influenced by imbalanced data compared to accuracy. It is calculated by the following equation:
| (1) |
where , , , and stand for true positives, true negatives, false positives, and false negatives respectively.
The MCC value ranges from -1 to 1, where -1 indicates a reverse correlation and 1 indicates a flawless correlation. A One-way Analysis of Variance (ANOVA) was performed to assess whether a particular number of fibers had a statistically significant, different mean MCC value in comparison to another number of fibers. The difference was considered statistically significant when the p-value was less than 0.05.
Furthermore, the influence of TTP on the performance of all classification models was analyzed by comparing the MCC, sensitivity and specificity for different TTP values. The classification models based on the number of fibers with significantly high MCC values for all TTP values were further analyzed. This was done by investigating the influence of the tumor-margin distance on their sensitivity, by determining the proportion of correctly classified tumor locations for various tumor-margin distances. Additionally, the differences in correctly versus incorrectly classified locations using the lowest TTP (5%) were analyzed.
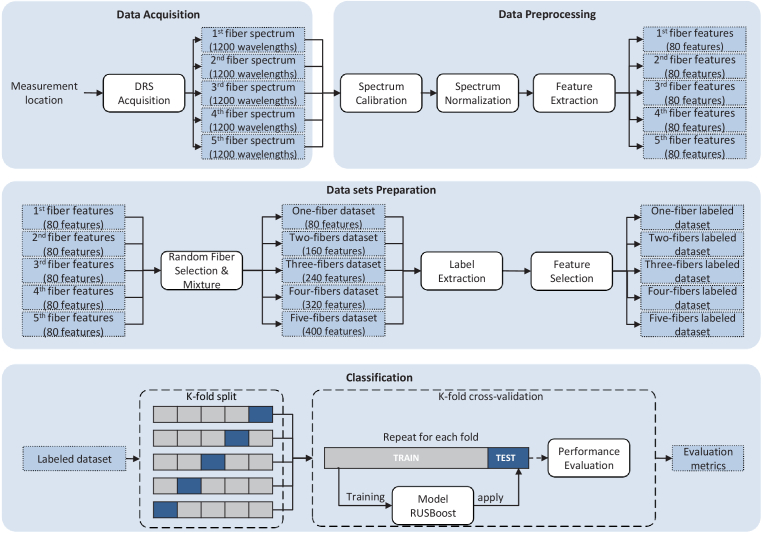
The entire workflow of data acquisition and analysis is displayed in Fig. 3.
Fig. 3.
Overview of the development and testing of all classification models. The process started with data acquisition, where 5 spectra were collected at each measurement location. The data was preprocessed by successively applying calibration, normalization, and feature extraction. In total, 80 features were extracted from each spectrum. Then 5 different data sets were built by using features from a different number of fibers (1-5). For each measurement location, the features from a randomly selected combination of fibers were used for each data set preparation. Subsequently, multiple data sets were built from the earlier data sets by labeling of the measurements (as tumorous and healthy) based on increasing cutoff points for tumor percentage. Thereafter, the most relevant features were selected from each data set. The labeled data sets were used to build RUSBoost classification models. The performance of the models was evaluated by an iterated 5-fold cross-validation method. Per patient, all spectra were assigned to one fold, ensuring that they were not split between the training and test set.
3. Results
3.1. Patient characteristics and measurement locations
In total, 1770 DRS spectra were obtained at 354 tissue locations from 100 breast specimens of 100 patients. An overview of the patient characteristics and measurement locations can be found in Table 1. The mean age of the patient population was 60,7 years (SD = 12,5) (Table 1). As far as the pathological diagnosis of the patients, 41 patients had IC of no special type (NST), 31 patients had IC NST combined with DCIS, 16 patients had an invasive lobular carcinoma (ILC), 10 patients had DCIS and 2 patients had lobular carcinoma in situ (LCIS) (Table 1). For the data analysis, the patient groups with IC NST, IC NST combined with DCIS and ILC were combined, as well as the group with DCIS and LCIS.
Table 1. Patient characteristics and measurement locations a .
| Patient characteristic / measurement location | Value |
|---|---|
| Characteristic N = 100 | |
| Age (years) (median, SD) | 60,7 (12,5) |
| Histological tumor type | |
| IC NST | 41 |
| IC NST + DCIS | 31 |
| ILC | 16 |
| DCIS | 10 |
| LCIS | 2 |
| Measurement locations (N = 354) | |
| IC within 2 from margin | 71 |
| DCIS within 2 from margin | 17 |
| Healthy tissue within 2 from margin | 266 |
IC NST = invasive carcinoma of no special type, DCIS = ductal carcinoma in situ,
ILC = invasive lobular carcinoma, LCIS = lobular carcinoma in situ;
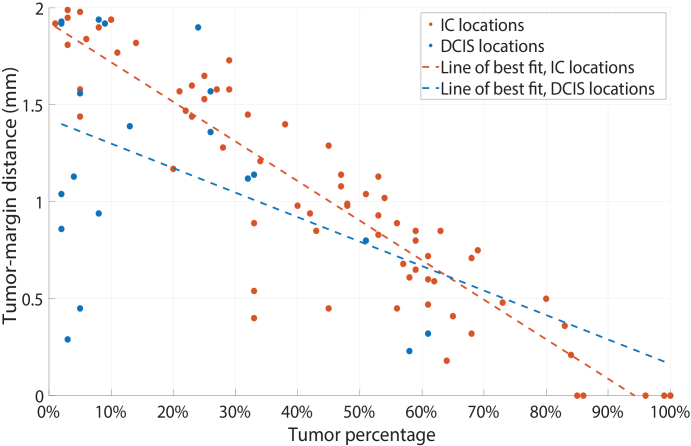
Of all measurement locations, there were 88 (25%) locations with tumor tissue within a distance of 2 from the margin and 266 (75%) locations with only healthy breast tissue. 71 (81%) of the tumor locations contained IC and 17 (19%) locations contained DCIS. In Fig. 4 the distance to the tumor is plotted against the tumor percentage for all IC within 2 from the margin locations (orange dots) and DCIS 2 from the margin locations (blue dots). The dashed lines represent the lines of best fit using linear regression analysis. From this figure, it is apparent that there is a negative, linear correlation between tumor percentage and tumor depth. This relationship is stronger for IC locations compared to DCIS locations.
Fig. 4.
Tumor-margin distance compared to the tumor percentage of all measurement locations. The orange dots represent IC locations, and the blue dots represent DCIS locations. The dashed lines are corresponding lines of best fit.
3.2. Selected features
The MRMR analysis yielded a different number of optimum features per fiber combination data set, due to a different input number of features as can be seen in Fig. 3. The number of features varied from 5 to 35 features for each data set. We ranked the top 10 selected features with the highest importance scores per data set, and investigated the frequency of each of these features across all data sets. The 10 features with the highest frequencies are ranked in Table 2. As shown in Table 2, all of the displayed selected features are in the near-infrared wavelength range, where fat and water are the most important absorbers.
Table 2. Frequency rank of features among the top 10 features with the highest importance scores of all data sets.
| Frequency rank | Selected features |
|---|---|
| 1 | Maximum difference between the slope and the measured spectrum between 1224 nm and 1331 nm |
| 2 | Wavelength of the right inflection point of the peak between 1008 nm and 1053 nm |
| 3 | Maximum difference between the slope and the measured spectrum between 1142 nm and 1225 nm |
| 4 | Slope of the measured spectrum between 999 nm and 1034 nm |
| 5 | Slope of the measured spectrum between 1213 nm and 1248 nm |
| 6 | Wavelength of the right inflection point of the peak between 1021 nm and 1102 nm |
| 7 | Slope of the measured spectrum between 1112 nm and 1147 nm |
| 8 | Slope of the measured spectrum between 883 nm and 1149 nm |
| 9 | Slope of the measured spectrum between 1024 nm and 1059 nm |
| 10 | Slope of the measured spectrum between 1395 and 1430 nm |
3.3. Effect of different numbers of fibers on classification performance
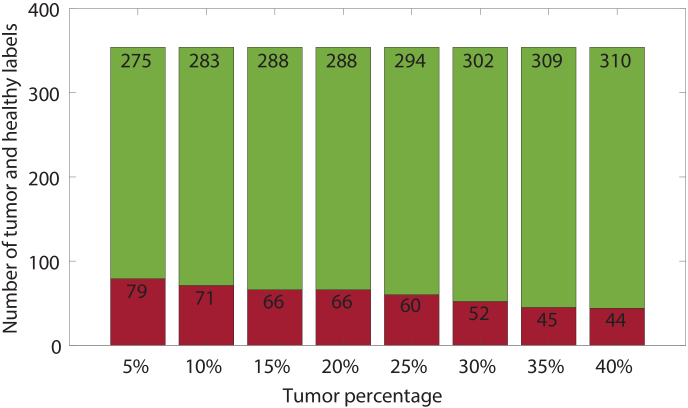
Different classification models were developed for each number of fibers based on features from 1, 2, 3, 4 or 5 fibers, and TTP values from 5%, 10%, 15%, 20%, 25%, 30%, 35% or 40%. For assigning the labels, a maximum value of 40% was used as TTP, since a higher TTP led to insufficient tumor labels in the training set. Figure 5 displays the distribution of tumor labels and healthy labels for different TTPs. As the TTP increases, the number of tumor labels decreases, while the total number of measurements remains equal. At the lowest TTP, 79 (22%) of all 354 measurement locations are labeled as tumor, while at the highest TTP, 44 (12%) of all locations are labeled as tumor.
Fig. 5.
Distribution of tumor labels (red bars) and healthy labels (green bars) in the overall data set for different TTPs.
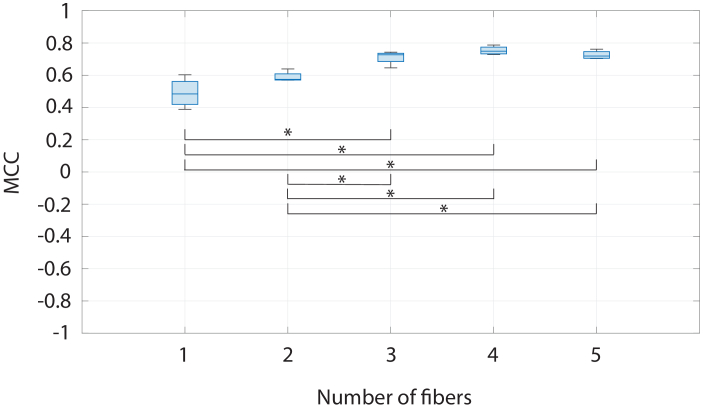
The results of classifications for all numbers of fibers are demonstrated in Fig. 6. In this plot, each box visualizes the MCC values of all classification models over different TTPs for each fiber combination, where each MCC value in a box represents an average of all cross-validations per model. The minimum, maximum, first quartile and third quartile of all MCC values are displayed. The asterisks in this figure indicate the statistically significant differences between the performance of different fiber combinations, according to the One-way ANOVA test. Overall, the single-fiber classification models showed the lowest classification performance (median MCC 0.48, interquartile range (IQR) 0.14), while the classification models of 4 fibers showed the highest classification performance (median MCC 0.75, IQR 0.04). The median MCC of all classification models of 2 fibers, 3 fibers and 5 fibers were 0.57 (IQR 0.04), 0.73 (IQR 0.05), 0.72 (IQR 0.04), respectively. There were statistically significant differences (p-value < 0.05) between the performance of the models based on 1 fiber and 2 fibers compared to the models based on 3 or more fibers. From the plot it can be observed that the classification performance increases significantly with an increasing number of fibers, but reaches a plateau after 3 fibers.
Fig. 6.
Classification performance for different numbers of fibers. Each box is composed of all average MCC values of models based on different TTP values and the same number of fibers. The lines with an asterisk indicate a p-value of 0.05.
3.4. Effect of tumor percentage on classification performance
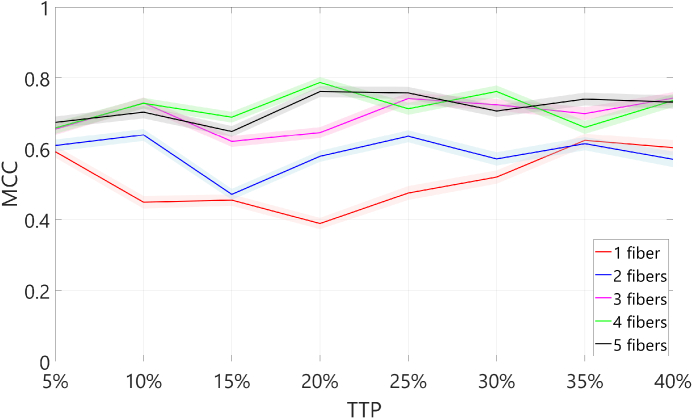
We investigated the effect of tumor percentages on the tissue discrimination performance. Therefore, we repeated the experiments by training the classification model for all numbers of fibers while the data labels were adjusted based on tumor percentage. In Fig. 7, each colored line depicts the average MCC value of each classification model based on a different TTP, for a particular number of fibers. The shaded areas represent the accompanying average standard deviations (SD). The best performance is obtained when 4 fibers are used and the TTP is set at 20%, with a MCC value of 0.79 (SD 0.015). The lowest classification performance was obtained when using 1 fiber while setting the TTP at 20%, with a MCC value of 0.39 (SD 0.016). In general, at all TTP values, the use of 3, 4 or 5 fibers outperforms the use of 1 or 2 fibers. Another observation is that utilizing 3 or more fibers resulted in a SD of the MCC of 0.08, while the SD of the MCC of 3 fibers decreased to 0.03. This illustrates the robust performance of 3 to 5 fibers over different TTPs, while the performance of the models based on 1 and 2 fibers changes significantly over different TTPs.
Fig. 7.
Classification performance of models based on different TTPs. Each line color represents a different number of fibers. The TTP is displayed on the x-axis and the MCC on the y-axis. The shaded areas indicate the standard deviations.
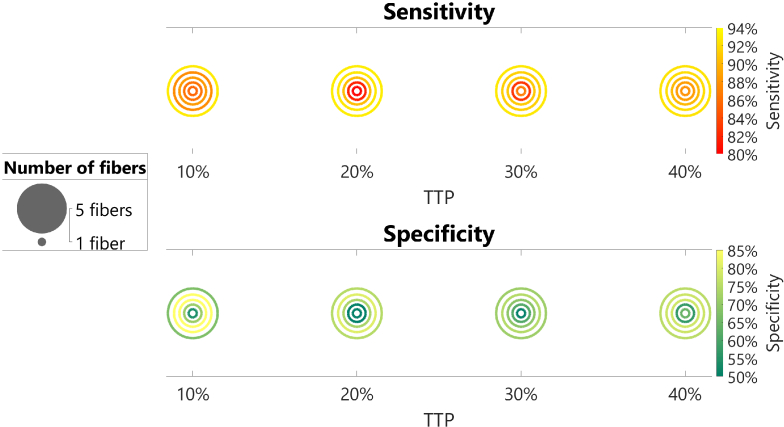
The calculated sensitivity and specificity of each classification model are depicted in Fig. 8. In general, all classification models have a high sensitivity, ranging between 80% and 93%. However, the specificity varies widely across different models, ranging from 50% to 86%. The highest sensitivity of 93% was achieved using 5 fibers and a TTP of 20%. This model had a specificity of 75%. On the other hand, the highest specificity of 86% was obtained with 4 fibers and a TTP of 10%. This model had a sensitivity of 88%. Among all possible numbers of fibers and TTP values, higher sensitivity and specificity can always be achieved when using 3 to 5 fibers compared to 1 or 2 fibers. The exact values of sensitivity and specificity for all classification models can be found in Supplement 1 (885.6KB, pdf) (Section 1).
Fig. 8.
Sensitivity and specificity of all classification models. In both diagrams, 4 sets of rings are present, with each set containing 5 rings of different sizes and colors. The size represents the number of fibers, while the color represents sensitivity in the upper diagram and specificity in the lower diagram.
3.5. Effect of tumor-margin distance on classification performance
In general, the previous experiment indicates that the use of 3 to 5 fibers outperforms the use of 1 to 2 fibers significantly. Thus, for the remainder of this study, we have analyzed the effects of the tumor-margin distance on the classification performance for only 3, 4, and 5 fibers.
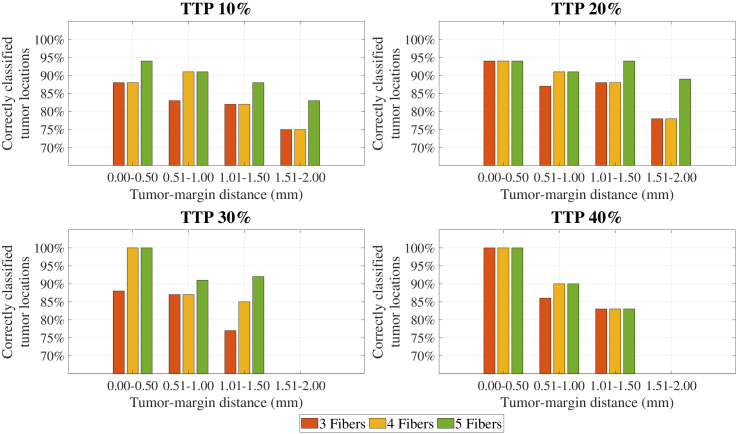
Figure 9 displays the percentage of locations with tumor tissue that are correctly classified when using different numbers of fibers at various tumor-margin distances. The tumor margin distance has been divided into 4 bins of 0.5 . Each graph represents a similar experiment but with a different TTP value (10%, 20%, 30%, and 40%). It is worth mentioning that with a TTP of 30% or 40%, there were no locations with tumor tissue deeper than 1.50 .
Fig. 9.
The percentage of correctly classified locations at different tumor-margin distances for different TTPs. Each bar color represents a different number of fibers, while each of the 4 graphs represents a different TTP.
In general, all graphs show a similar trend, where the percentage of correctly classified tumor locations decreases with an increase in the distance to the tumor. The percentage of correctly classified tumor locations varies from 75% to 100%, depending on the TTP and the number of fibers. Among the models based on a TTP of 30%, the use of 4 or 5 fibers gives the highest sensitivity for the shortest tumor-margin distance category, while for a TTP of 40%, it can be observed that all selected numbers of fibers have the same sensitivity. In these scenarios, 100% of all locations with a tumor-margin distance of are classified correctly. Furthermore, for a tumor-margin distance , 5 fibers give the highest percentage of correctly classified locations for all different TTP values.
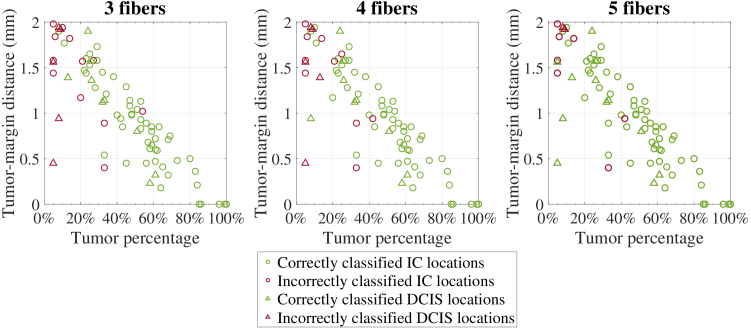
Furthermore, in Fig. 10, the tumor-margin distance of all correctly and incorrectly classified IC and DCIS locations is plotted against the tumor tissue percentage. The distribution of locations in this graph demonstrates that DCIS locations with a low tumor percentage (0-20%) in combination with a low tumor-margin distance (0-1 ) are existent, while this is not the case for IC locations. All graphs show a similar trend, where the number of misclassified locations increases with an increasing tumor-margin distance. Furthermore, the total number of misclassified locations decreases with an increasing number of fibers. In essence, it shows that in a scenario where the lowest possible cut-off point for tumor percentage would be used, the highest chance of correct classification for each tumor location would occur when using 5 fibers. In this scenario, 89% of all IC locations and 86% of all DCIS locations get classified correctly, regardless of tumor-margin-distance. Furthermore, 94% of all locations with a tumor-margin distance get classified correctly, regardless of tumor percentage. The specificity of distinguishing tumorous tissue from healthy tissue is 75% when using 3 fibers, 78% when using 4 fibers and 74% when using 5 fibers.
Fig. 10.
Tumor-margin distance compared to the tumor percentage of all correctly and incorrectly classified IC and DCIS locations when using classification models based on a TTP of 5% for 3, 4, and 5 fibers.
4. Discussion
The first goal of this study was to develop breast tissue classification models using optical spectral features and to investigate the optimal number of optical fibers for accurate discrimination of tumorous breast tissue from healthy tissue. In order to do so, we compared the performance of several classification models using 1 to 5 fibers.
As for the first research question concerning the number of optical fibers, it was found that in general, experiments with 3 to 5 fibers had a substantially higher performance compared to the use of 1 to 2 fibers. This could be explained by the fact that malignant breast lesions often possess an irregular shape, and therefore could easily have a significant variation in the tumor-margin distance over a relatively short trajectory. A DRS probe with 1 or 2 emitting fiber(s) and 1 receiving fiber collects optical information of a smaller tissue volume compared to a DRS probe with a similar tip diameter, but containing 3, 4 or 5 optical emitting fibers encircling 1 receiving fiber. Combining the features of multiple fibers enables the algorithm to give a more accurate classification result regarding the sampled volume. We found no significant difference between the models using 3, 4 or 5 fibers. One possible explanation for this might be that 3 fibers already provide sufficient data from the probed volume, meaning that more fibers would not provide additional information regarding the tumor presence in that volume. Another possible explanation might be that the addition of features beyond the features from 3 fibers leads to redundant information and noise, which may cause overfitting during the training phase.
The second goal of this study was to assess how the performance of different numbers of fibers depended on the tumor percentage. For this purpose, the experiments were repeated several times each time with different tumor percentage threshold values for labels assignment. The evaluation metrics showed that for all TTP values the models based on 3 to 5 fibers outperformed the models based on 1 to 2 fibers. It was also shown that the models based on 3 to 5 fibers have more robust performance with similar MCC over all TTP values, while in the single and double fiber models the MCC value changes significantly over the TTPs.
The third goal was to investigate the performance of different numbers of fibers in comparison with the tumor-margin distance. Concerning this, we investigated the number of correctly classified tumor locations per tumor-margin distance category for the best set of models. It was found that the percentage of correctly classified tumor locations decreased with an increase in the tumor-margin distance. This suggests that spectra collected from locations with deeper tumors are optically less different to spectra of healthy tissue, compared to spectra collected from locations with more superficial tumors. Therefore, deeper tumor locations are more difficult to correctly classify. For tumors deeper than 1.0 , 5 fibers had the highest sensitivity regardless of the TTP. A possible explanation is that when you have the highest number of fibers on the same tissue surface area, there is a higher chance of measuring tumorous tissue when it is present within 2 .
Among the patients included in this study, there were 5 patients with a positive resection margin according to Dutch guidelines. The clinical consequences for these patients were that 3 patients had to undergo a re-excision, and 2 patients had to undergo additional boost radiotherapy. The unnecessary burden for these patients would have been prevented if DRS was applied on the resection margins after surgery, since all these positive margin locations were correctly identified by the classification models using 3, 4 or 5 fibers. This illustrates the clinical value of this technology in practice.
It is noteworthy that during this research, we have put maximum effort to correlate the measured tissue locations to the corresponding pathological outcome. However, this correlation has an inherent shortcoming since the H&E section is a 2D image of a few cell layers, while the probed tissue is a 3D volume. Therefore, the tissue areas in the H&E section will not completely represent the probed tissue volume. Furthermore, we have not investigated the impact of benign tissue structures with high nuclei densities on the margin assessment accuracy. This would be an interesting point to investigate in the future.
In order to integrate DRS into a clinically applicable tool, it is important to conduct a large clinical study using DRS in vivo directly on the breast tissue to be resected during BCS, to validate the performance of the classification models. Moreover, it should be investigated which tumor percentage should be used as a threshold point for achieving the most clinically relevant performance. DRS could be applied for margin assessment using two different methods: 1) a DRS probe for classification of suspicious margin locations on the specimen directly after excision, ensuring additional resection of any tumor tissue which was left behind in the breast, 2) a surgical resection tool allowing the combination of DRS measurements, real-time classification, and tissue resection based on the classification results. For the latter method, one emitting fiber and one receiving fiber would suffice, since you could move the probe over an entire tissue surface area allowing quick measurements and classification in a continuous manner. It is important to mention that in such a study, the measured locations in vivo could be marked using sutures or surgical clips, followed by a similar pathology analysis as conducted in this study. When investigating both methods, the usability of both tools should be evaluated among surgeons. When these questions are investigated, the next step would be to set up a clinical study to evaluate the effect of a DRS-integrated tool during breast-conserving surgeries on clinical end-points such as the number of positive resection margins, and the resection volumes in relation to the tumor volumes.
5. Conclusion
In this study, we have investigated the optimum number of fibers for distinguishing tumorous breast tissue from healthy breast tissue on the resection margin. The results demonstrate that in general, classification models based on 3 or more fibers lead to a 52% increase in the MCC value compared to 1 fiber models, regardless of tumor percentage as well as the distance to the tumor. The models based on 3 to 5 fibers also show a more robust performance over different tumor percentages. Although using 4 and 5 fibers slightly outperform 3 fibers in some experiments, there was no significant difference between their performances. Furthermore, when looking at the models based on 3 to 5 fibers, the percentage of correctly classified tumor locations varies from 75% to 100% depending on the tumor percentage, the tumor-margin distance and the number of fibers. In conclusion, to achieve reliable and robust performance in using DRS for surgical margin assessment, we require at least 3 fibers to be able to detect small tumor percentages up to 2 in depth, with 5 fibers providing the highest detection accuracy. A large clinical in vivo DRS study would be the next step towards reaching the ultimate goal of intraoperatively evaluating surgical margins during breast-conserving surgeries.
Acknowledgments
The authors thank all employees from the NKI-AvL Core Facility Molecular Pathology & Biobanking (CFMPB), all surgeons and nurses from the Department of Surgery, and all pathologists and pathologist assistants from the Department of Pathology for their assistance.
Disclosures
The authors declare no conflicts of interest.
Data Availability
Data underlying the results presented in this paper are not publicly available at the time but may be obtained from the authors upon reasonable request.
Supplemental document
See Supplement 1 (885.6KB, pdf) for supporting content.
References
- 1.Chiappa C., Rovera F., Corben A. D., Fachinetti A., De Berardinis V., Marchionini V., Rausei S., Boni L., Dionigi G., Dionigi R., “Surgical margins in breast conservation,” Int. J. Surg. 11, S69–S72 (2013). 10.1016/S1743-9191(13)60021-7 [DOI] [PubMed] [Google Scholar]
- 2.Provenzano E., Bossuyt V., Viale G., Cameron D., Badve S., Denkert C., MacGrogan G., Penault-Llorca F., Boughey J., Curigliano G., Dixon J. M., Esserman L., Fastner G., Kuehn T., Peintinger F., von Minckwitz G., White J., Yang W., Symmans W. F., “Standardization of pathologic evaluation and reporting of postneoadjuvant specimens in clinical trials of breast cancer: recommendations from an international working group,” Mod. Pathol. 28(9), 1185–1201 (2015). 10.1038/modpathol.2015.74 [DOI] [PubMed] [Google Scholar]
- 3.Nayyar A., Gallagher K. K., McGuire K. P., “Definition and management of positive margins for invasive breast cancer,” Surg. Clin. 98(4), 761–771 (2018). 10.1016/j.suc.2018.03.008 [DOI] [PubMed] [Google Scholar]
- 4.Dunne C., Burke J. P., Morrow M., Kell M. R., “Effect of margin status on local recurrence after breast conservation and radiation therapy for ductal carcinoma in situ,” in Database of Abstracts of Reviews of Effects (DARE): Quality-assessed Reviews [Internet], (Centre for Reviews and Dissemination (UK), 2009). [DOI] [PubMed] [Google Scholar]
- 5.Spivack B., Khanna M. M., Tafra L., Juillard G., Giuliano A. E., “Margin status and local recurrence after breast-conserving surgery,” Arch. Surg. 129(9), 952–957 (1994). 10.1001/archsurg.1994.01420330066013 [DOI] [PubMed] [Google Scholar]
- 6.Meric F., Mirza N. Q., Vlastos G., Buchholz T. A., Kuerer H. M., Babiera G. V., Singletary S. E., Ross M. I., Ames F. C., Feig B. W., Krishnamurthy S., Perkins G. H., McNeese M. D., Strom E. A., Valero V., Hunt K. K., “Positive surgical margins and ipsilateral breast tumor recurrence predict disease-specific survival after breast-conserving therapy,” Cancer 97(4), 926–933 (2003). 10.1002/cncr.11222 [DOI] [PubMed] [Google Scholar]
- 7.Singletary S. E., “Surgical margins in patients with early-stage breast cancer treated with breast conservation therapy,” The Am. journal of surgery 184(5), 383–393 (2002). 10.1016/S0002-9610(02)01012-7 [DOI] [PubMed] [Google Scholar]
- 8.Bodilsen A., Bjerre K., Offersen B. V., Vahl P., Amby N., Dixon J. M., Ejlertsen B., Overgaard J., Christiansen P., “Importance of margin width in breast-conserving treatment of early breast cancer,” J. Surg. Oncol. 113(6), 609–615 (2016). 10.1002/jso.24224 [DOI] [PubMed] [Google Scholar]
- 9.Morrow M., Van Zee K. J., Solin L. J., Houssami N., Chavez-MacGregor M., Harris J. R., Horton J., Hwang S., Johnson P. L., Marinovich M. L., Schnitt S. J., Wapnir I., Moran M. S., “Society of surgical oncology-american society for radiation oncology-american society of clinical oncology consensus guideline on margins for breast-conserving surgery with whole-breast irradiation in ductal carcinoma in situ,” Pract. Radiat. Oncol. 6(5), 287–295 (2016). 10.1016/j.prro.2016.06.011 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.de Koning S. G. B., V. Peeters M.-J. T., Jóźwiak K., Bhairosing P. A., Ruers T. J., “Tumor resection margin definitions in breast-conserving surgery: systematic review and meta-analysis of the current literature,” Clin. Breast Cancer 18(4), e595–e600 (2018). 10.1016/j.clbc.2018.04.004 [DOI] [PubMed] [Google Scholar]
- 11.McCahill L. E., Single R. M., Bowles E. J. A., Feigelson H. S., James T. A., Barney T., Engel J. M., Onitilo A. A., “Variability in reexcision following breast conservation surgery,” JAMA 307(5), 467–475 (2012). 10.1001/jama.2012.43 [DOI] [PubMed] [Google Scholar]
- 12.Blair S. L., Thompson K., Rococco J., Malcarne V., Beitsch P. D., Ollila D. W., “Attaining negative margins in breast-conservation operations: is there a consensus among breast surgeons?” J. Am. Coll. Surg. 209(5), 608–613 (2009). 10.1016/j.jamcollsurg.2009.07.026 [DOI] [PubMed] [Google Scholar]
- 13.Pilewskie M., Morrow M., “Margins in breast cancer: How much is enough?” Cancer 124(7), 1335–1341 (2018). 10.1002/cncr.31221 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Azu M., Abrahamse P., Katz S. J., Jagsi R., Morrow M., “What is an adequate margin for breast-conserving surgery? surgeon attitudes and correlates,” Ann. Surg. Oncol. 17(2), 558–563 (2010). 10.1245/s10434-009-0765-1 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Moran M. S., Schnitt S. J., Giuliano A. E., Harris J. R., Khan S. A., Horton J., Klimberg S., Chavez-MacGregor M., Freedman G., Houssami N., Johnson P. L., Morrow M., “Society of surgical oncology-american society for radiation oncology consensus guideline on margins for breast-conserving surgery with whole-breast irradiation in stages i and ii invasive breast cancer,” Int. J. Radiat. Oncol. 88(3), 553–564 (2014). 10.1016/j.ijrobp.2013.11.012 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Nederland N. B. O., “Nabon (2012). mammacarcinoom. landelijke richtlijn, versie: 2.0,” (2018).
- 17.Olsen M. A., Nickel K. B., Margenthaler J. A., Wallace A. E., Mines D., Miller J. P., Fraser V. J., Warren D. K., “Increased risk of surgical site infection among breast-conserving surgery re-excisions,” Ann. Surg. Oncol. 22(6), 2003–2009 (2015). 10.1245/s10434-014-4200-x [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Collette S., Collette L., Budiharto T., et al. , “Predictors of the risk of fibrosis at 10 years after breast conserving therapy for early breast cancer - a study based on the eortc trial 22881-10882 ’boost versus no boost’,” Eur. J. Cancer 44(17), 2587–2599 (2008). 10.1016/j.ejca.2008.07.032 [DOI] [PubMed] [Google Scholar]
- 19.Wazer D. E., DiPetrillo T., Schmidt-Ullrich R., Weld L., Smith T., Marchant D., Robert N., “Factors influencing cosmetic outcome and complication risk after conservative surgery and radiotherapy for early-stage breast carcinoma,” J. Clin. Oncol. 10(3), 356–363 (1992). 10.1200/JCO.1992.10.3.356 [DOI] [PubMed] [Google Scholar]
- 20.Heil J., Breitkreuz K., Golatta M., Czink E., Dahlkamp J., Rom J., Schuetz F., Blumenstein M., Rauch G., Sohn C., “Do reexcisions impair aesthetic outcome in breast conservation surgery? exploratory analysis of a prospective cohort study,” Ann. Surg. Oncol. 19(2), 541–547 (2012). 10.1245/s10434-011-1947-1 [DOI] [PubMed] [Google Scholar]
- 21.Hau E., Browne L., Capp A., Delaney G. P., Fox C., Kearsley J. H., Millar E., Nasser E. H., Papadatos G., Graham P. H., “The impact of breast cosmetic and functional outcomes on quality of life: long-term results from the st. george and wollongong randomized breast boost trial,” Breast Cancer Res. Treat. 139(1), 115–123 (2013). 10.1007/s10549-013-2508-z [DOI] [PubMed] [Google Scholar]
- 22.Waljee J. F., Hu E. S., Ubel P. A., Smith D. M., Newman L. A., Alderman A. K., “Effect of esthetic outcome after breast-conserving surgery on psychosocial functioning and quality of life,” J. Clin. Oncol. 26(20), 3331–3337 (2008). 10.1200/JCO.2007.13.1375 [DOI] [PubMed] [Google Scholar]
- 23.Volders J. H., Negenborn V. L., Haloua M. H., Krekel N. M., Jóźwiak K., Meijer S., van den Tol P. M., “Cosmetic outcome and quality of life are inextricably linked in breast-conserving therapy,” J. Surg. Oncol. 115(8), 941–948 (2017). 10.1002/jso.24615 [DOI] [PubMed] [Google Scholar]
- 24.Pataky R., Baliski C., “Reoperation costs in attempted breast-conserving surgery: a decision analysis,” Curr. Oncol. 23(5), 314–321 (2016). 10.3747/co.23.2989 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Abe S. E., Hill J. S., Han Y., Walsh K., Symanowski J. T., Hadzikadic-Gusic L., Flippo-Morton T., Sarantou T., Forster M., White Jr R. L., “Margin re-excision and local recurrence in invasive breast cancer: a cost analysis using a decision tree model,” J. Surg. Oncol. 112(4), 443–448 (2015). 10.1002/jso.23990 [DOI] [PubMed] [Google Scholar]
- 26.Clough K. B., Cuminet J., Fitoussi A., Nos C., Mosseri V., “Cosmetic sequelae after conservative treatment for breast cancer: classification and results of surgical correction,” Ann. Plast. Surg. 41(5), 471–481 (1998). 10.1097/00000637-199811000-00004 [DOI] [PubMed] [Google Scholar]
- 27.Sneeuw K., Aaronson N., Yarnold J., Broderick M., Regan J., Ross G., Goddard A., “Cosmetic and functional outcomes of breast conserving treatment for early stage breast cancer. 1. comparison of patients’ ratings, observers’ ratings and objective assessments,” Radiother. Oncol. 25(3), 153–159 (1992). 10.1016/0167-8140(92)90261-R [DOI] [PubMed] [Google Scholar]
- 28.Cochrane R., Valasiadou P., Wilson A., Al-Ghazal S., Macmillan R., “Cosmesis and satisfaction after breast-conserving surgery correlates with the percentage of breast volume excised,” J. Br. Surg. 90(12), 1505–1509 (2003). 10.1002/bjs.4344 [DOI] [PubMed] [Google Scholar]
- 29.Taylor M. E., Perez C. A., Halverson K. J., Kuske R. R., Philpott G. W., Garcia D. M., Mortimer J. E., Myerson R. J., Radford D., Rush C., “Factors influencing cosmetic results after conservation therapy for breast cancer,” Int. J. Radiat. Oncol. Biol. Phys. 31(4), 753–764 (1995). 10.1016/0360-3016(94)00480-3 [DOI] [PubMed] [Google Scholar]
- 30.Vrieling C., Collette L., Fourquet A., Hoogenraad W. J., Horiot J.-C., Jager J. J., Pierart M., Poortmans P. M., Struikmans H., Maat B., Van Limbergen E., Bartelink H., “The influence of patient, tumor and treatment factors on the cosmetic results after breast-conserving therapy in the eortc ’boost vs. no boost’ trial,” Radiother. Oncol. 55(3), 219–232 (2000). 10.1016/S0167-8140(00)00210-3 [DOI] [PubMed] [Google Scholar]
- 31.Hashem T., Morsi A., Farahat A., Zaghloul T., Hamed A., “Correlation of specimen/breast volume ratio to cosmetic outcome after breast conserving surgery,” Indian J. Surg. Oncol. 10(4), 668–672 (2019). 10.1007/s13193-019-00973-y [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Krekel N., Zonderhuis B., Muller S., Bril H., van Slooten H.-J., de Lange de Klerk E., van den Tol P., Meijer S., “Excessive resections in breast-conserving surgery: a retrospective multicentre study,” The breast journal 17(6), 602–609 (2011). 10.1111/j.1524-4741.2011.01198.x [DOI] [PubMed] [Google Scholar]
- 33.Valejo F. A. M., Tiezzi D. G., Mandarano L. R. M., d. Sousa C. B., d. Andrade J. M., “Volume of breast tissue excised during breast-conserving surgery in patients undergoing preoperative systemic therapy,” Revista Brasileira de Ginecologia e Obstet. 35(5), 221–225 (2013). 10.1590/S0100-72032013000500006 [DOI] [PubMed] [Google Scholar]
- 34.Shin Y. D., Choi Y. J., Kim D. H., Park S. S., Choi H., Kim D. J., Park S., Yun H. Y., Song Y. J., “Comparison of outcomes of surgeon-performed intraoperative ultrasonography-guided wire localization and preoperative wire localization in nonpalpable breast cancer patients undergoing breast-conserving surgery: a retrospective cohort study,” Medicine 96(50), e9340 (2017). 10.1097/MD.0000000000009340 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Al-Ghazal S. K., Fallowfield L., Blamey R., “Does cosmetic outcome from treatment of primary breast cancer influence psychosocial morbidity?” Eur. J. Surg. Oncol. 25(6), 571–573 (1999). 10.1053/ejso.1999.0708 [DOI] [PubMed] [Google Scholar]
- 36.Doyle T. E., Factor R. E., Ellefson C. L., Sorensen K. M., Ambrose B. J., Goodrich J. B., Hart V. P., Jensen S. C., Patel H., Neumayer L. A., “High-frequency ultrasound for intraoperative margin assessments in breast conservation surgery: a feasibility study,” BMC Cancer 11(1), 444 (2011). 10.1186/1471-2407-11-444 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Krekel N. M. A., Zonderhuis B. M., Schreurs H. W. H., L. Cardozo A. M. F., Rijna H., van der Veen H., Muller S., Poortman P., de Widt L., de Roos W. K., Bosch A. M., Taets van Amerongen A. H. M., Bergers E., van der Linden M. H. M., de Lange de Klerk E. S. M., Winters H. A. H., Meijer S., van den Tol P. M. P., “Ultrasound-guided breast-sparing surgery to improve cosmetic outcomes and quality of life. a prospective multicentre randomised controlled clinical trial comparing ultrasound-guided surgery to traditional palpation-guided surgery (cobalt trial),” BMC Surg. 11(1), 8–10 (2011). 10.1186/1471-2482-11-8 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Pleijhuis R., Langhout G., Helfrich W., Themelis G., Sarantopoulos A., Crane L., Harlaar N., De Jong J., Ntziachristos V., Van Dam G., “Near-infrared fluorescence (nirf) imaging in breast-conserving surgery: assessing intraoperative techniques in tissue-simulating breast phantoms,” Eur. J. Surg. Oncol. 37(1), 32–39 (2011). 10.1016/j.ejso.2010.10.006 [DOI] [PubMed] [Google Scholar]
- 39.Haka A. S., Volynskaya Z. I., Gardecki J. A., Nazemi J., Shenk R., Wang N., Dasari R. R., Fitzmaurice M., Feld M. S., “Diagnosing breast cancer using raman spectroscopy: prospective analysis,” J. Biomed. Opt. 14(5), 054023 (2009). 10.1117/1.3247154 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Ha R., Friedlander L. C., Hibshoosh H., Hendon C., Feldman S., Ahn S., Schmidt H., Akens M. K., Fitzmaurice M., Wilson B. C., Mango V. L., “Optical coherence tomography: A novel imaging method for post-lumpectomy breast margin assessment-a multi-reader study,” Acad. Radiol. 25(3), 279–287 (2018). 10.1016/j.acra.2017.09.018 [DOI] [PubMed] [Google Scholar]
- 41.Foo K. Y., Kennedy K. M., Zilkens R., Allen W. M., Fang Q., Sanderson R. W., Anstie J., Dessauvagie B. F., Latham B., Saunders C. M., Chin L., Kennedy B. F., “Optical palpation for tumor margin assessment in breast-conserving surgery,” Biomed. Opt. Express 12(3), 1666–1682 (2021). 10.1364/BOE.415888 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Pappo I., Spector R., Schindel A., Morgenstern S., Sandbank J., Leider L. T., Schneebaum S., Lelcuk S., Karni T., “Diagnostic performance of a novel device for real-time margin assessment in lumpectomy specimens,” J. Surg. Res. 160(2), 277–281 (2010). 10.1016/j.jss.2009.02.025 [DOI] [PubMed] [Google Scholar]
- 43.Li R., Wang P., Lan L., Lloyd F. P., Goergen C. J., Chen S., Cheng J.-X., “Assessing breast tumor margin by multispectral photoacoustic tomography,” Biomed. Opt. Express 6(4), 1273–1281 (2015). 10.1364/BOE.6.001273 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Pradipta A. R., Tanei T., Morimoto K., Shimazu K., Noguchi S., Tanaka K., “Emerging technologies for real-time intraoperative margin assessment in future breast-conserving surgery,” Adv. Sci. 7(9), 1901519 (2020). 10.1002/advs.201901519 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Keating J. J., Fisher C., Batiste R., Singhal S., “Advances in intraoperative margin assessment for breast cancer,” Curr. Surg. Rep. 4(4), 15 (2016). 10.1007/s40137-016-0136-3 [DOI] [Google Scholar]
- 46.St John E. R., Al-Khudairi R., Ashrafian H., Athanasiou T., Takats Z., Hadjiminas D. J., Darzi A., Leff D. R., “Diagnostic accuracy of intraoperative techniques for margin assessment in breast cancer surgery,” Ann. Surg. 265(2), 300–310 (2017). 10.1097/SLA.0000000000001897 [DOI] [PubMed] [Google Scholar]
- 47.Gomes A. J., Backman V., “Algorithm for automated selection of application-specific fiber-optic reflectance probes,” J. Biomed. Opt. 18(2), 027012 (2013). 10.1117/1.JBO.18.2.027012 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.De Boer L., Molenkamp B., Bydlon T., Hendriks B., Wesseling J., Sterenborg H., Ruers T., “Fat/water ratios measured with diffuse reflectance spectroscopy to detect breast tumor boundaries,” Breast Cancer Res. Treat. 152(3), 509–518 (2015). 10.1007/s10549-015-3487-z [DOI] [PubMed] [Google Scholar]
- 49.de Boer L. L., Kho E., Van de Vijver K. K., Vranken Peeters M.-J. T., van Duijnhoven F., Hendriks B. H., Sterenborg H. J., Ruers T. J., “Optical tissue measurements of invasive carcinoma and ductal carcinoma in situ for surgical guidance,” Breast Cancer Res. 23(1), 59 (2021). 10.1186/s13058-021-01436-5 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Volynskaya Z., Haka A. S., Bechtel K. L., Fitzmaurice M., Shenk R., Wang N., Nazemi J., Dasari R. R., Feld M. S., “Diagnosing breast cancer using diffuse reflectance spectroscopy and intrinsic fluorescence spectroscopy,” J. Biomed. Opt. 13(2), 024012 (2008). 10.1117/1.2909672 [DOI] [PubMed] [Google Scholar]
- 51.Soares J. S., Barman I., Dingari N. C., Volynskaya Z., Liu W., Klein N., Plecha D., Dasari R. R., Fitzmaurice M., “Diagnostic power of diffuse reflectance spectroscopy for targeted detection of breast lesions with microcalcifications,” Proc. Natl. Acad. Sci. 110(2), 471–476 (2013). 10.1073/pnas.1215473110 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Keller M. D., Majumder S. K., Kelley M. C., Meszoely I. M., Boulos F. I., Olivares G. M., Mahadevan-Jansen A., “Autofluorescence and diffuse reflectance spectroscopy and spectral imaging for breast surgical margin analysis,” Lasers Surg. Med. 42(1), 15–23 (2010). 10.1002/lsm.20865 [DOI] [PubMed] [Google Scholar]
- 53.Majumder S. K., Keller M. D., Boulos F. I., Kelley M. C., Mahadevan-Jansen A., “Comparison of autofluorescence, diffuse reflectance, and raman spectroscopy for breast tissue discrimination,” J. Biomed. Opt. 13(5), 054009 (2008). 10.1117/1.2975962 [DOI] [PubMed] [Google Scholar]
- 54.Evers D. J., Nachabe R., Vranken Peeters M.-J., van der Hage J. A., Oldenburg H. S., Rutgers E. J., Lucassen G. W., Hendriks B. H., Wesseling J., Ruers T. J., “Diffuse reflectance spectroscopy: towards clinical application in breast cancer,” Breast Cancer Res. Treat. 137(1), 155–165 (2013). 10.1007/s10549-012-2350-8 [DOI] [PubMed] [Google Scholar]
- 55.Nachabé R., Evers D. J., Hendriks B. H. W., Lucassen G. W., van der Voort M., Rutgers E. J., Peeters M.-J. V., Van der Hage J. A., Oldenburg H. S., Wesseling J., Ruers T. J. M., “Diagnosis of breast cancer using diffuse optical spectroscopy from 500 to 1600 nm: comparison of classification methods,” J. Biomed. Opt. 16(8), 087010 (2011). 10.1117/1.3611010 [DOI] [PubMed] [Google Scholar]
- 56.Nachabe R., Hendriks B. H., Desjardins A. E., van der Voort M., van der Mark M. B., Sterenborg H. J., “Estimation of lipid and water concentrations in scattering media with diffuse optical spectroscopy from 900 to 1600 nm,” J. Biomed. Opt. 15(3), 037015 (2010). 10.1117/1.3454392 [DOI] [PubMed] [Google Scholar]
- 57.Geldof F., Dashtbozorg B., Hendriks B. H., Sterenborg H. J., Ruers T. J., “Layer thickness prediction and tissue classification in two-layered tissue structures using diffuse reflectance spectroscopy,” Sci. Rep. 12(1), 1698 (2022). 10.1038/s41598-022-05751-5 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Kho E., Dashtbozorg B., De Boer L. L., Van de Vijver K. K., Sterenborg H. J., Ruers T. J., “Broadband hyperspectral imaging for breast tumor detection using spectral and spatial information,” Biomed. Opt. Express 10(9), 4496–4515 (2019). 10.1364/BOE.10.004496 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Geladi P., MacDougall D., Martens H., “Linearization and scatter-correction for near-infrared reflectance spectra of meat,” Appl. Spectrosc. 39(3), 491–500 (1985). 10.1366/0003702854248656 [DOI] [Google Scholar]
- 60.De Boer L. L., Bydlon T. M., Van Duijnhoven F., Vranken Peeters M.-J. T., Loo C. E., Winter-Warnars G. A., Sanders J., Sterenborg H. J., Hendriks B. H., Ruers T. J., “Towards the use of diffuse reflectance spectroscopy for real-time in vivo detection of breast cancer during surgery,” J. Transl. Med. 16(1), 367 (2018). 10.1186/s12967-018-1747-5 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Peng H., Ding C., Long F., “Minimum redundancy-maximum relevance feature selection,” (2005).
- 62.Seiffert C., Khoshgoftaar T. M., Van Hulse J., Napolitano A., “Rusboost: A hybrid approach to alleviating class imbalance,” IEEE Trans. Syst., Man, Cybern. A 40(1), 185–197 (2010). 10.1109/TSMCA.2009.2029559 [DOI] [Google Scholar]
- 63.Tong T., Ledig C., Guerrero R., Schuh A., Koikkalainen J., Tolonen A., Rhodius H., Barkhof F., Tijms B., Lemstra A. W., Soininen H., Remes A. M., Waldemar G., Hasselbalch S., Mecocci P., Baroni M., Lötjönen J., van der Flier W., Rueckert D., “Five-class differential diagnostics of neurodegenerative diseases using random undersampling boosting,” NeuroImage: Clin. 15, 613–624 (2017). 10.1016/j.nicl.2017.06.012 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64.Jeong D.-H., Kim S.-E., Choi W.-H., Ahn S.-H., “A comparative study on the influence of undersampling and oversampling techniques for the classification of physical activities using an imbalanced accelerometer dataset,” in Healthcare, vol. 10 (MDPI, 2022), p. 1255. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 65.Tanha J., Abdi Y., Samadi N., Razzaghi N., Asadpour M., “Boosting methods for multi-class imbalanced data classification: an experimental review,” J. Big Data 7(1), 70 (2020). 10.1186/s40537-020-00349-y [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
Data underlying the results presented in this paper are not publicly available at the time but may be obtained from the authors upon reasonable request.