An innovative inertial extra-proximal gradient algorithm for solving convex optimization problems with application to image and signal processing

Abstract

This study introduces an innovative approach to address convex optimization problems, with a specific focus on applications in image and signal processing. The research aims to develop a self-adaptive extra proximal algorithm that incorporates an inertial term to effectively tackle challenges in convex optimization. The study's significance lies in its contribution to advancing optimization techniques in the realm of image deblurring and signal reconstruction. The proposed methodology involves creating a novel self-adaptive extra proximal algorithm, analyzing its convergence rigorously to ensure reliability and effectiveness. Numerical examples, including image deblurring and signal reconstruction tasks using only 10% of the original signal, illustrate the practical applicability and advantages of the algorithm. By introducing an inertial term within the extra proximal framework, the algorithm demonstrates potential for faster convergence and improved optimization outcomes, addressing real-world challenges of image enhancement and signal reconstruction. The algorithm's incorporation of an inertial term showcases its potential for faster convergence and improved optimization outcomes. This research significantly contributes to the field of optimization techniques, particularly in the context of image and signal processing applications.

1. Introduction

One of the very important tools for modeling and solving various real-world problems is convex optimization theory. The theory can be applied in variety of fields like machine learning, game theory, economics, control theory among others, see Refs. [[1], [2], [3], [4], [5], [6], [7], [8], [9], [10]] for more details.

Consider a function $\gamma$ that is not differentiable but convex and a set $\mathcal{S}$ that is convex, the standard convex optimization problem aim for solving

$$\gamma \left({\xi }^{*}\right)=\underset{\xi \in \mathcal{S}}{\min }\gamma \left(\xi \right)\text{.}$$ (1.1)

Researchers have over the years derived various techniques for locating ${\xi }^{*}=\mathrm{argmin}\gamma \left(\xi \right)$. For example Newton methods, regula-falsi methods and others have been employed to minimize the function $\gamma$, but when $\gamma$ fails to be differentiable/smooth, then the proximal point algorithm (PPA) introduced in Ref. [11], is the most prevalent and desirable technique. For any starting point ${\xi }_0\in \mathcal{S}$, Martinet in Ref. [11] recommend the recursive rule for the generated sequence $\left({\xi }_h\right)$ for finding the solution (1.1).

$${\xi }_{h+1}=\underset{t}{\mathrm{argmin}}\left(\gamma \left(t\right)+{\Vert {\xi }_h-t\Vert }_2^2\right)\text{.}$$ (1.2)

Since the right part of (1.2) is a minimization of a strongly convex operator, then we will surely have just one solution which is referred to as the proximal operator:

$$\text{pro}{\mathrm{x}}_{\gamma }\left(\xi \right)=\underset{t}{\mathrm{argmin}}\left(\gamma \left(t\right)+{\Vert \xi -t\Vert }_2^2\right)$$ (1.3)

which can be written mostly as,

$$\text{pro}{\mathrm{x}}_{{\mathrm{\Lambda }}_h\gamma }\left(\xi \right)=\underset{t}{\mathrm{argmin}}\left(\gamma \left(t\right)+\frac{1}{2{\mathrm{\Lambda }}_h}{\Vert \xi -t\Vert }_2^2\right)$$ (1.4)

for some ${\mathrm{\Lambda }}_h>0$.

Martinet expressed the view that each weak cluster points in the sequence of (1.2) solve the optimization problem (1.1). The procedure has attracted the interest of many researchers because it is straightforward and has the ability to search for the solution of large scale optimization problem. Hence, the theory have been extended in many ways, for example see Refs. [12],[13],[14],[15],[16],[17] ,[[18], [19], [20], [21]][,[[22], [23], [24]] and the many references therein. The mathematical model of temperature-dependent flow of power-law nanofluid over a variable stretching Riga sheet was study by Ref. [24]. Following refs. [[25], [26], [27], [28]] have several other noteworthy studies. Priority-aware resource scheduling for UAV-mounted mobile edge computing networks was study by Ref. [29]. references [[29], [30], [31], [32], [33], [34], [35]] encompass various other significant investigations.

The existence of a strong link between the various problems related to the fixed point problem, namely, variational inequality and minimization, has been shown, This allows the P.P.A to be utilized to solve these problems and other related problems. For example, the $\mathrm{argmin}$ of the minimization problem (1.1) is also the zeros of the sub-differential of $\gamma$ symbolized as $\partial \gamma \left(\xi \right)$ which in-turn is the fixed point of $\text{pro}{\mathrm{x}}_{{\mathrm{\Lambda }}_h\gamma }$, i.e.

$${\xi }^{*}=\arg \min \gamma \left(\xi \right)\text{if}\text{and}\text{only}\text{if}0\in \partial \gamma \left({\xi }^{*}\right)\text{if}\text{and}\text{only}\text{if}{\xi }^{*}=\left(\text{pro}{\mathrm{x}}_{{\mathrm{\Lambda }}_h\gamma }\right){\xi }^{*}\text{.}$$ (1.5)

Our objective in this endeavor is to explore ways of solving the minimization problem stated in (1.1). The algorithm's core lies in optimizing convex problems, enhancing outcomes in diverse scenarios. Its contributions encompass both image and signal domains, making it a valuable tool for enhancing quality, accuracy, and analysis in data-driven applications. By efficiently tackling convex optimization challenges, this algorithm finds relevance in various tasks, including image processing, signal reconstruction, and sparse signal recovery and sparse signal recovers. The loss function involved in this problem is denoted as $p\left(\xi \right)+\mathrm{\Xi }\left(\xi \right)$, and it is defined on a real Hilbert space $\mathcal{H}$. The operator $\mathrm{\Xi }:\mathcal{H}\to \mathbb{R}$ is both smooth and convex, whereas $p:\mathcal{H}\to (-\infty ,+\infty ]$ is lower semicontinuous, proper, and convex, but it is not necessarily smooth or differentiable.

$$\underset{\xi \in \mathcal{H}}{\min }p\left(\xi \right)+\mathrm{\Xi }\left(\xi \right)\text{.}$$ (1.6)

We can represent the collection of solutions of (1.6) as $\mathrm{\Omega }$. It is evident that ${\xi }^{*}$ achieves the minimum value for $p+\mathrm{\Xi }$ if and only if

$$0\in \left(\partial p+\nabla \mathrm{\Xi }\right)\left(\xi \right)\text{.}$$ (1.7)

From the relationships in (1.5), the forward-backward algorithm (also known as the shrinkage thresholding algorithm) is defined as:

$${\xi }_{h+1}=\left(\text{pro}{\mathrm{x}}_{{\mathrm{\Lambda }}_{h}p}\left({\xi }_h-{\mathrm{\Lambda }}_h\nabla \mathrm{\Xi }\left({\xi }_h\right)\right)\right)\text{,}$$ (1.8)

The value assigned to the step-size, denoted as ${\mathrm{\Lambda }}_h$, falls within the open interval between 0 and $\frac{2}{B}$, where $B$ represents the Lipschitz constant of the gradient of $\mathrm{\Xi }$. More insights on the method and its practical uses can be obtained by referring to Refs. [6,18–20,23,24,29], including the sources cited therein.

The inertial proximal scheme was proposed by F. Alvarez and H. Attouch in 2001 [36]. The method is inspired by the heavy ball with friction dynamical system, and given any two points ${\xi }_0,{\xi }_1\in \mathcal{S}$, the sequence $\left({\xi }_{\kappa }\right)$ is defined using the iterative rule:

$$\{\begin{array}{l}{t}_h=x_h+{\phi }_h\left({\xi }_h-{\xi }_{h-1}\right)\\ {\xi }_{h+1}=\text{pro}{\mathrm{x}}_{{\mathrm{\Lambda }}_h\gamma }\left(t_h\right)\end{array}$$ (1.9)

Further details about the scheme can be found in the original source [36].

After the convergence properties of the inertial proximal scheme were discovered, researchers in the field put in significant efforts to improve the algorithm in various ways. For instance, A. Beck and M. Teboulle [23] developed the Fast Inertia Shrinkage Thresholding Algorithm (FISTA) in 2009. To implement FISTA, two initial values ${\xi }_0$ and ${\xi }_1$ are chosen from a set $\mathcal{S}$, and $t_0$ is set to 1. The update rule involves four steps, including the calculation of $t_{h+1}$, ${\phi }_h$, $y_h$, and ${\xi }_{h+1}$, which make use of various parameters such as ${\mathrm{\Lambda }}_h$, $\nabla \mathrm{\Xi }\left(y_h\right)$, and the proximal operator. The algorithm is given as:

$$t_{h+1}=\frac{1+{\left(1+4t_{h-1}^2\right)}^{1/2}}{2}$$

$${\phi }_h=\frac{t_{h-1}-1}{t_h}$$

$$y_h={\xi }_h+{\phi }_h\left({\xi }_h-{\xi }_{h-1}\right)$$

$${\xi }_{h+1}=\text{pro}{\mathrm{x}}_{{\mathrm{\Lambda }}_{h}p}\left(y_h-{\mathrm{\Lambda }}_h\nabla \mathrm{\Xi }\left(y_h\right)\right)$$ (1.10)

Tseng [10] introduced a modified shrinkage thresholding approach or a method that utilizes a step-size line-search technique in 2000. This method can be defined as follows: given $\mathrm{{\rm Y}}>0$, $\varkappa \in \left(\mathrm{0,1}\right)$, $\sigma \in \left(\mathrm{0,1}\right)$, and ${\xi }_0,{\xi }_1\in \mathcal{S}$, we have:

$$y_h=\text{pro}{\mathrm{x}}_{\mathrm{\Lambda }hp}\left({\xi }_h-\mathrm{\Lambda }h\nabla \mathrm{\Xi }\left({\xi }_h\right)\right)$$

$$\xi h+1=\text{prox}{\mathrm{\Lambda }}_{h}p\left(y_h-{\mathrm{\Lambda }}_h\left(\nabla \mathrm{\Xi }\left(y_h\right)-\nabla \mathrm{\Xi }\left({\xi }_h\right)\right)\right)$$ (1.11)

Here, ${\mathrm{\Lambda }}_h$ is the maximum value of $\mathrm{\Lambda }\in \mathrm{{\rm Y}},\mathrm{{\rm Y}}\varkappa ,\mathrm{{\rm Y}}{\varkappa }^2,...$ that satisfies $\mathrm{\Lambda }\left|\nabla \mathrm{\Xi }\left(y_h\right)-\nabla \mathrm{\Xi }\left({\xi }_h\right)\right|\le \left|y_h-{\xi }_h\right|$.

A novel modified forward-backward splitting method was recently introduced by Padcharoen et al. [37] in 2021. Their definition of the method is as follows: Let ${\xi }_0$ and ${\xi }_1$ be elements of $\mathcal{S}$. Then, we can compute

$$t_h={\xi }_h+{\phi }_h\left({\xi }_h-{\xi }_{h-1}\right)\text{.}$$

$$y_h=\text{pro}{\mathrm{x}}_{\mathrm{\Lambda }p}\left(t_h-{\mathrm{\Lambda }}_h\nabla \mathrm{\Xi }\left(t_h\right)\right)$$

$${\xi }_{h+1}=y_h-{\mathrm{\Lambda }}_h\left(\nabla \mathrm{\Xi }\left(y_h\right)-\nabla \mathrm{\Xi }\left(t_h\right)\right)$$ (1.12)

This method can be used to solve optimization problems effectively and efficiently. Suparat Kesornprom and Prasit Cholamjiak in Ref. [22] showed that the algorithm in (1.13) weakly converges to the solution of (1.6).

Kesornprom S. and Cholamjiak P. introduced a new inertial forward-backward method for solving the problem given in (1.6) [22]. This method is a recent addition to the class of proximal type algorithms. For $h\ge 1$, the algorithm computes ${\xi }_{h+1}$ using the following steps:

$$t_h={\xi }_h+\phi h\left({\xi }_h-\xi h-1\right)$$

$$y_h=\text{pro}{\mathrm{x}}_{\mathrm{\Lambda }p}\left(t_h-\mathrm{\Lambda }h\nabla \mathrm{\Xi }\left(t_h\right)\right)\text{.}$$

$${\xi }_{h+1}=y_h-{\mathrm{\Lambda }}_h\left(\nabla \mathrm{\Xi }\left(y_h\right)-\nabla \mathrm{\Xi }\left(t_h\right)\right)$$ (1.13)

Here, ${\xi }_0$ and ${\xi }_1$ are elements of $\mathcal{S}$, and ${\mathrm{\Lambda }}_1$ and ${\phi }_1$ are positive constants. Additionally, $\sigma \in \left(\mathrm{0,1}\right)$, and ${\mathrm{\Lambda }}_{h+1}$ is defined as follows:

$${\mathrm{\Lambda }}_{h+1}=\{\begin{array}{l}\min \left\{\frac{\sigma \Vert t_h-y_h\Vert }{\Vert \nabla \mathrm{\Xi }\left(t_h\right)-\nabla \mathrm{\Xi }\left(y_h\right)\Vert },{\mathrm{\Lambda }}_h\right\}\\ {\mathrm{\Lambda }}_h\end{array}\begin{array}{l}\text{if}\Vert \nabla \mathrm{\Xi }\left(t_h\right)-\nabla \mathrm{\Xi }\left(y_h\right)\Vert \ne 0\\ \text{otherwise}\end{array}$$

The authors proved in Ref. [22] that the algorithm in (1.13) converges weakly to the solution of (1.6), which makes it an effective tool for solving this type of problem.

The results discussed above provided motivation for us to propose a modified inertial extra-proximal-gradient algorithm. This algorithm is designed to converge to the solution of a convex optimization problem given in (1.6). We then applied this algorithm to an image and signal reconstruction problem.

2. Preliminary

The focus of this section will be to present a selection of widely recognized lemmas, propositions, and definitions hat are necessary to prove the main theorem in a satisfactory manner.

For any sequence ${\xi }_h\subseteq \mathcal{H}$, we define ${\omega }_h\left({\xi }_h\right)$ as the weak $\omega$-limit, which is a set containing ${\xi }^{*}\in \mathcal{H}$ such that there exists some subsequence $h_j$ of $h$ with ${\xi }_{h_j}$ weakly converging to ${\xi }^{*}$. We also have both weak (${\xi }_h\rightharpoonup {\xi }^{*}$) and strong (${\xi }_h\to {\xi }^{*}$) convergence of ${\xi }_h$ to ${\xi }^{*}$. Additionally, the subdifferential of $g$ is defined as

$$\partial p\left(\xi \right)=\left\{u\in \mathcal{H}|⟨u,t-\xi ⟩\le p\left(t\right)-g\left(\xi \right),t\in \mathcal{H}\right\}\text{.}$$

Lemma 2.1 (see Refs. [17],[18]) Consider a real Hilbert space $\mathcal{H}$, the following statements are valid:

J1 for every ${\xi }_1,{\xi }_2\in \mathcal{H}$, $\Vert {\xi }_1+{\xi }_2\Vert ={\Vert {\xi }_1\Vert }^2+2⟨{\xi }_1,{\xi }_2⟩+{\Vert {\xi }_2\Vert }^2$.

J2 $\text{for}\text{every}\xi ,{\xi }_2\in \mathcal{H}$, $\Vert \xi +{\xi }_2\Vert \le {\Vert \xi \Vert }^2+2⟨\xi +{\xi }_2,{\xi }_2⟩$.

J3 $\text{for}\text{every}\alpha \in \mathbb{R},\xi ,{\xi }_2\in \mathcal{H}\Vert \alpha \xi -\left(\alpha -1\right){\xi }_2\Vert =\alpha {\Vert \xi \Vert }^2-\left(1-\alpha \right){\Vert {\xi }_2\Vert }^2-\alpha \left(1-\alpha \right){\Vert \xi -{\xi }_2\Vert }^2$.

J4 $\text{for}\text{every}\xi ,{\xi }_2,{\xi }_{3}in\mathcal{H}$, $\Vert \xi -{\xi }_2-{\xi }_3\Vert ={\Vert \xi \Vert }^2+{\Vert {\xi }_2\Vert }^2+{\Vert {\xi }_3\Vert }^2+2⟨\xi ,{\xi }_3⟩-2⟨\xi ,{\xi }_2⟩-2⟨\xi ,{\xi }_3⟩$.

Lemma 2.2 (see Ref. [22]). Suppose that ${\mathrm{\xi }}_{\mathrm{h}}$ is quasi-Fejer convergent to a point within the set $\mathcal{S}$. Then, we can deduce the following:

• I.$\left\{{\xi }_h\right\}$ is bounded.
• II.If every weak accumulation point of ${\xi }_h$ lies in $\mathcal{S}$, then ${\xi }_h$ converges weakly to a point within $\mathcal{S}$.

Lemma 2.3 (see Ref. [22]). Suppose we have real, positive sequences ${\mathrm{\tau }}_{\mathrm{h}}$, ${\mathrm{\beta }}_{\mathrm{h}}$, and ${\mathrm{\eta }}_{\mathrm{h}}$ such that:

$${\eta }_{h+1}\le \left(1+{\beta }_h\right){\eta }_h+{\tau }_h,h\ge 1\text{.}$$

If the infinite sums ${\sum }_{h=1}^{\infty }{\beta }_h$ and ${\sum }_{h=1}^{\infty }{\tau }_h$ are both finite, then the limit of ${\eta }_h$ as $h$ approaches infinity exists.

Lemma 2.4 (see Ref. [22]). Consider a subdifferential operator $\partial \mathrm{g}$ that is maximal monotone. addition, the graph of $\partial \mathrm{g}$, $\mathrm{G}\left(\partial \mathrm{g}\right)=\left\{\left(\mathrm{\xi },\mathrm{v}\right)\in \mathcal{H}\times \mathcal{H}:\mathrm{v}\in \partial \mathrm{g}\left(\mathrm{\xi }\right)\right\}$ is demiclosed, that is, if a sequence $\left\{\left({\mathrm{\xi }}_{\mathrm{h}},{\mathrm{v}}_{\mathrm{h}}\right)\right\}\subset \mathrm{G}\left(\partial \mathrm{g}\right)$ satisfying the conditions that $\left\{{\mathrm{\xi }}_{\mathrm{h}}\right\}$ converges weakly to ${\mathrm{\xi }}^{*}$ and $\left\{{\mathrm{v}}_{\mathrm{h}}\right\}$ converges strongly to ${\mathrm{v}}^{*}$, then $\left(\mathrm{\xi },\mathrm{v}\right)\in \mathrm{G}\left(\partial \mathrm{g}\right)$.

Lemma 2.5 (see Ref. [22]) Suppose we have real, positive sequences ${\mathrm{\eta }}_{\mathrm{h}}$ and ${\mathrm{\beta }}_{\mathrm{h}}$ such that:

$${\mathrm{\eta }}_{\mathrm{h}+1}\le \left(1+{\mathrm{\beta }}_{\mathrm{h}}\right){\mathrm{\eta }}_{\mathrm{h}}+{\mathrm{\beta }}_{\mathrm{h}}{\mathrm{\eta }}_{\mathrm{h}-1},\mathrm{h}\ge 1\text{.}$$

Then, we have ${\mathrm{\eta }}_{\mathrm{h}+1}\le \mathrm{\kappa }\cdot {\prod }_{\mathrm{i}=1}^{\mathrm{h}}\left(1+2{\mathrm{\beta }}_{\mathrm{i}}\right)$, where $\mathrm{\kappa }=\max \left\{{\mathrm{\eta }}_1,{\mathrm{\eta }}_2\right\}$. Furthermore, if ${\sum }_{\mathrm{h}=1}^{\infty }{\mathrm{\beta }}_{\mathrm{h}}<\infty$, then the sequence ${\mathrm{\eta }}_{\mathrm{h}}$ is bounded.

Definition 2.1 (see Ref. [22]) Consider a subset $\mathcal{S}$ of $\mathcal{H}$ such that $\mathcal{S}\ne \varnothing$. We define a sequence ${\mathrm{\xi }}_{\mathrm{h}}$ in $\mathcal{H}$ to be quasi-Fejer convergent to a point in $\mathcal{S}$ if and only if, for every $\mathrm{\xi }\in \mathcal{S}$, there exists a positive sequence ${ϵ}_{\mathrm{h}}$ satisfying ${\sum }_{\mathrm{h}=1}^{\infty }{ϵ}_{\mathrm{h}}<+\infty$, and $\parallel {\mathrm{\xi }}_{\mathrm{h}+1}-{\mathrm{\xi }}^{*}{\parallel }^2\le \parallel {\mathrm{\xi }}_{\mathrm{h}}-{\mathrm{\xi }}^{*}{\parallel }^2+{ϵ}_{\mathrm{h}}$ for every $\mathrm{h}\ge 1$. If the sequence ${ϵ}_{\mathrm{h}}$ is null, then we can conclude that ${\mathrm{\xi }}_{\mathrm{h}}$ is Fejer convergent to a point in $\mathcal{S}$.

Definition 2.2 (see Ref. [22]) Consider a nonlinear point to set function $\mathrm{\gamma }:\mathcal{S}\to 2^{\mathcal{H}}$, the graph of $\mathrm{\gamma }$ is the set

$$G\left(\gamma \right)=\left\{\left(\xi ,p\right)p\in \gamma \left(\xi \right)\right\}$$

for every $\xi$ and $p$ in the set $\mathcal{S}$, the operator $\gamma$ is said to be non-expansive if,

$$\Vert \gamma \xi -\gamma p\Vert \le \parallel \xi -p\parallel$$

If for any $\xi$ and $p$ belonging to a set $\mathcal{S}$, and $u$ and $v$ belonging to $\gamma \xi$ and $\gamma p$ respectively, the inequality $⟨u-v,\xi -p⟩\ge 0$ holds, then the operator $\gamma$ can be referred to as monotone.

$\gamma$ is a maximal monotone operator if the graph if its graph is not entirely contained within the graph of any other monotone operator.

$\gamma$ is strongly monotone if we can find $\mathrm{\Lambda }>0$ such that

$$⟨\gamma \xi -\gamma p,\xi -p⟩\ge \mathrm{\Lambda }{\Vert \xi -p\Vert }^{2}forall\xi ,p\in \mathcal{S}$$

If there exists a positive value $\mathrm{\Lambda }$ such that for any $\xi$ and $p$ in set $\mathcal{S}$, the inequality $⟨\gamma \xi -\gamma p,\xi -p⟩\ge \mathrm{\Lambda }{\left|\xi -p\right|}^2$ holds, then $\gamma$ is said to be strongly monotone.

The function $F$ is considered to be firmly non-expansive if, for any two points $\xi$ and $p$ in a set $\mathcal{S}$, the following inequality holds:

$$⟨\gamma \xi -\gamma p,\xi -p⟩\ge {\Vert \gamma \xi -\gamma p\Vert }^2$$

3. Convergence analysis

Our interest in this section is to show that algorithm (3.1) converges weakly to a point in the set of solution $\mathrm{\Omega }$ of (1.6). In this section, we will also state and proof some new useful lemmas that will assist in showing convergence.

C1 The feasible region for the convex optimization problem (1.6) has at least one solution, which means that it is not empty, and it is given in the set below:

$$\mathrm{\Omega }=\mathrm{argmin}\left(l+\mathrm{\Xi }\right)\ne \varnothing$$

C2 $l,\mathrm{\Xi }:\mathcal{H}\to (-\infty ,+\infty ]$ are two convex, proper and lower semi-continuous operators.

C3 $l$ is smooth on $\mathcal{H}$ and $\nabla \mathrm{\Xi }$ is Lipschitz continuous on $\mathcal{H}$ with the Lipschitz constant $K$ $>$ 0. (1.6).

The function $l$ is smooth over the set $\mathcal{H}$, and the gradient of $\mathrm{\Xi }$ is bounded by a Lipschitz constant $K$ over $\mathcal{H}$, where $K$ is a positive value, this is. This relationship is expressed in equation (1.6).

We will now present a method for solving equation (1.6), which we call the "inertial extra forward-backward technique".

Algorithm 3.1 An Initial extra-proximal Extra Forward and Backward Method (IEFBM)

Initialize-step: Let ${\xi }_0={\xi }_1\in \mathcal{H},{\mathrm{\Lambda }}_1,{\phi }_1,{\mathrm{\Phi }}_1>0$ and $\sigma \in \left(\mathrm{0,1}\right)$.

Recursive Step: for $h\ge 1$, the following computation for ${\xi }_{h+1}$ is performed:

1st-step Compute the inertial term: $t_h={\xi }_h+{\mathrm{\Phi }}_h\left({\xi }_h-{\xi }_{h-1}\right)$.

2nd-step Compute the proximal gradient descent two times in a progressive manner:

$$y_h=\text{prox}\left(t_h-{\mathrm{\Lambda }}_h\nabla \mathrm{\Xi }\left(t_h\right)\right)$$

$$z_h=\text{prox}\left(y_h-{\phi }_h\nabla \mathrm{\Xi }\left(y_h\right)\right)$$

3rd-tep Compute ${\xi }_{h+1}$ step:

$${\xi }_{h+1}=z_h-{\mathrm{\Lambda }}_h\left(\nabla \mathrm{\Xi }\left(y_h\right)-\nabla \mathrm{\Xi }\left(t_h\right)\right)-{\phi }_h\left(\nabla \mathrm{\Xi }\left(z_h\right)-\nabla \mathrm{\Xi }\left(y_h\right)\right)$$

$${\mathrm{\Lambda }}_{h+1}=\{\begin{array}{l}\min \left\{\frac{\sigma \Vert t_h-y_h\Vert }{\Vert \nabla \mathrm{\Xi }\left(t_h\right)-\nabla \mathrm{\Xi }\left(y_h\right)\Vert },{\mathrm{\Lambda }}_h\right\}\\ {\mathrm{\Lambda }}_h\end{array}\begin{array}{l}\text{if}\Vert \nabla \mathrm{\Xi }\left(t_h\right)-\nabla \mathrm{\Xi }\left(y_h\right)\Vert \ne 0\\ \text{otherwise}\end{array}$$

$${\phi }_{h+1}=\{\begin{array}{l}\min \left\{\frac{\sigma \Vert z_h-y_h\Vert }{\Vert \nabla \mathrm{\Xi }\left(z_h\right)-\nabla \mathrm{\Xi }\left(y_h\right)\Vert },{\mathrm{\Lambda }}_h\right\}\\ {\mathrm{\Lambda }}_h\end{array}\begin{array}{l}\text{if}\Vert \nabla \mathrm{\Xi }\left(z_h\right)-\nabla \mathrm{\Xi }\left(y_h\right)\Vert \ne 0\\ \text{otherwise}\end{array}$$

4th-step stop when $\parallel {\xi }_h-{\xi }_{h+1}\parallel <ϵ$, otherwise, set $h=h+1$ and move control to the first step

Lemma 3.1 Suppose that the sequence ${\mathrm{\xi }}_{\mathrm{h}}$ is produced by Algorithm 3.1. Then

$${\Vert {\xi }_{h+1}-{\xi }^{*}\Vert }^2\le {\Vert t_h-{\xi }^{*}\Vert }^2-\left[\left(1-\frac{{\mathrm{\Lambda }}_h^2{\sigma }^2}{{\mathrm{\Lambda }}_{h+1}^2}\right)+\frac{2\sigma }{{\mathrm{\Lambda }}_{h+1}}\cdot \left(1+\frac{{\mathrm{\Lambda }}_h}{{\mathrm{\Lambda }}_{h+1}}\right)\left(1-\frac{{\mathrm{\Lambda }}_h{\phi }_h\sigma }{{\phi }_{h+1}}\right)\right]{\Vert y_h-t_h\Vert }^2-\left(1-\frac{{\phi }_h^2{\sigma }^2}{{\phi }_{h+1}^2}\right){\Vert z_h-y_h\Vert }^2$$

for ${\xi }^{*}$ in the solution set

Proof. Assuming that (1.6) has a solution, say ${\xi }^{*}$ we can proceed to deduce the following:

$${\Vert {\xi }_{h+1}-{\xi }^{*}\Vert }^2={\Vert z_h-{\mathrm{\Lambda }}_h\left(\nabla \mathrm{\Xi }\left(y_h\right)-\nabla \mathrm{\Xi }\left(t_h\right)\right)-{\phi }_h\left(\nabla \mathrm{\Xi }\left(z_h\right)-\nabla \mathrm{\Xi }\left(y_h\right)\right)-{\xi }^{*}\Vert }^2$$

$$={\Vert z_h-{\xi }^{*}-{\mathrm{\Lambda }}_h\left(\nabla \mathrm{\Xi }\left(y_h\right)-\nabla \mathrm{\Xi }\left(t_h\right)\right)-{\phi }_h\left(\nabla \mathrm{\Xi }\left(z_h\right)-\nabla \mathrm{\Xi }\left(y_h\right)\right)\Vert }^2$$

$$={\Vert z_h-{\xi }^{*}\Vert }^2+{\mathrm{\Lambda }}_h^2{\Vert \left(\nabla \mathrm{\Xi }\left(y_h\right)-\nabla \mathrm{\Xi }\left(t_h\right)\right)\Vert }^2$$

$$+{\phi }_h^2{\Vert \left(\nabla \mathrm{\Xi }\left(z_h\right)-\nabla \mathrm{\Xi }\left(y_h\right)\right)\Vert }^2-2⟨z_h-{\xi }^{*},{\mathrm{\Lambda }}_h\left(\nabla \mathrm{\Xi }\left(y_h\right)-\nabla \mathrm{\Xi }\left(t_h\right)\right)⟩$$

$$-2⟨z_h-{\xi }^{*},{\phi }_h\left(\nabla \mathrm{\Xi }\left({\mathrm{z}}_{\mathrm{n}}\right)-\nabla \mathrm{\Xi }\left(y_h\right)\right)⟩$$

$$+2⟨{\mathrm{\Lambda }}_h(\nabla \mathrm{\Xi }\left(z_h\right)-\nabla \mathrm{\Xi }\left(y_h\right),{\phi }_h\left(\nabla \mathrm{\Xi }\left(y_h\right)-\nabla \mathrm{\Xi }\left(t_h\right)\right)⟩$$

$$\le {\Vert z_h-{\xi }^{*}\Vert }^2+{\mathrm{\Lambda }}_h^2{\Vert \left(\nabla \mathrm{\Xi }\left(y_h\right)-\nabla \mathrm{\Xi }\left(t_h\right)\right)\Vert }^2$$

$$+{\phi }_h^2{\Vert \left(\nabla \mathrm{\Xi }\left(z_h\right)-\nabla \mathrm{\Xi }\left(y_h\right)\right)\Vert }^2-2⟨z_h-y_h,{\mathrm{\Lambda }}_h\left(\nabla \mathrm{\Xi }\left(y_h\right)-\nabla \mathrm{\Xi }\left(t_h\right)\right)⟩$$

$$-2⟨y_h-{\xi }^{*},{\mathrm{\Lambda }}_h\left(\nabla \mathrm{\Xi }\left(y_h\right)-\nabla \mathrm{\Xi }\left(t_h\right)\right)⟩$$

$$-2⟨z_h-{\xi }^{*},{\phi }_h\left(\nabla \mathrm{\Xi }\left(z_h\right)-\nabla \mathrm{\Xi }\left(y_h\right)\right)⟩$$

$$+2{\mathrm{\Lambda }}_h{\phi }_h⟨\left(\nabla \mathrm{\Xi }\left(z_h\right)-\nabla \mathrm{\Xi }\left(y_h\right)\right),\left(\nabla \mathrm{\Xi }\left(y_h\right)-\nabla \mathrm{\Xi }\left(t_h\right)\right)⟩$$

$$\le {\Vert z_h-{\xi }^{*}\Vert }^2+{\mathrm{\Lambda }}_h^2{\Vert \left(\nabla \mathrm{\Xi }\left(y_h\right)-\nabla \mathrm{\Xi }\left(t_h\right)\right)\Vert }^2$$

$$+{\phi }_h^2{\Vert \left(\nabla \mathrm{\Xi }\left(z_h\right)-\nabla \mathrm{\Xi }\left(y_h\right)\right)\Vert }^2-2\parallel z_h-y_h\parallel \parallel \nabla \mathrm{\Xi }\left(y_h\right)-\nabla \mathrm{\Xi }\left(t_h\right)\parallel$$

$$-2⟨y_h-{\xi }^{*},{\mathrm{\Lambda }}_h\left(\nabla \mathrm{\Xi }\left(y_h\right)-\nabla \mathrm{\Xi }\left(t_h\right)\right)⟩$$ (3.1)

$$-2⟨z_h-{\xi }^{*},{\phi }_h\left(\nabla \mathrm{\Xi }\left(z_h\right)-\nabla \mathrm{\Xi }\left(y_h\right)\right)⟩+$$

$$2{\mathrm{\Lambda }}_h{\phi }_h\Vert \nabla \mathrm{\Xi }\left(z_h\right)-\nabla \mathrm{\Xi }\left(y_h\right)\Vert \parallel \nabla \mathrm{\Xi }\left(y_h\right)-\nabla \mathrm{\Xi }\left(t_h\right)\parallel$$

The following conclusions are draw from the hypothesis in algorithm 3.1,

$${\mathrm{\Lambda }}_{h+1}=\min \left\{{\mathrm{\Lambda }}_h,\frac{\sigma \Vert t_h-y_h\Vert }{\Vert \nabla \mathrm{\Xi }\left(t_h\right)-\nabla \mathrm{\Xi }\left(y_h\right)\Vert }\right\}\le \frac{\sigma \Vert t_h-y_h\Vert }{\Vert \nabla \mathrm{\Xi }\left(t_h\right)-\nabla \mathrm{\Xi }\left(y_h\right)\Vert }\text{.}$$

Therefore,

$$\parallel \nabla \mathrm{\Xi }\left(t_h\right)-\nabla \mathrm{\Xi }\left(y_h\right)\parallel \le \frac{\sigma }{{\mathrm{\Lambda }}_{h+1}}\parallel t_h-y_h\parallel \text{.}$$ (3.2)

Similarly,

$$\Vert \nabla \mathrm{\Xi }\left(y_h\right)-\nabla \mathrm{\Xi }\left(z_h\right)\Vert \le \frac{\sigma }{{\phi }_{h+1}}\parallel y_h-z_h\parallel$$ (3.3)

it is easy to see that

$$\Vert z_h-y_h\Vert \le \left(1+\frac{{\mathrm{\Lambda }}_h}{{\mathrm{\Lambda }}_{h+1}}\right)\parallel t_h-y_h\parallel \text{.}$$ (3.4)

Hence, substituting it into equation (3.3) we have,

$$\Vert \nabla \mathrm{\Xi }\left(y_h\right)-\nabla \mathrm{\Xi }\left(z_h\right)\Vert \le \frac{\sigma }{{\phi }_{h+1}}\cdot \left(1+\frac{{\mathrm{\Lambda }}_h}{{\mathrm{\Lambda }}_{h+1}}\right)\parallel t_h-y_h\parallel \text{.}$$ (3.5)

Now, let us compute ${\Vert z_h-{\xi }^{*}\Vert }^2$,

$${\Vert z_h-{\xi }^{*}\Vert }^2={\Vert z_h-y_h+y_h-{\xi }^{*}\Vert }^2$$

$$={\Vert z_h-y_h\Vert }^2+{\Vert y_h-{\xi }^{*}\Vert }^2+2⟨z_h-y_h,y_h-{\xi }^{*}⟩$$

$$={\Vert y_h-{\xi }^{*}\Vert }^2-{\Vert z_h-y_h\Vert }^2+2⟨z_h-y_h,z_h-{\xi }^{*}⟩$$

$$={\Vert t_h-{\xi }^{*}\Vert }^2-{\Vert y_h-t_h\Vert }^2-{\Vert z_h-y_h\Vert }^2$$

$$+2⟨y_h-t_h,y_h-{\xi }^{*}⟩+2⟨z_h-y_h,z_h-{\xi }^{*}⟩\text{.}$$ (3.6)

Substituting (3.4), (3.5) and (3.6) into (3.1) we have,

$${\Vert {\xi }_{h+1}-{\xi }^{*}\Vert }^2\le {\Vert t_h-{\xi }^{*}\Vert }^2-{\Vert y_h-t_h\Vert }^2-{\Vert z_h-y_h\Vert }^2+{\mathrm{\Lambda }}_h^2{\Vert \left(\nabla \mathrm{\Xi }\left(y_h\right)-\nabla \mathrm{\Xi }\left(t_h\right)\right)\Vert }^2$$

$$+{\phi }_h^2{\Vert \left(\nabla \mathrm{\Xi }\left(z_h\right)-\nabla \mathrm{\Xi }\left(y_h\right)\right)\Vert }^2-\frac{2\sigma }{{\mathrm{\Lambda }}_{h+1}}\cdot \left(1+\frac{{\mathrm{\Lambda }}_h}{{\mathrm{\Lambda }}_{h+1}}\right){\Vert t_h-y_h\Vert }^2+$$

$$\frac{2{\mathrm{\Lambda }}_h{\phi }_h{\sigma }^2}{{\phi }_{h+1}{\mathrm{\Lambda }}_{h+1}}\cdot \left(1+\frac{{\mathrm{\Lambda }}_h}{{\mathrm{\Lambda }}_{h+1}}\right){\Vert t_h-y_h\Vert }^2+2⟨y_h-t_h,y_h-{\xi }^{*}⟩+$$

$$2⟨z_h-y_h,z_h-{\xi }^{*}⟩-2⟨y_h-{\xi }^{*},{\mathrm{\Lambda }}_h\left(\nabla \mathrm{\Xi }\left(y_h\right)-\nabla \mathrm{\Xi }\left(t_h\right)\right)⟩$$

$$-2⟨z_h-{\xi }^{*},{\phi }_h\left(\nabla \mathrm{\Xi }\left(z_h\right)-\nabla \mathrm{\Xi }\left(y_h\right)\right)⟩$$

$$\le {\Vert t_h-{\xi }^{*}\Vert }^2-\left(1-\frac{{\mathrm{\Lambda }}_h^2{\sigma }^2}{{\mathrm{\Lambda }}_{h+1}^2}\right){\Vert y_h-t_h\Vert }^2-\left(1-\frac{{\phi }_h^2{\sigma }^2}{{\phi }_{h+1}^2}\right){\Vert z_h-y_h\Vert }^2-$$

$$\frac{2\sigma }{{\mathrm{\Lambda }}_{h+1}}\cdot \left(1+\frac{{\mathrm{\Lambda }}_h}{{\mathrm{\Lambda }}_{h+1}}\right)\left(1-\frac{{\mathrm{\Lambda }}_h{\phi }_h\sigma }{{\phi }_{h+1}}\right){\Vert t_h-y_h\Vert }^2$$ (3.7)

$$-2{\mathrm{\Lambda }}_h⟨t_h-y_h+\left(\nabla \mathrm{\Xi }\left(y_h\right)-\nabla \mathrm{\Xi }\left(t_h\right)\right),y_h-{\xi }^{*}⟩$$

$$-2{\phi }_h⟨y_h-z_h+\left(\nabla \mathrm{\Xi }\left(z_h\right)-\nabla \mathrm{\Xi }\left(y_h\right)\right),z_h-{\xi }^{*}⟩\text{.}$$

From Algorithm (3.1) we have, $z_h=\text{pro}{\mathrm{x}}_{{\phi }_{h}g}\left(y_h-{\phi }_h\nabla \mathrm{\Xi }\left(y_h\right)\right)\Rightarrow y_h-{\phi }_h\nabla \mathrm{\Xi }\left(y_h\right)-z_h\in {\phi }_h\partial g\left(z_h\right)\text{.}$ Let ${\xi }_h\in \partial g\left(z_h\right)$ then we have that

$${\xi }_h=\frac{1}{{\phi }_h}\left(y_h-{\phi }_h\nabla \mathrm{\Xi }\left(y_h\right)-z_h\right)\text{.}$$

Since ${\xi }^{*}$ is an element of the set of solution, $\mathrm{\Omega }$ defined in (1.6), then $0\in \left(\nabla \mathrm{\Xi }+\partial g\right){\xi }^{*}$. Therefore,

$$⟨\nabla \mathrm{\Xi }\left(z_h\right)+{\xi }_h,z_h-{\xi }^{*}⟩\ge 0\text{.}$$ (3.8)

We obtain,

$$\frac{1}{{\phi }_h}⟨y_h-z_h+{\phi }_h\nabla \mathrm{\Xi }\left(z_h\right)-{\phi }_h\nabla \mathrm{\Xi }\left(y_h\right),z_h-{\xi }^{*}⟩\ge 0$$

$$\Rightarrow ⟨y_h-z_h+{\phi }_h\nabla \mathrm{\Xi }\left(z_h\right)-{\phi }_h\nabla \mathrm{\Xi }\left(y_h\right),z_h-{\xi }^{*}⟩\ge 0\text{.}$$ (3.9)

Similarly, since $y_h=\text{pro}{\mathrm{x}}_{{\mathrm{\Lambda }}_{h}p}\left(t_h-{\mathrm{\Lambda }}_h\nabla \mathrm{\Xi }\left(t_h\right)\right)$ and if we let ${\eta }_h\in \partial f\left(y_h\right)$ we can have that,

$$⟨\nabla \mathrm{\Xi }\left(y_h\right)+{\eta }_h,y_h-{\xi }^{*}⟩\ge 0\text{.}$$ (3.10)

Hence, we have

$$⟨t_h-y_h+{\mathrm{\Lambda }}_h\nabla \mathrm{\Xi }\left(y_h\right)-{\mathrm{\Lambda }}_h\nabla \mathrm{\Xi }\left(t_h\right),y_h-{\xi }^{*}⟩\ge 0\text{.}$$ (3.11)

Using (3.8), (3.10) we obtain,

$${\Vert {\xi }_{h+1}-{\xi }^{*}\Vert }^2\le {\Vert t_h-{\xi }^{*}\Vert }^2-\left[\left(1-\frac{{\mathrm{\Lambda }}_h^2{\sigma }^2}{{\mathrm{\Lambda }}_{h+1}^2}\right)+\frac{2\sigma }{{\mathrm{\Lambda }}_{h+1}}\cdot \left(1+\frac{{\mathrm{\Lambda }}_h}{{\mathrm{\Lambda }}_{h+1}}\right)\left(1-\frac{{\mathrm{\Lambda }}_h{\phi }_h\sigma }{{\phi }_{h+1}}\right)\right]\cdot$$

$${\Vert y_h-t_h\Vert }^2-\left(1-\frac{{\phi }_h^2{\sigma }^2}{{\phi }_{h+1}^2}\right)\Vert z_h-y_h\Vert$$ (3.12)

Lemma 3.2 Let Algorithm 3.1. generates $\left\{{\mathrm{\xi }}_{\mathrm{h}}\right\}$ then If ${\sum }_{\mathrm{h}=1}^{\infty }{\mathrm{\Phi }}_{\mathrm{h}}<\infty$, we obtain that

$$\underset{h\to \infty }{\lim }\parallel {\xi }_h-{\xi }^{*}\parallel$$

exists for every ${\xi }^{*}\in \mathrm{\Omega }$, the solution set.

Proof. Since ${\xi }^{*}$ is an element of the set of solution, then from lemma 3.1 we obtain,

$$\Vert {\xi }_{h+1}-{\xi }^{*}\Vert \le \parallel t_h-{\xi }^{*}\parallel$$

Notice that

$$\parallel {\xi }_{h+1}-{\xi }^{*}\parallel \le \Vert t_h-{\xi }^{*}\Vert \le \parallel {\xi }_h-{\mathrm{\Phi }}_h\left({\xi }_h-{\xi }_{h-1}\right)-{\xi }^{*}\parallel$$

$$\le \Vert {\xi }_h-{\xi }^{*}\Vert +{\mathrm{\Phi }}_h\Vert {\xi }_h-{\xi }_{h-1}\Vert$$

$$\le \Vert {\xi }_h-{\xi }^{*}\Vert +{\mathrm{\Phi }}_h\Vert {\xi }_h-{\xi }^{*}\Vert +\mathrm{\Phi }\Vert {\xi }_{h-1}-{\xi }^{*}\Vert$$

$$\le \left(1+{\mathrm{\Phi }}_h\right)\Vert {\xi }_h-{\xi }^{*}\Vert +{\mathrm{\Phi }}_h\parallel {\xi }_{h-1}-{\xi }^{*}\parallel \text{,}$$

hence, we obtained

$$\Vert {\xi }_{h+1}-{\xi }^{*}\Vert \le \left(1+{\mathrm{\Phi }}_h\right)\Vert {\xi }_h-{\xi }^{*}\Vert +{\mathrm{\Phi }}_h\parallel {\xi }_{h-1}-{\xi }^{*}\parallel \text{.}$$ (3.13)

Using Lemma 2.5, we derive that

$$\Vert {\xi }_{h+1}-{\xi }^{*}\Vert \le \kappa \prod _{m=1}^h\left(1+2{\mathrm{\Phi }}_m\right)$$

where $\kappa =\max \left\{\Vert {\xi }_1-{\xi }^{*}\Vert ,\Vert {\xi }_2-{\xi }^{*}\Vert \right\}$. Since, ${\sum }_{h=1}^{\infty }{\mathrm{\Phi }}_h<+\infty$, by Lemma 2.5, we have that $\left\{{\xi }_h-{\xi }^{*}\right\}$ is bounded, that is ${\sum }_{h=1}^{\infty }{\mathrm{\Phi }}_h\parallel {\xi }_{h-1}-{\xi }^{*}\parallel <+\infty$. Therefore, using (3.12) and Lemma 2.3 we can conclude that ${\lim }_{h\to \infty }\parallel {\xi }_h-{\xi }^{*}\parallel$ exists. This complete the proof.

Lemma 3.3 Let Algorithm 3.1 generates $\left\{{\xi }_h\right\}$. If ${\sum }_{h=1}^{\infty }{\Phi }_h<\infty$, then

$$\underset{h\to \infty }{\lim }\parallel {\xi }_{h+1}-{\xi }_h\parallel =0$$

Proof.

$$\parallel {\xi }_{h+1}-{\xi }_h\parallel \le \Vert {\xi }_{h+1}-{\xi }_h\Vert =\parallel {\xi }_{h+1}-z_h+z_h-{\xi }_h\parallel$$

$$\le \Vert {\xi }_{h+1}-z_h\Vert +\Vert z_h-{\xi }_h\Vert \text{,}$$ (3.14)

it is enough to show that $\Vert {\xi }_{h+1}-z_h\Vert \to 0and\Vert z_h-{\xi }_h\Vert \to 0$.

We obtain,

$$\Vert {\xi }_{h+1}-z_h\Vert \le \Vert {\mathrm{\Lambda }}_h\left(\nabla \mathrm{\Xi }\left(y_h\right)-\nabla \mathrm{\Xi }\left(t_h\right)\right)-{\phi }_h\left(\nabla \mathrm{\Xi }\left(z_h\right)-\nabla \mathrm{\Xi }\left(y_h\right)\right)\Vert$$

$$\le {\mathrm{\Lambda }}_h\Vert \nabla \mathrm{\Xi }\left(y_h\right)-\nabla \mathrm{\Xi }\left(t_h\right)\parallel +{\phi }_h\parallel \nabla \mathrm{\Xi }\left(z_h\right)-\nabla \mathrm{\Xi }\left(y_h\right)\Vert$$ (3.15)

from Algorithm 3.1. Now, since $\nabla \mathrm{\Xi }$ is uniformly continuous,

$${\mathrm{\Lambda }}_h\Vert \nabla \mathrm{\Xi }\left(y_h\right)-\nabla \mathrm{\Xi }\left(t_h\right)\parallel +{\phi }_h\parallel \nabla \mathrm{\Xi }\left(z_h\right)-\nabla \mathrm{\Xi }\left(y_h\right)\Vert \to 0$$

From (3.15), we have

$$\Vert {\xi }_{h+1}-z_h\Vert \to 0ash\to \infty \text{.}$$ (3.16)

We also know that,

$$\Vert z_h-{\xi }_h\Vert \le \Vert z_h-t_h\parallel +\parallel t_h-{\xi }_h\Vert$$

$$\le \Vert z_h-y_h\parallel +\parallel y_h-t_h\parallel +\parallel t_h-{\xi }_h\Vert$$ (3.17)

From the inertial step in algorithm 3.1, we have

$$\Vert t_h-{\xi }_h\Vert =\Vert {\xi }_h+{\mathrm{\Phi }}_h\left({\xi }_h-{\xi }_{h-1}\right)-{\xi }_h\Vert ={\mathrm{\Phi }}_h\Vert {\xi }_h-{\xi }_{h-1}\Vert \to 0\left(h\to \infty \right)$$

Therefore

$$\Vert t_h-{\xi }_h\Vert \to 0ash\to \infty \text{.}$$ (3.18)

From (3.12) we have that

$${\Vert {\xi }_{h+1}-{\xi }^{*}\Vert }^2\le {\Vert t_h-{\xi }^{*}\Vert }^2-\left(\left(1-\frac{{\mathrm{\Lambda }}_h^2{\sigma }^2}{{\mathrm{\Lambda }}_{h+1}^2}\right)+\frac{2\sigma }{{\mathrm{\Lambda }}_{h+1}}\cdot \left(1+\frac{{\mathrm{\Lambda }}_h}{{\mathrm{\Lambda }}_{h+1}}\right)\left(1-\frac{{\mathrm{\Lambda }}_h{\phi }_h\sigma }{{\phi }_{h+1}}\right)\right)$$

$$\cdot {\Vert y_h-t_h\Vert }^2-\left(1-\frac{{\phi }_h^2{\sigma }^2}{{\phi }_{h+1}^2}\right){\Vert z_h-y_h\Vert }^2$$

$$\le {\Vert {\xi }_h-{\xi }^{*}\Vert }^2+{\mathrm{\Phi }}_h{\Vert \left({\xi }_h-{\xi }_{h-1}\right)\Vert }^2+2{\mathrm{\Phi }}_h\Vert {\xi }_h-{\xi }^{*}\Vert \parallel {\xi }_h-{\xi }_{h-1}\parallel -$$

$$\left(\left(1-\frac{{\mathrm{\Lambda }}_h^2{\sigma }^2}{{\mathrm{\Lambda }}_{h+1}^2}\right)+\frac{2\sigma }{{\mathrm{\Lambda }}_{h+1}}\cdot \left(1+\frac{{\mathrm{\Lambda }}_h}{{\mathrm{\Lambda }}_{h+1}}\right)\left(1-\frac{{\mathrm{\Lambda }}_h{\phi }_h\sigma }{{\phi }_{h+1}}\right)\right){\Vert y_h-t_h\Vert }^2$$ (3.19)

The fact that ${\mathrm{\Phi }}_h\Vert {\xi }_h-{\xi }_{h-1}\Vert \to 0ash\to \infty$ and that ${\lim }_{h\to \infty }\parallel {\xi }_h-{\xi }^{*}\parallel$ exists $-$ a conclusion from Lemma 3.2, we can conclude from (3.19) that

$$\Vert y_h-t_h\Vert \to 0ash\to \infty \text{,}$$

lastly, from 3.4 we can easy see that,

$$\parallel z_h-y_h\parallel \to 0ash\to \infty \text{.}$$

We have that,

$$\Vert z_h-{\xi }_h\Vert \to 0ash\to \infty \text{,}$$ (3.20)

hence, using the result of (3.20), (3.16) in (3.14) we conclude that

$$\parallel {\xi }_{h+1}-{\xi }_h\parallel \to 0ash\to \infty$$

This completes the proof.

Theorem 3.1 Suppose Algorithm 3.1 produces the sequence ${\mathrm{\xi }}_{\mathrm{h}}$. If the infinite series ${\sum }_{\mathrm{h}=1}^{\infty }{\mathrm{\alpha }}_{\mathrm{h}}$ converges to a finite value, then the sequence ${\mathrm{\xi }}_{\mathrm{h}}$ weakly converges to an element that belongs to the set of solutions $\mathrm{\Omega }$ defined by the problem in (1.6).

Proof. Given that the sequence ${\xi }_h$ is bounded, we can identify a subset of the sequence, denoted by ${\xi }_{h_k}$, such that $\parallel {\xi }_{h_k}-{\xi }^{*}\parallel \rightharpoonup 0$, where ${\xi }^{*}$ is a member of $\mathcal{H}$. By applying Lemma 3.3, it follows that $\parallel {\xi }_{h_k+1}-{\xi }^{*}\parallel \rightharpoonup 0$ for ${\xi }^{*}\in \mathcal{H}$. Using Algorithm 3.1 we get that,

$$\frac{y_{h_k}-z_{h_k}}{{\phi }_{h_k}}-\nabla \mathrm{\Xi }\left(y_{h_k}\right)+\nabla \mathrm{\Xi }\left(z_{h_k}\right)\in \partial l\left(z_{h_k}\right)+\nabla \mathrm{\Xi }\left(z_{h_k}\right)$$ (3.21)

From equation (3.20), we can deduce that $\Vert z_h-{\xi }_h\Vert \to 0$. As a result, it follows that $z_{h_k}$ weakly converges to ${\xi }^{*}$. By applying Lemma 2.4 and taking the limit as $k$ approaches infinity in equation (3.21), while considering the maximal property of the operator $\left(\partial l+\nabla \mathrm{\Xi }\right)$ and the uniform continuity of $\nabla \mathrm{\Xi }$, we can establish that:

$$0\in \left(\partial l+\nabla \mathrm{\Xi }\right)\left({\xi }^{*}\right)\text{or}\left({\xi }^{*},0\right)\in \mathrm{G}\left(\nabla \mathrm{\Xi }+\partial l\right)$$

Thus, we can conclude that ${\xi }^{*}$ belongs to the solution set of the maximal operator $\left(\partial g+\nabla \mathrm{\Xi }\right)$, i.e., ${\xi }^{*}\in \mathrm{\Omega }$. Additionally, we observe from inequality (3.19) that the sequence $\left\{{\xi }_h\right\}$ is a quasi-Fejer sequence. Therefore, using Lemma 2.2, we can establish that the sequence $\left\{{\xi }_h\right\}$ weakly converges to a point, say ${\xi }^{*}$ in the solution set $\mathrm{\Omega }$. This completes the proof.

4. Application of the propose algorithm to image and signal reconstruction

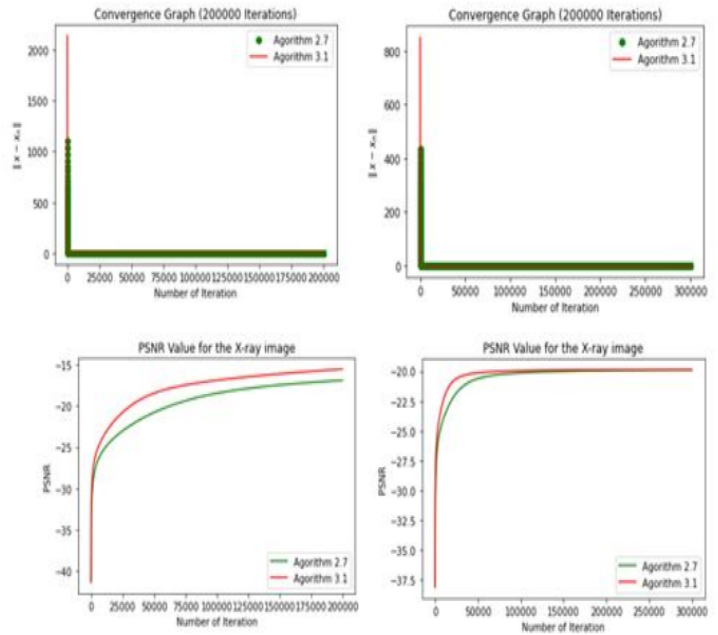
Our objective in this section is to furnish an illustration to show the application of the propose algorithm to image restoration and signal reconstruction respectively, and to exhibit the applicability, stability and efficacy of our newly introduced algorithm. To show how our proposed algorithm faired, we compared it with the very recent scheme introduced by Suparat Kesornprom and Prasit Cholamjiak [22].

Our initial issue pertains to the restoration of the original image from a blurred image, and we will employ the peak-signal-to-noise ratio (P.S.N.R), as presented by K. H. Thung and P. Raveendran [38], as a metric to gauge the efficacy of both methods in producing high-quality images. Given that $\xi$ is the original image and ${\xi }_h$ is the reconstructed image, then the P.S.N.R is defined follows:

$$\mathrm{P}.\mathrm{S}.\mathrm{N}.\mathrm{R}=10\cdot \text{lo}{\mathrm{g}}_{10}\left(\frac{255^2}{{\Vert {\xi }_h-\xi \Vert }^2}\right)$$

It is noted that, a greater P.S.N.R typically implies a better quality of reconstruction. This numerical experiment was conducted using JupyterLab (Python 3) on an 8 Giga Byte of RAM with a core i5 processor.

It is a commonly accepted fact that all images consist of a dimension of $N\times M$ pixels, and the values of each pixel are restricted to the range of $\left[\mathrm{0,255}\right]$. The process of image deblurring or masking is expressed through the following system of linear equations:

$$l=B\xi +u$$ (4.1)

The blurring matrix is denoted by $B$, and the original image is represented by $\xi$, which belongs to the $R^{\mathit{Dim}}$ space. The blurred or degraded image, also referred to as the observed image or measurement, is represented by $t$ in the $R^{\mathit{Dim}}$ space, and $u$ denotes the noise that has been incorporated into the image.

In order to obtain an estimation of the initial image, it is necessary to determine the solution to the optimization dilemma expressed in Equation 4.2 below

$$\underset{\xi \in \mathcal{S}}{\min }\left\{\frac{1}{2}{\Vert B\xi -t\Vert }_2^2+\eta {\Vert \xi \Vert }_1\right\}\text{,}$$ (4.2)

where $\eta ,{\Vert \cdot \Vert }_1$ and ${\Vert \cdot \Vert }_2$ are the positive parameter, the ${\mathcal{l}}_1$-norm, and the Euclidean norm respectively. It is widely known that the ${\mathcal{l}}_1-$ norm is convex but not smooth and the Euclidean norm is a both convex and differentiable/smooth.

The optimization problem in (4.2) can easily be written in the form of (1.6) by setting $p\left(\xi \right)=\frac{1}{2}{\Vert B\xi -t\Vert }_2^2$ and $\mathrm{\Xi }\left(\xi \right)=\eta {\Vert \xi \Vert }_1$ we shall use our newly introduced algorithm, (3.1) to restore the original image or something very close to it given a masked image in Fig. 1.

Fig. 1.

The images on the left represent the original images see Refs. [39,40], while the images on the right show the masked images, with respective PSNR values of −65.9 and −60.2.

The algorithm is initialized with the following parameters:

$\sigma =0.1,{\mathrm{\Lambda }}_1=0.0001,{\phi }_1=0.0001,\eta =\frac{h+1}{30\cdot J\left(h+2\right)}$ where $J=\parallel B^T\cdot B\parallel$.

The computational result is documented in Table 1.

Table 1.

Extra-proximal gradient algorithm convergence table.

Image-Type	$\mathit{n}\_\mathit{i}\mathit{t}\mathit{e}\mathit{r}$	C.P.U-Time	Algorithm 3.1 (P.S.N.R Scores)	CPU-Time	Algorithm 1.13 (P.S.N.R Scores)
Bioimage	20000	112.8	−21.6	82.1	−23.7
	40000	224.7	−19.2	160.8	−21.6
	60000	363.5	−18.0	265.1	−20.2
	120000	720.3	−16.6	497.9	−18.0
	200000	1184.9	−15.4	958.2	−16.6
House.jpg	20000	35	−20.9	27.0	−22.3
	40000	71.1	−20.2	55.0	−20.9
	60000	104.3	−20.1	85.2	−20.4
	120000	218.4	−19.9	183.4	−20.1
	200000	384.5	−19.9	322.9	−19.9

For the second example, we will employ our algorithm to reconstruct a sinusoidal signal from a.

10% sample.

We used the following initialization: $\sigma =0.5,{\mathrm{\Lambda }}_1=0.5,{\phi }_1=0.5,\eta =\frac{h+1}{30\cdot J\left(h+2\right)}$ where

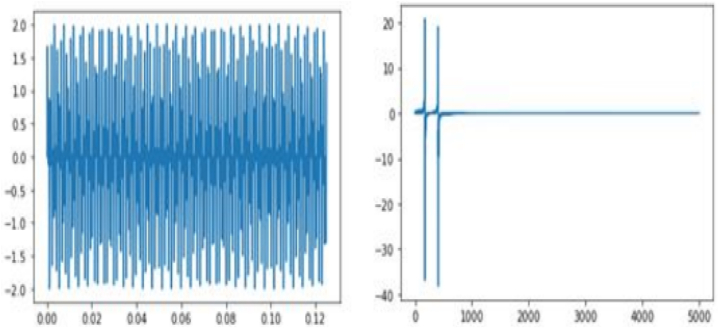
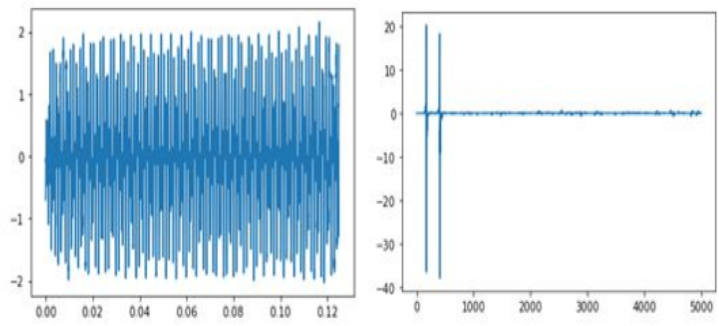
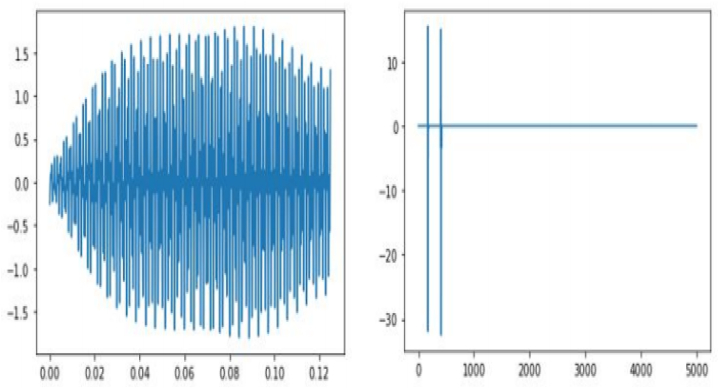
$J=\parallel A^T\cdot A\parallel$. employing our propose algorithm with the 10% sample from the original signal, the following results were observed after 40000 iterations. Table 1 show the extra-proximal gradient algorithm convergence. The image on the left was obtained using algorithm 3.1, while the image on the right was produced by implementing algorithm 1.13 (see Fig. 2). The P.S.N.R and convergence plot obtained from the reconstructed image data are illustrated in Fig. 3. The graph on the left corresponds to the y, whereas the transformed graph on the right corresponds to the axis of yt (see Fig. 4). The graphical representation of the 10% sample data is display in Fig. 5. The signal reconstructed using algorithm (3.1) can be represented uniquely in both the time domain and frequency domain is display in Fig. 6.

Fig. 2.

The image on the left was obtained using algorithm 3.1, while the image on the right was produced by implementing algorithm 1.13.

Fig. 3.

The P.S.N.R and convergence plot obtained from the reconstructed image data are illustrated in the figure. The plot on the left depicts the outcome obtained from algorithm 3.1, while the plot on the right exhibits the results produced by executing algorithm 1.13.

Fig. 4.

The graph on the left corresponds to the y, whereas the transformed graph on the right corresponds to the axis of yt.

Fig. 5.

A graphical representation of the 10% sample data.

Fig. 6.

The signal reconstructed using algorithm (3.1) can be represented uniquely in both the time domain and frequency domain.

The graphical representation of the reconstructed signal employing cvxpy is display in Fig. 7.

Fig. 7.

The graphical representation of the reconstructed signal employing cvxpy.

5. Conclusions

The main purpose of this work is to introduce an initial extra proximal forward-backward algorithm that is capable of searching for the solution of a convex minimization problem, and to demonstrate through analytical means that the algorithm converges weakly to the problem's solution. Employing the $L_1$ regularization model, we present two applications of our algorithm: Firstly, we use it to restore a blurred image in image restoration. Secondly, we use it to reconstruct a basic signal from only 10% of the original signal. Furthermore, We also present a graphically representation of the resulting data. The introduced algorithm finds meaningful applications in various domains. It can enhance the quality of medical images, aiding in accurate diagnoses.

Author contribution statement

Joshua Olilima & Adesanmi Mogbademu: Conceived and designed the experiments; performed the experiments; Wrote the paper. M. Asif Memon & Adebowale Martins Obalalu: Analyzed and interpreted the data; Wrote the paper. Hudson Akewe & Jamel Seidu: Contributed reagents, materials, analysis tools or data; wrote the paper.

Data availability statement

No data was used for the research described in the article.

Declaration of competing interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.