Chitosan Polysaccharides from a Polarizable Multiscale Approach

Abstract

We report simulations of chitosan polysaccharides in the aqueous phase, at infinite dilute conditions and zero ionic strength. Those simulations are performed by means of a polarizable multiscale modeling scheme that relies on a polarizable all atom force field to model solutes and on a polarizable solvent coarse grained approach. Force field parameters are assigned only from quantum chemistry ab initio data. We simulate chitosan monomer units, dimers and 50-long chains. Regarding the 50-long chains we simulate three sets of ten randomly built chain replica at three different pH conditions (corresponding to different chain protonation states, the chain degree of deacetylation is 85%). Our simulations show the persistence length of 50-long chitosan chains at strong acidic conditions (pH <5) to be 24 ± 2 nm (at weak/negligible ionic strength conditions), and to be 1 order of magnitude shorter at usual pH conditions. Our simulation data support the most recent simulation and experimental studies devoted to chitosan polysaccharides in the aqueous phase.

1. Introduction

Chitosan is a linear polysaccharide derived by N-deacetylation of 2-acetamide-2-deoxy-β-d-glucopyranose (GlcNac) monomer units of chitin, which is one of the more abundant polysaccharides on Earth.¹ The deacetylation process of chitin, which can be readily performed at the industrial scale, yields chitosan chains comprising both acetamide and deacetylated 2-amino-2-deoxy-β-d-glucopyranose (GlcN) units. The biodegrability and biocompatibility properties of chitosan as well as its ability to be shaped into several forms and conformations explain its great interest in many research and industrial fields from biomedical applications (as matrix for tissue engineering² or to functionalize graphene-based materials for drug delivery purposes,³⁻⁵ for instance), to food science and packaging,^6,7 adhesive field,⁸ energy field,⁹ and cosmetic and personal care applications.¹⁰⁻¹²

Besides the ability of chitosan/chitin pyranose rings to potentially adopt different conformations (puckers) as shown for different carbohydrates¹³⁻¹⁷ (to strengthen interactions of oligosaccharides with biomolecules,¹⁶ for instance), another remarkable properties of chitosans arise from the presence of an amino group in GlcN monomer unit, amino group whose pK_a is included between 6 and 7.¹⁸ That yields chitosan chains that behave as weak polyelectrolytes¹⁹ with a sizable portion of their monomer units (from 10 to 20%) already protonated at usual pH conditions (protonated monomer unit will be denoted GlcNH⁺). That favors the solubility of chitosan in mild acidic solutions. Moreover, the interactions among chitosan −NH⁺₃ cationic heads and acid anionic heads and counterions from the chemical environment are at the origin of the chitosan ability to acquire specific organizations and conformations depending on the nature of the latter acids and ions.^20,21 The chitosan degree of deacetylation, DA, is thus a key parameter to modulate the properties of chitosan chains,¹⁸ as it allows us to modulate the magnitude as well as the balance of hydrophobic, electrostatic, and hydrogen bonding effects on the interactions of chitosan chains among them and with their environment.

As all glycan polymers, the difficulty in developing in silico strategies to investigate and more likely to optimize chitosan chains for specific applications arises from the nature of the intermolecular interactions between chitosan and its chemical partners, the chain length and the size of the chitosan assemblies that can appear in solution or deposit on particular surfaces. Besides popular all atom pairwise force field approaches,^22,23 a promising attempt to model realistic chitosan systems consists of using coarse grained approaches to model chitosan and implicit methods to account for the chemical environment (in particular the solvent water), see in particular the recent attempts detailed in refs (24−28). As compared to explicit all atom simulations that have been performed to investigate the properties of chitosan chains,^4,29−31 chitosan films and membranes³² (here we may also quote ab initio molecular dynamics simulations³³), and chitosan-decorated graphenes,⁵ as well as the chitin decrystallization process,³⁴ the length of the chitosan chains that can be readily modeled using a coarse grained approach is at least 2 orders of magnitude larger. However, it is far from obvious to check whether a coarse grained approach is able to capture the strength and balance of microscopic phenomena modulating the properties of chitosan chains in complex environments, in particular microscopic polarization effects that are pivotal to understanding the properties in the aqueous phase from monatomic ions to polyelectrolytes.³⁵⁻³⁹

Here we present a multiscale approach combining an ab initio-based all atom polarizable force field to model chitosan chains and a polarizable coarse grained approach developed by one of us to handle the solvent water in order to model medium-sized chitosan systems. The all atom polarizable force field can be used with any kind of solvent approaches (from implicit to all atom ones) as it is built by taking into account only quantum chemistry ab initio data regarding GlcN/GlcNac monomer units and small hydrogen bonded aggregates (comprising only methanol, dimethyl ether, amine, ammonium, or N,N-dimethylacetamide entities). Polarization is modeled in our all atom force field and solvent coarse-grained model from the induced dipole moment approach. Alternative theoretical approaches to handle polarization microscopic effects have been proposed, see in particular the recent all atom polarizable force field based on Drude oscillators to model the behavior of mannopyrannose disaccharides in aqueous phase.⁴⁰

Our multiscale approach may be used to perform in depth analyses of the microscopic factors modulating the interactions among chitosan chains and between chitosan chains and their chemical partners (like the solvent, acids and counterions). However, it may also be used to provide reference data from which to assess and/or calibrate full coarse-grained approaches to efficiently model large chitosan assemblies according to bottom-up schemes.^25,41−43 Before to use our multiscale approach to simulate complex chitosan chain networks in aqueous phase, we detail here our modeling approach (in particular the all atom polarizable force field, the protocol to assign its parameters, our water coarse grained approach and its coupling to all atom force fields). Then, to assess our modeling approach, we discuss simulation data obtained from it regarding chitosan monomers, dimers, and 50-long chains dissolved in the aqueous phase at infinite dilution conditions and at the ionic strength zero limit. Regarding the 50-long chitosan chains (whose DA is 85%), we simulate in aqueous phase three sets of ten replica. The protonation state of the amine moieties for each set corresponds to low, intermediate and usual pH conditions (namely pH 4.5, 6.2, and 7), respectively. We focus here our discussions on comparing our new data to available experimental and simulation results (from all atom force field and/or coarse grained approaches) to assess the reliability of our approach.

2. Methods and Computational Details

2.1. Quantum Computations

All quantum computations discussed below were performed by means of the GAUSSIAN09 package of programs,⁴⁴ using the frozen core, FC, approximation. The binding energy of small molecular clusters are extrapolated to the Complete Basis Set, CBS, limit from computations performed the MP2(FC) level of theory used in conjunction with aug-cc-VXZ basis sets (X = D, T, and Q) according to the protocol detailed in refs (45 and 46). The geometrical data that we used to assign the model parameters correspond to cluster geometries optimized at the MP2/aug-cc-pVTZ level theory.

2.2. All Atom Polarizable Force Field for Chitosan Chains

In the following, N is the total number of atoms considered and N_μ is the total number of polarizable atoms. The potential energy U is the sum of six terms:

1

The repulsive U^rep, Coulombic U^qq′, and dispersion U^disp terms are defined as

2

3

4

Here, r_ij is the distance between atoms i and j, q_i are static atomic charges, and a_ij, b_ij, and r^*_ij are adjustable parameters. The repulsive term U^rep is truncated for distances larger than 5.0 Å. U^rel is introduced to handle intramolecular degrees of freedom, namely covalent bonds A–B and covalent angles A–B–C, and 1–4 torsional dihedral angles A–B–C–D, using standard harmonic stretching U^st, bending U^bd, and cosine-based U^vt potentials as defined in the CHARMM version 2.7 force field.⁴⁷

The polarization energy component U^pol is defined from an induced dipole moment approach in which only non-hydrogen atoms are polarizable centers (and whose polarizability, denoted α_i, is taken as isotropic). U^pol and the atomic induced dipole moments p_i obey

5

6

T_ij is the dipolar interaction tensor and E^q_i is the electric field generated on the polarizable center i by the surrounding static charges q_j. T_ij and E^q_i are both damped at short-range as proposed by Thole⁴⁸ (see our earlier study⁴⁹ for details).

The many-body anisotropic short-range energy term U^hb is introduced to accurately model hydrogen bond, HB, networks as those occurring among water, alcohol, and ether-oxide molecules/moieties, see refs (50) and (51). That terms is defined as

7

The sum runs over all the possible X···H–Y HBs whose geometric parameters r_hb (the hydrogen bond length) and the angles θ and ϕ are defined in Figure 1. The functions f and g are Gaussian or a product of Gaussian functions:

8

r_e,hb, θ_e, ϕ_e, γ_r, γ_θ, and γ_ϕ are adjustable parameters that depend on the HB nature. To account for the chemical environment effect on the strength of a local HB among water molecules and/or alcohol heads, D_e is taken as a linear function of the local density ρ_yh of H–Y* bonds (that are different from the hydrogen donor H–Y one) surrounding the hydrogen acceptor atom X: D_e = d_e(1 – ξρ_yh), with d_e and ξ two adjustable parameters depending on the nature of the hydrogen acceptor moiety. ρ_yh is estimated according to

9

The sum runs on the H–Y* bonds. U^hb terms is used to model local inter atomic interactions among oxygens (amine nitrogens) and all the possible H–Y groups. In the case of oxygen-based HB aggregates, its origin may be argued from electronic charge redistribution effects from oxygen lone pairs toward anti bonding H–O orbitals.⁴⁹ However, we also showed it to be related to dispersion effects in the particular case of the isolated water dimer.⁵² That explains why we do not take into account a specific U^disp term to model any kind of X···H–Y HB. Nevertheless as dispersion is pivotal to model microscopic interactions involving aliphatic carbon moieties CH_n, we model interactions among aliphatic carbons and between them and non hydrogen atoms that are separated by more than 2 covalent bonds using U^disp (together with U^rep, U^qq′, and U^pol). As for U^pol, we do not account for dispersion tied to hydrogens.

Figure 1.

Definition of the geometrical parameters (r, θ, ϕ) of the energy term U^lh in the particular case of O···H–X hydrogen bonds. For hydrogen bonds corresponding to a nitrogen proton acceptor atom, the axis X is the vector connecting the nitrogen to the center of mass of the three atoms covalently bonded to it and the angle θ is the angle between X and the hydrogen bond axis.

2.3. Force Field Parameters

The Coulombic charges correspond to those of earlier studies^51,53,54 with the exception of aliphatic carbon atoms, whose charge is set to reproduce the total charge of the GlcN/GlcNH⁺/GlcNac units. Regarding aliphatic carbon dispersion, we consider our former values of the parameter r^*_ij that we assigned to reproduce ab initio computations.^53,54 Regarding the energy terms U^rep, U^pol, and U^hb, we use for the present study a refined set of parameters to accurately model small water/methanol/dimethyl ether-oxide/methylamine/dimethylacetamide aggregates according to the parameter assignment protocol detailed in ref (50). However, we consider as target quantities (like HB geometries and aggregate binding energies) data from quantum ab initio computations at the MP2(FC) level of theory extrapolated at the CBS limit (see Figure S1 of the Supporting Information). As compared to our original study⁵⁰ dealing about water/alcohol/ether-oxide systems that yields a slightly altered set of parameters (mostly regarding the terms U^rep and U^hb).

Most the stretching and bending parameters (target bond lengths and angle values as well as harmonic constants) are taken from the CHARMM version 2.7 force field.⁴⁷ A few parameters, like those corresponding to CH–NH₂ and CH₃–O–CH–O–CH moieties are assigned to reproduce the covalent bond lengths and covalent angle values of those groups within the GlcN monomer unit. The stretching and harmonic constants are assigned to mean values of the CHARMM force field corresponding to C–O and C–N groups.

Regarding the parameters of the torsional term U^vt, we systematically assigned them to best reproduce torsional energy profiles computed from quantum ab initio computations performed at the MP2(FC)/aug-cc-pVTZ level of theory. The torsional parameters corresponding to H–C–O–C and H–O–C–C/H dihedral angles are assigned from energy profiles corresponding to the ethanol and dimethyl ether-oxide molecules, whereas those corresponding to dihedral angles C–O–C–O, C–O–C–C, and O_alcool–C–C–C/O are assigned to reproduce the energy profile of the dihedral angles ω_n=1–5 of the GlcN and GlcNac monomer units, see Figure 2 for definition. Quantum and best model energy profiles are provided as Supporting Information, see Figures 2 and 3.

Figure 2.

Top: definition of the GlcN (left) and GlcNac (right) monomer units and of their dihedral angles ω_n. Bottom: comparison of the relative energies of the monomer conformations discussed in the text (left: GlcN; right: GlcNac), from quantum and model computations. The conformers are shown in Figures S4 and S6 (see the Supporting Information). Note the rings of the two monomers are here in a ⁴C₁ conformation. The three Bercès’ dihedral angles (τ₁, τ₂, τ₃) to investigate pyranose ring conformations correspond to (∠ C₂C₃C₄C₅, ∠ C₃C₄C₅C₆, ∠ C₄C₅C₆O₁) according to the atom numbering of the GlcNac monomer unit.

Figure 3.

Top: definition of the GlcN–GlcNac dimer and of its dihedral angles (Θ, Ψ). The dimer conformation shown corresponds to the most stable conformation of the energy maps at (Θ = 75°, Ψ = 105°) (bottom left is from B3LYP/6-31+G(d,p) computations, bottom right is from the model). The energy contours correspond to increments of 1 kcal mol^–1.

Once the above parameters were assigned, we generated a set of GlcN, GlcNH⁺, and GlcNac conformers from in vacuo MD simulations at the 50 ns scale that were sampled every 1 ps. The sampled conformer sets were post processed using a clustering algorithm⁵⁵ (based on the root-mean-square deviation of all the atomic coordinates, RMSD, along the simulation). 9, 3, and 12 main clusters were identified for GlcN, GlcNH⁺ and GlcNac, respectively. Conformations corresponding to the center of mass of each cluster were then optimized using ab initio computations, at the MP2(FC)/aug-cc-pVTZ level of theory, and the torsional force field parameters of the dihedral angles C–O–C–C occurring within the monomer six-membered rings were then refined to best fit these new quantum data.

2.4. Polarizable Pseudo-Particle Solvent Coarse-Grained Approach

The Polarizable Pseudo-Particle solvent coarse-grained approach PPP relies on polarizable pseudoparticles (denoted as ppp) to model triatomic water molecules. The ppp’s interact with the solute and they are allowed to relax at its vicinity. Their isotropic polarizability α_s obeys the Clausius–Mosotti relation.^53,56 Denoting ε_s and ρ_s, the dielectric constant and the molecular density of liquid water, yields

10

α_s does not correspond to an atomic or molecular polarizability (which models only the perturbation of an electronic cloud due to an external electric field). α_s accounts for both the water molecular electronic polarization effects arising from solute electric fields but also for the water molecule orientational polarization.⁵⁷ For the present purpose we set the size of the ppp’s to that of a single water molecule. That yields α_s = 2.35 ų.

An important assumption of PPP is the use of the local approximation: the magnitude of the induced dipole moment p^s_j of ppp j is only a function of the solute electric field E^j_solute acting on it. Intrasolvent polarization effects are thus neglected. To prevent potential solute/solvent overpolarization effects arising from that assumption,⁵⁷ saturation of the p^s_j’s is introduced according to

11

here 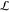is the Langevin function and μ_s is the ppp saturation dipole value. The corresponding solvent/solute polarization energy is then

12

We showed that long-range solute/solvent electrostatic contributions corresponding to neutral solute groups rapidly converge.^56,58 For our present study we thus only account for the induced dipole and static charge components of the electric fields E^j_solute that corresponds to solute atom/ppp distances that are smaller than the cut off distance R^pol_cut = 12 Å. A priori such an assumption is not valid to accurately model the hydration of ionic species and the 50-long chitosan chains that we model to assess our approach comprise from 7 to 42 cationic – NH⁺₃ heads. However, our aim is to simulate those chitosan chains at the ionic strength zero limit, i.e. we will not account for counterions. In that case solute/solvent long-range electrostatic effects are less crucial⁵⁸ and we thus also truncate long-range ammonium/solvent electrostatic effects, however according to the shell-based truncation scheme.⁵⁸ For the present study, the shell extends up to R^pol_cut from any non hydrogen chitosan atom (i.e., all the ppp’s belonging to such a shell undergo the E^j_solute component arising from all the chitosan cationic heads).

Nonelectrostatic interactions among ppp’s and solute atoms are modeled by means of a Lennard–Jones-like potential 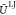(53) whose parameters are assigned to best reproduce both the first hydration shell structure and the hydration Gibbs free energy of a training set of small solutes.⁵⁸ That training molecule/ion set to model chitosan is detailed in Table S1 of the Supporting Information.

Interactions among ppp’s are modeled by means of a standard additive Lennard-Jones U^LJ energy term and by means of a many-body term that is a function of the solvent local density at the vicinity of a ppp.⁵⁶ Both these terms are truncated for inter particle distances greater than 7 Å. Their parameters are assigned to reproduce the water density (0.0335 molecule per ų) and the two regimes of the free energy corresponding to the creation of an empty cavity in water at ambient conditions according to the Lum–Chandler–Weeks theory of hydrophobicity.⁵⁹

Because of the distance-based truncation of solute/solvent interactions, it is straightforward to model the hydration of a solute at infinite dilution conditions as embedded in a ppp box. We just need to neglect interactions among solute images as using periodic boundary conditions (which are only used to preserve the solvent mean density along a MD simulation). Lastly as our multi scale simulation approach retains the notion of solvent particle, it allows us to account explicitly for solute/solvent microscopic interactions.

2.5. MD Simulation Details

The simulated systems correspond to ppp cubic boxes in which the solute is embedded. The box dimensions are large enough to ensure the minimal distance between any solute atom and the box boundary to be larger than R^pol_cut. The systems are simulated using periodic conditions as discussed above. Along the simulations the solute center of mass is periodically reset at the box center and the ppp coordinates are then reset accordingly. The box dimensions are first relaxed by performing a NPT MD run of 2 ns. The final simulation snapshot is then considered as the starting point of the MD NVT production runs.

The temperature and pressure are monitored along the MD simulations using the Nosé–Hoover barostat⁶⁰ (NPT simulations) and General Gaussian Moment Thermostat (NVT runs).⁶¹ The barostat and thermostat coupling constants are set to 2.5 ps. All the solute X–H bond lengths and H–X–H bending angle values are constrained using the RATTLE procedure (the convergence criterium is set to 10^–5 Å).

For small systems (up to hydrated dimers) the induced dipole moments are solved iteratively until the mean and largest differences in their values between two successive iterations are smaller than 10^–6 and 25 × 10^–6 Debye, respectively. The Newtonian equations of motion are solved using a basic Multiple Time Steps, MTS, algorithm with two time steps: 0.25 fs (stretching and bending intra molecular forces), 2 fs (all the other kinds of forces). For larger chitosan systems, we used a three level MTS scheme devoted to polarizable force field based on induced dipoles.⁶² In that case the three time steps are 0.25 fs (stretching and bending intra molecular forces), 2 fs (torsional, repulsion and hydrogen bond forces as well as short-range dispersion, Coulombic, and polarization forces), and 6 fs (long-range Coulombic, dispersion, and polarization forces). The cutoff distance to compute short-range forces is set to 8 Å, and we iteratively converge the induced dipole moments (atomic and ppp ones) until the mean difference in the dipole values between two successive iterations is less than 10^–6 Debye. That protocol to solve the equations of motion for large hydrated chitosan systems yields a reasonable shifting rate of the total energy (no more than 0.005% of the total energy per ns).

All molecular modeling computations and simulations were performed with our own code POLARIS(MD).⁶³

2.6. Hydration Free Energy Computations

Hydration free energies are computed from a two steps approach. Each step consists in a 32 windows Thermodynamical Integration, TI, scheme.⁶⁴ Each TI window corresponds to a MD simulation performed in the NPT ensemble at ambient conditions and at 30 ns scale. The potential energy derivatives are numerically computed each 250 fs once a starting relaxation phase of 500 ps is achieved.

The first step consists in linearly downscaling to zero the solute Coulombic charges and polarizabilities. During the second step, atomic charges and polarizabilities are set to zero and the solute atoms are linearly mutated into ghost centers fully decoupled from the solvent. To prevent numerical instabilities during the second step,⁶⁵ atom/ppp distances r_ij are incremented by the quantity (1 – λ) as computing the atom/ppp nonpolar energy term U^LJ. λ is the scaling parameter monitoring the linear downscaling of solute/solvent interactions in TI schemes.

For our purpose, we compute the hydration Gibbs free energies ΔG_solv at ambient conditions by simulating a single solute molecule dissolved in a solvent box. ΔG_solv is the sum of two components ΔG_elec and ΔG_np, each corresponding to the above two steps, respectively. As discussed above in Section 2.4 the solutes are dissolved in our computations at infinite dilution conditions and at the ionic strength zero limit (i.e., no counterion is taken into account even for the protonated GlcNH⁺ monomer). The hydration energies and structural properties for the training set of small molecules and ions considered to assign solute/ppp parameters and computed from our multi scale approach are summarized in Table S1 of the Supporting Information.

2.7. Hamiltonian Replica Exchange Simulations

To investigate the potential surface energy of GlcN–GlcN, GlcN–GlcNH⁺, and GlcN–GlcNac dimers in the aqueous phase, we use the Hamiltonian Replica Exchange, HRE, protocol detailed in ref (66). Potential exchanges among replica are checked each 500 fs. The potential energy of each replica is shifted by an amount of energy δU^HRE estimated on the fly to reach an exchange averaged rate of 40%.⁶⁶δU^HRE is re evaluated periodically by checking the exchange rate along 10 ps subportions of the MD trajectories. All the solute/solvent energy terms are scaled by a parameter λ^HRE (ranging from 0.2 to 1.0) as well as all the energy terms modeling the solute intra molecular degrees of freedom at the exception of the harmonic stretching and bending energy terms. We systematically consider 16 replica and the MD runs were performed at the 500 ns scale. The set of λ^HRE values that we used is provided as Supporting Information.

3. Results and Discussion

3.1. Force Field Accuracy In Vacuo

The conformations of the 9, 3, and 12 main conformers identified from sampling high temperature simulations in vacuo of the monomer units GlcN, GlcNH⁺, and GlcNac (see Section 2.2) are shown in Figures S4–S6 of Supporting Information. Regardless of the monomer unit, from 50 to 70% of these conformers are in a chair conformation, whereas the other conformers are in a skew boat conformation that is stabilized by an intramolecular hydrogen bond between the alcoholic and the ether-oxide groups neighboring the ring oxygen.

In Figure 2, we compare the relative energy of the neutral GlcN and GlcNac conformers (wrt their corresponding most stable conformer) from our model to quantum ab initio MP2(FC)/aug-cc-pVTZ and DFT B3LYP/6-31+G(d,p) computations. Our model is able to reproduce the differences in energy between the 9 GlcN conformers from quantum methods within about 0.5 kcal mol^–1 on average, a value that matches the mean difference in energy between MP2 and B3LYP (about 0.4 kcal mol^–1). Importantly and as predicted by quantum methods, our model shows the three GlcN chair conformers (labeled 5, 6, and 8 in Figure S4 of the Supporting Information) to be almost iso-energetic and to be from 3 to 4 kcal mol^–1 more stable than the six other chair and skew boat conformers. A similar agreement between our model and quantum data is reached for GlcNac conformers. However, our computations show a larger mean difference in the relative energies (about 1.0 kcal mol^–1) between quantum MP2 and B3LYP computations for GlcNac conformers compared to GlcN ones.

The energy agreement between our model and quantum data is equivalent to that recently reported for empirical models devoted to different 5- and 6-membered ring monosaccharides and adjusted to reproduce high level quantum data at the CCSD(T)/6-311+G(d,p) level of theory using machine learning techniques⁶⁷ as well as to semiempirical approaches recalibrated to match quantum MP2/cc-pVDZ⁶⁸ or RB3LYP/6-311++G(d,p) data.⁶⁹

Regarding the 3 main conformers of GlcNH⁺, our model and quantum methods agree on their energy ordering, even if the difference in energy between the two most stable chair conformers is shown by our model to be larger than using quantum methods by +1 kcal mol^–1. Note the model parameters to handle hydrogen bonds among ethanol, dimethyl ether-oxide, amine, and acetamide moieties are here assigned to reproduce quantum ab initio MP2(FC) data extrapolated at the CBS limit. As compared to quantum MP2(FC)/aug-cc-pVTZ and B3LYP/6-31+G(d,p) data, the binding energies of small hydrogen bonded aggregates extrapolated at the MP2/CBS limit are systematically less stable by at least 0.3 up to 2 kcal mol^–1 (see among others the data discussed in refs (70) and (71), as well as in Figure S1 of the Supporting Information). In our opinion, that explains most of the above energy differences between our model and quantum MP2/B3LYP methods.

We computed the energy map U(Θ, Ψ) corresponding to the pair of dihedral angles (Θ, Ψ) of the GlcN–GlcNac dimer in vacuo from quantum B3LYP/6-31+G(d,p) computations and our model. For efficiency reasons we constrain a set of internal dihedral angles (see the dimer Z-matrix that we used provided as Supporting Information). Hence U(Θ, Ψ) does not correspond to the optimal (fully relaxed) energy map. The dimer, dihedral angle definitions, and energy maps are shown in Figure 3. Regarding the stretching, bending and torsional parameters of the glycosidic linkage C–O–C interconnecting the monomer units, note here that they correspond to the parameter sets that we assigned to model monomers to model the C–O–CH₃ moiety. In particular, the stretching and bending parameters are taken from the CHARMM force field version 2.7 whereas the torsional parameters regarding the dihedral angles XCOC, X = H, O, and C, are those assigned to best reproduce the torsional energy profiles corresponding to the dihedral angles ω₁ and ω₃ (see Figure S2 of the Supporting Information). Nevertheless the model and quantum B3LYP maps are close: they show the existence of three almost isoenergetic (within 1 kcal mol^–1) main minima located at (75°, 105°), (270°, 180°), and (285°, 270°) and of a local minimum at (0°, 300°) higher in energy by about +7 kcal mol^–1. In our opinion and as discussed above for monomer units, the difference in energy among the three main minima in vacuo of the GlcN–GlcNac dimer between our model and B3LYP results (at most of 1 kcal mol^–1) arises again from the difference in describing hydrogen bonds between quantum B3LYP/6-31+G(d,p) and MP2(FC)/CBS methods. This is why we do not further refined our force field parameters to match B3LYP data for the present purpose.

In all, the above results show our ab initio-based force field approach to be able to model GlcN/GlcNac/GlcNH⁺ monomer units and the GlcN–GlcNac dimer in vacuo with an accuracy equivalent to available efficient quantum methods.

3.2. Monomer Units in the Aqueous Phase

We performed 500 ns MD simulations of the three monomer units embedded in a cubic box comprising about 2 000 ppp’s in the NPT ensemble. The trajectories are sampled each 6 ps once an initial relaxation phase of 10 ns is achieved. From those sampling sets, we first investigated the 6-membered ring conformations from the ring dihedral angles (τ₁, τ₂, τ₃) proposed by Bercès et al.⁷² (see Figure 2 for angle definitions). The temporal evolutions of those angles for the three monomer units along the 400 ns last segment of the simulations are shown in Figure S7 of the Supporting Information and the corresponding mean Bercès’ angle values are summarized in Table 1.

Table 1. Selected Monomer Unit GlcN, GlcNH⁺ and GlcNac NMR Coupling Constants (in Hz) and Bercès’ Dihedral Angles (τ₁, τ₂, τ₃) Computed along NPT MD Simulations in the Aqueous Phase at 500 ns Scale^a.

	GlcN	GlcNH+	GlcNac	Sim.	Exp.
Coupling constants
3J(a)H5,H6R	5.18	5.01	5.27	5.25–6.28	5.57–6.0
3J(a)H5,H6S	4.47	3.52	3.26	1.70–2.96	1.85–2.27
3J(b)H5,H6R	5.06	5.01	5.26	4.77–6.09
3J(b)H5,H6S	4.87	2.96	3.66	1.58–2.91
3JH2,HN	-	-	9.77	8.35–10.39	9.07
Dihedral angles
τ1	–52.3°	–54.5°	–52.2°
τ2	52.1°	54.7°	49.0°
τ3	–51.2°	–55.1°	–56.3°

^aWe use the standard labeling of the coupling constants (see ref (76) for instance). At the exception of ³J_H2,HN, the coupling constant are computed by considering the dihedral angle ∠O₁C₆CO. a and b: constants computed from the relations of Stenutz et al.⁷⁵ and Tafazolli and Ghiasi,⁷⁶ respectively. For GlcNac, the mean dihedral values correspond to the most abundant ⁴C₁ conformations. The standard deviation regarding the dihedral angles is about 7°, regardless of the angle and the monomer unit. Sim. and Exp.: coupling constant values from earlier simulation and experimental studies reported in ref (74).

The conformations of GlcN and GlcNH⁺ rings along our simulations correspond to ⁴C₁ as usually reported (see among others refs⁷³.⁷⁴, and references mentioned therein). In the particular case of GlcN we rarely observe the ²S_o ring conformation. For GlcNac we observe a 20:1 equilibrium between conformations ⁴C₁ and ¹C₄. Such an equilibrium was also observed along microsecond scale all atom simulations using a pairwise force field.¹⁵ However, ⁴C₁ is much more abundant and ¹C₄ is only a transient conformation along the latter μs scale simulations compared to our own. Our simulation approach predicts a free energy difference ΔG_c between ⁴C₁ and ¹C₄ conformations to be about +1.7 kcal mol^–1 for GlcNac, a value that is slightly lower than earlier reported ΔG_c values using pairwise force fields^15,73,74 (from +2.5 to +3.5 kcal mol^–1).

Regarding the exocylic hydroxyl moiety neighboring the ring oxygen O₆, we computed the distribution functions of the dihedral angle ω₁ (namely the angle ∠C₅C₆CO) for the three monomer units (see Figure S8 of Supporting Information). Denoting gg, gt, and tg as the conformers corresponding to ω₁ value windows [0°, 120°], [120°, 240°], and [240°, 360°], our distribution functions show their respective weights along our simulations to be about 68, 30, and 2% for GlcN and GlcNH⁺, and 55, 32, and 13% for GlcNac. Our weights for conformers gg to tg are in line with earlier data from all atom simulations based on pairwise force fields (see refs (73) and (74) and the reference mentioned therein).

From the distribution functions of the dihedral angle ω^′₁= ∠O₁C₆CO, we estimated the NMR coupling constants ³J_H5,H6R/S using the formula proposed by Stenutz et al.⁷⁵ and Tafazolli and Ghiasi.⁷⁶ Our coupling constants are in line with earlier simulations and available experimental data (see Table 1), at the remarkable exception of the constant ³J_H5,H6S for GlcN that is clearly outside of the expected range of values (about 4.60 Hz whereas all the reported values are smaller 3 Hz). That high GlcN³J_H5,H6S value arises from a non negligible weight of GlcN structures whose ω^′₁ value is close to 0° along our simulation (see Figure S9 of the Supporting Information). In our opinion, that may result from an artifact of our all atom force field that underestimates the energy barrier of the ω^′₁ torsional energy profile at ω^′₁= 0° (see Figure S2 of the Supporting Information). Lastly we also computed the coupling constant ³J_H2,HN corresponding to the dihedral angle ω₅ for GlcNac (see Figure 2 for definition) according to the relation proposed by Mobli and Almond:⁷⁷ we get 9.77 Hz a value higher than experiment by about 1 Hz, but which is included in the range of earlier MD simulation values (from 8.35⁷⁴ to 10.39⁷⁷ Hz).

The pseudoparticles ppp’s correspond to water molecules that are allowed to relax around the solute in MD simulations. We thus compute along the hydrated monomer trajectories the atom/solvent ppp radial distribution functions g^X_ppp(r) and their corresponding integrals n^X_ppp(r) that are shown in Figure 4 for alcohol O^alc and ether-oxide O^ether oxygens. The functions g^X_ppp(r) are normalized to the ppp density at ambient conditions (ρ_ppp = 0.0335 particles per ų). The normalized g^X_ppp(r) functions centered at O^alc and at O^ether are close regardless of the neutral monomer unit. They present a first peak at about 2.85/2.90 Å and a second minimum at about 3.8/3.5 Å for O^alc and O^ether, respectively. The heights of their first peak are about 2.65 and 0.95 and the mean coordination numbers N^X_ppp (corresponding to n^X_ppp(r) values at the second g^X_ppp(r) minimum) are about 5.9 and 2.5 ± 0.5 ppp for the both the latter kinds of oxygen. These hydration structural data are in line with those corresponding to the small training molecules (methanol and dimethyl etheroxide) taken into account to assign our solvent model parameters. The coordination numbers N^X_ppp are however smaller by about 0.5 ppp for chitosan monomers compared to the latter molecules as expected from the presence of a solvent inaccessible volume corresponding to the monomer 6-membered ring.

Figure 4.

Mean radial distribution functions g^X_ppp(r) (full lines) and their integrals n^X_ppp(r) (dashed lines) for hydrated GlcN, GlcNH⁺, and GlcNac monomer units, as centered at their alcohol and ether oxide atoms. Black, gray, and violet: functions centered at alcohol atoms (for GlcN, GlcNac, and GlcNH⁺, respectively). Blue, light blue, and green: functions centered at etheroxide atoms (GlcN, GlcNac, and GlcNH⁺, respectively).

We computed the Gibbs hydration free energy ΔG_solv of the three monomer units from the protocol detailed above. Our computed ΔG_solv values are −21.4, −24.1, and −77.0 ± 0.1 kcal mol^–1 for GlcN, GlcNac and GlcNH⁺, respectively. The difference in ΔG_solv between the neutral units GlcN and GlcNac matches the difference between the methyl-amine and the dimethyl-acetamide (about +2.7 and +3.5 ± 0.2 kcal mol^–1, respectively, see also Table S1 of Supporting Information). Regarding GlcNH⁺, its ΔG_solv agrees with that of methyl ammonium within 0.6 kcal mol^–1 (however we note a noticeable weaker(stronger) weight of the electrostatic(nonpolar) component for GlcNH⁺ compared to methyl ammonium, see Table S1 of the Supporting Information). To our best knowledge no experimental data is available regarding the hydration energies of monosaccharides. However, our computed ΔG_solv’s for the GlcN and GlcNac neutral units are in line with earlier theoretical estimates regarding different glucose epimers^78,79 (they range between −20 and −23 kcal mol^–1), as well as with the magnitude of monomer unit contributions to the total hydration free energy of chitosan chains (mainly ranging from −15 to −22 kcal mol^–1).³⁰

We estimated the three monomer unit volumes in aqueous phase from the dilution method. We performed MD simulations at the 250 ns scale of the monomers dissolved in boxes comprising from about 1 000 up to 9 250 ppp’s in the NPT ensemble. Once an initial phase of 10 ns is achieved, we collected volume data along the trajectories each 5 ps. In Figure 5 we plot the ratios of the mass density ρ_m of the box including the monomer scaled by the corresponding mass density ρ_s of a pure aqueous box as a function of the monomer mass fraction. Those ratios are all linear functions of the mass fraction. We then estimate the monomer volumes v_M from the linear regression function slopes s according to v_M = (1 + s)M_M/(ρ_pppM_w) (M_M and M_w are the monomer and water molecular masses, respectively).

Figure 5.

Ratios of the mass density ρ_M for hydrated chitosan monomer simulation boxes and of ρ_s for pure ppp boxes as a function of the monomer mass fraction within the simulation boxes. Black, blue, and light blue symbols: data corresponding to GlcNac, GlcN, and GlcNH⁺ units, respectively. The uncertainties are computed from the standard deviations of the densities ρ_M and ρ_s along MD trajectories and by assuming these data to be temporally uncorrelated. In dashed lines: linear regression fit, the Pearson regression coefficients here are all larger than 0.99. The uncertainty regarding the linear regression slope s is about 5% on average.

The volumes v_M are 0.152, 0.125, and 0.095 ± 0.012 nm^–3 for GlcNac, GlcN and GlcNH⁺, respectively. Accounting for a single water molecule companion per chain unit in aqueous phase, the latter volumes are then larger by about 15%. Our monomer volumes are in line with a recent estimate of 0.163 nm^–3 (regardless of the monomer kind) computed from simulations of chitosan polymers comprising from 10 to 40 units at low pH value and corresponding to DA = 60%.⁸⁰

In all our approach is thus able to reproduce most of the well accepted hydration properties of GlcN, GlcNH⁺, and GlcNac monomer units.

3.3. Dimers in the Aqueous Phase

We performed HRE simulations at the 500 ns scale of the six dimers GlcN–GlcN, GlcN–GlcNH⁺, GlcN–GlcNac, GlcNac–GlcNac, GlcNac–GlcN, and GlcNac–GlcNH⁺ as embedded in cubic solvent boxes comprising about 2 000 ppp’s (the relaxed box dimension at ambient conditions is 4.03 nm). From dimer conformations sampled along the reference HRE trajectories (corresponding to λ^HRE = 1.0) we computed the angular distributions P(Θ, Ψ) and the corresponding free energy maps F(Θ, Ψ) defined as

13

here k_B and T are the Boltzmann constant and the simulation target temperature (300 K). The six F(Θ, Ψ) maps are shown in Figure 6.

Figure 6.

Chitosan dimer free energy map F(Θ, Ψ) in the aqueous phase. The cruciform symbols are located at the bassin centers corresponding to the original dihedral angle distribution P(Θ, Ψ) according to the protocol detailed in ref (81). (a) GlcN–GlcNac; (b) GlcN–GlcN; (c: GlcN–GlcNH⁺; (d) GlcNH⁺–GlcNH⁺; (e) GlcNac–GlcNac; (f) GlcNH⁺–GlcNac. The data in gray are the populations (in %) of 4C₁ and ¹C₄ ring conformations in HRE reference simulations for dimer units A and B (see Figure 3 for definition). Examples of the Bercès’ dihedral angle τ₃ distributions from which the ring populations are computed are shown in Figure S10 of the Supporting Information.

Regarding the GlcN–GlcNac dimer and as compared to its energy map in vacuo U(Θ, Ψ) (see Figure 3), its two in vacuo minima located at (270°, 180°) and (285°, 270°) are shifted in the aqueous phase toward weaker and larger Ψ values, respectively. Moreover the in vacuo minimum at (75°, 105°) is destabilized in aqueous phase by about 2 kcal mol^–1, whereas the in vacuo high energy minimum at (0°, 300°) is stabilized by solvent effects (by about 3 kcal mol^–1) and shifted to larger Θ values.

The F(Θ, Ψ) maps are close regardless of the dimer. The three aqueous minima discussed above for GlcN–GlcNac are usually observed for all the other dimers, even if the local minimum at (75°, 105°) is a priori higher in energy for dimers GlcNH⁺–GlcNH⁺, GlcNac–GlcNac, and GlcNH⁺–GlcNac than for the three other dimers. We note also a weak energy barrier ΔG* (weaker than +2 kcal mol^–1) connecting the two aqueous minima located at about (280°, 105°) and (280°, 360°), at the exception of dimer GlcNH⁺–GlcNac for which that energy barrier is at least twice as large.

Our dimer results support free energy maps F(Θ, Ψ) reported from earlier studies from metadynamics^25,80 and HRE⁷⁴ simulations using pairwise force fields. In particular and as already discussed for pairwise force field approaches, we note a relatively weak portion of the maps to correspond to low energy levels, i.e., higher at most by +2 kcal mol^–1 from the global minimum located at about (280°, 105°). That suggests a relative rigidity of the conformation between two monomer units in chitosan chains, regardless of their kind. However:

• The aqueous local minimum located at about (200°, 90°) usually reported from pairwise force field approaches^25,80 is systematically a (low energy) point of the bassins corresponding to the global minimum located at (280°, 105°) in our polarizable approach.

• We note a noticeable sensitivity of the energy barrier ΔG* to the pairwise force field used: that energy barrier can be close to our data (as in ref (80)) or much higher in energy than ours (it ranges from +5 to +8 kcal mol^–1 in ref (25)). Note here the existence of a local minimum located (200°, 90°) to be also dependent on the pairwise force field used (see for instance the F(Θ, Ψ) maps for GlcNH⁺–GlcNac dimers reported in refs (25) and (80)).

Recently the F(Θ, Ψ) maps of mannopyrannose disaccharides in aqueous phase computed from both a standard pairwise force field and a polarizable Drude oscillator-based approach have been reported.⁴⁰ As for our polarizable force field, the map portions at the vicinity of the F(Θ, Ψ) global minima from the Drude approach are also flatter than from the pairwise force field approach. Lastly about the global minimum of our F(Θ, Ψ) maps and of the earlier simulation studies mentioned above, we may note that its location agree with the (Θ, Ψ) values reported from X-ray crystallographic experimental studies of chitosan and chitin chains.⁸²⁻⁸⁴

Regarding the 6-membered rings of hydrated dimers, the ring of the dimer first unit A (see Figure 3) is more flexible in aqueous solution along HRE reference simulations for dimers GlcN–GlcNac, GlcN–GlcN, GlcN–GlcNH⁺, and GlcNH⁺–GlcNH⁺, as compared to single monomer units GlcN and GlcNH⁺. For those four dimers, the ring A conformation oscillates between ⁴C₁ and ¹C₄, ⁴C₁ being still the most abundant (the main conformation populations are reported in Figure 6). The ring conformation of the dimer unit B is systematically more rigid and corresponds to a ⁴C₁ conformation. The difference in behavior between A and B rings arises from inter unit interactions (hydrogen bonds) between amino, ammonium and N-acetyl groups of unit A with the hydroxyl moieties of B that favor ring A¹C₄ conformation for particular (Θ, Ψ) angle values. For the two last dimers GlcNac–GlcNac and GlcNH⁺–GlcNac, both their rings A and B are in a ⁴C₁ conformation along HRE reference simulations. Contrary to single monomer units, our simulation approach thus predicts a somehow enhanced flexibility of GlcN and GlcNH⁺ 6-membered rings in hydrated dimers.

3.4. Chitosan Chains in the Aqueous Phase

We consider 3 different chitosan chains denoted chitosan^h, chitosan^t, and chitosan^l whose DA is 85% and whose degree of polymerization, DP, is 50. Their compositions (expressed in %) in GlcN, GlcNH⁺, and GlcNac units are (71,14,15), (42.5,42.5,15), and (0,85,15). The experimental pK_a of chitosan amino groups varies from 6.2 to 7.2,¹⁸ which suggests our proportions of protonated GlcNH⁺ units in chitosan^l, chitosan^t, and chitosan^h to be a priori expected for aqueous solutions whose pH is <4.5 and about 6 and 7, respectively. We assume thus the protonation states of chitosan^l, chitosan^t, and chitosan^h to correspond to the latter three pH conditions.

For each chain kind, we built 10 replica whose unit sequences are randomly set (the sequences are summarized in the Supporting Information). Each replica is embedded in a cubic box fulfilled with water polarizable pseudo particles ppp’s. The box dimensions are large enough to match the largest dimension of a replica in a linear conformation. That yields boxes comprising about 680k ppp’s. For the present purpose we do not account for counterions. We model thus the chains at the ionic strength zero limit. For each replica, the box volumes are first relaxed by performing 2 ns NPT simulations along which the chains conformations are restrained to their starting linear geometries. The final snapshots of the NPT runs are then used as starting points for a new series of NVT simulations performed at the 100 ns scale.

The NVT trajectories are sampled each 6 ps once an initial relaxation phase of 10 ns is achieved. All the mean quantities discussed below are computed from those sampled sets. Simulations at the 100 ns scale are a priori too short to perform an exhaustive sampling of the potential energy surface of complex molecular systems (like our hydrated chitosan chains) and thus to estimate accurate mean data. However, averaging data over a set of replica has been shown to provide accurate estimates of physical quantities, like the coefficient of diffusion.⁸⁵ We will thus discuss the below mean data computed over the full set of replica for each chitosan chain. In particular, we focus here our discussions on quantities like the chain gyration radius R_g, the monomer unit contour length l_cm (computed from the positions of the oxygen atoms O_c of the glycosidic linkages interconnecting two adjacent monomer units) and the temporal correlation function C_k from which the chain persistence length L_p can be estimated according to

14

Here b_l is the vector defined by two neighboring O_c and b_l is its norm. b̅ is the mean value of the b_l computed over all the chain units. The bracket corresponds to temporal averages. Several relations have been proposed to estimate the persistence length L_p,⁸⁶ in particular from the mean square of the chain end to end distance R_ee and the chain counter length L_c = (DP – 1)l_cm that is valid for chains in coil regime:

15

The persistence length L_p is a priori a quantity defined for long chains and which is independent from their length. In particular, for infinite chain length, the persistence length L_p is defined as the average projection of the end to end vector R_ee on the tangent of the chain contour at one chain end. Because of the length of our chains and to prevent confusion, we will denote 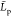the persistence length values for our chains that we compute from the above relations. That yields us to assume the largest value of 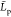to be at most equal to L_c (and thus about ) for a chain in a rigid rod conformation.

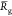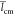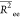We summarize in Table 2 the mean values and averaged over the 10 replica for our three kinds of chitosan chains. The mean chain end to end distances (that we assume to be the distances between the first and the last methyl-oxide oxygens) and their mean square values are summarized in Table S2 of Supporting Information. These data show the progressive increase of the chain flexibility as the chain protonation decreases (i.e., pH increases). For instance the 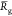and 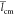values decreases from 6.5 to 3.3 nm and from 0.5 to 0.2 nm as the chain protonation decreases. We note also the spread in the replica R_g and l_cm values to increase as the chain protonation decreases. Lastly and in line with those results, the plots of Figure 7 show the spread in the replica C_k functions to noticeably increase as the chain protonation decreases.

Table 2. Chitosan Chain Conformation Data.^a.

chitosanl	6.49 (6.39, 6.53, 0.05)	0.499 (0.516, 0.454, 0.024)	24.0*
chitosant	5.16 (3.69, 6.24, 1.01)	0.365 (0.226, 0.486, 0.094)	9.5 (9.9)
chitosanh	3.32 (1.56, 4.98, 1.41)	0.199 (0.055, 0.324, 0.109)	1.6 (2.8)

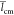^a, , and 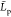mean gyration radius, mean monomer unit contour length, and mean chain persistence length, respectively. Bold data: value averaged over the 10 replica (for the persistence length, the mean value is computed from averaging the replica C_k functions and superscript * indicates the mean end to end distance, see main text).Values in parentheses: smallest, largest, and standard deviation data within the replica set, at the exception of 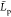data, for which the values in parentheses are computed from eq 15. All data in nm.

Figure 7.

(a–c) Correlation functions C_k for each replica (gray lines and symbols) and mean function 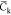(black lines and symbols) averaged over the full replica set for chitosan^l, chitosan^t, and chitosan^h, respectively. Here the chain curvature distance s between two chain units i and i + k is set to kb̅. Red and blue dashed lines: single and double exponential functions best fitting the functions 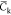, respectively (the largest and weakest persistence lengths from the double exponential fit are 20.5 and 0.4 nm for chitosan^t and 4.3 and 1.2 nm for chitosan^h). (d) mean persistence length 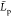for each kind of chitosan chains as a function of the pH (the error bars correspond to the standard deviations among replica and scaled by the square root of their number). For pH 4.5, the 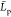value is the mean end to end distance of chitosan^l (24.0 ± 2 nm, see main text). The black dashed line corresponds to the linear regression of data (the Pearson coefficient is >0.99, and the slope is −8.7 ± 0.5 nm).

All the replica l_cm values (included within 0.454 and 0.515 nm) for chitosan^l agree with available estimates corresponding to both low pH and low ionic strength (≤4.5 and ≤0.01 M, respectively): 0.49 nm (experimental, DA = 40%),⁸⁷ 0.46 nm (all atom simulations using pairwise force field, DA = 40%),⁸⁰ and 0.515 nm (experimental, DA = 5%).⁸⁸ Our 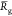values for chitosan^l (6.5 nm) are also in line with recent data from all atom simulations extrapolated to our chain length scale (about 6.2 nm).⁸⁰

The chain conformations at the end of our 100 ns scale simulations are shown in Figure 8. For chitosan^h replica (low protonation state, pH of about 7) the final conformations range from globular (compact) to worm-like chain conformations. For chitosan^t (pH of about 6), they range from almost fully linear ones to partially folded (with however a large chain portion that is still in a linear conformation), whereas for chitosan^l (pH ≤4.5) they all correspond to an almost fully linear conformation. To our opinion, the large conformational variability along the MD trajectories for chitosan^h and chitosan^t replica arises mainly from the chaotic effects inherent to MD simulations rather than from the difference in the replica chain sequence (even if the effect of those differences may not be fully neglected, in particular for chitosan^t). 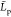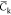Assuming the latter hypothesis and following the ideas of Maginn and co-workers to compute diffusion coefficients,⁸⁵ we estimate a mean persistence length value for each kind of chitosan chain from the mean function averaged over the replica C_k functions. From the plots of Figure 7, the replica C_k functions are equally distributed above and under the limit defined by the mean functions 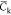, regardless of the chain type.

Figure 8.

(a, b) Final conformations of chitosan^h and chitosan^t replica (for each chain, the replica conformations are superimposed to minimize the root-mean-square deviation in the non hydrogen atom coordinates). (c) A representative conformation of chitosan^l replica. All the conformations are shown at the same scale.

The conformation of the fully protonated chains chitosan^l is almost linear (rod-like) along all our simulations. That yields estimates of the mean 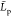value to be larger than the mean chain distance from both eqs 14 and 15. We thus set that 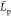value to the mean end to end distance 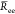value (about 24 ± 2 nm). For the chains chitosan^h and chitosan^t that we assume to be in a coil regime (from both their functions C_k and the simulation snapshots shown in Figures 7 and 8), the 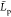values computed from eqs 14 and 15 agree within less than 1 nm. However, the mean functions 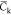averaged over the replica for those two kinds of chains more likely obey a double exponential decay rather than a single one, as it may be a priori expected from the chain polyelectrolyte nature,⁸⁹ see Figure 7.

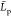decreases from 24 down to 2 nm as the chain protonation state decreases and it linearly depends on pH, see Figure 7d. Our simulations correspond to infinite dilution conditions and to the ionic strength zero limit. For low pH, the order of magnitude of our 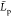value agree with recent estimates from coarse grained simulations²⁵ (about 90 nm, DA = 90% and DP = 1000) and experiments⁹⁰ (about 50 nm, DA ≈ 95% and DP > 200) corresponding to low pH (≤4.5) and to low ionic strength conditions (within the 0.001–0.01 M range). However, for such conditions, earlier experimental^87,91 and recent simulation-based^80,92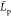 estimates are 1 order of magnitude smaller than the latter ones. 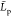Regarding the latter recent simulation studies, their estimate corresponds to concentrated chitosan chain networks⁹² or it is computed from all atom simulations taking explicitly into account counterions,⁸⁰ and all atom simulations of salty solutions are highly sensitive to the accuracy in modeling ion pair interactions in aqueous phase.^93,94

Polymer conformations in aqueous phase result from a competition between intra chain and chain/solvent interactions. Following the ideas of Hansen and Abbott,⁹⁵ we define a set of four reduced energies u that all obey u = U̅/Φ. Here, U̅ is the mean value of an energy component along a MD simulation, namely the chain/solvent polarization U^pol_ps and nonpolar U^LJ_ps energies (see Section 2.4), as well as the intramolecular chain Coulombic U^int_qq and polarization U^int_pol ones. Φ is the chain volume defined from the monomer unit mean volumes discussed in Section 3.2. We summarize in Table 3 the reduced energies averaged over the replica set for each kind of chain. Even if the replica chain sequences are randomly set, we can compare here the chain internal Coulombic and polarization energy data among replica of a given chain type as those replica comprise the same number of identical chemical bonds. Regarding the other intramolecular chain energy components (like dispersion or repulsion), the dependence of their mean values along MD simulations to the chain composition and sequence is much weaker compared to the Coulombic and polarization components (see Table S3 of the Supporting Information).

Table 3. Chitosan Chain Reduced Energy Data^a.

	Q	Φ
chitosanl	42	5.18	–779 (22)	–490 (2)	363 (9)	–220 (3)
chitosant	21	5.81	–359 (59)	–386 (4)	133 (9)	–165 (22)
chitosanh	7	6.24	–160 (35)	–332 (4)	80 (3)	–90 (12)
(*)	0	6.46	–10	–295	–4	–72

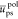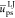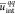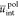^aQ is the chain total charge (in e) and Φ is the chain volume computed from monomer unit volumes (in nm^–3). The reduced energies , , and correspond to the solute/solvent polarization, solute/solvent nonpolar, chain intramolecular Coulombic, and chain intramolecular polarization energies, respectively, averaged over the replica sets. In parentheses, the standard deviation to the mean value corresponding to each replica set. (*): linear extrapolation of chain data wrt Q (the Pearson coefficient are all larger than 0.97 for the three energies). All data in kcal mol^–1 nm^–3.

For each chain type, the four reduced energies are close, regardless of the replica. Mean reduced energies u̅ (as averaged over replica) are thus reliable quantities that do not depend on the chain sequence. As expected all the electrostatic (Coulombic and polarization) mean reduced energies decrease in magnitude as the chain total charge decreases. So also do the chain/solvent nonpolar energy 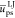(that arises from stronger non polar ammonium/solvent interactions as compared to neutral moieties, see Table S1 of the Supporting Information). Interestingly, all our mean reduced energies are linearly correlated to the chain total charge (see Table 3). We also computed the difference in the solvent mean reduced energy corresponding to neat water and in the presence of chitosan chains. 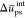is not sensitive to the chain type and sequence: it amounts to +110 ± 10 kcal mol^–1 nm^–3 on average.

Because of their non dependence to the chain sequence, the chain/solvent mean reduced energies 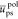and 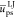can be used to build simple indexes from which to anticipate the behavior of chitosan chains in different solvents (modeled from the present solvent coarse grained approach). Interestingly, the mean intramolecular chain Coulombic energy 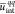appears to be a simple and reliable index to predict chain structural data and their variability in aqueous solution for particular chain protonation states and thus at particular pH conditions. That is suggested by the plots of u^qq_int as a function of the gyration radius for all the replica, see Figure 9. Because of the weak deviation in the magnitude of u^qq_int regardless of the chain conformation, short MD simulations of hydrated chitosan chains are expected to provide accurate enough u^qq_int values from which to infer chain structural data like gyration radius or mean persistence length, for instance. We will further investigate that assumption for longer chitosan chains (corresponding also to different DA) and for longer simulation durations from coarse grained approaches built to reproduce the present simulation data.

Figure 9.

Chain Coulombic reduced energies u^qq_int computed along MD simulations for each replica as a function of the replica gyration radius. Black, blue and red symbols: data corresponding to chitosan^h, chitosan^t, and chitosan^l. The dashed lines delimit the expected range of the gyration radius for intermediate u^qq_int values. The inset plot shows the linear dependence of 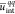(the scale axis is the same as for the main graph) on the pH corresponding to the chain protonation states (the Pearson coefficient is larger than 0.97).

4. Conclusion

We have detailed a new polarizable multiscale approach to model chitosan chains in aqueous environments. That approach is based on a all atom force field (including anisotropic many body energy terms to model hydrogen bonds) to handle the solute (here chitosan chains) and on a coarse grained solvent model. Polarization effects (arising from both the response of an electronic cloud to external electric fields and to microscopic reorientation effects due to the presence of a solute in the particular case of the coarse grained solvent model) are modeled using an induced dipole moment scheme. A main feature of our all atom force field to model chitosan chains is its parameter set that is assigned to reproduce only quantum ab initio data regarding a training set a small molecules and aggregates (like the methanol dimer and GlcN/GlcNH⁺/GlcNac monomer units).

Regarding chitosan monomers and dimers, estimates of hydration Gibbs free energies and structural properties (monomers) as well as molecular conformations (dimers) computed from our approach are in line with all the available data from earlier simulation studies based on all atom pairwise force fields. We also investigated the behavior of 50-long chitosan chains corresponding to a DA of 85%, as dissolved in aqueous phase at infinite dilution conditions, at the ionic strength zero limit and at three pH conditions (namely <4.5, and about 6 and 7, respectively). For that purpose we simulated 10 replica per pH condition, each replica corresponding to a random sequence of GlcN, GlcNH⁺, and GlcNac monomer units. For those chains, the order of magnitude of the persistence length is at the 24 nm scale for pH ≤4.5 and it decreases down to 2 nm at usual pH condition for our 50-long chains. That suggests that the persistence lengths of longer chains have to be at least 24 nm at low pH conditions, which is in line the conclusion of recent experimental⁹⁰ and coarse grained simulation²⁵ studies for low pH solutions.

In all our results regarding chitosan monomers, dimers and medium-sized chains support the reliability of our approach and thus its use to model more complex aqueous solutions comprising chitosan chain networks in the presence of surfactants and counterions, solutions in which strong polarization effects are expected to occur because of the presence of organic polarizable chain (chitosan) and of multiple charged entities (the chains as well as counterions and surfactants).

Lastly, our study shows that it is now possible to build new kinds of sophisticated simulation approaches by only accounting for results from available quantum chemistry methods without considering any experimental data. That is now possible because of the huge computational resources that are presently available. These new ab initio-based modeling approach are of particular interest to theoretically investigate new chemical systems ahead of experiment. Moreover they may be also considered to complement data from popular simulation approaches (based on efficient pairwise force fields) to better assess the reliability of the conclusions that we may draw from molecular modeling simulations, in particular for polyelectrolyte solutions in which microscopic dynamical polarization effects can play a pivotal role or to be negligible depending on the local ionic structures (see the discussions in ref (39)).

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acsomega.3c01584.

• The force field parameters, as well as the hydration energies and structural data regarding small molecules and chitosan monomer units, the Z-matrix of the GlyN dimer investigated using quantum chemistry methods, the set of Hamiltonian Replica Exchange scaling factors, and the sequences (compositions) of the 50-long chitosan chains (PDF)

The authors declare the following competing financial interest(s): Fabien Lonfort is a full employee of L'Oreal involved in research activities.