Skip to main content
NCBI home page
ACS Omega logoLink to ACS Omega
. 2023 Sep 19;8(39):36471–36478. doi: 10.1021/acsomega.3c05501

Thermodynamic Analysis and Pyrolysis Mechanism of 4,4′-Azobis-1,2,4-triazole

Kaiyi Qin 1, Mimi Zhu 1, Mingmin Zhang 1, Linan Zhang 1, Benduan Cheng 1, Qiuhan Lin 1,*
PMCID: PMC10552472  PMID: 37810696

Abstract

graphic file with name ao3c05501_0010.jpg

The nonisothermal thermal decomposition kinetics of 4,4′-azobis-1,2,4-triazole (ATRZ) at different heating rates (5, 10, 15, and 20 °C·min–1) were investigated by thermogravimetry (TG) and differential scanning calorimetry (DSC) studies. The thermal decomposition kinetic parameters such as apparent activation energy (E) and pre-exponential factor (A) were calculated by the Kissinger, Ozawa, and Šatava-Šestak methods. The E and A values calculated by the above three methods are very close, which are 391.1 kJ·mol–1/1034.92 s–1, 381.1 kJ·mol–1/1034.30 s–1, and 393.4 kJ·mol–1/1035.76 s–1, respectively. Then, the decomposition mechanism function of ATRZ is analyzed by the calculated results. The results show that the decomposition temperature of ATRZ is about 300 °C and the exothermic decomposition speed is fast. The decomposition pathway of ATRZ was analyzed by pyrolysis-gas chromatography–mass spectrometry (PY-GC-MS). The thermal decomposition kinetic equation of the ATRZ was deduced.

1. Introduction

In recent years, research on high-nitrogen materials represented by azo compounds in the field of energetic materials has attracted extensive attention, especially nitrogen-rich heterocyclic-based energetic compounds. Nitrogen-rich energy-containing heterocyclic compounds such as tetrazole, triazole, pyrazole, imidazole, and oxadiazole are very promising candidates.1,2 Singly or doubly bonded polynitrogen compounds can decompose into N2, and their energy release is very large and fast, which makes them attractive as potential explosives or propellants.3−5 Compared with traditional energetic materials, high-nitrogen materials have a large number of N–N, C–N, and N=N high-energy bonds, which causes these materials to have a higher positive heat of formation to obtain higher heat,6 rather than through intermolecular or intramolecular redox reactions, such as traditional polynitro explosives such as 2,4,6-trinitrotoluene (TNT) or pentaerythritol tetranitrate (PETN).7 Compared with traditional explosives, high-nitrogen materials have higher density and better oxygen balance (as shown in Table 1), which gives this kind of material a great advantage in the field of energetic materials, which has attracted a lot of attention from researchers from all over the world.8 Research results in recent years have shown that azotriazole compounds have excellent energy properties. Their structures have multiple nitrogen atoms that are directly connected, and there are many C–N and N–N single or double bonds, which endow them with good energy characteristics.9−15 Among them, when the N-NH2 coupling reaction generates the azo group, the N4 [N–N=N–N] chain with high energy can be generated, and this (N–N=N–N)-linked triazole compound can not only increase the nitrogen content but also provide more substitutable sites for the synthesis of polynitrogen or polynitro-containing energetic materials. Compared with a single triazole ring, it has greatly improved energy density, heat of formation, detonation velocity, and detonation pressure.12,16−20 Therefore, these compounds have received extensive attention as energetic materials.21 At present, in the field of energetic materials, people are eager to find materials with better performance, stronger stability, and higher safety. In recent years, more and more research on azo compounds has been carried out, which mainly reflects that these compounds have high heat of formation and density, as well as thermal stability compared to conventional energetic materials. This shows that azo-energetic compounds are expected to be called new materials to replace traditional explosives such as trinitrotoluene (TNT), pentaerythritol tetranitrate (PETN), cyclotrimethylenetrinitramine (RDX), or cyclotetramethylenetetranitramine (HMX).7

Table 1. Properties of ATRZ and Several Energetic Materials.

material thermal stability (°C) density(g·cm–3) detonation velocity(km·s–1) detonation pressure (GPa) oxygen balance (%)
ATRZ 310 1.62 7.43 22.73 –97.56
RDX 230 1.68 8.64 32.93 –21.61
TNT 300 1.65 6.92 20.12 –73.96
HMX 280 1.91 9.01 32.46 –21.61
PETN 200 1.78 8.60 31.75 +3.52
Open in a new tab

Numerous studies have reported the synthesis and characterization of azo-energetic materials. However, studies on the fundamental thermodynamics of these compounds are limited, such as activation energy, exothermic decomposition process, and mechanism function. 4,4′-Azobis-1,2,4-triazole (ATRZ) is a typical high-energy azo compound, which is a polynitrogen compound formed by introducing an azo bond to the nitrogen atom of the triazole ring. The introduction of azo bonds on the nitrogen heterocycle can be carried out by HgO, Br2, chloramine, etc. through N-NH2 on the nitrogen heterocycle,22,23 but the yields of the above methods for introducing azo bonds on the nitrogen atom of the triazole ring are relatively low.22 Therefore, this work used Sodium Dichloro Iso Cyanurate (SDIC) to oxidatively couple 4-amino-1,2,4-triazole to obtain 4,4′-azobis-1,2,4-triazole in higher-yield azoles.24

The purpose of this study is to explore the relevant kinetic data of the thermal decomposition of ATRZ to provide a basis for future research on azo-energetic materials. The validation method chosen in this paper is reasonable to obtain valid kinetic parameters, and the mechanism function obtained by the method and data analysis are also unique. In this paper, TG and DSC analyses were used to study the thermal decomposition process of ATRZ at different heating rates,25,26 and the kinetic parameters were obtained by the model-free method and the model fitting method.27 The possible decomposition mechanisms were discussed by the PY-GC-MS analysis.28

2. Experiment

2.1. Synthesis

Synthesis of 4,4′-azobis-1,2,4-triazole (ATRZ): In a 500 mL flask, 200 mL of water and 28 g of SDIC (0.24 mol) were added and stirred until a clear solution was obtained. Then, 50 mL of glacial acetic acid was added and the mixture was continued to stir until the solution was clear. Then, a solution of 20 g of 4-amino-1,2,4-triazole (0.24 mol) dissolved in 20 mL of water was added dropwise, and the temperature was controlled at 15–20 °C. After the completion of the dropwise addition, stirring was continued for 1 h to complete the reaction. The mixture was filtered and washed to obtain transparent crystals.81H NMR (500 MHz; CD3OD, 25 °C, TMS): δ = 9.42 ppm (4H, s); IR (KBr): ν = 3112, 1487, 1365, 1316, 1168 cm–1; elemental analysis (%) for ATRZ (164): C, 29.27; H, 2.44; N, 68.29; found: C, 30.17; H, 2.58; N, 67.25.

ATRZ is composed of two triazole rings and azo bonds and has a symmetrical coplanar molecular structure. The ATRZ molecule contains one N=N double bond, four N–N single bonds, and four C=N double bonds, which theoretically have a high energy storage capacity. In addition, the molecule does not contain nitro, which imparts better safety. The structural formula of ATRZ is shown in Figure 1.

Figure 1.

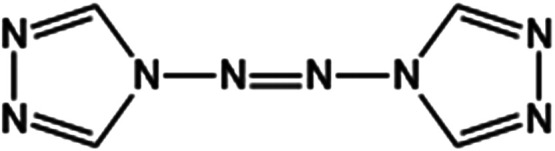
Figure 1

Open in a new tab

ATRZ structure.

2.2. Experimental Equipment and Conditions

The instruments for thermal dynamics research were STA 449F5 Jupiter (NETZSCH, Germany) and DSC 204F1 Phoenix (NETZSCH, Germany). The instrument for pyrolysis mechanism research was PY-GC-MS (Agilent, 7890B+5977B+3030D).

The ATRZ was studied by using TG and DSC analyses under a nitrogen atmosphere with the flow rates of 40 mL·min–1 purge gas and 60 mL·min–1 guard gas for DSC and 20 mL·min–1 purge gas and 20 mL·min–1 guard gas for TG analysis. The sample dosage was about 0.23 mg. The heating rate was 5, 10, 15, and 20 °C·min–1 from 30 to 400 °C. The pyrolysis temperature of PY-GC-MS is 400 °C. The TG, DSC, and PY-GC-MS data were analyzed and studied using Origin software.

3. Thermodynamic Theory

By using Kissinger and Ozawa methods, the kinetic parameters of a solid-state reaction can be obtained without the knowledge of the reaction mechanism.

The Kissinger method and Ozawa method are commonly used in thermodynamic analysis to calculate thermodynamic parameters (apparent activation energy (E) and pre exponential factor (A)).25 The Kissinger29 method can help researchers evaluate kinetic parameters without calculating E for each conversion value of the solid reaction. The apparent activation energy (E) and the pre-exponential factor (A) can be obtained from the slope −/(RTP) and intercept ln (AR/E) of the ln (β/TP) versus 1/TP plot, respectively. The Ozawa method30 is simple and suitable for reactions that cannot be analyzed by other methods. It is widely used, along with the Kissinger method, to determine the apparent activation energy (E). The apparent activation energy (E) can be obtained from a logarithmic plot of the heating rates. The curve of logβ for 1/TP represents a linear function with an intercept of 0.4567E/R. The E calculated by this method is independent of the thermal decomposition mechanism.

Using the DSC data, the kinetic factors (E, A) of the thermal decomposition reaction of ATRZ were obtained using the Kissinger, Ozawa, and Šatava-Šestak methods. The calculation method is shown in Table 2.

Table 2. Calculation Methods Used in This Studya.

method expression heating rate function
Kissinger 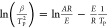Inline graphic multiple free
Ozawa Inline graphic multiple/single free
Šatava-Šesták Inline graphic single G(α)
Open in a new tab
a

The best-fitting integral functional form of Ozawa and Šatava-Šesták: G(α) = −ln(1−α).

where f(α) and G(α) are the differential and integral kinetic mechanism functions, respectively; E is the apparent activation energy; A is the pre-exponential factor; β is the heating rate; To is the temperature onset point at which the DSC curve begins to deviate from the baseline; R is the molar gas constant (8.314 J·mol–1·K–1); α is the conversion rate; T is the temperature K at time t; and TP is the peak temperature of the DSC curve. The 41 functional forms of the kinetic model used in this paper are in Table S1 and can be found in ref (31).

4. Results and Discussion

4.1. Thermal Analysis

DSC curves of ATRZ under different heating rates in a nitrogen environment are shown in Figure 2. It can be seen from Figure 2 that there is a group of extremely small endothermic peaks in the temperature range of 175–200 °C. This can be attributed to the melting of the ATRZ sample. The exothermic peak is found in the temperature range of 270–330 °C. The characteristic temperature and heating rate of the DSC curve are shown in Table 3. It can be seen from Table 3 that at 5 °C·min–1, the thermal decomposition temperature starts from 282.0 °C and basically ends at 310.5 °C. The initial temperature (T) of the DSC curve for thermal decomposition at a higher heating rate, peak temperature (TP), and final temperature (Te) from 282.0, 308.9, and 310.5 °C at 5 °C·min–1 increase to 295.4, 318.5, and 321.1 °C at 20 °C·min–1, respectively.

Figure 2.

Figure 2

Open in a new tab

DSC curves of ATRZ at different heating rates.

Table 3. Characteristic Temperature and Heating Rate of DSC Curvesa.

β (°C·min–1) To (°C) TP (°C) Te (°C)
5 282.0 308.9 310.5
10 287.0 315.5 317.0
15 291.4 316.7 318.5
20 295.4 318.5 321.1
Open in a new tab
a

β: heating rate; To, TP, Te: onset, peak, and end temperatures of the DSC curve, respectively.

DSC images showed that ATRZ was rapidly exothermic in a small temperature range, showing an obvious exothermic peak. The peak temperatures of the exothermic peaks at four heating rates (5, 10, 15, 20 °C·min–1) in this work are 308.9, 315.5, 316.7, and 318.5 °C, respectively, which are almost close to the peak temperatures of the exothermic peaks at the same heating rates in the literature (312.7, 317.7, 320.4, 322.7 °C and 306.1, 309.3, 310.1, 310.9 °C).32,33

TG and DTG curves of ATRZ at different heating rates under a nitrogen atmosphere are shown in Figures 3 and 4, respectively. The specific data of ATRZ are listed in Table 4. It can be seen from Table 4 that the weight loss of the sample starts from 283.7 °C at 5 °C·min–1. With the increase of heating rate, the initial temperature of the TG curve (To) and weight loss (%) increases from 283.7 °C at 5 °C·min–1, 97.40% at 20 °C·min–1 to 299.5 °C, 96.87%.

Figure 3.

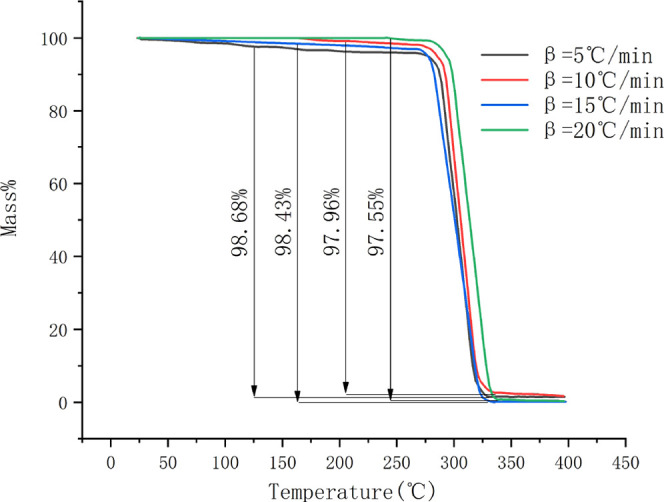
Figure 3

Open in a new tab

TG curves of ATRZ at different heating rates.

Figure 4.

Figure 4

Open in a new tab

DTG curves of ATRZ at different heating rates.

Table 4. Relevant Information of the TG Curves of ATRZ.

β (°C·min–1) To (°C) mass (%)
5 283.7 97.40
10 288.4 97.36
15 295.9 96.99
20 299.5 96.87
Open in a new tab

4.2. Determination of Parameters Related to Thermal Decomposition Kinetics

The experimental data measured in this work were inserted into the Kissinger, Ozawa, and Šatava-Šesták equations in Table 2, and the dynamic parameters (E and A) of the thermal decomposition of ATRZ were calculated. The results obtained are given in Table 5.

Table 5. Kinetic Parameters Calculated by Kissinger, Ozawa, and Šatava-Šesták Methodsa.

method E (kJ·mol–1) lg A (s–1) r2 d
Kissinger 391.1 34.92 0.99204 0.00939
Ozawa 381.1 34.30 0.99252 0.00177
Šatava-Šesták 393.4 35.76 0.99798 0.00240
Average 388.5 34.99 0.99418 0.00452
Open in a new tab
a

r: correlation coefficient; d: standard deviation of E.

According to the data in Table 5, the E values of ATRZ thermal decomposition stage calculated by Kissinger, Ozawa, and Šatava-Šesták methods are EK = 391.1 kJ·mol–1, EO = 381.1 kJ·mol–1, and ES = 393.4 kJ·mol–1, respectively. The E values calculated by these three methods are quite comparable, indicating that these values can be used as a reference for determining possible kinetic mechanism functions.

The DSC curve data were analyzed using a nonisothermal multiple scan rate method (equal transformation rate method,34 model-free function method, model-free method25,35). Based on the difference in temperature and exothermic rate at the same conversion in the DSC curve, a system of equations is listed to solve the values of E and A. It can be seen from Figure 5 that the fitted lines are nearly parallel, which indicates that the method is suitable for this system within the transformation range studied. This fact indicates that there is only one reaction mechanism corresponding to it in the thermal decomposition stage.36

Figure 5.

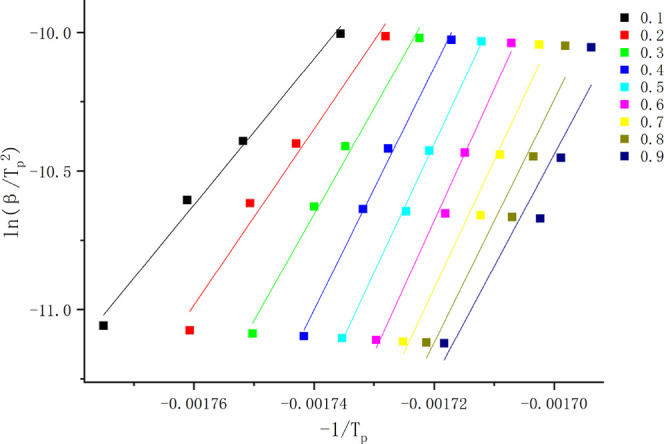
Figure 5

Open in a new tab

Thermal decomposition phase diagram at different conversion rates by the Kissinger method.

4.3. Determination of the Parameters Related to Thermal Decomposition Kinetics

The Šatava-Šesták method combined with the relevant data in Tables 2 and 5 was used to explore the best thermodynamic mechanism function among 41 kinetic mechanism functions. The activation energy ES calculated by the Šatava-Šesták method was compared with the activation energy EO calculated by the Ozawa method. The activation energy obtained satisfied the condition (EO – ES)/EO ≤ 0.1. The relationship between ln AS obtained by the Šatava-Šesták method and ln AK obtained by the Kissinger method is (ln AS – ln AK)/ln AS ≤ 0.5. Only when the above two conditions are satisfied, the integral function G(α) is the integral form of the reaction mechanism function of thermal decomposition.

By calculation and screening, the No. 16 function (refer to Table S1) is selected as the best integral function of the thermal decomposition reaction, and the values of E and A obtained by Kissinger, Ozawa, and Šatava-Šesták methods are the most close, with a good correlation and a low standard deviation. The reaction model at this stage is random nucleation and subsequent growth, n = 1, m = 1, the integral and differential forms are shown in eqs 1 and 2, respectively.

4.3. 1
4.3. 2

According to the reaction rate differential formula Inline graphic, the thermal decomposition kinetic equation of ATRZ at the heating rate of 10 °C min–1 is shown in eq 3. Refer to Table 5 for specific values.

4.3. 3

According to the Arrhenius equation Inline graphic, the reaction rate equation of ATRZ in the stage is shown in eq 4.

4.3. 4

4.4. Pyrolysis Mechanism

The pyrolysis process of ATRZ was studied by PY-GC-MS, and the decomposition pathway and mechanism of ATRZ were analyzed. The PY-GC-MS image of the ATRZ is shown in Figure 6. Various fragment structures and products in the thermal decomposition process of ATRZ are listed in Table 6.

Figure 6.

Figure 6

Open in a new tab

PY-GC-MS total-ion chromatogram of ATRZ at 400 °C. (a) ATRZ ion chromatogram of the whole time period. (b) ATRZ ion chromatogram of the first 10 min.

Table 6. Product Structural Assignments During ATRZ Pyrolysis.

4.4.

Open in a new tab

According to the thermal cracking and mass spectrometry detection of ATRZ at 400 °C by PY-GC-MS in Figure 6 and Table 6, the pyrolysis pathway of ATRZ was inferred, as shown in Scheme 1. Scheme 2 shows the fragment structures obtained by further recombination of the initial thermal decomposition fragments of ATRZ through a coupling reaction. First, the bonds of the ATRZ ring system with azo break and decompose into intermediates (1) (m/z 96) and (2) (m/z 68) and N2. The intermediate (2) can also be obtained by further removing a molecule of N2 from intermediate (1). The intermediate (2) opens the triazole ring through two different bond-breaking methods, further resulting in smaller fragments (3) (m/z 41), (4) (m/z 27), and (5) (m/z 13). Fragment (6) (m/z 26) was obtained by coupling two fragments (5) (m/z 13) through C=C double-bond formation. A fragment (4) is coupled with a fragment (6) through the formation of a C–C single bond to obtain intermediate (7) (m/z 53). The intermediate (7) performs H proton transfer to produce product No. 3 (m/z 53). Two fragments (4) and one fragment (6) are coupled through the formation of two C–C single bonds to obtain intermediate (8) (m/z 80). The intermediate (8) is further dehydrogenated to produce product No. 7 (m/z 78). Two fragments (4) are coupled with one fragment (6) to form a ring to produce products 5 (m/z 80) and 6 (m/z 80). The three fragments (4) are coupled to form a ring to produce product No. 4 (m/z 81).

Scheme 1. Main Decomposition Path of ATRZ.

Scheme 1

Open in a new tab

Scheme 2. Fragment Structures Obtained by Further Recombination of the Initial Thermal Decomposition Fragments of ATRZ.

Scheme 2

Open in a new tab

5. Conclusions

Thermogravimetry (TG) and differential scanning calorimetry (DSC) analyses were used to analyze the thermal properties of ATRZ. When the heating rate was 5 °C·min–1, the DSC curve showed an exothermic peak in the range of 282.0–310.5 °C. With the increase in the heating rate, the characteristic temperature of the DSC curve moved to a higher temperature. When the heating rate was 5 °C·min–1, the weight loss curve of TG started from 283.7 °C. With the increase of the heating rate, the initial decomposition temperature also increased, which was almost consistent with the initial decomposition temperature measured by the DSC curve.

The kinetic parameters of the thermal decomposition of ATRZ were calculated by the Kissinger, Ozawa, and Šatava-Šestak methods. The thermal decomposition kinetic parameters of the ATRZ obtained by different calculation methods are basically the same. The E and lgA values calculated by the Kissinger, Ozawa, and Šatava-Šestak methods are 391.1, 381.1, and 393.4 kJ·mol–1 and 34.92, 34.30, and 35.76 s–1, respectively. Among the 41 mechanism functions, function 16 is selected as the most suitable mechanism function, and the reaction model is random nucleation and subsequent growth, n = 1, m = 1, the integral and differential forms are shown in eqs 1a and 2a, respectively.

5. 1a
5. 2a

The kinetic equation of the ATRZ thermal decomposition stage is shown in eq 3a.

5. 3a

The thermal decomposition path of the ATRZ was investigated by PY-GC-MS analysis. The thermal decomposition reaction of ATRZ involves the breaking of the N–N single bond in the molecule and the ring opening of the triazole ring. ATRZ undergoes complete thermal decomposition to generate smaller fragments, which are coupled to produce new products.

Acknowledgments

This work was supported by the National Natural Science Foundation of China (22375095) and the Natural Science Foundation of Jiangsu Province (BK20191291).

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acsomega.3c05501.

  • In this paper, the best mechanism function of the ATRZ thermal decomposition process is calculated by using 41 kinds of kinetic model functions and combining them with the thermal decomposition data of ATRZ under different conversion rates. The 41 kinds of kinetic model functions are shown in Table S1 (PDF)

Author Contributions

† K.Q. and M.Z. contributed equally to this work. The manuscript was written through contributions of all authors. All authors have given approval to the final version of the manuscript.

The authors declare no competing financial interest.

Supplementary Material

ao3c05501_si_001.pdf (1.1MB, pdf)

References

  1. Tuoping H.; Wenhua B.; Xiaoqin H.; et al. Construction of Metal–Organic Frameworks with Novel {Zn8O13} SBU or Chiral Channels throughin SituLigand Reaction. Cryst. Growth Des. 2010, 10 (8), 3324. 10.1021/cg100725j. [DOI] [Google Scholar]
  2. Yingxiang Y.; Liuqin Z.; Qinfang P.; et al. High anhydrous proton conductivity of imidazole-loaded mesoporous polyimides over a wide range from subzero to moderate temperature. J. Am. Chem. Soc. 2015, 137 (2), 913. 10.1021/ja511389q. [DOI] [PubMed] [Google Scholar]
  3. Yuangang X.; Qian W.; Cheng S.; et al. A series of energetic metal pentazolate hydrates. Nature 2017, 549 (7670), 78. 10.1038/nature23662. [DOI] [PubMed] [Google Scholar]
  4. Hirshberg B.; Gerber R. B.; Krylov A. I. Calculations predict a stable molecular crystal of N8. Nat. Chem. 2014, 6 (1), 52. 10.1038/nchem.1818. [DOI] [PubMed] [Google Scholar]
  5. Christe K. O. Polynitrogen chemistry enters the ring. Science 2017, 355 (6323), 351 10.1126/science.aal5057. [DOI] [PubMed] [Google Scholar]
  6. Fischer D.; Klapoetke T. M.; Stierstorfer J. 1,5-Di(nitramino)tetrazole: High Sensitivity and Superior Explosive Performance. Angew. Chem., Int. Ed. 2015, 54 (35), 10299–10302. 10.1002/anie.201502919. [DOI] [PubMed] [Google Scholar]
  7. Qu Y.; Babailov S. P. Azo-linked high-nitrogen energetic materials. J. Mater. Chem. A 2018, 6 (5), 1915–1940. 10.1039/C7TA09593G. [DOI] [Google Scholar]
  8. Qi C.; Li S.-H.; Li Y.-C.; et al. A novel stable high-nitrogen energetic material: 4,4 ′-azobis(1,2,4-triazole). J. Mater. Chem. 2011, 21 (9), 3221–3225. 10.1039/c0jm02970j. [DOI] [Google Scholar]
  9. Singh R. P.; Ga H.; Meshri D. T.. et al. Nitrogen-rich Heterocycles; Klapotke T. M., Ed.; High Energy Density Materials, 2007; pp 35–83. [Google Scholar]
  10. Klapoetke T. M.; Sabate C. M. Bistetrazoles: Nitrogen-rich, high-performing, insensitive energetic compounds. Chem. Mater. 2008, 20, 3629–3637. 10.1021/cm703657k. [DOI] [Google Scholar]
  11. Tao G.-H.; Guo Y.; Parrish D. A.; et al. Energetic 1,5-diamino-4H-tetrazolium nitro-substituted azolates. J. Mater. Chem. 2010, 20 (15), 2999–3005. 10.1039/b925267c. [DOI] [Google Scholar]
  12. Guo Y.; Gao H.; Twamley B.; et al. Energetic nitrogen rich salts of N,N-bis 1(2)H-tetrazol-5-yl amine. Adv. Mater. 2007, 19 (19), 2884–2888. 10.1002/adma.200602647. [DOI] [Google Scholar]
  13. Joo Y.-H.; Shreeve J. N. M. High-Density Energetic Mono- or Bis(Oxy)-5-Nitroiminotetrazoles. Angew. Chem., Int. Ed. 2010, 49 (40), 7320–7323. 10.1002/anie.201003866. [DOI] [PubMed] [Google Scholar]
  14. Huynh M. H. V.; Hiskey M. A.; Hartline E. L.; et al. Polyazido high-nitrogen compounds: Hydrazo- and azo-1,3,5-triazine. Angew. Chem., Int. Ed. 2004, 43 (37), 4924–4928. 10.1002/anie.200460366. [DOI] [PubMed] [Google Scholar]
  15. Klapoetke T. M.; Piercey D. G. 1,1 ′-Azobis(tetrazole): A Highly Energetic Nitrogen-Rich Compound with a N-10 Chain. Inorg. Chem. 2011, 50 (7), 2732–2734. 10.1021/ic200071q. [DOI] [PubMed] [Google Scholar]
  16. Qi C.; Li S.-H.; Li Y.-C.; et al. Synthesis and Promising Properties of a New Family of High-Nitrogen Compounds: Polyazido- and Polyamino-Substituted N,N′-Azo-1,2,4-triazoles. Chem. - Eur. J. 2012, 18 (51), 16562–16570. 10.1002/chem.201202428. [DOI] [PubMed] [Google Scholar]
  17. Li Y.-C.; Qi C.; Li S.-H.; et al. 1,1 ′-Azobis-1,2,3-triazole: A High-Nitrogen Compound with Stable N-8 Structure and Photochromism. J. Am. Chem. Soc. 2010, 132 (35), 12172–12173. 10.1021/ja103525v. [DOI] [PubMed] [Google Scholar]
  18. Liu W.; Li S.-H.; Li Y.-C.; et al. Nitrogen-rich salts based on polyamino substituted N,N ′-azo-1,2,4-triazole: a new family of high-performance energetic materials. J. Mater. Chem. A 2014, 2 (38), 15978–15986. 10.1039/C4TA03016H. [DOI] [Google Scholar]
  19. Sivabalan R.; Anniyappan M.; Pawar S. J.; et al. Synthesis, characterization and thermolysis studies on triazole and tetrazole based high nitrogen content high energy materials. J. Hazard. Mater. 2006, 137 (2), 672–680. 10.1016/j.jhazmat.2006.03.038. [DOI] [PubMed] [Google Scholar]
  20. Li Z.-M.; Zhang J.-G.; Cui Y.; et al. A Novel Nitrogen-Rich Cadmium Coordination Compound Based on 1,5-Diaminotetrazole: Synthesis, Structure Investigation, and Thermal Properties. J. Chem. Eng. Data 2010, 55 (9), 3109–3116. 10.1021/je100001b. [DOI] [Google Scholar]
  21. Li X.; Sun Q.; Lin Q.; et al. N-N=N-N -linked fused triazoles with pi-pi stacking and hydrogen bonds: Towards thermally stable, Insensitive, and highly energetic materials. Chem. Eng. J. 2021, 406, 126817 10.1016/j.cej.2020.126817. [DOI] [Google Scholar]
  22. Porath B.; Munzenberg R.; Heymanns P.; et al. First synthesis and investigation of two hydroxyalkyl-substituted 2-tetrazenes. Eur. J. Org. Chem. 1998, 1998 (7), 1431–1440. . [DOI] [Google Scholar]
  23. Delalu H.; Elkhatib M.; Peyrot L.; et al. Synthesis and NMR investigation of 3,4-diazabicyclo 4.3.0 non-2-ene and N,N ′-azo-3-azabicyclo 3.3.0 octane. X-ray crystal structure analysis of a new tetrazene derivative. J. Heterocycl. Chem. 1999, 36 (3), 681–686. 10.1002/jhet.5570360317. [DOI] [Google Scholar]
  24. Li Y.; Li S.; Qi C.; et al. Synthesis and Performance of A Novel Poly-nitrogen Compound 1,1 ′-Azobis-1,2,3-triazole. Acta Chim. Sin. 2011, 69 (18), 2159–2165. [Google Scholar]
  25. Liu R.; Zhang T.; Yang L.; et al. DSC/DPTA Thermal Analysis Kinetics and Their Applications. Chin. J. Explos. Propellants 2013, 36 (5), 16–21. [Google Scholar]
  26. Ziru L. Review and prospect of thermal analysis technology applied to study thermal properties of energetic materials. FirePhysChem. 2021, 1 (3), 129–138. 10.1016/j.fpc.2021.05.002. [DOI] [Google Scholar]
  27. Jankovic B. Kinetic analysis of the nonisothermal decomposition of potassium metabisulfite using the model-fitting and isoconversional (model-free) methods. Chem. Eng. J. 2008, 139 (1), 128–135. 10.1016/j.cej.2007.07.085. [DOI] [Google Scholar]
  28. Du X.; Li X.; Zou M.; et al. Thermal kinetic study of 1-amino-1,2,3-triazolium nitrate. J. Therm. Anal. Calorim. 2014, 115 (2), 1195–1203. 10.1007/s10973-013-3405-8. [DOI] [Google Scholar]
  29. Kissinger H. E. Reaction Kinetics in Differential Thermal Analysis. Anal. Chem. 2002, 29 (11), 1702–1706. 10.1021/ac60131a045. [DOI] [Google Scholar]
  30. Ozawa T. A New Method of Analyzing Thermogravimetric Data. Bull. Chem. Soc. Jpn. 1965, 38 (11), 1881–1886. 10.1246/bcsj.38.1881. [DOI] [Google Scholar]
  31. Liu R.; Zhou Z.; Yin Y.; et al. Dynamic vacuum stability test method and investigation on vacuum thermal decomposition of HMX and CL-20. Thermochim. Acta 2012, 537, 13–19. 10.1016/j.tca.2012.02.025. [DOI] [Google Scholar]
  32. Pan Q.; Zhang H.; Guo X.; et al. Pyrolysis Kinetics and Combustion Behaviors of a High-Nitrogen Compound, 4,4 ′-Azobis(1,2,4-triazole). Int. J. Mol. Sci. 2022, 23 (19), 11313 10.3390/ijms231911313. [DOI] [PMC free article] [PubMed] [Google Scholar]
  33. Jia C.; Li Y.; Zhang S.; et al. Thermogravimetric analysis, kinetic study, and pyrolysis-GC/MS analysis of 1,1 ′-azobis-1,2,3-triazole and 4,4 ′-azobis-1,2,4-triazole. Chem. Cent. J. 2018, 12, 22 10.1186/s13065-018-0381-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
  34. Brown M. E.; Maciejewski M.; Vyazovkin S.; et al. Computational aspects of kinetic analysis Part A: The ICTAC kinetics project-data, methods and results. Thermochim. Acta 2000, 355 (1–2), 125–143. 10.1016/S0040-6031(00)00443-3. [DOI] [Google Scholar]
  35. Janković B. Kinetic analysis of the nonisothermal decomposition of potassium metabisulfite using the model-fitting and isoconversional (model-free) methods. Chem. Eng. J. 2007, 139 (1), 128–135. 10.1016/j.cej.2007.07.085. [DOI] [Google Scholar]
  36. Yan Q.-L.; Li X.-H.; Wang H.; et al. Thermal decomposition and kinetics studies on 1,4-dinitropiperazine (DNP). J. Hazard. Mater. 2008, 151 (2–3), 515–521. 10.1016/j.jhazmat.2007.06.019. [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

ao3c05501_si_001.pdf (1.1MB, pdf)

Articles from ACS Omega are provided here courtesy of American Chemical Society

RESOURCES