Skin-interfaced soft microfluidics systems with modular and reusable electronics for in-situ capacitive sensing of sweat loss, rate and conductivity

Abstract

Important insights into human health can be obtained through the non-invasive collection and detailed analysis of sweat, a biofluid that contains a wide range of essential biomarkers. Skin-interfaced microfluidic platforms, characterized by soft materials and thin geometries, offer a collection of capabilities for in-situ capture, storage, and analysis of sweat and its constituents. In ambulatory uses cases, the ability to provide real-time feedback on sweat loss, rate and content, without visual inspection of the device, can be important. This paper introduces a low-profile skin-interfaced system that couples disposable microfluidic sampling devices with reusable ‘stick-on’ electrodes and wireless readout electronics that remain isolated from the sweat. An ultra-thin capping layer on the microfluidic platform permits high-sensitivity, contactless capacitive measurements of both sweat loss and electrolyte concentration. This architecture avoids the potential for corrosion of the sensing components and eliminates need for cleaning/sterilizing the electronics, thereby resulting in a cost-effective platform that is simple to use. Optimized electrode designs follow from a combination of extensive benchtop testing, analytical calculations and FEA simulations for two sensing configurations: (1) sweat rate and loss, and (2) sweat conductivity, which contains information about electrolyte content. Both configurations couple to a flexible, wireless electronics platform that digitizes and transmits information to Bluetooth-enabled devices. On-body field testing during physical exercise validates the performance of the 63 system in scenarios of practical relevance to human health and performance.

Graphical Abstract

Stick-on electrodes capacitively coupled to single-use microfluidic channels enable contactless analysis of sweat in a soft wearable format with real-time wireless data collection.

Introduction

Sweat, as a biofluid that can be captured with completely non-invasive sampling procedures, can provide a valuable collection of data with relevance to human health¹. Quantitative measurements of sweat constituents, such as electrolytes, metabolites and proteins, is particularly attractive in the context of medical diagnostics^2,3 and athletic performance⁴. Real-time analysis of sweat has immediate relevance in developing individualized hydration strategies to control electrolyte balance and to limit dehydration or overhydration during physical activity⁵. The utility of sweat for physiological monitoring is of rapidly growing interest due to the recent emergence of various classes of skin-interfaced digital devices that enable collection and analysis of sweat in the field, without the need for bulky laboratory instruments. Of specific interest are skin-like, or ‘epidermal’ microfluidic systems, sometimes referred to as epifluidic technologies, that consist of low-profile, micromolded channels embedded in soft elastomeric materials for in-situ measurements of sweat rate⁶ and quantitative measurements of constituent concentrations through colorimetric⁷, fluorescence⁸, electrochemical⁹, or impedance-based¹⁰ techniques. Such platforms can measure a variety of physiological parameters via eccrine sweat, across a range of practical applications, including uses in extreme environments¹¹. These possibilities expand the capabilities and scope of those associated with traditional methods that utilize absorbent pads for sweat collection, with subsequent analysis performed in centralized facilities using conventional laboratory equipment^4,12.

Electrolyte concentration in sweat is a key biomarker of interest, but its value is influenced by sweat rate due to the fundamental secretion and reabsorption mechanisms associated with the sweat ducts.^{3, 13} As such, measurements of both rate and electrolyte composition are necessary for conclusive analysis. Previous studies of sweat rate and electrolyte content often utilize visual observation within epifluidic devices, but such approaches require visual access and reference color charts to control for variable lighting conditions^{7, 14}. Other continuous mode embodiments provide real-time digital feedback on rate and/or electrolyte content through direct contact between the collected sweat and measurement electrodes^{10, 15, 16, 17}. These platforms, however, have drawbacks such as limited robustness due to the presence of air bubbles at the electrode interface¹⁵ and practical difficulties in cleaning and sterilizing the electrodes and associated electronics after each cycle of use. Most importantly, galvanic contacts with sweat require a protective encapsulation of the measurement electrodes with chemically inert metals such as gold to avoid corrosion reactions, thereby increasing manufacturing costs and preventing their deployment at scale. Here, we report a platform that utilizes non-contact electrodes capacitively coupled to the sweat as it travels through a microfluidic device. Combining this construct with Bluetooth-based electronics for data capture and wireless transmission enables continuous and real-time measurements of sweat conductivity and dynamics.

Capacitively-coupled approaches provide attractive means to measure fluid levels and to distinguish between different types of fluids. Dielectric properties of aqueous solutions have been studied widely in the literature especially in the mid-20^th century¹⁸, but little information is available on the dielectric properties of human sweat¹⁹. Many types of microfluidic lab-on-a-chip technologies use capacitance-based measurements, to detect droplets size and speed²⁰, to infer their content in the case of simple mixtures²¹, but also to provide quantitative measurements in the context of biological materials including single cell analysis^22,23. Some systems offer options in which electrodes contact fluid droplets directly, by measuring the double layer capacitance with two metal electrodes²⁴ or by evaluating the capacitance between a fluid channel and one metal electrode in its close vicinity with no electrical contact to the fluid²⁵. More interestingly, non-contact measurements are possible with interdigitated electrode pairs^{20, 26} in optimized geometries²⁷, as described in several examples in the literature^28–30. This paper describes adaptations and extensions of these basic concepts for the study of sweat using skin-interfaced microfluidic platforms. The approach optimizes the sensitivity through the use of ultra-thin capping layers on the channels as a sensing interface that offers sufficiently large changes in capacitance for accurate measurement using simple, compact readout electronics. Another important feature is in the electrical decoupling of the system from the underlying skin, to allow accurate, in situ measurements.^{31, 32} A combination of experiments, analytical calculations and FEA simulations reveal the essential effects, to enable optimization of the measurement system and electrode geometries. Tailoring the layouts allows for measurement of both sweat rate and sweat conductivity from the capacitance values. A low-profile, custom readout circuit enables accurate wireless operation during human subject field studies on healthy volunteers.

Results and discussion

Skin-interfaced capacitance-based electronics and microfluidics design

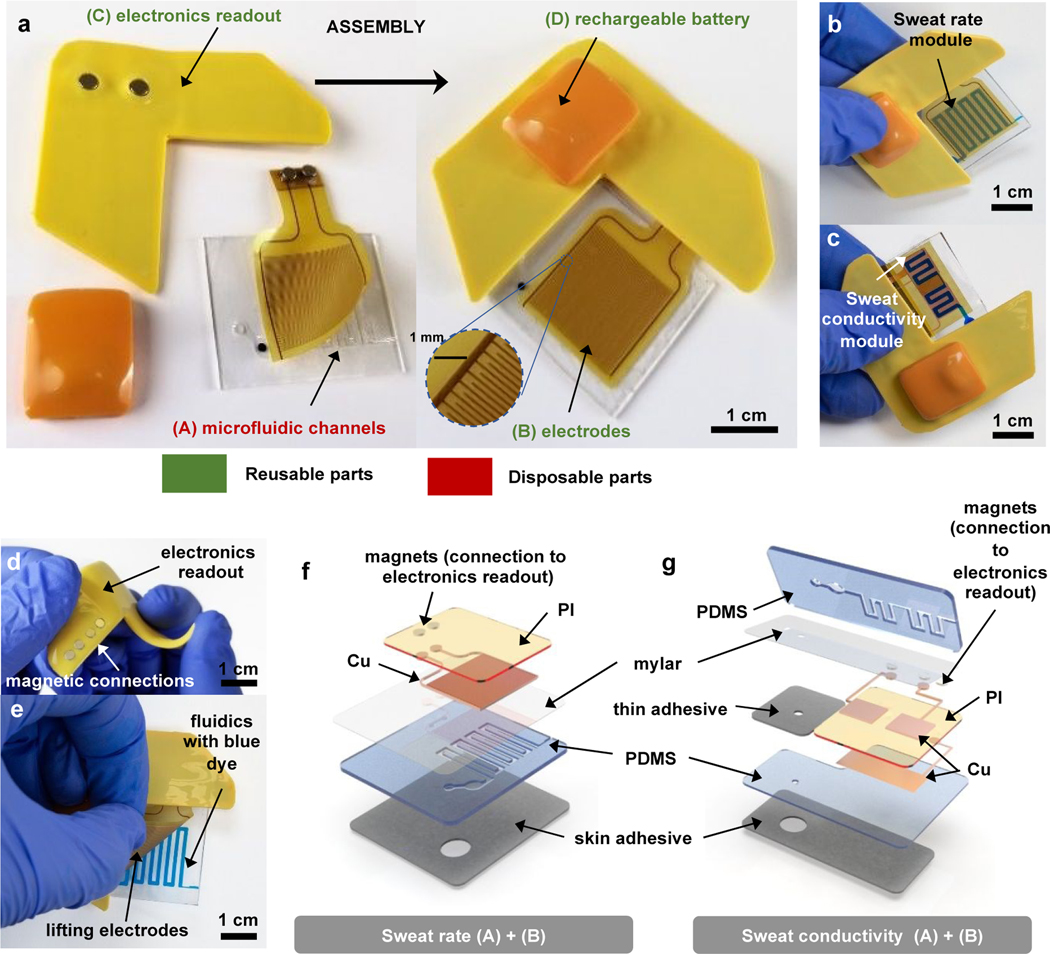
The capacitance sensing module and microfluidics system consists of a collection of several sub-modules: (A) a soft skin-mounted disposable microfluidic system, (B) flexible, repositionable and reusable electrodes, (C) a reusable electronics readout platform to digitize and transmit information collected by the electrodes wirelessly to a Bluetooth-enabled device (e.g. tablet), and (D) a rechargeable battery (Figure 1a). The geometries of modules (A) and (B) are optimized for measurements of sweat rate and conductivity. Modules (C) and (D) are the same for both types of measurements, as described in detail in the section on “electronics readout design”. Coupling between modules (B), (C) and (D) occurs through a magnetic interfacing scheme. Fully assembled devices for sweat rate and sweat conductivity measurements are shown in Figure 1b and 1c, with blue dye to enhance the visual contrast of the microfluidic channels. All components have low-profile, flexible designs, as shown in Figure 1d for the electronics readout, and electrodes (B) benefit from repositionable adhesive coupling to fluidics module (A), as illustrated in Figure 1e.

Figure 1. Pictures and schematic illustrations of a wireless microfluidics and electronics device with capabilities in digital measurements of sweat loss, sweat rate and sweat conductivity.

a. General overview of device assembly, showing disposable (A) and reusable (B, C, D) parts: microfluidics channels (A) are assembled to electrodes (B) through a thin silicone adhesive coating. Electrodes connection to electronics readout (C) ensured through magnets allows wirelessly transmission of data, using battery (D) as a powering source, connected through magnets to (C).

b. Fully assembled device for sweat rate measurements, with blue dyed liquid in the microfluidic channel to aid visualization.

c. Fully assembled device for sweat conductivity measurements, with blue dyed liquid in the microfluidic channel to aid visualization.

d. Bending of the electronics readout part, showing high flexibility and low profile.

e. Peeling of reusable electrodes from the microfluidics module, illustrating reusability of parts (B, C, D).

f. Exploded view schematic illustrations of parts (A) and (B) for the sweat rate device.

g. Exploded view schematic illustrations of parts (A) and (B) for the sweat conductivity device.

For measurements of sweat rate, module (A) consists of three layers of polymeric materials shown in Figure 1f: a thin polyester film (Mylar) as a uniform capping layer, a polydimethylsiloxane (PDMS) microfluidic layer fabricated via molding using soft lithography techniques to define a collection of microchannels, an inlet to the skin to allow entry of sweat and an outlet to the surrounding ambient air to suppress back-pressure. A medical-grade acrylic adhesive layer with an opening that aligns to the inlet bonds the device to the skin. Sweat enters through the inlet as a consequence of secretory fluidic pressures generated at the surface of the skin by eccrine sweat glands and fills progressively the channels³³. The upper surface of the Mylar film serves as the foundation for a thin layer of silicone adhesive that allows repositionable contact to module (B), as shown in Figure 1e. Module (B) consists of a flexible polyimide (PI) / copper (Cu) clad sheet patterned with an interdigitated array of electrodes. A set of magnets soldered to connection pads serve as an electrical and mechanical interface to module (C). Figure 1b shows the assembled device, and Figure 1f presents an exploded view to highlight the details of modules (A) and (B).

Devices for measurement of sweat conductivity exploit similar stacks of materials, but with two important modifications to the geometry: (i) electrodes take the form of two pads that cover separate zones of the microchannel, with a small channel that connects the two, as inspired by designs for capacitively coupled contactless conductivity detection in other contexts^{34, 35}; (ii) microchannels and Mylar film integrate on top of an additional flat layer of PDMS, with module (B) inserted in between to minimize the influence of the skin on the measurements. Module (B) presents electrodes on one side and an electrical ground plane of Cu on the other side, in between the electrodes and the skin. This plane, along with the electrodes, connects to module (C) using the magnetic coupling scheme described previously. Figure 1c shows the completed device, and Figure 1g presents an exploded view to highlight the details of parts (A) and (B). Fabrication protocols are in the Materials and Methods section. A thin, conformal coating of parylene-C, not shown in the illustration, protects the PI layer and electrodes in module (B) from moisture.

Materials, mechanics, and design considerations for optimal capacitive coupling

Capacitive coupling between the electrodes and microfluidic channels strongly depends on the distance between the liquid and electrodes, relevant for measurements of both rate²⁰ and conductivity³⁵. As expected, the sensitivity improves with decreasing distance. The soft microfluidics platforms involve an assembly of two PDMS layers, one cast against a mold that forms trenches, and another that is flat and mounts on top of first as a capping layer to define closed channels^{7, 14}. The thickness of the capping layers in previously reported systems are in the range of ten to hundreds of micrometers. With PDMS (Young’s modulus ~1–2 MPa), mechanical collapse of the structures^{36, 37} and wrinkling of the capping layer could limit the dimensions of the channels and the thickness of the capping layer. The use of Mylar (Young’s modulus 1–3 GPa) instead of PDMS for the capping layer bypasses these limitations, where a seal to the PDMS channel layer occurs through covalent bonding³⁸. Supplementary Figure S1a describes the assembly process. A 2.5 μm thick Mylar film treated in a UVO-cleaner and immersed in a 2% volume solution of aminopropyltriethoxysilane (APTES) in DI water, subsequently washed, dried and placed on a sacrificial soft silicone elastomer layer facilitates handling and bonding during the assembly. Specifically, a UVO-treated PDMS channel layer laminated onto the Mylar sheet forms covalent bonding upon contact. Supplementary Figure S1b highlights considerations for different materials and thickness criteria. The bonding strength evaluated via mechanical testing (Figure S2) confirms the utility of the APTES functionalization approach³⁸ in achieving robust 191 integration.

Geometry optimization and benchtop testing of sweat rate

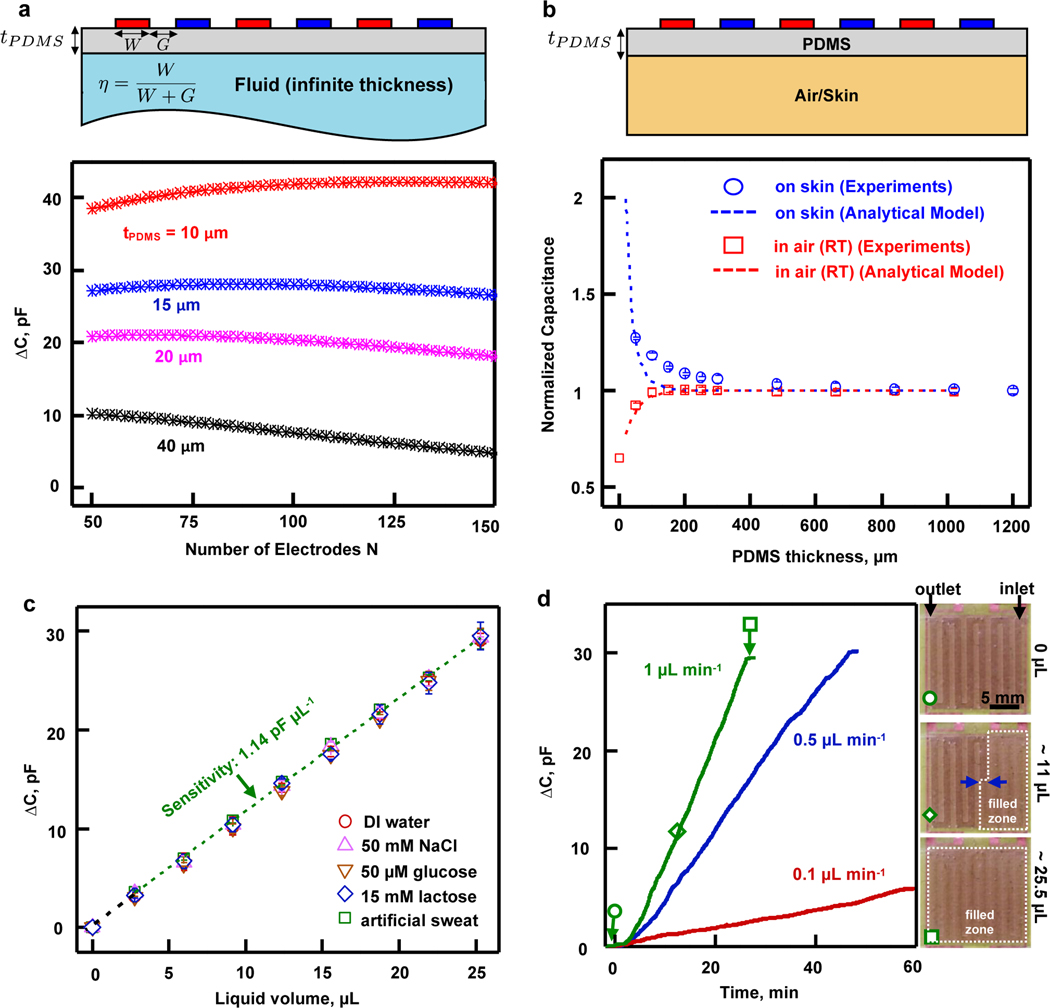
Capacitive measurements of fluid levels are sensitive to the electrode geometry^20,26,27. For on-body sweat measurements, an additional constraint is that the configuration must be highly sensitive to sweat in the channels adjacent to the electrodes, but insensitive to the underlying skin surface. The design parameters reported here involve interdigitated arrays of copper (9 μm in thickness) electrodes, with spacings G, widths W, lengths $\text{L}=1.5\text{cm}$, and a total number of electrodes N across a total width of 1.5 cm (Figure 2a), on a layer of PI (25 μm in thickness) as a substrate. An analytical model for the capacitance of the interdigitated electrodes based on conformal mapping techniques³⁹ provides geometrical design guidelines. The capacitance is a function of number of electrodes N, metallization ratio $\text{η}$ ($\frac{W}{W+G}$, defined in Figure 2a) and layer thickness to wavelength ratio $\text{t}/\lambda$, where $\lambda =2(\text{W}+\text{G})$. For fixed total device length $\text{L}(\text{L}=\text{N}\lambda /2)$, the independent variables can be redefined as $\text{η}$, $\text{t}$ and $\text{N}$. Figure 2a shows the difference between the capacitance associated with the array when the material present at a distance ${\text{t}}_{\text{PDMS}}$ (separated by a PDMS layer) changes from water to air, as a function of N with $\text{η}=0.37$. Results confirm that decreasing the separation of the electrodes from the material under test (i.e. ${\text{t}}_{\text{PDMS}}$) increases the sensitivity. For a separation thickness fixed to the lowest value accessible given experimental constraints (corresponding to minimal capping layer and adhesive thicknesses), the number of electrodes that cover a domain of constant area only slightly affects sensitivity. The optimal value of $\text{N}$ depends on considerations in the sensitivity of the system to the surrounding medium. Specifically, the measurement must be sensitive to the liquid inside the channels but not to the skin underneath. As a result, $\text{N}$ is chosen to yield an effective sensing distance of several hundred microns around the electrodes, to approach the maximum sensitivity defined by the curve on Figure 2a. The geometry used for benchtop analysis involves a photolithography mask with $\text{N}=76$, $\text{L}=1.51\text{cm}$, $\text{W}=100\text{μm}$ and $\text{G}=100\text{μm}$, resulting in samples with $\text{W}=75+/-5\text{μm}$ and $\text{G}=125+/-5\text{μm}$ after the etching process.

Figure 2. Geometry optimization and benchtop evaluation of sweat rate channels and electrodes.

a. An interdigitated array of electrodes with width W and spacing G covers an infinite area filled either by air or liquid, with a thickness ${\text{t}}_{\text{PDMS}}$ ($\text{η}=0.375$, area 1.5 cm × 1.5 cm). The graph shows analytical simulation results of the capacitance difference for the bottom half space between two situations: filled with water and filled with air, as a function of the number of electrodes, for a constant area, for multiple ${\text{t}}_{\text{PDMS}}$.

b. A bulk piece of PDMS of thickness ${\text{t}}_{\text{PDMS}}$ separates an interdigitated electrodes array of dimensions $\text{W}=75\text{μm}$, $\text{G}=125\text{μm}$, covering an area 1.5 cm × 1.5 cm, from a material under test which is either air or skin. The graph shows the capacitance measured experimentally with an impedance analyzer at 25 kHz (open symbols) and analytical simulations (dashed lines) for air (in red) and skin (in blue), normalized by the capacitance values at large thicknesses of PDMS ($\text{η}=0.375$, $\text{L}=1.5\text{cm}$, $\lambda =400\text{μm}$, $\text{N}=76$)). The results provide guidelines for insulation of the device from the skin by a layer of PDMS.

c. Capacitance change (between empty and filled channel) measured with the FDC1004 chip as a function of liquid volume in the channels for DI water (red circles), 50 mM NaCl (purple upwards pointed triangles), 50 μM glucose (brown downwards pointed triangles), 15 mM lactate (blue diamonds) and artificial sweat solution (green squares) at room temperature in air. All liquids show the same linear relation between capacitance change and volume. The results confirm the robustness of the sweat rate measurement, independent of sweat composition. Sensitivity is 1.14 pF. μL⁻¹. Error bars correspond to measurements on 3 different samples.

d. Continuous, real-time capacitance change recorded with the FDC1004 chip when artificial sweat flows into the microchannels at rates of 0.1 (pink), 0.5 (blue) and 1 μL.min⁻¹ (green) at room temperature in air. Orange symbols correspond to images showing the integrated sweat rate platform filled at 1 μL.min⁻¹ with 0 μL (empty, circle), 11 μL (partially filled, diamond) and 25.5 μL (completely filled, square) of liquid.

The thickness of the PDMS (${\text{t}}_{\text{PDMS}}$) underneath the electrodes must be sufficient to avoid significant contributions of the skin, while minimizing the overall thickness of the device. For a given optimal electrode geometry, the model constrains a few parameters ($N=76$, $\text{η}=0.375$ and $\lambda =400\text{μm}$) to explore the dependence on $t_{PDMS}$, as a means to evaluate the critical PDMS thickness beyond which the capacitance no longer changes depends on $t_{PDMS}$. Fig. 2b shows the capacitance as a function of ${\text{t}}_{\text{PDMS}}$ for an optimal electrodes geometry ($N=76$, $\text{η}=0.375$ and $\lambda =400\text{μm}$) when in air at room temperature (red) and on skin (blue). Open symbols correspond to experiments and dashed lines to the analytical model. Capacitances are normalized by the value in the limit of large ${\text{t}}_{\text{PDMS}}$, to provide guidelines on the minimum t_PDMS for which contributions from the skin are at the level of a few percent. The raw data appears in Supplementary Figure S3. Supplementary Figure S4 shows the full spectral results captured with the impedance analyzer. The frequency of 25 kHz corresponds to a convenient value for the operation of the miniaturized capacitance-to-digital converter FDC1004 available for the electronics readout. Experiments described in the following use ${\text{t}}_{\text{PDMS}}=800+/-50\text{μm}$.

The depths of the microfluidic channels are 200 +/− 10 μm, the capping layer consists of the Mylar sheet described previously and the silicone adhesive has a thickness of 7.6 μm. These choices yield capacitances that span the dynamic range of the FDC1004 sensor, as shown in Figure S5. The data also indicate that the increased temperature and the presence of skin underneath do not affect the results.

Systematic experiments using a syringe pump apparatus perfusing various liquids similar to human sweat (DI water, 50 mM NaCl, 50 μM glucose, 15 mM lactate solutions in DI water, and commercial artificial sweat) through the microfluidic channels establish a relationship between capacitance and sweat rate/loss. The studies involve filling the microfluidic channels with one of those liquids and measuring the change in capacitance as a function of the volume V. Results, shown in Figure 2c, highlight that the change in capacitance is proportional to V with no dependence on the composition of the liquid within physiologically relevant concentrations of electrolytes and metabolites. This measurement relies on the limited variation of the real part of the dielectric constant over the physiological range of electrolyte concentrations¹⁸, as the main parameter that affects capacitance measurements with the interdigitated array. This result allows for accurate sweat rate measurements, independent of variations in sweat composition. As a consequence, calibration results derived from Figure 2c have a sensitivity of 1.14 pF.μL⁻¹. Figure 2d shows continuous-mode measurements across multiple filling rates, controlled with a syringe pump. Figure 2d images (right panel) show different levels of sweat fill extent corresponding to three experimental points in the plot. These experiments establish the basis for on-body trials for sweat rate, without dependence on (i) detailed composition of the sweat across the physiological range, (ii) temperature, or (iii) the subjacent skin layer.

Geometry optimization and benchtop testing of sweat conductivity

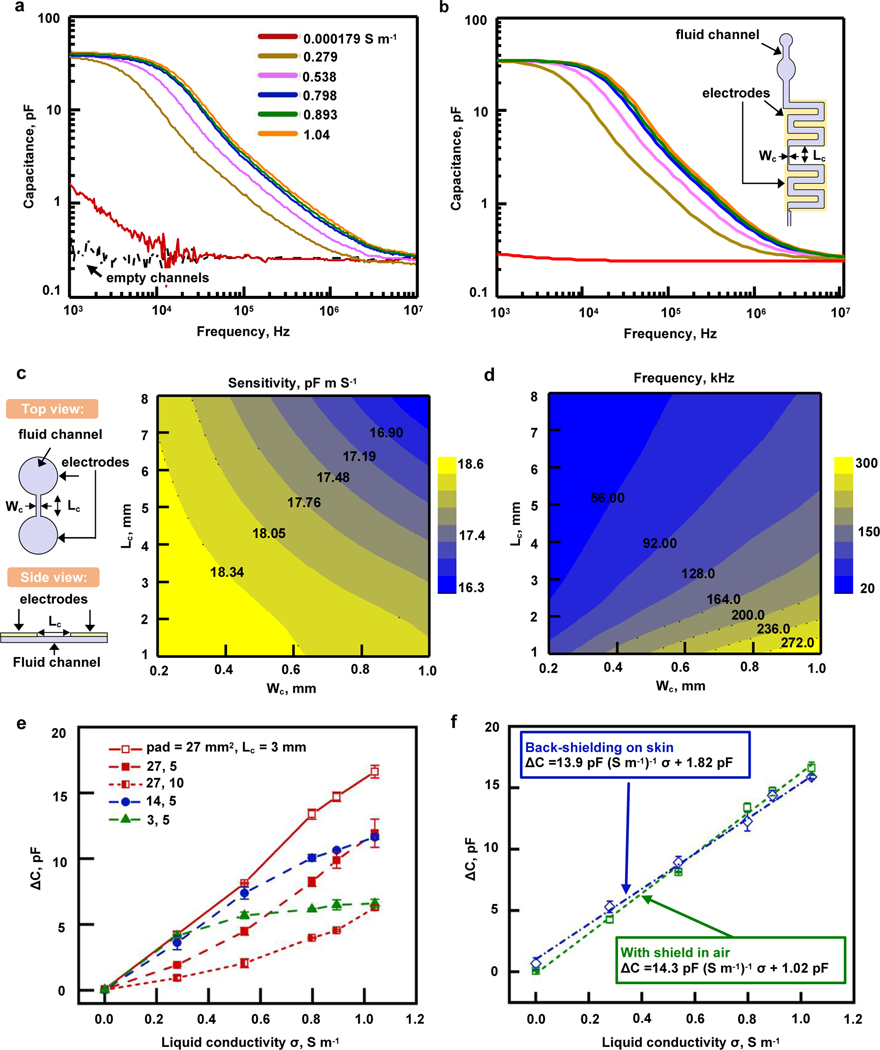
Given that the capacitance measurements described above are independent of the composition of sweat, measurements of sweat conductivity require a dramatic change in the geometry of the channels and electrodes. The approach presented here derives from the from C⁴D techniques used in capillary electrophoresis.^{34, 35} The geometry consists of two microchannels with dimensions in the mm-range that connect by a narrow and long microchannel. One large electrode couples capacitively to each of the large microchannels, in a manner such that the capacitance of a pair of such electrodes exhibits a frequency spectrum that depends on the conductivity of the liquid, as detailed by Cahill et al⁴⁰. Capacitance measurement using that geometry thus permits a contactless determination of liquid conductivity. Figure 3a shows an example of frequency spectra for multiple liquid conductivities (physiologically relevant for human sweat), for an optimized geometry selected according to considerations detailed below. A sharp decrease of capacitance occurs at a frequency value that increases with conductivity. Measurements at a given frequency close to that of these large variations (here 25kHz, which corresponds to FDC1004 chip operation frequency) serve as the basis for determining the conductivity. The data of Supplementary Figure S6 demonstrate that increasing the areas of the microchannels and electrodes improves the sensitivity. To avoid collapse^{36, 37}, the geometries of these channels take the form of serpentine rather than circular shapes, as shown in Figure 1g and the inset of Figure 3b. Experiments involve layers of PDMS (800 +/− 50 μm in thickness) with trenches (200 +/− 10 μm in depth) covered by a capping layer of Mylar (2.5 μm in thickness) coated with a silicone adhesive (5.4 μm in thickness; corresponding to a spin-coating speed of 4500 280 rpm). Figure 3b summarizes the results of FEA for the geometry (inset) used in the experiments in Figure 3a, highlighting excellent agreement with no adjustable parameters. Limiting the overall size of the device (i) improves the wearability, and (ii) provides a continuous measurement with reasonably small amount of sweat analyzed at a given time. Increasing the sizes of the large microchannels would require an excessive amount of sweat, potentially more than that collected in typical exercising conditions. The geometry selected here corresponds to a volume of 12 μL to enable the conductivity measurement. This volume is several times smaller than that collected during a representative exercising session¹⁴.

Figure 3. Geometry optimization and benchtop evaluation of sweat conductivity channels and electrodes.

a. Typical capacitance spectra for a sweat conductivity sensor comprising a pair of coplanar electrodes integrated with microfluidic systems (pad area $\text{p}=27{\text{mm}}^2$, channel length ${\text{L}}_{\text{c}}=3\text{mm}$) at room temperature in air. The initially empty channels (dashed black line) are filled with different conductive solutions (solid colored lines) with conductivities ranging from 0.000179 (red line) to 1.04 S m-1 (orange line). Those liquids (also used for Figure 3e and f measurements) include DI water, NaCl solutions with multiple concentrations, as well as commercial artificial sweat. The capacitance behavior varies distinctively from 2 kHz to 3 MHz in response to the different conductive liquids. At a given frequency within the range of the sharp decrease of capacitance, the values recorded for different conductivities are different and thus allow a measurement of conductivity through capacitance.

b. Corresponding FEA results of the capacitance for different conductive solutions using the sensor geometry (inset) with channel length ${\mathbf{\text{L}}}_{\mathbf{\text{c}}}=3\text{mm}$ and channel width ${\mathbf{\text{W}}}_{\mathbf{\text{c}}}=0.2\text{mm}$, with same color code as in part a of this figure. The results show excellent agreement with experimental results without any parameter fitting.

c. FEA contour of maximum sensitivity based on a parametric study of the connecting channel width ${\mathbf{\text{W}}}_{\mathbf{\text{c}}}$ and length ${\mathbf{\text{L}}}_{\mathbf{\text{c}}}$ (shown in the schematic on the left) between circular channels in a simplified model of the actual geometry. The size of the circular channels is adjusted to maintain a constant volume while the connecting channel dimensions vary. To maximize the sensitivity, the results suggest that the dimensions of ${\mathbf{\text{W}}}_{\mathbf{\text{c}}}$ and ${\mathbf{\text{L}}}_{\mathbf{\text{c}}}$ must be small.

d. FEA contour of the value of the frequency when the sensor reaches maximum sensitivity. The connecting channel width ${\mathbf{\text{W}}}_{\mathbf{\text{c}}}$ and length ${\mathbf{\text{L}}}_{\mathbf{\text{c}}}$ are varied, as explained in part c of this figure. For given dimensions of the connecting channel, the sensitivity is maximum at the simulated frequency, which corresponds to ideal frequency for the measurement.

e. Experiments showing the influence of geometry (pad size p, length of connecting channel l) on the relationship between the capacitance difference between filled and empty channels and the conductivity of the liquid. Measurements are taken at 25 kHz, and the highest sensitivity is achieved with $\text{p}=27{\text{mm}}^2$, l=3 mm (for a total sensor size at the cm scale).

f. Results with the final stack of materials for the sensor to be used on skin including a additional layer of PDMS (as shown in Fig. 1f) that allows for a back-shielding (shielding plane in between skin and electrodes). The difference in capacitance between filled and empty channels is linear as a function of liquid conductivity for the geometry chosen ($\text{p}=27{\text{mm}}^2$, l=3 mm) and the influence of skin is small as shown by the difference between blue (on skin) and green (in air) curves in the presence of a shielding plane. Sensitivity on skin is 13.9 pF (S.m⁻¹)⁻¹.

FEA simulations at the operating frequency of 25 kHz provide insights into appropriate geometries, especially the dimensions of connecting channel (width, ${\text{W}}_{\text{c}}$; length, ${\text{L}}_{\text{c}}$) as defined in the schematic illustration of Figure 3c. Details of this 3D model, based on the electric current flow in conductive and capacitive media over a frequency domain⁴¹, are in the Materials and Methods section. The minimum value of ${\text{W}}_{\text{c}}$ is 200 μm, to facilitate the filling of the channel due to pressure supplied by the sweat glands³³. A simplified model with two disks linked by a straight channel reveals the influence of the dimensions. Computational studies vary the parameters ${\text{W}}_{\text{c}}$, ${\text{L}}_{\text{c}}$ as well as the radius of the disks in a manner that maintains a constant total volume of 12 μL. Details on differences between this simplified model and the actual geometry are shown in Supplementary Figure S6. Figure 3c highlights the maximum sensitivity of the capacitance to conductivity across a broad range of frequencies. Here, the sensitivity corresponds to the partial derivative of the capacitance over the dimensionless electrical conductivity at a conductivity of $\sigma =1\text{S}.{\text{m}}^{-1}$. The contour plot demonstrates that a combination of small ${\text{W}}_{\text{c}}$ and ${\text{L}}_{\text{c}}$ provides the best sensitivity. Figure 3d shows the frequency at which the maximum sensitivity from Figure 3c occurs for various values of ${\text{W}}_{\text{c}}$ and ${\text{L}}_{\text{c}}$, i.e. the frequency for which the curves in Figures 3a and 3b are most separated for different conductivities. At 25 kHz and at a conductivity of 1S/m, this simplified model suggests that the dimensions should be ${\text{W}}_{\text{c}}=(0.2-0.3)\text{mm}$ and ${\text{L}}_{\text{c}}=\left(5-6\text{mm}\right)$ to maximize the sensitivity.

Figure 3e provides experimental results on geometry optimization, using ${\text{W}}_{\text{c}}=0.2\text{mm}$ for various pad areas, p, defined as the area of each set of serpentine channel, and channel length L_c. Experiments confirm that increasing the sizes of the pads increases the capacitance, consistent with numerical results in Supplementary Figure S6. Results also demonstrate that the case of $\text{p}=27{\text{mm}}^2$ and ${\text{L}}_{\text{c}}=3\text{mm}$ exhibits a linear relationship between the change in capacitance (at 25 kHz) with the largest slope over the entire range of conductivity. As suggested previously, the measured capacitances span a significant fraction of the operating range of the FDC1004 chip. Further experiments (including on-body testing), as well as 315 examples shown in Figure 3a and 3b exploit this optimized geometry.

The millimeter-scale electrodes and spacings for this conductivity system lead to a high level of sensitivity to the skin underneath. For that reason, the device design includes a shielding copper plane between the measurement system and the skin. The full stack of materials appears above and in Figure 1g. The results of Figure 3f demonstrate that this shielding leads to behaviors that are similar on skin and in air. In both cases, the change in capacitance for filled and empty channels depends linearly on the conductivity of the liquid. The experiments shown in Figure 3a, e, and f involve multiple NaCl solutions and an artificial sweat solution (0.893 S.m⁻¹). These results establish a calibration curve that can be used for on-body trials, with a sensitivity on skin of 13.9 pF (S.m⁻¹)⁻¹_.

Digital signals and readout design

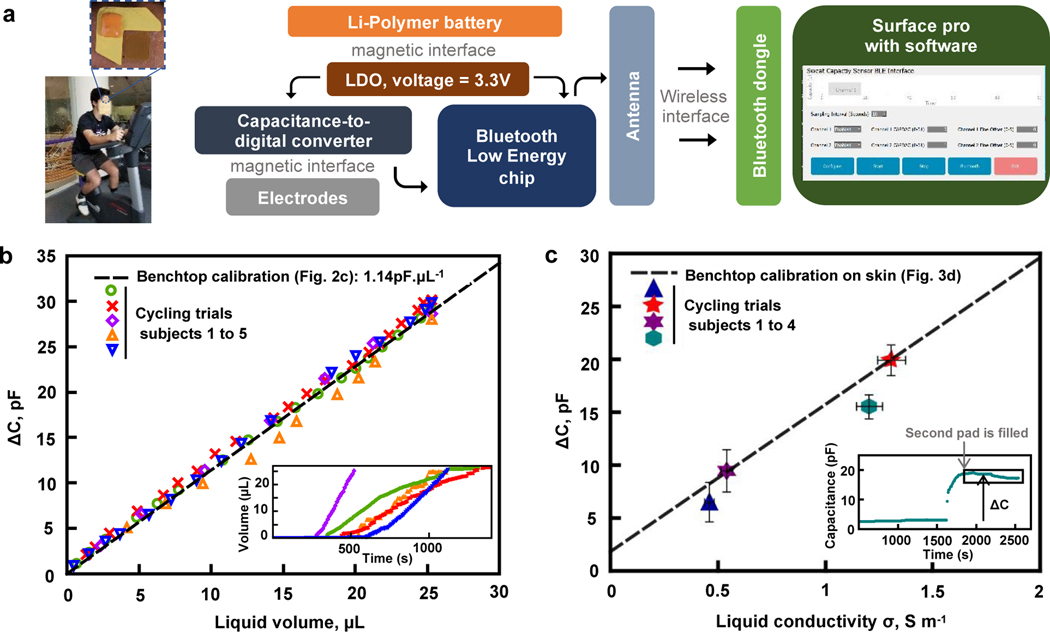
Wireless digital analysis of sweat rate and conductivity, in real-time, is critically important for practical applications of this technology. Rapid prototyping techniques form flexible electronics boards of polyimide and copper, on which components can be soldered to yield a functional electronics system for capacitive readout and wireless Bluetooth transmission capabilities. The design includes the following electronics subsystems: (i) a capacitance-to-digital converter (FDC 1004, Texas Instruments) that supports a measurement range of +/− 15pF around an offset that can be set between 0 and 100 pF, (ii) a microcontroller (nFR52832, Nordic Semiconductor) that captures data from the capacitance-to-digital converter and transmits information wirelessly and, (iii) a Li-Polymer battery (12 to 45mAh) that provides power to the system. A software routine on a tablet serves as a user-friendly interface to connect to the sensors, start/stop the acquisition process and set the parameters to control the measurement range and sampling frequency. The overall operating scheme is in Figure 4a and electronics schematics are in Supplementary Figure S7. Encapsulating the electronics in a low modulus silicone elastomer provides a safe and soft interface to the skin. Bluetooth transmission allows robust data collection, with no dropouts observed within a 5 m distance between the device and a Bluetooth dongle connected to the tablet.

Figure 4. Wireless on-body operation and in-situ on-body analysis of sweat collected during gym exercising.

a. Image illustrating the positioning of the device and exercising activity of the volunteers and schematic description of the system for on body-trials: battery and readout electronics that connect to the electrodes allow for real-time measurement. Transmission to the tablet occurs through a Bluetooth chip and antenna present on the electronics board, for communication to a dongle plugged into the computer via USB connection.

b. Sweat rate on-body trials: difference between current capacitance and initial capacitance recorded continuously through the tablet while the actual volume present in the channels is determined through pictures taken at random intervals, for 5 subjects. The dashed black line is the benchtop calibration from Fig. 2c (no fitting parameter). Error bars are comparable to the sizes of the symbols. Inset: temporal evolution of the volume of sweat in the patch (measured through capacitance values) for all 5 subjects, with same color code as the main figure.

c. Plot of sweat conductivity on-body trials: the difference between the average of the capacitance of the filled device and the initial capacitance as a function of the sweat conductivity (value at 22°C). Error bars refer to the dilution precision on the × axis and to both the standard variation within the trial and systematic error on the Y axis. Inset: temporal evolution of the measured capacitance as a function of time for one trial, illustrating how ΔC is measured.

On-body field trials during physical exercise

Intimate skin coupling requires wearable devices that can bend and conform to curvilinear surface of the human body. Data presented in Supplementary Information Figure S8 show that the geometry and choice of materials allow bending (but not stretching) to a degree that allows accurate measurements in typical mounting locations on the body. Human subject testing involves evaluations on healthy young adult volunteers during exercise on stationary bikes. Detailed protocols are in the Materials and Methods section. Devices attach to the skin on the forehead and capacitance data passes wirelessly, in real time, to a tablet (Figure 4a). Images captured at defined time intervals allow for secondary measurements of the filling front with a dye to facilitate visibility of the sweat. Measurements of sweat conductivity rely on small samples pipetted from the device during exercising (for droplets at the outlet) and at the end of the exercising session (for liquid left inside the channel). Dilution followed by measurements with a conductivity meter yields an average conductivity for the trial, as another comparative measure. All measurements of capacitance ($\text{ΔC}$) correspond to the difference between the capacitance at a particular time and that captured before the start of the exercising session.

Figure 4b shows on-body results of sweat rate compared to the benchtop calibration obtained in Figure 2c, indicating strong agreement between bench and on-body results. Inset of Figure 4b shows the temporal evolution of measured volume for all subjects, highlighting that the benchtop calibration holds for both low (red crosses) and high (purple diamonds) sweat rates. The volume indicated in abscissa corresponds to the actual volume minus 3.4 μL of dead volume near the inlet, where it interacts with the blue dye. This dead volume space can be reduced in devices that do not require the dye. For one subject (represented with orange triangles), a small delamination of the electrodes likely occurred during sweat flow, causing a reduction in the value of $\text{ΔC}$.

Figure 4c shows on-body measurements of sweat conductivity. The capacitance increases slightly (by ~0.5 pF) as the sweat fills the first pad. Upon filling of the second pad, the capacitance rises to a large value, and recording of the electrolyte content becomes possible. Data in Figure 4c correspond to the difference between the baseline and the average of the recorded data once the device is filled and continuously collects more recent sweat, as illustrated in the inset. Standard laboratory procedures involve measurements of conductivity of an entire sample of sweat, as a single averaged value. Such an evaluation provides a certain level of validation but fails to capture the full temporal evolution. Figure 4c shows that the calibration curve observed on skin with solutions of various conductivities in Figure 3f is in good agreement with averaged data recorded during exercise. This measurement is also sensitive to the temperature inside the channels, as the conductivity varies with temperature. A detailed discussion on the effect of temperature on the results for benchtop experiments in controlled conditions is in Figure S9. As an additional point, observed changes in capacitance over time, which manifest often as a decrease in our trials, suggest that the conductivity of the sweat decreases during this period. The limited number of trials in this study coupled to the effects of possible residual ions on the skin or of temperature variations prevent firm conclusions. Further investigations of these trends are necessary, especially as some recent studies report strong variations from person to person for temporal variations of ionic charge during exercising¹⁷. Details on the experimental protocol for on-body trials are in the Materials and Methods section.

Conclusions

The flexible, skin-mounted platforms presented here illustrate an important, non-contact approach in interfacing electronics modules and capacitance-based electrodes with microfluidic systems for sweat collection. Electrodes coupled capacitively to single-use microfluidics are capable of real-time measurements of sweat rate and sweat conductivity during physical exercise. Optimized channel and electrode designs, together with an ultrathin capping layer, enable reliable and accurate measurements from a lightweight, conformal platform that can mount on most regions of the body. A magnetic coupling scheme allows for repeated use of an electronics module that digitizes and transmits capacitive measurements to a tablet. Field trials establish the practical utility of the technology for use in fitness and sports with potential utility in other contexts, including medical monitoring and diagnostics.

Materials and methods

Fabrication of flexible and reusable electrode platforms:

Preparation starts with the fabrication of a chromium (Cr) photomask, exposed with a maskless aligner (30 mJ.cm⁻²; MLA150; Heidelberg Instruments), developed in 1:4 mixture of developer AZ400k (Microchemicals) and DI water, rinsed with DI water, etched with Cr etchant (CEP-200 chromium etchant; Microchrome Technology Products), and subsequently cleaned with DI water, acetone and isopropanol. To form the electrodes, polydimethylsiloxane (20:1 base:curing agent weight ratio, Sylgard 184, Dow Corning) spin-coated at 1500 rpm for 30s onto a glass slide (Fisherbrand) yielded a sticky layer as a support for lamination of a flexible polyimide (PI, 25 μm)-copper (Cu, 9 μm) clad foil (Pyralux AC092500EV; DuPont). Curing at 70°C for 3 h created strong bonds between the support and the clad sheet, with Cu facing up. Standard photolithography techniques then patterned the Cu: after spinning a layer of phototoresist (AZ4620P; Microchemicals) at 3000 rpm for 30 s and baking on a hotplate at 110 °C for 2 min, exposure with ultraviolet (UV) light (10 mJ cm⁻²) through our photomask, developing (in 1:4 mixture of developer AZ400k; Microchemicals) and rinsing with DI water formed patterns of photoresist. Cu wet etching (HFCE100 copper etchant; Transene), DI water rinsing, and subsequent resist removal by rinsing with acetone and isopropanol yielded a PI-Cu foil with electrodes in desired geometries. Upon release from the glass slide, deposition of a 1 μm conformal coating of parylene-C provided a protective layer on the entire sample, excluding connection pads protected with Kapton tape during deposition (SCS Labcoater 2 Parylene system, Specialty Coating Systems). Figure S10a summarizes this process.

Fabrication of an ultra-thin capping layer for the microfluidics channels:

Microfluidic channels were formed using soft lithography techniques. More precisely, spin coating KMPR 1010 (Microchem) at 3000 rpm for 30 s formed a 15 μm thick layer of photoresist on a 1mm-thick, 4 inch silicon wafer. Baking at 100°C on a hotplate for 3 min, exposing to UV light (10 mJ.cm⁻²) through a photomask (fabricated using similar technique as for the previously decribed photomask), post-baking for 2 min at 110°C, immersing in developer (AZ 917 MIF; Integrated Micro Materials) and rinsing with DI water yielded a wafer with patterned photoresist. Deep reactive ion etching (STS Pegasus ICP-DRIE, SPTS Technologies Ltd) then created trenches to depths of 200 +/−10 μm on the surface of the wafer. Pouring liquid PDMS (10:1 base:curing agent, Sylgard 184, Dow Corning) on the mold, spin coating at 100 rpm and curing at 120°C on a hotplate formed the channel layer (thickness 800+/−50 μm). Figure S10b summarizes this procedure. For channels designed for measurements of sweat rate, a 1.5 mm diameter circular punch (Reusable biopsy punch, World Precision Instruments) formed holes at the inlet of the channel layer. A Mylar film with thickness of 2.5 μm (Spectromembrane, Chemplex) served as a capping layer. After treating in a UVO-cleaner for 4 min, immersing in a solution of (3-Aminopropyl)triethoxysilane (Sigma-Aldrich) in DI water at a 1:50 volume ratio for at least 1 h, and rinsing with DI water, lamination of the Mylar film on a sacrificial soft elastomer layer (Ecoflex 30, Smooth-On) yielded a platform to facilitate assembly with PDMS channels. After a 4-min UVO-treatment, laminating the PDMS channels onto the Mylar sealed the channels. Release from the Ecoflex layer and baking overnight at 70°C in an oven yielded strongly bonded microchannels with an ultra thin capping layer, as illustrated in Figure S1a.

For channels designed to measure sweat conductivity, a 1.5 mm diameter hole formed in the Mylar allowed sweat to enter the channels. Assembly of the layer containing the channels (PDMS trenches and Mylar capping layer) onto a flat 800+/−50 μm PDMS layer with a 1.5 mm hole aligned with that of the Mylar, relied on a JMS#903 adhesive (Label Innovation) around the inlet zone. This process yielded a device that allowed insertion and removal of the electrodes and the shield plane in between the bottom PDMS layer and the Mylar layer, as shown in Figure 1g.

In both systems, the Mylar served as a foundation for repositionable adhesives (MG1010 adhesive, Dow Corning) spin-coated at 3500 rpm for the sweat rate channel and at 4500 rpm for the sweat conductivity channel for 5 min resulted in a thin (7.6 μm or 5.4 μm) coatings. After drying for 5 min at 70°C and cooling down to room temperature, bleached Kraft paper with silicone release (3M) laminated onto the adhesive coating protected it from dust and damage.

Analytical model for optimizing sweat rate sensor

A 2-D analytical model determined the optimal number of electrodes and the thickness of the dielectric (capping) layer. Due to symmetry and periodicity³⁹, the total capacitance can be written as

$$C\approx (N-1)\frac{C_I}{2}$$ (1)

where $N$ is the number of electrodes in the system, and $C_I$ is the half capacitance of one 468 interior electrode with respect to the ground plane as shown in Figure S11a.

For a half plane space consisting of two layers as in Figure 2a, the capacitance $C_I$ is a function of two non-dimensional geometric parameters $\text{η}$ and $\frac{t}{\lambda }$. The solution of $C_I$ is obtained with conformal mapping techniques, and the contributions from different layers are summed up in a parallel scheme $\left({\epsilon }_1<{\epsilon }_2\right)$ or serial scheme $\left({\epsilon }_1>{\epsilon }_2\right)$ as shown in Figure S11b. The complete derivation of $C_I$ and $C_E$ can be found in the analytical model³⁵.

FEA simulations for optimizing sweat conductivity sensor:

3-D finite element analysis was performed using commercial FEA software (COMSOL) to determine the frequency dependent capacitive behavior for fluid conductivities and to optimize the connecting channel length for maximum sensitivity⁴¹. Voltage applied at electrodes and a corresponding current response gives the complex impedance $Z^{\ast }$. The equivalent capacitance $C$ is then determined as

$$C=Im\left(\frac{1}{\omega Z^{\ast }}\right)$$ (3)

and the sensitivity is defined as the partial derivative of the capacitance over the electrical conductivity $\partial C/\partial \sigma$. The electrode pads, microchannels, fluid, and material layers are modeled using 4-node tetrahedral elements. To account for the Parylene-C/adhesive/mylar multilayer structure, we consider a homogeneous dielectric layer of 9 μm thickness. Convergence test of the mesh size had been performed to ensure accuracy. The total number of elements in the models is approximately ~910,000. A parameters table is provided in Supplementary Information Figure S12.

Preparation of standard test solutions:

Mixing NaCl (certified ACS; Fisher Chemicals), D (+) glucose or (L+) lactic acid (Sigma-Aldrich) in DI water yielded single-analyte solutions with physiologically relevant sodium chloride (NaCl, 25 to 100 mM) ⁴², glucose (50 μM) ^14,33 and lactate (15 mM)⁴³ concentrations. An artificial sweat solution containing several electrolytes, minerals, metabolites and amino acids (stabilized artificial eccrine perspiration 1700 – 0020; Pickering Laboratories) and DI water (HPLC grade; Fisher chemicals) served as additional test solutions. Probing the DI water, NaCl and artificial sweat solutions with a 497 conductivity meter (SevenMulti, Mettler Toledo) yielded their conductivities.

Benchtop testing of devices with an impedance analyzer:

An impedance analyzer (E4990A; Keysight Technologies) served as a system for quantifying the sensor capacitance. Inserting polytetrafluorethylene tubing (PTFE; Cole-Parmer Instrument Company) and sealing the microchannel inlet with epoxy facilitated the introduction of a test fluid using a syringe. For consecutive tests with solutions of various conductivities, injection of fluids in an order of increasing conductivity with separate syringes minimized the effect of contamination. Characterization at room temperature involved connecting the electrodes via alligator clips to the measurement instrument and suspending the assembled device at least 3 cm above the work surface to minimize parasitic capacitances during measurements. Performing a frequency sweep from 1 kHz to 10 MHz then yielded the capacitance spectra.

Fabrication of wireless readout electronics:

Designing the electronics layout with e-CAD software and cutting with a LPKF Protolaser U4 yielded a double-sided flexible electronics board cut in a 75 μm Cu / 18 μm PI / 75 μm Cu sheet (Pyralux, DuPont). Soldering of the following components then yielded a functional electronics readout platform (once connected magnetically to a Li-Polymer battery (12mAh to 45mAh)): nRF52832 (Nordics Semiconductor) Bluetooth Low Energy chip, 2.4Ghz ceramic antenna (Johanson Technology), ISL9016 (Renesas Electronics) LDO to reduce operating voltage to 3.3V, FDC1004 (Texas Instruments) capacitance-to-digital converter, as well as multiple passive components (402 and 201 sizes). High temperature neodymium magnets soldered to the board facilitated reversible connectivity between the modules: four 0.04” thick 0.1” diameter magnets (McMaster) for connection to the electrodes and shield, and two 0.06” thick 1/8” diameter magnets (McMaster) for connection to the battery. Magnets of opposite polarity soldered on the electrodes and on the battery allowed for a secure connection, with an alternation in the orientations of the magnets so that only one mounting position is possible. The flexible board and the battery were then encapsulated in thin low modulus silicone shell (Silbione 4420 RTV, Elkem Silicones, mixed with Silc-Pig silicone dye, Smooth-On) to yield in a soft platform without exposed electronic components or wiring. Validation of the performance of the electronics was performed using capacitors of known values. Measurements on the electronics readout part (C) with a power profile system show that the average current is 780 μA when connected to the BLE host at the operating frequency, which allows to run multiple exercising sessions with one charged battery.

In situ measurements of sweat rate and conductivity from human trials:

Testing involved healthy young adult volunteers, cycling at moderate to high intensity at ambient temperature and humidity conditions. Prior to the trial, skin-safe adhesive (1524, 3M) cut to appropriate shapes (board outline and a 6mm diameter hole at the inlet to allow sweat to enter the device) and treated on one side with a UVO-cleaner (to allow secure bonding to the device) provided an easy-to-peel adhesive interface to the skin. Before attachment of the device, cleaning of skin by rubbing with an isopropyl alcohol prep pad (Dynarex) limited contamination of new sweat samples with residual ions present on the skin. Microfluidics and electrodes patches laminated on skin coupled through magnets to the electronic readout unit, which transmitted data to the tablet (Surface Pro, Microsoft) through a Bluetooth dongle (Nordics Semiconductor nRF52 development kit), placed at a distance between 2 and 5 m from the subject, with a sampling frequency of 0.1 Hz, which is sufficient to capture variations over physiologically relevant timescales. The ability of the sensors to detect rapid changes in flow rate and conductivity depend mainly on their geometry. For sweat rate measurements, the characteristic dimensions of the interdigitated electrodes allow assessments of fluid progression in the channel at appropriate scales. For sweat conductivity, the sensor must fill with sweat (at least 12 μL) for an initial measurement, with a continuous capability thereafter, as sweat in the sensor is progressively replaced. Data collection included sweat rate and/or conductivity from one or two patches placed on the forehead, on one or two tablets. Mounting on the forehead corresponds to a case for which wireless transmission of data to a tablet is especially relevant, as visual inspection cannot be performed easily by the individual wearing the device. In addition, the relatively high sweat rates that occur at that location facilitate validation of the device during medium intensity exercising sessions by ensuring a complete filling of the channels. The microfluidic structures were used only once. The electrodes and electronics were sanitized and reused. Photographs of the sweat rate device captured at random time intervals during each exercising session allowed comparison to reference data for sweat rate, with blue dye to enhance visibility (Americolor Soft Gel Paste, Blue). Measurements of conductivity of diluted sweat were performed with a laboratory bench conductivity meter (SevenCompact S230 with InLab751 4 mm probe, Mettler Toledo) as reference data for sweat conductivity. For the conductivity measurement system, sweat collected from the channels with a micropipette contained no dye to avoid any potential contamination issues, and conductivity measurements at two temperatures were linearly extrapolated to a temperature of 22°C, corresponding to the temperature at which benchtop validation was performed.