The giant flexoelectric effect in a luffa plant-based sponge for green devices and energy harvesters

Significance

Designing soft materials that permit the facile conversion of mechanical deformation into electricity is of significant technological importance. In this work, using fundamental science principles and the exotic phenomenon of flexoelectricity, we design a natural vegetable-based luffa sponge to “act” as a strong piezoelectric material suitable for energy harvesting, sensing and myriad other applications. We demonstrate applications of our developed materials in the context of sensing, actuation, and electrical energy harvesting for speech/voice recognition, pressure sensing, and powering light-emitting diodes. The natural luffa material is biodegradable, abundantly available and thus “green”. The developments we report constitute a paradigm for green and flexible sensors and energy harvesters with unique advantages of light weight, low cost, and full biodegradability.

Abstract

Soft materials that can produce electrical energy under mechanical stimulus or deform significantly via moderate electrical fields are important for applications ranging from soft robotics to biomedical science. Piezoelectricity, the property that would ostensibly promise such a realization, is notably absent from typical soft matter. Flexoelectricity is an alternative form of electromechanical coupling that universally exists in all dielectrics and can generate electricity under nonuniform deformation such as flexure and conversely, a deformation under inhomogeneous electrical fields. The flexoelectric coupling effect is, however, rather modest for most materials and thus remains a critical bottleneck. In this work, we argue that a significant emergent flexoelectric response can be obtained by leveraging a hierarchical porous structure found in biological materials. We experimentally illustrate our thesis for a natural dry luffa vegetable-based sponge and demonstrate an extraordinarily large mass- and deformability-specific electromechanical response with the highest-density-specific equivalent piezoelectric coefficient known for any material (50 times that of polyvinylidene fluoride and more than 10 times that of lead zirconate titanate). Finally, we demonstrate the application of the fabricated natural sponge as green, biodegradable flexible smart devices in the context of sensing (e.g., for speech, touch pressure) and electrical energy harvesting.

Materials that permit interconversion of electrical fields and mechanical deformation have been intensely researched. This coupling enables sensors (1), actuators (2), energy harvesters (3, 4), biomedical devices (1), soft robotics (5), and artificial muscles (6, 7), among many other applications. The most expedient type of direct electromechanical coupling, piezoelectricity, is largely restricted to hard, brittle, and environmentally unfriendly ceramics (8) and a sparse collection of polymers that demonstrate rather low performance [e.g., PVDF (Polyvinylidene fluoride)] (9). In short, environmentally friendly, biodegradable, high-performance, and low-cost piezoelectrics are virtually nonexistent.

In this work, we exploit an electromechanical coupling mechanism that is universally present in all dielectric materials—flexoelectricity (10–14) —and demonstrate a paradigm to create a mechanically soft, biodegradable, green material with an emergent “giant” flexoelectric effect.

Flexoelectricity refers to the ability of a material to produce an electric field under nonuniform deformation or alternatively, a mechanical response under inhomogeneous electric fields. This effect is rather weak but present in all insulators (14). Past studies have shown that this effect is appreciable only under extremely large strain gradients (typically observed at the nanoscale) (14) or materials with unusually large flexoelectric coupling (such as hard ferroelectric ceramics) (15–18). Despite the rather small values of flexoelectricity in typical materials, intense research over the last two decades points to tantalizing prospects for this exotic phenomenon, e.g., creating artificial piezoelectric materials without using piezoelectric materials (11, 19, 20) [including mechanical metamaterials (21) or hierarchical structures (22, 23)], bone-injury repair and remodeling (24), mammalian hearing mechanism (25–27) including musical perception (28), neuronal activity (29, 30), energy harvesting (23, 31), and sensors and actuators (32–34). Extensive experimental and theoretical work has ensued to understand the fundamental underpinnings of this phenomenon for both hard and soft materials. We refer the reader to several review articles that summarize the progress in this field, with an emphasis that ranges from two dimensional materials to biology (12, 14, 35–37).

The flexoelectric effect is generally weak at the macroscale, which is an impediment to its wide applications. There have been some limited studies to amplify this effect, e.g., design at purely polymer chain level for elastomers (38) and electrets (39–41). Zhang et al. (22), and Yan et al. (23) have realized ultrahigh flexoelectric output in porous materials by exploiting the random orientation and irregularly arranged ligaments. A macroscopic load, indeed; any sort of mechanical stimulus, will lead to local flexure of the ligaments at the microscale. In other words, even if the underlying material of the porous material is nonpiezoelectric, the ligaments will produce an electrical polarization due to flexoelectricity and bending of the ligaments. Since the ligament size is often in the microscale, considerable electrical activity can be generated in a small representative unit cell of a porous material. We remark that while the size effect of flexoelectricity is at the nanoscale for hard materials, in soft materials, the same output may be obtained at three order of magnitude higher length scale (39). A key requirement, for an emergent macroscopic response that resembles piezoelectricity due to electromechanical activity at the microscale, is that the representative unit cell must break mirror symmetry (20). Predicated on this premise, and guided by our theory (see SI Appendix and Materials and Methods sections), we demonstrate the key idea on an abundantly available, low-cost, biodegradable material, derived from the cucumber-family vegetable—luffa sponge (LS).

The inspiration from nature is well justified. Many biomaterials have excellent mechanical properties and natural and intricate hierarchical structures (layered or porous structures). Most biomaterials, especially those derived from plants, have a porous structure and thus do not require additional manufacturing steps and of course are abundant, sustainable, biocompatible, and biodegradable (42, 43). Among them, the dry LS is a typical porous and fibrous natural material (Fig. 1), which is light-weight, low density, and exhibits impressive flexibility and elasticity (44). In prior works, Zhang et al. (22) established a computational model for the flexoelectricity of porous structures, providing a design framework for enhancing the electrical output of such structures. Thereafter, based on theoretical guidance, Yan et al. (23) successfully synthesized an artificial porous composite material with an ultrahigh flexoelectric enabled piezoelectric-like effect. They also successfully demonstrated its utility as an electric generator to recharge devices. However, natural materials are preferable since complex composite fabrication processes can be avoided. Perhaps even more importantly, natural materials are biodegradable, abundant, and economical. Here, we exploit the distinctive porous structure of a green and naturally derived LS to create a dramatically amplified flexoelectric effect. While our results are demonstrated for this specific biomaterial, the central idea may be used in the context of other similar biomaterials.

Fig. 1.

The LS can be utilized as a flexoelectric generator for charging smart devices.

Materials

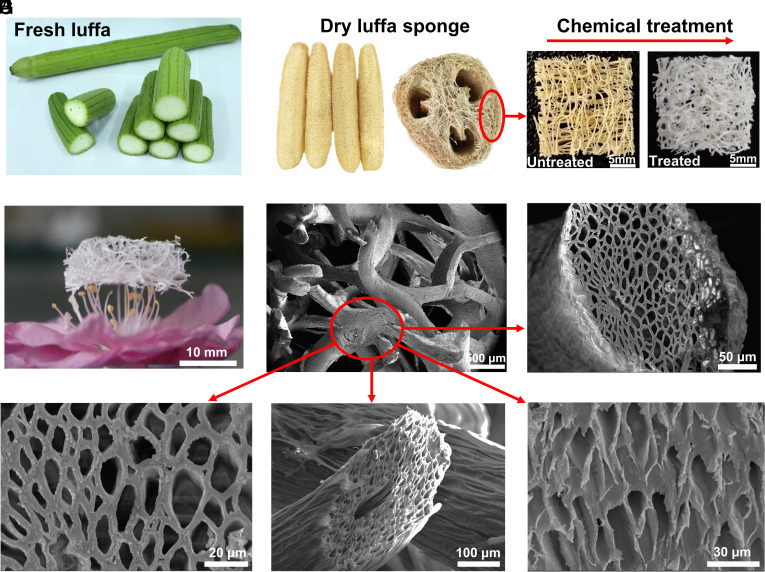
In the current work, the dry LS derived from sun curing the matured luffa vegetable was commercially sourced. The flexoelectric property of the original dry LS is limited as consistent with the polymeric constituents. Furthermore, we believe that its mechanical elasticity is limited due to the presence of lignin and hemicellulose (45, 46). Therefore, a chemical treatment was performed to remove the lignin and hemicellulose from the natural dry LS, and the detailed treatment procedure can be found in Materials and Methods—Luffa sample treatment and briefly summarized in Fig. 2. As shown in Fig. 2B, the dry LS, as bought, possesses a natural three-dimensional porous interconnected network structure. The treatment successfully removes the majority of hemicelluloses and lignin leaving behind mainly the type-I cellulose crystal form characterized by FT-IR (Fourier-transform infrared spectroscopy) spectra and X-ray diffraction as shown in SI Appendix, Fig. S2. The scanning electron microscopy (SEM) image in Fig. 2E illustrates that the diameter of a macroscopic single fiber ligament is about 250 to 350 μm. Dry luffa is a hierarchical porous material, and Fig. 2 F–I show the cross-sections and oblique sections of a fiber. The final motif is similar to the honeycomb structure. The diameter of the hole is ca. 13.8 μm, and the thickness of the wall is ca. 2.7 μm.

Fig. 2.

Morphological characteristics of luffa. Photos of the (A) fresh luffa, (B) dry LS, (C) natural untreated luffa (Left) and chemical-treated LS (Right), and (D) LS placed on the stamen to illustrate its lightweight characteristic. SEM images of the (E) macroscopic LS with fibers and pores, (F) and (G) cross-section of a fiber, (H) and (I) oblique section of a luffa fiber.

Results

Flexoelectricity-Mediated Electromechanical Response of the LS.

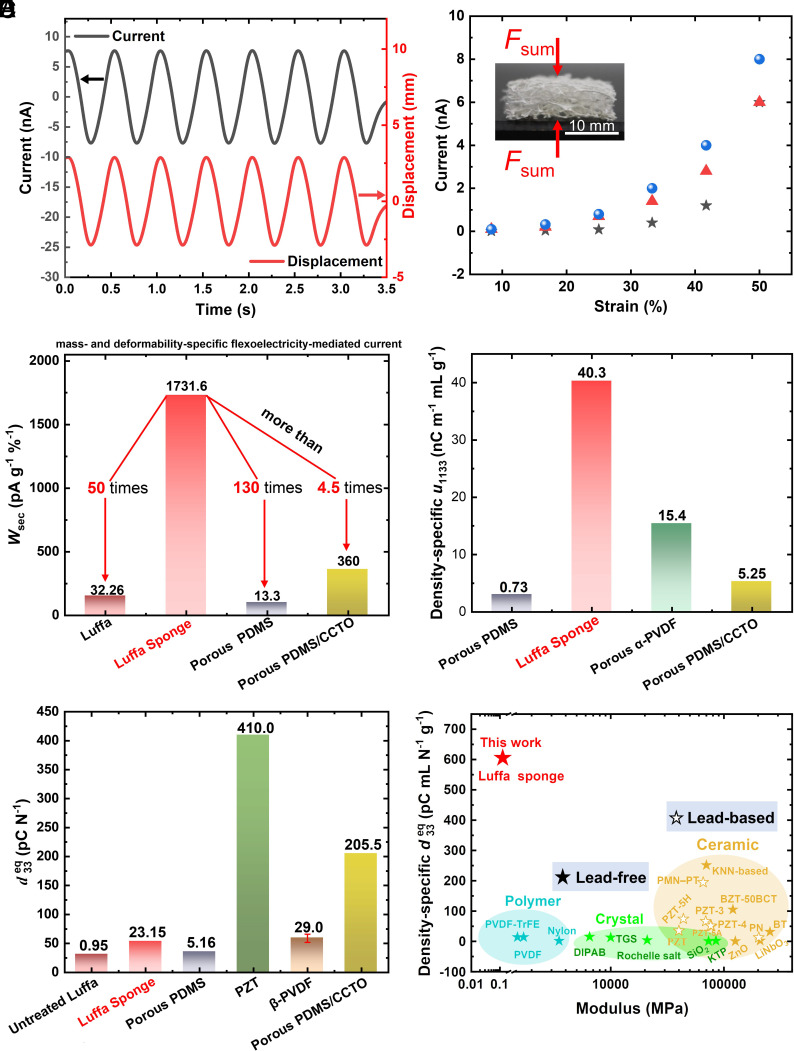
As highlighted earlier, the LS due to its natural hierarchical porous structure with randomly oriented ligaments engenders considerable strain gradient in the microscale fibers and walls for any macroscopic loading. We can therefore expect a significant microscopic flexoelectric response, and provided, there is reflection symmetry breaking at the microscale, a pronounced macroscopic piezoelectric-mimicking output. Through differential testing, we have systematically ruled out the role of other electromechanical coupling mechanisms such as electret effect, native piezoelectricity of the underlying material, or triboelectricity (SI Appendix, The mechanism underpinning the electromechanical coupling of the LS). The electric output of macroscopic cubic LS samples (20 × 20 × 6 mm³) is shown in Fig. 3. As evident, Fig. 3A displays the flexoelectric-induced polarization current (left axis) of the treated LS and the real-time applied displacement (right axis) variations versus time, and smooth and reproducible signals at 2 Hz with high consistency may be noted. We observe that (Fig. 3B) the current generated by the LS increases with the increase of applied strain, which is up to 8 nA under 50% strain. It is important to highlight that an untreated luffa will experience destructive damage under the applied strain of more than 30%, and the maximum output current is only 210 pA (SI Appendix, Fig. S3A). The mass- and deformability-specific flexoelectricity-mediated current is defined as W_sec = I_max/(mε), where I_max, m, and ε represent the maximum current, the mass of the sample, and the applied macroscopic compression strain, respectively. As a pure natural material, the W_sec of the treated LS is 1731.6 pAg⁻¹ %⁻¹, which is 50 times and 130 times higher than those of the untreated luffa and porous polydimethylsiloxane (PDMS) (22), respectively, and even more than the optimized porous composite material (23), as shown in Fig. 3C. The comparison of the density-specific equivalent flexoelectric coefficient μ₁₁₃₃ is shown in Fig. 3D, and that of the LS is 40.3 nCm⁻¹ mL g⁻¹, which is 55 times and 2.6 times that of porous PDMS and porous α-PVDF, respectively.

Fig. 3.

The performance of the LS and comparison with piezoelectric materials. (A) The current (left axis, black) of the LS and the real-time applied displacement (right axis, red) at 2 Hz. (B) The relationship between current and applied strain of the LS of three samples. (C) The mass- and deformability-specific flexoelectricity-mediated current W_sec of the treated LS, untreated luffa, porous PDMS, and porous PDMS/calcium copper titanate (CCTO) composite (23). (D) The density-specific μ₁₁₃₃ of the LS, porous PDMS, porous α-PVDF, and porous PDMS/CCTO composite (23). (E) The equivalent piezoelectric coefficient $d_{33}^{\mathit{eq}}$   of the treated LS, untreated luffa, porous PDMS, PZT, porous β-PVDF, and porous PDMS/CCTO composite. (F) The density-specific $d_{33}^{\mathit{eq}}$  of the treated LS and common piezoelectric materials, including PZT-3, PZT-4, PZT-5H (47, 48), PZT-5A, Ba(Zr_0.2Ti_0.8)O₃-50(Ba_0.7Ca_0.3)TiO₃ (BZT-50BCT) (49), PZT (50), ZnO, LiNbO₃, Nylon, Rochelle salt, triglycine sulfate (TGS), KTiOPO₄ (KTP) (51), PVDF, PVDF-TrFE (52), diisopropylammonium bromide (DIPAB) (53), (K,Na)NbO₃ (KNN)-Based (48, 54), BaTiO₃ (BT), PbNb₂O₆ (PN) (55), Pb(Mg_1/3Nb_2/3)O₃-PbTiO₃ (PMN-PT) (56), and SiO₂ (57).

The LS produces local flexoelectricity under compression due to the bending of ligaments but macroscopically behaves like a piezoelectric material. In this sense, the longitudinal equivalent piezoelectric coefficient, $d_{33}^{\mathit{eq}}$ is calculated by the definition of the charge polarized per load as

$$d_{33}^{eq}=\frac{\mathrm{d}Q}{\mathrm{d}F}=\frac{\mathrm{d}\left(\frac{\mathrm{i}}{2\pi f}\right)}{\mathrm{d}\left(E\epsilon A\right)}=\frac{1}{2\pi fEA}\frac{\mathrm{d}i}{\mathrm{d}\epsilon },$$ [1]

where i, ε, f, E, and A are the current, compressive strain, frequency of alternating applied load, equivalent compressive modulus, and the cross-sectional area of the LS sample, respectively. As shown in Fig. 3E, $d_{33}^{\mathit{eq}}$ of the LS is 23.15 pC/N, which is comparable to that of the piezoelectric polymer β-PVDF, whereas it is much smaller than that of the porous composite (23) as well as the commonly used piezoelectric ceramic lead zirconate titanate (PZT) (50). The density-specific $d_{33}^{\mathit{eq}}$ of the LS is compared to those of the common piezoelectric materials with the corresponding elastic moduli as shown in Fig. 3F. The LS possesses an exceptionally low modulus yet exhibits the highest-density-specific equivalent piezoelectric coefficient, which is 50 times higher than that of β-PVDF and over 10 times higher than that of PZT.

Theoretical Analysis—Flexoelectricity under Macroscopic Compression.

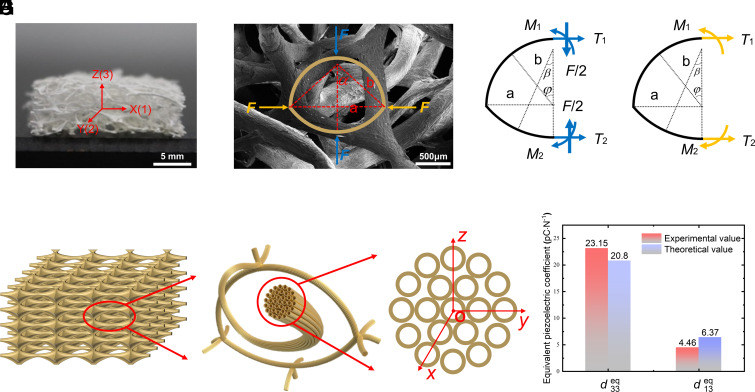
The LS has obvious growth traces along the macroscopic axial direction, which leads to the differences in morphology as well as the mechanical properties between the axial and radial structures of the sponge. In order to quantitatively calculate the flexoelectric effect in the LS, a theoretical analysis is performed. Fig. 4A shows the sample and its porous structure, and Fig. 4B is an SEM image, where a representative unit cell model of the larger porous structure is constructed as shown in Fig. 4 C and D. The unit cell is taken as a frame structure composed of two circular arcs, namely, the upper half circle with radius of a and lower arc with radius of b. The Z direction is along the radial direction of the LS. Fig. 4E represents the LS sample with layers of unit cells. The smaller porous structure inside the fiber is more like a honeycomb structure, which can be modeled as multiple circular cross-sections through holes as shown in Fig. 4 F and G.

Fig. 4.

Theoretical model description. (A) A picture of a sample. (B) A unit cell representing the macroscopic porous structure. (C) Half unit cell with vertical applied force F [blue ones in (B)] and (D) half unit cell with horizontal applied force F [orange ones in (B)]. (E) The schematic plot representing the macroscopic LS with layers of unit cells. (F) A unit cell showing through holes porous structures along a fiber, and (G) the cross-section of a fiber. (H) Comparison of experimental and theoretical values of equivalent piezoelectric coefficients of the LS.

It is assumed that each unit cell bears the same deformation form during the compression of the LS cuboid sample, and the left half unit cell is analyzed for convenience with the force F along the defined positive directions as shown in Fig. 4 C and D. When the external alternating load F_sum(t) is applied vertically (Z) or horizontally (X) to the surface of the macroscopic LS sample, the load is evenly distributed across each unit cell of the contact area. The vertically and horizontally compressive force F on the unit cell are F = F_sum(t)/n₁n₂ and F = F_sum(t)/n₂n₃, respectively, where n₁, n₂, and n₃ are the number of layers of unit cells along the X, Y, and Z directions of the sample, respectively. Through a theoretical analysis, we have derived the flexoelectric output of the macroscopic LS, as detailed in the Materials and Methods—Theoretical calculation of flexoelectric charges and SI Appendix, Theoretical model. The theoretical equivalent piezoelectric coefficients ( $d_{33}^{\mathit{eq}}$   and $d_{13}^{\mathit{eq}}$   ) can be expressed by Eq. 2,

$$d_{\mathrm{i}3}^{eq}=\frac{\mathrm{d}}{\mathrm{d}{F}_{\mathrm{s}\mathrm{u}\mathrm{m}}}{Q}_{\mathrm{i}3}\left(F_{\mathrm{sum}}\right),$$ [2]

where the subscript i (i = 1 or 3) denotes the direction of the F_sum(t), and the subscript “3” represents the polarization direction. Q is the flexoelectric charge in the macroscopic LS sample.

Two theoretical equivalent piezoelectric coefficients ( $d_{33}^{\mathit{eq}}$   and $d_{13}^{\mathit{eq}}$   ) of the LS are compared with the experimental data, which agree very well with each other, as shown in Fig. 4H. Based on the theoretical model, the dependence of the current on different parameters is shown in SI Appendix, Fig. S5. The current increases with the increase of the applied force, F_sum, and the decrease of Young’s modulus, E, section moment of inertia, I, and fiber diameter, δ.

Applications of the LS as Sensors and Electric Generators.

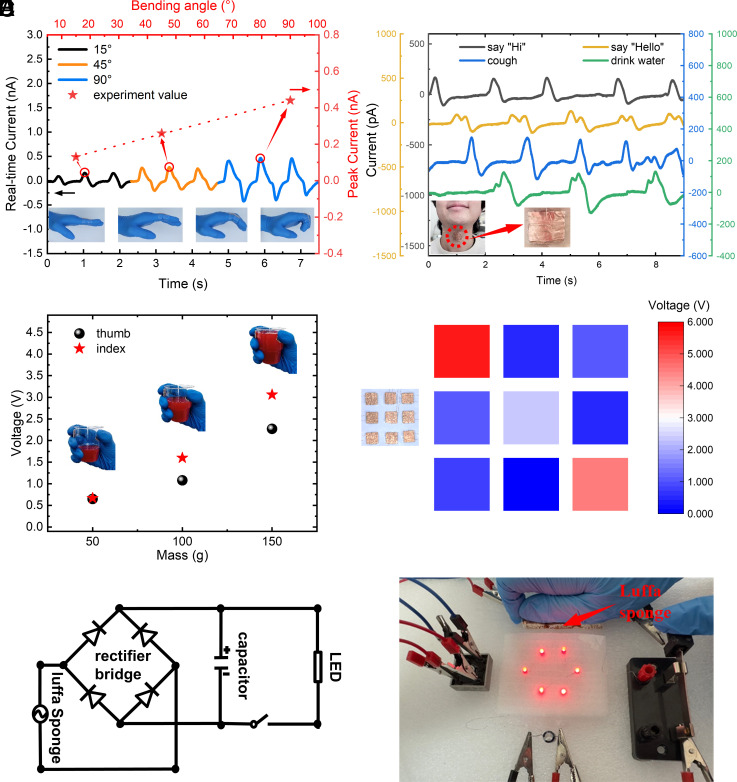
In recent years, the flexible strain sensors have attracted significant attention with applications in consumer biomedical devices such as health monitors and other related fields (58). Here, we illustrate the prospect of the LS as passive flexible sensors, as well as the strain gradient electric generator (SGG). The LS sensor can detect the bending of fingers, where the real-time current waveform (left y axis) exhibits the remarkable stability once the finger bends the same angle as shown in Fig. 5A. And the peak current (right y axis) changes linearly with the variation of different bending angles that facilitates the sensing of the bending angle. The LS sensor is highly capable of sensing even miniscule pressure changes arising from throat movement during coughing and drinking, as shown in Fig. 5B. In addition, the LS sensor distinguishes sounding “Hi” and “Hello”, indicating its potential usage for speech/voice recognition (Fig. 5B). Fig. 5C illustrates the uses as a pressure sensor, where two LS sensors were pasted on the thumb and forefinger each. When a beaker with water of 50 g, 100 g, and 150 g is picked up, the sensors exhibit different responses to the different loads. The electrical signal is linearly proportional to the loads (Fig. 5 A and C), which marks the advantage of the LS sensors. As illustrated in Fig. 5D, the LS precisely identifies the profile of a hand via the contour plot of electrical signals by using a multichannel data acquisition approach (59), which is dependent on the specific location of dynamic pressure.

Fig. 5.

Application of flexoelectricity of the LS. Sensor applications for (A) bending angle of fingers (the left y axis represents the real-time current waveform, and the right y axis represents the corresponding peak current.), (B) movement of the throat, (C) pressure sensor, and (D) arrays of the pressure sensor. (E) Circuit diagram of the SGG. (F) LS SGG lights up six LEDs.

Apart from applications as flexible and sensitive sensors, the LS is also a promising green electric-energy harvester. A circuit diagram as shown in Fig. 5E was used to charge a capacitor (4.7 μF), which was then used to charge light-emitting diodes (LEDs). Here, six LEDs were powered after the capacitor charged for ca. 7 min by uniaxial compression on three LS samples with the total size of 20 × 60 × 6 mm³ as shown in Fig. 5F and Movie S1. The LS can be arrayed (or cut to the required size) to obtain the required electrical output, so as to realize its power supply function to charge the headset, mouse, watch, and other smart electronic devices.

Concluding Remarks

We have investigated the flexoelectric effect in the natural LS, which is a low-cost, biodegradable, biocompatible, ultralight biomaterial. After the chemical treatment, the LS sample with the size of 20 × 20 × 6 mm³ generates an electric current of 8 nA under 50% applied strain. The density-specific equivalent-specific piezoelectric coefficients of the LS are highest among known materials including the often-used PZT. We demonstrate potential applications of LSs in the field of wearable sensors for monitoring human movement (such as finger bending, vocal cord vibration, and speech recognition) and pressure detection. Moreover, the LS is a SGG, which can convert mechanical energy into electric energy to power devices.

Materials and Methods

Materials and Chemicals.

Native dry luffa was used to fabricate the LSs. Originally, the outer-layer part of luffa was selected and cut into the dimension of 20 × 20 × Z mm³. The hydrogen peroxide (H₂O₂, 35 wt%) and sodium hydroxide (NaOH) were purchased from Yongda Chemistry Co. Ltd. (Tianjin, China). All of these chemicals were used as received without further purification. Deionized water was used as the solvent or clean the LS.

Luffa Sample Treatment.

Initially, the natural dried LSs (untreated luffa) were boiled in a 6 wt% NaOH solution at 100 °C for 8 h to remove hemicellulose. Then, the samples were kept in boiling pure water for 3 h. Thereafter, the samples were further boiled within the 15 wt% H₂O₂ solution at 80 °C for 8 h to remove the lignin. Then, the samples were kept in boiling pure water for 3 h and dried at 60 °C for 12 h using an oven. Finally, the treated samples were cut into the dimension of 20 × 20 × 6 mm³, and the mass m = 0.10 g.

Theoretical Calculation of Flexoelectric Charges.

Under external loads (horizontal or vertical), the flexoelectric polarizations of the upper and lower parts of the unit cell are set as P_U(φ) and P_L(φ), respectively, and the charge output (Q_net) of the unit cell can be expressed as

$$\begin{array}{c}{Q}_{\mathrm{net}} = 2\left({\iint }_{0\le \phi \le \frac{\pi }{2},z^2+y^2={\delta }^2} P_U\left(\phi \right)\cos \phi \mathrm{d}S\cos \phi \right.\hfill \\ -\left.{\iint }_{0\le \beta \le \alpha ,z^2+y^2={\delta }^2} P_L\left(\beta \right)\cos \beta \mathrm{d}S\cos \beta \right),\hfill \end{array}$$ [A1]

Therefore, the total flexoelectric charges, Q_sum, of the whole sample can be calculated as

$$Q_{\mathrm{sum}}=n_1{n}_2{Q}_{\mathrm{net}}.$$ [A2]

Equipment.

The morphology and structure of the LSs were characterized by field emission SEM (Hitachi SU-8020, Tokyo, Japan) after coating Pt nanoparticles on the surface (Cressington 108 Auto). FTIR (GCMS-QP2020 NX) was performed over a range of 400 to 4,000 cm⁻¹ to analyze the changes in composition before and after the chemical delignification treatment. The crystal structure and crystallinity of the cellulose in LSs were characterized by X-ray diffraction (D8 DISCOVER). The dynamic mechanical analyzer (TA ElectroForce-DMA3200, USA) was used for dynamic uniaxial compression and mechanical property test. A low noise current preamplifier (Stanford Research SR-570, USA) was used to measure and convert the current signal to voltage signal, in which a low noise gain mode and a low-pass filter method were chosen. An electrostatic eliminator (KEYENCE SJ-F036, Japan) was used to remove the electrostatic charge. Finally, the oscilloscope (Tektronix MDO-3034, USA) was used to record the real-time voltage signal.

Supplementary Material

Appendix 01 (PDF)

Movie S1.

The luffa sponge is a promising green electric-energy harvester. Three luffa sponge samples with the total size of 20×60×6 mm3 charge a capacitor (4.7 μF) for ca. 7 minutes by uniaxial compression, which is then used to charge six LEDs.

Data, Materials, and Software Availability

All study data are included in the article and/or supporting information.