Task-based assessment of digital mammography microcalcification detection with deep learning denoising algorithms using in silico and physical phantom studies

Abstract.

Purpose

Recent research suggests that image quality degradation with reduced radiation exposure in mammography can be mitigated by postprocessing mammograms with denoising algorithms based on convolutional neural networks. Breast microcalcifications, along with extended soft-tissue lesions, are the primary breast cancer biomarkers in a clinical x-ray examination, with the former being more sensitive to quantum noise. We test one such publicly available denoising method to observe if an improvement in detection of small microcalcifications can be achieved when deep learning-based denoising is applied to half-dose phantom scans.

Approach

An existing denoiser model (that was previously trained on clinical data) was applied to mammograms of an anthropomorphic physical phantom with hydroxyapatite microcalcifications. In addition, another model trained and tested using all synthetic (Monte Carlo) data was applied to a similar digital compressed breast phantom. Human reader studies were conducted to assess and compare image quality in a set of binary signal detection 4-AFC experiments, with proportion of correct responses used as a performance metric.

Results

In both physical phantom/clinical system and simulation studies, we saw no apparent improvement in small microcalcification signal detection in denoised half-dose mammograms. However, in a Monte Carlo study, we observed a noticeable jump in 4-AFC scores, when readers analyzed denoised half-dose images processed by the neural network trained on a dataset composed of 50% signal-present (SP) and 50% signal-absent regions of interest (ROIs).

Conclusions

Our findings conjecture that deep-learning denoising algorithms may benefit from enriching training datasets with SP ROIs, at least in cases with clusters of 5 to 10 microcalcifications, each of size $\lesssim 240\mu \mathrm{m}$.

1. Introduction

One of the most effective means for reducing breast cancer mortality is the screening of asymptomatic women using digital mammography (DM).¹ Two of the most important clinical signs of breast cancer observed on a mammogram are: (1) the characteristics of a tumor soft-tissue mass and (2) presentations of mineral deposits as specks referred to as microcalcifications.² Mammography is one of the most challenging radiological imaging techniques because it requires both good conspicuity of low-contrast tumor masses, as well as of fine, high-resolution details associated with microcalcifications. Since the breast is radiosensitive, it is also important that mammography systems are designed to maximize image quality while also limiting the mean glandular dose.

Detection of breast microcalcifications in mammograms is particularly important because they often are an early indication of in situ breast cancer that makes up to 34% of all newly diagnosed breast cancers detected in mammography.³ It has been previously shown through phantom studies that detection of microcalcifications is largely limited by the radiation dose to the breast.^4,5 One recent study by Chan et al.⁶ conducted a microcalcification phantom study showing that with a decrease of dose from 2.07 to 1.34 mGy, radiologists recorded decreased sensitivity and increased false positives.

Thus any effort to reduce the radiation dose to the breast with mammography must carefully consider whether microcalcification detection accuracy would be penalized. Several recent research efforts have focused on the development of image processing methods to reduce noise in mammographic images, some with the goal of reducing radiation dose to the breast. Lately, studies using deep-learning convolutional neural network (DL-CNN)-based techniques have focused on the potential of reducing radiation dose to the breast by restoring mammography images acquired using a lower-dose protocol to obtain image quality similar to that achieved with a conventional dose protocol.

Shan et al.⁷ explored the use of DL-CNNs for restoring low-dose digital mammograms and investigated various network loss functions, including mean-square error (MSE), mean-absolute error (MAE), structural similarity index (SSIM),⁸ and perceptual loss (PL).⁹ For training the DL-CNN, they used a large number of image patches extracted from retrospective DM exams acquired on a clinical system, using a procedure to add quantum noise to full-dose scans to simulate varying radiation dose levels. To evaluate the denoising algorithm, an anthropomorphic breast phantom was used to acquire images at different dose levels, and performance was assessed using signal-to-noise ratio (SNR) and mean-normalized-square error (MNSE). Results suggested that one PL loss function (PL4) was able to achieve similar noise levels of the full-dose image when applied to reduced dose images, while achieving smaller bias than the other loss functions tested. In a follow up study, Vimieiro et al.¹⁰ enhanced the loss function to impose fidelity of the image noise correlation between full-dose and low-dose mammograms. In another study, Gao et al.¹¹ trained a DL-CNN using a loss function consisting of a weighted combination of MSE and adversarial loss to improve microcalcification conspicuity in breast tomosynthesis images. Although this study did not evaluate whether the method could be used on low-dose images to recover image quality to be similar to full-dose images, the algorithm showed improvements by training the network with simulated data acquired from a digital anthropomorphic breast phantom.

Training of these new DL-based denoising algorithms to restore low-dose images is a challenging endeavor. One approach is to acquire full-dose and low-dose mammograms from a large ensemble of patients for use in training the denoising algorithm. Unfortunately, this approach raises ethical issues in that patients would have to receive increased radiation dose over a conventional dose protocol. Another approach for procuring training data used by Shan et al.⁷ is to implement a simulation procedure to add quantum noise to full-dose clinical images. Adding simulated noise to images is difficult in that it requires accurate modeling of the imaging system, as well as the postacquisition image processing implemented by the vendor. Another potential challenge with using clinical data to train the network is that the training data should include representations of different clinical diagnostic features, e.g., image patches containing microcalcification clusters. To obviate these difficulties, Gao et al. trained a DL-CNN using realistic anthropomorphic digital breast phantoms and in silico modeling of the breast imaging system, and they concluded that the DL-CNN trained using this data was applicable to clinical human subjects.

Assessing performance of new DL-CNN algorithms in improving the accuracy of microcalcification detection in low-dose images represents an additional challenge. Common figure-of-merits used to analyze performance are visual assessment, SNR, contrast-to-noise ratio (CNR), MNSE, and SSIM. Visual assessment of denoised images is subjective and not necessarily predictive of clinical performance. The SNR and CNR do not account for the effect of noise correlations in the image that could affect microcalcification detection, and the MNSE and SSIM are global image metrics that do not relate specifically to microcalcification detection accuracy. A recent work aimed to objectively evaluate performance of DL-based denoising methods by use of numerical observers.¹²

Since microcalcification detection accuracy is especially sensitive to quantum noise, while the detectability of masses is only lightly dependent on radiation dose,¹³ we focus here on the evaluation of microcalcification detection with denoising algorithms. Two approaches for the objective assessment of microcalcification detection performance with DL-CNN denoising algorithms are proposed. The first approach used a previously described physical anthropomorphic breast phantom with inserted microcalcification clusters of small size.¹⁴ Although it is unclear if physical breast phantoms can be used to collect enough training data to train the denoising network, the approach could be used to evaluate networks previously trained on clinical data. The second approach used in silico computational methods with a previously developed anthropomorphic digital breast phantom¹⁵ and GPU accelerated Monte-Carlo software¹⁶ for simulating the imaging acquisition process. With this latter approach, a large ensemble of image data with small microcalcification clusters can be generated for training and testing of DL-CNN breast imaging denoising algorithms. We demonstrate the use of these testing approaches by evaluating performance of a recently developed DL-CNN-based algorithm^7,10 for denoising low-dose mammography images. The latest implementation of this algorithm uses a weighted loss function comprised of two components; a PL and another term that calculates the difference in the power spectra of the input and output images. The goal of this second term is to constrain the processed image to have similar noise correlation (i.e., power spectrum) as the original image.

2. Methods

This study consists of two separate experiments. In both, we used an existing PyTorch deep-learning denoising model provided to us by its developers.^7,10 In the first set of experiments, the denoising model was trained (by the algorithm creators) using clinical data and applied to images of a physical breast phantom with embedded microcalcifications acquired on the Hologic Selenia Dimensions DM system. In the second set of experiments, a cohort of digital anthropomorphic breast phantoms was generated with embedded microcalcification clusters, and mammograms were simulated with Monte Carlo x-ray transport software. These synthetic images were then used for training and testing of the deep-learning denoising algorithm. The following sections explain the denoising software we tested and details of data preparation.

2.1. Existing DL-Denoising Model Applied to Experimental Phantom Data

To restore low-dose phantom images collected on our Hologic Selenia Dimensions DM system, we used an existing pretrained deep-learning model. Details of its implementation and training are given by Shan et al.,⁷ and the source code is available from USP-LAVI GitHub repository.^17,18 To briefly summarize the authors developments, a HResNet network (modification of a ResNet architecture¹⁹ optimized for better modeling of the noise distribution in low-dose DM) has been investigated with seven different loss functions. Specifically, the authors experimented with MSE, MAE, SSIM,⁸ and PL [compares similarity between two images in a high-level feature space of the VGG-16 network²⁰] loss functions PL1 through PL4, with a numerical index indicating whether the PL was computed on early or later layers in the VGG-16 for four different feature spaces. The algorithm was trained on image data extracted from 400 clinical mammograms (CC/MLO/left/right breasts) of 100 patients from the Barretos Cancer Hospital in Brazil, all collected using the Hologic Selenia Dimensions DM system. In order to have a matching dataset of low-dose mammograms the authors injected quantum and electronic noise into the full-dose images, taking into account detector crosstalk. Two new image sets with dose reduction factors of 50% and 75% were produced. After this image restoration, models were trained using 256,000 $64\times 64{\mathrm{px}}^2$ randomly selected breast background patches [matched pairs of full-dose and low-dose regions of interest (ROIs)]. It was concluded that, among others, the PL4 loss function-based model preserved most image details without excessive smoothness. Therefore, we chose this model for denoising low-dose phantom data.

2.2. Physical Phantom Imaging for a Testing Set

For testing the above denoising model in the human observer studies, we imaged our previously described²¹ anthropomorphic 2D-printed paper breast phantom, which mimics $\sim 30\%$-glandular tissue composition and a 40-mm-thick compressed breast. Signals used in the observer detection task were defined as clusters of microcalcifications. Several “inserts,” with many hydroxyapatite microcalcification cluster patterns arranged in each, allowed us to produce sufficient number of nonrepeated random cluster configurations. Such an “insert” was placed in the paper phantom to produce signal-present (SP) ROIs in x-ray images. A typical cluster is localized in a $5{\mathrm{mm}}^2$ area and contains on average 5 to 7 calcifications of random shapes with individual specks sizes varying from $\sim 150$ to $180\mu \mathrm{m}$. Phantom mammograms were acquired on a Hologic Selenia Dimension mammography unit. Figure 1(a) shows a sample acquisition. Automatic exposure control (AEC) was used for full-dose scans of the phantom, and manual exposure corresponding to a $\times 0.5$ of AEC dose was used for low-dose acquisitions. All together two datasets with $N=250$ unique SP ROIs and 750 signal-absent (SA) ROIs were acquired with the full-dose and low-dose settings. The $\mathrm{HResNet}+\mathrm{PL}4$ denoising model, as described above, was used to process low-dose mammograms. Since the original deep-learning model was trained using “for processing” (e.g., raw) clinical mammograms, we used the same kind of output in a test dataset. Table 1 lists the machine exposure parameters used for collecting experimental data.

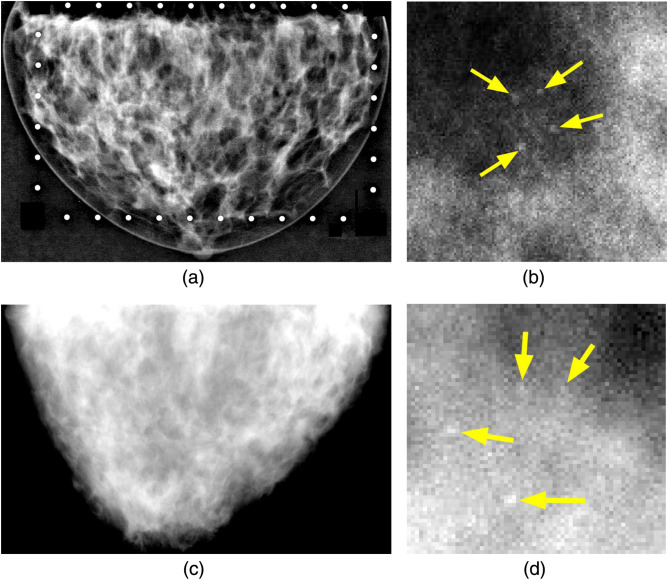
Fig. 1.

Examples of physical and simulated phantom mammograms and microcalcification clusters. (a) Experimental phantom mammogram, where bright circles around the breast are fiducial markers used for ROI extraction. (b) Physical cluster of HA calcifications. (c) Monte Carlo simulation. (d) Synthetic cluster. Arrows indicate individual speck locations in (b) and (d).

Table 1.

Techniques used for collecting phantom mammograms for denoising algorithm testing.

Modality	Spectrum	kVp	Full dose (AEC) (mAs)	Half dose (mAs)	Presentation intent type
DM	W-Rh	31	125	60	Raw

2.3. Simulated Mammography Data

For the in silico study, a large number of synthetic mammograms were generated using MC-GPU x-ray transport and simulation software.¹⁶ An ensemble of VICTRE²² compressed breast phantoms of scattered density type was used. Voxelized phantoms are based on Graff’s model¹⁵ and were of the size $121\times 87\times 57{\mathrm{mm}}^3$.

SP mammograms (with microcalcification clusters present) were modeled by inserting spherical specks of sizes $100\mu \mathrm{m}\lesssim d\lesssim 240\mu \mathrm{m}$, five per random cluster/multiple clusters per phantom, into a central slice of the phantom. A single cluster occupies approximately a $4\times 4{\mathrm{mm}}^2$ area. Microcalcifications were modeled as hydroxyapatite with voxels making up the specks assigned varying density values ranging from 1.1 to $1.4{\mathrm{g}/\mathrm{cm}}^3$. These density values were determined by trial and error from pilot 4-AFC reader studies with a human observer to obtain desired signal contrast and resulting PC score in the microcalcification detection task. We aimed to approximately match the reader’s PC performance achieved in the study with experimental mammograms of the anthropomorphic breast phantom, e.g., PC $\gtrsim 80\%$ for a full-dose exposure. Figure 1 shows physical and simulated phantom x-ray images, as well as corresponding SP regions.

2.4. Deep-Learning Denoising Model with Combined PL + PS Loss Function Training

For the study with Monte Carlo generated data, we employed an improved version of the denoising algorithm by the same group (Laboratory of Computer Vision, University of São Paulo, Brazil), presented at the IWBI 2022 conference.¹⁰ Similar to the original work, our implementation used a combination of two loss functions: one to impose fidelity in the noise correlations (2D power spectrum or PS-2D) and one that optimizes visual perception (perception loss or PL) in VGG-16 network. The PS-2D component was defined as the mean-normalized-absolute erro between the 2D power spectrum of the prediction (e.g., model output image) and the target (ground-truth high-dose image); whereas the PL component compares similarity between two images in a high-level feature space in the early or later layers of the VGG-16 (thus dubbed PL1 through PL4) and is equivalent to the MSE but defined in a feature space instead of a pixel space. Specifically, the combined loss function was expressed as

$${\mathcal{L}}_{\mathrm{PL}+\mathrm{PS}}={\mathcal{L}}_{\mathrm{PL}4}+\lambda ·{\mathcal{L}}_{\mathrm{PS}\text{-}2\mathrm{D}},$$ (1)

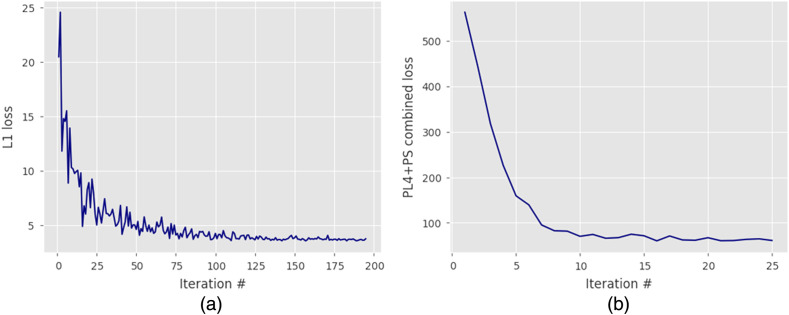
where the PS-2D component’s weight was set to $\lambda =0.037$, as was determined optimal in the algorithm’s developers experiments, and that appeared to produce good results with our own data. Following the original approach, we first pretrained the denoising model using an L1-norm loss function and then used a saved model as an input to train the final model with the $\mathrm{PS}\text{-}2\mathrm{D}+\mathrm{PL}4$ loss function. Convergence criteria in both cases were satisfied when the loss value achieved a stable plateau, as shown in Fig. 2. Pretraining with a simple L1-norm loss function was done to obtain a solution reasonably close to the input image, before fine-tuning the algorithm with a more complex combined loss function, to avoid possible divergence in the optimization process. Learning rates and other neural network hyperparameters were the same as in the original work. Figure 2 shows the learning progression for both steps.

Fig. 2.

Pretraining and training of the denoising algorithm: (a) pretraining with L1-norm loss function and (b) fine-tuning with combined $\mathrm{PS}\text{-}2\mathrm{D}+\mathrm{PL}4$ loss function.

Model training was done patchwise using a large number ($\sim \mathrm{248,000}$) of matched full-dose and half-dose $64\times 64{\mathrm{px}}^2$ image pairs. We explored two approaches for the algorithm training: (1) all ROIs used in the training set were extracted from breast background regions in mammograms without microcalcifications (e.g., SA images only) and (2) half of ROIs used in the training set ($\sim \mathrm{124,000}$) were SA, while the other half contained microcalcifications. The idea was to see if enriching the training set with ROIs containing microcalcifications would have an effect on the observer performance. Finally, the resulting PyTorch models were used for denoising of (whole) low-dose mammograms for the reader studies.

2.5. 4-AFC Visual Experiment with Human Observers

The observer study, using phantom images acquired on the Hologic Selenia Dimensions system, consisted of the three reading sessions with full-dose, low-dose, and DL-denoised low-dose ROIs. The image patches were 16-bit grayscale $100\times 100{\mathrm{px}}^2$ ($\sim 7\times 7{\mathrm{mm}}^2$) DICOM crops. The same ROIs (locations within the image) were used in all sessions, with their order randomized between each session and each participant. Default window level and window width were set to maximize the contrast of each crop (e.g., using full range for window width and having widow level at the midpoint) with readers being able to adjust magnification, brightness, and contrast for individual “windows” in the 4-AFC interface. We employed the University of Leuven, Belgium, 4-AFC GUI display software²³ to conduct the readings. A room with controlled light environment and a medical-grade DICOM-calibrated display BARCO MDCC-6130 were used for all human observer experiments. Four readers with biomedical engineering degrees and medical imaging background were recruited from our laboratory to do the readings. The resulting data were analyzed to produce a proportion of correct (PC) responses score for each reader, and data bootstrapping was implemented to estimate confidence intervals on PC.

Similar reading sessions were carried out with ROIs extracted from simulated mammograms of the digital breast phantom and DL-denoised data processed by the $\mathrm{HResNet}/\mathrm{PS}\text{-}2\mathrm{D}+\mathrm{PL}4$ model, which we trained ourselves. Each reader conducted four studies with full-dose, low-dose, and DL-denoised data processed with the model trained only using SA patches, as well as DL-denoised data processed with the model trained using 50% SA and 50% SP ROIs.

3. Results

3.1. DL-Denoising Performance Evaluation Using Existing Model Applied to Phantom Data Acquired on a Clinical Mammography Machine

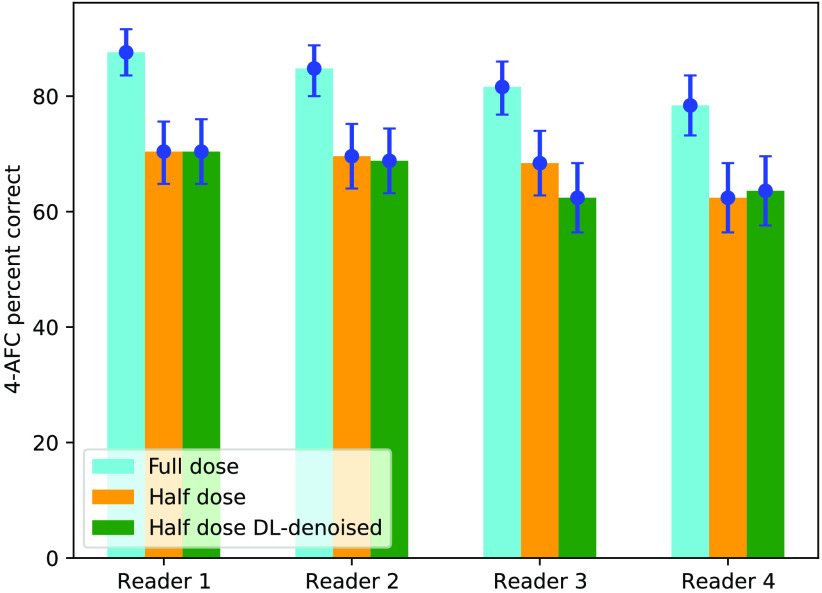
Figure 3 summarizes microcalcification detection performance in the 4-AFC study using an experimental breast phantom for four human readers. PC responses with 95% confidence intervals obtained from bootstrapping data and determining 2.5% and 97.5% percentiles, is compared for full-dose, half-dose, and DL-denoised half-dose images. From the plot, it can be noted that (1) there is a statistically significant difference between observers performance with full-dose and half-dose ROIs, and (2) denoising of low-dose data did not improve calcification detectability (PC values are provided in Table 2). For all readers, analyzing ROIs from denoised mammograms resulted in performance close to that obtained with original low-dose data, within measurement error bars.

Fig. 3.

4-AFC human reader study with physical breast phantom imaged on the Hologic DM system.

Table 2.

Results of the 4-AFC human observer experiment with physical breast phantom imaged on the Hologic DM system.

Reader #	1	2	3	4
${\mathrm{PC}}_{\mathrm{fulldose}}$ a	87.6 [83.6, 91.6]	84.8 [80.0, 88.8]	81.6 [76.8, 86.0]	78.4 [73.2, 83.6]
${\mathrm{PC}}_{\mathrm{halfdose}}$	70.4 [64.8, 75.6]	69.6 [64.0, 75.2]	68.4 [62.8, 74.0]	62.4 [56.4, 68.4]
${\mathrm{PC}}_{\mathrm{restored}}$	70.4 [64.8, 76.0]	68.8 [63.2, 74.4]	62.4 [56.4, 68.4]	63.6 [57.6, 69.6]

^aPC values and their 95% confidence intervals.

Figure 4 shows a typical SP ROI at full-dose, half-dose, and a half-dose image after denoising. Loss of finer details, including some microcalcifications, and higher pixel variance are apparent in the half-dose image. The restored image, on the other hand, although providing visually better resemblance of a full-dose image texture, still misses high-frequency detalization of full-dose data. MSE and SSIM comparison shows that denoising improves both quantities—MSE is reduced by 37% and SSIM is increased by 24% when comparing half-dose versus full-dose and restored versus full-dose image pairs. We speculate that “smoothing out” of the local fine structures, despite improved “global” image quality metrics, such as MSE and SSIM, is what causes human readers not to perform better with microcalcification detection in denoised ROIs.

Fig. 4.

Same SP ROI: (a) full-dose, (b) half-dose, and (c) restored half-dose images. Denoised mammogram has 37% better MSE and 24% better SSIM, compared to the half-dose one, when similarity is measured with respect to the full-dose image.

3.2. DL-Denoising Performance Evaluation Using Model Trained and Tested on Monte Carlo Mammograms

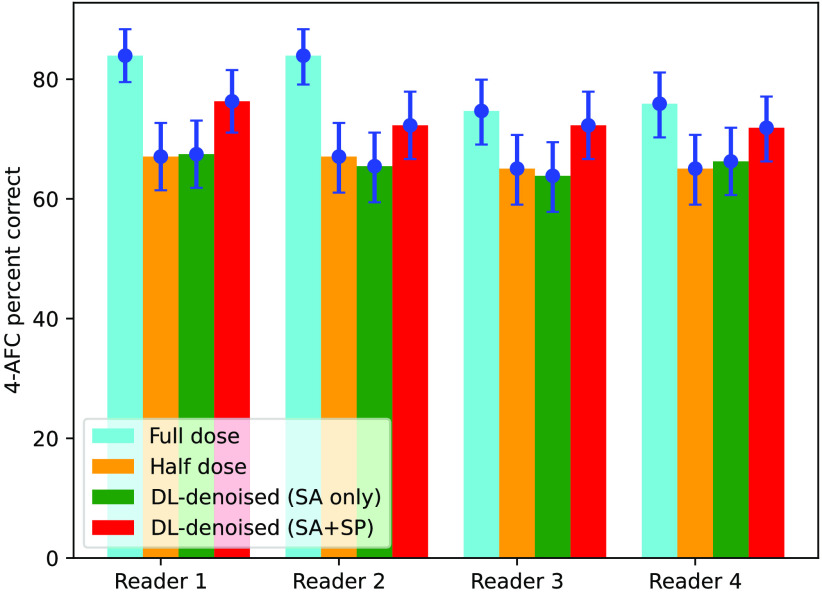
Human observer results for the study using Monte Carlo generated mammograms processed with the denoising algorithm that used the $\mathrm{PS}+\mathrm{PL}4$ loss function trained using only SA ROIs, as well as trained using both signal-absent and signal-present ($\mathrm{SA}+\mathrm{SP}$) ROIsare summarized in Fig. 5.

Fig. 5.

4-AFC human reader study with digital breast phantom MC-GPU mammograms.

Two interesting observations can be made from these data. First, there was no significant difference in detection performance observed between reading half-dose images and half-dose images processed with DL-denoising, when the model was trained using only SA data. This repeats our finding in the experiment with physical phantom. Second, when low-dose images are restored with the model trained on a combined $\mathrm{SA}+\mathrm{SP}$ set, it is observed (red color bars) that the 4-AFC PC score increased for all readers compared to PC obtained with the original low-dose images. $P$-value calculation shows that the likelihood of this improvement being a random chance is rather small ($\lesssim 5\%$ for 3 out of 4 readers, 10% for the remaining reader), e.g., denoising in this case provided statistically significant gain in readers performance. Although the processing algorithm did not produce images in which humans would achieve detection scores obtained with full-dose mammograms, the improving effect is nonnegligible and noteworthy. Human observer performance for simulated mammograms is detailed in Table 3

Table 3.

Results of the 4-AFC human observer experiment with Monte Carlo mammograms of digital breast phantoms.

Reader #	1	2	3	4
${\mathrm{PC}}_{\mathrm{fulldose}}$ a	83.94 [79.52, 88.35]	83.94 [79.12, 88.35]	74.70 [69.08, 79.92]	75.90 [70.28, 81.12]
${\mathrm{PC}}_{\text{halfdose}}$	67.07 [61.45, 72.69]	67.07 [61.04, 72.69]	65.06 [59.04, 70.68]	65.06 [59.04, 70.69]
${\mathrm{PC}}_{\text{restored}}^{\mathrm{SAonly}}$	67.47 [61.85, 73.09]	65.46 [59.44, 71.08]	63.86 [57.83, 69.48]	66.27 [60.64, 71.89]
${\mathrm{PC}}_{\text{restored}}^{\mathrm{SA}+\mathrm{SP}}$	76.31 [71.08, 81.53]	72.29 [66.67, 77.91]	72.29 [66.67, 77.91]	71.89 [66.27, 77.11]
$\mathrm{\Delta }\mathrm{PC}$ (%)b	13.78	7.78	11.11	10.50
$p$-valuec	0.011	0.103	0.041	0.051

^aPC values and their 95% confidence intervals.

^bPC increase from ${\mathrm{PC}}_{\text{halfdose}}$ to ${\mathrm{PC}}_{\text{restored}}^{\mathrm{SA}+\mathrm{SP}}$.

^cProbability that there is no difference between ${\mathrm{PC}}_{\text{halfdose}}$ and ${\mathrm{PC}}_{\text{restored}}^{\mathrm{SA}+\mathrm{SP}}$.

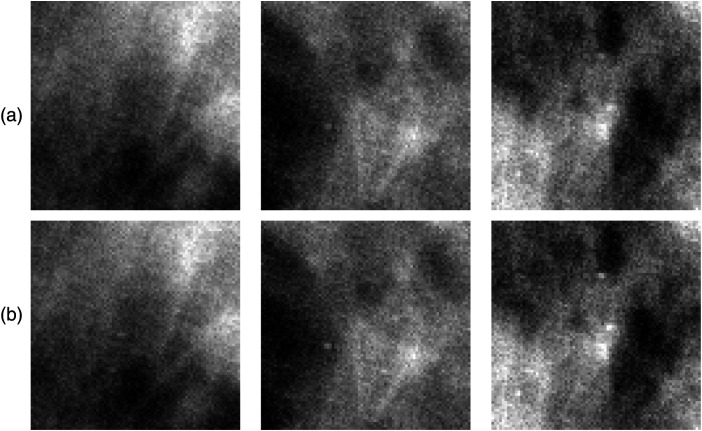
It is instructive to look at a few ROIs from restored mammograms, processed by the denoiser model trained with background images only versus processed by the model trained with both signal and background images (Fig. 6). Subjective visual inspection reveals very subtle differences in the way microcalcifications are rendered with one observation: crops from mammograms denoised using $\mathrm{SA}+\mathrm{SP}$ model exhibit slightly better signal contrast and definition, likely sufficient to make a difference in the PC score. This appears feasible, keeping in mind that in a 4-AFC trial there are three SA ROIs (possibly containing false-positive noise spikes), the reader has to analyze along with an SP ROI.

Fig. 6.

(a) Three SP crops from half-dose restored mammogram using denoiser model trained on SA only data. (b) Same crops using denoiser model trained on $\mathrm{SA}+\mathrm{SP}$ data. Same window level/window width is used in paired ROIs.

4. Discussion

Denoising algorithms that use convolutional neural networks have been previously developed for reducing noise in DM and DBT images. Noise reduction in screening mammography could potentially be used to reduce radiation dose or to improve image quality. Radiation dose in mammography is currently low, and further dose reduction might not be needed. Nevertheless, it is important from a regulatory aspect to understand how dose reduction combined with deep-learning denoising algorithms might affect the accuracy of microcalcification detection. That is the focus of this study; further studies will investigate whether image quality (without dose reduction) can be improved with denoising algorithms. There have been previous reports that suggested DL denoising networks have promise for potentially reducing the dose to the breast; however, the proper training and accurate evaluation of such algorithms is challenging. A recent study by Shan et al. discussed an analysis of seven trained denoising networks with different loss functions that were applied to phantom acquisitions acquired at full-dose and half-dose using a Hologic Selenia Dimensions DM system. The testing phantom consisted of slabs of breast equivalent material with calcium oxalate specks placed between the slabs to emulate microcalcifications. The denoised phantom images were analyzed using a number of figures-of-merit, including visual analysis, SNR, and normalized mean-square-error (NMSE). Using these metrics, it was concluded that one particular [perceptual] loss function (PL4) was optimal and was able to achieve virtually the same noise levels for half-dose and full-dose DM acquisitions. The objective assessment of image quality with DM is nontrivial because mammography requires good fidelity of both low-frequency structures, such as extended mass lesions, as well as of high-frequency objects, such as microcalcifications. Having said that, it is also a common wisdom that conspicuity of small, speck-like particles is more susceptible to quantum noise (e.g., reduce x-ray dose) than larger round lesions. We believe that denoising algorithms should be evaluated using task-based performance, such as the accuracy in detecting microcalcifications. Metrics, such as normalized-mean-squared error, provide a global measure of noise reduction, however, they do not necessarily assess the diagnostic tasks of interests, such as detection of smaller, high-frequency microcalcification clusters.

In this study, we describe two possible approaches for assessing deep-learning denoising algorithms applied to mammography. One approach uses in silico methods involving Monte Carlo simulation of a large cohort of anthropomorphic breast phantoms embedded with microcalcification clusters, and the other approach uses a previously published anthropomorphic physical phantom embedded with calcium hydroxyapatite microcalcification clusters. In both cases, acquisitions at both full-dose and half-dose settings are generated and DL denoising is applied to the half-dose images. Human observer performance was then evaluated using 4-AFC studies.

For the physical phantom study, the (existing) DL-denoising network was trained using 400 clinical mammograms acquired on a Hologic Selenia Dimensions. To avoid giving these patients extra radiation dose, half-dose images were computed by injecting quantum and electronic noise into the dataset. Although procedures for adding noise to mammography images have been reported on in the literature,^24–27 these approaches involve approximations, and the effect of these approximations on the training of the network is not fully understood. Thus from these 400 clinical mammograms, 256,000 patches were obtained for training the DL denoising network. It was not stated how many of these 256,000 patches contained microcalcification clusters, however, given the relative rarity of microcalcifications in clinical data, it is likely that only a very small proportion of training data contained microcalcification clusters. This pretrained DL denoising network was then applied to the half-dose images of our physical anthropomorphic breast phantom with embedded microcalcifications acquired on our Hologic Selenia Dimensions DM system. As observed in Fig. 3, there was no significant difference in observer performance between the restored half-dose images and the nonrestored half-dose images. Although the restored half-dose images looked visually appealing with reduced noise and showed better MSE and SSIM values, microcalcification detection accuracy did not improve, and the performance of the full-dose images were significantly better than the processed half-dose images.

For the in silico study reported here, the DL denoising network was trained with 248,000 Monte Carlo simulated full-dose and half-dose ROI pairs. In one case, the network was trained with only SA ROI images (SA only), and in another case, the network was trained with half SA and half SP ROI images ($\mathrm{SA}+\mathrm{SP}$). The results in Fig. 5 showed that performance obtained when denoising the half-dose images using the network trained with SA only was not significantly different than half-dose images without processing with DL denoising. Thus similar to the results from the physical phantom study, the DL denoiser produces images that visually appear to have less noise but does not improve microcalcification detection performance. However, when the DL denoiser was trained with $\mathrm{SA}+\mathrm{SP}$ images, microcalcification detection accuracy improved somewhat over the unprocessed half-dose images. From these data, one can infer that DL denoising networks can learn that microcalcifications are important diagnostic features in the image and that visualization should not be penalized by the noise reduction process. It should be pointed out that enriching the training dataset with more microcalcification clusters is straightforward when the training data are simulated; however, this would be more challenging if clinical patient data were used for training the denoising network. One practical approach that was not considered here would be to augment patient training data with simulated full-dose and half-dose images of microcalcification clusters.

It should be emphasized that the microcalcifications modeled in this report were purposely small in size, ranging from 150 to $180\mu \mathrm{m}$ for the physical phantom study and from 100 to $240\mu \mathrm{m}$ for the in silico study. In addition, the clusters modeled herein contained approximately five microcalcifications, whereas clusters found clinically contain $\sim 5$ to 15 or more microcalcifications on average. Because of these modeling choices, this study focused on studying the detection of more challenging clinical microcalcification cases. For bigger microcalcifications, there might be different trade-offs associated with use of DL denoising networks.

5. Conclusions

In this work, we investigated an advanced deep-learning based algorithm (actually two algorithms, with one being an improved version of the original) for image denoising in low-dose mammography, using human reader studies. In the first part, we applied an existing denoiser model trained on clinical images to mammograms of a physical phantom, whereas in the second part, we trained and tested the denoiser model (using developer’s code) using all synthetic data from Monte Carlo simulated mammography system. In this second set of experiments, the DL model used a combined loss function, that in a addition to a PL term had another term enforcing preservation of the breast background power spectrum between the original full-dose image and the restored one. In both studies, the detection task was finding (present or not present) clusters of small microcalcifications in ROI images by means of 4-AFC observer studies.

Our preliminary results suggest that for these challenging tasks deep-learning denoising software was not helpful in assisting humans readers, if it was trained using either clinical exam data (perhaps with some, but not many, images of microcalcifications present in a training set) or using modeled data without SP samples in a training dataset. However, when the training set was compiled using half data containing microcalcifications, i.e., 124k out of 248k ROIs were SP, we saw noticeable improvements in PC scores among all four human observers. Although “full” image restoration (when PC obtained on restored mammograms would have matched PC obtained on full-dose mammograms) was not achieved, the improvement effect is real, and we can conclude that enriching training data with ROIs containing microcalcifications may be worth of further investigation.

Biography

Biographies of the authors are not available.

Disclosures

The authors have no relevant conflicts of interest to disclose. The mention of commercial products herein is not to be construed as either an actual or implied endorsement of such products by the Department of Health and Human Services.