Active learning-based multistage sequential decision-making model with application on common bile duct stone evaluation

Abstract

Multistage sequential decision-making occurs in many real-world applications such as healthcare diagnosis and treatment. One concrete example is when the doctors need to decide to collect which kind of information from subjects so as to make the good medical decision cost-effectively. In this paper, an active learning-based method is developed to model the doctors' decision-making process that actively collects necessary information from each subject in a sequential manner. The effectiveness of the proposed model, especially its two-stage version, is validated on both simulation studies and a case study of common bile duct stone evaluation for pediatric patients.

1. Introduction

The multistage sequential decision-making occurs in many real-world applications when one wants to make accurate, efficient, and cost-effective decisions. For instance, it has been applied for addressing the trade-off between audit costs and expected overpayment recovery [8], or optimal investments in multiple projects based on experts' evaluations [10,11,19,23,25], etc. In recent years, active learning can be integrated with multistage sequential decision-making model [9,16,24]. Active learning is a special case of machine learning in which a learning algorithm can interactively query a user or some other information source to label new data points with the desired outputs [22].

In this paper, motivated by the need to assist the doctors to make reliable diagnostic decisions and treatment recommendations in a cost-effective and convenient manner, we propose to develop an active learning-based multistage sequential decision-making model. Our specific motivating example is as follows. Gallstone are solid particles that can form from cholesterol, bilirubin, and other substances within the gallbladder. These densities are often benign when localized to the gallbladder, but can cause pain, infection, and liver damage when they become stuck in the common bile duct (CBD) and impede the flow of bile into the digestive tract. A stone that becomes impacted in the CBD can be difficult to detect definitively, but its presence requires a procedural intervention, either intraoperative cholangiogram (IOC) or endoscopic retrograde cholangiopancreatography (ERCP). In particular, IOC is a safer but less efficient procedure to clean the stone. Meanwhile, the ERCP procedure is more efficient but carries the risk of complications, as it requires anesthesia and might lead to pancreatitis, infection, and bleeding. As a result, it is imperative to ensure that the ERCP procedure is only performed when there is a stone definitively obstructing the duct. This is particularly true in children [7]. Thus, it is important is to definitively predict the presence of a CBD stone in a child with high accuracy and specificity.

From the machine learning or statistical viewpoint, this seems to straightforward: one would use the historical or training data to determine those informative features that yield to high modeling accuracy and robust performance, and then recommend to collect as many informative features as possible from each subject. Unfortunately, from the clinical or medical viewpoint, this is an open problem, as it is often more time-consuming and more expensive to collect those more informative features, which might not be available when the doctors need to make a timely decision. For instance, in our real data set of the CBD stone evaluation application, from the machine learning or statistical viewpoint, the computed tomography (CT) scan would provide the most accurate prediction in the sense of being consistent with the outcome of the procedures IOC or ERCP. However, the majority (around 95%) of pediatric patients in our real data sets did not take the CT scan, partly due to the long waiting time and high cost, and partly due to the radiation-induced cancer risk of CT scan. Indeed, it is gradually noted [13] that children who have a CT scan are slightly more likely to develop cancer later in life. Also when a CT scan detects the presence of a CBD stone, one still needs the intervention procedure such as IOC or ERCP to remove the stone. Thus based on the current technology and medical understanding, the CT scan might not be a good approach for the prediction of a CBD stone from the clinical or medical viewpoint.

Indeed, as compared to many standard machine learning and statistical applications on computer sciences or engineering, the data sets on the CBD stone and many other biomedical applications are actually from active learning. To be more concrete, the medical doctors would follow their expertise and intuition to start those simpler and cheaper laboratory tests, and then ordered to collect more informative and more expensive features if needed. In other words, different subjects will have different explanatory variables, and we essentially deal with incomplete data. In the literature, the are many widely-used methods dealing with incomplete data, such as simple deletion on feature or record, mean/median/mode/zeros substitution, regression imputation, last observation carried forward, Expectation-Maximization (EM) algorithm, etc. [14,17]. However, these existing methods were developed often under the crucial assumption of missing-at-random. In our context, features or explanatory variables are not missing at random, as they are due to the doctors' decision.

Our proposed multistage sequential decision-making model aims to provide a new way to handle missing-not-at-random data, and provide a rigorous machine learning and statistical foundation to understand and support the medical doctors' decision. In this model, some patients are allowed to take fewer examinations if their symptoms are apparent according to early-stage features, whereas other patients will have a more comprehensive laboratory or imagining evaluation. This novel platform allows the healthcare provider to actively and sequentially collect only the necessary data rather than collecting all the comprehensive information for all patients. As a result, the diagnostic and treatment decision process will be faster, more convenient, and more cost effective at the population level, while retaining significant accuracy at the individual level.

The rationale of our proposed multistage sequential decision-making model is similar to those of classical sequential hypothesis testing and group sequential clinical trials, in which we will continue to collect more information unless we accumulate enough evidence to make a decision for each subject. A key technical idea is to model the doctor's decision process on each subject via an underlying continuous latent variable, and whether to collect new features correspond to whether this underlying latent variable crosses certain stopping boundaries or not. Statistically speaking, this leads to ordinal logistic regression models, or proportional odds model [15,18,26]. It allows us to classify a subject into one of three classifiers in a given stage: healthy or mild (‘0’), indeterminate (‘0.5’), and disease or severe (‘1’). For those subjects in the healthy/mild (‘0’) or disease/severe (‘1’) class, there are no need to collect more features in the next stages, as we are confident about the subject's status or treatment decision. For instance, for the CBD stone patients, we would recommend the IOC procedure for the ‘0’ class, and the ERCP procedure for the ‘1’ class. Meanwhile, for those subjects in the indeterminate (‘0.5’) class, we will need to collect more features in the next stages until we can reach a medical decision.

The contribution of our work is twofold. In terms of statistical analysis, a multistage decision-making model is proposed to fit an active learning data set that involves with missing-not-at-random data. In terms of healthcare applications, our model is useful for guiding the diagnostics and treatment of future patients by interactively querying a patient to collect additional clinical data when needed [20]. This will help the doctor making rapid efficient diagnostic decisions and treatment recommendations, especially when some features or laboratory results are more expensive, invasive, or time-consuming to collect than others. By recommending requisite testing to those patients in whom symptoms do not support a definitive medical decision, the proposed process is cost-effective and reliable at the population level. Also, the methodology and ideas are applicable to many other real-world applications beyond biomedical sciences in which one is allowed to actively and sequentially select a subset of explanatory variables for each subject/sample/product among a large number of explanatory variables when making decisions.

In Section 2, the proposed model is described. Section 3 discusses the novel approach to parameter estimation for the proposed model. In Section 4, the performance of the proposed methodology on synthetic data is reported. Finally, in Section 5, the analytical result on real clinical data is demonstrated.

2. Our proposed multistage sequential decision-making model

In this section, we present our proposed active learning-based multistage sequential decision-making model. For better understanding, we split into three subsections. The high-level general framework of our proposed model is demonstrated in Subsection 2.1, and the data presentation and organization is presented in Subsection 2.2. In Subsection 2.3, the mathematical details are presented based on the existing ordinal logistic regression model.

2.1. General framework

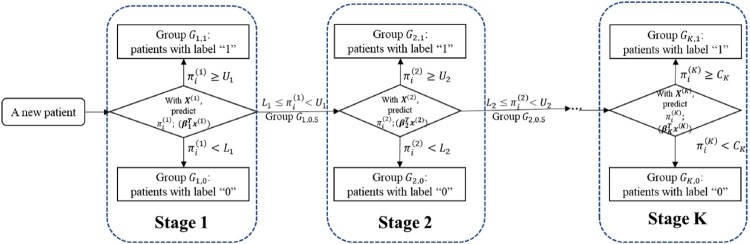
The proposed multistage sequential decision-making model is shown in Figure 1. At the high-level, the features of a subject's clinical data are classified into several different stages according to the relevant cost, invasiveness, time, subject's willingness to participate, etc. The earlier stages should involve those features that are patient-friendly, inexpensive, though potentially less informative. The latter stages could include those features that are more time-consuming, expensive, unpleasant, but potentially provide more information about the medical conditions of the subject. In this paper, we assume that the medical doctors will decide the number of stages and which features can be included in each stage based on their expertise.

Figure 1.

The framework of the proposed multistage sequential decision-making model, where K is the number of stages, ${\pi }_i^{(j)}$ is the probability of patient i having disease estimated in stage j, $U_j$ and $L_j$ is the cutoff points on the estimated probability in stage j, and $C_K$ is the single cutoff point in the last stage, K.

To be more concrete, assume there are K stages in the decision making. For each intermediate stage, it involves two cutoff values, $(L_k,U_k)$ for $k=1,\dots ,K-1$, whereas the final stage includes a single cutoff value $C_K$. At k-th stage, based on the cumulative observed features or data, an ordinal logistic regression model, which will be discussed in more details in Subsection 2.3, is applied as the classifier to estimate the probability of having disease for each subject. Denote such probability by ${\pi }_i^{(k)}$ for the i-th subject at the k-th stage. At each intermediate stage, and there are three possible outcomes for the i-th subject:

• If ${\pi }_i^{(k)}<L_k$, the subject will be labeled as healthy/mild (‘0’) and might undergo those less efficient but safer procedure such as IOC;

• If ${\pi }_i^{(1)}\ge U_k$, the subject will be labeled as disease/severe (‘1’), and might be proceeded for the risky but more efficient intervention such as ERCP;

• If ${\pi }_i^{(1)}\in [L_k,U_k)$, the subject will be labeled as indeterminate (‘0.5’) and be moved to the next stage to collect more features for better diagnostics.

Meanwhile, for the final K-th stage, there is a single cutoff value $C_K$, and it can be thought of as the special case of the intermediate stage with $L_K=U_K=C_K.$

In this paper, we first use the training data to estimate the parameters in our framework including the ordinal logistic model and the cutoff values, which will be discussed in Section 3. Next, when applying to a new subject in the testing data, we will arrive at a diagnosis and recommend treatments accordingly. In such a way, the necessary features will be collected sequentially and actively.

2.2. Data organization

In this subsection, let us present the data format and organization. As discussed earlier, the features are first divided into several categories, each corresponds to a certain stage in our multistage model based on the domain knowledge of the doctors. The criteria for feature grouping are flexible and can be adjusted according to real scenarios case-by-case: (1) For the features inside a category, the cost of collection and the information contained therein should be similar. For example, these features in a given category can be obtained simultaneously from one examination such as a blood test. (2) Each category should contain some useful information, and excess categories should be avoided. For example, there is no need to split each variable into one category, especially less informative variables, such as gender, age, and race.

To illustrate the data structure or organization for the proposed model, without loss of generality, we can take the training data as an example, and assume that it has the following structure:

• Stage 1: $$\begin{gathered} \{y_i^{(1)};x_{i,1}^{(1)},x_{i,2}^{(1)},\dots ,x_{i,p_1}^{(1)}\}=\{{\mathit{y}}^{(1)};{\mathit{X}}^{(1)}\},i=1,2,\dots ,N_1, \\ {y}_i^{(1)}\in \{‘0^{\prime },‘{0.5}^{\prime },‘1^{\prime }\}; \end{gathered}$$

• ··· 

• Stage k: $\{y_i^{(k)};x_{i,1}^{(1)},x_{i,2}^{(1)},\dots ,x_{i,p_1}^{(1)};\cdots ;x_{i,1}^{(k)},x_{i,2}^{(k)},\dots ,x_{i,p_k}^{(k)}\}=\{{\mathit{y}}^{(k)};{\mathit{X}}^{(k)}\},i=1,2,\dots ,N_k,y_i^{(k)}\in \{‘0^{\prime },‘{0.5}^{\prime },‘1^{\prime }\};$

• ··· 

• Stage K: $\{y_i^{(K)};x_{i,1}^{(1)},x_{i,2}^{(1)},\dots ,x_{i,p_1}^{(1)};\cdots ;x_{i,1}^{(K)},x_{i,2}^{(K)},\dots ,x_{i,p_K}^{(K)}\}=\{{\mathit{y}}^{(K)};{\mathit{X}}^{(K)}\},i=1,2,\dots ,N_K,y_i^{(K)}\in \{‘0^{\prime },‘1^{\prime }\}.$

Here the subscript i denotes the i-th subject in the training data, and the superscript (k) denotes the k-th stage. In addition, the parameter $p_k$ denotes the number of features collected in the k-th stage, and $N_k$ is the number of subjects who stops taking observations at the k-th stage in the training data. In other words, each subject's data are recorded in one and only one stage under our notation of data organization. Thus the total number of subjects in the training data is $N_1+\cdots +N_K,$ whereas the number of features or explanatory variables for a subject is adaptive, ranging from as few as $p_1$ to as large as $p_1+p_2+\cdots +p_K.$

2.3. Ordinal logistic regression model

In this subsection, we explicitly discuss the ordinal logistic regression model, which is the building block of the classifier in each stage in our proposed multistage model. There are many ways to present the ordinal logistic regression model. Here we choose one presentation that allows us to model the doctor's decision process as an underlying (continuous) latent variable $Y^{\ast }$ to summarize the cumulative information as a subject collects more features or data.

Let us begin with the (continuous) latent variable $Y^{\ast }$ over different stages. For the i-th subject in the training data, we model the cumulative information at the first stage as

$$Y_i^{\ast (1)}={\beta }_1^{(1)}{x}_{i,1}^{(1)}+\cdots +{\beta }_{p1}^{(1)}{x}_{i,p_1}^{(1)}.$$ (1)

Here we simplify the notation to omit the intercept coefficient, but the intercept can be included in the model in (1) by defining a constant explanatory variable $x_{i,1}^{(1)}\equiv 1$ for all subjects if we want.

When the i-th subject is assigned to collect more features in the second stage, we model the cumulative information at the end of the second stage as

$$Y_i^{\ast (2)}=Y_i^{\ast (1)}+{\beta }_1^{(2)}{x}_{i,1}^{(2)}+\cdots +{\beta }_{p_2}^{(2)}{x}_{i,p_2}^{(2)}.$$ (2)

In other words, the cumulative information at the second stage is based on those information from the first stage and the new information collected at the second stage. Likewise, for $k=1,2,\dots ,K$, the cumulative information at the k-th stage is recursively modeled as

$$Y_i^{\ast (k)}=Y_i^{\ast (k-1)}+{\beta }_1^{(k)}{x}_{i,1}^{(k)}+\cdots +{\beta }_{p_k}^{(k)}{x}_{i,p_k}^{(k)}.$$ (3)

Note that under (1)–(3), the latent variable $Y^{\ast }$ summarizes the cumulative information. Thus while different features will likely have different β values, the β value of a given feature is assumed to stay the same across different stages.

Next, we model the decision-making whether or not to collect new features at a given stage based on whether the randomized version of the corresponding underlying latent variables $Y^{\ast }$ cross certain cutoff values or not. To be more specific, at the end of the k-th stage for $k=1,\dots ,K-1,$ the i-th subject is classified as

$$Y_i^{(k)}=\{\begin{array}{ll}0,& \mathrm{if}{Y}_i^{(k)\ast }+{ϵ}_i^{(k)}<L_k^{\ast }\\ 0.5,& \mathrm{if}{L}_k^{\ast }\le Y_i^{(k)\ast }+{ϵ}_i^{(k)}<U_k^{\ast }\\ 1,& \mathrm{if}{Y}_i^{(k)\ast }+{ϵ}_i^{(k)}\ge U_k^{\ast }\end{array}$$ (4)

for some cutoff values $L_k^{\ast }$ and $U_k^{\ast }.$ For those subjects who have taken observations at the final K-th stage, they face a binary decision:

$$Y_i^{(K)}=\{\begin{array}{ll}0,& \mathrm{if}{Y}_i^{(K)\ast }+{ϵ}_i^{(K)}<C_K^{\ast }\\ 1,& \mathrm{if}{Y}_i^{(K)\ast }+{ϵ}_i^{(K)}\ge C_K^{\ast }\end{array}$$ (5)

for a single cutoff value $C_K^{\ast }.$

It is useful to add a couple of comments on the proposed classifiers in (4) and (5). First, the noises ${ϵ}_i^{(k)}$'s are assumed to be i.i.d. with a common cumulative distribution function (cdf) F. There are many possible choices for the cdf F of the noises such as logistic, probit, complementary log-log, and Cauchy. In this paper, we consider the logistic distribution with

$$F(t)=\frac{1}{1+e^{-t}}\text{ for }-\mathrm{\infty }<t<\mathrm{\infty }.$$ (6)

As a result, the classifier (4) is equivalent to the ordinal logistic regression model, and (5) is equivalent to the standard binary logistic regression model.

Second, the cutoff points $\{L_k^{\ast },U_k^{\ast },C_K^{\ast }\}$ applying on the latent variable $Y^{\ast }$ are different from $\{L_k,U_k,C_K\}$ applying on the probability estimation ${\pi }_i^{(k)}$ in the Figure 1. Instead, the former set needs to go through a logit transformation to get the latter as

$$Y_i^{\ast (k)}=\log \frac{{\pi }_i^{(k)}}{1-{\pi }_i^{(k)}}.$$

For simplicity, below we focus on the cutoff points $\{L_k^{\ast },U_k^{\ast },C_K^{\ast }\}$ in (4) and (5) for parameter estimation and model prediction.

3. Model parameter estimation

In this section, we discuss the parameter estimation of our multi-stage sequential decision-making model in (1) – (5) based on the training data in Subsection 2.2.

On the one hand, we face an ordinal logistic regression model in each intermediate stage and a standard binary logistic regression model in the final stage. A naive baseline approach is then to estimate the parameters in different stages separately by assuming the model parameters ${\mathit{\beta }}_i^{(k)}$'s are independent without considering the nested structure and potential correlations between the two adjacent stages. That is, conduct the ordinal logistic regression model for each stage independently with existing software packages. This naive baseline approach can be used to fit our training data, but it will lead to a non-smooth decision process across different stages, which might or might not be reasonable depending on applications and contexts.

On the other hand, under our proposed model in (1)–(5), the decision-making at a stage is based on the cumulative available features or data from all previous stages, and thus the model coefficients share consistent common parts. For instance, in the two-stage model, the feature data of the i-th subject in the second stage contains the feature in the first stage, e.g.:

$${\mathit{x}}_i^{(2)}=\{x_{i,1}^{(1)},x_{i,2}^{(1)},\dots ,x_{i,p_1}^{(1)};x_{i,1}^{(2)},x_{i,2}^{(2)},\dots ,x_{i,p_2}^{(2)}\}=\{{\mathit{x}}_i^{(1)};x_{i,1}^{(2)},x_{i,2}^{(2)},\dots ,x_{i,p_2}^{(2)}\}$$

and the coefficient ${\mathit{\beta }}^{(1)}$ at the first stage is part of ${\mathit{\beta }}^{(2)}$ at the second stage:

$${\mathit{\beta }}^{(2)}=\{{\beta }_1^{(1)},{\beta }_2^{(1)},\dots ,{\beta }_{p_1}^{(1)};{\beta }_1^{(2)},{\beta }_2^{(2)},\dots ,{\beta }_{p_2}^{(2)}\}=\{{\mathit{\beta }}^{(1)};{\beta }_1^{(2)},{\beta }_2^{(2)},\dots ,{\beta }_{p_2}^{(2)}\}$$

The corresponding medical meaning is that the doctor's decision process is cumulative, and the newly added features will not dramatically change the previous decision in the sense of not affecting the weights of existing ones. This makes the model more interpretable for doctors and patients.

It is useful to mention the number of parameters of our proposed model in (1)–(5) under the general setting of the K-stage model. At the k-th stage, the number of ${\mathit{\beta }}^{(k)}$ coefficients is $p_1+p_2+\dots +p_k$ if we assume that the intercept is part of $p_1$ parameters at the first stage, and the number of the cutoff value parameters are 2 at the k-th intermediate stage (and 1 at the final stage). In particular, under this new notation, for the i-th subject who stops at the k-th stage, the cumulative latent information in (3) at the previous r-stage can be re-written as

$$Y_i^{\ast (r)}={\mathit{\beta }}^{(r)\mathrm{\top }}{\mathit{x}}_i^{(r)}$$

for $r=1,\dots ,k.$ Had we followed the baseline to estimate each stage separately, the total number of parameters one would need to estimate is $\sum _{k=1}^K(p_1+p_2+\dots +p_k)+2K-1.$ Meanwhile, under the common coefficients assumption, the total number of the $\mathit{\beta }$ parameters to be estimated is only $p_1+p_2+\dots +p_K$, and the total number of cutoff value parameters is 2K−1, which significantly simplify the model complexity. Moreover, for a given training data set, the common coefficients assumption will lead to a more efficient parameter estimation in the sense of reduction the variance of parameter estimation, as it allows us to use all observations when estimating parameters.

Below we propose to use the maximum likelihood method to estimate the parameters in our proposed multistage model. Note that subjects are independent, and each subject will be made a final medical decision in one and only one stage. For the given i-th subject who makes a final decision at the k-th stage, note that it must be classified as ‘0.5’ in all previous r-th stage for $r=1,\dots ,k-1$ $(k>1)$. Note that when k = 1, there will be no previous stages and thus no requirements on results from the previous stage. To be more specific, when k>1, for a given y = 0 or 1,

$$\begin{array}{rl}P(Y_i^{(k)}=y)& =P(Y_i^{(k)}=y\text{ and }{Y}_i^{(r)}=0.5\text{ for all}r=1,\dots ,k-1)\\ & =P(Y_i^{(k)}=y|Y_i^{(1)}=\cdots Y_i^{(k-1)}=0.5)\\ & \times \prod _{r=1}^{k-1}P(Y_i^{(r)}=0.5|Y_i^{(1)}=\cdots Y_i^{(r-1)}=0.5)\end{array}$$

The good news is that while the cumulative (latent) information at the k-stage $Y_i^{\ast (r)}={\mathit{\beta }}^{(r)\mathrm{\top }}{\mathit{x}}_i^{(r)}$ is dependent between different r stages, the noises ${ϵ}_i^{(r)}$'s are independent across different r stages under our model assumption. This greatly simplify the computation of the likelihood function. Hence, for the general K-stage model, the joint log-likelihood function for all data is:

$$\begin{array}{rl}\log \mathcal{L}(\mathit{\beta },\mathit{L},\mathit{U})& =\sum _{k=1}^K\sum _{i=1}^{N_k}\{I(Y_i^{(k)}=0)\log F(L_k^{\ast }-{\mathit{\beta }}^{(k)\mathrm{\top }}{\mathit{x}}_i^{(k)})\\ & +I(Y_i^{(k)}=1)\log [1-F(U_k^{\ast }-{\mathit{\beta }}^{(k)\mathrm{\top }}{\mathit{x}}_i^{(k)})]\\ & +\sum _{r=1}^{k-1}I(Y_i^{(r)}=0.5)\log [F(U_r^{\ast }-{\mathit{\beta }}^{(r)\mathrm{\top }}{\mathit{x}}_i^{(r)})-F(L_r^{\ast }-{\mathit{\beta }}^{(r)\mathrm{\top }}{\mathit{x}}_i^{(r)})]\}\end{array}$$ (7)

where $L_K^{\ast }=U_K^{\ast }=C_K^{\ast }$ for the final K-th stage due to the single cutoff value.

Next, let us discuss the optimization algorithm to solve (7). When there is only one stage, i.e. when $K=1,$ McCullagh [1,18] presented a Fisher scoring algorithm to solve (7), and showed that a sufficiently large sample size guarantees a unique maximum of the likelihood function. Burridge and Pratt [1] showed that iterative algorithms usually converge rapidly to an estimator that has nice asymptotic properties. These properties allow one to develop efficient iteratively reweighted least squares (IRLS) algorithms to compute the MLEs. Indeed, there exist many well-developed software packages for fitting the ordinal logistic regression model [6], e.g. polr from MASS [21], the VGAM package [27], orm functions from the rms package [12] and brms package [5].

When estimating parameters from the joint-optimization problem in (7), we propose to adopt the IRLS algorithm that iteratively estimates the coefficients $\mathit{\beta }$ and the cutoff values $(\mathit{L},\mathit{U}),$ see the appendix for the technical details on the two-stage model. Numerically, we follow the framework of the existing $polr()$ function in the package MASS in R software, and adopt the $optim()$ function as an optimization solver. Recall that the $optim()$ is a function designed for general-purpose optimization based on Nelder–Mead, quasi-Newton and conjugate-gradient algorithms. In our numerical studies, when implementing the $optim()$ function in R, the Broyden–Fletcher–Goldfarb–Shanno algorithm (BFGS) method is chosen for optimization. This is because ‘BFGS’ is an iterative quasi-Newton method for solving unconstrained nonlinear optimization problems [3], and it appears to work best with analytic gradients which are true in our case.

4. Simulation study

In this section, a simulation study is conducted to assess the feasibility and effectiveness of our proposed model and methodology.

To highlight our main ideas, we focus on the two-stage model. First, a two-stage synthetic dataset, $\{(X^{(1)},Y^{(1)});(X^{(2)},Y^{(2)})\},$ is generated with prescribed coefficient ${\mathit{\beta }}^{(1)},{\mathit{\beta }}^{(2)}$ and classification threshold $\{L_1^{\ast },U_1^{\ast },C_2^{\ast }\}$. With the synthetic dataset and model parameters as ground truth, we conduct a baseline approach and the proposed algorithm with common coefficients assumption and estimate the parameters in both stages simultaneously. Finally, we compare the performance of the baseline method and proposed method with respect to prediction performance, stability, model interpretability, and simplicity.

For better presentation, we split this section into two subsections. Subsection 4.1 discusses the generation of synthetic training data, and Subsection 4.2 presents the fitness of the synthetic training data.

4.1. Synthetic data generation

Let us begin with the generation of synthetic data. Let $N_1=10,000$ denote the total number of synthetic subjects in the training data. We design the features of patients as follows: $X_1^{(1)}\sim Bernoulli(0.3)$, $X_2^{(1)}\sim N(-1,1)$, $X_3^{(1)}\sim N(1,1)$, $X_4^{(1)}\sim N(0,2)$, $X_1^{(2)}\sim Bernoulli(0.4)$, $X_2^{(2)}\sim N(-1,1)$, $X_3^{(2)}\sim N(0,1)$. For the first stage, we assume it includes the first 4 features: ${\mathit{X}}^{(1)}=\{X_1^{(1)},X_2^{(1)},X_3^{(1)},X_4^{(1)}\}$. Then, three new features, $\{X_1^{(2)},X_2^{(2)},X_3^{(2)}\}$, are added for the second stage, and thus the cumulative features for the second stage are: ${\mathit{X}}^{(2)}=\{{\mathit{X}}^{(1)};X_1^{(2)},X_2^{(2)},X_3^{(2)}\}=\{X_1^{(1)},X_2^{(1)},X_3^{(1)},X_4^{(1)};X_1^{(2)},X_2^{(2)},X_3^{(2)}\}$.

Next, we generated the continuous latent variable $Y^{\ast }$'s from the model in (1) – (3) without intercepts, and the β coefficients are designed as ${\beta }_1={\beta }_2={\beta }_3={\beta }_4=2$ and ${\beta }_5={\beta }_6={\beta }_7=4.$ The noises ${\mathit{\epsilon }}^{(k)}$'s are generated i.i.d. from the $Logistic(0,1)$ distribution that has location parameter 0 and the scale parameter 1. Note that if the error term $\mathit{\epsilon }$ follows logistic regression with other parameters, the estimation of $\mathit{\beta }$, $\mathit{L}$, and $\mathit{U}$ can be scaled according to the inherent model assumption in the probability formation in (4) and (5).

Finally, the observed response variables Y's in the training data are generated from (4) and (5) based on the continuous latent variable $Y^{\ast }$. The cutoff value parameters in our simulation are chosen as $L_1^{\ast }=-2.2,U_1^{\ast }=2.2$, and $C_2^{\ast }=\mathrm{0.5.}$ Here these cutoff values yield to $U_1=F(2.2)=0.9$ and $L_1=F(-2.2)=0.1$. We feel that 0.9 and 0.1 could be reasonable cutoff points on the probability of having diseases in Figure 1. With these pre-defined classification cutoff values, the latent variables $Y^{(1)\ast }$ can be stratified into 3 and 2 categories at the first and second stages, respectively, the corresponding observed label $Y_i^{(k)}$ can be obtained according to (4) and (5).

In our simulation studies, we adopt the Monte-Carlo method and run the data generation and parameter estimation 100 times, so as to provide reliable statistical inference.

4.2. Performance assessment

In this subsection, we fit our proposed multi-stage sequential decision-making model to the synthetic training data, and compare its performance with other methods.

Our proposed method is to estimate the model parameters via MLE, which is realized by the $optim()$ optimizaion solver in R that solves the optimization problem in (7). Our focus is to evaluate the mean and the standard deviation of the parameter estimation as well as the accuracy and stability of prediction.

For the purpose of comparison, we also consider the baseline approach that treats the data in two stages separately: a standard ordinal logistic regression is applied to data in the first stage via $polr()$ function in the MASS package in R, and a standard logistic regression is applied on data in the second stage via the $glm()$ function in R. Note that these two different R functions, $plor()$ and $glm(),$ are used to handle the ordinal response with three categories and binary responses, respectively.

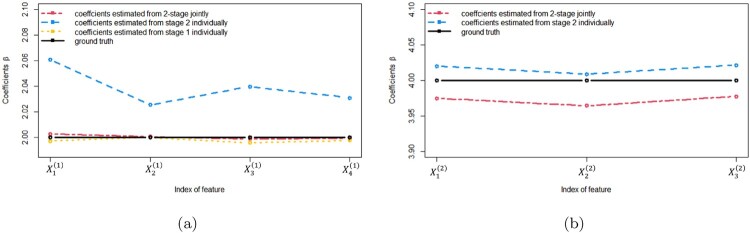
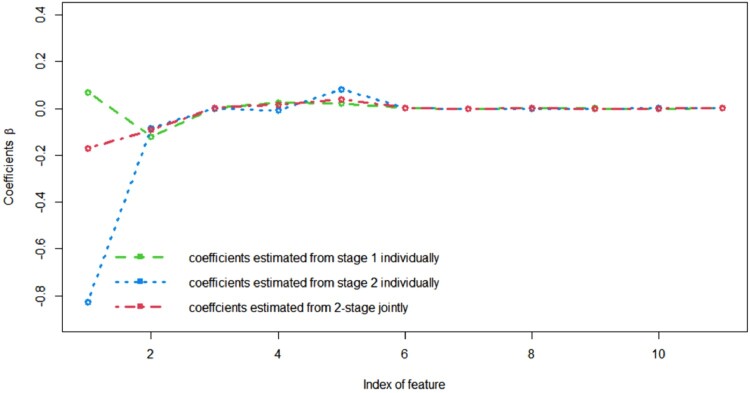
The comparison of the mean coefficients estimated from the two methods is visualized in Figure 2. Clearly, the coefficients estimated from the two methods are similar and both coincide well with ground truth, indicating that both methods have little or no bias when estimating parameters, proving the effectiveness of both methods on estimating. To quantify the subtle difference, we can utilize the (cumulative) mean square error (MSE), $\sum _{\ell =1}^k\sum _{j=1}^{p_{\ell }}({\hat{\beta }}_j^{(\ell )}-{\beta }_j^{(\ell )}{)}^2,$ to measure the distance between the estimated coefficients and the ground truth for all $p_1+\cdots +p_k$ β coefficients at the k-th stage. For the 4 coefficients in stage 1, the MSE of the estimation from the baseline method and the proposed method are $7.62\times {10}^{-6}$ and $2.25\times {10}^{-6}$, respectively. Likewise, in stage 2, the MSEs of all 7 coefficients for the baseline method and the proposed method are 0.0011 and 0.0003, respectively. We also conducted t-tests on the estimations of all 7 coefficients by all 3 models: with critical p-value = 0.01, only the baseline model in stage 2 gives the statistically different mean estimations from the ground truths of feature $\{X_1^{(1)},X_3^{(1)}\}$, although this model seems to have some advantage on feature $X_2^{(2)}$ in Figure 2(b). This indicates the improved estimation properties of the proposed methods on mean coefficients estimation.

Figure 2.

Mean coefficients estimation comparison among ground truth (black line), mean coefficients estimated from baseline approached individually (blue and yellow line), and mean coefficients estimated from proposed method jointly (red line). (a) for 4 β coefficients in stage 1 and (b) for 3 β coefficients in stage 2. This plot demonstrates that both methods have little bias on parameter estimation.

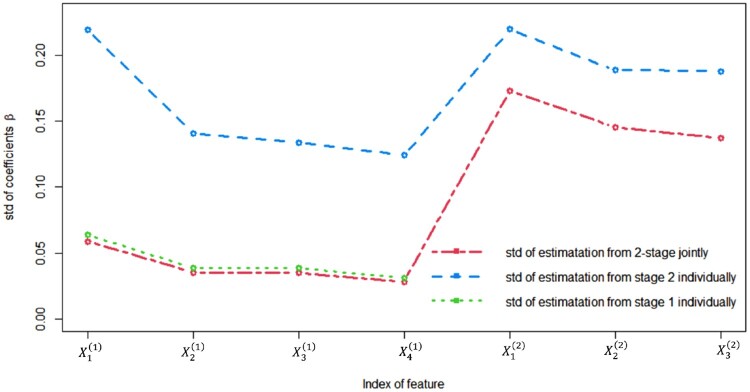
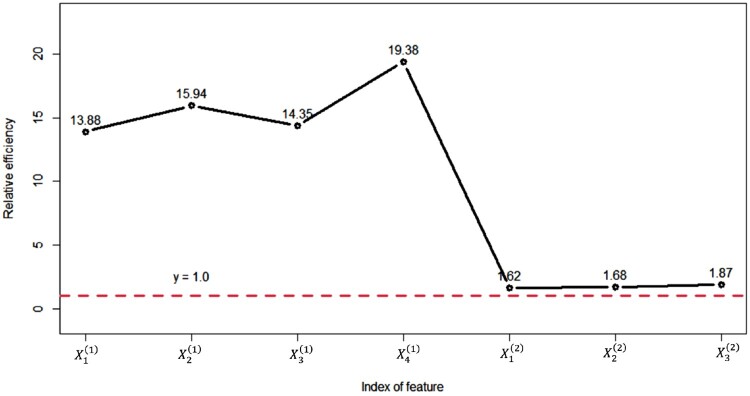
Figure 3 shows the standard deviation (std) of coefficients estimation from the methods. It can be seen that the standard deviation of estimation from the proposed method is significantly smaller than those from baseline methods in both stages. This is an important advantage of the proposed method since it supports the statistical efficiency of the proposed method. To better quantify this advantage for different parameters in different stages, for a given individual parameter ${\beta }_j,$ the relative efficiency of the proposed method with respect to the baseline method is defined as $e(T_1,T_2)=\frac{var(T_2)}{var(T_1)}.$ Such relative efficiency for all seven features are plotted in Figure 4, where $T_1$ and $T_2$ represent the estimates for seven ${\beta }_j$'s in the proposed method and baseline method, respectively. It can be seen that the relative efficiency of the estimates in the first stage is very large, e.g. as high as $\mathrm{19.38.}$ Meanwhile, for the estimate for the β coefficients in the second stage, there are some improvements in statistical efficiency, as the smallest relative efficiency is around 1.62. This implies that the statistical efficiency of the parameter estimation in the proposed methodology is improved as much as $1838\mathrm{\%}$ in the first stage and as much as $62\mathrm{\%}$ in the second stage. The reason behind this improved performance is straightforward: all available data are used by the proposed method in the parameter estimation, whereas only observed data in each stage is used for the parameter estimation in each stage.

Figure 3.

Standard deviation of coefficients estimation from two methods.

Figure 4.

Relative efficiency of the proposed method with respect to the baseline method.

For the estimation of cutoff points, the baseline method and the proposed method give the mean estimations as $\{-2.201,2.192,0.536\}$ and $\{-2.199,2.197,0.506\}$, respectively. And the standard of deviation of the estimations by the baseline and proposed methods are $\{0.061,0.064,0.178\}$ and $\{0.057,0.062,0.119\}$, respectively. Compared with the ground truth, $\{-2.2,2.2,0.5\}$, both methods are functional, yet the proposed approach yields a lower mean deviation and standard deviation.

Hence, from the parameter estimation viewpoint, the proposed 2-stage model provides a more efficient estimation since it involves all data in the parameter estimation. This is because of less number of model parameters and more observations to estimate the model parameters.

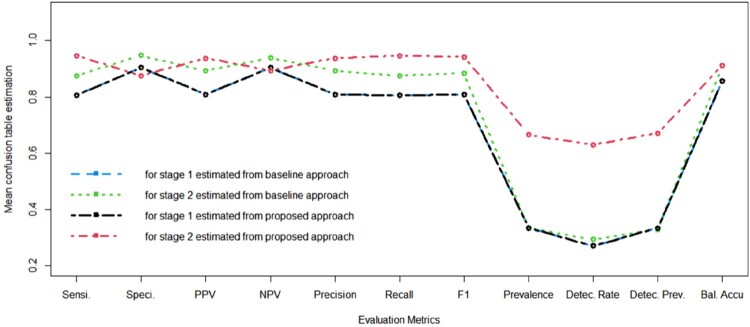
Furthermore, we also apply our proposed method to predict the testing data set, and compare its performance with the baseline method. Figure 5 shows the mean prediction metrics for prediction for two stages with coefficients estimated from the two methods respectively. The evaluation metrics include sensitivity (Sensi.), specificity (Speci.), positive predictive values (PPV), negative predictive values (NPV), and balanced accuracy, precision, recall, F1 value, prevalence, detection rate (Detec. Rate), detection prevalence (Detec. Prev.), and balanced accuracy (Bal. Accu). From the predictive performance comparison in Figure 5, there is no significant difference between the proposed method and baseline method for the first stage prediction, as we can see that the blue and black lines are too close to each other to distinguish them from each other visually. Meanwhile, the proposed method has a significant advantage for the prediction at the second stage with almost higher values in every criterion, especially the prevalence, and detection rate, and detection prevalence.

Figure 5.

Mean prediction metrics for 2 stages with coefficients estimated from baseline approach individually (blue and green line), and coefficients estimated from proposed method jointly (red and black line). Note that the blue and black lines are too close to each other to distinguish them from each other visually. The red line is almost higher than the green line in every dimension, demonstrating the advantages of the proposed method.

5. Case study

In this section, we apply our method to the real clinical data set in [7] on the presence of a CBD stone for pediatric patients mentioned in the introduction.

For this data set, there are 316 pediatric patients who underwent either IOC or ERCP procedure that provides a ground truth whether a CBD stone is present or not. In addition, each pediatric patient also collects some explanatory variables or features before the IOC or ERCP procedure. There are two categories of features. One is the demographic variables and routine laboratory test results such as age, gender, body mass index (BMI), hemolytic disease, total bilirubin, alanine transaminase (ALT), aspartate transaminase (AST), lipase, amalyse, gamma-glutamyl transferase (GGT), alkaline phosphatase. The other is the four imaging features including CBD diameter and the presence of CBDS by both ultrasound (US) and magnetic resonance imaging (MRI) examinations. While all 316 patients have observed features from the first category, only 189 of them have imaging data from the US and MRI examinations. The descriptive statistics were calculated for all variables of interest in Table 1.

Table 1.

Descriptive statistics for demographic, laboratory, and imaging data in case study.

	CBD stone present	No CBD stone present	p-value
Total patients	120	196
IOC	81	196
ERCP	39	0
Age $(\mathrm{yrs})$	$13.8\pm 3.3$	$13.6\pm 3.6$	0.883
Female	$81(67.5\mathrm{\%})$	$123(62.8\mathrm{\%})$	0.400
BMI $(\mathrm{kg}/{\mathrm{m}}^2)$	$25.7\pm 8.0$	$24.5\pm 8.7$	0.125
Hemolytic disease	$23(19.2\mathrm{\%})$	$49(25.0\mathrm{\%})$	0.270
Total bilirubin $(\mathrm{mg}/\mathrm{dL})$	$5.6\pm 8.3$	$2.6\pm 5.2$	<0.001
ALT (U/L)	$258.5\pm 195.8$	$132.9\pm 146.2$	<0.001
AST (U/L)	$153.3\pm 135.6$	$87.9\pm 110.6$	<0.001
Lipase (U/L)	$578.4\pm 1516.9$	$268.4\pm 517.8$	0.538
Amylase (U/L)	$113.6\pm 197.8$	$119.3\pm 190.9$	0.011
GGT (U/L)	$296.0\pm 202.0$	$232.5\pm 216.1$	0.024
Alkaline phosphatase (U/L)	$247.1\pm 189.6$	$179.7\pm 98.1$	0.014
CBD diameter (mm, by US)	$7.4\pm 3.8$	$5.6\pm 3.8$	<0.001
Presence of CBD stone (US)	$11(13.4\mathrm{\%})$	$3(3.1\mathrm{\%})$	0.012
CBD diameter (mm, by MRI)	$9.3\pm 3.8$	$8.3\pm 2.6$	0.420
Presence of CBD stone (MRI)	$28(54.9\mathrm{\%})$	$10(19.6\mathrm{\%})$	0.041

Now we fit this data set by a two-stage sequential decision-making model, so that we can learn the doctor's decision process. There are $N_1=316-189=127$ subjects who only have the features from the first category, and there are $N_2=189$ subjects who have the features from both categories. Here we assume that if a patient has available features in the second category, such patient would be labeled in the class of ‘0.5’ at the first stage. This is because the doctor is unsure about the patient's disease status and thus recommends to collect imaging data for further diagnostic interventions. In other words, for this real data, which kinds of features are collected for each patient is decided by the doctor's knowledge and experience, and the features are not missing at random but deliberately interfered with.

Figure 6 visualizes the coefficients for features in the first category estimated by baseline approach and proposed, respectively. It can be seen that with the baseline approach, the coefficients estimated by the two individual models are similar to each other for most features, $(X_2,\dots ,X_{11})$, but significantly different for $X_1$. In the proposed two-stage model, the coefficients estimated for all features seem to resemble a weighted average of the coefficients obtained from baseline individual models. Moreover, the estimated cutoff values are $\widehat{U_1^{\ast }}=4.183,\widehat{L_1^{\ast }}=0.751$, and $C_2^{\ast }=2.680$. Transforming back to the cutoff values on probability estimation ${\pi }_i^{(k)}$ in Figure 1, we get $\widehat{U_1}=0.985,\widehat{L_1}=0.679$, and $\widehat{C_2}=0.936$. This suggests that the doctors seem to be comfortable to recommend the safe IOC procedure, but are very cautious when recommending the risky ERCP procedure unless there is an overwhelming evidence on the presence of the CBD stone.

Figure 6.

Coefficients comparison between coefficients obtained from 2 methods for features in stages 1.

Given the parameters estimated by the proposed two-stage method, when a new patient arrives, we can mimic the doctor's decision by first recommending the patient undergo routine laboratory tests to collect those features in the first category, and then predicting the class ${\hat{Y}}^{(1)}$ accordingly. Based on the estimated cutoff values ${\hat{L}}_1$ and ${\hat{U}}_1$, the patient will be labeled as mild (‘0’), severe (‘1’), or indeterminate and proceeded to the next stage (‘0.5’). When the patient's status is indeterminate, additional US and MRI examinations are recommended to collect imaging data. In other words, only necessary data are actively learned for each patient, and the medical decisions are made sequentially. If the patient is classified as ‘1’ by our model, we would recommend an expedited intervention with ERCP, a high-risk procedure for pediatric patients that treats problems of the bile and pancreatic ducts. If the patient is classified as ‘0’ by our model, we would recommend the safer IOC procedure. This simplifies and expedites the diagnostic and intervention process, so that one can reach a solid medical decision in a cost-effective and objective way. Additionally, we can easily extend the two-stage model to the multi-stage model by increasing the number of stages and adjusting the features in each stage, especially if new efficient diagnostic tests are available.

6. Conclusion and discussion

In this paper, a multistage sequential decision-making model is developed to actively collect necessary diagnostic data for each subject. It allows the doctors, patients and their families to adaptively collect features and data to reach reliable healthcare clinical decision in a cost-effective way. The usefulness of our proposed method is illustrated in the simulation study and a real case study on the pediatric CBD stone patients.

This research provides a new direction in medical diagnosis and treatment by developing an multi-stage sequential decision-making model to actively observe those necessary features or data in a cost efficient way. There are several important topics for future research that are related to this work. First, the current research chooses the list of possible features based on the doctor's domain knowledge, and use the MLE to estimate the model parameters. Further studies can be done by adding more possible features at each stage and by adding the $L_1$ regularization term for feature or parameter selection of the model.

Second, in healthcare or medical settings, the penalty for mis-diagnosis or mis-treatment can vary dramatically. In particular, false-positive detection may lead to excess intervention or unnecessary procedures that are risky and harmful, whereas false-negative detection may result in missed or delayed treatment. For such scenarios, we might put weighted penalties on different types of mis-classification. When fitting the training data, we can modify the objective function from the log-likelihood function in (7) to the empirical risk function with penalties: $\underset{\mathit{\beta },\mathit{L},\mathit{U}}{min}[-\log \mathcal{L}(\mathit{\beta },\mathit{L},\mathit{U})-C_1\sum _{i}I({\hat{y}}_i=0,y_i=0.5\text{ or }1)-C_2\sum _{i}I({\hat{y}}_i=1,y_i=0\text{ or }0.5)]$, where the $C_1$ and $C_2$ denotes the costs for false-negative and false-positive detection, respectively. Gradient-based optimization algorithms can then be developed based on the surrogate objective function that smooths out the 0-1 loss function $I(\hat{y}!=y).$

Finally, our model and method is applicable to a broad range of sequential decision-making scenarios when the dimension of the feature is high-dimension but it is infeasible to collect all features simultaneously. In such a case, our method allows one to utilize active learning to observe or collect required information to make robust and cost-efficient decision.

Appendix 1. Likelihood and gradient for two-stage model

In this appendix, we provide a detailed explanation on the computation of the gradient of the likelihood function for two-stage model.

To simplify the notation, denote by $G_{1,j}$ the subset of subjects whose is classified as the class ‘j’ at the first stage for j = 0, 0.5 and 1, and denote by $G_{2,j}$ the same at the second stage for j = 0 or 1. Since only those subjects who are classified as ‘0.5’ (intermediate) will take observations at the second stage, we have $G_{1,0.5}=G_{2,0}\cup G_{2,1}.$

Under this new notation, the log-likelihood function can be re-written as:

$$\begin{array}{rl}\log \mathcal{L}(\mathit{\beta },\mathit{L},\mathit{U})=& \sum _{i\in G_{1,0}}\log F(L_1^{\ast }-{\mathit{\beta }}^{(1{)}^{\mathrm{\top }}}{\mathit{x}}_i^{(1)})\\ & +\sum _{i\in G_{1,0.5}}\log \{F(U_1^{\ast }-{\mathit{\beta }}^{(1)\mathrm{\top }}{\mathit{x}}_i^{(1)})-F(L_1^{\ast }-{\mathit{\beta }}^{(1)\mathrm{\top }}{\mathit{x}}_i^{(1)})\}\\ & +\sum _{i\in G_{1,1}}\log \{1-F(U_1^{\ast }-{\mathit{\beta }}^{(1{)}^{\mathrm{\top }}}{\mathit{x}}_i^{(1)})\}\\ & +\sum _{i\in G_{2,0}}\log F(C_2^{\ast }-{\mathit{\beta }}^{(2)\mathrm{\top }}{\mathit{x}}_i^{(2)})\\ & +\sum _{i\in G_{2,1}}\log \{1-F(C_2^{\ast }-{\mathit{\beta }}^{(2)\mathrm{\top }}{\mathit{x}}_i^{(2)})\}.\end{array}$$

It is important to note that for those features observed at the first stage, the corresponding β coefficients occur in all five terms in the log-likelihood function. This implies that its estimation uses all observations from all subjects, and thus it has a smaller variance than that of the baseline method which only uses the data from the first stage. Meanwhile, for those features observed at the second stage, the corresponding β coefficients occur in the last two terms for the observations in the second stage. This explains why the estimation of the β parameters in the second stage is similar to those of the baseline method in our simulation studies.

These facts allow us to easily to compute the derivatives of the log-likelihood function with respect to the β coefficient parameters. In particular, for those β coefficients for the features in the first stage, say, ${\beta }_m^{(1)}$ for $m=1,\dots ,p_1$, we have:

$$\begin{array}{rl}\frac{\mathrm{\partial }\log \mathcal{L}(\mathit{\beta },\mathit{L},\mathit{U})}{\mathrm{\partial }{\beta }_m^{(1)}}& =\sum _{i\in G_{1,0}}\frac{-x_{i,m}^{(1)}f(L_1^{\ast }-{\mathit{\beta }}^{(1)\mathrm{\top }}{\mathit{x}}_i^{(1)})}{F(L_1^{\ast }-{\mathit{\beta }}^{(1)\mathrm{\top }}{\mathit{x}}_i^{(1)})}\\ & +\sum _{i\in G_{1,0.5}}\frac{-x_{i,m}^{(1)}[f(U_1^{\ast }-{\mathit{\beta }}^{(1)\mathrm{\top }}{\mathit{x}}_i^{(1)})-f(L_1^{\ast }-{\mathit{\beta }}^{(1)\mathrm{\top }}{\mathit{x}}_i^{(1)})]}{F(U_1^{\ast }-{\mathit{\beta }}^{(1)\mathrm{\top }}{\mathit{x}}_i^{(1)})-F(L_1^{\ast }-{\mathit{\beta }}^{(1)\mathrm{\top }}{\mathit{x}}_i^{(1)})}\\ & +\sum _{i\in G_{1,1}}\frac{x_{i,m}^{(1)}f(U_1^{\ast }-{\mathit{\beta }}^{(1)\mathrm{\top }}{\mathit{x}}_i^{(1)})}{1-F(U_1^{\ast }-{\mathit{\beta }}^{(1)\mathrm{\top }}{\mathit{x}}_i^{(1)})}\\ & +\sum _{i\in G_{2,0}}\frac{x_{i,m}^{(2)}f(C_2^{\ast }-{\mathit{\beta }}^{(2)\mathrm{\top }}{\mathit{x}}_i^{(2)})}{F(C_2^{\ast }-{\mathit{\beta }}^{(2)\mathrm{\top }}{\mathit{x}}_i^{(2)})}\\ & +\sum _{i\in G_{2,1}}\frac{x_{i,m}^{(2)}f(C_2^{\ast }-{\mathit{\beta }}^{(2)\mathrm{\top }}{\mathit{x}}_i^{(2)})}{1-F(C_2^{\ast }-{\mathit{\beta }}^{(2)\mathrm{\top }}{\mathit{x}}_i^{(2)})}\end{array}$$

Here $f(t)=F^{\prime }(t)$ is the probability density function of the logistic distribution function $F(t)$ in (6). Likewise, for those β coefficients for the features in the second stage, say, ${\beta }_m^{(2)}$ for $m=1,\dots ,p_2$, we have:

$$\frac{\mathrm{\partial }\log \mathcal{L}(\mathit{\beta },\mathit{L},\mathit{U})}{\mathrm{\partial }{\beta }_m^{(2)}}=\sum _{i\in G_{2,0}}\frac{x_{i,m}^{(2)}f(C_2^{\ast }-{\mathit{\beta }}^{(2)\mathrm{\top }}{\mathit{x}}_i^{(2)})}{F(C_2^{\ast }-{\mathit{\beta }}^{(2)\mathrm{\top }}{\mathit{x}}_i^{(2)})}+\sum _{i\in G_{2,1}}\frac{x_{i,m}^{(2)}f(C_2^{\ast }-{\mathit{\beta }}^{(2)\mathrm{\top }}{\mathit{x}}_i^{(2)})}{1-F(C_2^{\ast }-{\mathit{\beta }}^{(2)\mathrm{\top }}{\mathit{x}}_i^{(2)})}.$$

As for the derivatives of the log-likelihood function with respect to three cutoff value parameters, $L_1^{\ast },U_1^{\ast }$ and $C_2^{\ast },$ note that each cutoff value parameter occurs in exactly two terms in the log-likelihood function.

$$\begin{array}{rl}\frac{\mathrm{\partial }\log \mathcal{L}(\mathit{\beta },\mathit{L},\mathit{U})}{\mathrm{\partial }{L}_1^{\ast }}& =\sum _{i\in G_{1,0}}\frac{f(L_1^{\ast }-{\mathit{\beta }}^{(1)\mathrm{\top }}{\mathit{x}}_i^{(1)})}{F(L_1^{\ast }-{\mathit{\beta }}^{(1)\mathrm{\top }}{\mathit{x}}_i^{(1)})}\\ & +\sum _{i\in G_{1,0.5}}\frac{-f(L_1^{\ast }-{\mathit{\beta }}^{(1)\mathrm{\top }}{\mathit{x}}_i^{(1)})}{F(U_1^{\ast }-{\mathit{\beta }}^{(1)\mathrm{\top }}{\mathit{x}}_i^{(1)})-F(L_1^{\ast }-{\mathit{\beta }}^{(1)\mathrm{\top }}{\mathit{x}}_i^{(1)})};\\ \frac{\mathrm{\partial }\log \mathcal{L}(\mathit{\beta },\mathit{L},\mathit{U})}{\mathrm{\partial }{U}_1^{\ast }}& =\sum _{i\in G_{1,0.5}}\frac{f(U_1^{\ast }-{\mathit{\beta }}^{(1)\mathrm{\top }}{\mathit{x}}_i^{(1)})}{F(U_1^{\ast }-{\mathit{\beta }}^{(1)\mathrm{\top }}{\mathit{x}}_i^{(1)})-F(L_1^{\ast }-{\mathit{\beta }}^{(1)\mathrm{\top }}{\mathit{x}}_i^{(1)})}\\ & +\sum _{i\in G_{1,1}}\frac{-f(U_1^{\ast }-{\mathit{\beta }}^{(1)\mathrm{\top }}{\mathit{x}}_i^{(1)})}{1-F(U_1^{\ast }-{\mathit{\beta }}^{(1)\mathrm{\top }}{\mathit{x}}_i^{(1)})};\\ \frac{\mathrm{\partial }\log \mathcal{L}(\mathit{\beta },\mathit{L},\mathit{U})}{\mathrm{\partial }{C}_2^{\ast }}& =\sum _{i\in G_{2,0}}\frac{f(C_2^{\ast }-{\mathit{\beta }}^{(2)\mathrm{\top }}{\mathit{x}}_i^{(2)})}{F(C_2^{\ast }-{\mathit{\beta }}^{(2)\mathrm{\top }}{\mathit{x}}_i^{(2)})}\\ & +\sum _{i\in G_{2,1}}\frac{-f(C_2^{\ast }-{\mathit{\beta }}^{(2)\mathrm{\top }}{\mathit{x}}_i^{(2)})}{1-F(C_2^{\ast }-{\mathit{\beta }}^{(2)\mathrm{\top }}{\mathit{x}}_i^{(2)})}.\end{array}$$

Clearly, we can also easily continue to compute the second-order or high-order derivatives if we want.

Given these derivatives, it is straightforward to implement either the (first-order) gradient descent algorithm that has a general form of

$${\mathit{\theta }}_{new}={\mathit{\theta }}_{old}+\lambda \frac{\mathrm{\partial }\log \mathcal{L}\left(\mathit{\theta }\right)}{\mathrm{\partial }\mathit{\theta }}{|}_{{\mathit{\theta }}_{Old}},$$

or the second-order Newton-Raphson algorithm that has a general form of

$${\mathit{\theta }}_{new}={\mathit{\theta }}_{old}-[\frac{{\mathrm{\partial }}^2\log \mathcal{L}\left(\mathit{\theta }\right)}{\mathrm{\partial }\mathit{\theta }\mathrm{\partial }{\mathit{\theta }}^T}{]}^{-1}\frac{\mathrm{\partial }\log \mathcal{L}\left(\mathit{\theta }\right)}{\mathrm{\partial }\mathit{\theta }}{|}_{{\mathit{\theta }}_{Old}}.$$

In our simulation studies and case study, we recursive apply the gradient descent algorithm to our model and training data. When convergence, we obtain the desired parameter estimates of our proposed model.

Disclosure statement

No potential conflict of interest was reported by the author(s).