Interpretable, predictive spatio-temporal models via enhanced pairwise directions estimation

Abstract

This article concerns predictive modeling for spatio-temporal data as well as model interpretation using data information in space and time. We develop a novel approach based on supervised dimension reduction for such data in order to capture nonlinear mean structures without requiring a prespecified parametric model. In addition to prediction as a common interest, this approach emphasizes the exploration of geometric information from the data. The method of Pairwise Directions Estimation (PDE) is implemented in our approach as a data-driven function searching for spatial patterns and temporal trends. The benefit of using geometric information from the method of PDE is highlighted, which aids effectively in exploring data structures. We further enhance PDE, referring to it as PDE+, by incorporating kriging to estimate the random effects not explained in the mean functions. Our proposal can not only increase prediction accuracy but also improve the interpretation for modeling. Two simulation examples are conducted and comparisons are made with several existing methods. The results demonstrate that the proposed PDE+ method is very useful for exploring and interpreting the patterns and trends for spatio-temporal data. Illustrative applications to two real datasets are also presented.

1. Introduction

Complicated phenomena in spatio-temporal data raise large challenges remaining to be overcome even in today's new era of computing. Kriging, as a method widely used in modeling such data, typically contains two components; namely, a stationary Gaussian process and a mean function. Interestingly, most kriging approaches assume a very simple structure for the mean function. For example, data at n locations over T time points are assumed to be observed according to

$$y(\mathbf{s},t)=\mu (\mathbf{s},t)+u(\mathbf{s},t)+\epsilon (\mathbf{s},t),$$

where $\mu (\mathbf{s},t)$ is a mean function, $u(\mathbf{s},t)$ is a zero-mean Gaussian process with a covariance function $C(\mathbf{s}-{\mathbf{s}}^{\ast },t-t^{\ast })\equiv \text{cov}(u(\mathbf{s},t),u({\mathbf{s}}^{\ast },t^{\ast }))$, and $\epsilon (\mathbf{s},t)$ is an additive white-noise. Usual choice of $\mu (\mathbf{s},t)$ is either a linear combination of ‘known’ covariates (i.e. universal kriging), or a constant not varying over space or time (i.e. ordinary kriging). It results in most analyses focusing on the covariance functions.

In Ref. [22], Martin and Simpson showed that ordinary kriging could obtain a poor prediction under the presence of strong trends. To explore the important spatial structures for spatio-temporal data, the renowned empirical orthogonal function (EOF) analysis is a commonly used method, which is based on principal component analysis; see Refs. [7,9] for review. Letting

$$z(\mathbf{s},t)=\mu (\mathbf{s},t)+u(\mathbf{s},t),$$ (1)

EOFs formulate the spatio-temporal data approximately in the summation form as

$$z(\mathbf{s},t)\approx \sum _{k=1}^K{\text{PC}}_k(t){\text{EOF}}_k(\mathbf{s}),$$ (2)

(see Refs. [3,26]). This linear combination of inner products of temporal and spatial functions in EOFs has close connection to many dimension reduction approaches for geostatistics in the literature. From the reduced rank perspective, a low-rank model for spatial data at a particular time point is considered in a form similar to (2) as

$$z(\mathbf{s})\approx \sum _{k=1}^K{\alpha }_k{\beta }_k(\mathbf{s}),$$ (3)

where ${\alpha }_k$'s are unknown scalars and ${\beta }_k(\mathbf{s})$ is either a fully known function or a parametric basis function depending on a few parameters (e.g. [2,6,29]). When several time points are involved, ${\alpha }_k$ in (3) can be further assumed as a time-varying random variables ${\alpha }_k(t)$ (see Refs. [8,10,27,28]). Some of these works assumed $({\alpha }_1(t),\dots ,{\alpha }_K(t){)}^{\mathrm{\prime }}$ to be independent and identically distributed (i.i.d.) over time, while others linked ${\alpha }_k(t-1)$ and ${\alpha }_k(t)$ for equal time spaces in an autoregressive way. The SpTimer package developed by Bakar and Sahu [1] utilizing the low-rank framework is implemented to hierarchical Bayesian modeling for space-time data. In contrast to stochastic ${\alpha }_k(t)$'s and parametric ${\beta }_k(\mathbf{s})$'s above, additive models provide a non-parametric perspective on (3). They used spline functions to represent ${\alpha }_k(t)$ and/or ${\beta }_k(\mathbf{s})$ (e.g. [16,24]). The mgcv package based on Ref. [30] is a convenient tool for additive models.

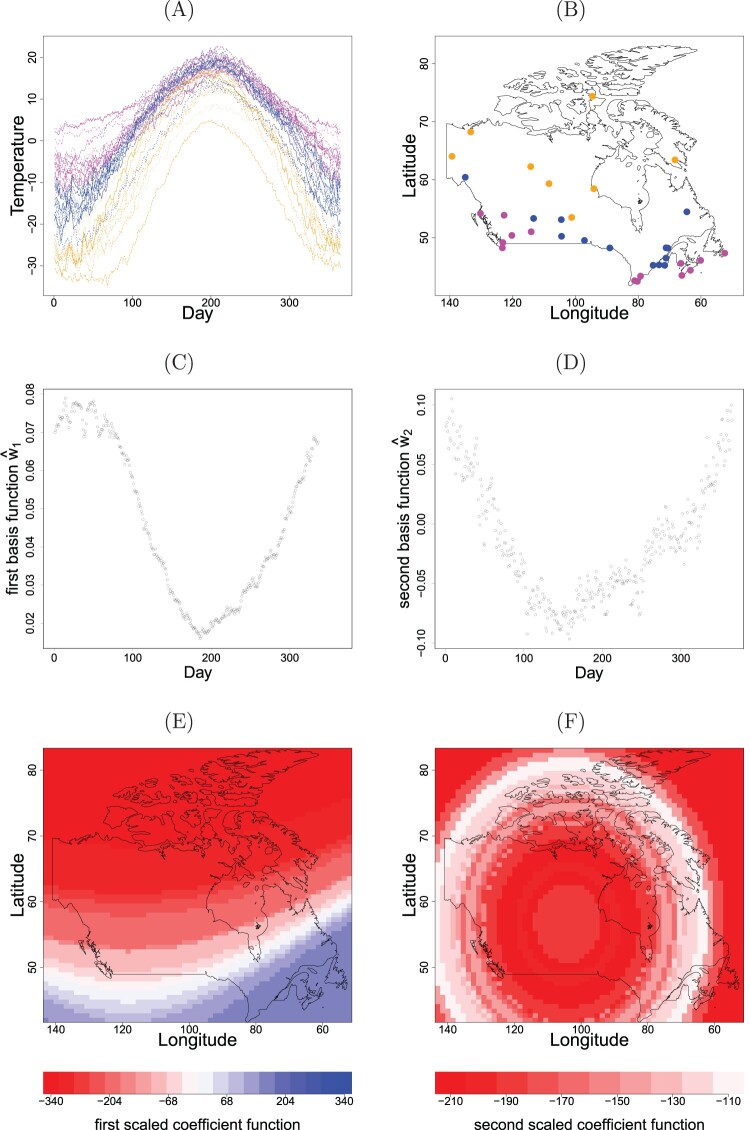
As a motivating example for illustrating the intriguing discovery, the data of average temperatures for each day of the year at 35 weather stations in Canada, shown in Figure 3(A,B), are considered. From Figure 3(A), a concave down pattern for daily temperatures is clearly observed. It seems to imply that a strong geometric information structure in the data. Two immediate questions are raised: are there any important time-related shapes hidden in those curves? Does the variation of curves relate to spatial patterns across the locations of stations? These questions stimulated us to investigate whether the inner products of spatial and temporal functions aid in exploring and interpreting the data. Our primary aim of the study is to gain an understanding of how temperature cycles at stations vary with location and/or with time. In general, this aim is not easy to accomplish. The aforementioned dimension reduction approaches turn the problem more tractable through different simplifications. For example, the EOFs impose the orthogonality on estimated components, the low-rank methods assume certain parametric function forms, and additive models use a large collection of smooth functions and rely on coefficient shrinkage to eliminate unneeded functions. In contrast, we relax those simplifications through an extension of supervised dimension reduction approach into the analysis without requiring pre-specified parametric functions.

Figure 3.

Plots of (A) the average daily temperatures over individual locations, (B) the spatial distribution of locations, (C) the first and (D) the second basis functions, and (E) the first and (F) the second scaled coefficient functions for Canadian Weather data.

Instead of directly taking $z(\mathbf{s},t)$ in (1), we assume $z(\mathbf{s},t)=\sum _{k=1}^K{\alpha }_k(t){\beta }_k(\mathbf{s})+u(\mathbf{s},t)$ with a substantially different mean distinct from typical kriging. The Pairwise Directions Estimation (PDE; [20]) is incorporated in our proposed method to estimate the $\sum _{k=1}^K{\alpha }_k(t){\beta }_k(\mathbf{s})$ in a data-driven way. In this article, we focus on explicitly finding both ${\alpha }_k(t)$ and ${\beta }_k(\mathbf{s})$ in order to detect potentially sophisticated mean structures in the spatio-temporal data.

Despite recent flourish of research on supervised dimension reduction (e.g. [4,17,20]), such time-relevant high-dimensional data remains to be challenging. We shall propose a novel approach to adaptively capture important spatial structures and temporal patterns for spatio-temporal data. Our main idea is to combine PDE and kriging, two quite flexible spatio-temporal modeling methods, into an ensemble learner, which not only increases the prediction accuracy of PDE, but also gives more comprehensive interpretation than typical kriging. The numerical results and real applications show that our proposed method not only gives explainable mean trends but may also produce more accurate model prediction.

The remainder of the paper is organized as follows. Section 2 introduces our approach. We use two simulation examples to illustrate and evaluate our proposed method in Section 3. Section 4 applies our method to two real datasets, and Section 5 concludes with discussion on future work.

2. Proposed method

Consider a sequence of processes, $\{z(\mathbf{s},t):\mathbf{s}\in \mathcal{D}\}$ for $t=1,\dots ,T$, defined on a d-dimensional spatial domain $\mathcal{D}\subset {\mathrm{\Re }}^d$ with $T\ge 1$. The processes are assumed to have a stationary spatio-temporal covariance function $\text{cov}(z(\mathbf{s},t),z({\mathbf{s}}^{\ast },t^{\ast }))$. The spatio-temporal random effects model of $y(\mathbf{s},t)$ with a measurement error ε is considered in this article as

$$\begin{array}{rl}y(\mathbf{s},t)& =z(\mathbf{s},t)+\epsilon (\mathbf{s},t),\end{array}$$ (4)

$$\begin{array}{rl}z(\mathbf{s},t)& =\mathit{w}(t)\mathit{f}(\mathbf{s})+u(\mathbf{s},t),\end{array}$$ (5)

for $t=1,\dots ,T$, where $\mathit{f}(\mathbf{s})=(f_1(\mathbf{s}),\dots ,f_{\kappa }(\mathbf{s}){)}^{\prime }$, $\mathit{w}(t)=(w_1(t),\dots ,w_{\kappa }(t))$, $u(\mathbf{s},t)$ is a zero-mean random effect with a covariance function $C(\mathbf{s}-{\mathbf{s}}^{\ast },t-t^{\ast })\equiv \text{cov}(u(\mathbf{s},t)\$,\$u({\mathbf{s}}^{\ast },t^{\ast }))$ for any pair of $(\mathbf{s},t)$ and $({\mathbf{s}}^{\ast },t^{\ast })$, and $\epsilon (\mathbf{s},t)$ $\sim N(0,{\sigma }_{\epsilon }^2(t))$ is an additive white-noise uncorrelated with $z(\mathbf{s},t)$. We assume that $u(\cdot ,t)$ and $\epsilon (\cdot ,t)$ are mutually uncorrelated. More specifically, $f_j({\mathbf{s}}_i)$ stands for $f_j({\mathit{\theta }}_j^{\prime }\mathbf{x}({\mathbf{s}}_i))$, where $\mathbf{x}({\mathbf{s}}_i)$ is a spatial-only covariate vector, and we can represent the inner-product term in (5) in terms of the summation as

$$\mathit{w}(t)\mathit{f}(\mathbf{s})=\sum _{j=1}^{\kappa }{w}_j(t)f_j(\mathbf{s}).$$ (6)

Here $w_j(t),j=1,\dots ,\kappa$, is an unknown basis function changing gradually with time t, and $f_j(\mathbf{s})$ is an unknown coefficient function standing for a certain spatial pattern. The function $f_j(\mathbf{s})$ depends on a $p\times 1$ vector $\mathbf{x}(\mathbf{s})$ through an unknown vector ${\mathit{\theta }}_j$ of weights. We refer to ${\mathit{\theta }}_j^{\prime }\mathbf{x}(\mathbf{s})$ as a variate. Hence, determining $f_j(\mathbf{s})$ amounts to finding both $f_j$ and ${\mathit{\theta }}_j$, which is a typical theme in supervised dimension reduction via constructing new variate ${\mathit{\theta }}_j^{\prime }\mathbf{x}(\mathbf{s})$ instead of using $\mathbf{x}(\mathbf{s})$ directly.

For covariates $\mathbf{x}(\mathbf{s})$ over ${\mathrm{\Re }}^d$, $(s_1,\dots ,s_d,s_1^2,\dots ,s_d^2{)}^{\prime }$ are considered in our simulation examples and real data applications. We certainly can incorporate more elaborate and domain-specific covariates into $\mathbf{x}(\mathbf{s})$, which may be useful for comprehending the spatio-temporal phenomenon.

Note that in the semi-parametric models of (4) and (5), only $\mathbf{x}(\mathbf{s})$ and $y(\mathbf{s},t)$ are observed, but other quantities are kept unknown. The aim of this study is to predict the process $z(\mathbf{s},t)$ by reconstructing those unknown terms $\mathit{w}(t)$, $\mathit{f}(\mathbf{s})$ and $u(\mathbf{s},t)$ based on the observed data $\mathbf{x}({\mathbf{s}}_i)$ and $y({\mathbf{s}}_i,t)$, $i=1,\dots ,n$; $t=1,\dots ,T$, as parsimonious as possible. To estimate those terms in (5), we begin with finding $\mathit{w}(t)$ and $\mathit{f}(\mathbf{s})$ via PDE proposed by Lue [20], and then estimate $u(\mathbf{s},t)$ by applying the kriging method for the spatio-temporal data (e.g. [7,25]). We briefly introduce the two key building blocks, PDE and kriging, and then propose our estimation method.

2.1. Pairwise directions estimation

Suppose that $y(\mathbf{s},t)$ at n distinct locations, ${\mathbf{s}}_1,\dots ,{\mathbf{s}}_n\in \mathcal{D}$, for $t=1,\dots ,T$ with a covariate vector $\mathbf{x}(\mathbf{s})$ are available. The original setting for time point t is not necessarily equal-spaced, but for simplicity, we assume them to be equal-spaced. For ease of illustration, we denote $\mathbf{y}(\cdot ,t)=(y({\mathbf{s}}_1,t),\dots ,y({\mathbf{s}}_n,t){)}^{\prime }$, $\mathbf{y}(\mathbf{s},\cdot )=(y(\mathbf{s},1),\dots ,y(\mathbf{s},T){)}^{\prime }$ and $\mathbf{Y}=(\mathbf{y}(\cdot ,1),\dots ,\mathbf{y}(\cdot ,T))$. The rationale behind using PDE to approximate the inner-product term in (5) is tentatively considering

$${\mathit{\varphi }}_j^{\prime }\mathbf{y}(\mathbf{s},\cdot )=g_j({\mathit{\theta }}_j^{\prime }\mathbf{x}(\mathbf{s}))+\tilde{e},1\le j\le \kappa ,$$ (7)

which originally deals with multivariate response data via a ”pairwise” model. After some algebra, (7) leads to the following model

$$y(\mathbf{s},t)=\sum _{j=1}^{\kappa }{\mathit{\varphi }}_j(t)g_j({\mathit{\theta }}_j^{\prime }\mathbf{x}(\mathbf{s}))+e(\mathbf{s},t),$$ (8)

for $t=1,\dots ,T$. In order to describe $y(\mathbf{s},t)$, we need to estimate a $T\times 1$ vector ${\mathit{\varphi }}_j$, a $p\times 1$ vector ${\mathit{\theta }}_j$ and a link function $g_j$, which all are totally unknown. Under (7), it is natural to pairwise find the solutions of ${\mathit{\varphi }}_j$ and ${\theta }_j$ via minimizing $\sum _i\{{\mathit{\varphi }}_j^{\prime }\mathbf{y}({\mathbf{s}}_i,\cdot )-g_j({\mathit{\theta }}_j^{\prime }\mathbf{x}({\mathbf{s}}_i)){\}}^2$. The estimation strategy is to find ${\mathit{\theta }}_j$ first and then estimate ${\mathit{\varphi }}_j$ and $g_j$ in an iterative way. We allow ${\mathit{\varphi }}_j$, $g_j$ and ${\mathit{\theta }}_j$ to be determined by the data with the number κ as small as possible.

The initial estimate ${\hat{\mathit{\theta }}}_j$ of ${\mathit{\theta }}_j,j=1,\dots ,\kappa$, can be found by two methods for efficiently implementing the PDE method. They are mrSIR and pe-mrPHD methods (for more details, see Refs. [18,19]). After initialization of ${\mathit{\theta }}_j$, we utilize an adaptive estimation of MAVE in Ref. [31] for a single-index case to obtain an initial estimate of ${\mathit{\varphi }}_j$ by solving the minimization problem:

$${min}_{{\tilde{d}}_{j_1},{\tilde{d}}_{j_2},{\mathit{\varphi }}_j}\sum _{\ell =1}^n\sum _{i=1}^n({\mathit{\theta }}_j^{\prime }\mathbf{x}({\mathbf{s}}_i)-\{{\tilde{d}}_{j_1\ell }+{\tilde{d}}_{j_2\ell }{\mathit{\varphi }}_j^{\prime }(\mathbf{y}({\mathbf{s}}_i,\cdot )-\mathbf{y}({\mathbf{s}}_{\ell },\cdot ))\}{)}^2{\delta }_{i\ell },$$ (9)

where ${\delta }_{i\ell }=K_{h_{\mathbf{Y}}}\{{\mathit{\varphi }}_j^{\prime }(\mathbf{y}({\mathbf{s}}_i,\cdot )-\mathbf{y}({\mathbf{s}}_{\ell },\cdot ))\}/\sum _{i=1}^n{K}_{h_{\mathbf{Y}}}\{{\mathit{\varphi }}_j^{\prime }(\mathbf{y}({\mathbf{s}}_i,\cdot )-\mathbf{y}({\mathbf{s}}_{\ell },\cdot ))\}$, K is a kernel function and $h_{\mathbf{Y}}$ is the bandwidth of $\mathbf{Y}$.

The iterative algorithm for estimating ${\mathit{\varphi }}_j$, ${\mathit{\theta }}_j$ and $g_j$ for $j=1,\dots ,\kappa$ in (8) via PDE proceeds in the following steps:

1. Initialize ${\hat{\mathit{\theta }}}_{j(0)}$, $j=1,\dots ,\kappa$, from mrSIR and/or pe-mrPHD, and then get ${\tilde{\mathit{\varphi }}}_{j(0)}$ as the minimizer of ${\mathit{\varphi }}_j$ in (9). Compute the estimated basis functions ${\hat{\mathit{\varphi }}}_{j(0)}={\hat{\mathbf{\Sigma }}}_{\mathbf{Y}}{\tilde{\mathit{\varphi }}}_{j(0)}$, where ${\hat{\mathbf{\Sigma }}}_{\mathbf{Y}}$ is the sample covariance of $\mathbf{Y}$ (see Lemma of [20]).

2. At the τ-th iteration, fit a linear regression model to $\mathbf{y}({\mathbf{s}}_i,\cdot )$ against $\{{\hat{\mathit{\varphi }}}_{j(\tau -1)}{\}}_{j=1}^{\kappa }$, i.e. assuming

   $$\mathbf{y}({\mathbf{s}}_i,\cdot )=g_{1i}{\hat{\mathit{\varphi }}}_{1(\tau -1)}+\cdots +g_{\kappa i}{\hat{\mathit{\varphi }}}_{\kappa (\tau -1)}+\mathit{e}({\mathbf{s}}_i,\cdot ),$$ (10)

   for $i=1,\dots ,n$, to obtain the estimated coefficients ${\hat{g}}_{ji(\tau )}$, $j=1,\dots ,\kappa$, where the $(\tau )$ in the subscript denotes the iteration number.

3. Obtain the updated estimate ${\tilde{\mathit{\varphi }}}_{j(\tau )}$ from (9) by replacing ${\mathit{\theta }}_j^{\prime }\mathbf{x}({\mathbf{s}}_i)$ with ${\hat{g}}_{ji(\tau )}$ and then compute the updated basis functions ${\hat{\mathit{\varphi }}}_{j(\tau )}={\hat{\mathbf{\Sigma }}}_{\mathbf{Y}}{\tilde{\mathit{\varphi }}}_{j(\tau )}$, $j=1,\dots ,\kappa$.

4. Repeat steps 2 and 3 until $||{\hat{\mathit{\varphi }}}_{j(\tau )}-{\hat{\mathit{\varphi }}}_{j(\tau -1)}||<\mathrm{\Delta },j=1,\dots ,\kappa$, for some given tolerance value Δ (e.g. $\mathrm{\Delta }=0.001$).

5. Use the final estimate ${\hat{\mathit{\varphi }}}_j$ in step 4 to obtain the final estimates ${\hat{\mathit{\theta }}}_j$ and ${\hat{g}}_j$, $j=1,\dots ,\kappa$, by solving the minimization problem:

   $${min}_{d_{j_1},d_{j_2},{\mathit{\theta }}_j}\sum _{\ell =1}^n\sum _{i=1}^n({\hat{\mathit{\varphi }}}_j^{\prime }\mathbf{y}({\mathbf{s}}_i,\cdot )-\{d_{j_1\ell }+d_{j_2\ell }{\mathit{\theta }}_j^{\prime }(\mathbf{x}({\mathbf{s}}_i)-\mathbf{x}({\mathbf{s}}_{\ell }))\}{)}^2{\delta }_{i\ell },$$

   where ${\delta }_{i\ell }=K_{h_{\mathbf{x}}}\{{\mathit{\theta }}_j^{\prime }(\mathbf{x}({\mathbf{s}}_i)-\mathbf{x}({\mathbf{s}}_{\ell }))\}/\sum _{i=1}^n{K}_{h_{\mathbf{x}}}\{{\mathit{\theta }}_j^{\prime }(\mathbf{x}({\mathbf{s}}_i)-\mathbf{x}({\mathbf{s}}_{\ell }))\}$ and $h_{\mathbf{x}}$ is the bandwidth of $\mathbf{x}(\mathbf{s})$. We use ${\hat{d}}_{j_1\ell },\ell =1,\dots ,n,$ to be the estimate of $g_j(\cdot )$ in (8).

In step 2 of the algorithm, $g_{ji}\equiv g_j({\mathit{\theta }}_j^{\prime }\mathbf{x}({\mathbf{s}}_i)),j=1,\dots ,\kappa$ obtained from the regression coefficients in (10), is a working estimate of $g_j$ at ${\mathbf{s}}_i$.

2.2. Function scaling estimation

The PDE captures the inner-product term, $\mathit{w}(t)\mathit{f}(\mathbf{s})$, of nonlinear mean structures in (5) without requiring a prespecified parametric model; namely, ${\hat{\mathit{\varphi }}}_j$ and ${\hat{g}}_j$ found by PDE in step 5 are used to respectively estimate $w_j$ and $f_j$ in (6) for $j=1,\dots ,\kappa$. In order to address the identifiability issue of functional estimation, we let the estimate ${\hat{w}}_j=({\hat{w}}_j(1),\dots ,{\hat{w}}_j(T){)}^{\mathrm{\prime }}$ be a normalized vector of unit norm, and then a scaling factor ${\hat{b}}_j(\mathbf{s})$ is introduced for prediction purpose. Under (5), we use $\sum _{j=1}^{\kappa }{\hat{w}}_j(t){\hat{b}}_j(\mathbf{s}){\hat{f}}_j(\mathbf{s})$ to approximate $\mathit{w}(t)\mathit{f}(\mathbf{s})$ via a linear fit. More specifically, $\hat{b}({\mathbf{s}}_i)=({\hat{b}}_1({\mathbf{s}}_i),\dots ,{\hat{b}}_{\kappa }({\mathbf{s}}_i){)}^{\prime }$ are the estimated coefficients obtained from the linear regression of $y({\mathbf{s}}_i,t)$ against $\{{\hat{f}}_j({\mathbf{s}}_i){\hat{w}}_j(t){\}}_{j=1}^{\kappa }$ for each $i=1,\dots ,n$. Then we refer to the jth scaled coefficient function ${\tilde{f}}_j(\mathbf{s})$ as the estimates $({\hat{b}}_j({\mathbf{s}}_1){\hat{f}}_j({\mathbf{s}}_1),\dots ,{\hat{b}}_j({\mathbf{s}}_n){\hat{f}}_j({\mathbf{s}}_n){)}^{\mathrm{\prime }}$, $j=1,\dots ,\kappa$. Based on the scaling procedure, it would not only improve the prediction accuracy, but also give appropriate magnitude for the inner products. In calculating $\hat{\mathbf{z}}({\mathbf{s}}_0,\cdot )$ at a predicted location ${\mathbf{s}}_0$, the scaled coefficients ${\hat{b}}_j({\mathbf{s}}_0){\hat{f}}_j({\mathbf{s}}_0),j=1,\dots ,\kappa$, can be obtained by using the average of k nearest neighbors around ${\hat{\mathit{\theta }}}_j^{\prime }\mathbf{x}({\mathbf{s}}_0)$ in the observed data (e.g. k = 3).

2.3. Incorporation of kriging

Since PDE does not take the random effects in (5) into account, we incorporate kriging to estimate this term for model prediction. The kriging method is dedicated to modeling the covariance function $C(\mathbf{s}-{\mathbf{s}}^{\ast },t-t^{\ast })\equiv \text{cov}(u(\mathbf{s},t),u({\mathbf{s}}^{\ast },t^{\ast }))$ that measures the strength of dependency between any pairs of variables at $(\mathbf{s},t)$ and $({\mathbf{s}}^{\ast },t^{\ast })$. In (5), $\mathit{w}(t)$ and $\mathit{f}(\mathbf{s})$ are unknown deterministic functions. When measurement errors are absent with $\epsilon (\cdot ,\cdot )=0$, an equivalence exists between the variogram $\nu (\mathbf{s}-{\mathbf{s}}^{\ast },t-t^{\ast })\equiv \text{var}((y(\mathbf{s},t)-y({\mathbf{s}}^{\ast },t^{\ast }))=E[(u(\mathbf{s},t)-u({\mathbf{s}}^{\ast },t^{\ast }){)}^2]$ and the covariance function $C(\cdot ,\cdot )$ under the second-order stationary assumption of $u(\mathbf{s},t)$, i.e. $E(u(\mathbf{s},t))$ is constant (assumed zero here) over $\mathbf{s}$ and t, and $\text{cov}(u(\mathbf{s},t),u({\mathbf{s}}^{\ast },t^{\ast }))$ only depends on $\mathbf{s}-{\mathbf{s}}^{\ast }$ and $t-t^{\ast }$; see Ref. [5] or [23]. Then the minimum-mean-squared-error linear prediction for $u(\mathbf{s},t)$ at $({\mathbf{s}}_0,t_0)$ of interest can be found by $E[u({\mathbf{s}}_0,t_0)|\mathbf{Y}]$ under the joint normality and assuming the parameters to be known; see Ref. [5].

We consider the isotropic product-sum model in this article with covariance in the form of

$$C(h_s,h_t)=C_s(h_s;{\mathit{\xi }}_1)+C_t(h_t;{\mathit{\xi }}_2)+k_0{C}_s(h_s;{\mathit{\xi }}_1)C_t(h_t;{\mathit{\xi }}_2)$$ (11)

for any pair of space-time points $(\mathbf{s},t)$ and $(\mathbf{s}+h_s,t+h_t)$ with valid covariance functions $C_s(h_s;{\mathit{\xi }}_1)$ and $C_t(h_t;{\mathit{\xi }}_2)$, respectively. We use exponential covariance functions for $C_s$ and $C_t$ in what follows, where both ${\mathit{\xi }}_1$ and ${\mathit{\xi }}_2$ contain two parameters for the marginal variance and the scale of $C_s$ or $C_t$, and $k_0$ is an additional parameter for the spatio-temporal interaction. When the first two terms on the right-hand side in (11) vanish, the covariance function becomes a separable model. Although other non-separable covariance functions can be applied in this framework, we mainly focus on (11) due to its ease of understanding and acceptable flexibility.

In the presence of measurement errors as (4), the variation of $y(\cdot ,\cdot )$ comes from both $u(\cdot ,\cdot )$ and $\epsilon (\cdot ,\cdot )$, and hence $\nu (\mathbf{s}-{\mathbf{s}}^{\ast },t-t^{\ast })=E[(u(\mathbf{s},t)-u({\mathbf{s}}^{\ast },t^{\ast }){)}^2]+E[(\epsilon (\mathbf{s},t)-\epsilon ({\mathbf{s}}^{\ast },t^{\ast }){)}^2]$. We shall instead consider a variogram model corresponding to the following covariance function between $(\mathbf{s},t)$ and $(\mathbf{s}+h_s,t+h_t)$:

$$C(h_s,h_t)+{\sigma }_{\epsilon }^2\cdot \mathbb{I}(h_s=0)\cdot \mathbb{I}(h_t=0),$$

where $\mathbb{I}$ is the indicator function, and ${\sigma }_{\epsilon }^2=\text{var}(\epsilon (\mathbf{s},t))$. For approximation of $u(\mathbf{s},t)$, we need to calculate the empirical variogram, namely, the sample version of $\nu (\mathbf{s}-{\mathbf{s}}^{\ast },t-t^{\ast })$, for the detrended process $y(\mathbf{s},t)-\mathit{w}(t)\mathit{f}(\mathbf{s})$. The estimation of parameters ${\sigma }_{\epsilon }^2$, $k_0$, ${\mathit{\xi }}_1$ and ${\mathit{\xi }}_2$ is based on least-squares variogram fitting, which is the default method implemented in the package $\mathtt{\text{gstat}}$. After obtaining $\hat{\mathit{w}}(t)\hat{\mathit{f}}(\mathbf{s})$ by PDE in Section 2.1, we apply kriging to estimate $u(\mathbf{s},t)$ based on the residuals $y(\mathbf{s},t)-\hat{\mathit{w}}(t)\hat{\mathit{f}}(\mathbf{s})$ through using

$$E[u({\mathbf{s}}_0,t_0)|\{y({\mathbf{s}}_i,t)-\sum _{j=1}^{\kappa }{\hat{w}}_j(t){\hat{f}}_j(\mathbf{s});i=1,\dots ,n,t=1,\dots ,T\}]$$

with plugging-in estimated parameters under the joint normality assumptions of $u(\cdot ,\cdot )$ and $\epsilon (\cdot ,\cdot )$ in (4) and (5). Here ${\hat{w}}_j(t)$ and ${\hat{f}}_j(\mathbf{s})$ are replaced respectively with ${\hat{\mathit{\varphi }}}_j$ and ${\hat{g}}_j$ found by PDE in its steps 4 and 5 for $j=1,\dots ,\kappa$. We perform a one-more-step iteration to obtain the final estimates for each component in (5), whose algorithm is given in Section 2.4.

2.4. Enhanced PDE

We propose a new enhanced method of PDE, called PDE+, through incorporating the PDE with kriging for modeling spatio-temporal data. In what follows, $\mathit{ϵ}(\mathbf{s},\cdot )$, $\widehat{\mathit{ϵ}}(\mathbf{s},\cdot )$, $\mathit{u}(\mathbf{s},\cdot )$, and $\hat{\mathit{u}}(\mathbf{s},\cdot )$ are defined in a similar way as $\mathbf{y}(\mathbf{s},\cdot )$ with respect to $\{y(\mathbf{s},t);t=1,\dots ,T\}$. The algorithm for PDE+ proceeds in the following two steps:

1. Apply PDE to the data $\{\mathbf{x}(\mathbf{s}),y(\mathbf{s},t)\}$ for obtaining $\hat{\mathit{f}}(\mathbf{s})$ and $\hat{\mathit{w}}(t)$, and then get the residuals $\mathit{ϵ}({\mathbf{s}}_i,\cdot )$ from a linear fit of $\mathbf{y}({\mathbf{s}}_i,\cdot )$ against $\{{\hat{w}}_j{\}}_{j=1}^{\kappa }$ for $i=1,\dots ,n$. Use kriging in Section 2.3 on $\mathit{ϵ}(\mathbf{s},\cdot )$ to get an initial estimate $\hat{\mathit{u}}(\mathbf{s},\cdot )$ of $\mathit{u}(\mathbf{s},\cdot )$.

2. Let $\widehat{\mathit{ϵ}}(\mathbf{s},\cdot )$ be the difference between $\mathbf{y}(\mathbf{s},\cdot )$ and $\hat{\mathit{u}}(\mathbf{s},\cdot )$ from step I, and then repeat step I once by treating the observed data as $\{\mathbf{x}(\mathbf{s}),\widehat{\mathit{ϵ}}(\mathbf{s},t)\}$.

The final predictive model of PDE+ is defined as the one in step II. The reason for taking once iteration on PDE+ is for computational efficiency. For prediction, we incorporate function scaling estimation procedure in Section 2.2 for measuring the prediction error based on the testing data. In this article, the dominant eigenvalue sequence and the scatterplots of $g_j$ on ${\mathit{\theta }}_j^{\prime }\mathbf{x}(\mathbf{s})$ are effectively used to determine the parameter κ in (7) in practice.

3. Numeric results

3.1. Simulation setups

We shall apply our proposed method for studying predictive modeling on spatio-temporal data through two simulated examples. Suppose that we observe data $y(\mathbf{s},t)$ at location $\mathbf{s}$ and time t. Let the spatial-only covariate vector be $\mathbf{x}(\mathbf{s})=(s_1,s_2,s_1^2,s_2^2{)}^{\prime }$, where $\mathbf{s}=(s_1,s_2{)}^{\prime }$, generated from given spatial locations and $f_j(\cdot )$ be the coefficient function for unknown spatial structure shared across t. Under (5), we think of elements of $\mathit{w}(t)$ and $\mathit{f}(\mathbf{s})$ as unknown deterministic functions. In all simulations and real applications, we have conducted the sample splitting procedure by removing some spatial locations and some time points (20% removal). To make comparisons with our proposal, we consider several existing methods. To evaluate the performance of prediction accuracy, we compute four indices, including two versions of prediction error criteria, namely root integrated mean squared error (RIMSE) and rooted prediction mean squared error (RPMSE), defined by

$$\begin{array}{rl}\mathrm{RIMSE}& =\frac{1}{n_t}\sum _{i=1}^{n_t}||\mathbf{y}({\mathbf{s}}_i,\cdot )-\hat{\mathbf{z}}({\mathbf{s}}_i,\cdot )||,\\ \mathrm{RPMSE}& ={(\frac{1}{n_{t}T}\sum _{t=1}^T\sum _{i=1}^{n_t}(y({\mathbf{s}}_i,t)-\hat{z}({\mathbf{s}}_i,t){)}^2)}^{1/2},\end{array}$$ (12)

where $n_t$ is the size of locations in the testing data, $\hat{z}({\mathbf{s}}_i,t)$ denotes the estimate of $z({\mathbf{s}}_i,t)$, and $\hat{\mathbf{z}}({\mathbf{s}}_i,\cdot )=(\hat{z}({\mathbf{s}}_i,1),\dots ,\hat{z}({\mathbf{s}}_i,T){)}^{\prime }$. We also assess the model prediction based on continuous ranked probability score (CRPS) and interval score (Iscore) discussed in Ref. [12]. For a specific real-value y, CRPS and Iscore are respectively defined as:

$$\begin{array}{rl}& \mathrm{CRPS}(F,y)=-{\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}\{F(v)-\mathbb{I}(v\ge y){\}}^2\mathrm{d}v,\end{array}$$ (13)

$$\begin{array}{rl}& \mathrm{Iscore}({\alpha }_0,y)=(I_U-I_L)+\frac{2}{{\alpha }_0}(I_L-y)\mathbb{I}(y<I_L)+\frac{2}{{\alpha }_0}(y-I_U)\mathbb{I}(y>I_U),\end{array}$$ (14)

where $F(\cdot )$ is the cumulative distribution of a probabilistic forecasting model, $[I_L,I_U]$ is its $(1-{\alpha }_0)$ prediction interval. We shall report the averaged CRPS and Iscore over all observed y values for ${\alpha }_0=10\mathrm{\%}$ in what follows. According to four indices above, the smaller the index levels, the higher is the prediction accuracy.

The cross-validation estimates of RIMSE, RPMSE, CRPS and Iscore are collected over 100 replications for each example. Seven other methods to be compared, referred to as naive, SpTimer, kriging-P, kriging-N, mgcv, OKFD and WMWC, are briefly described below.

The naive method takes the simple predictor $\hat{z}(\mathbf{s},t)=\frac{1}{n_t}\sum _{i=1}^{n_t}y({\mathbf{s}}_i,t)$, i.e. the sample mean of all locations at time t. The SpTimer method uses a hierarchical Bayesian approach for space-time data. Its model is given by

$$\begin{array}{rl}y(\mathbf{s},t)& =\alpha +R(\mathbf{s},t)+\varpi (\mathbf{s},t)\\ R(\mathbf{s},t)& =\rho R(\mathbf{s},t-1)+\varsigma (\mathbf{s},t),\end{array}$$

where $\varsigma (\mathbf{s},t)$'s are zero-mean spatial random effects independent over time with an isotropic stationary Matérn covariance function. This method has been implemented in an R package named SpTimer. The kriging method typically considers the term $\mathit{w}(t)\mathit{f}(\mathbf{s})$ in (5) as a constant μ. The ordinary kriging estimates $\mu +u({\mathbf{s}}_0,t_0)$ by $\sum _{i=1}^n\sum _{t=1}^T{p}_{it}({\mathbf{s}}_0,t_0)y({\mathbf{s}}_i,t)$, where $\{p_{it}({\mathbf{s}}_0,t_0)\}$ depend on the variogram $\nu (\cdot ,\cdot )$ under the constraint of $\sum _i\sum _t{p}_{it}({\mathbf{s}}_0,t_0)=1$, with plugging all estimated covariance parameters. We refer to this typical kriging as parametric kriging, or kriging-P for short. Instead of using parametric form, [32] recently proposed a non-parametric method to estimate the spatio-temporal mean function and covariance function. We refer to it as non-parametric kriging (kriging-N). If the assumptions of stationarity, constant mean, or isotropic structure lack to hold, such a non-parametric method expectedly performs better than kriging-P.

The mgcv method exploits additive models with tensor products. It assumes

$$E[y(\mathbf{s},t)]=q_1(s_1)+q_2(s_2)+q_3(t)+q_4(s_1,s_2)+q_5(s_1,t)+q_6(s_2,t)+q_7(s_1,s_2,t),$$ (15)

where $q_k$'s are constructed by superimposing several known basis functions and its noises are assumed to follow $N(0,{\sigma }_y^2)$ independently over space and time. With these higher-order interactions, the model tends to overfit, and hence some penalized approach is necessary. The famous R package mgcv provides convenient ways for determining an appropriate penalty.

There have been some research treating spatial-temporal data as a set of functional data, i.e. curves, at multiple locations, by specifying spatial correlations among curves [11,13–15]. The OKFD method used in Refs. [11,14] estimates a mean curve $\mu (\mathbf{s},t)=\mu (t)$ and a variance curve $\text{var}(y(\mathbf{s},t))={\sigma }^2(t)$ for all $\mathbf{s}$, followed by modeling the $\text{cov}(y(\mathbf{s},t),y({\mathbf{s}}^{\ast },t))$ based on a spatially stationary covariance model $C_s(\Vert \mathbf{s}-{\mathbf{s}}^{\ast }\Vert ,t)$. The OKFD was implemented in the R package geofd. Besides, the literature [13] and [15] discussed an expansion of $y(\mathbf{s},t)$ as $\mu (t)+\sum _{i=1}^K{\alpha }_k(t){\beta }_k(\mathbf{s})$, where the mean curve $\mu (t)$ and the components of ${\alpha }_k(t)$ and ${\beta }_k(\mathbf{s})$ are estimated based on weighted averages of quantities from all observed locations, without assuming spatial stationarity. This method is referred to as weighted-mean-weighted-component (WMWC).

Moreover, the original PDE method is also included in the comparisons. We can think of PDE+ as an ensemble learner combining both PDE and kriging. The comparisons among PDE, kriging, and PDE+ aid in numerically verifying that the proposed integration leads to better prediction of the data.

According to the algorithms of the above methods, the default values are used to set the turning parameters. We emphasize the accuracy of prediction as the indices in (12)–(14) and the findings of interesting pattern structures. The strategy for determining the structural dimension κ in model (7) is based on the maximal eigenvalue ratio criterion (MERC) proposed by Luo et al. [21]. More specifically, they suggested to select κ by $\hat{\kappa }={\text{arg max}}_{i=1,\dots ,p-1}{\hat{\lambda }}_i/{\hat{\lambda }}_{i+1}$, where ${\hat{\lambda }}_i$ is the estimated eigenvalue of the eigenvalue decomposition for mrSIR (or pe-mrPHD). For the two real data applications in the next section, both of the MERC are two. From simulations and practical applications in the next two sections, PDE successfully estimates the effective dimension reduction directions.

3.2. Comparison of simulation results

In each simulation run, we set T = 20 and generate $\mathbf{y}({\mathbf{s}}_i,\cdot )$ at n locations which consist of a learning set with size $n_{\ell }(=80\mathrm{\%}\times n)$ and a testing set with size $n_t(=20\mathrm{\%}\times n)$. We also exclude learning data at randomly sampled $4(=20\mathrm{\%}\times T)$ time points for validation purposes. The location set $\{{\mathbf{s}}_1,\dots ,{\mathbf{s}}_n\}$ is drawn from $\mathcal{D}=[-1,1{]}^2$ using simple random sampling. We set the number of slices for mrSIR to be 10 for all runs. We denote the absolute value of cosine angle between the estimate ${\hat{\mathit{\theta }}}_j$ and the true vector ${\mathit{\theta }}_j$ as $|\cos ({\hat{\mathit{\theta }}}_j)|$, $j=1,\dots ,\kappa$, for evaluating the accuracy of directional estimation.

Example 3.1

Consider a process, $\{z(\mathbf{s},t):\mathbf{s}\in [-1,1{]}^2\}$, generated according to (5) with trigonometric and quadratic structures by setting

$$\begin{array}{rl}{f}_1(\mathbf{s})& =\cos (0.5\pi ||\mathbf{s}-(-0.5,-0.5{)}^{\prime }|{|}^2),\\ f_2(\mathbf{s})& =\sin (0.5\pi ||\mathbf{s}-(0.5,0.5{)}^{\prime }|{|}^2),\end{array}$$ (16)

$$\begin{array}{rl}{w}_1(t)& =(0.5t-5{)}^2,w_2(t)=5\sin (0.1\pi t),\end{array}$$ (17)

for $t=1,\dots ,T$, and $u(\mathbf{s},t)$ being a zero-mean random effect with the covariance

$$\begin{array}{r}\mathrm{cov}(u(\mathbf{s},t),u({\mathbf{s}}^{\ast },t^{\ast }))=\{\begin{array}{ll}\exp (-0.5|\mathbf{s}-{\mathbf{s}}^{\ast }|)& \mathrm{if}t=t^{\ast };\\ 0& \mathrm{otherwise}.\end{array}\end{array}$$

Using (4), the data $\{y(\mathbf{s},t)\}$ with $\epsilon (\mathbf{s},t)\underset{\sim }{\mathrm{i}.\mathrm{i}.\mathrm{d}.}\mathrm{N}(0,0.25)$ over time and space are generated. With letting ${\mathit{\theta }}_1=(0.5,0.5,0.5,0.5{)}^{\prime }$ and ${\mathit{\theta }}_2=(-0.5,-0.5,0.5,0.5{)}^{\prime }$, the coefficient functions $f_j$'s can be reformulated as $f_1(\mathbf{s})=\cos (0.5\pi (2{\mathit{\theta }}_1^{\prime }\mathbf{x}(\mathbf{s})+0.5))$ and $f_2(\mathbf{s})=\sin (0.5\pi (2{\mathit{\theta }}_1^{\prime }\mathbf{x}(\mathbf{s})+0.5))$, where $\mathbf{x}(\mathbf{s})=(s_1,s_2,s_1^2,s_2^2{)}^{\prime }$. Both unknown vectors, ${\mathit{\theta }}_1$ and ${\mathit{\theta }}_2$, are sufficient dimension reduction directions needed to be estimated.

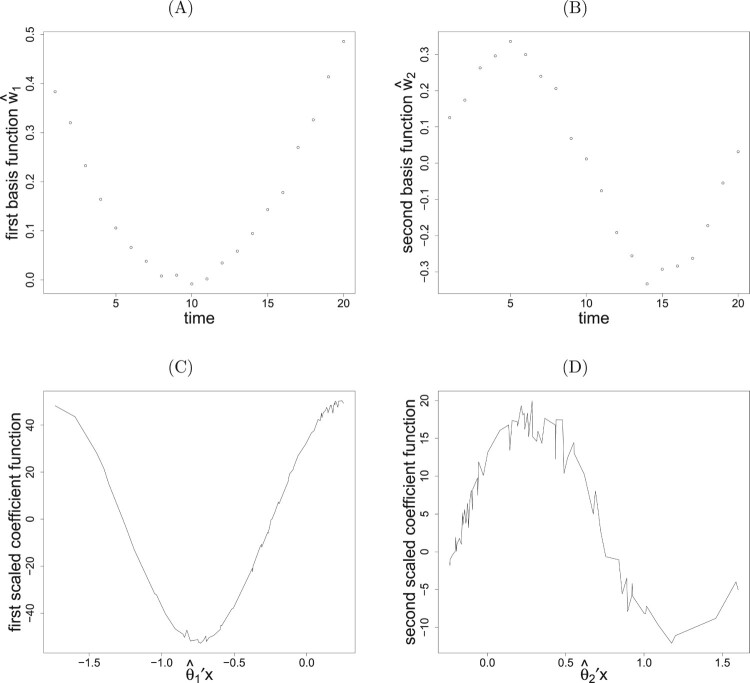
To illustrate the application of PDE+ via data visualization, a single run is taken. The data with n = 100 are generated according to models (16) and (17). We separately conduct the eigenvalue decomposition of mrSIR and pe-mrPHD for the learning data to obtain initial estimates ${\hat{\mathit{\theta }}}_j$'s. It turns out that the modified eigenvalues (0.73, 0.31, 0, 0) found by mrSIR suggest one $\mathbf{x}(\mathbf{s})$ variate. One significant direction is also found by pe-mrPHD with the eigenvalues (2.24, 1.83, 0.68, 0.29). By choosing $h_Y=3,h_{\mathbf{x}}=0.5$ and taking the two initial estimates ${\hat{\mathit{\theta }}}_j,j=1,2$, we proceed with the proposed algorithm to dimension reduction for $\mathbf{x}({\mathbf{s}}_i)$ and $y({\mathbf{s}}_i,t)$, $i=1,\dots ,n$; $t=1,\dots ,T$. After attaining the iterative convergence, two leading directions, (0.501, 0.506, 0.490, 0.502) ${}^{\prime }$ and (-0.496, -0.496, 0.515, 0.492) ${}^{\prime }$, for $\mathbf{x}(\mathbf{s})$ variates are found along with $|\cos ({\hat{\mathit{\theta }}}_1)|=0.999$ and $|\cos ({\hat{\mathit{\theta }}}_2)|=0.999$, which are consistently close to the theoretical vectors ${\mathit{\theta }}_j,j=1,2$. The scatterplot of the first estimated basis function, shown in Figure 1(A), reveals a noticeable quadratic pattern. Figure 1(B) shows a clear sine pattern for the second estimated basis function. Figure 1(C,D) displays coefficient functions which are very close to the true trigonometric patterns.

Figure 1.

Plots of (A) the first and (B) the second basis functions with (C) the first and (D) the second scaled coefficient functions for a randomly selected simulation from model in (16) and (17).

In reference to the sampling performance, the results based on 100 simulated replicates according to (16) and (17) are summarized in Table 1. It reports the mean and standard deviation for four indices obtained by all methods. PDE+ does outperform with the smallest averaged values of indices for this model and with the best prediction interval because of its capture of clear signal for functional patterns. For example, the mean of RIMSE obtained by PDE+ is about 5.18, which is about 27.6% $(=6.61/5.18-1)$ improvement over kriging-P; while the improvement with respect to RPMSE is more significant about 31.8% $(=1.74/1.32-1)$. Not surprisingly, PDE uses locally linear information via smoothing techniques to capture the function forms of $w_j$ and $f_j$, $j=1,\dots ,\kappa$, which make the rest of processes more well-suited for typical kriging models. Though the original PDE and kriging-P obtain similar results in this setup, the effectiveness of prediction is validated via combining the strengths of PDE and kriging into PDE+.

Table 1.

Averaged values of four indices in the testing locations obtained by methods for data generated from models in (16) and (17) in 100 replicates (values given in parentheses are the corresponding standard errors).

	PDE+				PDE	naive	SpTimer	kriging-P	kriging-N	mgcv	OKFD	WMWC
RIMSE	5.18				6.91	37.17	32.74	6.61	13.30	6.93	8.39	13.45
	(1.21)				(2.67)	(3.33)	(3.57)	(1.31)	(2.03)	(1.13)	(8.50)	(4.28)
RPMSE	1.32				1.79	8.91	8.79	1.74	3.27	1.71	2.07	3.11
	(0.46)				(0.85)	(0.63)	(0.83)	(0.44)	(0.54)	(0.40)	(2.03)	(0.95)
CRPS	0.05				0.10	5.57	5.43	0.17	1.06	0.25	0.25	0.22
	(0.06)				(0.12)	(5.97)	(5.85)	(0.38)	(0.78)	(0.37)	(0.31)	(0.48)
Iscore	0.19				0.25	4.35	4.31	0.22	0.37	0.25	0.33	0.48
	(0.27)				(0.37)	(5.34)	(5.30)	(0.45)	(0.17)	(0.38)	(0.43)	(0.82)

Both kriging-N and WMWC via removing a non-constant mean function prior to modeling the complicated covariance structure indeed pay some price in estimation. It is not appropriate for OKFD to ignore the correlation interactions between space and time in estimation. In contrast, the naive and SpTimer produce considerable error in prediction, however.

Example 3.2

Generate a process, $\{z(\mathbf{s},t):\mathbf{s}\in [-1,1{]}^2\}$, from (5) with setting

$$\begin{array}{rl}{f}_1(\mathbf{s})& =15/\{-0.75+\exp (||\mathbf{s}-(-0.5,-0.5{)}^{\prime }|{|}^2)\},\\ f_2(\mathbf{s})& =1.5(-2+||\mathbf{s}-(0.5,0.5{)}^{\prime }|{|}^2{)}^2,\end{array}$$ (18)

$$\begin{array}{rl}{w}_1(t)& =\arctan (0.1\pi t),w_2(t)=2\log (0.75+(0.1t-1{)}^2),\end{array}$$ (19)

for $t=1,\dots ,T$, and $u(\mathbf{s},t)$ being a zero-mean random effect with the covariance

$$\begin{array}{rl}\mathrm{cov}(u(\mathbf{s},t),u({\mathbf{s}}^{\ast },t^{\ast }))& =0.25\exp (-0.5||\mathbf{s}-{\mathbf{s}}^{\ast }||)\exp (-0.8||t-t^{\ast }||)\\ & +\exp (-0.5||\mathbf{s}-{\mathbf{s}}^{\ast }||)+0.5\exp (-0.8||t-t^{\ast }||).\end{array}$$

We also generate $\epsilon (\mathbf{s},t)\underset{\sim }{\mathrm{i}.\mathrm{i}.\mathrm{d}.}\mathrm{N}(0,0.5)$ over time and space. We need to estimate two sufficient dimension reduction vectors, ${\mathit{\theta }}_1=(0.5,0.5,0.5,0.5{)}^{\prime }$ and ${\mathit{\theta }}_2=(-0.5,-0.5,0.5,0.5{)}^{\prime }$, as previous mentioned.

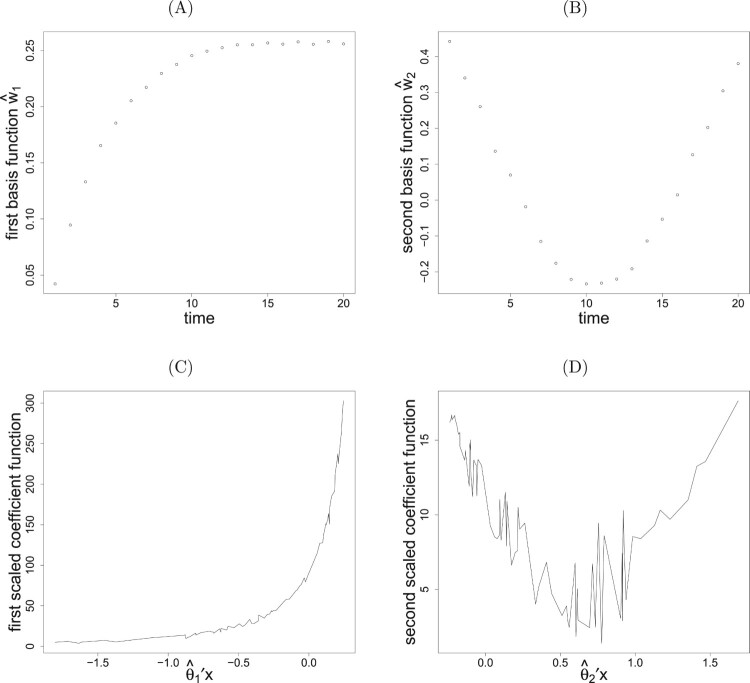
The data with n = 150 are generated according to models (18), (19) and (4) for a single run. Using the eigenvalue decomposition, the modified eigenvalues (1.50, 0.35, 0, 0) found by mrSIR suggest one $\mathbf{x}(\mathbf{s})$ variate and another significant direction is also found by pe-mrPHD with the eigenvalues (2.50, 1.93, 0.65, 0.50). Two leading directions for $\mathbf{x}(\mathbf{s})$ variates, ( 0.520, 0.480, 0.530, 0.467) ${}^{\prime }$ and $(-0.510,-0.488,0.517,0.483{)}^{\prime }$, are found by taking $h_Y=10,h_{\mathbf{x}}=0.5$, after attaining the iterative convergence. The estimates along with $|\cos ({\hat{\mathit{\theta }}}_1)|=0.998$ and $|\cos ({\hat{\mathit{\theta }}}_2)|=0.999$ are consistently close to the theoretical vectors ${\mathit{\theta }}_j,j=1,2$. The first two estimated basis functions, shown in Figure 2(A,B), reveal clear arctangent and quadratic patterns. Figure 2(C,D) displays estimated coefficient functions which are very close to the true views.

Figure 2.

Plots of (A) the first and (B) the second basis functions with (C) the first and (D) the second scaled coefficient functions for a randomly selected simulation from model in (18) and (19).

The results based on 100 simulation runs according to (18) and (19) are summarized in Table 2. As regards the predictive accuracy, PDE+ does outperform with the smallest averaged indices compared to other methods. The original PDE significantly outperforms kriging-P and kriging-N in this example. In contrast, other methods perform worse duo to lacking the capture of the substantial mean structure. The mean of RIMSE obtained by PDE+ is about 5.83, which is about 79% $(=10.44/5.83-1)$ improvement over kriging-P; while the improvement is more significant about 116% ( $=3.57/1.65-1)$ with respect to RPMSE, for example. In contrast, the naive and SpTimer produce considerable error in prediction, however.

Table 2.

Averaged values of four indices in the testing locations obtained by methods for data generated from models in (18) and (19) in 100 replicates (values given in parentheses are the corresponding standard errors).

	PDE+				PDE	naive	SpTimer	kriging-P	kriging-N	mgcv	OKFD	WMWC
RIMSE	5.83				6.43	65.38	61.05	10.44	17.57	13.55	10.44	12.10
	(1.35)				(1.59)	(8.66)	(7.29)	(5.05)	(4.14)	(2.61)	(19.86)	(4.64)
RPMSE	1.65				1.81	17.53	16.35	3.57	5.85	4.12	2.85	2.86
	(0.53)				(0.63)	(2.49)	(2.43)	(1.91)	(1.67)	(0.78)	(5.24)	(1.06)
CRPS	0.36				0.41	11.5	10.41	0.91	2.11	0.45	0.45	0.78
	(0.30)				(0.44)	(10.11)	(9.28)	(1.66)	(3.40)	(0.60)	(0.64)	(0.30)
Iscore	0.23				0.25	7.70	6.78	0.46	0.99	0.48	0.67	0.46
	(0.15)				(0.26)	(10.39)	(9.52)	(0.89)	(2.75)	(0.44)	(0.52)	(0.11)

4. Applications to real data

To illustrate the application of our approach to predictive modeling for empirical studies, we analyze two real datasets. In the following datasets, the longitudes and latitudes are available for given spatial locations. Additional information about elevation in the second dataset is usable. We set the respective spatial-only covariate vector to be $\mathbf{x}(\mathbf{s})=(s_1,s_2,s_1^2,s_2^2{)}^{\prime }$ and $\mathbf{x}(\mathbf{s})=(s_1,s_2,s_1^2,s_2^2,m{)}^{\prime }$, where $s_1$ is the longitude, $s_2$ is the latitude, and m is the elevation.

4.1. Canadian weather data

We applied the proposed method to a dataset of average temperatures over the years 1960–1994 for each day of the year at 35 weather stations in Canada. The data are available in the fda package on Comprehensive R Archive Network (CRAN). The observations $\{y(\mathbf{s},t)\}$ of interest are the average of temperatures measured on 35 location sites for 365 days.

The annual temperature cycle at 35 stations shown in Figure 3(A) indicates a clear concave-down pattern. The map of observation locations is shown in Figure 3(B). For illustration, we first standardize $\mathbf{x}(\mathbf{s})$ for being centered and removing scale. We randomly partition $\{\mathbf{y}({\mathbf{s}}_i,\cdot );i=1,\dots ,35\}$ into a learning set with size 30 and a testing set with size 5 for further comparison analysis. We exclude learning data at randomly sampled 73 $(=20\mathrm{\%}\times 365)$ days for validation purpose. Details in one single analysis run are demonstrated. We conduct the eigenvalue decomposition for the learning data to obtain initial estimates ${\hat{\mathit{\theta }}}_j$'s. Two significant directions are found by pe-mrPHD with the eigenvalues (2.71, 2.35, 1.20, 0.81). By choosing the bandwidths, $h_Y=3.5$ and $h_{\mathbf{x}}=1$, we proceed with the proposed algorithm to dimension reduction for $\mathbf{x}({\mathbf{s}}_i)$ and $y({\mathbf{s}}_i,t)$, $i=1,\dots ,30$; $t=1,\dots ,365$. After convergence, two leading directions are $(-0.109,-0.950,0.217,-0.198{)}^{\prime }$ and (0.314, 0.110, 0.900, 0.281) ${}^{\prime }$. It shows that there exist respective dominant effects, latitude and squared longitude, for the first two variates.

According to (5), both basis functions $w_j(t)$ and coefficient functions $f_j(\mathbf{s})$ affect $z(\mathbf{s},t)$ through the inner product form. Figure 3(C,D) displays the estimated basis functions which reveal similar concave patterns. Figure 3(C) displays that ${\hat{w}}_1$ is positive and has much higher values at the left and right sides along the horizontal axis (Day) (indicating a winter season), but lower values in the middle (indicating a summer season). The levels of function ${\hat{f}}_1(\mathbf{s})$ over spatial locations $\mathbf{s}$ shown in Figure 3(E) reveal a decreasing trend as the latitude increases. This figure also shows a large portion of locations with negative values for ${\hat{f}}_1(\mathbf{s})$. As a result, the influence of the first dominant component ${\hat{w}}_1(t){\hat{f}}_1(\mathbf{s})$ just goes consistently with the common sense that the larger latitude is, the lower temperature is in winter; the lower latitude is, the higher temperature is in summer. The shape of Figure 3(D) roughly contrasts the temperature difference between summer and winter, due to the two seasons with the opposite signs of the function value for ${\hat{w}}_2$. Figure 3(F) displays the levels of ${\hat{f}}_2(\mathbf{s})$ over locations, indicating the maximum of the absolute value of ${\hat{f}}_2(\mathbf{s})$ occurred nearly around the continental areas. Note that ${\hat{f}}_2$ is negative for all areas. Figure 3(F) indicates that the bright-red (continental) regions have greater temperature difference compared to the faint-red (coastal) regions. Consequently, the secondary component ${\hat{w}}_2(t){\hat{f}}_2(\mathbf{s})$ implies that continental areas tend to have lower temperatures in winter, and higher temperatures in summer compared to the coastal regions. The colors in Figure 3(A,B) are based on the corresponding temperature difference. The pattern in Figure 3(F) can be also found in Figure 3(B). More specifically, Figure 3(A) implies the temperature differences are greater in brown curves (continental areas) than in pink curves (coastal areas).

In reference to the sampling performance, the results based on 100 sets of random data partitions, as previously mentioned are summarized in Table 3. With including a three-term interaction in (15) (i.e. the $q_7$ term), mgcv produces a considerable error with the respective mean values of 2487.9, 235.8, 7.3, and 14.7 for RIMSE, RPMSE, CRPS and Iscore. The larger values of indices found by mgcv indicate its heavy overfitting. It should be aware of the constraint impact on model complexity, even though mgcv provides its automatic penalty determination. The results for mgcv shown in Table 3 are obtained through excluding the $q_7$ term. Interestingly, PDE captures the sharp functional patterns for $w_j(t)$ and $f_j(\mathbf{s})$, j = 1, 2, useful for improving model prediction. Not unexpectedly, PDE+ does outperform with the smallest averaged indices through integrating PDE for the dominant mean structure with kriging for estimating the random effect. From the outputs of Table 3 and Figure 3, PDE+ indeed shows an interpretable predictive model in addition to improving the accuracy of model prediction.

Table 3.

Averaged values of four indices in the testing locations obtained by methods for Canadian Weather data in 100 validations (values given in parentheses are the corresponding standard errors).

	PDE+				PDE	naive	SpTimer	kriging-P	kriging-N	mgcv	OKFD	WMWC
RIMSE	50.21				101.93	112.67	96.64	55.58	54.72	174.77	238.75	191.72
	(24.91)				(24.8)	(32.48)	(29.37)	(25.89)	(13.16)	(168.21)	(233.38)	(13.78)
RPMSE	3.01				5.79	6.68	6.47	3.32	3.14	13.31	17.76	10.16
	(1.88)				(1.63)	(2.06)	(2.09)	(1.47)	(0.82)	(15.77)	(19.54)	(0.73)
CRPS	0.72				2.24	2.73	2.61	0.76	1.11	1.84	2.14	7.06
	(0.59)				(1.51)	(3.22)	(3.23)	(0.86)	(1.01)	(1.99)	(1.23)	(4.12)
Iscore	0.47				1.11	1.78	1.72	0.50	0.47	1.95	2.72	4.61
	(0.31)				(0.93)	(2.99)	(2.98)	(0.48)	(0.39)	(1.69)	(1.38)	(4.01)

4.2. German PM ${}_{10}$ data

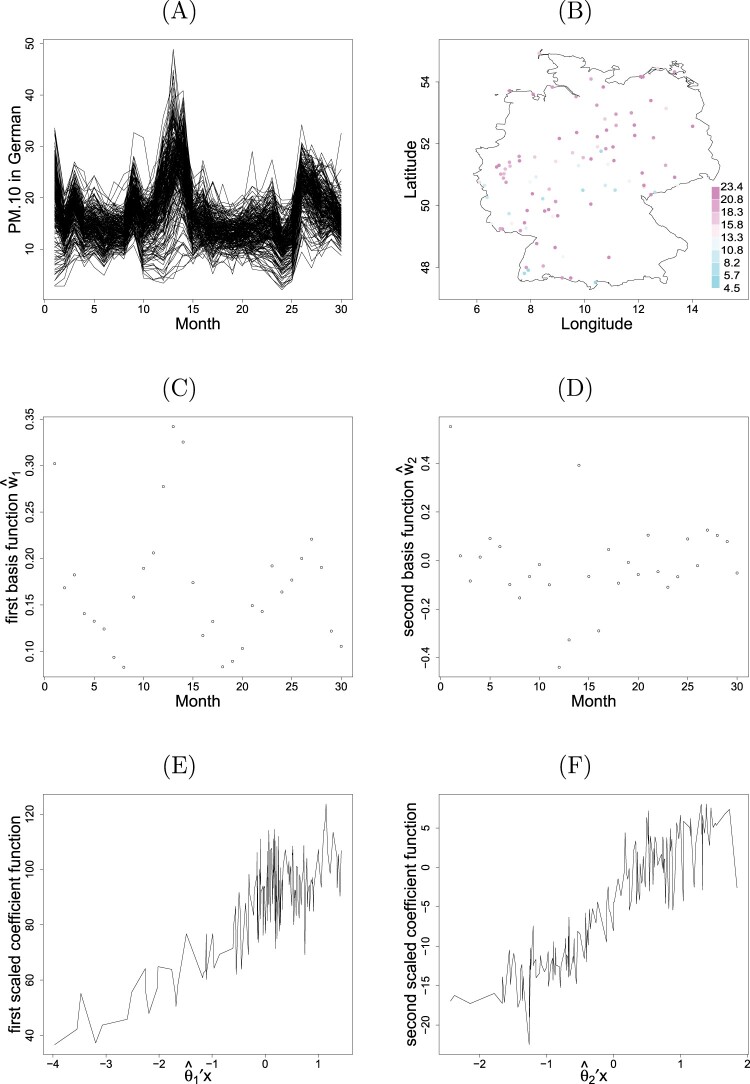
We applied the proposed method to a dataset of air quality obtained from European Commission's Airbase and air quality e-reporting repositories (AQER). The monthly averages of PM ${}_{10}$ concentrations within Germany between January 2016 and June 2018 are considered. The package saqgetr on CRAN was used to extract hourly PM ${}_{10}$ averages, and an aggregation to obtain monthly averages was performed at each of background stations. Totally 221 stations have complete monthly records over the 30 months considered. The monthly average concentrations for 221 stations shown in Figure 4(A) indicate several peaks occurring particularly at the beginning of years.

Figure 4.

Plots of (A) the monthly averages of PM ${}_{10}$ concentrations over individual locations, (B) the spatial distribution of locations, (C) the first and (D) the second basis functions, and (E) the first and (F) the second scaled coefficient functions for German PM ${}_{10}$ data.

In addition to location information, this dataset also contains elevation values. We will demonstrate that spatial covariates show two dominate effects in the PDE+ model. The map of station locations is shown in Figure 4(B), where the color gradients represent the average concentrations of PM ${}_{10}$ values over the 30 months of individual sites. For illustration, we first standardize $\mathbf{x}(\mathbf{s})$ for being centered and removing scale for further analysis. We randomly partition $\{\mathbf{y}({\mathbf{s}}_i,\cdot );i=1,\dots ,221\}$ into a learning data with size 177 and a testing data with size 44. We also exclude learning data at randomly sampled 6 $(=20\mathrm{\%}\times 30)$ months for validation purpose.

In one single analysis run, the eigenvalue decomposition is conducted for the learning data to obtain initial estimates ${\hat{\mathit{\theta }}}_j$'s. Two significant directions are found by pe-mrPHD with the eigenvalues (0.68, 0.60, 0.21, 0.17, 0.07). After the convergence of PDE algorithm with choosing the bandwidths $h_Y=6$ and $h_{\mathbf{x}}=1$, two leading directions, $(0.28,0.17,0.21,0.08,-0.91{)}^{\prime }$ and $(0.71,0.60,0.06,-0.08,0.35{)}^{\prime }$, for $\mathbf{x}(\mathbf{s})$ variates are obtained. It reveals that there exist respective dominant effects; namely, elevation (with negative association) for the first variate, and a linear combination of longitude and latitude (with approximately equal weight) for the second variate.

Recall that both $w_j(t)$ and $f_j(\mathbf{s})$ affect $z(\mathbf{s},t)$ through the inner product form. Figure 4(C) displays the first estimated basis function with a conceivable ‘W’ pattern reflecting the peaks of the data. It indicates that German PM ${}_{10}$ concentrations are higher in winter than in summer. Figure 4(E) shows a linearly increasing trend of ${\hat{f}}_1$ associated with a large negative elevation effect in ${\hat{\mathit{\theta }}}_1$. As a result, the influence of the first dominant component ${\hat{w}}_1(t){\hat{f}}_1(\mathbf{s})$ shows that the larger (smaller) the elevation levels, the smaller (larger) is the value of PM ${}_{10}$. Figure 4(D) displays a near equal-partitioned pattern fluctuating around zero in the vertical axis. Figure 4(F) exhibits a linearly increasing pattern along ${\hat{\mathit{\theta }}}_2^{\prime }\mathbf{x}(\mathbf{s})$, roughly standing for a direction from northeast to southwest, due to the equal-weight effect of longitude and latitude in ${\hat{\mathit{\theta }}}_2$. Consequently, the influence of the second component ${\hat{w}}_2(t){\hat{f}}_2(\mathbf{s})$ illustrates that the air pollution of PM ${}_{10}$ in Germany widely spreads over in the areas from northeast to southwest, similar to the colored pattern shown in Figure 4(B). Compared to Figure 4(E), the second component may serve as the complement part of influence on PM ${}_{10}$ due to the magnitudes.

The results based on 100 random data partitions for sampling performance are summarized in Table 4. To make a compatible comparison, kriging-P uses universal kriging with elevation being the covariate in the mean part. For methods without a natural way to include the covariates (e.g. OKFD and naive), we simply subtract the mean function obtained by a linear regression of $y(\mathbf{s},t)$ on elevation from $y(\mathbf{s},t)$. Again, PDE indeed captures the interesting functional patterns for $w_j(t)$ and $f_j(\mathbf{s})$, j = 1, 2. In the aspect of predictive accuracy, PDE+ does outperform with the smallest averaged indices, as shown in Table 4. More importantly, PDE+ can greatly help the explanation of the spatio-temporal trends, which is difficult for all other methods.

Table 4.

Averaged values of four indices in the testing locations obtained by methods for German PM ${}_{10}$ data in 100 validations (values given in parentheses are the corresponding standard errors).

	PDE+				PDE	naive	SpTimer	kriging-P	kriging-N	mgcv	OKFD	WMWC
RIMSE	17.28				27.64	19.17	18.32	17.68	24.78	18.95	90.19	90.79
	(1.98)				(1.95)	(1.19)	(0.98)	(3.49)	(1.40)	(1.07)	(2.79)	(9.90)
RPMSE	3.29				5.12	3.68	3.47	3.43	4.68	3.56	16.71	16.84
	(0.38)				(0.37)	(0.21)	(0.24)	(0.7)	(0.25)	(0.20)	(0.49)	(1.78)
CRPS	0.86				1.66	1.22	1.18	1.01	2.46	1.18	14.51	13.32
	(0.55)				(0.7)	(1.31)	(1.24)	(0.88)	(2.67)	(0.99)	(2.68)	(5.32)
Iscore	0.48				0.76	0.65	0.57	0.49	1.52	0.55	11.26	10.49
	(0.29)				(0.39)	(1.13)	(1.09)	(0.55)	(2.38)	(0.66)	(2.91)	(5.34)

5. Discussion

Exploring the mean structure for spatio-temporal data via dimension reduction is studied in this article. Effective dimension reduction is a much more challenging statistical issue on spatio-temporal data, which was less paid attention in the past decades. We focus on dimension reduction for the spatial covariates $\mathbf{x}(\mathbf{s})$ to increase the interpretability of the predictive model. Searching the optimum of possible linear combinations for $\mathbf{x}(\mathbf{s})$ is crucial for solving such a problem. Another important issue is to discover the connection of linear or nonlinear association with the spatio-temporal variables of interest. The PDE+ can successfully achieve the above goals. In simulations, the performance of PDE is comparable to kriging, while in real applications, kriging works better than PDE. Overall, PDE+, combining PDE and kriging, outperforms kriging in all situations. The proposed method based on dimension reduction effectively demonstrates its interpretable and accurate prediction from all the numerical results.

In contrast, few methods utilize a data-driven approach for providing the estimation of mean structures in the literature. Two exceptions investigated in the numerical examples are kriging-N and WMWC, which may trade stability off for flexibility. The number of unknown parameters in the data-driven estimation of $w_j(t)f_j(\mathbf{s})$ in (6) is relatively small compared to the available $n\times T$ data points. For example, $w_j(t)$ and ${\mathit{\theta }}_j$ in the jth component have respective T and p parameters, while $f_j(\mathbf{s})\equiv f_j({\mathit{\theta }}_j^{\prime }\mathbf{x}(\mathbf{s}))$ is merely a univariate smoother for the variate ${\mathit{\theta }}_j^{\prime }\mathbf{x}({\mathbf{s}}_i)$. Besides, the number of parameters in $C(\mathbf{s}-{\mathbf{s}}^{\ast },t-t^{\ast })$ for $u(\mathbf{s},t)$ is usually less than a dozen. Using the smaller number of parameters in PDE+ not only prevent the modeling from overfitting, but also allow it to be more easily interpretable. Hence, we can think of PDE+ as a parsimonious ensemble learner with great prediction ability as typical ensemble methods, but not being a hard-to-understand black box.

Appendix.

The codes for implementing the PDE+ method of this article are available at https://github.com/hhlue/PDEplus. We also illustrate how to extract the components of a PDE+ model, and how to predict based on PDE+, through a simulation in Example 3.1. In addition, the datasets of monthly German PM ${}_{10}$ concentrations in Section 4.2 can also be found from the same webpage.

Funding Statement

Lue's and Tzeng's research works were supported in part by grants from the Ministry of Science and Technology of Taiwan [grant numbers MOST107-2118-M-029-001 and MOST 107-2118-M-110-004-MY3], respectively.

Disclosure statement

No potential conflict of interest was reported by the author(s).