Hierarchical VAEs provide a normative account of motion processing in the primate brain

Abstract

The relationship between perception and inference, as postulated by Helmholtz in the 19th century, is paralleled in modern machine learning by generative models like Variational Autoencoders (VAEs) and their hierarchical variants. Here, we evaluate the role of hierarchical inference and its alignment with brain function in the domain of motion perception. We first introduce a novel synthetic data framework, Retinal Optic Flow Learning (ROFL), which enables control over motion statistics and their causes. We then present a new hierarchical VAE and test it against alternative models on two downstream tasks: (i) predicting ground truth causes of retinal optic flow (e.g., self-motion); and (ii) predicting the responses of neurons in the motion processing pathway of primates. We manipulate the model architectures (hierarchical versus non-hierarchical), loss functions, and the causal structure of the motion stimuli. We find that hierarchical latent structure in the model leads to several improvements. First, it improves the linear decodability of ground truth factors and does so in a sparse and disentangled manner. Second, our hierarchical VAE outperforms previous state-of-the-art models in predicting neuronal responses and exhibits sparse latent-to-neuron relationships. These results depend on the causal structure of the world, indicating that alignment between brains and artificial neural networks depends not only on architecture but also on matching ecologically relevant stimulus statistics. Taken together, our results suggest that hierarchical Bayesian inference underlines the brain’s understanding of the world, and hierarchical VAEs can effectively model this understanding.

1. Introduction

Intelligent interactions with the world require representation of its underlying composition. This inferential process has long been postulated to underlie human perception [1–9], and is paralleled in modern machine learning by generative models [10–17], which learn latent representations of their sensory inputs. The question of what constitutes a “good” representation has no clear answer [18, 19], but several desirable features have been proposed. In the field of neuroscience, studies focused on object recognition have suggested that effective representations “untangle” the various factors of variation in the input, rendering them linearly decodable [20, 21]. This intuitive notion of linear decodability has emerged in the machine learning community under different names such as “informativeness” [22] or “explicitness” [23]. Additionally, it has been suggested that “disentangled” representations are desirable, wherein distinct, informative factors of variations in the data are separated [24–29]. Artificial neural networks (ANNs) are also increasingly evaluated based on their alignment with biological neural processing [30–38], because of the shared goals of ANNs and the brain’s sensory processing [25, 39, 40]. Such alignment also provides the possibility of gaining insights into the brain by understanding the operations within an ANN [41–47].

In this work, we investigate how the combination of (i) model architecture, (ii) loss function, and (iii) training dataset, affects learned representations, and whether this is related to the brain-alignment of the ANN [41, 44]. We focus specifically on understanding the representation of motion because large sections of the visual cortex are devoted to processing motion [34], and the causes of retinal motion (moving objects and self-motion [48]) can be manipulated systematically. Crucially, motion in an image can be described irrespective of the identity and specific visual features that are moving, just as the identity of objects is invariant to how they are moving. This separation of motion and object processing mirrors the division of primate visual processing into dorsal (motion) and ventral (object) streams [49–51].

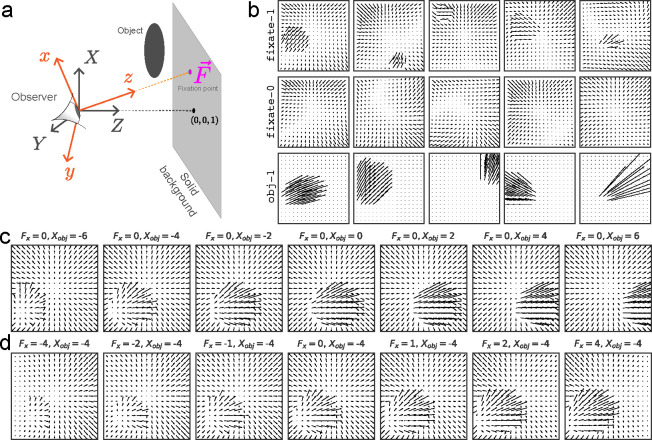
We designed a naturalistic motion simulation based on distributions of ground truth factors corresponding to the location and depth of objects, motion of these objects, motion of the observer, and observer’s direction of gaze (i.e., the fixation point; Fig. 1a). Using our simulated retinal flow, we then trained and evaluated an ensemble of autoencoder-based models on our simulation. We based our evaluation on (1) whether the models untangle and disentangle the ground truth factors in our simulation; and (2) the degree to which their latent spaces could be directly related to neural data recorded in the dorsal stream of primates (area MT).

Figure 1:

Retinal Optic Flow Learning (ROFL): a simulation platform for synthesizing naturalistic optic flow patterns. (a) The general setup includes a moving or stationary observer and a solid background, with optional moving object(s) in the scene. More details are provided in the appendix (section 13). (b) Example frames showcasing different categories (see Table 1 for definitions). (c, d) Demonstrating the causal effects of varying a single ground truth factor while keeping all others fixed: (c) $X_{obj}$, the $x$ component of object position (measured in retinal coordinates, orange), and (d) $F_x$, the $X$ component of the fixation point (measured in fixed coordinates, gray).

We introduce a new hierarchical variational autoencoder, the “compressed” Nouveau VAE (cNVAE) [52]. The cNVAE exhibited superior performance compared to other models across our multiple evaluation metrics. First, it discovered latent factors that accurately captured the ground truth factors in the simulation in a more disentangled manner than other models. Second, it achieved significant improvements in predicting neural responses compared to the previous state-of-the-art model [34], doubling the performance, with sparse mapping from its latent space to neural responses.

Taken together, these observations demonstrate the power of the synthetic data framework and show that a single inductive bias—hierarchical latent structure—leads to many desirable features of representations, including brain alignment.

2. Background & Related Work

Neuroscience and VAEs.

It has long been argued that perception reflects unconscious inference of the structure of the world constructed from sensory inputs. The concept of “perception as unconscious inference” has existed since at least the 19th century [1, 2], and more recently inspired Mumford [3] to conjecture that brains engage in hierarchical Bayesian inference to comprehend the world [3, 4]. These ideas led to the development of Predictive Coding [5, 9, 53–58], Bayesian Brain Hypothesis [6, 59–63], and Analysis-by-Synthesis [7], collectively suggesting that brains contain an internal generative model of the world [7, 8, 64]. A similar idea underlies modern generative models [15–17, 65–67], especially hierarchical variants of VAEs [52, 68–70].

The Nouveau VAE (NVAE) [52] and very deep VAE (vdvae) [68] demonstrated that deep hierarchical VAEs can generate realistic high-resolution images, overcoming the limitations of their non-hierarchical predecessors. However, neither work evaluated how the hierarchical latent structure changed the quality of learned representations. Additionally, both NVAE and vdvae have an undesirable property: their convolutional latents result in a latent space that is several orders of magnitude larger than the input space, defeating a main purpose of autoencoders: compression. Indeed, Hazami et al. [71] showed that a tiny subset (around 3%) of the vdvae latent space is sufficient for comparable input reconstruction. Here, we demonstrate that it is possible to compress hierarchical VAEs and focus on investigating their latent representations with applications to neuroscience data.

Evaluating ANNs on predicting biological neurons.

Several studies have focused on evaluating ANNs on their performance in predicting brain responses, but almost entirely on describing static (“ventral stream”) image processing [30, 33, 36]. In contrast, motion processing (corresponding to the dorsal stream) has only been considered thus far in Mineault et al. [34], who used a 3D ResNet (“DorsalNet”) to extract ground truth factors about self-motion from drone footage (“AirSim”, [72]) in a supervised manner. DorsalNet learned representations with receptive fields that matched known features of the primate dorsal stream and achieved state-of-the-art on predicting neural responses on the dataset that we consider here. In addition to our model architecture and training set, a fundamental difference between our approach and Mineault et al. [34] is that they trained their models using direct supervision. As such, their models have access to the ground truth factors at all times. Here, we demonstrate that it is possible to obtain ground truth factors “for free”, in a completely unsupervised manner, while achieving better performance in predicting responses of biological neurons.

Using synthetic data to train ANNs.

A core component of a reductionist approach to studying the brain is to characterize neurons based on their selectivity to a particular subset of pre-identified visual “features”, usually by presenting sets of “feature-isolating” stimuli [73]. In the extreme, stimuli are designed that remove all other features except the one under investigation [74]. While these approaches can inform how pre-selected feature sets are represented by neural networks, it is often difficult to generalize this understanding to more natural stimuli, which are not necessarily well-described by any one feature set. As a result, here we generate synthetic data representing a naturalistic distribution of natural motion stimuli. Such synthetic datasets allow us to manipulate the causal structure of the world, in order to make hypotheses about what aspects of the world matter for the representations learned by brains and ANNs [75]. Like previous work on synthesized textures [15], here we specifically manipulate the data generative structure to contain factors of variation due to known ground truth factors.

3. Approach: Data & Models

Retinal Optic Flow Learning (ROFL).

Our synthetic dataset framework, ROFL, generates the resulting optic flow from different world structures, self-motion trajectories, and object motion (Fig. 1a, see also [76]).

ROFL can be used to generate naturalistic flow fields that share key elements with those experienced in navigation through 3-D environments. Specifically, each frame contains global patterns that are due to self-motion, including rotation that can arise due to eye or head movement [77, 78]. In addition, local motion patterns can be present due to objects that move independently of the observer [48]. The overall flow pattern is also affected by the observer’s direction of gaze (fixation point [79], Fig. 1a).

ROFL generates flow vectors that are instantaneous in time, representing the velocity across the visual field resulting from the spatial configuration of the scene and motion vectors of self and object. Ignoring the time-evolution of a given scene (which can arguably be considered separably [80]) dramatically reduces the input space from [3 × H × W × T] to [2 × H × W], and allows a broader sampling of configurations without introducing changes in luminance and texture. As a result, we can explore the role of different causal structures in representation learning in ANNs.

The retinal flow patterns generated by a moving object depend on both the observer’s self-motion and the rotation of their eyes as they maintain fixation in the world, in addition to the motion of the object itself. For example, Fig. 1c demonstrates a situation where the observer is moving forward, and the object is moving to the right, with different object positions: an object on the left side will have its flow patterns distorted, while an object on the right will have its flow patterns largely unaffected because its flow vectors are parallel with that of the self-motion. In summary, ROFL allows us to simulate retinal optic flow with a known ground truth structure driven by object and self-motion.

The compressed NVAE (cNVAE).

The latent space of the NVAE is partitioned into groups, $\mathit{z}=\left\{{\mathit{z}}_1,{\mathit{z}}_2,\dots ,{\mathit{z}}_L\right\}$, where $L$ is the number of groups. The latent groups are serially dependent, meaning that the distribution of a given latent group depends on the value of the preceding latents, such that the prior is given by $p(\mathit{z})=p\left({\mathit{z}}_1\right)\cdot {\prod }_{\ell =2}^L p\left({\mathit{z}}_{\ell }\mid {\mathit{z}}_{<\ell }\right)$, and approximate posterior is given by $q(\mathit{z}\mid \mathit{x})={\prod }_{\ell =1}^L q\left({\mathit{z}}_{\ell }\mid {\mathit{z}}_{<\ell },\mathit{x}\right)$ (more details in section 9.1. Additionally, different latent groups in the NVAE operate at different spatial scales (Fig. 2, left), with multiple groups per scale. Crucially, such scale-dependent grouping is absent from non-hierarchical VAEs (Fig. 2, right).

Figure 2:

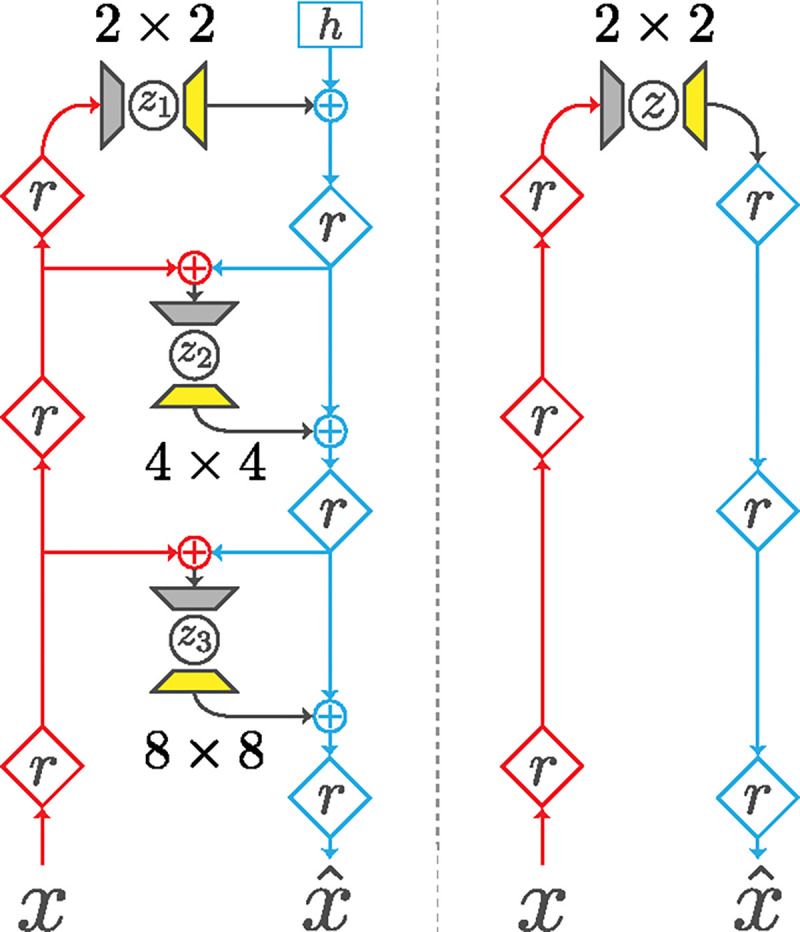
Architecture comparison. Left, compressed NVAE (cNVAE); right, non-hierarchical VAE. We modified the NVAE sampler layer (grey trapezoids) and introduced a deconvolution expand layer (yellow trapezoids). The encoder (inference) and decoder (generation) pathways are depicted in red and blue, respectively. $r$, residual block; $h$, trainable parameter; +, feature combination.

The cNVAE closely follows the NVAE [52], with one important difference: the original NVAE latent space is convolutional, and ours is not. We modified the sampler layers (grey trapezoids, Fig. 2) such that their receptive field sizes match the spatial scale they operate on. Thus, sampler layers integrate over spatial information before sampling from the approximate posterior. The spatial patterns of each latent dimension are then determined by expand modules (yellow trapezoids, Fig. 2), based on a deconvolution step. Further details about the processing of the sampler and expand layers are provided in Supplementary section 9.2.

Our modification of the NVAE serves two purposes. First, it decouples spatial information from the functionality of latent variables, allowing them to capture abstract features that are invariant to particular spatial locations. Second, it has the effect of compressing the input space into a lower-dimensional latent code. We explain this in more detail in Supplementary section 9.3.

Our model has the following structure: 3 latent groups operating at the scale of 2 × 2; 6 groups at the scale of 4 × 4; and 12 groups at the scale of 8 × 8 (Table 4, Fig. 2). Therefore, the model has 3 + 6 + 12 = 21 hierarchical latent groups in total. Each latent group has 20 latent variables, which results in an overall latent dimensionality of 21 × 20 = 420. See Table 4 and Supplementary section 9.3 for more details.

Alternative models.

We evaluated a range of unsupervised models alongside cNVAE, including standard (non-hierarchical) VAEs [11, 12], a hierarchical autoencoder with identical architecture as the cNVAE but trained only with reconstruction loss (cNAE), and an autoencoder (AE) counterpart for the VAE (Table 2). All models had the same latent dimensionality (Table 4), and approximately the same number of parameters and convolutional layers. We used endpoint error as our measure of reconstruction loss, which is the Euclidean norm of the difference between actual and reconstructed flow vectors. This metric works well with optical flow data [81].

Table 2:

Model details. Here, hierarchical means that there are parallel pathways for information to flow from the encoder to the decoder (Fig. 2), which is slightly different from the conventional notion. For variational models, this implies hierarchical dependencies between latents in a statistical sense [68]. This hierarchical dependence is reflected in the KL term for the cNVAE, where L is the number of hierarchical latent groups. See Supplementary section 9.3 for more details and section 9.1 for a derivation. All models have an equal # of latent dimensions (420, see Table 4), approximately the same # of convolutional layers, and # of parameters (~ 24 M). EPE, endpoint error.

Model	Architecture	Loss	Kullback–Leibler term (KL)
cNVAE	Hierarchical	EPE +β * KL	$\mathrm{K}\mathrm{L}={\sum }_{\ell =1}^L {\mathbb{E}}_{q\left({\mathit{z}}_{<\ell }\mid \mathit{x}\right)}\left[{\mathrm{K}\mathrm{L}}_{\ell }\right]$, where ${\mathrm{K}\mathrm{L}}_{\ell }:={𝒟}_{\mathrm{K}\mathrm{L}}\left[q\left({\mathit{z}}_{\ell }\mid \mathit{x},{\mathit{z}}_{<\ell }\right)\parallel p\left({\mathit{z}}_{\ell }\mid {\mathit{z}}_{<\ell }\right)\right]$
VAE	Non-hierarchical	EPE +β * KL	$\mathrm{K}\mathrm{L}={𝒟}_{\mathrm{K}\mathrm{L}}\left[q\right(\mathit{z}\mid \mathit{x})\parallel p(\mathit{z}\left)\right]$
cNAE	Hierarchical	EPE	-
AE	Non-hierarchical	EPE	-

Model representations.

We define a model’s internal representation to be either the mean of each Gaussian for variational models (i.e., samples drawn from $q(\mathit{z}\mid \mathit{x})$ at zero temperature), or the bottleneck activations for autoencoders. For hierarchical models (cNVAE, cNAE), we concatenate representations across all levels (Table 4).

Training details.

Models were trained for 160,000 steps at an input scale of 17 × 17, requiring slightly over a day on Quadro RTX 5000 GPUs. Please refer to Supplementary section 9.4 for additional details.

Disentanglement and $\beta$-VAEs.

A critical decision when optimizing VAEs involves determining the weight assigned to the KL term in the loss function compared to the reconstruction loss. Prior research has demonstrated that modifying a single parameter, denoted as $\beta$, which scales the KL term, can lead to the emergence of disentangled representations [82, 83]. Most studies employing VAEs for image reconstruction typically optimize the standard evidence lower bound (ELBO) loss, where $\beta$ is fixed at a value of 1 [11, 52, 68]. However, it should be noted that due to the dependence of the reconstruction loss on the input size, any changes in the dimensionality of the input will inevitably alter the relative contribution of the KL term, and thus the “effective” $\beta$ [82].

Furthermore, Higgins et al. [16] recently established a strong correspondence between the generative factors discovered by $\beta$-VAEs and the factors encoded by inferotemporal (IT) neurons in the primate ventral stream. The alignment between these factors and IT neurons exhibited a linear relationship with the value of $\beta$. In light of these findings, we explicitly manipulate the parameter $\beta$ within a range spanning from 0.01 to 10 to investigate the extent to which our results depend on its value.

4. Results

Our approach is based on the premise that the visual world contains a hierarchical structure. We use a simulation containing a hierarchical structure (ROFL, described above) and a hierarchical VAE (the cNVAE, above) to investigate how these choices affect the learned latent representations. While we are using a relatively simple simulation generated from a small number of ground truth factors, $\mathit{g}$, we do not specify how $\mathit{g}$ should be represented in our model or include $\mathit{g}$ in the loss. Rather, we allow the model to develop its own latent representation in a purely unsupervised manner. See Supplementary section 9.6 for more details on our approach.

We first consider hierarchical and non-hierarchical VAEs trained on the fixate-1 condition (see Table 1, throughout this work, fixate-1 is used unless stated otherwise). We extracted latent representations from each model and estimated the mutual information (MI) between the representations and ground truth factors such as self-motion, etc. For fixate-1, each data sample is uniquely determined using 11 ground truth factors (Table 1), and the models have latent dimensionality of 420 (Table 4). Thus, the resulting MI matrix has shape 11 × 420, where each entry shows how much information is contained in that latent variable about a given ground truth factor.

Table 1:

ROFL categories used in this paper. ground truth factors include fixation point (+2); velocity of the observer when self-motion is present (+3); and, object position & velocity (+6). Figure 1b showcases a few example frames for each category. The stimuli can be rendered at any given spatial scale N, yielding an input shape of 2 × N × N. Here we work with N = 17.

Category	Description	Dimensionality
fixate-1	A moving observer maintains fixation on a background point. In addition, the scene contains one independently moving object.	11 = 2 + 3 + 6
fixate-0	Same as fixate-1 but without the object.	5 = 2 + 3
obj-1	A single moving object, stationary observer.	8 = 2 + 6

Functional specialization emerges in the cNVAE.

Figure 3 shows the MI matrix for the latent space of cNVAE (top) and VAE (bottom). While both models achieved a good reconstruction of validation data (Fig. 14), the MI matrix for cNVAE exhibits clusters corresponding to distinct ground truth factors at different levels of the hierarchy. Specifically, object-related factors of variation are largely captured at the top 2 × 2 scale, while information about fixation point can be found across the hierarchy, and self-motion is largely captured by 8 × 8 latent groups. In contrast, non-hierarchical VAE has no such structure, suggesting that the inductive bias of hierarchy enhances the quality of latent spaces, which we quantify next.

Figure 3:

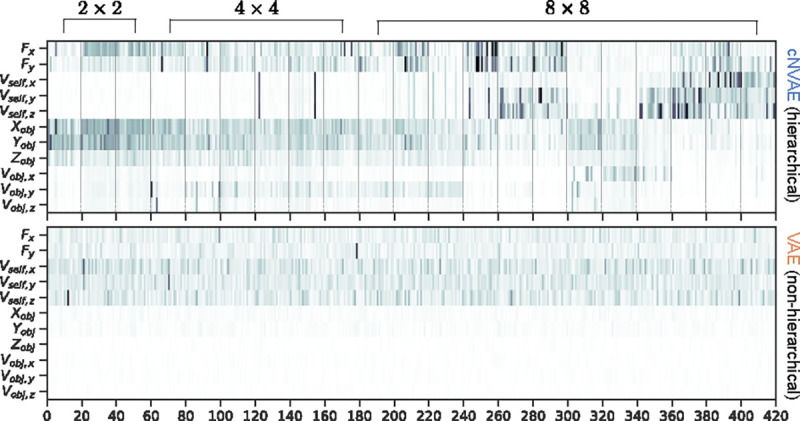
Mutual information between latent variables (x-axis) and ground truth factors (y-axis) is shown for cNVAE (top) and VAE (bottom). Dashed lines indicate 21 hierarchical latent groups of 20 latents each, comprising a 420-dimensional latent space. These groups operate at three different spatial scales, as indicated. In contrast, the VAE latent space lacks such grouping and operates solely at the spatial scale of 2 × 2 (see Fig. 2 and Table 4 for details on model latent configurations).

Evaluating the latent code.

To demonstrate the relationship between ground truth factors and latent representations discovered by the cNVAE visible in Fig. 3. we apply metrics referred to as “untangling” and “disentengling”. Additionally, in a separate set of experiments, we also evaluate model representations by relating them to MT neuron responses, which we call “brain-alignment”. We discuss each of these in detail in the following sections.

Untangling: the cNVAE untangles factors of variation.

One desirable feature of a latent representation is whether it makes information about ground truth factors easily (linearly) decodable [20, 21, 84]. This concept has been introduced in the context of core object recognition as “untangling”. Information about object identity that is “tangled” in the retinal input is untangled through successive nonlinear transforms, thus making it linearly available for higher brain regions to extract [20]. This concept is closely related to the “informativeness” metric of Eastwood and Williams [22] and “explicitness” metric of Ridgeway and Mozer [23].

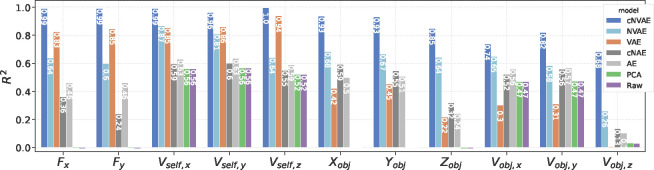
To assess the performance of our models, we evaluated the linear decodability of the ground truth factors, $\mathit{g}$, from model latent codes, $\mathit{z}$. Based on the $R^2$ scores obtained by predicting $\mathit{g}$ from $\mathit{z}$ using linear regression (Fig. 4), the cNVAE greatly outperforms competing models, faithfully capturing all ground truth factors. In contrast, the non-hierarchical VAE fails to capture object-related variables. Notably, the cNVAE can recover the fixation point location $\left(F_X,F_Y\right)$ in physical space almost perfectly. The fixation location has a highly nontrivial effect on the flow patterns, and varying it causes both global and local changes in the flow patterns (Fig. 1d).

Figure 4:

Hierarchical VAE untangles underlying factors of variation in data. The linear decodability of ground truth factors (x-axis) from different latent codes is shown. Untangling scores averaged across all ground truth factors are cNVAE = 0.898, NVAE = 0.639, VAE = 0.548, cNAE = 0.456, AE = 0.477, PCA = 0.236, and Raw = 0.235. For variational models, the best performing $\beta$ values were selected: cNVAE, $\beta =0.15$; VAE, $\beta =1.5$ (see Supplementary section 9.5 for more details).

Furthermore, cNVAE is the only model that reliably captures object position and velocity: especially note $V_{obj,z}$ (last column in Fig. 4). Inferring object motion from complex optic flow patterns involves two key components. First, the model must extract self-motion from flow patterns. Second, the model must understand how self-motion influences flow patterns globally. Only then can the model subtract self-motion from global flow vectors to obtain object motion. In vision science, this is known as the “flow-parsing hypothesis” [85–88]. Such flow-parsing is achieved by the cNVAE but none of the other models. See Supplementary section 11 for further discussion of this result and its implications.

Disentanglement: the cNVAE produces more disentangled representations.

The pursuit of disentanglement in neural representations has garnered considerable attention [23, 82, 89–97]. In particular, Locatello et al. [19] established that learning fully disentangled representations is fundamentally impossible without inductive biases. Prior efforts such as $\beta$-VAE [82] demonstrated that increasing the weight of the KL loss (indicated by $\beta$) promotes disentanglement in VAEs. More recently, Whittington et al. [89] demonstrated that simple biologically inspired constraints such as non-negativity and energy efficiency encourage disentanglement. Here, we demonstrate that another biological inductive bias, hierarchy in the latent space, will promote disentanglement of the latent representations learned by VAEs.

To evaluate the role of hierarchy, we adopted the DCI framework [22] which offers a well-rounded evaluation of latent representations. The approach involves training a simple decoder (e.g., lasso regression) that predicts data generative factors $\mathit{g}$ from a latent code $\mathit{z}$; followed by computing a matrix of relative importances (e.g., based on lasso weights) which is then used to evaluate different aspects of the code quality: Informativeness — measures whether $\mathit{z}$ contains easily accessible information about $\mathit{g}$ (similar to untangling from above). Disentanglement—measures whether individual latents correspond to individual generative factors. Completeness—measures how many $z_i$ are required to capture any single $g_j$. If a single latent contributes to $g_j$’s prediction, the score will be 1 (complete). If all latent variables equally contribute to $g_j$’s prediction, the score will be 0 (maximally overcomplete). Note that “completeness” is also referred to as “compactness” [23]. See Fig. 9 and Supplementary section 9.7.1 for more details, ref. [98] for a review, and ref. [99] for a recent extension of the DCI framework.

We follow the methods outlined by Eastwood and Williams [22] with two modifications: (1) we replaced lasso with linear regression to avoid the strong dependence on the lasso coefficient that we observed, and (2) we estimate the matrix of relative importances using a feature permutation-based algorithm (sklearn.inspection.permutation_importance), which measures the relative performance drop that results from shuffling a given latent.

We found that cNVAE outperforms competing models across all metrics for a broad range of $\beta$ values (Fig. 5). The observed pattern of an inverted U shape is consistent with previous work [82], which suggests that there is an optimal $\beta$ that can be empirically determined. In this case, cNVAE with $\beta =0.5$ achieved the best average DCI score. Further, we found that VAEs lacking hierarchical structure learn highly overcomplete codes, such that many latents contribute to predicting a single ground truth factor. In conclusion, the simple inductive bias of hierarchy in the latent space led to a substantial improvement in VAE performance across all components of the DCI metric.

Figure 5:

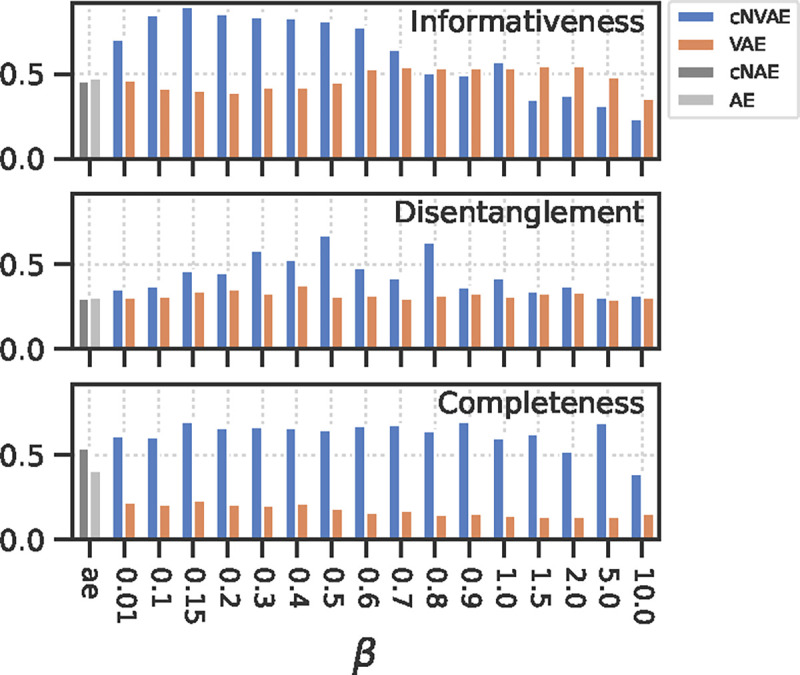
Evaluating the learned latent codes using the DCI framework [22]. Larger values are better for all metrics. Note that informativeness is closely related to untangling [20, 21]. See also Fig. 9.

Brain-alignment: the cNVAE aligns more closely with MT neurons.

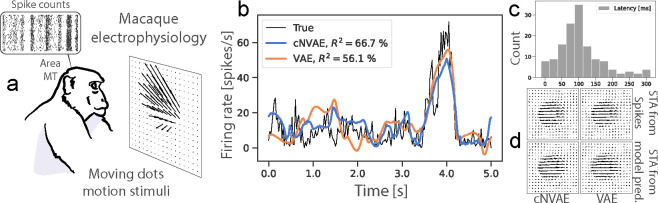
To evaluate the performance of models in predicting neuronal activity in response to motion stimuli, we used an existing dataset of N = 141 MT neurons recorded while presented with random dot kinematograms representing smoothly changing combinations of optic flow velocity fields [100, 101]. A subset of these neurons (N = 84) are publicly available on crcns.org and were recently used in Mineault et al. [34] that we compare to.

To measure neuronal alignment, we first determined the mapping from each model’s latent representation to MT neuron responses (binned spike counts, Fig. 6a). Here, the latent representation is defined as the mean of predicted Gaussian distributions for VAEs, and the bottleneck activations for AEs. We learn this linear latent-to-neuron mapping using ridge regression. Figure 6b shows the average firing rate of an example neuron along with model predictions. Because sensory neurons have a nonzero response latency, we determined each neuron’s optimal response latency, which maximized cross-validated performance. The resulting distribution of best-selected latencies (Fig. 6c) peaked around 100 ms: consistent with known MT latencies [100]. We also empirically optimized ridge coefficients to ensure each neuron has its best fit. Figure 6d shows that the models capture the receptive field properties of MT neurons as measured by the spike-triggered average stimulus. To evaluate performance, we follow methods established by Mineault et al. [34]: whenever repeated trials were available, we report Pearson’s $R$ on that held-out data, normalized by maximum explainable variance [102]. When repeats were not available, we performed 5-fold cross-validation and reported the held-out performance using Pearson’s $R$ between model prediction and spike trains.

Figure 6:

(a) Experimental setup form [100, 101]. (b) Both models explain MT neural variability well. (c) Distribution of best estimated latencies. (d) Spike-triggered averages (STA) are shown.

Evaluating brain alignment.

We use two measures of brain alignment: the success at predicting the neural response (Pearson’s $R$, Fig. 7. Table 3); and, the “alignment” between neurons and individual model latents (Fig. 8, [16]). These mirror the untangling and completeness metrics described above (more details are provided below).

Figure 7:

All models (pretrained on fixate-1) perform comparably in predicting MT neuron responses. Dashed line corresponds to the previous state-of-the-art on this data [103].

Table 3:

Both cNVAE and VAE perform well in predicting MT neuron responses, surpassing previous state-of-the-art models by more than a twofold improvement. Moreover, the clear gap between fixate-1 and other categories highlights the importance of pretraining data [104].

Model	Pretraining dataset	Performance, R (μ ± se; N = 141)
		β = 0.5	β = 0.8	β = 1	β = 5
cNVAE	fixate-1	.506 ± .018	.517 ± .017	.494 ± .018	.486 ± .016
	fixate-0	.428 ± .018	.450 ± .019	.442 ± .019	.469 ± .018
	obj-1	.471 ± .018	.465 ± .018	.477 ± .017	.468 ± .018
VAE	fixate-1	.508 ± .019	.481 ± .018	.494 ± .018	.509 ± .018
cNAE	fixate-1	.476 ± .018
AE	fixate-1	.495 ± .019
CPC [105]	AirSim [72]	.250 ± .020 (Mineault et al. [34])
DorsalNet	AirSim [72]	.251 ± .019 (Mineault et al. [34])

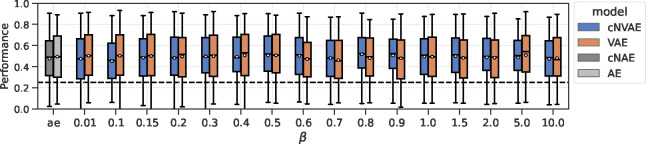
Figure 8:

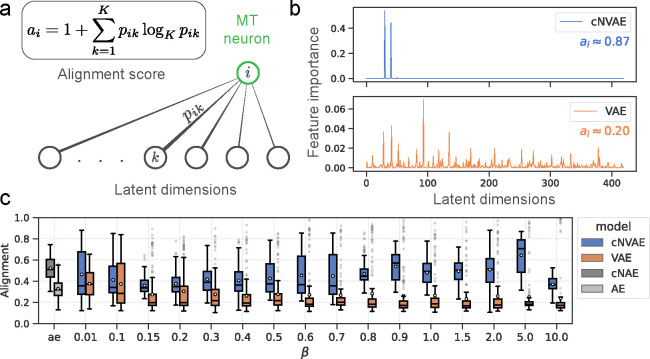
Hierarchical models (cNVAE, cNAE) are more aligned with MT neurons since they enable sparse latent-to-neuron relationships. (a) Alignment score measures the sparsity of permutation feature importances. $a_i=0$ when all latents are equally important in predicting neuron $i$; and, $a_i=1$ when a single latent predicts the neuron. (b) Feature importances are plotted for an example neuron (same as in Fig. 6b). cNVAE $(\beta =0.01)$ predicts this neuron’s response in a much sparser manner compared to non-hierarchical VAE $(\beta =5)$. Supplementary section 9.5 contains a discussion of our rationale in choosing these $\beta$ values. (c) Alignment across $\beta$ values, and autoencoders (ae).

All models predict MT neuron responses well.

After training a large ensemble of unsupervised models on fixate-1 and learning the neural mapping, we found that both hierarchical (cNVAE & cNAE) and non-hierarchical (VAE & AE) variants had similar ability to predict neural responses (Fig. 7). The performance did depend on the loss function itself, with the variational loss outperforming simple autoencoder reconstruction loss (Table 3).

Hierarchical VAEs are more aligned with MT neurons.

We next tested how these factors affect neural alignment, i.e., how closely neurons are related to individual latents in the model. Figure 8a demonstrates what we mean by “alignment”: a sparse latent-to-neuron relationship means larger alignment, indicative of a similar representational “form” [16]. See Fig. 10 for an illustration of this idea. To formalize this notion, we use feature permutation importance (described above), applied to the ridge regression models. This yields a 420-dimensional vector per neuron. Each dimension of this vector captures the importance of a given latent variable in predicting the responses of the neuron. We normalize these vectors and interpret them as the probability of importance. We then define alignment score $a_i$ of neuron $i$ as $a_i=1+{\sum }_{k=1}^K p_{ik}{\mathrm{l}\mathrm{o}\mathrm{g}}_K{p}_{ik}$, where $p_{ik}$ is interpreted as the importance of $k$–th latent variable in predicting neuron $i$ (Fig. 8a). This concept is closely related to the “completeness” score from the DCI framework as discussed above.

For almost all $\beta$ values, the cNVAE exhibited a greater brain alignment than non-hierarchical VAE (Fig. 8c; cNVAE > VAE, paired t–test; see Fig. 16 and Table 5). Similarly, for the autoencoders, we found that the hierarchical variant outperformed the non-hierarchical one (cNAE > AE). Based on these observations, we conclude that higher brain alignment is primarily due to hierarchical latent structure. However, note that hierarchy in the traditional sense did not matter: all these models had approximately the same number of convolutional layers and parameters.

Factors leading to brain-alignment.

To test the effect of the training dataset (i.e., category of ROFL) on model performance, we trained cNVAE models using fixate-0, fixate-1, and obj-1 categories (Table 1), while also exploring a variety of $\beta$ values. We found that fixate-1 clearly outperformed the other two ROFL categories (Table 3), suggesting that both global (e.g., self-motion) and local (e.g., object motion) sources of variation are necessary for learning MT-like representations. The effect of loss function was also visible: some $\beta$ values led to more alignment. But this effect was small compared to the effect of hierarchical architecture (Fig. 8c).

5. Discussion

We introduced a new framework for understanding and evaluating the representation of visual motion learned by artificial and biological neural networks. This framework provides a way to manipulate causes in the world and evaluate whether learned representations untangle and disentangle those causes. In particular, our framework makes it possible to test the influence of architecture (Fig. 2), loss function (Table 2), and training set (Table 1) on the learned representations, encompassing 3 out of the 4 core components of a recently proposed neuroconnectionist research programme [41]. Our framework brings hypothesis-testing to understand [biological] neural processing of vision and provides an interpretive framework to understand neurophysiological data.

The goal of the present work was to establish our framework and demonstrate its potential. To this end, we made several simplifying choices, such as training on individual flow frames rather than time-evolving videos. We provide a detailed discussion of study limitations in Supplementary section 8. Future work will address these by rendering images in simulations and using image-computable models, incorporating real eye-tracking and scene data in ROFL [80, 106], testing our approach on more data from other brain areas such as MST [107, 108], and using more sophisticated methods to measure representational alignment between ANNs and brains [109–112].

Conclusion.

We used synthetic data to test how causal structure in the world affects the representations learned by autoencoder-based models and evaluated the learned representations based on how they represent ground truth factors and how well they align with biological brains. We found that a single inductive bias, hierarchical latent structure, leads to desirable representations and increased brain alignment.

6. Code & Data

Our code and model checkpoints are available here: https://github.com/hadivafaii/ROFL-cNVAE.