Abstract
A widely assumed, but largely untested, tenet in ecology is that ecosystem stability tends to increase over succession. We rigorously test this idea using 60-year continuous data of old field succession across 480 plots nested within 10 fields. We found that ecosystem temporal stability increased over succession at the larger field scale (γ stability) but not at the local plot scale (α stability). Increased spatial asynchrony among plots within fields increased γ stability, while temporal increases in species stability and decreases in species asynchrony offset each other, resulting in no increase in α stability at the local scale. Furthermore, we found a notable positive diversity-stability relationship at the larger but not local scale, with the increased γ stability at the larger scale associated with increasing functional diversity later in succession. Our results emphasize the importance of spatial scale in assessing ecosystem stability over time and how it relates to biodiversity.
Continuous 60-year monitoring shows ecosystem stability increased over succession at the larger but not local spatial scale.
INTRODUCTION
Unraveling the temporal dynamics of plant communities over succession has been a central goal of ecology over the last century (1–4). Classical ecological theories posit that, as succession proceeds, plant communities would develop toward a more steady state where ecosystem functions are relatively constant despite perturbations (5). As a result, ecosystem temporal stability, a crucial dimension of stability that quantifies the invariability of ecosystem properties over time (6–8), has generally been assumed to increase during succession. This idea holds a central position in theories of succession and the field of restoration ecology (9–12). However, despite its widespread acceptance and intuitive appeal, this assumption remains largely untested, in large part due to a paucity of long-term continuous successional data.
Recent advances in succession research have highlighted that trajectories and rates of succession may depend on the spatial scale considered, as the ecological mechanisms responsible for successional processes vary across spatial scales (13–15). At larger spatial scales, community dynamics tend to follow a deterministic and predictable path, converging to steady-state conditions over time (9). At smaller scales, probabilistic processes, such as dispersal and demographic stochasticity, may dominate community assembly, resulting in considerable community instability, even in later successional stages (1, 14, 16). Thus, we hypothesize that ecosystem temporal stability is less likely to increase with succession at the fine local scale but more likely to increase over succession at sufficiently larger scales.
Recently, a hierarchical framework has been developed to partition ecosystem temporal stability to its lower-level components (17, 18). Within this framework, community stability at the larger scale (i.e., γ stability) is determined by the average stability of all local communities (i.e., α stability) and spatial asynchrony across local communities. Spatial asynchrony refers to the degree of asynchrony in community dynamics across localities. This compensation effect acts as a stabilizing mechanism, enhancing overall stability at the larger scale. Similarly, α stability at the local scale is determined by two components: species stability and species asynchrony. Species stability reflects the average temporal stability of all species within a local community, while species asynchrony represents the asynchronous population dynamics among these species. This framework has been applied to various ecological systems, facilitating our understanding of the underlying processes of temporal stability across spatial scales (19–22). However, this framework has rarely been applied to understand the stability of successional systems (23).
Diversity has long been considered a major determinant of ecosystem temporal stability (24–26). A growing number of studies have shown that increasing species diversity tends to increase ecosystem stability in various habitats (7, 27–31), although neutral and negative effects have also been reported (32, 33). Classical succession theories predict a temporal increase in diversity potentially leading to increased stability in later successional stages (5). However, recent research has revealed that plant diversity does not always increase over succession and may vary across spatial scales (14, 34). Therefore, it remains largely unknown to which extent changes in plant diversity across scales would contribute to changes in temporal stability over succession. Furthermore, previous studies on biodiversity-stability relationships have focused largely on taxonomic diversity, particularly species richness. Ecologists have recently begun to explore whether phylogenetic and functional diversity are better predictors of community stability than taxonomic diversity, as they are better at capturing the evolutionary and ecological differences among species (35–37). If phylogenetically and functionally dissimilar species tend to co-occur more frequently in later successional stages (38–40), then this could lead to greater asynchronous dynamics among species and, in turn, increased temporal stability. Conversely, if phylogenetically and functionally similar species dominate later in succession (41), then we might expect reduced asynchrony and temporal stability. However, it remains unknown how changes in taxonomic, phylogenetic, and functional diversity over time relate to changes in ecosystem stability over succession.
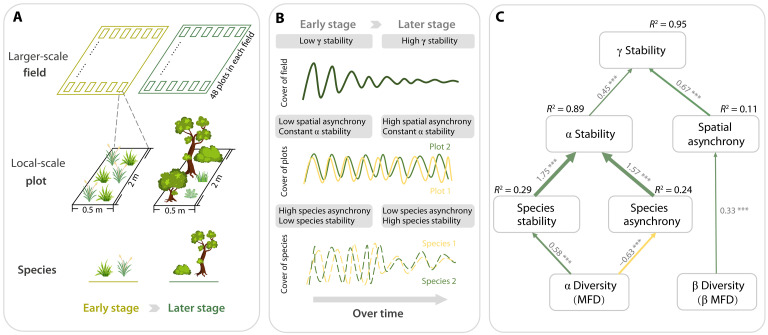
In this study, we use the long-term data from the Buell-Small old field succession study to investigate how ecosystem temporal stability across spatial scales changes with succession. Our study includes 10 abandoned agricultural fields, each containing 48 regularly distributed plots (of 1 m2) that were continuously monitored for over 60 years (fig. S1). This provides a unique opportunity to examine changes in temporal stability from the local plot scale to the larger field scale. We aim to examine (i) whether plant communities become more stable during succession at both local and larger spatial scales, and (ii) how the changes in taxonomic, phylogenetic, and functional biodiversity affect the temporal stability over succession at the two spatial scales.
RESULTS
Temporal stability over succession across spatial scales
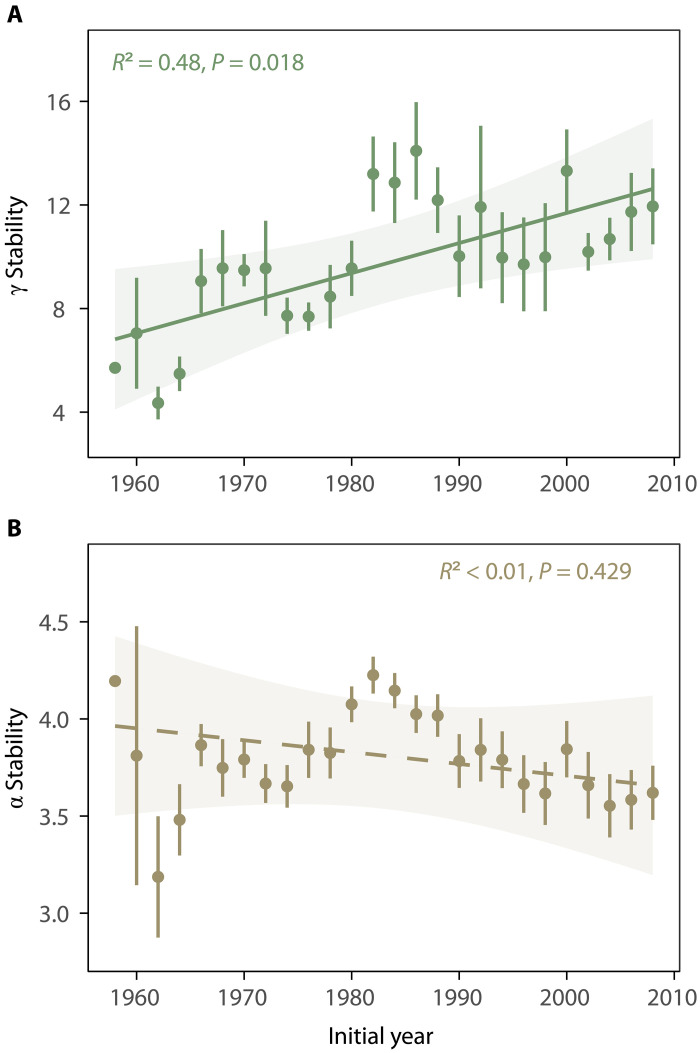
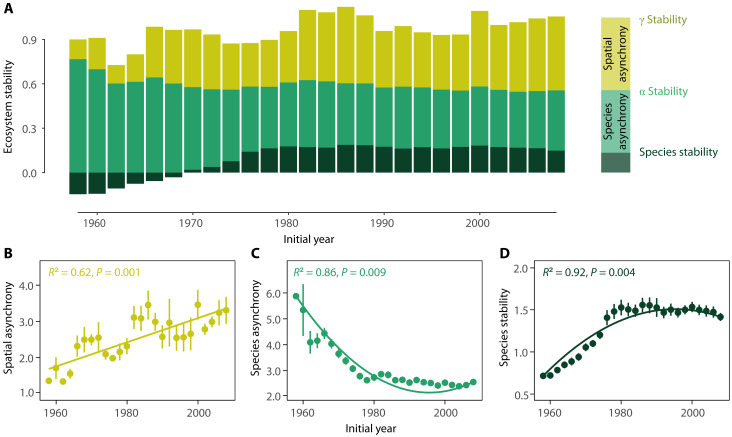
Ecosystem temporal stability, measured as the inverse of the coefficient of variation of plant cover for sequential 10-year rolling windows, showed contrasting trends over succession at the two spatial scales. Specifically, temporal stability increased with time at the larger field scale (γ stability) but not the local plot scale (α stability) (Fig. 1, P = 0.018 for γ stability and P = 0.429 for α stability). The increased γ stability at the field scale was mainly driven by an increase in spatial asynchrony among plots within the same field over time (Fig. 2, A and B, P = 0.001). Conversely, at the plot scale, the temporal increase in species stability (Fig. 2D, P = 0.004) was offset by a decrease in species asynchrony (Fig. 2C, P = 0.009), resulting in the nonsignificant relationship between α stability and time. These results are robust to the use of either rolling windows with different lengths of time intervals (from 8 to 14 years; fig. S2) or non-overlapping time windows (fig. S3). Similar results were found when data were detrended (figs. S4 and S5) and when different asynchrony indices were used (fig. S6). Results were also qualitatively similar when using successional age instead of the calendar year (figs. S7 and S8). Moreover, by arranging the 480 plots into quadrats of varying sizes, we found that the increase in temporal stability over succession became more pronounced at larger quadrat scales, confirming the scale-dependent changes in ecosystem temporal stability over succession (fig. S9).
Fig. 1. Temporal trends in γ and α stability.
γ stability (A), but not α stability (B), significantly increased over time during the 60-year succession. Points show 10-year temporal stability averaged across all observed fields (γ stability, A) or temporal stability averaged across all 48 plots among 10 fields of the same period (α stability, B). Error bars represent SEs. The x axis represents the initial year in each 10-year rolling window. Temporal trend lines, obtained from linear models accounting for temporal autocorrelation, are solid if significant (P < 0.05) and dashed if not significant.
Fig. 2. Visualized temporal trends of species stability, species asynchrony, and spatial asynchrony over succession.
In (A), the widths of the shades represent the logarithm-transformed mean values of species stability (dark green), species asynchrony (bright green), and spatial asynchrony (dark yellow) within each 10-year time interval. Mathematically, at the logarithm-transformed scale, the α stability can be viewed as the sum of species stability and species synchrony, and the γ stability can be viewed as the sum of α stability and spatial synchrony. Spatial asynchrony (B) and species stability (D) significantly increased, but species asynchrony (C) significantly decreased over time. The x axis represents the initial year of each 10-year rolling window. Temporal trend lines were fitted using linear (B) and quadratic regression [(C) and (D)] that account for temporal autocorrelation, respectively.
Diversity-stability relationship across spatial scales
At both plot and field scales, species richness peaked at the mid-successional stage (fig. S10, A, D and G). In contrast, phylogenetic diversity [measured as incidence- and abundance-based mean pairwise phylogenetic distance (MPD and MPDab)] and functional diversity [measured as incidence- and abundance-based mean pairwise functional distance (MFD and MFDab)] significantly increased over time (fig. S10, B, C, E, F, G, and H). Therefore, fewer, but phylogenetically and functionally more dissimilar species, co-occurred later in succession (fig. S10). However, the diversity-stability relationships varied between the plot and field scales. At the field scale, functional diversity consistently increased ecosystem temporal stability (Fig. 3, A and D) and was identified as a better predictor of γ stability than taxonomic and phylogenetic diversity in both univariate and univariate models (tables S1 and S2). This result indicates that high temporal stability of the fields in late successional stages is strongly associated with their high functional diversity in these stages. Similarly, we found general positive relationships between spatial asynchrony and β diversity of the 48 plots within each field (Fig. 3, B and E), and functional β diversity was identified as a better predictor of spatial asynchrony than taxonomic and phylogenetic β diversity (table S1), indicating the strong stabilizing effects of the increased functional dissimilarity among plots later in succession. In contrast, at the plot scale, changes in α stability were not associated with changes in α diversity over succession, regardless of whether taxonomic, phylogenetic, or functional diversity measures were used (Fig. 3, C and F). Specifically, the opposing effects of α diversity on species stability and species asynchrony generally cancelled each other out, resulting in a nonsignificant relationship between diversity and stability at the plot scale (fig. S11 and table S1).
Fig. 3. The diversity-stability relationships across spatial scales.
Effect sizes of taxonomic, phylogenetic, and functional diversity on γ stability (A), spatial asynchrony (B), and α stability (C) were determined as standardized coefficients from univariate linear mixed-effects models that account for temporal autocorrelation, estimated separately for each predictor variable. Solid circles indicate significant effects, and open circles indicate nonsignificant effects. Descriptions of the diversity indices are provided in Materials and Methods. In addition, the regression trends of functional diversity-stability relationships are shown (D to F). γ Stability and spatial asynchrony were log10-transformed. Colored points correspond to values of each field in each moving window. The conditional R2 for each diversity index is reported. Regression lines are solid if significant (P < 0.05) and dashed if not significant, while green bands represent a 95% confidence interval (CI).
We then constructed a structural equation model (SEM) to elucidate the influences of biodiversity changes over succession on ecosystem temporal stability across spatial scales. Our SEM showed that, at the field scale, increasing functional β diversity later in succession significantly enhanced γ stability primarily by promoting spatial asynchrony among plots (Fig. 4C and fig. S12). In contrast, at the plot scale, an increase in functional α diversity led to higher species stability, but this stabilizing effect was counteracted by reduced species asynchrony as functional α diversity increased in later successional stages, resulting in a weak relationship between functional diversity and stability at the plot scale (Figs. 3F and 4C). Consequently, the stronger stabilizing effects of functional β diversity on spatial asynchrony, coupled with the weaker stabilizing effects of functional α diversity on α stability, led to the emergence of a positive diversity-stability relationship at the field scale but not at the plot scale.
Fig. 4. Schematic showing the changes of ecosystem stability over succession across spatial scales and how they relate to biodiversity.
(A) We monitored the dynamic plant cover of 332 species in 480 plots nested within 10 fields over approximately 60 years, assessing changes in ecosystem temporal stability at both the larger field scale (γ stability) and the local plot scale (α stability). (B) As succession unfolded, the increase in species stability was offset by a decrease in species asynchrony, resulting in no increase in α stability at the local scale. In contrast, increased spatial asynchrony among plots substantially enhanced γ stability at the larger scale later in succession. (C) The SEM revealed that functional diversity significantly enhanced γ stability over succession primarily by promoting spatial asynchrony among plots. Green and yellow arrows denote positive and negative significant associations, respectively. Standardized path coefficients are shown next to each path, and asterisks indicate significant paths (*P < 0.05, **P < 0.01, and ***P < 0.001). The widths of significant paths are scaled by standardized path coefficients. The a priori SEM and a full SEM with all causal and correlated paths are provided in the Supplementary Materials (fig. S12).
DISCUSSION
Ecosystem temporal stability has long been a central topic in ecology, due to its vital role in maintaining sustainable ecosystem functioning and services to humanity. Although there is growing interest in understanding how stability varies across time and space, there remains a dearth of data available to directly assess the changes in temporal stability over long time periods. In addition, much research on temporal stability across spatial scales has relied on the artificial aggregation of separate local communities (19–21), and empirical studies sampling at nested spatial scales data have been rare [but see (42, 43)]. By leveraging the well-replicated and fully nested time series on 60 years of succession, we provide unequivocal evidence that ecosystem temporal stability increased with succession at the larger field scale but did not systematically increase at the local plot scale. These results highlight the necessity of considering spatial scale to better understand ecosystem dynamics over time.
At the larger scale, we found that γ stability monotonically increased with succession (Fig. 1A), primarily due to increased spatial asynchrony among local communities (Fig. 2A). Early in succession, different plots shared similar pioneer species that formed a single vegetation layer, which synchronized their responses to environmental fluctuations. Therefore, α stability of local plots almost directly scaled up to determine the γ stability of the field (Fig. 2A). However, as succession proceeds, the effects of factors such as dispersal limitation, habitat heterogeneity, and demographic stochasticity may become more pronounced over time, causing local plots to develop in progressively divergent trajectories (15). In our study, the local plots within each field significantly diverged over time, resulting in distinct vegetation assemblages in later successional stages (14). These dissimilar plots exhibited strong asynchronous responses to environmental fluctuations, characterized by high spatial asynchrony, which predominantly contributed to the increased γ stability during later successional stages (Figs. 2B and 4C). These results contrast with recent grassland studies that covered short observational periods (i.e., typically range from 3 to 5 years), which found that α stability has a greater effect on larger scale γ stability than spatial asynchrony (19, 20, 44). This discrepancy may result from our focus on a successional system over a much longer time scale, which enables local plots to diverge in both environmental conditions and community structures, resulting in greater asynchronous responses among them (14). Recent studies highlighted that the strong stabilizing effects of spatial asynchrony are more likely to emerge in relatively large spatial scales with greater spatial heterogeneity and species turnover (42, 43, 45). Our results extend these findings and suggest that long temporal scales are critical to capture the stabilizing effects of spatial asynchrony in empirical studies.
Furthermore, we detected a positive diversity-stability relationship at the larger scale, with functional diversity emerging as a superior predictor of γ stability (Fig. 3A and table S1). This finding corroborates previous studies which demonstrated that functional diversity explains more variation in ecosystem function and stability than taxonomic diversity (37, 46, 47). In our study, taxonomic γ diversity decreased but functional γ diversity increased in later successional stages (fig. S10, A and C). As a result, fields in later successional stages were characterized by the dominance of fewer yet functionally dissimilar species (figs. S13 and S14). These species, occupying a broader range of ecological niches, could better buffer against environmental fluctuations, consequently contributing to increased γ stability (37, 48). Further, we showed that the positive functional diversity-stability relationship at the larger scale was mainly generated by the strong positive effect of functional β diversity on spatial asynchrony (Fig. 4C). Specifically, different plots in later successional stages were characterized by functionally dissimilar species (figs. S13 and S14), resulting in greater asynchronous responses of plots to environmental fluctuations, thereby generating increased γ stability at the large scale. These findings underscore that conserving functional diversity at the larger scale should be prioritized during successional restoration.
In contrast, α stability at the local scale did not increase over time (Fig. 1B), indicating that local plots within a field still showed considerable variability later in succession. Early in succession, local plots were dominated by short-lived herbaceous species and underwent rapid species turnover (49). These early pioneer species showed low species stability due to their fast growth rates and short life spans but exhibited asynchronous and individualistic population dynamics in response to environmental fluctuations (50). Therefore, species asynchrony generated by species compensation and replacement within plots mainly contributed to community stability at early successional stages (Fig. 2A). As succession proceeded, perennial shrubs and other woody species continued to colonize and ultimately dominate communities (49). These long-lived species provided great species stability due to their low year-to-year variation in individual growth (50, 51). However, they are more likely to share the same ecological strategies adapted to local habitats later in succession (52) and would therefore exhibit parallel responses to natural environmental fluctuations. Together, the decreased species asynchrony and increased species stability cancelled each other out, resulting in a nonsignificant stability-time relationship at the plot scale.
We also detected a nonsignificant diversity-stability relationship at the local scale (Fig. 3C). This result can be attributed to the nonsignificant or opposing effects of diversity on species stability and species asynchrony, which nullified each other (fig. S11). These results confirm the recent theoretical predictions, empirical evidence, and meta-analysis that found species stability and species asynchrony are often governed by different ecological processes and exhibit distinct relationships with diversity (8, 53). For instance, although functionally dissimilar species co-occurred within the same plot at the later successional stages, these species generally exhibited higher species stability but more synchronous population dynamics, resulting in a nonsignificant functional diversity-stability relationship at the local scale (Fig. 3F). Our study thus provides compelling empirical evidence that the effects of functional diversity on stability are scale dependent, with the stabilizing effects of functional diversity being more pronounced at larger spatial scales compared to within local plots. This emphasizes the importance of using sufficiently large sampling areas to capture the stabilizing effects of diversity measures.
While being effective in demonstrating scale-dependent changes in ecosystem temporal stability over succession, several limitations of our study are worth noting. First, similar to recent studies (21, 42), we used total cover as a surrogate for ecosystem function in calculating temporal stability. Further investigations using alternative metrics, such as biomass, would be beneficial to generalize the observed patterns. Second, our 1-m2 permanent plots may better capture the dynamics of herbaceous species compared to woody species. While our conclusions remained robust when organizing plots into quadrats of different sizes (fig. S9), future studies could benefit from using multiple nested plots to comprehensively characterize species with different life forms at various spatial scales. Third, we calculated functional diversity based on species-level trait means, and our results could be strengthened by incorporating intraspecific trait variation and plastic responses of species traits over succession in future studies (54). In addition, factors like dispersal limitation, environmental heterogeneity, and demographic stochasticity likely play crucial roles in regulating temporal stability and synchrony across spatial scales. Unfortunately, data on these relevant covariates (e.g., soil nutrients) over succession were not available in our study. Accounting for these factors in future research could provide valuable insights into the underlying mechanisms driving biodiversity-stability relationships across spatial scales and offer useful implications for ecological restoration during succession (55).
In conclusion, our findings provide strong evidence for the scale dependence of the stability-time relationship and diversity-stability relationship over long-term succession. These findings have important implications for succession theory and restoration practice. First, our study suggests that it is inappropriate to assume that stability would always increase with successional development. It is critical to rigorously evaluate the changes in ecosystem stability using long-term and multiscale approaches. Second, we show that although there was no positive diversity-stability relationship at the local scale, it is critical to preserving biodiversity at larger scales, where functional diversity is important for stabilizing meta-communities. In particular, preserving functional β diversity among local communities should provide stable and sustainable ecosystem functions at broader spatial scales.
MATERIALS AND METHODS
Study sites and experimental design
Our study was based on 60-year time-series data from the Buell-Small Succession Study (BSS), the longest continuous study project on post-agricultural secondary succession (56). The BSS is located in the William L. Hutcheson Memorial Forest Center of New Jersey, USA (40°30′N, 74°34′W) and comprises 10 agricultural fields (each 0.5 to 1 ha) abandoned in pairs from 1958 to 1966 (57). Since abandonment, 48 permanent plots (0.5 m by 2.0 m) were established within each field, resulting in a total of 480 plots. Plot arrangement was regular in each field, with plots occurring over approximately the same area within each field (fig. S1). This hierarchical experimental design offered a unique opportunity to assess how the ecosystem temporal stability changes over succession across spatial scales.
The plant species composition was surveyed in late July by visually estimating the cover for all species present in each plot with the aid of a sampling frame. As plant canopies may overlap, total cover in each plot may exceed 100%. Sampling was conducted every year from 1958 to 1979 and then switched to alternate years since 1979, with half of the fields (240 plots) sampled each year (58). To maintain even replication, we condensed the data into 2-year intervals, merging data from odd-numbered years with the even-numbered years that immediately preceded them. To quantify temporal changes in stability, we analyzed 10-year rolling windows between 1958 and 2017 separated by 2-year intervals. Together, we calculated the temporal stability at both the field and plot levels for a total of 26 intervals (1958–1967 to 2008–2017). In addition, we also calculated temporal stability using multiple time intervals (from 8-year to 16-year rolling windows) to see whether our results were robust to the choice of time window length (fig. S2). We also quantified temporal changes in stability using non-overlapping time intervals (e.g., 1958–1967, 1968–1977, 1978–1987, 1988–1997, 1998–2007, and 2008–2017) to rule out confounding influences of temporal autocorrelation (fig. S3). In addition, since the 10 fields were abandoned in different years, analyses were also conducted on the basis of field age instead of the calendar year, to remove the influence of abandonment times in our study (figs. S7 and S8). Our results showed that the temporal patterns of stability and asynchrony at both field and plot scales were robust to these different methodical choices; therefore, we present results based on calendar year using 10-year rolling window in the main text, and all other results are included in the Supplementary Materials.
Temporal stability components
We regarded each plot within the field as a local community (α scale), and each field contains 48 plots as a metacommunity at the large scale (γ scale). Following recent literature (21, 42), we calculated temporal stability using total cover as a proxy for ecosystem function. Temporal stability indices at different spatial levels were defined as the ratio of temporal mean to its SD of total cover at each 10-year time interval. We calculated five temporal stability components, including γ stability, α stability, species stability, spatial asynchrony, and species asynchrony. For each field, γ stability represents the temporal stability of the total coverage of all plots within the field. Similarly, α stability represents the stability of community cover in each plot, which was calculated by taking the average across the 48 plots within each field, weighted by the total coverage of each plot. In addition, species stability was calculated as the average population stability weighted by species coverage within each plot and then averaged across all plots within the field. The mathematical formulas are (59)
where μi,k denotes the temporal mean of species i in local community k, and vij,kl denotes the temporal covariance between species i in local community k and species j in local community l, respectively.
To account for directional changes in plant coverage during succession, we also calculated γ, α, and species stability using detrended data to remove the potential influence of directional trends. At the field level, detrending was performed by regressing the annually measured field plant cover against the calendar year in each 10-year time window and then calculating the variance of the residuals of each regression (7). For each field, detrended γ stability was calculated as the 10-year mean plant cover divided by the detrended SD. A similar approach was used to detrend α stability and species stability for each plot and species. Stability with and without detrending produced consistent temporal patterns; consequently, we present results of stability without detrending in the main text and present detrended stability analyses in the Supplementary Materials (figs. S4 and S5).
We then define species asynchrony as the ratio of α stability to species stability and spatial asynchrony as the ratio of γ stability to α stability. These two asynchrony indices are vital contributors to multispatial scale stability in a spatial hierarchical framework of ecosystem stability (17, 59). We also calculated three other species and spatial asynchrony indices (60–62), to make sure that our results are robust to the measures used (fig. S6).
To assess the influence of sampling scales on ecological stability over time, the 480 plots were organized into non-overlapping quadrats of four different sizes: 10 m by 10 m, 20 m by 20 m, 30 m by 30 m, and 40 m by 40 m. In each resampling run, we randomly generated quadrats covering all fields for each quadrat size, ensuring that the quadrats did not overlap and each quadrat contained at least one plot. The coverage of all species within each quadrat was aggregated to represent the coverage of the local community. This resampling process was repeated 1000 times for each quadrat size. Subsequently, we calculated the average temporal stability among all quadrats with the same size to obtain stability at the respective spatial scales in each 10-year rolling window (fig. S9).
Community phylogeny and functional traits
We constructed a phylogeny for the 332 species that occurred in the BSS during 1958–2017, using BEAST version 1.7.5 (63). Briefly, we accessed GenBank database to acquire three sequenced genes (rbcL, matK and ITS), and one representative of the early diverging seed plant Cycas revoluta was selected as an outgroup species. Sequences were subsequently aligned using MUSCLE (64), and the optimal nucleotide substitution model was determined according to Akaike’s Information Criterion (AIC) by jModeltest v.2.1. (65). Complete details of phylogeny construction can be found in (39).
We selected nine functional traits related to plant growth, fundamental functional trade-offs, and successional strategy in our analysis, including plant height, seed mass, specific leaf area (SLA), leaf dry matter content (LDMC), growth form (graminoid, forb, vine, shrub, and tree), life span (annual, biennial, and perennial), pollination mode (biotic and abiotic), seed dispersal (biotic and abiotic), and clonal reproduction (true and false). Plant height, SLA, and LDMC are often associated with the competitive ability and adaption strategy of plants to changing light environments and nutrient conditions during succession (50, 66). Seed dispersal, seed mass, pollination made, and clonal reproduction are strongly related to the dispersal ability and colonization of species (67). Leaf traits of each species, including SLA and LDMC, were collected from 10 or more individuals within the study region whenever possible, following the protocols outlined by Cornelissen et al. (67). Data on plant height, seed mass, and all five categorical traits, as well as any missing leaf traits, were obtained from open databases and primary literature [e.g., US Department of Agriculture Plants Database and TRY Plant Trait Database; (68, 69)]. To visualize the shifts in functional trait spaces during succession, we performed a principal components analysis (PCA) using the four continuous traits for each year (fig. S13). For the PCA, we performed phylogenetic trait imputation to fill the missing trait data using the random forest algorithm with the missForest (70) package in R 4.0.4 (71).
Multiple facets of diversity
For taxonomic diversity, we apply a unified diversity concept based on Hill numbers with different order q to estimate α and γ diversity (72). When q = 0, the metric is identical to species richness; when q = 1, it is identical to the exponential of the Shannon index; when q = 2, it is the inverse Simpson index. At the plot scale, we defined α diversity as averaged Hill numbers of diversity per plot. At the larger field scale, γ diversity was calculated as the total Hill numbers across all plots for each field. Taxonomic β diversity, which represents the compositional dissimilarity of plots within each field, was calculated as the mean pairwise Jaccard, Sørensen, and Bray-Curtis dissimilarity indices between the 48 plots within each field.
For phylogenetic diversity, we used the MPD and MPDab as measures, and MPDab was weighted by the coverage of species. Specifically, phylogenetic γ diversity was measured as MPD and MPDab of the whole field, phylogenetic α diversity was measured as MPD and MPDab of each plot, and phylogenetic β diversity (βMPD and βMPDab) was measured as mean pairwise comparisons of MPD between the taxa of the 48 plots within each field. We used an identical framework to calculate functional α, β, and γ diversity (e.g., MFD, MFDab, βMFD, and βMFDab), using functional distances among species instead of their phylogenetic distances. The functional distance was calculated as Gower distance based on the nine traits to represent the distances of species in multivariate trait space. We also calculated functional dispersion of each continuous trait, as well as their combination, to assess the temporal changes in the dispersion of functional traits in multidimensional space at the field scale.
All diversity metrics were calculated for each sampling year, and the mean values of each 10-year window were used in subsequent analyses. The analyses were performed using the vegan (73), picante (74), and FD (75) packages in R.
Statistical analyses
To explore how stability changed over succession at larger and local scales, γ and α stability were modeled, respectively, as functions of the initial sampling year of each 10-year window, using generalized least squares (GLS) regression. Similarly, we used linear and quadratic GLS models to assess how spatial asynchrony, species asynchrony, and species stability change over succession. To account for potential temporal autocorrelation in the time series residuals, we specified a first-order autoregressive (AR1) correlation structure in these GLS models.
To examine whether and how the temporal change of stability was related to the change of diversity at both local and larger scales, we performed univariate linear mixed-effect models (LMMs) using the nlme package (76) in R. The LMMs modeled different temporal stability components, calculated over sequential 10-year rolling windows, as functions of the average diversity within each rolling window. Field was included as a random factor in all LMMs, and an AR1 correlation structure was used to account for temporal autocorrelation. Specifically, γ stability was fitted as a function of taxonomic, phylogenetic, and functional γ diversity measures, and spatial asynchrony was fitted as a function of taxonomic, phylogenetic, and functional β diversity measures. The response variables were log10-transformed in LMMs to ensure the normality of residuals and homogeneity of variance. Similarity, α stability, as well as species asynchrony and species stability, was fitted as functions of multiple facets of α diversity (including Hill numbers, MPD, MPDab, MFD, and MFDab). Marginal and conditional R2 values of these univariate models were calculated using the MuMIn package (77), and the standardized coefficient of each variable was calculated and compared using the effectsize package (78) in R.
To further investigate the relative importance of taxonomic, phylogenetic, and functional diversity measures on different stability components, we also fitted multivariate LMMs for each stability component. Before the regression analyses, we checked the correlation between diversity indices at the α, β, and γ levels, respectively, to identify potential multicollinearity among diversity indices (fig. S15). Highly correlated diversity indices (here, Pearson’s r > 0.7) were alternatively included in our multivariate models. The same random effect and autocorrelation structure were used for multivariate LMMs, and the model with the lowest corrected AIC was identified as the best-fitting model. For the best model, we assessed the variance inflation factor (VIF) to evaluate the risk of multicollinearity, ensuring that all selected predictors had VIF < 3.
In addition, we constructed a SEM to disentangle direct and indirect drivers of γ stability at the larger spatial scale, based on the a priori theoretical framework [fig. S12A; (18)]. Specifically, we examined how functional α and β diversity (i.e., MFD and βMFD) directly and indirectly affected the different components of temporal stability, as functional diversity emerged as a superior predictor of stability components in our univariate and multivariate models (tables S1 and S2). To avoid potential confounding effects, we excluded the successional year from the a priori model due to its significant correlation with diversity throughout the succession. The SEM was fitted using LMMs with the field as the random effect and incorporating temporal autocorrelation structure in each model using the piecewiseSEM package (79). The global model fit was assessed via Fisher’s C statistic (P > 0.05), and Shipley’s test of d-separation was used to ensure that we did not miss any potential pathways.
Acknowledgments
We are grateful to the originators of the BSS, H. Buell (1901–1995), M. Buell (1905–1975), and J. Small (1900–1977), and many field workers who sampled the fields every year for the past 60 years. We sincerely thank M. Xu for providing valuable guidance and assistance in the data analysis.
Funding: This work was financially supported by the National Natural Science Foundation of China (NSFC3222051 and NSFC31971553), the Shanghai Rising-Star Program (20QA1402900), and the Fundamental Research Funds for the Central Universities to S.P.L.
Author contributions: S.P.L. and L.J. developed and framed research questions. S.J.M. carried out the field experiment and collected data. Y.M. and S.P.L. analyzed the data and wrote the first draft with great support from S.W. and L.J. All authors contributed to the development and revision of the manuscript.
Competing interests: The authors declare that they have no competing interests.
Data and materials availability: All data needed to evaluate the conclusions in the paper are present in the paper and/or the Supplementary Materials. The data and R code used in this study are available at figshare (https://doi.org/10.6084/m9.figshare.24051111.v2). The future iterations of this dataset will be updated and available upon request from S.J.M.
Supplementary Materials
This PDF file includes:
Figs. S1 to S15
Tables S1 and S2
REFERENCES AND NOTES
- 1.Gleason H. A., The individualistic concept of the plant association. Bull. Torrey. Bot. Club 53, 7–26 (1926). [Google Scholar]
- 2.J. O. Luken, “Directing ecological succession” (Chapman and Hall, London, 1990). [Google Scholar]
- 3.D. C. Glenn-Lewin, R. K. Peet, T. T. Veblen, “Plant succession: Theory and prediction” (Chapman and Hall, London, 1992). [Google Scholar]
- 4.K. PrachL. R. Walker, “Comparative plant succession among terrestrial biomes of the World” (Cambridge University Press, Cambridge, 2020). [Google Scholar]
- 5.Odum E. P., The strategy of ecosystem development. Science 164, 262–270 (1969). [DOI] [PubMed] [Google Scholar]
- 6.McCann K. S., The diversity–stability debate. Nature 405, 228–233 (2000). [DOI] [PubMed] [Google Scholar]
- 7.Tilman D., Reich P. B., Knops J. M., Biodiversity and ecosystem stability in a decade-long grassland experiment. Nature 441, 629–632 (2006). [DOI] [PubMed] [Google Scholar]
- 8.Xu Q., Yang X., Yan Y., Wang S., Loreau M., Jiang L., Consistently positive effect of species diversity on ecosystem, but not population, temporal stability. Ecol. Lett. 24, 2256–2266 (2021). [DOI] [PubMed] [Google Scholar]
- 9.F. E. Clements, “Plant succession: An analysis of the development of vegetation” (Carnegie Institution of Washington, 1916).
- 10.Palmer M. A., Ambrose R. F., Poff N. L., Ecological theory and community restoration ecology. Restor. Ecol. 5, 291–300 (1997). [Google Scholar]
- 11.Young T. P., Chase J. M., Huddleston R. T., Community succession and assembly. Ecol. Restor. 19, 5–18 (2001). [Google Scholar]
- 12.Pickett S. T. A., Cadenasso M. L., Meiners S. J., Ever since Clements: From succession to vegetation dynamics and understanding to intervention. Appl. Veg. Sci. 12, 9–21 (2009). [Google Scholar]
- 13.Cook W. M., Yao J., Foster B. L., Holt R. D., Patrick L. B., Secondary succession in an experimentally fragmented landscape: Community patterns across space and time. Ecology 86, 1267–1279 (2005). [Google Scholar]
- 14.Li S. P., Cadotte M. W., Meiners S. J., Pu Z., Fukami T., Jiang L., Convergence and divergence in a long-term old-field succession: The importance of spatial scale and species abundance. Ecol. Lett. 19, 1101–1109 (2016). [DOI] [PubMed] [Google Scholar]
- 15.Breugel M., Craven D., Lai H. R., Baillon M., Turner B. L., Hall J. S., Soil nutrients and dispersal limitation shape compositional variation in secondary tropical forests across multiple scales. J. Ecol. 107, 566–581 (2019). [Google Scholar]
- 16.Vellend M., Srivastava D. S., Anderson K. M., Brown C. D., Jankowski J. E., Kleynhans E. J., Kraft N. J. B., Letaw A. D., Macdonald A. A. M., Maclean J. E., Myers-Smith I. H., Norris A. R., Xue X., Assessing the relative importance of neutral stochasticity in ecological communities. Oikos 123, 1420–1430 (2014). [Google Scholar]
- 17.Wang S., Loreau M., Ecosystem stability in space: α, β and γ variability. Ecol. Lett. 17, 891–901 (2014). [DOI] [PubMed] [Google Scholar]
- 18.Wang S., Loreau M., Biodiversity and ecosystem stability across scales in metacommunities. Ecol. Lett. 19, 510–518 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Wilcox K. R., Tredennick A. T., Koerner S. E., Grman E., Hallett L. M., Avolio M. L., La Pierre K. J., Houseman G. R., Isbell F., Johnson D. S., Alatalo J. M., Baldwin A. H., Bork E. W., Boughton E. H., Bowman W. D., Britton A. J., Cahill J. F. Jr., Collins S. L., Du G., Eskelinen A., Gough L., Jentsch A., Kern C., Klanderud K., Knapp A. K., Kreyling J., Luo Y., McLaren J. R., Megonigal P., Onipchenko V., Prevey J., Price J. N., Robinson C. H., Sala O. E., Smith M. D., Soudzilovskaia N. A., Souza L., Tilman D., White S. R., Xu Z., Yahdjian L., Yu Q., Zhang P., Zhang Y., Asynchrony among local communities stabilises ecosystem function of metacommunities. Ecol. Lett. 20, 1534–1545 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Zhang Y., Feng J., Loreau M., He N., Han X., Jiang L., Nitrogen addition does not reduce the role of spatial asynchrony in stabilising grassland communities. Ecol. Lett. 22, 563–571 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Hautier Y., Zhang P., Loreau M., Wilcox K. R., Seabloom E. W., Borer E. T., Byrnes J. E. K., Koerner S. E., Komatsu K. J., Lefcheck J. S., Hector A., Adler P. B., Alberti J., Arnillas C. A., Bakker J. D., Brudvig L. A., Bugalho M. N., Cadotte M., Caldeira M. C., Carroll O., Crawley M., Collins S. L., Daleo P., Dee L. E., Eisenhauer N., Eskelinen A., Fay P. A., Gilbert B., Hansar A., Isbell F., Knops J. M. H., MacDougall A. S., McCulley R. L., Moore J. L., Morgan J. W., Mori A. S., Peri P. L., Pos E. T., Power S. A., Price J. N., Reich P. B., Risch A. C., Roscher C., Sankaran M., Schutz M., Smith M., Stevens C., Tognetti P. M., Virtanen R., Wardle G. M., Wilfahrt P. A., Wang S., General destabilizing effects of eutrophication on grassland productivity at multiple spatial scales. Nat. Commun. 11, 5375 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Liang M., Liang C., Hautier Y., Wilcox K. R., Wang S., Grazing-induced biodiversity loss impairs grassland ecosystem stability at multiple scales. Ecol. Lett. 24, 2054–2064 (2021). [DOI] [PubMed] [Google Scholar]
- 23.Li W., Zhou X., Xiang Z., Li J., Wang S., Loreau M., Jiang L., Biomass temporal stability increases at two spatial scales during secondary succession. J. Ecol. 111, 1575–1586 (2023). [Google Scholar]
- 24.C. S. Elton, “The ecology of invasions by animals and plants” (University of Chicago Press, 1958). [Google Scholar]
- 25.McNaughton S. J., Diversity and stability of ecological communities: A comment on the role of empiricism in ecology. Am. Nat. 111, 515–525 (1977). [Google Scholar]
- 26.R. M. May, “Stability and complexity in model ecosystems” (Princeton University Press, Princeton, 1973). [Google Scholar]
- 27.Steiner C. F., Long Z., Krumins J. A., Morin P. J., Temporal stability of aquatic food webs: Partitioning the effects of species diversity, species composition and enrichment. Ecol. Lett. 8, 819–828 (2005). [Google Scholar]
- 28.Isbell F. I., Polley H. W., Wilsey B. J., Biodiversity, productivity and the temporal stability of productivity: Patterns and processes. Ecol. Lett. 12, 443–451 (2009). [DOI] [PubMed] [Google Scholar]
- 29.Jiang L., Joshi H., Patel S. N., Predation alters relationships between biodiversity and temporal stability. Am. Nat. 173, 389–399 (2009). [DOI] [PubMed] [Google Scholar]
- 30.van der Plas F., Biodiversity and ecosystem functioning in naturally assembled communities. Biol. Rev. Camb. Philos. Soc. 94, 1220–1245 (2019). [DOI] [PubMed] [Google Scholar]
- 31.Wagg C., Roscher C., Weigelt A., Vogel A., Ebeling A., de Luca E., Roeder A., Kleinspehn C., Temperton V. M., Meyer S. T., Scherer-Lorenzen M., Buchmann N., Fischer M., Weisser W. W., Eisenhauer N., Schmid B., Biodiversity-stability relationships strengthen over time in a long-term grassland experiment. Nat. Commun. 13, 7752 (2022). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Petchey O. L., Casey T., Jiang L., McPhearson P. T., Price J., Species richness, environmental fluctuations, and temporal change in total community biomass. Oikos 99, 231–240 (2002). [Google Scholar]
- 33.Valdivia N., Molis M., Observational evidence of a negative biodiversity-stability relationship in intertidal epibenthic communities. Aquat. Biol. 4, 263–271 (2009). [Google Scholar]
- 34.Ladouceur E., Isbell F., Clark A. T., Harpole W. S., Reich P. B., Tilman G. D., Chase J. M., The recovery of plant community composition following passive restoration across spatial scales. J. Ecol. 111, 814–829 (2023). [Google Scholar]
- 35.Cadotte M. W., Dinnage R., Tilman D., Phylogenetic diversity promotes ecosystem stability. Ecology 93, S223–S233 (2012). [Google Scholar]
- 36.Pu Z., Daya P., Tan J., Jiang L., Phylogenetic diversity stabilizes community biomass. J. Plant Ecol. 7, 176–187 (2014). [Google Scholar]
- 37.Craven D., Eisenhauer N., Pearse W. D., Hautier Y., Isbell F., Roscher C., Bahn M., Beierkuhnlein C., Bonisch G., Buchmann N., Byun C., Catford J. A., Cerabolini B. E. L., Cornelissen J. H. C., Craine J. M., De Luca E., Ebeling A., Griffin J. N., Hector A., Hines J., Jentsch A., Kattge J., Kreyling J., Lanta V., Lemoine N., Meyer S. T., Minden V., Onipchenko V., Polley H. W., Reich P. B., van Ruijven J., Schamp B., Smith M. D., Soudzilovskaia N. A., Tilman D., Weigelt A., Wilsey B., Manning P., Multiple facets of biodiversity drive the diversity-stability relationship. Nat. Ecol. Evol. 2, 1579–1587 (2018). [DOI] [PubMed] [Google Scholar]
- 38.Purschke O., Schmid B. C., Sykes M. T., Poschlod P., Michalski S. G., Durka W., Kuhn I., Winter M., Prentice H. C., Contrasting changes in taxonomic, phylogenetic and functional diversity during a long-term succession: Insights into assembly processes. J. Ecol. 101, 857–866 (2013). [Google Scholar]
- 39.Li S. P., Cadotte M. W., Meiners S. J., Hua Z. S., Jiang L., Shu W. S., Species colonisation, not competitive exclusion, drives community overdispersion over long-term succession. Ecol. Lett. 18, 964–973 (2015). [DOI] [PubMed] [Google Scholar]
- 40.Letcher S. G., Phylogenetic structure of angiosperm communities during tropical forest succession. Proc. Biol. Sci. 277, 97–104 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Letten A. D., Keith D. A., Tozer M. G., Phylogenetic and functional dissimilarity does not increase during temporal heathland succession. Proc. Biol. Sci. 281, 20142102 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Liang M., Baiser B., Hallett L. M., Hautier Y., Jiang L., Loreau M., Record S., Sokol E. R., Zarnetske P. L., Wang S., Consistent stabilizing effects of plant diversity across spatial scales and climatic gradients. Nat. Ecol. Evol. 6, 1669–1675 (2022). [DOI] [PubMed] [Google Scholar]
- 43.Qiao X., Geng Y., Zhang C., Han Z., Zhang Z., Zhao X., von Gadow K., Spatial asynchrony matters more than alpha stability in stabilizing ecosystem productivity in a large temperate forest region. Glob. Ecol. Biogeogr. 31, 1133–1146 (2022). [Google Scholar]
- 44.Wang S., Loreau M., de Mazancourt C., Isbell F., Beierkuhnlein C., Connolly J., Deutschman D. H., Doležal J., Eisenhauer N., Hector A., Jentsch A., Kreyling J., Lanta V., Lepš J., Polley H. W., Reich P. B., van Ruijven J., Schmid B., Tilman D., Wilsey B., Craven D., Biotic homogenization destabilizes ecosystem functioning by decreasing spatial asynchrony. Ecology 102, e03332 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.van der Plas F., Hennecke J., Chase J. M., van Ruijven J., Barry K. E., Universal beta-diversity-functioning relationships are neither observed nor expected. Trends Ecol. Evol. 38, 532–544 (2023). [DOI] [PubMed] [Google Scholar]
- 46.Flynn D. F., Mirotchnick N., Jain M., Palmer M. I., Naeem S., Functional and phylogenetic diversity as predictors of biodiversity–ecosystem-function relationships. Ecology 92, 1573–1581 (2011). [DOI] [PubMed] [Google Scholar]
- 47.Petchey O. L., Hector A., Gaston K. J., How do different measures of functional diversity perform? Ecology 85, 847–857 (2004). [Google Scholar]
- 48.Schnabel F., Liu X., Kunz M., Barry K. E., Bongers F. J., Bruelheide H., Fichtner A., Härdtle W., Li S., Pfaff C.-T., Schmid B., Schwarz J. A., Tang Z., Yang B., Bauhus J., von Oheimb G., Ma K., Wirth C., Species richness stabilizes productivity via asynchrony and drought-tolerance diversity in a large-scale tree biodiversity experiment. Sci. Adv. 7, eabk1643 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Ladwig L. M., Meiners S. J., Spatiotemporal dynamics of lianas during 50 years of succession to temperate forest. Ecology 91, 671–680 (2010). [DOI] [PubMed] [Google Scholar]
- 50.Májeková M., de Bello F., Doležal J., Lepš J., Plant functional traits as determinants of population stability. Ecology 95, 2369–2374 (2014). [Google Scholar]
- 51.Lepš J., Osbornová-Kosinová J., Rejmánek M., Community stability, complexity and species life history strategies. Vegetatio 50, 53–63 (1982). [Google Scholar]
- 52.Lohbeck M., Poorter L., Lebrija-Trejos E., Martinez-Ramos M., Meave J. A., Paz H., Perez-Garcia E. A., Romero-Perez I. E., Tauro A., Bongers F., Successional changes in functional composition contrast for dry and wet tropical forest. Ecology 94, 1211–1216 (2013). [DOI] [PubMed] [Google Scholar]
- 53.Thibaut L. M., Connolly S. R., Understanding diversity–stability relationships: Towards a unified model of portfolio effects. Ecol. Lett. 16, 140–150 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Violle C., Enquist B. J., McGill B. J., Jiang L., Albert C. H., Hulshof C., Jung V., Messier J., The return of the variance: Intraspecific variability in community ecology. Trends Ecol. Evol. 27, 244–252 (2012). [DOI] [PubMed] [Google Scholar]
- 55.Isbell F., Tilman D., Polasky S., Binder S., Hawthorne P., Low biodiversity state persists two decades after cessation of nutrient enrichment. Ecol. Lett. 16, 454–460 (2013). [DOI] [PubMed] [Google Scholar]
- 56.Cadenasso M. L., Meiners S. J., Pickett S. T. A., The success of succession: A symposium commemorating the 50th anniversary of the Buell-Small Succession Study. Appl. Veg. Sci. 12, 3–8 (2009). [Google Scholar]
- 57.Buell M. F., Buell H. F., Small J. A., Invasion of trees in secondary succession on the New Jersey Piedmont. Bull. Torrey. Bot. Club 98, 67–74 (1971). [Google Scholar]
- 58.Pickett S. T. A., Population patterns through twenty years of oldfield succession. Vegetatio 49, 45–59 (1982). [Google Scholar]
- 59.Wang S., Lamy T., Hallett L. M., Loreau M., Stability and synchrony across ecological hierarchies in heterogeneous metacommunities: Linking theory to data. Ecography 42, 1200–1211 (2019). [Google Scholar]
- 60.Loreau M., de Mazancourt C., Species synchrony and its drivers: Neutral and nonneutral community dynamics in fluctuating environments. Am. Nat. 172, E48–E66 (2008). [DOI] [PubMed] [Google Scholar]
- 61.Gross K., Cardinale B. J., Fox J. W., Gonzalez A., Loreau M., Polley H. W., Reich P. B., van Ruijven J., Species richness and the temporal stability of biomass production: A new analysis of recent biodiversity experiments. Am. Nat. 183, 1–12 (2014). [DOI] [PubMed] [Google Scholar]
- 62.Lepš J., Götzenberger L., Valencia E., de Bello F., Accounting for long-term directional trends on year-to-year synchrony in species fluctuations. Ecography 42, 1728–1741 (2019). [Google Scholar]
- 63.Drummond A. J., Suchard M. A., Xie D., Rambaut A., Bayesian phylogenetics with BEAUti and the BEAST 1.7. Mol. Biol. Evol. 29, 1969–1973 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64.Edgar R. C., MUSCLE: Multiple sequence alignment with high accuracy and high throughput. Nucleic Acids Res. 32, 1792–1797 (2004). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 65.Posada D., jModelTest: Phylogenetic model averaging. Mol. Biol. Evol. 25, 1253–1256 (2008). [DOI] [PubMed] [Google Scholar]
- 66.Lasky J. R., Uriarte M., Boukili V. K., Chazdon R. L., Trait-mediated assembly processes predict successional changes in community diversity of tropical forests. Proc. Natl. Acad. Sci. U.S.A. 111, 5616–5621 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 67.Cornelissen J., Lavorel S., Garnier E., Díaz S., Buchmann N., Gurvich D., Reich P., Ter Steege H., Morgan H., Van Der Heijden M., Pausas J. G., Poorter H., A handbook of protocols for standardised and easy measurement of plant functional traits worldwide. Aust. J. Bot. 51, 335–380 (2003). [Google Scholar]
- 68.Kattge J., Bönisch G., Díaz S., Lavorel S., Prentice I. C., Leadley P., Tautenhahn S., Werner G. D. A., Aakala T., Abedi M., Acosta A. T. R., Adamidis G. C., Adamson K., Aiba M., Albert C. H., Alcántara J. M., Carolina Alcázar C., Aleixo I., Ali H., Amiaud B., Ammer C., Amoroso M. M., Anand M., Anderson C., Anten N., Antos J., Apgaua D. M. G., Ashman T.-L., Asmara D. H., Asner G. P., Aspinwall M., Atkin O., Aubin I., Baastrup-Spohr L., Bahalkeh K., Bahn M., Baker T., Baker W. J., Bakker J. P., Baldocchi D., Baltzer J., Banerjee A., Baranger A., Barlow J., Barneche D. R., Baruch Z., Bastianelli D., Battles J., Bauerle W., Bauters M., Bazzato E., Beckmann M., Beeckman H., Beierkuhnlein C., Bekker R., Belfry G., Belluau M., Beloiu M., Benavides R., Benomar L., Berdugo-Lattke M. L., Berenguer E., Bergamin R., Bergmann J., Carlucci M. B., Berner L., Bernhardt-Römermann M., Bigler C., Bjorkman A. D., Blackman C., Blanco C., Blonder B., Blumenthal D., Bocanegra-González K. T., Boeckx P., Bohlman S., Böhning-Gaese K., Boisvert-Marsh L., Bond W., Bond-Lamberty B., Boom A., Boonman C. C. F., Bordin K., Boughton E. H., Boukili V., Bowman D. M. J. S., Bravo S., Brendel M. R., Broadley M. R., Brown K. A., Bruelheide H., Brumnich F., Bruun H. H., Bruy D., Buchanan S. W., Bucher S. F., Buchmann N., Buitenwerf R., Bunker D. E., Bürger J., Burrascano S., Burslem D. F. R. P., Butterfield B. J., Byun C., Marques M., Scalon M. C., Caccianiga M., Cadotte M., Cailleret M., Camac J., Camarero J. J., Campany C., Campetella G., Campos J. A., Cano-Arboleda L., Canullo R., Carbognani M., Carvalho F., Casanoves F., Castagneyrol B., Catford J. A., Cavender-Bares J., Cerabolini B. E. L., Cervellini M., Chacón-Madrigal E., Chapin K., Chapin F. S., Chelli S., Chen S.-C., Chen A., Cherubini P., Chianucci F., Choat B., Chung K.-S., Chytrý M., Ciccarelli D., Coll L., Collins C. G., Conti L., Coomes D., Cornelissen J. H. C., Cornwell W. K., Corona P., Coyea M., Craine J., Craven D., Cromsigt J. P. G. M., Csecserits A., Cufar K., Cuntz M., da Silva A. C., Dahlin K. M., Dainese M., Dalke I., Fratte M. D., Dang-Le A. T., Danihelka J., Dannoura M., Dawson S., de Beer A. J., De Frutos A., De Long J. R., Dechant B., Delagrange S., Delpierre N., Derroire G., Dias A. S., Diaz-Toribio M. H., Dimitrakopoulos P. G., Dobrowolski M., Doktor D., Dřevojan P., Dong N., Dransfield J., Dressler S., Duarte L., Ducouret E., Dullinger S., Durka W., Duursma R., Dymova O., E-Vojtkó A., Eckstein R. L., Ejtehadi H., Elser J., Emilio T., Engemann K., Erfanian M. B., Erfmeier A., Esquivel-Muelbert A., Esser G., Estiarte M., Domingues T. F., Fagan W. F., Fagúndez J., Falster D. S., Fan Y., Fang J., Farris E., Fazlioglu F., Feng Y., Fernandez-Mendez F., Ferrara C., Ferreira J., Fidelis A., Finegan B., Firn J., Flowers T. J., Flynn D. F. B., Fontana V., Forey E., Forgiarini C., François L., Frangipani M., Frank D., Frenette-Dussault C., Freschet G. T., Fry E. L., Fyllas N. M., Mazzochini G. G., Gachet S., Gallagher R., Ganade G., Ganga F., García-Palacios P., Gargaglione V., Garnier E., Garrido J. L., de Gasper A. L., Gea-Izquierdo G., Gibson D., Gillison A. N., Giroldo A., Glasenhardt M.-C., Gleason S., Gliesch M., Goldberg E., Göldel B., Gonzalez-Akre E., Gonzalez-Andujar J. L., González-Melo A., González-Robles A., Graae B. J., Granda E., Graves S., Green W. A., Gregor T., Gross N., Guerin G. R., Günther A., Gutiérrez A. G., Haddock L., Haines A., Hall J., Hambuckers A., Han W., Harrison S. P., Hattingh W., Hawes J. E., He T., He P., Heberling J. M., Helm A., Hempel S., Hentschel J., Hérault B., Hereş A.-M., Herz K., Heuertz M., Hickler T., Hietz P., Higuchi P., Hipp A. L., Hirons A., Hock M., Hogan J. A., Holl K., Honnay O., Hornstein D., Hou E., Hough-Snee N., Hovstad K. A., Ichie T., Igić B., Illa E., Isaac M., Ishihara M., Ivanov L., Ivanova L., Iversen C. M., Izquierdo J., Jackson R. B., Jackson B., Jactel H., Jagodzinski A. M., Jandt U., Jansen S., Jenkins T., Jentsch A., Jespersen J. R. P., Jiang G.-F., Johansen J. L., Johnson D., Jokela E. J., Joly C. A., Jordan G. J., Joseph G. S., Junaedi D., Junker R. R., Justes E., Kabzems R., Kane J., Kaplan Z., Kattenborn T., Kavelenova L., Kearsley E., Kempel A., Kenzo T., Kerkhoff A., Khalil M. I., Kinlock N. L., Kissling W. D., Kitajima K., Kitzberger T., Kjøller R., Klein T., Kleyer M., Klimešová J., Klipel J., Kloeppel B., Klotz S., Knops J. M. H., Kohyama T., Koike F., Kollmann J., Komac B., Komatsu K., König C., Kraft N. J. B., Kramer K., Kreft H., Kühn I., Kumarathunge D., Kuppler J., Kurokawa H., Kurosawa Y., Kuyah S., Laclau J.-P., Lafleur B., Lallai E., Lamb E., Lamprecht A., Larkin D. J., Laughlin D., Le Bagousse-Pinguet Y., le Maire G., le Roux P. C., le Roux E., Lee T., Lens F., Lewis S. L., Lhotsky B., Li Y., Li X., Lichstein J. W., Liebergesell M., Lim J. Y., Lin Y.-S., Linares J. C., Liu C., Liu D., Liu U., Livingstone S., Llusià J., Lohbeck M., López-García Á., Lopez-Gonzalez G., Lososová Z., Louault F., Lukács B. A., Lukeš P., Luo Y., Lussu M., Ma S., Pereira C. M. R., Mack M., Maire V., Mäkelä A., Mäkinen H., Malhado A. C. M., Mallik A., Manning P., Manzoni S., Marchetti Z., Marchino L., Marcilio-Silva V., Marcon E., Marignani M., Markesteijn L., Martin A., Martínez-Garza C., Martínez-Vilalta J., Mašková T., Mason K., Mason N., Massad T. J., Masse J., Mayrose I., Carthy J. M., McCormack M. L., Culloh K. M., Mc Fadden I. R., Mc Gill B. J., Mc Partland M. Y., Medeiros J. S., Medlyn B., Meerts P., Mehrabi Z., Meir P., Melo F. P. L., Mencuccini M., Meredieu C., Messier J., Mészáros I., Metsaranta J., Michaletz S. T., Michelaki C., Migalina S., Milla R., Miller J. E. D., Minden V., Ming R., Mokany K., Moles A. T., Attila Molnár V., Molofsky J., Molz M., Montgomery R. A., Monty A., Moravcová L., Moreno-Martínez A., Moretti M., Mori A. S., Mori S., Morris D., Morrison J., Mucina L., Mueller S., Muir C. D., Müller S. C., Munoz F., Myers-Smith I. H., Myster R. W., Nagano M., Naidu S., Narayanan A., Natesan B., Negoita L., Nelson A. S., Neuschulz E. L., Ni J., Niedrist G., Nieto J., Niinemets Ü., Nolan R., Nottebrock H., Nouvellon Y., Novakovskiy A., Network T. N., Nystuen K. O., O’Grady A., O’Hara K., O’Reilly-Nugent A., Oakley S., Oberhuber W., Ohtsuka T., Oliveira R., Öllerer K., Olson M. E., Onipchenko V., Onoda Y., Onstein R. E., Ordonez J. C., Osada N., Ostonen I., Ottaviani G., Otto S., Overbeck G. E., Ozinga W. A., Pahl A. T., Paine C. E. T., Pakeman R. J., Papageorgiou A. C., Parfionova E., Pärtel M., Patacca M., Paula S., Paule J., Pauli H., Pausas J. G., Peco B., Penuelas J., Perea A., Peri P. L., Petisco-Souza A. C., Petraglia A., Petritan A. M., Phillips O. L., Pierce S., Pillar V. D., Pisek J., Pomogaybin A., Poorter H., Portsmuth A., Poschlod P., Potvin C., Pounds D., Powell A. S., Power S. A., Prinzing A., Puglielli G., Pyšek P., Raevel V., Rammig A., Ransijn J., Ray C. A., Reich P. B., Reichstein M., Reid D. E. B., Réjou-Méchain M., de Dios V. R., Ribeiro S., Richardson S., Riibak K., Rillig M. C., Riviera F., Robert E. M. R., Roberts S., Robroek B., Roddy A., Rodrigues A. V., Rogers A., Rollinson E., Rolo V., Römermann C., Ronzhina D., Roscher C., Rosell J. A., Rosenfield M. F., Rossi C., Roy D. B., Royer-Tardif S., Rüger N., Ruiz-Peinado R., Rumpf S. B., Rusch G. M., Ryo M., Sack L., Saldaña A., Salgado-Negret B., Salguero-Gomez R., Santa-Regina I., Santacruz-García A. C., Santos J., Sardans J., Schamp B., Scherer-Lorenzen M., Schleuning M., Schmid B., Schmidt M., Schmitt S., Schneider J. V., Schowanek S. D., Schrader J., Schrodt F., Schuldt B., Schurr F., Garvizu G. S., Semchenko M., Seymour C., Sfair J. C., Sharpe J. M., Sheppard C. S., Sheremetiev S., Shiodera S., Shipley B., Shovon T. A., Siebenkäs A., Sierra C., Silva V., Silva M., Sitzia T., Sjöman H., Slot M., Smith N. G., Sodhi D., Soltis P., Soltis D., Somers B., Sonnier G., Sørensen M. V., Sosinski E. E. Jr., Soudzilovskaia N. A., Souza A. F., Spasojevic M., Sperandii M. G., Stan A. B., Stegen J., Steinbauer K., Stephan J. G., Sterck F., Stojanovic D. B., Strydom T., Suarez M. L., Svenning J.-C., Svitková I., Svitok M., Svoboda M., Swaine E., Swenson N., Tabarelli M., Takagi K., Tappeiner U., Tarifa R., Tauugourdeau S., Tavsanoglu C., te Beest M., Tedersoo L., Thiffault N., Thom D., Thomas E., Thompson K., Thornton P. E., Thuiller W., Tichý L., Tissue D., Tjoelker M. G., Tng D. Y. P., Tobias J., Török P., Tarin T., Torres-Ruiz J. M., Tóthmérész B., Treurnicht M., Trivellone V., Trolliet F., Trotsiuk V., Tsakalos J. L., Tsiripidis I., Tysklind N., Umehara T., Usoltsev V., Vadeboncoeur M., Vaezi J., Valladares F., Vamosi J., van Bodegom P. M., van Breugel M., Van Cleemput E., van de Weg M., van der Merwe S., van der Plas F., van der Sande M. T., van Kleunen M., Van Meerbeek K., Vanderwel M., Vanselow K. A., Vårhammar A., Varone L., Valderrama M. Y. V., Vassilev K., Vellend M., Veneklaas E. J., Verbeeck H., Verheyen K., Vibrans A., Vieira I., Villacís J., Violle C., Vivek P., Wagner K., Waldram M., Waldron A., Walker A. P., Waller M., Walther G., Wang H., Wang F., Wang W., Watkins H., Watkins J., Weber U., Weedon J. T., Wei L., Weigelt P., Weiher E., Wells A. W., Wellstein C., Wenk E., Westoby M., Westwood A., White P. J., Whitten M., Williams M., Winkler D. E., Winter K., Womack C., Wright I. J., Wright S. J., Wright J., Pinho B. X., Ximenes F., Yamada T., Yamaji K., Yanai R., Yankov N., Yguel B., Zanini K. J., Zanne A. E., Zelený D., Zhao Y.-P., Zheng J., Zheng J., Ziemińska K., Zirbel C. R., Zizka G., Zo-Bi I. C., Zotz G., Wirth C., Glob. Chang. Biol. 26, 119–188 (2020). [DOI] [PubMed] [Google Scholar]
- 69.USDA, NRCS. The PLANTS Database, Version 3.1 (http://plants.usda.gov), National Plant Data Center, Baton Rouge, LA 70874–4490 USA. (2001)
- 70.Stekhoven D. J., Bühlmann P., MissForest—Non-parametric missing value imputation for mixed-type data. Bioinformatics 28, 112–118 (2012). [DOI] [PubMed] [Google Scholar]
- 71.R Core Team, R: A language and environment for statistical computing (R Foundation for Statistical Computing, 2020).
- 72.Chao A., Chiu C., Jost L., Unifying species diversity, phylogenetic diversity, functional diversity, and related similarity and differentiation measures through hill numbers. Annu. Rev. Ecol. Evol. Syst. 45, 297–324 (2014). [Google Scholar]
- 73.J. Oksanen, F. G. Blanchet, M. Friendly, R. Kindt, P. Legendre, D. McGlinn, P. R. Minchin, R. B. O’Hara, G. L. Simpson, P. Solymos, M. H. H. Stevens, E. Szoecs, H. Wagner, vegan: Community Ecology Package. R package version 2.5-3 (2018).
- 74.Kembel S. W., Cowan P. D., Helmus M. R., Cornwell W. K., Morlon H., Ackerly D. D., Blomberg S. P., Webb C. O., Picante: R tools for integrating phylogenies and ecology. Bioinformatics 26, 1463–1464 (2010). [DOI] [PubMed] [Google Scholar]
- 75.Laliberté E., Legendre P., A distance-based framework for measuring functional diversity from multiple traits. Ecology 91, 299–305 (2010). [DOI] [PubMed] [Google Scholar]
- 76.J. Pinheiro, D. Bates, S. DebRoy, D. Sarkar, R Core Team, nlme: Linear and Nonlinear Mixed Effects Models, R package version 3.1-131 (2017).
- 77.K. Bartón, MuMIn: Multi-Model Inference. R package version 1.40.4. https://CRAN.R-project.org/package=MuMIn. Bates (2018).
- 78.Ben-Shachar M. S., Lüdecke D., Makowski D., effectsize: Estimation of effect size indices and standardized parameters. J. Open Source Softw. 5, 2815 (2020). [Google Scholar]
- 79.Lefcheck J. S., piecewiseSEM: Piecewise structural equation modelling in R for ecology, evolution, and systematics. Methods Ecol. Evol. 7, 573–579 (2016). [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Figs. S1 to S15
Tables S1 and S2