Summary
Ovarian cancer is the deadliest gynecologic malignancy in women, with a 46% five-year overall survival rate. The objective of the study was to investigate the effects of non-homologous end-joining (NHEJ) genes on clinical outcomes of ovarian cancer patients. To determine if these genes act as prognostic biomarkers of mortality and disease progression, the expression profiles of 48 NHEJ-associated genes were analyzed using an array of statistical and machine learning techniques: logistic regression models, decision trees, naive-Bayes, two sample t-tests, support vector machines, hierarchical clustering, principal component analysis, and neural networks. In this process, the correlation of genes with patient survival and disease progression and recurrence was noted. Also, multiple features from the gene set were found to have significant predictive capabilities. APTX, BRCA1, PAXX, LIG1, and TP53 were identified as most important out of all the candidate genes for predicting clinical outcomes of ovarian cancer patients.
Subject areas: Clinical genetics, Diagnostics, Genes
Graphical abstract
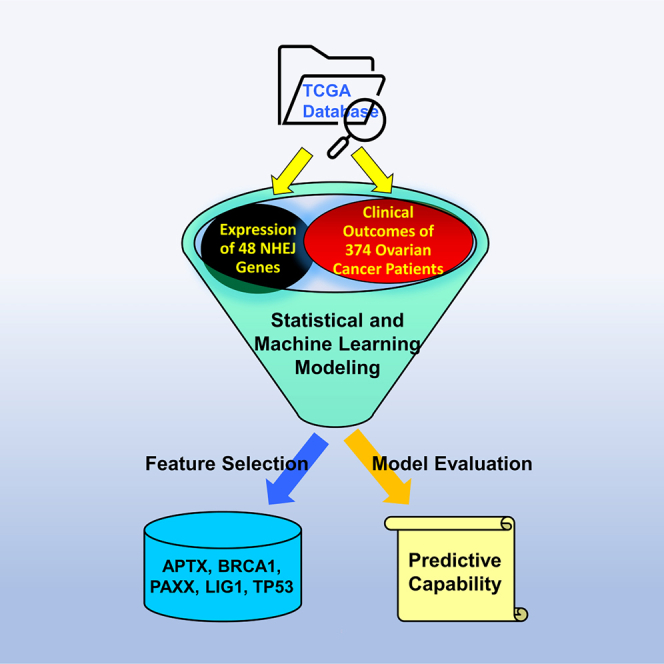
Highlights
-
•
NHEJ gene expression can be used as biomarkers of prognosis in ovarian cancer
-
•
APTX, BRCA1, PAXX, LIG1, and TP53 were identified as the most impactful genes
-
•
A higher quality and quantity of data are required to train complex prediction models
Clinical genetics; Diagnostics; Genes
Introduction
Cells are constantly monitoring for any DNA damage caused by environmental insults or incurred during DNA replication. When identified, multiple DNA repair pathways can be employed to repair the abnormality. The most lethal type of DNA damage, DNA double-strand break (DSB), is repaired by the error-free homologous recombination (HR) pathway or the error-prone non-homologous end-joining (NHEJ) pathway.1 DNA damage that starts as a single-strand break (SSB) is repaired mainly using poly ADP-ribose polymerase (PARP) through the process of base excision repair.2 If the SSB is left unrepaired, it can progress to a DSB, which is usually repaired through the HR pathway. When this pathway is unavailable, cells resort to the NHEJ pathway.3 In cancer cells with HR deficiency, the use of a PARP inhibitor leaves the cancer cells with the NHEJ pathway as the only option for repairing DSBs.4,5 It is postulated that when cells use the NHEJ repair mechanism, it leads to deleterious mutations or chromosomal abnormalities that promote cell death.6 Thus, many cancers, such as ovarian and breast cancers with defective HR repair, are susceptible to the cytotoxicity of PARP inhibitors through synthetic lethality. However, NHEJ repair could also act as a double-edged sword. Using this error-prone repair mechanism, surviving cancer cells can acquire advantageous mutations that lead to resistance to therapy.7
The NHEJ pathway can be further divided to two sub-pathways: classical or canonical NHEJ (cNHEJ) and alternative NHEJ (altNHEJ). cNHEJ involves the direct rejoining and ligation of two broken ends of a DSB. This process often leads to a small insertion or deletion (1–5 bp) at the break point. By contrast, altNHEJ requires additional end resection of both ends to generate a small microhomology sequence for pairing and joining. This process can result in a large insertion or deletion at the repaired junction. In mammalian cells, cNHEJ evolves to serve as a predominant mechanism to repair DSBs throughout the cell cycle and maintain genomic stability.6 altNHEJ functions as a backup repair mechanism when critical components for cNHEJ and HR pathways are unavailable. Therefore, the error-prone and mutagenic nature of NHEJ may be mainly attributable to altNHEJ.3 If NHEJ is not available, single strand annealing (SSA) is last in the hierarchy, being the most mutagenic.8 SSA is treated as an alternative to altNHEJ, specifically geared toward repairing resected DSBs in the S/G2 phase of the cell.9
The connections between genes involved in NHEJ and ovarian cancer outcomes remain largely unknown. However, the involvement of NHEJ pathways in cell death and mutagenic processes implies that these genes may serve as a biomarker of cancer mortality. Furthermore, the levels of NHEJ gene expression quantify the activity of the DNA repair process and potentially provide an indicator of the cancer cell’s fate in response to treatment.10 Thus, a mathematical model that correlates these genes with cancer mortality may hold promise to predict treatment and survival outcomes in patients. However, complex problems such as this may require a sophisticated model.
There are many genes involved in the NHEJ mechanism. Of them, 48 of the most prominent genes related to DNA repair, with relationships with NHEJ, were chosen for investigation. In early experimentation, classic statistical techniques were unable to check for intricate relationships with prognosis. As such, a stronger method was desired to thoroughly analyze these genes to predict prognosis. As opposed to classical methods, deep learning is a novel approach that has rapidly improved the success of models by leveraging large amounts of data to learn difficult patterns. For this approach, a neural network model was created. A subset of the data is used to train and tune the network’s parameters. Then, the model is evaluated on the remaining “testing” set of data.11 With that in mind, a major contributor to creating a successful deep learning model includes a large dataset size or data augmentation. The latter helps the model from overfitting and achieve higher accuracy by artificially increasing the amount of training data available.12 Due to the similarity of breast cancer to ovarian cancer, as shown by clinical responses to PARP inhibitors,13 breast cancer data were included in the training dataset for the deep learning approach.
Results
Linear regression shows APTX, RAD52, TP53BP1, and PMS1 correlate with survival
Linear regression was conducted to take a classic statistical approach to modeling patient’ survival. The model attempted to predict the length of survival as a function of the 48 gene expressions. The results produced an estimate, standard error, a t-value, and a p value. RAD52 and TP53BP1 were noted to be significant (p < 0.05) and negatively correlated with survival. APTX and PMS1 were also significant at a higher alpha level (p < 0.1) and positively correlated (Table S1). However, the mean squared error (MSE) for this model, 692.975, was higher than the control MSE of predicting average survival, 591.318, implying it was not making strong predictions.
Logistic regression identifies APTX, RAD52, TP53BP1, PMS1, and CTBP1 as predictors of survival
Logistic regression was conducted to supplement the results of the linear regression. The analysis produced an estimate, standard error, a t-value, and p value. RAD52, TP53BP1, CTBP1, PMS1, and APTX were statistically significant (p < 0.1). Of those genes, RAD52 and TP53BP1 were negatively correlated with survival and APTX, PMS1, and CTBP1 were positively correlated (Table 1). All the other genes gave no indication of their true relationship with patients’ survival. In addition, the balanced accuracy of the model was 0.5000, which implies this model was not effective.
Table 1.
Logistic regression of 48 genes to survival outcome conducted on the ovarian cancer dataset
| Gene | Estimate | Std. Error | t value | Pr(>|t|) |
|---|---|---|---|---|
| TP53BP1 | −0.077836 | 0.041337 | −1.883 | 0.0606 |
| RAD52 | −0.063386 | 0.032482 | −1.951 | 0.0519 |
| MRE11 | −0.061275 | 0.039049 | −1.569 | 0.1176 |
| POLQ | −0.058071 | 0.049820 | −1.166 | 0.2446 |
| XRCC5 | −0.056447 | 0.037277 | −1.514 | 0.1309 |
| XRCC1 | −0.047599 | 0.036273 | −1.312 | 0.1904 |
| XRCC7 | −0.037603 | 0.041710 | −0.902 | 0.3680 |
| MSH6 | −0.034452 | 0.062775 | −0.549 | 0.5835 |
| EXD2 | −0.027621 | 0.034477 | −0.801 | 0.4236 |
| RBBP8 | −0.020403 | 0.029359 | −0.695 | 0.4876 |
| APLF | −0.019839 | 0.033619 | −0.590 | 0.5555 |
| RIF1 | −0.016524 | 0.039430 | −0.419 | 0.6754 |
| LIG4 | −0.013188 | 0.031801 | −0.415 | 0.6786 |
| EXO1 | −0.010461 | 0.051082 | −0.205 | 0.8379 |
| PAXX | −0.008699 | 0.033950 | −0.256 | 0.7979 |
| H2AX | −0.007304 | 0.035200 | −0.208 | 0.8357 |
| XRCC6 | −0.006841 | 0.033174 | −0.206 | 0.8367 |
| PNKP | −0.005799 | 0.038298 | −0.151 | 0.8797 |
| LIG3 | −0.003759 | 0.028825 | −0.130 | 0.8963 |
| BRCA1 | −0.002899 | 0.038271 | −0.076 | 0.9397 |
| RAD1 | −0.002605 | 0.034548 | −0.075 | 0.9399 |
| ERCC1 | 0.001512 | 0.036701 | 0.041 | 0.9672 |
| RAD50 | 0.003361 | 0.033791 | 0.099 | 0.9208 |
| NBN | 0.005523 | 0.031675 | 0.174 | 0.8617 |
| ATR | 0.006529 | 0.041340 | 0.158 | 0.8746 |
| MSH3 | 0.008567 | 0.041481 | 0.207 | 0.8365 |
| RPA1 | 0.010596 | 0.032621 | 0.325 | 0.7455 |
| XRCC4 | 0.013539 | 0.036136 | 0.375 | 0.7082 |
| RAD51 | 0.018338 | 0.039797 | 0.461 | 0.6452 |
| TP53 | 0.018412 | 0.028813 | 0.639 | 0.5233 |
| MLH1 | 0.023919 | 0.035277 | 0.678 | 0.4982 |
| ERCC4 | 0.024449 | 0.031275 | 0.782 | 0.4349 |
| WRN | 0.024710 | 0.034415 | 0.718 | 0.4733 |
| DCLRE1C | 0.026012 | 0.035011 | 0.743 | 0.4580 |
| NHEJ1 | 0.026084 | 0.036593 | 0.713 | 0.4765 |
| PARP1 | 0.031145 | 0.042478 | 0.733 | 0.4640 |
| PARP3 | 0.033195 | 0.031000 | 1.071 | 0.2850 |
| POLM | 0.033783 | 0.032540 | 1.038 | 0.2999 |
| MLH3 | 0.036035 | 0.034967 | 1.031 | 0.3035 |
| LIG1 | 0.036274 | 0.043006 | 0.843 | 0.3996 |
| TDP1 | 0.040557 | 0.036737 | 1.104 | 0.2704 |
| MSH2 | 0.043464 | 0.063100 | 0.689 | 0.4914 |
| POLL | 0.045968 | 0.031495 | 1.460 | 0.1454 |
| PMS1 | 0.052444 | 0.030650 | 1.711 | 0.0880 |
| CTBP1 | 0.052678 | 0.030728 | 1.714 | 0.0874 |
| ATM | 0.056676 | 0.044617 | 1.270 | 0.2049 |
| APTX | 0.058779 | 0.031894 | 1.843 | 0.0662 |
| BRCA2 | 0.060350 | 0.039121 | 1.543 | 0.1239 |
Logistic regression for the gene dataset was conducted and each gene was ordered by the estimates. Positive estimates of gene expression are associated with improved survival whereas the negative estimates contribute to poor survival probability. Standard error, a t-value, and a p value for each gene in the logistic regression model was generated. P-values under 0.1 were bolded.
Logistic regression identifies BRCA1, BRCA2, PAXX, and DCLRE1C as predictors of progression
Logistic regression was conducted to assess gene correlation and predictive capabilities on progression. The analysis produced an estimate, standard error, a t-value, and p value. BRCA1 (p < 0.01), BRCA2 (p < 0.1), PAXX (p < 0.05), and DCLRE1C (p < 0.05) were statistically significant. Of those genes, BRCA1, BRCA2 and PAXX were negatively correlated with progression and just DCLRE1C was positively correlated (Table 2). Similar to survival, using just the statistically significant genes, the balanced accuracy of the model was still low at 0.5185.
Table 2.
Logistic regression of 48 genes to progression outcome conducted on the ovarian cancer dataset
| Gene | Estimate | Std. Error | t value | Pr(>|t|) |
|---|---|---|---|---|
| BRCA1 | −0.1242976 | 0.0415754 | −2.990 | 0.00305 |
| BRCA2 | −0.0736006 | 0.0416912 | −1.765 | 0.07862 |
| PAXX | −0.0706452 | 0.0331574 | −2.131 | 0.03402 |
| MSH6 | −0.0648559 | 0.0648274 | −1.000 | 0.31798 |
| ATM | −0.0619214 | 0.0476275 | −1.300 | 0.19466 |
| XRCC1 | −0.0504561 | 0.0372236 | −1.355 | 0.17638 |
| PNKP | −0.0449848 | 0.0397142 | −1.133 | 0.25833 |
| APLF | −0.0350988 | 0.0338855 | −1.036 | 0.30121 |
| LIG4 | −0.0297795 | 0.0345028 | −0.863 | 0.38884 |
| EXO1 | −0.0269956 | 0.0535367 | −0.504 | 0.61450 |
| PMS1 | −0.0265631 | 0.0303097 | −0.876 | 0.38159 |
| TDP1 | −0.0263480 | 0.0394532 | −0.668 | 0.50481 |
| EXD2 | −0.0254016 | 0.0368288 | −0.690 | 0.49096 |
| XRCC6 | −0.0240855 | 0.0349407 | −0.689 | 0.49121 |
| XRCC5 | −0.0228620 | 0.0371049 | −0.616 | 0.53831 |
| APTX | −0.0191056 | 0.0345156 | −0.554 | 0.58035 |
| NBN | −0.0186892 | 0.0318944 | −0.586 | 0.55838 |
| POLM | −0.0180680 | 0.0331872 | −0.544 | 0.58659 |
| RAD52 | −0.0141432 | 0.0420137 | −0.337 | 0.73665 |
| POLQ | −0.0094281 | 0.0517068 | −0.182 | 0.85545 |
| RAD1 | −0.0076254 | 0.0349897 | −0.218 | 0.82764 |
| MSH3 | −0.0064148 | 0.0422258 | −0.152 | 0.87936 |
| PARP3 | −0.0053147 | 0.0334938 | −0.159 | 0.87404 |
| RPA1 | −0.0003987 | 0.0363523 | −0.011 | 0.99126 |
| TP53 | 0.0001413 | 0.0302283 | 0.005 | 0.99627 |
| RIF1 | 0.0006736 | 0.0413518 | 0.016 | 0.98702 |
| XRCC4 | 0.0022986 | 0.0381269 | 0.060 | 0.95197 |
| RBBP8 | 0.0040682 | 0.0298129 | 0.136 | 0.89156 |
| NHEJ1 | 0.0044331 | 0.0367863 | 0.121 | 0.90417 |
| LIG3 | 0.0103901 | 0.0705623 | 0.147 | 0.88305 |
| LIG1 | 0.0125968 | 0.0473550 | 0.266 | 0.79043 |
| RAD50 | 0.0134041 | 0.0345507 | 0.388 | 0.69835 |
| POLL | 0.0181209 | 0.0320230 | 0.566 | 0.57195 |
| CTBP1 | 0.0218878 | 0.0310270 | 0.705 | 0.48113 |
| XRCC7 | 0.0312191 | 0.0429683 | 0.727 | 0.46812 |
| H2AX | 0.0313751 | 0.0385220 | 0.814 | 0.41608 |
| ERCC4 | 0.0315063 | 0.0306286 | 1.029 | 0.30455 |
| TP53BP1 | 0.0321815 | 0.0418084 | 0.770 | 0.44212 |
| MSH2 | 0.0341919 | 0.0658308 | 0.519 | 0.60391 |
| WRN | 0.0406368 | 0.0376392 | 1.080 | 0.28126 |
| ATR | 0.0408894 | 0.0450884 | 0.907 | 0.36527 |
| ERCC1 | 0.0438548 | 0.0381047 | 1.151 | 0.25078 |
| MLH3 | 0.0473954 | 0.0485356 | 0.977 | 0.32968 |
| MRE11 | 0.0542806 | 0.0394192 | 1.377 | 0.16964 |
| MLH1 | 0.0570253 | 0.0371401 | 1.535 | 0.12584 |
| RAD51 | 0.0639152 | 0.0396143 | 1.613 | 0.10781 |
| PARP1 | 0.0670000 | 0.0436469 | 1.535 | 0.12593 |
| DCLRE1C | 0.0916141 | 0.0392333 | 2.335 | 0.02026 |
Logistic regression for the gene dataset was conducted and each gene was ordered by the estimates. Positive estimates of gene expression are associated with likelihood for progression whereas the negative estimates contribute to low progression probability. Standard error, a t-value, and a p value for each gene in the logistic regression model was generated. P-values under 0.1 were bolded.
Logistic regression demonstrates strong predictive capabilities of recurrence using MLH3, BRCA2, LIG1, H2AX, TP53, NBN, MLH1, and RAD52
Logistic regression was conducted to assess gene correlation and predictive capabilities on recurrence. The analysis produced an estimate, standard error, a t-value, and p value. MLH3 (p < 0.01), BRCA2 (p < 0.005), and LIG1 (p < 0.1) were statistically significant and negatively correlated with recurrence. In addition, H2AX (p < 0.1), TP53 (p < 0.05), NBN (p < 0.05), MLH1 (p < 0.05), and RAD52 (p < 0.01) were statistically significant and positively correlated (Table 3). Using just the statistically significant genes resulted in a balanced accuracy of 0.6397.
Table 3.
Logistic regression of 48 genes to recurrence outcome conducted on the ovarian cancer dataset
| Gene | Estimate | Std. Error | t value | Pr(>|t|) |
|---|---|---|---|---|
| MLH3 | −0.1436620 | 0.0508329 | −2.826 | 0.00506 |
| BRCA2 | −0.1229546 | 0.0434042 | −2.833 | 0.00496 |
| LIG3 | −0.0960805 | 0.0733806 | −1.309 | 0.19152 |
| LIG1 | −0.0912946 | 0.0479346 | −1.905 | 0.05789 |
| MSH3 | −0.0576118 | 0.0442279 | −1.303 | 0.19381 |
| XRCC5 | −0.0561888 | 0.0382077 | −1.471 | 0.14255 |
| RAD51 | −0.0554070 | 0.0411657 | −1.346 | 0.17944 |
| PAXX | −0.0516596 | 0.0345574 | −1.495 | 0.13610 |
| ERCC4 | −0.0406260 | 0.0504662 | −0.805 | 0.42151 |
| POLM | −0.0379293 | 0.0343613 | −1.104 | 0.27064 |
| WRN | −0.0337736 | 0.0395686 | −0.854 | 0.39411 |
| PMS1 | −0.0323849 | 0.0315185 | −1.027 | 0.30510 |
| POLL | −0.0280872 | 0.0334922 | −0.839 | 0.40242 |
| XRCC7 | −0.0236921 | 0.0450393 | −0.526 | 0.59929 |
| APTX | −0.0219715 | 0.0355848 | −0.617 | 0.53746 |
| PNKP | −0.0185921 | 0.0412459 | −0.451 | 0.65252 |
| MSH2 | −0.0154689 | 0.0681421 | −0.227 | 0.82059 |
| RPA1 | −0.0019469 | 0.0380689 | −0.051 | 0.95925 |
| PARP3 | −0.0015842 | 0.0347633 | −0.046 | 0.96369 |
| DCLRE1C | −0.0009017 | 0.0410132 | −0.022 | 0.98248 |
| ATR | −0.0007959 | 0.0466153 | −0.017 | 0.98639 |
| RAD1 | 0.0031648 | 0.0360723 | 0.088 | 0.93015 |
| BRCA1 | 0.0060448 | 0.0409094 | 0.148 | 0.88264 |
| XRCC6 | 0.0061608 | 0.0364277 | 0.169 | 0.86583 |
| CTBP1 | 0.0066763 | 0.0324354 | 0.206 | 0.83707 |
| EXD2 | 0.0072041 | 0.0383797 | 0.188 | 0.85125 |
| POLQ | 0.0114784 | 0.0533366 | 0.215 | 0.82977 |
| APLF | 0.0127893 | 0.0366496 | 0.349 | 0.72739 |
| RBBP8 | 0.0133334 | 0.0310312 | 0.430 | 0.66777 |
| MSH6 | 0.0185962 | 0.0675222 | 0.275 | 0.78321 |
| LIG4 | 0.0279871 | 0.0363777 | 0.769 | 0.44235 |
| MRE11 | 0.0281447 | 0.0412834 | 0.682 | 0.49598 |
| XRCC4 | 0.0342550 | 0.0403606 | 0.849 | 0.39678 |
| RAD50 | 0.0374275 | 0.0363462 | 1.030 | 0.30404 |
| NHEJ1 | 0.0408071 | 0.0380589 | 1.072 | 0.28457 |
| PARP1 | 0.0414107 | 0.0448986 | 0.922 | 0.35718 |
| RIF1 | 0.0422092 | 0.0426535 | 0.990 | 0.32325 |
| TP53BP1 | 0.0426385 | 0.0435148 | 0.980 | 0.32802 |
| ERCC1 | 0.0475018 | 0.0399575 | 1.189 | 0.23555 |
| XRCC1 | 0.0490576 | 0.0404126 | 1.214 | 0.22583 |
| TDP1 | 0.0608796 | 0.0413757 | 1.471 | 0.14234 |
| EXO1 | 0.0630913 | 0.0546782 | 1.154 | 0.24956 |
| ATM | 0.0633327 | 0.0488009 | 1.298 | 0.19546 |
| H2AX | 0.0751909 | 0.0396955 | 1.894 | 0.05926 |
| TP53 | 0.0774415 | 0.0315229 | 2.457 | 0.01465 |
| NBN | 0.0788570 | 0.0333537 | 2.364 | 0.01877 |
| MLH1 | 0.0867637 | 0.0397749 | 2.181 | 0.03001 |
| RAD52 | 0.1173069 | 0.0437177 | 2.683 | 0.00774 |
Logistic regression for the gene dataset was conducted and each gene was ordered by the estimates. Positive estimates of gene expression are associated with likelihood for recurrence whereas the negative estimates contribute to low recurrence probability. Standard error, a t-value, and a p value for each gene in the logistic regression model was generated. P-values under 0.1 were bolded.
T-test identifies genes correlating with prognosis
To further analyze genes using classic statistical methods, two-sample t-tests were conducted. P-values and a correlation indication were generated for each gene and outcome. Among the survival outcome, DCLRE1C (p < 0.05), TDP1 (p < 0.05), PARP3 (p < 0.05), APTX (p < 0.05), and PMS1 (p < 0.05), were positively correlated. In the progression outcome, MRE11 (p < 0.05) was positively correlated while PAXX (p < 0.005) was negatively correlated. Finally, NBN (p < 0.05), ATM (p < 0.05), TP53 (p < 0.05), and MLH1 (p < 0.05) were positively correlated and BRCA2 (p < 0.05), PNKP (p < 0.05), and PAXX (p < 0.05) were negatively correlated with recurrence (Table 4).
Table 4.
Two sample t-tests for survival, progression, and recurrence
| Gene | Survival (p) | Survival positive correlation | Progression (p) | Progression positive correlation | Recurrence | Recurrence positive correlation |
|---|---|---|---|---|---|---|
| XRCC6 | 0.1365 | TRUE | 0.4762 | TRUE | 0.1414 | TRUE |
| XRCC5 | 0.3400 | FALSE | 0.4559 | FALSE | 0.3177 | TRUE |
| XRCC7 | 0.3347 | FALSE | 0.1218 | TRUE | 0.2297 | TRUE |
| LIG4 | 0.3816 | TRUE | 0.1728 | FALSE | 0.2789 | FALSE |
| LIG3 | 0.3274 | FALSE | 0.2043 | TRUE | 0.2824 | TRUE |
| LIG1 | 0.3058 | TRUE | 0.3732 | FALSE | 0.1334 | FALSE |
| XRCC4 | 0.2605 | TRUE | 0.3199 | FALSE | 0.4431 | TRUE |
| NHEJ1 | 0.2924 | TRUE | 0.0833 | TRUE | 0.1103 | TRUE |
| XRCC1 | 0.0599 | FALSE | 0.1989 | FALSE | 0.3436 | TRUE |
| DCLRE1C | 0.0209 | TRUE | 0.0654 | TRUE | 0.2610 | FALSE |
| TP53BP1 | 0.2826 | FALSE | 0.0775 | TRUE | 0.1005 | TRUE |
| BRCA1 | 0.3101 | TRUE | 0.1357 | FALSE | 0.1996 | TRUE |
| BRCA2 | 0.1017 | TRUE | 0.0521 | FALSE | 0.0134 | FALSE |
| EXO1 | 0.1077 | TRUE | 0.4149 | FALSE | 0.2766 | TRUE |
| EXD2 | 0.4229 | TRUE | 0.3532 | TRUE | 0.4824 | TRUE |
| POLM | 0.2072 | TRUE | 0.4002 | TRUE | 0.2672 | FALSE |
| POLL | 0.2428 | TRUE | 0.1369 | TRUE | 0.2618 | TRUE |
| POLQ | 0.2806 | TRUE | 0.4212 | FALSE | 0.1701 | FALSE |
| RAD50 | 0.1986 | TRUE | 0.0601 | TRUE | 0.1568 | TRUE |
| MRE11 | 0.4411 | FALSE | 0.0382 | TRUE | 0.0615 | TRUE |
| NBN | 0.2461 | TRUE | 0.1567 | TRUE | 0.0306 | TRUE |
| TDP1 | 0.0160 | TRUE | 0.4932 | FALSE | 0.4327 | TRUE |
| RBBP8 | 0.2539 | TRUE | 0.2660 | TRUE | 0.1830 | TRUE |
| CTBP1 | 0.2030 | TRUE | 0.4875 | FALSE | 0.4219 | TRUE |
| APLF | 0.2423 | TRUE | 0.4109 | FALSE | 0.4268 | TRUE |
| PARP1 | 0.1572 | TRUE | 0.1688 | TRUE | 0.1550 | TRUE |
| PARP3 | 0.0180 | TRUE | 0.1810 | TRUE | 0.3649 | TRUE |
| PNKP | 0.4876 | TRUE | 0.0553 | FALSE | 0.0365 | FALSE |
| APTX | 0.0109 | TRUE | 0.1646 | FALSE | 0.4179 | FALSE |
| WRN | 0.3309 | TRUE | 0.1074 | TRUE | 0.2218 | FALSE |
| PAXX | 0.3906 | TRUE | 0.0010 | FALSE | 0.0261 | FALSE |
| RIF1 | 0.4603 | TRUE | 0.4129 | FALSE | 0.4573 | TRUE |
| RAD52 | 0.0707 | FALSE | 0.4665 | TRUE | 0.0502 | TRUE |
| RAD51 | 0.2935 | TRUE | 0.2066 | TRUE | 0.4841 | TRUE |
| ATM | 0.3451 | TRUE | 0.1067 | TRUE | 0.0424 | TRUE |
| ATR | 0.1619 | TRUE | 0.1270 | TRUE | 0.3542 | TRUE |
| TP53 | 0.2473 | TRUE | 0.4517 | FALSE | 0.0169 | TRUE |
| H2AX | 0.3463 | FALSE | 0.4039 | FALSE | 0.1224 | TRUE |
| ERCC1 | 0.1258 | FALSE | 0.4466 | FALSE | 0.3870 | FALSE |
| ERCC4 | 0.2544 | TRUE | 0.1472 | TRUE | 0.2574 | TRUE |
| RPA1 | 0.1940 | TRUE | 0.3106 | TRUE | 0.0904 | TRUE |
| MSH2 | 0.1508 | TRUE | 0.2731 | TRUE | 0.1099 | TRUE |
| MSH3 | 0.1816 | TRUE | 0.1493 | TRUE | 0.2319 | TRUE |
| RAD1 | 0.2231 | TRUE | 0.2883 | FALSE | 0.1843 | FALSE |
| MSH6 | 0.2942 | TRUE | 0.4480 | FALSE | 0.0527 | TRUE |
| PMS1 | 0.0454 | TRUE | 0.4965 | TRUE | 0.4373 | FALSE |
| MLH1 | 0.0513 | TRUE | 0.1560 | TRUE | 0.0341 | TRUE |
| MLH3 | 0.0677 | TRUE | 0.1051 | TRUE | 0.1437 | FALSE |
p values were generated for the gene expression variables when compared to survival, progression, and recurrence. The test determines if the mean is different whether the patient has the outcome or not. Any p values below 0.05 were bolded. In addition, the “Positive Correlation” columns relate if higher gene expression associates with the survival, progression, or recurrence outcome.
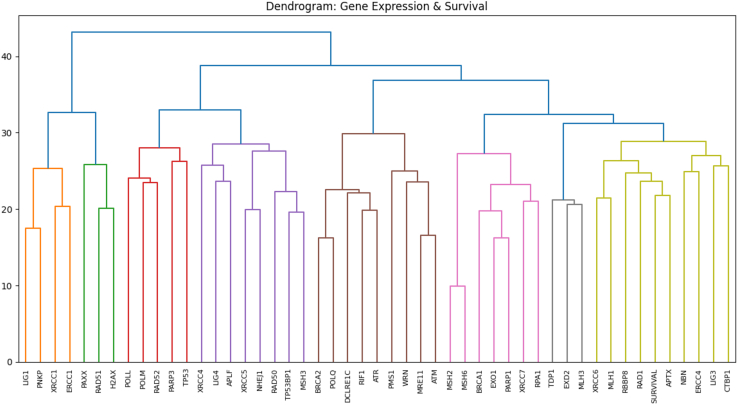
Hierarchical clustering forms a gene cluster with the survival outcome
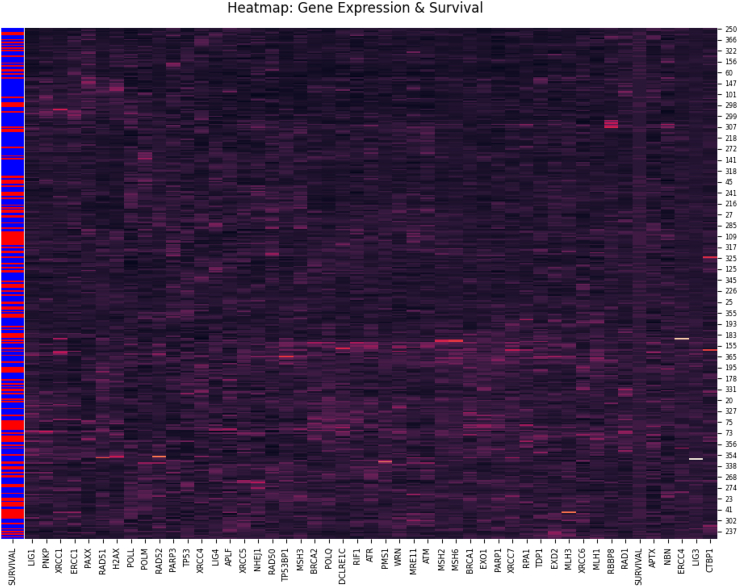
A dendrogram was generated to visualize the results of the hierarchical clustering analysis. The results showed that APTX, RAD1, RBBP8, MLH1, XRCC6, NBN, ERCC4, LIG3, and CTBP1 were part of the same cluster (yellow) with the survival variable (Figure 1). In addition, the hierarchical clustering analysis produced a heatmap that plots correlations between gene variables and patients. In this graph, there were some groups of patients with matching brightness, indicating close distance. These similar patients were likely easier to discern via modeling since the row coloring show that the most of them are also grouped by survival outcome (Figure 2).
Figure 1.
Dendrogram from hierarchical clustering of 48 genes
The dendrogram displays the relatedness between variables. Major clusters are colored on the figure. It is in scale, with lower branches indicating a closer similarity.
Figure 2.
Heatmap from hierarchical clustering of 48 genes
Shows the similarity between gene expression and patients. The brighter the color indicates a higher value, showing where correlation is. The first column are labels for survival, with blue representing deceased and red surviving patients.
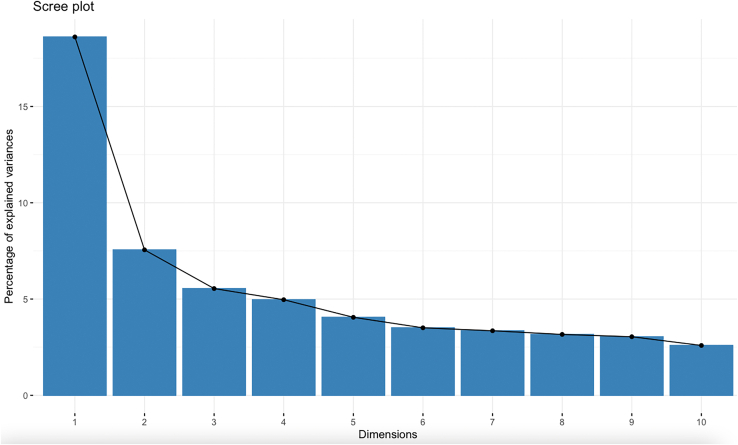
Dimensionality cannot be reduced with principal component analysis
Principal component analysis (PCA) was performed to assess redundancies in the data and to note relationships between the gene expression data as a whole and survival. According to the scree plot, a significant portion of the data was lost in the principal components. The first five components covered roughly 40% of the data while the entire ten components covered around 60% (Figure 3). As a result, no separation was observed when graphing alive and deceased patients using the first 2 PCA scores (Figure S1). Furthermore, EXO1, POLQ, XRCC7, TP53BP1, and PARP1 had the highest contributions to the principal components (Figure S2).
Figure 3.
Scree plot for PCA
The scree plot displayed the amount of retained information.
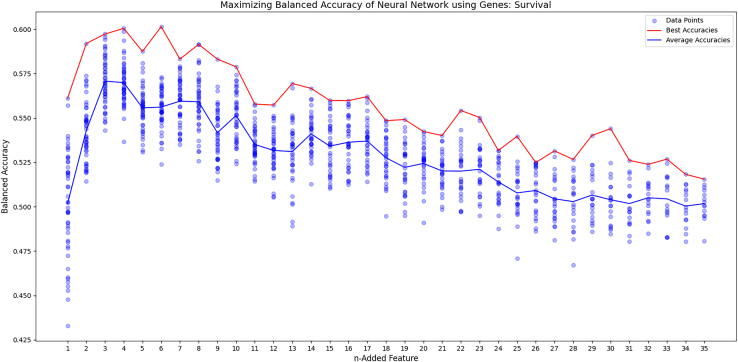
Forward feature selection optimizes neural network
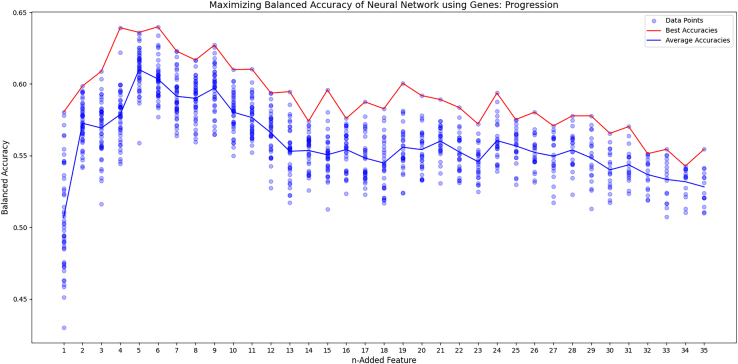
To create an effective neural network, forward feature selection was conducted to reduce the amount of irrelevant inputs to the model. In addition, feature selection graphs were generated for each outcome, displaying the trend of accuracy as each feature was added. The survival curve reached peak balanced accuracy with four genes, RBBP8, APTX, ERCC1, and LIG3, and then decreased after that (Figure 4). The progression curve was best on average after five, using PAXX, LIG1, BRCA1, MSH2, and POLQ, before it trended downward (Figure 5). The recurrence graph peaked after seven, with ERCC4, XRCC1, TP53, RIF1, LIG3, LIG1, and APLF. However, it didn’t consistently trend downward like the survival and progression graphs (Figure 6). In each graph, after seven genes, the max accuracy was stagnant, even though other relevant genes were present. This indicates that more data was likely needed to fit the model.
Figure 4.
Forward feature selection for survival
The figure graphs the results of the forward feature selection as each gene is added. The blue line is the average of each trial and the red line is the best trial.
Figure 5.
Forward feature selection for progression
The figure graphs the results of the forward feature selection as each gene is added. The blue line is the average of each trial and the red line is the best trial.
Figure 6.
Forward feature selection for recurrence
The figure graphs the results of the forward feature selection as each gene is added. The blue line is the average of each trial and the red line is the best trial.
Neural network makes strong predictions but breast cancer data fails to augment dataset
A bar graph was generated to compare the balanced accuracy of the neural network with and without the breast cancer data as training augmentation. Three gene sets were tested: all the genes, the best from the forward feature selection, and the best from the logistic regression feature selection. Using the top three from the forward feature selection, RBBP8, APTX, and ERRC1, produced the best balanced accuracy for predicting survival at 0.5776. In addition, in all three trials, the breast cancer data lowered the accuracy, indicating that it can’t serve as a method for data augmentation (See Figure S3). For predicting progression, the top four from the forward feature selection, PAXX, LIG1, BRCA1, and MSH2 reached a max balanced accuracy of 0.6310. Lastly, a balanced accuracy of 0.5953 was achieved predicting recurrence using the first six genes from the feature selection, ERCC4, XRCC1, TP53, RIF1, LIG3, and LIG1.
NHEJ related genes predicts prognosis using assorted machine learning methods
The optimal model for predicting survival was the support vector machine (SVM) using TP53BP1, CTBP1, APTX, RAD52, and PMS1 as the features with a balanced accuracy of 0.5887. For progression, the neural network performed the best with 0.6310 balanced accuracy using PAXX, LIG1, BRCA1, and MSH2. Finally, for predicting recurrence, the logistic regression was strongest at 0.6397 balanced accuracy using BRCA2, LIG1, NBN, RAD52, TP53, H2AX, MLH1, and MLH3 (See all model performance in Table S2).
Simulation determines baseline accuracy for significance
Based on the simulation experiment, the 95% percentile of balanced accuracy that can be achieved from a purely randomly generated dataset maxes out at 0.5546, using the decision tree model. The logistic regression, naive-Bayes, and SVM reached 0.5223, 0.5480, and 0.5425 balanced accuracy respectively. Typically, for each model, the average balanced accuracy was 0.5 (+/− 0.05). Lastly, on average, 4.64 genes were found to have significant p-values out of the 48 genes (See Table S3).
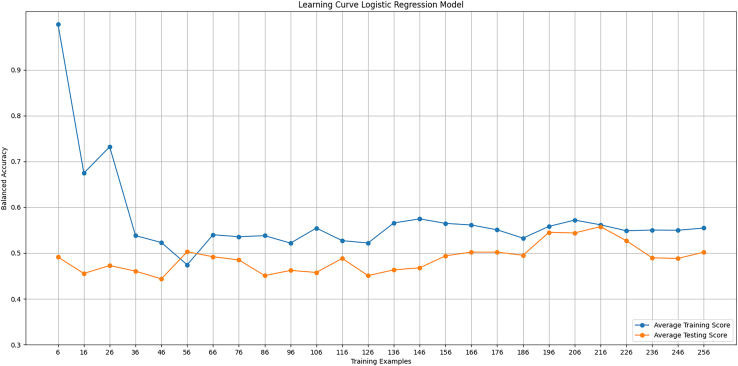
Learning curve demonstrates logistic regression as high-bias method
Learning curves were generated for the logistic regression model predicting survival. The curve showed that the model reached its potential with the features given. Yet it was an “under-fit” to the data as the performance was not very strong (Figure 7).
Figure 7.
Learning curve, logistic regression model
A learning curve was generated for the logistic regression model. Balanced accuracy evaluated training and testing as a function of the number of training examples. A high training score with few examples is expected since its trivial for the model to fit parameters to only a few data points.
Learning curves indicates deep learning methods potentially will improve with more data
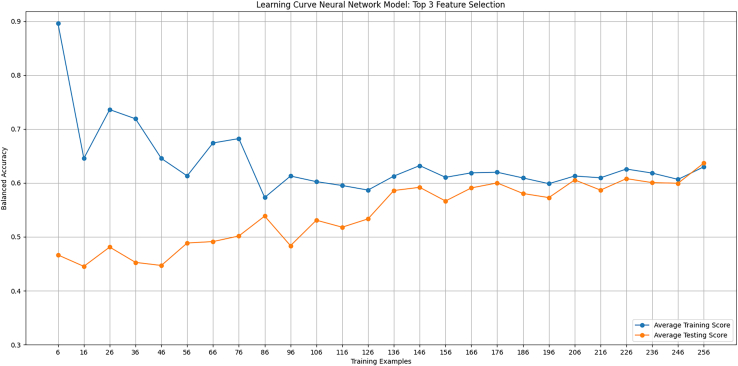
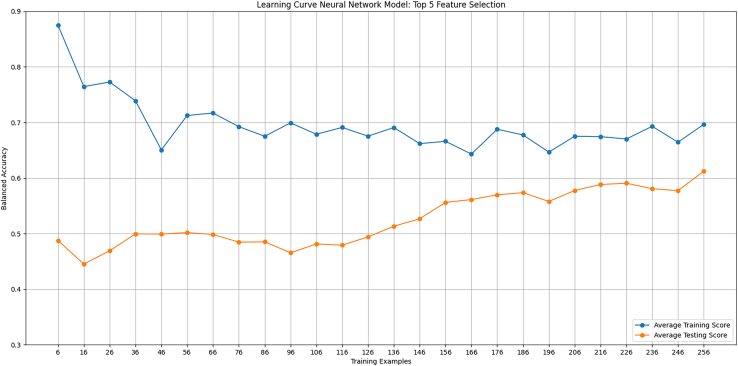
Learning curves were generated for the neural network model in predicting survival when training on a different number of genes. The first curve used the top three genes from the forward feature selection. The curve showed optimal training, needing each patient to reach equal balanced accuracy among the training and testing data (Figure 8). The second curve included the top five genes from the feature selection. This iteration demonstrated that increasing the number of features causes an overfit, trending toward more data equalizing the training and testing scores (Figure 9).
Figure 8.
Learning curve, optimal neural network model
A learning curve was generated for the neural network training on the top three genes from the forward feature selection. Balanced accuracy evaluated training and testing as a function of the number of training examples. A high training score with few examples is expected since its trivial for the neural network to fit parameters to only a few data points.
Figure 9.
Learning curve, neural network model
A learning curve was generated for the neural network training on the top five genes from the forward feature selection. Balanced accuracy evaluated training and testing as a function of the number of training examples. A high training score with few examples is expected since its trivial for the neural network to fit parameters to only a few data points.
Discussion
The machine learning models: logistic regression, decision tree, support vector machines, naive-Bayes, and neural network indicated the predictive capabilities of the genes on survival, progression, and recurrence outcomes. Balanced accuracy was used as the scoring metric because it achieves equal weighting of correct positive and negative predictions. The feature selection effectively improved this metric while also identifying which genes can act as biomarkers of prognosis. Since the models are assessed on unfamiliar examples, the balanced accuracy reliably showed the model’s effectiveness and generalization to new data.
Since the sample size is limited, a lower limit of accuracy was calculated to discern a statistically significant result. The simulation demonstrated that 95% of randomly generated datasets would not produce balanced accuracy above the threshold of 0.555. Since the threshold is beaten by our models, such as the SVM predicting survival achieving 0.5887, the accuracy is acceptable. It is statistically improbable for the actual gene expressions used to have shown correlation with prognosis purely by chance in such a sample.
In addition, the simulation confirmed that some genes are expected to be statistically significant in the t-test, purely by chance. This indicates that lone t-test results should be taken with skepticism. Rather, overlapping results with the feature selections are needed to corroborate the relevance of the gene.
This report demonstrated that NHEJ has an impact on the prognosis outcomes of ovarian cancer patients. Through multiple methods of statistical inference, several NHEJ genes that take a leading role in the clinical outcomes of ovarian cancer are identified. Based on the result of the logistic regression, and further supported by the linear regression, APTX, RAD52, TP53BP1, PMS1, and CTBP1 correlate with patients’ survival outcomes. The two-sample t-test analysis showed that DCLRE1C, PARP3, TDP1, APTX, and PMS1 likely exhibit significant differences between alive and deceased patients. In the forward feature selection, the genes RBBP8, APTX, ERCC1, and LIG3 were identified as optimal for predictions. Moreover, our hierarchical clustering analysis revealed that RBBP8, LIG3, and APTX are clustering with survival outcomes, among other genes. Because the scree plot demonstrated that significant information was lost in its dimensionality reduction, the results of the PCA are questionable.
The results for top genes correlated with the survival outcome was presented as a table for clarity (Table 5). One interesting association that was noted was that genes with positive survival outcomes typically promoted cNHEJ and SSA while those with negative survival outcomes promoted altNHEJ. CTBP1 and RAD52 were the sole exceptions to this trend. In addition, TP53BP1 has been supported to have a role in both pathways, so its effect is ambiguous. PMS1, MLH1, and RAD52 are also known mismatch repair (MMR) genes,14 so their involvement in MMR rather than SSA might also be related to this trend. This casual observation is only sufficient for hypothesis generation, requiring further validation.
Table 5.
Survival gene correlations and role in NHEJ
| Gene | Correlation | Analysis | Role in DNA repair | Reference |
|---|---|---|---|---|
| APTX | Positive | Logistic Regression (p < 0.1), T-Test (p < 0.05), Forward Feature Selection, Hierarchical Clustering |
cNHEJ | Seol et al.15; Wang et al.16; Chiruvella et al.17 |
| DCLRE1C | Positive | T-Test (p < 0.05) | cNHEJ | Moscariello et al.18; Chiruvella et al.17 |
| PARP3 | Positive | T-Test (p < 0.05) | cNHEJ | Beck et al.19, Chiruvella et al.17 |
| PMS1 | Positive | Logistic Regression (p < 0.1), T-Test (p < 0.05) |
SSA | Blasiak20 |
| TDP1 | Positive | T-Test (p < 0.05) | cNHEJ | Chiruvella et al.17 |
| CTBP1 | Positive | Logistic Regression (p < 0.1), Hierarchical Clustering |
altNHEJ | Shamanna et al.21 |
| MLH1 | Positive | Hierarchical Clustering | SSA | Blasiak20; Sugawara22 |
| TP53BP1 | Negative | Logistic Regression (p < 0.1) | cNHEJ, altNHEJ | Xiong et al.23; Lei24 |
| RAD52 | Negative | Logistic Regression (p < 0.1) | SSA | Stefanovie25 |
A table was compiled to include each gene with a found correlation with survival. The relationship, either positive or negative, was listed along with the analysis it was found in. Finally, the role in NHEJ is listed with its reference.
In predicting progression, the result of the logistic regression showed BRCA1, BRCA2, PAXX, and DCLRE1C are correlated. The two-sample t-test analysis corroborated PAXX’s relationship with progression and it further added MRE11. In the forward feature selection, BRCA1 and PAXX appeared again. In addition to BRCA1 and PAXX, LIG1, MSH2, and POLQ were used to achieve optimal progression predictions with the neural network. The recurrence logistic regression incorporated BRCA2, LIG1, H2AX, TP53, NBN, MLH1, and RAD52. The t-test found significance in BRCA2, TP53, NBN and MLH1 as well and further revealed PNKP, PAXX, and ATM as relevant. Yet the feature selection found ERCC4, XRCC1, TP53, RIF1, LIG3, and LIG1 were best for the neural network, the only overlap being TP53 and LIG1.
An interesting thing noted was the neural network and logistic regression didn’t have complete overlap in their feature sets with each other and the t-test. This likely indicates that the models could reach higher predictive capabilities by including all the relevant features discovered. It also narrows the upmost critical factors, with APTX in survival, PAXX and BRCA1 in progression, and TP53 and LIG1 in recurrence being shared by both feature selections conducted.
In the learning curves, the logistic regression model showed a high bias issue indicating that it needs to have more complexity. Transitioning to the neural network, there is a high variance issue, showing that the data became insufficient to train the survival models with at least five or six genes. We extrapolated from this that more data can potentially increase the accuracy of the model, since it will allow more features to be included. It was theorized that since breast cancer is similar to ovarian cancer, shown by similar response to PARP inhibitors,13 the model might be able to apply it to its learning process. The incorporation of breast cancer data into the training of our neural network didn’t improve the accuracy. As a result, it is critical that efforts are made to increase data from ovarian cancer patients.
It is important to note that all our models disregarded treatment information, demographics, and other indicators of prognosis. This was to ensure all predictive capabilities came from the gene data. But in the future, by including an array of different biomarkers and collecting more clinical data, a predictive model could be created to achieve a higher accuracy.26 Or, by emulating our methodology, other sets of genes can be analyzed cost-effectively. At the time, only high-grade serous ovarian cancer data were available. In the future, different types should be investigated to determine the generalization of the findings. Finally, NHEJ genes showed evidence through modeling to be able to predict survival, progression, and recurrence. Thus, further inquiry is necessary to assess the genes’ role in regard to each outcome.
Limitations of the study
The study was likely limited by the dataset size. Training a deep learning model requires a large number of examples and the learning curves implied that more are needed. More data would improve confidence in the generalization of results to new patients. In addition, there is concern in the reliability of the recurrence and progression factors. These data were inferred from clinical notes, which may be missing information. As a result, recurrence or progression could be mislabeled in the analysis. Lastly, computational strength limited the reliability of the neural network results. Training a deep learning model is stochastic, so the model will not perform the same every time it is trained. To counteract this, the experiment is repeated multiple times, averaging the accuracies to balance the element of randomness. In the forward feature selection, for each gene set, only 30 models total were trained and evaluated. In rare cases, the model group might get lucky in testing, leading to inflated accuracy. Thus, outliers might appear in the result of the forward feature selection. Ideally, each gene set could be tested more thoroughly.
STAR★Methods
Key resources table
| REAGENT or RESOURCE | SOURCE | IDENTIFIER |
|---|---|---|
| Deposited data | ||
| Cleaned data and R and Python code | This paper | RRID:SCR_003193; https://doi.org/10.5281/zenodo.8123030 |
| Software and algorithms | ||
| PCA software | GraphPad, Prism 9.02 | www.graphpad.com |
| Deep learning library | Tensorflow | https://www.tensorflow.org/ |
| Dendrogram generation | SciPy | https://scipy.org/ |
| Clustermap generation | Seaborn | https://seaborn.pydata.org/ |
| Python graphing library | matplotlib | https://matplotlib.org/ |
| Python programming language | Python | https://www.python.org/ |
| Model evaluations | caret | https://cran.r-project.org/package=caret |
| Decision tree classifier | rpart | https://cran.r-project.org/package=rpart |
| Naive-bayes and SVM classifiers | e1071 | https://cran.r-project.org/package=e1071 |
| R programming language | R Project | https://www.r-project.org/ |
| Other | ||
| Source of data | TCGA Web Program | https://www.cancer.gov/ |
| Protein names to gene names | ProteinAtlas | https://www.proteinatlas.org |
| Gene names to Ensembl ID | GeneCards | www.genecards.org |
Resource availability
Lead contact
Further information and requests for resources, including raw data, should be directed to and will be fulfilled by the lead contact, Z Ping Lin (z.ping.lin@yale.edu).
Materials availability
The source of the data and code in performed analyses are all open-source. The data files used in this study can be obtained through the TCGA web program.
Experimental model and study participant details
Ovarian cancer patients
The prognosis and gene expressions of the ovarian cancer patients were extracted from The Cancer Genome Atlas (RRID:SCR_003193).27 Given the nature of the cancer, the origin of the data was only female patients. The sample of ovarian cancer patients were majority white women (% = 0.86631) around an age mean of 59.58 (sd = 11.3), being classified as high-grade serous ovarian adenocarcinomas.27 61.22% of the ovarian cancer patients had a deceased outcome, 26.73% with progression, and 35.29% with recurrence. Lastly, the majority, 72.46% of patients had a FIGO stage as Stage IIIC. The remaining patients made up 15.24% as Stage IV, 4.01% as Stage IIC, 3.74% as Stage IIIB, and 4.55% as the remaining stages.
Method details
Data collection
A set of 48 proteins involved in the NHEJ repair mechanism were identified. Firstly, the NHEJ process will recognize, using the Ku heterodimer, and stabilize the DSB with main NHEJ factors like DNA-PKcs or Ligase IV. From there, Artemis, PNKP, APLF, WRN, and aprataxin, among other proteins, are recruited to bridge the ends and processes them. The next step is litigation of the broken ends via Ligase IV, XLF, and XRCC4.2 Alternatively, proteins that are involved in the promotion of other pathways, such as HR or SSA, were considered relevant for their antagonistic effect on NHEJ.28
Proteins from DNA repair are important to include since the relative activity between pathways could give a quantification of failed NHEJ. As a result, the standard for picking proteins was reported involvement in NHEJ or participation in other pathways with association with NHEJ activity.
Data was scraped from the Human Protein Atlas database to map the of proteins to genes.29 The final list of genes included XRCC6, XRCC5, XRCC7, LIG4, LIG3, LIG1, XRCC4, NHEJ1, XRCC1, DCLRE1C, TP53BP1, BRCA1, BRCA2, EXO1, EXD2, POLM, POLL, POLQ, RAD50, MRE11, NBN, TDP1, RBBP8, CTBP1, APLF, PARP1, PARP3, PNKP, APTX, WRN, PAXX, RIF1, RAD52, RAD51, ATM, ATR, TP53, H2AX, ERCC1, ERCC4, RPA1, MSH2, MSH3, RAD1, MSH6, PMS1, MLH1, and MLH3.2,15,16,17,18,19,20,21,23,25,17,18,19,20,21,23,25,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46 Following this, the Ensembl IDs, the reference number for each gene, were determined using the Human Gene database, GeneCards.47,48 FPKM (fragments per kilobase of transcript per million reads mapped)49 expression levels from 374 ovarian cancer patients and 279 breast cancer patients (653 total) were extracted from the Cancer Genome Atlas (TCGA, December 2020).27 The other data fields were patient ID, survival status, survival in days, progression status, recurrence status, age, race, ICD10 Code, FIGO stage, neoplasm histologic grade, tumor size, lymphatic invasion status, total dose, number of treatment cycles, treatment start date and end date, therapy type, drug name, and regimen indication. Progression and recurrence status was inferred from treatment regimen indication and were noted to potentially be inaccurate. Some entries were left as null because they were either missing, unavailable, or irrelevant to the study. 52 patients were missing a progression outcome and another 52 were missing a recurrence outcome. More detailed dataset statistics are listed in the Zenodo repository.50
The entire set of data was organized into a table and each gene’s expression was normalized. The categorical data points of tumor stage, grade, recurrence, and progression were converted to numerical labels and normalized as well. Dataset preparation was conducted using the R programming language.51
Quantification and statistical analysis
General information
Summary statistics were computed on the dataset using a spreadsheet. The patients used in this analysis were assumed to be independent and randomly selected from the population. Additionally, the central limit theorem justifies the sample being treated as normal.52 N represents the number of patients used in a given analysis.
10-Fold cross validation
The ovarian cancer patients were reordered randomly and separated into ten distinct sets. These sets were the same in each cross validation conducted. Iterating over each set, one was used as the testing set while the other nine were used as training data.53 The evaluation metric, balanced accuracy, was then averaged across the ten iterations. Balanced accuracy was chosen because it equally weighted positive and negative predictive strength.54
Linear and logistic regression
Linear and logistic regression was chosen to approach modeling starting with low complexity. It also provides clear feature importance. The correlation between each gene expression and survival time was calculated using linear regression (n=374) in R. With regression as the goal, alive patients were given a 20-year survival time and the linear regression model was fitted by minimizing squared residuals for length of survival (Table S1). Logistic regression was included to attempt classification of survival (n=374) (Table 1), progression (n=322) (Table 2), and recurrence (n=322) (Table 3). The positive cases (patient survival, cancer progression, cancer recurrence) were denoted as “1” and all others were “0”. The model predicts class probability, in the range 0-1. The threshold for predicting positive or negative was chosen to be 0.5. To evaluate purely the gene capabilities, they were the only predictors used in this analysis. The analysis also produced a coefficient and error for each feature. From this, t-values and p-values were generated. P-values less than 0.1 were chosen as within the threshold for significance in the feature selection, in order to have an adequate subset of data to create models. For the survival models, the corresponding coefficients and p-value of each gene were used to indicate confidence in their positive or negative correlation with survival. The linear regression was evaluated using mean absolute distance, comparing to a baseline of predicting average survival every time. The classifiers were evaluated using balanced accuracy over a 10-fold cross validation.
Decision tree, naive-bayes, support vector machine
To attempt a wider variety of models, a decision tree, a naive-bayes classifier, and a support vector machine were created in R using the rpart, caret, and e1071 packages.55,56,57 The intent was to predict survival (n=374), progression (n=322), and recurrence (n=322) using gene expression as the sole predictors. The features selected from the logistic regression analysis were used in training these models. However, an additional trial was conducted to use every gene, testing for relationships missed by the logistic regression feature selection. Balanced accuracy over a 10-fold cross validation were used to evaluate the models and compare them (Table S2). For the naive-bayes, the Laplace parameter was set to 0. For the support vector machines, the linear, polynomial, sigmoid, and radial kernels were all tested to choose the optimal one.
Two sample T-Test
A two sample t-test was performed using R software to compare the average gene expressions of patients over all three binary variables: survival (n=374), progression (n=322), and recurrence (n=322). Looking at each outcome individually, the data was separated into positive and negative sets. The mean and standard deviation of the sets were calculated. The hypothesis for the t-test, whether a positive or negative outcome had higher gene expression, was chosen based on which set had the higher mean. Then, two-sample t-statistics were computed. Finally, a Student’s t-distribution was used to calculate the p-value (Table 4). P-values under 0.05 were considered statistically significant.
Baseline accuracy calculation using simulation
With a small sample size, there was concern that the accuracy could be achieved by random variation in the dataset. To further corroborate the accuracy as significant, a simulation was performed in which the logistic regression, decision tree, naive-bayes, and SVM models were re-trained on a randomly generated dataset of the same number of patients and genes. The values drawn followed a normal distribution. Over 100 trials, the balanced accuracy from each model was recorded. The two sample T-Test was also conducted to count the number of significant genes. Lastly, the average and 95% percentile values were calculated.
Hierarchical clustering
Hierarchical clustering was performed to note the relatedness between gene expression variables and survival (n=374). The gene expression variables were isolated to evaluate their predictive capabilities. This analysis was performed on the dataset using SciPy, Matplotlib, and Seaborn software in Python.58,59,60,61 Agglomerative-type clustering was used applying the “ward" linkage method. The results were presented as a heatmap (Figure 2) and dendrogram (Figure 1) to depict the clusters of related genes and ovarian cancer patient outcomes.
Principal component analysis
A principal component analysis (PCA) was performed using the Prism software program (GraphPad) to determine redundancies that can be eliminated in the dataset and the significance of each gene in the dataset (n=374).62 The gene variables were isolated in this analysis to evaluate them as predictors. The first two principal components were plotted in comparison to survival (Figure S1). In addition, a scree plot (Figure 3) and feature representation plot (Figure S2) was generated.
Neural network
To analyze complex patterns in the data and attempt higher accuracy than current machine learning procedures, a neural network was created. The deep learning approach was implemented using TensorFlow in Python.63,64 A neural network was designed using two hidden layers, 19 neurons in the first layer and 10 in the second, to predict prognosis. ReLU was used as activation functions for the hidden layers and the sigmoid function was used on output. The training data held the first 80% of the ovarian cancer patients. This training set was used for “Model A”. For “Model B”, an augmented training group was created by combining breast cancer data with the first training set. “Model B” was only included to predict survival since the recurrence and progression prognoses were unknown for the breast cancer patients. All 274 breast cancer patients were added to help the model predict ovarian cancer prognosis. The validation set held the next 10% of the ovarian cancer patients. The testing set held the remaining 10% of ovarian cancer patients. In predicting progression and recurrence, 52 patients had to be dropped because their clinical outcomes were unknown. This change was reflected in the sizes of each set proportionally (survival had a 300|37|37 split, progression and recurrence had a 258|32|32 split). The models were tested with different hyper-parameters to determine their optimal design, including class weighting to value positive and negative outcomes equally. In addition, feature selection was performed using the forward feature selection technique (Figures 7, 8, and 9). The process begins with no genes. The next-best performing gene was added to the training features iteratively until 35 genes were chosen.65 Balanced accuracy over three repetitions of 10-fold cross-validation was used for choosing the next gene. The results of this method were graphed using Matplotlib to visualize the increase in best accuracy and average accuracy. Different gene sets were tested to maximize performance. Finally, the models were evaluated on the three binary outcomes: survival (n=374), progression (n=322), and recurrence (n=322), over ten repetitions of 10-fold cross validation. The 10-fold cross-validation was identical to that used in the other machine learning models. Averaged balanced accuracy was used for comparing models. Lastly, Model B was judged against to Model A in three trials: training with all the genes, the best from the forward feature selection, and the genes from the logistic regression feature selection. A bar graph was created using Matplotlib to visualize the differences (Figure S3).
Learning curves
Learning curves were generated for the survival outcome (n=374) with the logistic regression and neural network models. The logistic regression learning curve used the features from the logistic regression feature selection (Figure 7). Two learning curves were made for the neural network, training on the top three (Figure 8) and five (Figure 9) from the forward feature selection. This was done with Matplotlib by plotting training and testing scores when the model learned on differing amounts of examples, incrementing with 1/25 of the training set at a time. The training set consisted of 70% of the ovarian cancer patients and the testing had the remaining 30%. Balanced accuracy was used as the evaluation metric. The logistic regression model was created in R and the neural network was built in Python. The neural network scores for each training set size were averaged over six repetitions.
Acknowledgments
The results published here are in whole based upon data generated by the TCGA Research Network: https://www.cancer.gov/tcga. This work was supported by the Discovery to Cure Program at Yale University. Z.P.L. and E.S.R. are Discovery to Cure Fellows. In addition, we thank Catherine Piscitelli, Director of the Amity High School Science Research Program, for her guidance and support throughout the conception and execution of the project.
Author contributions
Conceptualization, Z.P.L.; Methodology, E.S.L.; Software, E.S.L.; Formal Analysis, E.S.L.; Writing – Original Draft, E.S.L.; Writing – Review and Editing, Z.P.L.; Supervision, Z.P.L. and E.S.R.; Project Administration, E.S.R.; Funding Acquisition, E.S.R.
Declaration of interests
The authors declare that they have no competing interest.
Published: September 15, 2023
Footnotes
Supplemental information can be found online at https://doi.org/10.1016/j.isci.2023.107934.
Contributor Information
Z. Ping Lin, Email: z.ping.lin@yale.edu.
Elena S. Ratner, Email: elena.ratner@yale.edu.
Supplemental information
Data and code availability
-
•
The cleaned dataset has been deposited in the Zenodo repository as “data.csv”. This paper analyzes existing, publicly available data from the TCGA web program. The accession numbers are listed in the key resources table.
-
•
All original code has been deposited in the Zenodo repository and is publicly available as of the date of publication. Additionally, all 3rd party packages used in the code are open source. DOIs are listed in the key resources table.
-
•
Any additional information required to reanalyze the data can be addressed by the lead contact upon request.
References
- 1.Vítor A.C., Huertas P., Legube G., de Almeida S.F. Studying DNA Double-Strand Break Repair: An Ever-Growing Toolbox. Front. Mol. Biosci. 2020;7:24. doi: 10.3389/fmolb.2020.00024. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Davis A.J., Chen D.J. DNA double strand break repair via non-homologous end-joining. Transl. Cancer Res. 2013;2:130–143. doi: 10.3978/j.issn.2218-676X.2013.04.02. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Bétermier M., Bertrand P., Lopez B.S. Is non-homologous end-joining really an inherently error-prone process? PLoS Genet. 2014;10 doi: 10.1371/journal.pgen.1004086. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Pennington K.P., Walsh T., Harrell M.I., Lee M.K., Pennil C.C., Rendi M.H., Thornton A., Norquist B.M., Casadei S., Nord A.S., et al. Germline and somatic mutations in homologous recombination genes predict platinum response and survival in ovarian, fallopian tube, and peritoneal carcinomas. Clin. Cancer Res. 2014;20:764–775. doi: 10.1158/1078-0432.CCR-13-2287. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Patel A.G., Sarkaria J.N., Kaufmann S.H. Nonhomologous end joining drives poly(ADP-ribose) polymerase (PARP) inhibitor lethality in homologous recombination-deficient cells. Proc. Natl. Acad. Sci. USA. 2011;108:3406–3411. doi: 10.1073/pnas.1013715108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Rodgers K., McVey M. Error-Prone Repair of DNA Double-Strand Breaks. J. Cell. Physiol. 2016;231:15–24. doi: 10.1002/jcp.25053. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Ratner E.S., Sartorelli A.C., Lin Z.P. Poly (ADP-ribose) polymerase inhibitors: on the horizon of tailored and personalized therapies for epithelial ovarian cancer. Curr. Opin. Oncol. 2012;24:564–571. doi: 10.1097/CCO.0b013e3283564230. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Mansour W.Y., Schumacher S., Rosskopf R., Rhein T., Schmidt-Petersen F., Gatzemeier F., Haag F., Borgmann K., Willers H., Dahm-Daphi J. Hierarchy of nonhomologous end-joining, single-strand annealing and gene conversion at site-directed DNA double-strand breaks. Nucleic Acids Res. 2008;36:4088–4098. doi: 10.1093/nar/gkn347. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Bhargava R., Onyango D.O., Stark J.M. Regulation of Single-Strand Annealing and its Role in Genome Maintenance. Trends Genet. 2016;32:566–575. doi: 10.1016/j.tig.2016.06.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Bai J.P.F., Alekseyenko A.V., Statnikov A., Wang I.-M., Wong P.H. Strategic applications of gene expression: from drug discovery/development to bedside. AAPS J. 2013;15:427–437. doi: 10.1208/s12248-012-9447-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Kumar Sarvepalli S. Deep Learning in Neural Networks: The Science behind an Artificial Brain. 2015. [DOI]
- 12.Alzubaidi L., Zhang J., Humaidi A.J., Al-Dujaili A., Duan Y., Al-Shamma O., Santamaría J., Fadhel M.A., Al-Amidie M., Farhan L. Review of deep learning: concepts, CNN architectures, challenges, applications, future directions. J. Big Data. 2021;8:53. doi: 10.1186/s40537-021-00444-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Weil M.K., Chen A.P. PARP inhibitor treatment in ovarian and breast cancer. Curr. Probl. Cancer. 2011;35:7–50. doi: 10.1016/j.currproblcancer.2010.12.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Plys A.J., Rogacheva M.V., Greene E.C., Alani E. The unstructured linker arms of Mlh1-Pms1 are important for interactions with DNA during mismatch repair. J. Mol. Biol. 2012;422:192–203. doi: 10.1016/j.jmb.2012.05.030. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Seol J.-H., Shim E.Y., Lee S.E. Microhomology-mediated end joining: Good, bad and ugly. Mutat. Res. 2018;809:81–87. doi: 10.1016/j.mrfmmm.2017.07.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Wang C., Lees-Miller S.P. Detection and repair of ionizing radiation-induced DNA double strand breaks: new developments in nonhomologous end joining. Int. J. Radiat. Oncol. Biol. Phys. 2013;86:440–449. doi: 10.1016/j.ijrobp.2013.01.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Chiruvella K.K., Liang Z., Wilson T.E. Repair of double-strand breaks by end joining. Cold Spring Harbor Perspect. Biol. 2013;5:a012757. doi: 10.1101/cshperspect.a012757. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Moscariello M., Wieloch R., Kurosawa A., Li F., Adachi N., Mladenov E., Iliakis G. Role for Artemis nuclease in the repair of radiation-induced DNA double strand breaks by alternative end joining. DNA Repair. 2015;31:29–40. doi: 10.1016/j.dnarep.2015.04.004. [DOI] [PubMed] [Google Scholar]
- 19.Beck C., Boehler C., Guirouilh Barbat J., Bonnet M.-E., Illuzzi G., Ronde P., Gauthier L.R., Magroun N., Rajendran A., Lopez B.S., et al. PARP3 affects the relative contribution of homologous recombination and nonhomologous end-joining pathways. Nucleic Acids Res. 2014;42:5616–5632. doi: 10.1093/nar/gku174. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Blasiak J. Single-Strand Annealing in Cancer. Int. J. Mol. Sci. 2021;22:2167. doi: 10.3390/ijms22042167. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Shamanna R.A., Lu H., de Freitas J.K., Tian J., Croteau D.L., Bohr V.A. WRN regulates pathway choice between classical and alternative non-homologous end joining. Nat. Commun. 2016;7 doi: 10.1038/ncomms13785. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Sugawara N., Goldfarb T., Studamire B., Alani E., Haber J.E. Heteroduplex rejection during single-strand annealing requires Sgs1 helicase and mismatch repair proteins Msh2 and Msh6 but not Pms1. Proc. Natl. Acad. Sci. USA. 2004;101:9315–9320. doi: 10.1073/pnas.0305749101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Xiong X., Du Z., Wang Y., Feng Z., Fan P., Yan C., Willers H., Zhang J. 53BP1 promotes microhomology-mediated end-joining in G1-phase cells. Nucleic Acids Res. 2015;43:1659–1670. doi: 10.1093/nar/gku1406. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Lei T., Du S., Peng Z., Chen L. Multifaceted regulation and functions of 53BP1 in NHEJ-mediated DSB repair (Review) Int. J. Mol. Med. 2022;50:90. doi: 10.3892/ijmm.2022.5145. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Stefanovie B., Hengel S.R., Mlcouskova J., Prochazkova J., Spirek M., Nikulenkov F., Nemecek D., Koch B.G., Bain F.E., Yu L., et al. DSS1 interacts with and stimulates RAD52 to promote the repair of DSBs. Nucleic Acids Res. 2020;48:694–708. doi: 10.1093/nar/gkz1052. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Chen R.-C., Dewi C., Huang S.-W., Caraka R.E. Selecting critical features for data classification based on machine learning methods. J. Big Data. 2020;7:52. doi: 10.1186/s40537-020-00327-4. [DOI] [Google Scholar]
- 27.Cancer Genome Atlas Research Network Integrated genomic analyses of ovarian carcinoma. Nature. 2011;474:609–615. doi: 10.1038/nature10166. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Her J., Bunting S.F. How cells ensure correct repair of DNA double-strand breaks. J. Biol. Chem. 2018;293:10502–10511. doi: 10.1074/jbc.TM118.000371. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Uhlen M., Oksvold P., Fagerberg L., Lundberg E., Jonasson K., Forsberg M., Zwahlen M., Kampf C., Wester K., Hober S., et al. Towards a knowledge-based Human Protein Atlas. Nat. Biotechnol. 2010;28:1248–1250. doi: 10.1038/nbt1210-1248. [DOI] [PubMed] [Google Scholar]
- 30.Han J., Ruan C., Huen M.S.Y., Wang J., Xie A., Fu C., Liu T., Huang J. BRCA2 antagonizes classical and alternative nonhomologous end-joining to prevent gross genomic instability. Nat. Commun. 2017;8:1470. doi: 10.1038/s41467-017-01759-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Saha J., Davis A.J. Unsolved mystery: the role of BRCA1 in DNA end-joining. J. Radiat. Res. 2016;57(Suppl 1):i18–i24. doi: 10.1093/jrr/rrw032. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Iwasaki D., Hayashihara K., Shima H., Higashide M., Terasawa M., Gasser S.M., Shinohara M. The MRX Complex Ensures NHEJ Fidelity through Multiple Pathways Including Xrs2-FHA-Dependent Tel1 Activation. PLoS Genet. 2016;12 doi: 10.1371/journal.pgen.1005942. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.He D., Li T., Sheng M., Yang B. Exonuclease 1 (Exo1) Participates in Mammalian Non-Homologous End Joining and Contributes to Drug Resistance in Ovarian Cancer. Med. Sci. Mon. Int. Med. J. Exp. Clin. Res. 2020;26 doi: 10.12659/MSM.918751. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Mateos-Gomez P.A., Gong F., Nair N., Miller K.M., Lazzerini-Denchi E., Sfeir A. Mammalian polymerase θ promotes alternative NHEJ and suppresses recombination. Nature. 2015;518:254–257. doi: 10.1038/nature14157. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Löbrich M., Jeggo P. A Process of Resection-Dependent Nonhomologous End Joining Involving the Goddess Artemis. Trends Biochem. Sci. 2017;42:690–701. doi: 10.1016/j.tibs.2017.06.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Layer J.V., Cleary J.P., Brown A.J., Stevenson K.E., Morrow S.N., Van Scoyk A., Blasco R.B., Karaca E., Meng F.-L., Frock R.L., et al. Parp3 promotes long-range end joining in murine cells. Proc. Natl. Acad. Sci. USA. 2018;115:10076–10081. doi: 10.1073/pnas.1801591115. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Verma P., Greenberg R.A. Noncanonical views of homology-directed DNA repair. Genes Dev. 2016;30:1138–1154. doi: 10.1101/gad.280545.116. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Di Domenico E.G., Romano E., Del Porto P., Ascenzioni F. Multifunctional role of ATM/Tel1 kinase in genome stability: from the DNA damage response to telomere maintenance. BioMed Res. Int. 2014;2014 doi: 10.1155/2014/787404. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Daley J.M., Sung P. RIF1 in DNA break repair pathway choice. Mol. Cell. 2013;49:840–841. doi: 10.1016/j.molcel.2013.02.019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Menon V., Povirk L. Involvement of p53 in the repair of DNA double strand breaks: multifaceted Roles of p53 in homologous recombination repair (HRR) and non-homologous end joining (NHEJ) Subcell. Biochem. 2014;85:321–336. doi: 10.1007/978-94-017-9211-0_17. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Bennardo N., Cheng A., Huang N., Stark J.M. Alternative-NHEJ is a mechanistically distinct pathway of mammalian chromosome break repair. PLoS Genet. 2008;4 doi: 10.1371/journal.pgen.1000110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Eckelmann B.J., Bacolla A., Wang H., Ye Z., Guerrero E.N., Jiang W., El-Zein R., Hegde M.L., Tomkinson A.E., Tainer J.A., Mitra S. XRCC1 promotes replication restart, nascent fork degradation and mutagenic DNA repair in BRCA2-deficient cells. NAR Cancer. 2020;2:zcaa013. doi: 10.1093/narcan/zcaa013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Chang H.H.Y., Pannunzio N.R., Adachi N., Lieber M.R. Non-homologous DNA end joining and alternative pathways to double-strand break repair. Nat. Rev. Mol. Cell Biol. 2017;18:495–506. doi: 10.1038/nrm.2017.48. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Stinson B.M., Loparo J.J. Repair of DNA Double-Strand Breaks by the Nonhomologous End Joining Pathway. Annu. Rev. Biochem. 2021;90:137–164. doi: 10.1146/annurev-biochem-080320-110356. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Ochi T., Blackford A.N., Coates J., Jhujh S., Mehmood S., Tamura N., Travers J., Wu Q., Draviam V.M., Robinson C.V., et al. DNA repair. PAXX, a paralog of XRCC4 and XLF, interacts with Ku to promote DNA double-strand break repair. Science. 2015;347:185–188. doi: 10.1126/science.1261971. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Jiang M., Jia K., Wang L., Li W., Chen B., Liu Y., Wang H., Zhao S., He Y., Zhou C. Alterations of DNA damage repair in cancer: from mechanisms to applications. Ann. Transl. Med. 2020;8:1685. doi: 10.21037/atm-20-2920. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Safran M., Rosen N., Twik M., BarShir R., Stein T.I., Dahary D., Fishilevich S., Lancet D. In: Practical Guide to Life Science Databases. Abugessaisa I., Kasukawa T., editors. Springer Nature Singapore; 2021. The GeneCards Suite; pp. 27–56. [DOI] [Google Scholar]
- 48.Stelzer G., Rosen N., Plaschkes I., Zimmerman S., Twik M., Fishilevich S., Stein T.I., Nudel R., Lieder I., Mazor Y., et al. The GeneCards Suite: From Gene Data Mining to Disease Genome Sequence Analyses. CP in Bioinformatics. 2016;54:1.30.1–1.30.33. doi: 10.1002/cpbi.5. [DOI] [PubMed] [Google Scholar]
- 49.Zhao S., Ye Z., Stanton R. Misuse of RPKM or TPM normalization when comparing across samples and sequencing protocols. RNA. 2020;26:903–909. doi: 10.1261/rna.074922.120. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.EthanLavi GeneExpressionPaperCode. 2023. [DOI]
- 51.R Core Team . R Foundation for Statistical Computing; 2022. R: A Language and Environment for Statistical Computing.https://www.R-project.org/ [Google Scholar]
- 52.Kwak S.G., Kim J.H. Central limit theorem: the cornerstone of modern statistics. Korean J. Anesthesiol. 2017;70:144–156. doi: 10.4097/kjae.2017.70.2.144. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Yadav S., Shukla S. 2016 IEEE 6th International Conference on Advanced Computing (IACC) IEEE; 2016. Analysis of k-Fold Cross-Validation over Hold-Out Validation on Colossal Datasets for Quality Classification; pp. 78–83. [DOI] [Google Scholar]
- 54.Brodersen K.H., Ong C.S., Stephan K.E., Buhmann J.M. 2010 20th International Conference on Pattern Recognition. IEEE; 2010. The Balanced Accuracy and Its Posterior Distribution; pp. 3121–3124. [DOI] [Google Scholar]
- 55.Therneau T., Atkinson B. Rpart: Recursive Partitioning and Regression Trees. R Package version 4.1.16. 2022. https://CRAN.R-project.org/package=rpart
- 56.Kuhn M. Caret: Classification and Regression Training. R package version 6.0-93. 2022. https://CRAN.R-project.org/package=caret
- 57.Meyer D., Dimitriadou E., Hornik K., Weingessel A., Leisch F. e1071: Misc Functions of the Department of Statistics, Probability Theory Group (Formerly: E1071), TU Wien. R package version 1.7-12. 2022. https://CRAN.R-project.org/package=e1071
- 58.Rossum G. van, Drake F.L. Python Software Foundation; 2010. The Python Language Reference Release 3.0.1 [Repr.] [Google Scholar]
- 59.Virtanen P., Gommers R., Oliphant T.E., Haberland M., Reddy T., Cournapeau D., Burovski E., Peterson P., Weckesser W., Bright J., et al. SciPy 1.0: fundamental algorithms for scientific computing in Python. Nat. Methods. 2020;17:261–272. doi: 10.1038/s41592-019-0686-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Waskom M. seaborn: statistical data visualization. JOSS. 2021;6:3021. doi: 10.21105/joss.03021. [DOI] [Google Scholar]
- 61.Hunter J.D. Matplotlib: A 2D Graphics Environment. Comput. Sci. Eng. 2007;9:90–95. doi: 10.1109/MCSE.2007.55. [DOI] [Google Scholar]
- 62.Principal Component Analysis Was Performed Using GraphPad Prism Version 9.0.2 for Mac, GraphPad Software, San Diego, California USA, www.graphpad.com.
- 63.Abadi, M., Agarwal, A., Barham, P., Brevdo, E., Chen, Z., Citro, C., Corrado, G.S., Davis, A., Dean, J., Devin, M., et al. (2016). TensorFlow: Large-Scale Machine Learning on Heterogeneous Distributed Systems.
- 64.TensorFlow Developers TensorFlow. 2022. [DOI]
- 65.Guyon I., Elisseeff A. An introduction to variable and feature selection. J. Mach. Learn. Res. 2003;3:1157–1182. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
-
•
The cleaned dataset has been deposited in the Zenodo repository as “data.csv”. This paper analyzes existing, publicly available data from the TCGA web program. The accession numbers are listed in the key resources table.
-
•
All original code has been deposited in the Zenodo repository and is publicly available as of the date of publication. Additionally, all 3rd party packages used in the code are open source. DOIs are listed in the key resources table.
-
•
Any additional information required to reanalyze the data can be addressed by the lead contact upon request.