Abstract
The demographic transition toward an aging society is a global phenomenon. An increase in the aging population directly challenges the government positions and public expenditures as it directly affects a country's aggregate demand and, thus, the country's income level. This paper investigates the impact of an aging population on the size of government spending. Using an updated dataset of 87 countries from 1996 to 2017, we study the aggregate level and each composition of government expenditures. Furthermore, we investigate whether the aging population influences the allocation of government spending toward different categories and economic growth changes. The paper uses the generalized method of moment (GMM) model for the dynamic panel data analysis to address the endogeneity problem. Our main findings suggest that an increase in the old-age population significantly induces higher aggregate government spending but only in developed countries and in particular on the spending in the social protection and environment categories. However, the aging society leads to lower government expenditure on education. Other critical findings reveal that changes in some compositions of government spending toward cultural expenditures impact growth slowdown, while an allocation toward education spending positively impacts economic growth.
Keywords: Aging population, Government spending, Composition government spending, Dynamic panel data analysis, Generalized method of moment (GMM)
1. Introduction
The demographic transition toward an aging society is a global phenomenon. According to Ref. [1], the global fertility rate for women of childbearing age dropped from 3.2 births per woman in 1990 to only 2.5 in 2019. Even in Sub-Saharan Africa, the region with the highest fertility rate, it dropped from 6.3 in 1990 to 4.6 in 2019; furthermore, fertility rates in other areas around the world also declined.1 In addition, the average life expectancy at birth increased from 65 years during 1990–1995 to 71 years during 2010–2015 [2]. The decline in fertility rates and a longer life span are the main reasons countries worldwide have an increasing proportion of their aging population and are continually moving toward an aging society.
As the life cycle theory says, the most productive labor is in middle age, and most aging people and children consume much more than they produce. An increase in the aging population influences the slowdown in economic growth through the shortage of effective labor participation and changes the patterns of consumption and investment [3,4]. Moreover, a more significant proportion of the aging population also reduces the effectiveness of fiscal policy shocks and shoots the healthcare and social security budgets to the ceiling (see more in Refs. [5,6,7], among others). The aging society substantially increases the pressure on public expenditures, as an increase in the elderly population results in a higher demand for programs and support for older people (See more in Ref. [8] for Brazil case; Ref. [9] for both advanced and emerging G20 countries) [10] reports significantly larger US healthcare spending to GDP by 30% as the aging population increases. Accordingly, the government requires more income to support the old-age pension system, public health services, and health care for the elderly directly affects long-term economic growth.
Research has shown the relationship between the size of government spending and economic growth in various ways. Ref. [[11], [12]] report a non-homothetic relationship between government spending and economic growth; the impacts of government spending on economic growth are varied according to a different stage of country's development (See more supportive arguments on [13]; interaction with political system [14] and [15] among others. Although many studies focus on the effect of government spending on growth, it remains to be seen how an aging society and the reallocation of government spending categories affect economic growth. This raises interesting questions of whether an increase in the aging population would impact an increase in government expenditures and thus, long-term economic growth.
Therefore, this paper analyzes the impact of an increase in the aging population on the size of government spending using both government spending at the aggregate level and in each spending component. Additionally, I compare developed and developing countries, since the impact of an aging population on government spending and economic growth in different countries may vary with income levels.
This research makes three main contributions to this field. First, this study analyzes the effects of a growing elderly proportion on government spending at the aggregate level and each composition of government spending. Second, we explore the interaction effect between aging populations and government spending as they affect economic development. Lastly, this study uses the generalized method of moments (GMM) for the dynamic panel data model to address the endogeneity problem and obtain an unbiased estimation.
The remainder of this paper is as follows: section 2 provides the stylized facts and reviews the literature; section 3 presents the data and identification strategy; section 4 shows the main results, together with discussion; and section 5 delivers the conclusions.
2. Stylized facts and literature review
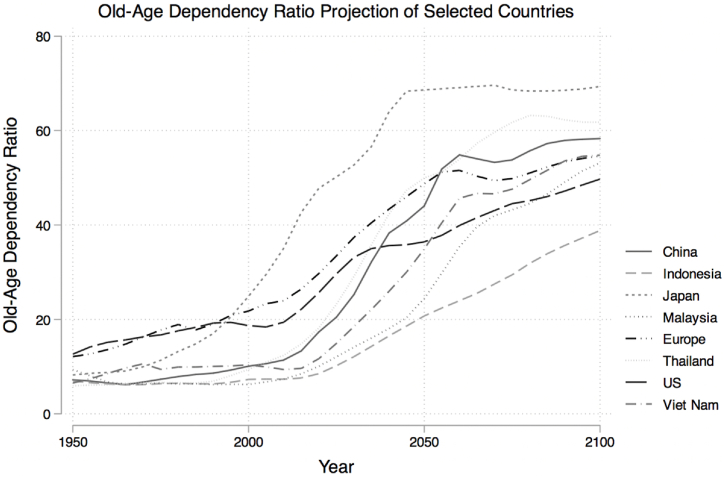
Entering the 2020s, many regions of the world face a demographic transition toward an aging society. As shown in Fig. 1, the old-age dependency ratio projections of the selected countries have been increasing since the 2000s. Before 2000, most countries still had a ratio of old-age population to a total population lower than 20% (a ratio that is applied to classify a society as a complete aging society), but this ratio gradually rose after 2000. In some countries like Japan, the ratio indicates that the country entered into a complete aging society even before 2000. The critical point is that demographic transition is not a process happening only in the high-income countries; we also observe that now middle-income countries, such as Thailand and Vietnam, will reach an old-age dependency ratio of 50% by 2050.
Fig. 1.
Old-age dependency ratio projection of selected countries. Source: Adapted from Ref. [16]. Notes: The figure presents eight the old-age dependency ratio for selected countries, where actual data are presented up to 2021 and thereafter the projected data. The old-age dependency ratio is calculated using the percentage of the population aged above 65 years to the working age population (age 15–64 years). Data sourced from the World Bank Databank.
An increase in the old-age dependency ratio stems from different factors. From the demographic perspective, as countries become more developed, the marginal cost of staying at home and taking care of children would be higher than entering the labor market. The female population attends higher education, thus, participating more in the labor market. This leads to a delay in bearing a child(ren) and a higher cost of childbearing. Furthermore, the greater the female population accessing higher education, the fewer children they decide to have. This affects a reduction in fertility rate and lowers the replacement rate worldwide.2 In terms of public health, improving access to health services helps to increase life expectancy at birth. Theoretically, Refs. [17,[18], [19]] suggest that investing in human capital also improves self-caring knowledge, thus, longer life expectancy.3 Overall, a reduction in fertility rate and having a long lifespan are the main reasons for the countries' aging society.
A shift in the demographic transition puts pressure on government policies and public finance. Ref. [20] finds that the aging population positively affects the size of government spending, especially in the categories related to the elderly, such as social protection, health care, and defense, using samples from OECD countries from 1990 to 1997.
Following ref. [21], the preference for public policies differs radically in different periods of life due to self-interest. Support may be required mainly for education during youth, while we may need a better infrastructure and social security programs in older age. Similarly, ref. [22] states that an increase in the old-age population raises social security and healthcare expenditures. Apart from government expenditures, ref. [23] show that a shift in the demographic structure toward an aging society affects other macroeconomic variables, such as investment, consumption, and income level.
In dynamic population literature, ref. [24] suggest that a greater proportion of the working-age population compared to other age ranges could help support higher economic growth. As the income level increases, savings are also increased, and the country can accumulate more physical capital for growth. On the other hand, a higher proportion of children or the old-age population than the working-age population hinders long-term economic growth, as expenditures related to children and old-age supportive programs have increased. This spending does not affect workers' effectiveness directly and reduces each country's savings. (See more in Refs. [25,26,27]). In addition, ref. [28] highlights the same issue in Japan using simple single-country regression.
Regarding the theoretical perspective, ref. [29] use an extended exogenous growth model with population dynamics to show that an increase in the old-age population instead helps increase the incentive to accumulate human capital. Although the accumulation of physical capital may be reduced due to less savings, investing in human capital sustains economic growth in the long run. Refs. [30,31] support that educated people tend to be more concerned about personal health issues, increasing their ability to work greater productivity; this induces higher economic growth. Nevertheless, ref. [32] argue that healthy old-age people come with a high cost of health care and other age-related expenditures. Many empirical works demonstrate that an increase in the old-age population tends to push public expenditures up, especially public health expenditures (see more in Refs. [33,34,20]).
An increase in government spending directly relates to a country's economic growth, especially at the beginning of development. Ref. [35] argues that the relationship between government spending and economic growth may not follow a homothetic direction. In addition, ref. [13] uses models with the simultaneous equation to empirically test both industrialized and developing countries to show that higher government spending induces higher growth only in the short-term.
Moreover, refs. [36], and [37] find that not all types of public expenditures enhance growth. Specifically, ref. [36] show that spending related to protection of property rights, law enforcement, defense, economic stability, and competitive market environment is essential and limits government duty. From a different perspective, ref. [37] focus more on the revenue side, where a higher government revenue affects the output level and government spending decisions.
Different allocations of public expenditures also matter to growth. Ref. [38] use the panel dataset of 56 countries (both developed and developing) from Government Fiscal Studies (GFS) and the International Monetary Fund (IMF) between 1970 and 2010 to test whether a change in the allocations of government spending affected growth. They find that a new allocation from other categories of government spending toward educational expenditure supports long-term growth, while an allocation to other categories does not significantly affect growth.
The literature focuses more on the aggregate perspective of government spending and growth. At the same time, there are few studies on each particular government spending component, not to mention in the context of an aging society. Once a country moves toward an aging society, a change in government expenditure allocation may differently impact long-term economic growth.
Therefore, this paper aims to investigate the impact of aging on economic growth through the channel of government spending at the aggregate level and each spending composition. Furthermore, we test whether a reallocation of government spending across categories affects economic growth when the country is aging.
3. Methodology
3.1. Data
We use unbalanced panel data from 87 industrialized and developing countries from 1996 to 2017 (see list of countries in Table 1).4 The primary independent variable is the old-age dependency ratio from World Bank Databank. For dependent variables, we use final government consumption (USD constant per capita) as a proxy of public spending. As we analyze the aggregate level and each component of government spending, we acquire the government spending classified by function from the GFS and IMF. Those spending categories include expenditures on general public services, defense, public order and safety, economic affairs, environmental protection, housing and community amenities, health, recreation, culture and religion, education, and social protection.
Table 1.
Selected countries classified by continent.
| Continent | Country |
|---|---|
| Asia | Afghanistan, Armenia, Azerbaijan, Bangladesh, Bhutan, China, India, Indonesia, Iran, Israel, Japan, Jordan, Kazakhstan, South Korea, Kuwait, Kyrgyz Republic, Macao, Malaysia, Mongolia, Myanmar, Nepal, Pakistan, the Philippines, Russian Federation, Singapore, Sri Lanka, Thailand, Turkey, Viet Nam |
| Africa | Algeria, Egypt, Ethiopia, Jamaica, Kenya, Liberia, Madagascar, Mauritius, Namibia, Nigeria, South Africa, Tunisia, Uganda |
| Europe | Albania, Belarus, Belgium, Bulgaria, Cyprus, Czech Republic, Denmark, Estonia, Finland, France, Georgia, Germany, Greece, Hungary, Ireland, Italy, Latvia, Lithuania, Moldova, Netherlands, Norway, Poland, Portugal, Romania, Slovak Republic, Slovenia, Spain, Sweden, Switzerland, Ukraine, United Kingdom |
| North America | Costa Rica, Dominican Republic, El Salvador, Guatemala, Jamaica, Mexico, USA |
| Oceania | Australia, New Zealand |
| South America | Argentina, Bolivia, Chile, Colombia, Uruguay |
Source: The author, data from and classified by the World Bank.
From the World Bank Databank we also include GDP per capita (constant USD), trade to GDP (%), total expenditure (constant USD), financial openness (from Ref. [39]), and control of corruption (from WDI) as control variables. In addition, we do a stationary test5 on our panel dataset before using these data to analyze the relationship between the aging population, government spending, and growth. They all become stationary after transforming to logarithmic form. The total sample descriptive statistics for all variables used in the econometric model are shown in Table 2. From the 2388 observations, 935 samples are from developed countries, and 1453 are from developing countries. The average GDP per capita of the total sample between 1996 and 2018 is 17,713.81 USD.
Table 2.
Descriptive statistic of selected variables (full sample).
| Variable | Unit | No. Obs | Mean | Std. Dev. | Min | Max |
|---|---|---|---|---|---|---|
| Year | year | 2388 | 1996 | 2018 | ||
| GDP per Capita | USD constant | 2388 | 17713.808 | 20784.559 | 187.52 | 111968.4 |
| Government Spending per Capita | USD constant | 2281 | 3254.587 | 4002.767 | 12.49 | 21977.28 |
| Financial Openness | Index | 2169 | 0.626 | 0.364 | 0 | 1 |
| Government Expenditure to GDP | Percentage | 2019 | 30.109 | 13.396 | 3.05 | 128.37 |
| Expenditure on Public Administrative to GDP | Percentage | 1885 | 6.901 | 3.978 | 0.46 | 38.82 |
| Expenditure on Defense to GDP | Percentage | 1787 | 1.898 | 1.796 | 0.02 | 17.33 |
| Expenditure on Order to GDP | Percentage | 1885 | 1.704 | 1.223 | 0.11 | 20.38 |
| Expenditure on Economics to GDP | Percentage | 1914 | 4.145 | 2.653 | 0.05 | 25.36 |
| Expenditure on Environment to GDP | Percentage | 1494 | 0.474 | 0.577 | −0.26 | 6.53 |
| Expenditure on Housing to GDP | Percentage | 1884 | 0.727 | 0.686 | −0.35 | 8.94 |
| Expenditure on Health to GDP | Percentage | 1919 | 3.212 | 2.555 | 0 | 12.7 |
| Expenditure on Culture to GDP | Percentage | 1796 | 0.685 | 0.574 | 0 | 5.03 |
| Expenditure on Education to GDP | Percentage | 1913 | 3.857 | 2.069 | 0.04 | 23.55 |
| Expenditure on Social Protection to GDP | Percentage | 1853 | 7.427 | 7.145 | 0 | 25.65 |
| Old-Age Dependency Ratio, ln | Logarithm | 2369 | 2.465 | 0.685 | −0.223 | 3.832 |
| Old-Age Population, ln | Logarithm | 2369 | 2.028 | 0.719 | −0.371 | 3.317 |
| GDP per Capita, ln | Logarithm | 2388 | 8.955 | 1.441 | 5.234 | 11.626 |
| Government Spending per Capita, ln | Logarithm | 2281 | 7.14 | 1.59 | 2.525 | 9.998 |
| Trade to GDP, ln | Logarithm | 2333 | 4.361 | 0.66 | −1.772 | 6.093 |
| Control of Corruption, ln | Logarithm | 2078 | 3.815 | 0.828 | −0.755 | 4.605 |
| Democracy | Dummy Variable | 2388 | 0.722 | 0.448 | 0 | 1 |
| Growth Rate of GDP per Capita (4 years), ln | Logarithm | 1656 | 2.317 | 0.999 | −4.237 | 4.839 |
| Government Debt to GDP, ln | Logarithm | 759 | 3.661 | 1.249 | −3.912 | 5.285 |
Source: The author, data from GFS and the World Bank.
The higher the income level for trade and financial openness, the more open the country. However, when considering the descriptive statistics for all interested variables classified by income level, as in Table 3, we find that the average income level diverges between groups. The average income per capita of developed countries is around 38,496.65 USD, while it is about 5091.61 USD and 634.89 USD for middle-income and low-income groups, respectively. Other variables also present the same picture; if the income level is high, the country usually has relatively high government spending. The average government spending for the high-income, middle-income, and low-income groups are 6932.08 USD, 838.38 USD and 78.51 USD, respectively.
Table 3.
Descriptive statistic of selected variables classified by income level.
| Level of Development |
Unit |
High-Income |
Middle-Income |
Low-Income |
|||
|---|---|---|---|---|---|---|---|
| Variables | No. Obs | Mean | No. Obs | Mean | No. Obs | Mean | |
| Year | 935 | 2007.589 | 1208 | 2006.91 | 245 | 2005.894 | |
| GDP per Capita | USD constant | 935 | 38496.647 | 1208 | 5091.605 | 245 | 634.893 |
| Government Spending per Capita | USD constant | 930 | 6932.08 | 1146 | 838.381 | 205 | 78.506 |
| Financial Openness | Index | 824 | 0.876 | 1106 | 0.489 | 239 | 0.4 |
| Government Expenditure to GDP | Percentage | 847 | 38 | 977 | 25.62 | 195 | 18.321 |
| Expenditure on Public Administrative to GDP | Percentage | 842 | 6.306 | 871 | 7.659 | 172 | 5.982 |
| Expenditure on Defense to GDP | Percentage | 803 | 1.939 | 820 | 1.852 | 164 | 1.93 |
| Expenditure on Order to GDP | Percentage | 841 | 1.577 | 886 | 1.896 | 158 | 1.302 |
| Expenditure on Economics to GDP | Percentage | 842 | 4.224 | 892 | 4.144 | 180 | 3.78 |
| Expenditure on Environment to GDP | Percentage | 728 | .631 | 647 | 0.368 | 119 | 0.093 |
| Expenditure on Housing to GDP | Percentage | 840 | 0.733 | 881 | 0.753 | 163 | 0.557 |
| Expenditure on Health to GDP | Percentage | 841 | 4.977 | 897 | 1.976 | 181 | 1.133 |
| Expenditure on Culture to GDP | Percentage | 825 | 0.953 | 826 | 0.507 | 145 | 0.166 |
| Expenditure on Education to GDP | Percentage | 842 | 4.547 | 890 | 3.45 | 181 | 2.645 |
| Expenditure on Social Protection to GDP | Percentage | 842 | 12.188 | 843 | 3.97 | 168 | 0.919 |
| Old-Age Dependency Ratio, ln | Logarithm | 935 | 2.784 | 1189 | 2.347 | 245 | 1.819 |
| GDP per Capita, ln | Logarithm | 935 | 10.436 | 1208 | 8.329 | 245 | 6.383 |
| Government Spending per Capita, ln | Logarithm | 930 | 8.683 | 1146 | 6.405 | 205 | 4.242 |
| Trade to GDP, ln | Logarithm | 930 | 4.546 | 1181 | 4.317 | 222 | 3.82 |
| Control of Corruption, ln | Logarithm | 826 | 4.418 | 1043 | 3.576 | 209 | 2.623 |
| Democracy | Dummy Variable | 935 | 0.857 | 1208 | 0.684 | 245 | 0.392 |
| Growth Rate of GDP per Capita (4 years), ln | Logarithm | 624 | 1.989 | 873 | 2.513 | 159 | 2.537 |
| Government Debt to GDP, ln | Logarithm | 262 | 3.495 | 454 | 3.727 | 43 | 3.978 |
Source: The author, data from GFS and the World Bank.
The average of all samples for the old-age dependency ratio is 2.465, while the average old-age dependency ratio of the high-income group is the highest (2.784) of the three income groups. We can see from the statistics that richer countries face dealing with an aging society before poorer ones.
3.2. Empirical strategy
This section illustrates the empirical strategies for analyzing the relationship between the old-age population, government spending, and economic growth.
3.2.1. Analysis of government spending at the aggregate level
We use the following Model (1) to answer the first objective of testing the relationship between government spending and the old-age population.
| (1) |
where is government spending of entity at time is an indicator related to the aging population (e.g., the old-age dependency ratio or the ratio of the old-age population to the total population), represents the GDP per capita, is the set of control variables, including financial openness, trade openness, and control of corruption, captures the country-specific effect, is a time dummy, and is the shock for each period. The set of control variables using in this model usually have impacts on the fiscal policy, especially government spending. Ref. [40] suggests that the quality of political institution induces the way government spend their money over the short-run fluctuations. Corrupted governments are more likely to spend more during the boom period and lowering their expenditure during recession. Moreover, countries with political instability cannot easily access to the international capital market during bad time. This means that financial openness also affects the government spending. Therefore, I include financial openness and corruption control as the control variables. Trade openness is also included as a control variable since many developing countries depend mostly on trade, which affect the budget position, and thus, government spending.
For the identification strategy, I analyze the impact of the old-age population on aggregate government spending trying various models. For example, first, we perform the ordinary least squared (OLS) and panel data with fixed and random effects to estimate the parameter , which are both of interest regarding their relationships with government spending. Both fixed and random effect models show that the coefficients for the old-age dependency ratio and the percentage of the old-age population are positively significant at 95%. The results imply that an increase in the percentage change of the old-age dependency ratio and the old-age population positively affects the expected value of government expenditures at the aggregate level (see Table 5, Table 4).
Table 4.
Regression results using various econometrics methods with old-age dependency ratio as a proxy for old-age populations).
| Variable | (OLS) | (FE) | (1DGMM) | (2DGMM) | (1SGMM) | (2SGMM) |
|---|---|---|---|---|---|---|
| Old__depend, ln | 0.0199*** | 0.0539+ | 0.0913 | −0.0154 | 0.0609** | 0.0642*** |
| (0.000) | (0.069) | (0.386) | (0.731) | (0.001) | (0.000) | |
| L. Gov Spending | 0.912*** | 0.714*** | 1.021*** | 1.061*** | 0.794*** | 0.798*** |
| (0.000) | (0.000) | (0.000) | (0.000) | (0.000) | (0.000) | |
| GDP per capita | 0.0835*** | 0.200*** | −0.261 | −0.204** | 0.147* | 0.137*** |
| (0.000) | (0.000) | (0.579) | (0.001) | (0.027) | (0.000) | |
| Trade to GDP | 0.00844+ | 0.00345 | 0.0272 | 0.0199* | 0.0199 | 0.0170** |
| (0.069) | (0.785) | (0.715) | (0.015) | (0.193) | (0.003) | |
| Control of corruption | 0.0116* | 0.0556*** | 0.0246 | 0.0246** | 0.0813** | 0.0879*** |
| (0.015) | (0.000) | (0.384) | (0.005) | (0.001) | (0.000) | |
| Financial Openness | −0.0134+ | −0.0167 | −0.0421 | −0.0238 | 0.0384 | 0.0304* |
| (0.095) | (0.348) | (0.438) | (0.448) | (0.199) | (0.026) | |
| Democracy_dummy | 0.0025 | 0.0298* | 0.0270 | 0.0205 | −0.0150 | −0.0211*** |
| (0.706) | (0.010) | (0.552) | (0.117) | (0.494) | (0.001) | |
| Constant | −0.214*** | −0.134 | −0.399+ | −0.362*** | ||
| (0.000) | (0.475) | (0.064) | (0.000) | |||
| N. Obs. | 1705 | 1705 | 1428 | 1428 | 1705 | 1705 |
| R-Squared | 0.996 | 0.854 | ||||
| Adjusted R-Squared | 0.996 | 0.843 | ||||
| AR (1) p-value | 0.00396 | 0.00462 | 0.00424 | 0.00842 | ||
| AR (2) p-value | 0.262 | 0.261 | 0.319 | 0.329 | ||
| Hansen p-value | 0.0908 | 0.0908 | 0.0831 | 0.0831 |
Note: This table estimates the relationship between Old-Age Populations, using Old-Age Dependency Ratio as a proxy, and Government Spending at the Aggregate Level. The Total Final Government Consumption per Capita in Logarithmic form is Dependent Variables. The Old-Age Dependency Ratio in Logarithmic form (Old_depend, ln) is the main Independent Variable. OLS represents the Ordinary Least Square Method: FE id Panel Data Model with Fixed Effect; 1DGMM and 2DGMM are one- and two-step Difference Generalized Methods of Moment, respectively, and 1SGMM and 2SGMM are one- and two-step System Generalized Methods of Moment, respectively. The p-value of Auto-Correlation 1st and 2nd order, including ' 'Hansen's post-Estimation Tests for Dynamic GMM are presented at the bottom Panel. The p-values are presented in parentheses and+p < 0.10, *p < 0.05, **p < 0.01, ***p < 0.001.
Source: Author's calculations.
Unlike the ordinary least squared (OLS) estimation, panel data with fixed effect helps reduce some unobserved common factors, which are time-invariant and common to all units affecting each. To choose the model with fixed or random effects, I perform the Hausman test with the null hypothesis that the difference in coefficients is not systematic. The statistical testing suggests rejection of the null hypothesis with 99% confidential intervals for both models using the old-age dependency ratio and the model using the percentage of old age population as main independent variables. This implies that the fixed effect model is preferable to the random effect model.
After testing which panel data model specifications fit more to our data (fixed or random effects), we further perform the dynamic panel data models with the generalized method of moment (GMM) estimators. I utilize the Generalized Method of Moments (GMM) estimator, initially introduced by Ref. [41]. Subsequently, it was refined and enhanced by Refs. [42,43]. The advantages of using GMM estimators are overcoming the endogeneity problem, which causes bias in the OLS and usually in the panel fixed effect model. Moreover, using GMM also helps to correct the heteroskedasticity and autocorrelation within individual units' errors.
In this model, we are interested in the coefficient which represents the marginal effect of the old-age population on aggregate government spending. We expect a positive sign: the more the old-age population increases, the higher the demand for public spending.
3.2.2. Analysis of each government spending composition
To analyze how the old-age population affects each government spending composition, we modify Equation (1) to Equation (2) to test the relationship between each government spending category and the old-age population.
| (2) |
where is government spending to GDP in category of entity at time . Categories include public spending on general public services, defense, expenditure on public order & safety, economic affairs, environmental protection, housing & community amenities, health, recreation, culture, & religion, education, and social protection. represents each spending category to GDP of the country from the previous period. is an indicator related to the aging population, e.g., the old-age dependency ratio or the ratio of the old-age population to the total population, which is the primary independent variable here. represents GDP per capita. is the set of control variables. capture country-specific effects. is a time dummy and is the shock for each period. Once again, we are interested in the coefficient which represents the marginal effect of the old-age population on each government spending category. We expect an increase in the old-age population to induce higher public spending on health and social protection categories.
3.2.3. Could reallocation of government spending enhance economic growth in the aging society?
This study further analyzes the reallocation of government spending that could enhance economic growth in the aging society (see Equation (3)). We modify the model from Ref. [38] to test whether the reallocation of government spending could enhance economic growth in an aging society. The model testing our conjecture is:
| (3) |
where represents the GDP growth rate per capita between year 0 and year . In this case, we follow [38] and set to 4 as many administrative periods last for four years, and it may take some time for government spending policy to be reallocated. is the GDP per capita of the previous period is the set of control variables. In this model, we also add total expenditure to GDP of the previous period to control that although there is some reallocation across spending categories, the overall expenditure remains unchanged. captures country-specific effect. is a time dummy and is the shock for each period. represents each government spending category as a proportion of GDP.
We omitted one component of the government spending to avoid exact multicollinearity. Consequently, the index only represents spending categories and the model is transformed into the following Equation (4):
| (4) |
where is an indicator related to the aging population, e.g., the old-age dependency ratio or the ratio of the old-age population to the total population. We expect the coefficient to be negative as an increase in the old-age population may reduce workers in the system, so as economic growth. capture country-specific effect. is a time dummy and is the shock for each period. denotes the interaction term between each category of government spending and the old-age variable. We are interested in the coefficient sign of this term as shows the marginal effect of and the interaction between the old-age population and the reallocation of government spending in the previous category (as we omitted it) to the new category in affecting economic growth. That is the derivative of with respect to :
This equation presents the effect on economic growth of the reallocation of government spending from the last category to the new one. The effect is the function of GDP per capita and the old-age dependency ratio.
4. Results and discussion
4.1. Effects of old-age population on government spending at the aggregate level
Table 4 shows the results of the baseline model using various econometric methods. This tests whether a change in the proportion of old-age population would affect government spending at the aggregate level. Almost all the regression results have a positive coefficient for the old-age dependency ratio (the main independent variable) except when we use the one- and two-step dynamic GMM with first difference. These indicate that an aging population significantly induces higher total government consumption. The difference GMM models show no significant results because the endogenous independent variable, which in this model is GDP per capita, has a Random walk distribution. This makes the system GMM model more favorable than the difference GMM models [44].
The system GMM model utilizes both the level and first difference of endogenous variables as internal instruments. In contrast, the difference GMM uses only the first difference of endogenous variables as an instrument. So, we have fewer observations for the first difference GMM model than for the system GMM model. Furthermore, after testing the post-estimation diagnostic, we can see from Table 4 that the system GMM model also overcomes the second order of error term auto-correlation as the p-value of AR(2) is higher than 0.05, and we can accept the null hypothesis based on the Hansen overidentification test at the 95% confidence level. Therefore, from now on, we will use the system GMM model as a method for further analysis.
Table 4 (columns 6 and 7) show that an increase of one percent in the old-age dependency ratio significantly induces an increase in government spending at the aggregate level of about 0.06% points at both the 95 and 99% confidence levels. Apart from our main interest in the independent variable, other control variables, such as trade to GDP, financial openness, and control of corruption, also positively affect government spending, while democracy induces lower public expenditure.
I also replicate all baseline models from Table 4 but uses the percentage of old-age population as a proxy for aging society instead of the old-age dependency ratio. The results, which are shown in Table 5 (in Appendix A. section), are quite similar and robust to the exercise from Table 4 as a higher proportion of aging population significantly affects a higher government spending for the 87 countries in the sample from 1996 to 2018.
The results from Table 5, Table 4 are consistent with the literature, which indicates that population aging presents a notable federal budgetary challenge, given that a significant portion of the federal budget is allocated towards old age entitlement programs, notably Social Security and Medicare, while simultaneously projecting per capita health costs to outpace GDP per capita growth in the future (see, for example, [45,46,47,48]).
However, there are interesting results when we group the countries by their income level into two groups (countries with income higher than 12,000 USD and those with an income level less than or equal to 12,000 USD). Table 6 illustrates that the old-age population would only cause higher government spending in the high-income group, and not for the middle- and low-income countries.
Table 6.
Regression results: Effect of old-age population on aggregate government spending by income group.
| Variable | (Income ≤ 12,000 USD) | (Income >12,000 USD) |
|---|---|---|
| Old_depend, ln | 0.00605 | 0.178*** |
| (0.126) | (0.000) | |
| L. Gov Spending | 0.918*** | 0.750*** |
| (0.000) | (0.000) | |
| GDP per capita | 0.00807 | 0.0938*** |
| (0.617) | (0.000) | |
| Trade to GDP | −0.0101 | 0.0431*** |
| (0.114) | (0.000) | |
| Control of corruption | 0.164*** | 0.0849*** |
| (0.000) | (0.000) | |
| Financial Openness | 0.0176 | −0.0469* |
| (0.262) | (0.028) | |
| Democracy_dummy | −0.00225 | 0.0139 |
| (0.794) | (0.110) | |
| N. Obs. | 702 | 1003 |
| AR (1) p-value | 0.00578 | 0.0222 |
| AR (2) p-value | 0.911 | 0.377 |
| Hansen p-value | 0.871 | 0.359 |
Note: This table estimates the relationship between Old-Age Populations, using Old-Age Dependency Ratio as a Proxy, and Government Spending at the Aggregate Level. The Total Final Government Consumption per Capita in Logarithmic form is Dependent Variables. The using Old-Age Dependency Ratio in Logarithmic form is the main Independent Variable. We use the two-step System generalized Methods of Moment to estimate interested parameters. Income > 12000 represents the Group of countries which the Level of Income above 12000 USD. Income ≤ 12000 represents the Group of countries which the Level of Income below or equal to 12000 USD. The p-value of Auto-Correlation 1st and 2nd order, including Hansen's post-Estimation Tests for Dynamic GMM are presented at the bottom Panel. The p-values are presented in parentheses and+p < 0.10, *p < 0.05, **p < 0.01, ***p < 0.001.
Source: Author's calculation
These results correspond to the other studies where, unlike in developed countries, the elderly in middle- and low-income countries usually depend on their own savings or family support rather than on public welfare [49,50,51]. Therefore, when we separate these two groups, the results show that an increase in the old-age dependency ratio leads to higher government spending only in developed countries.
4.2. Effects of old-age population on each compositional government spending
After testing the relationship between old-age population and government spending in total, we further analyze the effects of old-age on each government spending composition. Regarding the previous section, we again choose the system GMM model to estimate the parameter explaining the marginal effect of the old-age population on compositional government spending.
Each composition of government spending is a dependent variable, and the old-age population (proxied using the old-age dependency ratio) is the main independent variable. All control variables mentioned in section 3 are included in the model. Table 7 demonstrates that an increase in the old-age dependency ratio significantly leads to higher government spending, particularly in health, environment, and social protection expenditures. A one percent change in the old-age population induces a 1.626% change in the expenditure on social protection (see column 11 in Table 7). These results are consistent with the previous study on the positive effects of aging on health care and social security spending (see Refs. [52,53] for the study in Southeast Asian and European countries, respectively). Especially as people age, there is likely a decline in the transition rates from disabled states to the no-disability state [15].
Table 7.
Effects of old-age populations on each compositional government spending (as GDP percentage) using two-step system GMM with old-age dependency ratio as a proxy for old-age populations.
| Variable | (Public Admin) | (Defense) | (Order) | (Economic) | (Environment) | (Housing) | (Culture) | (Health) | (Education) | (Social Protection) |
|---|---|---|---|---|---|---|---|---|---|---|
| Old_depend, ln | −0.916** | 0.0166 | −0.0246 | 0.342+ | 0.0277* | −0.340*** | 0.0410+ | 0.0923+ | −0.174** | 1.626*** |
| (0.004) | (0.448) | (0.184) | (0.091) | (0.027) | (0.000) | (0.089) | (0.080) | (0.010) | (0.000) | |
| GDP per capita | 2.013*** | −0.0699** | 0.0328+ | −0.0512 | −0.00157 | 0.116* | 0.0976*** | 0.201*** | 0.191** | 1.463*** |
| (0.000) | (0.001) | (0.052) | (0.755) | (0.879) | (0.020) | (0.000) | (0.000) | (0.004) | (0.000) | |
| L.exp_pub_gdp | 0.212*** | |||||||||
| (0.000) | ||||||||||
| Trade to GDP | −0.166 | −0.0329 | 0.0490* | 0.792*** | 0.0240+ | 0.114* | 0.154*** | −0.0407 | 0.0969 | −0.0798 |
| (0.708) | (0.102) | (0.018) | (0.000) | (0.053) | (0.017) | (0.000) | (0.174) | (0.141) | (0.789) | |
| Control of corruption | −2.313*** | 0.0701** | −0.0709** | 0.00346 | 0.00288 | 0.0988+ | 0.000984 | −0.0778+ | 0.0110 | −1.238*** |
| (0.000) | (0.003) | (0.001) | (0.984) | (0.790) | (0.090) | (0.952) | (0.090) | (0.834) | (0.000) | |
| Financial Openness | −3.115*** | 0.173*** | −0.0126 | −0.0371 | 0.0297** | −0.117 | 0.0355 | 0.0328 | −0.0518 | 1.173* |
| (0.000) | (0.000) | (0.623) | (0.896) | (0.007) | (0.188) | (0.422) | (0.628) | (0.602) | (0.010) | |
| Democracy_dummy | 1.158** | −0.144*** | 0.0363 | −0.0752 | 0.0241** | −0.140* | −0.0520+ | 0.0625 | 0.227** | 0.329 |
| (0.008) | (0.000) | (0.129) | (0.662) | (0.007) | (0.034) | (0.088) | (0.136) | (0.006) | (0.322) | |
| L.exp_def_gdp | 0.888*** | |||||||||
| (0.000) | ||||||||||
| L.exp_order_gdp | 0.857*** | |||||||||
| (0.000) | ||||||||||
| L.exp_econ_gdp | 0.349*** | |||||||||
| (0.000) | ||||||||||
| L.exp_envi_gdp | 0.856*** | |||||||||
| (0.000) | ||||||||||
| L.exp_housing_gdp | 0.173*** | |||||||||
| (0.000) | ||||||||||
| L.exp_cult_gdp | 0.452*** | |||||||||
| (0.000) | ||||||||||
| L.exp_health_gdp | 0.874*** | |||||||||
| (0.000) | ||||||||||
| L.exp_edu_gdp | 0.792*** | |||||||||
| (0.000) | ||||||||||
| L.exp_socpro_gdp | 0.571*** | |||||||||
| (0.000) | ||||||||||
| Constant | −0.0583 | 0.632*** | 0.0431 | −1.305+ | −0.167* | −0.385 | −1.346*** | −1.325*** | −1.197** | −10.48*** |
| (0.978) | (0.000) | (0.641) | (0.094) | (0.011) | (0.165) | (0.000) | (0.000) | (0.005) | (0.000) | |
| N. Obs. | 1382 | 1344 | 1382 | 1407 | 1130 | 1380 | 1310 | 1409 | 1408 | 1354 |
| AR (1) p-value | 0.0205 | 0.0155 | 0.0397 | 0.00188 | 0.000456 | 0.0239 | 0.0105 | 0.00368 | 0.00000682 | 0.140 |
| AR (2) p-value | 0.169 | 0.782 | 0.358 | 0.0264 | 0.908 | 0.355 | 0.326 | 0.448 | 0.724 | 0.294 |
| Hansen p-value | 0.158 | 0.320 | 0.0791 | 0.0438 | 0.108 | 0.494 | 0.284 | 0.119 | 0.187 | 0.0695 |
Note: This table estimates the Effects of Old-Age Populations on each Compositional Government Spending using two-step System GMM. The Ratio of each Compositional Government Spending to GDP are Dependent Variables. The Old-Age Dependency Ratio (Old_depend, ln) is the main Independent Variable. For two-step System GMM, we let the Old-Age Dependency Ratio as Instrument, but put lagged Dependent Variable as Endogeneous with collapse option. The p-value of Auto-Correlation 1st and 2nd order, including Hansen's post-Estimation Tests are presented at the bottom Panel. The p-values are presented in parentheses and +p < 0.10, *p < 0.05, **p < 0.01, ***p < 0.001.
Source: Author's calculation.
Furthermore, we can see from the estimation results in Table 7 that as the country moves toward an aging society, the public spending on public administration, housing, and education are reduced perhaps because that once the country becomes aged, fewer children are born and spending related to education and public administration are lower. A change in the demographic structure reshapes how a government focuses on each spending category. In addition, housing spending reduces as the country has a larger aging population. There will be less demand for houses in aging society.
Furthermore, we also present the post-estimation tests in Table 7. The results suggest that our model does not suffer from second-order serial correlation and there is no problem with the weakness of instruments for model overidentification.
We also replicate a similar model using government spending composition to total expenditure instead of government spending composition as a percentage of GDP (See Table 8 in Appendix B.). The results in Table 8 confirm identical implications to those from Table 7. An increase in the old-age population significantly leads to higher government spending, especially in the social protection and public administration categories.
As expected, aging also reduces the spending on education.6 The results are consistent with previous studies. For example, ref. [[33], [54]] find that aging population induces higher spending on healthcare and social protections while contracting the spending in education using the data of Brazil based on the forecasting model with change in the age structure. Similar to ref. [55] who reveals positive effects of the proportion of elderly individuals on expenditure for pensions and social protection in 25 EU countries from 1995 to 2014, using panel data with the system GMM. Compared to total government revenue, the more significant positive impact on overall public expenditure reaffirms the adverse impact of population aging on the budget balance.
However, once we consider the different levels of income across the country (see Table 11), we find that the old-age population does not cause an increase in social protection or health expenditures in developing countries. Rather, it pushes the public spending on defense, which remains a puzzle as to why as the country becomes aged, there is a significant increase in public spending on defense. Ref. [56] suggest that public policy satisfaction differs across ages. People are likely to satisfy policies that ensure safety and life security as they age. Similarly, ref. [20] state that as the proportion of the old-age population increases, expenditure on defense tends to be higher due to the high demand for life safety and security. Moreover, ref. [57] uses the data from Japan National Election from 1972 to 2016 to test the public policy anticipation. He finds that older people are likelier to show interest and express their needs toward public policies than working-age people. As time passed, public policies related to aging became clearer, making old-age people more interested in this issue.
Table 11.
Effects of old-age populations on each compositional government spending (as percentage of GDP) using two-step system GMM with old-age dependency ratio as a proxy for old-age populations (sample: Developing).
| Variable | (Public Admin) | (Defense) | (Order) | (Economic) | (Environ ment) | (Housing) | (Culture) | (Health) | (Education) | (Social Protection) |
|---|---|---|---|---|---|---|---|---|---|---|
| Old_depend, ln | −3.823*** | 0.350*** | 0.0509 | −0.0856 | 0.0343 | −0.473*** | 0.0118 | −0.000214 | −0.390*** | 0.199 |
| (0.000) | (0.000) | (0.138) | (0.764) | (0.227) | (0.000) | (0.637) | (0.997) | (0.000) | (0.291) | |
| GDP per capita | 3.872*** | −0.413*** | −0.0450 | −0.0987 | −0.00233 | 0.330*** | 0.0186 | 0.0749+ | 0.154 | 0.873*** |
| (0.000) | (0.000) | (0.289) | (0.676) | (0.924) | (0.001) | (0.403) | (0.095) | (0.114) | (0.000) | |
| Trade to GDP | −0.168 | 0.0788 | 0.0967** | 0.915*** | 0.0686*** | 0.162** | 0.0614*** | 0.162*** | 0.241*** | −0.0956 |
| (0.643) | (0.166) | (0.005) | (0.000) | (0.000) | (0.007) | (0.000) | (0.001) | (0.000) | (0.506) | |
| Control of corruption | −1.671*** | 0.116*** | 0.00638 | 0.122+ | 0.0181* | 0.0344 | 0.00955 | 0.0329 | 0.137** | −0.224** |
| (0.000) | (0.000) | (0.713) | (0.073) | (0.042) | (0.410) | (0.334) | (0.138) | (0.001) | (0.001) | |
| Financial Openness | −1.544*** | 0.138* | 0.0561 | −0.441+ | 0.00308 | −0.171+ | −0.0179 | 0.170** | 0.0414 | 0.325+ |
| (0.001) | (0.034) | (0.106) | (0.059) | (0.855) | (0.087) | (0.127) | (0.002) | (0.563) | (0.089) | |
| Democracy_dummy | 0.464 | −0.0861* | 0.00180 | −0.104 | 0.0297*** | −0.0668 | −0.0186+ | 0.0335 | 0.0975+ | −0.00636 |
| (0.115) | (0.040) | (0.925) | (0.323) | (0.001) | (0.299) | (0.096) | (0.310) | (0.057) | (0.956) | |
| L.exp_pub_ gdp | 0.447*** | |||||||||
| (0.000) | ||||||||||
| L.exp_def_gdp | 0.898*** | |||||||||
| (0.000) | ||||||||||
| L.exp_order_gdp | 0.881*** | |||||||||
| (0.000) | ||||||||||
| L.exp_econ_gdp | 0.483*** | |||||||||
| (0.000) | ||||||||||
| L.exp_envi_gdp | 0.604*** | |||||||||
| (0.000) | ||||||||||
| L.exp_housing_gdp | 0.0959** | |||||||||
| (0.003) | ||||||||||
| L.exp_cult_gdp | 0.797*** | |||||||||
| (0.000) | ||||||||||
| L.exp_health_gdp | 0.766*** | |||||||||
| (0.000) | ||||||||||
| L.exp_edu_gdp | 0.772*** | |||||||||
| (0.000) | ||||||||||
| L.exp_socpro_gdp | 0.734*** | |||||||||
| (0.000) | ||||||||||
| Constant | −12.17*** | 1.926*** | 0.000253 | −0.709 | −0.361*** | −1.730** | −0.378* | −1.124*** | −0.962 | −5.896*** |
| (0.000) | (0.000) | (0.999) | (0.549) | (0.001) | (0.003) | (0.010) | (0.001) | (0.109) | (0.000) | |
| N. Obs. | 746 | 710 | 748 | 771 | 576 | 746 | 688 | 774 | 772 | 718 |
| AR (1) p-value | 0.0388 | 0.00557 | 0.0657 | 0.00466 | 0.00951 | 0.117 | 0.00384 | 0.0179 | 0.0000350 | 0.0425 |
| AR (2) p-value | 0.119 | 0.635 | 0.423 | 0.355 | 0.643 | 0.675 | 0.869 | 0.424 | 0.919 | 0.482 |
| Hansen p-value | 0.621 | 0.638 | 0.354 | 0.681 | 0.618 | 0.286 | 0.380 | 0.539 | 0.526 | 0.399 |
Note: This table estimates the Effects of Old-Age Populations on each Compositional Government Spending using two-step System GMM. The Ratio of each Compositional Government Spending to GDP are Dependent Variables. The Old-Age Dependency Ratio is the main Independent Variable. For two-step System GMM, we let the Old-Age Dependency Ratio as Instrument, but put lagged Dependent Variable as Endogeneous with collapse option. The p-value of Auto-Correlation 1st and 2nd order, including Hansen's post-Estimation Tests are presented at the bottom Panel. The p-values are presented in parentheses and + p < 0.10, *p < 0.05, **p < 0.01, ***p < 0.001.
Source: Author's calculation.
From the Median Voter Theorem, policies chosen by the government will eventually follow the preference of the median voters. Therefore, as the number of median voters becomes aged, policies become more conservative and less liberal. The idea of nationalism and policies preference for defense become critical for aging voters, which is reflected in a rise in the spending on defense in developing countries once the countries become more aged. Ref. [58] study the relationship between age and political ideas; they find that as people become older, the political idea tends to move towards Social Dominance Orientation (SDO) and Right-wing authoritarianism (RWA). SDO supports the thinking of social hierarchy, and the RWA supporters tend to follow the social norm and ruler's order; in other words more conservative ([59] for SDO definition and [60] for RWA definition as cited in Ref. [61]).
Looking at other spending compositions, the old-age dependency ratio still has significantly negative coefficients for spending on public administration, housing, and education. However, the negative effect of old-age population on public spending in education is larger in developing countries (44 countries) compared to the total sample of 87 countries. Comparing Column 10 in Table 7 with the same column in Table 11, the reduction in education spending in countries with income less than or equal to 12,000 USD is higher than for about 50% of the full sample. Although a shift in the demographic structure toward aging may reduce the number of children, and thus affect lower spending in education, education can be provided throughout the people's lifetime; for example, through training, re-skilling or upskilling during working age, or even a learning program to maintain physical and mental health when individuals become aged.
In summary, an increase in the old-age population is positively correlated to a higher government spending in health, environment, and social protection categories, while it reduces the spending, particularly on education and housing using the full sample. However, the results are different when we consider the income level of the countries, with an increase in the old-age population in the countries with income less than or equal to 12,000 USD pushes higher spending on defense rather than the usual related old-age population spending categories, such as health or social protection. For the countries with income higher than 12,000 USD, the results follow a similar pattern as for the full sample. However, the reductions in public administration, housing, and education as the countries age are shown in developing and developed countries.
4.3. Interaction of old-age population and government spending in affecting economic growth
We further analyze the interaction effect between aging population and reallocation of government spending on economic growth. The model is modified following the study of [38], as presented in Equation (4). Another study suggests that a reallocation of government spending in the health care and social protection categories toward education enhances economic growth in the long run. This study adds the aspect of an aging society to test whether a reallocation of government spending affects economic growth in an aging society.
Table 12 presents the regression estimates from the model in Equation (4). The header for each column represents a spending composition that has been omitted due to multicollinearity issues. Thus, those omitted spending categories will become the source of fund financing for other public spending categories. For example, in the second column in Table 12, we omit the government spending on public administration. We have the 4-year GDP per capita growth rate as a dependent variable.7 The interest-independent variable is the interaction effect terms between the old-age variable, government spending, and GDP growth. The results suggest that the previous 4-year GDP per capita (L4.GDP per capita) has increased, so the current 4-year growth rate of GDP per capita is reduced in each model. Looking at the population aging variable (L.Old_depen), we find that the population aging alone has no significant relationship with GDP growth. However, growth is impacted by the interaction between aging population and the reallocation of government spending in specific categories.
Table 12.
Effects of old-age populations and GDP per capita in affecting the allocation of compositional government spending (as percentage of GDP) using dynamic system GMM (with old-age dependency ratio as a proxy for old-age populations).
| Variable | (Public Admin) | (Defense) | (Order) | (Economic) | (Environ ment) | (Housing) | (Culture) | (Health) | (Education) | (Social Protection) |
|---|---|---|---|---|---|---|---|---|---|---|
| L4.GDP per capita | −2.131*** | −2.724*** | −2.569*** | −2.536*** | −2.898*** | −2.694*** | −2.318*** | −2.600*** | −2.233*** | −2.480 |
| (0.000) | (0.000) | (0.000) | (0.000) | (0.000) | (0.000) | (0.000) | (0.000) | (0.000) | (0.000) | |
| Trade to GDP | 0.0273 | 0.217 | 0.324 | 0.299 | 0.575+ | 0.386 | 0.283 | 0.215 | 0.496 | 0.131 |
| (0.942) | (0.553) | (0.390) | (0.468) | (0.073) | (0.319) | (0.491) | (0.556) | (0.181) | (0.740) | |
| Control of corruption | 1.670*** | 2.080*** | 2.070*** | 1.957*** | 2.487*** | 2.036*** | 2.382*** | 2.038*** | 1.942*** | 1.842*** |
| (0.000) | (0.000) | (0.000) | (0.000) | (0.000) | (0.000) | (0.000) | (0.000) | (0.000) | (0.000) | |
| Financial Openness | 0.316 | 0.183 | −0.136 | −0.344 | −0.395 | −0.310 | −0.139 | −0.160 | −0.0645 | −0.326 |
| (0.525) | (0.708) | (0.764) | (0.477) | (0.410) | (0.534) | (0.789) | (0.743) | (0.875) | (0.497) | |
| Democracy_dummy | −1.279* | −1.105* | −0.802+ | −1.025* | −0.828* | −0.858+ | −1.414** | −1.027* | −1.039* | −0.903* |
| (0.012) | (0.020) | (0.084) | (0.019) | (0.028) | (0.067) | (0.007) | (0.037) | (0.021) | (0.047) | |
| L4. Expenditure to GDP | 0.0278 | 0.0785 | −0.226** | −0.0233 | −0.230** | −0.145 | −0.138* | 0.0345 | −0.179* | −0.0190 |
| (0.310) | (0.281) | (0.007) | (0.539) | (0.006) | (0.115) | (0.018) | (0.685) | (0.012) | (0.579) | |
| L4. Old_depend, ln | 0.781 | −0.316 | −0.517 | −0.325 | −1.103 | −0.496 | −0.0655 | −0.0262 | 0.00619 | −0.0711 |
| (0.205) | (0.612) | (0.296) | (0.589) | (0.102) | (0.418) | (0.910) | (0.966) | (0.991) | (0.909) | |
| L4.exp_pub_ gdp | −0.328** | −0.114 | −0.316** | −0.247* | −0.191 | −0.0810 | −0.310* | −0.0747 | −0.255* | |
| (0.006) | (0.309) | (0.008) | (0.014) | (0.131) | (0.306) | (0.026) | (0.463) | (0.011) | ||
| L4.exp_def_gdp | −0.256 | 0.326 | 0.0519 | 0.205 | 0.218 | 0.174 | −0.0880 | −0.0641 | 0.0200 | |
| (0.401) | (0.321) | (0.857) | (0.431) | (0.552) | (0.319) | (0.794) | (0.829) | (0.941) | ||
| L4.exp_order_gdp | 0.164 | 0.0483 | −0.00798 | 1.266* | 0.187 | 0.193 | 0.0965 | −0.234 | −0.0266 | |
| (0.725) | (0.918) | (0.986) | (0.018) | (0.686) | (0.710) | (0.841) | (0.576) | (0.954) | ||
| L.exp_econ_gdp | 0.0382 | −0.0264 | 0.343+ | 0.275 | 0.197 | 0.504** | 0.0984 | 0.177 | 0.133 | |
| (0.791) | (0.883) | (0.059) | (0.153) | (0.276) | (0.007) | (0.599) | (0.292) | (0.383) | ||
| L.exp_envi_gdp | 3.188* | 2.305+ | 2.003 | 2.070 | 2.455+ | 0.639 | 2.563* | 1.459 | 2.307+ | |
| (0.011) | (0.074) | (0.119) | (0.115) | (0.068) | (0.666) | (0.037) | (0.293) | (0.096) | ||
| L4.exp_housing_gdp | −0.229 | −0.120 | 0.189 | −0.200 | 0.445 | −0.496 | −0.342 | −0.228 | −0.168 | |
| (0.601) | (0.792) | (0.673) | (0.647) | (0.386) | (0.351) | (0.440) | (0.624) | (0.701) | ||
| L4.exp_health_gdp | −0.180 | −0.512 | 0.272 | 0.0777 | 0.115 | 0.0117 | 0.903 | −0.197 | 0.429 | |
| (0.731) | (0.380) | (0.607) | (0.891) | (0.828) | (0.982) | (0.187) | (0.717) | (0.301) | ||
| L4.exp_cult_gdp | 1.676*** | 2.537*** | 2.541*** | 2.566*** | 2.691*** | 2.878*** | 2.366*** | 2.038*** | 2.318*** | |
| (0.000) | (0.000) | (0.000) | (0.000) | (0.000) | (0.000) | (0.000) | (0.000) | (0.000) | ||
| L4.exp_edu_gdp | −1.009** | −1.553*** | −1.124** | −1.195** | −1.522*** | −1.377*** | −0.973** | −1.277** | −1.230** | |
| (0.004) | (0.000) | (0.002) | (0.002) | (0.000) | (0.001) | (0.004) | (0.002) | (0.001) | ||
| L4.exp_socpro_gdp | 0.116 | 0.132 | 0.306+ | 0.159 | 0.444** | 0.317+ | 0.230 | 0.0387 | 0.305+ | |
| (0.402) | (0.434) | (0.086) | (0.410) | (0.006) | (0.096) | (0.261) | (0.818) | (0.067) | ||
| L4. Old_depend, ln X L4.exp_def_gdp X L4.GDP per capita | 0.0157 | 0.00429 | 0.00660 | 0.0109 | 0.00420 | 0.00705 | 0.0105 | 0.0193+ | 0.00804 | |
| (0.206) | (0.734) | (0.580) | (0.333) | (0.770) | (0.418) | (0.422) | (0.089) | (0.489) | ||
| L4. Old_depend, ln X L4.exp_order_gdp X L4.GDP per capita | −0.0235 | −0.0119 | −0.0154 | −0.0494+ | −0.0168 | −0.0204 | −0.0204 | −0.00191 | −0.0131 | |
| (0.346) | (0.637) | (0.545) | (0.091) | (0.501) | (0.451) | (0.451) | (0.936) | (0.605) |
| Variable | (Public Admin) | (Defense) | (Order) | (Economic) | (Environ ment) | (Housing) | (Culture) | (Health) | (Education) | (Social Protection) |
|---|---|---|---|---|---|---|---|---|---|---|
| L4. Old_depend, ln X L.exp_econ_gdp X L4.GDP per capita | −0.00130 | −0.00110 | −0.00351 | 0.00155 | −0.00112 | −0.0139* | −0.00418 | −0.000393 | −0.00354 | |
| (0.794) | (0.834) | (0.471) | (0.795) | (0.821) | (0.016) | (0.446) | (0.938) | (0.497) | ||
| L4. Old_depend, ln X L.exp_envi_gdp X L4.GDP per capita | −0.0991* | −0.0766+ | −0.0516 | −0.0562 | −0.0693 | 0.000690 | −0.0685+ | −0.0304 | −0.0622 | |
| (0.019) | (0.097) | (0.235) | (0.209) | (0.130) | (0.989) | (0.093) | (0.514) | (0.187) | ||
| L4. Old_depend, ln X L4.exp_housing_gdp X L4.GDP per capita | 0.00374 | −0.00489 | −0.00121 | 0.00723 | −0.000111 | 0.0203 | 0.0101 | 0.0138 | 0.00576 | |
| (0.851) | (0.811) | (0.951) | (0.722) | (0.996) | (0.364) | (0.595) | (0.537) | (0.775) | ||
| L4. Old_depend, ln X L4.exp_health_gdp X L4.GDP per capita | 0.00907 | 0.0173 | 0.00146 | 0.00371 | 0.00838 | 0.00839 | −0.0209 | 0.0157 | −0.00844 | |
| (0.641) | (0.409) | (0.942) | (0.860) | (0.659) | (0.674) | (0.414) | (0.449) | (0.557) | ||
| L4. Old_depend, ln X L4.exp_cult_gdp X L4.GDP per capita | −0.0665*** | −0.112*** | −0.0900*** | −0.0964*** | −0.105*** | −0.106*** | −0.0945*** | −0.0579* | −0.0886*** | |
| (0.001) | (0.000) | (0.000) | (0.000) | (0.000) | (0.000) | (0.000) | (0.012) | (0.000) | ||
| L4. Old_depend, ln X L4.exp_edu_gdp X L4.GDP per capita | 0.0389** | 0.0648*** | 0.0524*** | 0.0497** | 0.0705*** | 0.0619*** | 0.0410** | 0.0504** | 0.0506** | |
| (0.009) | (0.000) | (0.000) | (0.001) | (0.000) | (0.000) | (0.003) | (0.001) | (0.001) | ||
| L4. Old_depend, ln X L4.exp_socpro_gdp X L4.GDP per capita | −0.00436 | −0.00740 | −0.00272 | −0.00509 | −0.00738 | −0.00577 | −0.00225 | −0.00179 | −0.00201 | |
| (0.398) | (0.210) | (0.611) | (0.412) | (0.194) | (0.331) | (0.749) | (0.659) | (0.731) | ||
| L4. Old_depend, ln X L4.exp_pub_ gdp X L4.GDP per capita | 0.0131** | 0.0159** | 0.0163** | 0.0230*** | 0.0160** | 0.0114* | 0.0141** | 0.0120* | 0.0137* | |
| (0.008) | (0.002) | (0.002) | (0.000) | (0.002) | (0.037) | (0.003) | (0.013) | (0.006) | ||
| N. Obs. | 785 | 803 | 785 | 785 | 963 | 791 | 790 | 785 | 785 | 785 |
| AR (1) p-value | 0.896 | 0.306 | 0.250 | 0.245 | 0.285 | 0.190 | 0.661 | 0.339 | 0.381 | 0.347 |
| AR (2) p-value | 0.111 | 0.172 | 0.481 | 0.189 | 0.488 | 0.270 | 0.962 | 0.168 | 0.243 | 0.205 |
| Hansen p-value | 0.0000977 | 0.0000989 | 0.0000474 | 0.000135 | 0.0000987 | 0.0000942 | 0.000341 | 0.000327 | 0.0000778 | 0.000199 |
Note: This table estimates the Effects of Old-Age Populations and Reallocation of Government Spending across various functions on economic growth (4 years) using two-step System GMM. For two-step System GMM, we put lagged Dependent Variable as Endogeneous with collapse option. The p-value of Auto-Correlation 1st and 2nd order, including Hansen's post-Estimation Tests are presented at the bottom Panel. The p-values are presented in parentheses and + p < 0.10, *p < 0.05, **p < 0.01, ***p < 0.001.
Source: Author's calculation.
Considering the second column in Table 12 once again, the coefficient of the interaction terms (L4ln_Old_depen X L4exp_edu_gdp X L4ln_gdp_percapita) is positively significant (0.0389** at the 99% confidence level). When we trace educational spending (l4exp_edu_gdp), it has a significant negative sign (−1.009**) implying that omitting the expenditure for public administration and reallocating it to educational expenditure would help to improve economic growth by −1.009 + (0.0389*Old_depen* gdp_percapita).8 As the population aging and/or GDP per capita increase, the reallocation of government spending from public administration to education would improve economic growth.
According to the results shown in Table 12, we can summarize the implication of population aging and government spending reallocation on economic growth as in Table 13. Note also that the first column represents the omitted spending category or financing categories, while the header for columns 2–9 represent where the spending has been allocated.
Table 13.
Summary all results from Government Spending Reallocation Model.
| Growth rate of GDP per capita (4 years) | Public Admin | Defense | Order | Economic | Environment | Housing | Culture | Health | Education | Social Protection |
|---|---|---|---|---|---|---|---|---|---|---|
| Financing Component | ||||||||||
| (Public Admin) | X | |||||||||
| (Defense) | x | |||||||||
| (Order) | x | |||||||||
| (Economic) | x | |||||||||
| (Environment) | x | |||||||||
| (Housing) | x | |||||||||
| (Culture) | X | |||||||||
| (Health) | x | |||||||||
| (Education) | X | |||||||||
| (Social Protection) | x |
Note: This table estimates the Effects of Old-Age Populations and Reallocation of Government Spending across various functions on economic growth (4 years) using two-step System GMM. For two-step System GMM, we put lagged Dependent Variable as Endogeneous with collapse option. The p-value of Auto-Correlation 1st and 2nd order, including Hansen's post-Estimation Tests are presented at the bottom Panel. The p-values are presented in parentheses and *p < 0.05, **p < 0.01, ***p < 0.001.
Source: Author's calculation
The results shown in Table 13 suggest that the reallocations of government spending from any category toward expenditure for education help to improve economic growth in the aging countries, as we can see from the significantly positive signs for the whole column. The results are consistent to Ref. [38], [62]]. On the other hand, a reallocation of government spending from any category to expenditure for culture would hinder growth. Apart from these two main results, reallocations from the economic and environmental categories toward public administration also significantly promote economic growth. Here, the main result is that education is important for long-term economic growth; even if the population in the country ages, reallocating the expenditure toward this category can help to improve economic growth.
5. Conclusion
Population aging is a phenomenon that all countries are facing in this era. An increase in the old-age population challenges government policies as there is an increasing demand for more health support and other related issues. This paper successfully investigates the effect of an aging population on economic growth through the channel of government spending. We analyze both in aggregate and each government's compositional terms and test how reallocating government spending across composition can enhance economic growth in aging countries.
The main results suggest that first, an increase in the aging population does induce higher government spending in general, in particular for components, such as health, environment, and social protection. However, the results are controversial once we consider differences in income across countries. We find that higher income countries follow the same pattern as we suggest earlier, but not so for middle- and low-income countries. An increase in population aging does not induce higher government spending in general.
Considering the government spending composition, the old-age population rather induces higher defense spending in developing countries. I conjecture that it may be explained by an age-political preference. As the median voters become older, they are more likely to prefer conservatism and nationalist political profiles. This would enhance higher spending in the defense category. On the other hand, an increase in the aging population reduces education and housing public expenditures for all income groups because there is a reduced number of children and the elderly, resulting in a reduced demand for housing.
Lastly, we find that a reallocation of government spending from any categories toward education in the aging society would promote long-term economic growth, while any reallocation toward the cultural category would induce growth slowdown.
These results could be used as guidelines for public policy makers to allocate resources across government spending categories efficiently in the midst of an aging era.
Author contribution statement
Navarat Temsumrit: Conceived and designed the experiments; Performed the experiments; Analyzed and interpreted the data; Contributed reagents, materials, analysis tools or data; Wrote the paper.
Data availability statement
Data will be made available on request.
Declaration of competing interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper
Acknowledgment
I would like to offer my special thanks to supervisor on this project, Somskaow Bejranonda, Siwapong Dheera-aumpon, and anonymous referees for all their helpful guidance and enthusiastic support, as well as valuable comments during the PIER research exchange seminar and Thailand National Conference of Economists (NCE) 2022. The authors acknowledge funding from the Kasetsart University Research and Development Institute (KURDI) (Grant Number 20.64).
Footnotes
In North Africa and Western Asia, the fertility rate dropped from 4.4 to 2.9; in Central and South Asia, from 4.3 to 2.4; in East and South-Eastern Asia, from 2.5 to 1.8. In Latin America and the Caribbean, from 3.3 to 2.0; and in Oceania, from 4.5 to 3.4. In Australia and New Zealand, and in Europe and North America, fertility rates in 1990 was less than 2.0 births per woman. However, in 2020, the average birth rate in Australia and New Zealand was 1.8 births per woman and just 1.7 in Europe and North America [1].
An increase in life expectancy reciprocally affects individuals' decisions on investing more in their education. This affects positively the long-term economic growth, as a higher level of human capital helps the economy acquire more effective workers.
We exclude from the samples: all islands; countries depending heavily on oil exports; countries with a population less than one million; and countries with special authority, since these countries may bias our estimation.
We use the panel unit root test from Ref. [66].
For robustness checks, we try other proxies for the old-age population. That is we use the percentage of old-age population instead of using old-age dependency ratio as the main independent variable. The results are robust and confirm that the old-age population induces higher spending on particular categories e.g. health, social protection, and environment, while reducing public spending on education and housing. The results are shown in Tables 9 and 10 in Appendix B.
We follow [38] to use 4-year GDP growth rate as a change in the government spending policies responses to aging may take some time to see the effects.
−1.009 + (0.0389*Old_depen*gdp_percapita) when using average of old-age dependency ratio and GDP per capita of the 87 countries from descriptive statistic in Table 2, the marginal effect of aging population and government spending reallocation on economic growth will be −1.009 + (0.0389*2.465* 8.955) = −1.009 + 0.858 = −0.150, which is better than the case for no government expenditure reallocation.
Appendix.
Appendix A. Robustness checks using different proxies for model's main independent variable
Table 5.
Regression Results using Various Econometrics Methods with Percentage of Old-Age Population as a Proxy for Old-Age Populations.
| Variable | (OLS) | (FE) | (1DGMM) | (2DGMM) | (1SGMM) | (2SGMM) |
|---|---|---|---|---|---|---|
| Percentage Old pop | 0.0199*** | 0.0827* | 0.120 | 0.0253 | 0.0612*** | 0.0641*** |
| (0.000) | (0.012) | (0.393) | (0.607) | (0.000) | (0.000) | |
| L. Gov Spending | 0.913*** | 0.714*** | 1.011*** | 1.051*** | 0.791*** | 0.797*** |
| (0.000) | (0.000) | (0.000) | (0.000) | (0.000) | (0.000) | |
| GDP per capita | 0.0819*** | 0.196*** | −0.256 | −0.207** | 0.155* | 0.142*** |
| (0.000) | (0.000) | (0.614) | (0.002) | (0.019) | (0.000) | |
| Trade to GDP | 0.00772+ | 0.00327 | 0.0267 | 0.0199* | 0.0183 | 0.0163** |
| (0.096) | (0.796) | (0.717) | (0.015) | (0.220) | (0.002) | |
| Control of corruption | 0.0111* | 0.0562*** | 0.0247 | 0.0253** | 0.0726** | 0.0795*** |
| (0.021) | (0.000) | (0.376) | (0.004) | (0.002) | (0.000) | |
| Financial Openness | −0.0123 | −0.0171 | −0.0428 | −0.0261 | 0.0351 | 0.0312* |
| (0.126) | (0.337) | (0.432) | (0.488) | (0.202) | (0.017) | |
| Democracy_dummy | 0.00285 | 0.0298* | 0.0273 | 0.0195 | −0.0132 | −0.0204** |
| (0.665) | (0.010) | (0.551) | (0.144) | (0.546) | (0.001) | |
| Constant | −0.192*** | −0.130 | −0.383+ | −0.339*** | ||
| (0.000) | (0.476) | (0.071) | (0.000) | |||
| N. Obs. | 1705 | 1705 | 1428 | 1428 | 1705 | 1705 |
| R-Squared | 0.996 | 0.854 | ||||
| Adjusted R-Squared | 0.996 | 0.843 | ||||
| AR (1) p-value | 0.00409 | 0.00453 | 0.00424 | 0.00800 | ||
| AR (2) p-value | 0.262 | 0.262 | 0.308 | 0.318 | ||
| Hansen p-value | 0.0526 | 0.0526 | 0.0846 | 0.0846 |
Note: This table estimates the relationship between Old-Age Populations, using Percentage of Old-Age Population as a Proxy, and Government Spending at the Aggregate Level. The Total Final Government Consumption per Capita in Logarithmic form is Dependent Variables. The Percentage of Old-Age Population in Logarithmic form (Percentage Old pop) is the main Independent Variable. OLS represents the Ordinary Least Square Method: FE is Panel Data Model with Fixed Effect; 1DGMM and 2DGMM are one- and two-step Difference Generalized Methods of Moment, respectively, and 1SGMM and 2SGMM are one- and two-step System Generalized Methods of Moment, respectively. The p-value of Auto-Correlation 1st and 2nd order, including ' 'Hansen's post-Estimation Tests for Dynamic GMM are presented at the bottom Panel. The p-values are presented in parentheses and+p < 0.10, *p < 0.05, **p < 0.01, ***p < 0.001.
Source: Author's calculation.
Appendix B. Robustness checks using different proxies for model's main dependent variable
Table 8.
Effects of Old-Age Populations on Each Compositional Government Spending (as Percentage of Total Expenditure) Using Two-step System GMM with Old-Age Dependency Ratio as a Proxy for Old-Age Populations.
| Variable | (Public Admin) | (Defense) | (Order) | (Economic) | (Environ ment) | (Housing) | (Culture) | (Health) | (Education) | (Social Protection) |
|---|---|---|---|---|---|---|---|---|---|---|
| Old_depend, ln | −0.0238** | −0.000843 | −0.00427** | 0.00768+ | 0.00187*** | −0.0117*** | 0.00288*** | 0.00522* | −0.00607* | 0.0318*** |
| (0.001) | (0.555) | (0.008) | (0.071) | (0.000) | (0.000) | (0.000) | (0.019) | (0.027) | (0.000) | |
| GDP per capita, ln | 0.0242*** | −0.00286* | −0.00192 | −0.0209*** | −0.000431 | 0.00276* | 0.000125 | 0.00663*** | −0.00444+ | 0.0272*** |
| (0.000) | (0.041) | (0.110) | (0.000) | (0.186) | (0.027) | (0.810) | (0.000) | (0.067) | (0.000) | |
| Trade to GDP | −0.00898 | −0.00267+ | 0.00242+ | 0.0142*** | 0.00169*** | 0.00220 | 0.00460*** | 0.00255 | 0.00619** | −0.00188 |
| (0.252) | (0.088) | (0.096) | (0.000) | (0.000) | (0.134) | (0.000) | (0.237) | (0.003) | (0.716) | |
| Control of corruption | −0.0449*** | 0.000879 | −0.00208+ | 0.0172*** | 0.000431 | −0.000677 | 0.000568 | −0.000744 | 0.00697*** | −0.0188*** |
| (0.000) | (0.613) | (0.069) | (0.000) | (0.127) | (0.628) | (0.293) | (0.654) | (0.001) | (0.000) | |
| Financial Openness | −0.0468*** | 0.00502** | −0.00175 | −0.00564 | 0.00181** | −0.00119 | 0.00237* | 0.00401 | 0.00766+ | 0.0150+ |
| (0.000) | (0.008) | (0.379) | (0.377) | (0.002) | (0.559) | (0.034) | (0.194) | (0.055) | (0.082) | |
| Democracy_dummy | 0.0158+ | −0.0112*** | 0.00166 | −0.0185*** | 0.000283 | −0.00130 | −0.00296*** | 0.00579* | 0.00370 | 0.00235 |
| (0.065) | (0.000) | (0.243) | (0.001) | (0.370) | (0.522) | (0.000) | (0.015) | (0.182) | (0.623) | |
| L.pub_exp | 0.617*** | |||||||||
| (0.000) | ||||||||||
| L.def_exp | 0.799*** | |||||||||
| (0.000) | ||||||||||
| L.order_exp | 0.625*** | |||||||||
| (0.000) | ||||||||||
| L.econ_exp | 0.544*** | |||||||||
| (0.000) | ||||||||||
| L.envi_exp | 0.646*** | |||||||||
| (0.000) | ||||||||||
| L.housing_exp | 0.337*** | |||||||||
| (0.000) | ||||||||||
| L.cult_exp | 0.512*** | |||||||||
| (0.000) | ||||||||||
| L.health_exp | 0.634*** | |||||||||
| (0.000) | ||||||||||
| L.edu_exp | 0.729*** | |||||||||
| (0.000) | ||||||||||
| L.socpro_exp | 0.651*** | |||||||||
| (0.000) | ||||||||||
| Constant | 0.156*** | 0.0512*** | 0.0479*** | 0.123*** | −0.00825*** | 0.0140 | −0.0227*** | −0.0560*** | 0.0261* | −0.191*** |
| (0.001) | (0.000) | (0.000) | (0.000) | (0.000) | (0.112) | (0.000) | (0.000) | (0.029) | (0.000) | |
| N. Obs. | 1489 | 1489 | 1489 | 1489 | 1489 | 1489 | 1489 | 1489 | 1489 | 1489 |
| AR (1) p-value | 0.0000794 | 0.000849 | 0.000344 | 0.0000915 | 0.0139 | 0.0185 | 0.000149 | 0.0108 | 0.000209 | 0.00213 |
| AR (2) p-value | 0.102 | 0.166 | 0.0759 | 0.0783 | 0.358 | 0.395 | 0.426 | 0.187 | 0.0721 | 0.142 |
| Hansen p-value | 0.00840 | 0.418 | 0.0990 | 0.119 | 0.210 | 0.454 | 0.313 | 0.126 | 0.548 | 0.392 |
Note: This table estimates the relationship between Old-Age Populations and Government Spending in each Composition by their function using two-step System GMM. The Ratio of each Compositional Government Spending to Total Expenditures are Dependent Variables. The Old-Age Dependency Ratio is the main Independent Variable. For two-step System GMM, we put Old-Age Dependency Ratio as Instrument, but put lagged Dependent Variable as Endogeneous with collapse option. The p-value of Auto-Correlation 1st and 2nd order, including Hansen's post-Estimation Tests are presented at the bottom Panel. The p-values are presented in parentheses and+p < 0.10, *p < 0.05, **p < 0.01, ***p < 0.001.
Source: Author's calculation.
Table 9.
The Effects of Old-Age Populations on Each Compositional Government Spending (as Percentage of Total Expenditure) Using Two-step System GMM with Percentage of Old-Age Population as A Proxy for Old-Age Populations.
| Variable | (Public Admin) | (Defense) | (Order) | (Economic) | (Environ ment) | (Housing) | (Culture) | (Health) | (Education) | (Social Protection) |
|---|---|---|---|---|---|---|---|---|---|---|
| Percentage Old Pop, ln | −0.0248*** | −0.000603 | −0.00366* | 0.00734+ | 0.00186*** | −0.0118*** | 0.00285*** | 0.00380+ | −0.00630* | 0.0296*** |
| (0.000) | (0.686) | (0.030) | (0.078) | (0.000) | (0.000) | (0.000) | (0.100) | (0.020) | (0.000) | |
| GDP per capita, ln | 0.0243*** | −0.00286* | −0.00190 | −0.0202*** | −0.000520 | 0.00281* | 0.000101 | 0.00617*** | −0.00459+ | 0.0262*** |
| (0.000) | (0.046) | (0.135) | (0.000) | (0.124) | (0.027) | (0.849) | (0.000) | (0.062) | (0.000) | |
| Trade to GDP | −0.00813 | −0.00274+ | 0.00270+ | 0.0138*** | 0.00162*** | 0.00256+ | 0.00451*** | 0.00270 | 0.00648** | −0.00293 |
| (0.301) | (0.080) | (0.064) | (0.000) | (0.000) | (0.084) | (0.000) | (0.209) | (0.001) | (0.578) | |
| Control of corruption | −0.0434*** | 0.000790 | −0.00211+ | 0.0162*** | 0.000422 | −0.000193 | 0.000456 | −0.000244 | 0.00761*** | −0.0185*** |
| (0.000) | (0.646) | (0.064) | (0.001) | (0.128) | (0.884) | (0.398) | (0.878) | (0.000) | (0.000) | |
| Financial Openness | −0.0473*** | 0.00490** | −0.00220 | −0.00554 | 0.00195*** | −0.00144 | 0.00239* | 0.00467 | 0.00748+ | 0.0174+ |
| (0.000) | (0.009) | (0.268) | (0.384) | (0.001) | (0.484) | (0.034) | (0.120) | (0.062) | (0.051) | |
| Democracy_dummy | 0.0161+ | −0.0115*** | 0.00141 | −0.0184*** | 0.000317 | −0.00118 | −0.00296*** | 0.00639** | 0.00387 | 0.00318 |
| (0.062) | (0.000) | (0.327) | (0.001) | (0.330) | (0.559) | (0.000) | (0.008) | (0.161) | (0.520) | |
| L.pub_exp | 0.614*** | |||||||||
| (0.000) | ||||||||||
| L.def_exp | 0.795*** | |||||||||
| (0.000) | ||||||||||
| L.order_exp | 0.621*** | |||||||||
| (0.000) | ||||||||||
| L.econ_exp | 0.545*** | |||||||||
| (0.000) | ||||||||||
| L.envi_exp | 0.643*** | |||||||||
| (0.000) | ||||||||||
| L.housing_exp | 0.332*** | |||||||||
| (0.000) | ||||||||||
| L.cult_exp | 0.514*** | |||||||||
| (0.000) | ||||||||||
| L.health_exp | 0.638*** | |||||||||
| (0.000) | ||||||||||
| L.edu_exp | 0.728*** | |||||||||
| (0.000) | ||||||||||
| L.socpro_exp | 0.646*** | |||||||||
| (0.000) | ||||||||||
| Constant | 0.138** | 0.0515*** | 0.0442*** | 0.127*** | −0.00637** | 0.00567 | −0.0203*** | −0.0504*** | 0.0219+ | −0.161*** |
| (0.002) | (0.000) | (0.000) | (0.000) | (0.002) | (0.539) | (0.000) | (0.000) | (0.077) | (0.000) | |
| N. Obs. | 1489 | 1489 | 1489 | 1489 | 1489 | 1489 | 1489 | 1489 | 1489 | 1489 |
| AR (1) p-value | 0.0000804 | 0.000858 | 0.000339 | 0.0000901 | 0.0139 | 0.0187 | 0.000141 | 0.0107 | 0.000208 | 0.00216 |
| AR (2) p-value | 0.102 | 0.166 | 0.0755 | 0.0780 | 0.358 | 0.400 | 0.426 | 0.187 | 0.0721 | 0.143 |
| Hansen p-value | 0.00785 | 0.411 | 0.0917 | 0.114 | 0.216 | 0.484 | 0.332 | 0.120 | 0.537 | 0.408 |
Note: This table estimates the Effects of Old-Age Populations on each Compositional Government Spending using two-step System GMM. The Ratio of each Compositional Government Spending to Total Expenditure are Dependent Variables. The Percentage of Old-Age Population is the main Independent Variable. For two-step System GMM, we let the Percentage of Old-Age Population as Instrument, but put lagged Dependent Variable as Endogeneous with collapse option. The p-value of Auto-Correlation 1st and 2nd order, including Hansen's post-Estimation Tests are presented at the bottom Panel. The p-values are presented in parentheses and +p < 0.10, *p < 0.05, **p < 0.01, ***p < 0.001.
Source: Author's calculation.
Table 10.
The Effects of Old-Age Populations on Each Compositional Government Spending (as Percentage of GDP) Using Two-step System GMM with Percentage of Old-Age Population as A Proxy for Old-Age Populations.
| Variable | (Public Admin) | (Defense) | (Order) | (Economic) | (Environ ment) | (Housing) | (Culture) | (Health) | (Education) | (Social Protection) |
|---|---|---|---|---|---|---|---|---|---|---|
| Percentage Old Pop, ln | −0.759** | 0.0222 | −0.0596* | −0.103 | 0.0477** | −0.281*** | 0.0360+ | 0.0100 | −0.0750* | 1.516*** |
| (0.001) | (0.333) | (0.035) | (0.640) | (0.004) | (0.000) | (0.073) | (0.867) | (0.035) | (0.000) | |
| GDP per capita | 1.410*** | −0.0687** | 0.0599** | 0.425+ | 0.0326* | 0.102* | 0.0672*** | 0.147* | 0.0827+ | 1.318*** |
| (0.000) | (0.002) | (0.008) | (0.057) | (0.026) | (0.026) | (0.000) | (0.016) | (0.072) | (0.000) | |
| Trade to GDP | −0.416 | −0.0342+ | 0.104* | 0.708*** | 0.0585*** | 0.164*** | 0.136*** | −0.0125 | 0.0640* | −0.0948 |
| (0.146) | (0.088) | (0.015) | (0.000) | (0.001) | (0.001) | (0.000) | (0.788) | (0.036) | (0.745) | |
| Control of corruption | −1.756*** | 0.0656** | −0.118*** | −0.320 | −0.0181 | 0.0821 | 0.0123 | −0.0379 | −0.00637 | −1.181*** |
| (0.000) | (0.003) | (0.000) | (0.297) | (0.207) | (0.131) | (0.431) | (0.442) | (0.882) | (0.000) | |
| Financial Openness | −1.754*** | 0.172*** | −0.0137 | −0.589+ | 0.0475* | −0.137+ | 0.0381 | 0.0436 | 0.0398 | 1.362** |
| (0.001) | (0.000) | (0.701) | (0.084) | (0.030) | (0.092) | (0.301) | (0.557) | (0.485) | (0.003) | |
| Democracy_dummy | 1.081*** | −0.146*** | 0.0823* | 0.125 | 0.0429** | −0.0934 | −0.0433 | 0.0963+ | 0.165*** | 0.419 |
| (0.000) | (0.000) | (0.033) | (0.595) | (0.007) | (0.133) | (0.115) | (0.077) | (0.001) | (0.206) | |
| L.exp_pub_ gdp | 0.516*** | |||||||||
| (0.000) | ||||||||||
| L.exp_def_gdp | 0.888*** | |||||||||
| (0.000) | ||||||||||
| L.exp_order_gdp | 0.717*** | |||||||||
| (0.000) | ||||||||||
| L.exp_econ_gdp | 0.307*** | |||||||||
| (0.000) | ||||||||||
| L.exp_envi_gdp | 0.627*** | |||||||||
| (0.000) | ||||||||||
| L.exp_housing_gdp | 0.243*** | |||||||||
| (0.000) | ||||||||||
| L.exp_cult_gdp | 0.575*** | |||||||||
| (0.000) | ||||||||||
| L.exp_health_gdp | 0.902*** | |||||||||
| (0.000) | ||||||||||
| L.exp_edu_gdp | 0.870*** | |||||||||
| (0.000) | ||||||||||
| L.exp_socpro_gdp | 0.573*** | |||||||||
| (0.000) | ||||||||||
| Constant | 0.729 | 0.643*** | −0.0222 | −2.624* | −0.548*** | −0.729** | −1.073*** | −0.946* | −0.532* | −8.567*** |
| (0.666) | (0.000) | (0.904) | (0.011) | (0.000) | (0.010) | (0.000) | (0.032) | (0.016) | (0.000) | |
| N. Obs. | 1382 | 1344 | 1382 | 1407 | 1130 | 1380 | 1310 | 1409 | 1408 | 1354 |
| AR (1) p-value | 0.0136 | 0.0156 | 0.0392 | 0.00214 | 0.000508 | 0.0186 | 0.0132 | 0.00330 | 0.00000124 | 0.140 |
| AR (2) p-value | 0.0224 | 0.783 | 0.364 | 0.0403 | 0.804 | 0.302 | 0.337 | 0.445 | 0.782 | 0.295 |
| Hansen p-value | 0.148 | 0.313 | 0.175 | 0.194 | 0.398 | 0.395 | 0.390 | 0.293 | 0.132 | 0.0921 |
Note: This table estimates the Effects of Old-Age Populations on each Compositional Government Spending using two-step System GMM. The Ratio of each Compositional Government Spending to GDP are Dependent Variables. The Percentage of Old-Age Population is the main Independent Variable. For two-step System GMM, we let the Percentage of Old-Age Population as Instrument, but put lagged Dependent Variable as Endogeneous with collapse option. The p-value of Auto-Correlation 1st and 2nd order, including Hansen's post-Estimation Tests are presented at the bottom Panel. The p-values are presented in parentheses and +p < 0.10, *p < 0.05, **p < 0.01, ***p < 0.001.
Source: Author's calculation.
References
- 1.United Nations, Department of Economic and Social Affairs, Population Division . Department of Economic and Social Affairs, Population Division; 2020. World Fertility and Family Planning 2020: Highlights United Nations. 2020. [Google Scholar]
- 2.United Nations, Department of Economic and Social A airs, Population Division . 2017. World Population Prospects: the 2017 Revision, Methodology of the United Nations Population Estimates and Projections. Working Paper No. ESA/P/WP.250. [Google Scholar]
- 3.Maestas N., Mullen K.J., Powell D. The effect of population aging on economic growth, the labor force, and productivity. Am. Econ. J. Macroecon. 2023;15(2):306–332. [Google Scholar]
- 4.Mason A., Lee R., NTA Network Six ways population change will affect the global economy. Popul. Dev. Rev. 2022;48(1):51–73. [Google Scholar]
- 5.Morita H. On the relationship between fiscal multipliers and population aging in Japan: theory and empirics. Econ. Modell. 2022;108 [Google Scholar]
- 6.Yoshino N., Miyamoto H. Declined effectiveness of fiscal and monetary policies faced with aging population in Japan. Jpn. World Econ. 2017;42:32–44. [Google Scholar]
- 7.Yoshino N., Kim C.J., Sirivunnabood P. Aging population and its impacts on fiscal sustainability. Aging SocietieS. 2019 [Google Scholar]
- 8.Barbosa Filho F.D.H., Turra C.M., Franco Neto A.A.D.M. 2020. Brazil's Demographic Transition and its Effects on Public Spending. [Google Scholar]
- 9.Rouzet D., Sánchez A.C., Renault T., Roehn O. 2019. Fiscal Challenges and Inclusive Growth in Ageing Societies. [Google Scholar]
- 10.Dieleman J.L., Cao J., Chapin A., Chen C., Li Z., Liu A.…Murray C.J. US health care spending by payer and health condition, 1996-2016. JAMA. 2020;323(9):863–884. doi: 10.1001/jama.2020.0734. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Barro R.J. Government spending in a simple model of endogenous growth. J. Polit. Econ. 1990;98(5, Part 2):S103–S125. [Google Scholar]
- 12.Christie T. The effect of government spending on economic growth: testing the non‐linear hypothesis. Bull. Econ. Res. 2014;66(2):183–204. [Google Scholar]
- 13.Lin S.A. Government spending and economic growth. Appl. Econ. 1994;26(1):83–94. [Google Scholar]
- 14.Plümper T., Martin C.W. Democracy, government spending, and economic growth: a political-economic explanation of the Barro-effect. Publ. Choice. 2003;117(1–2):27–50. [Google Scholar]
- 15.Hou C., Ma Y., Yang X., Tao L., Zheng D., Liu X.…Guo X. Disability transitions and health expectancies among elderly people aged 65 years and over in China: a Nationwide Longitudinal Study. Aging Dis. 2019;10(6):1246. doi: 10.14336/AD.2019.0121. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Temsumrit N. Population aging, pension systems, and economic growth: applying an overlapping generations model to the informal sector. Asian Development Review. 2023 forthcoming. [Google Scholar]
- 17.Cervellati M., Sunde U. Human capital formation, life expectancy, and the process of development. Am. Econ. Rev. 2005;95(5):1653–1672. doi: 10.1257/000282805775014380. [DOI] [PubMed] [Google Scholar]
- 18.Cipriani G.P., Makris M. A model with self-fulfilling prophecies of longevity. Econ. Lett. 2006;91(1):122–126. [Google Scholar]
- 19.Gonzalez-Eiras M., Niepelt D. Ageing, government budgets, retirement, and growth. Eur. Econ. Rev. 2012;56(1):97–115. [Google Scholar]
- 20.Sanz I., Velázquez F.J. The role of ageing in the growth of government and social welfare spending in the OECD. Eur. J. Polit. Econ. 2007;23(4):917–931. [Google Scholar]
- 21.Scully G.W. Government expenditure and quality of life. Publ. Choice. 2001;108(1- 2):123–145. [Google Scholar]
- 22.Shelton C.A. The size and composition of government expenditure. J. Publ. Econ. 2007;91(11–12):2230–2260. [Google Scholar]
- 23.Goh S.K., McNown R., et al. Macroeconomic implications of population aging: evidence from Japan. J. Asian Econ. 2020 [Google Scholar]
- 24.Bloom D.E., Canning D., Sevilla J. National Bureau of Economic Research; 2001. Economic Growth and the Demographic Transition (No. w8685) [Google Scholar]
- 25.Bloom D.E., Canning D., Fink G. Implications of population ageing for economic growth. Oxf. Rev. Econ. Pol. 2010;26(4):583–612. [Google Scholar]
- 26.Hviding K., Mérette M. 1998. Macroeconomic Effects of Pension Reforms in the Context of Ageing Populations: Overlapping Generations Model Simulations for Seven OECD Countries. [Google Scholar]
- 27.Van Der Gaag N., de Beer J. From demographic dividend to demographic burden: the impact of population ageing on economic growth in Europe. Tijdschr. Econ. Soc. Geogr. 2015;106(1):94–109. [Google Scholar]
- 28.Oliver M. Population ageing and economic growth in Japan. International Journal of Sociology and Social Policy. 2015;35(11/12):841–-863. [Google Scholar]
- 29.Fougère M., Mérette M. Population ageing and economic growth in seven OECD countries. Econ. Modell. 1999;16(3):411–427. [Google Scholar]
- 30.Bloom D.E., Canning D., Sevilla J. National Bureau of Economic Research; 2001. The Effect of Health on Economic Growth: Theory and Evidence (No. w8587) [Google Scholar]
- 31.Ehrlich Isaac, Lui Francis T. Intergenerational trade, longevity, and economic growth. J. Polit. Econ. 1991;99:1029–1059. [Google Scholar]
- 32.Thiébaut S.P., Barnay T., Ventelou B. Ageing, chronic conditions and the evolution of future drugs expenditure: a five-year micro-simulation from 2004 to 2029. Appl. Econ. 2013;45(13):1663–1672. [Google Scholar]
- 33.Imam P. Demographic shift and the financial sector stability: the case of Japan. J. Popul. Ageing. 2013;6(4):269–303. [Google Scholar]
- 34.Nagarajan N.R., Teixeira A.A., Silva S.T. The impact of an ageing population on economic growth: an exploratory review of the main mechanisms. Análise Soc. 2016:4–35. [Google Scholar]
- 35.Barro R.J. Economic growth in a cross section of countries. Q. J. Econ. 1991;106(2):407–443. [Google Scholar]
- 36.Gwartney J.D., Lawson R., Holcombe R.G. Joint Economic Committee Washington; 1998. The Size and Functions of Government and Economic Growth. [Google Scholar]
- 37.Kneller R., Bleaney M.F., Gemmell N. Fiscal policy and growth:evidence from OECD countries. J. Publ. Econ. 1999;74(2):171–190. [Google Scholar]
- 38.Ormaechea M.S.A., Morozumi A. International Monetary Fund; 2013. Can a Government Enhance Long-Run Growth by Changing the Composition of Public Expenditure? Number 13-162. [Google Scholar]
- 39.Chinn M.D., Ito H. A new measure of financial openness. J. Comp. Pol. Anal. 2008;10(3):309–322. [Google Scholar]
- 40.Temsumrit N. Democracy, institutional quality and fiscal policy cycle: evidence from developing countries. Appl. Econ. 2022;54(1):75–98. [Google Scholar]
- 41.Holtz-Eakin D., Newey W., Rosen H.S. Estimating vector autoregressions with panel data. Econometrica: J. Econom. Soc. 1988:1371–1395. [Google Scholar]
- 42.Arellano M., Bond S. Some tests of specification for panel data: Monte Carlo evidence and an application to employment equations. Rev. Econ. Stud. 1991;58(2):277–297. [Google Scholar]
- 43.Arellano M., Bover O. Another look at the instrumental variable estimation of error-components models. J. Econom. 1995;68(1):29–51. [Google Scholar]
- 44.Blundell R., Bond S. Initial conditions and moment restrictions in dynamic panel data models. J. Econom. 1998;87(1):115–143. [Google Scholar]
- 45.Aksoy Y., Basso H.S., Smith R.P., Grasl T. Demographic structure and macroeconomic trends. Am. Econ. J. Macroecon. 2019;11(1):193–222. [Google Scholar]
- 46.Bodnár K., Nerlich C. 2022. The Macroeconomic and Fiscal Impact of Population Ageing (No. 296) ECB Occasional Paper. [Google Scholar]
- 47.Crowe D., Haas J., Millot V., Rawdanowicz Ł., Turban S. 2022. Population Ageing and Government Revenue: Expected Trends and Policy Considerations to Boost Revenue. [Google Scholar]
- 48.Sheiner L. Edward Elgar Publishing; 2021. The long-term impact of aging on the federal budget; pp. 93–117. (Fiscal Accountability and Population Aging). [Google Scholar]
- 49.Knodel J., Chayovan N. Inter‐generational family care for and by older people in Thailand. Int. J. Sociol. Soc. Pol. 2012;32(11/12):682–694. [Google Scholar]
- 50.Schröder-Butterfill E. Inter-generational family support provided by older people in Indonesia. Ageing Soc. 2004;24(4):497–530. doi: 10.1017/S0144686X0400234X. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Xu Y. Family support for old people in rural China. Soc. Pol. Adm. 2001;35(3):307–320. [Google Scholar]
- 52.Bosch-Farré C., Garre-Olmo J., Bonmatí-Tomàs A., Malagón-Aguilera M.C., Gelabert-Vilella S., Fuentes-Pumarola C., Juvinyà-Canal D. Prevalence and related factors of active and healthy ageing in Europe according to two models: results from the Survey of Health, Ageing and Retirement in Europe (SHARE) PLoS One. 2018;13(10) doi: 10.1371/journal.pone.0206353. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Korwatanasakul U., Sirivunnabood P., Majoe A. 2021. Demographic Transition and its Impacts on Fiscal Sustainability in East and Southeast Asia. [Google Scholar]
- 54.Miller T., Castanheira H.C. The fiscal impact of population aging in Brazil: 2005-2050. Rev. Bras. Estud. Popul. 2013;30:S5–S23. [Google Scholar]
- 55.Žokalj M. The impact of population aging on public finance in the European Union. Financ. Theor. Pract. 2016;40(4):383–412. [Google Scholar]
- 56.Busemeyer M.R., Goerres A., Weschle S. Attitudes towards redistributive spending in an era of demographic ageing: the rival pressures from age and income in 14 OECD countries. J. Eur. Soc. Pol. 2009;19(3):195–212. [Google Scholar]
- 57.Umeda M. The politics of aging: age difference in welfare issue Salience in Japan 1972–2016. Polit. Behav. 2020:1–23. [Google Scholar]
- 58.Zubielevitch E., Osborne D., Milojev P., Sibley C.G. Social dominance orientation and right-wing authoritarianism across the adult lifespan: an examination of aging and cohort effects. J. Pers. Soc. Psychol. 2022 doi: 10.1037/pspi0000400. Advance online publication. [DOI] [PubMed] [Google Scholar]
- 59.Altemeyer B. Univ. of Manitoba Press; 1983. Right-wing Authoritarianism. [Google Scholar]
- 60.Sidanius J., Pratto F. Cambridge University Press; 2001. Social Dominance: an Intergroup Theory of Social Hierarchy and Oppression. [Google Scholar]
- 61.Stanley S.K., Milfont T.L., Wilson M.S., Sibley C.G. The influence of social dominance orientation and right-wing authoritarianism on environmentalism: a five-year cross-lagged analysis. PLoS One. 2019;14(7) doi: 10.1371/journal.pone.0219067. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Kuehnel J. 2011. A Shift of Public Spending toward Spending on the Aging Population Hinders Economic Growth in Short-Term. [Google Scholar]
- 63.Becker G.S. Columbia University Press; 1960. An economic analysis of fertility; pp. 209–240. (Demographic and Economic Change in Developed Countries). [Google Scholar]
- 64.Becker G.S., Lewis H.G. On the interaction between the quantity and quality of children. J. Polit. Econ. 1973;81(2, Part 2):S279–S288. [Google Scholar]
- 65.Becker G.S., Murphy K.M., Tamura R. Human capital, fertility, and economic growth. J. Polit. Econ. 1990;98(5, Part 2):S12–S37. [Google Scholar]
- 66.Im K.S., Pesaran M.H., Shin Y. Testing for unit roots in heterogeneous panels. J. Econom. 2003;115(1):53–74. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
Data will be made available on request.