Abstract
Combined Cycle Power Plants (CCPP) are an effective method for Power generation due to their high thermal efficiency, low fuel consumption, and low greenhouse emissions. However, investing millions into building a power plant without knowledge of the power generation capacity seems unproductive. With the help of AI, we have tried to eliminate this conundrum. The present study focuses on the prediction of power produced by a 747 MW Combined Cycle Power Plant (CCPP) using a Back Propagation Neural Network (BPNN) and compares its results with the actual data from CCPP. BPNN is a regression-based prediction technique that is utilized in this study to develop a predictive model and train it using the following input features: Ambient Temperature, Ambient Pressure, Mass Flow rate of fuel in Gas Turbine 1, and Mass Flow rate of fuel in Gas Turbine 2. The Predictive Model with 10 neurons in the hidden layer was found to be most effective with Mean Squared Error (MSE) value, for the validation dataset, of 0.0063237. CCPP is also analyzed through a thermodynamic model, developed using EES. A detailed energy analysis is carried out and the results were compared with predicted and actual data. It was found that the thermal efficiency and total power generation of actual, predicted, and simulated models were 27.541% & 667.32 MW, 28.238% & 683.48 MW and 28.201% & 683.16 MW, respectively. A parametric study was further carried out to investigate the significance of operating parameters on power output and it was concluded that the temperatures across the Gas turbines have a significant impact on the performance of CCPP. Finally, Methane was replaced by 3 different fuels, one by one, and the effect of each fuel was investigated thermodynamically. It was found that the Lower Heating Value (LHV) of fuel was an important parameter in achieving a higher power output. It can be summarized from this research work that predictive models do have accuracy and such data science techniques can be used as a substitute for extensive thermodynamic calculations.
Keywords: Combined cycle power plant, Back propagation neural network, EES, Mean squared error, HRSG, Fuel, LHV
1. Introduction
As of February 2023, there are 188 power plants operating in Pakistan including 45 operated by Independent Power Producers (IPPs) [1]. The current electricity supply from these power plants stands at 21,200 MW [2] whereas the demand has exceeded 28,000 MW [3]. To address the shortfall of above 8000 MW, as of June 2023, the Pakistani government is seeking investment, as part of CPEC, for building new power plants [4]. The government of Pakistan (GoP) has undertaken small, medium, and long-term term initiatives to provide cheap, sustainable and continuous supply of electricity to consumers. These measures are part of Integrated Energy Plan (IEP) which will provide estimates of growth of production requirement and consumption of electricity till 2047.
Over the past few years, the GoP has been providing annual subsidies to energy sector [5] to provide relief to consumers as well as producers but this is not feasible in long term and so the need to establish self-sustaining and economically viable power generating project has become important for stakeholders due to uncertain economic condition of Pakistan. If investors could have the prior knowledge of the power output capacity, efficiency as well as economic viability of a project, they could make an informed decision about going through with the project. Prediction of the electrical power output and its related efficiency has been an area of concern for researchers recently to alleviate similar concerns. Artificial intelligence has the capacity to analyse huge data and provide useful insight about data [6] which may not be possible for human to assess via conventional means. This is evident from the increase in resource and energy efficiency within Chinese firms [7]. With Artificial Intelligence and Machine Learning techniques being frequently used nowadays, many researchers are also employing these techniques to make accurate predictions regarding power output in various trades and industries, in order to make their system economical and reliable.
The Algorithms for each machine learning models varies from one another and will lead to varying predictive efficiency so it becomes essential to identify which ML model to implement. A. Abdul Rasheed compared Deep learning with Random Forest, Gradient Boosting and Multi-layer perceptron by means of the two leading statistical measured called Root Mean Squared error (RMSE) and Mean Absolute error (MAE) and found that Deep learning method reduced the error rates by 35% for MAE and 48% for RMSE as compared to other techniques [8]. Bistline and Merrick worked on creating an open-source capacity planning model for a power plant. The motivation behind this step was to provide enough information to stakeholders to calculate investment, expected profits, retirement age of the plant and environmental issues associated with it. Since input data would vary for plant to plant and region to region, they realized that quality of data acquired from emerging markets lacked credibility and/or was in accurate. To overcome similar problem for regions where authentic data was unavailable, Bistline and Merrick used two statistical approaches namely, Linear regression and k-nearest-neighbour approach, to calculate unknown parameters for a known market (USA, in this case) and applying the learned functions onto the unknown region (Canada, in this case) to calculate the power plant parameters. They deduced that k-nearest-neighbour technique outperforms linear regression technique in accurate prediction of plant unknown data [9].
Hundi and Shahsavari came up with a solution to predict the power generation of a CCPP without using the thermodynamic or physics-based relationships. They used support vector machines, random forest regression, linear regression and Multi-Layer Perceptron (MLP) to come up with a power predictive model. The variables used as input in their study were humidity of the air, exhaust vacuum pressure, atmospheric pressure of the area and ambient temperature of the air. They collected recorded data of five years and used 75% of it to train their machine learning models and the remaining for testing. Their results showed random forests technique to be most accurate with R2, MAE and RMSE of 95.9%, 2.4 MW and 3.5 MW, respectively [10]. Hydro-power are known to provide cheap electricity and they account for almost 60% of all renewable energy available worldwide so it becomes essential to be able predict the hydro-power production capacity in a geographical location. Condemi et al. used different models to make accurate hydro-power capacity prediction for a real location in Northern Italy by using meteorological, climatic variables as well as volume of available water in the reservoir as input variables. A combination of different ANN algorithms namely: MLP, ELP and SVR were used by them in addition to Gaussian kernels, Polynomial and Linear. Principal Component Analysis (PCA), which is a feature reduction technique, was also implemented to try to reduce redundant input data. Their results showed that MLP outperforms all other techniques with RMSE and MAE of 0.2593 and 0.2128 TWh, respectively [11].
Ahmer Ali et al. came up with a power prediction model to predict the power generated by a Waste Heat Recovery (WHR) system deployed at a cement plant in Pakistan. They devised a Regression based predictive model using Feed Forward Back-Propagation neural network (FF-BPNN). The system was trained using steam pressure at turbine inlet, turbine inlet steam temperature, high pressure stage mass flowrate of steam as well as low pressure stage mass flowrate of steam. Simultaneously, a thermodynamic analysis was also carried out of the WHR system via Engineering Equation solver (EES) to calculate the power output analytically. It was calculated that the WHR system had a thermal efficiency of 19.75% and produced 10.06 MW of power. Similarly, the BPNN model was able to predict the output power accurately with a mean squared error of 0.283 while using 10 neurons in the hidden layers [12]. Pinar Tufekci carried out a study in which she presented an alternate solution to thermodynamic modelling for calculating the electric power output of a CCPP operating at full load. She used 4 input parameters namely: relative humidity of air, ambient temperature of air, exhaust pressure of steam and atmospheric pressure to predict the target variable i.e. electric power output. The data set used for this study took six years to be collected and the analysis was performed using 15 different machine learning regression methods to find the best algorithm with highest prediction accuracy. It was found that Bagging Rep Tree (BREP) method, which is a Meta-learning algorithm was the most accurate, among all regression methods, with a Root Mean-Squared Error (RMSE) and Mean Absolute Error (MAE) of 3.787 and 2.818, respectively [13].
M. Rashid et al. used PSO as the learning algorithm to train a FFNN for predicting the average hourly Power Output of a CCPP. The input variables utilized for the study were surrounding ambient temperature, atmospheric pressure of air, relative humidity and vacuum. Their model was trained with 10 hidden neurons for 50 iterations and the resulting Mean-Squared Error (MSE) for training and testing data was found to be 0.0001019 and 0.0055, respectively [14]. Derrick Adams et al. developed a machine learning model that used a deep learning algorithm along with least squared Support Vector Machine (SVM) in order to predict the Sulphur Oxides (SOx) and Nitrogen Oxides (NOx) emissions from the burning of Coal in a Power Plant. The commercially available data, provided by KEPCO, was used in this study for training and testing purposes and it was found that Deep Neural Network (DNN) model improved the accuracy of prediction of SOx and NOx by 39.24% and 26.58%, respectively while Least Square Support Vector Machine (LSSMV) model further increased the accuracy of prediction of SOx and NOx by 74.01% and 26.51%, respectively [15]. Bayram Akdemir also developed a Multi-layer Perceptron (MLP) model comprising of Artificial Neural Network (ANN) for prediction of Hourly Electric Power generation of a CCPP. His data included 4 variables and 9685 features whereas he used a two-fold cross validation technique for reliability of the application of MLP on his data. His predicted results had a MSE of 3.176 and R2 value of 0.96675 [16].
Many researchers have opted for many different methodologies in order to test the feasibility and effectiveness of CCPP. Ahmad et al. developed an analytical model to test the feasibility of a CCPP combined with a PV system and Inlet Air Cooling (IAC) system to tackle the harsh ambient conditions of Jordanian weather. Inlet air was cooled using mechanical chillers, which were driven by power from Steam Turbines. PV system was installed to generate excess steam for Steam Turbine to supplement for the power used by chillers. Authors used Engineering Equation Solver (EES) to solve the system and found that the fuel consumption of the system reduced by 8.4% while the power output and efficiency increased by 22.8% and 4.3%, respectively [17]. Similarly, Wang et al. used Ebsilon Software to compare the numerical results of their model with experimental data. Their proposed model consisted of a CCPP customized with Inlet Air Heating (IAH) system to overcome extreme winter weather. The air was heated using energy from HRSG before being supplied to compressor of GT. This resulted in drop of fuel consumption by 0.02 kg/s and 0.03 kg/s for 60% and 80% power load, respectively [18]. Gomez et al. proposed a CCPP model with Helium GT, which used the cold exergy of Liquefied Natural Gas (LNG) to reduce the temperature of Helium in compressor to cryogenic level. This system was modelled using EES and it was reported that the maximum efficiency attained was 56.72% [19].
Sabia et al. discussed the energy utilization during the shutdown and hot start-up phase of a CCPP. Three different pressures levels were selected for HRSG of CCPP and the experiment was simulated using ASPEN Plus Dynamic for comparison of actual plant data with simulated results. It was noted that ASPEN Plus Dynamic can perform accurately and provide close to actual results. The Best and Worst deviation of simulated results from actual was found to be 3.62% and 10.8%, respectively [20]. Abrosimov et al. evaluated the performance of High Temperature HRSG in Inverted Brayton Cycle coupled with Organic Rankine Cycle. The system was tested at three different ambient conditions using ASPEN HYSES software. It was found that the efficiency of the system decreased to 10.3% from 14.6% as the ambient temperatures increased from 5 °C to 35 °C [21]. Zuming Liu and I. A. Karimi compared a triple pressure reheat CCPP on two different platforms namely, ASPEN HYSES and GateCycle. The objective of the research was to distinguish the accuracies of both simulation software at part load 40%–100%. They found that the values deviated below 2% for all parameters. However, authors preferred ASPEN HYSES over GateCycle due to its ease of integration with variety of energy systems and ability to be dynamically for predicting real time CCPP values [22].
Jatin Sachdeva and Onkar Singh created a carbon free, 3-stage combined cycle power plant powered by solar. This mechanism consisted of Brayton cycle, Rankine Cycle and Organic Rankine Cycle with each consuming air, steam and R245fa, respectively. The cycle produces power at the rate of 333 kW per kg of topping cycle air at the thermal efficiency of 33.15% [23]. Divya Prakash and Onkar Singh also worked on another Carbon free CCPP by capturing the CO2 from flue gases and using it in to extract methane. This methane would further be used as fuel in another GT to generate additional power and hence reducing Carbon footprint. It was found that power output increased from 229.6 MW to 384.738 MW [24]. Dan-Teodor Balanescu and Vlad-Mario Homutescu also wanted to reduce the heat lost in flue gases from CCPP and so came up with a system of Brayton-Rankine-Organic Combine Cycle power plant. The downstream Organic Rankine Cycle used R134a and R123 as working fluids and it resulted in an improvement of 1.1% in the efficiency of plant and on average, the annual fuel savings was estimated to be 56000 Nm3 of natural gas [25]. Aliyu et al. conducted a complete thermodynamic analysis of each component of a triple pressure combined cycle power plant. It was found that HP evaporator, HP super-heater of HRSG, Stack and Pre-heater were components that have the potential to significantly improve the overall performance of CCPP. Exergetic efficiency was highest for Steam Turbine and Lowest for Condenser with values of 92% and 63%, respectively [26].
Current research work related to power generating plants, within Pakistan, is focused purely on thermal/thermo-electrical modelling which involves complex calculations and requires frequent assumptions to be made. Such analytical models require time and effort to be set up and refined before they can be used. Moreover, only an expert in the related field can develop such model or have the ability to utilise the model to generate an output. The power plant, in question, in this article has been previously worked upon to develop a thermodynamic model [27] and it is evident from this work that thermal analysis is difficult and laborious work and requires prior knowledge to work on. Moreover, the literature review also highlighted that no electrical power predictive model, for a CCPP, have been worked upon within Pakistan. The motivation for working on this research was to eliminate the complex and laborious calculations and from an easy solution for calculating output power. The benefits of utilizing AI based techniques to develop a predictive model is that they could be worked upon by anyone having no prior knowledge of thermal analysis, can be trained with any number of inputs available, does not require complex model to be developed, is quick to provide output and eliminates the requirement of making assumptions for variables not available.
This article includes a thermodynamic analysis of a Combined Cycle Power Plant situated in Kashmore, Sindh called “GENCO II, TPS Guddu”. The thermodynamic analysis is carried out using EES software and the results will be compared with the actual data obtained from TPS Guddu. Once, the EES model is validated, we will proceed towards the main objective of the article. A predictive model using a machine learning algorithm called “Back Propagation Neural Network” will be developed which requires a distinct number of inputs and outputs to train itself before it is ready to make any predictions. We will use Ambient Temperature, Ambient Pressure and Mass flow rate of fuel in both Gas Turbines as our input features to train the model for predicting our target value, which would be the total power output of the CCPP.
Once the predictive model is ready, it would be able to safely predict the power output of any day and any time by only using the 4 input features mentioned previously. This model would prove to be easy-to-use and could be applied by any non-technical person. The article would also present a relation between thermodynamic modelling via EES and machine learning techniques to compare the accuracy of both techniques.
1.1. System description
This article discusses the thermodynamic model and Power Generation prediction of an actual Combined Cycle Power Plant (CCPP). The plant consists of 2 Gas Turbine cycles producing 243 MW of electricity each, when running at full capacity. The exhaust flue gases from both these turbines, which are still at very high temperatures, are directed into Heat Recovery Steam Generator (HRSG), which acts as boiler in Rankine cycle, to produce steam. The Rankine Cycle produces 261 MW of electricity when running at full capacity and hence, the total capacity of the CCPP is 747 MW. Fig. 1 shows the flow diagram of complete stages within the mentioned CCPP.
Fig. 1.
Flow diagram of CCPP at Guddu.
1.2. Gas Turbine Cycle
Air, first enters the turbine at ambient temperature and pressure where it is pressurized up to 15 bar. The pressurized air then enters Combustion Chamber (CC) where it is mixed with fuel (Methane) to create an air-fuel mixture and combustion takes place. This air-fuel mixture then leaves the combustion chamber and enters the Gas turbine (GE PG9351- MS 9001 FA [28]), where it loses its pressure and temperature while generating power. The exhaust from this turbine is rerouted towards HRSG of Steam Cycle.
1.3. Steam Turbine Cycle
The Condenser, in Rankine Cycle, is maintained at 40 kPa. The water from Condenser first enters a Low Pressure (LP) Pump where it is pressurized up to 3400 kPa. The pressurized water then enters a LP Economiser where its temperature is risen but before it enters the LP Evaporator, the amount of water is divided into two unequal parts. One of these parts, enters the LP Evaporator followed by Superheater to convert into superheated steam. The remaining water enters an Intermediate Pressure (IP) Pump where it is pressurized up to 6000 kPa. The pressurized water then enters an IP Economiser where its temperature is risen but before it enters the IP Evaporator, the amount of water is further divided into two unequal parts. One of these parts enters the IP Evaporator followed by Superheater to convert into superheated steam. Finally, the remaining water enters a High Pressure (HP) Pump where it is pressurized up to 15500 kPa. The pressurized water then enters an HP Economiser followed by HP Evaporator and HP Super Heater to convert into superheated steam. This steam enters the HP turbine to generate power. HP turbine exhaust mixes with the superheated steam formed in IP superheater. It is then reheated in the reheater to raise its temperature before this mixture enters IP turbine to generate power. The exhaust from IP turbine and the superheated steam formed in LP superheater enters the LP turbine to generate power. The exhaust from LP turbine enters the condenser where it loses its heat, gets converted into water and the cycle is repeated.
It should be noted that Economiser, Evaporator, Superheater and Reheater are all part components that exists within HRSG. Fig. 2 shows the TS diagram of the CCPP under discussion.
Fig. 2.
TS diagram of CCPP at Guddu.
1.4. Analysis
Thermodynamic analysis of CCPP was carried out by using the governing equations of Steam Turbine and Gas Turbine Cycle considering Air as Real Gas. A thermodynamic model was formulated using EES software for complete analysis.
Following assumptions were made regarding the CCPP before an EES model was formulated. The assumptions were taken into consideration due to lack of available data.
-
1.
No pressure loss across Combustion Chamber in Gas Turbine Cycle (GTC).
-
2.
Air fuel ratio is equal to 24 as provided by manufacturer, in GE Turbine manual, for the given Gas Turbine [29].
-
3.
Pressure ratio across Gas Turbine is 15.3 [30].
-
4.
Compressor efficiency is equal to 95%.
-
5.
Flue gases exit temperature from Gas Turbine is 881K [30].
-
6.
Gas Turbine efficiency is 37% [31].
-
7.
Heat Recovery Steam Generator Efficiency is 85% [32].
-
8.
Efficiency of Low Pressure, Intermediate Pressure and High-Pressure Turbine, in Rankine Cycle of 84%, 94% and 88%, respectively.
-
9.
Efficiency of Low Pressure, Intermediate Pressure and High-Pressure Pump, in Rankine Cycle of 90%, each.
-
10.
Exhaust from Low Pressure Turbine, in Rankine Cycle, exits as Saturated Liquid.
-
11.
Stack Temperature is 323K.
Enthalpy at Compressor outlet () is calculated using equation (1) as mentioned below.
| (1) |
where is isentropic enthalpy at compressor exit, is enthalpy at compressor inlet and is efficiency of compressor.
Energy provided by fuel () during combustion is calculated using equation (2) as mentioned below.
| (2) |
where Lower Heating Value of the fuel is termed as LHV.
Enthalpy at Combustion Chamber outlet Enthalpy () was calculated using equation (3) as mentioned below.
| (3) |
Power consumed by Compressor is calculated using equation (4) as shown below.
| (4) |
Power generated by Turbine is calculated using equation (5) as shown below.
| (5) |
Net power produced by GTC is calculated using equation (6) as shown below.
| (6) |
Thermal Efficiency of GTC () is calculated using equation (7) as shown below.
| (7) |
Work done by Low Pressure Pump () is calculated using equation (8) as mentioned below.
| (8) |
where is the specific volume, and are pressures at inlet and outlet of Low-Pressure Pump and is the efficiency of Low-Pressure Pump.
Enthalpy at Low Pressure Pump exit () is calculated using equation (9) as mentioned below.
| (9) |
Enthalpy at Low Pressure Turbine inlet () is calculated using equation (10) as mentioned below.
| (10) |
where is the Low-Pressure Turbine efficiency and and is the isentropic enthalpy and actual enthalpy at Low Pressure Turbine outlet, respectively.
Work done by Intermediate Pressure Pump () is calculated using equation (11) as mentioned below.
| (11) |
where is the specific volume, and are pressures at inlet and outlet of Intermediate Pressure Pump and is the efficiency of Intermediate Pressure Pump.
Enthalpy at Intermediate Pressure Pump exit () is calculated using equation (12) as mentioned below.
| (12) |
Enthalpy at Intermediate Pressure Turbine inlet () is calculated using equation (13) as mentioned below.
| (13) |
where is the Intermediate Pressure Turbine efficiency and and is the isentropic enthalpy and actual enthalpy at Intermediate Pressure Turbine outlet, respectively.
Work done by High Pressure Pump () is calculated using equation (14) as mentioned below.
| (14) |
where is the specific volume, and are pressure at inlet and outlet of High-Pressure Pump and is the efficiency of High-Pressure Pump.
Enthalpy at High Pressure Pump exit () is calculated using equation (15) as mentioned below.
| (15) |
Enthalpy at High Pressure Turbine inlet () is calculated using equation (16) as mentioned below.
| (16) |
where is the High-Pressure Turbine efficiency and and is the isentropic enthalpy and actual enthalpy at High Pressure Turbine outlet, respectively.
Total Power produced by Triple Pressure Rankine cycle turbines is calculated using equation (17) as mentioned below.
| (17) |
Total Power consumed by Triple Pressure Rankine cycle pumps is calculated using equation (18) as mentioned below.
| (18) |
Total Net Power produced by Triple Pressure Rankine cycle is calculated using equation (19) as mentioned below.
| (19) |
Thermal Efficiency of Rankine Cycle () is calculated using equation (20) as mentioned below.
| (20) |
Total Power Produced by CCPP is calculated using equation (21) as mentioned below.
| (21) |
where is the net power producted by Rankine Cycle, and is the net power produced by Gas Turbine Cycle 1 and 2, respectively.
Thermal Efficiency of CCPP () is calculated using equation (22) as mentioned below.
| (22) |
where and is the energy provided by fuel in Gas Turbine cycle 1 and 2, respectively.
1.5. Back Propagation Neural Network
Back propagation Neural Network is a Linear Regression algorithm type that is categorized under Supervised Learning. Back propagation is a gradient descent method of weights adjustments of the neural network to minimize the loss function through activation function and improve the prediction accuracy. Commonly used activation functions include Sigmoidal, tan-sigmoidal and threshold. Fig. 3 shows the architecture of the BPNN used in this article. The input parameters considered are: Ambient Temperature, Ambient Pressure, Fuel flow rate in Gas Turbine Cycle 1 and Fuel flow rate in Gas Turbine Cycle 2. Similarly, only one output is being considered i.e. Power generated by CCPP.
Fig. 3.
BPNN architecture used in this article.
An algorithm usually undergoes a 4-step process to train as BPNN. This includes.
-
1.
Assign initial weights
-
2.
Feed Forward operation using Gradient Descent
-
3.
Back Propagation of errors using Loss Function
-
4.
Weights and Biases updated accordingly
When BPNN is run initially, small values of weights are assigned in the Feed Forward stage which helps in predicting the output. A loss function (error) in produced by comparing this result to the desired output. This loss function then travels back into the neural network and based upon this, the biases and weights of the network are adjusted. This cycle continues until such weights are assigned which results in minimum loss function.
The layers shown in Fig. 3 are denoted as i for input layer, j for hidden layer and k for output layer. Input training vector is denoted as A where A = [a1, a2, …..an] while the Target vector (desired value) is denoted as B where B = [b1, b2, …..bn]. Input layer “i” and Hidden layer “j” are connected through weight Rij where “j” is the Hidden network layer and “k” is the Output network layer and these layers are joined through weight Sjk. We initiate the network by assigning a small random to both weights Rij and Sjk and so when an input signal a1 is received by input unit, it is transmitted to all hidden network layer units. Inside each hidden layer, the sum p is calculated using equation (23) as mentioned below.
| (23) |
Where the biases are denoted as c and c = [c1, c2, ….cn]. If the activation function of a neuron is 1, their weight is called Biases. In the hidden layer, Activation function of neuron is calculated using equation (24) as mentioned below.
| (24) |
The resulting signal from the activation function is forwarded to the output layer and calculated using equation (25) as mentioned below.
| (25) |
This resulting signal is multiplied by the Sjk (weight of hidden and output layer) using equation (26) and equation (27) as mentioned below.
| (26) |
| (27) |
When all output units in the output layer have received a signal from the input units via hidden layers, an error is generated using equation (28) as mentioned below.
| (28) |
where is output unit error. In Back propagation, the output unit error travels back into the architecture through hidden layers where similar error is calculated and based on the results, the adjustments to biases and weights occurs according to equation (29) and equation (30) as mentioned below.
| (29) |
where is the difference deduced when error was fed back into the architecture via hidden layers.
| (30) |
Where varies between 0 and 1 and is known as learning rate.
The error, calculated between the predicted and actual value, dictates the value of the weights which are fed back into the hidden layers in order to minimize the error. This cycle is repeated until a desired output value is achieved.
Following are the main steps for BPNN algorithm.
-
1.
Organize and divide data into training, testing and validation Data set and select a training pattern.
-
2.
Input parameters selection, number of neurons in hidden layer and number of neurons in output layer.
-
3.
Select an optimal learning rate .
-
4.
Select random weights , , bias (c) and minimum error () to prepare the network.
-
5.
Training initiated by providing input parameters which passes through layers (Hidden and Output) while calculate the loss function.
-
6.
Error dictates the value of the assigned weights in hidden and output layers, which are adapted to minimize error.
-
7.
If error < , then you are set, otherwise repeat 5 and 6.
equation (31), shown below, is used to calculate Mean Squared Error.
| (31) |
Where the architecture of the BPNN used in Power Prediction is shown in Fig. 4.
Fig. 4.
BPNN power prediction architecture.
The flowchart of the steps to carry out BPNN for Power Prediction is in Fig. 5.
Fig. 5.
Flow chart of the BPNN for Power Prediction.
1.6. Model validation
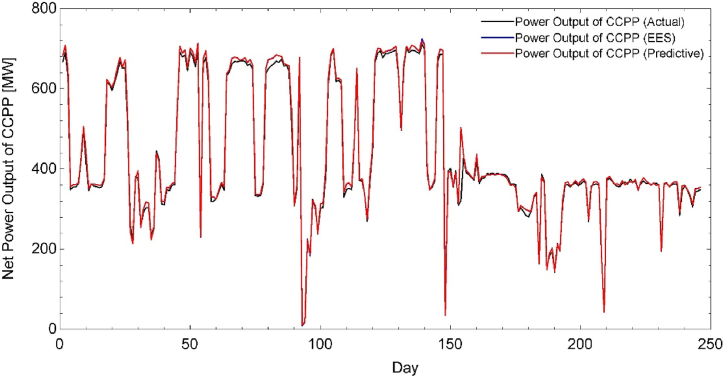
The model proposed in this study needs to be validated before we can proceed with discussion on the results obtained from this model. Fig. 6 shows a plot of Actual, Predictive and EES calculated Net Power Output of CCPP. The graph clearly shows an agreement among all 3 types of data and indicates that the predictive model is accurate. Similarly, the values obtained from thermodynamic model, developed in EES, also provides the values that are closer to the actual values, thereby confirming the accuracy of the model.
Fig. 6.
Comparison of actual, predicted and calculated power output of CCPP.
Furthermore, the efficiency of GT cycle, ST cycle and the overall efficiency of the CCPP was calculated by thermodynamic model in EES and compared against the actual and predicted efficiency and the results obtained are shown in Fig. 7. It is noted that actual and calculated efficiency of GT cycle 1 is 18.18% and 18.5%, respectively, which has a percentage error of 1.72%. The error is within acceptable range of 5% so it is safe to say that the predicted efficiency is accurate.
Fig. 7.
Comparison of actual, predicted and calculated efficiency of CCPP.
Similarly, the actual and calculated efficiency of Gas Turbine cycle 2 is 18.35% and 18.5%, respectively, which has a percentage error of 0.81%. The error is within acceptable range of 5% so it is safe to conclude that the Gas turbine 2 predicted efficiency is also accurate. The actual and calculated efficiency of Steam Turbine cycle is 14.67% and 15.34%, respectively, which has a percentage error of 4.36%. The error is within acceptable range of 5% so it can be concluded that the Steam Turbine cycle predicted efficiency is also accurate.
Furthermore, the actual overall efficiency of CCPP was also compared against the calculated and predicted efficiency. It was found that the actual, calculated and predicted efficiency of CCPP were 27.541%, 28.201% and 28.238%, respectively. The percentage error between actual and calculated efficiency was 2.34%, which is within the acceptable range of 5% while the percentage error between actual and predicted efficiency was 2.47%, which is also within the acceptable range of 5%. So, it can be concluded with certainty that the actual results of CCPP are in agreement with calculated and predicted results.
2. Results and discussion
This section discusses the results obtained from Thermodynamics Modelling through EES and Back Propagation Neural Network and compares its result against the actual data obtain from the Power Plant. Furthermore, a study is carried out by replacing the Fuel (Methane in our case) with Gasoline, LPG and Diesel, one by one, to calculate its Power Output by Thermodynamics Modelling followed by Power Output Prediction using BPNN.
Power Output of CCPP has also been calculated using a thermodynamic model, as shown previously, in EES. The calculated Power Output obtained from EES is plotted with actual Power Output of the CCPP and shown in Fig. 8.
Fig. 8.
Comparison of actual and calculated power output of CCPP.
The graph shows that the Actual Power Output plot coincides with the plot of EES and verifies the accuracy of the thermodynamic model used to calculate the Power Output.
Efficiency and the Net Power Output are the foremost feature of a CCPP. These two variables serve as the performance parameter of our model while the following variables would serve as operating parameters.
-
1.
GT 1 – Temperature and Pressure at Inlet
-
2.
GT 1 – Temperature at Outlet
-
3.
GT 2 – Temperature and Pressure at Inlet
-
4.
GT 2 – Temperature at Outlet
-
5.
HP ST – Temperature at Inlet
-
6.
IP ST – Temperature at Inlet
-
7.
Exhaust Mass Flow rate in Steam Turbine Cycle
A comparative analysis was conducted between the performance parameters and the operating parameters to understand the overall effect of operating parameters on the performance of the CCPP. Fig. 9 below shows Net Power Output and Efficiency of Gas Turbine cycle 1 against the Turbine Inlet temperature.
Fig. 9.
Turbine inlet temperature - GT1.
Increasing the Inlet temperature of air in Turbine from 2200 K to 2400 K led to an increase in Net Power Output due to higher energy content within the steam since a higher ΔT across the Turbine leads to a higher Power Output. Increasing temperature also results in improvement of the Gas Turbine Cycle efficiency but the gradient of Efficiency line is lower than Net Power Output which highlights the fact the higher temperature leads to a lower efficiency of the system.
Fig. 10 shows Net Power Output and Efficiency of Gas Turbine cycle 1 against the Turbine Outlet temperature.
Fig. 10.
Turbine outlet temperature - GT1.
This analysis was carried out by changing the Gas Turbine Outlet temperature from 650 K up to 900 K while ensuring all the parameters are not altered. It can be seen from the graph that an increase in temperature leads to a decrease in the Net Power Output and Efficiency. This is due to the loss of excess thermal energy from the turbine in form of higher temperature of exhaust that could have been utilized to produce more power. Thus, leading to a lower power output and efficiency.
Fig. 11 shows a graph of Net Power Output per kg of fuel and Efficiency against pressure at Turbine Inlet. The pressure at Turbine Inlet was increased from 1470 kPa up to 1520 kPa during the whole operation of 9 months and the corresponding Net Power Output per kg of fuel and Efficiency are plotted in the figure below. A higher-pressure ratio across the Turbine leads to a higher performance but the relationship is not linear. The Net Power Output and Efficiency does increase with increasing Inlet Pressure but after reaching a maximum, it starts decreasing. This explains that an optimal Inlet Pressure in needed to ensure higher performance of the Turbine.
Fig. 11.
Turbine inlet pressure - GT1.
Fig. 12 shows a similar trend as seen in Fig. 10. Increasing the Gas Turbine 2 Inlet Temperature from 2200 K up to 2400 K leads to an increase in Net Power Output and Efficiency as well. The Net Power Output increases from 169953 kW up to 232598 kW whereas the Efficiency increases from 13.68% up to 19.22%.
Fig. 12.
Turbine inlet temperature - GT2.
The relationship of Turbine Inlet Temperature with Net Power Output and Efficiency is direct and so we can be tempted to further increase the temperature to achieve higher performance. However, there is a potential risk of losing the integrity of the turbine blades due to excessive temperature which would pose a significant economic impact on the whole CCPP.
Fig. 13 below shows the relationship of Gas Turbine 2 Outlet Temperature with Net Power Output and Efficiency. Outlet Temperature has a direct relationship with Net Power Output and Efficiency and both performance parameters decrease with an increase in Outlet Temperature.
Fig. 13.
Turbine outlet temperature - GT2.
This analysis was carried out by changing the Gas Turbine Outlet temperature from 650 K up to 900 K while ensuring that the remaining parameters are not altered. The Net Power Output decreases from 283739 kW to 218830 kW while the Efficiency also reduces from 23.44% to 18.08%. This decrease is due to the loss of excess thermal energy from the turbine in form of higher temperature of exhaust that could have been utilized to produce more power. Thus, leading to a lower power output and efficiency.
Similarly, Fig. 14 shows a graph of Net Power Output per kg of fuel and Efficiency against Turbine Inlet pressure. The trend of this graph is similar to the trend seen in Fig. 11 since both graphs are for Gas Turbines having similar working principle. The Turbine Inlet pressure was increased from 1473 kPa up to 1523 kPa during the whole operation of 9 months and the corresponding Net Power Output per kg of fuel and Efficiency are plotted in the figure below. It was observed that the Net Power Output per kg of fuel increased from 9246 kW/kg to 9446 kW/kg while the Efficiency also increased from 18.49% to 18.89%.
Fig. 14.
Turbine inlet pressure - GT2.
The relationship of Pressure with Power and Efficiency is non-linear and the performance parameters increases with increase in Pressure to a moment before decreasing with further increase in Pressure. The impact of Inlet Pressure of Turbine variation on performance parameters is insignificant as compared Inlet Temperature of Turbine as seen from all the Gas Turbine graphs.
The parametric analysis was further carried on for Steam Turbine cycle as well and its performance parameters were also investigated against operational parameters. The effect of Inlet Temperature in High Pressure Turbine was investigated against Net Power Output and Efficiency of the Steam Turbine Cycle and the graph in Fig. 16 shows that a direct relationship exists between Inlet Temperature of HP Turbine and Net Power Output & Efficiency.
Fig. 16.
Intermediate pressure turbine inlet temperature – steam turbine.
Increasing the Inlet Temperature from 420 K up to 800 K which resulted in an increase in both Efficiency and Net Power Output of the Steam Turbine Cycle as seen in Fig. 15. The Net Power Output increased from 234735 kW to 259003 kW while the Efficiency also increased from 15.32% up to 16.9%. The higher temperature difference across the Turbine enables to a higher energy extraction by the Turbine leading to a significant Output Power as shown the by analysis.
Fig. 15.
High pressure turbine inlet temperature – steam turbine.
A similar analysis was carried out for Intermediate Pressure Turbine as shown in Fig. 16. The graph shows a non-linear relationship of Turbine Inlet Temperature with Net Power Output and Efficiency. The Intermediate Pressure Turbine Inlet Temperature was increased from 500 K up till 800 K to observe the performance parameters of the Steam turbine cycle. It was noticed that the least Net Power Output and Efficiency values were 120123 kW and 7.84%, respectively while the maximum Net Power Output and Efficiency values were 260731 kW and 17.02%, respectively. The non-linear behaviour of the graph suggests that the increase in Temperature do increase the Power and Efficiency of the Steam Turbine cycle due to a higher ΔT that exists across the Turbine. However, higher temperature also requires additional cooling of the components of the Power Plant in order to maintain proper functioning and lack of sufficient cooling of the components will lead to an efficiency reduction, as observed, and would also endanger the health of the component itself.
As mentioned previously, all the exhaust gases from both Gas Turbine Cycles are diverted towards HRSG which serves as the boiler of the Steam Turbine cycle. Fig. 17 below shows a plot of mass flow rate of exhaust in to steam turbine with Net Power Output and Efficiency.
Fig. 17.
Mass flow rate of exhaust – Steam Turbine.
The mass flow rate of exhaust, throughout the 9 months of observation, has a minimum value of 0.63 kg/s and a maximum value of 50.47 kg/s. The Net Power Output, against these values, showed a minimum value of 3078 kW and a maximum value of 248944 kW while the minimum efficiency achieved was 15.35% and maximum efficiency was 15.38%. The efficiency of Steam Turbine cycle was affected significantly by HP ST and IP ST Inlet Temperature as compared to exhaust gas mass flow rate.
The dataset used in this study was acquired through Distributed Control System (DCS) and contained dataset for 273 days i.e. from August 2020 till April 2021. Entire data set from DCS was analyzed and 4 Optimum Input parameters were selected against which the Predictive Model was trained. These 4 parameters were Temperature, Pressure, Mass Flow rate of Fuel in Gas Turbine Cycle 1 and Mass Flow rate of Fuel in Gas Turbine Cycle 2. The data was divided into 70:15:15 ratio, of which 70% was consumed in model training, 15% consumed in model testing and the last 15% consumed in validation of the system. During the predictive modelling via BPNN, different neurons are set in the hidden layer each time, starting from 5 neurons and going up to 100 neurons with different intervals. For each case, the results of the predictive model and its performance is assessed through the Regression Line plot of training, testing and validation as well as Validation performance curve with Mean Squared Value (MSE). The architecture of the BPNN is already shown in Fig. 4.
The 4 input parameters are fed into the BPNN where each get assigned a random weight. These parameters pass through hidden layers and output layers via forward propagation and a result is generated at the output. Consequently, an error is also calculated between this predictive and actual value. This error travel back into the system and based on this error, the hidden and output layer neuron's weights are adjusted. This cycle is repeated continuously until a desired output value is achieved.
Fig. 18 shows a plot of MSE against quantity of epochs for training, testing and validation data set with hidden layer consisting of 10 neurons. The MSE comes out to be 0.0063237 at 421 epochs after which the lines do not converge further and result stays constant.
Fig. 18.
Best Validation Performance at 10 neurons.
Fig. 19 shows the training, validation and testing regression plot when the hidden layer consists of 10 neurons. The plot gives an R = 1 value which demonstrated a strong correlation among the predicted and actual data. The performance of the BPNN by adjusting the hidden layer neurons is shown in Table 2. It can be noted from the table that the regression plot shows strong correlation or a close correlation for almost all the cases. The major difference occurs in the MSE value which highlights the sensitivity of the predictive model on the number of hidden neurons. It can be seen that there is no specific trend in the change of MSE in relation with the hidden neurons, however the results show that the least MSE was achieved at 10 hidden neurons where the value of MSE was 0.0063237, obtained at 421 epochs as shown in Table 1. The regression plot also shows R = 1 value which depicts a strong correlation between the actual and predictive value (see Fig. 20).
Fig. 19.
Training, Validation and Testing Regression Plot for dataset with 10 neurons, Plot (a) shows the coefficient of correlation for Training dataset, Plot (b) shows the coefficient of correlation for Validation dataset, Plot (c) shows the coefficient of correlation for Testing dataset and Plot (d) shows the overall coefficient of correlation.
Table 2.
Thermodynamic properties of fuels used.
| S.No. | Fuel | Lower Heating Value (LHV) – kJ/kg | Specific Heat Ratio (k) |
|---|---|---|---|
| 1 | Methane | 50000 | 1.33 |
| 2 | Diesel | 42910 | 1.28 |
| 3 | LPG | 46280 | 1.13 |
| 4 | Gasoline | 44150 | 1.044 |
Table 1.
BPNN result summary for different number of neurons.
| S.No. | Neurons in hidden layer | MSE | No. of epochs | R2 value - Training | R2 value - Validation | R2 value - Testing | R2 value - Overall |
|---|---|---|---|---|---|---|---|
| 1 | 5 | 0.029222 | 85 | 1 | 1 | 1 | 1 |
| 2 | 7 | 0.031184 | 37 | 1 | 1 | 1 | 1 |
| 3 | 9 | 0.0081228 | 53 | 1 | 1 | 1 | 1 |
| 4 | 10 | 0.0063237 | 421 | 1 | 1 | 1 | 1 |
| 5 | 12 | 0.039972 | 228 | 1 | 1 | 1 | 1 |
| 6 | 15 | 0.073641 | 73 | 1 | 1 | 1 | 1 |
| 7 | 20 | 0.27227 | 15 | 1 | 1 | 0.99997 | 0.99999 |
| 8 | 50 | 19.8004 | 6 | 0.99987 | 0.99982 | 0.99978 | 0.99985 |
| 9 | 75 | 14.6154 | 13 | 0.99996 | 0.99987 | 0.99377 | 0.99908 |
| 10 | 90 | 7059.3186 | 26 | 0.99602 | 0.93369 | 0.98103 | 0.98383 |
| 11 | 100 | 17659.894 | 304 | 0.82112 | 0.87503 | 0.87789 | 0.83675 |
Fig. 20.
Comparison of actual and predictive power output of CCPP.
Fig. 21 shows a plot of predictive Power Output of CCPP against the actual Power Output. The predicted values have been obtained for 10 neurons which gave the least MSE and showed a strong correlation of predicted values with the actual values. It can be seen from the plot that both graphs are almost identical to each other, hence verifying that the predicted values are acceptable.
Fig. 21.
Calculated Power Output of all fuels.
A study was carried out by replacing Methane, which was used as the fuel in CCPP, with a variety of fuels to compare their impact on the performance of CCPP. The fuels and their respective thermodynamic properties used in the study are shown in Table 2.
It can be seen that the comparison of Methane is carried out with Diesel, LPG and Gasoline as fuels using LHV and specific heat ratio as the distinguishing factor. The thermodynamic model prepared using EES was used again by replacing the existing LHV and Specific Heat Ratio values of Methane by that of Diesel, LPG and Gasoline, one by one. The Net Power Output calculated from the thermodynamic model using EES was plotted for all fuels and compared against the Net power Output of Methane.
The results were calculated for the entirety of the 9 months of data and the comparison is shown in Fig. 21. It can be clearly seen that the trend of Net Power Output is similar for all fuels, given that the thermodynamic model used is same. The difference in values arise from the different in LHV and Specific Heat Ratio for all 4 types of fuels used in the study. The graph shows that at any point, Methane produces more power while Diesel produces the least. Since, it is evident that the performance of the CCPP, for different fuel, is more dependent upon LHV than Specific Heat Ratio, it can be concluded that LHV is a dominant operating parameter.
Furthermore, this calculated result from all the fuels was used to train a Back Propagation Neural Network (BPNN). Hidden layer was the most important feature where the number of neurons was set at 10 when the least MSE was achieved. This was similar to the number of neurons set in hidden layer when Methane was used as the fuel. The predictive power output was calculated for Diesel, LPG and Gasoline using the data calculated from thermodynamic modelling in EES and this predictive result was compared with the predictive result of Methane and the analysis is shown in Fig. 22.
Fig. 22.
Predictive Power Output of all fuels.
The graph shows a similar trend for all fuels as Methane with Methane producing the highest Power Output while Diesel produces the lowest.
The reason for choosing the above mentioned 3 fuels for comparison with Methane was the fact that all these are some of the most commonly used fuels as source of energy and are widely accessible. It can be seen from Table 2 that Methane has the highest Lower Heating Value followed by LPG, Gasoline and Diesel, respectively. This indicates that Methane would produce the highest amount of thermal energy on combustion and Diesel would produce the least. This was further confirmed from the results plotted in Fig. 23. Fig. 23 shows a comparison of net power output and efficiency obtained by using all fuels mentioned above. It can be seen from Fig. 23 that the maximum net power output, by using Methane as fuel in CCPP, was 725 MW while the thermal efficiency of CCPP achieved was 28.85%. Similarly, the maximum net power output and efficiency by using LPG as fuel were, 631 MW and 27.17%. When Gasoline was considered as fuel for CCPP, the maximum net power output and efficiency of the cycle dropped to 578 MW and 26%, respectively. Diesel, with least LHV value, produced net power output and efficiency of 546 MW and 25.4%, respectively thereby confirming our initial synopsis that fuel with highest LHV will produce highest energy on consumption and will lead to a higher power generation.
Fig. 23.
Net power output and efficiency of all fuels.
3. Conclusion
This study discusses the Net Power Generation and Efficiency of an actual Combined Cycle Power Plant (CCPP). The plant consists of 2 Gas Turbine cycles producing 243 MW of electricity each and a Steam Turbine cycle producing 261 MW of electricity when running at full capacity and hence, the total capacity of the CCPP is 747 MW.
Predictive model for Net Power Generation of CCPP was based on Back Propagation Neural Network (BPNN) and utilized Fuel Mass Flow rate of GT-1, Fuel Mass Flow rate of GT-2, Ambient Pressure and Ambient Temperature as 4 input variables. Similarly, an EES based thermodynamic model of the CCPP was set up and the actual plant data was used to generate performance parameters such as Net Power Output, Efficiency, Power consumed by pumps and compressors. A sensitivity analyses was also carried out where different operating parameters were altered, one by one, to observe their effect on the performance parameters of CCPP. This was followed by a comparison of Predictive and EES results with actual data of the CCPP and inference made from this comparison is summarized as follows: BPNN is effective in the Net Power Generation prediction of CCPP as the MSE of BPNN predictive model was 0.0063237 at 421 epochs with hidden layer consisting of 10 neurons. The training, validation and testing regression plot of the dataset when hidden layer contains 10 neurons gave an R = 1 value which demonstrated a strong correlation between the actual and predicted data. This showed that the predictive model provided results that were in close agreement with the actual data of CCPP.
The simulated analysis on EES showed that the Net Power Output of GT-1, GT-2, Steam Turbine Cycle and CCPP was 224.26 MW, 223.89 MW, 235.01 MW and 683.16 MW, respectively while actual Net Power Output of GT-1, GT-2, Steam Turbine Cycle and CCPP was 220.41 MW, 222.1 MW, 224.81 MW and 667.32 MW, respectively. The simulated efficiency of CCPP was 28.201% while the actual efficiency was 27.541%. It was further deduced from the sensitivity analysis that the GT Inlet Temperature, GT Outlet Temperature, GT Inlet pressure, Inlet Temperature of HP Turbine and Inlet Temperature of IP Turbine are operating parameters that have a notable effect on the performance parameters of the CCPP.
Finally, after comparing the BPNN model results and simulated results from EES with actual data, it can be concluded that in BPNN model provided an efficient, time-saving and accurate alternative that could be used for predicting future data. BPNN is a data science technique that uses past data, statistics principles and machine learning algorithms to make prediction of desired data. Simulation results from EES were also accurate but required a complex thermodynamic model and detailed calculations before processing the results. This made this technique inefficient, time-consuming and error-prone since a slight modification of thermodynamic model, later on, would lead to inaccurate results.
It has been established via this article that energy analysis can be accurately predicted using AI based predictive models so it is recommended that future work should include exergy and exergoeconomic analysis and compare the results obtained via EES and AI based predictive models. Exergy analysis is essential for assessing any thermodynamic system and complements the energy analysis. Exergoeconomic can help identify how costly a system is. It presents a comparison between thermodynamic inefficiencies and cost of the product and provides a useful parameter to gauge the merit of a proposed thermodynamic system. Furthermore, Backpropagation neural network could be replaced by a variety of neural networks such Radial Basis Function along with MLP, SVM, Random Forest Regression, k nearest neighbour etc. to test the accuracy of each predictive model. Investigating Exergy, Exergoeconomic analysis along with an improved neural network would provide an opportunity to develop a robust model that would be beneficial for companies/stakeholders hoping to build a Power Plant by providing a cheap solution for prediction of power output using a few input parameters which would be readily available.
Author contribution statement
Adeel Asghar: Conceived and designed the experiments; Performed the experiments; Analyzed and interpreted the data; Wrote the paper.
Tahir Abdul Hussain Ratlamwala; Khurram Kamal: Conceived and designed the experiments; Performed the experiments; Wrote the paper.
Mohammed Alkahtani: Conceived and designed the experiments.
Emad Mohammad: Analyzed and interpreted the data; Contributed reagents, materials, analysis tools or data.
Senthan Mathavan: Analyzed and interpreted the data.
Data availability statement
Data will be made available on request.
Funding
This work was supported by Researchers Supporting Project number (RSP2023R274) King Saud University, Riyadh, Saudi Arabia.
Acknowledgement
This work was supported by Researchers Supporting Project number (RSP2023R274), King Saud University, Riyadh, Saudi Arabia.
Additional information
No additional information is available for this paper.
Declaration of competing interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Nomenclature
Power consumed by compressor (kW)
Power produced by Gas Turbine (kW)
Power consumed by Low Pressure Pump (kW)
Power consumed by High Pressure Pump (kW)
Power consumed by Intermediate Pressure Pump (kW)
Power produced by Intermediate Pressure Turbine (kW)
Power produced by high Pressure Turbine (kW)
Power produced by Low Pressure Turbine (kW)
- P
Pressure (kPa)
- T
Temperature (°K)
Thermal Energy (kW)
Mass flow rate (kg/s)
Weight of neurons between input and hidden layers
Weight of neurons between hidden and output layers
Subscript
- i
Input layer
- j
Hidden Layer
- k
Output Layer
- Net
Produced - Consumed
- GT1
Gas Turbine 1
- GT2
Gas Turbine 2
- ST
Steam Turbine
- Stack
Exit of HRSG
Greek Letters
- h
Enthalpy (kJ/kg)
- s
Entropy (kJ/kg.K)
- η
Thermal Efficiency
Thermal Efficiency of Gas Turbine Cycle
Thermal Efficiency of Steam Turbine Cycle
Thermal Efficiency of Combine Cycle Power Plant
- c
Biases in Back Propagation
Activation function in Back Propagation
Error at the Output Layer
- α
Learning Rate
Acronyms
- CCPP
Combine Cycle Power Plant
- TPS
Thermal Power Station
- CC
Combustion Chamber
- HRSG
Heat Recovery Steam Generator
- LNG
Liquefied Natural Gas
- LPG
Liquefied Petroleum gas
- HP
High Pressure
- IP
Intermediate Pressure
- LP
Low Pressure
- DCS
Distributed Control System
- EES
Engineering Equation Solver
- IEP
Integrated Energy Plan
- GoP
Government of Pakistan
- MW
Megawatt
- kW
Kilowatt
- TWh
Terawatt-hour
- LHV
Lower Heating Value
- BPNN
Back Propagation Neural network
- MSE
Mean Squared Error
- FFNN
Feed Forward Neural Network
- R2
Coefficient of Determination
- RMSE
Root Mean Squared Error
- ANN
Artificial Neural Network
References
- 1.Ministry of Energy (Power Division) 2023. COMMISSIONED IPPs & ITP.https://www.ppib.gov.pk/commisioned_ipps.html Feb. 22. [Google Scholar]
- 2.Rehman Usama. vol. 11. 2023. https://moderndiplomacy.eu/2023/03/11/energy-crisis-in-pakistan/ (Energy Crisis in Pakistan). Mar. [Google Scholar]
- 3.Desk Web. 2023. Longer Power Cuts in Pakistan as Electricity Shortfall Reaches 6516MW.https://en.dailypakistan.com.pk/24-Jun-2023/loadshedding-prolonged-in-pakistan-as-power-shortfall-reaches-6516mw Jun. 24. [Google Scholar]
- 4.Enerdata . vol. 23. 2023. https://www.enerdata.net/publications/daily-energy-news/pakistan-inaugurates-two-coal-fired-plants-165-gw-sindh-province.html (Pakistan Inaugurates Two Coal-Fired Plants (1.65 GW) in the Sindh Province). Mar. [Google Scholar]
- 5.Ahmad Ahmadani. 2023. https://profit.pakistantoday.com.pk/2023/06/11/powering-ahead-govt-boosts-subsidy-allocation-to-address-energy-sector-challenges-in-fy2023-24/ (Powering Ahead: Govt Boosts Subsidy Allocation to Address Energy Sector Challenges in FY2023-24). Jun. 11. [Google Scholar]
- 6.Xu Y., et al. Artificial intelligence: a powerful paradigm for scientific research. Innovation. Nov. 2021;2(4) doi: 10.1016/j.xinn.2021.100179. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Li J., Ma S., Qu Y., Wang J. The impact of artificial intelligence on firms' energy and resource efficiency: empirical evidence from China. Resour. Pol. May 2023;82 doi: 10.1016/j.resourpol.2023.103507. [DOI] [Google Scholar]
- 8.Rasheed A.A. Improving prediction efficiency by revolutionary machine learning models. Mater Today Proc. 2021 doi: 10.1016/j.matpr.2021.04.014. xxxx. [DOI] [Google Scholar]
- 9.Bistline J.E.T., Merrick J.H. Parameterizing open-source energy models: statistical learning to estimate unknown power plant attributes. Appl. Energy. 2020;269(April) doi: 10.1016/j.apenergy.2020.114941. [DOI] [Google Scholar]
- 10.Hundi P., Shahsavari R. Comparative studies among machine learning models for performance estimation and health monitoring of thermal power plants. Appl. Energy. 2020;265 doi: 10.1016/j.apenergy.2020.114775. March. [DOI] [Google Scholar]
- 11.Condemi C., Casillas-Pérez D., Mastroeni L., Jiménez-Fernández S., Salcedo-Sanz S. Hydro-power production capacity prediction based on machine learning regression techniques. Knowl Based Syst. 2021;222 doi: 10.1016/j.knosys.2021.107012. [DOI] [Google Scholar]
- 12.Ali A., Kamal K., Ratlamwala T.A.H., Fahad Sheikh M., Arsalan M. Power prediction of waste heat recovery system for a cement plant using back propagation neural network and its thermodynamic modeling. Int. J. Energy Res. 2021;45(6):9162–9178. doi: 10.1002/er.6444. [DOI] [Google Scholar]
- 13.Tüfekci P. Prediction of full load electrical power output of a base load operated combined cycle power plant using machine learning methods. Int. J. Electr. Power Energy Syst. 2014;60:126–140. doi: 10.1016/j.ijepes.2014.02.027. [DOI] [Google Scholar]
- 14.Rashid M., Kamal K., Zafar T., Sheikh Z., Shah A., Mathavan S. Proceedings of 2015 International Conference on Mechanical Engineering, Automation and Control Systems. MEACS 2015; 2016. Energy prediction of a combined cycle power plant using a particle swarm optimization trained feedforward neural network; pp. 1–5. [DOI] [Google Scholar]
- 15.Adams D., Oh D.H., Kim D.W., Lee C.H., Oh M. Prediction of SOx–NOx emission from a coal-fired CFB power plant with machine learning: plant data learned by deep neural network and least square support vector machine. J. Clean. Prod. 2020;270 doi: 10.1016/j.jclepro.2020.122310. [DOI] [Google Scholar]
- 16.Akdemir B. Prediction of hourly generated electric power using artificial neural network for combined cycle power plant. Int J Electrical Energy. 2016;4(2):91–95. doi: 10.18178/ijoee.4.2.91-95. [DOI] [Google Scholar]
- 17.Darwish Ahmad A., Abubaker A.M., Najjar Y.S.H., Manaserh Y.M.A. Power boosting of a combined cycle power plant in Jordan: an integration of hybrid inlet cooling & solar systems. Energy Convers. Manag. 2020;214(January) doi: 10.1016/j.enconman.2020.112894. [DOI] [Google Scholar]
- 18.Wang S., Liu Z., Cordtz R., Imran M., Fu Z. Performance prediction of the combined cycle power plant with inlet air heating under part load conditions. Energy Convers. Manag. 2019;200(September) doi: 10.1016/j.enconman.2019.112063. [DOI] [Google Scholar]
- 19.Gómez M.R., Garcia R.F., Gómez J.R., Carril J.C. Thermodynamic analysis of a Brayton cycle and Rankine cycle arranged in series exploiting the cold exergy of LNG (liquefied natural gas) Energy. 2014;66:927–937. doi: 10.1016/j.energy.2013.12.036. [DOI] [Google Scholar]
- 20.Sabia G., Heinze C., Alobaid F., Martelli E., Epple B. ASPEN dynamics simulation for combined cycle power plant – validation with hot start-up measurement. Energy. 2019;187 doi: 10.1016/j.energy.2019.115897. [DOI] [Google Scholar]
- 21.Abrosimov K., Baccioli A., Bischi A. Extensive techno-economic assessment of combined inverted Brayton – organic Rankine cycle for high-temperature waste heat recovery. Energy. 2020;211 doi: 10.1016/j.energy.2020.118406. [DOI] [Google Scholar]
- 22.Liu Z., Karimi I.A. Simulation of a combined cycle gas turbine power plant in Aspen HYSYS. Energy Proc. 2019;158:3620–3625. doi: 10.1016/j.egypro.2019.01.901. [DOI] [Google Scholar]
- 23.Sachdeva J., Singh O. Thermodynamic analysis of solar powered triple combined Brayton, Rankine and organic Rankine cycle for carbon free power. Renew. Energy. 2019;139(2019):765–780. doi: 10.1016/j.renene.2019.02.128. [DOI] [Google Scholar]
- 24.Prakash D., Singh O. Thermo-economic study of combined cycle power plant with carbon capture and methanation. J. Clean. Prod. 2019;231:529–542. doi: 10.1016/j.jclepro.2019.05.217. [DOI] [Google Scholar]
- 25.Bǎlǎnescu D.T., Homutescu V.M. Performance analysis of a gas turbine combined cycle power plant with waste heat recovery in Organic Rankine Cycle. Procedia Manuf. 2019;32:520–528. doi: 10.1016/j.promfg.2019.02.248. [DOI] [Google Scholar]
- 26.Aliyu M., Alqudaihi A.B., Said S.A.M., Habib M.A. Energy , exergy and parametric analysis of a combined cycle power plant. Therm. Sci. Eng. Prog. 2020;15 doi: 10.1016/j.tsep.2019.100450. November 2019. [DOI] [Google Scholar]
- 27.Ali M.S., Shafique Q.N., Kumar D., Kumar S., Kumar S. Energy and exergy analysis of a 747-MW combined cycle power plant Guddu. Int. J. Ambient Energy. Nov. 2020;41(13):1495–1504. doi: 10.1080/01430750.2018.1517680. [DOI] [Google Scholar]
- 28.Authority P.B.Y., Ii P. vol. 6. l; 1999. pp. 1–21. (NATIONAL ELECTRIC POWER REGULATORY AUTHORITY Distribution Licensing Rules). [Google Scholar]
- 29.G. E. P. Systems, “Technology…Experience…Innovation”.
- 30.F. J. Brooks, “Characteristics”.
- 31.Pan Z., Lin Z., Fan K., Yang C., Ma X. Off-design performance of gas turbine power units with alternative load-control strategies. Energy Eng. J. Assoc. Energy Eng.: J Ass Energy Eng. 2021;118(1):119–141. doi: 10.32604/EE.2020.013585. [DOI] [Google Scholar]
- 32.Ali M.S., Shafique Q.N., Kumar D., Kumar S., Kumar S. vol. 41. Taylor & Francis; 2020. (Energy and Exergy Analysis of a 747-MW Combined Cycle Power Plant Guddu). 13. [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
Data will be made available on request.